Darstellung von Sharding

Hintergrund

Mit der Sharding-Darstellung wird angegeben, wie ein Tensor in Bezug auf eine Reihe verfügbarer Geräte gesplittet wird.

Die Sharding-Darstellung kann entweder:

• Manuell vom Nutzer als Sharding-Einschränkungen für Eingaben, Ausgaben oder Zwischenergebnisse angegeben.
• Wird bei der Sharding-Übertragung pro Vorgang transformiert.

Übersicht

Grundstruktur

Ein logischer Mesh ist eine mehrdimensionale Ansicht von Geräten, die durch eine Liste von Achsennamen und -größen definiert wird.

Die vorgeschlagene Sharding-Darstellung ist über ihren Namen an ein bestimmtes logisches Mesh gebunden und kann nur auf Achsennamen aus diesem Mesh verweisen. Beim Sharding eines Tensors wird angegeben, entlang welcher Achsen (eines bestimmten logischen Mesh) die einzelnen Dimensionen des Tensors gesplittet werden, sortiert von Haupt- zu Nebenachsen. Der Tensor wird entlang aller anderen Achsen des Netzes repliziert.

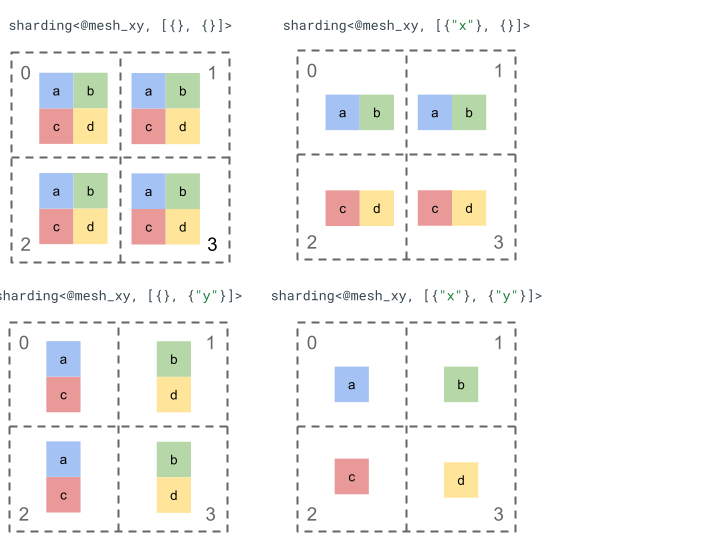
Sehen wir uns die Sharding-Darstellung mit einem einfachen Tensor der 2. Rangfolge und 4 Geräten an.

Wir geben den vier Geräten [0, 1, 2, 3] zuerst eine neue Form als zweidimensionales Array [[0, 1], [2, 3]], um ein Mesh mit zwei Achsen zu erstellen:

@mesh_xy = <["x"=2, "y"=2]>

Wir können dann den folgenden Tensor [[a, b], [c, d]] 2. Ordnung so segmentieren:

Weitere wichtige Komponenten

• Offene/Geschlossene Dimensionen: Dimensionen können entweder offen sein (können weiter nach verfügbaren Achsen segmentiert werden) oder geschlossen (sind fixiert und können nicht geändert werden).
• Explizit replizierte Achsen: Alle Achsen, die nicht zum Sharding einer Dimension verwendet werden, werden implizit repliziert. Beim Sharding können jedoch Achsen angegeben werden, die explizit repliziert werden und daher später nicht zum Sharding einer Dimension verwendet werden können.
• Achsenaufteilung und untergeordnete Achsen: Eine (vollständige) Mesh-Achse kann in mehrere untergeordnete Achsen aufgeteilt werden, die einzeln verwendet werden können, um eine Dimension zu teilen oder explizit zu replizieren.
• Mehrere logische Meshes: Unterschiedliche Shardings können an verschiedene logische Meshes gebunden werden, die unterschiedliche Achsen oder sogar eine andere Reihenfolge der logischen Geräte-IDs haben können.
• Prioritäten: Um ein Programm inkrementell zu partitionieren, können Dimensionen Sharding-Prioritäten zugewiesen werden. Diese bestimmen, in welcher Reihenfolge die Sharding-Einschränkungen pro Dimension im gesamten Modul weitergegeben werden.
• Teilbarkeit für das Sharding von Dimensionen: Eine Dimension kann nach Achsen gesplittet werden, deren Produkt der Größen nicht durch die Dimensionengröße teilbar ist.

Detaillierte Konfiguration

In diesem Abschnitt gehen wir auf die grundlegende Struktur und die einzelnen Hauptkomponenten ein.

Grundstruktur

Die Dimensionsshardings geben für jede Dimension des Tensors an, entlang welcher Achsen (oder Unterachsen) er von Haupt- zu Nebenachsen gesplittet wird. Alle anderen Achsen, die keine Dimensionen schardern, werden implizit (oder explizit) repliziert.

Wir beginnen mit einem einfachen Beispiel und erweitern es nach und nach, während wir weitere Funktionen beschreiben.

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>

Invarianten

• Die Anzahl der Dimensionsshardings muss mit dem Rang des Tensors übereinstimmen.
• Alle Achsennamen müssen im referenzierten Mesh vorhanden sein.
• Achsen oder untergeordnete Achsen dürfen in der Sharding-Darstellung nur einmal vorkommen. Jede Achsenebene wird entweder auf eine Dimension angewendet oder explizit repliziert.

Offene/geschlossene Dimensionen

Jede Dimension eines Tensors kann entweder offen oder geschlossen sein.

Öffnen

Eine offene Dimension kann weiter entlang zusätzlicher Achsen gesplittet werden. Das angegebene Dimensions-Sharding muss also nicht das endgültige Sharding dieser Dimension sein. Das ähnelt

• jax.sharding.PartitionSpec.UNCONSTRAINED
• GSPMD-unspecified_dims

Wenn eine Dimension geöffnet ist, fügen wir nach den Achsen, nach denen die Dimension bereits geSharded ist, ein ? hinzu (siehe Beispiel unten).

Geschlossen

Eine geschlossene Dimension kann nicht weiter gesplittet werden. Das angegebene Dimensions-Sharding ist also das endgültige Sharding dieser Dimension und kann nicht geändert werden. Ein häufiger Anwendungsfall hierfür ist, dass GSPMD in der Regel die Eingabe-/Ausgabeargumente eines Moduls nicht ändert oder dass bei jax.jit die vom Nutzer angegebene in_shardings statisch ist und sich nicht ändern kann.

Wir können das Beispiel oben um eine offene und eine geschlossene Dimension erweitern.

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>

Explizit replizierte Achsen

Eine explizite Reihe von Achsen, auf denen ein Tensor repliziert wird. Es kann zwar festgestellt werden, dass ein Tensor, der nicht entlang einer Achse geSharded ist, implizit auf dieser Achse repliziert wird (wie derzeit bei jax.sharding.PartitionSpec), aber wenn dies explizit angegeben ist, kann die Propagation diese Achsen nicht verwenden, um eine offene Dimension weiter entlang dieser Achsen zu Sharden. Bei der impliziten Replikation kann ein Tensor weiter partitioniert werden. Bei der expliziten Replikation kann der Tensor jedoch nicht entlang dieser Achse partitioniert werden.

Die Reihenfolge der replizierten Achsen hat keine Auswirkungen darauf, wie die Daten eines Tensors gespeichert werden. Aus Gründen der Konsistenz werden die Achsen jedoch in der Reihenfolge gespeichert, in der sie im Mesh der obersten Ebene angegeben sind. Beispiele:

@mesh_xy = <["c"=2, "a"=2, "b"=2]>

Die Achsen "a" und "c" sollen explizit repliziert werden. Die Reihenfolge sollte so sein:

replicated={"c", "a"}

Wir können unser Beispiel oben um eine explizit replizierte Achse erweitern.

@mesh_xyz = <["x"=2, "y"=4, "z"=2]>

// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would // be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>

Achsenaufteilung und untergeordnete Achsen

Ein logisches n-Achsen-Mesh wird erstellt, indem ein eindimensionales Gerätearray in ein n-dimensionales Array umgewandelt wird, wobei jede Dimension eine Achse mit einem benutzerdefinierten Namen bildet.

Mit demselben Verfahren können Sie im Compiler eine Achse der Größe k in m Unterachsen aufteilen, indem Sie das Mesh von [...,k,...] in [...,k1,...,km,...] umformen.

Motivation

Um die Gründe für die Aufteilung von Achsen zu verstehen, sehen wir uns das folgende Beispiel an:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>

Wir möchten das Ergebnis der Umwandlung so in Shards aufteilen, dass keine Kommunikation erforderlich ist (d.h. die Daten bleiben dort, wo sie sind). Da die Größe von "x" größer als die erste Dimension des Ergebnisses ist, müssen wir die Achse in zwei untergeordnete Achsen "x.0" und "x.1" mit jeweils einer Größe von 2 aufteilen und die erste Dimension auf "x.0" und die zweite Dimension auf "x.1" partitionieren.

Sharding für Funktionseingabe/-ausgabe

Es ist möglich, dass bei der Weiterleitung eine Eingabe oder Ausgabe der Hauptfunktion entlang einer untergeordneten Achse geSharded wird. Das kann bei einigen Frameworks ein Problem sein, da wir solche Shardings nicht ausdrücken können, um sie an den Nutzer zurückzugeben. In JAX können wir beispielsweise keine Unterachsen mit jax.sharding.NamedSharding ausdrücken.

In solchen Fällen haben wir mehrere Möglichkeiten:

• Sharding zulassen und in einem anderen Format zurückgeben (z.B. jax.sharding.PositionalSharding anstelle von jax.sharding.NamedSharding in JAX).
• Untergeordnete Achsen, die die Eingabe/Ausgabe in Shards aufteilen, sind nicht zulässig.

Derzeit sind untergeordnete Achsen für die Eingaben/Ausgaben in der Übertragungspipeline zulässig. Bitte lass es uns wissen, wenn du diese Funktion deaktivieren möchtest.

Darstellung

Genauso wie wir bestimmte volle Achsen aus dem Netz anhand ihres Namens referenzieren können, können wir bestimmte untergeordnete Achsen anhand ihrer Größe und des Produkts aller Größen der untergeordneten Achsen (mit demselben Achsennamen) links von ihnen (die für sie wichtig sind) referenzieren.

Um eine bestimmte Teilachse der Größe k aus einer vollständigen Achse "x" der Größe n zu extrahieren, ändern wir die Größe n (im Mesh) effektiv in [m, k, n/(m*k)] und verwenden die zweite Dimension als Teilachse. Eine untergeordnete Achse kann also durch zwei Zahlen, m und k, angegeben werden. Wir verwenden die folgende kompakte Schreibweise, um untergeordnete Achsen zu kennzeichnen: "x":(m)k.

• m>=1 ist die Vorabgröße dieser untergeordneten Achse. m muss ein Teiler von n sein. Die Vorabgröße ist das Produkt aller Größen der untergeordneten Achsen, die links von dieser untergeordneten Achse liegen (ist sie gleich 1, gibt es keine; ist sie größer als 1, entspricht sie einer oder mehreren untergeordneten Achsen).

• k>1 ist die tatsächliche Größe dieser Teilachse. k sollte ein Teiler von n sein.

• n/(m*k) ist die Nach-Größe. Er entspricht dem Produkt aller Größen der untergeordneten Achsen, die sich rechts von dieser untergeordneten Achse befinden (wenn er gleich 1 ist, gibt es keine; wenn er größer als 1 ist, entspricht er einer oder mehreren untergeordneten Achsen).

Die Anzahl der anderen Unterachsen spielt jedoch keine Rolle, wenn eine bestimmte Unterachse "x":(m)k verwendet wird. Andere Unterachsen müssen nicht im Tensor-Sharding referenziert werden, wenn sie keine Dimension aufteilen oder explizit repliziert werden.

Zurück zum Beispiel im Abschnitt zur Motivation: Wir können das Ergebnis so partitionieren:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
    : (tensor<8xf32>) -> tensor<2x4xf32>

Hier ist ein weiteres Beispiel für eine unterteilte Achse, bei der nur einige der untergeordneten Achsen verwendet werden.

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Axis "y" is effectively split into 3 sub-axes denoted as
//   "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>

Ähnlich sind die folgenden beiden Shardings semantisch äquivalent. Wir können uns mesh_xy als eine Aufteilung von mesh_full vorstellen.

@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>

sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>

Ausdrücklich replizierte untergeordnete Achsen

Untergeordnete Achsen können nicht nur zum Sharding von Dimensionen verwendet, sondern auch als explizit repliziert gekennzeichnet werden. Wir erlauben dies in der Darstellung, da sich untergeordnete Achsen genauso verhalten wie vollständige Achsen.Wenn Sie also eine Dimension entlang einer untergeordneten Achse der Achse "x" partitionieren, werden die anderen untergeordneten Achsen von "x" implizit repliziert. Sie können daher explizit repliziert werden, um anzugeben, dass eine untergeordnete Achse repliziert bleiben muss und nicht zum Partitionieren einer Dimension verwendet werden kann.

Beispiel:

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>

Replizierte Unterachsen derselben Vollachse sollten in aufsteigender Reihenfolge nach ihrer Vorabgröße sortiert werden, z. B.:

replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}

Invarianten

• Unterachsen, auf die in einem Tensor-Sharding verwiesen wird, dürfen sich nicht überschneiden, z.B. "x":(1)4 und "x":(2)4.

• In einem Tensor-Sharding referenzierte Unterachsen müssen so groß wie möglich sein. Wenn ein Dimensions-Sharding zwei benachbarte Unterachsen A und B in der richtigen Reihenfolge hat oder Unterachsen A und B explizit repliziert werden, dürfen sie nicht aufeinanderfolgen, z. B. "x":(1)2 und "x":(2)4, da sie durch eine einzelne "x":(1)8 ersetzt werden können.

Mehrere logische Netze

Ein logischer Mesh ist eine mehrdimensionale Ansicht von Geräten. Möglicherweise benötigen wir mehrere Ansichten der Geräte, um unsere Shardings darzustellen, insbesondere für beliebige Gerätezuweisungen.

Beispielsweise hat jax.sharding.PositionalSharding kein gemeinsames logisches Mesh. GSPMD unterstützt dies derzeit mit HloSharding, bei dem die Darstellung eine sortierte Liste von Geräten und Dimensionsgrößen sein kann. Dies kann jedoch nicht mit der oben beschriebenen Achsenaufteilung dargestellt werden.

Wir überwinden diese Einschränkung und behandeln bestehende Grenzfälle, indem wir auf der obersten Ebene des Programms mehrere logische Netze definieren. Jedes Mesh kann eine andere Anzahl von Achsen mit unterschiedlichen Namen sowie eine eigene beliebige Zuordnung für dieselbe Gruppe von Geräten haben. Das heißt, jedes Mesh bezieht sich auf dieselbe Gruppe von Geräten (anhand ihrer eindeutigen logischen ID), aber in einer beliebigen Reihenfolge, ähnlich wie bei der GSPMD-Darstellung.

Jede Sharding-Darstellung ist mit einem bestimmten logischen Mesh verknüpft und verweist daher nur auf Achsen aus diesem Mesh.

Ein Tensor, der einem logischen Mesh zugewiesen ist, kann von einer Operation verwendet werden, die einem anderen Mesh zugewiesen ist. Dazu wird der Tensor einfach so neu geSharded, dass er dem Ziel-Mesh entspricht. In GSPMD wird dies in der Regel getan, um sich überschneidende Raster zu lösen.

Unten finden Sie zwei Beispiele:

Nutzer können mehrere Meshes mit unterschiedlich benannten Achsen angeben (z.B. über jax.sharding.NamedSharding), die dieselbe Gerätereihenfolge haben. In diesem Beispiel ist <@mesh_0, "b"> mit <@mesh_1, "z">. identisch.

@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}

Prioritäten

Mithilfe der Priorität können bestimmte Partitionierungs- und Weiterleitungsentscheidungen gegenüber anderen priorisiert werden. Außerdem ist eine inkrementelle Partitionierung eines Programms möglich.

Prioritäten sind Werte, die einigen oder allen Dimensionen einer Sharding-Darstellung zugeordnet sind. Replizierte Achsen haben keine Prioritäten.

Beispiel:

@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>

//                                    |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>

Mit Prioritäten haben Nutzer eine detailliertere Kontrolle über die Replikation, z.B. zuerst Batchparallelität, dann Megatron und schließlich ZeRO-Sharding. Dies ermöglicht eine hohe Sicherheit bei der Partitionierung und eine bessere Fehlerbehebung durch detailliertere Sharding-Strategien (wir sehen, wie das Programm nach nur Megatron in Isolation aussieht).

Sie können jeder Dimensionssharding eine Priorität zuweisen (standardmäßig 0). Das bedeutet, dass alle Shardings mit der Priorität <i vor Shardings mit der Priorität i an das gesamte Programm weitergegeben werden.

Auch wenn eine Sharding-Einheit eine offene Dimension mit niedrigerer Priorität hat, z.B. {"z",?}p2, wird es bei der Weiterleitung nicht von einer anderen Tensor-Sharding-Methode mit höherer Priorität überschrieben. Eine solche offene Dimension kann jedoch weiter gesplittet werden, nachdem alle Shardings mit höherer Priorität propagiert wurden.

Mit anderen Worten: Prioritäten geben NICHT an, welches Dimensions-Sharding wichtiger ist als ein anderes. Es geht um die Reihenfolge, in der verschiedene Gruppen von Dimensions-Shardings auf das gesamte Programm angewendet werden sollen, und darum, wie Konflikte bei Zwischen-Tensoren ohne Anmerkungen gelöst werden sollen.

Invarianten

• Die Prioritäten beginnen bei 0 (höchste Priorität) und steigen an. Damit Nutzer Prioritäten einfach hinzufügen und entfernen können, sind Lücken zwischen den Prioritäten zulässig, z. B. werden p0 und p2 verwendet, aber nicht p1.

• Sharding einer leeren geschlossenen Dimension (z.B. {}) sollte keine Priorität haben, da dies keine Auswirkungen hat.

Teilbarkeit für Dimensionen

Eine Dimension mit der Größe d kann entlang von Achsen segmentiert werden, deren Produkt der Größen n ist, sodass d nicht durch n teilbar ist. In diesem Fall muss die Dimension in der Praxis aufgefüllt werden.

Beispiel:

@mesh_xy = <["x"=8, "y"=2, "z"=3]>

sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>

Grammatik

Jedes logische Mesh wird so definiert:

@mesh_name = <mesh_axis_1,...,mesh_axis_n>

mesh_axis ::= axis_name=axis_size

axis_name ::= str
axis_size ::= int

Die Sharding-Darstellung hat für einen Tensor mit Rang r die folgende Struktur:

sharding<@mesh_name, dim_shardings, replicated=replicated_axes}

mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}

dim_sharding ::=
  {axis_1,...,axis_k} |  // closed dimension
  {axis_1,...,axis_k,?}  // open dimension

axis ::=
  axis_name  |   // a full axis
  sub_axis             // a sub axis

axis_name ::= str

sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int