Background
The purpose of the sharding representation is to specify how a tensor is sharded with respect to a set of available devices.
Sharding representation can either be:
- Manually specified by the user as sharding constraints on inputs, outputs, or intermediates.
- Transformed per operation in the process of sharding propagation.
Overview
Basic structure
A logical mesh is a multi-dimensional view of devices, defined by a list of axis names and sizes.
The proposed sharding representation is bound to a specific logical mesh by its name, and can only reference axis names from that mesh. The sharding of a tensor specifies along which axes (of a specific logical mesh) each dimension of the tensor is sharded, ordered from major to minor. The tensor is replicated along all other axes of the mesh.
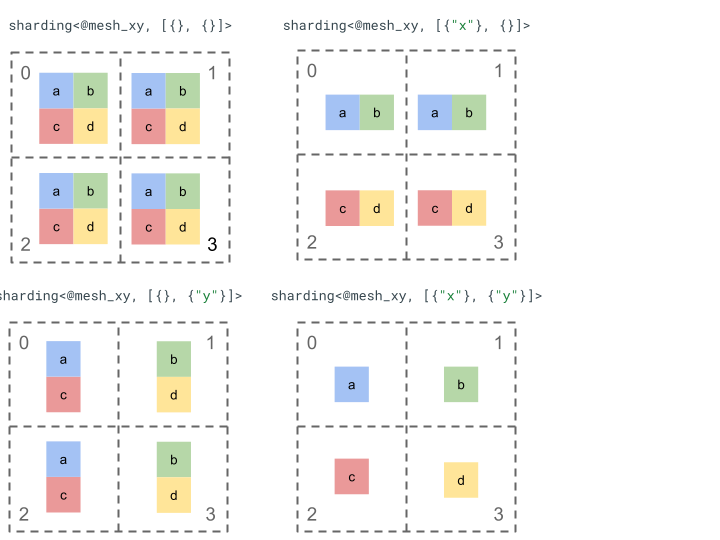
Let's explore the sharding representation with a simple rank 2 tensor and 4 devices.
We first reshape the 4 devices [0, 1, 2, 3] into a 2-d array [[0, 1], [2,
3]] to create a mesh with 2 axes:
@mesh_dm = <["d"=2, "m"=2]>
Where "d" represents the rows of the 2D matrix, while "m" the columns.
We can then shard the following rank 2 tensor [[a, b], [c, d]] as follows:
Other key components
- Open/Closed dimensions - dimensions can either be open - can be further sharded on available axes; or closed - are fixed and can't be changed.
- Explicitly replicated axes - all axes that are not used to shard a dimension are implicitly replicated, but the sharding can specify axes that are explicitly replicated and therefore cannot be used to shard a dimension later on.
- Axis splitting and sub-axes - a (full) mesh axis can be split into multiple sub-axes that can be individually used to shard a dimension or be explicitly replicated.
- Multiple logical meshes - different shardings can be bound to different logical meshes, which can have different axes or even a different order of logical device ids.
- Priorities - to partition a program incrementally, priorities can be attached to dimension shardings, which determine in which order per-dimension sharding constraints will be propagated throughout the module.
- Dimension sharding divisibility - a dimension can be sharded on axes whose product of sizes doesn't divide the dimension size.
Detailed Design
We expand the basic structure and each key component in this section.
Basic structure
The dimension shardings tell us for each dimension of the tensor, along which axes (or sub-axes) it is sharded from major to minor. All other axes that don't shard a dimension are implicitly replicated (or explicitly replicated).
We will start with a simple example and extend it as we describe additional features.
@mesh_xyz = <["x"=2, "y"=4, "z"=2]>
// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor
// dimension is sharded along axis "z" then further along axis "y".
// The local shape of this tensor (i.e. the shape on a single device),
// would be tensor<2x1xf32>.
sharding<@mesh_xyz, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>
Invariants
- The number of dimension shardings must match the rank of the tensor.
- All axis names must exist in the referenced mesh.
- Axes or sub-axes can only appear once in the sharding representation (each one either shards a dimension or is explicitly replicated).
Open/closed dimensions
Each dimension of a tensor can either be open or closed.
Open
An open dimension is open for propagation to further shard it along additional
axes, i.e. the specified dimension sharding doesn't have to be the final
sharding of that dimension. This is similar (but not exactly the same as) to
GSPMD's unspecified_dims.
If a dimension is open we add a ? following the axes that the dimension is
already sharded on (see example below).
Note that no sharding attribute on a tensor is equivalent to a fully open tensor sharding.
Closed
A closed dimension is one that isn't available for propagation to add further
sharding to, i.e. the specified dimension sharding is the final sharding of that
dimension and it can't be changed. A common use case of this is how GSPMD
(usually) doesn't modify the input/output arguments of a module, or how with
jax.jit, the user specified in_shardings are static - they can't change.
We can extend the example from above to have an open dimension and a closed dimension.
@mesh_xyz = <["x"=2, "y"=4, "z"=2]>
// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xyz, [{"x"}, {"z", ?}]> : tensor<4x8xf32>
Explicitly replicated axes
An explicit set of axes that a tensor is replicated on. While it can be
determined that a tensor not sharded on an axis is implicitly replicated on it
(like
jax.sharding.PartitionSpec
today), having it explicit makes sure that propagation cannot use these axes to
further shard an open dimension with those axes. With implicit replication, a
tensor can be further partitioned. But with explicit replication, nothing can
partition the tensor along that axis.
Ordering of replicated axes has no effect on how the data of a tensor is stored. But, for consistency only, the axes will be stored in the order they are specified in the top level mesh. For example, if the mesh is:
@mesh_cab = <["c"=2, "a"=2, "b"=2]>
And we want axes "a" and "c" to be explicitly replicated, the order should
be:
replicated={"c", "a"}
We can extend our example from above to have an explicitly replicated axis.
@mesh_xyz = <["x"=2, "y"=4, "z"=2]>
// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard any dimension. "z" doesn't shard any dimension here, so the
// local shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>
Axis splitting and sub-axes
A logical mesh of n axes is created by reshaping a 1-dimensional array of
devices into an n-dimensional array, where each dimension forms an axis with a
user-defined name.
The same process can be done in the compiler to split an axis of size k
further into m sub-axes, by reshaping the mesh from [...,k,...] into
[...,k1,...,km,...].
Motivation
To understand the motivation behind splitting axes, we will look at the following example:
@mesh_x = <["x"=4]>
%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>
We want to shard the result of the reshape in a way that would avoid
communication (i.e. keep the data where it is). Since the size of "x" is
greater than the 1st dimension of the result, we need to split the axis into two
sub-axes "x.0" and "x.1" of size 2 each, and shard the 1st dimension on
"x.0" and the 2nd dimension on "x.1".
Function Input/output shardings
It is possible that during propagation an input or output of the main function
will become sharded along a sub-axis. This can be a problem for some frameworks,
where we can't express such shardings to give back to the user (e.g. in JAX we
can't express sub-axes with
jax.sharding.NamedSharding).
We have a few options for dealing with such cases:
- Allow, and return the sharding in a different format (e.g.
jax.sharding.PositionalShardinginstead ofjax.sharding.NamedShardingin JAX). - Disallow, and all-gather sub-axes that shard the input/output.
Currently we allow sub-axes on the inputs/outputs in the propagation pipeline. Let us know if you want a way to disable this.
Representation
In the same way that we can reference specific full axes from the mesh by their name, we can reference specific sub-axes by their size and the product of all sub-axis (of the same axis name) sizes to their left (that are major to them).
To extract a specific sub-axis of size k from a full axis "x" of size n,
we effectively reshape the size n (in the mesh) into [m, k, n/(m*k)] and use
the 2nd dimension as the sub-axis. A sub-axis can thus be specified by two
numbers, m and k, and we use the following concise notation to denote
sub-axes: "x":(m)k.
m>=1is the pre-size of this sub-axis (mshould be a divisor ofn). The pre-size is the product of all sub-axis sizes to the left of (that are major to) this sub-axis (if equal to 1 it means there are none, If larger than 1 it corresponds to a single or multiple sub-axes).k>1is the actual size of this sub-axis (kshould be a divisor ofn).n/(m*k)is the post-size. It is the product of all sub-axis sizes to the right of (that are minor to) this sub-axis (if equal to 1 it means there are none, If larger than 1 it corresponds to a single or multiple sub-axes).
However, the number of other sub-axes doesn't make a difference when using a
specific sub-axis "x":(m)k, and any other sub-axis doesn't need to be
referenced in the tensor sharding if it doesn't shard a dimension or is
explicitly replicated.
Going back to the example in Motivation section, we can shard the result as follows:
@mesh_x = <["x"=4]>
%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
: (tensor<8xf32>) -> tensor<2x4xf32>
Here is another example of a split axis where only some of its sub-axes are used.
@mesh_xyz = <["x"=2, "y"=8, "z"=2]>
// Axis "y" is effectively split into 3 sub-axes denoted as
// "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>
Similarly, the following two shardings are semantically equivalent. We can think
of mesh_xy as a splitting of mesh_full.
@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>
sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>
Explicitly replicated sub-axes
In addition to sub-axes being used to shard dimension, they can also be marked
as explicitly replicated. We allow this in the representation because sub-axes
behave just like full axes, i.e. when you shard a dimension along a sub-axis of
axis "x", the other sub-axes of "x" are implicitly replicated, and therefore
can be explicitly replicated to indicate that a sub-axis must stay replicated
and can't be used to shard a dimension.
For example:
@mesh_xyz = <["x"=2, "y"=8, "z"=2]>
// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>
Replicated sub-axis of the same full axis should be ordered in increasing order by their pre-size, for example:
replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}
Invariants
Sub-axes referenced in a tensor sharding must not overlap, e.g.
"x":(1)4and"x":(2)4overlap.Sub-axes referenced in a tensor sharding must be as big as possible, i.e. If a dimension sharding has two adjacent sub-axes A and B in order, or sub-axes A and B are explicitly replicated, they must not be consecutive, e.g.
"x":(1)2and"x":(2)4as they can be replaced with a single"x":(1)8.
Multiple logical meshes
One logical mesh is a multi-dimensional view of devices. We may need multiple views of the devices to represent our shardings, especially for arbitrary device assignments.
For example,
jax.sharding.PositionalSharding does not have one common logical mesh.
GSPMD currently supports that with HloSharding, where the representation can be
an ordered list of devices and dimension sizes, but this can't be represented
with the axis splitting above.
We overcome this limitation and handle existing corner cases by defining multiple logical meshes at the top level of the program. Each mesh can have a different number of axes with different names, as well as its own arbitrary assignment for the same set of devices, i.e. each mesh refers to the same set of devices (by their unique logical ID) but with an arbitrary order, similar to the GSPMD representation.
Each sharding representation is linked to a specific logical mesh, therefore it will only reference axes from that mesh.
A tensor that is assigned to one logical mesh can be used by an op that is assigned to a different mesh, by naively resharding the tensor to match the destination mesh. In GSPMD this is what is usually done to resolve conflicting meshes.
Users can specify multiple meshes with different named axes (e.g. via
jax.sharding.NamedSharding), that have the same order of devices. Consider
this example, <@mesh_0, "b"> is identical to <@mesh_1, "z">:
@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
Priorities
Priority is a way to prioritize certain partitioning and propagation decisions over others, and allows for incremental partitioning of a program.
Priorities are values attached to some or all dimensions of a sharding representation (replicated axes don't have priorities).
For example:
@mesh_wxyz = <["w"=6, "x"=2, "y"=4, "z"=2]>
// |-> y is implicitly p0
%arg4 : sharding<@mesh_wxyz, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>
Priorities give users more fine grained control over propagation, e.g., batch parallelism first, then megatron, and finally ZeRO sharding. This allows for strong guarantees about what's partitioned and allows for better debuggability by having more fine grained sharding strategies (can see how the program looks after just megatron in isolation).
We allow attaching a priority to each dimension sharding (0 by default), which
indicates that all shardings with priority <i will be propagated to the entire
program before shardings with priority i.
Even if a sharding has an open dimension with lower priority, e.g., {"z",?}p2,
it won't be overridden by another tensor sharding with a higher priority during
propagation. However, such an open dimension can be further sharded after all
higher priority shardings have been propagated.
In other words, priorities are NOT about which dimension sharding is more important than another - it's the order in which distinct groups of dimension shardings should propagate to the entire program, and how conflicts on intermediate, unannotated tensors should be resolved.
Invariants
Priorities start at 0 (highest priority) and increase (to allow users to add and remove priorities easily, we allow gaps between priorities, e.g., p0 and p2 are used but p1 isn't).
An empty closed dimension sharding (i.e.,
{}), shouldn't have a priority, as this won't have any effect.
Dimension sharding divisibility
It's possible for a dimension of size d to be sharded along axes whose product
of sizes is n, such that d is not divisible by n (which in practice would
require the dimension to be padded).
For example:
@mesh_xyz = <["x"=8, "y"=2, "z"=3]>
sharding<@mesh_xyz, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>
Grammar
Each logical mesh is defined as follows:
@mesh_name = <mesh_axis_1,...,mesh_axis_n>
mesh_axis ::= axis_name=axis_size
axis_name ::= str
axis_size ::= int
The sharding representation will have the following structure for a tensor of rank r:
sharding<@mesh_name, dim_shardings, replicated=replicated_axes}
mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}
dim_sharding ::=
{axis_1,...,axis_k} | // closed dimension
{axis_1,...,axis_k,?} // open dimension
axis ::=
axis_name | // a full axis
sub_axis // a sub axis
axis_name ::= str
sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int
