本頁面由 Cloud Translation API 翻譯而成。

分割表示法

背景

分割表示法的目的，是針對一組可用的裝置，指定張量分割方式。

分割表示法可以是：

使用者手動指定的輸入、輸出或中間輸出項目區隔限制。
在分割傳播過程中，每個作業都會經過轉換。

總覽

基本結構

邏輯網格是裝置的多維度檢視畫面，由一組軸名和大小定義。

建議的分割表示法會根據名稱繫結至特定邏輯網格，且只能參照該網格中的軸名。張量的分割作業會指定沿著哪個軸 (特定邏輯網格) 分割張量的每個維度，並依序從主要到次要排列。張量會沿著網格的所有其他軸複製。

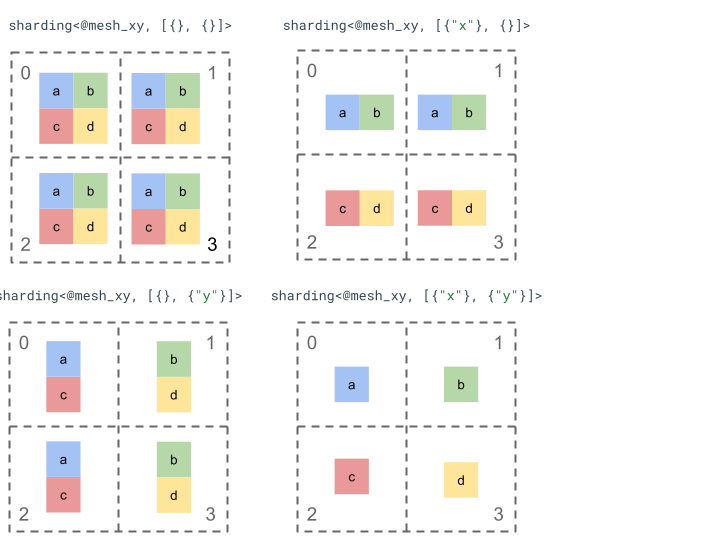
讓我們透過簡單的 2 階張量和 4 個裝置，瞭解分割表示法。

我們首先將 4 個裝置 [0, 1, 2, 3] 重塑為 2 維陣列 [[0, 1], [2, 3]]，以建立具有 2 個軸線的網格：

@mesh_xy = <["x"=2, "y"=2]>

接著，我們可以將下列 2 階張量 [[a, b], [c, d]] 切割如下：

秩為 2 的張量分割表示法

其他重要元件

開放式/封閉式維度：維度可以是開放式，可進一步在可用的軸上分割；或是封閉式，固定且無法變更。
明確複製的軸：所有未用於分割維度的軸都會隱含複製，但分割作業可以指定明確複製的軸，因此無法用於日後分割維度。
軸分割和子軸 - 可將 (完整) 網格軸分割成多個子軸，這些子軸可分別用於分割維度或明確複製。
多個邏輯網格：不同的分割作業可以綁定至不同的邏輯網格，這些網格可以有不同的軸，甚至邏輯裝置 ID 的順序也可能不同。
優先順序：為了逐步劃分程式，您可以將優先順序附加至維度分割作業，以決定各維度分割限制在整個模組中傳播的順序。
維度分割可分性：維度可在大小乘積不會除以維度大小的軸上分割。

縝密設計

我們會在本節中擴充基本結構和每個重要元件。

基本結構

維度分割作業會告訴我們，張量的每個維度沿著哪些軸 (或子軸) 從主要分割到次要分割。所有未分割維度的其他軸都會隱含複製 (或明確複製)。

我們將從簡單範例開始，並在說明其他功能時擴充範例。

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>

不變量

維度切割數量必須與張量的秩相符。
所有軸名稱都必須存在於參照的網格中。
軸或子軸只能在區隔表示法中出現一次 (每個軸都會區隔一個維度，或明確複製)。

開放式/封閉式維度

張量的每個維度都可以是開放式或封閉式。

開啟

開放式維度可供傳播，以便進一步沿著其他軸切割，也就是說，指定的維度切割不一定是該維度的最終切割。這與

jax.sharding.PartitionSpec.UNCONSTRAINED
GSPMD 的 unspecified_dims

如果維度是開放的，我們會在維度已分割的軸後方新增 ? (請參閱下方範例)。

已關閉

封閉維度是指無法透過傳播來進一步分割的維度，也就是說，指定的維度分割是該維度的最終分割，無法再變更。這項功能的常見用途是 GSPMD 通常不會修改模組的輸入/輸出引數，或是在 jax.jit 中，使用者指定的 in_shardings 是靜態的，無法變更。

我們可以擴充上述範例，以便使用開放式維度和封閉式維度。

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>

明確複製的軸

要複製張量的明確軸集。雖然可以判斷未在軸上分割的張量會在該軸上隱含複製 (例如今天的 jax.sharding.PartitionSpec)，但明確指定這項資訊可確保傳播無法使用這些軸，進一步透過這些軸分割開放維度。透過隱含複製功能，張量可以進一步分割。但在明確複製的情況下，沒有任何東西可以沿著該軸切割張量。

重複的軸順序不會影響張量的資料儲存方式。但為了保持一致性，軸會依照頂層網格中指定的順序儲存。舉例來說，如果網格是：

@mesh_xy = <["c"=2, "a"=2, "b"=2]>

我們希望軸 "a" 和 "c" 明確複製，因此順序應為：

replicated={"c", "a"}

我們可以擴充上述範例，讓軸明確複製。

@mesh_xyz = <["x"=2, "y"=4, "z"=2]>

// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would // be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>

軸分割和子軸

將裝置的 1 維陣列重新調整為 n 維陣列，即可建立 n 軸的邏輯網格，其中每個維度都會形成一個軸，並以使用者定義的名稱命名。

在編譯器中，您可以透過將網格從 [...,k,...] 重塑為 [...,k1,...,km,...]，執行相同的程序，將大小為 k 的軸進一步分割為 m 子軸。

動機

為了瞭解分割軸背後的動機，我們將參考以下範例：

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>

我們希望以避免通訊的方式分割重塑結果 (也就是保留資料所在位置)。由於 "x" 的大小大於結果的第 1 個維度，因此我們需要將軸分割成兩個子軸 "x.0" 和 "x.1"，每個大小為 2，並在 "x.0" 上分割第 1 個維度，在 "x.1" 上分割第 2 個維度。

函式輸入/輸出分割

在傳播期間，主函式的輸入或輸出可能會沿著子軸分割。這對某些架構來說可能會造成問題，因為我們無法以這種方式將分割作業傳回給使用者 (例如在 JAX 中，我們無法使用 jax.sharding.NamedSharding 表示子軸)。

我們有幾種方法可處理這類案件：

允許並以不同格式傳回分割作業 (例如 jax.sharding.PositionalSharding，而非 JAX 中的 jax.sharding.NamedSharding)。
禁止，以及會分割輸入/輸出的 all-gather 子軸。

目前，我們允許在傳播管道中對輸入/輸出內容使用子軸。如果你想知道如何停用這項功能，請告訴我們。

代表權

我們可以根據名稱參照網格中的特定完整軸，同樣地，我們也可以根據子軸的大小和左側所有子軸 (同軸名稱) 大小的乘積來參照特定子軸。

如要從大小為 n 的完整軸 "x" 中，擷取大小為 k 的特定子軸，我們可以有效地將大小為 n (在網格中) 的大小重塑為 [m, k, n/(m*k)]，並使用第 2 個維度做為子軸。因此，子軸可以由兩個數字 m 和 k 指定，我們使用以下簡潔的符號表示子軸："x":(m)k。

m>=1 是這個子軸的預先大小 (m 應為 n 的除數)。預先大小是這個子軸左側所有子軸大小 (對應於這個子軸) 的乘積 (如果等於 1，表示沒有任何子軸；如果大於 1，則對應於一個或多個子軸)。
k>1 是此子軸的實際大小 (k 應為 n 的除數)。
n/(m*k) 是後端大小。這個值是這個子軸右側 (次要於此子軸) 的所有子軸大小的乘積 (如果等於 1，表示沒有任何子軸；如果大於 1，則對應於單一或多個子軸)。

不過，使用特定子軸 "x":(m)k 時，其他子軸的數量不會造成差異，如果子軸未分割維度或已明確複製，則無須在張量分割中參照任何其他子軸。

回到「動機」一節的範例，我們可以將結果分割如下：

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
    : (tensor<8xf32>) -> tensor<2x4xf32>

以下是另一個分割軸的範例，其中只使用了部分子軸。

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Axis "y" is effectively split into 3 sub-axes denoted as
//   "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>

同樣地，以下兩個分割作業在語意上是等價的。我們可以將 mesh_xy 視為 mesh_full 的拆分。

@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>

sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>

明確複製的子軸

除了用於分割維度的子軸之外，也可以將子軸標示為明確複製的軸。我們允許在表示法中執行這項操作，因為子軸的行為與完整軸相同，也就是說，當您沿著軸 "x" 的子軸分割維度時，"x" 的其他子軸會隱含複製，因此可以明確複製，以表示子軸必須保持複製狀態，且無法用於分割維度。

例如：

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>

相同完整軸的複製子軸應依預先大小遞增排序，例如：

replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}

不變量

張量切割中參照的子軸不得重疊，例如 "x":(1)4 和 "x":(2)4 重疊。
張量切割中參照的子軸必須盡可能大，也就是說，如果維度切割有兩個相鄰的子軸 A 和 B，或子軸 A 和 B 明確複製，則這些子軸不得連續，例如 "x":(1)2 和 "x":(2)4，因為可以用單一 "x":(1)8 取代。

多個邏輯網格

一個邏輯網格是裝置的多維檢視畫面。我們可能需要多個裝置檢視畫面來代表分割作業，尤其是針對任意裝置指派作業。

例如，jax.sharding.PositionalSharding 沒有一個共同的邏輯網格。GSPMD 目前透過 HloSharding 支援這項功能，其中的呈現方式可以是裝置和維度大小的排序清單，但無法透過上述軸分割呈現。

我們在程式的頂層定義多個邏輯網格，藉此克服這項限制並處理現有的邊緣情況。每個網格可以有不同數量的軸，且名稱也不同，並且可為相同組裝置隨意指派，也就是說，每個網格都會參照相同組裝置 (透過其專屬邏輯 ID)，但會以任意順序排列，類似於 GSPMD 表示法。

每個分割表示法都會連結至特定邏輯網格，因此只會參照該網格中的軸。

指派給一個邏輯網格的張量，可由指派給不同網格的運算子使用，方法是簡單地重新切割張量，以符合目的地網格。在 GSPMD 中，這通常是解決相衝突的網格問題的方法。

請參考以下兩個範例：

使用者可以指定多個具有不同軸名稱 (例如透過 jax.sharding.NamedSharding) 且裝置順序相同的多個網格。在這個範例中，<@mesh_0, "b"> 與 <@mesh_1, "z">. 相同

@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}

優先順序

優先順序可用於將特定分區和傳播決策優先於其他決策，並允許逐步分區執行程式。

優先順序是附加至分割表示法部分或所有維度的值 (複製的軸沒有優先順序)。

例如：

@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>

//                                    |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>

優先順序可讓使用者更精細地控制傳播作業，例如先執行批次並行作業，然後再執行 megatron，最後再執行 ZeRO 分割作業。這可讓您確保分割的內容，並透過更精細的分割策略，讓程式更容易進行偵錯 (可查看在單獨情況下，程式在 megatron 之後的樣貌)。

我們允許為每個維度分割作業附加優先順序 (預設為 0)，這表示優先順序為 <i 的所有分割作業會先傳播至整個程式，再傳播優先順序為 i 的作業。

即使切割作業含有優先順序較低的開放式維度 (例如{"z",?}p2，在傳播期間，不會被其他優先順序較高的張量切割覆寫。不過，在所有優先順序較高的分割作業完成後，這類開放維度可以進一步分割。

換句話說，優先順序「不是」關乎哪個維度分割作業比其他作業更重要，而是指不同的維度分割作業群組應如何傳播至整個程式，以及如何解決中間未註解的張量衝突。

不變量

優先順序從 0 (最高優先順序) 開始，並依序增加 (為了讓使用者輕鬆新增及移除優先順序，我們允許優先順序之間有空格，例如 p0 和 p2 會使用，但 p1 不會)。
空白的封閉維度區隔 (即{}) 不應設有優先順序，因為這不會產生任何影響。

維度分割的可除性

大小為 d 的維度可能會沿著大小乘積為 n 的軸進行分割，因此 d 無法被 n 整除 (實際上需要對維度進行填充)。

例如：

@mesh_xy = <["x"=8, "y"=2, "z"=3]>

sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>

文法

每個邏輯網格定義如下：

@mesh_name = <mesh_axis_1,...,mesh_axis_n>

mesh_axis ::= axis_name=axis_size

axis_name ::= str
axis_size ::= int

對於秩序為 r 的張量，分割表示法會有下列結構：

sharding<@mesh_name, dim_shardings, replicated=replicated_axes}

mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}

dim_sharding ::=
  {axis_1,...,axis_k} |  // closed dimension
  {axis_1,...,axis_k,?}  // open dimension

axis ::=
  axis_name  |   // a full axis
  sub_axis             // a sub axis

axis_name ::= str

sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int