Propagação

Visão geral

A propagação de fragmentação usa as fragmentações especificadas pelo usuário para inferir as fragmentações não especificadas de tensores (ou dimensão específica de tensores). Ele percorre o fluxo de dados (cadeias de uso-def) do gráfico de computação em ambas as direções até que um ponto fixo seja alcançado. Ou seja, o fragmentação não pode mais mudar sem desfazer as decisões de fragmentação anteriores.

A propagação pode ser dividida em etapas. Cada etapa envolve analisar uma operação específica e propagar entre os tensores (operandos e resultados), com base nas características dessa operação. Usando uma matmul como exemplo, propagaríamos entre a dimensão não contraída de lhs ou rhs para a dimensão correspondente do resultado ou entre a dimensão contraída de lhs e rhs.

As características de uma operação determinam a conexão entre as dimensões correspondentes nas entradas e saídas e podem ser abstratas como uma regra de fragmentação por operação.

Sem a resolução de conflitos, uma etapa de propagação simplesmente propagaria o máximo possível, ignorando os eixos em conflito. Chamamos isso de eixos de divisão principais (mais longos) compatíveis.

Design detalhado

Hierarquia de resolução de conflitos

Criamos várias estratégias de resolução de conflitos em uma hierarquia:

1. Prioridades definidas pelo usuário. Em Representação de divisão, descrevemos como as prioridades podem ser anexadas a divisões de dimensão para permitir a partição incremental do programa, por exemplo, fazendo paralelismo de lote -> megatron -> divisão ZERO. Isso é feito aplicando a propagação em iterações. Na iteração i, propagamos todos os shardings de dimensão que têm prioridade <=i e ignoramos todos os outros. Também garantimos que a propagação não vai substituir fragmentações definidas pelo usuário com prioridade mais baixa (>i), mesmo que sejam ignoradas durante iterações anteriores.
2. Prioridades baseadas em operações. Nós propagamos os shardings com base no tipo de operação. As operações de "transmissão" (por exemplo, operações por elemento e remodelagem) têm a maior prioridade, enquanto as operações com transformação de forma (por exemplo, ponto e redução) têm prioridade menor.
3. Propagação agressiva. Propague os shardings com uma estratégia agressiva. A estratégia básica só propaga partições sem conflitos, enquanto a estratégia agressiva resolve conflitos. Uma maior agressividade pode reduzir o consumo de memória em detrimento da comunicação potencial.
4. Propagação básica. É a estratégia de propagação mais baixa na hierarquia, que não faz nenhuma resolução de conflito e, em vez disso, propaga eixos compatíveis entre todos os operandos e resultados.

Essa hierarquia pode ser interpretada como loops aninhados. Por exemplo, para cada prioridade do usuário, uma propagação completa de prioridade de operação é aplicada.

Regra de fragmentação de operações

A regra de fragmentação introduz uma abstração de cada operação que fornece ao algoritmo de propagação real as informações necessárias para propagar fragmentações de operandos para resultados ou entre operandos etc., sem precisar raciocinar sobre tipos de operação específicos e seus atributos. Isso é basicamente separar a lógica específica da operação e fornecer uma representação compartilhada (estrutura de dados) para todas as operações apenas para fins de propagação. Na forma mais simples, ele fornece apenas esta função:

GetOpShardingRule(Operation *) -> OpShardingRuleAttr

A regra permite que você escreva o algoritmo de propagação apenas uma vez de maneira genérica, com base nessa estrutura de dados (OpShardingRule), em vez de replicar partes semelhantes do código em muitas operações, reduzindo muito a possibilidade de bugs ou comportamento inconsistente em todas as operações.

Vamos voltar ao exemplo de matmul.

Uma codificação que encapsula as informações necessárias durante a propagação, ou seja, as relações entre as dimensões, pode ser gravada na forma de notação einsum:

(i, k), (k, j) -> (i, j)

Nessa codificação, cada dimensão é mapeada para um único fator.

Como a propagação usa esse mapeamento:se uma dimensão de um operando/resultado for fragmentada em um eixo, a propagação vai procurar o fator dessa dimensão nesse mapeamento e fragmentar outros operandos/resultados na respectiva dimensão com o mesmo fator. Além disso, (sujeito à discussão anterior sobre a replicação) também pode replicar outros operandos/resultados que não têm esse fator ao longo desse eixo.

Fatores compostos: estender a regra para remodelações

Em muitas operações, como matmul, só precisamos mapear cada dimensão para um único fator. No entanto, isso não é suficiente para reformulações.

A reformulação a seguir mescla duas dimensões em uma:

%out = mhlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>

Aqui, as dimensões 0 e 1 da entrada correspondem à dimensão 0 da saída. Digamos que começamos fornecendo fatores para a entrada:

(i,j,k) : i=2, j=4, k=32

Se quisermos usar os mesmos fatores para a saída, vamos precisar de uma única dimensão para fazer referência a vários fatores:

(i,j,k) -> ((ij), k) : i=2, j=4, k=32

O mesmo pode ser feito se a remodelagem dividir uma dimensão:

%out = mhlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32> ((ij), k) -> (i,j,k) : i=2, j=4, k=32

A dimensão de tamanho 8 aqui é basicamente composta pelos fatores 2 e 4, por isso chamamos os fatores de (i,j,k).

Esses fatores também podem funcionar em casos em que não há uma dimensão completa que corresponde a um dos fatores:

%out = mhlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32> ((ij), k) -> (i,(jk)) : i=2, j=4, k=4

Esse exemplo também enfatiza por que precisamos armazenar os tamanhos de fator, já que não podemos deduzir facilmente as dimensões correspondentes.

Algoritmo de propagação principal

Propague as partições ao longo dos fatores

No Shardy, temos a hierarquia de tensores, dimensões e fatores. Eles representam dados em níveis diferentes. Um fator é uma subdimensão. É uma hierarquia interna usada na propagação de fragmentação. Cada dimensão pode corresponder a um ou mais fatores. O mapeamento entre a dimensão e o fator é definido por OpShardingRule.

O Shardy propaga eixos de fragmentação ao longo de fatores, em vez de dimensões. Para fazer isso, temos três etapas, conforme mostrado na figura abaixo.

1. DimSharding do projeto para FactorSharding
2. Propague eixos de fragmentação no espaço do FactorSharding
3. Projetar o FactorSharding atualizado para receber o DimSharding atualizado

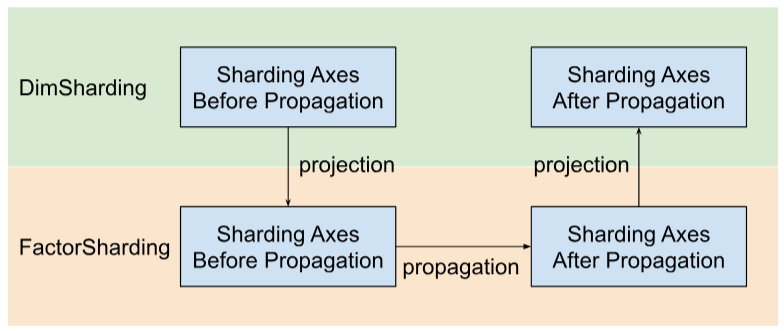
Visualização da propagação de fragmentação ao longo dos fatores

Usaremos a tabela a seguir para visualizar o problema e o algoritmo de propagação de fragmentação.

	F0	F1	F2	Eixos replicados explicitamente
T0
T1
T2

• Cada coluna representa um fator. F0 significa o fator com índice 0. Nós propagamos os shardings ao longo de fatores (colunas).
• Cada linha representa um tensor. T0 se refere ao tensor com índice 0. Os tensores são todos os operandos e resultados envolvidos em uma operação específica. Os eixos em uma linha não podem se sobrepor. Um eixo (ou subeixo) não pode ser usado para particionar um tensor várias vezes. Se um eixo for replicado explicitamente, não será possível usá-lo para particionar o tensor.

Assim, cada célula representa um fator de fragmentação. Um fator pode estar ausente em tensores parciais. Confira a tabela de C = dot(A, B) abaixo. As células que contêm um N implicam que o fator não está no tensor. Por exemplo, F2 está em T1 e T2, mas não em T0.

C = dot(A, B)	F0 Escurecer em lote	Dimensão F1 não contraída	F2: escurecimento sem contração	F3 Contratação de escurecimento	Eixos replicados explicitamente
T0 = A			N
T1 = B		N
T2 = C				N

Coletar e propagar eixos de fragmentação

Usamos um exemplo simples mostrado abaixo para visualizar a propagação.

	F0	F1	F2	Eixos replicados explicitamente
T0	"a"		"f"
T1	"a", "b"	"c", "d"	"g"
T2		"c", "e"

Etapa 1: Encontre eixos para propagar em cada fator (também conhecidos como os eixos de fragmentação principais (mais longos) compatíveis). Neste exemplo, propagamos ["a", "b"] ao longo de F0, propagamos ["c"] ao longo de F1 e não propagamos nada ao longo de F2.

Etapa 2: Expanda os shardings de fator para obter o resultado a seguir.

	F0	F1	F2	Eixos replicados explicitamente
T0	"a", "b"	"c"	"f"
T1	"a", "b"	"c", "d"	"g"
T2	"a", "b"	"c", "e"