Contexto
O objetivo da representação de fragmentação é especificar como um tensor é fragmentado em relação a um conjunto de dispositivos disponíveis.
A representação de fragmentação pode ser:
- Especificadas manualmente pelo usuário como restrições de fragmentação em entradas, saídas ou intermediárias.
- Transformado por operação no processo de propagação de fragmentação.
Visão geral
Estrutura básica
Uma malha lógica é uma visualização multidimensional de dispositivos, definida por uma lista de nomes e tamanhos de eixos.
A representação de fragmentação proposta é vinculada a uma malha lógica específica pelo nome e só pode referenciar nomes de eixos dessa malha. O sharding de um tensor especifica ao longo de quais eixos (de uma malha lógica específica), cada dimensão do tensor é dividida, ordenada de maior para menor. O tensor é replicado em todos os outros eixos da malha.
Vamos analisar a representação de fragmentação com um tensor de nível 2 simples e quatro dispositivos.
Primeiro, remodelamos os 4 dispositivos [0, 1, 2, 3] em uma matriz 2D [[0, 1], [2,
3]] para criar uma malha com dois eixos:
@mesh_xy = <["x"=2, "y"=2]>
Podemos dividir o seguinte tensor de rank 2 [[a, b], [c, d]] da seguinte maneira:
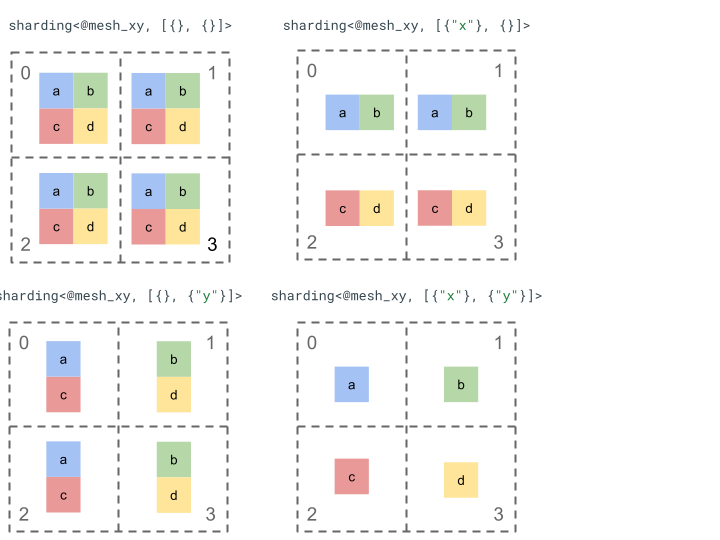
Outros componentes importantes
- Dimensões abertas/fechadas: as dimensões podem ser abertas, ou seja, podem ser divididas em partições nos eixos disponíveis, ou fechadas, ou seja, são fixas e não podem ser alteradas.
- Eixos replicados explicitamente: todos os eixos que não são usados para dividir uma dimensão são replicados implicitamente, mas o sharding pode especificar eixos que são replicados explicitamente e, portanto, não podem ser usados para dividir uma dimensão mais tarde.
- Divisão e subeixos do eixo: um eixo de malha (completo) pode ser dividido em vários subeixos que podem ser usados individualmente para dividir uma dimensão ou ser replicados explicitamente.
- Várias malhas lógicas: diferentes fragmentações podem ser vinculadas a diferentes malhas lógicas, que podem ter eixos diferentes ou até mesmo uma ordem diferente de IDs de dispositivos lógicos.
- Prioridades: para particionar um programa de forma incremental, é possível anexar prioridades a divisões de dimensão, que determinam em qual ordem as restrições de divisão por dimensão serão propagadas pelo módulo.
- Divisibilidade do fragmentação de dimensão: uma dimensão pode ser fragmentada em eixos cujo produto de tamanhos não divide o tamanho da dimensão.
Design detalhado
Nesta seção, vamos expandir a estrutura básica e cada componente principal.
Estrutura básica
Os shardings de dimensão informam para cada dimensão do tensor, ao longo de quais eixos (ou subeixos) ele é dividido de maior para menor. Todos os outros eixos que não fragmentam uma dimensão são replicados implicitamente (ou explicitamente).
Vamos começar com um exemplo simples e ampliá-lo à medida que descrevemos outros recursos.
@mesh_xy = <["x"=2, "y"=4, "z"=2]>
// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>
Invariantes
- O número de fragmentações de dimensão precisa corresponder ao rank do tensor.
- Todos os nomes de eixo precisam existir na malha referenciada.
- Os eixos ou subeixos só podem aparecer uma vez na representação de fragmentação. Cada um deles fragmenta uma dimensão ou é explicitamente replicado.
Dimensões abertas/fechadas
Cada dimensão de um tensor pode ser aberta ou fechada.
Abrir
Uma dimensão aberta está disponível para propagação e pode ser dividida em outros eixos, ou seja, o dimensionamento especificado não precisa ser o final. Isso é semelhante (mas não exatamente igual) a
jax.sharding.PartitionSpec.UNCONSTRAINEDunspecified_dimsdo GSPMD
Se uma dimensão estiver aberta, vamos adicionar um ? seguindo os eixos em que a dimensão já está particionada (veja o exemplo abaixo).
Fechado
Uma dimensão fechada é aquela que não está disponível para propagação para adicionar mais particionamento. Ou seja, o particionamento de dimensão especificado é o particionamento final dessa dimensão e não pode ser alterado. Um caso de uso comum para isso é como o GSPMD
(geralmente) não modifica os argumentos de entrada/saída de um módulo ou como, com
jax.jit, o in_shardings especificado pelo usuário é estático, ou seja, não pode mudar.
Podemos estender o exemplo acima para ter uma dimensão aberta e uma fechada.
@mesh_xy = <["x"=2, "y"=4, "z"=2]>
// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>
Eixos replicados explicitamente
Um conjunto explícito de eixos em que um tensor é replicado. Embora seja possível
determinar que um tensor não dividido em um eixo é replicado implicitamente nele
(como
jax.sharding.PartitionSpec
atualmente), ter isso de forma explícita garante que a propagação não possa usar esses eixos para
dividir ainda mais uma dimensão aberta com esses eixos. Com a replicação implícita, um
tensor pode ser particionado novamente. Mas, com a replicação explícita, nada pode
particionar o tensor ao longo desse eixo.
A ordem dos eixos replicados não afeta a forma como os dados de um tensor são armazenados. No entanto, para manter a consistência, os eixos serão armazenados na ordem em que são especificados na malha de nível superior. Por exemplo, se a malha for:
@mesh_xy = <["c"=2, "a"=2, "b"=2]>
E queremos que os eixos "a" e "c" sejam replicados explicitamente. A ordem precisa ser
a seguinte:
replicated={"c", "a"}
Podemos estender nosso exemplo acima para ter um eixo replicado explicitamente.
@mesh_xyz = <["x"=2, "y"=4, "z"=2]>
// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would // be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>
Divisão de eixos e eixos secundários
Uma malha lógica de eixos n é criada reformulando uma matriz unidimensional de
dispositivos em uma matriz n-dimensional, em que cada dimensão forma um eixo com um
nome definido pelo usuário.
O mesmo processo pode ser feito no compilador para dividir um eixo de tamanho k
em subeixos m, remodelando a malha de [...,k,...] em
[...,k1,...,km,...].
Motivação
Para entender a motivação por trás da divisão dos eixos, vamos analisar o seguinte exemplo:
@mesh_x = <["x"=4]>
%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>
Queremos dividir o resultado da reformulação de uma maneira que evite a
comunicação (ou seja, manter os dados onde estão). Como o tamanho de "x" é
maior que a primeira dimensão do resultado, precisamos dividir o eixo em dois
subeixos "x.0" e "x.1" de tamanho 2 cada e dividir a primeira dimensão em
"x.0" e a segunda em "x.1".
Fragmentações de entrada/saída de função
É possível que, durante a propagação, uma entrada ou saída da função principal
seja dividida em um eixo secundário. Isso pode ser um problema para alguns frameworks,
em que não podemos expressar esses shardings para devolver ao usuário. Por exemplo, no JAX,
não podemos expressar subeixos com
jax.sharding.NamedSharding.
Temos algumas opções para lidar com esses casos:
- Permitir e retornar o fragmentação em um formato diferente (por exemplo,
jax.sharding.PositionalShardingem vez dejax.sharding.NamedShardingno JAX). - Não permitir e todos os subeixos de coleta que fragmentam a entrada/saída.
No momento, permitimos subeixos nas entradas/saídas no pipeline de propagação. Informe se você quer desativar essa opção.
Representação
Da mesma forma que podemos referenciar eixos completos específicos da malha pelo nome, podemos referenciar eixos secundários específicos pelo tamanho e pelo produto de todos os tamanhos de eixos secundários (do mesmo nome) à esquerda (que são principais para eles) .
Para extrair um eixo secundário específico de tamanho k de um eixo completo "x" de tamanho n,
reformamos o tamanho n (na malha) em [m, k, n/(m*k)] e usamos
a segunda dimensão como o eixo secundário. Um eixo secundário pode ser especificado por dois
números, m e k, e usamos a seguinte notação concisa para denotar
eixos secundários: "x":(m)k.
m>=1é o pré-tamanho desse eixo secundário (mprecisa ser um divisor den). O pré-tamanho é o produto de todos os tamanhos de eixos secundários à esquerda (que são principais) desse eixo secundário. Se for igual a 1, significa que não há nenhum. Se for maior que 1, corresponde a um ou vários eixos secundários.k>1é o tamanho real desse eixo secundário (kprecisa ser um divisor den).n/(m*k)é o tamanho da postagem. É o produto de todos os tamanhos de eixos secundários à direita (que são menores que) esse eixo secundário. Se for igual a 1, significa que não há nenhum. Se for maior que 1, corresponde a um ou vários eixos secundários.
No entanto, o número de outros eixos secundários não faz diferença ao usar um
"x":(m)k de eixo secundário específico, e nenhum outro eixo secundário precisa ser
referenciado no particionamento de tensor se ele não particionar uma dimensão ou for
explicitamente replicado.
Voltando ao exemplo na seção Motivação, podemos dividir o resultado da seguinte maneira:
@mesh_x = <["x"=4]>
%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
: (tensor<8xf32>) -> tensor<2x4xf32>
Confira outro exemplo de eixo dividido em que apenas alguns dos subeixos são usados.
@mesh_xyz = <["x"=2, "y"=8, "z"=2]>
// Axis "y" is effectively split into 3 sub-axes denoted as
// "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>
Da mesma forma, os dois shardings a seguir são semanticamente equivalentes. Podemos pensar
em mesh_xy como uma divisão de mesh_full.
@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>
sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>
Subeixos replicados explicitamente
Além de os eixos secundários serem usados para dimensionar o fragmento, eles também podem ser marcados
como replicados explicitamente. Isso é permitido na representação porque os eixos secundários se comportam como eixos completos. Ou seja, quando você divide uma dimensão em um eixo secundário de "x", os outros eixos secundários de "x" são replicados implicitamente e, portanto, podem ser replicados explicitamente para indicar que um eixo secundário precisa permanecer replicado e não pode ser usado para dividir uma dimensão.
Exemplo:
@mesh_xyz = <["x"=2, "y"=8, "z"=2]>
// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>
Os eixos secundários replicados do mesmo eixo completo precisam ser ordenados em ordem crescente pelo tamanho prévio, por exemplo:
replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}
Invariantes
Os subeixos referenciados em um fragmentação de tensor não podem se sobrepor, por exemplo,
"x":(1)4e"x":(2)4se sobrepõem.Os eixos secundários referenciados em um fragmentação de tensor precisam ser o maior possível. Ou seja, se um fragmentação de dimensão tiver dois eixos secundários adjacentes A e B em ordem ou se os eixos A e B forem replicados explicitamente, eles não podem ser consecutivos, por exemplo,
"x":(1)2e"x":(2)4, porque podem ser substituídos por um único"x":(1)8.
Várias malhas lógicas
Uma malha lógica é uma visualização multidimensional de dispositivos. Talvez precisemos de várias visualizações dos dispositivos para representar nossos shardings, especialmente para atribuições arbitrárias de dispositivos.
Por exemplo,
jax.sharding.PositionalSharding não tem uma malha lógica comum.
No momento, o GSPMD oferece suporte a isso com o HloSharding, em que a representação pode ser
uma lista ordenada de dispositivos e tamanhos de dimensão, mas isso não pode ser representado
com a divisão de eixos acima.
Superamos essa limitação e tratamos os casos extremos definindo várias malhas lógicas no nível superior do programa. Cada malha pode ter um número diferente de eixos com nomes diferentes, além de uma atribuição arbitrária para o mesmo conjunto de dispositivos, ou seja, cada malha se refere ao mesmo conjunto de dispositivos (pelo ID lógico exclusivo), mas com uma ordem arbitrária, semelhante à representação do GSPMD.
Cada representação de fragmentação é vinculada a uma malha lógica específica. Portanto, ela somente vai referenciar eixos dessa malha.
Um tensor atribuído a uma malha lógica pode ser usado por uma operação atribuída a uma malha diferente, redimensionando o tensor para corresponder à malha de destino. No GSPMD, isso é o que geralmente é feito para resolver conflitos de malhas.
Confira dois exemplos abaixo:
Os usuários podem especificar várias malhas com eixos nomeados diferentes (por exemplo, via
jax.sharding.NamedSharding), que têm a mesma ordem de dispositivos. Neste
exemplo, <@mesh_0, "b"> é idêntico a <@mesh_1, "z">..
@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
Prioridades
A prioridade é uma maneira de priorizar determinadas decisões de particionamento e propagação em relação a outras e permite o particionamento incremental de um programa.
As prioridades são valores associados a algumas ou todas as dimensões de uma representação de fragmentação (os eixos replicados não têm prioridades).
Exemplo:
@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>
// |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>
As prioridades dão aos usuários um controle mais preciso sobre a propagação, por exemplo, o paralelismo em lote primeiro, depois o Megatron e, por fim, o sharding do ZeRO. Isso permite garantias fortes sobre o que é particionado e permite uma melhor capacidade de depuração com estratégias de fragmentação mais detalhadas (é possível conferir como o programa fica após o Megatron isoladamente).
Permitimos a vinculação de uma prioridade a cada divisão de dimensão (0 por padrão), o que
indica que todas as divisões com prioridade <i serão propagadas para todo o
programa antes das divisões com prioridade i.
Mesmo que um particionamento tenha uma dimensão aberta com prioridade mais baixa, por exemplo, {"z",?}p2,
não será substituído por outro fragmentação de tensor com uma prioridade mais alta durante
a propagação. No entanto, essa dimensão aberta pode ser dividida depois que todos os
fragmentos de maior prioridade forem propagados.
Em outras palavras, as prioridades NÃO se referem a qual divisão de dimensão é mais importante do que outra. É a ordem em que grupos distintos de divisões de dimensão precisam se propagar para todo o programa e como os conflitos em tensores intermediários não anotados precisam ser resolvidos.
Invariantes
As prioridades começam em 0 (prioridade mais alta) e aumentam.Para permitir que os usuários adicionem e removam prioridades com facilidade, permitimos lacunas entre as prioridades. Por exemplo, p0 e p2 são usados, mas p1 não é.
Um sharding de dimensão fechada vazio (ou seja,
{}), não deve ter prioridade, porque não vai ter nenhum efeito.
Divisibilidade do dimensionamento
É possível que uma dimensão de tamanho d seja dividida em eixos cujo produto
de tamanhos seja n, de modo que d não seja divisível por n (o que, na prática,
requer que a dimensão seja preenchida).
Exemplo:
@mesh_xy = <["x"=8, "y"=2, "z"=3]>
sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>
Gramática
Cada malha lógica é definida da seguinte maneira:
@mesh_name = <mesh_axis_1,...,mesh_axis_n>
mesh_axis ::= axis_name=axis_size
axis_name ::= str
axis_size ::= int
A representação de fragmentação terá a seguinte estrutura para um tensor de grau r:
sharding<@mesh_name, dim_shardings, replicated=replicated_axes}
mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}
dim_sharding ::=
{axis_1,...,axis_k} | // closed dimension
{axis_1,...,axis_k,?} // open dimension
axis ::=
axis_name | // a full axis
sub_axis // a sub axis
axis_name ::= str
sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int