背景
分片表示法旨在指定张量相对于一组可用设备的分片方式。
分片表示法可以是：
- 由用户手动指定为输入、输出或中间结果的分片约束条件。
- 在分片传播过程中，按操作进行转换。
概览
基本结构
逻辑网格是设备的多维视图，由轴名称和尺寸列表定义。
所提议的分片表示法会通过其名称绑定到特定逻辑网格，并且只能引用该网格中的轴名称。张量的分片会指定张量的每个维度沿哪些轴（特定逻辑网格的轴）进行分片，并按主轴到次轴的顺序排列。张量会沿网格的所有其他轴复制。
我们来探索一下使用简单的秩 2 张量和 4 个设备的分片表示法。
我们首先将 4 个设备 [0, 1, 2, 3] 重塑为 2 维数组 [[0, 1], [2,
3]]，以创建具有 2 个轴的网格：
@mesh_xy = <["x"=2, "y"=2]>
然后，我们可以按如下方式对秩为 2 的张量 [[a, b], [c, d]] 进行分片：
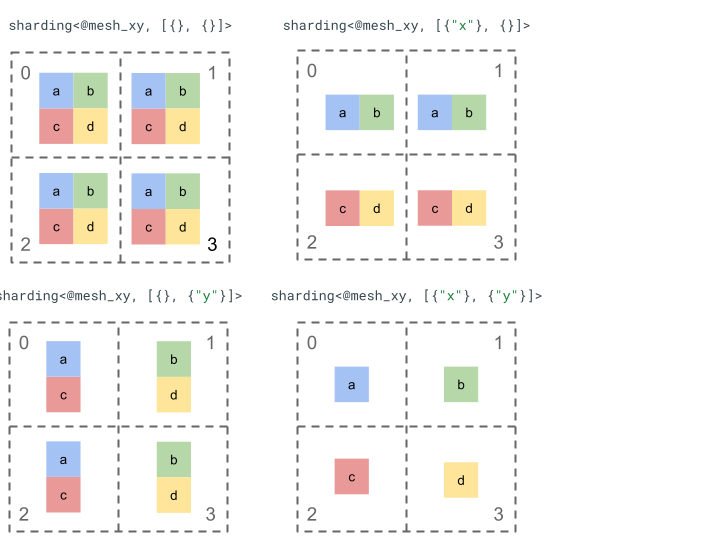
其他关键组件
- 开放式/封闭式维度 - 维度可以是开放式（可在可用轴上进一步分片）；也可以是封闭式（固定且无法更改）。
- 显式复制的轴 - 所有未用于分片维度的轴都是隐式复制的，但分片可以指定显式复制的轴，因此这些轴无法在日后用于分片维度。
- 轴拆分和子轴 - 一个（完整的）网格轴可以拆分为多个子轴，这些子轴可以单独用于对维度进行分片或进行显式复制。
- 多个逻辑网格 - 不同的分片可以绑定到不同的逻辑网格，这些逻辑网格可以具有不同的轴，甚至逻辑设备 ID 的顺序也可能不同。
- 优先级 - 如需增量分区程序，可以将优先级附加到维度分片，这些优先级决定了每个维度分片约束条件将以何种顺序传播到整个模块。
- 维度分片可分性 - 维度可沿尺寸乘积不等于维度大小的轴进行分片。
详细设计
在本部分中，我们将详细介绍基本结构和每个关键组件。
基本结构
维度分片可告诉我们张量的每个维度是沿哪些轴（或子轴）从主轴到次轴进行分片的。所有其他不对维度进行分片的轴都会隐式复制（或显式复制）。
我们将从一个简单的示例开始，并在介绍其他功能时对其进行扩展。
@mesh_xy = <["x"=2, "y"=4, "z"=2]>
// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>
不变量
- 维度分片数量必须与张量的秩一致。
- 所有轴名称都必须存在于所引用的网格中。
- 轴或子轴只能在分片表示法中出现一次（每个轴都对某个维度进行分片，或者显式复制）。
开放/封闭维度
张量的每个维度都可以是开放的，也可以是封闭的。
打开
开放维度可供传播，以便沿其他轴进一步分片，即指定的维度分片不一定是该维度的最终分片。这类似于
jax.sharding.PartitionSpec.UNCONSTRAINED- GSPMD 的
unspecified_dims
如果维度处于“打开”状态，我们会在该维度已分片的轴后面添加 ?（请参阅下面的示例）。
已关闭
已关闭的维度是指无法通过传播来添加进一步的分片的维度，即指定的维度分片是该维度的最终分片，并且无法更改。一个常见的用例是，GSPMD 通常不会修改模块的输入/输出参数，或者在 jax.jit 中，用户指定的 in_shardings 是静态的，无法更改。
我们可以扩展上面的示例，使其包含一个“打开”维度和一个“关闭”维度。
@mesh_xy = <["x"=2, "y"=4, "z"=2]>
// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>
显式复制的轴
张量复制到的明确轴集。虽然可以确定未沿某个轴分片的张量会在该轴上隐式复制（例如目前的 jax.sharding.PartitionSpec），但明确指定分片可确保传播无法使用这些轴进一步对具有这些轴的开放维度进行分片。借助隐式复制，张量可以进一步分区。但是，使用显式复制时，任何内容都无法沿该轴对张量进行分区。
复制轴的排序不会影响张量数据的存储方式。但仅出于一致性考虑，轴将按其在顶级网格中指定的顺序存储。例如，如果网格是：
@mesh_xy = <["c"=2, "a"=2, "b"=2]>
我们希望显式复制轴 "a" 和 "c"，顺序应为：
replicated={"c", "a"}
我们可以扩展上述示例，以实现显式复制的轴。
@mesh_xyz = <["x"=2, "y"=4, "z"=2]>
// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would // be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>
轴拆分和子轴
通过将设备的一维数组重塑为 n 维数组，创建 n 轴的逻辑网格，其中每个维度都形成一个具有用户定义名称的轴。
在编译器中，也可以执行相同的过程，通过将网格从 [...,k,...] 重新塑造成 [...,k1,...,km,...]，将大小为 k 的轴进一步拆分为 m 个子轴。
设计初衷
为了了解拆分轴背后的动机，我们将通过以下示例进行说明：
@mesh_x = <["x"=4]>
%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>
我们希望以避免通信的方式对重塑结果进行分片（即将数据保留在原位）。由于 "x" 的大小大于结果的第 1 个维度，因此我们需要将该轴拆分为两个大小为 2 的子轴 "x.0" 和 "x.1"，并在 "x.0" 上对第 1 个维度进行分片，在 "x.1" 上对第 2 个维度进行分片。
函数输入/输出分片
在传播期间，主函数的输入或输出可能会沿子轴分片。这对于某些框架来说可能是一个问题，因为我们无法表达此类分片以交还给用户（例如，在 JAX 中，我们无法使用 jax.sharding.NamedSharding 表达子轴）。
我们可以通过以下几种方式处理此类支持请求：
- 允许并以其他格式（例如 JAX 中的
jax.sharding.PositionalSharding而非jax.sharding.NamedSharding）返回分片。 - 禁止使用会对输入/输出进行分片的所有收集子轴。
目前，我们允许在传播流水线中的输入/输出上使用子轴。 如果您想知道如何停用此功能，请告诉我们。
表示法
就像我们可以通过名称引用网格的特定全轴一样，我们也可以通过大小以及左侧（对其而言是主要轴）所有子轴（具有相同轴名称）大小的乘积来引用特定子轴。
如需从大小为 n 的完整轴 "x" 中提取大小为 k 的特定子轴，我们可以有效地将大小为 n 的网格重新塑造成 [m, k, n/(m*k)]，并将第 2 个维度用作子轴。因此，子轴可以由两个数字 m 和 k 指定，我们使用以下简洁的表示法来表示子轴："x":(m)k。
m>=1是此子轴的预设尺寸（m应为n的除数）。预设尺寸是此子轴左侧（位于其上方）的所有子轴尺寸的乘积（如果等于 1，则表示没有子轴；如果大于 1，则表示对应于一个或多个子轴）。k>1是此子轴的实际大小（k应为n的除数）。n/(m*k)是后尺寸。它是此子轴右侧（次于此子轴）的所有子轴大小的乘积（如果等于 1，则表示没有子轴；如果大于 1，则表示对应于一个或多个子轴）。
不过，使用特定子轴 "x":(m)k 时，其他子轴的数量没有影响，并且如果任何其他子轴未对维度进行分片或已被显式复制，则无需在张量分片中引用该子轴。
回到“动机”部分中的示例，我们可以按如下方式对结果进行分片：
@mesh_x = <["x"=4]>
%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
: (tensor<8xf32>) -> tensor<2x4xf32>
下面是另一个分屏轴示例，其中仅使用了部分子轴。
@mesh_xyz = <["x"=2, "y"=8, "z"=2]>
// Axis "y" is effectively split into 3 sub-axes denoted as
// "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>
同样，以下两个分片在语义上是等效的。我们可以将 mesh_xy 视为 mesh_full 的分块。
@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>
sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>
显式复制的子轴
除了用于分片维度之外，子轴还可以标记为显式复制。我们允许在表示法中这样做，因为子轴的行为与完整轴完全相同，即当您沿轴 "x" 的子轴分片维度时，"x" 的其他子轴会被隐式复制，因此可以显式复制，以指明子轴必须保持复制状态，不能用于分片维度。
例如：
@mesh_xyz = <["x"=2, "y"=8, "z"=2]>
// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>
同一完整轴的复制子轴应按其预先大小从小到大排序，例如：
replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}
不变量
张量分片中引用的子轴不得重叠，例如
"x":(1)4和"x":(2)4重叠。张量分片中引用的子轴必须尽可能大，即如果维度分片中有两个相邻的子轴 A 和 B，或者子轴 A 和 B 被显式复制，则它们不得是连续的，例如
"x":(1)2和"x":(2)4，因为它们可以替换为单个"x":(1)8。
多个逻辑网格
一个逻辑网格是设备的多维视图。我们可能需要多个设备视图来表示分片，尤其是对于任意设备分配。
例如，jax.sharding.PositionalSharding 没有一个通用的逻辑网格。GSPMD 目前支持使用 HloSharding 实现此功能，其中表示法可以是设备和尺寸维度的有序列表，但无法使用上述轴拆分来表示。
我们通过在程序的顶层定义多个逻辑网格来克服此限制并处理现有极端情况。每个网格可以有不同数量的轴，具有不同的名称，并且可以为同一组设备进行自己的任意分配，即每个网格都引用同一组设备（通过其唯一的逻辑 ID），但顺序是任意的，类似于 GSPMD 表示法。
每个分片表示法都与特定的逻辑网格相关联，因此它只会引用该网格中的轴。
分配给一个逻辑网格的张量可以被分配给其他网格的运算使用，只需简单地重新分片张量以匹配目标网格即可。在 GSPMD 中，通常会执行此操作来解决冲突的网格。
下面提供了两个示例：
用户可以指定多个具有不同命名轴（例如通过 jax.sharding.NamedSharding）的网格，这些网格具有相同的设备顺序。在此示例中，<@mesh_0, "b"> 与 <@mesh_1, "z">. 完全相同
@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
优先级
优先级是一种方法，可将某些分区+传播决策的优先级设为高于其他决策，并允许对程序进行增量分区。
优先级是附加到分片表示法的一些或所有维度的值（复制轴没有优先级）。
例如：
@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>
// |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>
优先级可让用户更精细地控制传播，例如先批量并行处理，然后是 Megatron，最后是 ZeRO 分片。这样可以对分区内容做出强有力的保证，并通过采用更精细的分片策略（可以查看仅使用 Megatron 后程序的显示效果），实现更好的调试能力。
我们允许为每个维度分片附加优先级（默认为 0），这表示优先级为 <i 的所有分片都将在优先级为 i 的分片之前传播到整个程序。
即使分片具有优先级较低的未关闭维度（例如{"z",?}p2，它不会在传播过程中被优先级更高的其他张量分片替换。不过，在所有更高优先级的分片都传播完毕后，此类未分片的维度可以进一步分片。
换句话说，优先级不是指哪个维度分片比另一个更重要，而是指不同的维度分片组应向整个程序传播的顺序，以及如何解决未加注解的中间张量上的冲突。
不变量
优先级从 0（最高优先级）开始递增（为了让用户能够轻松添加和移除优先级，我们允许优先级之间存在空缺，例如，使用 p0 和 p2，但不使用 p1）。
空的闭合维度分片（即
{}），不应设置优先级，因为这不会产生任何影响。
维度分片可分割性
大小为 d 的维度可以沿大小乘积为 n 的轴进行分片，这样 d 就不能被 n 整除（这在实践中需要对维度进行填充）。
例如：
@mesh_xy = <["x"=8, "y"=2, "z"=3]>
sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>
语法
每个逻辑网格的定义如下：
@mesh_name = <mesh_axis_1,...,mesh_axis_n>
mesh_axis ::= axis_name=axis_size
axis_name ::= str
axis_size ::= int
对于秩为 r 的张量，分片表示法将具有以下结构：
sharding<@mesh_name, dim_shardings, replicated=replicated_axes}
mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}
dim_sharding ::=
{axis_1,...,axis_k} | // closed dimension
{axis_1,...,axis_k,?} // open dimension
axis ::=
axis_name | // a full axis
sub_axis // a sub axis
axis_name ::= str
sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int