Reprezentacja w ramach fragmentacji

Tło

Przedstawienie w postaci fragmentacji służy do określenia sposobu podziału tensora z uwzględnieniem zestawu dostępnych urządzeń.

Reprezentacja fragmentacji może być:

  • Ręcznie określone przez użytkownika jako ograniczenia podziału na podzbiory w przypadku danych wejściowych, danych wyjściowych lub pośrednich.
  • Przekształcone na podstawie operacji w procesie propagacji podziału.

Omówienie

Struktura podstawowa

Sieć logiczna to wielowymiarowa perspektywa urządzeń określona przez listę nazw i rozmiarów osi.

Proponowana reprezentacja dzielenia na części jest powiązana z określonym szkieletem logicznym za pomocą nazwy i może odwoływać się tylko do nazw osi z tego szkieletu. Dzielenie na części tensora określa, wzdłuż których osi (konkretnej siatki logicznej) poszczególne wymiary tensora są dzielone na części, w kolejności od głównej do podrzędnej. Tensor jest powielany wzdłuż wszystkich innych osi siatki.

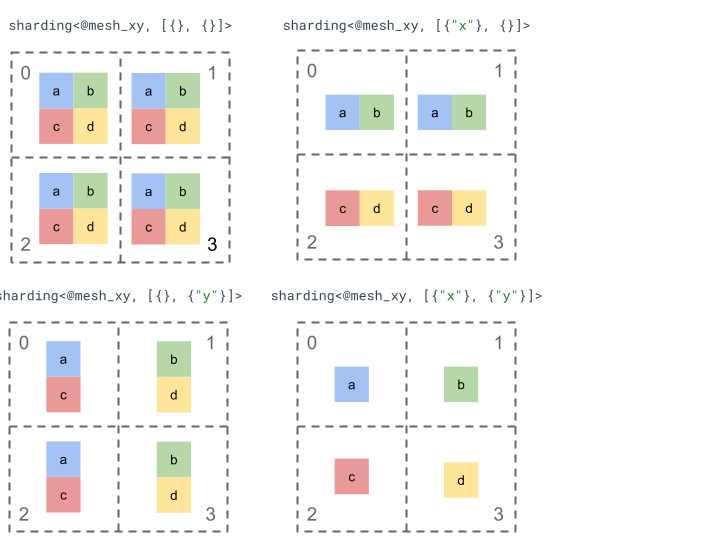
Przyjrzyjmy się reprezentowaniu dzielenia za pomocą prostego tensora 2-rzędowego i 4 urządzeń.

Najpierw zmieniamy kształt 4 urządzeń [0, 1, 2, 3] na tablicę dwuwymiarową [[0, 1], [2, 3]], aby utworzyć siatkę z 2 ośmi:

@mesh_xy = <["x"=2, "y"=2]>

Następnie możemy podzielić ten tensor rzędu 2 [[a, b], [c, d]] w następujący sposób:

Reprezentacja szarżowania tensora 2-rzędowego

Inne kluczowe komponenty

  • Otwarte/zamknięte wymiary – wymiary mogą być otwarte (można je dalej dzielić na dostępne osie) lub zamknięte (są stałe i nie można ich zmieniać).
  • Wyraźnie powielane osie – wszystkie osie, które nie są używane do dzielenia wymiaru, są powielane domyślnie, ale dzielenie może określać osie, które są powielane wyraźnie, i w konsekwencji nie mogą być używane do późniejszego dzielenia wymiaru.
  • Podział i podosi osi – (pełna) oś siatki może zostać podzielona na wiele podosi, które można stosować indywidualnie do podziału wymiaru lub powielać.
  • Wiele siatek logicznych – różne podziały mogą być powiązane z różnymi siatkami logicznymi, które mogą mieć różne osie lub nawet inną kolejność identyfikatorów logicznych urządzeń.
  • Priorytety – aby stopniowo dzielić program, możesz dołączać priorytety do podziału wymiarów, które określają, w jakiej kolejności ograniczenia podziału wymiarów będą propagowane w module.
  • Dzielenie wymiaru na części zamienne – wymiar można dzielić na części zamienne na osiach, których iloczyn rozmiarów nie dzieli się na rozmiar wymiaru.

Szczegółowy projekt

W tej sekcji omówimy szczegółowo podstawową strukturę i poszczególne kluczowe komponenty.

Struktura podstawowa

Podziały wymiarów podają, według których osi (lub podosi) tensor jest dzielony na mniejsze elementy, poczynając od głównej osi. Wszystkie inne osie, które nie dzielą wymiaru, są replikowane domyślnie (lub wyraźnie replikowane).

Zaczniemy od prostego przykładu, a potem opiszemy dodatkowe funkcje.

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>

Niezmienniki

  • Liczba podziałów wymiaru musi być zgodna z rangą tensora.
  • Wszystkie nazwy osi muszą występować w meshu, do którego się odwołujesz.
  • Osie lub pod-osie mogą występować tylko raz w reprezentacji dzielenia (każda z nich dzieli wymiar lub jest wyraźnie powielana).

Wymiary otwarte i zamknięte

Każdy wymiar tensora może być otwarty lub zamknięty.

Otwórz

Otwarty wymiar jest dostępny do propagowania, aby można było go podzielić na dodatkowe osie, co oznacza, że podział określonego wymiaru nie musi być ostatecznym podziałem tego wymiaru. Jest to podobne (ale nie identyczne) z

Jeśli wymiar jest otwarty, dodajemy ? po osiach, na których wymiar jest już podzielony na fragmenty (patrz przykład poniżej).

Zamknięte

Zamknięty wymiar to taki, którego nie można propagować, aby dodać do niego dalszego podziału, czyli podział określonego wymiaru jest ostatnim podziałem tego wymiaru i nie można go zmienić. Typowym zastosowaniem jest to, że GSPMD zazwyczaj nie modyfikuje argumentów wejściowych/wyjściowych modułu ani nie zmienia parametrów jax.jit określonych przez użytkownika, które są statyczne.in_shardings

Możemy rozszerzyć przykład z powyżej, aby zawierał wymiar otwarty i zamknięty.

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>

Wyraźnie powielane osie

Wyraźny zbiór osi, na których powiela się tensor. Można stwierdzić, że tensor, który nie jest dzielony na segmenty wzdłuż osi, jest na niej domyślnie powielany (jak w przypadku tensorajax.sharding.PartitionSpec dzisiaj). Dzięki temu propagacja nie może używać tych osi do dalszego dzielenia na segmenty wymiaru otwartego za pomocą tych osi. Dzięki replikacji domyślnej tensor może zostać podzielony na kolejne partycje. Jednak w przypadku jawnej replikacji nic nie może podzielić tensora wzdłuż tej osi.

Kolejność powielonych osi nie ma wpływu na sposób przechowywania danych tensora. Jednak ze względu na spójność osie będą przechowywane w kolejności, w jakiej zostały określone w siatce najwyższego poziomu. Jeśli na przykład siatka jest:

@mesh_xy = <["c"=2, "a"=2, "b"=2]>

Chcemy, aby osie "a" i "c" były wyraźnie powielane, więc kolejność powinna być taka:

replicated={"c", "a"}

Możemy rozszerzyć nasz przykład z powyżej, aby uzyskać wyraźnie powieloną oś.

@mesh_xyz = <["x"=2, "y"=4, "z"=2]>

// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would // be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>

Dzielenie osi i osi podrzędnych

Logiczne siatki osi n są tworzone przez zmianę kształtu jednowymiarowej tablicy urządzeń w tablicę n-wymiarową, gdzie każda z osi ma nazwę zdefiniowaną przez użytkownika.

Ten sam proces można wykonać w kompilatorze, aby podzielić oś o rozmiarze k na m podosi, zmieniając kształt siatki z [...,k,...] na [...,k1,...,km,...].

Motywacja

Aby zrozumieć, dlaczego osi można dzielić, rozważmy ten przykład:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>

Chcemy podzielić na segmenty wynik przekształcania w sposób, który pozwoli uniknąć komunikacji (czyli utrzymać dane w ich obecnym miejscu). Ponieważ rozmiar "x" jest większy niż rozmiar 1. wymiaru wyniku, musimy podzielić oś na 2 podosi "x.0" i "x.1" o rozmiarze 2 każda oraz podzielić 1. wymiar na "x.0" i 2. wymiar na "x.1".

Dzielenie na fragmenty wejść i wyjść funkcji

Podczas propagacji dane wejściowe lub wyjściowe funkcji głównej mogą zostać podzielone na podosi. Może to być problemem w przypadku niektórych frameworków, w których nie możemy wyrazić takich podziałów, aby przekazać je użytkownikowi (np. w JAX nie możemy wyrazić podosi za pomocą jax.sharding.NamedSharding).

W takich przypadkach mamy kilka opcji:

  • Dopuszczanie i zwracanie podziału na fragmenty w innym formacie (np. jax.sharding.PositionalSharding zamiast jax.sharding.NamedSharding w JAX).
  • Nie zezwalaj na podosi, które dzielą dane wejściowe/wyjściowe.

Obecnie zezwalamy na podosi w przypadku wejść i wyjść w systemie propagacji. Daj nam znać, jeśli chcesz, abyśmy Ci to umożliwili.

Reprezentacja

Podobnie jak możemy odwoływać się do określonych pełnych osi z siatki po ich nazwie, możemy odwoływać się do określonych podosi po ich rozmiarze i iloczynie wszystkich rozmiarów podosi (o tej samej nazwie) po lewej stronie (które są dla nich głównymi) .

Aby wyodrębnić konkretną podrzędną o rozmiarze k z pełnej osi "x" o rozmiarze n, zmieniamy rozmiar n (w sieci) na [m, k, n/(m*k)] i używamy 2. wymiaru jako podrzędnej. Oś podrzędną można więc określić za pomocą 2 liczb: m i k. Aby oznaczyć osie podrzędne, używamy tej zwięzłej notacji: "x":(m)k.

  • m>=1 to wstępny rozmiar tej podosi (m powinien być dzielnikiem wartości n). Wstępny rozmiar to iloczyn wszystkich rozmiarów podosi po lewej stronie tej podosi (jeśli jest równy 1, oznacza, że nie ma żadnych, jeśli jest większy niż 1, odpowiada jednej lub wielu podosiom).

  • k>1 to rzeczywisty rozmiar tej podosi (k powinien być dzielnikiem wartości n).

  • n/(m*k) to rozmiar posta. Jest to iloczyn wszystkich rozmiarów podrzędnych po prawej stronie tej podrzędnej (czyli tych, które są mniejsze od niej) (jeśli jest równa 1, oznacza, że nie ma żadnych, jeśli jest większa od 1, odpowiada jednej lub wielu podrzędnym).

Jednak liczba innych podosi nie ma znaczenia, gdy używasz określonej podosi "x":(m)k, a w przypadku innych osi nie musisz ich uwzględniać w podziale tensora, jeśli nie dzielą one wymiaru ani nie są wyraźnie powielane.

Wracając do przykładu w sekcji Motywacja, możemy podzielić wynik w ten sposób:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
    : (tensor<8xf32>) -> tensor<2x4xf32>

Oto kolejny przykład podzielonej osi, w której używane są tylko niektóre z jej podosi.

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Axis "y" is effectively split into 3 sub-axes denoted as
//   "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>

Podobnie 2 poniżej podane przykłady są semantycznie równoważne. mesh_xy można traktować jako rozszczepienie mesh_full.

@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>

sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>

Wyraźnie powielone podosi

Oprócz tego, że podosi używa się do wymiaru fragmentów, można je też oznaczyć jako wyraźnie powielone. Dopuszczamy to w reprezentacji, ponieważ podosi zachowują się tak samo jak pełne osie. Oznacza to, że gdy dzielisz wymiar wzdłuż podosi osi "x", inne podosi "x" są automatycznie powielane, a dlatego można je powielać w sposób jawny, aby wskazać, że pod-oś musi pozostać powielona i nie może być używana do dzielenia wymiaru.

Na przykład:

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>

Powtórzone podosi tej samej pełnej osi powinny być uporządkowane w rosnącej kolejności według ich rozmiaru wstępnego, na przykład:

replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}

Niezmienniki

  • Osie podrzędne, do których odwołuje się podział tensora, nie mogą się pokrywać, np. "x":(1)4 i "x":(2)4 nie mogą się pokrywać.

  • Podosi, do których odwołuje się podział tensora, muszą być jak największe, tzn. jeśli podział wymiaru ma 2 sąsiednie podosi A i B lub podosi A i B są wyraźnie powielane, nie mogą być one kolejne, np. "x":(1)2 i "x":(2)4, ponieważ można je zastąpić pojedynczą wartością "x":(1)8.

Wiele siatek logicznych

Jedna sieć logiczna to wielowymiarowy widok urządzeń. Możemy potrzebować wielu widoków urządzeń, aby reprezentować nasze partycjonowanie, zwłaszcza w przypadku dowolnych przypisań urządzeń.

Na przykład wymiar jax.sharding.PositionalSharding nie ma jednej wspólnej siatki logicznej. GSPMD obsługuje obecnie sharding HLO, w którym reprezentacja może być uporządkowaną listą urządzeń i wymiarów, ale nie można jej przedstawić za pomocą dzielenia osi.

Aby pokonać to ograniczenie i rozwiązać istniejące problemy, zdefiniowaliśmy wiele siatek logicznych na najwyższym poziomie programu. Każda siatka może mieć inną liczbę osi o różnych nazwach, a także własne dowolne przypisanie do tego samego zestawu urządzeń, czyli każda siatka odnosi się do tego samego zestawu urządzeń (na podstawie ich unikalnych identyfikatorów logicznych), ale w dowolnej kolejności, podobnie jak w reprezentacji GSPMD.

Każda reprezentacja dzielenia jest powiązana z konkretną siatką logiczną, dlatego będzie odwoływać się tylko do osi z tej siatki.

Tensor przypisany do jednej siatki logicznej może być używany przez operację przypisaną do innej siatki, przez naiwne ponowne podzielenie tensora tak, aby pasował do siatki docelowej. W GSPMD jest to zwykle sposób na rozwiązanie konfliktu siatek.

Poniżej przedstawiamy 2 przykłady:

Użytkownicy mogą określić wiele siatek z różnymi nazwami osi (np. za pomocą jax.sharding.NamedSharding), które mają ten sam porządek urządzeń. W tym przykładzie <@mesh_0, "b"> jest identyczne z <@mesh_1, "z">.

@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}

Priorytety

Priorytet to sposób na nadawanie priorytetów niektórym decyzjom dotyczącym partycjonowania i propagowania, a także umożliwia partycjonowanie przyrostowe programu.

Priorytety to wartości przypisane do niektórych lub wszystkich wymiarów reprezentacji dzielenia (osi powielonych nie mają priorytetów).

Na przykład:

@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>

//                                    |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>

Priorytety zapewniają użytkownikom bardziej szczegółową kontrolę nad propagowaniem, np. najpierw równoległość pakietów, następnie megatron, a na końcu podział ZeRO. Pozwala to uzyskać silne gwarancje dotyczące tego, co jest dzielone, oraz ułatwia debugowanie dzięki bardziej szczegółowym strategiom dzielenia (można zobaczyć, jak wygląda program po zastosowaniu tylko megatronu).

Do każdego podziału wymiaru można przypisać priorytet (domyślnie 0), co oznacza, że wszystkie podziały o priorytecie <i zostaną rozpowszechnione na cały program przed podziałami o priorytecie i.

Nawet jeśli podział ma wymiar otwarty o niższym priorytecie, np. {"z",?}p2, nie zostanie zastąpiony przez inny podział tensora o wyższym priorytecie podczas propagacji. Taki otwarty wymiar można jednak podzielić na części po propagowaniu wszystkich podziałów o wyższym priorytecie.

Inaczej mówiąc, priorytety NIE określają, które podziały wymiarów są ważniejsze od innych – określają one kolejność, w jakiej odrębne grupy podziałów wymiarów powinny być propagowane do całego programu, oraz sposób rozwiązywania konfliktów w pośrednich nieanotowanych tensorach.

Niezmienniki

  • Priorytety zaczynają się od 0 (najwyższy priorytet) i rosną (aby umożliwić użytkownikom łatwe dodawanie i usuwanie priorytetów, zezwalamy na luki między priorytetami, np. używane są priorytety p0 i p2, ale nie p1).

  • pusty podział wymiaru zamkniętego (np. {}), nie powinien mieć priorytetu, ponieważ nie będzie to miało żadnego wpływu.

Dzielność podziału wymiarów

Wymiar o wielkości d może być dzielony na części wzdłuż osi, których iloczyn wynosi n, tak aby d nie był podzielny przez n (co w praktyce wymagałoby uzupełnienia wymiaru).

Na przykład:

@mesh_xy = <["x"=8, "y"=2, "z"=3]>

sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>

Gramatyka

Każda siatka logiczna jest zdefiniowana w ten sposób:

@mesh_name = <mesh_axis_1,...,mesh_axis_n>

mesh_axis ::= axis_name=axis_size

axis_name ::= str
axis_size ::= int

W przypadku tensora o rangę r reprezentacja dzielenia będzie mieć następującą strukturę:

sharding<@mesh_name, dim_shardings, replicated=replicated_axes}

mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}

dim_sharding ::=
  {axis_1,...,axis_k} |  // closed dimension
  {axis_1,...,axis_k,?}  // open dimension

axis ::=
  axis_name  |   // a full axis
  sub_axis             // a sub axis

axis_name ::= str

sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int