Fondo
El propósito de la representación de fragmentación es especificar cómo se fragmenta un tensor con respecto a un conjunto de dispositivos disponibles.
La representación de fragmentación puede ser una de las siguientes:
- El usuario las especifica manualmente como restricciones de fragmentación en entradas, salidas o elementos intermedios.
- Se transforma por operación en el proceso de propagación de fragmentación.
Descripción general
Estructura básica
Una malla lógica es una vista multifacética de los dispositivos, definida por una lista de nombres y tamaños de ejes.
La representación de fragmentación propuesta está vinculada a una malla lógica específica por su nombre y solo puede hacer referencia a los nombres de los ejes de esa malla. La fragmentación de un tensor especifica a lo largo de qué ejes (de una malla lógica específica) se fragmenta cada dimensión del tensor, ordenada de mayor a menor. El tensor se replica a lo largo de todos los demás ejes de la malla.
Exploremos la representación del fragmentación con un tensor de rango 2 simple y 4 dispositivos.
Primero, cambiamos la forma de los 4 dispositivos [0, 1, 2, 3] en un array 2D [[0, 1], [2,
3]] para crear una malla con 2 ejes:
@mesh_xy = <["x"=2, "y"=2]>
Luego, podemos dividir el siguiente tensor de rango 2 [[a, b], [c, d]] de la siguiente manera:
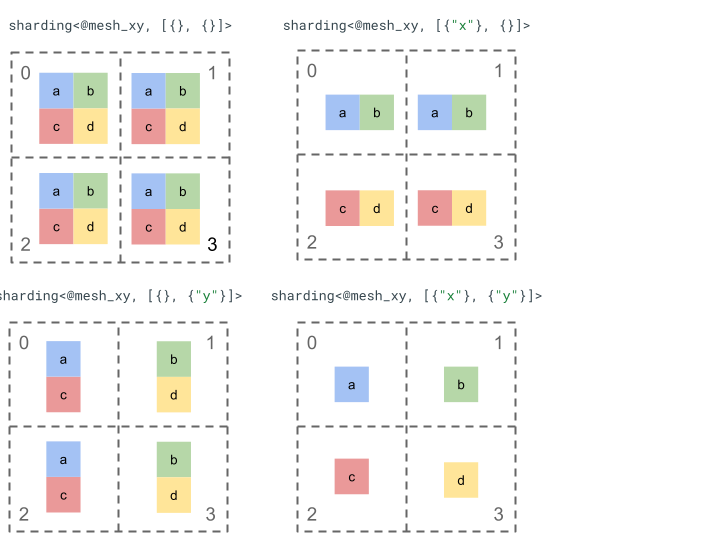
Otros componentes clave
- Dimensiones abiertas o cerradas: Las dimensiones pueden ser abiertas (se pueden dividir en más fragmentos en los ejes disponibles) o cerradas (son fijas y no se pueden cambiar).
- Ejes replicados de forma explícita: Todos los ejes que no se usan para particionar una dimensión se replican de forma implícita, pero el particionado puede especificar ejes que se replican de forma explícita y, por lo tanto, no se pueden usar para particionar una dimensión más adelante.
- División de ejes y subejes: Un eje de malla (completo) se puede dividir en varios subejes que se pueden usar de forma individual para dividir una dimensión o replicarse de forma explícita.
- Múltiples mallas lógicas: Se pueden vincular diferentes particiones a diferentes mallas lógicas, que pueden tener diferentes ejes o incluso un orden diferente de IDs de dispositivos lógicos.
- Prioridades: Para particionar un programa de forma incremental, las prioridades se pueden adjuntar a los fragmentos de dimensión, que determinan en qué orden se propagarán las restricciones de fragmentación por dimensión en todo el módulo.
- Divisibilidad del particionado de dimensiones: Una dimensión se puede particionar en ejes cuyo producto de tamaños no divide el tamaño de la dimensión.
Diseño detallado
En esta sección, expandimos la estructura básica y cada componente clave.
Estructura básica
Los particionamientos de dimensión nos indican, para cada dimensión del tensor, a lo largo de qué ejes (o subejes) se particiona de mayor a menor. Todos los demás ejes que no fragmentan una dimensión se replican de forma implícita (o explícita).
Comenzaremos con un ejemplo simple y lo ampliaremos a medida que describamos funciones adicionales.
@mesh_xy = <["x"=2, "y"=4, "z"=2]>
// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>
Invarianzas
- La cantidad de particiones de dimensión debe coincidir con el rango del tensor.
- Todos los nombres de los ejes deben existir en la malla a la que se hace referencia.
- Los ejes o subejes solo pueden aparecer una vez en la representación de fragmentación (cada uno fragmenta una dimensión o se reproduce de forma explícita).
Dimensiones abiertas o cerradas
Cada dimensión de un tensor puede ser abierta o cerrada.
Abrir
Una dimensión abierta está disponible para la propagación para particionarla aún más en ejes adicionales, es decir, el particionado de dimensión especificado no tiene que ser el particionado final de esa dimensión. Esto es similar (pero no exactamente igual) a unspecified_dims de GSMPD.
Si una dimensión está abierta, agregamos un ? después de los ejes en los que la dimensión ya está fragmentada (consulta el ejemplo a continuación).
Cerrado
Una dimensión cerrada es aquella que no está disponible para la propagación para agregar más fragmentación, es decir, la fragmentación de dimensión especificada es la fragmentación final de esa dimensión y no se puede cambiar. Un caso de uso común de esto es cómo GSPMD (por lo general) no modifica los argumentos de entrada y salida de un módulo, o cómo, con jax.jit, el in_shardings especificado por el usuario es estático (no puede cambiar).
Podemos extender el ejemplo anterior para tener una dimensión abierta y una cerrada.
@mesh_xy = <["x"=2, "y"=4, "z"=2]>
// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>
Ejes replicados de forma explícita
Es un conjunto explícito de ejes en los que se replica un tensor. Si bien se puede determinar que un tensor no particionado en un eje se replica de forma implícita en él (como jax.sharding.PartitionSpec en la actualidad), tenerlo explícito garantiza que la propagación no pueda usar estos ejes para particionar aún más una dimensión abierta con esos ejes. Con la replicación implícita, un tensor puede particionarse aún más. Sin embargo, con la replicación explícita, nada puede
particionar el tensor a lo largo de ese eje.
El orden de los ejes replicados no tiene efecto en la forma en que se almacenan los datos de un tensor. Sin embargo, solo por coherencia, los ejes se almacenarán en el orden en que se especifiquen en la malla de nivel superior. Por ejemplo, si la malla es:
@mesh_xy = <["c"=2, "a"=2, "b"=2]>
Y queremos que los ejes "a" y "c" se repliquen de forma explícita, el orden debe ser el siguiente:
replicated={"c", "a"}
Podemos extender nuestro ejemplo anterior para tener un eje replicado de forma explícita.
@mesh_xyz = <["x"=2, "y"=4, "z"=2]>
// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>
División de ejes y ejes secundarios
Para crear una malla lógica de ejes n, se modifica la forma de un array de dispositivos de 1 dimensión en un array de n dimensiones, en el que cada dimensión forma un eje con un nombre definido por el usuario.
Se puede realizar el mismo proceso en el compilador para dividir un eje de tamaño k en subejes m. Para ello, se debe cambiar la forma de la malla de [...,k,...] a [...,k1,...,km,...].
Motivación
Para comprender la motivación detrás de la división de ejes, veremos el siguiente ejemplo:
@mesh_x = <["x"=4]>
%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>
Queremos particionar el resultado de la reasignación de forma tal que evite la comunicación (es decir, mantener los datos donde están). Dado que el tamaño de "x" es mayor que la 1ª dimensión del resultado, debemos dividir el eje en dos subejes "x.0" y "x.1" de tamaño 2 cada uno, y dividir la 1ª dimensión en "x.0" y la 2ª dimensión en "x.1".
División de entradas y salidas de funciones
Es posible que, durante la propagación, una entrada o salida de la función principal
se fragmente a lo largo de un eje secundario. Esto puede ser un problema para algunos frameworks, en los que no podemos expresar esos particionados para devolverlos al usuario (p.ej., en JAX, no podemos expresar subejes con jax.sharding.NamedSharding).
Tenemos algunas opciones para abordar estos casos:
- Permite y muestra el fragmentación en un formato diferente (p.ej.,
jax.sharding.PositionalShardingen lugar dejax.sharding.NamedShardingen JAX). - No se permiten subejes de recopilación total que fragmenten la entrada o la salida.
Actualmente, permitimos subejes en las entradas o salidas de la canalización de propagación. Avísanos si quieres inhabilitar esta función.
Representación
De la misma manera que podemos hacer referencia a ejes completos específicos de la malla por su nombre, podemos hacer referencia a subejes específicos por su tamaño y el producto de todos los subejes (del mismo nombre de eje) a su izquierda (que son importantes para ellos).
Para extraer un subeje específico de tamaño k de un eje completo "x" de tamaño n, cambiamos de forma efectiva el tamaño n (en la malla) a [m, k, n/(m*k)] y usamos la 2ª dimensión como el subeje. Por lo tanto, un subeje se puede especificar con dos números, m y k, y usamos la siguiente notación concisa para denotar subejes: "x":(m)k.
m>=1es el tamaño previo de este eje secundario (mdebe ser un divisor den). El tamaño previo es el producto de todos los tamaños de eje secundario a la izquierda de este eje secundario (si es igual a 1, significa que no hay ninguno; si es mayor que 1, corresponde a un solo eje secundario o a varios).k>1es el tamaño real de este subeje (kdebe ser un divisor den).n/(m*k)es el tamaño posterior. Es el producto de todos los tamaños de subeje a la derecha de este subeje (si es igual a 1, significa que no hay ninguno; si es mayor que 1, corresponde a un solo subeje o a varios).
Sin embargo, la cantidad de otros subejes no hace diferencia cuando se usa un
subeje "x":(m)k específico, y no es necesario hacer referencia a ningún otro subeje
en la división de tensores si no divide una dimensión o se replica
de forma explícita.
Volviendo al ejemplo de la sección Motivación, podemos particionar el resultado de la siguiente manera:
@mesh_x = <["x"=4]>
%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
: (tensor<8xf32>) -> tensor<2x4xf32>
Este es otro ejemplo de un eje dividido en el que solo se usan algunos de sus subejes.
@mesh_xyz = <["x"=2, "y"=8, "z"=2]>
// Axis "y" is effectively split into 3 sub-axes denoted as
// "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>
Del mismo modo, los siguientes dos particionamientos son semánticamente equivalentes. Podemos pensar en mesh_xy como una división de mesh_full.
@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>
sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>
Ejes secundarios replicados de forma explícita
Además de los subejes que se usan para particionar la dimensión, también se pueden marcar
como replicados de forma explícita. Permitimos esto en la representación porque los subejes se comportan de la misma manera que los ejes completos, es decir, cuando se fragmenta una dimensión a lo largo de un subeje del eje "x", los otros subejes de "x" se replican de forma implícita y, por lo tanto, se pueden replicar de forma explícita para indicar que un subeje debe permanecer replicado y no se puede usar para fragmentar una dimensión.
Por ejemplo:
@mesh_xyz = <["x"=2, "y"=8, "z"=2]>
// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>
Los subejes replicados del mismo eje completo deben ordenarse en orden creciente según su tamaño previo, por ejemplo:
replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}
Invarianzas
Los subejes a los que se hace referencia en una fragmentación de tensores no deben superponerse, p.ej.,
"x":(1)4y"x":(2)4se superponen.Los subejes a los que se hace referencia en una fragmentación de tensores deben ser lo más grandes posible, es decir, si una fragmentación de dimensiones tiene dos subejes adyacentes A y B en orden, o si los subejes A y B se replican de forma explícita, no deben ser consecutivos, p. ej.,
"x":(1)2y"x":(2)4, ya que se pueden reemplazar por un solo"x":(1)8.
Múltiples mallas lógicas
Una malla lógica es una vista multidimensionada de los dispositivos. Es posible que necesitemos varias vistas de los dispositivos para representar nuestros particionados, especialmente para las asignaciones de dispositivos arbitrarias.
Por ejemplo, jax.sharding.PositionalSharding no tiene una malla lógica común.
Actualmente, GSPMD admite eso con HloSharding, en el que la representación puede ser una lista ordenada de dispositivos y tamaños de dimensión, pero esto no se puede representar con la división de ejes anterior.
Superamos esta limitación y manejamos los casos extremos existentes definiendo varios mallas lógicas en el nivel superior del programa. Cada malla puede tener una cantidad diferente de ejes con nombres diferentes, así como su propia asignación arbitraria para el mismo conjunto de dispositivos, es decir, cada malla se refiere al mismo conjunto de dispositivos (por su ID lógico único), pero con un orden arbitrario, similar a la representación de GSMPD.
Cada representación de fragmentación está vinculada a una malla lógica específica, por lo que solo hará referencia a los ejes de esa malla.
Una operación que se asigna a una malla lógica puede usar un tensor que se asigna a una malla diferente. Para ello, se vuelve a particionar el tensor de forma ingenua para que coincida con la malla de destino. En GSPMD, esto es lo que se suele hacer para resolver mallas en conflicto.
Los usuarios pueden especificar varias mallas con diferentes ejes nombrados (p.ej., a través de jax.sharding.NamedSharding) que tienen el mismo orden de dispositivos. En este ejemplo, <@mesh_0, "b"> es idéntico a <@mesh_1, "z">:
@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
Prioridades
La prioridad es una forma de priorizar ciertas decisiones de partición y propagación sobre otras, y permite la partición incremental de un programa.
Las prioridades son valores adjuntos a algunas o todas las dimensiones de una representación de fragmentación (los ejes replicados no tienen prioridades).
Por ejemplo:
@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>
// |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>
Las prioridades les brindan a los usuarios un control más detallado sobre la propagación, p.ej., primero el paralelismo por lotes, luego megatron y, por último, el fragmentación de ZeRO. Esto permite garantías sólidas sobre lo que se particiona y permite una mejor depuración, ya que tiene estrategias de fragmentación más detalladas (puedes ver cómo se ve el programa después de solo megatron de forma aislada).
Permitimos adjuntar una prioridad a cada división de dimensión (0 de forma predeterminada), lo que indica que todas las divisiones con prioridad <i se propagarán a todo el programa antes de las divisiones con prioridad i.
Incluso si un fragmento tiene una dimensión abierta con una prioridad más baja, p.ej., {"z",?}p2, no se anulará con otro fragmento de tensor con una prioridad más alta durante la propagación. Sin embargo, una dimensión abierta de este tipo se puede particionar aún más después de que se hayan propagado todos los particionamientos de prioridad más alta.
En otras palabras, las prioridades NOT se refieren a qué partición de dimensión es más importante que otra, sino al orden en el que los grupos distintos de particiones de dimensión deben propagarse a todo el programa y cómo se deben resolver los conflictos en los tensores intermedios sin anotaciones.
Invarianzas
Las prioridades comienzan en 0 (prioridad más alta) y aumentan (para permitir que los usuarios agreguen y quiten prioridades fácilmente, permitimos brechas entre las prioridades, p.ej., se usan p0 y p2, pero no p1).
Un fragmento de dimensión cerrada vacío (es decir,
{}), no debe tener una prioridad, ya que no tendrá ningún efecto.
Divisibilidad del particionado de dimensiones
Es posible que una dimensión de tamaño d se particione en ejes cuyo producto de tamaños sea n, de modo que d no sea divisible por n (lo que, en la práctica, requeriría que la dimensión se rebase).
Por ejemplo:
@mesh_xy = <["x"=8, "y"=2, "z"=3]>
sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>
Gramática
Cada malla lógica se define de la siguiente manera:
@mesh_name = <mesh_axis_1,...,mesh_axis_n>
mesh_axis ::= axis_name=axis_size
axis_name ::= str
axis_size ::= int
La representación del fragmentación tendrá la siguiente estructura para un tensor de rango r:
sharding<@mesh_name, dim_shardings, replicated=replicated_axes}
mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}
dim_sharding ::=
{axis_1,...,axis_k} | // closed dimension
{axis_1,...,axis_k,?} // open dimension
axis ::=
axis_name | // a full axis
sub_axis // a sub axis
axis_name ::= str
sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int
