การนําเสนอการแยกกลุ่ม

ข้อมูลเบื้องต้น

วัตถุประสงค์ของการแสดงการแยกเป็นกลุ่มคือเพื่อระบุวิธีแยกกลุ่มของเทนเซอร์ตามชุดอุปกรณ์ที่ใช้ได้

การนำเสนอการแยกข้อมูลอาจเป็นอย่างใดอย่างหนึ่งต่อไปนี้

• ผู้ใช้ระบุด้วยตนเองเป็นข้อจำกัดการแยกข้อมูลในอินพุต เอาต์พุต หรือข้อมูลกลาง
• เปลี่ยนรูปแบบตามการดำเนินการในกระบวนการกระจายข้อมูลการแยกส่วน

ภาพรวม

โครงสร้างพื้นฐาน

เมชเชิงตรรกะคือมุมมองอุปกรณ์หลายมิติที่กําหนดโดยรายการชื่อและขนาดแกน

การนำเสนอการแยกส่วนข้อมูลที่เสนอจะเชื่อมโยงกับเมชเชิงตรรกะหนึ่งๆ ตามชื่อ และสามารถอ้างอิงชื่อแกนจากเมชนั้นเท่านั้น การแยกกลุ่มของเทนเซอร์จะระบุตามแกน (ของเมชเชิงตรรกะหนึ่งๆ) ที่จะแยกกลุ่มมิติข้อมูลแต่ละรายการของเทนเซอร์ โดยเรียงลำดับจากหลักไปรอง ระบบจะทําซ้ำเทนเซอร์ตามแกนอื่นๆ ทั้งหมดของเมช

มาสำรวจการนำเสนอการแยกส่วนด้วยเทนเซอร์อันดับ 2 ธรรมดาและอุปกรณ์ 4 เครื่อง

ก่อนอื่น เราจะเปลี่ยนรูปร่างของอุปกรณ์ 4 เครื่อง [0, 1, 2, 3] เป็นอาร์เรย์ 2 มิติ [[0, 1], [2, 3]] เพื่อสร้างเมชที่มี 2 แกนดังนี้

@mesh_xy = <["x"=2, "y"=2]>

จากนั้นเราก็สามารถแบ่งกลุ่มเทนเซอร์อันดับ 2 [[a, b], [c, d]] ดังต่อไปนี้

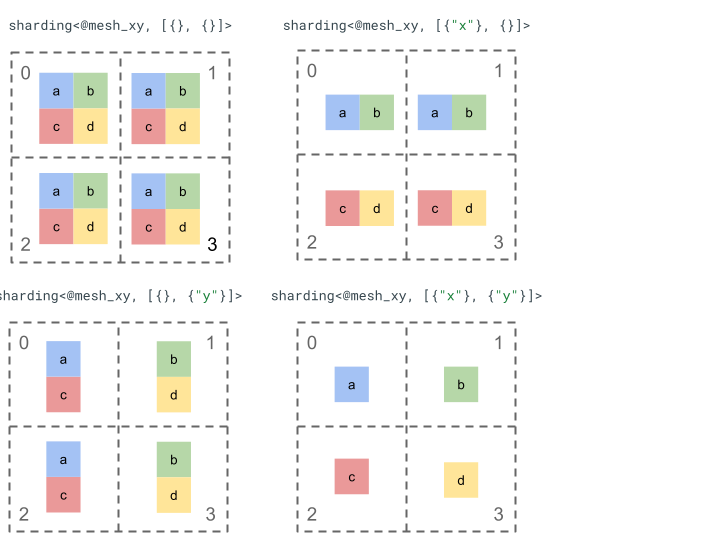
องค์ประกอบหลักอื่นๆ

• มิติข้อมูลแบบเปิด/ปิด - มิติข้อมูลอาจเป็นแบบเปิด ซึ่งจะแบ่งกลุ่มเพิ่มเติมได้ในแกนที่ใช้ได้ หรือแบบปิด ซึ่งจะคงที่และเปลี่ยนแปลงไม่ได้
• แกนที่ทำซ้ำโดยชัดแจ้ง - ระบบจะทําซ้ำแกนทั้งหมดที่ไม่ได้ใช้สําหรับการแยกกลุ่มมิติข้อมูลโดยนัย แต่การแยกกลุ่มสามารถระบุแกนที่ทำซ้ำโดยชัดแจ้ง ดังนั้นจึงใช้แยกกลุ่มมิติข้อมูลในภายหลังไม่ได้
• การแยกแกนและแกนย่อย - แกนเมช (แบบเต็ม) สามารถแยกออกเป็นแกนย่อยหลายแกนซึ่งสามารถใช้แยกมิติข้อมูลหรือทำซ้ำได้อย่างชัดเจน
• เมชเชิงตรรกะหลายรายการ - คุณสามารถเชื่อมโยงการแยกส่วนที่แตกต่างกันกับเมชเชิงตรรกะที่แตกต่างกันได้ ซึ่งอาจมีแกนที่แตกต่างกันหรือแม้แต่ลําดับรหัสอุปกรณ์เชิงตรรกะที่แตกต่างกัน
• ลําดับความสําคัญ - หากต้องการแบ่งพาร์ติชันโปรแกรมทีละส่วน คุณสามารถแนบลําดับความสําคัญกับการแยกกลุ่มมิติข้อมูล ซึ่งจะกําหนดลําดับการเผยแพร่ข้อจํากัดการแยกกลุ่มต่อมิติข้อมูลทั่วทั้งโมดูล
• การหารที่เป็นไปได้ของการแยกกลุ่มมิติข้อมูล - ระบบจะแยกกลุ่มมิติข้อมูลตามแกนซึ่งผลคูณของขนาดไม่ได้หารขนาดมิติข้อมูล

การออกแบบในรายละเอียด

เราจะขยายโครงสร้างพื้นฐานและองค์ประกอบหลักแต่ละอย่างในส่วนนี้

โครงสร้างพื้นฐาน

การแยกมิติข้อมูลจะบอกเราสำหรับมิติข้อมูลแต่ละมิติของเทมพอร์ ซึ่งตามแกน (หรือแกนย่อย) ที่มีการแยกจากแกนหลักเป็นแกนย่อย ส่วนแกนอื่นๆ ทั้งหมดที่ไม่ได้แบ่งมิติข้อมูลจะได้รับการทําซ้ำโดยนัย (หรือทําซ้ำโดยชัดแจ้ง)

เราจะเริ่มต้นด้วยตัวอย่างง่ายๆ แล้วขยายตัวอย่างไปเรื่อยๆ ขณะที่อธิบายฟีเจอร์เพิ่มเติม

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>

อินตัวแปร

• จำนวนการแยกกลุ่มมิติข้อมูลต้องตรงกับลําดับชั้นของเทนเซอร์
• ชื่อแกนทั้งหมดต้องอยู่ในเมชที่อ้างอิง
• แกนหรือแกนย่อยจะปรากฏได้เพียงครั้งเดียวในการแสดงการแยกข้อมูล (แต่ละแกนจะแยกมิติข้อมูลหรือทำซ้ำอย่างชัดแจ้ง)

มิติข้อมูลแบบเปิด/ปิด

มิติข้อมูลแต่ละมิติของเทนเซอร์อาจเป็นแบบเปิดหรือแบบปิดก็ได้

เปิด

มิติข้อมูลที่เปิดอยู่พร้อมสําหรับการนำไปใช้งานเพื่อแบ่งตามแกนเพิ่มเติม กล่าวคือ การแยกมิติข้อมูลที่ระบุไม่จำเป็นต้องเป็นการแยกมิติข้อมูลครั้งสุดท้าย ซึ่งคล้ายกับ (แต่ไม่เหมือนกับ)

• jax.sharding.PartitionSpec.UNCONSTRAINED
• unspecified_dims ของ GSPMD

หากมิติข้อมูลเปิดอยู่ เราจะเพิ่ม ? ต่อจากแกนที่มีการแบ่งมิติข้อมูลอยู่แล้ว (ดูตัวอย่างด้านล่าง)

ปิด

มิติข้อมูลที่ปิดคือมิติข้อมูลที่ไม่สามารถนำไปใช้เพื่อเพิ่มการแยกส่วนได้ กล่าวคือ การแยกมิติข้อมูลที่ระบุคือการแยกมิติข้อมูลครั้งสุดท้ายของมิติข้อมูลนั้นและไม่สามารถเปลี่ยนแปลงได้ กรณีการใช้งานที่พบบ่อยของกรณีนี้คือวิธีที่ GSPMD (โดยปกติ) ไม่แก้ไขอาร์กิวเมนต์อินพุต/เอาต์พุตของโมดูล หรือวิธีที่ jax.jit ที่ผู้ใช้ระบุจะคงที่เมื่อใช้ jax.jit ซึ่งจะเปลี่ยนแปลงไม่ได้in_shardings

เราขยายตัวอย่างจากด้านบนให้มีมิติข้อมูลแบบเปิดและมิติข้อมูลแบบปิดได้

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>

แกนที่มีการจําลองอย่างชัดแจ้ง

ชุดแกนที่ชัดเจนซึ่งมีการทําซ้ำเทนเซอร์ แม้ว่าจะระบุได้ว่ามีการทําซ้ำเทนเซอร์ที่ไม่ได้มีการแบ่งกลุ่มตามแกนโดยนัย (เช่น jax.sharding.PartitionSpec ในปัจจุบัน) แต่การระบุให้ชัดเจนจะช่วยให้มั่นใจได้ว่าการนำไปใช้งานจะไม่ใช้แกนเหล่านี้เพื่อแบ่งกลุ่มมิติข้อมูลที่เปิดอยู่ด้วยแกนเหล่านั้นอีก เมื่อใช้การทําซ้ำโดยนัย คุณจะสามารถแบ่งพาร์ติชันเทนเซอร์เพิ่มเติมได้ แต่หากใช้การทําซ้ำอย่างชัดแจ้ง จะไม่มีสิ่งใดแบ่งพาร์ติชันเทนเซอร์ตามแกนนั้นได้

การจัดลําดับของแกนที่ทําซ้ำจะไม่มีผลต่อวิธีจัดเก็บข้อมูลของเทมพอร์ แต่ระบบจะจัดเก็บแกนตามลําดับที่ระบุไว้ในเมชระดับบนสุดเพื่อความสอดคล้องกันเท่านั้น เช่น หากตาข่ายมีลักษณะดังนี้

@mesh_xy = <["c"=2, "a"=2, "b"=2]>

และเราต้องการให้ทำซ้ำแกน "a" และ "c" อย่างชัดเจน โดยลำดับควรเป็นดังนี้

replicated={"c", "a"}

เราขยายตัวอย่างจากด้านบนให้มีแกน X ที่ซ้ำกันอย่างชัดเจนได้

@mesh_xyz = <["x"=2, "y"=4, "z"=2]>

// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would // be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>

การแยกแกนและแกนย่อย

ตาข่ายเชิงตรรกะของแกน n จะสร้างขึ้นโดยการเปลี่ยนรูปร่างอาร์เรย์ 1 มิติของอุปกรณ์เป็นอาร์เรย์ n มิติ โดยที่แต่ละมิติจะสร้างแกนที่มีชื่อที่ผู้ใช้กำหนด

คุณทำขั้นตอนเดียวกันนี้ในคอมไพเลอร์เพื่อแยกแกนขนาด k ออกเป็นแกนย่อย m ได้โดยการเปลี่ยนรูปร่างของเมชจาก [...,k,...] เป็น [...,k1,...,km,...]

แรงจูงใจ

มาดูตัวอย่างต่อไปนี้เพื่อทำความเข้าใจแรงจูงใจในการแยกแกน

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>

เราต้องการแบ่งกลุ่มผลลัพธ์ของการรีเชปในลักษณะที่จะหลีกเลี่ยงการสื่อสาร (เช่น เก็บข้อมูลไว้ที่เดิม) เนื่องจากขนาดของ "x" มากกว่ามิติข้อมูล 1 ของผลลัพธ์ เราจึงต้องแยกแกนออกเป็น 2 แกนย่อย "x.0" และ "x.1" ขนาดละ 2 แกน และแยกมิติข้อมูล 1 ไว้ใน "x.0" และมิติข้อมูล 2 ไว้ใน "x.1"

การแยกส่วนอินพุต/เอาต์พุตของฟังก์ชัน

ในระหว่างการนำไปใช้งาน อินพุตหรือเอาต์พุตของฟังก์ชันหลักอาจมีการแบ่งตามแกนย่อย ซึ่งอาจทำให้เกิดปัญหากับเฟรมเวิร์กบางรายการที่เราไม่สามารถแสดงการแยกกลุ่มดังกล่าวเพื่อแสดงต่อผู้ใช้ (เช่น ใน JAX เราไม่สามารถแสดงแกนย่อยด้วย jax.sharding.NamedSharding)

เรามีตัวเลือกในการดำเนินการกับกรณีดังกล่าว ดังนี้

• อนุญาตและแสดงผลการจัดสรรในรูปแบบอื่น (เช่น jax.sharding.PositionalSharding แทน jax.sharding.NamedSharding ใน JAX)
• ไม่อนุญาตและแกนย่อยการรวบรวมทั้งหมดที่แบ่งกลุ่มอินพุต/เอาต์พุต

ปัจจุบันเราอนุญาตให้ใช้แกนย่อยในอินพุต/เอาต์พุตในไปป์ไลน์การนำไปใช้งาน โปรดแจ้งให้เราทราบหากต้องการวิธีปิดใช้ฟีเจอร์นี้

การแสดง

ในทำนองเดียวกับที่เราอ้างอิงแกนหลักที่เฉพาะเจาะจงจากตาข่ายตามชื่อ เรายังอ้างอิงแกนย่อยที่เฉพาะเจาะจงตามขนาดและผลคูณของขนาดแกนย่อยทั้งหมด (ที่มีชื่อแกนเดียวกัน) ทางด้านซ้าย (ซึ่งเป็นแกนหลักของแกนย่อยนั้น) ได้อีกด้วย

หากต้องการดึงข้อมูลแกนย่อยขนาด k ที่เฉพาะเจาะจงออกจากแกนเต็ม "x" ขนาด n เราจะเปลี่ยนรูปร่างขนาด n (ในตาข่าย) เป็น [m, k, n/(m*k)] อย่างมีประสิทธิภาพ และใช้มิติข้อมูลที่ 2 เป็นแกนย่อย ดังนั้น คุณจึงระบุแกนย่อยได้ด้วยตัวเลข 2 ตัว ได้แก่ m และ k และเราใช้สัญลักษณ์ต่อไปนี้เพื่อระบุแกนย่อย "x":(m)k

• m>=1 คือขนาดก่อนการแปลงของแกนย่อยนี้ (m ควรเป็นตัวหารของ n) ขนาดก่อนการแปลงคือผลคูณของขนาดแกนย่อยทั้งหมดทางด้านซ้ายของ (ซึ่งเป็นแกนหลักของ) แกนย่อยนี้ (หากเท่ากับ 1 แสดงว่าไม่มีค่า หากมากกว่า 1 แสดงว่าสอดคล้องกับแกนย่อยเดียวหรือหลายแกน)

• k>1 คือขนาดจริงของแกนย่อยนี้ (k ควรเป็นตัวหารของ n)

• n/(m*k) คือ post-size ค่านี้คือผลคูณของขนาดแกนย่อยทั้งหมดทางด้านขวาของ (ซึ่งอยู่ต่ำกว่า) แกนย่อยนี้ (หากเท่ากับ 1 หมายความว่าไม่มีค่า หากมากกว่า 1 แสดงว่าสอดคล้องกับแกนย่อยเดียวหรือหลายแกนย่อย)

อย่างไรก็ตาม จำนวนแกนย่อยอื่นๆ จะไม่ส่งผลต่อการใช้แกนย่อย "x":(m)k ที่เฉพาะเจาะจง และไม่จำเป็นต้องอ้างอิงแกนย่อยอื่นๆ ในการแยกกลุ่มเทนเซอร์หากไม่ได้แยกกลุ่มมิติข้อมูลหรือมีการทําซ้ำอย่างชัดแจ้ง

กลับไปที่ตัวอย่างในส่วนแรงจูงใจ เราจะแบ่งกลุ่มผลลัพธ์ได้ดังนี้

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
    : (tensor<8xf32>) -> tensor<2x4xf32>

นี่เป็นตัวอย่างอีกแบบหนึ่งของแกนแยกที่ใช้เฉพาะแกนย่อยบางแกน

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Axis "y" is effectively split into 3 sub-axes denoted as
//   "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>

ในทํานองเดียวกัน การแยกข้อมูล 2 รายการต่อไปนี้มีความหมายเทียบเท่ากัน เราอาจคิดว่า mesh_xy เป็นการแยก mesh_full

@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>

sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>

แกนย่อยที่จำลองโดยชัดแจ้ง

นอกจากจะใช้แกนย่อยเพื่อแบ่งมิติข้อมูลแล้ว คุณยังทําเครื่องหมายแกนย่อยว่ามีการทําสําเนาอย่างชัดเจนได้ด้วย เราอนุญาตการทําเช่นนี้ในการแสดงผลเนื่องจากแกนย่อยทํางานเหมือนกับแกนเต็ม เช่น เมื่อคุณแบ่งมิติข้อมูลตามแกนย่อยของแกนกลาง "x" ระบบจะทําสําเนาแกนย่อยอื่นๆ ของ "x" โดยนัย และจึงทําสําเนาได้อย่างชัดเจนเพื่อระบุว่าแกนย่อยต้องได้รับการทําสําเนาอยู่เสมอและไม่สามารถนําไปใช้แบ่งมิติข้อมูล

เช่น

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>

ควรจัดเรียงแกนย่อยที่ซ้ำกันของแกนเต็มเดียวกันตามลําดับจากน้อยไปมากตามขนาดก่อน เช่น

replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}

อินตัวแปร

• แกนย่อยที่อ้างอิงในการจัดสรร Tensor ต้องไม่ซ้อนทับกัน เช่น "x":(1)4 และ "x":(2)4 ซ้อนทับกัน

• แกนย่อยที่อ้างอิงในการจัดสรร Tensor ต้องมีขนาดใหญ่ที่สุดเท่าที่จะเป็นไปได้ เช่น หากการจัดสรรมิติข้อมูลมีแกนย่อย A และ B ที่อยู่ติดกัน 2 แกนตามลําดับ หรือมีการทําซ้ำแกนย่อย A และ B อย่างชัดเจน แกนย่อยเหล่านี้ต้องไม่อยู่ติดกัน เช่น "x":(1)2 และ "x":(2)4 เนื่องจากสามารถแทนที่ด้วย "x":(1)8 เพียงแกนเดียว

เมชตรรกะหลายรายการ

เมชเชิงตรรกะ 1 รายการคือมุมมองอุปกรณ์แบบหลายมิติ เราอาจต้องใช้มุมมองหลายมุมมองของอุปกรณ์เพื่อแสดงการแยกข้อมูล โดยเฉพาะสำหรับการกำหนดอุปกรณ์แบบกำหนดเอง

เช่น jax.sharding.PositionalSharding ไม่มีเมชตรรกะทั่วไปรายการเดียว ปัจจุบัน GSPMD รองรับการแสดงผลด้วย HloSharding ซึ่งการแสดงผลอาจเป็นรายการอุปกรณ์และขนาดมิติข้อมูลที่เรียงลําดับ แต่ไม่สามารถแสดงผลด้วยการแยกแกนด้านบน

เราเอาชนะข้อจำกัดนี้และจัดการกับกรณีที่เกิดขึ้นจริงที่มีอยู่ด้วยการกําหนดเมชเชิงตรรกะหลายรายการที่ระดับบนสุดของโปรแกรม แต่ละเมชอาจมีแกนจำนวนต่างกันโดยใช้ชื่อต่างกัน รวมถึงการกำหนดค่าที่ไม่เจาะจงสำหรับชุดอุปกรณ์เดียวกัน กล่าวคือ เมชแต่ละรายการอ้างอิงถึงชุดอุปกรณ์เดียวกัน (ตามรหัสตรรกะที่ไม่ซ้ำกัน) แต่มีลําดับที่ไม่เจาะจง ซึ่งคล้ายกับการแสดง GSPMD

การนําเสนอการแยกแต่ละรายการจะลิงก์กับเมชตรรกะหนึ่งๆ ดังนั้นจึงจะอ้างอิงเฉพาะแกนจากเมชนั้น

การดำเนินการที่มอบหมายให้กับเมชอื่นสามารถใช้เทนเซอร์ที่มอบหมายให้กับเมชเชิงตรรกะหนึ่งได้ โดยการแบ่งกลุ่มเทนเซอร์ใหม่ให้ตรงกับเมชปลายทาง ใน GSPMD การดำเนินการนี้มักทำเพื่อแก้ไขตาข่ายที่ขัดแย้งกัน

เรามีตัวอย่าง 2 ตัวอย่างด้านล่าง

ผู้ใช้สามารถระบุตาข่ายหลายรายการที่มีแกนตั้งชื่อต่างกัน (เช่น ทางผ่าน jax.sharding.NamedSharding) ซึ่งมีลําดับอุปกรณ์เดียวกัน ในตัวอย่างนี้ <@mesh_0, "b"> เหมือนกับ <@mesh_1, "z">.

@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}

ลำดับความสำคัญ

ลําดับความสําคัญเป็นวิธีจัดลําดับความสําคัญของการตัดสินใจการแบ่งพาร์ติชันและการนำไปใช้งานบางรายการเหนือกว่ารายการอื่นๆ และช่วยให้สามารถแบ่งพาร์ติชันโปรแกรมได้มากขึ้น

ลําดับความสําคัญคือค่าที่แนบมากับมิติข้อมูลบางรายการหรือทั้งหมดของการแสดงผลการแยกข้อมูล (แกนข้อมูลที่ทําซ้ำจะไม่มีลําดับความสําคัญ)

เช่น

@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>

//                                    |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>

ลําดับความสําคัญช่วยให้ผู้ใช้ควบคุมการนำไปใช้งานแบบละเอียดยิ่งขึ้น เช่น การทำงานแบบขนานแบบเป็นกลุ่มก่อน จากนั้นจึงใช้ Megatron และสุดท้ายใช้การแยกกลุ่ม ZeRO วิธีนี้ช่วยให้มั่นใจได้มากขึ้นเกี่ยวกับสิ่งที่มีการแบ่งพาร์ติชันและช่วยให้แก้ไขข้อบกพร่องได้ดียิ่งขึ้นด้วยกลยุทธ์การแยกส่วนแบบละเอียดยิ่งขึ้น (ดูลักษณะการทำงานของโปรแกรมหลังจากแยก Megatron ออกมาเพียงอย่างเดียวได้)

เราอนุญาตให้แนบลําดับความสําคัญกับการแยกข้อมูลมิติข้อมูลแต่ละรายการ (0 โดยค่าเริ่มต้น) ซึ่งบ่งชี้ว่าระบบจะเผยแพร่การแยกข้อมูลทั้งหมดที่มีลําดับความสําคัญ <i ไปยังทั้งโปรแกรมก่อนการแยกข้อมูลที่มีลําดับความสําคัญ i

แม้ว่าการแยกข้อมูลจะมีมิติข้อมูลที่เปิดอยู่ซึ่งมีลําดับความสําคัญต่ำกว่า เช่น {"z",?}p2 จะไม่ถูกลบล้างโดยการแยกกลุ่มเทนเซอร์อื่นที่มีลําดับความสําคัญสูงกว่าในระหว่างการนำไปใช้งาน อย่างไรก็ตาม มิติข้อมูลที่เปิดอยู่ดังกล่าวสามารถแบ่งกลุ่มเพิ่มเติมได้หลังจากที่มีการนำไปใช้กับข้อมูลการแยกกลุ่มที่มีลําดับความสําคัญสูงกว่าทั้งหมดแล้ว

กล่าวคือ ลําดับความสําคัญไม่ได้เกี่ยวกับว่าการแยกกลุ่มมิติข้อมูลใดสําคัญกว่ากัน แต่เป็นลําดับที่กลุ่มการแยกกลุ่มมิติข้อมูลที่ต่างกันควรเผยแพร่ไปยังทั้งโปรแกรม และวิธีแก้ไขข้อขัดแย้งในเทนเซอร์ระดับกลางที่ไม่มีคําอธิบายประกอบ

อินตัวแปร

• ลำดับความสำคัญเริ่มต้นที่ 0 (สำคัญที่สุด) และเพิ่มขึ้น (เราอนุญาตให้มีลำดับความสำคัญเว้นวรรคกันเพื่อให้ผู้ใช้เพิ่มและนำลำดับความสำคัญออกได้ง่ายๆ เช่น ใช้ p0 และ p2 แต่ไม่ได้ใช้ p1)

• การแยกกลุ่มมิติข้อมูลที่ปิดอยู่ซึ่งว่างเปล่า (เช่น {}) ไม่ควรมีลําดับความสําคัญเนื่องจากจะไม่มีผล

การหารที่หารได้ของการจัดสรรกลุ่มมิติข้อมูล

มิติข้อมูลขนาด d อาจมีการแบ่งตามแกนที่มีผลคูณของขนาดเป็น n เช่น d หารด้วย n ไม่ได้ (ซึ่งในทางปฏิบัติจะต้องมีการเติมค่าลงในมิติข้อมูล)

เช่น

@mesh_xy = <["x"=8, "y"=2, "z"=3]>

sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>

ไวยากรณ์

เมชเชิงตรรกะแต่ละรายการมีคำจำกัดความดังนี้

@mesh_name = <mesh_axis_1,...,mesh_axis_n>

mesh_axis ::= axis_name=axis_size

axis_name ::= str
axis_size ::= int

การนำเสนอการแยกข้อมูลจะมีโครงสร้างต่อไปนี้สำหรับเทนเซอร์ที่มีลําดับชั้น r

sharding<@mesh_name, dim_shardings, replicated=replicated_axes}

mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}

dim_sharding ::=
  {axis_1,...,axis_k} |  // closed dimension
  {axis_1,...,axis_k,?}  // open dimension

axis ::=
  axis_name  |   // a full axis
  sub_axis             // a sub axis

axis_name ::= str

sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int