Sharding প্রতিনিধিত্ব

পটভূমি

শর্ডিং উপস্থাপনার উদ্দেশ্য হল উপলব্ধ ডিভাইসগুলির একটি সেটের ক্ষেত্রে একটি টেনসর কীভাবে শার্ড করা হয় তা নির্দিষ্ট করা।

শেয়ারিং প্রতিনিধিত্ব হতে পারে:

• ইনপুট, আউটপুট বা ইন্টারমিডিয়েটগুলিতে শার্ডিং সীমাবদ্ধতা হিসাবে ব্যবহারকারীর দ্বারা ম্যানুয়ালি নির্দিষ্ট করা হয়েছে।
• শার্ডিং প্রচারের প্রক্রিয়ায় প্রতি অপারেশনে রূপান্তরিত।

ওভারভিউ

মৌলিক কাঠামো

একটি যৌক্তিক জাল হল ডিভাইসগুলির একটি বহুমাত্রিক দৃশ্য, যা অক্ষের নাম এবং আকারের একটি তালিকা দ্বারা সংজ্ঞায়িত করা হয়।

প্রস্তাবিত শার্ডিং উপস্থাপনাটি তার নামের দ্বারা একটি নির্দিষ্ট লজিক্যাল জালের সাথে আবদ্ধ, এবং শুধুমাত্র সেই জাল থেকে অক্ষের নাম উল্লেখ করতে পারে। একটি টেনসরের শার্ডিং নির্দিষ্ট করে কোন অক্ষ বরাবর (একটি নির্দিষ্ট লজিক্যাল মেশের), টেনসরের প্রতিটি ডাইমেনশন শার্ড করা হয়েছে, বড় থেকে ছোট পর্যন্ত অর্ডার করা হয়েছে। টেনসরটি জালের অন্যান্য সমস্ত অক্ষ বরাবর প্রতিলিপি করা হয়।

আসুন একটি সাধারণ র‌্যাঙ্ক 2 টেনসর এবং 4টি ডিভাইস সহ শার্ডিং উপস্থাপনাটি অন্বেষণ করি।

আমরা প্রথমে 4টি ডিভাইস [0, 1, 2, 3] একটি 2-ডি অ্যারেতে [[0, 1], [2, 3]] 2টি অক্ষ সহ একটি জাল তৈরি করি:

@mesh_xy = <["x"=2, "y"=2]>

তারপরে আমরা নিম্নোক্ত র্যাঙ্ক 2 টেনসর [[a, b], [c, d]] কে নিম্নরূপ শর্ড করতে পারি:

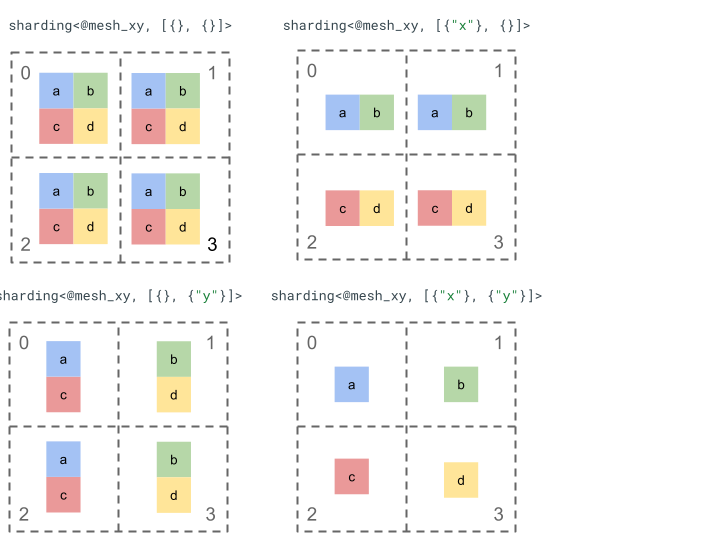
অন্যান্য মূল উপাদান

• খোলা/বন্ধ মাত্রা - মাত্রাগুলি হয় খোলা হতে পারে - উপলব্ধ অক্ষগুলিতে আরও শার্ড করা যেতে পারে; বা বন্ধ - স্থির এবং পরিবর্তন করা যাবে না।
• স্পষ্টভাবে প্রতিলিপি করা অক্ষ - সমস্ত অক্ষ যেগুলি একটি মাত্রাকে শার্ড করার জন্য ব্যবহার করা হয় না সেগুলি পরোক্ষভাবে প্রতিলিপি করা হয়, তবে শার্ডিং এমন অক্ষগুলিকে নির্দিষ্ট করতে পারে যেগুলি স্পষ্টভাবে প্রতিলিপি করা হয়েছে এবং তাই পরবর্তীতে একটি মাত্রা শার্ড করতে ব্যবহার করা যাবে না৷
• অক্ষ বিভাজন এবং উপ-অক্ষ - একটি (পূর্ণ) জাল অক্ষকে একাধিক উপ-অক্ষে বিভক্ত করা যেতে পারে যেগুলি পৃথকভাবে একটি মাত্রা শার্ড করতে বা স্পষ্টভাবে প্রতিলিপি করা যেতে পারে।
• একাধিক লজিক্যাল মেশ - বিভিন্ন শার্ডিংগুলি বিভিন্ন লজিক্যাল মেশের সাথে আবদ্ধ হতে পারে, যার বিভিন্ন অক্ষ বা এমনকি লজিক্যাল ডিভাইস আইডির ভিন্ন ক্রম থাকতে পারে।
• অগ্রাধিকার - একটি প্রোগ্রামকে ক্রমবর্ধমানভাবে বিভাজন করার জন্য, অগ্রাধিকারগুলি মাত্রা শার্ডিংয়ের সাথে সংযুক্ত করা যেতে পারে, যা নির্ধারণ করে যে প্রতি-মাত্রা শার্ডিং সীমাবদ্ধতাগুলি সমগ্র মডিউল জুড়ে প্রচার করা হবে।
• ডাইমেনশন শার্ডিং বিভাজ্যতা - একটি ডাইমেনশন অক্ষের উপর শার্ড করা যেতে পারে যার মাপের গুণফল ডাইমেনশন সাইজকে ভাগ করে না।

বিস্তারিত ডিজাইন

আমরা এই বিভাগে মৌলিক কাঠামো এবং প্রতিটি মূল উপাদান প্রসারিত করি।

মৌলিক কাঠামো

ডাইমেনশন শার্ডিংগুলি টেনসরের প্রতিটি ডাইমেনশনের জন্য আমাদের জানায়, কোন অক্ষগুলি (বা সাব-অক্ষগুলি ) বরাবর এটি বড় থেকে ছোট পর্যন্ত শার্ড করা হয়েছে। অন্য সমস্ত অক্ষ যেগুলি একটি মাত্রাকে শার্ড করে না সেগুলি পরোক্ষভাবে প্রতিলিপি করা হয় (বা স্পষ্টভাবে প্রতিলিপি করা হয় )।

আমরা একটি সাধারণ উদাহরণ দিয়ে শুরু করব এবং অতিরিক্ত বৈশিষ্ট্যগুলি বর্ণনা করার সাথে সাথে এটিকে প্রসারিত করব।

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>

অপরিবর্তনীয়

• ডাইমেনশন শার্ডিংয়ের সংখ্যা অবশ্যই টেনসরের র্যাঙ্কের সাথে মেলে।
• সমস্ত অক্ষের নাম অবশ্যই উল্লেখিত জালের মধ্যে থাকতে হবে।
• অক্ষ বা উপ-অক্ষগুলি শার্ডিং উপস্থাপনায় শুধুমাত্র একবার উপস্থিত হতে পারে (প্রত্যেকটি হয় একটি মাত্রাকে শার্ড করে বা স্পষ্টভাবে প্রতিলিপি করা হয়)।

খোলা/বন্ধ মাত্রা

একটি টেনসরের প্রতিটি মাত্রা হয় খোলা বা বন্ধ হতে পারে।

খোলা

একটি ওপেন ডাইমেনশন বিস্তারের জন্য উন্মুক্ত থাকে যাতে এটিকে অতিরিক্ত অক্ষ বরাবর আরও শার্ড করা যায়, অর্থাৎ নির্দিষ্ট ডাইমেনশন শার্ডিংকে সেই ডাইমেনশনের চূড়ান্ত শার্ডিং হতে হবে না। এটি একই রকম (কিন্তু ঠিক একই রকম নয়)

• jax.sharding.PartitionSpec.UNCONSTRAINED
• GSPMD-এর unspecified_dims

একটি মাত্রা খোলা থাকলে আমরা একটি যোগ করব ? অক্ষগুলি অনুসরণ করুন যেগুলির উপর মাত্রাটি ইতিমধ্যেই শার্ড করা হয়েছে (নীচের উদাহরণ দেখুন)।

বন্ধ

একটি ক্লোজড ডাইমেনশন হল এমন একটি যা প্রচারের জন্য উপলব্ধ নয় যাতে আরও শার্ডিং যোগ করা যায়, অর্থাৎ নির্দিষ্ট মাত্রা শার্ডিং হল সেই মাত্রার চূড়ান্ত শার্ডিং এবং এটি পরিবর্তন করা যায় না। এটির একটি সাধারণ ব্যবহারের ক্ষেত্রে হল GSPMD (সাধারণত) একটি মডিউলের ইনপুট/আউটপুট আর্গুমেন্টগুলিকে কীভাবে পরিবর্তন করে না, বা jax.jit এর সাথে, in_shardings নির্দিষ্ট করা ব্যবহারকারী স্থির থাকে - তারা পরিবর্তন করতে পারে না।

আমরা একটি খোলা মাত্রা এবং একটি বন্ধ মাত্রা থাকতে উপরের থেকে উদাহরণটি প্রসারিত করতে পারি।

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>

স্পষ্টভাবে প্রতিলিপি করা অক্ষ

অক্ষের একটি সুস্পষ্ট সেট যাতে একটি টেনসর প্রতিলিপি করা হয়। যদিও এটি নির্ধারণ করা যেতে পারে যে একটি অক্ষের উপর কোন টেনসর শেড করা হয়নি সেটির উপর নিহিতভাবে প্রতিলিপি করা হয়েছে (যেমন jax.sharding.PartitionSpec আজ), এটি সুস্পষ্টভাবে থাকা নিশ্চিত করে যে প্রচার এই অক্ষগুলিকে সেই অক্ষগুলির সাথে একটি খোলা মাত্রাকে আরও সংক্ষিপ্ত করতে এই অক্ষগুলি ব্যবহার করতে পারে না। অন্তর্নিহিত প্রতিলিপি সহ, একটি টেনসরকে আরও বিভাজন করা যেতে পারে । কিন্তু সুস্পষ্ট প্রতিলিপি সহ, কিছুই সেই অক্ষ বরাবর টেনসরকে বিভাজন করতে পারে না।

প্রতিলিপিকৃত অক্ষের ক্রম একটি টেনসরের ডেটা কীভাবে সংরক্ষণ করা হয় তার উপর কোন প্রভাব ফেলে না। কিন্তু, শুধুমাত্র সামঞ্জস্যের জন্য, অক্ষগুলি উপরের স্তরের জালে নির্দিষ্ট করা ক্রমে সংরক্ষণ করা হবে। উদাহরণস্বরূপ, যদি জাল হয়:

@mesh_xy = <["c"=2, "a"=2, "b"=2]>

এবং আমরা চাই "a" এবং "c" অক্ষগুলি স্পষ্টভাবে প্রতিলিপি করা হোক, ক্রমটি হওয়া উচিত:

replicated={"c", "a"}

একটি স্পষ্টভাবে প্রতিলিপিকৃত অক্ষ থাকতে আমরা উপরে থেকে আমাদের উদাহরণ প্রসারিত করতে পারি।

@mesh_xyz = <["x"=2, "y"=4, "z"=2]>

// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would // be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>

অক্ষ বিভাজন এবং উপ-অক্ষ

n অক্ষগুলির একটি যৌক্তিক জাল তৈরি করা হয় একটি 1-মাত্রিক অ্যারেকে এন-ডাইমেনশনাল অ্যারেতে রূপান্তর করে, যেখানে প্রতিটি মাত্রা ব্যবহারকারী-সংজ্ঞায়িত নামের সাথে একটি অক্ষ গঠন করে।

[...,k,...] থেকে [...,k1,...,km,...] এ জালকে পুনরায় আকার দিয়ে, k আকারের একটি অক্ষকে m সাব-অক্ষে বিভক্ত করার জন্য একই প্রক্রিয়াটি কম্পাইলারে করা যেতে পারে। [...,k1,...,km,...] ।

প্রেরণা

বিভক্ত অক্ষের পিছনে প্রেরণা বোঝার জন্য, আমরা নিম্নলিখিত উদাহরণটি দেখব:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>

আমরা পুনঃআকৃতির ফলাফলকে এমনভাবে ভাগ করতে চাই যা যোগাযোগ এড়াতে পারে (অর্থাৎ ডেটা যেখানে আছে সেখানে রাখুন)। যেহেতু "x" এর আকার ফলাফলের 1ম মাত্রার চেয়ে বড়, তাই আমাদের অক্ষটিকে দুটি উপ-অক্ষ "x.0" এবং "x.1" আকার 2-এ বিভক্ত করতে হবে এবং 1ম মাত্রাকে শার্ড করতে হবে "x.0" এবং "x.1" -এ ২য় মাত্রা।

ফাংশন ইনপুট/আউটপুট শার্ডিং

এটা সম্ভব যে প্রচারের সময় প্রধান ফাংশনের একটি ইনপুট বা আউটপুট একটি সাব-অক্ষ বরাবর সংক্ষিপ্ত হয়ে যাবে। এটি কিছু ফ্রেমওয়ার্কের জন্য একটি সমস্যা হতে পারে, যেখানে আমরা ব্যবহারকারীকে ফেরত দেওয়ার জন্য এই ধরনের শার্ডিংগুলি প্রকাশ করতে পারি না (যেমন JAX-এ আমরা jax.sharding.NamedSharding এর সাথে সাব-অ্যাক্সগুলি প্রকাশ করতে পারি না)।

এই ধরনের মামলা মোকাবেলা করার জন্য আমাদের কাছে কয়েকটি বিকল্প রয়েছে:

• অনুমতি দিন, এবং একটি ভিন্ন ফর্ম্যাটে শার্ডিং ফেরত দিন (যেমন jax.sharding.PositionalSharding jax.sharding.NamedSharding এর পরিবর্তে JAX-এ NamedSharding)।
• অননুমোদিত, এবং ইনপুট/আউটপুট শার্ড করে এমন সাব-অ্যাক্সগুলিকে সংগ্রহ করুন।

বর্তমানে আমরা প্রচার পাইপলাইনে ইনপুট/আউটপুটগুলিতে উপ-অক্ষের অনুমতি দিই। আপনি যদি এটি নিষ্ক্রিয় করার একটি উপায় চান তাহলে আমাদের জানান।

প্রতিনিধিত্ব

একইভাবে আমরা জাল থেকে নির্দিষ্ট পূর্ণ অক্ষগুলিকে তাদের নামের দ্বারা উল্লেখ করতে পারি, আমরা নির্দিষ্ট উপ-অক্ষগুলিকে তাদের আকার এবং সমস্ত উপ-অক্ষের (একই অক্ষের নামের) মাপের গুণফলকে তাদের বাম দিকে উল্লেখ করতে পারি (যেগুলি হল তাদের প্রধান)।

n আকারের একটি পূর্ণ অক্ষ "x" থেকে k আকারের একটি নির্দিষ্ট উপ-অক্ষ বের করতে, আমরা কার্যকরভাবে n (জালের মধ্যে) আকারটিকে [m, k, n/(m*k)] তে পরিবর্তন করি এবং 2য় ব্যবহার করি উপ-অক্ষ হিসাবে মাত্রা। একটি উপ-অক্ষ এইভাবে দুটি সংখ্যা দ্বারা নির্দিষ্ট করা যেতে পারে, m এবং k , এবং আমরা উপ-অক্ষগুলি বোঝাতে নিম্নলিখিত সংক্ষিপ্ত স্বরলিপি ব্যবহার করি: "x":(m)k ।

• m>=1 হল এই সাব-অক্ষের প্রাক-আকার ( m একটি n এর ভাজক হওয়া উচিত)। প্রাক-আকার হল এই সাব-অক্ষের বাম দিকের সমস্ত উপ-অক্ষের আকারের গুণফল (যেগুলি 1 এর সমান হলে এর মানে কোনওটি নেই, 1 এর থেকে বড় হলে এটি একটি একক বা একাধিক সাবের সাথে মিলে যায়) -অক্ষ)।

• k>1 হল এই উপ-অক্ষের প্রকৃত আকার ( k একটি n এর ভাজক হওয়া উচিত)।

• n/(m*k) হল পোস্ট-সাইজ । এটি এই সাব-অক্ষের ডানদিকের (যার থেকে ছোট) সমস্ত সাব-অক্ষের মাপের গুণফল (যদি 1 এর সমান হয় তবে এর মানে কোনটি নেই, 1 এর চেয়ে বড় হলে এটি একটি একক বা একাধিক উপ-অক্ষের সাথে মিলে যায়) .

যাইহোক, একটি নির্দিষ্ট সাব-অক্ষ "x":(m)k ব্যবহার করার সময় অন্যান্য উপ-অক্ষের সংখ্যা কোন পার্থক্য করে না, এবং অন্য কোন উপ-অক্ষকে টেনসর শার্ডিং-এ উল্লেখ করার প্রয়োজন নেই যদি এটি একটি মাত্রা শার্ড করে না বা স্পষ্টভাবে প্রতিলিপি করা হয় না।

অনুপ্রেরণা বিভাগে উদাহরণে ফিরে গিয়ে, আমরা নিম্নরূপ ফলাফলটি ভাগ করতে পারি:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
    : (tensor<8xf32>) -> tensor<2x4xf32>

এখানে একটি বিভক্ত অক্ষের আরেকটি উদাহরণ যেখানে শুধুমাত্র এর কিছু উপ-অক্ষ ব্যবহার করা হয়।

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Axis "y" is effectively split into 3 sub-axes denoted as
//   "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>

একইভাবে, নিম্নলিখিত দুটি শার্ডিং শব্দার্থগতভাবে সমতুল্য। আমরা mesh_xy কে mesh_full এর বিভাজন হিসাবে ভাবতে পারি।

@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>

sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>

স্পষ্টভাবে প্রতিলিপি করা উপ-অক্ষ

শার্ড ডাইমেনশনে উপ-অক্ষগুলি ব্যবহার করা ছাড়াও, সেগুলিকে স্পষ্টভাবে প্রতিলিপি হিসাবে চিহ্নিত করা যেতে পারে। আমরা উপস্থাপনায় এটির অনুমতি দিই কারণ উপ-অক্ষগুলি সম্পূর্ণ অক্ষের মতো আচরণ করে, অর্থাত্ আপনি যখন অক্ষ "x" এর একটি উপ-অক্ষ বরাবর একটি মাত্রা সংক্ষিপ্ত করেন, তখন "x" এর অন্যান্য উপ-অক্ষগুলি স্পষ্টভাবে প্রতিলিপি করা হয় এবং তাই হতে পারে একটি সাব-অক্ষের প্রতিলিপি থাকতে হবে এবং একটি মাত্রা শার্ড করার জন্য ব্যবহার করা যাবে না তা নির্দেশ করার জন্য স্পষ্টভাবে প্রতিলিপি করা হয়েছে।

যেমন:

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>

একই পূর্ণ অক্ষের প্রতিলিপিকৃত উপ-অক্ষগুলিকে তাদের প্রাক-আকার অনুসারে ক্রমবর্ধমান ক্রমানুসারে অর্ডার করা উচিত, উদাহরণস্বরূপ:

replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}

অপরিবর্তনীয়

• একটি টেনসর শার্ডিং-এ উল্লেখ করা সাব-অক্ষগুলিকে ওভারল্যাপ করা উচিত নয়, যেমন "x":(1)4 এবং "x":(2)4 ওভারল্যাপ।

• একটি টেনসর শার্ডিং-এ উল্লেখ করা সাব-অ্যাক্সগুলি অবশ্যই যতটা সম্ভব বড় হতে হবে, যেমন একটি ডাইমেনশন শার্ডিং-এ যদি দুটি সংলগ্ন সাব-অক্ষ A এবং B ক্রমানুসারে থাকে, অথবা সাব-অক্ষ A এবং B স্পষ্টভাবে প্রতিলিপি করা হয়, সেগুলি অবশ্যই পরপর হতে হবে না, যেমন "x":(1)2 এবং "x":(2)4 কারণ এগুলিকে একটি একক "x":(1)8 দিয়ে প্রতিস্থাপন করা যেতে পারে।

একাধিক লজিক্যাল মেশ

একটি যৌক্তিক জাল ডিভাইসগুলির একটি বহুমাত্রিক দৃশ্য। আমাদের শার্ডিংগুলিকে প্রতিনিধিত্ব করার জন্য আমাদের ডিভাইসগুলির একাধিক দৃশ্যের প্রয়োজন হতে পারে, বিশেষত নির্বিচারে ডিভাইসের অ্যাসাইনমেন্টের জন্য।

উদাহরণস্বরূপ, jax.sharding.PositionalSharding একটি সাধারণ লজিক্যাল মেশ নেই । GSPMD বর্তমানে HloSharding এর সাথে এটিকে সমর্থন করে, যেখানে উপস্থাপনাটি ডিভাইস এবং মাত্রার আকারের একটি অর্ডারকৃত তালিকা হতে পারে, কিন্তু উপরে অক্ষ বিভক্ত করে এটি উপস্থাপন করা যাবে না।

আমরা এই সীমাবদ্ধতা কাটিয়ে উঠি এবং প্রোগ্রামের শীর্ষ স্তরে একাধিক লজিক্যাল মেশ সংজ্ঞায়িত করে বিদ্যমান কর্নার কেসগুলি পরিচালনা করি। প্রতিটি জালের বিভিন্ন নাম সহ বিভিন্ন সংখ্যক অক্ষ থাকতে পারে, সেইসাথে একই ডিভাইসের সেটের জন্য তার নিজস্ব স্বেচ্ছাচারী অ্যাসাইনমেন্ট থাকতে পারে, অর্থাৎ প্রতিটি জাল একই ডিভাইসের সেটকে বোঝায় (তাদের অনন্য লজিক্যাল আইডি দ্বারা) কিন্তু একটি নির্বিচারে আদেশের সাথে, GSPMD প্রতিনিধিত্বের অনুরূপ।

প্রতিটি শার্ডিং উপস্থাপনা একটি নির্দিষ্ট লজিক্যাল মেশের সাথে সংযুক্ত, তাই এটি শুধুমাত্র সেই জাল থেকে অক্ষগুলিকে উল্লেখ করবে।

একটি যৌক্তিক জালের সাথে বরাদ্দ করা একটি টেনসর একটি অপের দ্বারা ব্যবহার করা যেতে পারে যা একটি ভিন্ন জালের সাথে বরাদ্দ করা হয়, গন্তব্য জালের সাথে মেলে টেনসরটিকে নির্বোধভাবে রিশার্ড করে। জিএসপিএমডিতে এটি সাধারণত বিরোধপূর্ণ মেশগুলি সমাধান করার জন্য করা হয়।

আমরা নীচে দুটি উদাহরণ প্রদান করি:

ব্যবহারকারীরা বিভিন্ন নামযুক্ত অক্ষ সহ একাধিক মেশ নির্দিষ্ট করতে পারেন (যেমন jax.sharding.NamedSharding এর মাধ্যমে), যেগুলির ডিভাইসগুলির একই ক্রম রয়েছে৷ এই উদাহরণে, <@mesh_0, "b"> <@mesh_1, "z">.

@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}

অগ্রাধিকার

অগ্রাধিকার হল নির্দিষ্ট পার্টিশনিং+প্রচারের সিদ্ধান্তকে অন্যদের উপর অগ্রাধিকার দেওয়ার একটি উপায়, এবং একটি প্রোগ্রামের ক্রমবর্ধমান বিভাজন করার অনুমতি দেয়।

অগ্রাধিকারগুলি হল একটি শার্ডিং উপস্থাপনার কিছু বা সমস্ত মাত্রার সাথে সংযুক্ত মান (প্রতিলিপিকৃত অক্ষগুলির অগ্রাধিকার নেই)।

যেমন:

@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>

//                                    |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>

অগ্রাধিকারগুলি ব্যবহারকারীদের প্রচারের উপর আরও সূক্ষ্ম দানাদার নিয়ন্ত্রণ দেয়, যেমন, প্রথমে ব্যাচ সমান্তরালতা, তারপরে মেগাট্রন এবং অবশেষে জিরো শার্ডিং। এটি পার্টিশন করা সম্পর্কে দৃঢ় গ্যারান্টি দেয় এবং আরও সূক্ষ্ম দানাদার শার্ডিং কৌশলগুলির মাধ্যমে আরও ভাল ডিবাগবিলিটির অনুমতি দেয় (বিচ্ছিন্নভাবে মেগাট্রনটি কীভাবে দেখায় তা দেখতে পারেন)।

আমরা প্রতিটি ডাইমেনশন শার্ডিংয়ের সাথে একটি অগ্রাধিকার সংযুক্ত করার অনুমতি দিই (ডিফল্টরূপে 0), যা নির্দেশ করে যে অগ্রাধিকার সহ সমস্ত শার্ডিং <i i সাথে শার্ডিংয়ের আগে সমগ্র প্রোগ্রামে প্রচার করা হবে।

এমনকি যদি একটি শার্ডিংয়ের নিম্ন অগ্রাধিকার সহ একটি খোলা মাত্রা থাকে, যেমন, {"z",?}p2 , এটি প্রচারের সময় উচ্চ অগ্রাধিকার সহ অন্য টেনসর শার্ডিং দ্বারা ওভাররাইড করা হবে না। যাইহোক, সমস্ত উচ্চ অগ্রাধিকার শর্ডিংগুলি প্রচারিত হওয়ার পরে এই ধরনের একটি খোলা মাত্রা আরও শার্ড করা যেতে পারে।

অন্য কথায়, কোন ডাইমেনশন শার্ডিং অন্যের চেয়ে বেশি গুরুত্বপূর্ণ সে বিষয়ে অগ্রাধিকারগুলি নয় - এটি সেই ক্রম যাতে ডাইমেনশন শার্ডিংয়ের স্বতন্ত্র গোষ্ঠীগুলি সমগ্র প্রোগ্রামে প্রচারিত হওয়া উচিত, এবং কীভাবে মধ্যবর্তী, অনির্ধারিত টেনসরগুলির দ্বন্দ্বগুলি সমাধান করা উচিত৷

অপরিবর্তনীয়

• অগ্রাধিকারগুলি 0 থেকে শুরু হয় (সর্বোচ্চ অগ্রাধিকার) এবং বৃদ্ধি পায় (ব্যবহারকারীদের সহজে অগ্রাধিকার যোগ করতে এবং সরানোর জন্য, আমরা অগ্রাধিকারগুলির মধ্যে ফাঁকের অনুমতি দিই, যেমন, p0 এবং p2 ব্যবহার করা হয় কিন্তু p1 নয়)।

• একটি খালি ক্লোজড ডাইমেনশন শার্ডিং (যেমন, {} ) এর কোনো অগ্রাধিকার থাকা উচিত নয়, কারণ এটি কোনো প্রভাব ফেলবে না।

ডাইমেনশন শার্ডিং বিভাজ্যতা

d আকারের একটি ডাইমেনশনকে অক্ষের সাথে শেড করা সম্ভব যার মাপের গুণফল n , যেমন d n দ্বারা বিভাজ্য নয় (যার অনুশীলনে মাত্রাটি প্যাড করা প্রয়োজন)।

যেমন:

@mesh_xy = <["x"=8, "y"=2, "z"=3]>

sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>

ব্যাকরণ

প্রতিটি যৌক্তিক জাল নিম্নরূপ সংজ্ঞায়িত করা হয়:

@mesh_name = <mesh_axis_1,...,mesh_axis_n>

mesh_axis ::= axis_name=axis_size

axis_name ::= str
axis_size ::= int

র্যাঙ্ক r এর টেনসরের জন্য শার্ডিং প্রতিনিধিত্বের নিম্নলিখিত কাঠামো থাকবে:

sharding<@mesh_name, dim_shardings, replicated=replicated_axes}

mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}

dim_sharding ::=
  {axis_1,...,axis_k} |  // closed dimension
  {axis_1,...,axis_k,?}  // open dimension

axis ::=
  axis_name  |   // a full axis
  sub_axis             // a sub axis

axis_name ::= str

sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int