Cette page a été traduite par l'API Cloud Translation.

Représentation de la segmentation

Contexte

L'objectif de la représentation du fractionnement est de spécifier comment un tenseur est fractionné par rapport à un ensemble d'appareils disponibles.

La représentation de la segmentation peut être:

Spécifiées manuellement par l'utilisateur en tant que contraintes de fractionnement sur les entrées, les sorties ou les intermédiaires.
Transformé par opération lors du processus de propagation du partitionnement.

Présentation

Structure de base

Une maille logique est une vue multidimensionnelle des appareils, définie par une liste de noms et de tailles d'axes.

La représentation de fractionnement proposée est liée à un maillage logique spécifique par son nom et ne peut faire référence qu'aux noms d'axes de ce maillage. Le fractionnement d'un tenseur spécifie le long desquels axes (d'un maillage logique spécifique) chaque dimension du tenseur est fractionnée, dans l'ordre croissant. Le tenseur est répliqué sur tous les autres axes du maillage.

Examinons la représentation du fractionnement avec un tenseur de rang 2 simple et quatre appareils.

Nous remodelons d'abord les quatre appareils [0, 1, 2, 3] en tableau à deux dimensions [[0, 1], [2, 3]] pour créer un maillage à deux axes:

@mesh_xy = <["x"=2, "y"=2]>

Nous pouvons ensuite diviser le tenseur de rang 2 [[a, b], [c, d]] suivant comme suit:

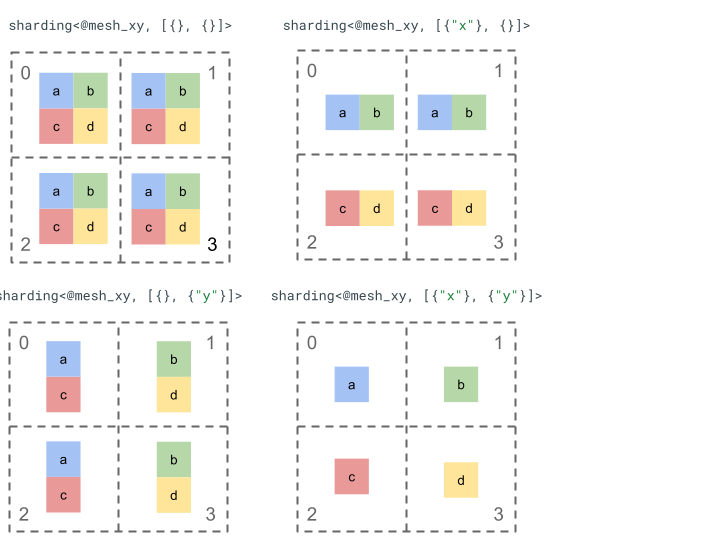
$Représentation du fractionnement d'un tenseur de rang 2$

Autres composants clés

Dimensions ouvertes/fermées : les dimensions peuvent être ouvertes (elles peuvent être fractionnées sur les axes disponibles) ou fermées (elles sont fixes et ne peuvent pas être modifiées).
Axes répliqués explicitement : toutes les axes qui ne sont pas utilisées pour fractionner une dimension sont répliquées implicitement, mais le fractionnement peut spécifier des axes répliqués explicitement et ne peut donc pas être utilisé pour fractionner une dimension ultérieurement.
Séparation des axes et sous-axes : une axe de maillage (complète) peut être divisée en plusieurs sous-axes pouvant être utilisés individuellement pour fractionner une dimension ou être répliqués explicitement.
Plusieurs maillages logiques : différents fractionnements peuvent être liés à différents maillages logiques, qui peuvent avoir des axes différents ou même un ordre différent d'ID d'appareils logiques.
Priorités : pour partitionner un programme de manière incrémentielle, des priorités peuvent être associées aux fractionnements de dimension, qui déterminent dans quel ordre les contraintes de fractionnement par dimension seront propagées dans tout le module.
Divisibilité de la partitionnement de dimension : une dimension peut être partitionnée sur des axes dont le produit des tailles ne divise pas la taille de la dimension.

Conception détaillée

Dans cette section, nous développons la structure de base et chaque composant clé.

Structure de base

Les fractionnements de dimension nous indiquent, pour chaque dimension du tenseur, le long desquels (ou des sous-axes) il est fractionné de majeur à mineur. Tous les autres axes qui ne fractionnent pas une dimension sont répliqués implicitement (ou répliqués explicitement).

Nous allons commencer par un exemple simple et l'étendre à mesure que nous décrivons des fonctionnalités supplémentaires.

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>

Invariants

Le nombre de fractionnements de dimension doit correspondre au rang du tenseur.
Tous les noms d'axes doivent exister dans le maillage référencé.
Les axes ou sous-axes ne peuvent apparaître qu'une seule fois dans la représentation du fractionnement (chacun fractionne une dimension ou est répliqué explicitement).

Dimensions "Ouvert/Fermé"

Chaque dimension d'un tenseur peut être ouverte ou fermée.

Ouvrir

Une dimension ouverte peut être propagée pour être tronquée sur d'autres axes. Autrement dit, le fractionnement de dimension spécifié n'a pas besoin d'être le fractionnement final de cette dimension. Cela est semblable (mais pas tout à fait identique) à

jax.sharding.PartitionSpec.UNCONSTRAINED
unspecified_dims de la GSPMD

Si une dimension est ouverte, nous ajoutons un ? après les axes sur lesquels la dimension est déjà partitionnée (voir exemple ci-dessous).

Fermé

Une dimension fermée ne peut pas être propagée pour ajouter d'autres partitions. Autrement dit, le fractionnement de dimension spécifié est le fractionnement final de cette dimension et ne peut pas être modifié. Un cas d'utilisation courant est le fait que GSPMD (généralement) ne modifie pas les arguments d'entrée/sortie d'un module, ou que, avec jax.jit, les in_shardings spécifiés par l'utilisateur sont statiques et ne peuvent pas changer.

Nous pouvons étendre l'exemple ci-dessus pour obtenir une dimension ouverte et une dimension fermée.

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>

Axes répliqués explicitement

Ensemble explicite d'axes sur lesquels un tenseur est répliqué. Bien qu'il soit possible de déterminer qu'un tenseur non segmenté sur une axe est répliqué implicitement dessus (comme jax.sharding.PartitionSpec aujourd'hui), le rendre explicite garantit que la propagation ne peut pas utiliser ces axes pour segmenter davantage une dimension ouverte avec ces axes. Avec la réplication implicite, un tenseur peut être partitionné davantage. Toutefois, avec la réplication explicite, rien ne peut partitionner le tenseur le long de cette axe.

L'ordre des axes répliqués n'a aucune incidence sur le stockage des données d'un tenseur. Toutefois, pour des raisons de cohérence uniquement, les axes seront stockés dans l'ordre dans lequel ils sont spécifiés dans le maillage de premier niveau. Par exemple, si la maille est:

@mesh_xy = <["c"=2, "a"=2, "b"=2]>

Nous voulons que les axes "a" et "c" soient répliqués explicitement. L'ordre doit être le suivant:

replicated={"c", "a"}

Nous pouvons étendre notre exemple ci-dessus pour obtenir une axe répliquée explicitement.

@mesh_xyz = <["x"=2, "y"=4, "z"=2]>

// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would // be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>

Fractionnement des axes et sous-axes

Un maillage logique d'axes n est créé en remodelant un tableau unidimensionnel d'appareils en tableau n-dimensionnel, où chaque dimension forme un axe avec un nom défini par l'utilisateur.

Le même processus peut être effectué dans le compilateur pour diviser une axe de taille k en sous-axes m, en remodelant le maillage de [...,k,...] en [...,k1,...,km,...].

Motivation

Pour comprendre la motivation derrière le fractionnement des axes, nous allons examiner l'exemple suivant:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>

Nous souhaitons diviser le résultat de la refonte de manière à éviter la communication (c'est-à-dire conserver les données telles qu'elles sont). Étant donné que la taille de "x" est supérieure à la première dimension du résultat, nous devons diviser l'axe en deux sous-axes "x.0" et "x.1" de taille 2 chacun, et introduire des fragments pour la première dimension sur "x.0" et la deuxième dimension sur "x.1".

Divisions d'entrée/sortie de fonction

Il est possible qu'au cours de la propagation, une entrée ou une sortie de la fonction principale soit fractionnée le long d'un sous-axe. Cela peut poser problème pour certains frameworks, où nous ne pouvons pas exprimer de tels fractionnements à restituer à l'utilisateur (par exemple, dans JAX, nous ne pouvons pas exprimer de sous-axes avec jax.sharding.NamedSharding).

Plusieurs options s'offrent à vous dans ce cas:

Autorisez et renvoyez le fractionnement dans un autre format (par exemple, jax.sharding.PositionalSharding au lieu de jax.sharding.NamedSharding dans JAX).
Interdiction et sous-axes "all-gather" qui fractionnent l'entrée/la sortie.

Pour le moment, nous autorisons les sous-axes sur les entrées/sorties dans le pipeline de propagation. N'hésitez pas à nous contacter si vous souhaitez désactiver cette fonctionnalité.

Représentation

De la même manière que nous pouvons référencer des axes complets spécifiques du maillage par leur nom, nous pouvons référencer des sous-axes spécifiques par leur taille et le produit de toutes les tailles de sous-axe (du même nom d'axe) à leur gauche (qui sont majeures pour eux) .

Pour extraire un sous-axe spécifique de taille k à partir d'un axe complet "x" de taille n, nous remodelons efficacement la taille n (dans le maillage) en [m, k, n/(m*k)] et utilisons la deuxième dimension comme sous-axe. Un sous-axe peut donc être spécifié par deux nombres, m et k, et nous utilisons la notation concise suivante pour désigner les sous-axes: "x":(m)k.

m>=1 correspond à la pré-taille de ce sous-axe (m doit être un diviseur de n). La pré-taille correspond au produit de toutes les tailles de sous-axe à gauche de (qui sont majeures par rapport à) ce sous-axe (si elle est égale à 1, cela signifie qu'il n'y en a pas, si elle est supérieure à 1, elle correspond à un ou plusieurs sous-axes).
k>1 correspond à la taille réelle de ce sous-axe (k doit être un diviseur de n).
n/(m*k) correspond à la post-taille. Il s'agit du produit de toutes les tailles de sous-axes à droite de (qui sont inférieures à) ce sous-axe (s'il est égal à 1, cela signifie qu'il n'y en a pas, s'il est supérieur à 1, il correspond à un ou plusieurs sous-axes).

Toutefois, le nombre d'autres sous-axes n'a pas d'incidence lorsque vous utilisez un sous-axe "x":(m)k spécifique. Aucun autre sous-axe n'a besoin d'être référencé dans le fractionnement de tensor s'il ne fractionne pas une dimension ou s'il est répliqué explicitement.

Pour en revenir à l'exemple de la section Motivation, nous pouvons diviser le résultat comme suit:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
    : (tensor<8xf32>) -> tensor<2x4xf32>

Voici un autre exemple d'axe fractionné où seuls certains de ses sous-axes sont utilisés.

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Axis "y" is effectively split into 3 sub-axes denoted as
//   "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>

De même, les deux partitionnements suivants sont sémantiquement équivalents. On peut considérer mesh_xy comme un fractionnement de mesh_full.

@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>

sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>

Sous-axes répliqués explicitement

En plus d'être utilisés pour fractionner la dimension, les sous-axes peuvent également être marqués comme répliqués explicitement. Nous autorisons cela dans la représentation, car les sous-axes se comportent comme des axes complets. Autrement dit, lorsque vous partitionnez une dimension le long d'un sous-axe de l'axe "x", les autres sous-axes de "x" sont répliqués implicitement et peuvent donc être répliqués explicitement pour indiquer qu'un sous-axe doit rester répliqué et ne peut pas être utilisé pour partitionner une dimension.

Exemple :

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>

Les sous-axes répliqués du même axe complet doivent être triés par ordre croissant en fonction de leur pré-taille, par exemple:

replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}

Invariants

Les sous-axes référencés dans un fractionnement de tenseur ne doivent pas se chevaucher, par exemple "x":(1)4 et "x":(2)4.
Les sous-axes référencés dans un fractionnement de tenseur doivent être aussi grands que possible, c'est-à-dire que si un fractionnement de dimension comporte deux sous-axes A et B adjacents dans l'ordre, ou que les sous-axes A et B sont répliqués explicitement, ils ne doivent pas être consécutifs (par exemple, "x":(1)2 et "x":(2)4, car ils peuvent être remplacés par un seul "x":(1)8).

Plusieurs maillages logiques

Un maillage logique est une vue multidimensionnelle des appareils. Nous pouvons avoir besoin de plusieurs vues des appareils pour représenter nos fractionnements, en particulier pour les attributions d'appareils arbitraires.

Par exemple, jax.sharding.PositionalSharding ne dispose pas d'un maillage logique commun. GSPMD est actuellement compatible avec HloSharding, où la représentation peut être une liste ordonnée d'appareils et de tailles de dimension, mais cela ne peut pas être représenté avec la division des axes ci-dessus.

Nous surmontons cette limitation et gérons les cas particuliers existants en définissant plusieurs maillages logiques au niveau supérieur du programme. Chaque maillage peut avoir un nombre d'axes différents avec des noms différents, ainsi que sa propre attribution arbitraire pour le même ensemble d'appareils, c'est-à-dire que chaque maillage fait référence au même ensemble d'appareils (par leur ID logique unique) mais avec un ordre arbitraire, semblable à la représentation GSPMD.

Chaque représentation de fractionnement est associée à un maillage logique spécifique. Par conséquent, elle ne fait référence qu'aux axes de ce maillage.

Un tenseur attribué à un maillage logique peut être utilisé par une opération attribuée à un autre maillage, en retriantaillant naïvement le tenseur pour qu'il corresponde au maillage de destination. Dans GSPMD, c'est généralement ce qui est fait pour résoudre les maillages en conflit.

Vous trouverez deux exemples ci-dessous:

Les utilisateurs peuvent spécifier plusieurs maillages avec des axes nommés différents (par exemple, via jax.sharding.NamedSharding), qui ont le même ordre d'appareils. Dans cet exemple, <@mesh_0, "b"> est identique à <@mesh_1, "z">..

@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}

Priorités

La priorité permet de donner la priorité à certaines décisions de partitionnement et de propagation par rapport à d'autres, et permet de partitionner de manière incrémentielle un programme.

Les priorités sont des valeurs associées à certaines ou à toutes les dimensions d'une représentation de fractionnement (les axes répliqués n'ont pas de priorités).

Exemple :

@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>

//                                    |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>

Les priorités offrent aux utilisateurs un contrôle plus précis sur la propagation, par exemple, le parallélisme par lot d'abord, puis le mégatron, et enfin le partitionnement ZeRO. Cela permet de garantir ce qui est partitionné et de faciliter le débogage grâce à des stratégies de partitionnement plus précises (vous pouvez voir à quoi ressemble le programme après seulement Megatron en isolation).

Nous autorisons l'ajout d'une priorité à chaque fractionnement de dimension (0 par défaut), ce qui indique que tous les fractionnements avec priorité <i seront propagés à l'ensemble du programme avant les fractionnements avec priorité i.

Même si un fractionnement comporte une dimension ouverte de priorité inférieure, par exemple : {"z",?}p2, il ne sera pas remplacé par un autre fractionnement de tensor avec une priorité plus élevée lors de la propagation. Toutefois, une telle dimension ouverte peut être partitionnée une fois que toutes les partitions de priorité supérieure ont été propagées.

En d'autres termes, les priorités ne PAS indiquent quel fractionnement de dimension est plus important qu'un autre. Il s'agit de l'ordre dans lequel des groupes distincts de fractionnements de dimension doivent se propager à l'ensemble du programme, et de la manière dont les conflits sur les tenseurs intermédiaires non annotés doivent être résolus.

Invariants

Les priorités commencent à 0 (priorité la plus élevée) et augmentent (pour permettre aux utilisateurs d'ajouter et de supprimer facilement des priorités, nous autorisons des écarts entre les priorités. Par exemple, p0 et p2 sont utilisés, mais p1 ne l'est pas).
Un fractionnement de dimension fermée vide (c'est-à-dire, {}) ne doit pas avoir de priorité, car cela n'aura aucun effet.

Divisibilité du fractionnement des dimensions

Il est possible qu'une dimension de taille d soit partitionnée selon des axes dont le produit des tailles est n, de sorte que d ne soit pas divisible par n (ce qui nécessiterait en pratique de rembourrer la dimension).

Exemple :

@mesh_xy = <["x"=8, "y"=2, "z"=3]>

sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>

Grammaire

Chaque maillage logique est défini comme suit:

@mesh_name = <mesh_axis_1,...,mesh_axis_n>

mesh_axis ::= axis_name=axis_size

axis_name ::= str
axis_size ::= int

La représentation du fractionnement aura la structure suivante pour un tenseur de rang r:

sharding<@mesh_name, dim_shardings, replicated=replicated_axes}

mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}

dim_sharding ::=
  {axis_1,...,axis_k} |  // closed dimension
  {axis_1,...,axis_k,?}  // open dimension

axis ::=
  axis_name  |   // a full axis
  sub_axis             // a sub axis

axis_name ::= str

sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int