تمثيل التقسيم إلى أجزاء

تنظيم صفحاتك في مجموعات يمكنك حفظ المحتوى وتصنيفه حسب إعداداتك المفضّلة.

الخلفية

الغرض من تمثيل التجزئة هو تحديد كيفية تقسيم مصفوفة كثيفة بالاستناد إلى مجموعة من الأجهزة المتاحة.

يمكن أن يكون تمثيل التجزئة إما:

• يحدّدها المستخدم يدويًا على أنّها قيود تقسيم على المدخلات أو المخرجات أو الوسائط.
• يتم تحويلها لكل عملية في عملية نشر التجزئة.

نظرة عامة

البنية الأساسية

الشبكة المنطقية هي عرض متعدد الأبعاد للأجهزة، ويتم تحديدها من خلال قائمة بأسماء محور وأحجامه.

يكون تمثيل التجزئة المقترَح مرتبطًا بشبكة منطقية معيّنة من خلال اسمها، ولا يمكنه الإشارة إلا إلى أسماء المحاور من تلك الشبكة. تُحدِّد عملية تقسيم مصفوفة كثيفة المحاور (لشبكة منطقية معيّنة) التي يتم تقسيم كل سمة من سمات المصفوفة الكثيفة على طولها، بترتيب من الرئيسي إلى الثانوي. يتم تكرار المتجه على طول جميع المحاور الأخرى للشبكة.

لنطّلِع على تمثيل التجزئة باستخدام مصفوفة بسيطة من الترتيب 2 و4 أجهزة.

نعيد أولاً تشكيل الأجهزة الأربعة [0, 1, 2, 3] إلى صفيف ثنائي الأبعاد [[0, 1], [2, 3]] لإنشاء شبكة ذات محورَين:

@mesh_xy = <["x"=2, "y"=2]>

يمكننا بعد ذلك تقسيم مصفوفة [[a, b], [c, d]] من الترتيب الثاني على النحو التالي:

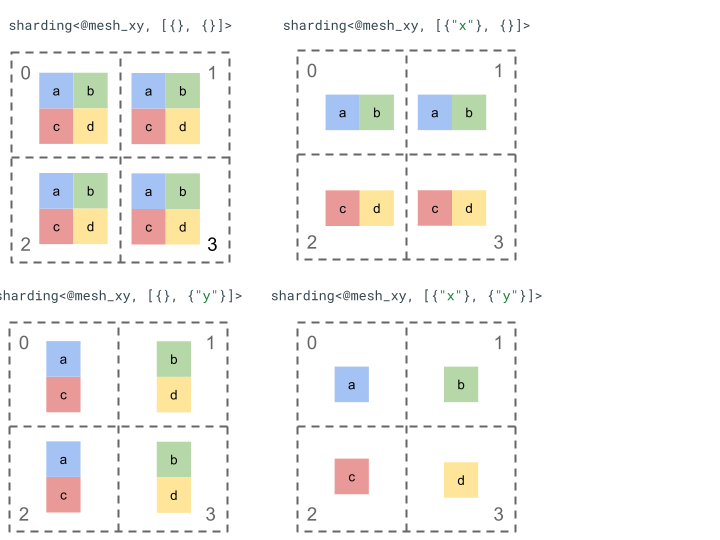
المكوّنات الرئيسية الأخرى

• السمات المفتوحة/المغلقة: يمكن أن تكون السمات إما مفتوحة - يمكن تقسيمها بشكل أكبر على المحاور المتاحة، أو مغلقة - تكون ثابتة ولا يمكن تغييرها.
• الأعمدة التي تتم إعادة نسخها بشكل صريح: تتم إعادة نسخ جميع الأبعاد التي لا تُستخدَم لتقسيم سمة بشكل ضمني، ولكن يمكن أن يحدِّد التقسيم الأبعاد التي تتم إعادة نسخها بشكل صريح، وبالتالي لا يمكن استخدامها لتقسيم سمة لاحقًا.
• تقسيم المحاور والمحاور الفرعية: يمكن تقسيم محور الشبكة (الكامل) إلى محاور فرعية متعددة يمكن استخدامها بشكلٍ فردي لتقسيم سمة أو تكرارها بشكلٍ صريح.
• شبكات منطقية متعدّدة: يمكن ربط عمليات تحليل مختلفة بشبكات منطقية مختلفة، والتي يمكن أن تتضمّن محورين مختلفين أو حتى ترتيبًا مختلفًا لأرقام تعريف الأجهزة المنطقية.
• الأولويات: لتقسيم برنامج بشكل تدريجي، يمكن إرفاق الأولويات بتقسيم السمات، ما يحدّد الترتيب الذي سيتم فيه نشر قيود تقسيم السمات لكل سمة في الوحدة.
• قابلية تقسيم السمات: يمكن تقسيم سمة على محاور لا يقسم منتج مقاساتها حجم السمة.

التصميم التفصيلي

نوسّع البنية الأساسية وكل مكوّن رئيسي في هذا القسم.

البنية الأساسية

تُعلمنا تقسيمات السمات لكل سمة من سمات المصفوفة، والتي يتم تقسيمها على طول محورين (أو محورَين فرعيَّين) من الرئيسي إلى الفرعي. تتمّ إعادة نسخ جميع المحاور الأخرى التي لا تقسم سمة بشكل ضمني (أو بشكل صريح).

سنبدأ بمثال بسيط ونوسّعه أثناء وصفنا لمزيد من الميزات.

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>

القيم الثابتة

• يجب أن يتطابق عدد تقسيمات السمات مع ترتيب المصفوفة.
• يجب أن تكون جميع أسماء المحاور متوفّرة في الشبكة المُشار إليها.
• لا يمكن أن تظهر المحاور أو المحاور الفرعية إلا مرة واحدة في تمثيل التجزئة (يؤدي كل محور إلى تجزئة سمة أو يتم تكرار محوره صراحةً).

السمات المفتوحة/المغلقة

يمكن أن تكون كل سمة من سمات مصفوفة تانسور مفتوحة أو مغلقة.

فتح

تكون السمة المفتوحة متاحة للنشر لتقسيمها بشكل أكبر على محورين إضافيين، أي أنّه ليس من الضروري أن يكون تقسيم السمة المحدّد هو التقسيم النهائي لهذه السمة. وهذا مشابه (ولكن ليس مطابقًا تمامًا) لunspecified_dims في GSPMD.

إذا كانت السمة مفتوحة، نضيف ? بعد المحاور التي تم تقسيم السمة حسبها (راجِع المثال أدناه).

النشاط التجاري مغلق

السمة المغلقة هي سمة غير متاحة للنشر لإضافة المزيد من التحليل إلى تحليلها، أي أنّ تقسيم السمة المحدّد هو التقسيم النهائي لهذه السمة ولا يمكن تغييره. ومن حالات الاستخدام الشائعة لهذا الإجراء، الطريقة التي لا تعدّل بها GSPMD (عادةً) وسيطات الإدخال/الإخراج لمكوّن، أو الطريقة التي تكون بها in_shardings التي حدّدها المستخدم ثابتة باستخدام jax.jit، ولا يمكن تغييرها.

يمكننا توسيع المثال أعلاه للحصول على سمة مفتوحة وسمة مغلقة.

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>

المحاور التي تم تكرارها صراحةً

مجموعة صريحة من المحاور التي يتم تكرار مصفوفة تينسور عليها على الرغم من أنّه يمكن تحديد أنّ مصفوفة لاتّصال لا يتم تقسيمها على محور يتم نسخها ضمنيًا عليه (مثل jax.sharding.PartitionSpec اليوم)، فإنّ تحديدها بشكل صريح يضمن أنّ الانتشار لا يمكنه استخدام هذه المحاور لمزيد من تقسيم سمة مفتوحة باستخدام هذه المحاور. باستخدام النسخ التلقائي، يمكن تقسيم ملف ملف tensor بشكل أكبر. ولكن مع التكرار الصريح، لا يمكن لأي شيء تقسيم المصفوفة على طول هذا المحور.

لا يؤثّر ترتيب المحاور المكرّرة في كيفية تخزين بيانات مصفوفة تينسور. ولكن من أجل الاتساق فقط، سيتم تخزين المحاور بالترتيب الذي يتم فيه تحديدها في شبكة المستوى الأعلى. على سبيل المثال، إذا كانت الشبكة:

@mesh_xy = <["c"=2, "a"=2, "b"=2]>

ونريد تكرار محورَي "a" و"c" بشكل صريح، ويجب أن يكون الترتيب على النحو التالي:

replicated={"c", "a"}

يمكننا توسيع مثالنا أعلاه للحصول على محور مكرّر بشكل صريح.

@mesh_xyz = <["x"=2, "y"=4, "z"=2]>

// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>

تقسيم المحاور والمحاور الفرعية

يتم إنشاء شبكة منطقية من n محور من خلال إعادة تشكيل صفيف أحادي الأبعاد من الأجهزة إلى صفيف ذي n أبعاد، حيث يشكّل كلّ سمة محورًا باسم يحدّده المستخدم.

يمكن تنفيذ العملية نفسها في المُجمِّع لتقسيم محور بحجم k إلى m محور فرعي، وذلك من خلال إعادة تشكيل الشبكة من [...,k,...] إلى [...,k1,...,km,...].

الحافز

لفهم السبب وراء تقسيم المحاور، سنلقي نظرة على المثال التالي:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>

نريد تقسيم نتيجة إعادة التنسيق بطريقة تتجنّب التواصل (أي إبقاء البيانات في مكانها). بما أنّ حجم "x" هو أكبر من السمة الأولى للنتيجة، علينا تقسيم المحور إلى محورَين فرعيَّين "x.0" و"x.1" بحجم 2 لكل منهما، وتقسيم السمة الأولى على "x.0" والسمة الثانية على "x.1".

تقسيم الإدخال/الإخراج للدالة

من الممكن أن تصبح مدخلات أو مخرجات الدالة الرئيسية مجزّأة على طول محور فرعي أثناء النشر. يمكن أن يشكّل ذلك مشكلة لبعض الأطر، حيث لا يمكننا التعبير عن عمليات التجزئة هذه لإعادتها إلى المستخدم (على سبيل المثال، في JAX، لا يمكننا التعبير عن المحاور الفرعية باستخدام jax.sharding.NamedSharding).

لدينا بعض الخيارات للتعامل مع هذه الحالات:

• السماح بتقسيم البيانات وعرضها بتنسيق مختلف (مثل jax.sharding.PositionalSharding بدلاً من jax.sharding.NamedSharding في JAX)
• لا تسمح بالأعمدة الفرعية التي تجمع كل الإدخالات أو المخرجات.

نسمح حاليًا باستخدام المحاور الفرعية في الإدخالات/المخرجات في مسار النشر. يُرجى إعلامنا إذا أردت طريقة لإيقاف هذه الميزة.

التمثيل

بالطريقة نفسها التي يمكننا بها الإشارة إلى محاور كاملة معيّنة من الشبكة باستخدام اسمها، يمكننا الإشارة إلى محاور فرعية معيّنة حسب حجمها ومنتج جميع أحجام المحور الفرعي (الذي يحمل اسم المحور نفسه) على يساره (أي المحاور الرئيسية).

لاستخراج محور فرعي معيّن بحجم k من محور كامل "x" بحجم n، نعيد تشكيل الحجم n (في الشبكة) بفعالية إلى [m, k, n/(m*k)] ونستخدم السمة الثانية كمحور فرعي. وبالتالي، يمكن تحديد محور فرعي باستخدام رقمين، m وk، ونستخدم الرمز الموجز التالي للإشارة إلى المحاور الفرعية: "x":(m)k.

• m>=1 هو الحجم المُسبَق لهذا المحور الفرعي (يجب أن يكون m مقسومًا عليه n). الحجم المُسبَق هو حاصل ضرب جميع أحجام المحاور الفرعية على يمين هذا المحور الفرعي (إذا كان يساوي 1، يعني ذلك أنّه لا يتوفّر أي محور فرعي، وإذا كان أكبر من 1، يعني ذلك أنّه يتطابق مع محور فرعي واحد أو أكثر).

• k>1 هو الحجم الفعلي لهذا المحور الفرعي (يجب أن يكون k مقسومًا عليه n).

• ‫n/(m*k) هو مقاس المشاركة. وهو حاصل ضرب جميع أحجام المحاور الفرعية على يسار هذا المحور الفرعي (إذا كان يساوي 1، يعني ذلك أنّه لا يوجد أي محور فرعي، وإذا كان أكبر من 1، يعني ذلك أنّه يتوافق مع محور فرعي واحد أو أكثر).

ومع ذلك، لا يُحدث عدد المحاور الفرعية الأخرى فرقًا عند استخدام محور فرعي معيّن "x":(m)k، ولا يلزم الإشارة إلى أي محور فرعي آخر في تجزئة مصفوفة تينسور إذا لم يكن يجزئ سمة أو يتم تكراره صراحةً.

بالعودة إلى المثال في قسم "الدافع"، يمكننا تقسيم النتيجة على النحو التالي:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
    : (tensor<8xf32>) -> tensor<2x4xf32>

في ما يلي مثال آخر على محور مُقسَّم يتم فيه استخدام بعض محاوره الفرعية فقط.

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Axis "y" is effectively split into 3 sub-axes denoted as
//   "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>

وبالمثل، فإنّ القسمتَين التاليتَين متساويتان من الناحية الدلالية. يمكننا اعتبار mesh_xy عملية تقسيم mesh_full.

@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>

sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>

المحاور الفرعية التي تم تكرارها صراحةً

بالإضافة إلى المحاور الفرعية المستخدَمة لتقسيم السمة، يمكن أيضًا وضع علامة عليها بأنّها مكرّرة صراحةً. نسمح بذلك في التمثيل لأنّ المحاور الفرعية تتصرّف تمامًا مثل المحاور الكاملة، أي عند تقسيم سمة على طول محور فرعي من محور "x"، تتمّ تكرار المحاور الفرعية الأخرى للمحور "x" بشكل ضمني، وبالتالي يمكن تكرارها بشكل صريح للإشارة إلى أنّه يجب أن يظلّ محور فرعي مكرّرًا ولا يمكن استخدامه لتقسيم سمة.

على سبيل المثال:

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>

يجب ترتيب المحور الفرعي المكرّر للمحور الكامل نفسه بترتيب تصاعدي حسب الحجم المحدّد مسبقًا، على سبيل المثال:

replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}

القيم الثابتة

• يجب ألا تتداخل المحاور الفرعية المُشار إليها في تقسيم مصفوفة تانسور، مثل تداخل "x":(1)4 و"x":(2)4.

• يجب أن تكون المحاور الفرعية المُشار إليها في تقسيم مصفوفة تانسور أكبر قدر ممكن، أي إذا كان تقسيم السمة يتضمّن محورَين فرعيَّين متجاورَين أ و ب بالترتيب، أو تم تكرار المحاور الفرعية أ و ب بشكل صريح، يجب ألّا تكون متتالية، على سبيل المثال، "x":(1)2 و"x":(2)4 لأنّه يمكن استبدالهما ب"x":(1)8 واحد.

شبكات منطقية متعددة

الشبكة المنطقية هي عرض متعدد الأبعاد للأجهزة. قد نحتاج إلى عدة طرق لعرض الأجهزة لتمثيل تقسيماتنا، خاصةً عند تحديد الأجهزة بشكل عشوائي.

على سبيل المثال، jax.sharding.PositionalSharding لا يحتوي على شبكة منطقية مشتركة واحدة. تتيح ميزة GSPMD حاليًا ذلك باستخدام HloSharding، حيث يمكن أن يكون التمثيل قائمة مرتبة للأجهزة وأحجام السمات، ولكن لا يمكن تمثيل ذلك باستخدام تقسيم المحور أعلاه.

نتغلب على هذا القيد ونتعامل مع الحالات الشاذة الحالية من خلال تحديد شبكات منطقية متعدّدة في أعلى مستوى من البرنامج. يمكن أن تحتوي كل شبكة على عدد مختلف من المحاور بأسماء مختلفة، بالإضافة إلى تحديد عشوائي لها للمجموعة نفسها من الأجهزة، أي أنّ كل شبكة تشير إلى المجموعة نفسها من الأجهزة (حسب رقم التعريف المنطقي الفريد لها) ولكن بترتيب عشوائي، على غرار تمثيل GSPMD.

يرتبط كل تمثيل لتقسيم البيانات بشبكة منطقية معيّنة، وبالتالي لن يشير سوى إلى المحاور من تلك الشبكة.

يمكن أن يستخدم إجراء تمّ تعيينه لشبكة منطقية واحدة مصفوفة تمّ تعيينها لشبكة مختلفة، وذلك من خلال إعادة تقسيم المصفوفة بشكلٍ عفوي لمطابقة الشبكة المقصودة. في GSPMD، يتم عادةً إجراء ذلك لحلّ تعارضات الشبكات.

يمكن للمستخدمين تحديد شبكات متعددة باستخدام محاور مُسمّاة مختلفة (مثلاً من خلال jax.sharding.NamedSharding)، والتي تتضمّن ترتيب الأجهزة نفسه. في المثال التالي،<@mesh_0, "b"> مطابق لـ<@mesh_1, "z">:

@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}

الأولويات

الأولوية هي طريقة لمنح الأولوية لقرارات تقسيم ونشر معيّنة مقارنةً بغيرها، كما تتيح التقسيم المتزايد لبرنامج.

الأولويات هي قيم مرتبطة ببعض أو كل سمات تمثيل التجزئة (لا تتضمّن المحاور المكرّرة أولويات).

على سبيل المثال:

@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>

//                                    |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>

تمنح الأولويات للمستخدمين إمكانية التحكّم بشكل أدق في النشر، مثل معالجة ملف برمجي المهام بالتوازي أولاً، ثم Megatron، وأخيراً تحليل ملف برمجي ZeRO. يتيح ذلك تقديم ضمانات قوية بشأن ما يتم تقسيمه، كما يتيح إمكانية تصحيح الأخطاء بشكل أفضل من خلال توفُّر استراتيجيات تقسيم أكثر دقة (يمكنك الاطّلاع على شكل البرنامج بعد استخدام Megatron فقط بشكل منفصل).

نسمح بإرفاق الأولوية بكل عملية تقسيم سمة (0 تلقائيًا)، ما يشير إلى أنّه سيتم نشر جميع عمليات التقسيم ذات الأولوية <i على البرنامج بالكامل قبل عمليات التقسيم ذات الأولوية i.

حتى إذا كانت شريحة البيانات تتضمّن سمة مفتوحة ذات أولوية أقل، مثلاً {"z",?}p2، لن يتم إلغاءه من خلال تقسيم مصفوفة آخر بأولوية أعلى أثناء الانتشار. ومع ذلك، يمكن تقسيم هذه السمة المفتوحة إلى أقسام أخرى بعد أن تتم إعادة توجيه كل القسمات التي لها أولوية أعلى.

بعبارة أخرى، NOT ترتبط الأولويات بتحديد عملية تقسيم السمات التي هي أكثر أهمية من غيرها، بل هي الترتيب الذي يجب أن تنتشر به مجموعات مختلفة من عمليات تقسيم السمات إلى البرنامج بأكمله، وكيفية حلّ التعارضات في المتسلسلات غير المُشارَك عليها.

القيم الثابتة

• تبدأ الأولويات من 0 (أعلى أولوية) وتزداد (للسماح للمستخدمين بإضافة وإزالة الأولويات بسهولة، نسمح بفواصل بين الأولويات، على سبيل المثال، يتم استخدام p0 و p2 ولكن لا يتم استخدام p1).

• تقسيم سمة مغلقة فارغة (أي {})، يجب ألا يكون لها أولوية، لأنّ ذلك لن يؤثر في أيّ شيء.

قابلية تقسيم السمات

من الممكن تقسيم سمة بحجم d على محاور يكون حاصل ضرب أحجامها هو n، بحيث لا يكون d قابلاً للقسمة على n (ما قد يتطلّب في الممارسة ملء السمة).

على سبيل المثال:

@mesh_xy = <["x"=8, "y"=2, "z"=3]>

sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>

القواعد اللغوية

يتم تعريف كل شبكة منطقية على النحو التالي:

@mesh_name = <mesh_axis_1,...,mesh_axis_n>

mesh_axis ::= axis_name=axis_size

axis_name ::= str
axis_size ::= int

سيكون تمثيل التجزئة بالبنية التالية لمكثف من الترتيب r:

sharding<@mesh_name, dim_shardings, replicated=replicated_axes}

mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}

dim_sharding ::=
  {axis_1,...,axis_k} |  // closed dimension
  {axis_1,...,axis_k,?}  // open dimension

axis ::=
  axis_name  |   // a full axis
  sub_axis             // a sub axis

axis_name ::= str

sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int