نمایندگی شاردینگ

پس زمینه

هدف از نمایش تقسیم بندی مشخص کردن نحوه تقسیم بندی یک تانسور با توجه به مجموعه ای از دستگاه های موجود است.

نمایش شاردینگ می تواند به صورت زیر باشد:

• به صورت دستی توسط کاربر به عنوان محدودیت های اشتراک گذاری در ورودی ها، خروجی ها یا واسطه ها مشخص شده است.
• به ازای هر عملیات در فرآیند انتشار شاردینگ تبدیل شده است.

نمای کلی

ساختار اساسی

مش منطقی یک نمای چند بعدی از دستگاه ها است که با لیستی از نام محورها و اندازه ها تعریف می شود.

نمایش تقسیم بندی پیشنهادی با نام خود به یک مش منطقی خاص متصل است و فقط می تواند به نام محورها از آن مش ارجاع دهد. تقسیم بندی یک تانسور مشخص می کند که در امتداد کدام محورها (از یک شبکه منطقی خاص)، هر بعد تانسور، از بزرگ به کوچک مرتب شده است. تانسور در امتداد تمام محورهای دیگر مش تکرار می شود.

بیایید نمایش اشتراک گذاری را با یک تانسور رتبه 2 ساده و 4 دستگاه بررسی کنیم.

ابتدا 4 دستگاه [0, 1, 2, 3] به یک آرایه 2 بعدی [[0, 1], [2, 3]] تغییر شکل می دهیم تا یک شبکه با دو محور ایجاد کنیم:

@mesh_xy = <["x"=2, "y"=2]>

سپس می توانیم تانسور رتبه 2 زیر [[a, b], [c, d]] به صورت زیر تقسیم کنیم:

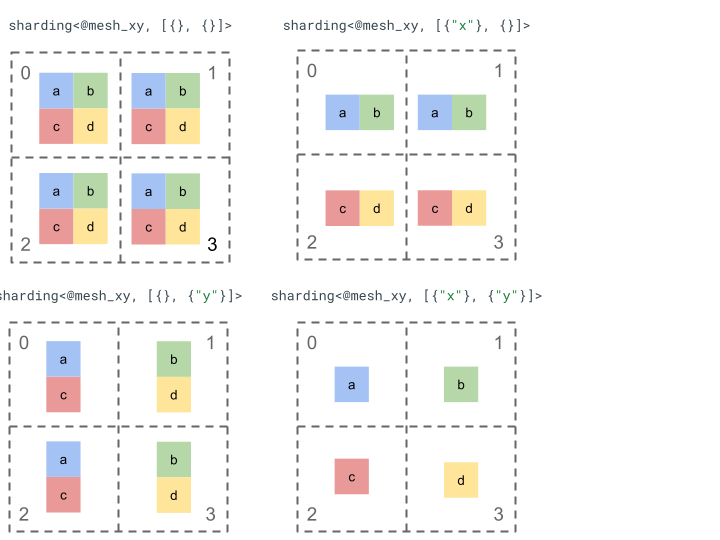
سایر اجزای کلیدی

• ابعاد باز/بسته - ابعاد می‌توانند باز باشند - می‌توانند بیشتر بر روی محورهای موجود خرد شوند. یا بسته - ثابت هستند و قابل تغییر نیستند.
• محورهایی که به طور صریح تکرار می شوند - همه محورهایی که برای خرد کردن یک بعد استفاده نمی شوند به طور ضمنی تکرار می شوند، اما تقسیم بندی می تواند محورهایی را مشخص کند که به صراحت تکرار می شوند و بنابراین نمی توان از آنها برای خرد کردن یک بعد بعد استفاده کرد.
• تقسیم محور و محورهای فرعی - یک محور مش (کامل) را می توان به محورهای فرعی متعددی تقسیم کرد که می توانند به صورت جداگانه برای خرد کردن یک بعد یا به طور صریح تکرار شوند.
• مش های منطقی چندگانه - شاردینگ های مختلف را می توان به مش های منطقی مختلفی متصل کرد، که می توانند محورهای مختلف یا حتی ترتیب متفاوتی از شناسه های منطقی دستگاه داشته باشند.
• اولویت ها - برای پارتیشن بندی یک برنامه به صورت تدریجی، اولویت ها را می توان به تقسیم بندی های ابعادی متصل کرد، که تعیین می کند محدودیت های تقسیم بندی در هر بعد به چه ترتیبی در سراسر ماژول منتشر می شود.
• تقسیم‌پذیری تقسیم‌بندی ابعاد - یک بعد را می‌توان بر روی محورهایی خرد کرد که حاصل ضرب اندازه‌های آن اندازه ابعاد را تقسیم نمی‌کند.

طراحی دقیق

ما ساختار اصلی و هر جزء کلیدی را در این بخش گسترش می دهیم.

ساختار اساسی

تقسیم‌بندی ابعاد برای هر بعد تانسور به ما می‌گوید که در امتداد کدام محورها (یا محورهای فرعی ) از اصلی به فرعی تقسیم می‌شود. تمام محورهای دیگری که یک بعد را تکه تکه نمی کنند به طور ضمنی تکرار می شوند (یا به طور صریح تکرار می شوند ).

ما با یک مثال ساده شروع می کنیم و آن را به عنوان ویژگی های اضافی توضیح می دهیم.

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>

متغیرها

• تعداد تقسیم‌بندی ابعاد باید با رتبه تانسور مطابقت داشته باشد.
• همه نام محورها باید در مش ارجاع شده وجود داشته باشد.
• محورها یا محورهای فرعی فقط می توانند یک بار در نمایش شاردینگ ظاهر شوند (هر کدام یک بعد را تکثیر می کنند یا به صراحت تکرار می شوند).

ابعاد باز/بسته

هر بعد از یک تانسور می تواند باز یا بسته باشد.

باز کنید

یک بعد باز برای انتشار باز است تا بیشتر آن را در امتداد محورهای اضافی خرد کند، یعنی تقسیم بعد مشخص شده لازم نیست که تقسیم بندی نهایی آن بعد باشد. این شبیه (اما نه دقیقاً مشابه) است

• jax.sharding.PartitionSpec.UNCONSTRAINED
• unspecified_dims GSPMD

اگر یک بعد باز است یک ? به دنبال محورهایی که ابعاد قبلاً بر روی آنها تقسیم شده است (نمونه زیر را ببینید).

بسته شد

بعد بسته، ابعادی است که برای انتشار برای افزودن به اشتراک گذاری بیشتر در دسترس نیست، یعنی تقسیم بندی بعد مشخص شده، تقسیم بندی نهایی آن بعد است و نمی توان آن را تغییر داد. یک مورد معمول استفاده از آن این است که چگونه GSPMD (معمولاً) آرگومان های ورودی/خروجی یک ماژول را تغییر نمی دهد، یا اینکه چگونه با jax.jit ، کاربر مشخص شده in_shardings ثابت است - آنها نمی توانند تغییر کنند.

می‌توانیم مثال را از بالا گسترش دهیم تا یک بعد باز و یک بعد بسته داشته باشیم.

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>

محورهای صراحتاً تکرار شده

مجموعه ای از محورهای صریح که یک تانسور روی آن تکثیر می شود. در حالی که می توان تشخیص داد که تانسوری که روی یک محور تکه تکه نشده است به طور ضمنی روی آن تکثیر می شود (مانند jax.sharding.PartitionSpec امروز)، داشتن صریح آن اطمینان حاصل می کند که انتشار نمی تواند از این محورها برای تقسیم بعدی بعد باز با آن محورها استفاده کند. با همانندسازی ضمنی، یک تانسور را می توان بیشتر تقسیم کرد. اما با تکرار صریح، هیچ چیز نمی تواند تانسور را در امتداد آن محور تقسیم کند.

ترتیب محورهای تکرار شده تاثیری بر نحوه ذخیره داده های یک تانسور ندارد. اما، فقط برای سازگاری، محورها به ترتیبی که در مش سطح بالایی مشخص شده اند ذخیره می شوند. به عنوان مثال، اگر مش است:

@mesh_xy = <["c"=2, "a"=2, "b"=2]>

و ما می خواهیم محورهای "a" و "c" به صراحت تکرار شوند، ترتیب باید به صورت زیر باشد:

replicated={"c", "a"}

می‌توانیم مثال خود را از بالا بسط دهیم تا یک محور صریحاً تکرار شده داشته باشیم.

@mesh_xyz = <["x"=2, "y"=4, "z"=2]>

// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would // be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>

شکاف محور و محورهای فرعی

یک شبکه منطقی از n محور با تغییر شکل یک آرایه 1 بعدی از دستگاه ها به یک آرایه n بعدی ایجاد می شود که در آن هر بعد یک محور با نام تعریف شده توسط کاربر را تشکیل می دهد.

همین فرآیند را می توان در کامپایلر انجام داد تا یک محور به اندازه k بیشتر به m محورهای فرعی تقسیم کرد، با تغییر شکل مش از [...,k,...] به [...,k1,...,km,...] .

انگیزه

برای درک انگیزه پشت محورهای تقسیم، به مثال زیر نگاه می کنیم:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>

ما می خواهیم نتیجه تغییر شکل را به گونه ای تقسیم کنیم که از ارتباط جلوگیری شود (یعنی داده ها را در جایی که هستند نگه داریم). از آنجایی که اندازه "x" بزرگتر از بعد 1 نتیجه است، باید محور را به دو محور فرعی "x.0" و "x.1" با اندازه 2 تقسیم کنیم و بعد اول را بر روی آن خرد کنیم. "x.0" و بعد دوم در "x.1" .

عملکرد اشتراک گذاری ورودی/خروجی

ممکن است در حین انتشار، ورودی یا خروجی تابع اصلی در امتداد یک محور فرعی خرد شود. این می‌تواند برای برخی از فریم‌ورک‌ها مشکل‌ساز باشد، جایی که نمی‌توانیم چنین تقسیم‌بندی‌هایی را برای بازپرداخت به کاربر بیان کنیم (مثلاً در JAX نمی‌توانیم محورهای فرعی را با jax.sharding.NamedSharding بیان کنیم).

ما چند گزینه برای مقابله با چنین مواردی داریم:

• اجازه دهید، و شاردینگ را در قالب دیگری برگردانید (مثلاً jax.sharding.PositionalSharding به جای jax.sharding.NamedSharding در JAX).
• محورهای فرعی را که ورودی/خروجی را خرد می کنند، مجاز نکنید و همه آنها را جمع آوری کنید.

در حال حاضر ما به محورهای فرعی روی ورودی/خروجی ها در خط لوله انتشار اجازه می دهیم. اگر راهی برای غیرفعال کردن آن می‌خواهید به ما اطلاع دهید.

نمایندگی

همانطور که می‌توانیم محورهای کامل مشخصی از مش را با نام آنها ارجاع دهیم، می‌توانیم به محورهای فرعی خاص با اندازه آنها و حاصل ضرب اندازه‌های زیر محورها (با همان نام محور) در سمت چپ آنها (که عبارتند از عمده به آنها) .

برای استخراج یک محور فرعی خاص به اندازه k از یک محور کامل "x" با اندازه n ، اندازه n (در مش) را به طور موثر به [m, k, n/(m*k)] تغییر می دهیم و از 2 استفاده می کنیم. بعد به عنوان محور فرعی بنابراین یک محور فرعی را می توان با دو عدد m و k مشخص کرد و از نماد مختصر زیر برای نشان دادن محورهای فرعی استفاده می کنیم: "x":(m)k .

• m>=1 پیش اندازه این محور فرعی است ( m باید مقسوم علیه n باشد). پیش اندازه حاصلضرب تمام اندازه های زیر محور در سمت چپ (که عمده به) این محور فرعی است (اگر برابر با 1 باشد، به این معنی است که هیچ یک وجود ندارد، اگر بزرگتر از 1 باشد، مربوط به یک زیر یک یا چندگانه است. -تبر).

• k>1 اندازه واقعی این محور فرعی است ( k باید مقسوم علیه n باشد).

• n/(m*k) اندازه پست است. حاصلضرب تمام اندازه‌های زیرمحور در سمت راست (که جزئی هستند) این محور فرعی است (اگر برابر با 1 باشد به این معنی است که هیچ‌یک وجود ندارد، اگر بزرگ‌تر از 1 باشد مربوط به یک یا چند محور فرعی است) .

با این حال، تعداد محورهای فرعی دیگر هنگام استفاده از یک محور فرعی خاص "x":(m)k تفاوتی ایجاد نمی کند، و هر محور فرعی دیگری نیازی به ارجاع در تقسیم بندی تانسور ندارد. یک بعد را تکه تکه نمی کند یا به صراحت تکرار می شود.

با بازگشت به مثال در بخش انگیزه ، می توانیم نتیجه را به صورت زیر تقسیم کنیم:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
    : (tensor<8xf32>) -> tensor<2x4xf32>

در اینجا مثال دیگری از یک محور تقسیم شده است که در آن فقط برخی از محورهای فرعی آن استفاده می شود.

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Axis "y" is effectively split into 3 sub-axes denoted as
//   "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>

به طور مشابه، دو تقسیم بندی زیر از نظر معنایی معادل هستند. ما می توانیم mesh_xy را به عنوان یک تقسیم mesh_full در نظر بگیریم.

@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>

sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>

محورهای فرعی به صراحت تکرار شده است

علاوه بر اینکه از محورهای فرعی برای ابعاد خرد شده استفاده می‌شود، می‌توان آنها را به‌عنوان صراحتاً تکرار شده نیز علامت‌گذاری کرد. ما این را در نمایش مجاز می‌دانیم زیرا محورهای فرعی دقیقاً مانند محورهای کامل رفتار می‌کنند، یعنی وقتی یک بعد را در امتداد یک محور فرعی از محور "x" تقسیم می‌کنید، سایر محورهای فرعی "x" به طور ضمنی تکرار می‌شوند، و بنابراین می‌توانند به صراحت تکرار می شود تا نشان دهد که یک محور فرعی باید تکرار شود و نمی توان از آن برای خرد کردن یک بعد استفاده کرد.

به عنوان مثال:

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>

محورهای فرعی تکرار شده همان محور کامل باید به ترتیب افزایش بر اساس اندازه اولیه آنها ترتیب داده شوند، به عنوان مثال:

replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}

متغیرها

• محورهای فرعی ارجاع شده در تقسیم بندی تانسور نباید همپوشانی داشته باشند، به عنوان مثال "x":(1)4 و "x":(2)4 همپوشانی دارند.

• محورهای فرعی که در تقسیم بندی تانسور ارجاع داده می شوند باید تا حد امکان بزرگ باشند، به عنوان مثال اگر یک تقسیم بعدی دارای دو محور فرعی A و B در مجاورت یکدیگر باشد، یا محورهای فرعی A و B به صراحت تکرار شوند، آنها نباید متوالی باشند، مثلا "x":(1)2 و "x":(2)4 که می توانند با یک "x":(1)8 جایگزین شوند.

مش های منطقی متعدد

یکی از مش های منطقی، نمای چند بعدی از دستگاه ها است. ما ممکن است به چندین نما از دستگاه ها برای نشان دادن به اشتراک گذاری های خود نیاز داشته باشیم، به خصوص برای تخصیص دلخواه دستگاه.

برای مثال، jax.sharding.PositionalSharding یک مش منطقی مشترک ندارد . GSPMD در حال حاضر با HloSharding از آن پشتیبانی می‌کند، جایی که نمایش می‌تواند فهرستی از دستگاه‌ها و اندازه‌های ابعادی باشد، اما نمی‌توان آن را با تقسیم محور بالا نشان داد.

ما بر این محدودیت غلبه می کنیم و با تعریف چندین مش منطقی در سطح بالای برنامه، موارد گوشه موجود را مدیریت می کنیم. هر مش می‌تواند تعداد محورهای متفاوتی با نام‌های متفاوت داشته باشد، همچنین تخصیص دلخواه خود برای مجموعه‌ای از دستگاه‌ها، یعنی هر مش به مجموعه‌ای از دستگاه‌ها (با شناسه منطقی منحصربه‌فردشان) اشاره دارد، اما با ترتیب دلخواه، مشابه نمایش GSPMD.

هر نمایش شاردینگ به یک مش منطقی خاص مرتبط است، بنابراین فقط به محورهای آن مش اشاره می کند.

تانسوری که به یک مش منطقی اختصاص داده می‌شود، می‌تواند توسط عملیاتی که به مش دیگری اختصاص داده می‌شود، با ساده‌لوحانه‌سازی مجدد تانسور برای مطابقت با مش مقصد استفاده شود. در GSPMD این کاری است که معمولا برای حل مش های متضاد انجام می شود.

در زیر دو مثال ارائه می دهیم:

کاربران می‌توانند مش‌های متعددی را با محورهای نام‌گذاری متفاوت (مثلاً از طریق jax.sharding.NamedSharding ) که ترتیب دستگاه‌های یکسانی دارند، مشخص کنند. در این مثال، <@mesh_0, "b"> با <@mesh_1, "z">.

@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}

اولویت ها

اولویت راهی برای اولویت دادن به تصمیمات پارتیشن بندی + انتشار بر سایرین است و امکان پارتیشن بندی تدریجی یک برنامه را فراهم می کند.

اولویت ها مقادیری هستند که به برخی یا همه ابعاد یک نمایش تقسیم بندی متصل می شوند (محورهای تکراری اولویت ندارند).

به عنوان مثال:

@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>

//                                    |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>

اولویت‌ها به کاربران کنترل دقیق‌تری بر انتشار می‌دهند، به‌عنوان مثال، ابتدا موازی‌سازی دسته‌ای، سپس مگاترون، و در نهایت تقسیم‌بندی ZeRO. این اجازه می دهد برای تضمین قوی در مورد آنچه پارتیشن بندی شده است و برای اشکال زدایی بهتر با داشتن استراتژی های ریز دانه دانه بیشتر اجازه می دهد تا (می توانید ببینید که چگونه برنامه پس از مگاترون در انزوا نگاه می کند).

ما اجازه می‌دهیم یک اولویت به هر تقسیم‌بندی بعد (به طور پیش‌فرض 0) الصاق کنیم، که نشان می‌دهد همه تقسیم‌بندی‌های با اولویت <i قبل از تقسیم‌بندی با اولویت i به کل برنامه منتشر می‌شوند.

حتی اگر یک تقسیم بندی دارای یک بعد باز با اولویت پایین تر باشد، به عنوان مثال، {"z",?}p2 , در حین انتشار توسط تقسیم بندی تانسور دیگری با اولویت بالاتر لغو نمی شود. با این حال، چنین بعد باز می‌تواند پس از انتشار همه خرده‌کاری‌های با اولویت بالاتر، بیشتر خرد شود.

به عبارت دیگر، اولویت‌ها این نیست که کدام بعد مهم‌تر از دیگری است - این ترتیبی است که گروه‌های متمایز از تقسیم‌بندی ابعاد باید در کل برنامه منتشر شوند و چگونه تضادها در تانسورهای میانی و بدون حاشیه‌نویسی باید حل شوند.

متغیرها

• اولویت‌ها از 0 شروع می‌شوند (بالاترین اولویت) و افزایش می‌یابند (برای اینکه به کاربران اجازه دهیم اولویت‌ها را به راحتی اضافه و حذف کنند، فاصله بین اولویت‌ها را مجاز می‌کنیم، به عنوان مثال، p0 و p2 استفاده می‌شوند اما p1 استفاده نمی‌شود).

• اشتراک گذاری ابعاد بسته خالی (یعنی {} ) نباید اولویت داشته باشد، زیرا این کار هیچ تأثیری نخواهد داشت.

تقسیم پذیری ابعاد

ممکن است ابعادی به اندازه d در امتداد محورهایی که حاصل ضرب اندازه آنها n است تقسیم شود، به طوری که d بر n قابل تقسیم نباشد (که در عمل مستلزم اضافه کردن ابعاد است).

به عنوان مثال:

@mesh_xy = <["x"=8, "y"=2, "z"=3]>

sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>

گرامر

هر مش منطقی به صورت زیر تعریف می شود:

@mesh_name = <mesh_axis_1,...,mesh_axis_n>

mesh_axis ::= axis_name=axis_size

axis_name ::= str
axis_size ::= int

نمایش شاردینگ ساختار زیر را برای تانسور رتبه r خواهد داشت:

sharding<@mesh_name, dim_shardings, replicated=replicated_axes}

mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}

dim_sharding ::=
  {axis_1,...,axis_k} |  // closed dimension
  {axis_1,...,axis_k,?}  // open dimension

axis ::=
  axis_name  |   // a full axis
  sub_axis             // a sub axis

axis_name ::= str

sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int