Sfondo
Lo scopo della rappresentazione dello sharding è specificare in che modo un tensore viene suddiviso in parti rispetto a un insieme di dispositivi disponibili.
La rappresentazione del partizionamento può essere:
- Specificati manualmente dall'utente come vincoli di suddivisione in input, output o intermediari.
- Trasformato per operazione durante il processo di propagazione dello sharding.
Panoramica
Struttura di base
Una mesh logica è una visualizzazione multidimensionale dei dispositivi, definita da un elenco di nomi e dimensioni degli assi.
La rappresentazione dello sharding proposta è associata a una mesh logica specifica per il suo nome e può fare riferimento solo ai nomi degli assi di quella mesh. La suddivisione di un tensore specifica lungo quali assi (di una mesh logica specifica) viene suddivisa ogni dimensione del tensore, in ordine dal maggiore al minore. Il tensore viene replicato su tutti gli altri assi della mesh.
Esploriamo la rappresentazione dello sharding con un semplice tensore di rango 2 e 4 dispositivi.
Per prima cosa, rimodelliamo i 4 dispositivi [0, 1, 2, 3] in un array 2D [[0, 1], [2,
3]] per creare una mesh con 2 assi:
@mesh_xy = <["x"=2, "y"=2]>
Possiamo quindi suddividere il seguente tensore di rango 2 [[a, b], [c, d]] come segue:
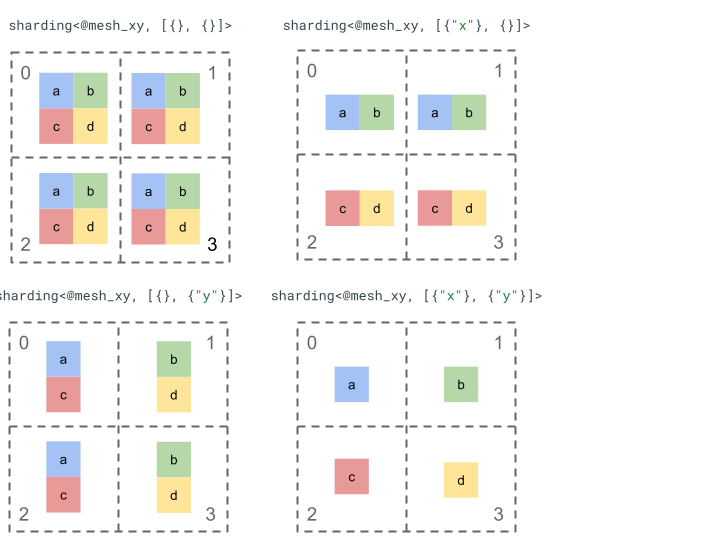
Altri componenti chiave
- Dimensioni aperte/chiuse: le dimensioni possono essere aperte, quindi possono essere ulteriormente suddivise in base agli assi disponibili, oppure chiuse, quindi fisse e non modificabili.
- Assi replicati esplicitamente: tutti gli assi che non vengono utilizzati per suddividere una dimensione vengono replicati implicitamente, ma il suddivisione può specificare assi replicati esplicitamente e pertanto non possono essere utilizzati per suddividere una dimensione in un secondo momento.
- Suddivisione degli assi e assi secondari: un asse della maglia (completo) può essere suddiviso in più assi secondari che possono essere utilizzati singolarmente per suddividere una dimensione o essere replicati esplicitamente.
- Più mesh logici: è possibile associare diversi sharding a mesh logici diversi, che possono avere assi diversi o anche un ordine diverso degli ID dispositivo logici.
- Priorità: per partizionare un programma in modo incrementale, le priorità possono essere associate ai suddivisioni delle dimensioni, che determinano in quale ordine i vincoli di suddivisione per dimensione verranno propagati nel modulo.
- Divisibilità del frazionamento delle dimensioni: una dimensione può essere frazionata in base ad assi il cui prodotto delle dimensioni non divide la dimensione.
Progetto dettagliato
In questa sezione espandiamo la struttura di base e ogni componente chiave.
Struttura di base
I partizionamenti delle dimensioni ci indicano per ogni dimensione del tensore lungo quali assi (o sottoassi) viene suddiviso dal maggiore al minore. Tutti gli altri assi che non eseguono lo shard di una dimensione vengono replicati implicitamente (o esplicitamente).
Inizieremo con un esempio semplice e lo estenderemo man mano che descriviamo altre funzionalità.
@mesh_xy = <["x"=2, "y"=4, "z"=2]>
// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>
Invariati
- Il numero di suddivisioni delle dimensioni deve corrispondere al rango del tensore.
- Tutti i nomi degli assi devono esistere nel mesh a cui viene fatto riferimento.
- Gli assi o gli assi secondari possono apparire una sola volta nella rappresentazione dello sharding (ognuno suddivide una dimensione o viene replicato esplicitamente).
Dimensioni aperte/chiuse
Ogni dimensione di un tensore può essere aperta o chiusa.
Apri
Una dimensione aperta è disponibile per la propagazione per suddividerla ulteriormente in base ad altri assi, ovvero lo sharding della dimensione specificata non deve essere necessariamente quello finale. È simile (ma non esattamente uguale) a unspecified_dims di GSMPD.
Se una dimensione è aperta, aggiungi un ? dopo gli assi su cui è già suddivisa (vedi l'esempio di seguito).
Chiuso
Una dimensione chiusa non è disponibile per la propagazione a cui aggiungere un ulteriore suddivisione, ovvero la suddivisione della dimensione specificata è la suddivisione finale della dimensione e non può essere modificata. Un caso d'uso comune è il modo in cui GSPMD
(di solito) non modifica gli argomenti di input/output di un modulo o il modo in cui con
jax.jit, gli in_shardings specificati dall'utente sono statici e non possono cambiare.
Possiamo estendere l'esempio riportato sopra per avere una dimensione aperta e una chiusa.
@mesh_xy = <["x"=2, "y"=4, "z"=2]>
// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>
Assi replicati esplicitamente
Un insieme esplicito di assi su cui viene replicato un tensore. Anche se è possibile determinare che un tensore non suddiviso in parti su un asse viene replicato implicitamente su di esso (come accade oggi per jax.sharding.PartitionSpec), la sua esplicitazione garantisce che la propagazione non possa utilizzare questi assi per suddividere ulteriormente una dimensione aperta con questi assi. Con la replica implicita, un
tensore può essere ulteriormente partizionato. Tuttavia, con la replica esplicita, nulla può
partizionare il tensore lungo quell'asse.
L'ordinamento degli assi replicati non influisce sul modo in cui vengono archiviati i dati di un tensore. Tuttavia, solo per coerenza, gli assi verranno memorizzati nell'ordine in cui sono specificati nel mesh di primo livello. Ad esempio, se la maglia è:
@mesh_xy = <["c"=2, "a"=2, "b"=2]>
Vogliamo che gli assi "a" e "c" vengano replicati esplicitamente, quindi l'ordine dovrebbe essere:
replicated={"c", "a"}
Possiamo estendere l'esempio precedente per avere un asse replicato esplicitamente.
@mesh_xyz = <["x"=2, "y"=4, "z"=2]>
// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>
Suddivisione degli assi e assi secondari
Una mesh logica di assi n viene creata modificando la forma di un array 1D di dispositivi in un array n-dimensionale, in cui ogni dimensione forma un asse con un nome definito dall'utente.
La stessa procedura può essere eseguita nel compilatore per suddividere ulteriormente un asse di dimensioni k in m assi secondari, rimodellando la mesh da [...,k,...] in [...,k1,...,km,...].
Motivazione
Per comprendere il motivo alla base della suddivisione degli assi, esamineremo il seguente esempio:
@mesh_x = <["x"=4]>
%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>
Vogliamo suddividere il risultato della trasformazione in modo da evitare la comunicazione (ovvero mantenere i dati invariati). Poiché la dimensione di "x" è superiore alla prima dimensione del risultato, dobbiamo suddividere l'asse in due assi secondari "x.0" e "x.1" di dimensione 2 ciascuno e suddividere la prima dimensione su "x.0" e la seconda dimensione su "x.1".
Sharding di input/output delle funzioni
È possibile che durante la propagazione un input o un output della funzione principale venga suddiviso in un sottoasse. Questo può essere un problema per alcuni framework,
in cui non possiamo esprimere questi suddivisioni da restituire all'utente (ad es. in JAX non possiamo esprimere gli assi secondari con
jax.sharding.NamedSharding).
Abbiamo alcune opzioni per gestire questi casi:
- Consenti e restituisci lo sharding in un formato diverso (ad es.
jax.sharding.PositionalShardinginstead ofjax.sharding.NamedShardingin JAX). - Non consentire e sottoassi all-gather che eseguono lo shard di input/output.
Al momento consentiamo assi secondari per gli input/output nella pipeline di propagazione. Facci sapere se vuoi un modo per disattivare questa funzionalità.
Rappresentazione
Allo stesso modo in cui possiamo fare riferimento ad assi completi specifici della mesh in base al nome, possiamo fare riferimento a assi secondari specifici in base alle dimensioni e al prodotto di tutte le dimensioni degli assi secondari (con lo stesso nome dell'asse) a sinistra (che sono principali per loro).
Per estrarre un asse secondario specifico di dimensione k da un asse completo "x" di dimensione n,
modifichiamo in modo efficace la dimensione n (nella mesh) in [m, k, n/(m*k)] e utilizziamo
la seconda dimensione come asse secondario. Un asse secondario può quindi essere specificato da due
numeri, m e k, e utilizziamo la seguente notazione concisa per indicare
gli assi secondari: "x":(m)k.
m>=1è la predimensione di questo asse secondario (mdeve essere un divisore din). La predimensione è il prodotto di tutte le dimensioni degli assi secondari a sinistra di (che sono maggiori di) questo asse secondario (se è uguale a 1 significa che non ce ne sono, se è maggiore di 1 corrisponde a uno o più assi secondari).k>1è la dimensione effettiva di questo asse secondario (kdeve essere un divisore din).n/(m*k)è la dimensione post. È il prodotto di tutte le dimensioni dei sottoassi a destra di (che sono inferiori a) questo sottoasse (se è uguale a 1, significa che non ce ne sono, se è maggiore di 1, corrisponde a uno o più sottoassi).
Tuttavia, il numero di altri assi secondari non fa alcuna differenza quando si utilizza un asse secondario specifico "x":(m)k e non è necessario fare riferimento a nessun altro asse secondario nello sharding del tensore se non esegue lo sharding di una dimensione o viene replicato esplicitamente.
Tornando all'esempio nella sezione Motivazione, possiamo suddividere il risultato come segue:
@mesh_x = <["x"=4]>
%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
: (tensor<8xf32>) -> tensor<2x4xf32>
Ecco un altro esempio di un'asse suddiviso in cui vengono utilizzati solo alcuni dei relativi assi secondari.
@mesh_xyz = <["x"=2, "y"=8, "z"=2]>
// Axis "y" is effectively split into 3 sub-axes denoted as
// "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>
Analogamente, i seguenti due shard sono semanticamente equivalenti. Possiamo pensare
mesh_xy come una scissione di mesh_full.
@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>
sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>
Assi secondari replicati esplicitamente
Oltre a essere utilizzati per suddividere la dimensione, gli assi secondari possono anche essere contrassegnati come replicati esplicitamente. Lo consentiamo nella rappresentazione perché gli assi secondari si comportano esattamente come gli assi completi, ovvero quando esegui lo shard di una dimensione lungo un asse secondario dell'asse "x", gli altri assi secondari di "x" vengono replicati in modo implicito e quindi possono essere replicati in modo esplicito per indicare che un asse secondario deve rimanere replicato e non può essere utilizzato per eseguire lo shard di una dimensione.
Ad esempio:
@mesh_xyz = <["x"=2, "y"=8, "z"=2]>
// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>
L'asse secondario replicato dello stesso asse completo deve essere ordinato in ordine crescente in base alle dimensioni predefinite, ad esempio:
replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}
Invariati
Gli assi secondari a cui si fa riferimento in uno sharding del tensore non devono sovrapporsi, ad esempio
"x":(1)4e"x":(2)4si sovrappongono.Gli assi secondari a cui si fa riferimento in uno sharding del tensore devono essere il più grandi possibile, ovvero se un sharding delle dimensioni ha due assi secondari adiacenti A e B in ordine o se gli assi secondari A e B sono replicati esplicitamente, non devono essere consecutivi, ad esempio
"x":(1)2e"x":(2)4, in quanto possono essere sostituiti da un singolo"x":(1)8.
Più mesh logici
Una mesh logica è una visualizzazione multidimensionale dei dispositivi. Potremmo aver bisogno di più visualizzazioni dei dispositivi per rappresentare i nostri shard, in particolare per le assegnazioni arbitrarie dei dispositivi.
Ad esempio,
jax.sharding.PositionalSharding non ha una maglia logica comune.
Al momento GSPMD supporta questa funzionalità con HloSharding, in cui la rappresentazione può essere un elenco ordinato di dispositivi e dimensioni, ma non può essere rappresentata con la suddivisione dell'asse sopra indicata.
Superiamo questa limitazione e gestiamo i casi limite esistenti definendo più mesh logici a livello superiore del programma. Ogni mesh può avere un numero diverso di assi con nomi diversi, nonché la propria assegnazione arbitraria per lo stesso insieme di dispositivi, ovvero ogni mesh si riferisce allo stesso insieme di dispositivi (in base al relativo ID logico univoco), ma con un ordine arbitrario, simile alla rappresentazione GSMPD.
Ogni rappresentazione di sharding è collegata a una mesh logica specifica, pertanto farà riferimento solo agli assi di quella mesh.
Un tensore assegnato a una mesh logica può essere utilizzato da un'operazione assegnata a una mesh diversa, ridistribuendo il tensore in modo ingenuo in modo che corrisponda alla mesh di destinazione. In GSPMD, questo è ciò che viene solitamente fatto per risolvere i reticoli in conflitto.
Gli utenti possono specificare più maglie con assi denominati diversi (ad es. viajax.sharding.NamedSharding), che hanno lo stesso ordine di dispositivi. Considera questo esempio: <@mesh_0, "b"> è identico a <@mesh_1, "z">:
@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
Priorità
La priorità è un modo per dare la priorità ad alcune decisioni di partizione e propagazione rispetto ad altre e consente la partizione incrementale di un programma.
Le priorità sono valori associati ad alcune o a tutte le dimensioni di una rappresentazione con suddivisione (gli assi replicati non hanno priorità).
Ad esempio:
@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>
// |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>
Le priorità offrono agli utenti un controllo più granulare sulla propagazione, ad esempio, prima il parallelismo batch, poi Megatron e infine lo sharding ZeRO. In questo modo, si ottengono forti garanzie su ciò che viene partizionato e si migliora la possibilità di eseguire il debug grazie a strategie di suddivisione più granulari (puoi vedere l'aspetto del programma dopo solo Megatron in isolamento).
Consentiamo di associare una priorità a ogni suddivisione della dimensione (0 per impostazione predefinita), che indica che tutti i suddivisioni con priorità <i verranno propagate all'intero programma prima di quelle con priorità i.
Anche se uno sharding ha una dimensione aperta con priorità inferiore, ad esempio {"z",?}p2,
non verrà sostituito da un altro sharding del tensore con una priorità più alta durante la propagazione. Tuttavia, una dimensione aperta può essere ulteriormente suddivisa dopo la propagazione di tutti gli sharding con priorità più elevata.
In altre parole, le priorità NOT riguardano quale suddivisione delle dimensioni è più importante di un'altra, ma l'ordine in cui gruppi distinti di suddivisioni delle dimensioni devono essere propagati all'intero programma e la modalità di risoluzione dei conflitti sui tensori intermedi non annotati.
Invariati
Le priorità iniziano da 0 (priorità più alta) e aumentano (per consentire agli utenti di aggiungere e rimuovere facilmente le priorità, consentiamo spazi tra le priorità, ad es. vengono utilizzati p0 e p2, ma non p1).
Un suddivisione delle dimensioni chiuse vuota (ad es.
{}), non deve avere una priorità, poiché non avrà alcun effetto.
Suddivisione delle dimensioni
È possibile che una dimensione di dimensioni d venga suddivisa in parti lungo assi il cui prodotto
delle dimensioni è n, in modo che d non sia divisibile per n (il che in pratica richiederebbe
di aggiungere spazi aggiuntivi alla dimensione).
Ad esempio:
@mesh_xy = <["x"=8, "y"=2, "z"=3]>
sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>
Grammatica
Ogni mesh logico è definito come segue:
@mesh_name = <mesh_axis_1,...,mesh_axis_n>
mesh_axis ::= axis_name=axis_size
axis_name ::= str
axis_size ::= int
La rappresentazione dello shard avrà la seguente struttura per un tensore di rango r:
sharding<@mesh_name, dim_shardings, replicated=replicated_axes}
mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}
dim_sharding ::=
{axis_1,...,axis_k} | // closed dimension
{axis_1,...,axis_k,?} // open dimension
axis ::=
axis_name | // a full axis
sub_axis // a sub axis
axis_name ::= str
sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int
