Parçalama Temsili

Arka plan

Bölme temsilinin amacı, bir tenzorun mevcut cihazlar kümesine göre nasıl bölündüğünü belirtmektir.

Bölme temsili şu şekilde olabilir:

• Girişler, çıkışlar veya ara öğeler üzerinde parçalama kısıtlamaları olarak kullanıcı tarafından manuel olarak belirtilir.
• Bölme yayma sürecinde işlem başına dönüştürülür.

Genel Bakış

Temel yapı

Mantıksal ağ, cihazların eksen adları ve boyutları listesiyle tanımlanan çok boyutlu bir görünümüdür.

Önerilen bölme temsili, adıyla belirli bir mantıksal ağa bağlıdır ve yalnızca bu ağdaki eksen adlarını referans alabilir. Bir tensörün bölümlenmesi, tensörün her boyutunun hangi eksenler (belirli bir mantıksal örgünün) boyunca, büyükten küçüğe sırayla bölümlendiğini belirtir. Tensör, ağın diğer tüm eksenleri boyunca kopyalanır.

Basit bir 2. sıralı tenör ve 4 cihazla bölümleme gösterimini keşfedelim.

Öncelikle 2 eksenli bir ağ oluşturmak için 4 cihazı [0, 1, 2, 3] 2 boyutlu bir dizi [[0, 1], [2, 3]] olarak yeniden şekillendiririz:

@mesh_xy = <["x"=2, "y"=2]>

Ardından aşağıdaki 2. sıralı tenzor [[a, b], [c, d]]'ü aşağıdaki gibi parçalara ayırabiliriz:

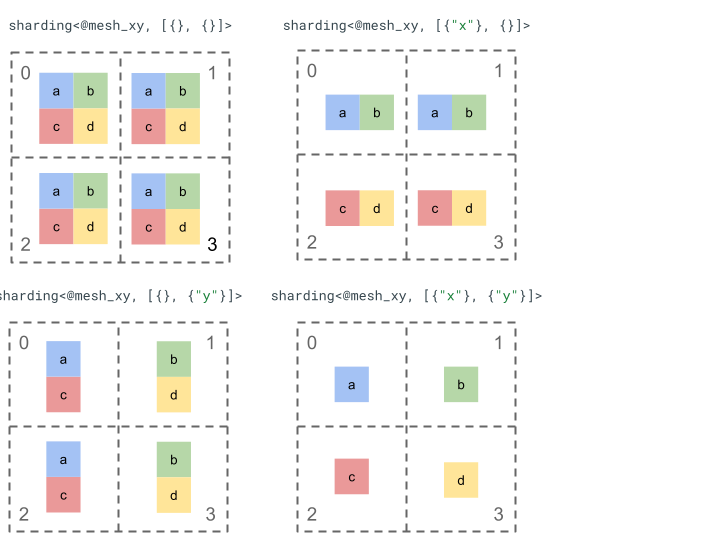
Diğer önemli bileşenler

• Açık/Kapalı boyutlar: Boyutlar açık olabilir (mevcut eksenler üzerinde daha fazla bölünebilir) veya kapalı olabilir (sabit olup değiştirilemez).
• Açıkça kopyalanan eksenler: Bir boyutu bölme işleminde kullanılmayan tüm eksenler açıkça kopyalanır ancak bölme işlemi, açıkça kopyalanan eksenleri belirtebilir ve bu nedenle daha sonra bir boyutu bölme işleminde kullanılamaz.
• Ekseni bölme ve alt eksenler: Bir (tam) ağ ekseni, bir boyutu bölme veya açıkça çoğaltmak için ayrı ayrı kullanılabilecek birden çok alt eksene bölünebilir.
• Birden fazla mantıksal ağ: Farklı bölme işlemleri farklı mantıksal ağlara bağlanabilir. Bu ağlar farklı eksenlere veya hatta farklı mantıksal cihaz kimliği sırasına sahip olabilir.
• Öncelikler: Bir programı kademeli olarak bölümlemek için boyut bölmelerine öncelik eklenebilir. Bu öncelik, boyut başına bölme kısıtlamalarının modülde hangi sırayla dağıtılacağını belirler.
• Boyut bölme işleminin bölünebilirliği: Bir boyut, boyutlarının çarpımı boyut boyutunu bölmeyen eksenlerde bölünebilir.

Ayrıntılı Tasarım

Bu bölümde temel yapıyı ve her bir temel bileşeni ayrıntılı olarak ele alıyoruz.

Temel yapı

Boyut bölme işlemleri, tensörün her boyutu için hangi eksenler (veya alt eksenler) boyunca büyükten küçüğe doğru bölündüğünü bize bildirir. Bir boyutu bölmeyen diğer tüm eksenler dolaylı olarak çoğaltılır (veya açıkça çoğaltılır).

Basit bir örnekle başlayıp ek özellikleri açıklarken bu örneği genişleteceğiz.

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st tensor dimension is sharded along axis "x" and the 2nd tensor dimension is
// sharded along axis "z" then further along axis "y". The local shape of this tensor (i.e. the shape on a single device), would be tensor<2x1xf32>.
sharding<@mesh_xy, [{"x"}, {"z", "y"}]> : tensor<4x8xf32>

Değişmezler

• Boyut bölmelerinin sayısı, tensörün rütbesiyle eşleşmelidir.
• Tüm eksen adları, referans verilen ağda bulunmalıdır.
• Eksenler veya alt eksenler, bölme temsilinde yalnızca bir kez görünebilir (her biri bir boyutu böler veya açıkça çoğaltılır).

Açık/kapalı boyutlar

Bir tensörün her boyutu açık veya kapalı olabilir.

Aç

Açık boyutlar, ek eksenler boyunca daha fazla bölme işlemine tabi tutulmak üzere dağıtılabilir. Yani belirtilen boyut bölme işleminin, söz konusu boyutun nihai bölme işlemi olması gerekmez. Bu,

• jax.sharding.PartitionSpec.UNCONSTRAINED
• GSPMD'nin unspecified_dims

Bir boyut açıksa boyutun zaten bölümlendirildiği eksenlerin ardından bir ? ekleriz (aşağıdaki örneğe bakın).

Kapalı

Kapalı boyut, daha fazla bölme eklemek için dağıtım için kullanılamayan boyuttur. Yani belirtilen boyut bölme işlemi, söz konusu boyutun nihai bölme işlemidir ve değiştirilemez. Bunun yaygın bir kullanım alanı, GSPMD'nin (genellikle) bir modülün giriş/çıkış bağımsız değişkenlerini değiştirmemesi veya jax.jit ile kullanıcı tarafından belirtilen in_shardings'ın statik olması (değiştirilememesi) şeklindedir.

Yukarıdaki örneği, açık ve kapalı bir boyut içerecek şekilde genişletebiliriz.

@mesh_xy = <["x"=2, "y"=4, "z"=2]>

// The 1st dimension is closed, therefore it can't be further sharded and {"x"}
// will remain its sharding. The 2nd dimension is open, and can therefore be
// further sharded during propagation, e.g. by "y".
sharding<@mesh_xy, [{"x"}, {"z", ?}]> : tensor<4x8xf32>

Açıkça kopyalanan eksenler

Bir tensörün kopyalandığı açık bir eksen grubu. Bir eksende bölümlenmemiş bir tensörün bu eksende dolaylı olarak çoğaltıldığı belirlenebilir (bugün olduğu gibi jax.sharding.PartitionSpec). Ancak açık olarak belirtilmesi, yayılmanın bu eksenleri kullanarak açık bir boyutu bu eksenlerle daha da bölümlemesini önler. Örtük çoğaltma ile bir tensör daha fazla bölümlenebilir ve bölünebilir. Ancak açık çoğaltma durumunda, hiçbir şey tensörü bu eksen boyunca bölemez.

Kopyalanan eksenlerin sıralaması, bir tenzorun verilerinin nasıl depolandığını etkilemez. Ancak yalnızca tutarlılık için eksenler, üst düzey örgede belirtildikleri sırayla saklanır. Örneğin, ağ:

@mesh_xy = <["c"=2, "a"=2, "b"=2]>

Ayrıca "a" ve "c" eksenlerinin açıkça kopyalanmasını istiyoruz. Sıralama şu şekilde olmalıdır:

replicated={"c", "a"}

Yukarıdaki örneğimizi, açıkça kopyalanan bir eksene sahip olacak şekilde genişletebiliriz.

@mesh_xyz = <["x"=2, "y"=4, "z"=2]>

// Since "y" is explicitly replicated, it can't be used to shard the 2nd
// dimension that is open. However, "z" is implicitly replicated so it can be
// used to shard that dimension. The local shape of this tensor (i.e. the
// shape on a single device), would // be tensor<2x8xf32>.
sharding<@mesh_xyz, [{"x"}, {?}], replicated={"y"}> : tensor<4x8xf32>

Eksen bölme ve alt eksenler

1 boyutlu bir cihaz dizisi n boyutlu bir diziye yeniden şekillendirilerek n eksenlerinden oluşan mantıksal bir ağ oluşturulur. Bu ağda her boyut, kullanıcı tanımlı bir ada sahip bir eksen oluşturur.

Aynı işlem, k boyutunda bir ekseni m alt eksene bölmek için derleyicide de yapılabilir. Bu işlem için [...,k,...] örgüsü [...,k1,...,km,...] olarak yeniden şekillendirilir.

Motivasyon

Eksenleri bölme motivasyonunu anlamak için aşağıdaki örneği inceleyeceğiz:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 : (tensor<8xf32>) -> tensor<2x4xf32>

Yeniden biçimlendirmenin sonucunu, iletişimi önleyecek şekilde (ör. verileri olduğu yerde tutacak şekilde) parçalara ayırmak istiyoruz. "x" boyutu, sonucun 1. boyutundan büyük olduğundan ekseni her biri 2 boyutunda iki alt eksene ("x.0" ve "x.1") bölmemiz ve 1. boyutu "x.0"'ta, 2. boyutu ise "x.1"'de bölmemiz gerekir.

İşlev giriş/çıkış bölme işlemleri

Yayma sırasında ana işlevin giriş veya çıkışının bir alt eksen boyunca bölümlenmesi mümkündür. Bu, kullanıcıya geri vermek için bu tür bölme işlemlerini ifade edemediğimiz bazı çerçeveler için sorun olabilir (ör. JAX'te alt eksenleri jax.sharding.NamedSharding ile ifade edemeyiz).

Bu tür durumlarda birkaç seçeneğimiz vardır:

• Bölme işlemine izin verin ve farklı bir biçimde döndürün (ör. JAX'te jax.sharding.NamedSharding yerine jax.sharding.PositionalSharding).
• Giriş/çıkışı bölen alt eksenlere izin vermeyin ve tümünü toplayın.

Şu anda, dağıtım ardışık düzenindeki girişlerde/çıkışlarda alt eksenlere izin veriyoruz. Bu özelliği devre dışı bırakmak isterseniz lütfen bize bildirin.

Representation

Örgüdeki belirli tam eksenlere adlarına göre referans verdiğimiz gibi, belirli alt eksenlere de boyutlarına ve sollarındaki tüm alt eksen (aynı eksen adında) boyutlarının çarpımına (kendileri için ana olan) göre referans verebiliriz.

n boyutunda bir tam eksen "x"'ten k boyutunda belirli bir alt eksen ayıklamak için n boyutunu (örgedeki) etkili bir şekilde [m, k, n/(m*k)] olarak yeniden şekillendiririz ve 2. boyutu alt eksen olarak kullanırız. Bu nedenle, bir alt eksen m ve k olmak üzere iki sayı ile belirtilebilir. Alt eksenleri belirtmek için aşağıdaki kısa gösterimi kullanırız: "x":(m)k.

• m>=1, bu alt eksenin ön boyutudur (m, n'nin böleni olmalıdır). Ön boyut, bu alt eksenin solunda (bu alt eksenden büyük) olan tüm alt eksen boyutlarının çarpımıdır (1'e eşitse hiçbir alt eksen olmadığı, 1'den büyükse tek veya birden fazla alt eksene karşılık geldiği anlamına gelir).

• k>1, bu alt eksenin gerçek boyutudur (k, n'nin böleni olmalıdır).

• n/(m*k), post-size değeridir. Bu alt eksenin sağında (bu alt eksenden küçük) tüm alt eksen boyutlarının çarpımıdır (1'e eşitse hiçbir alt eksen olmadığı, 1'den büyükse tek veya birden fazla alt eksene karşılık geldiği anlamına gelir).

Ancak belirli bir alt eksen "x":(m)k kullanıldığında diğer alt eksenlerin sayısı fark etmez ve bir boyutu bölemezse veya açıkça çoğaltılmazsa diğer alt eksenlerin tensör bölme işleminde referans gösterilmesi gerekmez.

Motivasyon bölümündeki örneğe dönecek olursak sonucu aşağıdaki gibi bölebiliyoruz:

@mesh_x = <["x"=4]>

%arg0 : tensor<8xf32> {sdy.sharding=<@mesh_x, [{"x"}]>}
%0 = reshape %arg0 {sdy.sharding_per_value=<[<@mesh_x, [{"x":(1)2}, {"x":(2)2}]>]>}
    : (tensor<8xf32>) -> tensor<2x4xf32>

Alt eksenlerinin yalnızca bazılarının kullanıldığı bölünmüş eksene dair başka bir örnek aşağıda verilmiştir.

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Axis "y" is effectively split into 3 sub-axes denoted as
//   "y":(1)2, "y":(2)2, "y":(4)2
// in order, but only "y":(2)2 is used, to shard the 2nd dimension. The local
// shape of this tensor (i.e. the shape on a single device), would be
// tensor<2x4xf32>.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}]> : tensor<4x8xf32>

Benzer şekilde, aşağıdaki iki bölme semantik olarak eşdeğerdir. mesh_xy'ü mesh_full'un bölünmesi olarak düşünebiliriz.

@mesh_full = <"devices"=8>
@mesh_xy = <"x"=4, "y"=2>

sharding<@mesh_xy, [{"x"},{ "y"}]> : tensor<4x4xf32>
sharding<@mesh_full, [{"devices":(1)4}, {"devices":(4)2}]> : tensor<4x4xf32>

Açıkça çoğaltılan alt eksenler

Boyutu bölme amacıyla kullanılan alt eksenler, açıkça çoğaltılmış olarak da işaretlenebilir. Alt eksenler tam eksenler gibi davrandığından, temsilde buna izin verilir.Yani bir boyutu "x" ekseninin bir alt ekseni boyunca bölerseniz "x"'nin diğer alt eksenleri dolaylı olarak çoğaltılır. Bu nedenle, bir alt eksenin çoğaltılmış kalması ve bir boyutu bölme için kullanılamaması gerektiğini belirtmek üzere açıkça çoğaltılabilir.

Örneğin:

@mesh_xyz = <["x"=2, "y"=8, "z"=2]>

// Sub-axis "y":(1)2 is explicitly replicated and "y":(4)2 is implicitly replicated.
sharding<@mesh_xyz, [{"x"}, {"y":(2)2}], replicated={"y":(1)2}> : tensor<4x8xf32>

Aynı tam eksenin kopyalanan alt eksenleri, ön boyutlarına göre artan düzende sıralanır. Örneğin:

replicated={"y":(4)2, "x", "y":(1)2} ~> replicated={"x", "y":(1)2, "y":(4)2}

Değişmezler

• Bir tensör bölme işleminde referans verilen alt eksenler çakışmamalıdır (ör. "x":(1)4 ve "x":(2)4 çakışmamalıdır).

• Bir tensör bölme işleminde referans verilen alt eksenler mümkün olduğunca büyük olmalıdır. Yani, bir boyut bölme işleminde sırayla A ve B olmak üzere iki bitişik alt eksen varsa veya A ve B alt eksenleri açıkça kopyalanmışsa bunlar tek bir "x":(1)8 ile değiştirilebileceğinden ardışık olmamalıdır (ör. "x":(1)2 ve "x":(2)4).

Birden fazla mantıksal ağ

Mantıksal ağ, cihazların çok boyutlu bir görünümüdür. Özellikle rastgele cihaz atamaları için bölmelerimizi temsil etmek üzere cihazların birden fazla görünümüne ihtiyacımız olabilir.

Örneğin, jax.sharding.PositionalSharding'nin ortak bir mantıksal örgüsü yoktur. GSPMD şu anda HloSharding ile bunu desteklemektedir. Burada temsil, cihazların ve boyut boyutlarının sıralı bir listesi olabilir ancak bu, yukarıdaki eksen bölme ile temsil edilemez.

Programın üst düzeyinde birden fazla mantıksal ağ tanımlayarak bu sınırlamayı aşar ve mevcut özel durumları ele alırız. Her ağ, farklı adlara sahip farklı sayıda eksene ve aynı cihaz grubu için kendi rastgele atamasına sahip olabilir. Yani her ağ, aynı cihaz grubunu (benzersiz mantıksal kimliklerine göre) ifade eder ancak GSPMD temsiline benzer şekilde rastgele bir sırayla ifade eder.

Her bir bölme temsili belirli bir mantıksal ağa bağlıdır. Bu nedenle, yalnızca söz konusu ağdaki eksenlere referans verir.

Bir mantıksal ağa atanmış bir tensör, farklı bir ağa atanmış bir işlem tarafından kullanılabilir. Bu işlem, hedef ağ ile eşleşecek şekilde tenzoru basitçe yeniden böler. GSPMD'de, çakışan ağları çözmek için genellikle bu işlem yapılır.

Aşağıda iki örnek verilmiştir:

Kullanıcılar, farklı adlandırılmış eksenleri olan (ör. jax.sharding.NamedSharding aracılığıyla) ve aynı cihaz sırasına sahip birden fazla ağ belirtebilir. Bu örnekte <@mesh_0, "b">, <@mesh_1, "z">. ile aynıdır.

@mesh_0 = {<["a"=4, "b"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}
@mesh_1 = {<["x"=2, "y"=2, "z"=2]>, device_ids=[0, 1, 2, 3, 4, 5, 6, 7]}

Öncelikler

Öncelik, belirli bölümlendirme ve dağıtım kararlarını diğerlerinden daha öncelikli hale getirmenin bir yoludur ve bir programın artımlı bölümlendirilmesine olanak tanır.

Öncelikler, bir bölme temsilinin bazı veya tüm boyutlarına eklenmiş değerlerdir (kopyalanan eksenlerin önceliği yoktur).

Örneğin:

@mesh_xy = <["w"=6, "x"=2, "y"=4, "z"=2]>

//                                    |-> y is implicitly p0
%arg4 : sharding<@mesh_xy, [{"x"}p1, {"y"}, {"z",?}p2], replicated={} }>

Öncelikler, kullanıcılara dağıtım üzerinde daha ayrıntılı kontrol sağlar (ör. önce toplu paralellik, ardından megatron ve son olarak ZeRO bölümlendirme). Bu sayede, hangi verilerin bölümleneceği konusunda güçlü garantiler verilebilir ve daha ayrıntılı bölümleme stratejileri sayesinde daha iyi hata ayıklama yapılabilir (yalnızca megatron'un izole olarak çalıştırılmasının ardından programın nasıl göründüğünü görebilirsiniz).

Her boyut bölme işlemine bir öncelik (varsayılan olarak 0) eklemenize izin verilir. Bu, <i önceliğine sahip tüm bölme işlemlerinin, i önceliğine sahip bölme işlemlerinden önce programın tamamına dağıtılacağını gösterir.

Bir bölme işleminde daha düşük öncelikli açık bir boyut olsa bile (ör. {"z",?}p2, dağıtım sırasında daha yüksek önceliğe sahip başka bir tenör bölme işlemi tarafından geçersiz kılınmaz. Ancak bu tür açık boyutlar, tüm yüksek öncelikli parçalara ayrıldıktan sonra daha fazla parçaya ayrılabilir.

Diğer bir deyişle, öncelikler HANGİ boyut bölme işleminin diğerinden daha önemli olduğuyla ilgili değildir. Farklı boyut bölme grubu gruplarının programın tamamına nasıl dağıtılacağı ve ara, notlandırılmamış tenzorlardaki anlaşmazlıkların nasıl çözüleceğiyle ilgilidir.

Değişmezler

• Öncelikler 0'dan (en yüksek öncelik) başlar ve artar (kullanıcıların öncelik eklemesine ve kaldırmasına kolayca izin vermek için öncelikler arasında boşluklara izin verilir. Örneğin, p0 ve p2 kullanılır ancak p1 kullanılmaz).

• Boş kapalı boyut bölme (ör. {}) öncelikli olmamalıdır.

Boyut bölme bölünebilirliği

d boyutunda bir boyutun, boyutlarının çarpımı n olan eksenler boyunca bölünmesi mümkündür. Bu durumda d, n'e bölünemez (bu da pratikte boyutun doldurulmasını gerektirir).

Örneğin:

@mesh_xy = <["x"=8, "y"=2, "z"=3]>

sharding<@mesh_xy, [{"x"}, {"y"}, {"z"}]> : tensor<7x3x8xf32>

Dilbilgisi

Her mantıksal ağ şu şekilde tanımlanır:

@mesh_name = <mesh_axis_1,...,mesh_axis_n>

mesh_axis ::= axis_name=axis_size

axis_name ::= str
axis_size ::= int

Sıralama temsili, r rütbesine sahip bir tensör için aşağıdaki yapıya sahiptir:

sharding<@mesh_name, dim_shardings, replicated=replicated_axes}

mesh_name ::= str
dim_shardings ::= [dim_sharding_1,...,dim_sharding_r]
replicated_axes ::= {axis_1,...,axis_m}

dim_sharding ::=
  {axis_1,...,axis_k} |  // closed dimension
  {axis_1,...,axis_k,?}  // open dimension

axis ::=
  axis_name  |   // a full axis
  sub_axis             // a sub axis

axis_name ::= str

sub_axis ::= axis_name:(pre_size)size
pre_size ::= int
size ::= int