Обзор
Распространение сегментирования использует указанные пользователем сегменты для вывода неуказанных сегментов тензоров (или конкретных размеров тензоров). Он пересекает поток данных (цепочки use-def) вычислительного графа в обоих направлениях до тех пор, пока не будет достигнута фиксированная точка, т. е. сегментирование больше не может измениться без отмены предыдущих решений о сегментировании.
Распространение можно разбить на этапы. Каждый шаг включает в себя рассмотрение конкретной операции и распространение между тензорами (операндами и результатами) в зависимости от характеристик этой операции. Взяв в качестве примера матмуль, мы будем осуществлять распространение между несжимающимся измерением левой или правой стороны до соответствующего измерения результата или между сжимающимся измерением левой и правой стороны.
Характеристики операции определяют связь между соответствующими измерениями на ее входах и выходах и могут быть абстрагированы как правило сегментирования для каждой операции.
Без разрешения конфликта шаг распространения будет просто распространяться настолько, насколько это возможно, игнорируя при этом конфликтующие оси; мы называем это (самой длинной) совместимой основной осью шардинга.
Детальный проект
Иерархия разрешения конфликтов
Мы составляем несколько стратегий разрешения конфликтов в иерархии:
- Определяемые пользователем приоритеты . В разделе «Представление сегментирования» мы описали, как можно присвоить приоритеты сегментированию измерений, чтобы обеспечить постепенное секционирование программы, например, выполнение пакетного параллелизма -> мегатрон -> сегментирование ZeRO. Это достигается за счет применения распространения в итерациях — на итерации
iмы распространяем все сегменты измерений, имеющие приоритет<=iи игнорируем все остальные. Мы также следим за тем, чтобы распространение не переопределяло определенные пользователем сегменты с более низким приоритетом (>i), даже если они были проигнорированы во время предыдущих итераций. - Приоритеты, основанные на операциях . Мы распространяем шардинги в зависимости от типа операции. «Проходящие» операции (например, поэлементные операции и изменение формы) имеют наивысший приоритет, тогда как операции с преобразованием формы (например, расстановка точек и уменьшение) имеют более низкий приоритет.
- Агрессивная пропаганда. Распространяйте шардинги, используя агрессивную стратегию. Базовая стратегия распространяет шардинги только без конфликтов, тогда как агрессивная стратегия разрешает конфликты. Более высокая агрессивность может уменьшить объем памяти за счет потенциального обмена данными.
- Основное распространение. Это самая низкая стратегия распространения в иерархии, которая не выполняет никакого разрешения конфликтов, а вместо этого распространяет оси, совместимые между всеми операндами и результатами.

Эту иерархию можно интерпретировать как вложенные циклы for. Например, для каждого приоритета пользователя применяется полное распространение приоритета операции.
Правило сегментирования операции
Правило сегментирования вводит абстракцию каждой операции, которая обеспечивает фактический алгоритм распространения информацией, необходимой для распространения сегментирования от операндов к результатам или между операндами, без необходимости рассуждать о конкретных типах операций и их атрибутах. По сути, это исключает логику, специфичную для операции, и обеспечивает общее представление (структуру данных) для всех операций только с целью распространения. В своей простейшей форме он просто предоставляет следующую функцию:
GetOpShardingRule(Operation *) -> OpShardingRuleAttr
Правило позволяет нам написать алгоритм распространения только один раз в общем виде, основанном на этой структуре данных ( OpShardingRule ), вместо репликации одинаковых фрагментов кода во многих операциях, что значительно снижает вероятность ошибок или несогласованного поведения между операциями.
Вернемся к примеру с matmul.
Кодировка, которая инкапсулирует информацию, необходимую во время распространения, т. е. отношения между измерениями, может быть записана в форме нотации einsum:
(i, k), (k, j) -> (i, j)
В этой кодировке каждое измерение отображается в один фактор.
Как распространение использует это сопоставление: если измерение операнда/результата сегментировано вдоль оси, распространение будет искать фактор этого измерения в этом сопоставлении и сегментировать другие операнды/результаты вдоль их соответствующего измерения с тем же коэффициентом – и (с учетом более раннего обсуждения репликации) потенциально также реплицировать другие операнды/результаты, которые не имеют этого фактора вдоль этой оси.
Составные факторы: расширение правила для изменения формы
Во многих операциях, например в matmul, нам нужно сопоставить каждое измерение только с одним фактором. Однако для переформирования этого недостаточно.
Следующее изменение формы объединяет два измерения в одно:
%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>
Здесь оба измерения 0 и 1 входа соответствуют размерности 0 выхода. Скажем, мы начнем с ввода коэффициентов на вход:
(i,j,k) : i=2, j=4, k=32
Вы можете видеть, что если мы хотим использовать одни и те же факторы для выходных данных, нам понадобится одно измерение для ссылки на несколько факторов:
(i,j,k) -> ((ij), k) : i=2, j=4, k=32
То же самое можно сделать, если изменение формы должно было разделить измерение:
%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>
Здесь,
((ij), k) -> (i,j,k) : i=2, j=4, k=32
Размерность размера 8 здесь по существу состоит из факторов 2 и 4, поэтому мы называем факторы (i,j,k) факторами.
Эти факторы также могут работать в случаях, когда нет полного измерения, соответствующего одному из факторов:
%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4
Этот пример также подчеркивает, почему нам нужно хранить размеры факторов, поскольку мы не можем легко вывести их из соответствующих измерений.
Базовый алгоритм распространения
Распространение сегментов по факторам
В Шарди у нас есть иерархия тензоров, измерений и факторов. Они представляют данные на разных уровнях. Фактор – это подизмерение. Это внутренняя иерархия, используемая при распространении шардинга. Каждое измерение может соответствовать одному или нескольким факторам. Сопоставление между измерением и фактором определяется OpShardingRule .

Шарди распределяет оси сегментирования по факторам, а не по измерениям . Для этого нам нужно сделать три шага, как показано на рисунке ниже:
- Проект
DimShardingвFactorSharding - Распространение осей шардинга в пространстве
FactorSharding - Спроецируйте обновленный
FactorSharding, чтобы получить обновленныйDimSharding
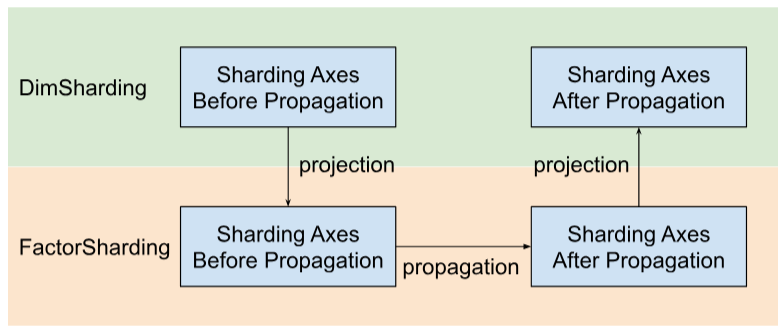
Визуализация распространения шардинга по факторам
Мы будем использовать следующую таблицу для визуализации проблемы и алгоритма распространения сегментирования.
| Ф0 | Ф1 | Ф2 | Явно реплицированные оси | |
|---|---|---|---|---|
| Т0 | ||||
| Т1 | ||||
| Т2 |
- Каждый столбец представляет фактор. F0 означает фактор с индексом 0. Распространяем шардинги по факторам (столбцам).
- Каждая строка представляет тензор. T0 относится к тензору с индексом 0. Тензоры — это все операнды и результаты, используемые для конкретной операции. Оси подряд не могут перекрываться. Ось (или подось) не может использоваться для многократного разделения одного тензора. Если ось явно реплицируется, мы не можем использовать ее для разделения тензора.
Таким образом, каждая ячейка представляет собой факторный сегмент. В частичных тензорах может отсутствовать коэффициент. Таблица для C = dot(A, B) приведена ниже. Ячейки, содержащие N означают, что фактор не входит в тензор. Например, F2 находится в T1 и T2, но не в T0.
C = dot(A, B) | F0 Дозирование тусклое | F1 Несжимающийся тусклый | F2 Несжимающийся тусклый свет | F3 Уменьшение яркости | Явно реплицированные оси |
|---|---|---|---|---|---|
| Т0 = А | Н | ||||
| Т1 = Б | Н | ||||
| Т2 = С | Н |
Собирайте и распространяйте оси шардинга
Мы используем простой пример, показанный ниже, чтобы визуализировать распространение.
| Ф0 | Ф1 | Ф2 | Явно реплицированные оси | |
|---|---|---|---|---|
| Т0 | "а" | "ф" | ||
| Т1 | «а», «б» | «в», «д» | "г" | |
| Т2 | «в», «е» |
Шаг 1. Найдите оси для распространения вдоль каждого фактора (так называемые (самые длинные) совместимые основные оси сегментирования). В этом примере мы распространяем ["a", "b"] вдоль F0, распространяем ["c"] вдоль F1 и ничего не распространяем вдоль F2.
Шаг 2. Разверните сегменты фактора, чтобы получить следующий результат.
| Ф0 | Ф1 | Ф2 | Явно реплицированные оси | |
|---|---|---|---|---|
| Т0 | «а», «б» | "с" | "ф" | |
| Т1 | «а», «б» | «в», «д» | "г" | |
| Т2 | «а», «б» | «в», «е» |
Операции потока данных
Приведенное выше описание шага распространения применимо к большинству операций. Однако бывают случаи, когда правило сегментирования не подходит. Для этих случаев Шарди определяет операции потока данных .
Граница потока данных некоторой операции X определяет мост между набором источников и набором целей , так что все источники и цели должны быть сегментированы одинаковым образом. Примерами таких операций являются stablehlo::OptimizationBarrierOp , stablehlo::WhileOp , stablehlo::CaseOp , а также sdy::ManualComputationOp . В конечном счете, любая операция, реализующая ShardableDataFlowOpInterface , считается операцией потока данных.
Операция может иметь несколько ребер потока данных, ортогональных друг другу. Например:
y_0, ..., y_n = while (x_0, ..., x_n)
((pred_arg_0,... , pred_arg_n) { ... })
((body_arg_0,..., body_arg_n) {
...
return return_value_0, ..., return_value_n
})
При этом op имеет n ребер потока данных: i-е ребро потока данных находится между источниками x_i , return_value_i и целями y_i , pred_arg_i , body_arg_i .
Shardy будет распространять сегменты между всеми источниками и целями границы потока данных, как если бы это была обычная операция с источниками в качестве операндов и целями в качестве результатов, а также идентификатором sdy.op_sharding_rule . Это означает, что прямое распространение происходит от источников к целям, а обратное распространение — от целей к источникам.
Пользователь должен реализовать несколько методов, описывающих, как получить источники и цели каждого ребра потока данных через их владельца , а также как получить и установить сегменты владельцев ребер. Владелец — это указанная пользователем цель границы потока данных, используемая при распространении Шарди. Пользователь может выбрать его произвольно, но он должен быть статичным.
Например, учитывая custom_op , определенный ниже:
y_1, ..., y_n = custom_op (x_1, ..., x_n)
((body_arg_1,..., body_arg_n) {
...
return return_value_1, ..., return_value_n
})
Этот custom_op имеет два типа ребер потока данных: n ребер между return_value_i (источниками) и y_i (целями) и n ребер между x_i (источниками) и body_arg_i (целями). В этом случае владельцы ребер те же, что и цели.
Обзор
Распространение сегментирования использует указанные пользователем сегменты для вывода неуказанных сегментов тензоров (или конкретных размеров тензоров). Он пересекает поток данных (цепочки use-def) вычислительного графа в обоих направлениях до тех пор, пока не будет достигнута фиксированная точка, т. е. сегментирование больше не может измениться без отмены предыдущих решений о сегментировании.
Распространение можно разбить на этапы. Каждый шаг включает в себя рассмотрение конкретной операции и распространение между тензорами (операндами и результатами) в зависимости от характеристик этой операции. Взяв в качестве примера матмуль, мы будем осуществлять распространение между несжимающимся измерением левой или правой стороны до соответствующего измерения результата или между сжимающимся измерением левой и правой стороны.
Характеристики операции определяют связь между соответствующими измерениями на ее входах и выходах и могут быть абстрагированы как правило сегментирования для каждой операции.
Без разрешения конфликта шаг распространения будет просто распространяться настолько, насколько это возможно, игнорируя при этом конфликтующие оси; мы называем это (самой длинной) совместимой основной осью шардинга.
Детальный проект
Иерархия разрешения конфликтов
Мы составляем несколько стратегий разрешения конфликтов в иерархии:
- Определяемые пользователем приоритеты . В разделе «Представление сегментирования» мы описали, как можно присвоить приоритеты сегментированию измерений, чтобы обеспечить постепенное секционирование программы, например, выполнение пакетного параллелизма -> мегатрон -> сегментирование ZeRO. Это достигается за счет применения распространения в итерациях — на итерации
iмы распространяем все сегменты измерений, имеющие приоритет<=iи игнорируем все остальные. Мы также следим за тем, чтобы распространение не переопределяло определенные пользователем сегменты с более низким приоритетом (>i), даже если они были проигнорированы во время предыдущих итераций. - Приоритеты, основанные на операциях . Мы распространяем шардинги в зависимости от типа операции. «Проходящие» операции (например, поэлементные операции и изменение формы) имеют наивысший приоритет, тогда как операции с преобразованием формы (например, расстановка точек и уменьшение) имеют более низкий приоритет.
- Агрессивная пропаганда. Распространяйте шардинги, используя агрессивную стратегию. Базовая стратегия распространяет шардинги только без конфликтов, тогда как агрессивная стратегия разрешает конфликты. Более высокая агрессивность может уменьшить объем памяти за счет потенциального обмена данными.
- Основное распространение. Это самая низкая стратегия распространения в иерархии, которая не выполняет никакого разрешения конфликтов, а вместо этого распространяет оси, совместимые между всеми операндами и результатами.

Эту иерархию можно интерпретировать как вложенные циклы for. Например, для каждого приоритета пользователя применяется полное распространение приоритета операции.
Правило сегментирования операции
Правило сегментирования вводит абстракцию каждой операции, которая обеспечивает фактический алгоритм распространения информацией, необходимой для распространения сегментирования от операндов к результатам или между операндами, без необходимости рассуждать о конкретных типах операций и их атрибутах. По сути, это исключает логику, специфичную для операции, и обеспечивает общее представление (структуру данных) для всех операций только с целью распространения. В своей простейшей форме он просто предоставляет следующую функцию:
GetOpShardingRule(Operation *) -> OpShardingRuleAttr
Правило позволяет нам написать алгоритм распространения только один раз в общем виде, основанном на этой структуре данных ( OpShardingRule ), вместо репликации одинаковых фрагментов кода во многих операциях, что значительно снижает вероятность ошибок или несогласованного поведения между операциями.
Вернемся к примеру с matmul.
Кодировка, которая инкапсулирует информацию, необходимую во время распространения, т. е. отношения между измерениями, может быть записана в форме нотации einsum:
(i, k), (k, j) -> (i, j)
В этой кодировке каждое измерение отображается в один фактор.
Как распространение использует это сопоставление: если измерение операнда/результата сегментировано вдоль оси, распространение будет искать фактор этого измерения в этом сопоставлении и сегментировать другие операнды/результаты вдоль их соответствующего измерения с тем же коэффициентом – и (с учетом более раннего обсуждения репликации) потенциально также реплицировать другие операнды/результаты, которые не имеют этого фактора вдоль этой оси.
Составные факторы: расширение правила для изменения формы
Во многих операциях, например в matmul, нам нужно сопоставить каждое измерение только с одним фактором. Однако для переформирования этого недостаточно.
Следующее изменение формы объединяет два измерения в одно:
%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>
Здесь оба измерения 0 и 1 входа соответствуют размерности 0 выхода. Скажем, мы начнем с ввода коэффициентов на вход:
(i,j,k) : i=2, j=4, k=32
Вы можете видеть, что если мы хотим использовать одни и те же факторы для выходных данных, нам понадобится одно измерение для ссылки на несколько факторов:
(i,j,k) -> ((ij), k) : i=2, j=4, k=32
То же самое можно сделать, если изменение формы должно было разделить измерение:
%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>
Здесь,
((ij), k) -> (i,j,k) : i=2, j=4, k=32
Размерность размера 8 здесь по существу состоит из факторов 2 и 4, поэтому мы называем факторы (i,j,k) факторами.
Эти факторы также могут работать в случаях, когда нет полного измерения, соответствующего одному из факторов:
%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4
Этот пример также подчеркивает, почему нам нужно хранить размеры факторов, поскольку мы не можем легко вывести их из соответствующих измерений.
Базовый алгоритм распространения
Распространение сегментов по факторам
В Шарди у нас есть иерархия тензоров, измерений и факторов. Они представляют данные на разных уровнях. Фактор – это подизмерение. Это внутренняя иерархия, используемая при распространении шардинга. Каждое измерение может соответствовать одному или нескольким факторам. Сопоставление между измерением и фактором определяется OpShardingRule .

Шарди распределяет оси сегментирования по факторам, а не по измерениям . Для этого нам нужно сделать три шага, как показано на рисунке ниже:
- Проект
DimShardingвFactorSharding - Распространение осей шардинга в пространстве
FactorSharding - Спроецируйте обновленный
FactorSharding, чтобы получить обновленныйDimSharding

Визуализация распространения шардинга по факторам
Мы будем использовать следующую таблицу для визуализации проблемы и алгоритма распространения сегментирования.
| Ф0 | Ф1 | Ф2 | Явно реплицированные оси | |
|---|---|---|---|---|
| Т0 | ||||
| Т1 | ||||
| Т2 |
- Каждый столбец представляет фактор. F0 означает фактор с индексом 0. Распространяем шардинги по факторам (столбцам).
- Каждая строка представляет тензор. T0 относится к тензору с индексом 0. Тензоры — это все операнды и результаты, используемые для конкретной операции. Оси подряд не могут перекрываться. Ось (или подось) не может использоваться для многократного разделения одного тензора. Если ось явно реплицируется, мы не можем использовать ее для разделения тензора.
Таким образом, каждая ячейка представляет собой факторный сегмент. В частичных тензорах может отсутствовать коэффициент. Таблица для C = dot(A, B) приведена ниже. Ячейки, содержащие N означают, что фактор не входит в тензор. Например, F2 находится в T1 и T2, но не в T0.
C = dot(A, B) | F0 Дозирование тусклое | F1 Несжимающийся тусклый | F2 Несжимающийся тусклый свет | F3 Уменьшение яркости | Явно реплицированные оси |
|---|---|---|---|---|---|
| Т0 = А | Н | ||||
| Т1 = Б | Н | ||||
| Т2 = С | Н |
Собирайте и распространяйте оси шардинга
Мы используем простой пример, показанный ниже, чтобы визуализировать распространение.
| Ф0 | Ф1 | Ф2 | Явно реплицированные оси | |
|---|---|---|---|---|
| Т0 | "а" | "ф" | ||
| Т1 | «а», «б» | «в», «д» | "г" | |
| Т2 | «в», «е» |
Шаг 1. Найдите оси для распространения вдоль каждого фактора (так называемые (самые длинные) совместимые основные оси сегментирования). В этом примере мы распространяем ["a", "b"] вдоль F0, распространяем ["c"] вдоль F1 и ничего не распространяем вдоль F2.
Шаг 2. Разверните сегменты фактора, чтобы получить следующий результат.
| Ф0 | Ф1 | Ф2 | Явно реплицированные оси | |
|---|---|---|---|---|
| Т0 | «а», «б» | "с" | "ф" | |
| Т1 | «а», «б» | «в», «д» | "г" | |
| Т2 | «а», «б» | «в», «е» |
Операции потока данных
Приведенное выше описание шага распространения применимо к большинству операций. Однако бывают случаи, когда правило сегментирования не подходит. Для этих случаев Шарди определяет операции потока данных .
Граница потока данных некоторой операции X определяет мост между набором источников и набором целей , так что все источники и цели должны быть сегментированы одинаковым образом. Примерами таких операций являются stablehlo::OptimizationBarrierOp , stablehlo::WhileOp , stablehlo::CaseOp , а также sdy::ManualComputationOp . В конечном счете, любая операция, реализующая ShardableDataFlowOpInterface , считается операцией потока данных.
Операция может иметь несколько ребер потока данных, ортогональных друг другу. Например:
y_0, ..., y_n = while (x_0, ..., x_n)
((pred_arg_0,... , pred_arg_n) { ... })
((body_arg_0,..., body_arg_n) {
...
return return_value_0, ..., return_value_n
})
При этом op имеет n ребер потока данных: i-е ребро потока данных находится между источниками x_i , return_value_i и целями y_i , pred_arg_i , body_arg_i .
Shardy будет распространять сегменты между всеми источниками и целями границы потока данных, как если бы это была обычная операция с источниками в качестве операндов и целями в качестве результатов, а также идентификатором sdy.op_sharding_rule . Это означает, что прямое распространение происходит от источников к целям, а обратное распространение — от целей к источникам.
Пользователь должен реализовать несколько методов, описывающих, как получить источники и цели каждого ребра потока данных через их владельца , а также как получить и установить сегменты владельцев ребер. Владелец — это указанная пользователем цель границы потока данных, используемая при распространении Шарди. Пользователь может выбрать его произвольно, но он должен быть статичным.
Например, учитывая custom_op , определенный ниже:
y_1, ..., y_n = custom_op (x_1, ..., x_n)
((body_arg_1,..., body_arg_n) {
...
return return_value_1, ..., return_value_n
})
Этот custom_op имеет два типа ребер потока данных: n ребер между return_value_i (источниками) и y_i (целями) и n ребер между x_i (источниками) и body_arg_i (целями). В этом случае владельцы ребер те же, что и цели.
Обзор
Распространение сегментирования использует указанные пользователем сегменты для вывода неуказанных сегментов тензоров (или конкретных размеров тензоров). Он пересекает поток данных (цепочки use-def) вычислительного графа в обоих направлениях до тех пор, пока не будет достигнута фиксированная точка, т. е. сегментирование больше не может измениться без отмены предыдущих решений о сегментировании.
Распространение можно разбить на этапы. Каждый шаг включает в себя рассмотрение конкретной операции и распространение между тензорами (операндами и результатами) в зависимости от характеристик этой операции. Взяв в качестве примера матмуль, мы будем осуществлять распространение между несжимающимся измерением левой или правой стороны до соответствующего измерения результата или между сжимающимся измерением левой и правой стороны.
Характеристики операции определяют связь между соответствующими измерениями на ее входах и выходах и могут быть абстрагированы как правило сегментирования для каждой операции.
Без разрешения конфликта шаг распространения будет просто распространяться настолько, насколько это возможно, игнорируя при этом конфликтующие оси; мы называем это (самой длинной) совместимой основной осью шардинга.
Детальный проект
Иерархия разрешения конфликтов
Мы составляем несколько стратегий разрешения конфликтов в иерархии:
- Определяемые пользователем приоритеты . В разделе «Представление сегментирования» мы описали, как можно присвоить приоритеты сегментированию измерений, чтобы обеспечить постепенное секционирование программы, например, выполнение пакетного параллелизма -> мегатрон -> сегментирование ZeRO. Это достигается за счет применения распространения в итерациях — на итерации
iмы распространяем все сегменты измерений, имеющие приоритет<=iи игнорируем все остальные. Мы также следим за тем, чтобы распространение не переопределяло определенные пользователем сегменты с более низким приоритетом (>i), даже если они были проигнорированы во время предыдущих итераций. - Приоритеты, основанные на операциях . Мы распространяем шардинги в зависимости от типа операции. «Проходящие» операции (например, поэлементные операции и изменение формы) имеют наивысший приоритет, тогда как операции с преобразованием формы (например, расстановка точек и уменьшение) имеют более низкий приоритет.
- Агрессивная пропаганда. Распространяйте шардинги, используя агрессивную стратегию. Базовая стратегия распространяет шардинги только без конфликтов, тогда как агрессивная стратегия разрешает конфликты. Более высокая агрессивность может уменьшить объем памяти за счет потенциального обмена данными.
- Основное распространение. Это самая низкая стратегия распространения в иерархии, которая не выполняет никакого разрешения конфликтов, а вместо этого распространяет оси, совместимые между всеми операндами и результатами.

Эту иерархию можно интерпретировать как вложенные циклы for. Например, для каждого приоритета пользователя применяется полное распространение приоритета операции.
Правило сегментирования операции
Правило сегментирования вводит абстракцию каждой операции, которая обеспечивает фактический алгоритм распространения информацией, необходимой для распространения сегментирования от операндов к результатам или между операндами, без необходимости рассуждать о конкретных типах операций и их атрибутах. По сути, это исключает логику, специфичную для операции, и обеспечивает общее представление (структуру данных) для всех операций только с целью распространения. В своей простейшей форме он просто предоставляет следующую функцию:
GetOpShardingRule(Operation *) -> OpShardingRuleAttr
Правило позволяет нам написать алгоритм распространения только один раз в общем виде, основанном на этой структуре данных ( OpShardingRule ), вместо репликации одинаковых фрагментов кода во многих операциях, что значительно снижает вероятность ошибок или несогласованного поведения между операциями.
Вернемся к примеру с matmul.
Кодировка, которая инкапсулирует информацию, необходимую во время распространения, т. е. отношения между измерениями, может быть записана в форме нотации einsum:
(i, k), (k, j) -> (i, j)
В этой кодировке каждое измерение отображается в один фактор.
Как распространение использует это сопоставление: если измерение операнда/результата сегментировано вдоль оси, распространение будет искать фактор этого измерения в этом сопоставлении и сегментировать другие операнды/результаты вдоль их соответствующего измерения с тем же коэффициентом – и (с учетом более раннего обсуждения репликации) потенциально также реплицировать другие операнды/результаты, которые не имеют этого фактора вдоль этой оси.
Составные факторы: расширение правила для изменения формы
Во многих операциях, например в matmul, нам нужно сопоставить каждое измерение только с одним фактором. Однако для переформирования этого недостаточно.
Следующее изменение формы объединяет два измерения в одно:
%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>
Здесь оба измерения 0 и 1 входа соответствуют размерности 0 выхода. Скажем, мы начнем с ввода коэффициентов на вход:
(i,j,k) : i=2, j=4, k=32
Вы можете видеть, что если мы хотим использовать одни и те же факторы для выходных данных, нам понадобится одно измерение для ссылки на несколько факторов:
(i,j,k) -> ((ij), k) : i=2, j=4, k=32
То же самое можно сделать, если изменение формы должно было разделить измерение:
%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>
Здесь,
((ij), k) -> (i,j,k) : i=2, j=4, k=32
Размерность размера 8 здесь по существу состоит из факторов 2 и 4, поэтому мы называем факторы (i,j,k) факторами.
Эти факторы также могут работать в случаях, когда нет полного измерения, соответствующего одному из факторов:
%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4
Этот пример также подчеркивает, почему нам нужно хранить размеры факторов, поскольку мы не можем легко вывести их из соответствующих измерений.
Базовый алгоритм распространения
Распространение сегментов по факторам
В Шарди у нас есть иерархия тензоров, измерений и факторов. Они представляют данные на разных уровнях. Фактор – это подизмерение. Это внутренняя иерархия, используемая при распространении шардинга. Каждое измерение может соответствовать одному или нескольким факторам. Сопоставление между измерением и фактором определяется OpShardingRule .

Шарди распределяет оси сегментирования по факторам, а не по измерениям . Для этого нам нужно сделать три шага, как показано на рисунке ниже:
- Проект
DimShardingвFactorSharding - Распространение осей шардинга в пространстве
FactorSharding - Спроецируйте обновленный
FactorSharding, чтобы получить обновленныйDimSharding

Визуализация распространения шардинга по факторам
Мы будем использовать следующую таблицу для визуализации проблемы и алгоритма распространения сегментирования.
| Ф0 | Ф1 | Ф2 | Явно реплицированные оси | |
|---|---|---|---|---|
| Т0 | ||||
| Т1 | ||||
| Т2 |
- Каждый столбец представляет фактор. F0 означает фактор с индексом 0. Распространяем шардинги по факторам (столбцам).
- Каждая строка представляет тензор. T0 относится к тензору с индексом 0. Тензоры — это все операнды и результаты, используемые для конкретной операции. Оси подряд не могут перекрываться. Ось (или подось) не может использоваться для многократного разделения одного тензора. Если ось явно реплицируется, мы не можем использовать ее для разделения тензора.
Таким образом, каждая ячейка представляет собой факторный сегмент. В частичных тензорах может отсутствовать коэффициент. Таблица для C = dot(A, B) приведена ниже. Ячейки, содержащие N означают, что фактор не входит в тензор. Например, F2 находится в T1 и T2, но не в T0.
C = dot(A, B) | F0 Дозирование тусклое | F1 Несжимающийся тусклый | F2 Несжимающийся тусклый свет | F3 Уменьшение яркости | Явно реплицированные оси |
|---|---|---|---|---|---|
| Т0 = А | Н | ||||
| Т1 = Б | Н | ||||
| Т2 = С | Н |
Собирайте и распространяйте оси шардинга
Мы используем простой пример, показанный ниже, чтобы визуализировать распространение.
| Ф0 | Ф1 | Ф2 | Явно реплицированные оси | |
|---|---|---|---|---|
| Т0 | "а" | "ф" | ||
| Т1 | «а», «б» | «в», «д» | "г" | |
| Т2 | «в», «е» |
Шаг 1. Найдите оси для распространения вдоль каждого фактора (так называемые (самые длинные) совместимые основные оси сегментирования). В этом примере мы распространяем ["a", "b"] вдоль F0, распространяем ["c"] вдоль F1 и ничего не распространяем вдоль F2.
Шаг 2. Разверните сегменты фактора, чтобы получить следующий результат.
| Ф0 | Ф1 | Ф2 | Явно реплицированные оси | |
|---|---|---|---|---|
| Т0 | «а», «б» | "с" | "ф" | |
| Т1 | «а», «б» | «в», «д» | "г" | |
| Т2 | «а», «б» | «в», «е» |
Операции потока данных
Приведенное выше описание шага распространения применимо к большинству операций. Однако бывают случаи, когда правило сегментирования не подходит. Для этих случаев Шарди определяет операции потока данных .
Граница потока данных некоторой операции X определяет мост между набором источников и набором целей , так что все источники и цели должны быть сегментированы одинаковым образом. Примерами таких операций являются stablehlo::OptimizationBarrierOp , stablehlo::WhileOp , stablehlo::CaseOp , а также sdy::ManualComputationOp . В конечном счете, любая операция, реализующая ShardableDataFlowOpInterface , считается операцией потока данных.
Операция может иметь несколько ребер потока данных, ортогональных друг другу. Например:
y_0, ..., y_n = while (x_0, ..., x_n)
((pred_arg_0,... , pred_arg_n) { ... })
((body_arg_0,..., body_arg_n) {
...
return return_value_0, ..., return_value_n
})
При этом op имеет n ребер потока данных: i-е ребро потока данных находится между источниками x_i , return_value_i и целями y_i , pred_arg_i , body_arg_i .
Shardy будет распространять сегменты между всеми источниками и целями границы потока данных, как если бы это была обычная операция с источниками в качестве операндов и целями в качестве результатов, а также идентификатором sdy.op_sharding_rule . Это означает, что прямое распространение происходит от источников к целям, а обратное распространение — от целей к источникам.
Пользователь должен реализовать несколько методов, описывающих, как получить источники и цели каждого ребра потока данных через их владельца , а также как получить и установить сегменты владельцев ребер. Владелец — это указанная пользователем цель границы потока данных, используемая при распространении Шарди. Пользователь может выбрать его произвольно, но он должен быть статичным.
Например, учитывая custom_op , определенный ниже:
y_1, ..., y_n = custom_op (x_1, ..., x_n)
((body_arg_1,..., body_arg_n) {
...
return return_value_1, ..., return_value_n
})
Этот custom_op имеет два типа ребер потока данных: n ребер между return_value_i (источниками) и y_i (целями) и n ребер между x_i (источниками) и body_arg_i (целями). В этом случае владельцы ребер те же, что и цели.
Обзор
Распространение сегментирования использует указанные пользователем сегменты для вывода неуказанных сегментов тензоров (или конкретных размеров тензоров). Он пересекает поток данных (цепочки use-def) вычислительного графа в обоих направлениях до тех пор, пока не будет достигнута фиксированная точка, т. е. сегментирование больше не может измениться без отмены предыдущих решений о сегментировании.
Распространение можно разбить на этапы. Каждый шаг включает в себя рассмотрение конкретной операции и распространение между тензорами (операндами и результатами) в зависимости от характеристик этой операции. Взяв в качестве примера матмуль, мы будем осуществлять распространение между несжимающимся измерением левой или правой стороны до соответствующего измерения результата или между сжимающимся измерением левой и правой стороны.
Характеристики операции определяют связь между соответствующими измерениями на ее входах и выходах и могут быть абстрагированы как правило сегментирования для каждой операции.
Без разрешения конфликта шаг распространения будет просто распространяться настолько, насколько это возможно, игнорируя при этом конфликтующие оси; мы называем это (самой длинной) совместимой основной осью шардинга.
Детальный проект
Иерархия разрешения конфликтов
Мы составляем несколько стратегий разрешения конфликтов в иерархии:
- Определяемые пользователем приоритеты . В разделе «Представление сегментирования» мы описали, как можно присвоить приоритеты сегментированию измерений, чтобы обеспечить постепенное секционирование программы, например, выполнение пакетного параллелизма -> мегатрон -> сегментирование ZeRO. Это достигается за счет применения распространения в итерациях — на итерации
iмы распространяем все сегменты измерений, имеющие приоритет<=iи игнорируем все остальные. Мы также следим за тем, чтобы распространение не переопределяло определенные пользователем сегменты с более низким приоритетом (>i), даже если они были проигнорированы во время предыдущих итераций. - Приоритеты, основанные на операциях . Мы распространяем шардинги в зависимости от типа операции. «Проходящие» операции (например, поэлементные операции и изменение формы) имеют наивысший приоритет, тогда как операции с преобразованием формы (например, расстановка точек и уменьшение) имеют более низкий приоритет.
- Агрессивная пропаганда. Распространяйте шардинги, используя агрессивную стратегию. Базовая стратегия распространяет шардинги только без конфликтов, тогда как агрессивная стратегия разрешает конфликты. Более высокая агрессивность может уменьшить объем памяти за счет потенциального обмена данными.
- Основное распространение. Это самая низкая стратегия распространения в иерархии, которая не выполняет никакого разрешения конфликтов, а вместо этого распространяет оси, совместимые между всеми операндами и результатами.

Эту иерархию можно интерпретировать как вложенные циклы for. Например, для каждого приоритета пользователя применяется полное распространение приоритета операции.
Правило сегментирования операции
Правило сегментирования вводит абстракцию каждой операции, которая обеспечивает фактический алгоритм распространения информацией, необходимой для распространения сегментирования от операндов к результатам или между операндами, без необходимости рассуждать о конкретных типах операций и их атрибутах. По сути, это исключает логику, специфичную для операции, и обеспечивает общее представление (структуру данных) для всех операций только с целью распространения. В своей простейшей форме он просто предоставляет следующую функцию:
GetOpShardingRule(Operation *) -> OpShardingRuleAttr
Правило позволяет нам написать алгоритм распространения только один раз в общем виде, основанном на этой структуре данных ( OpShardingRule ), вместо репликации одинаковых фрагментов кода во многих операциях, что значительно снижает вероятность ошибок или несогласованного поведения между операциями.
Вернемся к примеру с matmul.
Кодировка, которая инкапсулирует информацию, необходимую во время распространения, т. е. отношения между измерениями, может быть записана в форме нотации einsum:
(i, k), (k, j) -> (i, j)
В этой кодировке каждое измерение отображается в один фактор.
Как распространение использует это сопоставление: если измерение операнда/результата сегментировано вдоль оси, распространение будет искать фактор этого измерения в этом сопоставлении и сегментировать другие операнды/результаты вдоль их соответствующего измерения с тем же коэффициентом – и (с учетом более раннего обсуждения репликации) потенциально также реплицировать другие операнды/результаты, которые не имеют этого фактора вдоль этой оси.
Составные факторы: расширение правила для изменения формы
Во многих операциях, например в matmul, нам нужно сопоставить каждое измерение только с одним фактором. Однако для переформирования этого недостаточно.
Следующее изменение формы объединяет два измерения в одно:
%out = stablehlo.reshape(%in) : (tensor<2x4x32xf32>) -> tensor<8x32xf32>
Здесь оба измерения 0 и 1 входа соответствуют размерности 0 выхода. Скажем, мы начнем с ввода коэффициентов на вход:
(i,j,k) : i=2, j=4, k=32
Вы можете видеть, что если мы хотим использовать одни и те же факторы для выходных данных, нам понадобится одно измерение для ссылки на несколько факторов:
(i,j,k) -> ((ij), k) : i=2, j=4, k=32
То же самое можно сделать, если изменение формы должно было разделить измерение:
%out = stablehlo.reshape(%in) : (tensor<8x32xf32>) -> tensor<2x4x32xf32>
Здесь,
((ij), k) -> (i,j,k) : i=2, j=4, k=32
Размерность размера 8 здесь по существу состоит из факторов 2 и 4, поэтому мы называем факторы (i,j,k) факторами.
Эти факторы также могут работать в случаях, когда нет полного измерения, соответствующего одному из факторов:
%out = stablehlo.reshape(%in) : (tensor<8x4xf32>) -> tensor<2x16xf32>
// ((ij), k) -> (i,(jk)) : i=2, j=4, k=4
Этот пример также подчеркивает, почему нам нужно хранить размеры факторов, поскольку мы не можем легко вывести их из соответствующих измерений.
Базовый алгоритм распространения
Распространение сегментов по факторам
В Шарди у нас есть иерархия тензоров, измерений и факторов. Они представляют данные на разных уровнях. Фактор – это подизмерение. Это внутренняя иерархия, используемая при распространении шардинга. Каждое измерение может соответствовать одному или нескольким факторам. Сопоставление между измерением и фактором определяется OpShardingRule .

Шарди распределяет оси сегментирования по факторам, а не по измерениям . Для этого нам нужно сделать три шага, как показано на рисунке ниже:
- Проект
DimShardingвFactorSharding - Распространение осей шардинга в пространстве
FactorSharding - Спроецируйте обновленный
FactorSharding, чтобы получить обновленныйDimSharding

Визуализация распространения шардинга по факторам
Мы будем использовать следующую таблицу для визуализации проблемы и алгоритма распространения сегментирования.
| Ф0 | Ф1 | Ф2 | Явно реплицированные оси | |
|---|---|---|---|---|
| Т0 | ||||
| Т1 | ||||
| Т2 |
- Каждый столбец представляет фактор. F0 означает фактор с индексом 0. Распространяем шардинги по факторам (столбцам).
- Каждая строка представляет тензор. T0 относится к тензору с индексом 0. Тензоры — это все операнды и результаты, используемые для конкретной операции. Оси подряд не могут перекрываться. Ось (или подось) не может использоваться для многократного разделения одного тензора. Если ось явно реплицируется, мы не можем использовать ее для разделения тензора.
Таким образом, каждая ячейка представляет собой факторный сегмент. В частичных тензорах может отсутствовать коэффициент. Таблица для C = dot(A, B) приведена ниже. Ячейки, содержащие N означают, что фактор не входит в тензор. Например, F2 находится в T1 и T2, но не в T0.
C = dot(A, B) | F0 Дозирование тусклое | F1 Несжимающийся тусклый | F2 Несжимающийся тусклый свет | F3 Уменьшение яркости | Явно реплицированные оси |
|---|---|---|---|---|---|
| Т0 = А | Н | ||||
| Т1 = Б | Н | ||||
| Т2 = С | Н |
Собирайте и распространяйте оси шардинга
Мы используем простой пример, показанный ниже, чтобы визуализировать распространение.
| Ф0 | Ф1 | Ф2 | Явно реплицированные оси | |
|---|---|---|---|---|
| Т0 | "а" | "ф" | ||
| Т1 | «а», «б» | «в», «д» | "г" | |
| Т2 | «в», «е» |
Шаг 1. Найдите оси для распространения вдоль каждого фактора (так называемые (самые длинные) совместимые основные оси сегментирования). В этом примере мы распространяем ["a", "b"] вдоль F0, распространяем ["c"] вдоль F1 и ничего не распространяем вдоль F2.
Шаг 2. Разверните сегменты фактора, чтобы получить следующий результат.
| Ф0 | Ф1 | Ф2 | Явно реплицированные оси | |
|---|---|---|---|---|
| Т0 | «а», «б» | "с" | "ф" | |
| Т1 | «а», «б» | «в», «д» | "г" | |
| Т2 | «а», «б» | «в», «е» |
Операции потока данных
Приведенное выше описание шага распространения применимо к большинству операций. Однако бывают случаи, когда правило сегментирования не подходит. Для этих случаев Шарди определяет операции потока данных .
Граница потока данных некоторой операции X определяет мост между набором источников и набором целей , так что все источники и цели должны быть сегментированы одинаковым образом. Примерами таких операций являются stablehlo::OptimizationBarrierOp , stablehlo::WhileOp , stablehlo::CaseOp , а также sdy::ManualComputationOp . В конечном счете, любая операция, реализующая ShardableDataFlowOpInterface , считается операцией потока данных.
Операция может иметь несколько ребер потока данных, ортогональных друг другу. Например:
y_0, ..., y_n = while (x_0, ..., x_n)
((pred_arg_0,... , pred_arg_n) { ... })
((body_arg_0,..., body_arg_n) {
...
return return_value_0, ..., return_value_n
})
При этом op имеет n ребер потока данных: i-е ребро потока данных находится между источниками x_i , return_value_i и целями y_i , pred_arg_i , body_arg_i .
Shardy будет распространять сегменты между всеми источниками и целями границы потока данных, как если бы это была обычная операция с источниками в качестве операндов и целями в качестве результатов, а также идентификатором sdy.op_sharding_rule . Это означает, что прямое распространение происходит от источников к целям, а обратное распространение — от целей к источникам.
Пользователь должен реализовать несколько методов, описывающих, как получить источники и цели каждого ребра потока данных через их владельца , а также как получить и установить сегменты владельцев ребер. Владелец — это указанная пользователем цель границы потока данных, используемая при распространении Шарди. Пользователь может выбрать его произвольно, но он должен быть статичным.
Например, учитывая custom_op , определенный ниже:
y_1, ..., y_n = custom_op (x_1, ..., x_n)
((body_arg_1,..., body_arg_n) {
...
return return_value_1, ..., return_value_n
})
Этот custom_op имеет два типа ребер потока данных: n ребер между return_value_i (источниками) и y_i (целями) и n ребер между x_i (источниками) и body_arg_i (целями). В этом случае владельцы ребер те же, что и цели.

