Ce document décrit l'analyse d'indexation HLO, qui vous permet de calculer symboliquement des cartes d'indexation pour les opérations HLO. La carte d'indexation est une fonction qui met en correspondance les indices d'un tenseur avec ceux d'un autre, par exemple les indices de sortie d'une instruction HLO avec les indices d'entrée de l'instruction HLO ou inversement.
Exemple
Pour une annonce de tensor<20xf32> à tensor<10x20x30xf32>
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
La carte d'indexation de la sortie vers l'entrée est (i, j, k) -> (j) pour i in
[0, 10], j in [0, 20] et k in [0, 30].
Motivation
Le GPU XLA utilise plusieurs solutions sur mesure pour raisonner la coalescence, l'opérande l'utilisation et les schémas d'emplacement (plus de détails ci-dessous). L'objectif de l'analyse d'indexation est de fournir un composant réutilisable pour ces cas d'utilisation. Analyse de l'indexation est basé sur l'infrastructure Affine Map de MLIR et ajoute une sémantique HLO.
Coalescing
Le raisonnement de la coalescence de la mémoire devient réalisable dans les cas non triviaux, lorsque nous savons quels éléments/tranches des entrées sont lus pour calculer un élément du de sortie.
Utilisation des opérandes
L'utilisation de l'opérande dans XLA indique la part de chaque entrée de l'instruction est utilisé en supposant que sa sortie est entièrement utilisée. Actuellement, l'utilisation n'est pas non plus pour un cas générique. L'analyse de l'indexation permet de calculer précisément l'utilisation.
Mosaïque
Une carte/une tranche est un sous-ensemble hyper-rectangulaire d'un tenseur paramétré par des décalages, des tailles et des pas. La propagation des cartes permet de calculer les paramètres de carte du producteur/consommateur de l'opération à l'aide des paramètres de cartes de l'opération elle-même. Il existe déjà une bibliothèque qui le fait pour softmax et dot. La propagation des cartes peut être plus générique et robustes si elles sont exprimées via l'indexation de cartes.
Fonction et domaine
La carte d'indexation est une fonction f(x) = f(d, r, rt)
qui mappe le multi-index d d'un Tensor A à des éléments/plages de
B. Le paramètre r fait référence aux plages d'indices de
Les dimensions présentes dans le Tensor B, mais pas dans le Tensor A. La
rt fait référence aux valeurs d'exécution, par exemple pour une opération de collecte.
Par exemple, si nous obtenons une réduction de tensor<2x4x8x16xf32> à
tensor<4x8xf32>, la carte d'indexation de la sortie 2D à l'entrée 4D est
(d0, d1) -> (r0, d0, d1, r1), où d_i sont les variables de dimension
correspondent aux index du Tensor de sortie. Les variables de plage r_j encodent plusieurs valeurs. Autrement dit, pour calculer un élément (d0, d1) de la sortie, nous avons besoin d'éléments (r0, d0, d1, r1) de l'entrée, où r0 in [0, 1] et r1 in [0, 15].
Ce mappage peut être construit à partir des attributs des instructions HLO les mappages d'instructions non fusionnées peuvent être composés pour obtenir l'indexation pour une fusion. Le mappage comporte également un domaine, qui spécifie quels éléments du Tensor le mappage existe.
f(x) s.t.
lb <= g(x) <= ub
Comme nous voulons minimiser les calculs, nous avons besoin d'une bibliothèque des calculs. XLA dépend déjà de MLIR. Nous utilisons donc mlir::AffineMap au lieu d'écrire une autre bibliothèque d'arithmétique symbolique.
Un AffineMap type se présente comme suit :
(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)
AffineMap comporte deux types de paramètres : les dimensions et les symboles. Les dimensions correspondent aux variables de dimension d, les symboles correspondent aux variables de plage r et aux variables RT rt. AffineMap ne contient aucune métadonnées sur les plages des dimensions. Nous devons donc fournir ces données nous-mêmes.
struct Interval {
int64_t lower;
int64_t upper;
};
// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
Interval bounds;
};
// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
Interval range;
};
// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
Interval feasible_values;
const HloInstruction* hlo;
// This is a map from the iteration space of the corresponding indexing map to
// the iteration space of `hlo`. It shows what element of `hlo` we need to
// extract to get the runtime value for the RTVar.
mlir::AffineMap map;
};
class IndexingMap {
mlir::AffineMap affine_map_;
std::vector<DimVar> dim_vars_;
std::vector<RangeVar> range_vars_;
std::vector<RTVar> rt_vars_;
llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};
dim_vars_ encode les contraintes de zone inclusive pour la dimension.
d de la carte d'indexation, qui coïncident généralement avec la valeur
forme du Tensor de sortie pour des opérations telles que la transposition, la réduction, l'élément par élément, le point, mais
il existe quelques
exceptions comme
HloConcatenateInstruction.
range_vars_ encode les valeurs possibles que les paramètres r peuvent prendre.
rt_vars_ stockera les instructions hlo associées ainsi que leur accès
et les valeurs possibles pendant l'exécution. Par exemple, le décalage est dynamique pour une HloDynamicSliceInstruction 1D. Le RTVar correspondant aura une
HloInstruction* qui génère un Tensor de rang-0 avec l'accès (d0) -> ()
car pour chaque élément de la sortie, nous extrayons le même élément
à partir du Tensor de décalage pour calculer l'index de l'entrée. Nous pouvons
également supposer
que le décalage de la tranche est toujours compris entre 0 et
tensor_size - slice_size - 1
Examinons des exemples pour comprendre ce que tout cela signifie.
Indexer des cartes pour des opérations non fusionnées
Elementwise
Pour les opérations élémentaires, la carte d'indexation est une identité.
p0 = f32[10, 20] parameter(0)
p1 = f32[10, 20] parameter(1)
add = f32[10, 20] add(p0, p1)
Les mappages de sortie vers entrée :
- sortie -> input_i :
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Les mappages d'entrée/sortie
- input_i -> output:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Mégaphone
La diffusion signifie que certaines dimensions seront supprimées lorsque nous mapperons la sortie sur l'entrée et ajoutées lorsque nous mapperons l'entrée sur la sortie.
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
Carte de sortie vers entrée :
(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]
Mappage des entrées aux sorties
(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]
Notez que nous avons maintenant s à droite pour l'entrée et la sortie.
le mappage. Ce sont les symboles qui représentent des plages de valeurs. Par exemple, dans ce cas particulier, chaque élément d'entrée avec l'indice d0 est mappé sur une tranche 10x1x30 de la sortie.
Constante et Iota
Ils ne comportent aucun paramètre d'entrée. Il n'y a donc rien à calculer pour l'indexation.
DynamicSlice
DynamicSlice est identique à un segment d'application, à l'exception des décalages qui sont dynamiques.
src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}
Mappage de la sortie à l'entrée pour src :
(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
hlo: of1 = s32[] parameter(1)
(d0, d1, d2) -> ()
s1 in [0, 0]
hlo: of2 = s32[] parameter(2)
(d0, d1, d2) -> ()
s2 in [0, 226]
hlo: of3 = s32[] parameter(3)
(d0, d1, d2) -> ()
Notez que nous avons maintenant s sur le côté droit pour le mappage entrée-sortie.
Ce sont les symboles qui représentent les valeurs d'exécution. Par exemple, dans ce cas particulier, pour chaque élément de la sortie avec les indices d0, d1, d2, nous accédons aux décalages de tranche of1, of2 et of3 pour calculer l'indice de l'entrée.
Les intervalles pour les variables d'exécution sont dérivés en partant du principe que l'intégralité
reste dans les limites.
Mappage de la sortie à l'entrée pour of1, of2 et of3 :
(d0, d1, d2) -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
DynamicUpdateSlice
src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)
La sortie vers le mappage d'entrée pour src est simple. Elle peut être rendue
plus précise en
le domaine est limité aux index non mis à jour, mais les cartes sont actuellement indexées
ne sont pas compatibles avec les contraintes d'égalité.
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]
Le résultat du mappage d'entrée pour upd:
(d0, d1)[s0, s1] -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
hlo: of1 = s32[] parameter(2)
(d0, d1) -> ()
s1 in [0, 20]
hlo: of2 = s32[] parameter(3)
(d0, d1) -> ()
Notez que nous avons maintenant s sur le côté droit pour le mappage entrée-sortie.
Ce sont les symboles qui représentent les valeurs d'exécution. Par exemple, dans ce cas particulier, pour chaque élément de la sortie avec les indices d0, d1, nous accédons aux décalages de tranche of1 et of2 pour calculer l'indice de l'entrée. Les intervalles pour les variables d'exécution sont dérivés en supposant que l'ensemble de la tranche reste dans les limites.
Le résultat du mappage d'entrée pour of1 et of2:
(d0, d1) -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]
Réunir
Seule la collecte simplifiée est acceptée. Voir [gather_simplifier].(https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h).
operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
offset_dims={1,2,3},
collapsed_slice_dims={},
start_index_map={0,1},
index_vector_dim=1,
slice_sizes={7,8,4}
Le résultat du mappage d'entrée pour operand:
(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 1)
Notez que nous avons maintenant s sur le côté droit pour le mappage entrée-sortie.
Ce sont les symboles qui représentent les valeurs d'exécution. Par exemple, dans ce
pour chaque élément de la sortie comportant les index d0, d1, d2, d3 que nous
extraire les éléments (d0, 0) et (d0, 1) du Tensor indices.
Le résultat du mappage d'entrée pour indices:
(d0, d1, d2, d3)[s0] -> (d0, s0)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 1]
La variable de plage s0 indique que nous avons besoin de la ligne entière (d0, *) de la
Tensor indices pour calculer un élément de sortie.
Transposer
La carte d'indexation pour la transposition est une permutation des dimensions d'entrée/sortie.
p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}
Carte de sortie vers entrée :
(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]
Le mappage d'entrée et de sortie:
(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]
Inverser
Le mappage d'indexation pour l'inversion remplace les dimensions inversées par upper_bound(d_i) -
d_i :
p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}
Carte de sortie vers entrée :
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
Mappage des entrées aux sorties :
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
Réduction (variadic)
La réduction variadique comporte plusieurs entrées et plusieurs inits. La carte de sortie vers l'entrée ajoute les dimensions réduites. Il se comporte donc comme l'inverse d'une annonce d'une certaine manière.
p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
dimensions={0}, to_apply=max
Les mappages de sortie vers entrée :
- output -> input_j:
(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]
- sortie -> init_j:
(d0) -> ()
domain:
d0 in [0, 9]
Les mappages d'entrée/sortie :
- entrée_i -> output_j:
(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]
- init_i -> output_j:
()[s0] -> (s0)
domain:
s0 in [0, 9]
for i, j = 0, ... INPUT_COUNT.
Tranche
L'indexation de la sortie à l'entrée pour les tranches aboutit à un mappage d'indexation en plusieurs parties qui est valide pour chaque élément de la sortie. Le mappage de l'entrée à la sortie est limité à une plage striée des éléments de l'entrée.
p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
slice={[5:10:1], [3:20:7], [0:50:2]}
Carte de sortie vers entrée :
(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]
Le mappage d'entrée et de sortie:
(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]
Remodeler
Les remodelages se présentent sous différentes saveurs.
Réduire la forme
Il s'agit d'une « linéarisation » de N-D à 1D.
p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)
La sortie sur le mappage d'entrée:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
Le mappage d'entrée et de sortie:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
Développer la forme
Il s'agit d'une opération inverse de "réduire la forme". Elle transforme une entrée 1D en sortie N-D.
p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)
La sortie sur le mappage d'entrée:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
Mappage des entrées aux sorties :
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
Remodelage générique
Il s'agit des opérations de remodelage qui ne peuvent pas être représentées par une seule expansion ou réduire la forme. Elles ne peuvent être représentées que sous la forme d'une composition de deux formes d'expansion ou de réduction ou plus.
Exemple 1: Linéarisation-délinéarisation
p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)
Ce remodelage peut être représenté par la composition de la forme de réduction
tensor<4x8xf32> à tensor<32xf32>, puis une forme développée pour
tensor<2x4x4xf32>
Carte de sortie vers entrée :
(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]
Le mappage d'entrée et de sortie:
(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
Exemple 2 : Sous-formes développées et réduites
p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)
Cette refonte peut être représentée comme une composition de deux refontes. Le premier
réduit les dimensions les plus externes tensor<4x8x12xf32> en tensor<32x12xf32>
La dimension la plus interne tensor<32x12xf32> s'étend
tensor<32x3x4xf32>
La sortie sur le mappage d'entrée:
(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]
Mappage des entrées aux sorties :
(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]
Bitcast
Une opération de bitcast peut être représentée sous la forme d'une séquence de transposition-remodelage-transposition. Par conséquent, ses cartes d'indexation ne sont qu'une composition de cartes d'indexation pour séquence.
Concaténer
Le mappage sortie-entrée pour la concaténation est défini pour toutes les entrées, mais avec domaines qui ne se chevauchent pas, c'est-à-dire qu'une seule des entrées sera utilisée à la fois.
p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}
La sortie aux entrées mappe :
- sortie -> entrée 1 :
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- sortie -> entrée 2 :
(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]
- sortie -> entrée 3:
(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]
Les entrées des cartes de sortie :
- entrée 1 -> sortie:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- entrée 2 -> sortie:
(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]
- Entrée 3 -> Sortie :
(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]
Point
L'indexation des mappages par points est très semblable à celle de la fonction Réduire.
p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
lhs_batch_dims={0}, rhs_batch_dims={0},
lhs_contracting_dims={2}, rhs_contracting_dims={1}
La sortie aux entrées mappe :
- output -> input_1:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
- output -> input_2:
(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
Les entrées des cartes de sortie :
- entrée_1 -> sortie:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]
- entrée_2 -> sortie:
(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]
Pad
L'indexation de PadOp est l'inverse de l'indexation SliceOp.
p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0
La configuration de marge intérieure 1_4_1x4_8_0 indique lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1.
La sortie des mappages d'entrée:
- sortie -> entrée:
(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]
- sortie -> init :
(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]
ReduceWindow
ReduceWindow dans XLA effectue également un remplissage. Par conséquent, les cartes d'indexation peuvent être calculées en tant que composition de l'indexation ReduceWindow qui n'effectue aucun remplissage et de l'indexation de PadOp.
c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
window={size=1x512 pad=0_0x0_0}, to_apply=max
La sortie des mappages d'entrée:
- sortie -> entrée:
(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]
- sortie -> init:
(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]
Indexer Maps pour Fusion
La carte d'indexation pour l'opération de fusion est une composition de cartes d'indexation pour chaque opération du cluster. Il peut arriver que certaines entrées soient lues plusieurs fois avec des schémas d'accès différents.
Une entrée, plusieurs cartes d'indexation
Voici un exemple pour p0 + transpose(p0).
f {
p0 = f32[1000, 1000] parameter(0)
transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}
Les mappages d'indexation de la sortie vers l'entrée pour p0 seront (d0, d1) -> (d0, d1) et
(d0, d1) -> (d1, d0) Cela signifie que pour calculer un élément de la sortie, nous pouvons avoir besoin de lire le paramètre d'entrée deux fois.
Une entrée, indexation dédupliquée de la carte
Dans certains cas, les cartes d'indexation sont en fait les mêmes, ce qui n'est pas immédiatement évident.
f {
p0 = f32[20, 10, 50] parameter(0)
lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}
Dans ce cas, le mappage d'indexation de la sortie vers l'entrée pour p0 est simplement
(d0, d1, d2) -> (d2, d0, d1)
Softmax
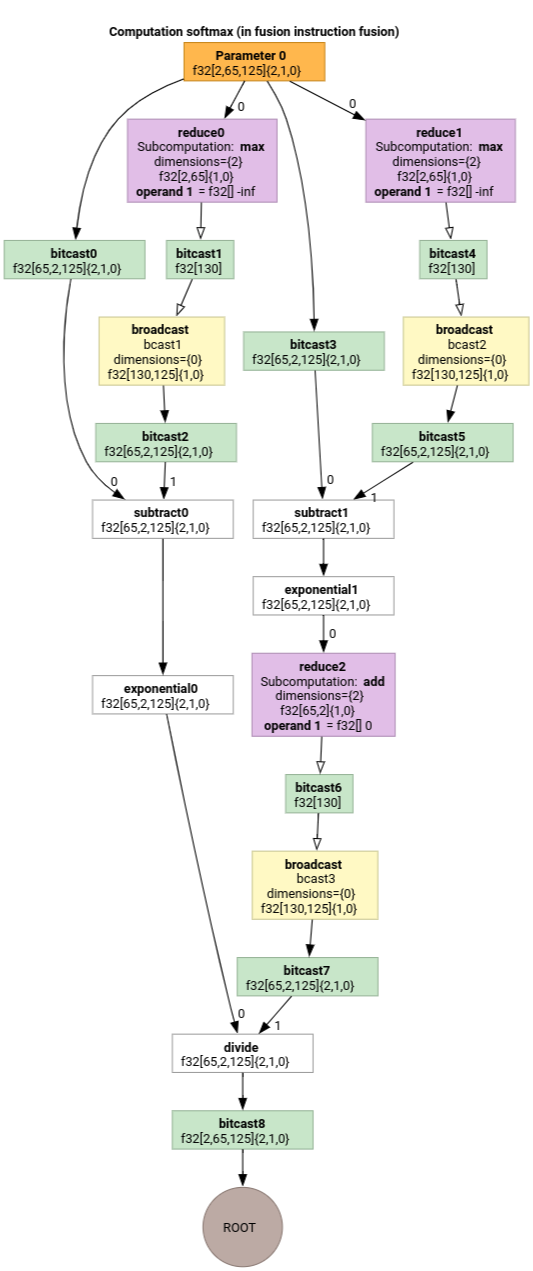
Les mappages d'indexation de sortie vers entrée pour parameter 0 pour softmax :
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]
et
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
où s0 fait référence à la dimension la plus interne de l'entrée.
Indexing Map Simplifier
Le simplificateur par défaut de mlir::AffineMap en amont ne peut pas
sur les plages de dimensions/symboles. Par conséquent, il ne peut pas
simplifier les expressions avec mod et div de manière efficace.
Nous pouvons exploiter les connaissances sur les bornes inférieure et supérieure des sous-expressions dans les cartes affines pour les simplifier encore plus.
Le simplificateur peut réécrire les expressions suivantes.
(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16)pour d dans[0, 6] x [0, 14]devient(d0, d1) -> (d0, d1)(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10)pourdi in [0, 9]devient(d0, d1, d2) -> (d0, d1, d2).(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8)pourd_i in [0, 9]devient(d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8).(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9)pendant d dans[0, 9] x [0, 10]devient(d0, d1) -> (d0).
Le simplifieur de carte d'indexation nous permet de comprendre que certaines des refontes en chaîne dans HLO s'annulent mutuellement.
p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)
Après la composition des cartes d'indexation et leur simplification, nous obtenons
(d0, d1, d2) -> (d0, d1, d2).
La simplification de l'indexation des cartes simplifie également les contraintes.
- Les contraintes de type
lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_boundsont réécrites en tant queupdated_lower_bound <= affine_expr <= updated_upped_bound. - Les contraintes toujours satisfaites, comme
d0 + s0 in [0, 20]pourd0 in [0, 5]ets0 in [1, 3]sont éliminés. - Les expressions affines dans les contraintes sont optimisées comme la carte affine d'indexation ci-dessus.
Pour en savoir plus, consultez indexing_map_test.cc.

