The following describes the semantics of operations defined in the
XlaBuilder
interface. Typically, these operations map one-to-one to operations defined in
the RPC interface in
xla_data.proto.
A note on nomenclature: the generalized data type XLA deals with is an N-dimensional array holding elements of some uniform type (such as 32-bit float). Throughout the documentation, array is used to denote an arbitrary-dimensional array. For convenience, special cases have more specific and familiar names; for example a vector is a 1-dimensional array and a matrix is a 2-dimensional array.
Learn more about the structure of an Op in Shapes and layout and Tiled Layout.
Abs
See also
XlaBuilder::Abs.
Element-wise abs x -> |x|.
Abs(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
For StableHLO information see StableHLO - abs.
Add
See also
XlaBuilder::Add.
Performs element-wise addition of lhs and rhs.
Add(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Add:
Add(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - add.
AddDependency
See also
HloInstruction::AddDependency.
AddDependency may appear in HLO dumps, but they are not intended to be
constructed manually by end users.
AfterAll
See also
XlaBuilder::AfterAll.
AfterAll takes a variadic number of tokens and produces a single token. Tokens
are primitive types which can be threaded between side-effecting operations to
enforce ordering. AfterAll can be used as a join of tokens for ordering an
operation after a set of operations.
AfterAll(tokens)
| Arguments | Type | Semantics |
|---|---|---|
tokens |
vector of XlaOp |
variadic number of tokens |
For StableHLO information see StableHLO - after_all.
AllGather
See also
XlaBuilder::AllGather.
Performs concatenation across replicas.
AllGather(operand, all_gather_dimension, shard_count, replica_groups,
channel_id, layout, use_global_device_ids)
| Arguments | Type | Semantics |
|---|---|---|
operand
|
XlaOp
|
Array to concatenate across replicas |
all_gather_dimension |
int64 |
Concatenation dimension |
shard_count
|
int64
|
The size of each replica group |
replica_groups
|
vector of vectors of
int64 |
Groups between which the concatenation is performed |
channel_id
|
optional
ChannelHandle |
Optional channel ID for cross-module communication |
layout
|
optional Layout
|
Creates a layout pattern that will capture the matched layout in the argument |
use_global_device_ids
|
optional bool
|
Returns true if the ids in the ReplicaGroup config represent a global id |
replica_groupsis a list of replica groups between which the concatenation is performed (replica id for the current replica can be retrieved usingReplicaId). The order of replicas in each group determines the order in which their inputs are located in the result.replica_groupsmust either be empty (in which case all replicas belong to a single group, ordered from0toN - 1), or contain the same number of elements as the number of replicas. For example,replica_groups = {0, 2}, {1, 3}performs concatenation between the replicas0and2, and1and3.shard_countis the size of each replica group. We need this in cases wherereplica_groupsare empty.channel_idis used for cross-module communication: onlyall-gatheroperations with the samechannel_idcan communicate to each other.use_global_device_idsReturns true if the ids in the ReplicaGroup config represent a global id of (replica_id * partition_count + partition_id) instead of a replica id. This enables more flexible grouping of devices if this all-reduce is both cross-partition and cross-replica.
The output shape is the input shape with the all_gather_dimension made
shard_count times larger. For example, if there are two replicas and the
operand has the value [1.0, 2.5] and [3.0, 5.25] respectively on the two
replicas, then the output value from this op where all_gather_dim is 0 will
be [1.0, 2.5, 3.0,5.25] on both replicas.
The API of AllGather is internally decomposed into 2 HLO instructions
(AllGatherStart and AllGatherDone).
See also
HloInstruction::CreateAllGatherStart.
AllGatherStart, AllGatherDone serve as primitives in HLO. These ops may
appear in HLO dumps, but they are not intended to be constructed manually by end
users.
For StableHLO information see StableHLO - all_gather.
AllReduce
See also
XlaBuilder::AllReduce.
Performs a custom computation across replicas.
AllReduce(operand, computation, replica_groups, channel_id,
shape_with_layout, use_global_device_ids)
| Arguments | Type | Semantics |
|---|---|---|
operand
|
XlaOp
|
Array or a non-empty tuple of arrays to reduce across replicas |
computation |
XlaComputation |
Reduction computation |
replica_groups
|
ReplicaGroup vector
|
Groups between which the reductions are performed |
channel_id
|
optional
ChannelHandle |
Optional channel ID for cross-module communication |
shape_with_layout
|
optional Shape
|
Defines the layout of the data transferred |
use_global_device_ids
|
optional bool
|
Returns true if the ids in the ReplicaGroup config represent a global id |
- When
operandis a tuple of arrays, the all-reduce is performed on each element of the tuple. replica_groupsis a list of replica groups between which the reduction is performed (replica id for the current replica can be retrieved usingReplicaId).replica_groupsmust either be empty (in which case all replicas belong to a single group), or contain the same number of elements as the number of replicas. For example,replica_groups = {0, 2}, {1, 3}performs reduction between the replicas0and2, and1and3.channel_idis used for cross-module communication: onlyall-reduceoperations with the samechannel_idcan communicate to each other.shape_with_layout: forces the layout of the AllReduce to the given layout. This is used to guarantee the same layout for a group of AllReduce ops compiled separately.use_global_device_idsReturns true if the ids in the ReplicaGroup config represent a global id of (replica_id * partition_count + partition_id) instead of a replica id. This enables more flexible grouping of devices if this all-reduce is both cross-partition and cross-replica.
The output shape is the same as the input shape. For example, if there are two
replicas and the operand has the value [1.0, 2.5] and [3.0, 5.25]
respectively on the two replicas, then the output value from this op and
summation computation will be [4.0, 7.75] on both replicas. If the input is a
tuple, the output is a tuple as well.
Computing the result of AllReduce requires having one input from each replica,
so if one replica executes an AllReduce node more times than another, then the
former replica will wait forever. Since the replicas are all running the same
program, there are not a lot of ways for that to happen, but it is possible when
a while loop's condition depends on data from infeed and the data that is
infeed causes the while loop to iterate more times on one replica than
another.
The API of AllReduce is internally decomposed into 2 HLO instructions
(AllReduceStart and AllReduceDone).
See also
HloInstruction::CreateAllReduceStart.
AllReduceStart and AllReduceDone serve as primitives in HLO. These ops may
appear in HLO dumps, but they are not intended to be constructed manually by end
users.
CrossReplicaSum
See also
XlaBuilder::CrossReplicaSum.
Performs AllReduce with a summation computation.
CrossReplicaSum(operand, replica_groups)
| Arguments | Type | Semantics |
|---|---|---|
operand
|
XlaOp | Array or a non-empty tuple of arrays to reduce across replicas |
replica_groups
|
vector of vectors of
int64 |
Groups between which the reductions are performed |
Returns the sum of the operand value within each subgroup of replicas. All replicas supply one input to the sum and all replicas receive the resulting sum for each subgroup.
AllToAll
See also
XlaBuilder::AllToAll.
AllToAll is a collective operation that sends data from all cores to all cores. It has two phases:
- The scatter phase. On each core, the operand is split into
split_countnumber of blocks along thesplit_dimensions, and the blocks are scattered to all cores, e.g., the ith block is sent to the ith core. - The gather phase. Each core concatenates the received blocks along the
concat_dimension.
The participating cores can be configured by:
replica_groups: each ReplicaGroup contains a list of replica ids participating in the computation (the replica id for the current replica can be retrieved usingReplicaId). AllToAll will be applied within subgroups in the specified order. For example,replica_groups = { {1,2,3}, {4,5,0} }means that an AllToAll will be applied within replicas{1, 2, 3}, and in the gather phase, and the received blocks will be concatenated in the same order of 1, 2, 3. Then, another AllToAll will be applied within replicas 4, 5, 0, and the concatenation order is also 4, 5, 0. Ifreplica_groupsis empty, all replicas belong to one group, in the concatenation order of their appearance.
Prerequisites:
- The dimension size of the operand on the
split_dimensionis divisible bysplit_count. - The operand's shape is not tuple.
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups, layout, channel_id)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
n dimensional input array |
split_dimension
|
int64
|
A value in the interval
[0,n) that names the
dimension along which the
operand is split |
concat_dimension
|
int64
|
A value in the interval
[0,n) that names the
dimension along which the
split blocks are
concatenated |
split_count
|
int64
|
The number of cores that
participate in this
operation. If
replica_groups is empty,
this should be the number of
replicas; otherwise, this
should be equal to the
number of replicas in each
group. |
replica_groups
|
ReplicaGroupvector
|
Each group contains a list of replica ids. |
layout |
optional Layout |
user-specified memory layout |
channel_id
|
optional ChannelHandle
|
unique identifier for each send/recv pair |
See xla::shapes for more information on shapes and layouts..
For StableHLO information see StableHLO - all_to_all.
AllToAll - Example 1.
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(
x,
/*split_dimension=*/ 1,
/*concat_dimension=*/ 0,
/*split_count=*/ 4);
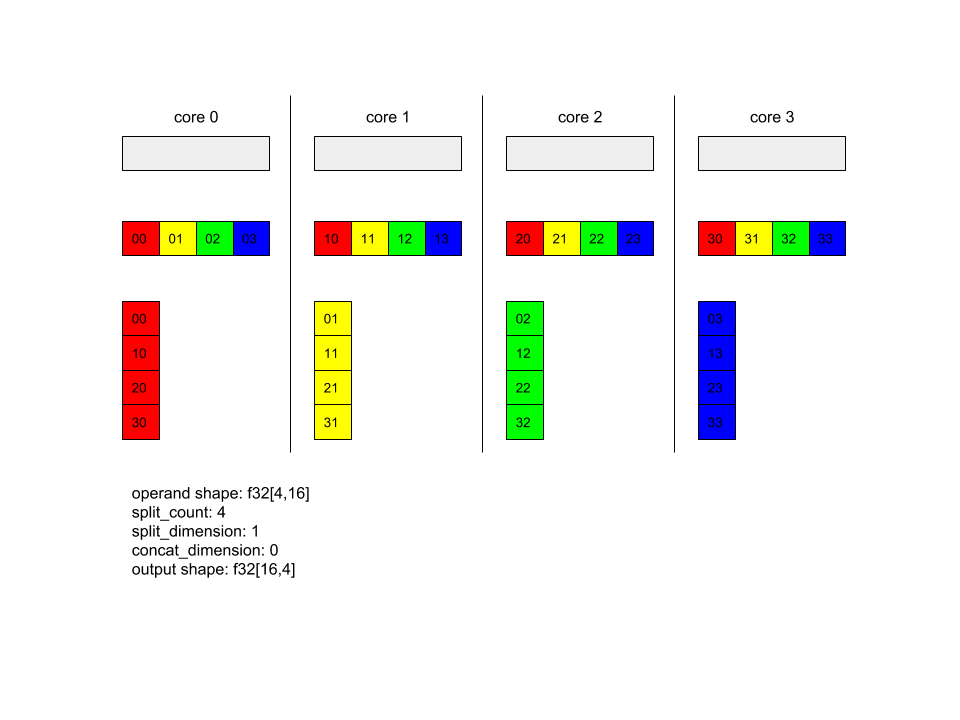
In the above example, there are 4 cores participating in the Alltoall. On each core, the operand is split into 4 parts along dimension 1, so each part has shape f32[4,4]. The 4 parts are scattered to all cores. Then each core concatenates the received parts along dimension 0, in the order of core 0-4. So the output on each core has shape f32[16,4].
AllToAll - Example 2 - StableHLO
In the above example, there are 2 replicas participating in the AllToAll. On each replica, the operand has shape f32[2,4]. The operand is split into 2 parts along dimension 1, so each part has shape f32[2,2]. The 2 parts are then exchanged across the replicas according to their position in the replica group. Each replica collects its corresponding part from both operands and concatenates them along dimension 0. As a result, the output on each replica has shape f32[4,2].
RaggedAllToAll
See also
XlaBuilder::RaggedAllToAll.
RaggedAllToAll performs a collective all-to-all operation, where the input and output are ragged tensors.
RaggedAllToAll(input, input_offsets, send_sizes, output, output_offsets,
recv_sizes, replica_groups, channel_id)
| Arguments | Type | Semantics |
|---|---|---|
input |
XlaOp |
N array of type T |
input_offsets |
XlaOp |
N array of type T |
send_sizes |
XlaOp |
N array of type T |
output |
XlaOp |
N array of type T |
output_offsets |
XlaOp |
N array of type T |
recv_sizes |
XlaOp |
N array of type T |
replica_groups
|
ReplicaGroup vector
|
Each group contains a list of replica ids. |
channel_id
|
optional ChannelHandle
|
unique identifier for each send/recv pair |
Ragged tensors are defined by a set of three tensors:
data: thedatatensor is “ragged” along its outermost dimension, along which each indexed element has variable size.offsets': theoffsetstensor indexes the outermost dimension of thedatatensor, and represents the starting offset of each ragged element of thedatatensor.sizes: thesizestensor represents the size of each ragged element of thedatatensor, where the size is specified in units of sub-elements. A sub-element is defined as the suffix of the ‘data’ tensor shape obtained by removing the outermost “ragged” dimension.- The
offsetsandsizestensors must have the same size.
An example ragged tensor:
data: [8,3] =
{ {a,b,c},{d,e,f},{g,h,i},{j,k,l},{m,n,o},{p,q,r},{s,t,u},{v,w,x} }
offsets: [3] = {0, 1, 4}
sizes: [3] = {1, 3, 4}
// Index 'data' at 'offsets'[0], 'sizes'[0]' // {a,b,c}
// Index 'data' at 'offsets'[1], 'sizes'[1]' // {d,e,f},{g,h,i},{j,k,l}
// Index 'data' at 'offsets'[2], 'sizes'[2]' // {m,n,o},{p,q,r},{s,t,u},{v,w,x}
output_offsets must be sharded in a way that each replica has offsets in the
target replica output perspective.
For i-th output offset, the current replica will send
input[input_offsets[i]:input_offsets[i]+input_sizes[i]] update to i-th
replica that will be written to
output_i[output_offsets[i]:output_offsets[i]+send_sizes[i]] in i-th replica
output.
For example, if we have 2 replicas:
replica 0:
input: [1, 2, 2]
output:[0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 2]
output_offsets: [0, 0]
recv_sizes: [1, 1]
replica 1:
input: [3, 4, 0]
output: [0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 1]
output_offsets: [1, 2]
recv_sizes: [2, 1]
// replica 0's result will be: [1, 3, 0, 0]
// replica 1's result will be: [2, 2, 4, 0]
The ragged all-to-all HLO has the following arguments:
input: ragged input data tensor.output: ragged output data tensor.input_offsets: ragged input offsets tensor.send_sizes: ragged send sizes tensor.output_offsets: array of ragged offsets in the target replica output.recv_sizes: ragged recv sizes tensor.
The *_offsets and *_sizes tensors must all have the same shape.
Two shapes are supported for the *_offsets and *_sizes tensors:
[num_devices]where ragged-all-to-all may send at most one update to each remote device in the replica group. For example:
for (remote_device_id : replica_group) {
SEND input[input_offsets[remote_device_id]],
output[output_offsets[remote_device_id]],
send_sizes[remote_device_id] }
[num_devices, num_updates]where ragged-all-to-all may send up tonum_updatesupdates the same remote device (each at different offsets), for each remote device in the replica group.
For example:
for (remote_device_id : replica_group) {
for (update_idx : num_updates) {
SEND input[input_offsets[remote_device_id][update_idx]],
output[output_offsets[remote_device_id][update_idx]]],
send_sizes[remote_device_id][update_idx] } }
And
See also
XlaBuilder::And.
Performs element-wise AND of two tensors lhs and rhs.
And(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for And:
And(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - and.
Async
See also HloInstruction::CreateAsyncStart,
HloInstruction::CreateAsyncUpdate,
HloInstruction::CreateAsyncDone.
AsyncDone, AsyncStart, and AsyncUpdate are internal HLO instructions used
for Asynchronous operations and serve as primitives in HLO. These ops may appear
in HLO dumps but they are not intended to be constructed manually by end users.
Atan2
See also
XlaBuilder::Atan2.
Performs element-wise atan2 operation on lhs and rhs.
Atan2(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Atan2:
Atan2(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - atan2.
BatchNormGrad
See also
XlaBuilder::BatchNormGrad
and the original batch normalization paper
for a detailed description of the algorithm.
Calculates gradients of batch norm.
BatchNormGrad(operand, scale, batch_mean, batch_var, grad_output, epsilon,
feature_index)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp | n dimensional array to be normalized (x) |
scale |
XlaOp | 1 dimensional array (\(\gamma\)) |
batch_mean |
XlaOp | 1 dimensional array (\(\mu\)) |
batch_var |
XlaOp | 1 dimensional array (\(\sigma^2\)) |
grad_output |
XlaOp | Gradients passed to BatchNormTraining (\(\nabla y\)) |
epsilon |
float |
Epsilon value (\(\epsilon\)) |
feature_index |
int64 |
Index to feature dimension in operand |
For each feature in the feature dimension (feature_index is the index for the
feature dimension in operand), the operation calculates the gradients with
respect to operand, offset, and scale across all the other dimensions. The
feature_index must be a valid index for the feature dimension in operand.
The three gradients are defined by the following formulas (assuming a
4-dimensional array as operand and with feature dimension index l, batch
size m and spatial sizes w and h):
\[ \begin{split} c_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sigma^2_l+\epsilon} \right) \\\\ d_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \\\\ \nabla x_{ijkl} &= \frac{\gamma_{l} }{\sqrt{\sigma^2_{l}+\epsilon} } \left( \nabla y_{ijkl} - d_l - c_l (x_{ijkl} - \mu_{l}) \right) \\\\ \nabla \gamma_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sqrt{\sigma^2_{l}+\epsilon} } \right) \\\\\ \nabla \beta_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \end{split} \]
The inputs batch_mean and batch_var represent moments values across batch
and spatial dimensions.
The output type is a tuple of three handles:
| Outputs | Type | Semantics |
|---|---|---|
grad_operand
|
XlaOp | gradient with respect to
input operand
(\(\nabla x\)) |
grad_scale
|
XlaOp | gradient with respect to
input **scale **
(\(\nabla\gamma\)) |
grad_offset
|
XlaOp | gradient with respect to
input
offset(\(\nabla\beta\)) |
For StableHLO information see StableHLO - batch_norm_grad.
BatchNormInference
See also
XlaBuilder::BatchNormInference
and the original batch normalization paper
for a detailed description of the algorithm.
Normalizes an array across batch and spatial dimensions.
BatchNormInference(operand, scale, offset, mean, variance, epsilon,
feature_index)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp | n dimensional array to be normalized |
scale |
XlaOp | 1 dimensional array |
offset |
XlaOp | 1 dimensional array |
mean |
XlaOp | 1 dimensional array |
variance |
XlaOp | 1 dimensional array |
epsilon |
float |
Epsilon value |
feature_index |
int64 |
Index to feature dimension in operand |
For each feature in the feature dimension (feature_index is the index for the
feature dimension in operand), the operation calculates the mean and variance
across all the other dimensions and uses the mean and variance to normalize each
element in operand. The feature_index must be a valid index for the feature
dimension in operand.
BatchNormInference is equivalent to calling BatchNormTraining without
computing mean and variance for each batch. It uses the input mean and
variance instead as estimated values. The purpose of this op is to reduce
latency in inference, hence the name BatchNormInference.
The output is an n-dimensional, normalized array with the same shape as input
operand.
For StableHLO information see StableHLO - batch_norm_inference.
BatchNormTraining
See also
XlaBuilder::BatchNormTraining
and the original batch normalization paper
for a detailed description of the algorithm.
Normalizes an array across batch and spatial dimensions.
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
n dimensional array to be normalized (x) |
scale |
XlaOp |
1 dimensional array (\(\gamma\)) |
offset |
XlaOp |
1 dimensional array (\(\beta\)) |
epsilon |
float |
Epsilon value (\(\epsilon\)) |
feature_index |
int64 |
Index to feature dimension in operand |
For each feature in the feature dimension (feature_index is the index for the
feature dimension in operand), the operation calculates the mean and variance
across all the other dimensions and uses the mean and variance to normalize each
element in operand. The feature_index must be a valid index for the feature
dimension in operand.
The algorithm goes as follows for each batch in operand \(x\) that contains m
elements with w and h as the size of spatial dimensions (assuming operand
is a 4 dimensional array):
Calculates batch mean \(\mu_l\) for each feature
lin feature dimension: \(\mu_l=\frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h x_{ijkl}\)Calculates batch variance \(\sigma^2_l\): $\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
Normalizes, scales and shifts: \(y_{ijkl}=\frac{\gamma_l(x_{ijkl}-\mu_l)}{\sqrt[2]{\sigma^2_l+\epsilon} }+\beta_l\)
The epsilon value, usually a small number, is added to avoid divide-by-zero errors.
The output type is a tuple of three XlaOps:
| Outputs | Type | Semantics |
|---|---|---|
output
|
XlaOp
|
n dimensional array with the same shape as input
operand (y) |
batch_mean |
XlaOp |
1 dimensional array (\(\mu\)) |
batch_var |
XlaOp |
1 dimensional array (\(\sigma^2\)) |
The batch_mean and batch_var are moments calculated across the batch and
spatial dimensions using the formulas above.
For StableHLO information see StableHLO - batch_norm_training.
Bitcast
See also
HloInstruction::CreateBitcast.
Bitcast may appear in HLO dumps, but they are not intended to be constructed
manually by end users.
BitcastConvertType
See also
XlaBuilder::BitcastConvertType.
Similar to a tf.bitcast in TensorFlow, performs an element-wise bitcast
operation from a data shape to a target shape. The input and output size must
match: e.g. s32 elements become f32 elements via bitcast routine, and one
s32 element will become four s8 elements. Bitcast is implemented as a
low-level cast, so machines with different floating-point representations will
give different results.
BitcastConvertType(operand, new_element_type)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
array of type T with dims D |
new_element_type |
PrimitiveType |
type U |
The dimensions of the operand and the target shape must match, apart from the last dimension which will change by the ratio of the primitive size before and after the conversion.
The source and destination element types must not be tuples.
For StableHLO information see StableHLO - bitcast_convert.
Bitcast-converting to primitive type of different width
BitcastConvert HLO instruction supports the case where the size of the output
element type T' is not equal to the size of the input element T. As the
whole operation is conceptually a bitcast and does not change the underlying
bytes, the shape of the output element has to change. For B = sizeof(T), B' =
sizeof(T'), there are two possible cases.
First, when B > B', the output shape gets a new minor-most dimension of size
B/B'. For example:
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
The rule remains the same for effective scalars:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
Alternatively, for B' > B the instruction requires the last logical dimension
of the input shape to be equal to B'/B, and this dimension is dropped during
the conversion:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
Note that conversions between different bitwidths are not elementwise.
Broadcast
See also
XlaBuilder::Broadcast.
Adds dimensions to an array by duplicating the data in the array.
Broadcast(operand, broadcast_sizes)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The array to duplicate |
broadcast_sizes |
ArraySlice<int64> |
The sizes of the new dimensions |
The new dimensions are inserted on the left, i.e. if broadcast_sizes has
values {a0, ..., aN} and the operand shape has dimensions {b0, ..., bM} then
the shape of the output has dimensions {a0, ..., aN, b0, ..., bM}.
The new dimensions index into copies of the operand, i.e.
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
For example, if operand is a scalar f32 with value 2.0f, and
broadcast_sizes is {2, 3}, then the result will be an array with shape
f32[2, 3] and all the values in the result will be 2.0f.
For StableHLO information see StableHLO - broadcast.
BroadcastInDim
See also
XlaBuilder::BroadcastInDim.
Expands the size and number of dimensions of an array by duplicating the data in the array.
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The array to duplicate |
out_dim_size
|
ArraySlice<int64>
|
The sizes of the dimensions of the target shape |
broadcast_dimensions
|
ArraySlice<int64>
|
Which dimension in the target shape each dimension of the operand shape corresponds to |
Similar to Broadcast, but allows adding dimensions anywhere and expanding existing dimensions with size 1.
The operand is broadcast to the shape described by out_dim_size.
broadcast_dimensions maps the dimensions of operand to the dimensions of the
target shape, i.e. the i'th dimension of the operand is mapped to the
broadcast_dimension[i]'th dimension of the output shape. The dimensions of
operand must have size 1 or be the same size as the dimension in the output
shape they are mapped to. The remaining dimensions are filled with dimensions of
size 1. Degenerate-dimension broadcasting then broadcasts along these degenerate
dimensions to reach the output shape. The semantics are described in detail on
the broadcasting page.
Call
See also
XlaBuilder::Call.
Invokes a computation with the given arguments.
Call(computation, operands...)
| Arguments | Type | Semantics |
|---|---|---|
computation
|
XlaComputation
|
computation of type T_0, T_1, ...,
T_{N-1} -> S with N parameters of
arbitrary type |
operands |
sequence of N XlaOps |
N arguments of arbitrary type |
The arity and types of the operands must match the parameters of the
computation. It is allowed to have no operands.
CompositeCall
See also
XlaBuilder::CompositeCall.
Encapsulates an operation made up (composed) of other StableHLO operations, taking inputs and composite_attributes and producing results. The semantics of the op are implemented by the decomposition attribute. The composite op can be replaced with its decomposition without changing program semantics. In cases where inlining the decomposition does not provide the same op semantics, prefer using custom_call.
The version field (defaults to 0) is used to denote when a composite's semantics change.
This op is implemented as a kCall with attribute is_composite=true. The
decomposition field is specified by the computation attribute. The frontend
attributes store the remaining attributes prefixed with composite..
Example CompositeCall op:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
CompositeCall(computation, operands..., name, attributes, version)
| Arguments | Type | Semantics |
|---|---|---|
computation
|
XlaComputation
|
computation of type T_0, T_1, ...,
T_{N-1} -> S with N parameters of
arbitrary type |
operands |
sequence of N XlaOps |
variadic number of values |
name |
string |
name of the composite |
attributes
|
optional string
|
optional stringified dictionary of attributes |
version
|
optional int64
|
number to version updates to semantics of the composite op |
An op’s decomposition isn’t a field called, but instead appears as a to_apply
attribute that points to the function which contains the lower-level
implementation, i.e. to_apply=%funcname
More information on composite and decomposition can be found on StableHLO Specification.
Cbrt
See also
XlaBuilder::Cbrt.
Element-wise cubic root operation x -> cbrt(x).
Cbrt(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Cbrt also supports the optional result_accuracy argument:
Cbrt(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
For StableHLO information see StableHLO - cbrt.
Ceil
See also
XlaBuilder::Ceil.
Element-wise ceil x -> ⌈x⌉.
Ceil(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
For StableHLO information see StableHLO - ceil.
Cholesky
See also
XlaBuilder::Cholesky.
Computes the Cholesky decomposition of a batch of symmetric (Hermitian) positive definite matrices.
Cholesky(a, lower)
| Arguments | Type | Semantics |
|---|---|---|
a
|
XlaOp
|
an array of a complex or floating-point type with > 2 dimensions. |
lower |
bool |
whether to use the upper or lower triangle of a. |
If lower is true, computes lower-triangular matrices l such that $a = l .
l^T$. If lower is false, computes upper-triangular matrices u such that
\(a = u^T . u\).
Input data is read only from the lower/upper triangle of a, depending on the
value of lower. Values from the other triangle are ignored. Output data is
returned in the same triangle; the values in the other triangle are
implementation-defined and may be anything.
If a has greater than 2 dimensions, a is treated as a batch of matrices,
where all except the minor 2 dimensions are batch dimensions.
If a is not symmetric (Hermitian) positive definite, the result is
implementation-defined.
For StableHLO information see StableHLO - cholesky.
Clamp
See also
XlaBuilder::Clamp.
Clamps an operand to within the range between a minimum and maximum value.
Clamp(min, operand, max)
| Arguments | Type | Semantics |
|---|---|---|
min |
XlaOp |
array of type T |
operand |
XlaOp |
array of type T |
max |
XlaOp |
array of type T |
Given an operand and minimum and maximum values, returns the operand if it is in
the range between the minimum and maximum, else returns the minimum value if the
operand is below this range or the maximum value if the operand is above this
range. That is, clamp(a, x, b) = min(max(a, x), b).
All three arrays must be the same shape. Alternatively, as a restricted form of
broadcasting, min and/or max can be a scalar of type T.
Example with scalar min and max:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
For StableHLO information see StableHLO - clamp.
Collapse
See also
XlaBuilder::Collapse.
and the tf.reshape operation.
Collapses dimensions of an array into one dimension.
Collapse(operand, dimensions)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
array of type T |
dimensions |
int64 vector |
in-order, consecutive subset of T's dimensions. |
Collapse replaces the given subset of the operand's dimensions by a single
dimension. The input arguments are an arbitrary array of type T and a
compile-time-constant vector of dimension indices. The dimension indices must be
an in-order (low to high dimension numbers), consecutive subset of T's
dimensions. Thus, {0, 1, 2}, {0, 1}, or {1, 2} are all valid dimension sets, but
{1, 0} or {0, 2} are not. They are replaced by a single new dimension, in the
same position in the dimension sequence as those they replace, with the new
dimension size equal to the product of original dimension sizes. The lowest
dimension number in dimensions is the slowest varying dimension (most major)
in the loop nest which collapses these dimensions, and the highest dimension
number is fastest varying (most minor). See the tf.reshape operator if more
general collapse ordering is needed.
For example, let v be an array of 24 elements:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
Clz
See also
XlaBuilder::Clz.
Element-wise count leading zeros.
Clz(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
CollectiveBroadcast
See also
XlaBuilder::CollectiveBroadcast.
Broadcasts data across replicas. Data is sent from the first replica id in each
group to the other ids in the same group. If a replica id is not in any replica
group, the output on that replica is a tensor consisting of 0(s) in shape.
CollectiveBroadcast(operand, replica_groups, channel_id)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
replica_groups
|
ReplicaGroupvector
|
Each group contains a list of replica ids |
channel_id
|
optional ChannelHandle
|
unique identifier for each send/recv pair |
For StableHLO information see StableHLO - collective_broadcast.
CollectivePermute
See also
XlaBuilder::CollectivePermute.
CollectivePermute is a collective operation that sends and receives data across replicas.
CollectivePermute(operand, source_target_pairs, channel_id, inplace)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
n dimensional input array |
source_target_pairs
|
<int64, int64> vector
|
A list of (source_replica_id, target_replica_id) pairs. For each pair, the operand is sent from source replica to target replica. |
channel_id
|
optional ChannelHandle
|
Optional channel ID for cross-module communication |
inplace
|
optional bool
|
flag whether permutation should be done in place |
Note that there are the following restrictions on the source_target_pairs:
- Any two pairs should not have the same target replica id, and they should not have the same source replica id.
- If a replica id is not a target in any pair, then the output on that replica is a tensor consisting of 0(s) with the same shape as the input.
The API of CollectivePermute operation is internally decomposed into 2 HLO
instructions (CollectivePermuteStart and CollectivePermuteDone).
See also
HloInstruction::CreateCollectivePermuteStart.
CollectivePermuteStart and CollectivePermuteDone serve as primitives in HLO.
These ops may appear in HLO dumps, but they are not intended to be constructed
manually by end users.
For StableHLO information see StableHLO - collective_permute.
Compare
See also
XlaBuilder::Compare.
Performs element-wise comparison of lhs and rhs of the following:
Eq
See also
XlaBuilder::Eq.
Performs element-wise equal-to comparison of lhs and rhs.
\(lhs = rhs\)
Eq(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Eq:
Eq(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
Support a total order over the floating point numbers exists for Eq, by enforcing:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
EqTotalOrder(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
For StableHLO information see StableHLO - compare.
Ne
See also
XlaBuilder::Ne.
Performs element-wise not equal-to comparison of lhs and rhs.
\(lhs != rhs\)
Ne(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Ne:
Ne(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
Support a total order over the floating point numbers exists for Ne, by enforcing:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
NeTotalOrder(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
For StableHLO information see StableHLO - compare.
Ge
See also
XlaBuilder::Ge.
Performs element-wise greater-or-equal-than comparison of lhs and rhs.
\(lhs >= rhs\)
Ge(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Ge:
Ge(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
Support a total order over the floating point numbers exists for Gt, by enforcing:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
GtTotalOrder(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
For StableHLO information see StableHLO - compare.
Gt
See also
XlaBuilder::Gt.
Performs element-wise greater-than comparison of lhs and rhs.
\(lhs > rhs\)
Gt(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Gt:
Gt(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - compare.
Le
See also
XlaBuilder::Le.
Performs element-wise less-or-equal-than comparison of lhs and rhs.
\(lhs <= rhs\)
Le(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Le:
Le(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
Support a total order over the floating point numbers exists for Le, by enforcing:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LeTotalOrder(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
For StableHLO information see StableHLO - compare.
Lt
See also
XlaBuilder::Lt.
Performs element-wise less-than comparison of lhs and rhs.
\(lhs < rhs\)
Lt(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Lt:
Lt(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
Support a total order over the floating point numbers exists for Lt, by enforcing:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LtTotalOrder(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
For StableHLO information see StableHLO - compare.
Complex
See also
XlaBuilder::Complex.
Performs element-wise conversion to a complex value from a pair of real and
imaginary values, lhs and rhs.
Complex(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Complex:
Complex(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - complex.
ConcatInDim (Concatenate)
See also
XlaBuilder::ConcatInDim.
Concatenate composes an array from multiple array operands. The array has the same number of dimensions as each of the input array operands (which must have the same number of dimensions as each other) and contains the arguments in the order that they were specified.
Concatenate(operands..., dimension)
| Arguments | Type | Semantics |
|---|---|---|
operands
|
sequence of N XlaOp
|
N arrays of type T with dimensions [L0, L1, ...]. Requires N >= 1. |
dimension
|
int64
|
A value in the interval [0, N) that
names the dimension to be concatenated
between the operands. |
With the exception of dimension all dimensions must be the same. This is
because XLA does not support "ragged" arrays. Also note that 0-dimensional
values cannot be concatenated (as it's impossible to name the dimension along
which the concatenation occurs).
1-dimensional example:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
//Output: {2, 3, 4, 5, 6, 7}
2-dimensional example:
let a = { {1, 2},
{3, 4},
{5, 6} };
let b = { {7, 8} };
Concat({a, b}, 0)
//Output: { {1, 2},
// {3, 4},
// {5, 6},
// {7, 8} }
Diagram:
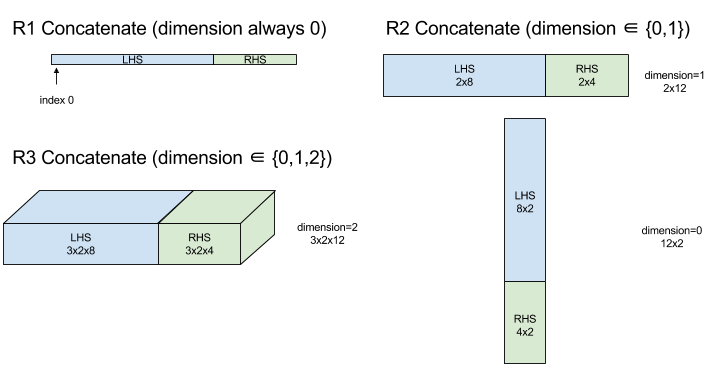
For StableHLO information see StableHLO - concatenate.
Conditional
See also
XlaBuilder::Conditional.
Conditional(predicate, true_operand, true_computation, false_operand,
false_computation)
| Arguments | Type | Semantics |
|---|---|---|
predicate |
XlaOp |
Scalar of type PRED |
true_operand |
XlaOp |
Argument of type \(T_0\) |
true_computation |
XlaComputation |
XlaComputation of type \(T_0 \to S\) |
false_operand |
XlaOp |
Argument of type \(T_1\) |
false_computation |
XlaComputation |
XlaComputation of type \(T_1 \to S\) |
Executes true_computation if predicate is true, false_computation if
predicate is false, and returns the result.
The true_computation must take in a single argument of type \(T_0\) and will
be invoked with true_operand which must be of the same type. The
false_computation must take in a single argument of type \(T_1\) and will be
invoked with false_operand which must be of the same type. The type of the
returned value of true_computation and false_computation must be the same.
Note that only one of true_computation and false_computation will be
executed depending on the value of predicate.
Conditional(branch_index, branch_computations, branch_operands)
| Arguments | Type | Semantics |
|---|---|---|
branch_index |
XlaOp |
Scalar of type S32 |
branch_computations |
sequence of N XlaComputation |
XlaComputations of type \(T_0 \to S , T_1 \to S , ..., T_{N-1} \to S\) |
branch_operands |
sequence of N XlaOp |
Arguments of type \(T_0 , T_1 , ..., T_{N-1}\) |
Executes branch_computations[branch_index], and returns the result. If
branch_index is an S32 which is < 0 or >= N, then branch_computations[N-1]
is executed as the default branch.
Each branch_computations[b] must take in a single argument of type \(T_b\) and
will be invoked with branch_operands[b] which must be of the same type. The
type of the returned value of each branch_computations[b] must be the same.
Note that only one of the branch_computations will be executed depending on
the value of branch_index.
For StableHLO information see StableHLO - if.
Constant
See also
XlaBuilder::ConstantLiteral.
Produces an output from a constant literal.
Constant(literal)
| Arguments | Type | Semantics |
|---|---|---|
literal |
LiteralSlice |
constant view of an existing Literal |
For StableHLO information see StableHLO - constant.
ConvertElementType
See also
XlaBuilder::ConvertElementType.
Similar to an element-wise static_cast in C++, ConvertElementType performs
an element-wise conversion operation from a data shape to a target shape. The
dimensions must match, and the conversion is an element-wise one; e.g. s32
elements become f32 elements via an s32-to-f32 conversion routine.
ConvertElementType(operand, new_element_type)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
array of type T with dims D |
new_element_type |
PrimitiveType |
type U |
The dimensions of the operand and the target shape must match. The source and destination element types must not be tuples.
A conversion such as T=s32 to U=f32 will perform a normalizing int-to-float
conversion routine such as round-to-nearest-even.
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
For StableHLO information see StableHLO - convert.
Conv (Convolution)
See also
XlaBuilder::Conv.
Computes a convolution of the kind used in neural networks. Here, a convolution can be thought of as a n-dimensional window moving across a n-dimensional base area and a computation is performed for each possible position of the window.
Conv Enqueues a convolution instruction onto the computation, which uses the
default convolution dimension numbers with no dilation.
The padding is specified in a short-hand way as either SAME or VALID. SAME
padding pads the input (lhs) with zeroes so that the output has the same shape
as the input when not taking striding into account. VALID padding simply means
no padding.
Conv(lhs, rhs, window_strides, padding, feature_group_count,
batch_group_count, precision_config, preferred_element_type)
| Arguments | Type | Semantics |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-dimensional array of inputs |
rhs
|
XlaOp
|
(n+2)-dimensional array of kernel weights |
window_strides |
ArraySlice<int64> |
n-d array of kernel strides |
padding |
Padding |
enum of padding |
feature_group_count
|
int64 | the number of feature groups |
batch_group_count |
int64 | the number of batch groups |
precision_config
|
optional
PrecisionConfig |
enum for level of precision |
preferred_element_type
|
optional
PrimitiveType |
enum of scalar element type |
Increasing levels of controls are available for Conv:
Let n be the number of spatial dimensions. The lhs argument is an
(n+2)-dimensional array describing the base area. This is called the input,
even though of course the rhs is also an input. In a neural network, these are
the input activations. The n+2 dimensions are, in this order:
batch: Each coordinate in this dimension represents an independent input for which convolution is carried out.z/depth/features: Each (y,x) position in the base area has a vector associated to it, which goes into this dimension.spatial_dims: Describes thenspatial dimensions that define the base area that the window moves across.
The rhs argument is an (n+2)-dimensional array describing the convolutional
filter/kernel/window. The dimensions are, in this order:
output-z: Thezdimension of the output.input-z: The size of this dimension timesfeature_group_countshould equal the size of thezdimension in lhs.spatial_dims: Describes thenspatial dimensions that define the n-d window that moves across the base area.
The window_strides argument specifies the stride of the convolutional window
in the spatial dimensions. For example, if the stride in the first spatial
dimension is 3, then the window can only be placed at coordinates where the
first spatial index is divisible by 3.
The padding argument specifies the amount of zero padding to be applied to the
base area. The amount of padding can be negative -- the absolute value of
negative padding indicates the number of elements to remove from the specified
dimension before doing the convolution. padding[0] specifies the padding for
dimension y and padding[1] specifies the padding for dimension x. Each
pair has the low padding as the first element and the high padding as the second
element. The low padding is applied in the direction of lower indices while the
high padding is applied in the direction of higher indices. For example, if
padding[1] is (2,3) then there will be a padding by 2 zeroes on the left and
by 3 zeroes on the right in the second spatial dimension. Using padding is
equivalent to inserting those same zero values into the input (lhs) before
doing the convolution.
The lhs_dilation and rhs_dilation arguments specify the dilation factor to
be applied to the lhs and rhs, respectively, in each spatial dimension. If the
dilation factor in a spatial dimension is d, then d-1 holes are implicitly
placed between each of the entries in that dimension, increasing the size of the
array. The holes are filled with a no-op value, which for convolution means
zeroes.
Dilation of the rhs is also called atrous convolution. For more details, see
tf.nn.atrous_conv2d. Dilation of the lhs is also called transposed
convolution. For more details, see tf.nn.conv2d_transpose.
The feature_group_count argument (default value 1) can be used for grouped
convolutions. feature_group_count needs to be a divisor of both the input and
the output feature dimension. If feature_group_count is greater than 1, it
means that conceptually the input and output feature dimension and the rhs
output feature dimension are split evenly into many feature_group_count
groups, each group consisting of a consecutive subsequence of features. The
input feature dimension of rhs needs to be equal to the lhs input feature
dimension divided by feature_group_count (so it already has the size of a
group of input features). The i-th groups are used together to compute
feature_group_count for many separate convolutions. The results of these
convolutions are concatenated together in the output feature dimension.
For depthwise convolution the feature_group_count argument would be set to the
input feature dimension, and the filter would be reshaped from
[filter_height, filter_width, in_channels, channel_multiplier] to
[filter_height, filter_width, 1, in_channels * channel_multiplier]. For more
details, see tf.nn.depthwise_conv2d.
The batch_group_count (default value 1) argument can be used for grouped
filters during backpropagation. batch_group_count needs to be a divisor of the
size of the lhs (input) batch dimension. If batch_group_count is greater
than 1, it means that the output batch dimension should be of size input batch
/ batch_group_count. The batch_group_count must be a divisor of the output
feature size.
The output shape has these dimensions, in this order:
batch: The size of this dimension timesbatch_group_countshould equal the size of thebatchdimension in lhs.z: Same size asoutput-zon the kernel (rhs).spatial_dims: One value for each valid placement of the convolutional window.
The figure above shows how the batch_group_count field works. Effectively, we
slice each lhs batch into batch_group_count groups, and do the same for the
output features. Then, for each of these groups we do pairwise convolutions and
concatenate the output along the output feature dimension. The operational
semantics of all the other dimensions (feature and spatial) remain the same.
The valid placements of the convolutional window are determined by the strides and the size of the base area after padding.
To describe what a convolution does, consider a 2d convolution, and pick some
fixed batch, z, y, x coordinates in the output. Then (y,x) is a
position of a corner of the window within the base area (e.g. the upper left
corner, depending on how you interpret the spatial dimensions). We now have a 2d
window, taken from the base area, where each 2d point is associated to a 1d
vector, so we get a 3d box. From the convolutional kernel, since we fixed the
output coordinate z, we also have a 3d box. The two boxes have the same
dimensions, so we can take the sum of the element-wise products between the two
boxes (similar to a dot product). That is the output value.
Note that if output-z is e.g., 5, then each position of the window produces 5
values in the output into the z dimension of the output. These values differ
in what part of the convolutional kernel is used - there is a separate 3d box of
values used for each output-z coordinate. So you could think of it as 5
separate convolutions with a different filter for each of them.
Here is pseudo-code for a 2d convolution with padding and striding:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
precision_config is used to indicate the precision configuration. The level
dictates whether hardware should attempt to generate more machine code
instructions to provide more accurate dtype emulation when needed (i.e.
emulating f32 on a TPU that only supports bf16 matmuls). Values may be
DEFAULT, HIGH, HIGHEST. Additional details
in the MXU sections.
preferred_element_type is a scalar element of higher/lower precision output
types used for accumulation. preferred_element_type recommends the
accumulation type for the given operation, however it is not guaranteed. This
allows for some hardware backends to instead accumulate in a different type and
convert to the preferred output type.
For StableHLO information see StableHLO - convolution.
ConvWithGeneralPadding
See also
XlaBuilder::ConvWithGeneralPadding.
ConvWithGeneralPadding(lhs, rhs, window_strides, padding,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Same as Conv where padding configuration is explicit.
| Arguments | Type | Semantics |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-dimensional array of inputs |
rhs
|
XlaOp
|
(n+2)-dimensional array of kernel weights |
window_strides |
ArraySlice<int64> |
n-d array of kernel strides |
padding
|
ArraySlice<
pair<int64,int64>> |
n-d array of (low, high) padding |
feature_group_count
|
int64 | the number of feature groups |
batch_group_count |
int64 | the number of batch groups |
precision_config
|
optional
PrecisionConfig |
enum for level of precision |
preferred_element_type
|
optional
PrimitiveType |
enum of scalar element type |
ConvWithGeneralDimensions
See also
XlaBuilder::ConvWithGeneralDimensions.
ConvWithGeneralDimensions(lhs, rhs, window_strides, padding,
dimension_numbers, feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Same as Conv where dimension numbers are explicit.
| Arguments | Type | Semantics |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-dimensional array of inputs |
rhs
|
XlaOp
|
(n+2)-dimensional array of kernel weights |
window_strides
|
ArraySlice<int64>
|
n-d array of kernel strides |
padding |
Padding |
enum of padding |
dimension_numbers
|
ConvolutionDimensionNumbers
|
the number of dimensions |
feature_group_count
|
int64 | the number of feature groups |
batch_group_count
|
int64 | the number of batch groups |
precision_config
|
optional PrecisionConfig
|
enum for level of precision |
preferred_element_type
|
optional PrimitiveType
|
enum of scalar element type |
ConvGeneral
See also
XlaBuilder::ConvGeneral.
ConvGeneral(lhs, rhs, window_strides, padding, dimension_numbers,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Same as Conv where dimension numbers and padding
configuration is explicit
| Arguments | Type | Semantics |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-dimensional array of inputs |
rhs
|
XlaOp
|
(n+2)-dimensional array of kernel weights |
window_strides
|
ArraySlice<int64>
|
n-d array of kernel strides |
padding
|
ArraySlice<
pair<int64,int64>>
|
n-d array of (low, high) padding |
dimension_numbers
|
ConvolutionDimensionNumbers
|
the number of dimensions |
feature_group_count
|
int64 | the number of feature groups |
batch_group_count
|
int64 | the number of batch groups |
precision_config
|
optional PrecisionConfig
|
enum for level of precision |
preferred_element_type
|
optional PrimitiveType
|
enum of scalar element type |
ConvGeneralDilated
See also
XlaBuilder::ConvGeneralDilated.
ConvGeneralDilated(lhs, rhs, window_strides, padding, lhs_dilation,
rhs_dilation, dimension_numbers, feature_group_count, batch_group_count,
precision_config, preferred_element_type, window_reversal)
Same as Conv where padding configuration, dilation
factors, and dimension numbers are explicit.
| Arguments | Type | Semantics |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-dimensional array of inputs |
rhs
|
XlaOp
|
(n+2)-dimensional array of kernel weights |
window_strides
|
ArraySlice<int64>
|
n-d array of kernel strides |
padding
|
ArraySlice<
pair<int64,int64>>
|
n-d array of (low, high) padding |
lhs_dilation
|
ArraySlice<int64>
|
n-d lhs dilation factor array |
rhs_dilation
|
ArraySlice<int64>
|
n-d rhs dilation factor array |
dimension_numbers
|
ConvolutionDimensionNumbers
|
the number of dimensions |
feature_group_count
|
int64 | the number of feature groups |
batch_group_count
|
int64 | the number of batch groups |
precision_config
|
optional PrecisionConfig
|
enum for level of precision |
preferred_element_type
|
optional PrimitiveType
|
enum of scalar element type |
window_reversal
|
optional vector<bool>
|
flag used to logically reverse dimension before applying the convolution |
Copy
See also
HloInstruction::CreateCopyStart.
Copy is internally decomposed into 2 HLO instructions CopyStart and
CopyDone. Copy along with CopyStart and CopyDone serve as primitives in
HLO. These ops may appear in HLO dumps, but they are not intended to be
constructed manually by end users.
Cos
See
alsoXlaBuilder::Cos.
Element-wise cosine x -> cos(x).
Cos(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Cos also supports the optional result_accuracy argument:
Cos(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
For StableHLO information see StableHLO - cosine.
Cosh
See also
XlaBuilder::Cosh.
Element-wise hyperbolic cosine x -> cosh(x).
Cosh(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Cosh also supports the optional result_accuracy argument:
Cosh(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
CustomCall
See also
XlaBuilder::CustomCall.
Call a user-provided function within a computation.
CustomCall documentation is provided in Developer details - XLA Custom Calls
For StableHLO information see StableHLO - custom_call.
Div
See also
XlaBuilder::Div.
Performs element-wise division of dividend lhs and divisor rhs.
Div(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
Integer division overflow (signed/unsigned division/remainder by zero or signed
division/remainder of INT_SMIN with -1) produces an implementation defined
value.
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Div:
Div(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - divide.
Domain
See also
HloInstruction::CreateDomain.
Domain may appear in HLO dumps, but it is not intended to be constructed
manually by end users.
Dot
See also
XlaBuilder::Dot.
Dot(lhs, rhs, precision_config, preferred_element_type)
| Arguments | Type | Semantics |
|---|---|---|
lhs |
XlaOp |
array of type T |
rhs |
XlaOp |
array of type T |
precision_config
|
optional
PrecisionConfig |
enum for level of precision |
preferred_element_type
|
optional
PrimitiveType |
enum of scalar element type |
The exact semantics of this operation depend on the ranks of the operands:
| Input | Output | Semantics |
|---|---|---|
vector [n] dot vector [n] |
scalar | vector dot product |
matrix [m x k] dot vector
[k] |
vector [m] | matrix-vector multiplication |
matrix [m x k] dot matrix
[k x n] |
matrix [m x n] | matrix-matrix multiplication |
The operation performs sum of products over the second dimension of lhs (or
the first if it has 1 dimension) and the first dimension of rhs. These are the
"contracted" dimensions. The contracted dimensions of lhs and rhs must be of
the same size. In practice, it can be used to perform dot products between
vectors, vector/matrix multiplications or matrix/matrix multiplications.
precision_config is used to indicate the precision configuration. The level
dictates whether hardware should attempt to generate more machine code
instructions to provide more accurate dtype emulation when needed (i.e.
emulating f32 on a TPU that only supports bf16 matmuls). Values may be
DEFAULT, HIGH, HIGHEST. Additional details
in the MXU sections.
preferred_element_type is a scalar element of higher/lower precision output
types used for accumulation. preferred_element_type recommends the
accumulation type for the given operation, however it is not guaranteed. This
allows for some hardware backends to instead accumulate in a different type and
convert to the preferred output type.
For StableHLO information see StableHLO - dot.
DotGeneral
See also
XlaBuilder::DotGeneral.
DotGeneral(lhs, rhs, dimension_numbers, precision_config,
preferred_element_type)
| Arguments | Type | Semantics |
|---|---|---|
lhs |
XlaOp |
array of type T |
rhs |
XlaOp |
array of type T |
dimension_numbers
|
DotDimensionNumbers
|
contracting and batch dimension numbers |
precision_config
|
optional
PrecisionConfig |
enum for level of precision |
preferred_element_type
|
optional
PrimitiveType |
enum of scalar element type |
Similar to Dot, but allows contracting and batch dimension numbers to be
specified for both the lhs and rhs.
| DotDimensionNumbers Fields | Type | Semantics |
|---|---|---|
lhs_contracting_dimensions
|
repeated int64 | lhs contracting dimension
numbers |
rhs_contracting_dimensions
|
repeated int64 | rhs contracting dimension
numbers |
lhs_batch_dimensions
|
repeated int64 | lhs batch dimension
numbers |
rhs_batch_dimensions
|
repeated int64 | rhs batch dimension
numbers |
DotGeneral performs the sum of products over contracting dimensions specified in
dimension_numbers.
Associated contracting dimension numbers from the lhs and rhs do not need to
be the same but must have the same dimension sizes.
Example with contracting dimension numbers:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { { 6.0, 12.0},
{15.0, 30.0} }
Associated batch dimension numbers from the lhs and rhs must have the same
dimension sizes.
Example with batch dimension numbers (batch size 2, 2x2 matrices):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> {
{ {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| Input | Output | Semantics |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | batch matmul |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | batch matmul |
It follows that the resulting dimension number starts with the batch dimension,
then the lhs non-contracting/non-batch dimension, and finally the rhs
non-contracting/non-batch dimension.
precision_config is used to indicate the precision configuration. The level
dictates whether hardware should attempt to generate more machine code
instructions to provide more accurate dtype emulation when needed (i.e.
emulating f32 on a TPU that only supports bf16 matmuls). Values may be
DEFAULT, HIGH, HIGHEST. Additional details
can be found in the MXU sections.
preferred_element_type is a scalar element of higher/lower precision output
types used for accumulation. preferred_element_type recommends the
accumulation type for the given operation, however it is not guaranteed. This
allows for some hardware backends to instead accumulate in a different type and
convert to the preferred output type.
For StableHLO information see StableHLO - dot_general.
ScaledDot
See also
XlaBuilder::ScaledDot.
ScaledDot(lhs, lhs_scale, rhs, rhs_scale, dimension_number,
precision_config,preferred_element_type)
| Arguments | Type | Semantics |
|---|---|---|
lhs |
XlaOp |
array of type T |
rhs |
XlaOp |
array of type T |
lhs_scale |
XlaOp |
array of type T |
rhs_scale |
XlaOp |
array of type T |
dimension_number
|
ScatterDimensionNumbers
|
Dimension numbers for scatter operation |
precision_config
|
PrecisionConfig
|
enum for level of precision |
preferred_element_type
|
optional PrimitiveType
|
enum of scalar element type |
Similar to DotGeneral.
Creates a scaled dot op with operands 'lhs', 'lhs_scale', 'rhs', and 'rhs_scale', with contracting and batch dimensions specified in 'dimension_numbers'.
RaggedDot
See also
XlaBuilder::RaggedDot.
For a breakdown of RaggedDot computation see
StableHLO - chlo.ragged_dot
DynamicReshape
See also
XlaBuilder::DynamicReshape.
This operation is functionally identical to reshape, but the result shape is specified dynamically via output_shape.
DynamicReshape(operand, dim_sizes, new_size_bounds, dims_are_dynamic)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
N dimensional array of type T |
dim_sizes |
vector of XlaOP |
N dimensional vector sizes |
new_size_bounds |
vector of int63 |
N dimensional vector of bounds |
dims_are_dynamic |
vector of bool |
N dimensional dynamic dim |
For StableHLO information see StableHLO - dynamic_reshape.
DynamicSlice
See also
XlaBuilder::DynamicSlice.
DynamicSlice extracts a sub-array from the input array at dynamic
start_indices. The size of the slice in each dimension is passed in
size_indices, which specify the end point of exclusive slice intervals in each
dimension: [start, start + size). The shape of start_indices must be
1-dimensional, with dimension size equal to the number of dimensions of
operand.
DynamicSlice(operand, start_indices, slice_sizes)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
N dimensional array of type T |
start_indices
|
sequence of N XlaOp
|
List of N scalar integers containing the starting indices of the slice for each dimension. Value must be greater than or equal to zero. |
size_indices
|
ArraySlice<int64>
|
List of N integers containing the slice size for each dimension. Each value must be strictly greater than zero, and start + size must be less than or equal to the size of the dimension to avoid wrapping modulo dimension size. |
The effective slice indices are computed by applying the following
transformation for each index i in [1, N) before performing the slice:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - slice_sizes[i])
This ensures that the extracted slice is always in-bounds with respect to the operand array. If the slice is in-bounds before the transformation is applied, the transformation has no effect.
1-dimensional example:
let a = {0.0, 1.0, 2.0, 3.0, 4.0};
let s = {2};
DynamicSlice(a, s, {2});
// Result: {2.0, 3.0}
2-dimensional example:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2});
//Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
For StableHLO information see StableHLO - dynamic_slice.
DynamicUpdateSlice
See also
XlaBuilder::DynamicUpdateSlice.
DynamicUpdateSlice generates a result which is the value of the input array
operand, with a slice update overwritten at start_indices.
The shape of update determines the shape of the sub-array of the result which
is updated.
The shape of start_indices must be 1-dimensional, with dimension size equal to
the number of dimensions of operand.
DynamicUpdateSlice(operand, update, start_indices)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
N dimensional array of type T |
update
|
XlaOp
|
N dimensional array of type T containing the slice update. Each dimension of update shape must be strictly greater than zero, and start + update must be less than or equal to the operand size for each dimension to avoid generating out-of-bounds update indices. |
start_indices
|
sequence of N XlaOp
|
List of N scalar integers containing the starting indices of the slice for each dimension. Value must be greater than or equal to zero. |
The effective slice indices are computed by applying the following
transformation for each index i in [1, N) before performing the slice:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
This ensures that the updated slice is always in-bounds with respect to the operand array. If the slice is in-bounds before the transformation is applied, the transformation has no effect.
1-dimensional example:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s)
// Result: {0.0, 1.0, 5.0, 6.0, 4.0}
2-dimensional example:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s)
// Result:
// { {0.0, 1.0, 2.0},
// {3.0, 12.0, 13.0},
// {6.0, 14.0, 15.0},
// {9.0, 16.0, 17.0} }
For StableHLO information see StableHLO - dynamic_update_slice.
Erf
See also
XlaBuilder::Erf.
Element-wise error function x -> erf(x) where:
\(\text{erf}(x) = \frac{2}{\sqrt{\pi} }\int_0^x e^{-t^2} \, dt\).
Erf(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Erf also supports the optional result_accuracy argument:
Erf(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
Exp
See also
XlaBuilder::Exp.
Element-wise natural exponential x -> e^x.
Exp(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Exp also supports the optional result_accuracy argument:
Exp(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
For StableHLO information see StableHLO - exponential.
Expm1
See also
XlaBuilder::Expm1.
Element-wise natural exponential minus one x -> e^x - 1.
Expm1(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Expm1 also supports the optional result_accuracy argument:
Expm1(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
For StableHLO information see StableHLO - exponential_minus_one.
Fft
See also
XlaBuilder::Fft.
The XLA FFT operation implements the forward and inverse Fourier Transforms for real and complex inputs/outputs. Multidimensional FFTs on up to 3 axes are supported.
Fft(operand, ftt_type, fft_length)
| Arguments | Type | Semantics |
|---|---|---|
operand
|
XlaOp
|
The array we are Fourier transforming. |
fft_type |
FftType |
See the table below. |
fft_length
|
ArraySlice<int64>
|
The time-domain lengths
of the axes being
transformed. This is
needed in particular for
IRFFT to right-size the
innermost axis, since
RFFT(fft_length=[16])
has the same output
shape as
RFFT(fft_length=[17]). |
FftType |
Semantics |
|---|---|
FFT |
Forward complex-to-complex FFT. Shape is unchanged. |
IFFT |
Inverse complex-to-complex FFT. Shape is unchanged. |
RFFT
|
Forward real-to-complex FFT. Shape of the innermost axis is
reduced to fft_length[-1] // 2 + 1 if fft_length[-1] is a
non-zero value, omitting the reversed conjugate part of the
transformed signal beyond the Nyquist frequency. |
IRFFT
|
Inverse real-to-complex FFT (i.e. takes complex, returns real).
Shape of the innermost axis is expanded to fft_length[-1] if
fft_length[-1] is a non-zero value, inferring the part of the
transformed signal beyond the Nyquist frequency from the reverse
conjugate of the 1 to fft_length[-1] // 2 + 1 entries. |
For StableHLO information see StableHLO - fft.
Multidimensional FFT
When more than 1 fft_length is provided, this is equivalent to applying a
cascade of FFT operations to each of the innermost axes. Note that for the
real->complex and complex->real cases, the innermost axis transform is
(effectively) performed first (RFFT; last for IRFFT), which is why the innermost
axis is the one which changes size. Other axis transforms will then be
complex->complex.
Implementation details
CPU FFT is backed by Eigen's TensorFFT. GPU FFT uses cuFFT.
Floor
See also
XlaBuilder::Floor.
Element-wise floor x -> ⌊x⌋.
Floor(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
For StableHLO information see StableHLO - floor.
Fusion
See also
HloInstruction::CreateFusion.
Fusion operation represents HLO instructions and serves as a primitive in HLO.
This op may appear in HLO dumps but is not intended to be constructed manually
by end users.
Gather
The XLA gather operation stitches together several slices (each slice at a potentially different runtime offset) of an input array.
For StableHLO information see StableHLO - gather.
General Semantics
See also
XlaBuilder::Gather.
For a more intuitive description, see the "Informal Description" section below.
gather(operand, start_indices, dimension_numbers, slice_sizes,
indices_are_sorted)
| Arguments | Type | Semantics |
|---|---|---|
operand
|
XlaOp
|
The array we’re gathering from. |
start_indices
|
XlaOp
|
Array containing the starting indices of the slices we gather. |
dimension_numbers
|
GatherDimensionNumbers
|
The dimension in
start_indices that
"contains" the starting
indices. See below for a
detailed description. |
slice_sizes
|
ArraySlice<int64>
|
slice_sizes[i] is the
bounds for the slice on
dimension i. |
indices_are_sorted
|
bool
|
Whether the indices are guaranteed to be sorted by the caller. |
For convenience, we label dimensions in the output array not in offset_dims
as batch_dims.
The output is an array with batch_dims.size + offset_dims.size dimensions.
The operand.rank must equal the sum of offset_dims.size and
collapsed_slice_dims.size. Also, slice_sizes.size has to be equal to
operand.rank.
If index_vector_dim is equal to start_indices.rank we implicitly consider
start_indices to have a trailing 1 dimension (i.e. if start_indices was of
shape [6,7] and index_vector_dim is 2 then we implicitly consider the
shape of start_indices to be [6,7,1]).
The bounds for the output array along dimension i is computed as follows:
If
iis present inbatch_dims(i.e. is equal tobatch_dims[k]for somek) then we pick the corresponding dimension bounds out ofstart_indices.shape, skippingindex_vector_dim(i.e. pickstart_indices.shape.dims[k] ifk<index_vector_dimandstart_indices.shape.dims[k+1] otherwise).If
iis present inoffset_dims(i.e. equal tooffset_dims[k] for somek) then we pick the corresponding bound out ofslice_sizesafter accounting forcollapsed_slice_dims(i.e. we pickadjusted_slice_sizes[k] whereadjusted_slice_sizesisslice_sizeswith the bounds at indicescollapsed_slice_dimsremoved).
Formally, the operand index In corresponding to a given output index Out is
calculated as follows:
Let
G= {Out[k] forkinbatch_dims}. UseGto slice out a vectorSsuch thatS[i] =start_indices[Combine(G,i)] where Combine(A, b) inserts b at positionindex_vector_diminto A. Note that this is well defined even ifGis empty: IfGis empty thenS=start_indices.Create a starting index,
Sin, intooperandusingSby scatteringSusingstart_index_map. More precisely:Sin[start_index_map[k]] =S[k] ifk<start_index_map.size.Sin[_] =0otherwise.
Create an index
Oinintooperandby scattering the indices at the offset dimensions inOutaccording to thecollapsed_slice_dimsset. More precisely:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]] ifk<offset_dims.size(remapped_offset_dimsis defined below).Oin[_] =0otherwise.
InisOin+Sinwhere + is element-wise addition.
remapped_offset_dims is a monotonic function with domain [0,
offset_dims.size) and range [0, operand.rank) \ collapsed_slice_dims. So
if, e.g., offset_dims.size is 4, operand.rank is 6 and
collapsed_slice_dims is {0, 2} then remapped_offset_dims is {0→1,
1→3, 2→4, 3→5}.
If indices_are_sorted is set to true then XLA can assume that start_indices
are sorted (in ascending order, after scattering its values according to
start_index_map) by the user. If they are not then the semantics are
implementation defined.
Informal Description and Examples
Informally, every index Out in the output array corresponds to an element E
in the operand array, computed as follows:
We use the batch dimensions in
Outto look up a starting index fromstart_indices.We use
start_index_mapto map the starting index (whose size may be less than operand.rank) to a "full" starting index into theoperand.We dynamic-slice out a slice with size
slice_sizesusing the full starting index.We reshape the slice by collapsing the
collapsed_slice_dimsdimensions. Since all collapsed slice dimensions must have a bound of 1, this reshape is always legal.We use the offset dimensions in
Outto index into this slice to get the input element,E, corresponding to output indexOut.
index_vector_dim is set to start_indices.rank - 1 in all of the examples
that follow. More interesting values for index_vector_dim do not change the
operation fundamentally, but make the visual representation more cumbersome.
To get an intuition on how all of the above fits together, let's look at an
example that gathers 5 slices of shape [8,6] from a [16,11] array. The
position of a slice into the [16,11] array can be represented as an index
vector of shape S64[2], so the set of 5 positions can be represented as a
S64[5,2] array.
The behavior of the gather operation can then be depicted as an index
transformation that takes [G,O0,O1], an index in
the output shape, and maps it to an element in the input array in the following
way:
We first select an (X,Y) vector from the gather indices array using G.
The element in the output array at index
[G,O0,O1] is then the element in the input
array at index [X+O0,Y+O1].
slice_sizes is [8,6], which decides the range of O0 and
O1, and this in turn decides the bounds of the slice.
This gather operation acts as a batch dynamic slice with G as the batch
dimension.
The gather indices may be multidimensional. For instance, a more general
version of the example above using a "gather indices" array of shape [4,5,2]
would translate indices like this:
Again, this acts as a batch dynamic slice G0 and
G1 as the batch dimensions. The slice size is still [8,6].
The gather operation in XLA generalizes the informal semantics outlined above in the following ways:
We can configure which dimensions in the output shape are the offset dimensions (dimensions containing
O0,O1in the last example). The output batch dimensions (dimensions containingG0,G1in the last example) are defined to be the output dimensions that are not offset dimensions.The number of output offset dimensions explicitly present in the output shape may be smaller than the input number of dimensions. These "missing" dimensions, which are listed explicitly as
collapsed_slice_dims, must have a slice size of1. Since they have a slice size of1the only valid index for them is0and eliding them does not introduce ambiguity.The slice extracted from the "Gather Indices" array ((
X,Y) in the last example) may have fewer elements than the input array's number of dimensions, and an explicit mapping dictates how the index should be expanded to have the same number of dimensions as the input.
As a final example, we use (2) and (3) to implement tf.gather_nd:
G0 and G1 are used to slice out a starting index
from the gather indices array as usual, except the starting index has only one
element, X. Similarly, there is only one output offset index with the value
O0. However, before being used as indices into the input array,
these are expanded in accordance to "Gather Index Mapping" (start_index_map in
the formal description) and "Offset Mapping" (remapped_offset_dims in the
formal description) into [X,0] and [0,O0] respectively,
adding up to [X,O0]. In other words, the output index
[G0,G1,O0] maps to the input index
[GatherIndices[G0,G1,0],O0]
which gives us the semantics for tf.gather_nd.
slice_sizes for this case is [1,11]. Intuitively this means that every
index X in the gather indices array picks an entire row and the result is the
concatenation of all these rows.
GetDimensionSize
See also
XlaBuilder::GetDimensionSize.
Returns the size of the given dimension of the operand. The operand must be array shaped.
GetDimensionSize(operand, dimension)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
n dimensional input array |
dimension
|
int64
|
A value in the interval [0, n) that specifies the
dimension |
For StableHLO information see StableHLO - get_dimension_size.
GetTupleElement
See also
XlaBuilder::GetTupleElement.
Indexes into a tuple with a compile-time-constant value.
The value must be a compile-time-constant so that shape inference can determine the type of the resulting value.
This is analogous to std::get<int N>(t) in C++. Conceptually:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
See also tf.tuple.
GetTupleElement(tuple_data, index)
| Argument | Type | Semantics |
|---|---|---|
tuple_data |
XlaOP |
The tuple |
index |
int64 |
Index of tuple shape |
For StableHLO information see StableHLO - get_tuple_element.
Imag
See also
XlaBuilder::Imag.
Element-wise imaginary part of a complex (or real) shape. x -> imag(x). If the
operand is a floating point type, returns 0.
Imag(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
For StableHLO information see StableHLO - imag.
Infeed
See also
XlaBuilder::Infeed.
Infeed(shape, config)
| Argument | Type | Semantics |
|---|---|---|
shape
|
Shape
|
Shape of the data read from the Infeed interface. The layout field of the shape must be set to match the layout of the data sent to the device; otherwise its behavior is undefined. |
config |
optional string |
Configuration of the op. |
Reads a single data item from the implicit Infeed streaming interface of the
device, interpreting the data as the given shape and its layout, and returns a
XlaOp of the data. Multiple Infeed operations are allowed in a computation,
but there must be a total order among the Infeed operations. For example, two
Infeed's in the code below have a total order since there is a dependency
between the while loops.
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
Nested tuple shapes are not supported. For an empty tuple shape, the Infeed operation is effectively a no-op and proceeds without reading any data from the Infeed of the device.
For StableHLO information see StableHLO - infeed.
Iota
See also
XlaBuilder::Iota.
Iota(shape, iota_dimension)
Builds a constant literal on device rather than a potentially large host
transfer. Creates an array that has specified shape and holds values starting at
zero and incrementing by one along the specified dimension. For floating-point
types, the produced array is equivalent to ConvertElementType(Iota(...)) where
the Iota is of integral type and the conversion is to the floating-point type.
| Arguments | Type | Semantics |
|---|---|---|
shape |
Shape |
Shape of the array created by Iota() |
iota_dimension |
int64 |
The dimension to increment along. |
For example, Iota(s32[4, 8], 0) returns
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
Iota(s32[4, 8], 1) returns
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
For StableHLO information see StableHLO - iota.
IsFinite
See also
XlaBuilder::IsFinite.
Tests whether each element of operand is finite, i.e., is not positive or
negative infinity, and is not NaN. Returns an array of PRED values with the
same shape as the input, where each element is true if and only if the
corresponding input element is finite.
IsFinite(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
For StableHLO information see StableHLO - is_finite.
Log
See also
XlaBuilder::Log.
Element-wise natural logarithm x -> ln(x).
Log(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Log also supports the optional result_accuracy argument:
Log(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
For StableHLO information see StableHLO - log.
Log1p
See also
XlaBuilder::Log1p.
Element-wise shifted natural logarithm x -> ln(1+x).
Log1p(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Log1p also supports the optional result_accuracy argument:
Log1p(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
For StableHLO information see StableHLO - log_plus_one.
Logistic
See also
XlaBuilder::Logistic.
Element-wise logistic function computation x -> logistic(x).
Logistic(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Logistic also supports the optional result_accuracy argument:
Logistic(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
For StableHLO information see StableHLO - logistic.
Map
See also
XlaBuilder::Map.
Map(operands..., computation, dimensions)
| Arguments | Type | Semantics |
|---|---|---|
operands |
sequence of N XlaOps |
N arrays of types T0..T{N-1} |
computation
|
XlaComputation
|
Computation of type T_0, T_1,
.., T_{N + M -1} -> S with N
parameters of type T and M of
arbitrary type. |
dimensions |
int64 array |
Array of map dimensions |
static_operands
|
sequence of N XlaOps
|
Static ops for the map operation |
Applies a scalar function over the given operands arrays, producing an array
of the same dimensions where each element is the result of the mapped function
applied to the corresponding elements in the input arrays.
The mapped function is an arbitrary computation with the restriction that it has
N inputs of scalar type T and a single output with type S. The output has
the same dimensions as the operands except that the element type T is replaced
with S.
For example: Map(op1, op2, op3, computation, par1) maps elem_out <-
computation(elem1, elem2, elem3, par1) at each (multi-dimensional) index in the
input arrays to produce the output array.
For StableHLO information see StableHLO - map.
Max
See also
XlaBuilder::Max.
Performs element-wise max operation on tensors lhs and rhs.
Max(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Max:
Max(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - maximum.
Min
See also
XlaBuilder::Min.
Performs element-wise min operation on lhs and rhs.
Min(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Min:
Min(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - minimum.
Mul
See also
XlaBuilder::Mul.
Performs element-wise product of lhs and rhs.
Mul(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Mul:
Mul(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - multiply.
Neg
See also
XlaBuilder::Neg.
Element-wise negation x -> -x.
Neg(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
For StableHLO information see StableHLO - negate
Not
See also
XlaBuilder::Not.
Element-wise logical not x -> !(x).
Not(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
For StableHLO information see StableHLO - not.
OptimizationBarrier
See also
XlaBuilder::OptimizationBarrier.
Blocks any optimization pass from moving computations across the barrier.
OptimizationBarrier(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Ensures that all inputs are evaluated before any operators that depend on the barrier's outputs.
For StableHLO information see StableHLO - optimization_barrier.
Or
See also
XlaBuilder::Or.
Performs element-wise OR of lhs and rhs .
Or(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Or:
Or(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - or.
Outfeed
See also
XlaBuilder::Outfeed.
Writes inputs to the outfeed.
Outfeed(operand, shape_with_layout, outfeed_config)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
array of type T |
shape_with_layout |
Shape |
Defines the layout of the data transferred |
outfeed_config |
string |
Constant of config for the Outfeed instruction |
shape_with_layout communicates the laid out shape that we want to outfeed.
For StableHLO information see StableHLO - outfeed.
Pad
See also
XlaBuilder::Pad.
Pad(operand, padding_value, padding_config)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
array of type T |
padding_value
|
XlaOp
|
scalar of type T to fill in the added
padding |
padding_config
|
PaddingConfig
|
padding amount on both edges (low, high) and between the elements of each dimension |
Expands the given operand array by padding around the array as well as between
the elements of the array with the given padding_value. padding_config
specifies the amount of edge padding and the interior padding for each
dimension.
PaddingConfig is a repeated field of PaddingConfigDimension, which contains
three fields for each dimension: edge_padding_low, edge_padding_high, and
interior_padding.
edge_padding_low and edge_padding_high specify the amount of padding added
at the low-end (next to index 0) and the high-end (next to the highest index) of
each dimension respectively. The amount of edge padding can be negative -- the
absolute value of negative padding indicates the number of elements to remove
from the specified dimension.
interior_padding specifies the amount of padding added between any two
elements in each dimension; it may not be negative. Interior padding occurs
logically before edge padding, so in the case of negative edge padding, elements
are removed from the interior-padded operand.
This operation is a no-op if the edge padding pairs are all (0, 0) and the
interior padding values are all 0. The figure below shows examples of different
edge_padding and interior_padding values for a two-dimensional array.
For StableHLO information see StableHLO - pad.
Parameter
See also
XlaBuilder::Parameter.
Parameter represents an argument input to a computation.
PartitionID
See also
XlaBuilder::BuildPartitionId.
Produces partition_id of the current process.
PartitionID(shape)
| Arguments | Type | Semantics |
|---|---|---|
shape |
Shape |
Shape of the data |
PartitionID may appear in HLO dumps but it is not intended to be constructed
manually by end users.
For StableHLO information see StableHLO - partition_id.
PopulationCount
See also
XlaBuilder::PopulationCount.
Computes the number of bits set in each element of operand.
PopulationCount(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
For StableHLO information see StableHLO - popcnt.
Pow
See also
XlaBuilder::Pow.
Performs element-wise exponentiation of lhs by rhs.
Pow(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Pow:
Pow(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - power.
Real
See also
XlaBuilder::Real.
Element-wise real part of a complex (or real) shape. x -> real(x). If the
operand is a floating point type, Real returns the same value.
Real(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
For StableHLO information see StableHLO - real.
Recv
See also
XlaBuilder::Recv.
Recv, RecvWithTokens, and RecvToHost are operations that serve as
communication primitives in HLO. These ops typically appear in HLO dumps as part
of low-level input/output or cross-device transfer, but they are not intended to
be constructed manually by end users.
Recv(shape, handle)
| Arguments | Type | Semantics |
|---|---|---|
shape |
Shape |
shape of the data to receive |
handle |
ChannelHandle |
unique identifier for each send/recv pair |
Receives data of the given shape from a Send instruction in another
computation that shares the same channel handle. Returns a
XlaOp for the received data.
For StableHLO information see StableHLO - recv.
RecvDone
See also
HloInstruction::CreateRecv and HloInstruction::CreateRecvDone.
Similar to Send, the client API of Recv operation represents
synchronous communication. However, the instruction is internally decomposed
into 2 HLO instructions (Recv and RecvDone) to enable asynchronous data
transfers.
Recv(const Shape& shape, int64 channel_id)
Allocates resources required to receive data from a Send instruction
with the same channel_id. Returns a context for the allocated resources, which
is used by a following RecvDone instruction to wait for the completion of the
data transfer. The context is a tuple of {receive buffer (shape), request
identifier (U32)} and it can only be used by a RecvDone instruction.
Given a context created by a Recv instruction, waits for the data transfer to
complete and return the received data.
Reduce
See also
XlaBuilder::Reduce.
Applies a reduction function to one or more arrays in parallel.
Reduce(operands..., init_values..., computation, dimensions_to_reduce)
| Arguments | Type | Semantics |
|---|---|---|
operands
|
Sequence of N XlaOp
|
N arrays of types T_0,...,
T_{N-1}. |
init_values
|
Sequence of N XlaOp
|
N scalars of types
T_0,..., T_{N-1}. |
computation
|
XlaComputation
|
computation of type
T_0,..., T_{N-1}, T_0,
...,T_{N-1} ->
Collate(T_0,...,
T_{N-1}). |
dimensions_to_reduce
|
int64 array
|
unordered array of dimensions to reduce. |
Where:
- N is required to be greater or equal to 1.
- The computation has to be "roughly" associative (see below).
- All input arrays must have the same dimensions.
- All initial values have to form an identity under
computation. - If
N = 1,Collate(T)isT. - If
N > 1,Collate(T_0, ..., T_{N-1})is a tuple ofNelements of typeT.
This operation reduces one or more dimensions of each input array into scalars.
The number of dimensions of each returned array is
number_of_dimensions(operand) - len(dimensions). The output of the op is
Collate(Q_0, ..., Q_N) where Q_i is an array of type T_i, the
dimensions of which are described below.
Different backends are allowed to reassociate the reduction computation. This can lead to numerical differences, as some reduction functions like addition are not associative for floats. However, if the range of the data is limited, floating-point addition is close enough to be associative for most practical uses.
For StableHLO information see StableHLO - reduce.
Examples
When reducing across one dimension in a single 1D array with values [10, 11,
12, 13], with reduction function f (this is computation) then that could be
computed as
f(10, f(11, f(12, f(init_value, 13)))
but there are also many other possibilities, e.g.
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
The following is a rough pseudo-code example of how reduction could be implemented, using summation as the reduction computation with an initial value of 0.
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
Here's an example of reducing a 2D array (matrix). The shape has 2 dimensions, dimension 0 of size 2 and dimension 1 of size 3:
Results of reducing dimensions 0 or 1 with an "add" function:
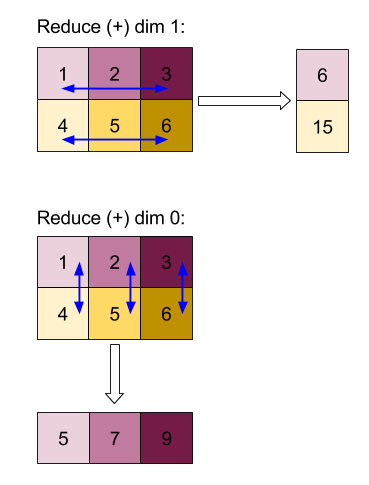
Note that both reduction results are 1D arrays. The diagram shows one as column and another as row just for visual convenience.
For a more complex example, here is a 3D array. Its number of dimensions is 3, dimension 0 of size 4, dimension 1 of size 2 and dimension 2 of size 3. For simplicity, the values 1 to 6 are replicated across dimension 0.
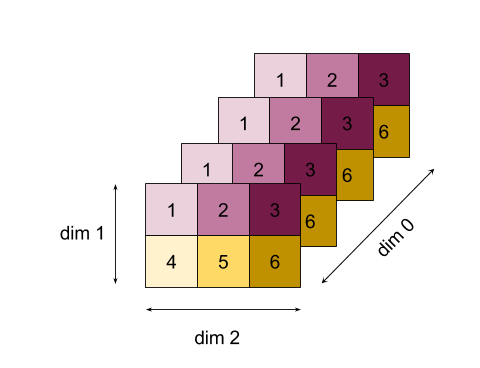
Similarly to the 2D example, we can reduce just one dimension. If we reduce dimension 0, for example, we get a 2-dimensional array where all values across dimension 0 were folded into a scalar:
| 4 8 12 |
| 16 20 24 |
If we reduce dimension 2, we also get a 2-dimensional array where all values across dimension 2 were folded into a scalar:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
Note that the relative order between the remaining dimensions in the input is preserved in the output, but some dimensions may get assigned new numbers (since the number of dimensions changes).
We can also reduce multiple dimensions. Add-reducing dimensions 0 and 1 produces
the 1D array [20, 28, 36].
Reducing the 3D array over all its dimensions produces the scalar 84.
Variadic Reduce
When N > 1, reduce function application is slightly more complex, as it is
applied simultaneously to all inputs. The operands are supplied to the
computation in the following order:
- Running reduced value for the first operand
- ...
- Running reduced value for the N'th operand
- Input value for the first operand
- ...
- Input value for the N'th operand
For example, consider the following reduction function, which can be used to compute the max and the argmax of a 1-D array in parallel:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
For 1-D Input arrays V = Float[N], K = Int[N], and init values
I_V = Float, I_K = Int, the result f_(N-1) of reducing across the only
input dimension is equivalent to the following recursive application:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
Applying this reduction to an array of values, and an array of sequential indices (i.e. iota), will co-iterate over the arrays, and return a tuple containing the maximal value and the matching index.
ReducePrecision
See also
XlaBuilder::ReducePrecision.
Models the effect of converting floating-point values to a lower-precision format (such as IEEE-FP16) and back to the original format. The number of exponent and mantissa bits in the lower-precision format can be specified arbitrarily, although all bit sizes may not be supported on all hardware implementations.
ReducePrecision(operand, exponent_bits, mantissa_bits)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
array of floating-point type T. |
exponent_bits |
int32 |
number of exponent bits in lower-precision format |
mantissa_bits |
int32 |
number of mantissa bits in lower-precision format |
The result is an array of type T. The input values are rounded to the nearest
value representable with the given number of mantissa bits (using "ties to even"
semantics), and any values that exceed the range specified by the number of
exponent bits are clamped to positive or negative infinity. NaN values are
retained, although they may be converted to canonical NaN values.
The lower-precision format must have at least one exponent bit (in order to
distinguish a zero value from an infinity, since both have a zero mantissa), and
must have a non-negative number of mantissa bits. The number of exponent or
mantissa bits may exceed the corresponding value for type T; the corresponding
portion of the conversion is then simply a no-op.
For StableHLO information see StableHLO - reduce_precision.
ReduceScatter
See also
XlaBuilder::ReduceScatter.
ReduceScatter is a collective operation that effectively does an AllReduce and
then scatters the result by splitting it into shard_count blocks along the
scatter_dimension and replica i in the replica group receives the ith
shard.
ReduceScatter(operand, computation, scatter_dimension, shard_count,
replica_groups, channel_id, layout, use_global_device_ids)
| Arguments | Type | Semantics |
|---|---|---|
operand
|
XlaOp
|
Array or a non-empty tuple of arrays to reduce across replicas. |
computation |
XlaComputation |
Reduction computation |
scatter_dimension |
int64 |
Dimension to scatter. |
shard_count
|
int64
|
Number of blocks to split
scatter_dimension |
replica_groups
|
ReplicaGroup vector
|
Groups between which the reductions are performed |
channel_id
|
optional
ChannelHandle |
Optional channel ID for cross-module communication |
layout
|
optional Layout
|
user-specified memory layout |
use_global_device_ids |
optional bool |
user-specified flag |
- When
operandis a tuple of arrays, the reduce-scatter is performed on each element of the tuple. replica_groupsis a list of replica groups between which the reduction is performed (replica id for the current replica can be retrieved usingReplicaId). The order of replicas in each group determines the order in which the all-reduce result will be scattered.replica_groupsmust either be empty (in which case all replicas belong to a single group), or contain the same number of elements as the number of replicas. When there are more than one replica groups, they all must be of the same size. For example,replica_groups = {0, 2}, {1, 3}performs reduction between the replicas0and2, and1and3and then scatters the result.shard_countis the size of each replica group. We need this in cases wherereplica_groupsare empty. Ifreplica_groupsis not empty,shard_countmust be equal to the size of each replica group.channel_idis used for cross-module communication: onlyreduce-scatteroperations with the samechannel_idcan communicate with each other.layoutSee xla::shapes for more information on layouts.use_global_device_idsis a user-specified flag. Whenfalse(default) the numbers inreplica_groupsareReplicaIdwhentruethereplica_groupsrepresent a global id of (ReplicaID*partition_count+partition_id). For example:- With 2 replicas and 4 partitions,
- replica_groups={ {0,1,4,5},{2,3,6,7} } and use_global_device_ids=true
- group[0] = (0,0), (0,1), (1,0), (1,1)
- group[1] = (0,2), (0,3), (1,2), (1,3)
- where each pair is (replica_id, partition_id).
The output shape is the input shape with the scatter_dimension made
shard_count times smaller. For example, if there are two replicas and the
operand has the value [1.0, 2.25] and [3.0, 5.25] respectively on the two
replicas, then the output value from this op where scatter_dim is 0 will be
[4.0] for the first replica and [7.5] for the second replica.
For StableHLO information see StableHLO - reduce_scatter.
ReduceScatter - Example 1 - StableHLO
In the above example, there are 2 replicas participating in the ReduceScatter. On each replica, the operand has shape f32[2,4]. An all-reduce (sum) is performed across the replicas, producing a reduced value of shape f32[2,4] on each replica. This reduced value is then split into 2 parts along dimension 1, so each part has shape f32[2,2]. Each replica within the process group receives the part corresponding to its position in the group. As a result, the output on each replica has shape f32[2,2].
ReduceWindow
See also
XlaBuilder::ReduceWindow.
Applies a reduction function to all elements in each window of a sequence of N
multi-dimensional arrays, producing a single or a tuple of N multi-dimensional
arrays as output. Each output array has the same number of elements as the
number of valid positions of the window. A pooling layer can be expressed as a
ReduceWindow. Similar to Reduce, the applied computation is
always passed the init_values on the left-hand side.
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| Arguments | Type | Semantics |
|---|---|---|
operands
|
N XlaOps
|
A sequence of N
multi-dimensional arrays of
types T_0,..., T_{N-1}, each
representing the base area on
which the window is placed. |
init_values
|
N XlaOps
|
The N starting values for the reduction, one for each of the N operands. See Reduce for details. |
computation
|
XlaComputation
|
Reduction function of type T_0,
..., T_{N-1}, T_0, ..., T_{N-1}
-> Collate(T_0, ..., T_{N-1}),
to apply to elements in each
window of all the input
operands. |
window_dimensions
|
ArraySlice<int64>
|
array of integers for window dimension values |
window_strides
|
ArraySlice<int64>
|
array of integers for window stride values |
base_dilations
|
ArraySlice<int64>
|
array of integers for base dilation values |
window_dilations
|
ArraySlice<int64>
|
array of integers for window dilation values |
padding
|
Padding
|
padding type for window (Padding::kSame, which pads so as to have the same output shape as input if the stride is 1, or Padding::kValid, which uses no padding and "stops" the window once it no longer fits) |
Where:
- N is required to be greater or equal to 1.
- All input arrays must have the same dimensions.
- If
N = 1,Collate(T)isT. - If
N > 1,Collate(T_0, ..., T_{N-1})is a tuple ofNelements of type(T0,...T{N-1}).
For StableHLO information see StableHLO - reduce_window.
ReduceWindow - Example 1
Input is a matrix of size [4x6] and both window_dimensions and window_stride_dimensions are [2x3].
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
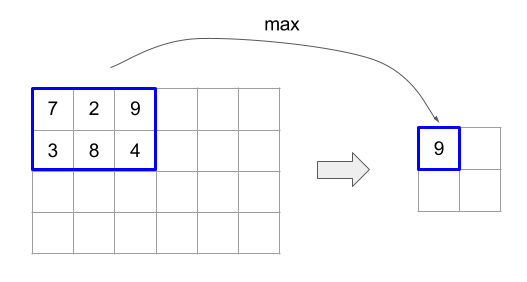
Stride of 1 in a dimension specifies that the position of a window in the dimension is 1 element away from its adjacent window. In order to specify that no windows overlap with each other, window_stride_dimensions should be equal to window_dimensions. The figure below illustrates the use of two different stride values. Padding is applied to each dimension of the input and the calculations are the same as though the input came in with the dimensions it has after padding.
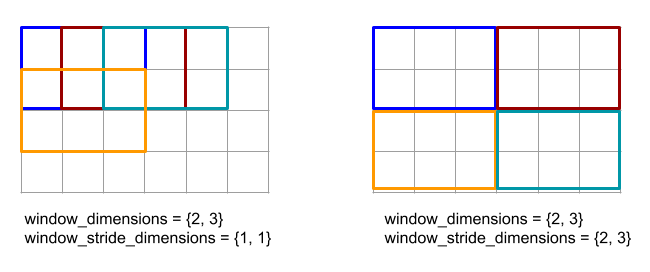
For a non-trivial padding example, consider computing reduce-window minimum
(initial value is MAX_FLOAT) with dimension 3 and stride 2 over the input
array [10000, 1000, 100, 10, 1]. Padding kValid computes minimums over two
valid windows: [10000, 1000, 100] and [100, 10, 1], resulting in the
output [100, 1]. Padding kSame first pads the array so that the shape after
the reduce-window would be the same as input for stride one by adding initial
elements on both sides, getting [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE]. Running reduce-window over the padded array operates on three
windows [MAX_VALUE, 10000, 1000], [1000, 100, 10], [10, 1, MAX_VALUE], and
yields [1000, 10, 1].
The evaluation order of the reduction function is arbitrary and may be
non-deterministic. Therefore, the reduction function should not be overly
sensitive to reassociation. See the discussion about associativity in the
context of Reduce for more details.
ReduceWindow - Example 2 - StableHLO
In the above example:
Input) The operand has an input shape of S32[3,2]. With a values of
[[1,2],[3,4],[5,6]]
Step 1) Base dilation with factor 2 along the row dimension inserts holes between each row of the operand. Padding of 2 rows at the top and 1 row at the bottom is applied after dilation. As a result, the tensor becomes taller.
Step 2) A window of shape [2,1] is defined, with window dilation [3,1]. This means each window selects two elements from the same column, but the second element is taken three rows below the first rather than directly beneath it.
Step 3) The windows are then slid across the operand with stride [4,1]. This
causes the window to move down four rows at a time, while shifting one column at
a time horizontally. Padding cells are filled with the init_value (in this
case init_value = 0). Values 'falling into' dilation cells are ignored.
Because of the stride and padding, some windows overlap only zeros and holes,
while others overlap real input values.
Step 4) Within each window, the elements are combined using the reduction function (a, b) → a + b, starting from an initial value of 0. The top two windows see only padding and holes, so their results are 0. The bottom windows capture the values 3 and 4 from the input and return those as results.
Results) The final output has shape S32[2,2], with values: [[0,0],[3,4]]
Rem
See also
XlaBuilder::Rem.
Performs element-wise remainder of dividend lhs and divisor rhs.
The sign of the result is taken from the dividend, and the absolute value of the result is always less than the divisor's absolute value.
Rem(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Rem:
Rem(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - remainder.
ReplicaId
See also
XlaBuilder::ReplicaId.
Returns the unique ID (U32 scalar) of the replica.
ReplicaId()
The unique ID of each replica is an unsigned integer in the interval [0, N),
where N is the number of replicas. Since all the replicas are running the same
program, a ReplicaId() call in the program will return a different value on
each replica.
For StableHLO information see StableHLO - replica_id.
Reshape
See also
XlaBuilder::Reshape.
and the Collapse operation.
Reshapes the dimensions of an array into a new configuration.
Reshape(operand, dimensions)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
array of type T |
dimensions |
int64 vector |
vector of sizes of new dimensions |
Conceptually, reshape first flattens an array into a one-dimensional vector of
data values, and then refines this vector into a new shape. The input arguments
are an arbitrary array of type T, a compile-time-constant vector of dimension
indices, and a compile-time-constant vector of dimension sizes for the result.
The dimensions vector determines the size of the output array. The value at
index 0 in dimensions is the size of dimension 0, the value at index 1 is the
size of dimension 1, and so on. The product of the dimensions dimensions must
equal the product of the operand's dimension sizes. When refining the collapsed
array into the multidimensional array defined by dimensions, the dimensions in
dimensions are ordered from slowest varying (most major) and to fastest
varying (most minor).
For example, let v be an array of 24 elements:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
As a special case, reshape can transform a single-element array to a scalar and vice versa. For example,
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
For StableHLO information see StableHLO - reshape.
Reshape (explicit)
See also
XlaBuilder::Reshape.
Reshape(shape, operand)
Reshape op that uses an explicit target shape.
| Arguments | Type | Semantics |
|---|---|---|
shape |
Shape |
Output shape of type T |
operand |
XlaOp |
array of type T |
Rev (reverse)
See also
XlaBuilder::Rev.
Rev(operand, dimensions)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
array of type T |
dimensions |
ArraySlice<int64> |
dimensions to reverse |
Reverses the order of elements in the operand array along the specified
dimensions, generating an output array of the same shape. Each element of the
operand array at a multidimensional index is stored into the output array at a
transformed index. The multidimensional index is transformed by reversing the
index in each dimension to be reversed (i.e., if a dimension of size N is one of
the reversing dimensions, its index i is transformed into N - 1 - i).
One use for the Rev operation is to reverse the convolution weight array along
the two window dimensions during the gradient computation in neural networks.
For StableHLO information see StableHLO - reverse.
RngNormal
See also
XlaBuilder::RngNormal.
Constructs an output of a given shape with random numbers generated following the \(N(\mu, \sigma)\) normal distribution. The parameters \(\mu\) and \(\sigma\), and output shape have to have a floating point elemental type. The parameters furthermore have to be scalar valued.
RngNormal(mu, sigma, shape)
| Arguments | Type | Semantics |
|---|---|---|
mu |
XlaOp |
Scalar of type T specifying mean of generated numbers |
sigma
|
XlaOp
|
Scalar of type T specifying standard deviation of generated |
shape |
Shape |
Output shape of type T |
For StableHLO information see StableHLO - rng.
RngUniform
See also
XlaBuilder::RngUniform.
Constructs an output of a given shape with random numbers generated following the uniform distribution over the interval \([a,b)\). The parameters and output element type have to be a boolean type, an integral type or a floating point types, and the types have to be consistent. The CPU and GPU backends currently only support F64, F32, F16, BF16, S64, U64, S32 and U32. Furthermore, the parameters need to be scalar valued. If \(b <= a\) the result is implementation-defined.
RngUniform(a, b, shape)
| Arguments | Type | Semantics |
|---|---|---|
a |
XlaOp |
Scalar of type T specifying lower limit of interval |
b |
XlaOp |
Scalar of type T specifying upper limit of interval |
shape |
Shape |
Output shape of type T |
For StableHLO information see StableHLO - rng.
RngBitGenerator
See also
XlaBuilder::RngBitGenerator.
Generates an output with a given shape filled with uniform random bits using the specified algorithm (or backend default) and returns an updated state (with the same shape as initial state) and the generated random data.
Initial state is the initial state of the current random number generation. It and the required shape and valid values are dependent on the algorithm used.
The output is guaranteed to be a deterministic function of the initial state but it is not guaranteed to be deterministic between backends and different compiler versions.
RngBitGenerator(algorithm, initial_state, shape)
| Arguments | Type | Semantics |
|---|---|---|
algorithm |
RandomAlgorithm |
PRNG algorithm to be used. |
initial_state |
XlaOp |
Initial state for the PRNG algorithm. |
shape |
Shape |
Output shape for generated data. |
Available values for algorithm:
rng_default: Backend specific algorithm with backend specific shape requirements.rng_three_fry: ThreeFry counter-based PRNG algorithm. Theinitial_stateshape isu64[2]with arbitrary values. Salmon et al. SC 2011. Parallel random numbers: as easy as 1, 2, 3.rng_philox: Philox algorithm to generate random numbers in parallel. Theinitial_stateshape isu64[3]with arbitrary values. Salmon et al. SC 2011. Parallel random numbers: as easy as 1, 2, 3.
For StableHLO information see StableHLO - rng_bit_generator.
RngGetAndUpdateState
See also
HloInstruction::CreateRngGetAndUpdateState.
The API of the various Rng operations are internally decomposed into HLO
instructions including RngGetAndUpdateState.
RngGetAndUpdateState serves as a primitive in HLO. This op may appear in HLO
dumps, but it is not intended to be constructed manually by end users.
Round
See also
XlaBuilder::Round.
Element-wise rounding, ties away from zero.
Round(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
RoundNearestAfz
See also
XlaBuilder::RoundNearestAfz.
Performs element-wise rounding towards the nearest integer, breaking ties away from zero.
RoundNearestAfz(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
For StableHLO information see StableHLO - round_nearest_afz.
RoundNearestEven
See also
XlaBuilder::RoundNearestEven.
Element-wise rounding, ties to the nearest even.
RoundNearestEven(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
For StableHLO information see StableHLO - round_nearest_even.
Rsqrt
See also
XlaBuilder::Rsqrt.
Element-wise reciprocal of square root operation x -> 1.0 / sqrt(x).
Rsqrt(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Rsqrt also supports the optional result_accuracy argument:
Rsqrt(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
For StableHLO information see StableHLO - rsqrt.
Scan
See also
XlaBuilder::Scan.
Applies a reduction function to an array across a given dimension, producing a final state and an array of intermediate values.
Scan(operands..., to_apply, scan_dimension, is_reverse, is_associative)
| Arguments | Type | Semantics |
|---|---|---|
operands |
Sequence of m+k XlaOps |
The first m operands are inputs (arrays to scan), the remaining k operands are inits (initial carries). |
to_apply |
XlaComputation |
Computation of type i_0, ..., i_{m-1}, c_0, ..., c_{k-1} -> (o_0, ..., o_{n-1}, c'_0, ..., c'_{k-1}). |
scan_dimension |
int64 |
The dimension to scan across. |
is_reverse |
bool |
If true, scan in reverse order. |
is_associative |
bool (tri-state) |
If true, the operation is associative. |
The function to_apply is applied sequentially to elements in inputs along
scan_dimension. If is_reverse is false, elements are processed in order
0 to N-1, where N is the size of scan_dimension. If is_reverse is true,
elements are processed from N-1 down to 0.
The to_apply function takes m + k operands:
mcurrent elements frominputs.kcarry values from the previous step (orinitsfor the first element). It returns a tuple containingnoutput values andknew carry values.
The Scan operation produces a tuple of n + k values:
- The
noutput arrays, each with the same shape asinputs(except for element type), containing the output values for each step. - The final
kcarry values after processing all elements.
The types of the m inputs must match the types of the first m parameters of
to_apply (except for the scan dimension). The types of the k carries must
match the types of the next k parameters and the last k return values of
to_apply. The types of the n outputs must match the types of the first n
return values of to_apply (except for the scan dimension).
For example, for initial carry i, input [a, b, c], function f, and
scan_dimension=0, is_reverse=false, where f(x, s) -> (y, s'):
- Step 0:
f(a, i) -> (y0, s0) - Step 1:
f(b, s0) -> (y1, s1) - Step 2:
f(c, s1) -> (y2, s2)
The output of Scan is ([y0, y1, y2], s2).
Scatter
See also
XlaBuilder::Scatter.
The XLA scatter operation generates a sequence of results which are the values
of the input array operands, with several slices (at indices specified by
scatter_indices) updated with the sequence of values in updates using
update_computation.
Scatter(operands..., scatter_indices, updates..., update_computation,
dimension_numbers, indices_are_sorted, unique_indices)
| Arguments | Type | Semantics |
|---|---|---|
operands |
Sequence of N XlaOp |
N arrays of types T_0, ..., T_N to be scattered into. |
scatter_indices |
XlaOp |
Array containing the starting indices of the slices that must be scattered to. |
updates |
Sequence of N XlaOp |
N arrays of types T_0, ..., T_N. updates[i] contains the values that must be used for scattering operands[i]. |
update_computation |
XlaComputation |
Computation to be used for combining the existing values in the input array and the updates during scatter. This computation should be of type T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N). |
index_vector_dim |
int64 |
The dimension in scatter_indices that contains the starting indices. |
update_window_dims |
ArraySlice<int64> |
The set of dimensions in updates shape that are window dimensions. |
inserted_window_dims |
ArraySlice<int64> |
The set of window dimensions that must be inserted into updates shape. |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
A dimensions map from the scatter indices to the operand index space. This array is interpreted as mapping i to scatter_dims_to_operand_dims[i] . It has to be one-to-one and total. |
dimension_number |
ScatterDimensionNumbers |
Dimension numbers for scatter operation |
indices_are_sorted |
bool |
Whether the indices are guaranteed to be sorted by the caller. |
unique_indices |
bool |
Whether the indices are guaranteed to be unique by the caller. |
Where:
- N is required to be greater or equal to 1.
operands[0], ...,operands[N-1] must all have the same dimensions.updates[0], ...,updates[N-1] must all have the same dimensions.- If
N = 1,Collate(T)isT. - If
N > 1,Collate(T_0, ..., T_N)is a tuple ofNelements of typeT.
If index_vector_dim is equal to scatter_indices.rank we implicitly consider
scatter_indices to have a trailing 1 dimension.
We define update_scatter_dims of type ArraySlice<int64> as the set of
dimensions in updates shape that are not in update_window_dims, in ascending
order.
The arguments of scatter should follow these constraints:
Each
updatesarray must haveupdate_window_dims.size + scatter_indices.rank - 1dimensions.Bounds of dimension
iin eachupdatesarray must conform to the following:- If
iis present inupdate_window_dims(i.e. equal toupdate_window_dims[k] for somek), then the bound of dimensioniinupdatesmust not exceed the corresponding bound ofoperandafter accounting for theinserted_window_dims(i.e.adjusted_window_bounds[k], whereadjusted_window_boundscontains the bounds ofoperandwith the bounds at indicesinserted_window_dimsremoved). - If
iis present inupdate_scatter_dims(i.e. equal toupdate_scatter_dims[k] for somek), then the bound of dimensioniinupdatesmust be equal to the corresponding bound ofscatter_indices, skippingindex_vector_dim(i.e.scatter_indices.shape.dims[k], ifk<index_vector_dimandscatter_indices.shape.dims[k+1] otherwise).
- If
update_window_dimsmust be in ascending order, not have any repeating dimension numbers, and be in the range[0, updates.rank).inserted_window_dimsmust be in ascending order, not have any repeating dimension numbers, and be in the range[0, operand.rank).operand.rankmust equal the sum ofupdate_window_dims.sizeandinserted_window_dims.size.scatter_dims_to_operand_dims.sizemust be equal toscatter_indices.shape.dims[index_vector_dim], and its values must be in the range[0, operand.rank).
For a given index U in each updates array, the corresponding index I in
the corresponding operands array into which this update has to be applied is
computed as follows:
- Let
G= {U[k] forkinupdate_scatter_dims}. UseGto look up an index vectorSin thescatter_indicesarray such thatS[i] =scatter_indices[Combine(G,i)] where Combine(A, b) inserts b at positionsindex_vector_diminto A. - Create an index
SinintooperandusingSby scatteringSusing thescatter_dims_to_operand_dimsmap. More formally:Sin[scatter_dims_to_operand_dims[k]] =S[k] ifk<scatter_dims_to_operand_dims.size.Sin[_] =0otherwise.
- Create an index
Wininto eachoperandsarray by scattering the indices atupdate_window_dimsinUaccording toinserted_window_dims. More formally:Win[window_dims_to_operand_dims(k)] =U[k] ifkis inupdate_window_dims, wherewindow_dims_to_operand_dimsis the monotonic function with domain [0,update_window_dims.size) and range [0,operand.rank) \inserted_window_dims. (For example, ifupdate_window_dims.sizeis4,operand.rankis6, andinserted_window_dimsis {0,2} thenwindow_dims_to_operand_dimsis {0→1,1→3,2→4,3→5}).Win[_] =0otherwise.
IisWin+Sinwhere + is element-wise addition.
In summary, the scatter operation can be defined as follows.
- Initialize
outputwithoperands, i.e. for all indicesJ, for all indicesOin theoperands[J] array:
output[J][O] =operands[J][O] - For every index
Uin theupdates[J] array and the corresponding indexOin theoperand[J] array, ifOis a valid index foroutput:
(output[0][O], ...,output[N-1][O]) =update_computation(output[0][O], ..., ,output[N-1][O],updates[0][U], ...,updates[N-1][U])
The order in which updates are applied is non-deterministic. So, when multiple
indices in updates refer to the same index in operands, the corresponding
value in output will be non-deterministic.
Note that the first parameter that is passed into the update_computation will
always be the current value from the output array and the second parameter
will always be the value from the updates array. This is important
specifically for cases when the update_computation is not commutative.
If indices_are_sorted is set to true then XLA can assume that
scatter_indices are sorted (in ascending order, after scattering its values
according to scatter_dims_to_operand_dims) by the user. If they are not then
the semantics are implementation defined.
If unique_indices is set to true then XLA can assume that all elements
scattered to are unique. So XLA could use non-atomic operations. If
unique_indices is set to true and the indices being scattered to are not
unique then the semantics is implementation defined.
Informally, the scatter op can be viewed as an inverse of the gather op, i.e. the scatter op updates the elements in the input that are extracted by the corresponding gather op.
For a detailed informal description and examples, refer to the
"Informal Description" section under Gather.
For StableHLO information see StableHLO - scatter.
Scatter - Example 1 - StableHLO
In the above image, each row of the table is an example of one update index example. Let's review stepwise from left(Update Index) to right(Result Index):
Input) input has shape S32[2,3,4,2]. scatter_indices have shape
S64[2,2,3,2]. updates have shape S32[2,2,3,1,2].
Update Index) As part of the input we are given update_window_dims:[3,4]. This
tell us that updates's dim 3 and dim 4 are window dimensions, highlighted in
yellow. This allows us to derive that update_scatter_dims = [0,1,2].
Update Scatter Index) Shows us the extracted updated_scatter_dims for each.
(The non-yellow of column Update Index)
Start Index) Looking at the scatter_indices tensor image we can see that our
values from the previous step (Update scatter Index), give us the location of
the start index. From index_vector_dim we are also told the dimension of the
starting_indices that contains the starting indices, which for
scatter_indices is dim 3 with a size 2.
Full Start Index) scatter_dims_to_operand_dims = [2,1] tells us the first
element of the index vector goes to operand dim 2. The second element of the
index vector goes to operand dim 1. The remaining operand dimensions are filled
with 0.
Full Batching Index) We can see the purple highlighted area is shown in this column(full batching index), the update scatter index column, and update index column.
Full Window Index) Computed from the update_window_dimensions [3,4].
Result Index) The addition of Full Start Index, Full Batching Index, and Full
Window Index in the operand tensor. Notice the green highlighted regions
correspond to the operand figure as well. The last row is skipped because it
falls outside of operand tensor.
Select
See also
XlaBuilder::Select.
Constructs an output array from elements of two input arrays, based on the values of a predicate array.
Select(pred, on_true, on_false)
| Arguments | Type | Semantics |
|---|---|---|
pred |
XlaOp |
array of type PRED |
on_true |
XlaOp |
array of type T |
on_false |
XlaOp |
array of type T |
The arrays on_true and on_false must have the same shape. This is also the
shape of the output array. The array pred must have the same dimensionality as
on_true and on_false, with the PRED element type.
For each element P of pred, the corresponding element of the output array is
taken from on_true if the value of P is true, and from on_false if the
value of P is false. As a restricted form of broadcasting,
pred can be a scalar of type PRED. In this case, the output array is taken
wholly from on_true if pred is true, and from on_false if pred is
false.
Example with non-scalar pred:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
Example with scalar pred:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
Selections between tuples are supported. Tuples are considered to be scalar
types for this purpose. If on_true and on_false are tuples (which must have
the same shape!) then pred has to be a scalar of type PRED.
For StableHLO information see StableHLO - select
SelectAndScatter
See also
XlaBuilder::SelectAndScatter.
This operation can be considered as a composite operation that first computes
ReduceWindow on the operand array to select an element from each window, and
then scatters the source array to the indices of the selected elements to
construct an output array with the same shape as the operand array. The binary
select function is used to select an element from each window by applying it
across each window, and it is called with the property that the first
parameter's index vector is lexicographically less than the second parameter's
index vector. The select function returns true if the first parameter is
selected and returns false if the second parameter is selected, and the
function must hold transitivity (i.e., if select(a, b) and select(b, c) are
true, then select(a, c) is also true) so that the selected element does
not depend on the order of the elements traversed for a given window.
The function scatter is applied at each selected index in the output array. It
takes two scalar parameters:
- Current value at the selected index in the output array
- The scatter value from
sourcethat applies to the selected index
It combines the two parameters and returns a scalar value that's used to update
the value at the selected index in the output array. Initially, all indices of
the output array are set to init_value.
The output array has the same shape as the operand array and the source
array must have the same shape as the result of applying a ReduceWindow
operation on the operand array. SelectAndScatter can be used to
backpropagate the gradient values for a pooling layer in a neural network.
SelectAndScatter(operand, select, window_dimensions, window_strides, padding,
source, init_value, scatter)
| Arguments | Type | Semantics |
|---|---|---|
operand
|
XlaOp
|
array of type T over which the windows slide |
select
|
XlaComputation
|
binary computation of type T, T
-> PRED, to apply to all
elements in each window; returns
true if the first parameter is
selected and returns false if
the second parameter is selected |
window_dimensions
|
ArraySlice<int64>
|
array of integers for window dimension values |
window_strides
|
ArraySlice<int64>
|
array of integers for window stride values |
padding
|
Padding
|
padding type for window (Padding::kSame or Padding::kValid) |
source
|
XlaOp
|
array of type T with the values to scatter |
init_value
|
XlaOp
|
scalar value of type T for the initial value of the output array |
scatter
|
XlaComputation
|
binary computation of type T, T
-> T, to apply each scatter
source element with its
destination element |
The figure below shows examples of using SelectAndScatter, with the select
function computing the maximal value among its parameters. Note that when the
windows overlap, as in the figure (2) below, an index of the operand array may
be selected multiple times by different windows. In the figure, the element of
value 9 is selected by both of the top windows (blue and red) and the binary
addition scatter function produces the output element of value 8 (2 + 6).
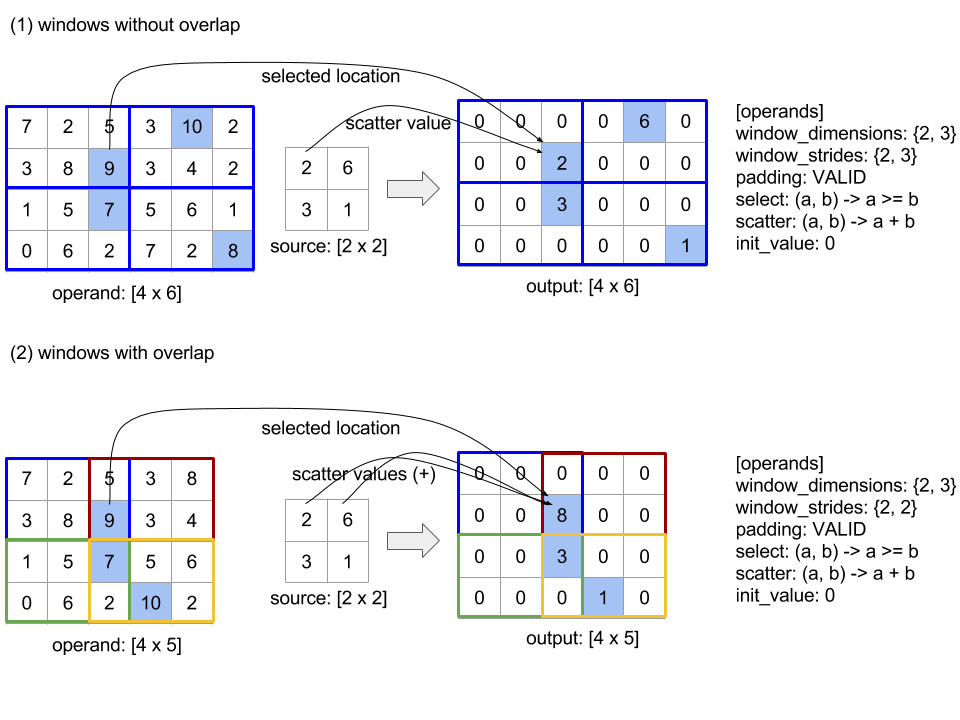
The evaluation order of the scatter function is arbitrary and may be
non-deterministic. Therefore, the scatter function should not be overly
sensitive to reassociation. See the discussion about associativity in the
context of Reduce for more details.
For StableHLO information see StableHLO - select_and_scatter.
Send
See also
XlaBuilder::Send.
Send, SendWithTokens, and SendToHost are operations that serve as
communication primitives in HLO. These ops typically appear in HLO dumps as part
of low-level input/output or cross-device transfer, but they are not intended to
be constructed manually by end users.
Send(operand, handle)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
data to send (array of type T) |
handle |
ChannelHandle |
unique identifier for each send/recv pair |
Sends the given operand data to a Recv instruction in another
computation that shares the same channel handle. Does not return any data.
Similar to the Recv operation, the client API of Send operation
represents synchronous communication, and is internally decomposed into 2 HLO
instructions (Send and SendDone) to enable asynchronous data transfers. See
also
HloInstruction::CreateSend and HloInstruction::CreateSendDone.
Send(HloInstruction operand, int64 channel_id)
Initiates an asynchronous transfer of the operand to the resources allocated by
the Recv instruction with the same channel id. Returns a context, which is
used by a following SendDone instruction to wait for the completion of the
data transfer. The context is a tuple of {operand (shape), request identifier
(U32)} and it can only be used by a SendDone instruction.
For StableHLO information see StableHLO - send.
SendDone
See also
HloInstruction::CreateSendDone.
SendDone(HloInstruction context)
Given a context created by a Send instruction, waits for the data transfer to
complete. The instruction does not return any data.
Scheduling of channel instructions
The execution order of the 4 instructions for each channel (Recv, RecvDone,
Send, SendDone) is as below.
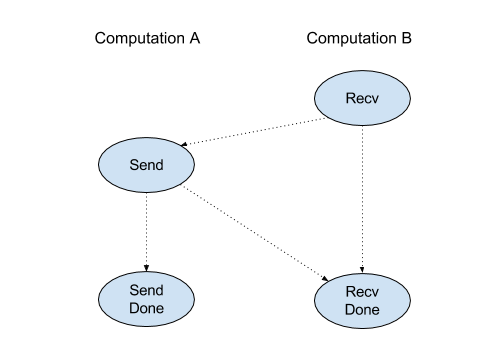
Recvhappens beforeSendSendhappens beforeRecvDoneRecvhappens beforeRecvDoneSendhappens beforeSendDone
When the backend compilers generate a linear schedule for each computation that communicates via channel instructions, there must not be cycles across the computations. For example, below schedules lead to deadlocks.
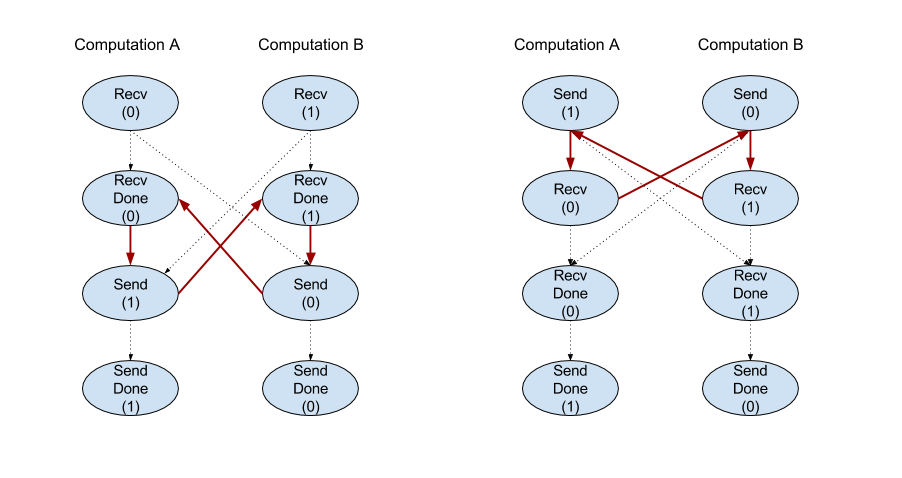
SetDimensionSize
See also
XlaBuilder::SetDimensionSize.
Sets the dynamic size of XlaOp's given dimension. The operand must be array shaped.
SetDimensionSize(operand, val, dimension)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
n dimensional input array. |
val |
XlaOp |
int32 representing the runtime dynamic size. |
dimension
|
int64
|
A value in the interval [0, n) that specifies the
dimension. |
Pass through the operand as result, with dynamic dimension tracked by the compiler.
Padded values will be ignored by downstream reduction ops.
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
ShiftLeft
See also
XlaBuilder::ShiftLeft.
Performs element-wise left-shift operation on lhs by rhs number of bits.
ShiftLeft(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for ShiftLeft:
ShiftLeft(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - shift_left.
ShiftRightArithmetic
See also
XlaBuilder::ShiftRightArithmetic.
Performs element-wise arithmetic right-shift operation on lhs by rhs number
of bits.
ShiftRightArithmetic(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for ShiftRightArithmetic:
ShiftRightArithmetic(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - shift_right_arithmetic.
ShiftRightLogical
See also
XlaBuilder::ShiftRightLogical.
Performs element-wise logical right-shift operation on lhs by rhs number of
bits.
ShiftRightLogical(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for ShiftRightLogical:
ShiftRightLogical(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - shift_right_logical.
Sign
See also
XlaBuilder::Sign.
Sign(operand) Element-wise sign operation x -> sgn(x) where
\[\text{sgn}(x) = \begin{cases} -1 & x < 0\\ -0 & x = -0\\ NaN & x = NaN\\ +0 & x = +0\\ 1 & x > 0 \end{cases}\]
using the comparison operator of the element type of operand.
Sign(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
For StableHLO information see StableHLO - sign.
Sin
Sin(operand) Element-wise sine x -> sin(x).
See also
XlaBuilder::Sin.
Sin(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Sin also supports the optional result_accuracy argument:
Sin(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
For StableHLO information see StableHLO - sine.
Slice
See also
XlaBuilder::Slice.
Slicing extracts a sub-array from the input array. The sub-array has the same number of dimensions as the input and contains the values inside a bounding box within the input array where the dimensions and indices of the bounding box are given as arguments to the slice operation.
Slice(operand, start_indices, limit_indices, strides)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
N dimensional array of type T |
start_indices
|
ArraySlice<int64>
|
List of N integers containing the starting indices of the slice for each dimension. Values must be greater than or equal to zero. |
limit_indices
|
ArraySlice<int64>
|
List of N integers containing the
ending indices (exclusive) for the
slice for each dimension. Each value
must be greater than or equal to the
respective start_indices value for
the dimension and less than or equal
to the size of the dimension. |
strides
|
ArraySlice<int64>
|
List of N integers that decides the
input stride of the slice. The slice
picks every strides[d] element in
dimension d. |
1-dimensional example:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4})
// Result: {2.0, 3.0}
2-dimensional example:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3})
// Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
For StableHLO information see StableHLO - slice.
Sort
See also
XlaBuilder::Sort.
Sort(operands, comparator, dimension, is_stable)
| Arguments | Type | Semantics |
|---|---|---|
operands |
ArraySlice<XlaOp> |
The operands to sort. |
comparator |
XlaComputation |
The comparator computation to use. |
dimension |
int64 |
The dimension along which to sort. |
is_stable |
bool |
Whether stable sorting should be used. |
If only one operand is provided:
If the operand is a 1-dimensional tensor (an array), the result is a sorted array. If you want to sort the array into ascending order, the comparator should perform a less-than comparison. Formally, after the array is sorted, it holds for all index positions
i, jwithi < jthat eithercomparator(value[i], value[j]) = comparator(value[j], value[i]) = falseorcomparator(value[i], value[j]) = true.If the operand has higher number of dimensions, the operand is sorted along the provided dimension. For example, for a 2-dimensional tensor (a matrix), a dimension value of
0will independently sort every column, and a dimension value of1will independently sort each row. If no dimension number is provided, then the last dimension is chosen by default. For the dimension which is sorted, the same sorting order applies as in the 1-dimensional case.
If n > 1 operands are provided:
All
noperands must be tensors with the same dimensions. The element types of the tensors may be different.All operands are sorted together, not individually. Conceptually the operands are treated as a tuple. When checking whether the elements of each operand at index positions
iandjneed to be swapped, the comparator is called with2 * nscalar parameters, where parameter2 * kcorresponds to the value at positionifrom thek-thoperand, and parameter2 * k + 1corresponds to the value at positionjfrom thek-thoperand. Usually, the comparator would thus compare parameters2 * kand2 * k + 1with each other and possibly use other parameter pairs as tie breakers.The result is a tuple that consists of the operands in sorted order (along the provided dimension, as above). The
i-thoperand of the tuple corresponds to thei-thoperand of Sort.
For example, if there are three operands operand0 = [3, 1],
operand1 = [42, 50], operand2 = [-3.0, 1.1], and the comparator compares
only the values of operand0 with less-than, then the output of the sort is the
tuple ([1, 3], [50, 42], [1.1, -3.0]).
If is_stable is set to true, the sort is guaranteed to be stable, that is, if
there are elements which are considered to be equal by the comparator, the
relative order of the equal values is preserved. Two elements e1 and e2 are
equal if and only if comparator(e1, e2) = comparator(e2, e1) = false. By
default, is_stable is set to false.
For StableHLO information see StableHLO - sort.
Sqrt
See also
XlaBuilder::Sqrt.
Element-wise square root operation x -> sqrt(x).
Sqrt(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Sqrt also supports the optional result_accuracy argument:
Sqrt(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
For StableHLO information see StableHLO - sqrt.
Sub
See also
XlaBuilder::Sub.
Performs element-wise subtraction of lhs and rhs.
Sub(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Sub:
Sub(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - subtract.
Tan
See also
XlaBuilder::Tan.
Element-wise tangent x -> tan(x).
Tan(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Tan also supports the optional result_accuracy argument:
Tan(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
For StableHLO information see StableHLO - tan.
Tanh
See also
XlaBuilder::Tanh.
Element-wise hyperbolic tangent x -> tanh(x).
Tanh(operand)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
Tanh also supports the optional result_accuracy argument:
Tanh(operand, result_accuracy)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to the function |
result_accuracy
|
optional ResultAccuracy
|
The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see
Result Accuracy.
For StableHLO information see StableHLO - tanh.
TopK
See also
XlaBuilder::TopK.
TopK finds the values and indices of the k largest or smallest elements for
the last dimension of the given tensor.
TopK(operand, k, largest)
| Arguments | Type | Semantics |
|---|---|---|
operand
|
XlaOp
|
The tensor from which to extract the top k elements.
The tensor must have greater or equal to one
dimensions. The size of the last dimension of the
tensor must be greater or equal to k. |
k |
int64 |
The number of elements to extract. |
largest
|
bool
|
Whether to extract the largest or smallest k
elements. |
For a 1-dimensional input tensor (an array), finds the k largest or smallest
entries in the array and outputs a tuple of two arrays (values, indices). Thus
values[j] is the j-th largest/smallest entry in operand, and its index is
indices[j].
For an input tensor with more than 1 dimension, computes the top k entries
along the last dimension, preserving all other dimensions (rows) in the output.
Thus, for an operand of shape [A, B, ..., P, Q] where Q >= k the output is
a tuple (values, indices) where:
values.shape = indices.shape = [A, B, ..., P, k]
If two elements within a row are equal, the lower-index element appears first.
Transpose
See also the tf.reshape operation.
Transpose(operand, permutation)
| Arguments | Type | Semantics |
|---|---|---|
operand |
XlaOp |
The operand to transpose. |
permutation |
ArraySlice<int64> |
How to permute the dimensions. |
Permutes the operand dimensions with the given permutation, so
∀ i . 0 ≤ i < number of dimensions ⇒
input_dimensions[permutation[i]] = output_dimensions[i].
This is the same as Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)).
For StableHLO information see StableHLO - transpose.
TriangularSolve
See also
XlaBuilder::TriangularSolve.
Solves systems of linear equations with lower or upper triangular coefficient
matrices by forward- or back-substitution. Broadcasting along leading
dimensions, this routine solves one of the matrix systems op(a) * x =
b, or x * op(a) = b, for the variable x, given a and b, where op(a)
is either op(a) = a, or op(a) = Transpose(a), or
op(a) = Conj(Transpose(a)).
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| Arguments | Type | Semantics |
|---|---|---|
a
|
XlaOp
|
a > 2 dimensional array of a complex or
floating-point type with shape [..., M,
M]. |
b
|
XlaOp
|
a > 2 dimensional array of the same type
with shape [..., M, K] if left_side is
true, [..., K, M] otherwise. |
left_side
|
bool
|
indicates whether to solve a system of the
form op(a) * x = b (true) or x *
op(a) = b (false). |
lower
|
bool
|
whether to use the upper or lower triangle
of a. |
unit_diagonal
|
bool
|
if true, the diagonal elements of a are
assumed to be 1 and not accessed. |
transpose_a
|
Transpose
|
whether to use a as is, transpose it or
take its conjugate transpose. |
Input data is read only from the lower/upper triangle of a, depending on the
value of lower. Values from the other triangle are ignored. Output data is
returned in the same triangle; the values in the other triangle are
implementation-defined and may be anything.
If the number of dimensions of a and b are greater than 2, they are treated
as batches of matrices, where all except the minor 2 dimensions are batch
dimensions. a and b must have equal batch dimensions.
For StableHLO information see StableHLO - triangular_solve.
Tuple
See also
XlaBuilder::Tuple.
A tuple containing a variable number of data handles, each of which has its own shape.
Tuple(elements)
| Arguments | Type | Semantics |
|---|---|---|
elements |
vector of XlaOp |
N array of type T |
This is analogous to std::tuple in C++. Conceptually:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
Tuples can be deconstructed (accessed) via the GetTupleElement operation.
For StableHLO information see StableHLO - tuple.
While
See also
XlaBuilder::While.
While(condition, body, init)
| Arguments | Type | Semantics |
|---|---|---|
condition
|
XlaComputation
|
XlaComputation of type T -> PRED which
defines the termination condition of the
loop. |
body
|
XlaComputation
|
XlaComputation of type T -> T which
defines the body of the loop. |
init
|
T
|
Initial value for the parameter of
condition and body. |
Sequentially executes the body until the condition fails. This is similar to
a typical while loop in many other languages except for the differences and
restrictions listed below.
- A
Whilenode returns a value of typeT, which is the result from the last execution of thebody. - The shape of the type
Tis statically determined and must be the same across all iterations.
The T parameters of the computations are initialized with the init value in
the first iteration and are automatically updated to the new result from body
in each subsequent iteration.
One main use case of the While node is to implement the repeated execution of
training in neural networks. Simplified pseudocode is shown below with a graph
that represents the computation. The code can be found in
while_test.cc.
The type T in this example is a Tuple consisting of an int32 for the
iteration count and a vector[10] for the accumulator. For 1000 iterations, the
loop keeps adding a constant vector to the accumulator.
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}
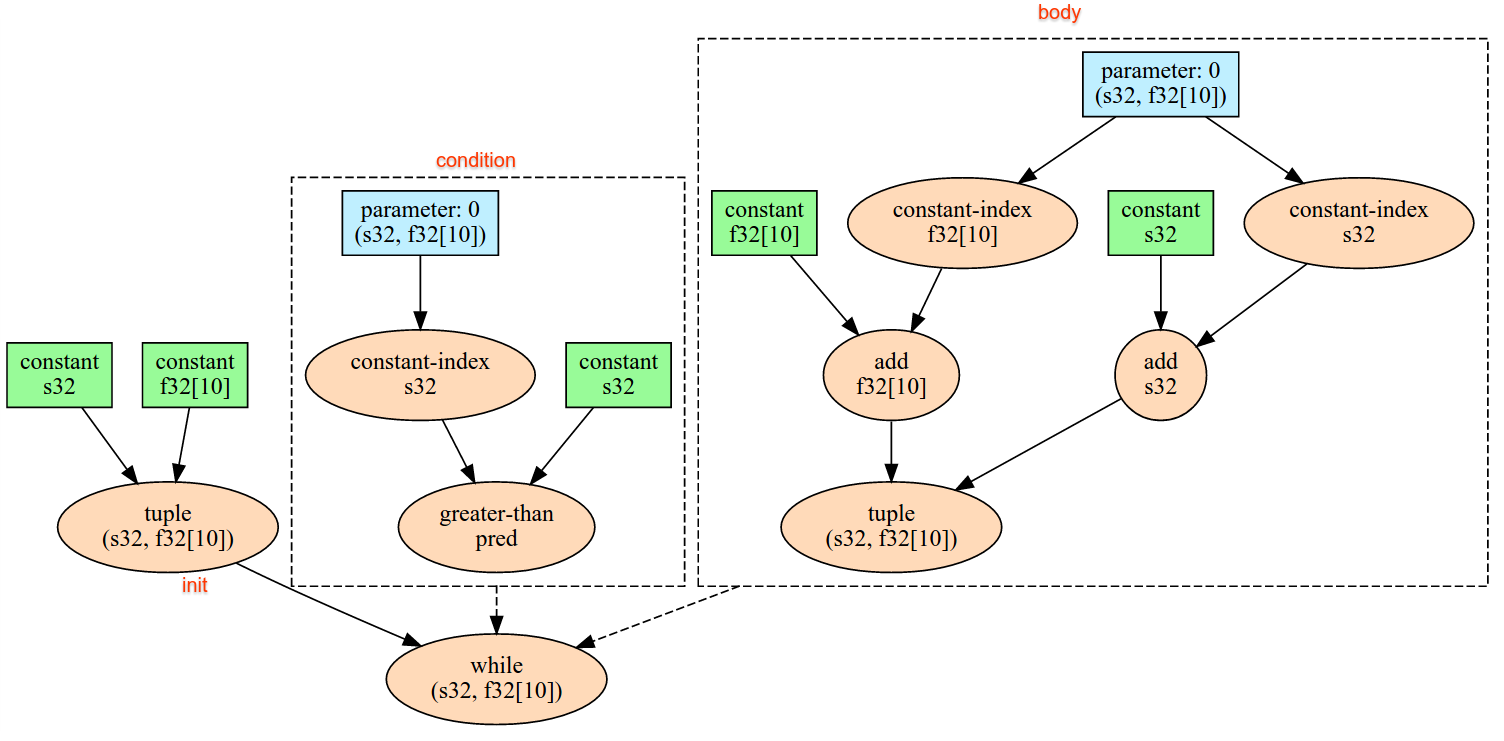
For StableHLO information see StableHLO - while.
Xor
See also
XlaBuilder::Xor.
Performs element-wise XOR of lhs and rhs.
Xor(lhs, rhs)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Xor:
Xor(lhs,rhs, broadcast_dimensions)
| Arguments | Type | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice |
Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page.
For StableHLO information see StableHLO - xor.








