Indexing analysis

This document describes the HLO indexing analysis, which lets you symbolically compute indexing maps for HLO ops. The indexing map is a function that maps indices of one tensor to the indices of another, e.g. indices of an HLO instruction output to indices of HLO instruction inputs or vice versa.

Example

For a broadcast from tensor<20xf32> to tensor<10x20x30xf32>

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

the indexing map from the output to input is (i, j, k) -> (j) for i in [0, 10], j in [0, 20] and k in [0, 30].

Motivation

XLA GPU uses several bespoke solutions to reason about coalescing, operand utilization, and tiling schemes (more details below). The goal of indexing analysis is providing a reusable component for such use cases. Indexing analysis is built on MLIR's Affine Map infrastructure and adds HLO semantics.

Coalescing

Reasoning about memory coalescing becomes feasible for non-trivial cases, when we know what elements/slices of the inputs are read to compute an element of the output.

Operand Utilization

Operand utilization in XLA indicates how much each input of the instruction is used assuming its output is fully used. Currently, utilization is also not computed for a generic case. Indexing analysis allows to compute utilization precisely.

Tiling

A tile/slice is hyper-rectangular subset of a tensor parameterized by offsets, sizes and strides. Tile propagation is a way to compute tile parameters of the producer/consumer of the op using the tiling parameters of the op itself. There is already a library that does it for softmax and dot. Tile propagation can be made more generic and robust if it is expressed via indexing maps.

Function and Domain

The indexing map is a function f(x) = f(d, r, rt) that maps a multi-index d of a tensor A to elements/ranges of tensor B. The parameter r refers to the ranges of indices of the dimensions that are present in tensor B, but not in tensor A. The parameter rt refers to the runtime values, e.g. indices for a gather op.

For example, if we have a reduction from tensor<2x4x8x16xf32> to tensor<4x8xf32>, then the indexing map from the 2D output to the 4D input is (d0, d1) -> (r0, d0, d1, r1), where d_i are the dimension variables that correspond to the indices of the output tensor. Range variables r_j encode multiple values, i.e. to compute a (d0, d1) element of the output, we need (r0, d0, d1, r1) elements of the input, where r0 in [0, 1] and r1 in [0, 15].

This mapping can be constructed from the attributes of HLO instructions or the mappings of unfused instructions can be composed to get indexing for a fusion. The mapping also has a domain, which specifies for what elements of the tensor the mapping exists.

f(x) s.t.

lb <= g(x) <= ub

Since we want to minimize recomputation, we need a library for symbolic computations. XLA already depends on MLIR, so we use mlir::AffineMap instead of writing a yet-another symbolic arithmetic library.

A typical AffineMap looks like

(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)

AffineMap has two types of parameters: dimensions and symbols. The dimensions correspond to the dimension variables d, symbols correspond to the range variables r and RT variables rt. AffineMap does not contain any metadata about ranges of the dimensions, so we have to provide this data ourselves.

struct Interval {
 int64_t lower;
 int64_t upper;
};

class IndexingMap {
   // Variable represents dimension, range or runtime variable.
  struct Variable {
    Interval bounds;
    // Name of the variable is used for nicer printing.
    std::string name = "";
  };

  mlir::AffineMap affine_map_;

  // DimVars represent dimensions of a tensor or of a GPU grid.
  std::vector<Variable> dim_vars_;

  // RangeVars represent ranges of values, e.g. to compute a single element of
  // the reduction's result we need a range of values from the input tensor.
  std::vector<Variable> range_vars_;

  // RTVars represent runtime values, e.g. a dynamic offset in
  // HLO dynamic-update-slice op.
  std::vector<Variable> rt_vars_;
  llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};

dim_vars_ encode the inclusive box constraints for the dimension variables d of the indexing map, which usually coincide with the shape of the output tensor for ops like transpose, reduce, elementwise, dot, but there are some exceptions like HloConcatenateInstruction.

range_vars_ encode possible values that r parameters can take.

rt_vars_ encode the feasible values in runtime. For example, the offset is dynamic for a 1D HloDynamicSliceInstruction. The corresponding RTVar will have the feasible values between 0 and tensor_size - slice_size - 1.

Let's study-by-example to understand what's all of the above actually means.

Indexing Maps for Unfused Ops

Elementwise

For elementwise ops the indexing map is an identity.

  p0 = f32[10, 20] parameter(0)
  p1 = f32[10, 20] parameter(1)
  add = f32[10, 20] add(p0, p1)

The output to input maps:

output -> input_i:

(d0, d1) -> (d0, d1),
domain:
d0 in [0, 9],
d1 in [0, 19]

The input to output maps

input_i -> output:

(d0, d1) -> (d0, d1),
domain:
d0 in [0, 9],
d1 in [0, 19]

Broadcast

Broadcasting means that some of the dimensions will be removed when we map output to input and added when we map input to output.

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

The output to input map:

(d0, d1, d2) -> (d1),
domain:
d0 in [0, 9],
d1 in [0, 19],
d2 in [0, 29]

The input to output map

(d0)[s0, s1] -> (s0, d0, s1),
domain:
d0 in [0, 19],
s0 in [0, 9],
s1 in [0, 29]

Note that now we have s on the right side for the input-to-output mapping. Those are the symbols that represent ranges of values. For example, in this particular case every element of input with index d0 is mapped to a 10x1x30 slice of the output.

Constant and Iota

Conveniently, they do not have any input parameters, so there is nothing to compute indexing for.

DynamicSlice

DynamicSlice is just like Slice, but the offsets are dynamic.

src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}

The output to input map for src:

(d0, d1, d2){rt0, rt1, rt2} -> (d0 + rt0, d1 + rt1, d2 + rt2),
domain:
d0 in [0, 0],
d1 in [0, 1],
d2 in [0, 31],
rt0 in [0, 1],
rt1 in [0, 0],
rt2 in [0, 226]

Note that now we have rt on the right side for the input-to-output mapping. Those are the symbols that represent runtime values. For example, in this particular case for every element of the output with indices d0, d1, d2 we access slice offsets of1, of2 and of3 to compute the index of the input. The intervals for the runtime variables are derived by assuming that the entire slice stays in bounds.

The output to input map for of1, of2 and of3:

(d0, d1, d2)  -> (),
domain:
d0 in [0, 0],
d1 in [0, 1],
d2 in [0, 31]

DynamicUpdateSlice

src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
    s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)

The output to input map for src is trivial. It can be made more precise by restricting the domain to the not-updated indices, but right now indexing maps do not support inqequality constraints.

(d0, d1) -> (d0, d1),
domain:
d0 in [0, 19],
d1 in [0, 29]

The output to input map for upd:

(d0, d1){rt0, rt1}  -> (d0 - rt0, d1 - rt1),
domain:
d0 in [0, 19],
d1 in [0, 29],
rt0 in [0, 15],
rt1 in [0, 20]

Note that now we have s on the right side for the input-to-output mapping. Those are the symbols that represent runtime values. For example, in this particular case for every element of the output with indices d0, d1 we access slice offsets of1 and of2 to compute the index of the input. The intervals for the runtime variables are derived by assuming that the entire slice stays in bounds.

The output to input map for of1 and of2:

(d0, d1)  -> (),
domain:
d0 in [0, 19],
d1 in [0, 29]

Gather

Only the simplified gather is supported. See gather_simplifier.h.

operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
  offset_dims={1,2,3},
  collapsed_slice_dims={},
  start_index_map={0,1},
  index_vector_dim=1,
  slice_sizes={7,8,4}

The output to input map for operand:

(d0, d1, d2, d3){rt0, rt1} -> (d1 + rt0, d2 + rt1, d3),
domain:
d0 in [0, 1805],
d1 in [0, 6],
d2 in [0, 7],
d3 in [0, 3],
rt0 in [0, 26],
rt1 in [0, 68]

Note that now we have rt symbols that represent runtime values.

The output to input map for indices:

(d0, d1, d2, d3)[s0] -> (d0, s0),
domain:
d0 in [0, 1805],
d1 in [0, 6],
d2 in [0, 7],
d3 in [0, 3],
s0 in [0, 1]

The range variable s0 shows that we need the entire row (d0, *) of the indices tensor to compute an element of the output.

Transpose

Indexing map for transpose is a permutation of input/output dimensions.

p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}

The output to input map:

(d0, d1, d2, d3) -> (d0, d3, d1, d2),
domain:
d0 in [0, 2],
d1 in [0, 5],
d2 in [0, 127],
d3 in [0, 12287],

The input to output map:

(d0, d1, d2, d3) -> (d0, d2, d3, d1),
domain:
d0 in [0, 2],
d1 in [0, 12287],
d2 in [0, 5],
d3 in [0, 127]

Reverse

Indexing map for reverse changes the reverted dimensions to upper_bound(d_i) - d_i:

p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}

The output to input map:

(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3),
domain:
d0 in [0, 0],
d1 in [0, 16],
d2 in [0, 8],
d3 in [0, 8]

The input to output map:

(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3),
domain:
d0 in [0, 0],
d1 in [0, 16],
d2 in [0, 8],
d3 in [0, 8]

(Variadic)Reduce

Variadic reduction have several inputs and several inits, the map from output to input adds the reduced dimensions. So, it behaves like an inverse to a broadcast in some sense.

p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
  dimensions={0}, to_apply=max

The output to input maps:

output -> input_j:

(d0)[s0] -> (s0, d0),
domain:
d0 in [0, 9],
s0 in [0, 255]

output -> init_j:

(d0) -> (),
domain:
d0 in [0, 9]

The input to output maps:

input_i -> output_j:

(d0, d1) -> (d1),
domain:
d0 in [0, 255],
d1 in [0, 9]

init_i -> output_j:

()[s0] -> (s0),
domain:
s0 in [0, 9]

for i, j = 0, ... INPUT_COUNT.

Slice

Indexing from output to input for slice results in a strided indexing map which is valid for every element of the output. Mapping from the input to output is restricted to a strided range of the elements in the input.

p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
  slice={[5:10:1], [3:20:7], [0:50:2]}

The output to input map:

(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2),
domain:
d0 in [0, 4],
d1 in [0, 2],
d2 in [0, 24]

The input to output map:

(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2),
domain:
d0 in [5, 9],
d1 in [3, 17],
d2 in [0, 48],
(d1 - 3) mod 7 in [0, 0],
d2 mod 2 in [0, 0]

Reshape

Reshapes come in different flavors.

Collapse shape

This is a "linearizing" reshape from N-D to 1D.

p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)

The output to input map:

(d0) -> (d0 floordiv 8, d0 mod 8),
domain:
d0 in [0, 31]

The input to output map:

(d0, d1) -> (d0 * 8 + d1),
domain:
d0 in [0, 3],
d1 in [0, 7]

Expand shape

This is an inverse "collapse shape" op, it reshapes a 1D input into N-D output.

p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)

The output to input map:

(d0, d1) -> (d0 * 8 + d1),
domain:
d0 in [0, 3],
d1 in [0, 7]

The input to output map:

(d0) -> (d0 floordiv 8, d0 mod 8),
domain:
d0 in [0, 31]

Generic reshape

These are the reshape ops that cannot be represented as a single expand or collapse shape. They can be only represented as a composition of 2 or more expand or collapse shapes.

Example 1: Linearization-delinearization.

p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)

This reshape can be represented as a composition of collapse shape of tensor<4x8xf32> to tensor<32xf32> and then a shape expansion to tensor<2x4x4xf32>.

The output to input map:

(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4),
domain:
d0 in [0, 1],
d1 in [0, 3],
d2 in [0, 3]

The input to output map:

(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4),
domain:
d0 in [0, 3],
d1 in [0, 7]

Example 2: Expanded and collapsed subshapes

p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)

This reshape can be represented as a composition of two reshapes. The first one collapses the outermost dimensions tensor<4x8x12xf32> to tensor<32x12xf32> and the second one expand the innermost dimension tensor<32x12xf32> into tensor<32x3x4xf32>.

The output to input map:

(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2),
domain:
d0 in [0, 31],
d1 in [0, 2]
d2 in [0, 3]

The input to output map:

(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4),
domain:
d0 in [0, 3],
d1 in [0, 7],
d2 in [0, 11]

Bitcast

A bitcast op can be represented as a sequence of transpose-reshape-transpose. Therefore, its indexing maps are just a composition of indexing maps for this sequence.

Concatenate

Output-to-input mapping for concat is defined for all inputs, but with non-overlapping domains, i.e. only one of the inputs will be used at a time.

p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}

The output to inputs maps:

output -> input 1:

(d0, d1, d2) -> (d0, d1, d2),
domain:
d0 in [0, 1],
d1 in [0, 4],
d2 in [0, 6]

output -> input 2:

(d0, d1, d2) -> (d0, d1 - 5, d2),
domain:
d0 in [0, 1],
d1 in [5, 15],
d2 in [0, 6]

output -> input 3:

(d0, d1, d2) -> (d0, d1 - 16, d2),
domain:
d0 in [0, 1],
d1 in [16, 32],
d2 in [0, 6]

The inputs to output maps:

input 1 -> output:

(d0, d1, d2) -> (d0, d1, d2),
domain:
d0 in [0, 1],
d1 in [0, 4],
d2 in [0, 6]

input 2 -> output:

(d0, d1, d2) -> (d0, d1 + 5, d2),
domain:
d0 in [0, 1],
d1 in [0, 10],
d2 in [0, 6]

input 3 -> output:

(d0, d1, d2) -> (d0, d1 + 16, d2),
domain:
d0 in [0, 1],
d1 in [0, 16],
d2 in [0, 6]

Dot

Indexing maps for dot are very similar to the ones of reduce.

p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
  lhs_batch_dims={0}, rhs_batch_dims={0},
  lhs_contracting_dims={2}, rhs_contracting_dims={1}

The output to inputs maps:

output -> input_1:

(d0, d1, d2)[s0] -> (d0, d1, s0),
domain:
d0 in [0, 3],
d1 in [0, 127],
d2 in [0, 63],
s0 in [0, 255]

output -> input_2:

(d0, d1, d2)[s0] -> (d0, s0, d2),
domain:
d0 in [0, 3],
d1 in [0, 127],
d2 in [0, 63],
s0 in [0, 255]

The inputs to output maps:

input_1 -> output:

(d0, d1, d2)[s0] -> (d0, d1, s0),
domain:
d0 in [0, 3],
d1 in [0, 127],
d2 in [0, 255],
s0 in [0, 63]

input_2 -> output:

(d0, d1, d2)[s0] -> (d0, s0, d1),
domain:
d0 in [0, 3],
d1 in [0, 255],
d2 in [0, 63],
s0 in [0, 127]

Pad

Indexing of PadOp is inverse of SliceOp indexing.

p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0

The padding config 1_4_1x4_8_0 denotes lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1.

The output to input maps:

output -> input:

(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4),
domain:
d0 in [1, 7],
d1 in [4, 7],
(d0 - 1) mod 2 in [0, 0]

output -> init:

(d0, d1) -> (),
domain:
d0 in [0, 11],
d1 in [0, 15]

ReduceWindow

ReduceWindow in XLA also performs padding. Therefore, the indexing maps can be computed as a composition of ReduceWindow indexing that does not do any padding and PadOp's indexing.

c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
  window={size=1x512 pad=0_0x0_0}, to_apply=max

The output to input maps:

output -> input:

(d0, d1)[s0] -> (d0, d1 + s0),
domain:
d0 in [0, 1023],
d1 in [0, 2],
s0 in [0, 511]

output -> init:

(d0, d1) -> (),
domain:
d0 in [0, 1023],
d1 in [0, 2]

Indexing Maps for Fusion

Indexing map for fusion op is a composition of indexing maps for every op in the cluster. It can happen that some inputs are read several times with different access patterns.

One input, several indexing maps

Here is an example for p0 + transpose(p0).

f {
  p0 = f32[1000, 1000] parameter(0)
  transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
  ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}

The output-to-input indexing maps for p0 will be (d0, d1) -> (d0, d1) and (d0, d1) -> (d1, d0). It means that to compute one element of the output we might need to read the input parameter twice.

One input, deduplicated indexing map

There are cases when the indexing maps are actually the same, even though it is not immediately obvious.

f {
  p0 = f32[20, 10, 50] parameter(0)
  lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
  lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
  lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
  rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
  rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
  rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
  ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}

The output-to-input indexing map for p0 in this case is just (d0, d1, d2) -> (d2, d0, d1).

Softmax

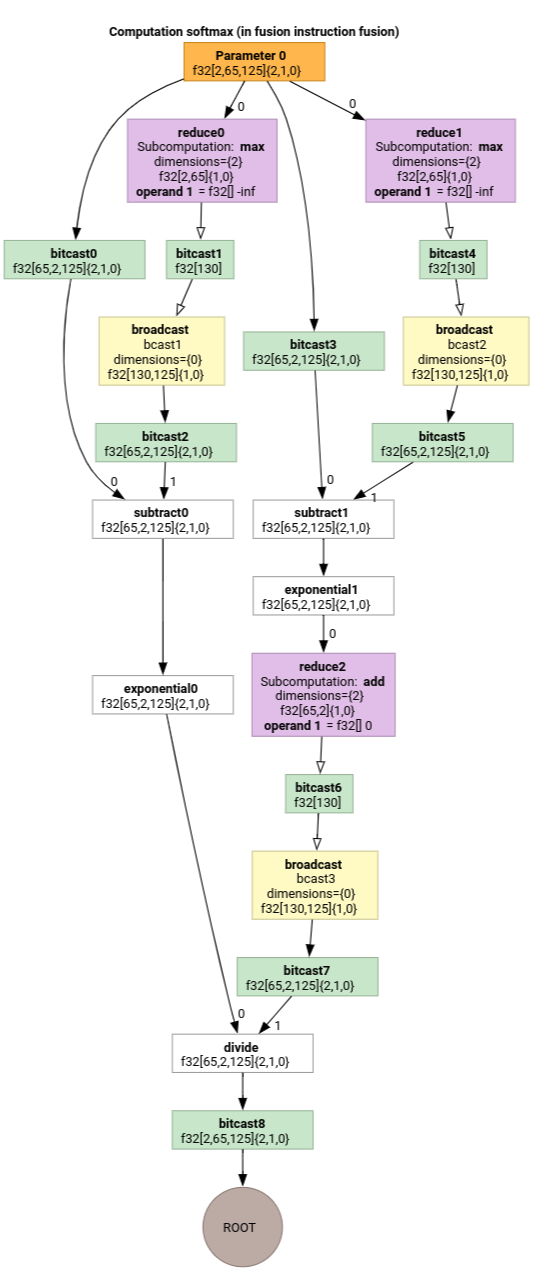
The output-to-input indexing maps for parameter 0 for softmax:

(d0, d1, d2)[s0] -> (d0, d1, s0),
domain:
d0 in [0, 1],
d1 in [0, 64],
d2 in [0, 124],
s0 in [0, 124]

and

(d0, d1, d2) -> (d0, d1, d2),
domain:
d0 in [0, 1],
d1 in [0, 64],
d2 in [0, 124]

where s0 refers to the inner-most dimension of the input.

For more examples see indexing_analysis_test.cc.

Indexing Map Simplifier

The default simplifier for mlir::AffineMap upstream cannot make any assumptions about the ranges of dimensions/symbols. Therefore, it cannot simplify expressions with mod and divefficiently.

We can leverage the knowledge about lower and upper bounds of the sub-expressions in the affine maps to simplify them even more.

The simplifier can rewrite the following expressions.

(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16) for d in [0, 6] x [0, 14] becomes (d0, d1) -> (d0, d1)
(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10) for di in [0, 9] becomes (d0, d1, d2) -> (d0, d1, d2).
(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8) for d_i in [0, 9] becomes (d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8).
(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9) for d in [0, 9] x [0, 10] becomes (d0, d1) -> (d0).

Indexing map simplifier allows us to understand that some of the chained reshapes in HLO cancel each other.

p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)

After the composition of indexing maps and their simplification we will get

(d0, d1, d2) -> (d0, d1, d2).

Indexing map simplification also simplifies the constraints.

Constraints of type lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_bound are rewritten as updated_lower_bound <= affine_expr <= updated_upped_bound.
Constraints that are always satisfied, e.g. d0 + s0 in [0, 20] for d0 in [0, 5] and s0 in [1, 3] are eliminated.
Affine expressions in the constraints are optimized as the indexing affine map above.

For more examples see indexing_map_test.cc.