In diesem Dokument wird die HLO-Indexierungsanalyse beschrieben, mit der Sie symbolisch Indexierungskarten für HLO-Operationen berechnen. Die Indexierungszuordnung ist eine Funktion, die Indizes eines Tensors mit den Indizes eines anderen, z.B. Indizes eines HLO in die Indexe von HLO-Anweisungseingaben und umgekehrt.
Beispiel
Für eine Übertragung von tensor<20xf32> nach tensor<10x20x30xf32>
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
Die Indexierungszuordnung von der Ausgabe in die Eingabe lautet (i, j, k) -> (j) für i in
[0, 10], j in [0, 20] und k in [0, 30].
Motivation
XLA GPU nutzt verschiedene maßgeschneiderte Lösungen für Koalescing, Operanden Auslastung und Tiling-Schemas (weitere Informationen weiter unten). Das Ziel der Indexierung eine wiederverwendbare Komponente für solche Anwendungsfälle bereitstellt. Indexierungsanalyse basiert auf der Affine Map-Infrastruktur von MLIR und fügt HLO-Semantik hinzu.
Koaleszenz
Die Überlegungen zur Speicherzusammenführung werden in nicht trivialen Fällen möglich, wenn wir wissen, welche Elemente/Scheiben der Eingaben gelesen werden, um ein Element der Ausgabe zu berechnen.
Operandauslastung
Die Operandennutzung in XLA gibt an, wie stark jede Eingabe der Anweisung verwendet wird, vorausgesetzt, die Ausgabe wird vollständig genutzt. Derzeit ist die Auslastung nicht für einen generischen Fall berechnet. Mit der Indexierungsanalyse lässt sich die Auslastung genau.
Kachelung:
Eine Kachel/ein Slice ist eine hyperrechteckige Teilmenge eines Tensors, der durch Offsets parametrisiert ist. Größen und Schritte. Die Kachelntfernung ist eine Möglichkeit, die Kachelnparameter des Erzeugers/Verbrauchers der Operation anhand der Parameter für die Kachelung der Operation selbst zu berechnen. Es gibt bereits eine Bibliothek, die das für Softmax und Dot-Produkt erledigt. Die Kachelntfernung kann allgemeiner und robuster gestaltet werden, wenn sie über Indexierungskarten ausgedrückt wird.
Funktion und Domain
Die Indexierungszuordnung ist eine Funktion f(x) = f(d, r, rt)
die einen Multiindex d eines Tensors A den Elementen/Bereichen von
Tensor B. Der Parameter r bezieht sich auf die Indexbereiche der Dimensionen, die im Tensor B, aber nicht im Tensor A vorhanden sind. Der Parameter rt bezieht sich auf die Laufzeitwerte, z. B. Indizes für eine „Gather“-Operation.
Wenn wir z. B. eine Reduzierung von tensor<2x4x8x16xf32> auf
tensor<4x8xf32> ist, wird die Indexierungszuordnung von der 2D-Ausgabe zur 4D-Eingabe
(d0, d1) -> (r0, d0, d1, r1), wobei d_i die Dimensionsvariablen sind, die
den Indizes des Ausgabetensors entsprechen. Bereichsvariablen r_j codieren
mehrere Werte, d.h., wir benötigen zum Berechnen eines (d0, d1)-Elements der Ausgabe
(r0, d0, d1, r1)-Elemente der Eingabe, wobei r0 in [0, 1] und
r1 in [0, 15]
Diese Zuordnung kann aus den Attributen der HLO-Anweisungen oder der Zuordnungen von nicht zusammengeführten Anweisungen können zusammengestellt werden, um die Indexierung für eine Fusion zu erhalten. Die Zuordnung hat auch eine Domäne, die angibt, für welche Elemente des Tensors die Zuordnung existiert.
f(x) mit
lb <= g(x) <= ub
Da wir die Neuberechnung minimieren möchten, benötigen wir eine Bibliothek für Berechnungen. XLA ist bereits von MLIR abhängig, daher verwenden wir mlir::AffineMap anstatt eine weitere symbolische arithmetische Bibliothek zu schreiben.
Ein typischer AffineMap sieht so aus:
(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)
AffineMap hat zwei Parametertypen: Dimensionen und Symbole. Die Dimensionen entsprechen den Dimensionsvariablen d, die Symbole den Bereichsvariablen r und den RT-Variablen rt. AffineMap enthält keine Metadaten zu Bereichen der Dimensionen. Diese Daten müssen wir also selbst angeben.
struct Interval {
int64_t lower;
int64_t upper;
};
// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
Interval bounds;
};
// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
Interval range;
};
// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
Interval feasible_values;
const HloInstruction* hlo;
// This is a map from the iteration space of the corresponding indexing map to
// the iteration space of `hlo`. It shows what element of `hlo` we need to
// extract to get the runtime value for the RTVar.
mlir::AffineMap map;
};
class IndexingMap {
mlir::AffineMap affine_map_;
std::vector<DimVar> dim_vars_;
std::vector<RangeVar> range_vars_;
std::vector<RTVar> rt_vars_;
llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};
dim_vars_: Codieren Sie die Einschränkungen für das Feld einschließlich der Dimension.
Variablen d der Indexierungszuordnung, die in der Regel mit den Variablen
Form des Ausgabetensors für Operationen wie Transponieren, Reduzieren, elementweise, Punkt, aber
gibt es Ausnahmen wie
HloConcatenateInstruction.
range_vars_ codiert mögliche Werte, die r-Parameter annehmen können.
rt_vars_ speichert die zugehörige Hlo-Anleitung zusammen mit der Zugriffsberechtigung
Mustern und den zulässigen Werten in der Laufzeit. Der Offset ist beispielsweise dynamisch,
für ein 1D-HloDynamicSliceInstruction. Die entsprechende RTVar hat ein
HloInstruction*, die einen Rang-0-Tensor mit dem (d0) -> ()-Zugriff erzeugt
Muster, weil wir für jedes Element der Ausgabe dasselbe Element extrahieren
vom Offset-Tensor, um den Index der Eingabe zu berechnen. Wir können auch davon ausgehen,
dass der Versatz des Slice immer zwischen 0 und
tensor_size - slice_size - 1.
Sehen wir uns anhand eines Beispiels an, was die oben genannten Punkte eigentlich bedeuten.
Karten für nicht zusammengeführte Vorgänge indexieren
Elementweise
Bei elementweisen Vorgängen ist die Indexierungszuordnung eine Identität.
p0 = f32[10, 20] parameter(0)
p1 = f32[10, 20] parameter(1)
add = f32[10, 20] add(p0, p1)
Die Ausgabe-zu-Eingabezuordnungen:
- output -> input_i:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Die Eingabe-/Ausgabezuordnungen
- input_i -> output:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Nachricht an alle
Bei der Übertragung werden einige Dimensionen entfernt, wenn wir den Output dem Input zuordnen, und hinzugefügt, wenn wir den Input dem Output zuordnen.
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
Die Ausgabe für die Eingabezuordnung:
(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]
Die Eingabe-zu-Ausgabe-Zuordnung
(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]
Beachten Sie, dass wir jetzt auf der rechten Seite s für die Zuordnung von Eingaben zu Ausgaben haben. Das sind die Symbole, die Wertebereiche darstellen. In diesem Fall wird beispielsweise jedem Eingabeelement mit dem Index d0 ein Ausschnitt der Ausgabe mit den Abmessungen 10 × 1 × 30 zugeordnet.
Konstante und Iota
Sie haben keine Eingabeparameter, sodass keine Indexierung berechnet werden muss.
DynamicSlice
„DynamicSlice“ funktioniert genauso wie „Slice“, die Abweichungen sind jedoch dynamisch.
src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}
Ausgabe-/Eingabezuordnung für src:
(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
hlo: of1 = s32[] parameter(1)
(d0, d1, d2) -> ()
s1 in [0, 0]
hlo: of2 = s32[] parameter(2)
(d0, d1, d2) -> ()
s2 in [0, 226]
hlo: of3 = s32[] parameter(3)
(d0, d1, d2) -> ()
Beachten Sie, dass wir jetzt auf der rechten Seite s für die Zuordnung von Eingaben zu Ausgaben haben.
Dies sind die Symbole, die Laufzeitwerte darstellen. In diesem Fall greifen wir beispielsweise für jedes Element der Ausgabe mit den Indizes d0, d1, d2 auf die Sliver-Abweichungen of1, of2 und of3 zu, um den Index der Eingabe zu berechnen.
Die Intervalle für die Laufzeitvariablen werden unter der Annahme abgeleitet, dass der gesamte Sliver innerhalb der Grenzen bleibt.
Ausgabe-/Eingabezuordnung für of1, of2 und of3:
(d0, d1, d2) -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
DynamicUpdateSlice
src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)
Die Zuordnung von Ausgabe zu Eingabe für src ist trivial. Sie können die Suche präzisieren, indem Sie die Domain auf die nicht aktualisierten Indexe beschränken. Derzeit werden in Indexierungskarten jedoch keine Ungleichungsbeschränkungen unterstützt.
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]
Ausgabe-/Eingabezuordnung für upd:
(d0, d1)[s0, s1] -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
hlo: of1 = s32[] parameter(2)
(d0, d1) -> ()
s1 in [0, 20]
hlo: of2 = s32[] parameter(3)
(d0, d1) -> ()
Beachten Sie, dass wir jetzt auf der rechten Seite s für die Zuordnung von Eingaben zu Ausgaben haben.
Das sind die Symbole für Laufzeitwerte. In diesem Beispiel
Sonderfall für jedes Element der Ausgabe mit den Indexen d0, d1, auf die wir zugreifen
die Slice-Offsets of1 und of2, um den Index der Eingabe zu berechnen. Die Intervalle
für die Laufzeitvariablen abgeleitet werden, indem angenommen wird, dass das gesamte Segment in
Grenzen festzulegen.
Die Ausgabe zur Eingabezuordnung für of1 und of2:
(d0, d1) -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]
Gather
Es wird nur die vereinfachte Erfassung unterstützt. Weitere Informationen finden Sie unter [gather_simplifier].(https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h).
operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
offset_dims={1,2,3},
collapsed_slice_dims={},
start_index_map={0,1},
index_vector_dim=1,
slice_sizes={7,8,4}
Die Ausgabe zur Eingabezuordnung für operand:
(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 1)
Beachten Sie, dass jetzt rechts s für die Eingabe/Ausgabe-Zuordnung angezeigt wird.
Das sind die Symbole für Laufzeitwerte. In diesem Beispiel
Für jedes Element der Ausgabe mit den Indexen d0, d1, d2, d3
die Elemente (d0, 0) und (d0, 1) aus dem indices-Tensor extrahieren.
Die Ausgabe zur Eingabezuordnung für indices:
(d0, d1, d2, d3)[s0] -> (d0, s0)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 1]
Die Bereichsvariable s0 zeigt, dass wir die gesamte Zeile (d0, *) des
Tensor indices, um ein Element der Ausgabe zu berechnen.
Transponieren
Die Indexzuordnung für die Transposition ist eine Permutation der Eingabe-/Ausgabedimensionen.
p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}
Die Ausgabe für die Eingabezuordnung:
(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]
Die Zuordnung von Eingaben zu Ausgaben:
(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]
Rückwärts
Mit der Indexierungszuordnung für die umgekehrte Reihenfolge werden die umgekehrten Dimensionen in upper_bound(d_i) -
d_i geändert:
p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}
Die Zuordnung von Ausgabe zu Eingabe:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
Die Zuordnung von Eingaben zu Ausgaben:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
(Variadic)Reduce
Die variadische Reduktion hat mehrere Eingaben und mehrere INITs. Die Zuordnung von Ausgabe zu Eingabe fügt die reduzierten Dimensionen hinzu. Es verhält sich also in gewisser Weise als Umkehrung einer Übertragung.
p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
dimensions={0}, to_apply=max
Die Ausgabe-zu-Eingabezuordnungen:
- output -> input_j:
(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]
- Ausgabe -> init_j:
(d0) -> ()
domain:
d0 in [0, 9]
Die Ein-/Ausgabe ordnet Folgendes zu:
- Eingabe_i -> output_j:
(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]
- init_i -> output_j:
()[s0] -> (s0)
domain:
s0 in [0, 9]
für i, j = 0, ... INPUT_COUNT.
Segment
Die Indexierung von der Ausgabe zur Eingabe für einen Ausschnitt führt zu einer Indexierungszuordnung, die für jedes Element der Ausgabe gültig ist. Die Zuordnung von Eingabe zu Ausgabe ist der auf einen abgestuften Bereich der Elemente in der Eingabe beschränkt ist.
p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
slice={[5:10:1], [3:20:7], [0:50:2]}
Die Ausgabe für die Eingabezuordnung:
(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]
Die Eingabe-/Ausgabezuordnung:
(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]
Neu gestalten
Es gibt verschiedene Arten von Shapes.
Form minimieren
Dies ist eine „Linearisierung“ von N-D in 1D umgewandelt.
p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)
Die Ausgabe für die Eingabezuordnung:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
Die Eingabe-/Ausgabezuordnung:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
Form maximieren
Dies ist eine umgekehrte „Zusammenfassen von Formen“-Operation, bei der eine 1D-Eingabe in eine n-dimensionale Ausgabe umgewandelt wird.
p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)
Die Zuordnung von Ausgabe zu Eingabe:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
Die Eingabe-/Ausgabezuordnung:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
Generische Umformung
Dies sind die Umformungsvorgänge, die nicht als einzelne Form zum Maximieren oder Minimieren dargestellt werden können. Sie können nur als Kombination aus mindestens zwei Elementen dargestellt werden. Formen maximieren oder minimieren.
Beispiel 1: Linearisierung und Delinearisierung
p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)
Diese Umformung kann als Zusammensetzung der Minimierungsform von
tensor<4x8xf32> in tensor<32xf32> und dann eine Formerweiterung auf
tensor<2x4x4xf32>
Die Zuordnungstabelle für Ausgabe und Eingabe:
(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]
Die Eingabe-/Ausgabezuordnung:
(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
Beispiel 2: Maximierte und minimierte untergeordnete Formen
p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)
Diese Umwandlung kann als Kombination aus zwei Umwandlungen dargestellt werden. Im ersten Fall werden die äußersten Dimensionen tensor<4x8x12xf32> zu tensor<32x12xf32> minimiert und im zweiten Fall wird die innerste Dimension tensor<32x12xf32> zu tensor<32x3x4xf32> maximiert.
Die Zuordnung von Ausgabe zu Eingabe:
(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]
Die Zuordnung von Eingaben zu Ausgaben:
(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]
Bitcast
Eine Bitcast-Operation kann als Sequenz von Transponieren-Neuformatieren-Transponieren dargestellt werden. Daher sind die Indexierungskarten nur eine Zusammensetzung von Indexierungskarten für diese Sequenz.
Konkatenieren
Die Ausgabe-zu-Eingabe-Zuordnung für die Verkettung ist für alle Eingaben definiert, aber mit Domains, die sich nicht überschneiden, d.h., es wird jeweils nur eine der Eingaben verwendet.
p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}
Die Ausgabe wird den Eingaben so zugeordnet:
- Ausgabe -> Eingabe 1:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- Ausgabe -> Eingabe 2:
(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]
- Ausgabe -> Eingabe 3:
(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]
Die Eingaben für die Ausgabe werden zugeordnet:
- Eingabe 1 –> Ausgabe:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- Eingabe 2 -> Ausgabe:
(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]
- Eingabe 3 –> Ausgabe:
(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]
Punkt
Die Indexierungskarten für dot ähneln denen von reduce.
p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
lhs_batch_dims={0}, rhs_batch_dims={0},
lhs_contracting_dims={2}, rhs_contracting_dims={1}
Die Ausgabe zu Eingaben ordnet Folgendes zu:
- Ausgabe -> input_1:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
- output -> input_2:
(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
Eingaben für Ausgabekarten:
- input_1 -> output:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]
- input_2 -> output:
(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]
Pad
Die Indexierung von PadOp ist das Gegenteil der Indexierung von SliceOp.
p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0
Die 1_4_1x4_8_0-Konfiguration für den Abstand steht für lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1.
Die Ausgabe wird den Eingabekarten zugeordnet:
- Ausgabe -> Eingabe:
(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]
- output -> init:
(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]
ReduceWindow
ReduceWindow in XLA führt auch ein Padding durch. Daher können die Indexierungszuordnungen berechnet als Zusammensetzung der ReduceWindow-Indexierung ohne Padding und die Indexierung durch PadOp.
c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
window={size=1x512 pad=0_0x0_0}, to_apply=max
Die Ausgabe-zu-Eingabezuordnungen:
- Ausgabe -> Eingabe:
(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]
- Ausgabe -> init:
(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]
Karten für Fusion indexieren
Die Indexierungskarte für die Fusionsoperation ist eine Zusammensetzung von Indexierungskarten für jede Operation im Cluster. Es kann vorkommen, dass einige Eingaben mehrere Male mit unterschiedlichen Zugriffsmuster haben.
Eine Eingabe, mehrere Indexierungszuordnungen
Hier ist ein Beispiel für p0 + transpose(p0).
f {
p0 = f32[1000, 1000] parameter(0)
transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}
Die Indexierungszuordnungen von Ausgabe zu Eingabe für p0 sind (d0, d1) -> (d0, d1) und
(d0, d1) -> (d1, d0) Das bedeutet, dass wir zum Berechnen eines Elements der Ausgabe den Eingabeparameter möglicherweise zweimal lesen müssen.
Eine Eingabe, deduplizierte Indexierungskarte
Es gibt Fälle, in denen die Indexierungszuordnungen tatsächlich identisch sind, obwohl sie nicht sofort offensichtlich.
f {
p0 = f32[20, 10, 50] parameter(0)
lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}
Die Zuordnungstabelle für die Ausgabe-zu-Eingabe-Indexierung für p0 ist in diesem Fall einfach (d0, d1, d2) -> (d2, d0, d1).
Softmax
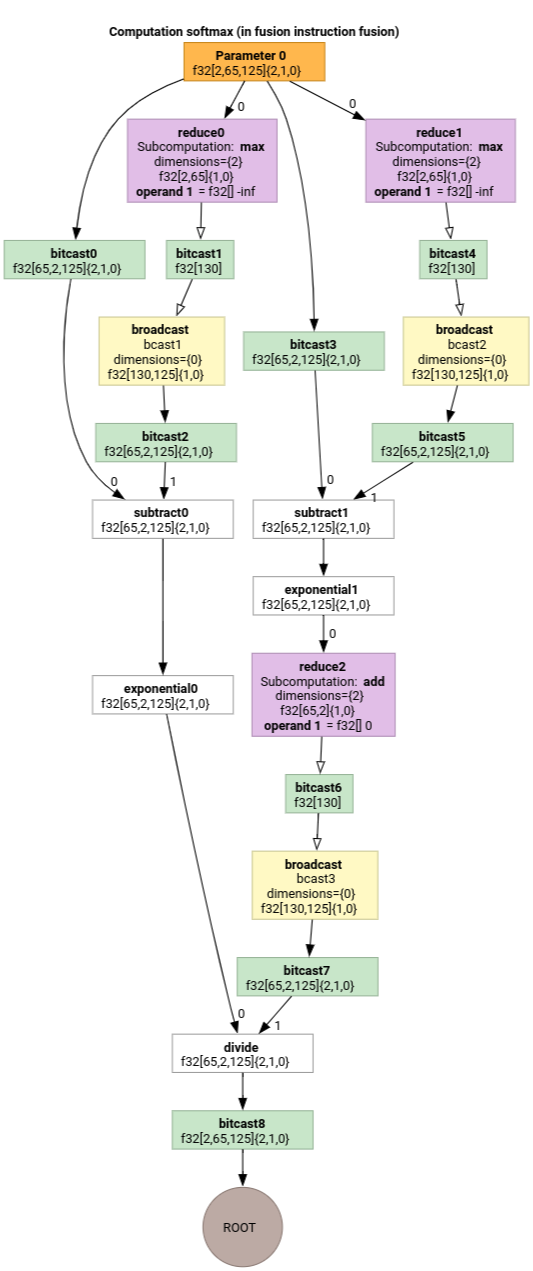
Die Zuordnung von Ausgabe zu Eingabe für parameter 0 für Softmax:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]
und
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
Dabei bezieht sich s0 auf die innerste Dimension der Eingabe.
Indexierungskartenvereinfacher
Mit der Standardvereinfachung für mlir::AffineMap-Upstream kann keine
zu den Dimensionen/Symbolen. Daher kann es auch nicht
Ausdrücke mit mod und div effizient vereinfachen.
Wir können das Wissen über die Unter- und Obergrenze Unterausdrücken in den affinen Maps, um sie noch weiter zu vereinfachen.
Der Vereinfacher kann die folgenden Ausdrücke umschreiben.
(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16)für d in[0, 6] x [0, 14]wird zu(d0, d1) -> (d0, d1)(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10)fürdi in [0, 9]wird zu(d0, d1, d2) -> (d0, d1, d2).(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8)fürd_i in [0, 9]wird zu(d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8).(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9)für d im[0, 9] x [0, 10]wird zu(d0, d1) -> (d0).
Durch die Indexierung der Kartenvereinfachung können wir erkennen, dass einige der verketteten verformen sich in HLO gegenseitig.
p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)
Nach der Zusammenstellung der Indexierungskarten und ihrer Vereinfachung erhalten wir
(d0, d1, d2) -> (d0, d1, d2).
Die Vereinfachung der Indexierung der Karte vereinfacht außerdem die Einschränkungen.
- Einschränkungen vom Typ
lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_boundwerden inupdated_lower_bound <= affine_expr <= updated_upped_boundumgeschrieben. - Einschränkungen, die immer erfüllt sind, z. B.
d0 + s0 in [0, 20]fürd0 in [0, 5]unds0 in [1, 3], werden entfernt. - Affine Ausdrücke in den Einschränkungen werden wie die oben beschriebene affine Indexierungskarte optimiert.
Weitere Beispiele finden Sie unter indexing_map_test.cc.

