Im Folgenden wird die Semantik der im XlaBuilder-Interface definierten Vorgänge beschrieben. In der Regel werden diese Vorgänge eins zu eins den Vorgängen zugeordnet, die in der RPC-Schnittstelle in xla_data.proto definiert sind.
Hinweis zur Nomenklatur: Der verallgemeinerte Datentyp, mit dem XLA arbeitet, ist ein N-dimensionales Array, das Elemente eines einheitlichen Typs (z. B. 32-Bit-Gleitkommazahl) enthält. In der gesamten Dokumentation wird array verwendet, um ein beliebiges mehrdimensionales Array zu bezeichnen. Sonderfälle haben zur besseren Übersicht spezifischere und vertrautere Namen. Ein Vektor ist beispielsweise ein eindimensionales Array und eine Matrix ein zweidimensionales Array.
Weitere Informationen zur Struktur eines Vorgangs finden Sie unter Formen und Layout und Gekacheltes Layout.
Bauchmuskeln
Siehe auch XlaBuilder::Abs.
Elementweiser Absolutwert x -> |x|.
Abs(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – abs.
Hinzufügen
Siehe auch XlaBuilder::Add.
Führt eine elementweise Addition von lhs und rhs durch.
Add(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für „Add“ gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Add(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Informationen zu StableHLO finden Sie unter StableHLO – add.
AddDependency
Siehe auch HloInstruction::AddDependency.
AddDependency kann in HLO-Dumps enthalten sein, sollte aber nicht manuell von Endnutzern erstellt werden.
AfterAll
Siehe auch XlaBuilder::AfterAll.
„AfterAll“ akzeptiert eine variable Anzahl von Tokens und gibt ein einzelnes Token aus. Tokens sind primitive Typen, die zwischen Operationen mit Nebeneffekten übergeben werden können, um die Reihenfolge zu erzwingen. AfterAll kann als Join von Tokens verwendet werden, um einen Vorgang nach einer Reihe von Vorgängen zu sortieren.
AfterAll(tokens)
| Argumente | Typ | Semantik |
|---|---|---|
tokens |
Vektor von XlaOp |
variadische Anzahl von Tokens |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – after_all.
AllGather
Siehe auch XlaBuilder::AllGather.
Führt die Verkettung über Replikate hinweg aus.
AllGather(operand, all_gather_dimension, shard_count, replica_groups,
channel_id, layout, use_global_device_ids)
| Argumente | Typ | Semantik |
|---|---|---|
operand
|
XlaOp
|
Array, das über Replikate hinweg verkettet werden soll |
all_gather_dimension |
int64 |
Verkettungsdimension |
shard_count
|
int64
|
Die Größe jeder Replikagruppe |
replica_groups
|
Vektor von Vektoren von
int64 |
Gruppen, zwischen denen die Verkettung erfolgt |
channel_id
|
optional
ChannelHandle |
Optionale Kanal-ID für die modulübergreifende Kommunikation |
layout
|
optional Layout
|
Erstellt ein Layoutmuster, das das übereinstimmende Layout im Argument erfasst. |
use_global_device_ids
|
optional bool
|
Gibt „true“ zurück, wenn die IDs in der ReplicaGroup-Konfiguration eine globale ID darstellen. |
replica_groupsist eine Liste von Replikagruppen, zwischen denen die Verkettung erfolgt. Die Replika-ID für die aktuelle Replika kann mitReplicaIdabgerufen werden. Die Reihenfolge der Replikas in jeder Gruppe bestimmt die Reihenfolge, in der sich ihre Eingaben im Ergebnis befinden.replica_groupsmuss entweder leer sein (in diesem Fall gehören alle Replikate zu einer einzelnen Gruppe, die von0bisN - 1sortiert ist) oder dieselbe Anzahl von Elementen wie die Anzahl der Replikate enthalten. Beispiel:replica_groups = {0, 2}, {1, 3}führt die Verkettung zwischen den Replikaten0und2sowie1und3durch.shard_countist die Größe jeder Replikagruppe. Wir benötigen diese Informationen, wennreplica_groupsleer ist.channel_idwird für die modulübergreifende Kommunikation verwendet: Nurall-gather-Vorgänge mit demselbenchannel_idkönnen miteinander kommunizieren.use_global_device_idsGibt „true“ zurück, wenn die IDs in der ReplicaGroup-Konfiguration eine globale ID von (replica_id * partition_count + partition_id) anstelle einer Replikat-ID darstellen. Dies ermöglicht eine flexiblere Gruppierung von Geräten, wenn diese All-Reduce-Operation sowohl partitionen- als auch replikübergreifend ist.
Die Ausgabedimension ist die Eingabedimension, wobei all_gather_dimension shard_count-mal größer ist. Wenn es beispielsweise zwei Replikate gibt und der Operand auf den beiden Replikaten die Werte [1.0, 2.5] bzw. [3.0, 5.25] hat, ist der Ausgabewert dieses Vorgangs, bei dem all_gather_dim gleich 0 ist, auf beiden Replikaten [1.0, 2.5, 3.0,5.25].
Die API von AllGather wird intern in zwei HLO-Anweisungen (AllGatherStart und AllGatherDone) zerlegt.
Siehe auch HloInstruction::CreateAllGatherStart.
AllGatherStart und AllGatherDone dienen als Primitiven in HLO. Diese Vorgänge können in HLO-Dumps enthalten sein, sie sind jedoch nicht dafür vorgesehen, von Endnutzern manuell erstellt zu werden.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – all_gather.
AllReduce
Siehe auch XlaBuilder::AllReduce.
Führt eine benutzerdefinierte Berechnung über Replikate hinweg aus.
AllReduce(operand, computation, replica_groups, channel_id,
shape_with_layout, use_global_device_ids)
| Argumente | Typ | Semantik |
|---|---|---|
operand
|
XlaOp
|
Array oder nicht leeres Tupel von Arrays, die über Replikate hinweg reduziert werden sollen |
computation |
XlaComputation |
Berechnung der Reduzierung |
replica_groups
|
ReplicaGroup vector
|
Gruppen, zwischen denen die Reduzierungen vorgenommen werden |
channel_id
|
optional
ChannelHandle |
Optionale Kanal-ID für die modulübergreifende Kommunikation |
shape_with_layout
|
optional Shape
|
Definiert das Layout der übertragenen Daten. |
use_global_device_ids
|
optional bool
|
Gibt „true“ zurück, wenn die IDs in der ReplicaGroup-Konfiguration eine globale ID darstellen. |
- Wenn
operandein Tupel von Arrays ist, wird die All-Reduce-Operation für jedes Element des Tupels ausgeführt. replica_groupsist eine Liste von Replikatgruppen, zwischen denen die Reduzierung erfolgt. Die Replikat-ID für das aktuelle Replikat kann mitReplicaIdabgerufen werden.replica_groupsmuss entweder leer sein (in diesem Fall gehören alle Replikate zu einer einzelnen Gruppe) oder dieselbe Anzahl von Elementen wie die Anzahl der Replikate enthalten. Beispiel:replica_groups = {0, 2}, {1, 3}führt eine Reduzierung zwischen den Replikaten0und2sowie1und3durch.channel_idwird für die modulübergreifende Kommunikation verwendet: Nurall-reduce-Vorgänge mit demselbenchannel_idkönnen miteinander kommunizieren.shape_with_layout: Erzwingt das Layout von AllReduce auf das angegebene Layout. Damit wird das gleiche Layout für eine Gruppe von AllReduce-Vorgängen garantiert, die separat kompiliert werden.use_global_device_idsGibt „true“ zurück, wenn die IDs in der ReplicaGroup-Konfiguration eine globale ID von (replica_id * partition_count + partition_id) anstelle einer Replikat-ID darstellen. Dies ermöglicht eine flexiblere Gruppierung von Geräten, wenn diese All-Reduce-Operation sowohl partitionen- als auch replikübergreifend ist.
Die Ausgabeform entspricht der Eingabeform. Wenn es beispielsweise zwei Replikate gibt und der Operand auf den beiden Replikaten die Werte [1.0, 2.5] bzw. [3.0, 5.25] hat, ist der Ausgabewert dieses Vorgangs und der Summenberechnung auf beiden Replikaten [4.0, 7.75]. Wenn die Eingabe ein Tupel ist, ist auch die Ausgabe ein Tupel.
Um das Ergebnis von AllReduce zu berechnen, ist eine Eingabe von jedem Replikat erforderlich. Wenn ein Replikat einen AllReduce-Knoten häufiger als ein anderes ausführt, wartet das erste Replikat unbegrenzt. Da auf allen Replikaten dasselbe Programm ausgeführt wird, gibt es nicht viele Möglichkeiten, wie das passieren kann. Es ist jedoch möglich, wenn die Bedingung einer While-Schleife von Daten aus infeed abhängt und die Daten, die infeed sind, dazu führen, dass die While-Schleife auf einem Replikat häufiger durchlaufen wird als auf einem anderen.
Die API von AllReduce wird intern in zwei HLO-Anweisungen (AllReduceStart und AllReduceDone) zerlegt.
Siehe auch HloInstruction::CreateAllReduceStart.
AllReduceStart und AllReduceDone dienen als Primitiven in HLO. Diese Vorgänge können in HLO-Dumps enthalten sein, sie sind jedoch nicht dafür vorgesehen, von Endnutzern manuell erstellt zu werden.
CrossReplicaSum
Siehe auch XlaBuilder::CrossReplicaSum.
Führt AllReduce mit einer Summenberechnung aus.
CrossReplicaSum(operand, replica_groups)
| Argumente | Typ | Semantik |
|---|---|---|
operand
|
XlaOp | Array oder nicht leeres Tupel von Arrays, die über Replikate hinweg reduziert werden sollen |
replica_groups
|
Vektor von Vektoren von
int64 |
Gruppen, zwischen denen die Reduzierungen vorgenommen werden |
Gibt die Summe des Operandenwerts in jeder Untergruppe von Replikaten zurück. Alle Replikate liefern einen Beitrag zur Summe und alle Replikate erhalten die resultierende Summe für jede Untergruppe.
AllToAll
Siehe auch XlaBuilder::AllToAll.
„AllToAll“ ist ein kollektiver Vorgang, bei dem Daten von allen Kernen an alle Kerne gesendet werden. Sie umfasst zwei Phasen:
- Die Streuungsphase. Auf jedem Kern wird der Operand in
split_countBlöcke entlang dersplit_dimensionsaufgeteilt und die Blöcke werden auf alle Kerne verteilt. Der i-te Block wird beispielsweise an den i-ten Kern gesendet. - Die Erfassungsphase. Jeder Kern verkettet die empfangenen Blöcke entlang der
concat_dimension.
Die teilnehmenden Kerne können so konfiguriert werden:
replica_groups: Jede ReplicaGroup enthält eine Liste von Replikat-IDs, die an der Berechnung beteiligt sind. Die Replikat-ID für das aktuelle Replikat kann mitReplicaIdabgerufen werden. „AllToAll“ wird in der angegebenen Reihenfolge auf Untergruppen angewendet.replica_groups = { {1,2,3}, {4,5,0} }bedeutet beispielsweise, dass ein AllToAll innerhalb von Replikaten{1, 2, 3}und in der Sammelphase angewendet wird und die empfangenen Blöcke in derselben Reihenfolge (1, 2, 3) verkettet werden. Anschließend wird ein weiteres AllToAll auf die Replikate 4, 5 und 0 angewendet. Die Verkettungsreihenfolge ist ebenfalls 4, 5, 0. Wennreplica_groupsleer ist, gehören alle Replikate zu einer Gruppe, in der Verkettungsreihenfolge ihres Erscheinens.
Voraussetzungen:
- Die Dimensionsgröße des Operanden auf der
split_dimensionist durchsplit_countteilbar. - Die Form des Operanden ist kein Tupel.
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups, layout, channel_id)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
n-dimensionales Eingabearray |
split_dimension
|
int64
|
Ein Wert im Intervall [0,n), der die Dimension angibt, entlang der der Operand aufgeteilt wird. |
concat_dimension
|
int64
|
Ein Wert im Intervall [0,n), der die Dimension angibt, entlang der die geteilten Blöcke verkettet werden. |
split_count
|
int64
|
Die Anzahl der Kerne, die an diesem Vorgang beteiligt sind. Wenn replica_groups leer ist, sollte dies die Anzahl der Replikate sein. Andernfalls sollte dies der Anzahl der Replikate in jeder Gruppe entsprechen. |
replica_groups
|
ReplicaGroupvector
|
Jede Gruppe enthält eine Liste von Replikat-IDs. |
layout |
optional Layout |
Vom Nutzer angegebenes Speicherlayout |
channel_id
|
optional ChannelHandle
|
Eindeutige Kennung für jedes Sende-/Empfangspaar |
Weitere Informationen zu Formen und Layouts finden Sie unter xla::shapes.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – all_to_all.
AllToAll – Beispiel 1
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(
x,
/*split_dimension=*/ 1,
/*concat_dimension=*/ 0,
/*split_count=*/ 4);
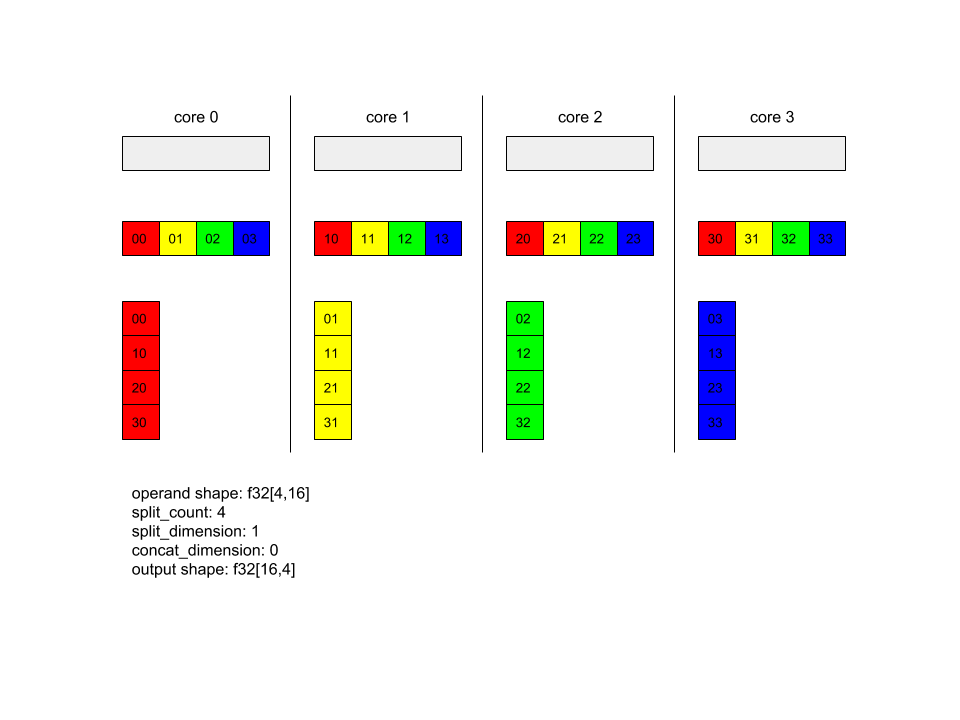
Im obigen Beispiel sind 4 Cores am Alltoall beteiligt. Auf jedem Kern wird der Operand entlang der Dimension 1 in vier Teile aufgeteilt, sodass jeder Teil die Form f32[4,4] hat. Die vier Teile sind auf alle Kerne verteilt. Anschließend werden die empfangenen Teile von jedem Kern entlang der Dimension 0 in der Reihenfolge der Kerne 0 bis 4 verkettet. Die Ausgabe auf jedem Kern hat also die Form f32[16,4].
AllToAll – Beispiel 2 – StableHLO
Im obigen Beispiel sind zwei Replikate am AllToAll-Vorgang beteiligt. Auf jeder Replik hat der Operand die Form f32[2,4]. Der Operand wird entlang der Dimension 1 in zwei Teile aufgeteilt. Jeder Teil hat also die Form f32[2,2]. Die beiden Teile werden dann entsprechend ihrer Position in der Replikatgruppe zwischen den Replikaten ausgetauscht. Jede Replik sammelt den entsprechenden Teil aus beiden Operanden und verkettet sie entlang der Dimension 0. Die Ausgabe auf jedem Replikat hat daher die Form f32[4,2].
RaggedAllToAll
Siehe auch XlaBuilder::RaggedAllToAll.
RaggedAllToAll führt einen kollektiven All-to-All-Vorgang aus, bei dem Ein- und Ausgabe unregelmäßige Tensoren sind.
RaggedAllToAll(input, input_offsets, send_sizes, output, output_offsets,
recv_sizes, replica_groups, channel_id)
| Argumente | Typ | Semantik |
|---|---|---|
input |
XlaOp |
N-Array vom Typ T |
input_offsets |
XlaOp |
N-Array vom Typ T |
send_sizes |
XlaOp |
N-Array vom Typ T |
output |
XlaOp |
N-Array vom Typ T |
output_offsets |
XlaOp |
N-Array vom Typ T |
recv_sizes |
XlaOp |
N-Array vom Typ T |
replica_groups
|
ReplicaGroup vector
|
Jede Gruppe enthält eine Liste von Replikat-IDs. |
channel_id
|
optional ChannelHandle
|
Eindeutige Kennung für jedes Sende-/Empfangspaar |
Ragged Tensors werden durch drei Tensoren definiert:
data: Derdata-Tensor ist entlang seiner äußersten Dimension „ragged“, d. h., jedes indexierte Element hat eine variable Größe.offsets: Der Tensoroffsetsindexiert die äußerste Dimension des Tensorsdataund stellt den Start-Offset jedes unregelmäßigen Elements des Tensorsdatadar.sizes: Dersizes-Tensor stellt die Größe jedes unregelmäßigen Elements desdata-Tensors dar. Die Größe wird in Einheiten von Unterelementen angegeben. Ein untergeordnetes Element wird als Suffix der „data“-Tensorform definiert, das durch Entfernen der äußersten „ragged“-Dimension erhalten wird.- Die Tensoren
offsetsundsizesmüssen dieselbe Größe haben.
Beispiel für einen unregelmäßigen Tensor:
data: [8,3] =
{ {a,b,c},{d,e,f},{g,h,i},{j,k,l},{m,n,o},{p,q,r},{s,t,u},{v,w,x} }
offsets: [3] = {0, 1, 4}
sizes: [3] = {1, 3, 4}
// Index 'data' at 'offsets'[0], 'sizes'[0]' // {a,b,c}
// Index 'data' at 'offsets'[1], 'sizes'[1]' // {d,e,f},{g,h,i},{j,k,l}
// Index 'data' at 'offsets'[2], 'sizes'[2]' // {m,n,o},{p,q,r},{s,t,u},{v,w,x}
output_offsets muss so aufgeteilt werden, dass jedes Replikat Offsets aus der Perspektive der Zielreplikatausgabe hat.
Für den i-ten Ausgabesatz sendet das aktuelle Replikat die input[input_offsets[i]:input_offsets[i]+input_sizes[i]]-Aktualisierung an das i-te Replikat, das in output_i[output_offsets[i]:output_offsets[i]+send_sizes[i]] im i-ten Replikat output geschrieben wird.
Wenn wir beispielsweise zwei Replikate haben:
replica 0:
input: [1, 2, 2]
output:[0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 2]
output_offsets: [0, 0]
recv_sizes: [1, 1]
replica 1:
input: [3, 4, 0]
output: [0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 1]
output_offsets: [1, 2]
recv_sizes: [2, 1]
// replica 0's result will be: [1, 3, 0, 0]
// replica 1's result will be: [2, 2, 4, 0]
Das unregelmäßige All-to-All-HLO hat die folgenden Argumente:
input: Ragged-Eingabedatentensor.output: Ragged-Ausgabedatentensor.input_offsets: Ragged-Eingabe-Offsets-Tensor.send_sizes: Tensor mit unregelmäßigen Sendegrößen.output_offsets: Array mit unregelmäßigen Offsets in der Ausgabe des Zielreplikats.recv_sizes: Ragged-Tensor für die Empfangsgrößen.
Die Tensoren *_offsets und *_sizes müssen alle dieselbe Form haben.
Für die Tensoren *_offsets und *_sizes werden zwei Formen unterstützt:
[num_devices]. Bei „Ragged-All-to-All“ kann maximal ein Update an jedes Remote-Gerät in der Replikatgruppe gesendet werden. Beispiel:
for (remote_device_id : replica_group) {
SEND input[input_offsets[remote_device_id]],
output[output_offsets[remote_device_id]],
send_sizes[remote_device_id] }
- Bei
[num_devices, num_updates], wo „ragged-all-to-all“ bis zunum_updatesUpdates an dasselbe Remote-Gerät sendet (jeweils mit unterschiedlichen Offsets), für jedes Remote-Gerät in der Replikagruppe.
Beispiel:
for (remote_device_id : replica_group) {
for (update_idx : num_updates) {
SEND input[input_offsets[remote_device_id][update_idx]],
output[output_offsets[remote_device_id][update_idx]]],
send_sizes[remote_device_id][update_idx] } }
Und
Siehe auch XlaBuilder::And.
Führt ein elementweises UND von zwei Tensoren lhs und rhs aus.
And(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für „And“ gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
And(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Informationen zu StableHLO finden Sie unter StableHLO.
Asynchron
Siehe auch HloInstruction::CreateAsyncStart,
HloInstruction::CreateAsyncUpdate,
HloInstruction::CreateAsyncDone.
AsyncDone, AsyncStart und AsyncUpdate sind interne HLO-Anweisungen, die für asynchrone Vorgänge verwendet werden und als Primitiven in HLO dienen. Diese Vorgänge können in HLO-Dumps enthalten sein, sie sind jedoch nicht dafür vorgesehen, von Endnutzern manuell erstellt zu werden.
Atan2
Siehe auch XlaBuilder::Atan2.
Führt eine elementweise atan2-Operation für lhs und rhs aus.
Atan2(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für Atan2 gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Atan2(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – atan2.
BatchNormGrad
Eine detaillierte Beschreibung des Algorithmus finden Sie auch unter XlaBuilder::BatchNormGrad und im ursprünglichen Batch-Normalisierungs-Paper.
Berechnet die Gradienten der Batch-Normalisierung.
BatchNormGrad(operand, scale, batch_mean, batch_var, grad_output, epsilon,
feature_index)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp | n-dimensionales Array, das normalisiert werden soll (x) |
scale |
XlaOp | Eindimensionales Array (\(\gamma\)) |
batch_mean |
XlaOp | Eindimensionales Array (\(\mu\)) |
batch_var |
XlaOp | Eindimensionales Array (\(\sigma^2\)) |
grad_output |
XlaOp | An BatchNormTraining (\(\nabla y\)) übergebene Farbverläufe |
epsilon |
float |
Epsilon-Wert (\(\epsilon\)) |
feature_index |
int64 |
Index für die Featuredimension in operand |
Für jedes Feature in der Feature-Dimension (feature_index ist der Index für die Feature-Dimension in operand) werden die Gradienten in Bezug auf operand, offset und scale über alle anderen Dimensionen hinweg berechnet. feature_index muss ein gültiger Index für die Feature-Dimension in operand sein.
Die drei Gradienten werden durch die folgenden Formeln definiert (unter der Annahme eines 4‑dimensionalen Arrays als operand und mit dem Index der Feature-Dimension l, der Batchgröße m und den räumlichen Größen w und h):
\[ \begin{split} c_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sigma^2_l+\epsilon} \right) \\\\ d_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \\\\ \nabla x_{ijkl} &= \frac{\gamma_{l} }{\sqrt{\sigma^2_{l}+\epsilon} } \left( \nabla y_{ijkl} - d_l - c_l (x_{ijkl} - \mu_{l}) \right) \\\\ \nabla \gamma_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sqrt{\sigma^2_{l}+\epsilon} } \right) \\\\\ \nabla \beta_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \end{split} \]
Die Eingaben batch_mean und batch_var stellen Momentwerte für Batch- und räumliche Dimensionen dar.
Der Ausgabetyp ist ein Tupel aus drei Handles:
| Ausgaben | Typ | Semantik |
|---|---|---|
grad_operand
|
XlaOp | Gradient in Bezug auf die Eingabe operand
(\(\nabla x\)) |
grad_scale
|
XlaOp | Gradient in Bezug auf die Eingabe **scale **
(\(\nabla\gamma\)) |
grad_offset
|
XlaOp | Gradient in Bezug auf die Eingabe
offset(\(\nabla\beta\)) |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – batch_norm_grad.
BatchNormInference
Eine detaillierte Beschreibung des Algorithmus finden Sie auch unter XlaBuilder::BatchNormInference und im ursprünglichen Batch-Normalisierungs-Paper.
Normalisiert ein Array über Batch- und räumliche Dimensionen hinweg.
BatchNormInference(operand, scale, offset, mean, variance, epsilon,
feature_index)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp | n-dimensionales Array, das normalisiert werden soll |
scale |
XlaOp | 1‑dimensionales Array |
offset |
XlaOp | 1‑dimensionales Array |
mean |
XlaOp | 1‑dimensionales Array |
variance |
XlaOp | 1‑dimensionales Array |
epsilon |
float |
Epsilon-Wert |
feature_index |
int64 |
Index für die Featuredimension in operand |
Für jedes Element in der Feature-Dimension (feature_index ist der Index für die Feature-Dimension in operand) werden der Mittelwert und die Varianz über alle anderen Dimensionen hinweg berechnet. Anschließend werden der Mittelwert und die Varianz verwendet, um jedes Element in operand zu normalisieren. Die feature_index muss ein gültiger Index für die Feature-Dimension in operand sein.
BatchNormInference entspricht dem Aufruf von BatchNormTraining, ohne mean und variance für jeden Batch zu berechnen. Stattdessen werden die Eingaben mean und variance als geschätzte Werte verwendet. Ziel dieses Vorgangs ist es, die Latenz bei der Inferenz zu verringern. Daher der Name BatchNormInference.
Die Ausgabe ist ein n-dimensionales, normalisiertes Array mit derselben Form wie die Eingabe operand.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – batch_norm_inference.
BatchNormTraining
Eine detaillierte Beschreibung des Algorithmus finden Sie auch unter XlaBuilder::BatchNormTraining und the original batch normalization paper.
Normalisiert ein Array über Batch- und räumliche Dimensionen hinweg.
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
n-dimensionales Array, das normalisiert werden soll (x) |
scale |
XlaOp |
Eindimensionales Array (\(\gamma\)) |
offset |
XlaOp |
Eindimensionales Array (\(\beta\)) |
epsilon |
float |
Epsilon-Wert (\(\epsilon\)) |
feature_index |
int64 |
Index für die Featuredimension in operand |
Für jedes Element in der Feature-Dimension (feature_index ist der Index für die Feature-Dimension in operand) werden der Mittelwert und die Varianz über alle anderen Dimensionen hinweg berechnet. Anschließend werden der Mittelwert und die Varianz verwendet, um jedes Element in operand zu normalisieren. Die feature_index muss ein gültiger Index für die Feature-Dimension in operand sein.
Der Algorithmus funktioniert für jeden Batch in operand \(x\) , der m Elemente mit w und h als Größe der räumlichen Dimensionen enthält, so (vorausgesetzt, operand ist ein vierdimensionales Array):
Berechnet den Batchmittelwert \(\mu_l\) für jedes Feature
lin der Feature-Dimension: \(\mu_l=\frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h x_{ijkl}\)Berechnet die Batch-Varianz \(\sigma^2_l\): $\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
Normalisiert, skaliert und verschiebt: \(y_{ijkl}=\frac{\gamma_l(x_{ijkl}-\mu_l)}{\sqrt[2]{\sigma^2_l+\epsilon} }+\beta_l\)
Der Epsilon-Wert, in der Regel eine kleine Zahl, wird hinzugefügt, um Division durch null zu vermeiden.
Der Ausgabetyp ist ein Tupel aus drei XlaOp:
| Ausgaben | Typ | Semantik |
|---|---|---|
output
|
XlaOp
|
n-dimensionales Array mit derselben Form wie die Eingabe operand (y) |
batch_mean |
XlaOp |
Eindimensionales Array (\(\mu\)) |
batch_var |
XlaOp |
Eindimensionales Array (\(\sigma^2\)) |
batch_mean und batch_var sind Momente, die mithilfe der oben genannten Formeln für die Batch- und räumlichen Dimensionen berechnet werden.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – batch_norm_training.
Bitcast
Siehe auch HloInstruction::CreateBitcast.
Bitcast kann in HLO-Dumps enthalten sein, sollte aber nicht manuell von Endnutzern erstellt werden.
BitcastConvertType
Siehe auch XlaBuilder::BitcastConvertType.
Ähnlich wie tf.bitcast in TensorFlow wird eine elementweise Bitcast-Operation von einer Datenform in eine Zielform ausgeführt. Die Eingabe- und Ausgabegröße müssen übereinstimmen: z.B. werden s32-Elemente über die Bitcast-Routine zu f32-Elementen und ein s32-Element wird zu vier s8-Elementen. Bitcast wird als Low-Level-Cast implementiert. Daher liefern Maschinen mit unterschiedlichen Gleitkommadarstellungen unterschiedliche Ergebnisse.
BitcastConvertType(operand, new_element_type)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Array vom Typ T mit Dimensionen D |
new_element_type |
PrimitiveType |
Typ U |
Die Dimensionen des Operanden und der Zielform müssen übereinstimmen, mit Ausnahme der letzten Dimension, die sich durch das Verhältnis der Primitivgröße vor und nach der Konvertierung ändert.
Die Quell- und Zielelementtypen dürfen keine Tupel sein.
Informationen zu StableHLO finden Sie unter StableHLO – bitcast_convert.
Bitcast-Konvertierung in einen primitiven Typ mit anderer Breite
Die BitcastConvert-HLO-Anweisung unterstützt den Fall, in dem die Größe des Ausgabeelementtyps T' nicht der Größe des Eingabeelements T entspricht. Da der gesamte Vorgang konzeptionell ein Bitcast ist und die zugrunde liegenden Bytes nicht geändert werden, muss sich die Form des Ausgabeelements ändern. Für B = sizeof(T), B' =
sizeof(T') gibt es zwei mögliche Fälle.
Erstens: Wenn B > B', erhält die Ausgabedimension eine neue untergeordnete Dimension der Größe B/B'. Beispiel:
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
Die Regel für effektive Skalare bleibt unverändert:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
Alternativ erfordert die Anleitung für B' > B, dass die letzte logische Dimension der Eingabeform gleich B'/B ist. Diese Dimension wird bei der Konvertierung entfernt:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
Beachten Sie, dass Konvertierungen zwischen verschiedenen Bitbreiten nicht elementweise erfolgen.
Nachricht an alle
Siehe auch XlaBuilder::Broadcast.
Fügt einem Array Dimensionen hinzu, indem die Daten im Array dupliziert werden.
Broadcast(operand, broadcast_sizes)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Das zu duplizierende Array |
broadcast_sizes |
ArraySlice<int64> |
Die Größen der neuen Dimensionen |
Die neuen Dimensionen werden links eingefügt. Wenn broadcast_sizes die Werte {a0, ..., aN} hat und die Operandenform die Dimensionen {b0, ..., bM} hat, hat die Form der Ausgabe die Dimensionen {a0, ..., aN, b0, ..., bM}.
Die neuen Dimensionen werden in Kopien des Operanden indexiert, d.h.
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
Wenn operand beispielsweise ein Skalar f32 mit dem Wert 2.0f ist und broadcast_sizes {2, 3} ist, ist das Ergebnis ein Array mit der Form f32[2, 3] und alle Werte im Ergebnis sind 2.0f.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – broadcast.
BroadcastInDim
Siehe auch XlaBuilder::BroadcastInDim.
Erhöht die Größe und Anzahl der Dimensionen eines Arrays, indem die Daten im Array dupliziert werden.
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Das zu duplizierende Array |
out_dim_size
|
ArraySlice<int64>
|
Die Größen der Dimensionen der Zielform |
broadcast_dimensions
|
ArraySlice<int64>
|
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Ähnlich wie bei Broadcast, aber es können Dimensionen an beliebiger Stelle hinzugefügt und vorhandene Dimensionen mit der Größe 1 erweitert werden.
Die operand wird auf die durch out_dim_size beschriebene Form übertragen.
broadcast_dimensions ordnet die Dimensionen von operand den Dimensionen der Zielform zu. Die i-te Dimension des Operanden wird also der broadcast_dimension[i]-ten Dimension der Ausgabeform zugeordnet. Die Dimensionen von operand müssen die Größe 1 haben oder dieselbe Größe wie die Dimension in der Ausgabedimension haben, auf die sie abgebildet werden. Die verbleibenden Dimensionen werden mit Dimensionen der Größe 1 gefüllt. Beim Broadcasting mit degenerierten Dimensionen wird dann entlang dieser degenerierten Dimensionen gesendet, um die Ausgabedimension zu erreichen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Anruf
Siehe auch XlaBuilder::Call.
Ruft eine Berechnung mit den angegebenen Argumenten auf.
Call(computation, operands...)
| Argumente | Typ | Semantik |
|---|---|---|
computation
|
XlaComputation
|
Berechnung vom Typ T_0, T_1, ...,
T_{N-1} -> S mit N Parametern beliebigen Typs |
operands |
Folge von N XlaOps |
N Argumente beliebigen Typs |
Die Stelligkeit und die Typen von operands müssen mit den Parametern von computation übereinstimmen. Es ist zulässig, kein operands zu haben.
CompositeCall
Siehe auch XlaBuilder::CompositeCall.
Kapselt einen Vorgang, der aus anderen StableHLO-Vorgängen besteht (zusammengesetzt), Eingaben und composite_attributes entgegennimmt und Ergebnisse erzeugt. Die Semantik des Vorgangs wird durch das Attribut „decomposition“ implementiert. Der zusammengesetzte Vorgang kann durch seine Zerlegung ersetzt werden, ohne die Programmsemantik zu ändern. Wenn durch das Inlining der Zerlegung nicht dieselbe Semantik für den Vorgang erzielt wird, sollten Sie „custom_call“ verwenden.
Das Feld „Version“ (Standardwert: 0) wird verwendet, um anzugeben, wann sich die Semantik eines Composites ändert.
Dieser Vorgang wird als kCall mit dem Attribut is_composite=true implementiert. Das Feld decomposition wird durch das Attribut computation angegeben. In den Frontend-Attributen werden die verbleibenden Attribute mit dem Präfix composite. gespeichert.
Beispiel für den Vorgang „CompositeCall“:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
CompositeCall(computation, operands..., name, attributes, version)
| Argumente | Typ | Semantik |
|---|---|---|
computation
|
XlaComputation
|
Berechnung vom Typ T_0, T_1, ...,
T_{N-1} -> S mit N Parametern beliebigen Typs |
operands |
Folge von N XlaOps |
variable Anzahl von Werten |
name |
string |
Name des Composites |
attributes
|
optional string
|
optionales in einen String umgewandeltes Attribut-Dictionary |
version
|
optional int64
|
Nummer für Versionsupdates für die Semantik des zusammengesetzten Vorgangs |
Die decomposition eines Vorgangs ist kein Feld, sondern wird als „to_apply“-Attribut angezeigt, das auf die Funktion verweist, die die Implementierung auf niedrigerer Ebene enthält, d. h. to_apply=%funcname.
Weitere Informationen zu Composite und Decomposition finden Sie in der StableHLO-Spezifikation.
Cbrt
Siehe auch XlaBuilder::Cbrt.
Elementweise Kubikwurzeloperation x -> cbrt(x).
Cbrt(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Cbrt unterstützt auch das optionale Argument result_accuracy:
Cbrt(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Informationen zu StableHLO finden Sie unter StableHLO – cbrt.
Aufrunden
Siehe auch XlaBuilder::Ceil.
Elementweise Obergrenze x -> ⌈x⌉.
Ceil(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – ceil.
Cholesky
Siehe auch XlaBuilder::Cholesky.
Berechnet die Cholesky-Zerlegung einer Reihe von symmetrischen (hermitischen) positiv definiten Matrizen.
Cholesky(a, lower)
| Argumente | Typ | Semantik |
|---|---|---|
a
|
XlaOp
|
Ein Array eines komplexen oder Gleitkommatyps mit mehr als zwei Dimensionen. |
lower |
bool |
ob das obere oder untere Dreieck von a verwendet werden soll. |
Wenn lower gleich true ist, werden die unteren Dreiecksmatrizen l so berechnet, dass $a = l .
l^T$. Wenn lower gleich false ist, werden obere Dreiecksmatrizen u berechnet, sodass\(a = u^T . u\).
Eingabedaten werden nur aus dem unteren/oberen Dreieck von a gelesen, je nach Wert von lower. Werte aus dem anderen Dreieck werden ignoriert. Ausgabedaten werden im selben Dreieck zurückgegeben. Die Werte im anderen Dreieck sind implementierungsdefiniert und können beliebig sein.
Wenn a mehr als zwei Dimensionen hat, wird a als Batch von Matrizen behandelt, wobei alle Dimensionen außer den beiden untergeordneten Dimensionen Batchdimensionen sind.
Wenn a nicht symmetrisch (hermitesch) positiv definit ist, ist das Ergebnis implementierungsdefiniert.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – cholesky.
Einschränken
Siehe auch XlaBuilder::Clamp.
Begrenzt einen Operanden auf den Bereich zwischen einem Mindest- und einem Höchstwert.
Clamp(min, operand, max)
| Argumente | Typ | Semantik |
|---|---|---|
min |
XlaOp |
Array vom Typ T |
operand |
XlaOp |
Array vom Typ T |
max |
XlaOp |
Array vom Typ T |
Gibt bei einem Operanden sowie einem Mindest- und einem Höchstwert den Operanden zurück, wenn er im Bereich zwischen dem Mindest- und dem Höchstwert liegt. Andernfalls wird der Mindestwert zurückgegeben, wenn der Operand unter diesem Bereich liegt, oder der Höchstwert, wenn der Operand über diesem Bereich liegt. Der Wert ist clamp(a, x, b) = min(max(a, x), b).
Alle drei Arrays müssen dieselbe Form haben. Alternativ können min und/oder max als eingeschränkte Form des Broadcasting ein Skalar vom Typ T sein.
Beispiel mit skalaren min und max:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
Weitere Informationen zu StableHLO finden Sie unter StableHLO – clamp.
Minimieren
Siehe auch XlaBuilder::Collapse.
und den Vorgang tf.reshape.
Reduziert die Dimensionen eines Arrays auf eine Dimension.
Collapse(operand, dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Array vom Typ T |
dimensions |
int64 vector |
in der richtigen Reihenfolge, aufeinanderfolgende Teilmenge der Dimensionen von T. |
Mit „Collapse“ wird die angegebene Teilmenge der Dimensionen des Operanden durch eine einzelne Dimension ersetzt. Die Eingabeargumente sind ein beliebiges Array vom Typ T und ein Compile-Zeitkonstantenvektor mit Dimensionsindexen. Die Dimensionsindexe müssen eine fortlaufende Teilmenge der Dimensionen von T in aufsteigender Reihenfolge (niedrige bis hohe Dimensionsnummern) sein. {0, 1, 2}, {0, 1} oder {1, 2} sind also gültige Dimensionssets, {1, 0} oder {0, 2} jedoch nicht. Sie werden durch eine einzelne neue Dimension ersetzt, die sich an derselben Position in der Dimensionsfolge befindet wie die Dimensionen, die sie ersetzt. Die Größe der neuen Dimension entspricht dem Produkt der ursprünglichen Dimensionsgrößen. Die niedrigste Dimensionsnummer in dimensions ist die am langsamsten variierende Dimension (wichtigste) im Schleifennest, in dem diese Dimensionen zusammengefasst werden. Die höchste Dimensionsnummer ist die am schnellsten variierende (unwichtigste). Wenn eine allgemeinere Reihenfolge für das Minimieren erforderlich ist, sehen Sie sich den Operator tf.reshape an.
Sei v beispielsweise ein Array mit 24 Elementen:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
Clz
Siehe auch XlaBuilder::Clz.
Zählt elementweise die führenden Nullen.
Clz(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
CollectiveBroadcast
Siehe auch XlaBuilder::CollectiveBroadcast.
Sendet Daten an alle Replikate. Daten werden von der ersten Replikat-ID in jeder Gruppe an die anderen IDs in derselben Gruppe gesendet. Wenn sich eine Replikat-ID in keiner Replikatgruppe befindet, ist die Ausgabe für dieses Replikat ein Tensor, der aus Nullen in shape besteht.
CollectiveBroadcast(operand, replica_groups, channel_id)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
replica_groups
|
ReplicaGroupvector
|
Jede Gruppe enthält eine Liste mit Replikat-IDs. |
channel_id
|
optional ChannelHandle
|
Eindeutige Kennung für jedes Sende-/Empfangspaar |
Informationen zu StableHLO finden Sie unter StableHLO – collective_broadcast.
CollectivePermute
Siehe auch XlaBuilder::CollectivePermute.
CollectivePermute ist ein kollektiver Vorgang, bei dem Daten zwischen Replikaten gesendet und empfangen werden.
CollectivePermute(operand, source_target_pairs, channel_id, inplace)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
n-dimensionales Eingabearray |
source_target_pairs
|
<int64, int64> vector
|
Eine Liste von Paaren (source_replica_id, target_replica_id). Für jedes Paar wird der Operand vom Quellreplikat an das Zielreplikat gesendet. |
channel_id
|
optional ChannelHandle
|
Optionale Channel-ID für die modulübergreifende Kommunikation |
inplace
|
optional bool
|
Flag, das angibt, ob die Permutation direkt erfolgen soll |
Beachten Sie die folgenden Einschränkungen für source_target_pairs:
- Zwei beliebige Paare dürfen nicht dieselbe Zielreplikat-ID und nicht dieselbe Quellreplikat-ID haben.
- Wenn eine Replikat-ID in keinem Paar ein Ziel ist, ist die Ausgabe für dieses Replikat ein Tensor, der aus Nullen mit derselben Form wie die Eingabe besteht.
Die API des CollectivePermute-Vorgangs wird intern in zwei HLO-Anweisungen (CollectivePermuteStart und CollectivePermuteDone) zerlegt.
Siehe auch HloInstruction::CreateCollectivePermuteStart.
CollectivePermuteStart und CollectivePermuteDone dienen als Primitiven in HLO.
Diese Vorgänge können in HLO-Dumps enthalten sein, sind aber nicht für die manuelle Erstellung durch Endnutzer vorgesehen.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – collective_permute.
Vergleichen
Siehe auch XlaBuilder::Compare.
Führt einen elementweisen Vergleich von lhs und rhs durch:
Eq
Siehe auch XlaBuilder::Eq.
Führt einen elementweisen Gleichheitsvergleich von lhs und rhs durch.
\(lhs = rhs\)
Eq(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für Eq gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Eq(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Für Eq ist eine totale Ordnung über den Gleitkommazahlen vorhanden, indem Folgendes erzwungen wird:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
EqTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Informationen zu StableHLO finden Sie unter StableHLO – compare.
Ne
Siehe auch XlaBuilder::Ne.
Führt einen elementweisen Ungleich-Vergleich von lhs und rhs durch.
\(lhs != rhs\)
Ne(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für Ne gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Ne(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Für Ne wird eine Gesamtordnung über den Gleitkommazahlen unterstützt, indem Folgendes erzwungen wird:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
NeTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Informationen zu StableHLO finden Sie unter StableHLO – compare.
Ge
Siehe auch XlaBuilder::Ge.
Führt einen elementweisen greater-or-equal-than von lhs und rhs durch.
\(lhs >= rhs\)
Ge(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für Ge gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Ge(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Für Gt ist eine Totalordnung über den Gleitkommazahlen vorhanden, indem Folgendes erzwungen wird:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
GtTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Informationen zu StableHLO finden Sie unter StableHLO – compare.
Gt
Siehe auch XlaBuilder::Gt.
Führt einen elementweisen Größer-als-Vergleich von lhs und rhs durch.
\(lhs > rhs\)
Gt(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für „Gt“ gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Gt(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Informationen zu StableHLO finden Sie unter StableHLO – compare.
Le
Siehe auch XlaBuilder::Le.
Führt einen elementweisen less-or-equal-than von lhs und rhs durch.
\(lhs <= rhs\)
Le(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für Le gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Le(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Für Le ist eine Gesamtordnung über den Gleitkommazahlen vorhanden, indem Folgendes erzwungen wird:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LeTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Informationen zu StableHLO finden Sie unter StableHLO – compare.
Lt
Siehe auch XlaBuilder::Lt.
Führt einen elementweisen Vergleich „Kleiner als“ von lhs und rhs durch.
\(lhs < rhs\)
Lt(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für „Lt“ gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Lt(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Für „Lt“ ist eine Gesamtbestellung über den Gleitkommazahlen vorhanden, indem Folgendes erzwungen wird:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LtTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Informationen zu StableHLO finden Sie unter StableHLO – compare.
Komplex
Siehe auch XlaBuilder::Complex.
Führt die elementweise Konvertierung in einen komplexen Wert aus einem Paar aus reellen und imaginären Werten, lhs und rhs, durch.
Complex(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für „Complex“ gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Complex(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Informationen zu StableHLO finden Sie unter StableHLO – complex.
ConcatInDim (Concatenate)
Siehe auch XlaBuilder::ConcatInDim.
Mit CONCATENATE wird ein Array aus mehreren Array-Operanden erstellt. Das Array hat dieselbe Anzahl von Dimensionen wie jeder der Eingabearray-Operanden (die dieselbe Anzahl von Dimensionen wie einander haben müssen) und enthält die Argumente in der Reihenfolge, in der sie angegeben wurden.
Concatenate(operands..., dimension)
| Argumente | Typ | Semantik |
|---|---|---|
operands
|
Sequenz von N XlaOp
|
N Arrays vom Typ T mit den Dimensionen [L0, L1, ...]. Erfordert N >= 1. |
dimension
|
int64
|
Ein Wert im Intervall [0, N), der die Dimension angibt, die zwischen den operands verkettet werden soll. |
Mit Ausnahme von dimension müssen alle Dimensionen identisch sein. Das liegt daran, dass XLA keine unregelmäßigen Arrays unterstützt. Außerdem können 0-dimensionale Werte nicht verkettet werden, da die Dimension, entlang der die Verkettung erfolgt, nicht benannt werden kann.
1‑dimensionales Beispiel:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
//Output: {2, 3, 4, 5, 6, 7}
2‑dimensionales Beispiel:
let a = { {1, 2},
{3, 4},
{5, 6} };
let b = { {7, 8} };
Concat({a, b}, 0)
//Output: { {1, 2},
// {3, 4},
// {5, 6},
// {7, 8} }
Diagramm:
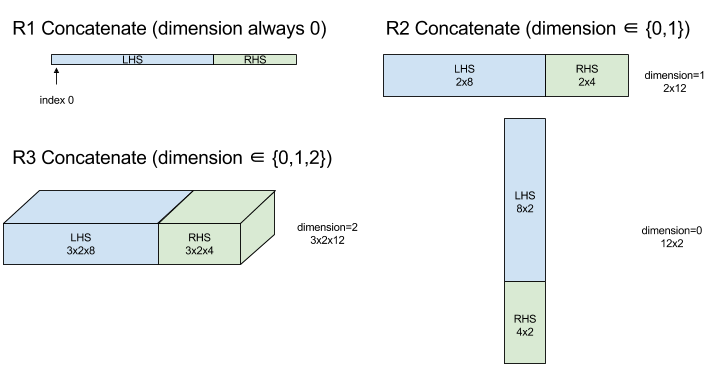
Weitere Informationen zu StableHLO finden Sie unter StableHLO – concatenate.
Bedingt
Siehe auch XlaBuilder::Conditional.
Conditional(predicate, true_operand, true_computation, false_operand,
false_computation)
| Argumente | Typ | Semantik |
|---|---|---|
predicate |
XlaOp |
Skalar vom Typ PRED |
true_operand |
XlaOp |
Argument vom Typ \(T_0\) |
true_computation |
XlaComputation |
XlaComputation vom Typ \(T_0 \to S\) |
false_operand |
XlaOp |
Argument vom Typ \(T_1\) |
false_computation |
XlaComputation |
XlaComputation vom Typ \(T_1 \to S\) |
Führt true_computation aus, wenn predicate gleich true ist, false_computation, wenn predicate gleich false ist, und gibt das Ergebnis zurück.
Die true_computation muss ein einzelnes Argument vom Typ \(T_0\) annehmen und wird mit true_operand aufgerufen, das vom selben Typ sein muss. Die false_computation muss ein einzelnes Argument vom Typ \(T_1\) annehmen und wird mit false_operand aufgerufen, das denselben Typ haben muss. Der Typ des zurückgegebenen Werts von true_computation und false_computation muss identisch sein.
Je nach Wert von predicate wird nur eine der beiden Optionen true_computation und false_computation ausgeführt.
Conditional(branch_index, branch_computations, branch_operands)
| Argumente | Typ | Semantik |
|---|---|---|
branch_index |
XlaOp |
Skalar vom Typ S32 |
branch_computations |
Sequenz von N XlaComputation |
XlaComputations vom Typ \(T_0 \to S , T_1 \to S , ..., T_{N-1} \to S\) |
branch_operands |
Sequenz von N XlaOp |
Argumente vom Typ \(T_0 , T_1 , ..., T_{N-1}\) |
Führt branch_computations[branch_index] aus und gibt das Ergebnis zurück. Wenn branch_index ein S32 ist, das < 0 oder >= N ist, wird branch_computations[N-1] als Standardzweig ausgeführt.
Jede branch_computations[b] muss ein einzelnes Argument vom Typ \(T_b\) entgegennehmen und wird mit branch_operands[b] aufgerufen, das denselben Typ haben muss. Der Typ des zurückgegebenen Werts der einzelnen branch_computations[b] muss identisch sein.
Je nach Wert von branch_index wird nur einer der branch_computations ausgeführt.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – if.
Konstante
Siehe auch XlaBuilder::ConstantLiteral.
Erstellt eine output aus einer konstanten literal.
Constant(literal)
| Argumente | Typ | Semantik |
|---|---|---|
literal |
LiteralSlice |
Konstante Ansicht eines vorhandenen Literal |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – constant.
ConvertElementType
Siehe auch XlaBuilder::ConvertElementType.
Ähnlich wie bei einem elementweisen static_cast in C++ wird mit ConvertElementType eine elementweise Konvertierungsoperation von einer Datenform in eine Zielform ausgeführt. Die Dimensionen müssen übereinstimmen und die Konvertierung erfolgt elementweise, z.B. werden s32-Elemente über eine s32-zu-f32-Konvertierungsroutine zu f32-Elementen.
ConvertElementType(operand, new_element_type)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Array vom Typ T mit Dimensionen D |
new_element_type |
PrimitiveType |
Typ U |
Die Dimensionen des Operanden und der Zielform müssen übereinstimmen. Die Quell- und Ziel-Elementtypen dürfen keine Tupel sein.
Bei einer Konvertierung wie T=s32 in U=f32 wird eine Normalisierungsroutine für die Konvertierung von Ganzzahlen in Gleitkommazahlen wie „round-to-nearest-even“ (auf die nächste gerade Zahl runden) ausgeführt.
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
Informationen zu StableHLO finden Sie unter StableHLO – convert.
Conv (Convolution)
Siehe auch XlaBuilder::Conv.
Berechnet eine Faltung, wie sie in neuronalen Netzen verwendet wird. Eine Faltung kann als n-dimensionales Fenster betrachtet werden, das sich über einen n-dimensionalen Basisbereich bewegt. Für jede mögliche Position des Fensters wird eine Berechnung durchgeführt.
Conv Stellt eine Faltungsanweisung in die Berechnungswarteschlange ein, die die Standard-Faltungsdimensionsnummern ohne Dilation verwendet.
Die Auffüllung wird in Kurzform als SAME oder VALID angegeben. Beim SAME-Padding wird die Eingabe (lhs) mit Nullen aufgefüllt, sodass die Ausgabe dieselbe Form wie die Eingabe hat, wenn kein Striding berücksichtigt wird. VALID-Padding bedeutet einfach kein Padding.
Conv(lhs, rhs, window_strides, padding, feature_group_count,
batch_group_count, precision_config, preferred_element_type)
| Argumente | Typ | Semantik |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-dimensionales Array von Eingaben |
rhs
|
XlaOp
|
(n+2)-dimensionales Array mit Kernelgewichten |
window_strides |
ArraySlice<int64> |
n-dimensionales Array von Kernel-Strides |
padding |
Padding |
enum für Padding |
feature_group_count
|
int64 | die Anzahl der Funktionsgruppen |
batch_group_count |
int64 | Anzahl der Batchgruppen |
precision_config
|
optional
PrecisionConfig |
Enum für den Genauigkeitsgrad |
preferred_element_type
|
optional
PrimitiveType |
enum des skalaren Elementtyps |
Für Conv sind verschiedene Steuerungsebenen verfügbar:
Sei n die Anzahl der räumlichen Dimensionen. Das lhs-Argument ist ein (n+2)-dimensionales Array, das die Grundfläche beschreibt. Dies wird als Eingabe bezeichnet, obwohl natürlich auch die rechte Seite eine Eingabe ist. In einem neuronalen Netzwerk sind das die Eingabeaktivierungen. Die n+2-Dimensionen sind in dieser Reihenfolge:
batch: Jede Koordinate in dieser Dimension stellt eine unabhängige Eingabe dar, für die die Faltung ausgeführt wird.z/depth/features: Jeder (y,x)-Position im Basisbereich ist ein Vektor zugeordnet, der in diese Dimension eingeht.spatial_dims: Beschreibt die räumlichen Dimensionen vonn, die den Basisbereich definieren, über den sich das Fenster bewegt.
Das rhs-Argument ist ein (n+2)-dimensionales Array, das den Faltungsfilter/Kernel/das Faltungsfenster beschreibt. Die Dimensionen sind in dieser Reihenfolge:
output-z: Diez-Dimension der Ausgabe.input-z: Die Größe dieser Dimension multipliziert mitfeature_group_countsollte der Größe der Dimensionzauf der linken Seite entsprechen.spatial_dims: Beschreibt die räumlichenn-Dimensionen, die das n-dimensionale Fenster definieren, das sich über den Basisbereich bewegt.
Das Argument window_strides gibt den Stride des Faltungsfensters in den räumlichen Dimensionen an. Wenn der Stride in der ersten räumlichen Dimension beispielsweise 3 ist, kann das Fenster nur an Koordinaten platziert werden, bei denen der erste räumliche Index durch 3 teilbar ist.
Das Argument padding gibt an, wie viel Nullenauffüllung auf den Basisbereich angewendet werden soll. Der Padding-Betrag kann negativ sein. Der absolute Wert des negativen Padding gibt die Anzahl der Elemente an, die vor der Faltung aus der angegebenen Dimension entfernt werden sollen. padding[0] gibt den Abstand für die Dimension y und padding[1] den Abstand für die Dimension x an. Jedes Paar hat das niedrige Padding als erstes und das hohe Padding als zweites Element. Das niedrige Padding wird in Richtung niedrigerer Indexe angewendet, das hohe Padding in Richtung höherer Indexe. Wenn padding[1] beispielsweise (2,3) ist, wird in der zweiten räumlichen Dimension links mit zwei Nullen und rechts mit drei Nullen aufgefüllt. Die Verwendung von Padding entspricht dem Einfügen dieser Nullwerte in die Eingabe (lhs) vor der Faltung.
Mit den Argumenten lhs_dilation und rhs_dilation wird der Dilation-Faktor angegeben, der in jeder räumlichen Dimension auf die linke bzw. rechte Seite angewendet werden soll. Wenn der Dilation-Faktor in einer räumlichen Dimension „d“ ist, werden implizit „d-1“ Lücken zwischen den einzelnen Einträgen in dieser Dimension eingefügt, wodurch sich die Größe des Arrays erhöht. Die Lücken werden mit einem No-Op-Wert gefüllt, was für die Faltung Nullen bedeutet.
Die Erweiterung der rechten Seite wird auch als Atrous-Faltung bezeichnet. Weitere Informationen finden Sie unter tf.nn.atrous_conv2d. Die Erweiterung der linken Seite wird auch als transponierte Faltung bezeichnet. Weitere Informationen finden Sie unter tf.nn.conv2d_transpose.
Das Argument feature_group_count (Standardwert 1) kann für gruppierte Faltungen verwendet werden. feature_group_count muss ein Teiler sowohl der Eingabe- als auch der Ausgabefeatured-Dimension sein. Wenn feature_group_count größer als 1 ist, bedeutet das, dass die Eingabe- und Ausgabefeature-Dimension und die rhs-Ausgabefeature-Dimension konzeptionell gleichmäßig in viele feature_group_count-Gruppen aufgeteilt werden, wobei jede Gruppe aus einer fortlaufenden Untersequenz von Features besteht. Die Eingabefeature-Dimension von rhs muss gleich der Eingabefeature-Dimension von lhs geteilt durch feature_group_count sein. Sie hat also bereits die Größe einer Gruppe von Eingabefeatures. Die i-ten Gruppen werden zusammen verwendet, um feature_group_count für viele separate Faltungen zu berechnen. Die Ergebnisse dieser Faltungen werden in der Ausgabefeatured-Dimension verkettet.
Bei der faltenden Schicht wird das feature_group_count-Argument auf die Eingabe-Feature-Dimension festgelegt und der Filter wird von [filter_height, filter_width, in_channels, channel_multiplier] in [filter_height, filter_width, 1, in_channels * channel_multiplier] umgeformt. Weitere Informationen finden Sie unter tf.nn.depthwise_conv2d.
Das Argument batch_group_count (Standardwert 1) kann für gruppierte Filter während der Backpropagation verwendet werden. batch_group_count muss ein Teiler der Größe der Batchdimension lhs (Eingabe) sein. Wenn batch_group_count größer als 1 ist, sollte die Ausgabebatchdimension die Größe input batch
/ batch_group_count haben. Die batch_group_count muss ein Teiler der Größe des Ausgabefeature sein.
Die Ausgabedimensionen sind in dieser Reihenfolge:
batch: Die Größe dieser Dimension multipliziert mitbatch_group_countsollte der Größe der Dimensionbatchin „lhs“ entsprechen.z: Hat dieselbe Größe wieoutput-zim Kernel (rhs).spatial_dims: Ein Wert für jede gültige Platzierung des Faltungsfensters.
Die Abbildung oben zeigt, wie das Feld batch_group_count funktioniert. Dazu wird jeder LHS-Batch in batch_group_count Gruppen unterteilt. Das Gleiche geschieht mit den Ausgabefunktionen. Anschließend führen wir für jede dieser Gruppen paarweise Faltungen durch und verketten die Ausgabe entlang der Ausgabefunktionsdimension. Die operationelle Semantik aller anderen Dimensionen (Feature und räumlich) bleibt unverändert.
Die gültigen Positionen des Faltungsfensters werden durch die Strides und die Größe der Grundfläche nach dem Padding bestimmt.
Um zu beschreiben, was eine Faltung bewirkt, betrachten wir eine 2D-Faltung und wählen einige feste batch-, z-, y- und x-Koordinaten in der Ausgabe aus. Dann ist (y,x) die Position einer Ecke des Fensters im Basisbereich (z.B. die obere linke Ecke, je nachdem, wie Sie die räumlichen Dimensionen interpretieren). Wir haben jetzt ein 2D-Fenster aus dem Basisbereich, in dem jeder 2D-Punkt einem 1D-Vektor zugeordnet ist. So erhalten wir einen 3D-Quader. Da wir die Ausgabekoordinate z festgelegt haben, erhalten wir aus dem Faltungs-Kernel auch einen 3D-Quader. Die beiden Begrenzungsrahmen haben dieselben Abmessungen. Wir können also die Summe der elementweisen Produkte zwischen den beiden Begrenzungsrahmen bilden (ähnlich einem Skalarprodukt). Das ist der Ausgabewert.
Wenn output-z beispielsweise 5 ist, werden für jede Position des Fensters 5 Werte in der Ausgabe in der Dimension z der Ausgabe generiert. Diese Werte unterscheiden sich darin, welcher Teil des Faltungskerns verwendet wird. Für jede output-z-Koordinate wird ein separater dreidimensionaler Wertebereich verwendet. Sie können sich das als fünf separate Faltungen mit jeweils einem anderen Filter vorstellen.
Hier ist Pseudocode für eine 2D-Faltung mit Padding und Striding:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
Mit precision_config wird die Konfiguration der Genauigkeit angegeben. Die Stufe bestimmt, ob die Hardware versuchen soll, mehr Maschinencode-Befehle zu generieren, um bei Bedarf eine genauere Dtype-Emulation zu ermöglichen (z.B. die Emulation von f32 auf einer TPU, die nur bf16-Matmuls unterstützt). Mögliche Werte sind DEFAULT, HIGH und HIGHEST. Weitere Informationen finden Sie in den MXU-Abschnitten.
preferred_element_type ist ein Skalarelement von Ausgabetypen mit höherer/niedrigerer Genauigkeit, das für die Akkumulierung verwendet wird. preferred_element_type empfiehlt den Akkumulationstyp für den angegebenen Vorgang, dies ist jedoch nicht garantiert. So können einige Hardware-Back-Ends stattdessen in einem anderen Typ akkumulieren und in den bevorzugten Ausgabetyp konvertieren.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – Convolution.
ConvWithGeneralPadding
Siehe auch XlaBuilder::ConvWithGeneralPadding.
ConvWithGeneralPadding(lhs, rhs, window_strides, padding,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Entspricht Conv, wobei die Padding-Konfiguration explizit ist.
| Argumente | Typ | Semantik |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-dimensionales Array von Eingaben |
rhs
|
XlaOp
|
(n+2)-dimensionales Array mit Kernelgewichten |
window_strides |
ArraySlice<int64> |
n-dimensionales Array von Kernel-Strides |
padding
|
ArraySlice<
pair<int64,int64>> |
n-dimensionales Array mit (niedrig, hoch)-Padding |
feature_group_count
|
int64 | die Anzahl der Funktionsgruppen |
batch_group_count |
int64 | Anzahl der Batchgruppen |
precision_config
|
optional
PrecisionConfig |
Enum für den Genauigkeitsgrad |
preferred_element_type
|
optional
PrimitiveType |
enum des skalaren Elementtyps |
ConvWithGeneralDimensions
Siehe auch XlaBuilder::ConvWithGeneralDimensions.
ConvWithGeneralDimensions(lhs, rhs, window_strides, padding,
dimension_numbers, feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Entspricht Conv, wobei die Dimensionsnummern explizit angegeben sind.
| Argumente | Typ | Semantik |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-dimensionales Array von Eingaben |
rhs
|
XlaOp
|
(n+2)-dimensionales Array mit Kernelgewichten |
window_strides
|
ArraySlice<int64>
|
n-dimensionales Array mit Kernel-Strides |
padding |
Padding |
enum für Padding |
dimension_numbers
|
ConvolutionDimensionNumbers
|
Anzahl der Dimensionen |
feature_group_count
|
int64 | Anzahl der Featuregruppen |
batch_group_count
|
int64 | Anzahl der Batchgruppen |
precision_config
|
optional PrecisionConfig
|
Aufzählung für den Genauigkeitsgrad |
preferred_element_type
|
optional PrimitiveType
|
enum des skalaren Elementtyps |
ConvGeneral
Siehe auch XlaBuilder::ConvGeneral.
ConvGeneral(lhs, rhs, window_strides, padding, dimension_numbers,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Wie Conv, wobei die Dimensionsnummern und die Padding-Konfiguration explizit angegeben werden.
| Argumente | Typ | Semantik |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-dimensionales Array von Eingaben |
rhs
|
XlaOp
|
(n+2)-dimensionales Array mit Kernelgewichten |
window_strides
|
ArraySlice<int64>
|
n-dimensionales Array mit Kernel-Strides |
padding
|
ArraySlice<
pair<int64,int64>>
|
n-dimensionales Array mit (low, high)-Padding |
dimension_numbers
|
ConvolutionDimensionNumbers
|
Anzahl der Dimensionen |
feature_group_count
|
int64 | Anzahl der Featuregruppen |
batch_group_count
|
int64 | Anzahl der Batchgruppen |
precision_config
|
optional PrecisionConfig
|
Aufzählung für den Genauigkeitsgrad |
preferred_element_type
|
optional PrimitiveType
|
enum des skalaren Elementtyps |
ConvGeneralDilated
Siehe auch XlaBuilder::ConvGeneralDilated.
ConvGeneralDilated(lhs, rhs, window_strides, padding, lhs_dilation,
rhs_dilation, dimension_numbers, feature_group_count, batch_group_count,
precision_config, preferred_element_type, window_reversal)
Entspricht Conv, wobei die Padding-Konfiguration, die Dilation-Faktoren und die Dimensionsnummern explizit angegeben werden.
| Argumente | Typ | Semantik |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-dimensionales Array von Eingaben |
rhs
|
XlaOp
|
(n+2)-dimensionales Array mit Kernelgewichten |
window_strides
|
ArraySlice<int64>
|
n-dimensionales Array mit Kernel-Strides |
padding
|
ArraySlice<
pair<int64,int64>>
|
n-dimensionales Array mit (low, high)-Padding |
lhs_dilation
|
ArraySlice<int64>
|
Array mit Faktoren für die n-dimensionale Dilation der linken Seite |
rhs_dilation
|
ArraySlice<int64>
|
Array mit Faktoren für die n-dimensionale RHS-Erweiterung |
dimension_numbers
|
ConvolutionDimensionNumbers
|
Anzahl der Dimensionen |
feature_group_count
|
int64 | Anzahl der Featuregruppen |
batch_group_count
|
int64 | Anzahl der Batchgruppen |
precision_config
|
optional PrecisionConfig
|
Aufzählung für den Genauigkeitsgrad |
preferred_element_type
|
optional PrimitiveType
|
enum des skalaren Elementtyps |
window_reversal
|
optional vector<bool>
|
Flag, das verwendet wird, um die Dimension logisch umzukehren, bevor die Faltung angewendet wird. |
Kopieren
Siehe auch HloInstruction::CreateCopyStart.
Copy wird intern in zwei HLO-Anweisungen zerlegt: CopyStart und CopyDone. Copy sowie CopyStart und CopyDone dienen als Primitiven in HLO. Diese Vorgänge können in HLO-Dumps enthalten sein, sind aber nicht dafür vorgesehen, von Endnutzern manuell erstellt zu werden.
COS
Siehe auch XlaBuilder::Cos.
Elementweiser Kosinus x -> cos(x).
Cos(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
„cos“ unterstützt auch das optionale Argument result_accuracy:
Cos(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – Kosinus.
Cosh
Siehe auch XlaBuilder::Cosh.
Elementweiser hyperbolischer Kosinus x -> cosh(x).
Cosh(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Cosh unterstützt auch das optionale Argument result_accuracy:
Cosh(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
.
CustomCall
Siehe auch XlaBuilder::CustomCall.
Eine vom Nutzer bereitgestellte Funktion in einer Berechnung aufrufen.
Die Dokumentation zu Custom Calls finden Sie unter Entwicklerdetails – XLA Custom Calls.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – custom_call.
Div
Siehe auch XlaBuilder::Div.
Führt eine elementweise Division von Dividend lhs und Divisor rhs aus.
Div(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Bei einem Ganzzahl-Divisionsüberlauf (Division/Rest mit Vorzeichen/ohne Vorzeichen durch Null oder Division/Rest mit Vorzeichen von INT_SMIN mit -1) wird ein implementierungsdefinierter Wert ausgegeben.
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für „Div“ gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Div(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – divide.
Domain
Siehe auch HloInstruction::CreateDomain.
Domain kann in HLO-Dumps vorkommen, sollte aber nicht manuell von Endnutzern erstellt werden.
Punkt
Siehe auch XlaBuilder::Dot.
Dot(lhs, rhs, precision_config, preferred_element_type)
| Argumente | Typ | Semantik |
|---|---|---|
lhs |
XlaOp |
Array vom Typ T |
rhs |
XlaOp |
Array vom Typ T |
precision_config
|
optional
PrecisionConfig |
Enum für den Genauigkeitsgrad |
preferred_element_type
|
optional
PrimitiveType |
enum des skalaren Elementtyps |
Die genaue Semantik dieses Vorgangs hängt von den Rängen der Operanden ab:
| Eingabe | Ausgabe | Semantik |
|---|---|---|
vector [n] dot vector [n] |
Skalar | Skalarprodukt von Vektoren |
Matrix [m × k] dot Vektor [k] |
Vektor [m] | Matrix-Vektor-Multiplikation |
Matrix [m × k] dot Matrix [k × n] |
Matrix [m × n] | Matrix-Matrix-Multiplikation |
Bei der Operation wird die Summe der Produkte über die zweite Dimension von lhs (oder die erste, wenn sie 1 Dimension hat) und die erste Dimension von rhs berechnet. Das sind die „kontrahierten“ Dimensionen. Die kontrahierten Dimensionen von lhs und rhs müssen dieselbe Größe haben. In der Praxis kann sie verwendet werden, um Skalarprodukte zwischen Vektoren, Vektor-/Matrix-Multiplikationen oder Matrix-/Matrix-Multiplikationen auszuführen.
Mit precision_config wird die Konfiguration der Genauigkeit angegeben. Die Stufe bestimmt, ob die Hardware versuchen soll, mehr Maschinencode-Befehle zu generieren, um bei Bedarf eine genauere Dtype-Emulation zu ermöglichen (z.B. die Emulation von f32 auf einer TPU, die nur bf16-Matmuls unterstützt). Mögliche Werte sind DEFAULT, HIGH und HIGHEST. Weitere Informationen finden Sie in den MXU-Abschnitten.
preferred_element_type ist ein Skalarelement von Ausgabetypen mit höherer/niedrigerer Genauigkeit, das für die Akkumulierung verwendet wird. preferred_element_type empfiehlt den Akkumulationstyp für den angegebenen Vorgang, dies ist jedoch nicht garantiert. So können einige Hardware-Back-Ends stattdessen in einem anderen Typ akkumulieren und in den bevorzugten Ausgabetyp konvertieren.
Informationen zu StableHLO finden Sie unter StableHLO – dot.
DotGeneral
Siehe auch XlaBuilder::DotGeneral.
DotGeneral(lhs, rhs, dimension_numbers, precision_config,
preferred_element_type)
| Argumente | Typ | Semantik |
|---|---|---|
lhs |
XlaOp |
Array vom Typ T |
rhs |
XlaOp |
Array vom Typ T |
dimension_numbers
|
DotDimensionNumbers
|
Kontrahierungs- und Batch-Dimensionsnummern |
precision_config
|
optional
PrecisionConfig |
Aufzählung für den Genauigkeitsgrad |
preferred_element_type
|
optional
PrimitiveType |
enum des skalaren Elementtyps |
Ähnlich wie „Dot“, aber es können Kontraktions- und Batch-Dimensionsnummern für lhs und rhs angegeben werden.
| DotDimensionNumbers-Felder | Typ | Semantik |
|---|---|---|
lhs_contracting_dimensions
|
repeated int64 | lhs Kontrahierende Dimensionszahlen |
rhs_contracting_dimensions
|
repeated int64 | rhs Kontrahierende Dimensionszahlen |
lhs_batch_dimensions
|
repeated int64 | lhs Batchdimension
Nummern |
rhs_batch_dimensions
|
repeated int64 | rhs Batchdimension
Nummern |
Mit DotGeneral wird die Summe der Produkte über die in dimension_numbers angegebenen Kontraktionsdimensionen berechnet.
Die zugehörigen Kontraktionsdimensionsnummern aus lhs und rhs müssen nicht identisch sein, aber dieselben Dimensionsgrößen haben.
Beispiel mit kontrahierten Dimensionsnummern:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { { 6.0, 12.0},
{15.0, 30.0} }
Die zugehörigen Batch-Dimensionsnummern aus lhs und rhs müssen dieselben Dimensionsgrößen haben.
Beispiel mit Batch-Dimensionsnummern (Batchgröße 2, 2×2-Matrizen):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> {
{ {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| Eingabe | Ausgabe | Semantik |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | Batch-Matrixmultiplikation |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | Batch-Matrixmultiplikation |
Die resultierende Dimensionsnummer beginnt also mit der Batch-Dimension, dann mit der lhs-Dimension (nicht kontrahierend/nicht Batch) und schließlich mit der rhs-Dimension (nicht kontrahierend/nicht Batch).
Mit precision_config wird die Konfiguration der Genauigkeit angegeben. Die Stufe bestimmt, ob die Hardware versuchen soll, mehr Maschinencode-Befehle zu generieren, um bei Bedarf eine genauere Dtype-Emulation zu ermöglichen (z.B. die Emulation von f32 auf einer TPU, die nur bf16-Matmuls unterstützt). Mögliche Werte sind DEFAULT, HIGH und HIGHEST. Weitere Informationen finden Sie in den MXU-Abschnitten.
preferred_element_type ist ein Skalarelement von Ausgabetypen mit höherer/niedrigerer Genauigkeit, das für die Akkumulierung verwendet wird. preferred_element_type empfiehlt den Akkumulationstyp für den angegebenen Vorgang, dies ist jedoch nicht garantiert. So können einige Hardware-Back-Ends stattdessen in einem anderen Typ akkumulieren und in den bevorzugten Ausgabetyp konvertieren.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – dot_general.
ScaledDot
Siehe auch XlaBuilder::ScaledDot.
ScaledDot(lhs, lhs_scale, rhs, rhs_scale, dimension_number,
precision_config,preferred_element_type)
| Argumente | Typ | Semantik |
|---|---|---|
lhs |
XlaOp |
Array vom Typ T |
rhs |
XlaOp |
Array vom Typ T |
lhs_scale |
XlaOp |
Array vom Typ T |
rhs_scale |
XlaOp |
Array vom Typ T |
dimension_number
|
ScatterDimensionNumbers
|
Dimensionsnummern für Scatter-Vorgang |
precision_config
|
PrecisionConfig
|
Aufzählung für den Genauigkeitsgrad |
preferred_element_type
|
optional PrimitiveType
|
enum des skalaren Elementtyps |
Ähnlich wie DotGeneral.
Erstellt einen skalierten Punktvorgang mit den Operanden „lhs“, „lhs_scale“, „rhs“ und „rhs_scale“, wobei die Kontraktions- und Batchdimensionen in „dimension_numbers“ angegeben werden.
RaggedDot
Siehe auch XlaBuilder::RaggedDot.
Eine Aufschlüsselung der Berechnung von RaggedDot finden Sie unter StableHLO – chlo.ragged_dot.
DynamicReshape
Siehe auch XlaBuilder::DynamicReshape.
Dieser Vorgang ist funktional identisch mit reshape, aber die Ergebnisform wird dynamisch über output_shape angegeben.
DynamicReshape(operand, dim_sizes, new_size_bounds, dims_are_dynamic)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
N-dimensionales Array vom Typ T |
dim_sizes |
Vektor von XlaOP |
N-dimensionale Vektorgrößen |
new_size_bounds |
Vektor von int63 |
N-dimensionaler Vektor von Grenzen |
dims_are_dynamic |
Vektor von bool |
N-dimensionale dynamische Dimension |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – dynamic_reshape.
DynamicSlice
Siehe auch XlaBuilder::DynamicSlice.
Mit DynamicSlice wird ein Unterarray aus dem Eingabearray an der dynamischen start_indices extrahiert. Die Größe des Slices in jeder Dimension wird in size_indices übergeben. Damit wird der Endpunkt der exklusiven Slice-Intervalle in jeder Dimension angegeben: [start, start + size). Die Form von start_indices muss eindimensional sein. Die Größe der Dimension muss der Anzahl der Dimensionen von operand entsprechen.
DynamicSlice(operand, start_indices, slice_sizes)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
N-dimensionales Array vom Typ T |
start_indices
|
Sequenz von N XlaOp
|
Liste mit N Skalar-Ganzzahlen, die die Startindexe des Slices für jede Dimension enthalten. Der Wert muss größer oder gleich null sein. |
size_indices
|
ArraySlice<int64>
|
Liste mit N Ganzzahlen, die die Segmentgröße für jede Dimension enthält. Jeder Wert muss größer als null sein und „start“ + „size“ muss kleiner oder gleich der Größe der Dimension sein, um einen Umbruch modulo der Dimensionsgröße zu vermeiden. |
Die effektiven Slice-Indexe werden berechnet, indem die folgende Transformation für jeden Index i in [1, N) angewendet wird, bevor der Slice ausgeführt wird:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - slice_sizes[i])
So wird sichergestellt, dass der extrahierte Ausschnitt immer innerhalb der Grenzen des Operanden-Arrays liegt. Wenn sich der Slice vor der Transformation innerhalb der Grenzen befindet, hat die Transformation keine Auswirkungen.
1‑dimensionales Beispiel:
let a = {0.0, 1.0, 2.0, 3.0, 4.0};
let s = {2};
DynamicSlice(a, s, {2});
// Result: {2.0, 3.0}
2‑dimensionales Beispiel:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2});
//Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
Weitere Informationen zu StableHLO finden Sie unter StableHLO – dynamic_slice.
DynamicUpdateSlice
Siehe auch XlaBuilder::DynamicUpdateSlice.
DynamicUpdateSlice generiert ein Ergebnis, das dem Wert des Eingabearrays operand entspricht, wobei ein Segment update bei start_indices überschrieben wird.
Die Form von update bestimmt die Form des aktualisierten Unterarrays des Ergebnisses.
Die Form von start_indices muss eindimensional sein. Die Größe der Dimension muss der Anzahl der Dimensionen von operand entsprechen.
DynamicUpdateSlice(operand, update, start_indices)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
N-dimensionales Array vom Typ T |
update
|
XlaOp
|
N-dimensionales Array vom Typ T mit der Slice-Aktualisierung. Jede Dimension der Aktualisierungsform muss größer als null sein und „start“ + „update“ muss für jede Dimension kleiner oder gleich der Operandengröße sein, damit keine Aktualisierungsindexe außerhalb des gültigen Bereichs generiert werden. |
start_indices
|
Sequenz von N XlaOp
|
Liste mit N Skalar-Ganzzahlen, die die Startindexe des Slices für jede Dimension enthalten. Der Wert muss größer oder gleich null sein. |
Die effektiven Slice-Indexe werden berechnet, indem die folgende Transformation für jeden Index i in [1, N) angewendet wird, bevor der Slice ausgeführt wird:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
So wird sichergestellt, dass der aktualisierte Ausschnitt immer innerhalb der Grenzen des Operanden-Arrays liegt. Wenn sich der Slice vor der Transformation innerhalb der Grenzen befindet, hat die Transformation keine Auswirkungen.
1‑dimensionales Beispiel:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s)
// Result: {0.0, 1.0, 5.0, 6.0, 4.0}
2‑dimensionales Beispiel:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s)
// Result:
// { {0.0, 1.0, 2.0},
// {3.0, 12.0, 13.0},
// {6.0, 14.0, 15.0},
// {9.0, 16.0, 17.0} }
Weitere Informationen zu StableHLO finden Sie unter StableHLO – dynamic_update_slice.
Erf
Siehe auch XlaBuilder::Erf.
Elementweise Fehlerfunktion x -> erf(x), wobei:
\(\text{erf}(x) = \frac{2}{\sqrt{\pi} }\int_0^x e^{-t^2} \, dt\).
Erf(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Erf unterstützt auch das optionale Argument result_accuracy:
Erf(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Exp
Siehe auch XlaBuilder::Exp.
Elementweise natürliche Exponentialfunktion x -> e^x.
Exp(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
„Exp“ unterstützt auch das optionale Argument result_accuracy:
Exp(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – Exponential.
Expm1
Siehe auch XlaBuilder::Expm1.
Elementweise natürliche Exponentialfunktion minus 1 x -> e^x - 1.
Expm1(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
„expm1“ unterstützt auch das optionale result_accuracy-Argument:
Expm1(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Informationen zu StableHLO finden Sie unter StableHLO – exponential_minus_one.
FFT
Siehe auch XlaBuilder::Fft.
Der XLA-FFT-Vorgang implementiert die Vorwärts- und Rücktransformation der Fourier-Transformation für reelle und komplexe Ein-/Ausgaben. Es werden mehrdimensionale FFTs auf bis zu drei Achsen unterstützt.
Fft(operand, ftt_type, fft_length)
| Argumente | Typ | Semantik |
|---|---|---|
operand
|
XlaOp
|
Das Array, das wir einer Fourier-Transformation unterziehen. |
fft_type |
FftType |
Siehe die folgende Tabelle. |
fft_length
|
ArraySlice<int64>
|
Die Längen der Zeitachse der Achsen, die transformiert werden. Dies ist insbesondere für IRFFT erforderlich, um die innerste Achse richtig zu dimensionieren, da RFFT(fft_length=[16]) dieselbe Ausgabedimension wie RFFT(fft_length=[17]) hat. |
FftType |
Semantik |
|---|---|
FFT |
Führt die komplexe FFT vorwärts aus. Die Form ist unverändert. |
IFFT |
Inverse komplex-zu-komplex-FFT. Die Form ist unverändert. |
RFFT
|
Vorwärts-FFT von reell zu komplex. Die Form der innersten Achse wird auf fft_length[-1] // 2 + 1 reduziert, wenn fft_length[-1] ein Wert ungleich null ist. Dabei wird der umgekehrte konjugierte Teil des transformierten Signals über der Nyquist-Frequenz hinaus weggelassen. |
IRFFT
|
Inverse reell-zu-komplex-FFT (d.h. nimmt komplexe Zahlen entgegen und gibt reelle Zahlen zurück).
Die Form der innersten Achse wird auf fft_length[-1] erweitert, wenn fft_length[-1] ein Wert ungleich null ist. Der Teil des transformierten Signals über der Nyquist-Frequenz wird aus dem umgekehrten Konjugat der Einträge von 1 bis fft_length[-1] // 2 + 1 abgeleitet. |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – fft.
Mehrdimensionale FFT
Wenn mehr als ein fft_length angegeben wird, entspricht dies der Anwendung einer Kaskade von FFT-Vorgängen auf jede der innersten Achsen. Beachten Sie, dass bei den Fällen „real“ –> „complex“ und „complex“ –> „real“ die Transformation der innersten Achse (effektiv) zuerst durchgeführt wird (RFFT; zuletzt für IRFFT). Daher ändert sich die Größe der innersten Achse. Andere Achsentransformationen sind dann komplex –> komplex.
Implementierungsdetails
Die CPU-FFT basiert auf TensorFFT von Eigen. GPU FFT verwendet cuFFT.
Etage
Siehe auch XlaBuilder::Floor.
Elementweise Untergrenze x -> ⌊x⌋.
Floor(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – floor.
Fusion
Siehe auch HloInstruction::CreateFusion.
Der Fusion-Vorgang stellt HLO-Anweisungen dar und dient als Primitive in HLO.
Dieser Vorgang kann in HLO-Dumps enthalten sein, sollte aber nicht manuell von Endnutzern erstellt werden.
Erfassen
Mit dem XLA-Vorgang „gather“ werden mehrere Slices (jeweils mit einem potenziell unterschiedlichen Laufzeit-Offset) eines Eingabearrays zusammengefügt.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – gather.
Allgemeine Semantik
Siehe auch XlaBuilder::Gather.
Eine intuitivere Beschreibung finden Sie im Abschnitt „Informelle Beschreibung“ unten.
gather(operand, start_indices, dimension_numbers, slice_sizes,
indices_are_sorted)
| Argumente | Typ | Semantik |
|---|---|---|
operand
|
XlaOp
|
Das Array, aus dem die Daten stammen. |
start_indices
|
XlaOp
|
Array mit den Startindexen der Segmente, die wir erfassen. |
dimension_numbers
|
GatherDimensionNumbers
|
Die Dimension in start_indices, die die Startindexe „enthält“. Eine detaillierte Beschreibung finden Sie unten. |
slice_sizes
|
ArraySlice<int64>
|
slice_sizes[i] sind die Grenzen für den Slice in Dimension i. |
indices_are_sorted
|
bool
|
Gibt an, ob die Indexe garantiert vom Aufrufer sortiert werden. |
Der Einfachheit halber bezeichnen wir Dimensionen im Ausgabearray nicht als offset_dims, sondern als batch_dims.
Die Ausgabe ist ein Array mit batch_dims.size + offset_dims.size Dimensionen.
operand.rank muss der Summe von offset_dims.size und collapsed_slice_dims.size entsprechen. Außerdem muss slice_sizes.size gleich operand.rank sein.
Wenn index_vector_dim gleich start_indices.rank ist, gehen wir implizit davon aus, dass start_indices eine nachgestellte 1-Dimension hat. Wenn start_indices also die Form [6,7] hat und index_vector_dim gleich 2 ist, gehen wir implizit davon aus, dass die Form von start_indices gleich [6,7,1] ist.
Die Grenzen für das Ausgabearray entlang der Dimension i werden so berechnet:
Wenn
iinbatch_dimsvorhanden ist (d.h. für ein bestimmteskgleichbatch_dims[k]ist), werden die entsprechenden Dimensionsgrenzen ausstart_indices.shapeausgewählt undindex_vector_dimwird übersprungen (d.h.start_indices.shape.dims[k] wird ausgewählt, wennk<index_vector_dimist, undstart_indices.shape.dims[k+1] andernfalls).Wenn
iinoffset_dimsvorhanden ist (d.h. gleichoffset_dims[k] für ein bestimmtesk), wählen wir die entsprechende Grenze ausslice_sizesaus, nachdem wircollapsed_slice_dimsberücksichtigt haben (d.h. wir wählenadjusted_slice_sizes[k] aus, wobeiadjusted_slice_sizesslice_sizesmit den Grenzen an den Indexpositionencollapsed_slice_dimsist).
Formal wird der Operandenindex In, der einem bestimmten Ausgabindex Out entspricht, so berechnet:
Sei
G= {Out[k] forkinbatch_dims}. VerwendeG, um einen VektorSzu erstellen, sodassS[i] =start_indices[Combine(G,i)], wobei Combine(A, b) b an der Positionindex_vector_dimin A einfügt. Dies ist auch dann definiert, wennGleer ist: WennGleer ist, giltS=start_indices.Erstellen Sie einen Startindex,
Sin, inoperand, indem SieSmitstart_index_mapaufteilen.SGenauer gesagt:Sin[start_index_map[k]] =S[k], wennk<start_index_map.size.Sin[_] =0andernfalls.
Erstelle einen Index
Oininoperand, indem du die Indexe an den Offsetdimensionen inOutgemäß demcollapsed_slice_dims-Satz verteilst. Genauer gesagt:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]], wennk<offset_dims.size(remapped_offset_dimswird unten definiert).Oin[_] =0andernfalls.
InistOin+Sin, wobei + die elementweise Addition ist.
remapped_offset_dims ist eine monotone Funktion mit dem Definitionsbereich [0, offset_dims.size) und dem Wertebereich [0, operand.rank) \ collapsed_slice_dims. Beispiel: Wenn offset_dims.size gleich 4, operand.rank gleich 6 und collapsed_slice_dims gleich {0, 2} ist, dann ist remapped_offset_dims gleich {0→1, 1→3, 2→4, 3→5}.
Wenn indices_are_sorted auf „true“ gesetzt ist, kann XLA davon ausgehen, dass start_indices vom Nutzer sortiert wurden (in aufsteigender Reihenfolge, nachdem die Werte gemäß start_index_map verteilt wurden). Andernfalls sind die Semantik implementierungsdefiniert.
Informelle Beschreibung und Beispiele
Informell entspricht jeder Index Out im Ausgabearray einem Element E im Operandenarray, das so berechnet wird:
Wir verwenden die Batchdimensionen in
Out, um einen Startindex ausstart_indicesabzurufen.Wir verwenden
start_index_map, um den Startindex (dessen Größe möglicherweise kleiner als operand.rank ist) einem „vollständigen“ Startindex inoperandzuzuordnen.Wir schneiden dynamisch einen Slice mit der Größe
slice_sizesaus dem vollständigen Startindex heraus.Wir passen das Segment an, indem wir die
collapsed_slice_dims-Dimensionen reduzieren. Da alle Dimensionen für zusammengefasste Slices eine Grenze von 1 haben müssen, ist diese Umformung immer zulässig.Wir verwenden die Offsetdimensionen in
Out, um in diesen Slice zu indexieren und das EingabeelementEabzurufen, das dem AusgabeelementOutentspricht.
In allen folgenden Beispielen ist index_vector_dim auf start_indices.rank – 1 festgelegt. Interessantere Werte für index_vector_dim ändern die Operation nicht grundlegend, machen die visuelle Darstellung aber umständlicher.
Um zu verstehen, wie alles zusammenpasst, sehen wir uns ein Beispiel an, in dem 5 Slices der Form [8,6] aus einem [16,11]-Array abgerufen werden. Die Position eines Slice im [16,11]-Array kann als Indexvektor der Form S64[2] dargestellt werden. Die Menge der fünf Positionen kann also als S64[5,2]-Array dargestellt werden.
Das Verhalten des Gather-Vorgangs kann dann als Indexumwandlung dargestellt werden, die [G,O0,O1], einen Index in der Ausgabedimension, verwendet und ihn auf folgende Weise einem Element im Eingabearray zuordnet:
Zuerst wird mit G ein (X,Y)-Vektor aus dem Array mit den Gather-Indizes ausgewählt.
Das Element im Ausgabearray am Index [G,O0,O1] ist dann das Element im Eingabearray am Index [X+O0,Y+O1].
slice_sizes ist [8,6], was den Bereich von O0 und O1 bestimmt. Dies wiederum bestimmt die Grenzen des Segments.
Dieser Sammelvorgang fungiert als dynamischer Batch-Slice mit G als Batch-Dimension.
Die Gather-Indizes können mehrdimensional sein. Eine allgemeinere Version des obigen Beispiels mit einem „gather indices“-Array der Form [4,5,2] würde Indexe so übersetzen:
Auch hier fungiert G0 als dynamischer Batch-Slice und G1 als Batch-Dimensionen. Die Segmentgröße ist weiterhin [8,6].
Der Gather-Vorgang in XLA verallgemeinert die oben beschriebene informelle Semantik auf folgende Weise:
Wir können konfigurieren, welche Dimensionen in der Ausgabedimension die Offsetdimensionen sind (Dimensionen mit
O0,O1im letzten Beispiel). Die Batchdimensionen der Ausgabe (Dimensionen mitG0,G1im letzten Beispiel) sind die Ausgabedimensionen, die keine Offsetdimensionen sind.Die Anzahl der Ausgabedimensionen, die explizit in der Ausgabeform vorhanden sind, kann kleiner sein als die Anzahl der Eingabedimensionen. Diese „fehlenden“ Dimensionen, die explizit als
collapsed_slice_dimsaufgeführt sind, müssen eine Slice-Größe von1haben. Da sie eine Segmentgröße von1haben, ist der einzige gültige Index für sie0. Das Auslassen führt daher nicht zu Unklarheiten.Das aus dem Array „Gather Indices“ extrahierte Segment ((
X,Y) im letzten Beispiel) kann weniger Elemente als die Anzahl der Dimensionen des Eingabearrays haben. Eine explizite Zuordnung gibt an, wie der Index erweitert werden soll, damit er dieselbe Anzahl von Dimensionen wie die Eingabe hat.
Als letztes Beispiel verwenden wir (2) und (3), um tf.gather_nd zu implementieren:
G0 und G1 werden wie gewohnt verwendet, um einen Startindex aus dem Array der Gather-Indizes herauszuschneiden. Der Startindex hat jedoch nur ein Element, X. Ebenso gibt es nur einen Ausgabeversetzungsindex mit dem Wert O0. Bevor sie jedoch als Indexe in das Eingabearray verwendet werden, werden sie gemäß „Gather Index Mapping“ (start_index_map in der formalen Beschreibung) und „Offset Mapping“ (remapped_offset_dims in der formalen Beschreibung) in [X,0] bzw. [0,O0] erweitert, was zu [X,O0] führt. Mit anderen Worten: Der Ausgabewertindex [G0,G1,O0] wird dem Eingabewertindex [GatherIndices[G0,G1,0],O0] zugeordnet, was uns die Semantik für tf.gather_nd liefert.
slice_sizes für diesen Fall ist [1,11]. Intuitiv bedeutet das, dass mit jedem Index X im Array „gather_indices“ eine ganze Zeile ausgewählt wird und das Ergebnis die Verkettung aller dieser Zeilen ist.
GetDimensionSize
Siehe auch XlaBuilder::GetDimensionSize.
Gibt die Größe der angegebenen Dimension des Operanden zurück. Der Operand muss ein Array sein.
GetDimensionSize(operand, dimension)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
n-dimensionales Eingabearray |
dimension
|
int64
|
Ein Wert im Intervall [0, n), der die Dimension angibt. |
Informationen zu StableHLO finden Sie unter StableHLO – get_dimension_size.
GetTupleElement
Siehe auch XlaBuilder::GetTupleElement.
Indizes in ein Tupel mit einem zur Kompilierzeit konstanten Wert.
Der Wert muss eine Kompilierzeitkonstante sein, damit die Typinferenz den Typ des resultierenden Werts bestimmen kann.
Das entspricht std::get<int N>(t) in C++. Konzeptionell:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
Siehe auch tf.tuple.
GetTupleElement(tuple_data, index)
| Argument | Typ | Semantik |
|---|---|---|
tuple_data |
XlaOP |
Das Tupel |
index |
int64 |
Index der Tupelform |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – get_tuple_element.
Imag
Siehe auch XlaBuilder::Imag.
Elementweiser imaginärer Teil einer komplexen (oder reellen) Form. x -> imag(x). Wenn der Operand ein Gleitkommatyp ist, wird 0 zurückgegeben.
Imag(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – imag.
Infeed
Siehe auch XlaBuilder::Infeed.
Infeed(shape, config)
| Argument | Typ | Semantik |
|---|---|---|
shape
|
Shape
|
Form der Daten, die über die Infeed-Schnittstelle gelesen werden. Das Feld „layout“ der Form muss so festgelegt werden, dass es mit dem Layout der Daten übereinstimmt, die an das Gerät gesendet werden. Andernfalls ist das Verhalten nicht definiert. |
config |
optional string |
Konfiguration des Vorgangs. |
Liest ein einzelnes Datenelement aus der impliziten Infeed-Streaming-Schnittstelle des Geräts, interpretiert die Daten als die angegebene Form und ihr Layout und gibt ein XlaOp der Daten zurück. Mehrere Infeed-Vorgänge sind in einer Berechnung zulässig, aber es muss eine Gesamtordnung zwischen den Infeed-Vorgängen geben. Die beiden Infeed im folgenden Code haben beispielsweise eine Gesamtordnung, da eine Abhängigkeit zwischen den while-Schleifen besteht.
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
Verschachtelte Tupelformen werden nicht unterstützt. Bei einer leeren Tupelform ist der Infeed-Vorgang effektiv ein No-Op und wird fortgesetzt, ohne Daten aus dem Infeed des Geräts zu lesen.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – Infeed.
Iota
Siehe auch XlaBuilder::Iota.
Iota(shape, iota_dimension)
Erstellt ein konstantes Literal auf dem Gerät anstelle eines potenziell großen Host-Transfers. Erstellt ein Array mit der angegebenen Form, das Werte ab null enthält, die entlang der angegebenen Dimension um eins erhöht werden. Bei Gleitkommatypen entspricht das erstellte Array ConvertElementType(Iota(...)), wobei Iota ein Ganzzahltyp ist und die Konvertierung in den Gleitkommatyp erfolgt.
| Argumente | Typ | Semantik |
|---|---|---|
shape |
Shape |
Form des Arrays, das von Iota() erstellt wurde |
iota_dimension |
int64 |
Die Dimension, entlang derer inkrementiert werden soll. |
Beispiel: Iota(s32[4, 8], 0) gibt Folgendes zurück:
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
Iota(s32[4, 8], 1) für Retouren
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
Weitere Informationen zu StableHLO finden Sie unter StableHLO – iota.
IsFinite
Siehe auch XlaBuilder::IsFinite.
Prüft, ob jedes Element von operand endlich ist, d.h. nicht positiv oder negativ unendlich und nicht NaN ist. Gibt ein Array von PRED-Werten mit derselben Form wie die Eingabe zurück, wobei jedes Element true ist, wenn das entsprechende Eingabeelement endlich ist.
IsFinite(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – is_finite.
Log
Siehe auch XlaBuilder::Log.
Elementweiser natürlicher Logarithmus x -> ln(x).
Log(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
„Log“ unterstützt auch das optionale Argument result_accuracy:
Log(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – log.
Log1p
Siehe auch XlaBuilder::Log1p.
Elementweiser verschobener natürlicher Logarithmus x -> ln(1+x).
Log1p(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Die Funktion „log1p“ unterstützt auch das optionale Argument result_accuracy:
Log1p(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – log_plus_one.
Logistisch
Siehe auch XlaBuilder::Logistic.
Elementweise Berechnung der logistischen Funktion x -> logistic(x).
Logistic(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Die Funktion „logistic“ unterstützt auch das optionale Argument result_accuracy:
Logistic(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – Logistik.
Karte
Siehe auch XlaBuilder::Map.
Map(operands..., computation, dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
operands |
Folge von N XlaOps |
N Arrays vom Typ T0..T{N-1} |
computation
|
XlaComputation
|
Berechnung vom Typ T_0, T_1,
.., T_{N + M -1} -> S mit N Parametern vom Typ T und M Parametern vom beliebigen Typ. |
dimensions |
int64-Array |
Array von Kartendimensionen |
static_operands
|
Folge von N XlaOps
|
Statische Vorgänge für den Kartenvorgang |
Wendet eine Skalarfunktion auf die angegebenen operands-Arrays an. Das Ergebnis ist ein Array mit denselben Dimensionen, in dem jedes Element das Ergebnis der zugeordneten Funktion ist, die auf die entsprechenden Elemente in den Eingabearrays angewendet wird.
Die zugeordnete Funktion ist eine beliebige Berechnung mit der Einschränkung, dass sie N Eingaben vom skalaren Typ T und eine einzelne Ausgabe vom Typ S hat. Die Ausgabe hat dieselben Dimensionen wie die Operanden, mit der Ausnahme, dass der Elementtyp T durch S ersetzt wird.
Beispiel: Map(op1, op2, op3, computation, par1) ordnet elem_out <-
computation(elem1, elem2, elem3, par1) an jedem (mehrdimensionalen) Index in den Eingabearrays zu, um das Ausgabearray zu erstellen.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – Map.
Max.
Siehe auch XlaBuilder::Max.
Führt die elementweise Max-Operation für die Tensoren lhs und rhs aus.
Max(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für Max gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Max(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – Maximum.
Min.
Siehe auch XlaBuilder::Min.
Führt eine elementweise Min-Operation für lhs und rhs aus.
Min(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für Min gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Min(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – Minimum.
Mul
Siehe auch XlaBuilder::Mul.
Berechnet das elementweise Produkt von lhs und rhs.
Mul(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für Mul gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Mul(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – multiply.
Neg
Siehe auch XlaBuilder::Neg.
Elementweise Negation x -> -x.
Neg(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – negate.
Nicht
Siehe auch XlaBuilder::Not.
Elementweises logisches NICHT x -> !(x).
Not(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Informationen zu StableHLO finden Sie unter StableHLO – nicht.
OptimizationBarrier
Siehe auch XlaBuilder::OptimizationBarrier.
Verhindert, dass Berechnungen über die Barriere hinweg verschoben werden.
OptimizationBarrier(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Sorgt dafür, dass alle Eingaben vor allen Operatoren ausgewertet werden, die von den Ausgaben der Barriere abhängen.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – optimization_barrier.
Oder
Siehe auch XlaBuilder::Or.
Führt ein elementweises ODER von lhs und rhs aus .
Or(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für „Oder“ gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Or(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Informationen zu StableHLO finden Sie unter StableHLO – oder.
Ausgang
Siehe auch XlaBuilder::Outfeed.
Schreibt Eingaben in den Outfeed.
Outfeed(operand, shape_with_layout, outfeed_config)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Array vom Typ T |
shape_with_layout |
Shape |
Definiert das Layout der übertragenen Daten |
outfeed_config |
string |
Konstante der Konfiguration für die Outfeed-Anweisung |
shape_with_layout gibt die angelegte Form an, die wir ausgeben möchten.
Informationen zu StableHLO finden Sie unter StableHLO – Outfeed.
Pad
Siehe auch XlaBuilder::Pad.
Pad(operand, padding_value, padding_config)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Array vom Typ T |
padding_value
|
XlaOp
|
Skalar vom Typ T, mit dem der hinzugefügte Padding-Bereich gefüllt werden soll |
padding_config
|
PaddingConfig
|
Abstand an beiden Rändern (niedrig, hoch) und zwischen den Elementen jeder Dimension |
Erweitert das angegebene operand-Array durch Auffüllen um das Array herum sowie zwischen den Elementen des Arrays mit dem angegebenen padding_value. padding_config gibt die Menge des Rand- und Innen-Paddings für jede Dimension an.
PaddingConfig ist ein wiederholtes Feld von PaddingConfigDimension, das für jede Dimension drei Felder enthält: edge_padding_low, edge_padding_high und interior_padding.
Mit edge_padding_low und edge_padding_high wird die Menge an Padding angegeben, die jeweils am unteren Ende (neben Index 0) und am oberen Ende (neben dem höchsten Index) jeder Dimension hinzugefügt wird. Der Betrag des Rand-Paddings kann negativ sein. Der absolute Wert des negativen Paddings gibt die Anzahl der Elemente an, die aus der angegebenen Dimension entfernt werden sollen.
interior_padding gibt den Abstand zwischen zwei Elementen in jeder Dimension an. Er darf nicht negativ sein. Die innere Auffüllung erfolgt logisch vor der Auffüllung von Rändern. Bei negativer Auffüllung von Rändern werden Elemente also aus dem inneren aufgefüllten Operanden entfernt.
Dieser Vorgang ist ein No-Op, wenn alle Edge-Padding-Paare (0, 0) und alle Werte für das innere Padding 0 sind. Die Abbildung unten zeigt Beispiele für verschiedene edge_padding- und interior_padding-Werte für ein zweidimensionales Array.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – pad.
Parameter
Siehe auch XlaBuilder::Parameter.
Parameter steht für eine Argumenteingabe für eine Berechnung.
PartitionID
Siehe auch XlaBuilder::BuildPartitionId.
Erstellt partition_id des aktuellen Prozesses.
PartitionID(shape)
| Argumente | Typ | Semantik |
|---|---|---|
shape |
Shape |
Form der Daten |
PartitionID kann in HLO-Dumps vorkommen, sollte aber nicht manuell von Endnutzern erstellt werden.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – partition_id.
PopulationCount
Siehe auch XlaBuilder::PopulationCount.
Berechnet die Anzahl der Bits, die in jedem Element von operand festgelegt sind.
PopulationCount(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Informationen zu StableHLO finden Sie unter StableHLO – popcnt.
Pow
Siehe auch XlaBuilder::Pow.
Führt die elementweise Potenzierung von lhs mit rhs aus.
Pow(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für Pow gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Pow(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Informationen zu StableHLO finden Sie unter StableHLO – power.
Real
Siehe auch XlaBuilder::Real.
Elementweiser Realteil einer komplexen (oder reellen) Form. x -> real(x). Wenn der Operand ein Gleitkommatyp ist, gibt Real denselben Wert zurück.
Real(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – real.
Recv
Siehe auch XlaBuilder::Recv.
Recv, RecvWithTokens und RecvToHost sind Vorgänge, die als Kommunikationsprimitive in HLO dienen. Diese Vorgänge sind in HLO-Dumps in der Regel Teil der Low-Level-Ein-/Ausgabe oder der geräteübergreifenden Übertragung, sie sind jedoch nicht für die manuelle Erstellung durch Endnutzer vorgesehen.
Recv(shape, handle)
| Argumente | Typ | Semantik |
|---|---|---|
shape |
Shape |
Form der zu empfangenden Daten |
handle |
ChannelHandle |
Eindeutige Kennung für jedes Sende-/Empfangspaar |
Empfängt Daten der angegebenen Form von einer Send-Anweisung in einer anderen Berechnung, die dasselbe Channel-Handle verwendet. Gibt einen XlaOp für die empfangenen Daten zurück.
Informationen zu StableHLO finden Sie unter StableHLO – recv.
RecvDone
Siehe auch HloInstruction::CreateRecv und HloInstruction::CreateRecvDone.
Ähnlich wie bei Send steht die Client-API des Vorgangs Recv für die synchrone Kommunikation. Die Anweisung wird jedoch intern in zwei HLO-Anweisungen (Recv und RecvDone) zerlegt, um asynchrone Datenübertragungen zu ermöglichen.
Recv(const Shape& shape, int64 channel_id)
Weist Ressourcen zu, die zum Empfangen von Daten aus einem Send-Befehl mit derselben channel_id erforderlich sind. Gibt einen Kontext für die zugewiesenen Ressourcen zurück, der von einer nachfolgenden RecvDone-Anweisung verwendet wird, um auf den Abschluss der Datenübertragung zu warten. Der Kontext ist ein Tupel aus {Empfangspuffer (Form), Anforderungs-ID (U32)} und kann nur von einem RecvDone-Befehl verwendet werden.
Wartet bei einem Kontext, der durch eine Recv-Anweisung erstellt wurde, darauf, dass die Datenübertragung abgeschlossen ist, und gibt die empfangenen Daten zurück.
Einschränken
Siehe auch XlaBuilder::Reduce.
Wendet eine Reduktionsfunktion parallel auf ein oder mehrere Arrays an.
Reduce(operands..., init_values..., computation, dimensions_to_reduce)
| Argumente | Typ | Semantik |
|---|---|---|
operands
|
Sequenz von N XlaOp
|
N Arrays vom Typ T_0,...,
T_{N-1}. |
init_values
|
Sequenz von N XlaOp
|
N Skalare vom Typ T_0,..., T_{N-1}. |
computation
|
XlaComputation
|
Berechnung vom Typ
T_0,..., T_{N-1}, T_0,
...,T_{N-1} ->
Collate(T_0,...,
T_{N-1}). |
dimensions_to_reduce
|
int64-Array
|
Ungeordnetes Array mit Dimensionen, die reduziert werden sollen. |
Wobei:
- N muss größer oder gleich 1 sein.
- Die Berechnung muss „ungefähr“ assoziativ sein (siehe unten).
- Alle Eingabearrays müssen dieselben Dimensionen haben.
- Alle Anfangswerte müssen unter
computationeine Identität bilden. - Wenn
N = 1, istCollate(T)T. - Wenn
N > 1, istCollate(T_0, ..., T_{N-1})ein Tupel ausN-Elementen vom TypT.
Bei dieser Operation werden eine oder mehrere Dimensionen jedes Eingabearrays in Skalare reduziert.
Die Anzahl der Dimensionen jedes zurückgegebenen Arrays ist number_of_dimensions(operand) - len(dimensions). Die Ausgabe des Vorgangs ist Collate(Q_0, ..., Q_N), wobei Q_i ein Array vom Typ T_i ist. Die Dimensionen werden unten beschrieben.
Verschiedene Backends dürfen die Berechnung der Reduzierung neu zuordnen. Dies kann zu numerischen Unterschieden führen, da einige Reduktionsfunktionen wie die Addition für Gleitkommazahlen nicht assoziativ sind. Wenn der Bereich der Daten jedoch begrenzt ist, ist die Gleitkommaaddition für die meisten praktischen Anwendungen assoziativ genug.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – reduce.
Beispiele
Wenn Sie ein eindimensionales Array mit Werten [10, 11,
12, 13] mit der Reduzierungsfunktion f (das ist computation) reduzieren, kann das so berechnet werden:
f(10, f(11, f(12, f(init_value, 13)))
Es gibt aber auch viele andere Möglichkeiten, z.B.:
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
Im Folgenden finden Sie ein grobes Pseudocode-Beispiel für die Implementierung der Reduzierung, wobei die Summe als Reduzierungsberechnung mit einem Anfangswert von 0 verwendet wird.
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
Hier ein Beispiel für das Reduzieren eines 2D-Arrays (einer Matrix). Die Form hat zwei Dimensionen, Dimension 0 mit der Größe 2 und Dimension 1 mit der Größe 3:
Ergebnisse der Reduzierung von Dimension 0 oder 1 mit einer „add“-Funktion:
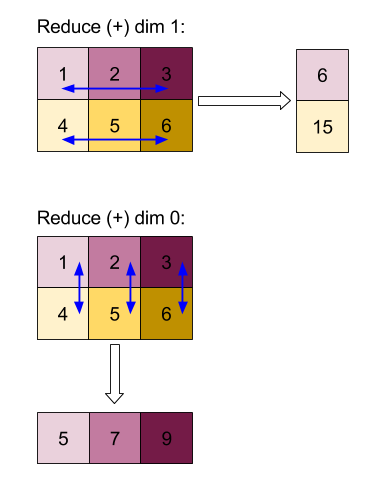
Beachten Sie, dass beide Reduzierungsergebnisse eindimensionale Arrays sind. Im Diagramm wird das eine als Spalte und das andere als Zeile dargestellt, um die Übersichtlichkeit zu erhöhen.
Hier ist ein komplexeres Beispiel mit einem 3D-Array. Die Anzahl der Dimensionen ist 3, Dimension 0 hat die Größe 4, Dimension 1 die Größe 2 und Dimension 2 die Größe 3. Der Einfachheit halber werden die Werte 1 bis 6 in Dimension 0 repliziert.
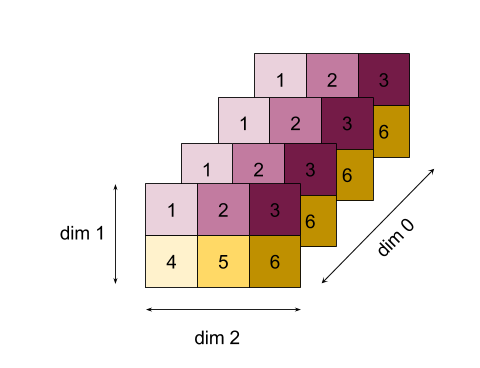
Ähnlich wie beim 2D-Beispiel können wir nur eine Dimension reduzieren. Wenn wir beispielsweise Dimension 0 reduzieren, erhalten wir ein zweidimensionales Array, in dem alle Werte über Dimension 0 in einen Skalar eingefügt wurden:
| 4 8 12 |
| 16 20 24 |
Wenn wir Dimension 2 reduzieren, erhalten wir ebenfalls ein zweidimensionales Array, in dem alle Werte aus Dimension 2 in einen Skalar gefaltet wurden:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
Die relative Reihenfolge der verbleibenden Dimensionen in der Eingabe wird in der Ausgabe beibehalten. Da sich die Anzahl der Dimensionen ändert, können einigen Dimensionen jedoch neue Zahlen zugewiesen werden.
Wir können auch mehrere Dimensionen reduzieren. Wenn Sie die Dimensionen 0 und 1 reduzieren, erhalten Sie das 1D-Array [20, 28, 36].
Wenn das 3D-Array über alle Dimensionen hinweg reduziert wird, ergibt sich der Skalar 84.
Variadic Reduce
Bei N > 1 ist die Anwendung der Reduce-Funktion etwas komplexer, da sie gleichzeitig auf alle Eingaben angewendet wird. Die Operanden werden in der folgenden Reihenfolge für die Berechnung bereitgestellt:
- Ausführen des reduzierten Werts für den ersten Operanden
- …
- Reduzierter Wert für den N-ten Operanden wird ausgeführt
- Eingabewert für den ersten Operanden
- …
- Eingabewert für den N-ten Operanden
Betrachten Sie beispielsweise die folgende Reduzierungsfunktion, mit der das Maximum und das Argmax eines eindimensionalen Arrays parallel berechnet werden können:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
Für 1‑D-Eingabearrays V = Float[N], K = Int[N] und Initialisierungswerte I_V = Float, I_K = Int entspricht das Ergebnis f_(N-1) der Reduzierung über die einzige Eingabedimension der folgenden rekursiven Anwendung:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
Wenn diese Reduzierung auf ein Array von Werten und ein Array von sequenziellen Indexen (d.h. iota) angewendet wird, werden die Arrays gemeinsam durchlaufen und ein Tupel mit dem Maximalwert und dem entsprechenden Index zurückgegeben.
ReducePrecision
Siehe auch XlaBuilder::ReducePrecision.
Modelliert die Auswirkungen der Konvertierung von Gleitkommawerten in ein Format mit niedrigerer Genauigkeit (z. B. IEEE-FP16) und zurück in das ursprüngliche Format. Die Anzahl der Exponenten- und Mantissenbits im Format mit niedrigerer Genauigkeit kann beliebig angegeben werden. Allerdings werden möglicherweise nicht alle Bitgrößen auf allen Hardwareimplementierungen unterstützt.
ReducePrecision(operand, exponent_bits, mantissa_bits)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Array vom Gleitkommatyp T. |
exponent_bits |
int32 |
Anzahl der Exponentenbits im Format mit geringerer Genauigkeit |
mantissa_bits |
int32 |
Anzahl der Mantissenbits im Format mit niedrigerer Genauigkeit |
Das Ergebnis ist ein Array vom Typ T. Die Eingabewerte werden auf den nächsten Wert gerundet, der mit der angegebenen Anzahl von Mantissenbits dargestellt werden kann (mit der Semantik „ties to even“). Alle Werte, die den durch die Anzahl der Exponentenbits angegebenen Bereich überschreiten, werden auf „positive“ oder „negative infinity“ (plus oder minus unendlich) begrenzt. NaN-Werte werden beibehalten, können aber in kanonische NaN-Werte umgewandelt werden.
Das Format mit niedrigerer Genauigkeit muss mindestens ein Exponentenbit haben, um einen Nullwert von einem Unendlichwert zu unterscheiden, da beide eine Nullmantisse haben. Außerdem muss es eine nicht negative Anzahl von Mantissenbits haben. Die Anzahl der Exponenten- oder Mantissenbits kann den entsprechenden Wert für den Typ T überschreiten. Der entsprechende Teil der Konvertierung ist dann einfach ein No-Op.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – reduce_precision.
ReduceScatter
Siehe auch XlaBuilder::ReduceScatter.
„ReduceScatter“ ist ein kollektiver Vorgang, der effektiv „AllReduce“ ausführt und das Ergebnis dann aufteilt, indem es in shard_count Blöcke entlang der scatter_dimension aufgeteilt wird. Die Replik i in der Replikgruppe empfängt den ith-Shard.
ReduceScatter(operand, computation, scatter_dimension, shard_count,
replica_groups, channel_id, layout, use_global_device_ids)
| Argumente | Typ | Semantik |
|---|---|---|
operand
|
XlaOp
|
Array oder nicht leeres Tupel von Arrays, die über Replikate hinweg reduziert werden sollen. |
computation |
XlaComputation |
Berechnung der Reduzierung |
scatter_dimension |
int64 |
Dimension für die Streuung. |
shard_count
|
int64
|
Anzahl der Blöcke, auf die scatter_dimension aufgeteilt werden soll |
replica_groups
|
ReplicaGroup vector
|
Gruppen, zwischen denen die Reduzierungen vorgenommen werden |
channel_id
|
optional
ChannelHandle |
Optionale Kanal-ID für die modulübergreifende Kommunikation |
layout
|
optional Layout
|
Vom Nutzer angegebenes Speicherlayout |
use_global_device_ids |
optional bool |
Vom Nutzer angegebenes Flag |
- Wenn
operandein Tupel von Arrays ist, wird die Reduce-Scatter-Operation für jedes Element des Tupels ausgeführt. replica_groupsist eine Liste von Replikagruppen, zwischen denen die Reduzierung erfolgt. Die Replikat-ID für das aktuelle Replikat kann mitReplicaIdabgerufen werden. Die Reihenfolge der Replikate in jeder Gruppe bestimmt die Reihenfolge, in der das All-Reduce-Ergebnis verteilt wird.replica_groupsmuss entweder leer sein (in diesem Fall gehören alle Replikate zu einer einzelnen Gruppe) oder dieselbe Anzahl an Elementen wie die Anzahl der Replikate enthalten. Wenn es mehrere Replikagruppen gibt, müssen sie alle dieselbe Größe haben. Beireplica_groups = {0, 2}, {1, 3}wird beispielsweise eine Reduzierung zwischen den Replikaten0und2sowie1und3durchgeführt und das Ergebnis dann verteilt.shard_countist die Größe jeder Replikagruppe. Wir benötigen diese Informationen, wennreplica_groupsleer ist. Wennreplica_groupsnicht leer ist, mussshard_countder Größe jeder Replikagruppe entsprechen.channel_idwird für die modulübergreifende Kommunikation verwendet: Nurreduce-scatter-Vorgänge mit demselbenchannel_idkönnen miteinander kommunizieren.layoutWeitere Informationen zu Layouts finden Sie unter xla::shapes.use_global_device_idsist ein vom Nutzer angegebenes Flag. Wennfalse(Standard) verwendet wird, sind die Zahlen inreplica_groupsReplicaId. Wenntrueverwendet wird, stellen diereplica_groupseine globale ID von (ReplicaID*partition_count+partition_id) dar. Beispiel:- Bei 2 Replikaten und 4 Partitionen
- replica_groups={ {0,1,4,5},{2,3,6,7} } and use_global_device_ids=true
- group[0] = (0,0), (0,1), (1,0), (1,1)
- group[1] = (0,2), (0,3), (1,2), (1,3)
- Dabei ist jedes Paar (replica_id, partition_id).
Die Ausgabedimensionen entsprechen den Eingabedimensionen, wobei die scatter_dimension-Dimension shard_count-mal kleiner ist. Wenn es beispielsweise zwei Replikate gibt und der Operand auf den beiden Replikaten die Werte [1.0, 2.25] bzw. [3.0, 5.25] hat, ist der Ausgabewert dieses Vorgangs, bei dem scatter_dim gleich 0 ist, [4.0] für das erste Replikat und [7.5] für das zweite Replikat.
Informationen zu StableHLO finden Sie unter StableHLO – reduce_scatter.
ReduceScatter – Beispiel 1 – StableHLO
Im obigen Beispiel sind zwei Replikate am ReduceScatter beteiligt. Auf jedem Replikat hat der Operand die Form f32[2,4]. Auf den Replikaten wird eine All-Reduce-Operation (Summe) ausgeführt, die auf jedem Replikat einen reduzierten Wert der Form f32[2,4] erzeugt. Dieser reduzierte Wert wird dann entlang der Dimension 1 in zwei Teile aufgeteilt, sodass jeder Teil die Form f32[2,2] hat. Jedes Replikat in der Prozessgruppe erhält den Teil, der seiner Position in der Gruppe entspricht. Daher hat die Ausgabe auf jedem Replikat die Form f32[2,2].
ReduceWindow
Siehe auch XlaBuilder::ReduceWindow.
Wendet eine Reduktionsfunktion auf alle Elemente in jedem Fenster einer Sequenz von N mehrdimensionalen Arrays an und gibt ein einzelnes oder ein Tupel von N mehrdimensionalen Arrays aus. Jedes Ausgabearray hat dieselbe Anzahl von Elementen wie die Anzahl der gültigen Positionen des Fensters. Ein Pooling-Layer kann als ReduceWindow ausgedrückt werden. Ähnlich wie bei Reduce wird die angewendete computation immer links von der init_values übergeben.
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| Argumente | Typ | Semantik |
|---|---|---|
operands
|
N XlaOps
|
Eine Sequenz von N mehrdimensionalen Arrays vom Typ T_0,..., T_{N-1}, die jeweils die Grundfläche darstellen, auf der das Fenster platziert wird. |
init_values
|
N XlaOps
|
Die N Startwerte für die Reduzierung, einer für jeden der N Operanden. Weitere Informationen finden Sie unter Reduzieren. |
computation
|
XlaComputation
|
Reduktionsfunktion vom Typ T_0,
..., T_{N-1}, T_0, ..., T_{N-1}
-> Collate(T_0, ..., T_{N-1}), die auf Elemente in jedem Fenster aller Eingabeoperanden angewendet werden soll. |
window_dimensions
|
ArraySlice<int64>
|
Array von Ganzzahlen für Fensterdimensionswerte |
window_strides
|
ArraySlice<int64>
|
Array von Ganzzahlen für Fenster-Stride-Werte |
base_dilations
|
ArraySlice<int64>
|
Array von Ganzzahlen für die Basis-Dilation-Werte |
window_dilations
|
ArraySlice<int64>
|
Array von Ganzzahlen für die Werte der Fenstererweiterung |
padding
|
Padding
|
Padding-Typ für das Fenster (Padding::kSame, das so aufgefüllt wird, dass die Ausgabegröße bei einem Stride von 1 mit der Eingabegröße übereinstimmt, oder Padding::kValid, bei dem keine Auffüllung verwendet wird und das Fenster „angehalten“ wird, sobald es nicht mehr passt) |
Wobei:
- N muss größer oder gleich 1 sein.
- Alle Eingabearrays müssen dieselben Dimensionen haben.
- Wenn
N = 1, istCollate(T)T. - Wenn
N > 1, istCollate(T_0, ..., T_{N-1})ein Tupel ausN-Elementen vom Typ(T0,...T{N-1}).
Weitere Informationen zu StableHLO finden Sie unter StableHLO – reduce_window.
ReduceWindow – Beispiel 1
Die Eingabe ist eine Matrix der Größe [4x6] und sowohl window_dimensions als auch window_stride_dimensions sind [2x3].
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
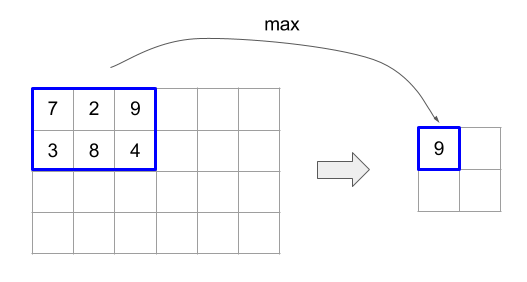
Ein Stride von 1 in einer Dimension gibt an, dass die Position eines Fensters in der Dimension 1 Element vom benachbarten Fenster entfernt ist. Wenn Sie angeben möchten, dass sich keine Fenster überlappen, muss window_stride_dimensions gleich window_dimensions sein. Die Abbildung unten veranschaulicht die Verwendung von zwei verschiedenen Schrittwerten. Padding wird auf jede Dimension der Eingabe angewendet. Die Berechnungen sind dieselben, als ob die Eingabe mit den Dimensionen erfolgt wäre, die sie nach dem Padding hat.
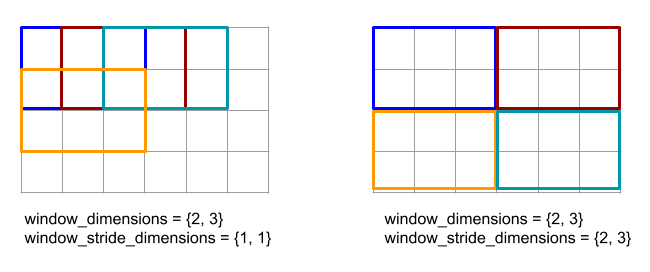
Ein nicht triviales Beispiel für Padding ist die Berechnung des Minimums im Reduzierungsfenster (Anfangswert ist MAX_FLOAT) mit Dimension 3 und Schrittweite 2 für das Eingabearray [10000, 1000, 100, 10, 1]. Beim Padding kValid werden die Minima für zwei gültige Fenster berechnet: [10000, 1000, 100] und [100, 10, 1]. Das Ergebnis ist [100, 1]. Beim Padding kSame wird das Array zuerst so aufgefüllt, dass die Form nach dem Reduce-Window dieselbe wie die Eingabe für den Stride 1 ist. Dazu werden auf beiden Seiten anfängliche Elemente hinzugefügt, sodass [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE] entsteht. Wenn Sie „reduce-window“ auf das aufgefüllte Array anwenden, werden drei Fenster [MAX_VALUE, 10000, 1000], [1000, 100, 10] und [10, 1, MAX_VALUE] verarbeitet und [1000, 10, 1] wird ausgegeben.
Die Auswertungsreihenfolge der Reduktionsfunktion ist beliebig und möglicherweise nicht deterministisch. Daher sollte die Reduktionsfunktion nicht zu empfindlich auf eine erneute Zuordnung reagieren. Weitere Informationen finden Sie in der Diskussion zur Assoziativität im Kontext von Reduce.
ReduceWindow – Beispiel 2 – StableHLO
Im obigen Beispiel:
Eingabe: Der Operand hat die Eingabeform S32[3,2]. Mit den Werten
[[1,2],[3,4],[5,6]]
Schritt 1: Durch die Basis-Dilation mit dem Faktor 2 entlang der Zeilendimension werden Lücken zwischen den einzelnen Zeilen des Operanden eingefügt. Nach der Erweiterung wird oben ein Padding von zwei Zeilen und unten ein Padding von einer Zeile angewendet. Dadurch wird der Tensor höher.
Schritt 2: Es wird ein Fenster mit der Form [2,1] und der Fenstererweiterung [3,1] definiert. Das bedeutet, dass in jedem Fenster zwei Elemente aus derselben Spalte ausgewählt werden. Das zweite Element befindet sich jedoch drei Zeilen unter dem ersten und nicht direkt darunter.
Schritt 3: Die Fenster werden dann mit dem Stride [4,1] über den Operanden geschoben. Dadurch wird das Fenster jeweils um vier Zeilen nach unten und um eine Spalte horizontal verschoben. Die Auffüllzellen werden mit init_value (in diesem Fall init_value = 0) gefüllt. Werte, die in die Dilation-Zellen fallen, werden ignoriert.
Aufgrund von Schrittweite und Padding überlappen sich einige Fenster nur mit Nullen und Lücken, während andere sich mit echten Eingabewerten überlappen.
Schritt 4: Innerhalb jedes Fensters werden die Elemente mithilfe der Reduzierungsfunktion (a, b) → a + b kombiniert, beginnend mit dem Startwert 0. In den beiden oberen Fenstern sind nur Padding und Löcher zu sehen, daher sind die Ergebnisse 0. In den unteren Fenstern werden die Werte 3 und 4 aus der Eingabe erfasst und als Ergebnisse zurückgegeben.
Ergebnisse) Die endgültige Ausgabe hat die Form S32[2,2] mit den Werten: [[0,0],[3,4]]
Rem
Siehe auch XlaBuilder::Rem.
Berechnet den elementweisen Rest von Dividend lhs und Divisor rhs.
Das Vorzeichen des Ergebnisses wird vom Dividenden übernommen und der absolute Wert des Ergebnisses ist immer kleiner als der absolute Wert des Divisors.
Rem(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für Rem gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Rem(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – remainder.
ReplicaId
Siehe auch XlaBuilder::ReplicaId.
Gibt die eindeutige ID (U32-Skalar) des Replikats zurück.
ReplicaId()
Die eindeutige ID jedes Replikats ist eine Ganzzahl ohne Vorzeichen im Intervall [0, N), wobei N die Anzahl der Replikate ist. Da auf allen Replikaten dasselbe Programm ausgeführt wird, gibt ein ReplicaId()-Aufruf im Programm auf jedem Replikat einen anderen Wert zurück.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – replica_id.
Umformen
Siehe auch XlaBuilder::Reshape.
und den Vorgang Collapse.
Ändert die Dimensionen eines Arrays in eine neue Konfiguration.
Reshape(operand, dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Array vom Typ T |
dimensions |
int64 vector |
Vektor der Größen der neuen Dimensionen |
Konzeptionell wird bei „reshape“ zuerst ein Array in einen eindimensionalen Vektor von Datenwerten umgewandelt und dann in eine neue Form gebracht. Die Eingabeargumente sind ein beliebiges Array vom Typ T, ein Compile-Zeitkonstantenvektor mit Dimensionsindexen und ein Compile-Zeitkonstantenvektor mit Dimensionsgrößen für das Ergebnis.
Der dimensions-Vektor bestimmt die Größe des Ausgabearrays. Der Wert an Index 0 in dimensions ist die Größe von Dimension 0, der Wert an Index 1 ist die Größe von Dimension 1 usw. Das Produkt der dimensions-Dimensionen muss dem Produkt der Dimensionsgrößen des Operanden entsprechen. Wenn das reduzierte Array in das mehrdimensionale Array umgewandelt wird, das durch dimensions definiert ist, werden die Dimensionen in dimensions von der langsamsten (wichtigsten) zur schnellsten (unwichtigsten) Variation sortiert.
Sei v beispielsweise ein Array mit 24 Elementen:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
Als Sonderfall kann mit „reshape“ ein Array mit einem Element in einen Skalar und umgekehrt umgewandelt werden. Beispiel:
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
Weitere Informationen zu StableHLO finden Sie unter StableHLO – reshape.
Umformen (explizit)
Siehe auch XlaBuilder::Reshape.
Reshape(shape, operand)
„Reshape“-Vorgang, bei dem eine explizite Zielform verwendet wird.
| Argumente | Typ | Semantik |
|---|---|---|
shape |
Shape |
Ausgabeform vom Typ T |
operand |
XlaOp |
Array vom Typ T |
Rev (reverse)
Siehe auch XlaBuilder::Rev.
Rev(operand, dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Array vom Typ T |
dimensions |
ArraySlice<int64> |
Umzukehrende Dimensionen |
Kehrt die Reihenfolge der Elemente im operand-Array entlang der angegebenen dimensions um und generiert ein Ausgabearray mit derselben Form. Jedes Element des Operanden-Arrays an einem mehrdimensionalen Index wird im Ausgabearray an einem transformierten Index gespeichert. Der mehrdimensionale Index wird transformiert, indem der Index in jeder umzukehrenden Dimension umgekehrt wird. Wenn eine Dimension der Größe N eine der umzukehrenden Dimensionen ist, wird ihr Index i in N – 1 – i transformiert.
Eine Anwendung für den Rev-Vorgang besteht darin, das Faltungs-Gewichts-Array während der Gradientenberechnung in neuronalen Netzwerken entlang der beiden Fensterdimensionen umzukehren.
Informationen zu StableHLO finden Sie unter StableHLO – reverse.
RngNormal
Siehe auch XlaBuilder::RngNormal.
Erstellt eine Ausgabe mit einer bestimmten Form mit Zufallszahlen, die gemäß der \(N(\mu, \sigma)\) Normalverteilung generiert werden. Die Parameter \(\mu\) und \(\sigma\)sowie die Ausgabedimension müssen einen Gleitkomma-Elementtyp haben. Die Parameter müssen außerdem skalare Werte haben.
RngNormal(mu, sigma, shape)
| Argumente | Typ | Semantik |
|---|---|---|
mu |
XlaOp |
Skalar vom Typ T, der den Mittelwert der generierten Zahlen angibt |
sigma
|
XlaOp
|
Skalar vom Typ T, der die Standardabweichung der generierten |
shape |
Shape |
Ausgabeform vom Typ T |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – rng.
RngUniform
Siehe auch XlaBuilder::RngUniform.
Erstellt eine Ausgabe mit einer bestimmten Form mit Zufallszahlen, die gemäß der Gleichverteilung über dem Intervall \([a,b)\)generiert werden. Die Parameter und der Ausgabeelementtyp müssen ein boolescher Typ, ein integraler Typ oder ein Gleitkommatyp sein und die Typen müssen konsistent sein. Die CPU- und GPU-Back-Ends unterstützen derzeit nur F64, F32, F16, BF16, S64, U64, S32 und U32. Außerdem müssen die Parameter skalare Werte haben. Wenn \(b <= a\) das Ergebnis ist, wird es durch die Implementierung definiert.
RngUniform(a, b, shape)
| Argumente | Typ | Semantik |
|---|---|---|
a |
XlaOp |
Skalar vom Typ T, der die Untergrenze des Intervalls angibt |
b |
XlaOp |
Skalar vom Typ T, der die Obergrenze des Intervalls angibt |
shape |
Shape |
Ausgabeform vom Typ T |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – rng.
RngBitGenerator
Siehe auch XlaBuilder::RngBitGenerator.
Generiert eine Ausgabe mit einer bestimmten Form, die mit gleichmäßig zufälligen Bits gefüllt ist, wobei der angegebene Algorithmus (oder das Backend-Standardverfahren) verwendet wird. Gibt einen aktualisierten Zustand (mit derselben Form wie der Anfangszustand) und die generierten Zufallsdaten zurück.
„Initial state“ ist der Ausgangszustand der aktuellen Zufallszahlengenerierung. Die Form und die gültigen Werte hängen vom verwendeten Algorithmus ab.
Die Ausgabe ist garantiert eine deterministische Funktion des Anfangszustands, aber sie ist nicht garantiert deterministisch zwischen Backends und verschiedenen Compilerversionen.
RngBitGenerator(algorithm, initial_state, shape)
| Argumente | Typ | Semantik |
|---|---|---|
algorithm |
RandomAlgorithm |
Der zu verwendende PRNG-Algorithmus. |
initial_state |
XlaOp |
Anfangszustand für den PRNG-Algorithmus. |
shape |
Shape |
Ausgabeform für generierte Daten. |
Verfügbare Werte für algorithm:
rng_default: Back-End-spezifischer Algorithmus mit Back-End-spezifischen Formatanforderungen.rng_three_fry: Counterbasierter PRNG-Algorithmus von ThreeFry. Die Form voninitial_stateistu64[2]mit beliebigen Werten. Salmon et al. SC 2011. Parallele Zufallszahlen: So einfach wie das Einmaleins.rng_philox: Philox-Algorithmus zum parallelen Generieren von Zufallszahlen. Die Form voninitial_stateistu64[3]mit beliebigen Werten. Salmon et al. SC 2011. Parallele Zufallszahlen: So einfach wie das Einmaleins.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – rng_bit_generator.
RngGetAndUpdateState
Siehe auch HloInstruction::CreateRngGetAndUpdateState.
Die API der verschiedenen Rng-Operationen wird intern in HLO-Anweisungen zerlegt, einschließlich RngGetAndUpdateState.
RngGetAndUpdateState dient als Primitiv in HLO. Diese Operation kann in HLO-Dumps enthalten sein, sie ist jedoch nicht für die manuelle Erstellung durch Endnutzer vorgesehen.
Runde
Siehe auch XlaBuilder::Round.
Elementweise Rundung, Bindungen von null weg.
Round(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
RoundNearestAfz
Siehe auch XlaBuilder::RoundNearestAfz.
Führt eine elementweise Rundung zur nächsten Ganzzahl durch, wobei bei Gleichstand von null weg gerundet wird.
RoundNearestAfz(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – round_nearest_afz.
RoundNearestEven
Siehe auch XlaBuilder::RoundNearestEven.
Elementweise Rundung, bei Gleichstand wird auf die nächste gerade Zahl gerundet.
RoundNearestEven(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – round_nearest_even.
Rsqrt
Siehe auch XlaBuilder::Rsqrt.
Elementweise Reziprok-Operation der Quadratwurzel x -> 1.0 / sqrt(x).
Rsqrt(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Rsqrt unterstützt auch das optionale Argument result_accuracy:
Rsqrt(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Informationen zu StableHLO finden Sie unter StableHLO – rsqrt.
Scannen
Siehe auch XlaBuilder::Scan.
Wendet eine Reduzierungsfunktion auf ein Array über eine bestimmte Dimension an und erzeugt einen Endzustand und ein Array von Zwischenwerten.
Scan(inputs..., inits..., to_apply, scan_dimension,
is_reverse, is_associative)
| Argumente | Typ | Semantik |
|---|---|---|
inputs |
Reihenfolge der m-XlaOps |
Die zu durchsuchenden Arrays. |
inits |
Reihenfolge der k-XlaOps |
Erste Übertragungen |
to_apply |
XlaComputation |
Berechnung vom Typ i_0, ..., i_{m-1}, c_0, ..., c_{k-1} -> (o_0, ..., o_{n-1}, c'_0, ..., c'_{k-1}). |
scan_dimension |
int64 |
Die Dimension, die gescannt werden soll. |
is_reverse |
bool |
Bei „true“ wird in umgekehrter Reihenfolge gescannt. |
is_associative |
bool (Tri-State) |
Wenn „true“, ist der Vorgang assoziativ. |
Die Funktion to_apply wird sequenziell auf Elemente in inputs entlang scan_dimension angewendet. Wenn is_reverse „false“ ist, werden die Elemente in der Reihenfolge 0 bis N-1 verarbeitet, wobei N die Größe von scan_dimension ist. Wenn is_reverse „true“ ist, werden Elemente von N-1 bis 0 verarbeitet.
Die to_apply-Funktion verwendet m + k Operanden:
maktuelle Elemente ausinputs.k– Übertragen Sie Werte aus dem vorherigen Schritt (oderinitsfür das erste Element).
Die Funktion to_apply gibt ein Tupel von n + k-Werten zurück:
n-Elemente vonoutputs.kneue Übertragungswerte.
Der Scanvorgang erzeugt ein Tupel von n + k-Werten:
- Die
n-Ausgabearrays mit den Ausgabewerten für jeden Schritt. - Die endgültigen
k-Übertragswerte nach der Verarbeitung aller Elemente.
Die Typen der m-Eingaben müssen mit den Typen der ersten m-Parameter von to_apply übereinstimmen, wobei eine zusätzliche Scan-Dimension hinzukommt. Die Typen der n-Ausgaben müssen mit den Typen der ersten n-Rückgabewerte von to_apply übereinstimmen, wobei eine zusätzliche Scan-Dimension hinzukommt. Die zusätzliche Scan-Dimension muss für alle Ein- und Ausgaben dieselbe Größe N haben. Die Typen der letzten k-Parameter und Rückgabewerte von to_apply sowie die k-Initialisierungen müssen übereinstimmen.
Beispiel (m, n, k == 1, N == 3): Für den ersten Übertrag i, die Eingabe [a, b, c], die Funktion f(x, c) -> (y, c') und scan_dimension=0, is_reverse=false:
- Schritt 0:
f(a, i) -> (y0, c0) - Schritt 1:
f(b, c0) -> (y1, c1) - Schritt 2:
f(c, c1) -> (y2, c2)
Die Ausgabe von Scan ist ([y0, y1, y2], c2).
Streudiagramm
Siehe auch XlaBuilder::Scatter.
Der XLA-Scatter-Vorgang generiert eine Folge von Ergebnissen, die die Werte des Eingabearrays operands sind. Dabei werden mehrere Slices (an den durch scatter_indices angegebenen Indexen) mit der Folge von Werten in updates aktualisiert, wobei update_computation verwendet wird.
Scatter(operands..., scatter_indices, updates..., update_computation,
dimension_numbers, indices_are_sorted, unique_indices)
| Argumente | Typ | Semantik |
|---|---|---|
operands |
Sequenz von N XlaOp |
N Arrays vom Typ T_0, ..., T_N, in die die Daten verteilt werden sollen. |
scatter_indices |
XlaOp |
Array mit den Startindexen der Segmente, die verteilt werden müssen. |
updates |
Sequenz von N XlaOp |
N Arrays vom Typ T_0, ..., T_N. updates[i] enthält die Werte, die für die Streuung von operands[i] verwendet werden müssen. |
update_computation |
XlaComputation |
Berechnung, die zum Kombinieren der vorhandenen Werte im Eingabearray und der Aktualisierungen während des Scatter-Vorgangs verwendet werden soll. Diese Berechnung sollte vom Typ T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N) sein. |
index_vector_dim |
int64 |
Die Dimension in scatter_indices, die die Startindexe enthält. |
update_window_dims |
ArraySlice<int64> |
Die Menge der Dimensionen in updates-Form, die Fensterdimensionen sind. |
inserted_window_dims |
ArraySlice<int64> |
Die Menge der Fensterdimensionen, die in die updates-Form eingefügt werden müssen. |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
Eine Dimensionszuordnung von den Scatter-Indizes zum Operandenindexbereich. Dieses Array wird als Zuordnung von i zu scatter_dims_to_operand_dims[i] interpretiert . Sie muss eineindeutig und total sein. |
dimension_number |
ScatterDimensionNumbers |
Dimensionsnummern für den Scatter-Vorgang |
indices_are_sorted |
bool |
Gibt an, ob die Indexe garantiert vom Aufrufer sortiert werden. |
unique_indices |
bool |
Gibt an, ob die Indexe vom Aufrufer garantiert eindeutig sind. |
Wobei:
- N muss größer oder gleich 1 sein.
operands[0], ...,operands[N-1] müssen alle dieselben Dimensionen haben.updates[0], ...,updates[N-1] müssen alle dieselben Dimensionen haben.- Wenn
N = 1, istCollate(T)T. - Wenn
N > 1, istCollate(T_0, ..., T_N)ein Tupel ausN-Elementen vom TypT.
Wenn index_vector_dim gleich scatter_indices.rank ist, gehen wir implizit davon aus, dass scatter_indices eine nachgestellte 1-Dimension hat.
Wir definieren update_scatter_dims vom Typ ArraySlice<int64> als die Menge der Dimensionen in updates-Form, die nicht in update_window_dims enthalten sind, in aufsteigender Reihenfolge.
Die Argumente von „scatter“ müssen die folgenden Einschränkungen erfüllen:
Jedes
updates-Array mussupdate_window_dims.size + scatter_indices.rank - 1Dimensionen haben.Die Grenzen der Dimension
iin jedemupdates-Array müssen den folgenden Anforderungen entsprechen:- Wenn
iinupdate_window_dimsvorhanden ist (d.h. für ein bestimmteskgleichupdate_window_dims[k]), darf die Grenze der Dimensioniinupdatesdie entsprechende Grenze vonoperandnach Berücksichtigung voninserted_window_dimsnicht überschreiten (d.h.adjusted_window_bounds[k], wobeiadjusted_window_boundsdie Grenzen vonoperandmit den Grenzen an den Indexpositioneninserted_window_dimsenthält). - Wenn
iinupdate_scatter_dimsvorhanden ist (d.h. für ein bestimmteskgleichupdate_scatter_dims[k]), muss die Grenze der Dimensioniinupdatesgleich der entsprechenden Grenze vonscatter_indicessein, wobeiindex_vector_dimübersprungen wird (d.h.scatter_indices.shape.dims[k], wennk<index_vector_dim, undscatter_indices.shape.dims[k+1] andernfalls).
- Wenn
update_window_dimsmuss in aufsteigender Reihenfolge vorliegen, darf keine sich wiederholenden Dimensionsnummern enthalten und muss im Bereich[0, updates.rank)liegen.inserted_window_dimsmuss in aufsteigender Reihenfolge vorliegen, darf keine sich wiederholenden Dimensionsnummern enthalten und muss im Bereich[0, operand.rank)liegen.operand.rankmuss der Summe vonupdate_window_dims.sizeundinserted_window_dims.sizeentsprechen.scatter_dims_to_operand_dims.sizemuss gleichscatter_indices.shape.dims[index_vector_dim] sein und seine Werte müssen im Bereich[0, operand.rank)liegen.
Für einen bestimmten Index U in jedem updates-Array wird der entsprechende Index I im entsprechenden operands-Array, in dem dieses Update angewendet werden muss, so berechnet:
- Sei
G= {U[k] fürkinupdate_scatter_dims}. Verwenden SieG, um einen IndexvektorSim Arrayscatter_indiceszu suchen, sodassS[i] =scatter_indices[Combine(G,i)], wobei Combine(A, b) b an den Positionenindex_vector_dimin A einfügt. - Erstellen Sie einen Index
Sininoperand, indem SieSmithilfe derscatter_dims_to_operand_dims-Karte streuen.SFormeller:Sin[scatter_dims_to_operand_dims[k]] =S[k], wennk<scatter_dims_to_operand_dims.size.Sin[_] =0andernfalls.
- Erstellt einen Index
Winin jedemoperands-Array, indem die Indexe beiupdate_window_dimsinUgemäßinserted_window_dimsverteilt werden. Formeller:Win[window_dims_to_operand_dims(k)] =U[k], wennkinupdate_window_dimsist, wobeiwindow_dims_to_operand_dimsdie monotone Funktion mit dem Definitionsbereich [0,update_window_dims.size) und dem Wertebereich [0,operand.rank) \inserted_window_dimsist. Wenn beispielsweiseupdate_window_dims.sizegleich4,operand.rankgleich6undinserted_window_dimsgleich {0,2} ist, dann istwindow_dims_to_operand_dimsgleich {0→1,1→3,2→4,3→5}).Win[_] =0andernfalls.
IistWin+Sin, wobei + die elementweise Addition ist.
Zusammenfassend lässt sich der Scatter-Vorgang so definieren:
- Initialisieren Sie
outputmitoperands, d.h. für alle IndexeJ, für alle IndexeOim Arrayoperands[J]:
output[J][O] =operands[J][O] - Für jeden Index
Uim Arrayupdates[J] und den entsprechenden IndexOim Arrayoperand[J] gilt: WennOein gültiger Index füroutputist, dann
(output[0][O], ...,output[N-1][O]) =update_computation(output[0][O], ...,output[N-1][O],updates[0][U], ...,updates[N-1][U])(output
Die Reihenfolge, in der Updates angewendet werden, ist nicht deterministisch. Wenn also mehrere Indexe in updates auf denselben Index in operands verweisen, ist der entsprechende Wert in output nicht deterministisch.
Der erste Parameter, der an update_computation übergeben wird, ist immer der aktuelle Wert aus dem Array output und der zweite Parameter ist immer der Wert aus dem Array updates. Das ist besonders wichtig, wenn die update_computation nicht kommutativ ist.
Wenn indices_are_sorted auf „true“ gesetzt ist, kann XLA davon ausgehen, dass scatter_indices vom Nutzer sortiert wurden (in aufsteigender Reihenfolge, nachdem die Werte gemäß scatter_dims_to_operand_dims verteilt wurden). Andernfalls sind die Semantik implementierungsdefiniert.
Wenn unique_indices auf „true“ gesetzt ist, kann XLA davon ausgehen, dass alle verteilten Elemente eindeutig sind. Daher konnte XLA nicht atomare Vorgänge verwenden. Wenn unique_indices auf „true“ gesetzt ist und die Indizes, auf die verteilt wird, nicht eindeutig sind, ist die Semantik implementierungsdefiniert.
Der Scatter-Vorgang kann informell als Umkehrung des Gather-Vorgangs betrachtet werden. Das heißt, der Scatter-Vorgang aktualisiert die Elemente in der Eingabe, die vom entsprechenden Gather-Vorgang extrahiert werden.
Eine detaillierte informelle Beschreibung und Beispiele finden Sie im Abschnitt „Informelle Beschreibung“ unter Gather.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – scatter.
Scatter – Beispiel 1 – StableHLO
Im Bild oben ist jede Zeile der Tabelle ein Beispiel für einen Aktualisierungsindex. Sehen wir uns die einzelnen Schritte von links(Index aktualisieren) nach rechts(Ergebnisindex) an:
Die Eingabe input hat die Form S32[2,3,4,2]. scatter_indices hat die Form S64[2,2,3,2]. updates hat die Form S32[2,2,3,1,2].
Update Index) As part of the input we are given update_window_dims:[3,4]. Das bedeutet, dass die Dimensionen 3 und 4 von updates Fensterdimensionen sind, die gelb hervorgehoben werden. Daraus lässt sich ableiten, dass update_scatter_dims = [0,1,2].
Update Scatter Index) Shows us the extracted updated_scatter_dims for each.
(Der nicht gelbe Teil der Spalte „Update Index“)
Startindex: Wenn wir uns das scatter_indices-Tensorbild ansehen, sehen wir, dass die Werte aus dem vorherigen Schritt (Update scatter Index) uns die Position des Startindex liefern. Aus index_vector_dim geht auch die Dimension des starting_indices hervor, die die Startindexe enthält. Für scatter_indices ist das Dimension 3 mit der Größe 2.
Der vollständige Startindex scatter_dims_to_operand_dims = [2,1] gibt an, dass das erste Element des Indexvektors in die Operandendimension 2 geht. Das zweite Element des Indexvektors wird auf die Operandendimension 1 angewendet. Die verbleibenden Operanden-Dimensionen werden mit 0 gefüllt.
Vollständiger Batching-Index: Der lila hervorgehobene Bereich wird in dieser Spalte(vollständiger Batching-Index), der Spalte „Update-Scatter-Index“ und der Spalte „Update-Index“ angezeigt.
Vollfensterindex) Berechnet aus dem update_window_dimensions [3,4].
Ergebnisindex: Die Summe aus dem Index für den vollständigen Start, dem Index für das vollständige Batching und dem Index für den vollständigen Zeitraum im operand-Tensor. Die grün hervorgehobenen Regionen entsprechen ebenfalls der Abbildung operand. Die letzte Zeile wird übersprungen, da sie außerhalb des operand-Tensors liegt.
Auswählen
Siehe auch XlaBuilder::Select.
Erstellt ein Ausgabearray aus Elementen von zwei Eingabearrays basierend auf den Werten eines Prädikatsarrays.
Select(pred, on_true, on_false)
| Argumente | Typ | Semantik |
|---|---|---|
pred |
XlaOp |
Array vom Typ PRED |
on_true |
XlaOp |
Array vom Typ T |
on_false |
XlaOp |
Array vom Typ T |
Die Arrays on_true und on_false müssen dieselbe Form haben. Das ist auch die Form des Ausgabearrays. Das Array pred muss dieselbe Dimensionalität wie on_true und on_false mit dem Elementtyp PRED haben.
Für jedes Element P von pred wird das entsprechende Element des Ausgabearrays aus on_true übernommen, wenn der Wert von P gleich true ist, und aus on_false, wenn der Wert von P gleich false ist. Als eingeschränkte Form des Broadcasting kann pred ein Skalar vom Typ PRED sein. In diesem Fall wird das Ausgabearray vollständig aus on_true übernommen, wenn pred gleich true ist, und aus on_false, wenn pred gleich false ist.
Beispiel mit nicht skalarer pred:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
Beispiel mit skalarer pred:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
Auswahlen zwischen Tupeln werden unterstützt. Tupel werden für diesen Zweck als skalare Typen betrachtet. Wenn on_true und on_false Tupel sind (die dieselbe Form haben müssen!), muss pred ein Skalar vom Typ PRED sein.
Informationen zu StableHLO finden Sie unter StableHLO – select.
SelectAndScatter
Siehe auch XlaBuilder::SelectAndScatter.
Dieser Vorgang kann als zusammengesetzter Vorgang betrachtet werden, bei dem zuerst ReduceWindow für das operand-Array berechnet wird, um ein Element aus jedem Fenster auszuwählen. Anschließend wird das source-Array auf die Indexe der ausgewählten Elemente verteilt, um ein Ausgabearray mit derselben Form wie das Operandenarray zu erstellen. Mit der binären select-Funktion wird ein Element aus jedem Fenster ausgewählt. Dazu wird sie auf jedes Fenster angewendet. Sie wird mit der Eigenschaft aufgerufen, dass der Indexvektor des ersten Parameters lexikografisch kleiner als der Indexvektor des zweiten Parameters ist. Die Funktion select gibt true zurück, wenn der erste Parameter ausgewählt ist, und false, wenn der zweite Parameter ausgewählt ist. Die Funktion muss transitiv sein (d. h., wenn select(a, b) und select(b, c) true sind, dann ist auch select(a, c) true), damit das ausgewählte Element nicht von der Reihenfolge der Elemente abhängt, die für ein bestimmtes Fenster durchlaufen werden.
Die Funktion scatter wird auf jeden ausgewählten Index im Ausgabearray angewendet. Er hat zwei skalare Parameter:
- Aktueller Wert am ausgewählten Index im Ausgabearray
- Der Streuungswert aus
source, der für den ausgewählten Index gilt
Die beiden Parameter werden kombiniert und es wird ein skalarer Wert zurückgegeben, mit dem der Wert am ausgewählten Index im Ausgabearray aktualisiert wird. Anfangs sind alle Indexe des Ausgabearrays auf init_value gesetzt.
Das Ausgabearray hat dieselbe Form wie das operand-Array und das source-Array muss dieselbe Form wie das Ergebnis der Anwendung einer ReduceWindow-Operation auf das operand-Array haben. Mit SelectAndScatter können die Gradientenwerte für eine Pooling-Schicht in einem neuronalen Netzwerk rückpropagiert werden.
SelectAndScatter(operand, select, window_dimensions, window_strides, padding,
source, init_value, scatter)
| Argumente | Typ | Semantik |
|---|---|---|
operand
|
XlaOp
|
Array vom Typ T, über das die Fenster gleiten |
select
|
XlaComputation
|
binäre Berechnung vom Typ T, T
-> PRED, die auf alle Elemente in jedem Fenster angewendet wird; gibt true zurück, wenn der erste Parameter ausgewählt ist, und false, wenn der zweite Parameter ausgewählt ist |
window_dimensions
|
ArraySlice<int64>
|
Array von Ganzzahlen für Fensterdimensionswerte |
window_strides
|
ArraySlice<int64>
|
Array von Ganzzahlen für Fenster-Stride-Werte |
padding
|
Padding
|
Padding-Typ für das Fenster (Padding::kSame oder Padding::kValid) |
source
|
XlaOp
|
Array vom Typ T mit den zu streuenden Werten |
init_value
|
XlaOp
|
Skalarwert vom Typ T für den Anfangswert des Ausgabearrays |
scatter
|
XlaComputation
|
binäre Berechnung vom Typ T, T
-> T, um jedes Scatter-Quellenelement mit seinem Zielelement anzuwenden |
In der Abbildung unten sehen Sie Beispiele für die Verwendung von SelectAndScatter. Die Funktion select berechnet den Maximalwert der Parameter. Wenn sich die Fenster überschneiden, wie in Abbildung 2 unten, kann ein Index des operand-Arrays mehrmals von verschiedenen Fenstern ausgewählt werden. In der Abbildung wird das Element mit dem Wert 9 sowohl vom oberen blauen als auch vom oberen roten Fenster ausgewählt. Die binäre Additionsfunktion scatter erzeugt das Ausgabeelement mit dem Wert 8 (2 + 6).
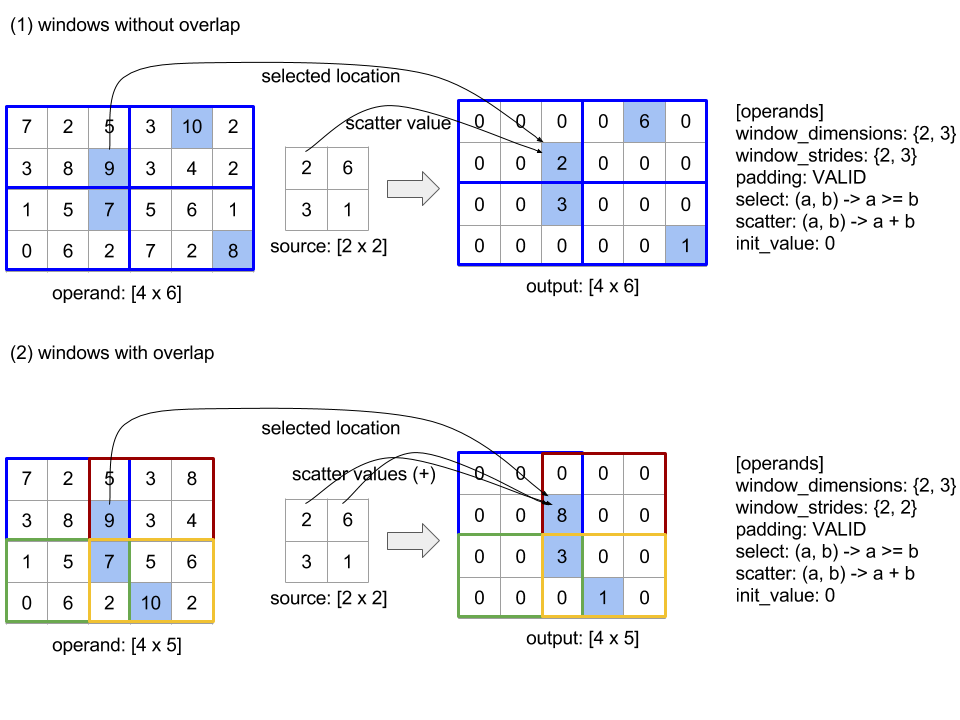
Die Auswertungsreihenfolge der Funktion scatter ist beliebig und kann nicht deterministisch sein. Daher sollte die scatter-Funktion nicht zu empfindlich auf eine erneute Zuordnung reagieren. Weitere Informationen finden Sie in der Diskussion zur Assoziativität im Kontext von Reduce.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – select_and_scatter.
Senden
Siehe auch XlaBuilder::Send.
Send, SendWithTokens und SendToHost sind Vorgänge, die als Kommunikationsprimitive in HLO dienen. Diese Vorgänge sind in HLO-Dumps in der Regel Teil der Low-Level-Ein-/Ausgabe oder der geräteübergreifenden Übertragung, sie sind jedoch nicht für die manuelle Erstellung durch Endnutzer vorgesehen.
Send(operand, handle)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Zu sendende Daten (Array vom Typ T) |
handle |
ChannelHandle |
Eindeutige Kennung für jedes Sende-/Empfangspaar |
Sendet die angegebenen Operanden an eine Recv-Anweisung in einer anderen Berechnung, die dasselbe Channel-Handle verwendet. Es werden keine Daten zurückgegeben.
Ähnlich wie beim Vorgang Recv stellt die Client-API des Vorgangs Send die synchrone Kommunikation dar und wird intern in zwei HLO-Anweisungen (Send und SendDone) zerlegt, um asynchrone Datenübertragungen zu ermöglichen. Siehe auch HloInstruction::CreateSend und HloInstruction::CreateSendDone.
Send(HloInstruction operand, int64 channel_id)
Leitet eine asynchrone Übertragung des Operanden an die Ressourcen ein, die durch die Recv-Anweisung mit derselben Channel-ID zugewiesen wurden. Gibt einen Kontext zurück, der von einer nachfolgenden SendDone-Anweisung verwendet wird, um auf den Abschluss der Datenübertragung zu warten. Der Kontext ist ein Tupel aus {Operand (Form), Anforderungs-ID (U32)} und kann nur von einem SendDone-Befehl verwendet werden.
Informationen zu StableHLO finden Sie unter StableHLO – send.
SendDone
Siehe auch HloInstruction::CreateSendDone.
SendDone(HloInstruction context)
Wartet in einem Kontext, der durch eine Send-Anweisung erstellt wurde, bis die Datenübertragung abgeschlossen ist. Mit der Anleitung werden keine Daten zurückgegeben.
Planung von Kanalanweisungen
Die Ausführungsreihenfolge der vier Anweisungen für jeden Channel (Recv, RecvDone, Send, SendDone) ist wie unten beschrieben.
Recvfindet vorSendstatt.Sendfindet vorRecvDonestatt.Recvfindet vorRecvDonestatt.Sendfindet vorSendDonestatt.
Wenn die Backend-Compiler einen linearen Zeitplan für jede Berechnung generieren, die über Channel-Anweisungen kommuniziert, darf es keine Zyklen zwischen den Berechnungen geben. Die folgenden Zeitpläne führen beispielsweise zu Deadlocks.
SetDimensionSize
Siehe auch XlaBuilder::SetDimensionSize.
Legt die dynamische Größe der angegebenen Dimension von XlaOp fest. Der Operand muss ein Array sein.
SetDimensionSize(operand, val, dimension)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
n-dimensionales Eingabearray. |
val |
XlaOp |
int32, das die dynamische Größe zur Laufzeit darstellt. |
dimension
|
int64
|
Ein Wert im Intervall [0, n), der die Dimension angibt. |
Der Operand wird als Ergebnis übergeben. Die dynamische Dimension wird vom Compiler erfasst.
Gepaddete Werte werden von nachgelagerten Reduktionsvorgängen ignoriert.
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
ShiftLeft
Siehe auch XlaBuilder::ShiftLeft.
Führt eine elementweise Linksverschiebung von lhs um rhs Bits aus.
ShiftLeft(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für ShiftLeft gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
ShiftLeft(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – shift_left.
ShiftRightArithmetic
Siehe auch XlaBuilder::ShiftRightArithmetic.
Führt eine elementweise arithmetische Rechtsverschiebung von lhs um rhs Bits durch.
ShiftRightArithmetic(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für ShiftRightArithmetic gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
ShiftRightArithmetic(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – shift_right_arithmetic.
ShiftRightLogical
Siehe auch XlaBuilder::ShiftRightLogical.
Führt eine elementweise logische Rechtsverschiebung von lhs um rhs Bits aus.
ShiftRightLogical(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für ShiftRightLogical gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
ShiftRightLogical(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – shift_right_logical.
Signieren
Siehe auch XlaBuilder::Sign.
Sign(operand) Elementweise Vorzeichenoperation x -> sgn(x), wobei
\[\text{sgn}(x) = \begin{cases} -1 & x < 0\\ -0 & x = -0\\ NaN & x = NaN\\ +0 & x = +0\\ 1 & x > 0 \end{cases}\]
mit dem Vergleichsoperator des Elementtyps von operand.
Sign(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Weitere Informationen zu StableHLO finden Sie unter StableHLO – sign.
Sinus
Sin(operand) Elementweise Sinusfunktion x -> sin(x):
Siehe auch XlaBuilder::Sin.
Sin(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Die Funktion „Sin“ unterstützt auch das optionale Argument result_accuracy:
Sin(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – Sinus.
Slice
Siehe auch XlaBuilder::Slice.
Beim Slicing wird ein Unterarray aus dem Eingabearray extrahiert. Das Unterarray hat dieselbe Anzahl von Dimensionen wie die Eingabe und enthält die Werte innerhalb eines umgebenden Rechtecks im Eingabearray, wobei die Dimensionen und Indexe des umgebenden Rechtecks als Argumente für den Slice-Vorgang angegeben werden.
Slice(operand, start_indices, limit_indices, strides)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
N-dimensionales Array vom Typ T |
start_indices
|
ArraySlice<int64>
|
Liste mit N Ganzzahlen, die die Startindexe des Slice für jede Dimension enthalten. Die Werte müssen größer oder gleich null sein. |
limit_indices
|
ArraySlice<int64>
|
Liste mit N Ganzzahlen, die die Endindexe (exklusiv) für den Slice für jede Dimension enthält. Jeder Wert muss größer oder gleich dem entsprechenden start_indices-Wert für die Dimension und kleiner oder gleich der Größe der Dimension sein. |
strides
|
ArraySlice<int64>
|
Liste mit N Ganzzahlen, die den Eingabestride des Slice festlegen. Mit dem Slice wird jedes strides[d]-Element in Dimension d ausgewählt. |
1‑dimensionales Beispiel:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4})
// Result: {2.0, 3.0}
2‑dimensionales Beispiel:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3})
// Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
Weitere Informationen zu StableHLO finden Sie unter StableHLO – slice.
Sortieren
Siehe auch XlaBuilder::Sort.
Sort(operands, comparator, dimension, is_stable)
| Argumente | Typ | Semantik |
|---|---|---|
operands |
ArraySlice<XlaOp> |
Die zu sortierenden Operanden. |
comparator |
XlaComputation |
Die zu verwendende Vergleichsberechnung. |
dimension |
int64 |
Die Dimension, nach der sortiert werden soll. |
is_stable |
bool |
Gibt an, ob stabiles Sortieren verwendet werden soll. |
Wenn nur ein Operand angegeben wird:
Wenn der Operand ein eindimensionaler Tensor (ein Array) ist, ist das Ergebnis ein sortiertes Array. Wenn Sie das Array in aufsteigender Reihenfolge sortieren möchten, sollte der Comparator einen „kleiner als“-Vergleich durchführen. Formal gilt nach dem Sortieren des Arrays für alle Indexpositionen
i, jmiti < jentwedercomparator(value[i], value[j]) = comparator(value[j], value[i]) = falseodercomparator(value[i], value[j]) = true.Wenn der Operand eine höhere Anzahl von Dimensionen hat, wird er entlang der angegebenen Dimension sortiert. Bei einem zweidimensionalen Tensor (einer Matrix) wird mit dem Dimensionswert
0jede Spalte unabhängig sortiert und mit dem Dimensionswert1jede Zeile unabhängig sortiert. Wenn keine Dimensionsnummer angegeben wird, wird standardmäßig die letzte Dimension ausgewählt. Für die sortierte Dimension gilt dieselbe Sortierreihenfolge wie im eindimensionalen Fall.
Wenn n > 1-Operanden angegeben werden:
Alle
n-Operanden müssen Tensoren mit denselben Dimensionen sein. Die Elementtypen der Tensoren können unterschiedlich sein.Alle Operanden werden zusammen sortiert, nicht einzeln. Konzeptionell werden die Operanden als Tupel behandelt. Beim Prüfen, ob die Elemente der einzelnen Operanden an den Indexpositionen
iundjgetauscht werden müssen, wird der Comparator mit2 * nskalaren Parametern aufgerufen. Dabei entspricht der Parameter2 * kdem Wert an der Positionides Operandenk-thund der Parameter2 * k + 1dem Wert an der Positionjdes Operandenk-th. Normalerweise werden also die Parameter2 * kund2 * k + 1miteinander verglichen und möglicherweise andere Parameterpaare als Tiebreaker verwendet.Das Ergebnis ist ein Tupel, das aus den Operanden in sortierter Reihenfolge (entlang der oben angegebenen Dimension) besteht. Der
i-th-Operand des Tupels entspricht demi-th-Operanden von „Sort“.
Wenn es beispielsweise drei Operanden operand0 = [3, 1], operand1 = [42, 50] und operand2 = [-3.0, 1.1] gibt und der Comparator nur die Werte von operand0 mit „kleiner als“ vergleicht, ist die Ausgabe der Sortierung das Tupel ([1, 3], [50, 42], [1.1, -3.0]).
Wenn is_stable auf „true“ gesetzt ist, ist die Sortierung garantiert stabil. Das bedeutet, dass die relative Reihenfolge der gleichen Werte beibehalten wird, wenn der Comparator Elemente als gleich betrachtet. Zwei Elemente e1 und e2 sind genau dann gleich, wenn comparator(e1, e2) = comparator(e2, e1) = false. Standardmäßig ist is_stable auf „false“ gesetzt.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – sort.
Sqrt
Siehe auch XlaBuilder::Sqrt.
Elementweise Quadratwurzeloperation x -> sqrt(x).
Sqrt(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
„Sqrt“ unterstützt auch das optionale Argument result_accuracy:
Sqrt(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – sqrt.
Untergeordnet
Siehe auch XlaBuilder::Sub.
Führt eine elementweise Subtraktion von lhs und rhs durch.
Sub(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für „Sub“ gibt es eine alternative Variante mit Unterstützung für Broadcasting in verschiedenen Dimensionen:
Sub(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – subtract.
Lederbraun
Siehe auch XlaBuilder::Tan.
Elementweise Tangente x -> tan(x).
Tan(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
„tan“ unterstützt auch das optionale Argument result_accuracy:
Tan(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – tan.
Tanh
Siehe auch XlaBuilder::Tanh.
Elementweiser hyperbolischer Tangens x -> tanh(x).
Tanh(operand)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
Tanh unterstützt auch das optionale Argument result_accuracy:
Tanh(operand, result_accuracy)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der Operand für die Funktion |
result_accuracy
|
optional ResultAccuracy
|
Die Genauigkeitstypen, die der Nutzer für unäre Operationen mit mehreren Implementierungen anfordern kann |
Weitere Informationen zu result_accuracy finden Sie unter Genauigkeit der Ergebnisse.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – tanh.
TopK
Siehe auch XlaBuilder::TopK.
Mit TopK werden die Werte und Indexe der k größten oder kleinsten Elemente für die letzte Dimension des angegebenen Tensors ermittelt.
TopK(operand, k, largest)
| Argumente | Typ | Semantik |
|---|---|---|
operand
|
XlaOp
|
Der Tensor, aus dem die obersten k-Elemente extrahiert werden sollen.
Der Tensor muss mindestens eine Dimension haben. Die Größe der letzten Dimension des Tensors muss größer oder gleich k sein. |
k |
int64 |
Die Anzahl der zu extrahierenden Elemente. |
largest
|
bool
|
Gibt an, ob die größten oder kleinsten k Elemente extrahiert werden sollen. |
Für einen eindimensionalen Eingabetensor (ein Array) werden die k größten oder kleinsten Einträge im Array ermittelt und ein Tupel aus zwei Arrays (values, indices) ausgegeben. values[j] ist also der j-größte/kleinste Eintrag in operand und sein Index ist indices[j].
Für einen Eingabetensor mit mehr als einer Dimension werden die k Einträge mit den höchsten Werten entlang der letzten Dimension berechnet. Alle anderen Dimensionen (Zeilen) bleiben in der Ausgabe erhalten.
Für einen Operanden mit der Form [A, B, ..., P, Q], wobei Q >= k, ist die Ausgabe also ein Tupel (values, indices), wobei gilt:
values.shape = indices.shape = [A, B, ..., P, k]
Wenn zwei Elemente in einer Zeile gleich sind, wird das Element mit dem niedrigeren Index zuerst angezeigt.
Transponieren
Weitere Informationen finden Sie unter tf.reshape.
Transpose(operand, permutation)
| Argumente | Typ | Semantik |
|---|---|---|
operand |
XlaOp |
Der zu transponierende Operand. |
permutation |
ArraySlice<int64> |
So werden die Dimensionen permutiert. |
Permutiert die Operanden-Dimensionen mit der angegebenen Permutation, sodass ∀ i . 0 ≤ i < number of dimensions ⇒
input_dimensions[permutation[i]] = output_dimensions[i].
Dies entspricht Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)).
Weitere Informationen zu StableHLO finden Sie unter StableHLO – transpose.
TriangularSolve
Siehe auch XlaBuilder::TriangularSolve.
Löst Systeme linearer Gleichungen mit unteren oder oberen Dreieckskoeffizientenmatrizen durch Vorwärts- oder Rückwärtssubstitution. Bei der Übertragung entlang der führenden Dimensionen wird eines der Matrixsysteme op(a) * x =
b oder x * op(a) = b für die Variable x gelöst, wobei a und b angegeben sind und op(a) entweder op(a) = a, op(a) = Transpose(a) oder op(a) = Conj(Transpose(a)) ist.
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| Argumente | Typ | Semantik |
|---|---|---|
a
|
XlaOp
|
ein mehr als zweidimensionales Array eines komplexen oder Gleitkommatyps mit der Form [..., M,
M]. |
b
|
XlaOp
|
ein mehrdimensionales Array desselben Typs mit der Form [..., M, K], wenn left_side „true“ ist, andernfalls [..., K, M]. |
left_side
|
bool
|
gibt an, ob ein System der Form op(a) * x = b (true) oder x *
op(a) = b (false) gelöst werden soll. |
lower
|
bool
|
ob das obere oder untere Dreieck von a verwendet werden soll. |
unit_diagonal
|
bool
|
Wenn true, werden die Diagonalelemente von a als 1 angenommen und nicht auf sie zugegriffen. |
transpose_a
|
Transpose
|
Gibt an, ob a unverändert verwendet, transponiert oder konjugiert transponiert werden soll. |
Eingabedaten werden nur aus dem unteren/oberen Dreieck von a gelesen, je nach Wert von lower. Werte aus dem anderen Dreieck werden ignoriert. Ausgabedaten werden im selben Dreieck zurückgegeben. Die Werte im anderen Dreieck sind implementierungsdefiniert und können beliebig sein.
Wenn die Anzahl der Dimensionen von a und b größer als 2 ist, werden sie als Batches von Matrizen behandelt, wobei alle Dimensionen außer den beiden untergeordneten Dimensionen Batchdimensionen sind. a und b müssen dieselben Batchdimensionen haben.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – triangular_solve.
Tupel
Siehe auch XlaBuilder::Tuple.
Ein Tupel mit einer variablen Anzahl von Daten-Handles, die jeweils eine eigene Form haben.
Tuple(elements)
| Argumente | Typ | Semantik |
|---|---|---|
elements |
Vektor von XlaOp |
N-Array vom Typ T |
Das entspricht std::tuple in C++. Konzeptionell:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
Tupel können mit dem Vorgang GetTupleElement dekonstruiert (auf sie kann zugegriffen) werden.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – Tuple.
Während
Siehe auch XlaBuilder::While.
While(condition, body, init)
| Argumente | Typ | Semantik |
|---|---|---|
condition
|
XlaComputation
|
XlaComputation vom Typ T -> PRED, der die Beendigungsbedingung der Schleife definiert. |
body
|
XlaComputation
|
XlaComputation vom Typ T -> T, die den Text der Schleife definiert. |
init
|
T
|
Anfangswert für den Parameter von condition und body. |
Führt die body sequenziell aus, bis die condition fehlschlägt. Das ähnelt einer typischen while-Schleife in vielen anderen Sprachen, mit Ausnahme der unten aufgeführten Unterschiede und Einschränkungen.
- Ein
While-Knoten gibt einen Wert vom TypTzurück, der das Ergebnis der letzten Ausführung vonbodyist. - Die Form des Typs
Twird statisch bestimmt und muss in allen Iterationen gleich sein.
Die T-Parameter der Berechnungen werden in der ersten Iteration mit dem Wert init initialisiert und in jeder nachfolgenden Iteration automatisch auf das neue Ergebnis von body aktualisiert.
Ein wichtiger Anwendungsfall für den While-Knoten ist die wiederholte Ausführung des Trainings in neuronalen Netzwerken. Unten sehen Sie vereinfachten Pseudocode mit einem Diagramm, das die Berechnung darstellt. Der Code befindet sich in while_test.cc.
Der Typ T in diesem Beispiel ist ein Tuple, der aus einem int32 für die Anzahl der Iterationen und einem vector[10] für den Akkumulator besteht. In 1.000 Schleifendurchläufen wird dem Akkumulator immer wieder ein konstanter Vektor hinzugefügt.
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}
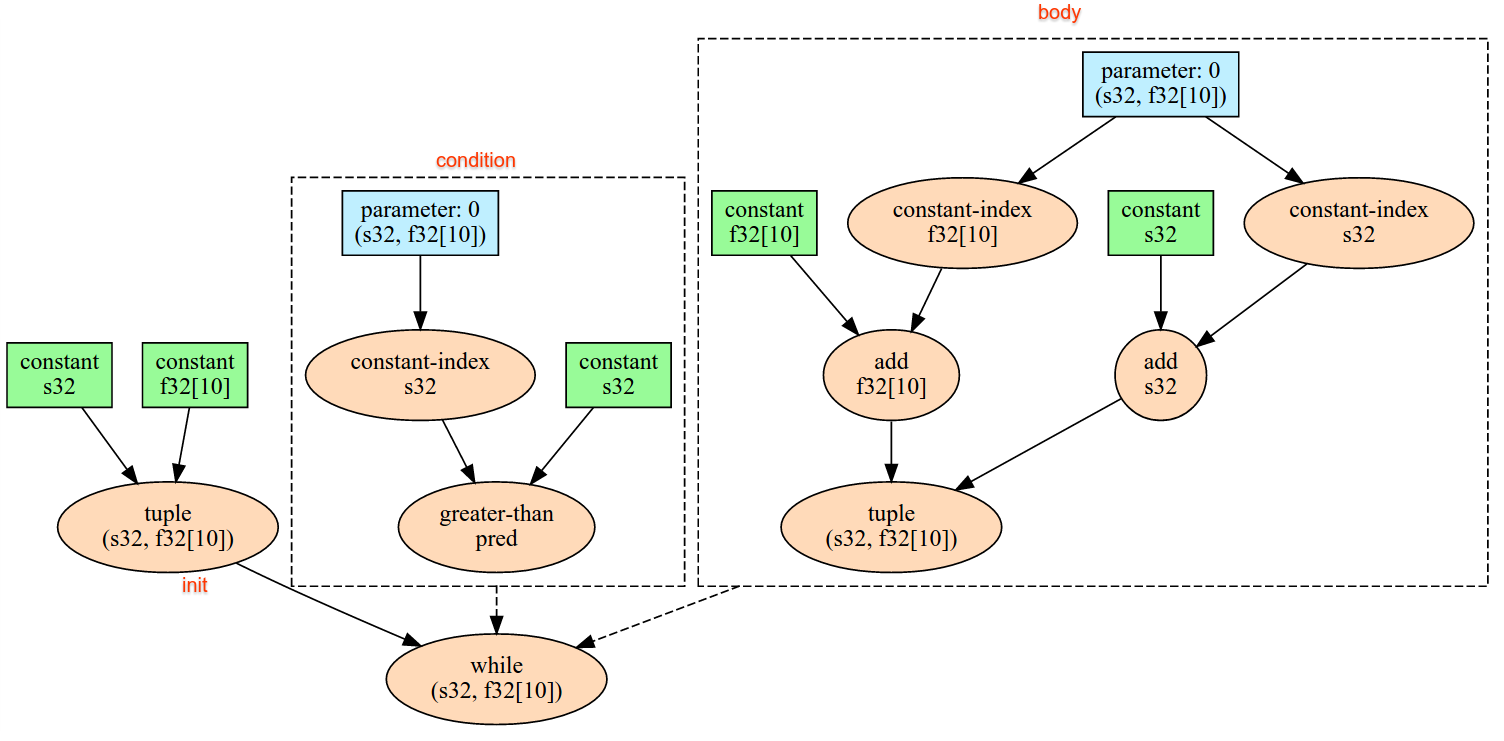
Weitere Informationen zu StableHLO finden Sie unter StableHLO – while.
Xor
Siehe auch XlaBuilder::Xor.
Führt ein elementweises XOR von lhs und rhs aus.
Xor(lhs, rhs)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
Die Formen der Argumente müssen entweder ähnlich oder kompatibel sein. In der Dokumentation zum Broadcasting finden Sie Informationen dazu, was es bedeutet, wenn Formen kompatibel sind. Das Ergebnis einer Operation hat eine Form, die sich aus dem Broadcasting der beiden Eingabearrays ergibt. In dieser Variante werden Operationen zwischen Arrays mit unterschiedlichen Rängen nicht unterstützt, es sei denn, einer der Operanden ist ein Skalar.
Für Xor gibt es eine alternative Variante mit Unterstützung für Broadcasting mit unterschiedlichen Dimensionen:
Xor(lhs,rhs, broadcast_dimensions)
| Argumente | Typ | Semantik |
|---|---|---|
| lhs | XlaOp | Linker Operand: Array vom Typ T |
| rhs | XlaOp | Linker Operand: Array vom Typ T |
| broadcast_dimension | ArraySlice |
Welcher Dimension im Ziel-Shape jede Dimension des Operanden-Shape entspricht |
Diese Variante des Vorgangs sollte für arithmetische Operationen zwischen Arrays unterschiedlichen Rangs verwendet werden, z. B. zum Addieren einer Matrix zu einem Vektor.
Der zusätzliche Operand „broadcast_dimensions“ ist ein Slice von Ganzzahlen, der die Dimensionen angibt, die zum Broadcasten der Operanden verwendet werden sollen. Die Semantik wird auf der Seite zum Broadcasting ausführlich beschrieben.
Weitere Informationen zu StableHLO finden Sie unter StableHLO – xor.








