موارد زیر، معنای عملیات تعریف شده در رابط XlaBuilder را شرح میدهد. معمولاً این عملیاتها به صورت یک به یک به عملیات تعریف شده در رابط RPC در xla_data.proto نگاشت میشوند.
نکتهای در مورد نامگذاری: نوع داده تعمیمیافته XLA با یک آرایه N بعدی سروکار دارد که عناصری از نوع یکنواخت (مانند اعشار ۳۲ بیتی) را در خود نگه میدارد. در سراسر مستندات، از آرایه برای نشان دادن یک آرایه با ابعاد دلخواه استفاده میشود. برای راحتی، موارد خاص نامهای مشخصتر و آشناتری دارند؛ به عنوان مثال، یک بردار یک آرایه ۱ بعدی و یک ماتریس یک آرایه ۲ بعدی است.
برای کسب اطلاعات بیشتر در مورد ساختار یک عملیات، به بخش شکلها و طرحبندی و بخش طرحبندی کاشیکاری شده مراجعه کنید.
شکم
همچنین به XlaBuilder::Abs مراجعه کنید.
در هر عنصر، abs x -> |x| .
Abs(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | عملوند تابع |
برای اطلاعات StableHLO به StableHLO - abs مراجعه کنید.
اضافه کردن
همچنین XlaBuilder::Add ببینید.
جمع lhs و rhs را به صورت عنصر به عنصر انجام میدهد.
Add(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| ل اچ اس | ایکس لا اوپ | عملوند سمت چپ: آرایهای از نوع T |
| rhs | ایکس لا اوپ | عملوند سمت چپ: آرایهای از نوع T |
شکل آرگومانها باید یا مشابه باشند یا سازگار. برای آشنایی با مفهوم سازگار بودن شکلها، به مستندات پخش مراجعه کنید. نتیجه یک عملیات، شکلی دارد که حاصل پخش دو آرایه ورودی است. در این نوع، عملیات بین آرایههایی با رتبههای مختلف پشتیبانی نمیشود ، مگر اینکه یکی از عملوندها اسکالر باشد.
یک نوع جایگزین با پشتیبانی از پخش چندبعدی برای Add وجود دارد:
Add(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| ل اچ اس | ایکس لا اوپ | عملوند سمت چپ: آرایهای از نوع T |
| rhs | ایکس لا اوپ | عملوند سمت چپ: آرایهای از نوع T |
| بُعد_پخش | آرایه برش | هر بُعد از شکل عملوند با کدام بُعد در شکل هدف مطابقت دارد؟ |
این نوع عملیات باید برای عملیات حسابی بین آرایههایی با رتبههای مختلف (مانند جمع کردن یک ماتریس به یک بردار) استفاده شود.
عملوند اضافی broadcast_dimensions برشی از اعداد صحیح است که ابعاد مورد استفاده برای پخش عملوندها را مشخص میکند. معانی آن به تفصیل در صفحه پخش توضیح داده شده است.
برای اطلاعات StableHLO به StableHLO - add مراجعه کنید.
افزودن وابستگی
همچنین HloInstruction::AddDependency مراجعه کنید.
AddDependency ممکن است در دامپهای HLO ظاهر شود، اما قرار نیست توسط کاربران نهایی به صورت دستی ساخته شوند.
بالاخره
همچنین به XlaBuilder::AfterAll مراجعه کنید.
AfterAll تعداد متغیری از توکنها را میگیرد و یک توکن واحد تولید میکند. توکنها انواع اولیهای هستند که میتوانند بین عملیات جانبی برای اعمال ترتیب، رشتهبندی شوند. AfterAll میتواند به عنوان اتصال توکنها برای ترتیب یک عملیات پس از مجموعهای از عملیاتها استفاده شود.
AfterAll(tokens)
| استدلالها | نوع | معناشناسی |
|---|---|---|
tokens | بردار XlaOp | تعداد متغیر توکنها |
برای اطلاعات StableHLO به StableHLO - after_all مراجعه کنید.
آلگَتِر
همچنین به XlaBuilder::AllGather مراجعه کنید.
عملیات الحاق را در بین کپیها انجام میدهد.
AllGather(operand, all_gather_dimension, shard_count, replica_groups, channel_id, layout, use_global_device_ids)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | آرایهای برای الحاق در سراسر کپیها |
all_gather_dimension | int64 | بُعد الحاق |
shard_count | int64 | اندازه هر گروه کپی |
replica_groups | بردار بردارهای int64 | گروههایی که الحاق بین آنها انجام میشود |
channel_id | ChannelHandle اختیاری | شناسه کانال اختیاری برای ارتباط بین ماژولها |
layout | Layout اختیاری | یک الگوی طرحبندی ایجاد میکند که طرحبندی منطبق در آرگومان را ثبت میکند. |
use_global_device_ids | bool اختیاری | اگر شناسههای موجود در پیکربندی ReplicaGroup نشاندهندهی یک شناسهی سراسری باشند، مقدار true را برمیگرداند. |
-
replica_groupsفهرستی از گروههای کپی است که الحاق بین آنها انجام میشود (شناسه کپی برای کپی فعلی را میتوان با استفاده ازReplicaIdبازیابی کرد). ترتیب کپیها در هر گروه، ترتیب قرارگیری ورودیهای آنها در نتیجه را تعیین میکند.replica_groupsیا باید خالی باشد (که در این صورت همه کپیها به یک گروه واحد تعلق دارند که از0تاN - 1مرتب شدهاند)، یا باید شامل تعداد عناصر یکسانی با تعداد کپیها باشد. به عنوان مثال،replica_groups = {0, 2}, {1, 3}الحاق بین کپیهای0و2و1و3را انجام میدهد. -
shard_countاندازه هر گروه replica است. ما در مواردی کهreplica_groupsخالی است به این نیاز داریم. -
channel_idبرای ارتباط بین ماژولها استفاده میشود: فقط عملیاتهایall-gatherباchannel_idیکسان میتوانند با یکدیگر ارتباط برقرار کنند. - اگر شناسههای موجود در پیکربندی ReplicaGroup به جای شناسه replica، نشاندهنده یک شناسه سراسری (replica_id * partition_count + partition_id) باشند، مقدار true را
use_global_device_ids. این امر گروهبندی انعطافپذیرتر دستگاهها را در صورتی که این all-reduce هم به صورت cross-partition و هم به صورت cross-replica باشد، امکانپذیر میسازد.
شکل خروجی، شکل ورودی است که all_gather_dimension آن shard_count چند برابر بزرگتر کرده است. برای مثال، اگر دو کپی وجود داشته باشد و عملوند به ترتیب مقدار [1.0, 2.5] و [3.0, 5.25] را در دو کپی داشته باشد، آنگاه مقدار خروجی از این عملیات که all_gather_dim برابر با 0 است، در هر دو کپی [1.0, 2.5, 3.0,5.25] خواهد بود.
رابط برنامهنویسی کاربردی (API) مربوط به AllGather به صورت داخلی به دو دستورالعمل HLO ( AllGatherStart و AllGatherDone ) تجزیه شده است.
همچنین HloInstruction::CreateAllGatherStart مراجعه کنید.
AllGatherStart و AllGatherDone به عنوان مقادیر اولیه در HLO عمل میکنند. این عملیات ممکن است در فایلهای HLO ظاهر شوند، اما قرار نیست توسط کاربران نهایی به صورت دستی ساخته شوند.
برای اطلاعات StableHLO به StableHLO - all_gather مراجعه کنید.
همهکاهش
همچنین به XlaBuilder::AllReduce مراجعه کنید.
یک محاسبه سفارشی را در سراسر کپیها انجام میدهد.
AllReduce(operand, computation, replica_groups, channel_id, shape_with_layout, use_global_device_ids)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | آرایه یا یک تاپل غیر تهی از آرایهها برای کاهش در کپیها |
computation | XlaComputation | محاسبه کاهش |
replica_groups | بردار ReplicaGroup | گروههایی که کاهشها بین آنها انجام میشود |
channel_id | ChannelHandle اختیاری | شناسه کانال اختیاری برای ارتباط بین ماژولها |
shape_with_layout | Shape اختیاری | طرحبندی دادههای منتقلشده را تعریف میکند |
use_global_device_ids | bool اختیاری | اگر شناسههای موجود در پیکربندی ReplicaGroup نشاندهندهی یک شناسهی سراسری باشند، مقدار true را برمیگرداند. |
- وقتی
operandیک چندتایی از آرایهها باشد، تمام کاهش روی هر عنصر چندتایی انجام میشود. -
replica_groupsفهرستی از گروههای کپی است که کاهش بین آنها انجام میشود (شناسه کپی برای کپی فعلی را میتوان با استفاده ازReplicaIdبازیابی کرد).replica_groupsیا باید خالی باشد (که در این صورت همه کپیها به یک گروه واحد تعلق دارند)، یا باید شامل تعداد عناصر یکسانی با تعداد کپیها باشد. به عنوان مثال،replica_groups = {0, 2}, {1, 3}کاهش را بین کپیهای0و2و1و3انجام میدهد. -
channel_idبرای ارتباط بین ماژولها استفاده میشود: فقط عملیاتهایall-reduceباchannel_idیکسان میتوانند با یکدیگر ارتباط برقرار کنند. -
shape_with_layout: طرحبندی AllReduce را به طرحبندی داده شده مجبور میکند. این برای تضمین طرحبندی یکسان برای گروهی از عملیات AllReduce که به طور جداگانه کامپایل شدهاند، استفاده میشود. - اگر شناسههای موجود در پیکربندی ReplicaGroup به جای شناسه replica، نشاندهنده یک شناسه سراسری (replica_id * partition_count + partition_id) باشند، مقدار true را
use_global_device_ids. این امر گروهبندی انعطافپذیرتر دستگاهها را در صورتی که این all-reduce هم به صورت cross-partition و هم به صورت cross-replica باشد، امکانپذیر میسازد.
شکل خروجی همان شکل ورودی است. برای مثال، اگر دو کپی وجود داشته باشد و عملوند به ترتیب مقدار [1.0, 2.5] و [3.0, 5.25] را در دو کپی داشته باشد، مقدار خروجی حاصل از این محاسبه عملیات و جمع در هر دو کپی [4.0, 7.75] خواهد بود. اگر ورودی یک چندتایی باشد، خروجی نیز یک چندتایی است.
محاسبه نتیجه AllReduce نیاز به داشتن یک ورودی از هر کپی دارد، بنابراین اگر یک کپی، گره AllReduce را بیشتر از دیگری اجرا کند، کپی قبلی برای همیشه منتظر خواهد ماند. از آنجایی که کپیها همه یک برنامه را اجرا میکنند، راههای زیادی برای وقوع این اتفاق وجود ندارد، اما زمانی که شرط یک حلقه while به دادههای infeed بستگی دارد و دادههای infeed باعث میشوند که حلقه while تعداد دفعات بیشتری روی یک کپی نسبت به دیگری تکرار شود، این امر امکانپذیر است.
رابط برنامهنویسی کاربردی AllReduce به صورت داخلی به دو دستورالعمل HLO ( AllReduceStart و AllReduceDone ) تجزیه شده است.
همچنین HloInstruction::CreateAllReduceStart مراجعه کنید.
AllReduceStart و AllReduceDone به عنوان مقادیر اولیه در HLO عمل میکنند. این عملیات ممکن است در فایلهای HLO ظاهر شوند، اما قرار نیست توسط کاربران نهایی به صورت دستی ساخته شوند.
CrossReplicaSum
همچنین به XlaBuilder::CrossReplicaSum مراجعه کنید.
AllReduce با محاسبه جمع انجام میدهد.
CrossReplicaSum(operand, replica_groups)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | ایکس لا اوپ | آرایه یا یک تاپل غیر تهی از آرایهها برای کاهش در کپیها |
replica_groups | بردار بردارهای int64 | گروههایی که کاهشها بین آنها انجام میشود |
مجموع مقدار عملوند را در هر زیرگروه از کپیها برمیگرداند. همه کپیها یک ورودی به مجموع میدهند و همه کپیها مجموع حاصل را برای هر زیرگروه دریافت میکنند.
همه به همه
همچنین به XlaBuilder::AllToAll مراجعه کنید.
AllToAll یک عملیات جمعی است که دادهها را از همه هستهها به همه هستهها ارسال میکند. این عملیات دو مرحله دارد:
- مرحله پراکندگی. در هر هسته، عملوند به تعداد بلوکهای
split_countدر امتدادsplit_dimensionsتقسیم میشود و بلوکها به تمام هستهها پراکنده میشوند، مثلاً بلوک iام به هسته iام ارسال میشود. - مرحله جمعآوری. هر هسته بلوکهای دریافتی را در امتداد
concat_dimensionبه هم متصل میکند.
هستههای شرکتکننده را میتوان با موارد زیر پیکربندی کرد:
-
replica_groups: هر ReplicaGroup شامل لیستی از شناسههای کپی است که در محاسبه شرکت میکنند (شناسه کپی برای کپی فعلی را میتوان با استفاده ازReplicaIdبازیابی کرد). AllToAll در زیرگروهها به ترتیب مشخص شده اعمال خواهد شد. به عنوان مثال،replica_groups = { {1,2,3}, {4,5,0} }به این معنی است که یک AllToAll در کپیهای{1, 2, 3}و در مرحله جمعآوری اعمال میشود و بلوکهای دریافتی به همان ترتیب 1، 2، 3 به هم متصل میشوند. سپس، AllToAll دیگری در کپیهای 4، 5، 0 اعمال میشود و ترتیب الحاق نیز 4، 5، 0 است. اگرreplica_groupsخالی باشد، همه کپیها به یک گروه تعلق دارند، به ترتیب الحاق ظاهر شدنشان.
پیشنیازها:
- اندازه بُعد عملوند روی
split_dimensionبرsplit_countبخشپذیر است. - شکل عملوند چندتایی نیست.
AllToAll(operand, split_dimension, concat_dimension, split_count, replica_groups, layout, channel_id)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | آرایه ورودی n بعدی |
split_dimension | int64 | مقداری در بازه [0,n) که نام بُعدی است که عملوند در امتداد آن تقسیم میشود |
concat_dimension | int64 | مقداری در بازه [0,n) که بُعدی را که بلوکهای تقسیمشده در امتداد آن به هم متصل میشوند، نامگذاری میکند. |
split_count | int64 | تعداد هستههایی که در این عملیات شرکت میکنند. اگر replica_groups خالی باشد، این باید تعداد کپیها باشد؛ در غیر این صورت، این باید برابر با تعداد کپیها در هر گروه باشد. |
replica_groups | بردار ReplicaGroup | هر گروه شامل لیستی از شناسههای کپی است. |
layout | Layout اختیاری | طرح حافظه مشخص شده توسط کاربر |
channel_id | ChannelHandle اختیاری | شناسه منحصر به فرد برای هر جفت ارسال/دریافت |
برای اطلاعات بیشتر در مورد شکلها و طرحبندیها، به xla::shapes مراجعه کنید.
برای اطلاعات StableHLO به StableHLO - all_to_all مراجعه کنید.
همه به همه - مثال ۱.
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(
x,
/*split_dimension=*/ 1,
/*concat_dimension=*/ 0,
/*split_count=*/ 4);
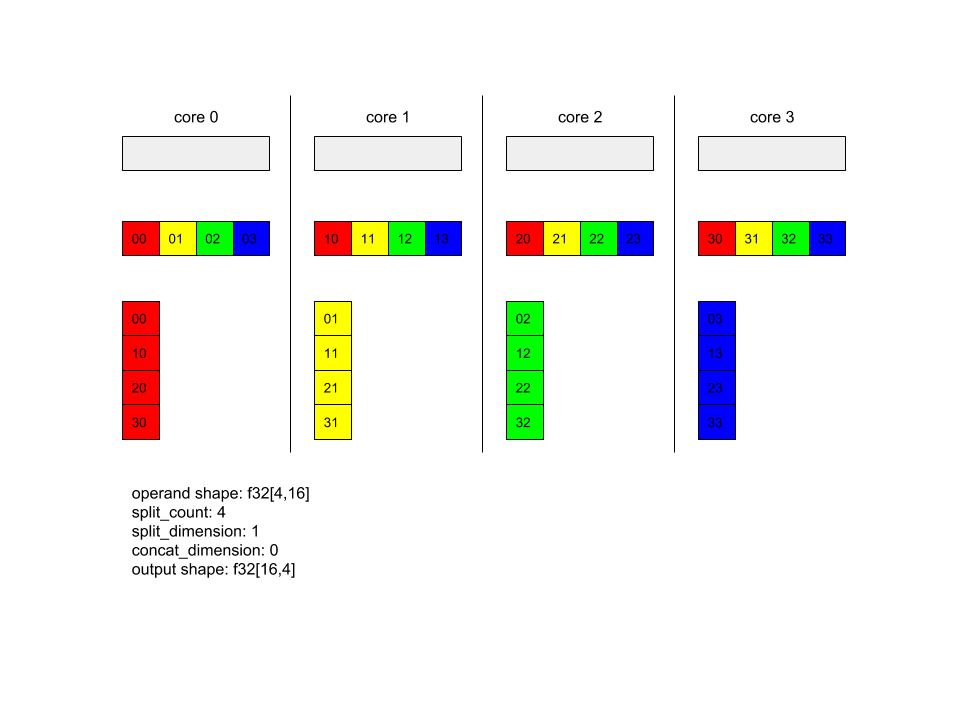
در مثال بالا، 4 هسته در Alltoall شرکت دارند. در هر هسته، عملوند به 4 قسمت در امتداد بُعد 1 تقسیم میشود، بنابراین هر قسمت شکل f32[4,4] را دارد. 4 قسمت در تمام هستهها پراکنده میشوند. سپس هر هسته، قسمتهای دریافتی را در امتداد بُعد 0، به ترتیب از هسته 0 تا 4، به هم متصل میکند. بنابراین خروجی در هر هسته شکل f32[16,4] را دارد.
AllToAll - مثال 2 - StableHLO
در مثال بالا، 2 کپی در AllToAll شرکت دارند. در هر کپی، عملوند به شکل f32[2,4] است. عملوند در امتداد بُعد 1 به 2 قسمت تقسیم میشود، بنابراین هر قسمت شکل f32[2,2] را دارد. سپس این 2 قسمت بر اساس موقعیتشان در گروه کپی، بین کپیها جابجا میشوند. هر کپی، قسمت مربوط به خود را از هر دو عملوند جمعآوری کرده و آنها را در امتداد بُعد 0 به هم متصل میکند. در نتیجه، خروجی در هر کپی به شکل f32[4,2] است.
همه چیز به همه
همچنین به XlaBuilder::RaggedAllToAll مراجعه کنید.
RaggedAllToAll یک عملیات همه به همه را به صورت جمعی انجام میدهد، که در آن ورودی و خروجی، تانسورهای ناهموار هستند.
RaggedAllToAll(input, input_offsets, send_sizes, output, output_offsets, recv_sizes, replica_groups, channel_id)
| استدلالها | نوع | معناشناسی |
|---|---|---|
input | XlaOp | N آرایه از نوع T |
input_offsets | XlaOp | N آرایه از نوع T |
send_sizes | XlaOp | N آرایه از نوع T |
output | XlaOp | N آرایه از نوع T |
output_offsets | XlaOp | N آرایه از نوع T |
recv_sizes | XlaOp | N آرایه از نوع T |
replica_groups | بردار ReplicaGroup | هر گروه شامل لیستی از شناسههای کپی است. |
channel_id | ChannelHandle اختیاری | شناسه منحصر به فرد برای هر جفت ارسال/دریافت |
تانسورهای ناهموار توسط مجموعهای از سه تانسور تعریف میشوند:
-
data: تانسورdataدر امتداد بیرونیترین بُعد خود «ناهموار» شده است، که در امتداد آن هر عنصر اندیسگذاری شده اندازه متغیری دارد. -
offsets': تانسورoffsets، بیرونیترین بُعد تانسورdataرا اندیسگذاری میکند و نشاندهندهی آفست شروع هر عنصر ناهموار تانسورdataاست. -
sizes: تانسورsizesنشاندهنده اندازه هر عنصر ناهموار از تانسورdataاست، که در آن اندازه بر حسب واحدهای زیرعناصر مشخص میشود. یک زیرعنصر به عنوان پسوند شکل تانسور «داده» که با حذف بیرونیترین بُعد «ناهموار» به دست میآید، تعریف میشود. - تانسورهای
offsetsوsizesباید اندازه یکسانی داشته باشند.
یک نمونه از تانسور ناهموار:
data: [8,3] =
{ {a,b,c},{d,e,f},{g,h,i},{j,k,l},{m,n,o},{p,q,r},{s,t,u},{v,w,x} }
offsets: [3] = {0, 1, 4}
sizes: [3] = {1, 3, 4}
// Index 'data' at 'offsets'[0], 'sizes'[0]' // {a,b,c}
// Index 'data' at 'offsets'[1], 'sizes'[1]' // {d,e,f},{g,h,i},{j,k,l}
// Index 'data' at 'offsets'[2], 'sizes'[2]' // {m,n,o},{p,q,r},{s,t,u},{v,w,x}
output_offsets باید به گونهای تقسیمبندی شوند که هر کپی، در دیدگاه خروجی کپی هدف، دارای آفست باشد.
برای i امین آفست خروجی، کپی فعلی، بهروزرسانی input[input_offsets[i]:input_offsets[i]+input_sizes[i]] را به کپی i ام ارسال میکند که در output_i[output_offsets[i]:output_offsets[i]+send_sizes[i]] در output کپی i ام نوشته خواهد شد.
برای مثال، اگر دو کپی داشته باشیم:
replica 0:
input: [1, 2, 2]
output:[0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 2]
output_offsets: [0, 0]
recv_sizes: [1, 1]
replica 1:
input: [3, 4, 0]
output: [0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 1]
output_offsets: [1, 2]
recv_sizes: [2, 1]
// replica 0's result will be: [1, 3, 0, 0]
// replica 1's result will be: [2, 2, 4, 0]
HLO نامرتب و همهکاره، استدلالهای زیر را دارد:
-
input: تانسور داده ورودی ناهموار. -
output: تانسور داده خروجی ناهموار. -
input_offsets: تانسور آفستهای ورودی ناهموار. -
send_sizes: تانسور اندازههای ارسال نامنظم. -
output_offsets: آرایهای از آفستهای ناهموار در خروجی کپی هدف. -
recv_sizes: تانسور اندازههای recv ناهموار.
تانسورهای *_offsets و *_sizes باید همگی شکل یکسانی داشته باشند.
دو شکل برای تانسورهای *_offsets و *_sizes پشتیبانی میشوند:
-
[num_devices]که در آن ragged-all-to-all میتواند حداکثر یک بهروزرسانی را به هر دستگاه از راه دور در گروه replica ارسال کند. برای مثال:
for (remote_device_id : replica_group) {
SEND input[input_offsets[remote_device_id]],
output[output_offsets[remote_device_id]],
send_sizes[remote_device_id] }
[num_devices, num_updates]که در آن ragged-all-to-all میتواند بهروزرسانیهایnum_updatesرا برای هر دستگاه راه دور در گروه replica تا همان دستگاه راه دور (هر کدام با آفستهای مختلف) ارسال کند.
برای مثال:
for (remote_device_id : replica_group) {
for (update_idx : num_updates) {
SEND input[input_offsets[remote_device_id][update_idx]],
output[output_offsets[remote_device_id][update_idx]]],
send_sizes[remote_device_id][update_idx] } }
و
همچنین XlaBuilder::And را ببینید.
عمل AND را به صورت عنصر به عنصر روی دو تانسور lhs و rhs انجام میدهد.
And(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| ل اچ اس | ایکس لا اوپ | عملوند سمت چپ: آرایهای از نوع T |
| rhs | ایکس لا اوپ | عملوند سمت چپ: آرایهای از نوع T |
شکل آرگومانها باید یا مشابه باشند یا سازگار. برای آشنایی با مفهوم سازگار بودن شکلها، به مستندات پخش مراجعه کنید. نتیجه یک عملیات، شکلی دارد که حاصل پخش دو آرایه ورودی است. در این نوع، عملیات بین آرایههایی با رتبههای مختلف پشتیبانی نمیشود ، مگر اینکه یکی از عملوندها اسکالر باشد.
یک نوع جایگزین با پشتیبانی از پخش چندبعدی برای And وجود دارد:
And(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| ل اچ اس | ایکس لا اوپ | عملوند سمت چپ: آرایهای از نوع T |
| rhs | ایکس لا اوپ | عملوند سمت چپ: آرایهای از نوع T |
| بُعد_پخش | آرایه برش | هر بُعد از شکل عملوند با کدام بُعد در شکل هدف مطابقت دارد؟ |
این نوع عملیات باید برای عملیات حسابی بین آرایههایی با رتبههای مختلف (مانند جمع کردن یک ماتریس به یک بردار) استفاده شود.
عملوند اضافی broadcast_dimensions برشی از اعداد صحیح است که ابعاد مورد استفاده برای پخش عملوندها را مشخص میکند. معانی آن به تفصیل در صفحه پخش توضیح داده شده است.
برای اطلاعات StableHLO به StableHLO - و مراجعه کنید.
ناهمگام
همچنین HloInstruction::CreateAsyncStart ، HloInstruction::CreateAsyncUpdate ، HloInstruction::CreateAsyncDone مراجعه کنید.
AsyncDone ، AsyncStart و AsyncUpdate دستورالعملهای داخلی HLO هستند که برای عملیات ناهمزمان استفاده میشوند و به عنوان مقادیر اولیه در HLO عمل میکنند. این عملیات ممکن است در فایلهای HLO ظاهر شوند، اما قرار نیست توسط کاربران نهایی به صورت دستی ساخته شوند.
آتان۲
همچنین به XlaBuilder::Atan2 مراجعه کنید.
عملیات atan2 را بر اساس عنصر روی lhs و rhs انجام میدهد.
Atan2(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| ل اچ اس | ایکس لا اوپ | عملوند سمت چپ: آرایهای از نوع T |
| rhs | ایکس لا اوپ | عملوند سمت چپ: آرایهای از نوع T |
شکل آرگومانها باید یا مشابه باشند یا سازگار. برای آشنایی با مفهوم سازگار بودن شکلها، به مستندات پخش مراجعه کنید. نتیجه یک عملیات، شکلی دارد که حاصل پخش دو آرایه ورودی است. در این نوع، عملیات بین آرایههایی با رتبههای مختلف پشتیبانی نمیشود ، مگر اینکه یکی از عملوندها اسکالر باشد.
یک نوع جایگزین با پشتیبانی از پخش چندبعدی برای Atan2 وجود دارد:
Atan2(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| ل اچ اس | ایکس لا اوپ | عملوند سمت چپ: آرایهای از نوع T |
| rhs | ایکس لا اوپ | عملوند سمت چپ: آرایهای از نوع T |
| بُعد_پخش | آرایه برش | هر بُعد از شکل عملوند با کدام بُعد در شکل هدف مطابقت دارد؟ |
این نوع عملیات باید برای عملیات حسابی بین آرایههایی با رتبههای مختلف (مانند جمع کردن یک ماتریس به یک بردار) استفاده شود.
عملوند اضافی broadcast_dimensions برشی از اعداد صحیح است که ابعاد مورد استفاده برای پخش عملوندها را مشخص میکند. معانی آن به تفصیل در صفحه پخش توضیح داده شده است.
برای اطلاعات StableHLO به StableHLO - atan2 مراجعه کنید.
BatchNormGrad
همچنین برای شرح مفصلی از الگوریتم، به XlaBuilder::BatchNormGrad و مقاله اصلی نرمالسازی دستهای مراجعه کنید.
گرادیانهای نرم دستهای را محاسبه میکند.
BatchNormGrad(operand, scale, batch_mean, batch_var, grad_output, epsilon, feature_index)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | ایکس لا اوپ | آرایه n بعدی که قرار است نرمالسازی شود (x) |
scale | ایکس لا اوپ | آرایه تک بعدی (\(\gamma\)) |
batch_mean | ایکس لا اوپ | آرایه تک بعدی (\(\mu\)) |
batch_var | ایکس لا اوپ | آرایه تک بعدی (\(\sigma^2\)) |
grad_output | ایکس لا اوپ | گرادیانهای ارسالی به BatchNormTraining (\(\nabla y\)) |
epsilon | float | مقدار اپسیلون (\(\epsilon\)) |
feature_index | int64 | اندیس گذاری برای بُعد ویژگی در operand |
برای هر ویژگی در بُعد ویژگی ( feature_index شاخص بُعد ویژگی در operand است)، این عملیات گرادیانها را نسبت به operand ، offset و scale در تمام ابعاد دیگر محاسبه میکند. feature_index باید یک شاخص معتبر برای بُعد ویژگی در operand باشد.
سه گرادیان با فرمولهای زیر تعریف میشوند (با فرض یک آرایه ۴ بعدی به عنوان operand و با شاخص بعد ویژگی l ، اندازه دسته m و اندازههای مکانی w و h ):
\[ \begin{split} c_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sigma^2_l+\epsilon} \right) \\\\ d_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \\\\ \nabla x_{ijkl} &= \frac{\gamma_{l} }{\sqrt{\sigma^2_{l}+\epsilon} } \left( \nabla y_{ijkl} - d_l - c_l (x_{ijkl} - \mu_{l}) \right) \\\\ \nabla \gamma_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sqrt{\sigma^2_{l}+\epsilon} } \right) \\\\\ \nabla \beta_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \end{split} \]
ورودیهای batch_mean و batch_var نشاندهنده مقادیر گشتاورها در ابعاد دستهای و مکانی هستند.
نوع خروجی یک تاپل از سه هندل است:
| خروجیها | نوع | معناشناسی |
|---|---|---|
grad_operand | ایکس لا اوپ | گرادیان نسبت به operand ورودی (\(\nabla x\)) |
grad_scale | ایکس لا اوپ | گرادیان نسبت به ورودی ** scale ** (\(\nabla\gamma\)) |
grad_offset | ایکس لا اوپ | گرادیان نسبت به offset ورودی (\(\nabla\beta\)) |
برای اطلاعات StableHLO به StableHLO - batch_norm_grad مراجعه کنید.
استنتاج BatchNorm
همچنین برای شرح مفصلی از الگوریتم، به XlaBuilder::BatchNormInference و مقاله اصلی نرمالسازی دستهای مراجعه کنید.
یک آرایه را در ابعاد دستهای و مکانی نرمالسازی میکند.
BatchNormInference(operand, scale, offset, mean, variance, epsilon, feature_index)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | ایکس لا اوپ | آرایه n بعدی که قرار است نرمالسازی شود |
scale | ایکس لا اوپ | آرایه تک بعدی |
offset | ایکس لا اوپ | آرایه تک بعدی |
mean | ایکس لا اوپ | آرایه تک بعدی |
variance | ایکس لا اوپ | آرایه تک بعدی |
epsilon | float | مقدار اپسیلون |
feature_index | int64 | اندیس گذاری برای بُعد ویژگی در operand |
برای هر ویژگی در بُعد ویژگی ( feature_index شاخصی برای بُعد ویژگی در operand است)، این عملیات میانگین و واریانس را در تمام ابعاد دیگر محاسبه میکند و از میانگین و واریانس برای نرمالسازی هر عنصر در operand استفاده میکند. feature_index باید یک شاخص معتبر برای بُعد ویژگی در operand باشد.
BatchNormInference معادل فراخوانی BatchNormTraining بدون محاسبه mean و variance برای هر دسته است. در این روش از mean و variance ورودی به عنوان مقادیر تخمینی استفاده میشود. هدف از این عملیات کاهش تأخیر در استنتاج است، از این رو BatchNormInference نام دارد.
خروجی یک آرایه n بعدی و نرمال شده با شکلی مشابه operand ورودی است.
برای اطلاعات StableHLO به StableHLO - batch_norm_inference مراجعه کنید.
آموزش BatchNorm
همچنین برای شرح مفصلی از الگوریتم، به XlaBuilder::BatchNormTraining و the original batch normalization paper مراجعه کنید.
یک آرایه را در ابعاد دستهای و مکانی نرمالسازی میکند.
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | آرایه n بعدی که قرار است نرمالسازی شود (x) |
scale | XlaOp | آرایه تک بعدی (\(\gamma\)) |
offset | XlaOp | آرایه تک بعدی (\(\beta\)) |
epsilon | float | مقدار اپسیلون (\(\epsilon\)) |
feature_index | int64 | اندیس گذاری برای بُعد ویژگی در operand |
برای هر ویژگی در بُعد ویژگی ( feature_index شاخصی برای بُعد ویژگی در operand است)، این عملیات میانگین و واریانس را در تمام ابعاد دیگر محاسبه میکند و از میانگین و واریانس برای نرمالسازی هر عنصر در operand استفاده میکند. feature_index باید یک شاخص معتبر برای بُعد ویژگی در operand باشد.
الگوریتم برای هر دسته در operand به شرح زیر است \(x\) که شامل m عنصر با w و h به عنوان اندازه ابعاد مکانی است (با فرض اینکه operand یک آرایه ۴ بعدی است):
میانگین دستهای را محاسبه میکند \(\mu_l\) برای هر ویژگی
lدر بُعد ویژگی:\(\mu_l=\frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h x_{ijkl}\)واریانس دستهای را محاسبه میکند \(\sigma^2_l\): $\sigma^2 l=\frac{1}{mwh}\sum {i=1}^m\sum {j=1}^w\sum {k=1}^h (x_{ijkl} - \mu_l)^2$
نرمالسازی، مقیاسبندی و تغییر مکان:\(y_{ijkl}=\frac{\gamma_l(x_{ijkl}-\mu_l)}{\sqrt[2]{\sigma^2_l+\epsilon} }+\beta_l\)
مقدار اپسیلون، که معمولاً عدد کوچکی است، برای جلوگیری از خطاهای تقسیم بر صفر اضافه میشود.
نوع خروجی یک چندتایی از سه XlaOp است:
| خروجیها | نوع | معناشناسی |
|---|---|---|
output | XlaOp | آرایه n بعدی با شکل مشابه operand ورودی (y) |
batch_mean | XlaOp | آرایه تک بعدی (\(\mu\)) |
batch_var | XlaOp | آرایه تک بعدی (\(\sigma^2\)) |
batch_mean و batch_var گشتاورهایی هستند که با استفاده از فرمولهای بالا در ابعاد دستهای و مکانی محاسبه میشوند.
برای اطلاعات StableHLO به StableHLO - batch_norm_training مراجعه کنید.
بیتکست
همچنین HloInstruction::CreateBitcast مراجعه کنید.
ممکن است Bitcast در فایلهای HLO ظاهر شود، اما قرار نیست توسط کاربران نهایی به صورت دستی ساخته شوند.
نوع تبدیل بیتکست
همچنین به XlaBuilder::BitcastConvertType مراجعه کنید.
مشابه tf.bitcast در TensorFlow، عملیات تبدیل بیت به بیت را بر اساس عنصر از یک شکل داده به شکل هدف انجام میدهد. اندازه ورودی و خروجی باید مطابقت داشته باشند: به عنوان مثال، عناصر s32 از طریق روال تبدیل بیت به عناصر f32 تبدیل میشوند و یک عنصر s32 به چهار عنصر s8 تبدیل میشود. تبدیل بیت به عنوان یک تبدیل سطح پایین پیادهسازی میشود، بنابراین ماشینهایی با نمایشهای مختلف ممیز شناور، نتایج متفاوتی خواهند داد.
BitcastConvertType(operand, new_element_type)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | آرایهای از نوع T با تیرههای D |
new_element_type | PrimitiveType | نوع U |
ابعاد عملوند و شکل هدف باید با هم مطابقت داشته باشند، به جز آخرین بُعد که به نسبت اندازه اولیه قبل و بعد از تبدیل تغییر خواهد کرد.
نوع عناصر منبع و مقصد نباید چندتایی باشند.
برای اطلاعات StableHLO به StableHLO - bitcast_convert مراجعه کنید.
تبدیل بیتکست به نوع اولیه با عرض متفاوت
دستورالعمل BitcastConvert HLO از حالتی پشتیبانی میکند که اندازه عنصر خروجی از نوع T' با اندازه عنصر ورودی T برابر نباشد. از آنجایی که کل عملیات از نظر مفهومی یک bitcast است و بایتهای زیرین را تغییر نمیدهد، شکل عنصر خروجی باید تغییر کند. برای B = sizeof(T), B' = sizeof(T') ، دو حالت ممکن وجود دارد.
اول، وقتی B > B' باشد، شکل خروجی یک بُعد فرعی جدید با اندازه B/B' میگیرد. برای مثال:
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
این قانون برای اسکالرهای مؤثر یکسان است:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
از طرف دیگر، برای B' > B دستورالعمل نیاز دارد که آخرین بُعد منطقی شکل ورودی برابر با B'/B باشد و این بُعد در طول تبدیل حذف میشود:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
توجه داشته باشید که تبدیل بین پهنای بیتهای مختلف به صورت عنصری انجام نمیشود.
پخش
همچنین به XlaBuilder::Broadcast مراجعه کنید.
با کپی کردن دادهها در آرایه، ابعاد آن را افزایش میدهد.
Broadcast(operand, broadcast_sizes)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | آرایهای که قرار است کپی شود |
broadcast_sizes | ArraySlice<int64> | اندازههای ابعاد جدید |
ابعاد جدید در سمت چپ درج میشوند، یعنی اگر broadcast_sizes دارای مقادیر {a0, ..., aN} باشد و شکل عملوند دارای ابعاد {b0, ..., bM} باشد، آنگاه شکل خروجی دارای ابعاد {a0, ..., aN, b0, ..., bM} خواهد بود.
ابعاد جدید به کپیهایی از عملوند، یعنی
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
برای مثال، اگر operand یک اسکالر f32 با مقدار 2.0f باشد و broadcast_sizes برابر با {2, 3} باشد، نتیجه یک آرایه با شکل f32[2, 3] خواهد بود و تمام مقادیر موجود در نتیجه 2.0f خواهند بود.
برای اطلاعات StableHLO به StableHLO - broadcast مراجعه کنید.
پخشدردیم
همچنین به XlaBuilder::BroadcastInDim مراجعه کنید.
با کپی کردن دادهها در آرایه، اندازه و تعداد ابعاد آن را افزایش میدهد.
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | آرایهای که قرار است کپی شود |
out_dim_size | ArraySlice<int64> | اندازه ابعاد شکل هدف |
broadcast_dimensions | ArraySlice<int64> | هر بُعد از شکل عملوند با کدام بُعد در شکل هدف مطابقت دارد؟ |
مشابه Broadcast است، اما امکان اضافه کردن ابعاد در هر جایی و گسترش ابعاد موجود با اندازه ۱ را فراهم میکند.
operand به شکلی که توسط out_dim_size توصیف شده است، پخش میشود. broadcast_dimensions ابعاد operand را به ابعاد شکل هدف نگاشت میکند، یعنی بعد iام عملوند به بعد broadcast_dimension[i]ام شکل خروجی نگاشت میشود. ابعاد operand باید اندازه ۱ داشته باشند یا به اندازه ابعادی در شکل خروجی که به آن نگاشت شدهاند، باشند. ابعاد باقیمانده با ابعادی با اندازه ۱ پر میشوند. سپس پخش با ابعاد منحط در امتداد این ابعاد منحط پخش میشود تا به شکل خروجی برسد. معانی به تفصیل در صفحه پخش شرح داده شده است.
تماس بگیرید
همچنین به XlaBuilder::Call مراجعه کنید.
با آرگومانهای داده شده، یک محاسبه را فراخوانی میکند.
Call(computation, operands...)
| استدلالها | نوع | معناشناسی |
|---|---|---|
computation | XlaComputation | محاسبه نوع T_0, T_1, ..., T_{N-1} -> S با N پارامتر از نوع دلخواه |
operands | توالی N XlaOp | N آرگومان از نوع دلخواه |
تعداد و نوع operands باید با پارامترهای computation مطابقت داشته باشد. مجاز است که هیچ operands نداشته باشد.
تماس ترکیبی
همچنین به XlaBuilder::CompositeCall مراجعه کنید.
عملیاتی را که از سایر عملیات StableHLO تشکیل شده است (مرکب شده) کپسوله میکند، ورودیها و composite_attributes را میگیرد و نتایج را تولید میکند. معنای op توسط ویژگی تجزیه پیادهسازی میشود. op ترکیبی را میتوان بدون تغییر معنای برنامه با تجزیه آن جایگزین کرد. در مواردی که inline کردن decomposition معنای op یکسانی را ارائه نمیدهد، استفاده از custom_call را ترجیح دهید.
فیلد نسخه (که مقدار پیشفرض آن 0 است) برای نشان دادن زمان تغییر معنای یک ترکیب استفاده میشود.
این عملیات به صورت یک kCall با ویژگی is_composite=true پیادهسازی شده است. فیلد decomposition توسط ویژگی computation مشخص میشود. ویژگیهای frontend، ویژگیهای باقیمانده را که با composite.
مثالی از عملیات CompositeCall:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
CompositeCall(computation, operands..., name, attributes, version)
| استدلالها | نوع | معناشناسی |
|---|---|---|
computation | XlaComputation | محاسبه نوع T_0, T_1, ..., T_{N-1} -> S با N پارامتر از نوع دلخواه |
operands | توالی N XlaOp | تعداد متغیر مقادیر |
name | string | نام کامپوزیت |
attributes | string اختیاری | دیکشنری رشتهای اختیاری از ویژگیها |
version | اختیاری int64 | شماره به نسخه، بهروزرسانیها به معناشناسی عملیات مرکب |
decomposition یک عملیات، فیلدی به نام نیست، بلکه به صورت یک ویژگی to_apply ظاهر میشود که به تابعی اشاره میکند که شامل پیادهسازی سطح پایینتر است، یعنی to_apply=%funcname
اطلاعات بیشتر در مورد ترکیب و تجزیه را میتوانید در StableHLO Specification بیابید.
سیبیآرتی
همچنین به XlaBuilder::Cbrt مراجعه کنید.
عملیات ریشه سوم به صورت عنصر به عنصر x -> cbrt(x) .
Cbrt(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | عملوند تابع |
Cbrt همچنین از آرگومان اختیاری result_accuracy پشتیبانی میکند:
Cbrt(operand, result_accuracy)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | عملوند تابع |
result_accuracy | ResultAccuracy اختیاری | انواع دقتی که کاربر میتواند برای عملیاتهای تکی با پیادهسازیهای متعدد درخواست کند |
برای اطلاعات بیشتر در مورد result_accuracy به بخش Result Accuracy مراجعه کنید.
برای اطلاعات StableHLO به StableHLO - cbrt مراجعه کنید.
سقف
همچنین به XlaBuilder::Ceil مراجعه کنید.
سقف عنصر-محور x -> ⌈x⌉ .
Ceil(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | عملوند تابع |
برای اطلاعات StableHLO به StableHLO - ceil مراجعه کنید.
چولسکی
همچنین به XlaBuilder::Cholesky مراجعه کنید.
تجزیه چولسکی دستهای از ماتریسهای متقارن (هرمیتی) مثبت معین را محاسبه میکند.
Cholesky(a, lower)
| استدلالها | نوع | معناشناسی |
|---|---|---|
a | XlaOp | آرایهای از نوع مختلط یا ممیز شناور با ابعاد > ۲. |
lower | bool | اینکه آیا از مثلث بالایی یا پایینی a استفاده شود. |
اگر lower true باشد، ماتریسهای پایین-مثلثی l را طوری محاسبه میکند که $a = l. l^T$. اگر lower false باشد، ماتریسهای بالا-مثلثی u طوری محاسبه میکند که\(a = u^T . u\).
دادههای ورودی فقط از مثلث پایینی/بالایی a خوانده میشوند، که به مقدار lower بستگی دارد. مقادیر مثلث دیگر نادیده گرفته میشوند. دادههای خروجی در همان مثلث بازگردانده میشوند؛ مقادیر موجود در مثلث دیگر، از نظر پیادهسازی تعریف شدهاند و میتوانند هر چیزی باشند.
اگر a بیشتر از ۲ بُعد داشته باشد، a به عنوان یک دسته از ماتریسها در نظر گرفته میشود، که در آن همه به جز ۲ بُعد فرعی، ابعاد دستهای هستند.
اگر a متقارن (هرمیتی) مثبت معین نباشد، نتیجه تعریفشده توسط پیادهسازی است.
برای اطلاعات StableHLO به StableHLO-cholesky مراجعه کنید.
گیره
همچنین به XlaBuilder::Clamp مراجعه کنید.
یک عملوند را در محدوده بین حداقل و حداکثر مقدار نگه میدارد.
Clamp(min, operand, max)
| استدلالها | نوع | معناشناسی |
|---|---|---|
min | XlaOp | آرایه از نوع T |
operand | XlaOp | آرایه از نوع T |
max | XlaOp | آرایه از نوع T |
با توجه به یک عملوند و مقادیر حداقل و حداکثر، اگر عملوند در محدوده بین حداقل و حداکثر باشد، مقدار حداقل را برمیگرداند، در غیر این صورت اگر عملوند کمتر از این محدوده باشد یا مقدار حداکثر را برمیگرداند اگر عملوند بالاتر از این محدوده باشد. یعنی، clamp(a, x, b) = min(max(a, x), b) .
هر سه آرایه باید شکل یکسانی داشته باشند. از طرف دیگر، به عنوان یک شکل محدود از پخش ، min و/یا max میتوانند یک اسکالر از نوع T باشند.
مثال با min و max اسکالر:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
برای اطلاعات StableHLO به گیره StableHLO مراجعه کنید.
جمع کردن
همچنین به XlaBuilder::Collapse و عملیات tf.reshape مراجعه کنید.
ابعاد یک آرایه را به یک بعد تبدیل میکند.
Collapse(operand, dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | آرایه از نوع T |
dimensions | بردار int64 | زیرمجموعهای متوالی و مرتب از ابعاد T. |
تابع Collapse زیرمجموعهی دادهشده از ابعاد عملوند را با یک بُعد واحد جایگزین میکند. آرگومانهای ورودی یک آرایهی دلخواه از نوع T و یک بردار ثابت زمان کامپایل از شاخصهای بُعد هستند. شاخصهای بُعد باید یک زیرمجموعهی متوالی و به ترتیب (اعداد با بُعد کم به زیاد) از ابعاد T باشند. بنابراین، {0، 1، 2}، {0، 1} یا {1، 2} همگی مجموعههای بُعد معتبری هستند، اما {1، 0} یا {0، 2} معتبر نیستند. آنها با یک بُعد جدید واحد، در همان موقعیت در دنباله بُعدهایی که جایگزین میشوند، جایگزین میشوند و اندازهی بُعد جدید برابر با حاصلضرب اندازههای بُعد اصلی است. کمترین عدد بُعد در dimensions ، کندترین بُعد متغیر (بزرگترین) در لانهی حلقه است که این ابعاد را جمع میکند و بالاترین عدد بُعد، سریعترین بُعد متغیر (کوچکترین) است. اگر به ترتیب کلیتر برای جمع کردن نیاز دارید، به عملگر tf.reshape مراجعه کنید.
برای مثال، فرض کنید v آرایهای با ۲۴ عنصر باشد:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
کلز
همچنین به XlaBuilder::Clz مراجعه کنید.
صفرهای پیشرو را به صورت عنصری بشمارید.
Clz(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | عملوند تابع |
پخش جمعی
همچنین به XlaBuilder::CollectiveBroadcast مراجعه کنید.
دادهها را در سراسر کپیها پخش میکند. دادهها از اولین شناسه کپی در هر گروه به شناسههای دیگر در همان گروه ارسال میشوند. اگر شناسه کپی در هیچ گروه کپی نباشد، خروجی روی آن کپی، تانسوری متشکل از 0(ها) به shape است.
CollectiveBroadcast(operand, replica_groups, channel_id)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | عملوند تابع |
replica_groups | بردار ReplicaGroup | هر گروه شامل لیستی از شناسههای کپی است. |
channel_id | ChannelHandle اختیاری | شناسه منحصر به فرد برای هر جفت ارسال/دریافت |
برای اطلاعات StableHLO به StableHLO - collective_broadcast مراجعه کنید.
CollectivePermute
همچنین به XlaBuilder::CollectivePermute مراجعه کنید.
CollectivePermute یک عملیات جمعی است که دادهها را بین کپیها ارسال و دریافت میکند.
CollectivePermute(operand, source_target_pairs, channel_id, inplace)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | آرایه ورودی n بعدی |
source_target_pairs | <int64, int64> | فهرستی از جفتهای (source_replica_id, target_replica_id). برای هر جفت، عملوند از کپی منبع به کپی هدف ارسال میشود. |
channel_id | ChannelHandle اختیاری | شناسه کانال اختیاری برای ارتباط بین ماژولها |
inplace | bool اختیاری | علامتگذاری کنید که آیا جایگشت باید در محل انجام شود یا خیر |
توجه داشته باشید که محدودیتهای زیر در مورد source_target_pairs وجود دارد:
- هیچ دو جفتی نباید شناسه کپی هدف یکسانی داشته باشند و همچنین نباید شناسه کپی منبع یکسانی داشته باشند.
- اگر یک شناسه کپی، هدف هیچ جفتی نباشد، خروجی روی آن کپی، تنسوری متشکل از 0(ها) با همان شکل ورودی است.
رابط برنامهنویسی کاربردی (API) عملیات CollectivePermute به صورت داخلی به دو دستورالعمل HLO ( CollectivePermuteStart و CollectivePermuteDone ) تجزیه شده است.
همچنین HloInstruction::CreateCollectivePermuteStart مراجعه کنید.
CollectivePermuteStart و CollectivePermuteDone به عنوان مقادیر اولیه در HLO عمل میکنند. این عملیات ممکن است در فایلهای HLO ظاهر شوند، اما قرار نیست توسط کاربران نهایی به صورت دستی ساخته شوند.
برای اطلاعات StableHLO به StableHLO - collective_permute مراجعه کنید.
مقایسه
همچنین به XlaBuilder::Compare مراجعه کنید.
مقایسه عنصری lhs و rhs موارد زیر را انجام میدهد:
معادله
همچنین به XlaBuilder::Eq مراجعه کنید.
Performs element-wise equal-to comparison of lhs and rhs .
\(lhs = rhs\)
Eq(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Eq:
Eq(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
Support a total order over the floating point numbers exists for Eq, by enforcing:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
EqTotalOrder(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
For StableHLO information see StableHLO - compare .
نه
See also XlaBuilder::Ne .
Performs element-wise not equal-to comparison of lhs and rhs .
\(lhs != rhs\)
Ne(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Ne:
Ne(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
Support a total order over the floating point numbers exists for Ne, by enforcing:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
NeTotalOrder(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
For StableHLO information see StableHLO - compare .
جی
See also XlaBuilder::Ge .
Performs element-wise greater-or-equal-than comparison of lhs and rhs .
\(lhs >= rhs\)
Ge(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Ge:
Ge(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
Support a total order over the floating point numbers exists for Gt, by enforcing:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
GtTotalOrder(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
For StableHLO information see StableHLO - compare .
Gt
See also XlaBuilder::Gt .
Performs element-wise greater-than comparison of lhs and rhs .
\(lhs > rhs\)
Gt(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Gt:
Gt(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - compare .
لو
See also XlaBuilder::Le .
Performs element-wise less-or-equal-than comparison of lhs and rhs .
\(lhs <= rhs\)
Le(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Le:
Le(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
Support a total order over the floating point numbers exists for Le, by enforcing:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LeTotalOrder(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
For StableHLO information see StableHLO - compare .
آن
See also XlaBuilder::Lt .
Performs element-wise less-than comparison of lhs and rhs .
\(lhs < rhs\)
Lt(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Lt:
Lt(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
Support a total order over the floating point numbers exists for Lt, by enforcing:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LtTotalOrder(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
For StableHLO information see StableHLO - compare .
پیچیده
See also XlaBuilder::Complex .
Performs element-wise conversion to a complex value from a pair of real and imaginary values, lhs and rhs .
Complex(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Complex:
Complex(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - complex .
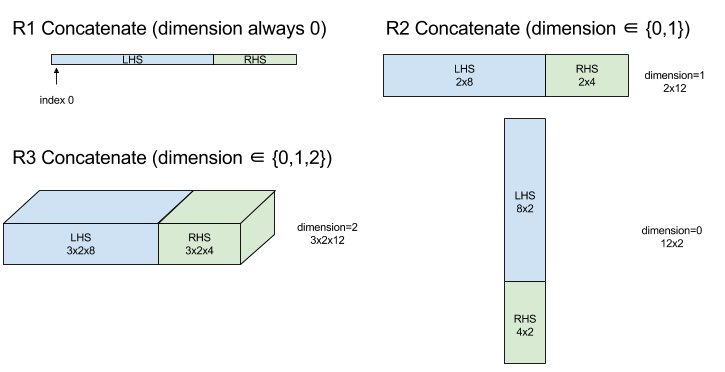
ConcatInDim (Concatenate)
See also XlaBuilder::ConcatInDim .
Concatenate composes an array from multiple array operands. The array has the same number of dimensions as each of the input array operands (which must have the same number of dimensions as each other) and contains the arguments in the order that they were specified.
Concatenate(operands..., dimension)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operands | sequence of N XlaOp | N arrays of type T with dimensions [L0, L1, ...]. Requires N >= 1. |
dimension | int64 | A value in the interval [0, N) that names the dimension to be concatenated between the operands . |
With the exception of dimension all dimensions must be the same. This is because XLA does not support "ragged" arrays. Also note that 0-dimensional values cannot be concatenated (as it's impossible to name the dimension along which the concatenation occurs).
1-dimensional example:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
//Output: {2, 3, 4, 5, 6, 7}
2-dimensional example:
let a = { {1, 2},
{3, 4},
{5, 6} };
let b = { {7, 8} };
Concat({a, b}, 0)
//Output: { {1, 2},
// {3, 4},
// {5, 6},
// {7, 8} }
Diagram:
For StableHLO information see StableHLO - concatenate .
Conditional
See also XlaBuilder::Conditional .
Conditional(predicate, true_operand, true_computation, false_operand, false_computation)
| استدلالها | نوع | معناشناسی |
|---|---|---|
predicate | XlaOp | Scalar of type PRED |
true_operand | XlaOp | Argument of type \(T_0\) |
true_computation | XlaComputation | XlaComputation of type \(T_0 \to S\) |
false_operand | XlaOp | Argument of type \(T_1\) |
false_computation | XlaComputation | XlaComputation of type \(T_1 \to S\) |
Executes true_computation if predicate is true , false_computation if predicate is false , and returns the result.
The true_computation must take in a single argument of type \(T_0\) and will be invoked with true_operand which must be of the same type. The false_computation must take in a single argument of type \(T_1\) and will be invoked with false_operand which must be of the same type. The type of the returned value of true_computation and false_computation must be the same.
Note that only one of true_computation and false_computation will be executed depending on the value of predicate .
Conditional(branch_index, branch_computations, branch_operands)
| استدلالها | نوع | معناشناسی |
|---|---|---|
branch_index | XlaOp | Scalar of type S32 |
branch_computations | sequence of N XlaComputation | XlaComputations of type \(T_0 \to S , T_1 \to S , ..., T_{N-1} \to S\) |
branch_operands | sequence of N XlaOp | Arguments of type \(T_0 , T_1 , ..., T_{N-1}\) |
Executes branch_computations[branch_index] , and returns the result. If branch_index is an S32 which is < 0 or >= N, then branch_computations[N-1] is executed as the default branch.
Each branch_computations[b] must take in a single argument of type \(T_b\) and will be invoked with branch_operands[b] which must be of the same type. The type of the returned value of each branch_computations[b] must be the same.
Note that only one of the branch_computations will be executed depending on the value of branch_index .
For StableHLO information see StableHLO - if .
ثابت
See also XlaBuilder::ConstantLiteral .
Produces an output from a constant literal .
Constant(literal)
| استدلالها | نوع | معناشناسی |
|---|---|---|
literal | LiteralSlice | constant view of an existing Literal |
For StableHLO information see StableHLO - constant .
ConvertElementType
See also XlaBuilder::ConvertElementType .
Similar to an element-wise static_cast in C++, ConvertElementType performs an element-wise conversion operation from a data shape to a target shape. The dimensions must match, and the conversion is an element-wise one; eg s32 elements become f32 elements via an s32 -to- f32 conversion routine.
ConvertElementType(operand, new_element_type)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | array of type T with dims D |
new_element_type | PrimitiveType | type U |
The dimensions of the operand and the target shape must match. The source and destination element types must not be tuples.
A conversion such as T=s32 to U=f32 will perform a normalizing int-to-float conversion routine such as round-to-nearest-even.
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
For StableHLO information see StableHLO - convert .
Conv (Convolution)
See also XlaBuilder::Conv .
Computes a convolution of the kind used in neural networks. Here, a convolution can be thought of as a n-dimensional window moving across a n-dimensional base area and a computation is performed for each possible position of the window.
Conv Enqueues a convolution instruction onto the computation, which uses the default convolution dimension numbers with no dilation.
The padding is specified in a short-hand way as either SAME or VALID. SAME padding pads the input ( lhs ) with zeroes so that the output has the same shape as the input when not taking striding into account. VALID padding simply means no padding.
Conv(lhs, rhs, window_strides, padding, feature_group_count, batch_group_count, precision_config, preferred_element_type)
| استدلالها | نوع | معناشناسی |
|---|---|---|
lhs | XlaOp | (n+2)-dimensional array of inputs |
rhs | XlaOp | (n+2)-dimensional array of kernel weights |
window_strides | ArraySlice<int64> | nd array of kernel strides |
padding | Padding | enum of padding |
feature_group_count | int64 | the number of feature groups |
batch_group_count | int64 | the number of batch groups |
precision_config | optional PrecisionConfig | enum for level of precision |
preferred_element_type | optional PrimitiveType | enum of scalar element type |
Increasing levels of controls are available for Conv :
Let n be the number of spatial dimensions. The lhs argument is an (n+2)-dimensional array describing the base area. This is called the input, even though of course the rhs is also an input. In a neural network, these are the input activations. The n+2 dimensions are, in this order:
-
batch: Each coordinate in this dimension represents an independent input for which convolution is carried out. -
z/depth/features: Each (y,x) position in the base area has a vector associated to it, which goes into this dimension. -
spatial_dims: Describes thenspatial dimensions that define the base area that the window moves across.
The rhs argument is an (n+2)-dimensional array describing the convolutional filter/kernel/window. The dimensions are, in this order:
-
output-z: Thezdimension of the output. -
input-z: The size of this dimension timesfeature_group_countshould equal the size of thezdimension in lhs. -
spatial_dims: Describes thenspatial dimensions that define the nd window that moves across the base area.
The window_strides argument specifies the stride of the convolutional window in the spatial dimensions. For example, if the stride in the first spatial dimension is 3, then the window can only be placed at coordinates where the first spatial index is divisible by 3.
The padding argument specifies the amount of zero padding to be applied to the base area. The amount of padding can be negative -- the absolute value of negative padding indicates the number of elements to remove from the specified dimension before doing the convolution. padding[0] specifies the padding for dimension y and padding[1] specifies the padding for dimension x . Each pair has the low padding as the first element and the high padding as the second element. The low padding is applied in the direction of lower indices while the high padding is applied in the direction of higher indices. For example, if padding[1] is (2,3) then there will be a padding by 2 zeroes on the left and by 3 zeroes on the right in the second spatial dimension. Using padding is equivalent to inserting those same zero values into the input ( lhs ) before doing the convolution.
The lhs_dilation and rhs_dilation arguments specify the dilation factor to be applied to the lhs and rhs, respectively, in each spatial dimension. If the dilation factor in a spatial dimension is d, then d-1 holes are implicitly placed between each of the entries in that dimension, increasing the size of the array. The holes are filled with a no-op value, which for convolution means zeroes.
Dilation of the rhs is also called atrous convolution. For more details, see tf.nn.atrous_conv2d . Dilation of the lhs is also called transposed convolution. For more details, see tf.nn.conv2d_transpose .
The feature_group_count argument (default value 1) can be used for grouped convolutions. feature_group_count needs to be a divisor of both the input and the output feature dimension. If feature_group_count is greater than 1, it means that conceptually the input and output feature dimension and the rhs output feature dimension are split evenly into many feature_group_count groups, each group consisting of a consecutive subsequence of features. The input feature dimension of rhs needs to be equal to the lhs input feature dimension divided by feature_group_count (so it already has the size of a group of input features). The i-th groups are used together to compute feature_group_count for many separate convolutions. The results of these convolutions are concatenated together in the output feature dimension.
For depthwise convolution the feature_group_count argument would be set to the input feature dimension, and the filter would be reshaped from [filter_height, filter_width, in_channels, channel_multiplier] to [filter_height, filter_width, 1, in_channels * channel_multiplier] . For more details, see tf.nn.depthwise_conv2d .
The batch_group_count (default value 1) argument can be used for grouped filters during backpropagation. batch_group_count needs to be a divisor of the size of the lhs (input) batch dimension. If batch_group_count is greater than 1, it means that the output batch dimension should be of size input batch / batch_group_count . The batch_group_count must be a divisor of the output feature size.
The output shape has these dimensions, in this order:
-
batch: The size of this dimension timesbatch_group_countshould equal the size of thebatchdimension in lhs. -
z: Same size asoutput-zon the kernel (rhs). -
spatial_dims: One value for each valid placement of the convolutional window.
The figure above shows how the batch_group_count field works. Effectively, we slice each lhs batch into batch_group_count groups, and do the same for the output features. Then, for each of these groups we do pairwise convolutions and concatenate the output along the output feature dimension. The operational semantics of all the other dimensions (feature and spatial) remain the same.
The valid placements of the convolutional window are determined by the strides and the size of the base area after padding.
To describe what a convolution does, consider a 2d convolution, and pick some fixed batch , z , y , x coordinates in the output. Then (y,x) is a position of a corner of the window within the base area (eg the upper left corner, depending on how you interpret the spatial dimensions). We now have a 2d window, taken from the base area, where each 2d point is associated to a 1d vector, so we get a 3d box. From the convolutional kernel, since we fixed the output coordinate z , we also have a 3d box. The two boxes have the same dimensions, so we can take the sum of the element-wise products between the two boxes (similar to a dot product). That is the output value.
Note that if output-z is eg, 5, then each position of the window produces 5 values in the output into the z dimension of the output. These values differ in what part of the convolutional kernel is used - there is a separate 3d box of values used for each output-z coordinate. So you could think of it as 5 separate convolutions with a different filter for each of them.
Here is pseudo-code for a 2d convolution with padding and striding:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
precision_config is used to indicate the precision configuration. The level dictates whether hardware should attempt to generate more machine code instructions to provide more accurate dtype emulation when needed (ie emulating f32 on a TPU that only supports bf16 matmuls). Values may be DEFAULT , HIGH , HIGHEST . Additional details in the MXU sections .
preferred_element_type is a scalar element of higher/lower precision output types used for accumulation. preferred_element_type recommends the accumulation type for the given operation, however it is not guaranteed. This allows for some hardware backends to instead accumulate in a different type and convert to the preferred output type.
For StableHLO information see StableHLO - convolution .
ConvWithGeneralPadding
See also XlaBuilder::ConvWithGeneralPadding .
ConvWithGeneralPadding(lhs, rhs, window_strides, padding, feature_group_count, batch_group_count, precision_config, preferred_element_type)
Same as Conv where padding configuration is explicit.
| استدلالها | نوع | معناشناسی |
|---|---|---|
lhs | XlaOp | (n+2)-dimensional array of inputs |
rhs | XlaOp | (n+2)-dimensional array of kernel weights |
window_strides | ArraySlice<int64> | nd array of kernel strides |
padding | ArraySlice< pair<int64,int64>> | nd array of (low, high) padding |
feature_group_count | int64 | the number of feature groups |
batch_group_count | int64 | the number of batch groups |
precision_config | optional PrecisionConfig | enum for level of precision |
preferred_element_type | optional PrimitiveType | enum of scalar element type |
ConvWithGeneralDimensions
See also XlaBuilder::ConvWithGeneralDimensions .
ConvWithGeneralDimensions(lhs, rhs, window_strides, padding, dimension_numbers, feature_group_count, batch_group_count, precision_config, preferred_element_type)
Same as Conv where dimension numbers are explicit.
| استدلالها | نوع | معناشناسی |
|---|---|---|
lhs | XlaOp | (n+2)-dimensional array of inputs |
rhs | XlaOp | (n+2)-dimensional array of kernel weights |
window_strides | ArraySlice<int64> | nd array of kernel strides |
padding | Padding | enum of padding |
dimension_numbers | ConvolutionDimensionNumbers | the number of dimensions |
feature_group_count | int64 | the number of feature groups |
batch_group_count | int64 | the number of batch groups |
precision_config | optional PrecisionConfig | enum for level of precision |
preferred_element_type | optional PrimitiveType | enum of scalar element type |
ConvGeneral
See also XlaBuilder::ConvGeneral .
ConvGeneral(lhs, rhs, window_strides, padding, dimension_numbers, feature_group_count, batch_group_count, precision_config, preferred_element_type)
Same as Conv where dimension numbers and padding configuration is explicit
| استدلالها | نوع | معناشناسی |
|---|---|---|
lhs | XlaOp | (n+2)-dimensional array of inputs |
rhs | XlaOp | (n+2)-dimensional array of kernel weights |
window_strides | ArraySlice<int64> | nd array of kernel strides |
padding | ArraySlice< pair<int64,int64>> | nd array of (low, high) padding |
dimension_numbers | ConvolutionDimensionNumbers | the number of dimensions |
feature_group_count | int64 | the number of feature groups |
batch_group_count | int64 | the number of batch groups |
precision_config | optional PrecisionConfig | enum for level of precision |
preferred_element_type | optional PrimitiveType | enum of scalar element type |
ConvGeneralDilated
See also XlaBuilder::ConvGeneralDilated .
ConvGeneralDilated(lhs, rhs, window_strides, padding, lhs_dilation, rhs_dilation, dimension_numbers, feature_group_count, batch_group_count, precision_config, preferred_element_type, window_reversal)
Same as Conv where padding configuration, dilation factors, and dimension numbers are explicit.
| استدلالها | نوع | معناشناسی |
|---|---|---|
lhs | XlaOp | (n+2)-dimensional array of inputs |
rhs | XlaOp | (n+2)-dimensional array of kernel weights |
window_strides | ArraySlice<int64> | nd array of kernel strides |
padding | ArraySlice< pair<int64,int64>> | nd array of (low, high) padding |
lhs_dilation | ArraySlice<int64> | nd lhs dilation factor array |
rhs_dilation | ArraySlice<int64> | nd rhs dilation factor array |
dimension_numbers | ConvolutionDimensionNumbers | the number of dimensions |
feature_group_count | int64 | the number of feature groups |
batch_group_count | int64 | the number of batch groups |
precision_config | optional PrecisionConfig | enum for level of precision |
preferred_element_type | optional PrimitiveType | enum of scalar element type |
window_reversal | optional vector<bool> | flag used to logically reverse dimension before applying the convolution |
کپی
See also HloInstruction::CreateCopyStart .
Copy is internally decomposed into 2 HLO instructions CopyStart and CopyDone . Copy along with CopyStart and CopyDone serve as primitives in HLO. These ops may appear in HLO dumps, but they are not intended to be constructed manually by end users.
Cos
See also XlaBuilder::Cos .
Element-wise cosine x -> cos(x) .
Cos(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
Cos also supports the optional result_accuracy argument:
Cos(operand, result_accuracy)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
For StableHLO information see StableHLO - cosine .
Cosh
See also XlaBuilder::Cosh .
Element-wise hyperbolic cosine x -> cosh(x) .
Cosh(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
Cosh also supports the optional result_accuracy argument:
Cosh(operand, result_accuracy)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
CustomCall
See also XlaBuilder::CustomCall .
Call a user-provided function within a computation.
CustomCall documentation is provided in Developer details - XLA Custom Calls
For StableHLO information see StableHLO - custom_call .
دیو
See also XlaBuilder::Div .
Performs element-wise division of dividend lhs and divisor rhs .
Div(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
Integer division overflow (signed/unsigned division/remainder by zero or signed division/remainder of INT_SMIN with -1 ) produces an implementation defined value.
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Div:
Div(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - divide .
دامنه
See also HloInstruction::CreateDomain .
Domain may appear in HLO dumps, but it is not intended to be constructed manually by end users.
نقطه
See also XlaBuilder::Dot .
Dot(lhs, rhs, precision_config, preferred_element_type)
| استدلالها | نوع | معناشناسی |
|---|---|---|
lhs | XlaOp | array of type T |
rhs | XlaOp | array of type T |
precision_config | optional PrecisionConfig | enum for level of precision |
preferred_element_type | optional PrimitiveType | enum of scalar element type |
The exact semantics of this operation depend on the ranks of the operands:
| ورودی | خروجی | معناشناسی |
|---|---|---|
vector [n] dot vector [n] | scalar | vector dot product |
matrix [mxk] dot vector [k] | vector [m] | matrix-vector multiplication |
matrix [mxk] dot matrix [kxn] | matrix [mxn] | matrix-matrix multiplication |
The operation performs sum of products over the second dimension of lhs (or the first if it has 1 dimension) and the first dimension of rhs . These are the "contracted" dimensions. The contracted dimensions of lhs and rhs must be of the same size. In practice, it can be used to perform dot products between vectors, vector/matrix multiplications or matrix/matrix multiplications.
precision_config is used to indicate the precision configuration. The level dictates whether hardware should attempt to generate more machine code instructions to provide more accurate dtype emulation when needed (ie emulating f32 on a TPU that only supports bf16 matmuls). Values may be DEFAULT , HIGH , HIGHEST . Additional details in the MXU sections .
preferred_element_type is a scalar element of higher/lower precision output types used for accumulation. preferred_element_type recommends the accumulation type for the given operation, however it is not guaranteed. This allows for some hardware backends to instead accumulate in a different type and convert to the preferred output type.
For StableHLO information see StableHLO - dot .
DotGeneral
See also XlaBuilder::DotGeneral .
DotGeneral(lhs, rhs, dimension_numbers, precision_config, preferred_element_type)
| استدلالها | نوع | معناشناسی |
|---|---|---|
lhs | XlaOp | array of type T |
rhs | XlaOp | array of type T |
dimension_numbers | DotDimensionNumbers | contracting and batch dimension numbers |
precision_config | optional PrecisionConfig | enum for level of precision |
preferred_element_type | optional PrimitiveType | enum of scalar element type |
Similar to Dot, but allows contracting and batch dimension numbers to be specified for both the lhs and rhs .
| DotDimensionNumbers Fields | نوع | معناشناسی |
|---|---|---|
lhs_contracting_dimensions | repeated int64 | lhs contracting dimension numbers |
rhs_contracting_dimensions | repeated int64 | rhs contracting dimension numbers |
lhs_batch_dimensions | repeated int64 | lhs batch dimension numbers |
rhs_batch_dimensions | repeated int64 | rhs batch dimension numbers |
DotGeneral performs the sum of products over contracting dimensions specified in dimension_numbers .
Associated contracting dimension numbers from the lhs and rhs do not need to be the same but must have the same dimension sizes.
Example with contracting dimension numbers:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { { 6.0, 12.0},
{15.0, 30.0} }
Associated batch dimension numbers from the lhs and rhs must have the same dimension sizes.
Example with batch dimension numbers (batch size 2, 2x2 matrices):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> {
{ {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| ورودی | خروجی | معناشناسی |
|---|---|---|
[b0, m, k] dot [b0, k, n] | [b0, m, n] | batch matmul |
[b0, b1, m, k] dot [b0, b1, k, n] | [b0, b1, m, n] | batch matmul |
It follows that the resulting dimension number starts with the batch dimension, then the lhs non-contracting/non-batch dimension, and finally the rhs non-contracting/non-batch dimension.
precision_config is used to indicate the precision configuration. The level dictates whether hardware should attempt to generate more machine code instructions to provide more accurate dtype emulation when needed (ie emulating f32 on a TPU that only supports bf16 matmuls). Values may be DEFAULT , HIGH , HIGHEST . Additional details can be found in the MXU sections .
preferred_element_type is a scalar element of higher/lower precision output types used for accumulation. preferred_element_type recommends the accumulation type for the given operation, however it is not guaranteed. This allows for some hardware backends to instead accumulate in a different type and convert to the preferred output type.
For StableHLO information see StableHLO - dot_general .
ScaledDot
See also XlaBuilder::ScaledDot .
ScaledDot(lhs, lhs_scale, rhs, rhs_scale, dimension_number, precision_config,preferred_element_type)
| استدلالها | نوع | معناشناسی |
|---|---|---|
lhs | XlaOp | array of type T |
rhs | XlaOp | array of type T |
lhs_scale | XlaOp | array of type T |
rhs_scale | XlaOp | array of type T |
dimension_number | ScatterDimensionNumbers | Dimension numbers for scatter operation |
precision_config | PrecisionConfig | enum for level of precision |
preferred_element_type | optional PrimitiveType | enum of scalar element type |
Similar to DotGeneral .
Creates a scaled dot op with operands 'lhs', 'lhs_scale', 'rhs', and 'rhs_scale', with contracting and batch dimensions specified in 'dimension_numbers'.
RaggedDot
See also XlaBuilder::RaggedDot .
For a breakdown of RaggedDot computation see StableHLO - chlo.ragged_dot
DynamicReshape
See also XlaBuilder::DynamicReshape .
This operation is functionally identical to reshape , but the result shape is specified dynamically via output_shape.
DynamicReshape(operand, dim_sizes, new_size_bounds, dims_are_dynamic)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | N dimensional array of type T |
dim_sizes | vector of XlaOP | N dimensional vector sizes |
new_size_bounds | vector of int63 | N dimensional vector of bounds |
dims_are_dynamic | vector of bool | N dimensional dynamic dim |
For StableHLO information see StableHLO - dynamic_reshape .
DynamicSlice
See also XlaBuilder::DynamicSlice .
DynamicSlice extracts a sub-array from the input array at dynamic start_indices . The size of the slice in each dimension is passed in size_indices , which specify the end point of exclusive slice intervals in each dimension: [start, start + size). The shape of start_indices must be 1-dimensional, with dimension size equal to the number of dimensions of operand .
DynamicSlice(operand, start_indices, slice_sizes)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | N dimensional array of type T |
start_indices | sequence of N XlaOp | List of N scalar integers containing the starting indices of the slice for each dimension. Value must be greater than or equal to zero. |
size_indices | ArraySlice<int64> | List of N integers containing the slice size for each dimension. Each value must be strictly greater than zero, and start + size must be less than or equal to the size of the dimension to avoid wrapping modulo dimension size. |
The effective slice indices are computed by applying the following transformation for each index i in [1, N) before performing the slice:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - slice_sizes[i])
This ensures that the extracted slice is always in-bounds with respect to the operand array. If the slice is in-bounds before the transformation is applied, the transformation has no effect.
1-dimensional example:
let a = {0.0, 1.0, 2.0, 3.0, 4.0};
let s = {2};
DynamicSlice(a, s, {2});
// Result: {2.0, 3.0}
2-dimensional example:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2});
//Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
For StableHLO information see StableHLO - dynamic_slice .
DynamicUpdateSlice
See also XlaBuilder::DynamicUpdateSlice .
DynamicUpdateSlice generates a result which is the value of the input array operand , with a slice update overwritten at start_indices . The shape of update determines the shape of the sub-array of the result which is updated. The shape of start_indices must be 1-dimensional, with dimension size equal to the number of dimensions of operand .
DynamicUpdateSlice(operand, update, start_indices)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | N dimensional array of type T |
update | XlaOp | N dimensional array of type T containing the slice update. Each dimension of update shape must be strictly greater than zero, and start + update must be less than or equal to the operand size for each dimension to avoid generating out-of-bounds update indices. |
start_indices | sequence of N XlaOp | List of N scalar integers containing the starting indices of the slice for each dimension. Value must be greater than or equal to zero. |
The effective slice indices are computed by applying the following transformation for each index i in [1, N) before performing the slice:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
This ensures that the updated slice is always in-bounds with respect to the operand array. If the slice is in-bounds before the transformation is applied, the transformation has no effect.
1-dimensional example:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s)
// Result: {0.0, 1.0, 5.0, 6.0, 4.0}
2-dimensional example:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s)
// Result:
// { {0.0, 1.0, 2.0},
// {3.0, 12.0, 13.0},
// {6.0, 14.0, 15.0},
// {9.0, 16.0, 17.0} }
For StableHLO information see StableHLO - dynamic_update_slice .
Erf
See also XlaBuilder::Erf .
Element-wise error function x -> erf(x) where:
\(\text{erf}(x) = \frac{2}{\sqrt{\pi} }\int_0^x e^{-t^2} \, dt\).
Erf(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
Erf also supports the optional result_accuracy argument:
Erf(operand, result_accuracy)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
تاریخ انقضا
See also XlaBuilder::Exp .
Element-wise natural exponential x -> e^x .
Exp(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
Exp also supports the optional result_accuracy argument:
Exp(operand, result_accuracy)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
For StableHLO information see StableHLO - exponential .
Expm1
See also XlaBuilder::Expm1 .
Element-wise natural exponential minus one x -> e^x - 1 .
Expm1(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
Expm1 also supports the optional result_accuracy argument:
Expm1(operand, result_accuracy)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
For StableHLO information see StableHLO - exponential_minus_one .
Fft
See also XlaBuilder::Fft .
The XLA FFT operation implements the forward and inverse Fourier Transforms for real and complex inputs/outputs. Multidimensional FFTs on up to 3 axes are supported.
Fft(operand, ftt_type, fft_length)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The array we are Fourier transforming. |
fft_type | FftType | See the table below. |
fft_length | ArraySlice<int64> | The time-domain lengths of the axes being transformed. This is needed in particular for IRFFT to right-size the innermost axis, since RFFT(fft_length=[16]) has the same output shape as RFFT(fft_length=[17]) . |
FftType | معناشناسی |
|---|---|
FFT | Forward complex-to-complex FFT. Shape is unchanged. |
IFFT | Inverse complex-to-complex FFT. Shape is unchanged. |
RFFT | Forward real-to-complex FFT. Shape of the innermost axis is reduced to fft_length[-1] // 2 + 1 if fft_length[-1] is a non-zero value, omitting the reversed conjugate part of the transformed signal beyond the Nyquist frequency. |
IRFFT | Inverse real-to-complex FFT (ie takes complex, returns real). Shape of the innermost axis is expanded to fft_length[-1] if fft_length[-1] is a non-zero value, inferring the part of the transformed signal beyond the Nyquist frequency from the reverse conjugate of the 1 to fft_length[-1] // 2 + 1 entries. |
For StableHLO information see StableHLO - fft .
Multidimensional FFT
When more than 1 fft_length is provided, this is equivalent to applying a cascade of FFT operations to each of the innermost axes. Note that for the real->complex and complex->real cases, the innermost axis transform is (effectively) performed first (RFFT; last for IRFFT), which is why the innermost axis is the one which changes size. Other axis transforms will then be complex->complex.
Implementation details
CPU FFT is backed by Eigen's TensorFFT. GPU FFT uses cuFFT.
طبقه
See also XlaBuilder::Floor .
Element-wise floor x -> ⌊x⌋ .
Floor(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
For StableHLO information see StableHLO - floor .
فیوژن
See also HloInstruction::CreateFusion .
Fusion operation represents HLO instructions and serves as a primitive in HLO. This op may appear in HLO dumps but is not intended to be constructed manually by end users.
جمع آوری
The XLA gather operation stitches together several slices (each slice at a potentially different runtime offset) of an input array.
For StableHLO information see StableHLO - gather .
General Semantics
See also XlaBuilder::Gather . For a more intuitive description, see the "Informal Description" section below.
gather(operand, start_indices, dimension_numbers, slice_sizes, indices_are_sorted)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The array we're gathering from. |
start_indices | XlaOp | Array containing the starting indices of the slices we gather. |
dimension_numbers | GatherDimensionNumbers | The dimension in start_indices that "contains" the starting indices. See below for a detailed description. |
slice_sizes | ArraySlice<int64> | slice_sizes[i] is the bounds for the slice on dimension i . |
indices_are_sorted | bool | Whether the indices are guaranteed to be sorted by the caller. |
For convenience, we label dimensions in the output array not in offset_dims as batch_dims .
The output is an array with batch_dims.size + offset_dims.size dimensions.
The operand.rank must equal the sum of offset_dims.size and collapsed_slice_dims.size . Also, slice_sizes.size has to be equal to operand.rank .
If index_vector_dim is equal to start_indices.rank we implicitly consider start_indices to have a trailing 1 dimension (ie if start_indices was of shape [6,7] and index_vector_dim is 2 then we implicitly consider the shape of start_indices to be [6,7,1] ).
The bounds for the output array along dimension i is computed as follows:
If
iis present inbatch_dims(ie is equal tobatch_dims[k]for somek) then we pick the corresponding dimension bounds out ofstart_indices.shape, skippingindex_vector_dim(ie pickstart_indices.shape.dims[k] ifk<index_vector_dimandstart_indices.shape.dims[k+1] otherwise).If
iis present inoffset_dims(ie equal tooffset_dims[k] for somek) then we pick the corresponding bound out ofslice_sizesafter accounting forcollapsed_slice_dims(ie we pickadjusted_slice_sizes[k] whereadjusted_slice_sizesisslice_sizeswith the bounds at indicescollapsed_slice_dimsremoved).
Formally, the operand index In corresponding to a given output index Out is calculated as follows:
Let
G= {Out[k] forkinbatch_dims}. UseGto slice out a vectorSsuch thatS[i] =start_indices[Combine(G,i)] where Combine(A, b) inserts b at positionindex_vector_diminto A. Note that this is well defined even ifGis empty: IfGis empty thenS=start_indices.Create a starting index,
Sin, intooperandusingSby scatteringSusingstart_index_map. More precisely:Sin[start_index_map[k]] =S[k] ifk<start_index_map.size.Sin[_] =0otherwise.
Create an index
Oinintooperandby scattering the indices at the offset dimensions inOutaccording to thecollapsed_slice_dimsset. More precisely:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]] ifk<offset_dims.size(remapped_offset_dimsis defined below).Oin[_] =0otherwise.
InisOin+Sinwhere + is element-wise addition.
remapped_offset_dims is a monotonic function with domain [ 0 , offset_dims.size ) and range [ 0 , operand.rank ) \ collapsed_slice_dims . So if, eg, offset_dims.size is 4 , operand.rank is 6 and collapsed_slice_dims is { 0 , 2 } then remapped_offset_dims is { 0 → 1 , 1 → 3 , 2 → 4 , 3 → 5 }.
If indices_are_sorted is set to true then XLA can assume that start_indices are sorted (in ascending order, after scattering its values according to start_index_map ) by the user. If they are not then the semantics are implementation defined.
Informal Description and Examples
Informally, every index Out in the output array corresponds to an element E in the operand array, computed as follows:
We use the batch dimensions in
Outto look up a starting index fromstart_indices.We use
start_index_mapto map the starting index (whose size may be less than operand.rank) to a "full" starting index into theoperand.We dynamic-slice out a slice with size
slice_sizesusing the full starting index.We reshape the slice by collapsing the
collapsed_slice_dimsdimensions. Since all collapsed slice dimensions must have a bound of 1, this reshape is always legal.We use the offset dimensions in
Outto index into this slice to get the input element,E, corresponding to output indexOut.
index_vector_dim is set to start_indices.rank - 1 in all of the examples that follow. More interesting values for index_vector_dim do not change the operation fundamentally, but make the visual representation more cumbersome.
To get an intuition on how all of the above fits together, let's look at an example that gathers 5 slices of shape [8,6] from a [16,11] array. The position of a slice into the [16,11] array can be represented as an index vector of shape S64[2] , so the set of 5 positions can be represented as a S64[5,2] array.
The behavior of the gather operation can then be depicted as an index transformation that takes [ G , O 0 , O 1 ], an index in the output shape, and maps it to an element in the input array in the following way:
We first select an ( X , Y ) vector from the gather indices array using G . The element in the output array at index [ G , O 0 , O 1 ] is then the element in the input array at index [ X + O 0 , Y + O 1 ].
slice_sizes is [8,6] , which decides the range of O 0 and O 1 , and this in turn decides the bounds of the slice.
This gather operation acts as a batch dynamic slice with G as the batch dimension.
The gather indices may be multidimensional. For instance, a more general version of the example above using a "gather indices" array of shape [4,5,2] would translate indices like this:
Again, this acts as a batch dynamic slice G 0 and G 1 as the batch dimensions. The slice size is still [8,6] .
The gather operation in XLA generalizes the informal semantics outlined above in the following ways:
We can configure which dimensions in the output shape are the offset dimensions (dimensions containing
O0,O1in the last example). The output batch dimensions (dimensions containingG0,G1in the last example) are defined to be the output dimensions that are not offset dimensions.The number of output offset dimensions explicitly present in the output shape may be smaller than the input number of dimensions. These "missing" dimensions, which are listed explicitly as
collapsed_slice_dims, must have a slice size of1. Since they have a slice size of1the only valid index for them is0and eliding them does not introduce ambiguity.The slice extracted from the "Gather Indices" array ((
X,Y) in the last example) may have fewer elements than the input array's number of dimensions, and an explicit mapping dictates how the index should be expanded to have the same number of dimensions as the input.
As a final example, we use (2) and (3) to implement tf.gather_nd :
G 0 and G 1 are used to slice out a starting index from the gather indices array as usual, except the starting index has only one element, X . Similarly, there is only one output offset index with the value O 0 . However, before being used as indices into the input array, these are expanded in accordance to "Gather Index Mapping" ( start_index_map in the formal description) and "Offset Mapping" ( remapped_offset_dims in the formal description) into [ X , 0 ] and [ 0 , O 0 ] respectively, adding up to [ X , O 0 ]. In other words, the output index [ G 0 , G 1 , O 0 ] maps to the input index [ GatherIndices [ G 0 , G 1 , 0 ], O 0 ] which gives us the semantics for tf.gather_nd .
slice_sizes for this case is [1,11] . Intuitively this means that every index X in the gather indices array picks an entire row and the result is the concatenation of all these rows.
GetDimensionSize
See also XlaBuilder::GetDimensionSize .
Returns the size of the given dimension of the operand. The operand must be array shaped.
GetDimensionSize(operand, dimension)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | n dimensional input array |
dimension | int64 | A value in the interval [0, n) that specifies the dimension |
For StableHLO information see StableHLO - get_dimension_size .
GetTupleElement
See also XlaBuilder::GetTupleElement .
Indexes into a tuple with a compile-time-constant value.
The value must be a compile-time-constant so that shape inference can determine the type of the resulting value.
This is analogous to std::get<int N>(t) in C++. Conceptually:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
See also tf.tuple .
GetTupleElement(tuple_data, index)
| استدلال | نوع | معناشناسی |
|---|---|---|
tuple_data | XlaOP | The tuple |
index | int64 | Index of tuple shape |
For StableHLO information see StableHLO - get_tuple_element .
Imag
See also XlaBuilder::Imag .
Element-wise imaginary part of a complex (or real) shape. x -> imag(x) . If the operand is a floating point type, returns 0.
Imag(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
For StableHLO information see StableHLO - imag .
Infeed
See also XlaBuilder::Infeed .
Infeed(shape, config)
| استدلال | نوع | معناشناسی |
|---|---|---|
shape | Shape | Shape of the data read from the Infeed interface. The layout field of the shape must be set to match the layout of the data sent to the device; otherwise its behavior is undefined. |
config | optional string | Configuration of the op. |
Reads a single data item from the implicit Infeed streaming interface of the device, interpreting the data as the given shape and its layout, and returns a XlaOp of the data. Multiple Infeed operations are allowed in a computation, but there must be a total order among the Infeed operations. For example, two Infeed 's in the code below have a total order since there is a dependency between the while loops.
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
Nested tuple shapes are not supported. For an empty tuple shape, the Infeed operation is effectively a no-op and proceeds without reading any data from the Infeed of the device.
For StableHLO information see StableHLO - infeed .
یوتا
See also XlaBuilder::Iota .
Iota(shape, iota_dimension)
Builds a constant literal on device rather than a potentially large host transfer. Creates an array that has specified shape and holds values starting at zero and incrementing by one along the specified dimension. For floating-point types, the produced array is equivalent to ConvertElementType(Iota(...)) where the Iota is of integral type and the conversion is to the floating-point type.
| استدلالها | نوع | معناشناسی |
|---|---|---|
shape | Shape | Shape of the array created by Iota() |
iota_dimension | int64 | The dimension to increment along. |
For example, Iota(s32[4, 8], 0) returns
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
Iota(s32[4, 8], 1) returns
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
For StableHLO information see StableHLO - iota .
IsFinite
See also XlaBuilder::IsFinite .
Tests whether each element of operand is finite, ie, is not positive or negative infinity, and is not NaN . Returns an array of PRED values with the same shape as the input, where each element is true if and only if the corresponding input element is finite.
IsFinite(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
For StableHLO information see StableHLO - is_finite .
ورود
See also XlaBuilder::Log .
Element-wise natural logarithm x -> ln(x) .
Log(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
Log also supports the optional result_accuracy argument:
Log(operand, result_accuracy)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
For StableHLO information see StableHLO - log .
Log1p
See also XlaBuilder::Log1p .
Element-wise shifted natural logarithm x -> ln(1+x) .
Log1p(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
Log1p also supports the optional result_accuracy argument:
Log1p(operand, result_accuracy)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
For StableHLO information see StableHLO - log_plus_one .
Logistic
See also XlaBuilder::Logistic .
Element-wise logistic function computation x -> logistic(x) .
Logistic(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
Logistic also supports the optional result_accuracy argument:
Logistic(operand, result_accuracy)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
For StableHLO information see StableHLO - logistic .
نقشه
See also XlaBuilder::Map .
Map(operands..., computation, dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operands | sequence of N XlaOp s | N arrays of types T 0..T {N-1} |
computation | XlaComputation | Computation of type T_0, T_1, .., T_{N + M -1} -> S with N parameters of type T and M of arbitrary type. |
dimensions | int64 array | Array of map dimensions |
static_operands | sequence of N XlaOp s | Static ops for the map operation |
Applies a scalar function over the given operands arrays, producing an array of the same dimensions where each element is the result of the mapped function applied to the corresponding elements in the input arrays.
The mapped function is an arbitrary computation with the restriction that it has N inputs of scalar type T and a single output with type S . The output has the same dimensions as the operands except that the element type T is replaced with S.
For example: Map(op1, op2, op3, computation, par1) maps elem_out <- computation(elem1, elem2, elem3, par1) at each (multi-dimensional) index in the input arrays to produce the output array.
For StableHLO information see StableHLO - map .
مکس
See also XlaBuilder::Max .
Performs element-wise max operation on tensors lhs and rhs .
Max(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Max:
Max(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - maximum .
حداقل
See also XlaBuilder::Min .
Performs element-wise min operation on lhs and rhs .
Min(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Min:
Min(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - minimum .
Mul
See also XlaBuilder::Mul .
Performs element-wise product of lhs and rhs .
Mul(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Mul:
Mul(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - multiply .
Neg
See also XlaBuilder::Neg .
Element-wise negation x -> -x .
Neg(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
For StableHLO information see StableHLO - negate
نه
See also XlaBuilder::Not .
Element-wise logical not x -> !(x) .
Not(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
For StableHLO information see StableHLO - not .
OptimizationBarrier
See also XlaBuilder::OptimizationBarrier .
Blocks any optimization pass from moving computations across the barrier.
OptimizationBarrier(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
Ensures that all inputs are evaluated before any operators that depend on the barrier's outputs.
For StableHLO information see StableHLO - optimization_barrier .
یا
See also XlaBuilder::Or .
Performs element-wise OR of lhs and rhs .
Or(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Or:
Or(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - or .
Outfeed
See also XlaBuilder::Outfeed .
Writes inputs to the outfeed.
Outfeed(operand, shape_with_layout, outfeed_config)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | array of type T |
shape_with_layout | Shape | Defines the layout of the data transferred |
outfeed_config | string | Constant of config for the Outfeed instruction |
shape_with_layout communicates the laid out shape that we want to outfeed.
For StableHLO information see StableHLO - outfeed .
پد
See also XlaBuilder::Pad .
Pad(operand, padding_value, padding_config)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | array of type T |
padding_value | XlaOp | scalar of type T to fill in the added padding |
padding_config | PaddingConfig | padding amount on both edges (low, high) and between the elements of each dimension |
Expands the given operand array by padding around the array as well as between the elements of the array with the given padding_value . padding_config specifies the amount of edge padding and the interior padding for each dimension.
PaddingConfig is a repeated field of PaddingConfigDimension , which contains three fields for each dimension: edge_padding_low , edge_padding_high , and interior_padding .
edge_padding_low and edge_padding_high specify the amount of padding added at the low-end (next to index 0) and the high-end (next to the highest index) of each dimension respectively. The amount of edge padding can be negative -- the absolute value of negative padding indicates the number of elements to remove from the specified dimension.
interior_padding specifies the amount of padding added between any two elements in each dimension; it may not be negative. Interior padding occurs logically before edge padding, so in the case of negative edge padding, elements are removed from the interior-padded operand.
This operation is a no-op if the edge padding pairs are all (0, 0) and the interior padding values are all 0. The figure below shows examples of different edge_padding and interior_padding values for a two-dimensional array.
For StableHLO information see StableHLO - pad .
پارامتر
See also XlaBuilder::Parameter .
Parameter represents an argument input to a computation.
PartitionID
See also XlaBuilder::BuildPartitionId .
Produces partition_id of the current process.
PartitionID(shape)
| استدلالها | نوع | معناشناسی |
|---|---|---|
shape | Shape | Shape of the data |
PartitionID may appear in HLO dumps but it is not intended to be constructed manually by end users.
For StableHLO information see StableHLO - partition_id .
PopulationCount
See also XlaBuilder::PopulationCount .
Computes the number of bits set in each element of operand .
PopulationCount(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
For StableHLO information see StableHLO - popcnt .
قدرت
See also XlaBuilder::Pow .
Performs element-wise exponentiation of lhs by rhs .
Pow(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Pow:
Pow(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - power .
واقعی
See also XlaBuilder::Real .
Element-wise real part of a complex (or real) shape. x -> real(x) . If the operand is a floating point type, Real returns the same value.
Real(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
For StableHLO information see StableHLO - real .
Recv
See also XlaBuilder::Recv .
Recv , RecvWithTokens , and RecvToHost are operations that serve as communication primitives in HLO. These ops typically appear in HLO dumps as part of low-level input/output or cross-device transfer, but they are not intended to be constructed manually by end users.
Recv(shape, handle)
| استدلالها | نوع | معناشناسی |
|---|---|---|
shape | Shape | shape of the data to receive |
handle | ChannelHandle | unique identifier for each send/recv pair |
Receives data of the given shape from a Send instruction in another computation that shares the same channel handle. Returns a XlaOp for the received data.
For StableHLO information see StableHLO - recv .
RecvDone
See also HloInstruction::CreateRecv and HloInstruction::CreateRecvDone .
Similar to Send , the client API of Recv operation represents synchronous communication. However, the instruction is internally decomposed into 2 HLO instructions ( Recv and RecvDone ) to enable asynchronous data transfers.
Recv(const Shape& shape, int64 channel_id)
Allocates resources required to receive data from a Send instruction with the same channel_id. Returns a context for the allocated resources, which is used by a following RecvDone instruction to wait for the completion of the data transfer. The context is a tuple of {receive buffer (shape), request identifier (U32)} and it can only be used by a RecvDone instruction.
Given a context created by a Recv instruction, waits for the data transfer to complete and return the received data.
کاهش
See also XlaBuilder::Reduce .
Applies a reduction function to one or more arrays in parallel.
Reduce(operands..., init_values..., computation, dimensions_to_reduce)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operands | Sequence of N XlaOp | N arrays of types T_0,..., T_{N-1} . |
init_values | Sequence of N XlaOp | N scalars of types T_0,..., T_{N-1} . |
computation | XlaComputation | computation of type T_0,..., T_{N-1}, T_0, ...,T_{N-1} -> Collate(T_0,..., T_{N-1}) . |
dimensions_to_reduce | int64 array | unordered array of dimensions to reduce. |
Where:
- N is required to be greater or equal to 1.
- The computation has to be "roughly" associative (see below).
- All input arrays must have the same dimensions.
- All initial values have to form an identity under
computation. - If
N = 1,Collate(T)isT. - If
N > 1,Collate(T_0, ..., T_{N-1})is a tuple ofNelements of typeT.
This operation reduces one or more dimensions of each input array into scalars. The number of dimensions of each returned array is number_of_dimensions(operand) - len(dimensions) . The output of the op is Collate(Q_0, ..., Q_N) where Q_i is an array of type T_i , the dimensions of which are described below.
Different backends are allowed to reassociate the reduction computation. This can lead to numerical differences, as some reduction functions like addition are not associative for floats. However, if the range of the data is limited, floating-point addition is close enough to be associative for most practical uses.
For StableHLO information see StableHLO - reduce .
مثالها
When reducing across one dimension in a single 1D array with values [10, 11, 12, 13] , with reduction function f (this is computation ) then that could be computed as
f(10, f(11, f(12, f(init_value, 13)))
but there are also many other possibilities, eg
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
The following is a rough pseudo-code example of how reduction could be implemented, using summation as the reduction computation with an initial value of 0.
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
Here's an example of reducing a 2D array (matrix). The shape has 2 dimensions, dimension 0 of size 2 and dimension 1 of size 3:
Results of reducing dimensions 0 or 1 with an "add" function:
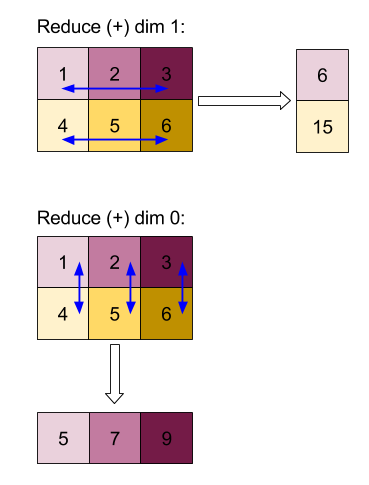
Note that both reduction results are 1D arrays. The diagram shows one as column and another as row just for visual convenience.
For a more complex example, here is a 3D array. Its number of dimensions is 3, dimension 0 of size 4, dimension 1 of size 2 and dimension 2 of size 3. For simplicity, the values 1 to 6 are replicated across dimension 0.
Similarly to the 2D example, we can reduce just one dimension. If we reduce dimension 0, for example, we get a 2-dimensional array where all values across dimension 0 were folded into a scalar:
| 4 8 12 |
| 16 20 24 |
If we reduce dimension 2, we also get a 2-dimensional array where all values across dimension 2 were folded into a scalar:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
Note that the relative order between the remaining dimensions in the input is preserved in the output, but some dimensions may get assigned new numbers (since the number of dimensions changes).
We can also reduce multiple dimensions. Add-reducing dimensions 0 and 1 produces the 1D array [20, 28, 36] .
Reducing the 3D array over all its dimensions produces the scalar 84 .
Variadic Reduce
When N > 1 , reduce function application is slightly more complex, as it is applied simultaneously to all inputs. The operands are supplied to the computation in the following order:
- Running reduced value for the first operand
- ...
- Running reduced value for the N'th operand
- Input value for the first operand
- ...
- Input value for the N'th operand
For example, consider the following reduction function, which can be used to compute the max and the argmax of a 1-D array in parallel:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
For 1-D Input arrays V = Float[N], K = Int[N] , and init values I_V = Float, I_K = Int , the result f_(N-1) of reducing across the only input dimension is equivalent to the following recursive application:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
Applying this reduction to an array of values, and an array of sequential indices (ie iota), will co-iterate over the arrays, and return a tuple containing the maximal value and the matching index.
ReducePrecision
See also XlaBuilder::ReducePrecision .
Models the effect of converting floating-point values to a lower-precision format (such as IEEE-FP16) and back to the original format. The number of exponent and mantissa bits in the lower-precision format can be specified arbitrarily, although all bit sizes may not be supported on all hardware implementations.
ReducePrecision(operand, exponent_bits, mantissa_bits)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | array of floating-point type T . |
exponent_bits | int32 | number of exponent bits in lower-precision format |
mantissa_bits | int32 | number of mantissa bits in lower-precision format |
The result is an array of type T . The input values are rounded to the nearest value representable with the given number of mantissa bits (using "ties to even" semantics), and any values that exceed the range specified by the number of exponent bits are clamped to positive or negative infinity. NaN values are retained, although they may be converted to canonical NaN values.
The lower-precision format must have at least one exponent bit (in order to distinguish a zero value from an infinity, since both have a zero mantissa), and must have a non-negative number of mantissa bits. The number of exponent or mantissa bits may exceed the corresponding value for type T ; the corresponding portion of the conversion is then simply a no-op.
For StableHLO information see StableHLO - reduce_precision .
ReduceScatter
See also XlaBuilder::ReduceScatter .
ReduceScatter is a collective operation that effectively does an AllReduce and then scatters the result by splitting it into shard_count blocks along the scatter_dimension and replica i in the replica group receives the ith shard.
ReduceScatter(operand, computation, scatter_dimension, shard_count, replica_groups, channel_id, layout, use_global_device_ids)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | Array or a non-empty tuple of arrays to reduce across replicas. |
computation | XlaComputation | Reduction computation |
scatter_dimension | int64 | Dimension to scatter. |
shard_count | int64 | Number of blocks to split scatter_dimension |
replica_groups | ReplicaGroup vector | Groups between which the reductions are performed |
channel_id | optional ChannelHandle | Optional channel ID for cross-module communication |
layout | optional Layout | user-specified memory layout |
use_global_device_ids | optional bool | user-specified flag |
- When
operandis a tuple of arrays, the reduce-scatter is performed on each element of the tuple. -
replica_groupsis a list of replica groups between which the reduction is performed (replica id for the current replica can be retrieved usingReplicaId). The order of replicas in each group determines the order in which the all-reduce result will be scattered.replica_groupsmust either be empty (in which case all replicas belong to a single group), or contain the same number of elements as the number of replicas. When there are more than one replica groups, they all must be of the same size. For example,replica_groups = {0, 2}, {1, 3}performs reduction between the replicas0and2, and1and3and then scatters the result. -
shard_countis the size of each replica group. We need this in cases wherereplica_groupsare empty. Ifreplica_groupsis not empty,shard_countmust be equal to the size of each replica group. -
channel_idis used for cross-module communication: onlyreduce-scatteroperations with the samechannel_idcan communicate with each other. -
layoutSee xla::shapes for more information on layouts. -
use_global_device_idsis a user-specified flag. Whenfalse(default) the numbers inreplica_groupsareReplicaIdwhentruethereplica_groupsrepresent a global id of (ReplicaID*partition_count+partition_id). For example:- With 2 replicas and 4 partitions,
- replica_groups={ {0,1,4,5},{2,3,6,7} } and use_global_device_ids=true
- group[0] = (0,0), (0,1), (1,0), (1,1)
- group[1] = (0,2), (0,3), (1,2), (1,3)
- where each pair is (replica_id, partition_id).
The output shape is the input shape with the scatter_dimension made shard_count times smaller. For example, if there are two replicas and the operand has the value [1.0, 2.25] and [3.0, 5.25] respectively on the two replicas, then the output value from this op where scatter_dim is 0 will be [4.0] for the first replica and [7.5] for the second replica.
For StableHLO information see StableHLO - reduce_scatter .
ReduceScatter - Example 1 - StableHLO
In the above example, there are 2 replicas participating in the ReduceScatter. On each replica, the operand has shape f32[2,4]. An all-reduce (sum) is performed across the replicas, producing a reduced value of shape f32[2,4] on each replica. This reduced value is then split into 2 parts along dimension 1, so each part has shape f32[2,2]. Each replica within the process group receives the part corresponding to its position in the group. As a result, the output on each replica has shape f32[2,2].
ReduceWindow
See also XlaBuilder::ReduceWindow .
Applies a reduction function to all elements in each window of a sequence of N multi-dimensional arrays, producing a single or a tuple of N multi-dimensional arrays as output. Each output array has the same number of elements as the number of valid positions of the window. A pooling layer can be expressed as a ReduceWindow . Similar to Reduce , the applied computation is always passed the init_values on the left-hand side.
ReduceWindow(operands..., init_values..., computation, window_dimensions, window_strides, padding)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operands | N XlaOps | A sequence of N multi-dimensional arrays of types T_0,..., T_{N-1} , each representing the base area on which the window is placed. |
init_values | N XlaOps | The N starting values for the reduction, one for each of the N operands. See Reduce for details. |
computation | XlaComputation | Reduction function of type T_0, ..., T_{N-1}, T_0, ..., T_{N-1} -> Collate(T_0, ..., T_{N-1}) , to apply to elements in each window of all the input operands. |
window_dimensions | ArraySlice<int64> | array of integers for window dimension values |
window_strides | ArraySlice<int64> | array of integers for window stride values |
base_dilations | ArraySlice<int64> | array of integers for base dilation values |
window_dilations | ArraySlice<int64> | array of integers for window dilation values |
padding | Padding | padding type for window (Padding::kSame, which pads so as to have the same output shape as input if the stride is 1, or Padding::kValid, which uses no padding and "stops" the window once it no longer fits) |
Where:
- N is required to be greater or equal to 1.
- All input arrays must have the same dimensions.
- If
N = 1,Collate(T)isT. - If
N > 1,Collate(T_0, ..., T_{N-1})is a tuple ofNelements of type(T0,...T{N-1}).
For StableHLO information see StableHLO - reduce_window .
ReduceWindow - Example 1
Input is a matrix of size [4x6] and both window_dimensions and window_stride_dimensions are [2x3].
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
Stride of 1 in a dimension specifies that the position of a window in the dimension is 1 element away from its adjacent window. In order to specify that no windows overlap with each other, window_stride_dimensions should be equal to window_dimensions. The figure below illustrates the use of two different stride values. Padding is applied to each dimension of the input and the calculations are the same as though the input came in with the dimensions it has after padding.
For a non-trivial padding example, consider computing reduce-window minimum (initial value is MAX_FLOAT ) with dimension 3 and stride 2 over the input array [10000, 1000, 100, 10, 1] . Padding kValid computes minimums over two valid windows: [10000, 1000, 100] and [100, 10, 1] , resulting in the output [100, 1] . Padding kSame first pads the array so that the shape after the reduce-window would be the same as input for stride one by adding initial elements on both sides, getting [MAX_VALUE, 10000, 1000, 100, 10, 1, MAX_VALUE] . Running reduce-window over the padded array operates on three windows [MAX_VALUE, 10000, 1000] , [1000, 100, 10] , [10, 1, MAX_VALUE] , and yields [1000, 10, 1] .
The evaluation order of the reduction function is arbitrary and may be non-deterministic. Therefore, the reduction function should not be overly sensitive to reassociation. See the discussion about associativity in the context of Reduce for more details.
ReduceWindow - Example 2 - StableHLO
In the above example:
Input) The operand has an input shape of S32[3,2]. With a values of [[1,2],[3,4],[5,6]]
Step 1) Base dilation with factor 2 along the row dimension inserts holes between each row of the operand. Padding of 2 rows at the top and 1 row at the bottom is applied after dilation. As a result, the tensor becomes taller.
Step 2) A window of shape [2,1] is defined, with window dilation [3,1]. This means each window selects two elements from the same column, but the second element is taken three rows below the first rather than directly beneath it.
Step 3) The windows are then slid across the operand with stride [4,1]. This causes the window to move down four rows at a time, while shifting one column at a time horizontally. Padding cells are filled with the init_value (in this case init_value = 0 ). Values 'falling into' dilation cells are ignored. Because of the stride and padding, some windows overlap only zeros and holes, while others overlap real input values.
Step 4) Within each window, the elements are combined using the reduction function (a, b) → a + b, starting from an initial value of 0. The top two windows see only padding and holes, so their results are 0. The bottom windows capture the values 3 and 4 from the input and return those as results.
Results) The final output has shape S32[2,2], with values: [[0,0],[3,4]]
رم
See also XlaBuilder::Rem .
Performs element-wise remainder of dividend lhs and divisor rhs .
The sign of the result is taken from the dividend, and the absolute value of the result is always less than the divisor's absolute value.
Rem(lhs, rhs)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Rem:
Rem(lhs,rhs, broadcast_dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - remainder .
ReplicaId
See also XlaBuilder::ReplicaId .
Returns the unique ID (U32 scalar) of the replica.
ReplicaId()
The unique ID of each replica is an unsigned integer in the interval [0, N) , where N is the number of replicas. Since all the replicas are running the same program, a ReplicaId() call in the program will return a different value on each replica.
For StableHLO information see StableHLO - replica_id .
تغییر شکل
See also XlaBuilder::Reshape . and the Collapse operation.
Reshapes the dimensions of an array into a new configuration.
Reshape(operand, dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | array of type T |
dimensions | int64 vector | vector of sizes of new dimensions |
Conceptually, reshape first flattens an array into a one-dimensional vector of data values, and then refines this vector into a new shape. The input arguments are an arbitrary array of type T, a compile-time-constant vector of dimension indices, and a compile-time-constant vector of dimension sizes for the result. The dimensions vector determines the size of the output array. The value at index 0 in dimensions is the size of dimension 0, the value at index 1 is the size of dimension 1, and so on. The product of the dimensions dimensions must equal the product of the operand's dimension sizes. When refining the collapsed array into the multidimensional array defined by dimensions , the dimensions in dimensions are ordered from slowest varying (most major) and to fastest varying (most minor).
For example, let v be an array of 24 elements:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
As a special case, reshape can transform a single-element array to a scalar and vice versa. For example,
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
For StableHLO information see StableHLO - reshape .
Reshape (explicit)
See also XlaBuilder::Reshape .
Reshape(shape, operand)
Reshape op that uses an explicit target shape.
| استدلالها | نوع | معناشناسی |
|---|---|---|
shape | Shape | Output shape of type T |
operand | XlaOp | array of type T |
Rev (reverse)
See also XlaBuilder::Rev .
Rev(operand, dimensions)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | array of type T |
dimensions | ArraySlice<int64> | dimensions to reverse |
Reverses the order of elements in the operand array along the specified dimensions , generating an output array of the same shape. Each element of the operand array at a multidimensional index is stored into the output array at a transformed index. The multidimensional index is transformed by reversing the index in each dimension to be reversed (ie, if a dimension of size N is one of the reversing dimensions, its index i is transformed into N - 1 - i).
One use for the Rev operation is to reverse the convolution weight array along the two window dimensions during the gradient computation in neural networks.
For StableHLO information see StableHLO - reverse .
RngNormal
See also XlaBuilder::RngNormal .
Constructs an output of a given shape with random numbers generated following the \(N(\mu, \sigma)\) normal distribution. The parameters \(\mu\) و \(\sigma\), and output shape have to have a floating point elemental type. The parameters furthermore have to be scalar valued.
RngNormal(mu, sigma, shape)
| استدلالها | نوع | معناشناسی |
|---|---|---|
mu | XlaOp | Scalar of type T specifying mean of generated numbers |
sigma | XlaOp | Scalar of type T specifying standard deviation of generated |
shape | Shape | Output shape of type T |
For StableHLO information see StableHLO - rng .
RngUniform
See also XlaBuilder::RngUniform .
Constructs an output of a given shape with random numbers generated following the uniform distribution over the interval \([a,b)\). The parameters and output element type have to be a boolean type, an integral type or a floating point types, and the types have to be consistent. The CPU and GPU backends currently only support F64, F32, F16, BF16, S64, U64, S32 and U32. Furthermore, the parameters need to be scalar valued. If \(b <= a\) the result is implementation-defined.
RngUniform(a, b, shape)
| استدلالها | نوع | معناشناسی |
|---|---|---|
a | XlaOp | Scalar of type T specifying lower limit of interval |
b | XlaOp | Scalar of type T specifying upper limit of interval |
shape | Shape | Output shape of type T |
For StableHLO information see StableHLO - rng .
RngBitGenerator
See also XlaBuilder::RngBitGenerator .
Generates an output with a given shape filled with uniform random bits using the specified algorithm (or backend default) and returns an updated state (with the same shape as initial state) and the generated random data.
Initial state is the initial state of the current random number generation. It and the required shape and valid values are dependent on the algorithm used.
The output is guaranteed to be a deterministic function of the initial state but it is not guaranteed to be deterministic between backends and different compiler versions.
RngBitGenerator(algorithm, initial_state, shape)
| استدلالها | نوع | معناشناسی |
|---|---|---|
algorithm | RandomAlgorithm | PRNG algorithm to be used. |
initial_state | XlaOp | Initial state for the PRNG algorithm. |
shape | Shape | Output shape for generated data. |
Available values for algorithm :
rng_default: Backend specific algorithm with backend specific shape requirements.rng_three_fry: ThreeFry counter-based PRNG algorithm. Theinitial_stateshape isu64[2]with arbitrary values. Salmon et al. SC 2011. Parallel random numbers: as easy as 1, 2, 3.rng_philox: Philox algorithm to generate random numbers in parallel. Theinitial_stateshape isu64[3]with arbitrary values. Salmon et al. SC 2011. Parallel random numbers: as easy as 1, 2, 3.
For StableHLO information see StableHLO - rng_bit_generator .
RngGetAndUpdateState
See also HloInstruction::CreateRngGetAndUpdateState .
The API of the various Rng operations are internally decomposed into HLO instructions including RngGetAndUpdateState .
RngGetAndUpdateState serves as a primitive in HLO. This op may appear in HLO dumps, but it is not intended to be constructed manually by end users.
گرد
See also XlaBuilder::Round .
Element-wise rounding, ties away from zero.
Round(operand)
| استدلالها | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
RoundNearestAfz
See also XlaBuilder::RoundNearestAfz .
Performs element-wise rounding towards the nearest integer, breaking ties away from zero.
RoundNearestAfz(operand)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | The operand to the function |
For StableHLO information see StableHLO - round_nearest_afz .
RoundNearestEven
See also XlaBuilder::RoundNearestEven .
Element-wise rounding, ties to the nearest even.
RoundNearestEven(operand)
| استدلالها | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
For StableHLO information see StableHLO - round_nearest_even .
Rsqrt
See also XlaBuilder::Rsqrt .
Element-wise reciprocal of square root operation x -> 1.0 / sqrt(x) .
Rsqrt(operand)
| استدلالها | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
Rsqrt also supports the optional result_accuracy argument:
Rsqrt(operand, result_accuracy)
| استدلالها | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
For StableHLO information see StableHLO - rsqrt .
اسکن
See also XlaBuilder::Scan .
Applies a reduction function to an array across a given dimension, producing a final state and an array of intermediate values.
Scan(inputs..., inits..., to_apply, scan_dimension, is_reverse, is_associative)
| استدلالها | نوع | Semantics |
|---|---|---|
inputs | Sequence of m XlaOp s | The arrays to scan. |
inits | Sequence of k XlaOp s | Initial carries. |
to_apply | XlaComputation | Computation of type i_0, ..., i_{m-1}, c_0, ..., c_{k-1} -> (o_0, ..., o_{n-1}, c'_0, ..., c'_{k-1}) . |
scan_dimension | int64 | The dimension to scan across. |
is_reverse | bool | If true, scan in reverse order. |
is_associative | bool (tri-state) | If true, the operation is associative. |
The function to_apply is applied sequentially to elements in inputs along scan_dimension . If is_reverse is false, elements are processed in order 0 to N-1 , where N is the size of scan_dimension . If is_reverse is true, elements are processed from N-1 down to 0 .
The to_apply function takes m + k operands:
-
mcurrent elements frominputs. -
kcarry values from the previous step (orinitsfor the first element).
The to_apply function returns a tuple of n + k values:
-
nelements ofoutputs. -
knew carry values.
The Scan operation produces a tuple of n + k values:
- The
noutput arrays, containing the output values for each step. - The final
kcarry values after processing all elements.
The types of the m inputs must match the types of the first m parameters of to_apply with an extra scan dimension. The types of the n outputs must match the types of the first n return values of to_apply with an extra scan dimension. The extra scan dimension among all inputs and outputs must have the same size N . The types of the last k parameters and return values of to_apply as well as the k inits must match.
For example ( m, n, k == 1, N == 3 ), for initial carry i , input [a, b, c] , function f(x, c) -> (y, c') , and scan_dimension=0 , is_reverse=false :
- Step 0:
f(a, i) -> (y0, c0) - Step 1:
f(b, c0) -> (y1, c1) - Step 2:
f(c, c1) -> (y2, c2)
The output of Scan is ([y0, y1, y2], c2) .
Scatter
See also XlaBuilder::Scatter .
The XLA scatter operation generates a sequence of results which are the values of the input array operands , with several slices (at indices specified by scatter_indices ) updated with the sequence of values in updates using update_computation .
Scatter(operands..., scatter_indices, updates..., update_computation, dimension_numbers, indices_are_sorted, unique_indices)
| استدلالها | نوع | Semantics |
|---|---|---|
operands | Sequence of N XlaOp | N arrays of types T_0, ..., T_N to be scattered into. |
scatter_indices | XlaOp | Array containing the starting indices of the slices that must be scattered to. |
updates | Sequence of N XlaOp | N arrays of types T_0, ..., T_N . updates[i] contains the values that must be used for scattering operands[i] . |
update_computation | XlaComputation | Computation to be used for combining the existing values in the input array and the updates during scatter. This computation should be of type T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N) . |
index_vector_dim | int64 | The dimension in scatter_indices that contains the starting indices. |
update_window_dims | ArraySlice<int64> | The set of dimensions in updates shape that are window dimensions . |
inserted_window_dims | ArraySlice<int64> | The set of window dimensions that must be inserted into updates shape. |
scatter_dims_to_operand_dims | ArraySlice<int64> | A dimensions map from the scatter indices to the operand index space. This array is interpreted as mapping i to scatter_dims_to_operand_dims[i] . It has to be one-to-one and total. |
dimension_number | ScatterDimensionNumbers | Dimension numbers for scatter operation |
indices_are_sorted | bool | Whether the indices are guaranteed to be sorted by the caller. |
unique_indices | bool | Whether the indices are guaranteed to be unique by the caller. |
Where:
- N is required to be greater or equal to 1.
-
operands[0], ...,operands[N-1] must all have the same dimensions. -
updates[0], ...,updates[N-1] must all have the same dimensions. - If
N = 1,Collate(T)isT. - If
N > 1,Collate(T_0, ..., T_N)is a tuple ofNelements of typeT.
If index_vector_dim is equal to scatter_indices.rank we implicitly consider scatter_indices to have a trailing 1 dimension.
We define update_scatter_dims of type ArraySlice<int64> as the set of dimensions in updates shape that are not in update_window_dims , in ascending order.
The arguments of scatter should follow these constraints:
Each
updatesarray must haveupdate_window_dims.size + scatter_indices.rank - 1dimensions.Bounds of dimension
iin eachupdatesarray must conform to the following:- If
iis present inupdate_window_dims(ie equal toupdate_window_dims[k] for somek), then the bound of dimensioniinupdatesmust not exceed the corresponding bound ofoperandafter accounting for theinserted_window_dims(ieadjusted_window_bounds[k], whereadjusted_window_boundscontains the bounds ofoperandwith the bounds at indicesinserted_window_dimsremoved). - If
iis present inupdate_scatter_dims(ie equal toupdate_scatter_dims[k] for somek), then the bound of dimensioniinupdatesmust be equal to the corresponding bound ofscatter_indices, skippingindex_vector_dim(iescatter_indices.shape.dims[k], ifk<index_vector_dimandscatter_indices.shape.dims[k+1] otherwise).
- If
update_window_dimsmust be in ascending order, not have any repeating dimension numbers, and be in the range[0, updates.rank).inserted_window_dimsmust be in ascending order, not have any repeating dimension numbers, and be in the range[0, operand.rank).operand.rankmust equal the sum ofupdate_window_dims.sizeandinserted_window_dims.size.scatter_dims_to_operand_dims.sizemust be equal toscatter_indices.shape.dims[index_vector_dim], and its values must be in the range[0, operand.rank).
For a given index U in each updates array, the corresponding index I in the corresponding operands array into which this update has to be applied is computed as follows:
- Let
G= {U[k] forkinupdate_scatter_dims}. UseGto look up an index vectorSin thescatter_indicesarray such thatS[i] =scatter_indices[Combine(G,i)] where Combine(A, b) inserts b at positionsindex_vector_diminto A. - Create an index
SinintooperandusingSby scatteringSusing thescatter_dims_to_operand_dimsmap. More formally:-
Sin[scatter_dims_to_operand_dims[k]] =S[k] ifk<scatter_dims_to_operand_dims.size. -
Sin[_] =0otherwise.
-
- Create an index
Wininto eachoperandsarray by scattering the indices atupdate_window_dimsinUaccording toinserted_window_dims. More formally:-
Win[window_dims_to_operand_dims(k)] =U[k] ifkis inupdate_window_dims, wherewindow_dims_to_operand_dimsis the monotonic function with domain [0,update_window_dims.size) and range [0,operand.rank) \inserted_window_dims. (For example, ifupdate_window_dims.sizeis4,operand.rankis6, andinserted_window_dimsis {0,2} thenwindow_dims_to_operand_dimsis {0→1,1→3,2→4,3→5}). -
Win[_] =0otherwise.
-
-
IisWin+Sinwhere + is element-wise addition.
In summary, the scatter operation can be defined as follows.
- Initialize
outputwithoperands, ie for all indicesJ, for all indicesOin theoperands[J] array:
output[J][O] =operands[J][O] - For every index
Uin theupdates[J] array and the corresponding indexOin theoperand[J] array, ifOis a valid index foroutput:
(output[0][O], ...,output[N-1][O]) =update_computation(output[0][O], ..., ,output[N-1][O],updates[0][U], ...,updates[N-1][U])
The order in which updates are applied is non-deterministic. So, when multiple indices in updates refer to the same index in operands , the corresponding value in output will be non-deterministic.
Note that the first parameter that is passed into the update_computation will always be the current value from the output array and the second parameter will always be the value from the updates array. This is important specifically for cases when the update_computation is not commutative .
If indices_are_sorted is set to true then XLA can assume that scatter_indices are sorted (in ascending order, after scattering its values according to scatter_dims_to_operand_dims ) by the user. If they are not then the semantics are implementation defined.
If unique_indices is set to true then XLA can assume that all elements scattered to are unique. So XLA could use non-atomic operations. If unique_indices is set to true and the indices being scattered to are not unique then the semantics is implementation defined.
Informally, the scatter op can be viewed as an inverse of the gather op, ie the scatter op updates the elements in the input that are extracted by the corresponding gather op.
For a detailed informal description and examples, refer to the "Informal Description" section under Gather .
For StableHLO information see StableHLO - scatter .
Scatter - Example 1 - StableHLO
In the above image, each row of the table is an example of one update index example. Let's review stepwise from left(Update Index) to right(Result Index):
Input) input has shape S32[2,3,4,2]. scatter_indices have shape S64[2,2,3,2]. updates have shape S32[2,2,3,1,2].
Update Index) As part of the input we are given update_window_dims:[3,4] . This tell us that updates 's dim 3 and dim 4 are window dimensions, highlighted in yellow. This allows us to derive that update_scatter_dims = [0,1,2].
Update Scatter Index) Shows us the extracted updated_scatter_dims for each. (The non-yellow of column Update Index)
Start Index) Looking at the scatter_indices tensor image we can see that our values from the previous step (Update scatter Index), give us the location of the start index. From index_vector_dim we are also told the dimension of the starting_indices that contains the starting indices, which for scatter_indices is dim 3 with a size 2.
Full Start Index) scatter_dims_to_operand_dims = [2,1] tells us the first element of the index vector goes to operand dim 2. The second element of the index vector goes to operand dim 1. The remaining operand dimensions are filled with 0.
Full Batching Index) We can see the purple highlighted area is shown in this column(full batching index), the update scatter index column, and update index column.
Full Window Index) Computed from the update_window_dimensions [3,4].
Result Index) The addition of Full Start Index, Full Batching Index, and Full Window Index in the operand tensor. Notice the green highlighted regions correspond to the operand figure as well. The last row is skipped because it falls outside of operand tensor.
انتخاب کنید
See also XlaBuilder::Select .
Constructs an output array from elements of two input arrays, based on the values of a predicate array.
Select(pred, on_true, on_false)
| استدلالها | نوع | Semantics |
|---|---|---|
pred | XlaOp | array of type PRED |
on_true | XlaOp | array of type T |
on_false | XlaOp | array of type T |
The arrays on_true and on_false must have the same shape. This is also the shape of the output array. The array pred must have the same dimensionality as on_true and on_false , with the PRED element type.
For each element P of pred , the corresponding element of the output array is taken from on_true if the value of P is true , and from on_false if the value of P is false . As a restricted form of broadcasting , pred can be a scalar of type PRED . In this case, the output array is taken wholly from on_true if pred is true , and from on_false if pred is false .
Example with non-scalar pred :
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
Example with scalar pred :
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
Selections between tuples are supported. Tuples are considered to be scalar types for this purpose. If on_true and on_false are tuples (which must have the same shape!) then pred has to be a scalar of type PRED .
For StableHLO information see StableHLO - select
SelectAndScatter
See also XlaBuilder::SelectAndScatter .
This operation can be considered as a composite operation that first computes ReduceWindow on the operand array to select an element from each window, and then scatters the source array to the indices of the selected elements to construct an output array with the same shape as the operand array. The binary select function is used to select an element from each window by applying it across each window, and it is called with the property that the first parameter's index vector is lexicographically less than the second parameter's index vector. The select function returns true if the first parameter is selected and returns false if the second parameter is selected, and the function must hold transitivity (ie, if select(a, b) and select(b, c) are true , then select(a, c) is also true ) so that the selected element does not depend on the order of the elements traversed for a given window.
The function scatter is applied at each selected index in the output array. It takes two scalar parameters:
- Current value at the selected index in the output array
- The scatter value from
sourcethat applies to the selected index
It combines the two parameters and returns a scalar value that's used to update the value at the selected index in the output array. Initially, all indices of the output array are set to init_value .
The output array has the same shape as the operand array and the source array must have the same shape as the result of applying a ReduceWindow operation on the operand array. SelectAndScatter can be used to backpropagate the gradient values for a pooling layer in a neural network.
SelectAndScatter(operand, select, window_dimensions, window_strides, padding, source, init_value, scatter)
| استدلالها | نوع | Semantics |
|---|---|---|
operand | XlaOp | array of type T over which the windows slide |
select | XlaComputation | binary computation of type T, T -> PRED , to apply to all elements in each window; returns true if the first parameter is selected and returns false if the second parameter is selected |
window_dimensions | ArraySlice<int64> | array of integers for window dimension values |
window_strides | ArraySlice<int64> | array of integers for window stride values |
padding | Padding | padding type for window (Padding::kSame or Padding::kValid) |
source | XlaOp | array of type T with the values to scatter |
init_value | XlaOp | scalar value of type T for the initial value of the output array |
scatter | XlaComputation | binary computation of type T, T -> T , to apply each scatter source element with its destination element |
The figure below shows examples of using SelectAndScatter , with the select function computing the maximal value among its parameters. Note that when the windows overlap, as in the figure (2) below, an index of the operand array may be selected multiple times by different windows. In the figure, the element of value 9 is selected by both of the top windows (blue and red) and the binary addition scatter function produces the output element of value 8 (2 + 6).
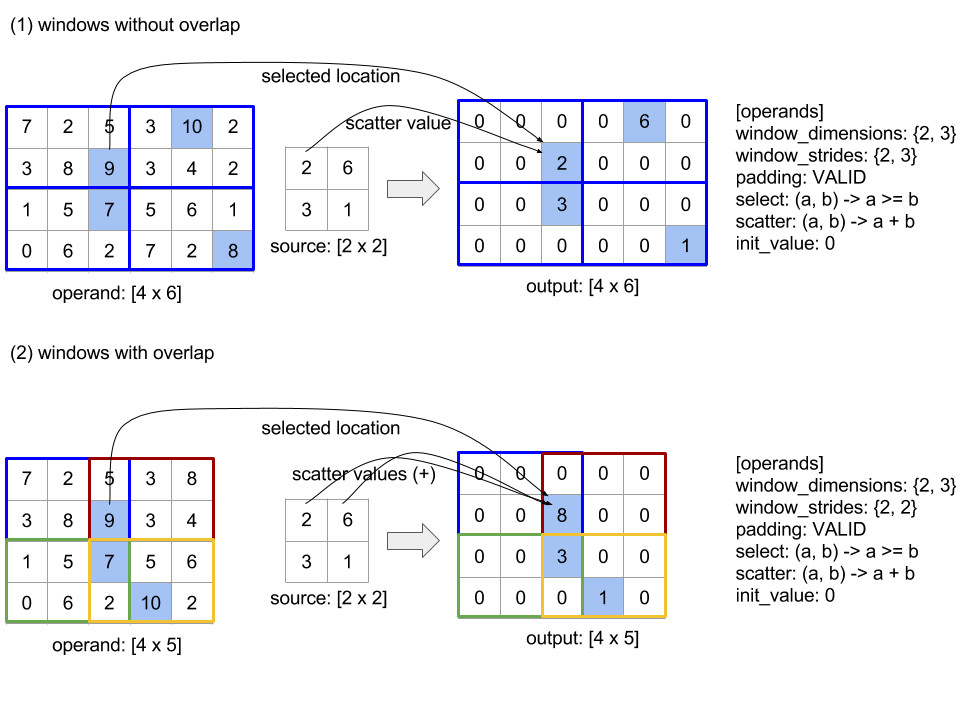
The evaluation order of the scatter function is arbitrary and may be non-deterministic. Therefore, the scatter function should not be overly sensitive to reassociation. See the discussion about associativity in the context of Reduce for more details.
For StableHLO information see StableHLO - select_and_scatter .
ارسال
See also XlaBuilder::Send .
Send , SendWithTokens , and SendToHost are operations that serve as communication primitives in HLO. These ops typically appear in HLO dumps as part of low-level input/output or cross-device transfer, but they are not intended to be constructed manually by end users.
Send(operand, handle)
| استدلالها | نوع | معناشناسی |
|---|---|---|
operand | XlaOp | data to send (array of type T) |
handle | ChannelHandle | unique identifier for each send/recv pair |
Sends the given operand data to a Recv instruction in another computation that shares the same channel handle. Does not return any data.
Similar to the Recv operation, the client API of Send operation represents synchronous communication, and is internally decomposed into 2 HLO instructions ( Send and SendDone ) to enable asynchronous data transfers. See also HloInstruction::CreateSend and HloInstruction::CreateSendDone .
Send(HloInstruction operand, int64 channel_id)
Initiates an asynchronous transfer of the operand to the resources allocated by the Recv instruction with the same channel id. Returns a context, which is used by a following SendDone instruction to wait for the completion of the data transfer. The context is a tuple of {operand (shape), request identifier (U32)} and it can only be used by a SendDone instruction.
For StableHLO information see StableHLO - send .
SendDone
See also HloInstruction::CreateSendDone .
SendDone(HloInstruction context)
Given a context created by a Send instruction, waits for the data transfer to complete. The instruction does not return any data.
Scheduling of channel instructions
The execution order of the 4 instructions for each channel ( Recv , RecvDone , Send , SendDone ) is as below.
-
Recvhappens beforeSend -
Sendhappens beforeRecvDone -
Recvhappens beforeRecvDone -
Sendhappens beforeSendDone
When the backend compilers generate a linear schedule for each computation that communicates via channel instructions, there must not be cycles across the computations. For example, below schedules lead to deadlocks.
SetDimensionSize
See also XlaBuilder::SetDimensionSize .
Sets the dynamic size of XlaOp's given dimension. The operand must be array shaped.
SetDimensionSize(operand, val, dimension)
| استدلالها | نوع | Semantics |
|---|---|---|
operand | XlaOp | n dimensional input array. |
val | XlaOp | int32 representing the runtime dynamic size. |
dimension | int64 | A value in the interval [0, n) that specifies the dimension. |
Pass through the operand as result, with dynamic dimension tracked by the compiler.
Padded values will be ignored by downstream reduction ops.
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
ShiftLeft
See also XlaBuilder::ShiftLeft .
Performs element-wise left-shift operation on lhs by rhs number of bits.
ShiftLeft(lhs, rhs)
| استدلالها | نوع | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for ShiftLeft:
ShiftLeft(lhs,rhs, broadcast_dimensions)
| Arguments | نوع | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - shift_left .
ShiftRightArithmetic
See also XlaBuilder::ShiftRightArithmetic .
Performs element-wise arithmetic right-shift operation on lhs by rhs number of bits.
ShiftRightArithmetic(lhs, rhs)
| Arguments | نوع | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for ShiftRightArithmetic:
ShiftRightArithmetic(lhs,rhs, broadcast_dimensions)
| Arguments | نوع | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - shift_right_arithmetic .
ShiftRightLogical
See also XlaBuilder::ShiftRightLogical .
Performs element-wise logical right-shift operation on lhs by rhs number of bits.
ShiftRightLogical(lhs, rhs)
| Arguments | نوع | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for ShiftRightLogical:
ShiftRightLogical(lhs,rhs, broadcast_dimensions)
| Arguments | نوع | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - shift_right_logical .
علامت
See also XlaBuilder::Sign .
Sign(operand) Element-wise sign operation x -> sgn(x) where
\[\text{sgn}(x) = \begin{cases} -1 & x < 0\\ -0 & x = -0\\ NaN & x = NaN\\ +0 & x = +0\\ 1 & x > 0 \end{cases}\]
using the comparison operator of the element type of operand .
Sign(operand)
| Arguments | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
For StableHLO information see StableHLO - sign .
گناه
Sin(operand) Element-wise sine x -> sin(x) .
See also XlaBuilder::Sin .
Sin(operand)
| Arguments | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
Sin also supports the optional result_accuracy argument:
Sin(operand, result_accuracy)
| Arguments | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
For StableHLO information see StableHLO - sine .
برش
See also XlaBuilder::Slice .
Slicing extracts a sub-array from the input array. The sub-array has the same number of dimensions as the input and contains the values inside a bounding box within the input array where the dimensions and indices of the bounding box are given as arguments to the slice operation.
Slice(operand, start_indices, limit_indices, strides)
| Arguments | نوع | Semantics |
|---|---|---|
operand | XlaOp | N dimensional array of type T |
start_indices | ArraySlice<int64> | List of N integers containing the starting indices of the slice for each dimension. Values must be greater than or equal to zero. |
limit_indices | ArraySlice<int64> | List of N integers containing the ending indices (exclusive) for the slice for each dimension. Each value must be greater than or equal to the respective start_indices value for the dimension and less than or equal to the size of the dimension. |
strides | ArraySlice<int64> | List of N integers that decides the input stride of the slice. The slice picks every strides[d] element in dimension d . |
1-dimensional example:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4})
// Result: {2.0, 3.0}
2-dimensional example:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3})
// Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
For StableHLO information see StableHLO - slice .
مرتب سازی
See also XlaBuilder::Sort .
Sort(operands, comparator, dimension, is_stable)
| Arguments | نوع | Semantics |
|---|---|---|
operands | ArraySlice<XlaOp> | The operands to sort. |
comparator | XlaComputation | The comparator computation to use. |
dimension | int64 | The dimension along which to sort. |
is_stable | bool | Whether stable sorting should be used. |
If only one operand is provided:
If the operand is a 1-dimensional tensor (an array), the result is a sorted array. If you want to sort the array into ascending order, the comparator should perform a less-than comparison. Formally, after the array is sorted, it holds for all index positions
i, jwithi < jthat eithercomparator(value[i], value[j]) = comparator(value[j], value[i]) = falseorcomparator(value[i], value[j]) = true.If the operand has higher number of dimensions, the operand is sorted along the provided dimension. For example, for a 2-dimensional tensor (a matrix), a dimension value of
0will independently sort every column, and a dimension value of1will independently sort each row. If no dimension number is provided, then the last dimension is chosen by default. For the dimension which is sorted, the same sorting order applies as in the 1-dimensional case.
If n > 1 operands are provided:
All
noperands must be tensors with the same dimensions. The element types of the tensors may be different.All operands are sorted together, not individually. Conceptually the operands are treated as a tuple. When checking whether the elements of each operand at index positions
iandjneed to be swapped, the comparator is called with2 * nscalar parameters, where parameter2 * kcorresponds to the value at positionifrom thek-thoperand, and parameter2 * k + 1corresponds to the value at positionjfrom thek-thoperand. Usually, the comparator would thus compare parameters2 * kand2 * k + 1with each other and possibly use other parameter pairs as tie breakers.The result is a tuple that consists of the operands in sorted order (along the provided dimension, as above). The
i-thoperand of the tuple corresponds to thei-thoperand of Sort.
For example, if there are three operands operand0 = [3, 1] , operand1 = [42, 50] , operand2 = [-3.0, 1.1] , and the comparator compares only the values of operand0 with less-than, then the output of the sort is the tuple ([1, 3], [50, 42], [1.1, -3.0]) .
If is_stable is set to true, the sort is guaranteed to be stable, that is, if there are elements which are considered to be equal by the comparator, the relative order of the equal values is preserved. Two elements e1 and e2 are equal if and only if comparator(e1, e2) = comparator(e2, e1) = false . By default, is_stable is set to false.
For StableHLO information see StableHLO - sort .
Sqrt
See also XlaBuilder::Sqrt .
Element-wise square root operation x -> sqrt(x) .
Sqrt(operand)
| Arguments | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
Sqrt also supports the optional result_accuracy argument:
Sqrt(operand, result_accuracy)
| Arguments | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
For StableHLO information see StableHLO - sqrt .
زیر
See also XlaBuilder::Sub .
Performs element-wise subtraction of lhs and rhs .
Sub(lhs, rhs)
| Arguments | نوع | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Sub:
Sub(lhs,rhs, broadcast_dimensions)
| Arguments | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - subtract .
برنزه
See also XlaBuilder::Tan .
Element-wise tangent x -> tan(x) .
Tan(operand)
| Arguments | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
Tan also supports the optional result_accuracy argument:
Tan(operand, result_accuracy)
| Arguments | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
For StableHLO information see StableHLO - tan .
Tanh
See also XlaBuilder::Tanh .
Element-wise hyperbolic tangent x -> tanh(x) .
Tanh(operand)
| Arguments | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
Tanh also supports the optional result_accuracy argument:
Tanh(operand, result_accuracy)
| Arguments | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to the function |
result_accuracy | optional ResultAccuracy | The types of accuracy the user can request for unary ops with multiple implementations |
For more information on result_accuracy see Result Accuracy .
For StableHLO information see StableHLO - tanh .
TopK
See also XlaBuilder::TopK .
TopK finds the values and indices of the k largest or smallest elements for the last dimension of the given tensor.
TopK(operand, k, largest)
| Arguments | نوع | Semantics |
|---|---|---|
operand | XlaOp | The tensor from which to extract the top k elements. The tensor must have greater or equal to one dimensions. The size of the last dimension of the tensor must be greater or equal to k . |
k | int64 | The number of elements to extract. |
largest | bool | Whether to extract the largest or smallest k elements. |
For a 1-dimensional input tensor (an array), finds the k largest or smallest entries in the array and outputs a tuple of two arrays (values, indices) . Thus values[j] is the j -th largest/smallest entry in operand , and its index is indices[j] .
For an input tensor with more than 1 dimension, computes the top k entries along the last dimension, preserving all other dimensions (rows) in the output. Thus, for an operand of shape [A, B, ..., P, Q] where Q >= k the output is a tuple (values, indices) where:
values.shape = indices.shape = [A, B, ..., P, k]
If two elements within a row are equal, the lower-index element appears first.
انتقال
See also the tf.reshape operation.
Transpose(operand, permutation)
| Arguments | نوع | Semantics |
|---|---|---|
operand | XlaOp | The operand to transpose. |
permutation | ArraySlice<int64> | How to permute the dimensions. |
Permutes the operand dimensions with the given permutation, so ∀ i . 0 ≤ i < number of dimensions ⇒ input_dimensions[permutation[i]] = output_dimensions[i] .
This is the same as Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)).
For StableHLO information see StableHLO - transpose .
TriangularSolve
See also XlaBuilder::TriangularSolve .
Solves systems of linear equations with lower or upper triangular coefficient matrices by forward- or back-substitution. Broadcasting along leading dimensions, this routine solves one of the matrix systems op(a) * x = b , or x * op(a) = b , for the variable x , given a and b , where op(a) is either op(a) = a , or op(a) = Transpose(a) , or op(a) = Conj(Transpose(a)) .
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| Arguments | نوع | Semantics |
|---|---|---|
a | XlaOp | a > 2 dimensional array of a complex or floating-point type with shape [..., M, M] . |
b | XlaOp | a > 2 dimensional array of the same type with shape [..., M, K] if left_side is true, [..., K, M] otherwise. |
left_side | bool | indicates whether to solve a system of the form op(a) * x = b ( true ) or x * op(a) = b ( false ). |
lower | bool | whether to use the upper or lower triangle of a . |
unit_diagonal | bool | if true , the diagonal elements of a are assumed to be 1 and not accessed. |
transpose_a | Transpose | whether to use a as is, transpose it or take its conjugate transpose. |
Input data is read only from the lower/upper triangle of a , depending on the value of lower . Values from the other triangle are ignored. Output data is returned in the same triangle; the values in the other triangle are implementation-defined and may be anything.
If the number of dimensions of a and b are greater than 2, they are treated as batches of matrices, where all except the minor 2 dimensions are batch dimensions. a and b must have equal batch dimensions.
For StableHLO information see StableHLO - triangular_solve .
چندتایی
See also XlaBuilder::Tuple .
A tuple containing a variable number of data handles, each of which has its own shape.
Tuple(elements)
| Arguments | نوع | Semantics |
|---|---|---|
elements | vector of XlaOp | N array of type T |
This is analogous to std::tuple in C++. Conceptually:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
Tuples can be deconstructed (accessed) via the GetTupleElement operation.
For StableHLO information see StableHLO - tuple .
در حالی که
See also XlaBuilder::While .
While(condition, body, init)
| Arguments | نوع | Semantics |
|---|---|---|
condition | XlaComputation | XlaComputation of type T -> PRED which defines the termination condition of the loop. |
body | XlaComputation | XlaComputation of type T -> T which defines the body of the loop. |
init | T | Initial value for the parameter of condition and body . |
Sequentially executes the body until the condition fails. This is similar to a typical while loop in many other languages except for the differences and restrictions listed below.
- A
Whilenode returns a value of typeT, which is the result from the last execution of thebody. - The shape of the type
Tis statically determined and must be the same across all iterations.
The T parameters of the computations are initialized with the init value in the first iteration and are automatically updated to the new result from body in each subsequent iteration.
One main use case of the While node is to implement the repeated execution of training in neural networks. Simplified pseudocode is shown below with a graph that represents the computation. The code can be found in while_test.cc . The type T in this example is a Tuple consisting of an int32 for the iteration count and a vector[10] for the accumulator. For 1000 iterations, the loop keeps adding a constant vector to the accumulator.
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}
For StableHLO information see StableHLO - while .
Xor
See also XlaBuilder::Xor .
Performs element-wise XOR of lhs and rhs .
Xor(lhs, rhs)
| Arguments | نوع | Semantics |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
The arguments' shapes have to be either similar or compatible. See the broadcasting documentation about what it means for shapes to be compatible. The result of an operation has a shape which is the result of broadcasting the two input arrays. In this variant, operations between arrays of different ranks are not supported, unless one of the operands is a scalar.
An alternative variant with different-dimensional broadcasting support exists for Xor:
Xor(lhs,rhs, broadcast_dimensions)
| Arguments | نوع | معناشناسی |
|---|---|---|
| lhs | XlaOp | Left-hand-side operand: array of type T |
| rhs | XlaOp | Left-hand-side operand: array of type T |
| broadcast_dimension | ArraySlice | Which dimension in the target shape each dimension of the operand shape corresponds to |
This variant of the operation should be used for arithmetic operations between arrays of different ranks (such as adding a matrix to a vector).
The additional broadcast_dimensions operand is a slice of integers specifying the dimensions to use for broadcasting the operands. The semantics are described in detail on the broadcasting page .
For StableHLO information see StableHLO - xor .









