בקטע הבא מוסבר על הסמנטיקה של הפעולות שמוגדרות בממשק XlaBuilder. בדרך כלל, הפעולות האלה ממופות אחת לאחת לפעולות שמוגדרות בממשק ה-RPC ב-xla_data.proto.
הערה לגבי מינוח: סוג הנתונים הכללי XLA מתייחס למערך N-ממדי שמכיל רכיבים מסוג אחיד כלשהו (כמו float של 32 ביט). בכל המסמכים, מערך מציין מערך רב-ממדי שרירותי. לנוחותכם, למקרים מיוחדים יש שמות ספציפיים ומוכרים יותר. לדוגמה, וקטור הוא מערך חד-ממדי ומטריצה היא מערך דו-ממדי.
מידע נוסף על המבנה של Op זמין במאמרים צורות ופריסה ופריסה של משבצות.
Abs
מידע נוסף זמין במאמר בנושא XlaBuilder::Abs.
ערך מוחלט של כל רכיב x -> |x|.
Abs(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
מידע על StableHLO זמין במאמר StableHLO - abs.
הוספה
מידע נוסף זמין במאמר בנושא XlaBuilder::Add.
מבצעת חיבור של lhs ו-rhs לפי רכיבים.
Add(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בשידור רב-ממדי עבור Add:
Add(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר בנושא StableHLO – הוספה.
AddDependency
מידע נוסף זמין במאמר בנושא HloInstruction::AddDependency.
יכול להיות ש-AddDependency יופיעו בקובצי dump של HLO, אבל הם לא מיועדים לבנייה ידנית על ידי משתמשי קצה.
AfterAll
מידע נוסף זמין במאמר בנושא XlaBuilder::AfterAll.
הפונקציה AfterAll מקבלת מספר משתנה של טוקנים ומפיקה טוקן יחיד. אסימונים (tokens)
הם סוגים פרימיטיביים שאפשר להעביר בין פעולות עם תופעות לוואי כדי
לאכוף סדר. אפשר להשתמש ב-AfterAll כדי להגדיר פעולה מסוימת אחרי קבוצה של פעולות.
AfterAll(tokens)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
tokens |
וקטור של XlaOp |
מספר משתנה של טוקנים |
למידע על StableHLO, ראו StableHLO – after_all.
AllGather
מידע נוסף זמין במאמר בנושא XlaBuilder::AllGather.
מבצע שרשור בין רפליקות.
AllGather(operand, all_gather_dimension, shard_count, replica_groups,
channel_id, layout, use_global_device_ids)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand
|
XlaOp
|
מערך לאיחוד בין עותקים |
all_gather_dimension |
int64 |
מאפיין שרשור |
shard_count
|
int64
|
הגודל של כל קבוצת רפליקות |
replica_groups
|
וקטור של וקטורים של
int64 |
קבוצות שביניהן מתבצעת השרשור |
channel_id
|
אופציונלי
ChannelHandle |
מזהה ערוץ אופציונלי לתקשורת בין מודולים |
layout
|
אופציונלי Layout
|
יוצר תבנית פריסה שתתעד את הפריסה התואמת בארגומנט |
use_global_device_ids
|
אופציונלי bool
|
הפונקציה מחזירה true אם המזהים בהגדרות של ReplicaGroup מייצגים מזהה גלובלי |
-
replica_groupsהיא רשימה של קבוצות רפליקות שביניהן מתבצעת השרשור (אפשר לאחזר את מזהה הרפליקה של הרפליקה הנוכחית באמצעותReplicaId). הסדר של הרפליקות בכל קבוצה קובע את הסדר שבו הקלט שלהן מופיע בתוצאה.replica_groupsהשדה הזה צריך להיות ריק (ואז כל העותקים שייכים לקבוצה אחת, מסודרים מ-0עדN - 1), או להכיל את אותו מספר רכיבים כמו מספר העותקים. לדוגמה, הפונקציהreplica_groups = {0, 2}, {1, 3}מבצעת שרשור בין העותקים0ו-2, ובין1ו-3. -
shard_countהוא הגודל של כל קבוצת עותקים. אנחנו צריכים את זה במקרים שבהם השדותreplica_groupsריקים. - הסימן
channel_idמשמש לתקשורת בין מודולים: רק פעולות עם אותוchannel_idיכולות לתקשר זו עם זו.all-gather use_global_device_idsהפונקציה מחזירה true אם המזהים בהגדרות של ReplicaGroup מייצגים מזהה גלובלי של (replica_id * partition_count + partition_id) במקום מזהה רפליקה. כך אפשר לקבץ מכשירים בצורה גמישה יותר אם הפעולה all-reduce היא גם חוצת מחיצות וגם חוצת עותקים.
צורת הפלט היא צורת הקלט עם all_gather_dimension שהוגדלה פי shard_count. לדוגמה, אם יש שני עותקים והאופרנד הוא [1.0, 2.5] ו-[3.0, 5.25] בהתאמה בשני העותקים, ערך הפלט מהפעולה הזו שבה all_gather_dim הוא 0 יהיה [1.0, 2.5, 3.0,5.25] בשני העותקים.
ממשק ה-API של AllGather מפורק באופן פנימי ל-2 הוראות HLO (AllGatherStart ו-AllGatherDone).
מידע נוסף זמין במאמר בנושא HloInstruction::CreateAllGatherStart.
AllGatherStart ו-AllGatherDone משמשים כפרימיטיבים ב-HLO. יכול להיות שהפעולות האלה יופיעו בקובצי dump של HLO, אבל הן לא מיועדות ליצירה ידנית על ידי משתמשי קצה.
מידע על StableHLO זמין במאמר StableHLO - all_gather.
AllReduce
מידע נוסף זמין במאמר בנושא XlaBuilder::AllReduce.
מבצעת חישוב בהתאמה אישית בין העותקים.
AllReduce(operand, computation, replica_groups, channel_id,
shape_with_layout, use_global_device_ids)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand
|
XlaOp
|
מערך או טופל לא ריק של מערכים לצמצום בין העותקים |
computation |
XlaComputation |
חישוב הצמצום |
replica_groups
|
ReplicaGroup וקטור
|
קבוצות שביניהן מתבצעות ההפחתות |
channel_id
|
אופציונלי
ChannelHandle |
מזהה ערוץ אופציונלי לתקשורת בין מודולים |
shape_with_layout
|
אופציונלי Shape
|
הגדרת הפריסה של הנתונים המועברים |
use_global_device_ids
|
אופציונלי bool
|
הפונקציה מחזירה true אם המזהים בהגדרות של ReplicaGroup מייצגים מזהה גלובלי |
- אם
operandהוא טאפל של מערכים, הפעולה all-reduce מתבצעת על כל רכיב בטאפל. -
replica_groupsהיא רשימה של קבוצות העתקים שביניהן מתבצעת ההפחתה (אפשר לאחזר את מזהה ההעתק של ההעתק הנוכחי באמצעותReplicaId). הרשימהreplica_groupsחייבת להיות ריקה (במקרה כזה כל ההעתקים שייכים לקבוצה אחת), או להכיל את אותו מספר של רכיבים כמו מספר ההעתקים. לדוגמה,replica_groups = {0, 2}, {1, 3}מבצע צמצום בין העותקים0ו-2, ובין1ו-3. - הסימן
channel_idמשמש לתקשורת בין מודולים: רק פעולות עם אותוchannel_idיכולות לתקשר זו עם זו.all-reduce -
shape_with_layout: כופה את הפריסה של AllReduce לפריסה שצוינה. הפרמטר הזה משמש כדי להבטיח את אותו פריסה לקבוצה של פעולות AllReduce שעברו קומפילציה בנפרד. use_global_device_idsהפונקציה מחזירה true אם המזהים בהגדרות של ReplicaGroup מייצגים מזהה גלובלי של (replica_id * partition_count + partition_id) במקום מזהה רפליקה. כך אפשר לקבץ מכשירים בצורה גמישה יותר אם הפעולה all-reduce היא גם חוצת מחיצות וגם חוצת עותקים.
צורת הפלט זהה לצורת הקלט. לדוגמה, אם יש שני עותקים והאופרנד הוא [1.0, 2.5] ו-[3.0, 5.25] בהתאמה בשני העותקים, ערך הפלט מהאופרציה הזו וחישוב הסכום יהיה [4.0, 7.75] בשני העותקים. אם הקלט הוא טאפל, הפלט יהיה גם הוא טאפל.
כדי לחשב את התוצאה של AllReduce, צריך לקבל קלט מכל עותק משוכפל. לכן, אם עותק משוכפל אחד מבצע צומת AllReduce יותר פעמים מעותק אחר, העותק הראשון ימתין לנצח. מכיוון שכל העותקים הרפליקציות מריצים את אותה תוכנית, אין הרבה דרכים שזה יכול לקרות, אבל זה אפשרי אם התנאי של לולאת while תלוי בנתונים מ-infeed והנתונים מ-infeed גורמים ללולאת while לבצע יותר איטרציות בעותק רפליקציה אחד מאשר בעותק רפליקציה אחר.
ממשק ה-API של AllReduce מפורק באופן פנימי ל-2 הוראות HLO (AllReduceStart ו-AllReduceDone).
מידע נוסף זמין במאמר בנושא HloInstruction::CreateAllReduceStart.
AllReduceStart ו-AllReduceDone משמשים כפרימיטיבים ב-HLO. יכול להיות שהפעולות האלה יופיעו בקובצי dump של HLO, אבל הן לא מיועדות ליצירה ידנית על ידי משתמשי קצה.
CrossReplicaSum
מידע נוסף זמין במאמר בנושא XlaBuilder::CrossReplicaSum.
מבצעת AllReduce עם חישוב סכום.
CrossReplicaSum(operand, replica_groups)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand
|
XlaOp | מערך או טופל לא ריק של מערכים לצמצום בין העותקים |
replica_groups
|
וקטור של וקטורים של
int64 |
קבוצות שביניהן מתבצעות ההפחתות |
הפונקציה מחזירה את סכום ערכי האופרנד בכל תת-קבוצה של העתקים. כל העותקים מספקים קלט אחד לסכום, וכל העותקים מקבלים את הסכום שמתקבל לכל קבוצת משנה.
AllToAll
מידע נוסף זמין במאמר בנושא XlaBuilder::AllToAll.
AllToAll היא פעולה קולקטיבית ששולחת נתונים מכל הליבות לכל הליבות. התהליך כולל שני שלבים:
- שלב הפיזור. בכל ליבה, האופרנד מפולג ל-
split_countמספר בלוקים לאורךsplit_dimensions, והבלוקים מפוזרים לכל הליבות, לדוגמה, הבלוק ה-i נשלח לליבה ה-i. - שלב האיסוף. כל ליבה משרשרת את הבלוקים שהתקבלו לאורך
concat_dimension.
אפשר להגדיר את הליבות המשתתפות באמצעות:
-
replica_groups: כל ReplicaGroup מכיל רשימה של מזהי רפליקות שמשתתפות בחישוב (אפשר לאחזר את מזהה הרפליקה הנוכחית באמצעותReplicaId). הפעולה AllToAll תתבצע בתוך קבוצות משנה בסדר שצוין. לדוגמה,replica_groups = { {1,2,3}, {4,5,0} }פירושו ש-AllToAll יוחל בתוך העותקים המשוכפלים{1, 2, 3}, ובשלב האיסוף, והבלוקים שהתקבלו יורכבו באותו סדר של 1, 2, 3. לאחר מכן, יוחל עוד AllToAll בעותקים 4, 5, 0, וסדר השרשור יהיה גם 4, 5, 0. אםreplica_groupsריק, כל העותקים שייכים לקבוצה אחת, לפי סדר השרשור של המופעים שלהם.
דרישות מוקדמות:
- הגודל של מימד האופרנד ב-
split_dimensionמתחלק ב-split_count. - הצורה של האופרנד היא לא טאפל.
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups, layout, channel_id)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך קלט n ממדי |
split_dimension
|
int64
|
ערך במרווח [0,n) שמציין את המאפיין שלפיו האופרנד מפולח |
concat_dimension
|
int64
|
ערך במרווח
[0,n) שבו מצוין שם המימד
שלאורכו הבלוקים המפוצלים
מחוברים |
split_count
|
int64
|
מספר ליבות המעבד שמשתתפות בפעולה הזו. אם השדה replica_groups ריק, צריך להזין כאן את מספר העותקים. אחרת, צריך להזין כאן מספר ששווה למספר העותקים בכל קבוצה. |
replica_groups
|
ReplicaGroupוקטור
|
כל קבוצה מכילה רשימה של מזהי העתקים. |
layout |
אופציונלי Layout |
פריסת זיכרון בהגדרת המשתמש |
channel_id
|
אופציונלי ChannelHandle
|
מזהה ייחודי לכל זוג של שליחה/קבלה |
מידע נוסף על צורות ופריסות זמין במאמר xla::shapes.
למידע על StableHLO, ראו StableHLO - all_to_all.
AllToAll – דוגמה 1.
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(
x,
/*split_dimension=*/ 1,
/*concat_dimension=*/ 0,
/*split_count=*/ 4);
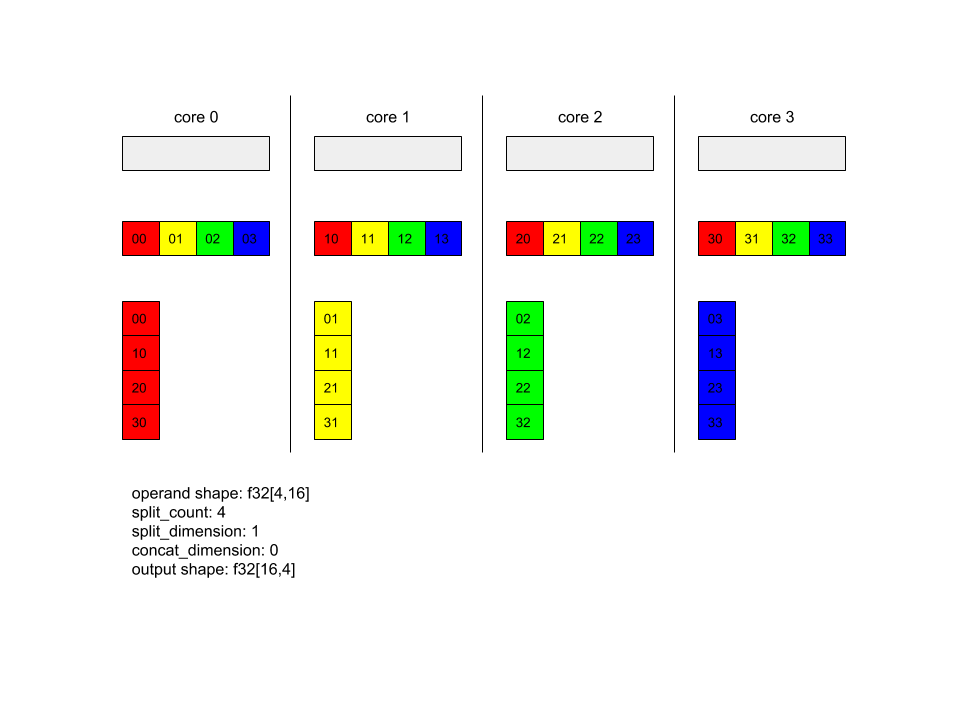
בדוגמה שלמעלה, יש 4 ליבות שמשתתפות ב-Alltoall. בכל ליבה, האופרנד מחולק ל-4 חלקים לאורך מימד 1, כך שלכל חלק יש צורה f32[4,4]. ארבעת החלקים מפוזרים בין כל הליבות. לאחר מכן, כל ליבה משרשרת את החלקים שהתקבלו לאורך מאפיין 0, לפי הסדר של ליבה 0 עד 4. לכן, הפלט בכל ליבה הוא בצורה f32[16,4].
AllToAll - Example 2 - StableHLO
בדוגמה שלמעלה, יש 2 רפליקות שמשתתפות ב-AllToAll. בכל רפליקה, לאופרנד יש צורה f32[2,4]. האופרנד מפוצל לשני חלקים לאורך מימד 1, כך שלכל חלק יש צורה f32[2,2]. לאחר מכן, שני החלקים מוחלפים בין העותקים בהתאם למיקום שלהם בקבוצת העותקים. כל רפליקה אוספת את החלק המתאים שלה משני האופרנדים ומשרשרת אותם לאורך מימד 0. כתוצאה מכך, הפלט בכל עותק זהה בצורה f32[4,2].
RaggedAllToAll
מידע נוסף זמין במאמר בנושא XlaBuilder::RaggedAllToAll.
RaggedAllToAll מבצע פעולה קולקטיבית של all-to-all, שבה הקלט והפלט הם טנסורים משוננים.
RaggedAllToAll(input, input_offsets, send_sizes, output, output_offsets,
recv_sizes, replica_groups, channel_id)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
input |
XlaOp |
מערך N מסוג T |
input_offsets |
XlaOp |
מערך N מסוג T |
send_sizes |
XlaOp |
מערך N מסוג T |
output |
XlaOp |
מערך N מסוג T |
output_offsets |
XlaOp |
מערך N מסוג T |
recv_sizes |
XlaOp |
מערך N מסוג T |
replica_groups
|
ReplicaGroup וקטור
|
כל קבוצה מכילה רשימה של מזהי עותקים. |
channel_id
|
אופציונלי ChannelHandle
|
מזהה ייחודי לכל זוג של שליחה/קבלה |
טנסורים לא סדירים מוגדרים על ידי קבוצה של שלושה טנסורים:
-
data: טנסורdataהוא 'משונן' לאורך הממד החיצוני ביותר שלו, שבו לכל רכיב באינדקס יש גודל משתנה. -
offsets': הטנזורoffsetsמבצע אינדוקס של הממד החיצוני ביותר של הטנזורdata, ומייצג את ההיסטארט של כל רכיב לא סדיר של הטנזורdata. -
sizes: טנסורsizesמייצג את הגודל של כל רכיב לא סדיר בטנסורdata, כאשר הגודל מצוין ביחידות של רכיבי משנה. רכיב משנה מוגדר כסיומת של צורת טנסור הנתונים שמתקבלת מהסרת המימד החיצוני ביותר של הנתונים. - הטנסורים
offsetsו-sizesצריכים להיות באותו גודל.
דוגמה לטנזור לא אחיד:
data: [8,3] =
{ {a,b,c},{d,e,f},{g,h,i},{j,k,l},{m,n,o},{p,q,r},{s,t,u},{v,w,x} }
offsets: [3] = {0, 1, 4}
sizes: [3] = {1, 3, 4}
// Index 'data' at 'offsets'[0], 'sizes'[0]' // {a,b,c}
// Index 'data' at 'offsets'[1], 'sizes'[1]' // {d,e,f},{g,h,i},{j,k,l}
// Index 'data' at 'offsets'[2], 'sizes'[2]' // {m,n,o},{p,q,r},{s,t,u},{v,w,x}
צריך לפצל את output_offsets כך שלכל העתק יהיו היסטים מנקודת המבט של פלט העתק היעד.
עבור היסט הפלט ה-i, העותק הנוכחי ישלח עדכון input[input_offsets[i]:input_offsets[i]+input_sizes[i]] לעותק ה-i שייכתב ל-output_i[output_offsets[i]:output_offsets[i]+send_sizes[i]] בעותק ה-i output.
לדוגמה, אם יש לנו 2 רפליקות:
replica 0:
input: [1, 2, 2]
output:[0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 2]
output_offsets: [0, 0]
recv_sizes: [1, 1]
replica 1:
input: [3, 4, 0]
output: [0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 1]
output_offsets: [1, 2]
recv_sizes: [2, 1]
// replica 0's result will be: [1, 3, 0, 0]
// replica 1's result will be: [2, 2, 4, 0]
ה-HLO המדורג all-to-all כולל את הארגומנטים הבאים:
-
input: טנסור של נתוני קלט לא אחידים. -
output: טנזור של נתוני פלט לא אחידים. -
input_offsets: טנזור של היסטים של קלט לא אחיד. -
send_sizes: טנזור של גדלים לא אחידים של שליחות. -
output_offsets: מערך של היסטים לא סדירים בפלט של העותק המשוכפל של היעד. -
recv_sizes: טנזור של גדלים לא אחידים של recv.
לכל הטנסורים *_offsets ו-*_sizes צריך להיות אותו צורה.
יש תמיכה בשתי צורות של טנסורים *_offsets ו-*_sizes:
-
[num_devices]שבו יכול להיות שיישלח עדכון אחד לכל מכשיר מרוחק בקבוצת העותקים. לדוגמה:
for (remote_device_id : replica_group) {
SEND input[input_offsets[remote_device_id]],
output[output_offsets[remote_device_id]],
send_sizes[remote_device_id] }
-
[num_devices, num_updates]שבהם ragged-all-to-all עשוי לשלוח עדnum_updatesעדכונים לאותו מכשיר מרוחק (כל אחד בהיסט שונה), לכל מכשיר מרוחק בקבוצת העותקים.
לדוגמה:
for (remote_device_id : replica_group) {
for (update_idx : num_updates) {
SEND input[input_offsets[remote_device_id][update_idx]],
output[output_offsets[remote_device_id][update_idx]]],
send_sizes[remote_device_id][update_idx] } }
וגם
מידע נוסף זמין במאמר בנושא XlaBuilder::And.
מבצעת פעולת AND בין שני טנסורים, lhs ו-rhs, ברמת הרכיב.
And(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בהרחבה רב-ממדית שונה עבור And:
And(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
למידע על StableHLO, ראו StableHLO - and.
אסינכרוני
ראו גם HloInstruction::CreateAsyncStart,
HloInstruction::CreateAsyncUpdate,
HloInstruction::CreateAsyncDone.
AsyncDone, AsyncStart ו-AsyncUpdate הן הוראות פנימיות של HLO שמשמשות לפעולות אסינכרוניות, והן פרימיטיבים ב-HLO. יכול להיות שהפעולות האלה יופיעו בפריקות של HLO, אבל הן לא מיועדות לבנייה ידנית על ידי משתמשי קצה.
Atan2
מידע נוסף זמין במאמר בנושא XlaBuilder::Atan2.
מבצע פעולת atan2 לפי רכיבים ב-lhs וב-rhs.
Atan2(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בהרחבת שידור מממד שונה עבור Atan2:
Atan2(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר StableHLO – atan2.
BatchNormGrad
תיאור מפורט של האלגוריתם מופיע גם במאמרים XlaBuilder::BatchNormGrad והמקורי בנושא נורמליזציה של קבוצות.
מחשבת את הגרדיאנטים של נורמליזציית אצווה.
BatchNormGrad(operand, scale, batch_mean, batch_var, grad_output, epsilon,
feature_index)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp | מערך n מימדי שיש לנרמל (x) |
scale |
XlaOp | מערך חד-ממדי (\(\gamma\)) |
batch_mean |
XlaOp | מערך חד-ממדי (\(\mu\)) |
batch_var |
XlaOp | מערך חד-ממדי (\(\sigma^2\)) |
grad_output |
XlaOp | מעברי צבע שהועברו אל BatchNormTraining (\(\nabla y\)) |
epsilon |
float |
ערך Epsilon (\(\epsilon\)) |
feature_index |
int64 |
אינדקס להצגת מאפיין ב-operand |
לכל מאפיין במאפיין התכונה (feature_index הוא האינדקס של מאפיין התכונה ב-operand), הפעולה מחשבת את הגרדיאנטים ביחס ל-operand, ל-offset ול-scale בכל שאר המאפיינים. הערך של feature_index חייב להיות אינדקס תקין של מאפיין התכונה ב-operand.
שלושת הגרדיאנטים מוגדרים באמצעות הנוסחאות הבאות (בהנחה שמערך 4 ממדי כ-operand, עם אינדקס ממד התכונה l, גודל אצווה m וגדלים מרחביים w ו-h):
\[ \begin{split} c_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sigma^2_l+\epsilon} \right) \\\\ d_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \\\\ \nabla x_{ijkl} &= \frac{\gamma_{l} }{\sqrt{\sigma^2_{l}+\epsilon} } \left( \nabla y_{ijkl} - d_l - c_l (x_{ijkl} - \mu_{l}) \right) \\\\ \nabla \gamma_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sqrt{\sigma^2_{l}+\epsilon} } \right) \\\\\ \nabla \beta_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \end{split} \]
הקלט batch_mean והקלט batch_var מייצגים ערכי רגעים במאפיינים של קבוצות ומרחבים.
סוג הפלט הוא טאפל של שלושה אובייקטים מסוג handle:
| פלט | סוג | סמנטיקה |
|---|---|---|
grad_operand
|
XlaOp | השיפוע ביחס לקלט operand
(\(\nabla x\)) |
grad_scale
|
XlaOp | הגרדיאנט ביחס לקלט **scale **
(\(\nabla\gamma\)) |
grad_offset
|
XlaOp | gradient with respect to
input
offset(\(\nabla\beta\)) |
מידע על StableHLO זמין במאמר StableHLO – batch_norm_grad.
BatchNormInference
תיאור מפורט של האלגוריתם מופיע גם במאמרים XlaBuilder::BatchNormInference והמקורי בנושא נורמליזציה של קבוצות.
מנרמלת מערך על פני מאפייני מיקום ומאפיינים של קבוצות.
BatchNormInference(operand, scale, offset, mean, variance, epsilon,
feature_index)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp | מערך n מימדי שצריך לנרמל |
scale |
XlaOp | מערך חד-ממדי |
offset |
XlaOp | מערך חד-ממדי |
mean |
XlaOp | מערך חד-ממדי |
variance |
XlaOp | מערך חד-ממדי |
epsilon |
float |
ערך אפסילון |
feature_index |
int64 |
אינדקס להצגת מאפיין ב-operand |
לכל מאפיין במאפיין feature (feature_index הוא האינדקס של המאפיין feature ב-operand), הפעולה מחשבת את הממוצע והשונות בכל שאר המאפיינים, ומשתמשת בממוצע ובשונות כדי לנרמל כל רכיב ב-operand. הערך של feature_index צריך להיות אינדקס חוקי למאפיין המאפיינים של התכונה ב-operand.
הפונקציה BatchNormInference שקולה לקריאה לפונקציה BatchNormTraining בלי לחשב את mean ואת variance לכל קבוצה. הוא משתמש בקלט mean ובקלט variance במקום זאת כערכים משוערים. מטרת הפעולה הזו היא להפחית את זמן האחזור בהסקת מסקנות, ומכאן השם BatchNormInference.
הפלט הוא מערך מנורמל n-ממדי עם צורה זהה לזו של הקלט operand.
מידע על StableHLO זמין במאמר StableHLO – batch_norm_inference.
BatchNormTraining
תיאור מפורט של האלגוריתם מופיע גם במאמרים XlaBuilder::BatchNormTraining וthe original batch normalization paper.
מנרמלת מערך על פני מימדים של אצווה ומימדים מרחביים.
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך n מימדי שיש לנרמל (x) |
scale |
XlaOp |
מערך חד-ממדי (\(\gamma\)) |
offset |
XlaOp |
מערך חד-ממדי (\(\beta\)) |
epsilon |
float |
ערך אפסילון (\(\epsilon\)) |
feature_index |
int64 |
אינדקס להצגת מאפיין ב-operand |
לכל מאפיין במאפיין feature (feature_index הוא האינדקס של המאפיין feature ב-operand), הפעולה מחשבת את הממוצע והשונות בכל שאר המאפיינים, ומשתמשת בממוצע ובשונות כדי לנרמל כל רכיב ב-operand. הערך של feature_index צריך להיות אינדקס חוקי למאפיין המאפיינים של התכונה ב-operand.
האלגוריתם פועל באופן הבא לכל אצווה ב-operand \(x\) שמכילה m רכיבים עם w ו-h כגודל הממדים המרחביים (בהנחה ש-operand הוא מערך 4 ממדי):
מחשבת את הממוצע של קבוצת הפריטים \(\mu_l\) לכל תכונה
lבממד התכונה: \(\mu_l=\frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h x_{ijkl}\)חישוב השונות של קבוצת תמונות \(\sigma^2_l\): $\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
נרמול, שינוי קנה מידה והזזה: \(y_{ijkl}=\frac{\gamma_l(x_{ijkl}-\mu_l)}{\sqrt[2]{\sigma^2_l+\epsilon} }+\beta_l\)
ערך האפסילון, בדרך כלל מספר קטן, מתווסף כדי למנוע שגיאות חלוקה באפס.
סוג הפלט הוא טאפל של שלושה ערכים מסוג XlaOp:
| פלט | סוג | סמנטיקה |
|---|---|---|
output
|
XlaOp
|
מערך n ממדי עם אותה צורה כמו הקלט
operand (y) |
batch_mean |
XlaOp |
מערך חד-ממדי (\(\mu\)) |
batch_var |
XlaOp |
מערך חד-ממדי (\(\sigma^2\)) |
הערכים batch_mean ו-batch_var הם רגעים שמחושבים על פני קבוצת הפריטים והמאפיינים המרחביים באמצעות הנוסחאות שלמעלה.
מידע על StableHLO זמין במאמר StableHLO - batch_norm_training.
Bitcast
מידע נוסף זמין במאמר בנושא HloInstruction::CreateBitcast.
Bitcast עשוי להופיע בקובצי dump של HLO, אבל הוא לא מיועד לבנייה ידנית על ידי משתמשי קצה.
BitcastConvertType
מידע נוסף זמין במאמר בנושא XlaBuilder::BitcastConvertType.
בדומה ל-tf.bitcast ב-TensorFlow, הפעולה מבצעת bitcast ברמת הרכיב מצורת נתונים לצורת יעד. הגודל של הקלט והפלט חייב להיות זהה: למשל, s32 רכיבים הופכים ל-f32 רכיבים באמצעות שגרת bitcast, ורכיב אחד של s32 יהפוך לארבעה רכיבים של s8. Bitcast מיושם כהעברה ברמה נמוכה, ולכן מכונות עם ייצוגים שונים של נקודות צפות יניבו תוצאות שונות.
BitcastConvertType(operand, new_element_type)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T עם מימדים D |
new_element_type |
PrimitiveType |
type U |
המידות של האופרנד ושל צורת היעד צריכות להיות זהות, למעט המימד האחרון שישתנה בהתאם ליחס בין גודל הפרימיטיב לפני ההמרה ואחריה.
סוגי הרכיבים של המקור והיעד לא יכולים להיות טופלים.
מידע על StableHLO זמין במאמר StableHLO - bitcast_convert.
Bitcast-converting to primitive type of different width
BitcastConvert ההוראה HLO תומכת במקרה שבו הגודל של סוג רכיב הפלט T' לא שווה לגודל של רכיב הקלט T. מכיוון שהפעולה כולה היא שידור ביט (bitcast) ולא משנה את הבייטים הבסיסיים, הצורה של רכיב הפלט צריכה להשתנות. עבור B = sizeof(T), B' =
sizeof(T'), יש שני מקרים אפשריים.
קודם כל, כש-B > B', צורת הפלט מקבלת מימד חדש קטן ביותר בגודל B/B'. לדוגמה:
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
הכלל נשאר זהה עבור סקלרים אפקטיביים:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
לחלופין, עבור B' > B ההוראה מחייבת שהמאפיין הלוגי האחרון של צורת הקלט יהיה שווה ל-B'/B, והמאפיין הזה מושמט במהלך ההמרה:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
שימו לב שהמרות בין רוחבי סיביות שונים לא מתבצעות ברמת הרכיב.
להודיע לכולם
מידע נוסף זמין במאמר בנושא XlaBuilder::Broadcast.
הפונקציה מוסיפה מאפיינים למערך על ידי שכפול הנתונים במערך.
Broadcast(operand, broadcast_sizes)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
המערך לשכפול |
broadcast_sizes |
ArraySlice<int64> |
הגודל של המאפיינים החדשים |
המימדים החדשים מוכנסים בצד ימין, כלומר אם ל-broadcast_sizes יש ערכים {a0, ..., aN} ולצורה של האופרנד יש מימדים {b0, ..., bM}, אז לצורה של הפלט יש מימדים {a0, ..., aN, b0, ..., bM}.
המאפיינים החדשים הם אינדקסים של עותקים של האופרנד, כלומר
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
לדוגמה, אם operand הוא סקלר f32 עם הערך 2.0f, ו-broadcast_sizes הוא {2, 3}, התוצאה תהיה מערך עם הצורה f32[2, 3] וכל הערכים בתוצאה יהיו 2.0f.
מידע על StableHLO זמין במאמר StableHLO – שידור.
BroadcastInDim
מידע נוסף זמין במאמר בנושא XlaBuilder::BroadcastInDim.
מרחיבה את הגודל ואת מספר המאפיינים של מערך על ידי שכפול הנתונים במערך.
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
המערך לשכפול |
out_dim_size
|
ArraySlice<int64>
|
הגדלים של המידות של צורת היעד |
broadcast_dimensions
|
ArraySlice<int64>
|
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
בדומה ל-Broadcast, אבל מאפשרת להוסיף מאפיינים בכל מקום ולהרחיב מאפיינים קיימים עם גודל 1.
הערך operand משודר לצורה שמתוארת על ידי out_dim_size.
broadcast_dimensions ממפה את המימדים של operand למימדים של צורת היעד, כלומר המימד ה-i של האופרנד ממופה למימד ה-broadcast_dimension[i] של צורת הפלט. הממדים של operand צריכים להיות בגודל 1 או באותו גודל כמו הממד בצורת הפלט שהם ממופים אליו. שאר המאפיינים יאוכלסו במאפיינים בגודל 1. לאחר מכן, מתבצע שידור (broadcast) של המימד המנוון לאורך המימדים המנוונים האלה כדי להגיע לצורת הפלט. הסמנטיקה מתוארת בפירוט בדף השידור.
התקשרות
מידע נוסף זמין במאמר בנושא XlaBuilder::Call.
מפעילה חישוב עם הארגומנטים הנתונים.
Call(computation, operands...)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
computation
|
XlaComputation
|
חישוב מסוג T_0, T_1, ...,
T_{N-1} -> S עם N פרמטרים מסוג שרירותי |
operands |
רצף של N XlaOps |
N ארגומנטים מסוג שרירותי |
הארות והסוגים של operands צריכים להתאים לפרמטרים של computation. מותר לא לכלול את operands.
CompositeCall
מידע נוסף זמין במאמר בנושא XlaBuilder::CompositeCall.
מכיל פעולה שמורכבת מפעולות אחרות של StableHLO, מקבלת קלט ו-composite_attributes ומפיקה תוצאות. הסמנטיקה של הפעולה מיושמת על ידי מאפיין הפירוק. אפשר להחליף את הפעולה המורכבת בפירוק שלה בלי לשנות את הסמנטיקה של התוכנית. במקרים שבהם הטמעה של הפירוק לא מספקת את אותה סמנטיקת פעולה, עדיף להשתמש ב-custom_call.
השדה version (ברירת המחדל היא 0) משמש לציון מתי הסמנטיקה של רכיב מורכב משתנה.
הפעולה הזו מיושמת כ-kCall עם המאפיין is_composite=true. השדה decomposition מוגדר על ידי המאפיין computation. מאפייני חזית האתר מאחסנים את שאר המאפיינים עם הקידומת composite..
דוגמה לפעולת CompositeCall:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
CompositeCall(computation, operands..., name, attributes, version)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
computation
|
XlaComputation
|
חישוב מסוג T_0, T_1, ...,
T_{N-1} -> S עם N פרמטרים מסוג שרירותי |
operands |
רצף של N XlaOps |
מספר ערכים משתנה |
name |
string |
שם המורכב |
attributes
|
אופציונלי string
|
מילון אופציונלי של מאפיינים בפורמט מחרוזת |
version
|
אופציונלי int64
|
מספר לעדכוני גרסה לסמנטיקה של הפעולה המורכבת |
ה-decomposition של פעולה הוא לא שדה שנקרא, אלא מופיע כמאפיין to_apply שמפנה לפונקציה שמכילה את ההטמעה ברמה הנמוכה יותר, כלומר to_apply=%funcname
מידע נוסף על קומפוזיציה ופירוק זמין במפרט של StableHLO.
Cbrt
מידע נוסף זמין במאמר בנושא XlaBuilder::Cbrt.
פעולת שורש שלישי לפי רכיבים x -> cbrt(x).
Cbrt(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Cbrt תומכת גם בארגומנט האופציונלי result_accuracy:
Cbrt(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
מידע על StableHLO זמין במאמר StableHLO – cbrt.
תקרה
מידע נוסף זמין במאמר בנושא XlaBuilder::Ceil.
פונקציית התקרה (ceil) לפי רכיבים x -> ⌈x⌉.
Ceil(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
מידע על StableHLO זמין במאמר StableHLO - ceil.
Cholesky
מידע נוסף זמין במאמר בנושא XlaBuilder::Cholesky.
מחשבת את פירוק צ'ולסקי של קבוצת מטריצות סימטריות (הרמיטיות) חיוביות מוגדרות.
Cholesky(a, lower)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
a
|
XlaOp
|
מערך מסוג מרוכב או מסוג נקודה צפה עם יותר מ-2 מימדים. |
lower |
bool |
אם להשתמש במשולש העליון או התחתון של a. |
אם lower הוא true, הפונקציה מחשבת מטריצות משולשות תחתונות l כך ש-$a = l .
l^T$. אם lower הוא false, המערכת מחשבת מטריצות משולשות עליונות u כך שמתקיים\(a = u^T . u\).
נתוני הקלט נקראים רק מהמשולש התחתון או העליון של a, בהתאם לערך של lower. המערכת מתעלמת מהערכים מהמשולש השני. נתוני הפלט מוחזרים באותו המשולש. הערכים במשולש השני מוגדרים בהטמעה ויכולים להיות כל דבר.
אם ל-a יש יותר מ-2 מאפיינים, המערכת מתייחסת ל-a כאל קבוצה של מטריצות, שבה כל המאפיינים חוץ מ-2 המאפיינים המשניים הם מאפייני קבוצה.
אם a לא סימטרי (הרמיטי) וחיובי מוגדר, התוצאה תלויה בהטמעה.
מידע על StableHLO זמין במאמר StableHLO – cholesky.
תיחום
מידע נוסף זמין במאמר בנושא XlaBuilder::Clamp.
הפונקציה מגבילה את האופרנד לטווח שבין ערך מינימלי לערך מקסימלי.
Clamp(min, operand, max)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
min |
XlaOp |
מערך מסוג T |
operand |
XlaOp |
מערך מסוג T |
max |
XlaOp |
מערך מסוג T |
בהינתן אופרנד וערכים מינימליים ומקסימליים, הפונקציה מחזירה את האופרנד אם הוא נמצא בטווח שבין הערך המינימלי לערך המקסימלי. אחרת, היא מחזירה את הערך המינימלי אם האופרנד נמוך מהטווח הזה, או את הערך המקסימלי אם האופרנד גבוה מהטווח הזה. כלומר, clamp(a, x, b) = min(max(a, x), b).
לכל שלושת המערכים צריך להיות אותו צורה. לחלופין, כצורה מוגבלת של שידור, min ו/או max יכולים להיות סקלר מסוג T.
דוגמה עם סקלר min ו-max:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
מידע על StableHLO זמין במאמר StableHLO - clamp.
כיווץ
מידע נוסף זמין במאמר בנושא XlaBuilder::Collapse.
והפעולה tf.reshape.
מצמצמת את המימדים של מערך למימד אחד.
Collapse(operand, dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T |
dimensions |
int64 וקטור |
קבוצת משנה רציפה של המאפיינים של T, לפי הסדר. |
הפונקציה Collapse מחליפה את קבוצת המשנה הנתונה של מימדי האופרנד במימד יחיד. ארגומנטי הקלט הם מערך שרירותי מסוג T ווקטור של אינדקסים של ממדים שהוא קבוע בזמן הקומפילציה. האינדקסים של המימדים חייבים להיות קבוצת משנה רציפה של המימדים של T, בסדר עולה (מספר המימד הנמוך לגבוה). לכן, {0, 1, 2}, {0, 1} או {1, 2} הם כולם קבוצות מימדים תקינות, אבל {1, 0} או {0, 2} לא תקינות. הם מוחלפים במאפיין חדש יחיד, באותו מיקום ברצף המאפיינים כמו המאפיינים שהם מחליפים, והגודל של המאפיין החדש שווה למכפלה של הגדלים של המאפיינים המקוריים. מספר המאפיין הנמוך ביותר ב-dimensions הוא המאפיין עם השינוי הכי איטי (הכי משמעותי) בקינון הלולאות שדוחס את המאפיינים האלה, ומספר המאפיין הכי גבוה הוא המאפיין עם השינוי הכי מהיר (הכי זניח). אם נדרש סדר כללי יותר של צמצום, אפשר לעיין באופרטור tf.reshape.
לדוגמה, נניח ש-v הוא מערך של 24 רכיבים:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
Clz
מידע נוסף זמין במאמר בנושא XlaBuilder::Clz.
ספירת אפסים מובילים בכל רכיב.
Clz(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
CollectiveBroadcast
מידע נוסף זמין במאמר בנושא XlaBuilder::CollectiveBroadcast.
משדר נתונים בין העותקים. הנתונים נשלחים ממזהה העותק הראשון בכל קבוצה למזהים האחרים באותה קבוצה. אם מזהה של רפליקה לא נמצא באף קבוצת רפליקות, הפלט ברפליקה הזו הוא טנסור שמורכב מאפסים ב-shape.
CollectiveBroadcast(operand, replica_groups, channel_id)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
replica_groups
|
ReplicaGroupוקטור
|
כל קבוצה מכילה רשימה של מזהי עותקים |
channel_id
|
אופציונלי ChannelHandle
|
מזהה ייחודי לכל זוג של שליחה/קבלה |
מידע על StableHLO זמין במאמר StableHLO - collective_broadcast.
CollectivePermute
מידע נוסף זמין במאמר בנושא XlaBuilder::CollectivePermute.
CollectivePermute היא פעולה קולקטיבית ששולחת ומקבלת נתונים בין רפליקות.
CollectivePermute(operand, source_target_pairs, channel_id, inplace)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך קלט n ממדי |
source_target_pairs
|
<int64, int64> וקטור
|
רשימה של זוגות (source_replica_id, target_replica_id). בכל זוג, האופרנד נשלח מהרפליקה של המקור לרפליקה של היעד. |
channel_id
|
אופציונלי ChannelHandle
|
מזהה ערוץ אופציונלי לתקשורת בין מודולים |
inplace
|
אופציונלי bool
|
סימון שמציין אם צריך לבצע את התמורה במקום |
שימו לב להגבלות הבאות על source_target_pairs:
- לשני זוגות שונים לא יכול להיות אותו מזהה של העותק המשוכפל של היעד, ולא יכול להיות להם אותו מזהה של העותק המשוכפל של המקור.
- אם מזהה רפליקה לא מוגדר כיעד באף זוג, הפלט ברפליקה הזו הוא טנסור שמורכב מאפסים עם אותה צורה כמו הקלט.
ה-API של פעולת CollectivePermute מפורק באופן פנימי ל-2 הוראות HLO (CollectivePermuteStart ו-CollectivePermuteDone).
מידע נוסף זמין במאמר בנושא HloInstruction::CreateCollectivePermuteStart.
CollectivePermuteStart ו-CollectivePermuteDone משמשים כפרימיטיבים ב-HLO.
יכול להיות שהפעולות האלה יופיעו בקובצי dump של HLO, אבל הן לא מיועדות לבנייה ידנית על ידי משתמשי קצה.
למידע על StableHLO, ראו StableHLO - collective_permute.
השוואה
מידע נוסף זמין במאמר בנושא XlaBuilder::Compare.
הפונקציה מבצעת השוואה בין lhs לבין rhs של הרכיבים הבאים:
Eq
מידע נוסף זמין במאמר בנושא XlaBuilder::Eq.
הפונקציה מבצעת השוואה שווה ל- בין lhs לבין rhs ברמת הרכיב.
\(lhs = rhs\)
Eq(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בהרחבת שידור לממדים שונים עבור משוואה:
Eq(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
קיימת תמיכה בסכום הזמנה כולל מעל המספרים הנקודתיים עבור Eq, על ידי אכיפה של:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
EqTotalOrder(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
מידע על StableHLO זמין במאמר StableHLO – השוואה.
Ne
מידע נוסף זמין במאמר בנושא XlaBuilder::Ne.
הפונקציה מבצעת השוואה של שונות בין lhs לבין rhs ברמת הרכיב.
\(lhs != rhs\)
Ne(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בשידור ממדים שונים עבור Ne:
Ne(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
קיימת תמיכה בסכום הזמנה כולל מעל המספרים הנקודתיים ב-Ne, על ידי אכיפה של:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
NeTotalOrder(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
מידע על StableHLO זמין במאמר StableHLO – השוואה.
Ge
מידע נוסף זמין במאמר בנושא XlaBuilder::Ge.
הפונקציה מבצעת השוואה greater-or-equal-than בין lhs ל-rhs ברמת הרכיב.
\(lhs >= rhs\)
Ge(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בהרחבת שידור לממדים שונים עבור Ge:
Ge(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
קיימת תמיכה בסכום הזמנה כולל מעל המספרים העשרוניים ב-Gt, על ידי אכיפה של:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
GtTotalOrder(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
מידע על StableHLO זמין במאמר StableHLO – השוואה.
Gt
מידע נוסף זמין במאמר בנושא XlaBuilder::Gt.
מבצע השוואה של lhs ו-rhs לפי גדול מ- ברמת הרכיב.
\(lhs > rhs\)
Gt(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בהרחבת שידור לממדים שונים עבור Gt:
Gt(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר StableHLO – השוואה.
Le
מידע נוסף זמין במאמר בנושא XlaBuilder::Le.
הפונקציה מבצעת השוואה less-or-equal-than בין כל רכיב של lhs לכל רכיב של rhs.
\(lhs <= rhs\)
Le(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בשידור בממדים שונים עבור Le:
Le(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
קיימת תמיכה בסכום הזמנה כולל מעל המספרים הנקודתיים הצפים עבור Le, על ידי אכיפה של:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LeTotalOrder(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
מידע על StableHLO זמין במאמר StableHLO – השוואה.
Lt
מידע נוסף זמין במאמר בנושא XlaBuilder::Lt.
הפונקציה מבצעת השוואה של קטן מ- בין כל רכיב ב-lhs לבין הרכיב התואם ב-rhs.
\(lhs < rhs\)
Lt(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בשידור רב-ממדי שונה עבור Lt:
Lt(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
קיימת תמיכה בסכום הזמנה כולל מעל המספרים הנקודתיים עבור Lt, על ידי אכיפה של:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LtTotalOrder(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
מידע על StableHLO זמין במאמר StableHLO – השוואה.
רמה למתקדמים מאוד
מידע נוסף זמין במאמר בנושא XlaBuilder::Complex.
מבצעת המרה של כל רכיב בנפרד לערך מרוכב מתוך זוג ערכים ממשיים ומדומים, lhs ו-rhs.
Complex(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בהרחבת שידור לממדים שונים עבור Complex:
Complex(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר StableHLO – complex.
ConcatInDim (שרשור)
מידע נוסף זמין במאמר בנושא XlaBuilder::ConcatInDim.
הפונקציה Concatenate יוצרת מערך מכמה אופרנדים של מערכים. למערך יש אותו מספר ממדים כמו לכל אחד מהאופרנדים של מערך הקלט (שחייבים להיות בעלי אותו מספר ממדים), והוא מכיל את הארגומנטים בסדר שבו הם צוינו.
Concatenate(operands..., dimension)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands
|
רצף של N XlaOp
|
N מערכים מסוג T עם מימדים [L0, L1, ...]. נדרש N >= 1. |
dimension
|
int64
|
ערך במרווח [0, N) שמציין את שם המאפיין שיוצמד בין operands. |
כל המימדים חייבים להיות זהים, למעט dimension. הסיבה לכך היא ש-XLA לא תומך במערכים לא סדירים. חשוב גם לזכור שאי אפשר לשרשר ערכים של מאפיינים עם 0 ממדים (כי אי אפשר לתת שם לממד שבו מתבצע השרשור).
דוגמה חד-ממדית:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
//Output: {2, 3, 4, 5, 6, 7}
דוגמה דו-ממדית:
let a = { {1, 2},
{3, 4},
{5, 6} };
let b = { {7, 8} };
Concat({a, b}, 0)
//Output: { {1, 2},
// {3, 4},
// {5, 6},
// {7, 8} }
תרשים:
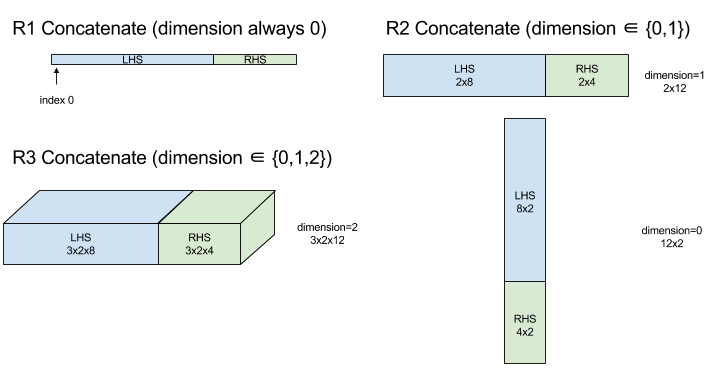
מידע על StableHLO זמין במאמר StableHLO – concatenate.
משפטי תנאי
מידע נוסף זמין במאמר בנושא XlaBuilder::Conditional.
Conditional(predicate, true_operand, true_computation, false_operand,
false_computation)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
predicate |
XlaOp |
סקלר מסוג PRED |
true_operand |
XlaOp |
ארגומנט מסוג \(T_0\) |
true_computation |
XlaComputation |
XlaComputation of type \(T_0 \to S\) |
false_operand |
XlaOp |
ארגומנט מסוג \(T_1\) |
false_computation |
XlaComputation |
XlaComputation of type \(T_1 \to S\) |
מבצעת את true_computation אם predicate הוא true, מבצעת את false_computation אם predicate הוא false ומחזירה את התוצאה.
הפונקציה true_computation חייבת לקבל ארגומנט יחיד מהסוג \(T_0\) , והיא תופעל עם true_operand, שחייב להיות מאותו סוג. הפונקציה
false_computation צריכה לקבל ארגומנט יחיד מהסוג \(T_1\) והיא תופעל עם false_operand שחייב להיות מאותו סוג. הסוג של הערך המוחזר של true_computation ושל false_computation חייב להיות זהה.
שימו לב שרק אחת מהפעולות true_computation ו-false_computation תתבצע, בהתאם לערך של predicate.
Conditional(branch_index, branch_computations, branch_operands)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
branch_index |
XlaOp |
סקלר מסוג S32 |
branch_computations |
רצף של N XlaComputation |
XlaComputations of type \(T_0 \to S , T_1 \to S , ..., T_{N-1} \to S\) |
branch_operands |
רצף של N XlaOp |
ארגומנטים מסוג \(T_0 , T_1 , ..., T_{N-1}\) |
מבצעת את הפעולה branch_computations[branch_index] ומחזירה את התוצאה. אם branch_index הוא S32 שקטן מ-0 או גדול מ-N או שווה לו, אז הפעולה branch_computations[N-1] מתבצעת כענף ברירת המחדל.
כל branch_computations[b] צריך לקבל ארגומנט יחיד מסוג \(T_b\) , והוא יופעל עם branch_operands[b] שצריך להיות מאותו סוג. הסוג של הערך המוחזר של כל branch_computations[b] חייב להיות זהה.
שימו לב שרק אחת מהפעולות branch_computations תבוצע, בהתאם לערך של branch_index.
מידע על StableHLO זמין במאמר בנושא StableHLO – if.
קבוע
מידע נוסף זמין במאמר בנושא XlaBuilder::ConstantLiteral.
הפונקציה מחזירה output מקבוע literal.
Constant(literal)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
literal |
LiteralSlice |
תצוגה קבועה של Literal |
מידע על StableHLO זמין במאמר StableHLO – קבוע.
ConvertElementType
מידע נוסף זמין במאמר בנושא XlaBuilder::ConvertElementType.
בדומה ל-static_cast ב-C++, ConvertElementType מבצעת פעולת המרה לפי רכיבים מצורת נתונים לצורת יעד. המימדים צריכים להיות זהים, וההמרה היא המרה של כל רכיב בנפרד. לדוגמה, s32 רכיבים הופכים ל-f32 רכיבים באמצעות שגרת המרה מ-s32 ל-f32.
ConvertElementType(operand, new_element_type)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T עם מימדים D |
new_element_type |
PrimitiveType |
type U |
המימדים של האופרנד ושל צורת היעד צריכים להיות זהים. סוגי הרכיבים של המקור והיעד לא יכולים להיות טופלים.
המרות כמו T=s32 ל-U=f32 יבצעו שגרת המרה של מספר שלם למספר עשרוני עם נורמליזציה, כמו עיגול למספר הזוגי הקרוב ביותר.
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
מידע על StableHLO זמין במאמר StableHLO – convert.
Conv (Convolution)
מידע נוסף זמין במאמר בנושא XlaBuilder::Conv.
מחשב קונבולוציה מהסוג שמשמש ברשתות נוירונים. אפשר לחשוב על קונבולוציה כחלון n-ממדי שנע על פני אזור בסיס n-ממדי, ומתבצע חישוב לכל מיקום אפשרי של החלון.
Conv Enqueues a convolution instruction onto the computation, which uses the
default convolution dimension numbers with no dilation.
הריפוד מצוין בקיצור כ-SAME או כ-VALID. הריפוד מסוג SAME מרפד את הקלט (lhs) באפסים כך שהפלט יהיה באותה צורה כמו הקלט, בלי להתחשב בצעדים. ריווח תקין פשוט אומר שאין ריווח.
Conv(lhs, rhs, window_strides, padding, feature_group_count,
batch_group_count, precision_config, preferred_element_type)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs
|
XlaOp
|
מערך קלט ב-(n+2) ממדים |
rhs
|
XlaOp
|
מערך במימד (n+2) של משקלי ליבה |
window_strides |
ArraySlice<int64> |
מערך n-d של צעדי ליבה |
padding |
Padding |
טיפוסים בני מנייה (enum) של ריווח |
feature_group_count
|
int64 | מספר קבוצות התכונות |
batch_group_count |
int64 | מספר קבוצות הבאצ'ים |
precision_config
|
אופציונלי
PrecisionConfig |
enum for level of precision |
preferred_element_type
|
אופציונלי
PrimitiveType |
enum של סוג רכיב סקלרי |
אמצעי בקרה ברמות שונות זמינים ל-Conv:
נסמן ב-n את מספר הממדים המרחביים. הארגומנט lhs הוא מערך (n+2)-ממדי שמתאר את שטח הבסיס. החלק הזה נקרא קלט,
אבל כמובן שגם הצד השמאלי הוא קלט. ברשת נוירונים, אלה הפעלות הקלט. המאפיינים n+2 הם, בסדר הזה:
-
batch: כל קואורדינטה בממד הזה מייצגת קלט עצמאי שעליו מתבצעת קונבולוציה. -
z/depth/features: לכל מיקום (y,x) באזור הבסיס יש וקטור שמשויך אליו, והוא נכנס למאפיין הזה. -
spatial_dims: מתאר את המידות המרחביות שלnשמגדירות את אזור הבסיס שהחלון נע לאורכו.
הארגומנט rhs הוא מערך (n+2)-ממדי שמתאר את המסנן/הליבה/החלון של הקונבולוציה. אלה המאפיינים, בסדר הזה:
-
output-z: המאפייןzשל הפלט. -
input-z: הגודל של המאפיין הזה כפולfeature_group_countצריך להיות שווה לגודל של המאפייןzבצד ימין. -
spatial_dims: מתאר אתnהמאפיינים המרחביים שמגדירים את חלון ה-n-d שנע על פני אזור הבסיס.
הארגומנט window_strides מציין את הצעד של חלון הקונבולוציה בממדים המרחביים. לדוגמה, אם הצעד במאפיין המרחבי הראשון הוא 3, אפשר למקם את החלון רק בקואורדינטות שבהן האינדקס המרחבי הראשון מתחלק ב-3.
הארגומנט padding מציין את מספר האפסים שיוספו לשטח הבסיס. הערך של הריפוד יכול להיות שלילי – הערך המוחלט של ריפוד שלילי מציין את מספר האלמנטים שיש להסיר מהממד שצוין לפני שמבצעים את הקונבולוציה. padding[0] מציין את הריווח של מאפיין y ו-padding[1] מציין את הריווח של מאפיין x. בכל זוג, הריווח התחתון הוא הרכיב הראשון והריווח העליון הוא הרכיב השני. המרווח הפנימי הנמוך מוחל בכיוון של אינדקסים נמוכים יותר, והמרווח הפנימי הגבוה מוחל בכיוון של אינדקסים גבוהים יותר. לדוגמה, אם
padding[1] הוא (2,3), אז יהיה ריפוד של 2 אפסים בצד שמאל ושל 3 אפסים בצד ימין בממד המרחבי השני. שימוש בריפוד שווה להוספת אותם ערכי אפס לקלט (lhs) לפני ביצוע הקונבולוציה.
הארגומנטים lhs_dilation ו-rhs_dilation מציינים את גורם ההרחבה שיש להחיל על lhs ו-rhs, בהתאמה, בכל ממד מרחבי. אם גורם ההרחבה בממד מרחבי הוא d, אז d-1 חורים מוצבים באופן מרומז בין כל אחת מהרשומות בממד הזה, וכך גודל המערך גדל. החורים האלה מתמלאים בערך no-op, שבמקרה של קונבולוציה הוא אפסים.
הרחבה של הצד הימני נקראת גם קונבולוציה אטרוסית. פרטים נוספים זמינים במאמר tf.nn.atrous_conv2d. הרחבה של הצד השמאלי נקראת גם קונבולוציה משוחפת. פרטים נוספים זמינים במאמר tf.nn.conv2d_transpose.
אפשר להשתמש בארגומנט feature_group_count (ערך ברירת המחדל הוא 1) עבור קונבולוציות מקובצות. feature_group_count צריך להיות מחלק של מימד התכונה של הקלט ושל הפלט. אם feature_group_count גדול מ-1, המשמעות היא שבאופן מושגי, המימד של תכונת הקלט והפלט והמימד של תכונת הפלט מחולקים באופן שווה לכמה קבוצות של feature_group_count, וכל קבוצה מורכבת מרצף עוקב של תכונות.rhs התכונה של קלט המימד rhs צריכה להיות שווה למימד של תכונת הקלט lhs חלקי feature_group_count (כך שהיא כבר כוללת את הגודל של קבוצת תכונות קלט). הקבוצות ה-i משמשות יחד לחישוב feature_group_count עבור הרבה קונבולוציות נפרדות. התוצאות של הקונבולוציות האלה משורשרות יחד בממד התכונה של הפלט.
במקרה של קונבולוציה עומקית, הארגומנט feature_group_count יוגדר למאפיין המימד של נתוני הקלט, והמסנן ישנה את הצורה מ-[filter_height, filter_width, in_channels, channel_multiplier] ל-[filter_height, filter_width, 1, in_channels * channel_multiplier]. פרטים נוספים זמינים במאמר tf.nn.depthwise_conv2d.
אפשר להשתמש בארגומנט batch_group_count (ערך ברירת המחדל הוא 1) כדי לסנן קבוצות במהלך הפצת שגיאות לאחור. batch_group_count צריך להיות מחלק של גודל הממד של אצווה lhs (קלט). אם batch_group_count גדול מ-1, המשמעות היא שגודל המנה של הפלט צריך להיות input batch
/ batch_group_count. הערך batch_group_count חייב להיות מחלק של גודל תכונת הפלט.
הפלט הוא טנזור עם המימדים הבאים, בסדר הזה:
-
batch: הגודל של המאפיין הזה כפולbatch_group_countצריך להיות שווה לגודל של המאפייןbatchבצד ימין. -
z: אותו גודל כמוoutput-zבקרנל (rhs). -
spatial_dims: ערך אחד לכל מיקום חוקי של חלון הקונבולוציה.
באיור שלמעלה אפשר לראות איך השדה batch_group_count פועל. למעשה, אנחנו מחלקים כל קבוצה של lhs ל-batch_group_count קבוצות, ועושים את אותו הדבר לגבי תכונות הפלט. לאחר מכן, לכל אחת מהקבוצות האלה אנחנו מבצעים קונבולוציות בזוגות ומשרשרים את הפלט לאורך הממד של תכונת הפלט. הסמנטיקה התפעולית של כל המאפיינים האחרים (מאפיינים מרחביים ומאפיינים של תכונות) נשארת ללא שינוי.
המיקומים התקינים של חלון הקונבולוציה נקבעים על ידי הצעדים וגודל אזור הבסיס אחרי הריפוד.
כדי לתאר מה עושה קונבולוציה, נתייחס לקונבולוציה דו-ממדית ונבחר כמה קואורדינטות קבועות batch, z, y, x בפלט. אז (y,x) הוא מיקום של פינת החלון בתוך אזור הבסיס (למשל, הפינה הימנית העליונה, בהתאם לאופן שבו מפרשים את המימדים המרחביים). עכשיו יש לנו חלון דו-ממדי, שנלקח מהאזור הבסיסי, שבו כל נקודה דו-ממדית משויכת לווקטור חד-ממדי, כך שמתקבלת תיבה תלת-ממדית. מליבת הקונבולוציה, מכיוון שתיקנו את קואורדינטת הפלט z, יש לנו גם תיבה תלת-ממדית. לשתי התיבות יש את אותם ממדים, ולכן אפשר לחשב את סכום המכפלות של הרכיבים בין שתי התיבות (בדומה למכפלה סקלרית). זה ערך הפלט.
הערה: אם הערך של output-z הוא למשל 5, אז כל מיקום של החלון יפיק 5 ערכים בפלט למאפיין z של הפלט. הערכים האלה שונים זה מזה בחלק של ליבת הקונבולוציה שמשמשת – יש תיבה תלת-ממדית נפרדת של ערכים שמשמשת לכל קואורדינטה של output-z. אפשר לחשוב על זה כעל 5 קונבולוציות נפרדות עם פילטר שונה לכל אחת מהן.
הנה פסאודו קוד עבור קונבולוציה דו-ממדית עם ריפוד ודילוג:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
הפרמטר precision_config משמש לציון הגדרת הדיוק. הרמה קובעת אם החומרה צריכה לנסות ליצור עוד הוראות של קוד מכונה כדי לספק הדמיה מדויקת יותר של dtype כשצריך (כלומר, הדמיה של f32 ב-TPU שתומך רק ב-bf16 matmuls). הערכים יכולים להיות DEFAULT, HIGH, HIGHEST. פרטים נוספים
בקטעים של MXU.
preferred_element_type הוא אלמנט סקלרי של סוגי פלט ברמת דיוק גבוהה או נמוכה יותר שמשמשים לצבירה. preferred_element_type ממליץ על סוג הצבירה לפעולה הנתונה, אבל אין בכך ערובה. כך אפשר לצבור נתונים בחלק מהעורפים של החומרה בסוג אחר ולהמיר אותם לסוג הפלט המועדף.
מידע על StableHLO זמין במאמר StableHLO – convolution.
ConvWithGeneralPadding
מידע נוסף זמין במאמר בנושא XlaBuilder::ConvWithGeneralPadding.
ConvWithGeneralPadding(lhs, rhs, window_strides, padding,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
זהה ל-Conv כאשר הגדרת הריפוד מפורשת.
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs
|
XlaOp
|
מערך קלט ב-(n+2) ממדים |
rhs
|
XlaOp
|
מערך במימד (n+2) של משקלי ליבה |
window_strides |
ArraySlice<int64> |
מערך n-d של צעדי ליבה |
padding
|
ArraySlice<
pair<int64,int64>> |
מערך n-d של (low, high) padding |
feature_group_count
|
int64 | מספר קבוצות התכונות |
batch_group_count |
int64 | מספר קבוצות הבאצ'ים |
precision_config
|
אופציונלי
PrecisionConfig |
enum for level of precision |
preferred_element_type
|
אופציונלי
PrimitiveType |
enum של סוג רכיב סקלרי |
ConvWithGeneralDimensions
מידע נוסף זמין במאמר בנושא XlaBuilder::ConvWithGeneralDimensions.
ConvWithGeneralDimensions(lhs, rhs, window_strides, padding,
dimension_numbers, feature_group_count, batch_group_count, precision_config,
preferred_element_type)
זהה ל-Conv, שבו מספרי המאפיינים מפורשים.
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs
|
XlaOp
|
מערך קלט עם (n+2) ממדים |
rhs
|
XlaOp
|
מערך של משקלי ליבה עם n+2 ממדים |
window_strides
|
ArraySlice<int64>
|
מערך n-ממדי של צעדי ליבה |
padding |
Padding |
טיפוסים בני מנייה (enum) של ריווח |
dimension_numbers
|
ConvolutionDimensionNumbers
|
מספר המאפיינים |
feature_group_count
|
int64 | מספר קבוצות התכונות |
batch_group_count
|
int64 | מספר קבוצות הבאצ'ים |
precision_config
|
אופציונלי PrecisionConfig
|
טיפוס בן מנייה (enum) לרמת הדיוק |
preferred_element_type
|
אופציונלי PrimitiveType
|
enum of scalar element type |
ConvGeneral
מידע נוסף זמין במאמר בנושא XlaBuilder::ConvGeneral.
ConvGeneral(lhs, rhs, window_strides, padding, dimension_numbers,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
אותו דבר כמו Conv, שבו מספרי המאפיינים והגדרת הריפוד מוגדרים באופן מפורש
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs
|
XlaOp
|
מערך קלט עם (n+2) ממדים |
rhs
|
XlaOp
|
מערך של משקלי ליבה עם n+2 ממדים |
window_strides
|
ArraySlice<int64>
|
מערך n-ממדי של צעדי ליבה |
padding
|
ArraySlice<
pair<int64,int64>>
|
מערך n-d של (low, high) padding |
dimension_numbers
|
ConvolutionDimensionNumbers
|
מספר המאפיינים |
feature_group_count
|
int64 | מספר קבוצות התכונות |
batch_group_count
|
int64 | מספר קבוצות הבאצ'ים |
precision_config
|
אופציונלי PrecisionConfig
|
טיפוס בן מנייה (enum) לרמת הדיוק |
preferred_element_type
|
אופציונלי PrimitiveType
|
enum of scalar element type |
ConvGeneralDilated
מידע נוסף זמין במאמר בנושא XlaBuilder::ConvGeneralDilated.
ConvGeneralDilated(lhs, rhs, window_strides, padding, lhs_dilation,
rhs_dilation, dimension_numbers, feature_group_count, batch_group_count,
precision_config, preferred_element_type, window_reversal)
זהה ל-Conv, שבו הגדרת הריפוד, גורמי ההרחבה ומספרי המאפיינים מפורטים.
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs
|
XlaOp
|
מערך קלט עם (n+2) ממדים |
rhs
|
XlaOp
|
מערך של משקלי ליבה עם n+2 ממדים |
window_strides
|
ArraySlice<int64>
|
מערך n-ממדי של צעדי ליבה |
padding
|
ArraySlice<
pair<int64,int64>>
|
מערך n-d של (low, high) padding |
lhs_dilation
|
ArraySlice<int64>
|
מערך גורמי הרחבה של צד ימין ב-n ממדים |
rhs_dilation
|
ArraySlice<int64>
|
n-d rhs dilation factor array |
dimension_numbers
|
ConvolutionDimensionNumbers
|
מספר המאפיינים |
feature_group_count
|
int64 | מספר קבוצות התכונות |
batch_group_count
|
int64 | מספר קבוצות הבאצ'ים |
precision_config
|
אופציונלי PrecisionConfig
|
טיפוס בן מנייה (enum) לרמת הדיוק |
preferred_element_type
|
אופציונלי PrimitiveType
|
enum of scalar element type |
window_reversal
|
אופציונלי vector<bool>
|
הדגל שמשמש להיפוך לוגי של המימד לפני שמחילים את הקונבולוציה |
העתקה
מידע נוסף זמין במאמר בנושא HloInstruction::CreateCopyStart.
הפונקציה Copy מפורקת באופן פנימי ל-2 הוראות HLO: CopyStart ו-CopyDone. Copy, יחד עם CopyStart ו-CopyDone, משמשים כפרימיטיבים ב-HLO. יכול להיות שהפעולות האלה יופיעו בקובצי dump של HLO, אבל הן לא מיועדות לבנייה ידנית על ידי משתמשי קצה.
Cos
ראו גםXlaBuilder::Cos.
קוסינוס לפי רכיבים x -> cos(x).
Cos(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Cos תומכת גם בארגומנט האופציונלי result_accuracy:
Cos(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
מידע על StableHLO זמין במאמר StableHLO – cosine.
Cosh
מידע נוסף זמין במאמר בנושא XlaBuilder::Cosh.
קוסינוס היפרבולי של כל רכיב x -> cosh(x).
Cosh(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
Cosh תומך גם בארגומנט האופציונלי result_accuracy:
Cosh(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
CustomCall
מידע נוסף זמין במאמר בנושא XlaBuilder::CustomCall.
להתקשר לפונקציה שסופקה על ידי המשתמש בתוך חישוב.
מסמכי התיעוד של CustomCall מופיעים במאמר פרטים למפתחים – קריאות מותאמות אישית של XLA
מידע על StableHLO זמין במאמר StableHLO – custom_call.
מח'
מידע נוסף זמין במאמר בנושא XlaBuilder::Div.
מבצעת חלוקה של המחולק lhs במחלק rhs לפי רכיבים.
Div(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
גלישה בחילוק של מספר שלם (חילוק/שארית של מספר חיובי/שלילי באפס או חילוק/שארית של INT_SMIN ב--1) מפיקה ערך שמוגדר על ידי ההטמעה.
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בשידור בממדים שונים עבור רכיב Div:
Div(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר בנושא StableHLO – divide.
דומיין
מידע נוסף זמין במאמר בנושא HloInstruction::CreateDomain.
Domain עשוי להופיע בקובצי dump של HLO, אבל הוא לא מיועד לבנייה ידנית על ידי משתמשי קצה.
נקודה
מידע נוסף זמין במאמר בנושא XlaBuilder::Dot.
Dot(lhs, rhs, precision_config, preferred_element_type)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs |
XlaOp |
מערך מסוג T |
rhs |
XlaOp |
מערך מסוג T |
precision_config
|
אופציונלי
PrecisionConfig |
enum for level of precision |
preferred_element_type
|
אופציונלי
PrimitiveType |
enum של סוג רכיב סקלרי |
הסמנטיקה המדויקת של הפעולה הזו תלויה בדרגות של האופרנדים:
| קלט | פלט | סמנטיקה |
|---|---|---|
וקטור [שם עצם] dot וקטור [שם עצם] |
סקלרי | מכפלה סקלרית של וקטורים |
מטריצה [m x k] dot וקטור [k] |
וקטור [m] | הכפלה של מטריצה בווקטור |
matrix [m x k] dot matrix
[k x n] |
מטריצה [m x n] | מטריצה-מטריצה כפל |
הפעולה מבצעת סכום של מכפלות בממד השני של lhs (או בממד הראשון אם יש לו ממד אחד) ובממד הראשון של rhs. אלה המאפיינים 'שמופיעים בחוזה'. המידות המצומצמות של lhs ו-rhs צריכות להיות באותו גודל. בפועל, אפשר להשתמש בה כדי לבצע מכפלה סקלרית בין וקטורים, מכפלות של וקטורים ומטריצות או מכפלות של מטריצות.
הפרמטר precision_config משמש לציון הגדרת הדיוק. הרמה קובעת אם החומרה צריכה לנסות ליצור עוד הוראות של קוד מכונה כדי לספק הדמיה מדויקת יותר של dtype כשצריך (כלומר, הדמיה של f32 ב-TPU שתומך רק ב-bf16 matmuls). הערכים יכולים להיות DEFAULT, HIGH, HIGHEST. פרטים נוספים
בקטעים של MXU.
preferred_element_type הוא אלמנט סקלרי של סוגי פלט ברמת דיוק גבוהה או נמוכה יותר שמשמשים לצבירה. preferred_element_type ממליץ על סוג הצבירה לפעולה הנתונה, אבל אין בכך ערובה. כך אפשר לצבור נתונים בחלק מהעורפים של החומרה בסוג אחר ולהמיר אותם לסוג הפלט המועדף.
מידע על StableHLO זמין במאמר בנושא StableHLO - dot.
DotGeneral
מידע נוסף זמין במאמר בנושא XlaBuilder::DotGeneral.
DotGeneral(lhs, rhs, dimension_numbers, precision_config,
preferred_element_type)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs |
XlaOp |
מערך מסוג T |
rhs |
XlaOp |
מערך מסוג T |
dimension_numbers
|
DotDimensionNumbers
|
מספרי מימדים של חוזים ושל פעולות בכמות גדולה |
precision_config
|
אופציונלי
PrecisionConfig |
טיפוס בן מנייה (enum) לרמת הדיוק |
preferred_element_type
|
אופציונלי
PrimitiveType |
enum of scalar element type |
בדומה ל-Dot, אבל מאפשר לציין מספרים של מאפיינים מצומצמים ומקבצים גם עבור lhs וגם עבור rhs.
| שדות DotDimensionNumbers | סוג | סמנטיקה |
|---|---|---|
lhs_contracting_dimensions
|
repeated int64 | lhs מספרים של מאפיינים מצטמצמים |
rhs_contracting_dimensions
|
repeated int64 | rhs מספרים של מאפיינים מצטמצמים |
lhs_batch_dimensions
|
repeated int64 | lhs מספרים של מאפיינים של קבוצות |
rhs_batch_dimensions
|
repeated int64 | rhs מספרים של מאפיינים של קבוצות |
הפונקציה DotGeneral מבצעת את סכום המכפלות על פני מאפיינים מצטמצמים שצוינו ב-dimension_numbers.
מספרי המימדים המשויכים לחוזה מ-lhs ומ-rhs לא צריכים להיות זהים, אבל הם חייבים להיות באותו גודל.
דוגמה עם מספרי מאפיינים מצטמצמים:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { { 6.0, 12.0},
{15.0, 30.0} }
מספרי המימדים המשויכים של אצווה מ-lhs ו-rhs חייבים להיות באותם גדלים.
דוגמה עם מספרי מאפיינים של קבוצות (גודל קבוצה 2, מטריצות 2x2):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> {
{ {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| קלט | פלט | סמנטיקה |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | batch matmul |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | batch matmul |
מכאן נובע שמספר המימד שמתקבל מתחיל במימד של הקבוצה, lhs מימד שאינו מתכווץ או קבוצתי, ולבסוף rhs מימד שאינו מתכווץ או קבוצתי.
הפרמטר precision_config משמש לציון הגדרת הדיוק. הרמה קובעת אם החומרה צריכה לנסות ליצור עוד הוראות של קוד מכונה כדי לספק הדמיה מדויקת יותר של dtype כשצריך (כלומר, הדמיה של f32 ב-TPU שתומך רק ב-bf16 matmuls). הערכים יכולים להיות DEFAULT, HIGH, HIGHEST. פרטים נוספים
זמינים בקטעים בנושא MXU.
preferred_element_type הוא אלמנט סקלרי של סוגי פלט ברמת דיוק גבוהה או נמוכה יותר שמשמשים לצבירה. preferred_element_type ממליץ על סוג הצבירה לפעולה הנתונה, אבל אין בכך ערובה. כך אפשר לצבור נתונים בחלק מהעורפים של החומרה בסוג אחר ולהמיר אותם לסוג הפלט המועדף.
מידע על StableHLO זמין במאמר בנושא StableHLO – dot_general.
ScaledDot
מידע נוסף זמין במאמר בנושא XlaBuilder::ScaledDot.
ScaledDot(lhs, lhs_scale, rhs, rhs_scale, dimension_number,
precision_config,preferred_element_type)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs |
XlaOp |
מערך מסוג T |
rhs |
XlaOp |
מערך מסוג T |
lhs_scale |
XlaOp |
מערך מסוג T |
rhs_scale |
XlaOp |
מערך מסוג T |
dimension_number
|
ScatterDimensionNumbers
|
מספרי מאפיינים לפעולת פיזור |
precision_config
|
PrecisionConfig
|
טיפוס בן מנייה (enum) לרמת הדיוק |
preferred_element_type
|
אופציונלי PrimitiveType
|
enum of scalar element type |
דומה ל-DotGeneral.
יוצר פעולת מכפלה נקודתית עם שינוי קנה מידה עם האופרנדים lhs, lhs_scale, rhs ו-rhs_scale, עם מימדים של כיווץ ואצווה שצוינו ב-dimension_numbers.
RaggedDot
מידע נוסף זמין במאמר בנושא XlaBuilder::RaggedDot.
לפירוט של חישוב RaggedDot אפשר לעיין במאמר StableHLO - chlo.ragged_dot
DynamicReshape
מידע נוסף זמין במאמר בנושא XlaBuilder::DynamicReshape.
הפעולה הזו זהה מבחינת הפונקציונליות ל-reshape, אבל הצורה של התוצאה מוגדרת באופן דינמי באמצעות output_shape.
DynamicReshape(operand, dim_sizes, new_size_bounds, dims_are_dynamic)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך N ממדי מסוג T |
dim_sizes |
וקטור של XlaOP |
גודלי וקטורים של N ממדים |
new_size_bounds |
וקטור של int63 |
וקטור של גבולות ב-N ממדים |
dims_are_dynamic |
וקטור של bool |
ממד דינמי של N מימדים |
מידע על StableHLO זמין במאמר StableHLO – dynamic_reshape.
DynamicSlice
מידע נוסף זמין במאמר בנושא XlaBuilder::DynamicSlice.
הפונקציה DynamicSlice מחלצת מערך משנה ממערך הקלט במיקום הדינמי start_indices. גודל הפלח בכל מאפיין מועבר בפרמטרים size_indices, שמציינים את נקודת הסיום של מרווחי פלחים בלעדיים בכל מאפיין: [התחלה, התחלה + גודל). הצורה של start_indices חייבת להיות חד-ממדית, והגודל של המימד צריך להיות שווה למספר המימדים של operand.
DynamicSlice(operand, start_indices, slice_sizes)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך N ממדי מסוג T |
start_indices
|
רצף של N XlaOp
|
רשימה של N מספרים שלמים סקלריים שמכילה את אינדקס ההתחלה של הפרוסה לכל מאפיין. הערך חייב להיות גדול מ-0 או שווה ל-0. |
size_indices
|
ArraySlice<int64>
|
רשימה של N מספרים שלמים שמכילה את גודל הפרוסה לכל מאפיין. כל ערך צריך להיות גדול מ-0, והסכום של start + size צריך להיות קטן או שווה לגודל המאפיין כדי למנוע חלוקה מודולרית של גודל המאפיין. |
כדי לחשב את אינדקסים של הפרוסות האפקטיביות, צריך להחיל את ההמרה הבאה על כל אינדקס i ב-[1, N) לפני שמבצעים את הפרוסה:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - slice_sizes[i])
כך מוודאים שהפרוסה שחולצה תמיד נמצאת בתוך הגבולות ביחס למערך האופרנד. אם הפרוסה נמצאת בתוך הגבולות לפני החלת השינוי, השינוי לא משפיע.
דוגמה חד-ממדית:
let a = {0.0, 1.0, 2.0, 3.0, 4.0};
let s = {2};
DynamicSlice(a, s, {2});
// Result: {2.0, 3.0}
דוגמה דו-ממדית:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2});
//Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
מידע על StableHLO זמין במאמר בנושא StableHLO – dynamic_slice.
DynamicUpdateSlice
מידע נוסף זמין במאמר בנושא XlaBuilder::DynamicUpdateSlice.
הפונקציה DynamicUpdateSlice יוצרת תוצאה שהיא הערך של מערך הקלט operand, עם פרוסת update שהוחלף ב-start_indices.
הצורה של update קובעת את הצורה של מערך המשנה של התוצאה שמתעדכנת.
הצורה של start_indices חייבת להיות חד-ממדית, עם גודל ממד ששווה למספר הממדים של operand.
DynamicUpdateSlice(operand, update, start_indices)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך N ממדי מסוג T |
update
|
XlaOp
|
מערך N ממדי מסוג T שמכיל את עדכון הפרוסה. כל מאפיין של צורת העדכון צריך להיות גדול מאפס, והסכום של start + update צריך להיות קטן או שווה לגודל האופרנד בכל מאפיין כדי למנוע יצירה של אינדקסים של עדכונים מחוץ לגבולות. |
start_indices
|
רצף של N XlaOp
|
רשימה של N מספרים שלמים סקלריים שמכילה את אינדקס ההתחלה של הפרוסה לכל מאפיין. הערך חייב להיות גדול מ-0 או שווה ל-0. |
כדי לחשב את אינדקסים של הפרוסות האפקטיביות, צריך להחיל את ההמרה הבאה על כל אינדקס i ב-[1, N) לפני שמבצעים את הפרוסה:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
כך אפשר לוודא שהפרוסה המעודכנת תמיד נמצאת בתוך גבולות המערך של האופרנד. אם הפרוסה נמצאת בתוך הגבולות לפני החלת השינוי, השינוי לא משפיע.
דוגמה חד-ממדית:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s)
// Result: {0.0, 1.0, 5.0, 6.0, 4.0}
דוגמה דו-ממדית:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s)
// Result:
// { {0.0, 1.0, 2.0},
// {3.0, 12.0, 13.0},
// {6.0, 14.0, 15.0},
// {9.0, 16.0, 17.0} }
למידע על StableHLO, ראו StableHLO – dynamic_update_slice.
Erf
מידע נוסף זמין במאמר בנושא XlaBuilder::Erf.
פונקציית השגיאה x -> erf(x) לפי רכיב, כאשר:
\(\text{erf}(x) = \frac{2}{\sqrt{\pi} }\int_0^x e^{-t^2} \, dt\).
Erf(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Erf תומכת גם בארגומנט האופציונלי result_accuracy:
Erf(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
תפוגה
מידע נוסף זמין במאמר בנושא XlaBuilder::Exp.
האקספוננט הטבעי של כל רכיב x -> e^x.
Exp(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Exp תומכת גם בארגומנט האופציונלי result_accuracy:
Exp(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
מידע על StableHLO זמין במאמר StableHLO – exponential.
Expm1
מידע נוסף זמין במאמר בנושא XlaBuilder::Expm1.
הפונקציה הטבעית של כל רכיב פחות אחד x -> e^x - 1.
Expm1(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Expm1 תומכת גם בארגומנט האופציונלי result_accuracy:
Expm1(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
מידע על StableHLO זמין במאמר StableHLO – exponential_minus_one.
FFT
מידע נוסף זמין במאמר בנושא XlaBuilder::Fft.
הפעולה XLA FFT מיישמת את טרנספורמציות פורייה הישירות וההפוכות עבור קלט/פלט ממשי ומרוכב. יש תמיכה ב-FFT רב-ממדי בעד 3 צירים.
Fft(operand, ftt_type, fft_length)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand
|
XlaOp
|
המערך שעליו מבצעים התמרת פורייה. |
fft_type |
FftType |
פרטים נוספים מופיעים בטבלה שבהמשך. |
fft_length
|
ArraySlice<int64>
|
האורכים של הצירים בתחום הזמן שעוברים טרנספורמציה. הפעולה הזו נדרשת במיוחד כדי ש-IRFFT יוכל להתאים את הגודל של הציר הפנימי ביותר, כי ל-RFFT(fft_length=[16]) יש את אותו צורה של פלט כמו ל-RFFT(fft_length=[17]). |
FftType |
סמנטיקה |
|---|---|
FFT |
FFT מורכב למורכב. הצורה לא משתנה. |
IFFT |
היפוך של FFT מורכב למורכב. הצורה לא משתנה. |
RFFT
|
העברה של FFT ממשי למרוכב. הצורה של הציר הפנימי ביותר מצטמצמת ל-fft_length[-1] // 2 + 1 אם fft_length[-1] הוא ערך שאינו אפס, ומשמיטה את החלק הצמוד ההפוך של האות שעבר טרנספורמציה מעבר לתדר נייקוויסט. |
IRFFT
|
היפוך של FFT מממשי למרוכב (כלומר, מקבלת מספר מרוכב ומחזירה מספר ממשי).
הצורה של הציר הפנימי ביותר מורחבת ל-fft_length[-1] אם fft_length[-1] הוא ערך שונה מאפס, ומסיקים את החלק של האות שעבר טרנספורמציה מעבר לתדר נייקוויסט מהצמוד ההפוך של הערכים 1 עד fft_length[-1] // 2 + 1. |
מידע על StableHLO זמין במאמר בנושא StableHLO – fft.
Multidimensional FFT
אם מציינים יותר מ-1, הפעולה שמתבצעת שקולה להחלת סדרה של פעולות FFT על כל אחד מהצירים הפנימיים ביותר.fft_length שימו לב: במקרים של real->complex ו-complex->real, הטרנספורמציה של הציר הפנימי ביותר מתבצעת (למעשה) קודם (RFFT; אחרון ב-IRFFT), ולכן הציר הפנימי ביותר הוא זה שגודלו משתנה. הטרנספורמציות האחרות של הצירים יהיו מורכבות->מורכבות.
פרטי ההטמעה
ה-FFT של המעבד מגובה על ידי TensorFFT של Eigen. GPU FFT משתמש ב-cuFFT.
קומה
מידע נוסף זמין במאמר בנושא XlaBuilder::Floor.
הפונקציה floor לפי רכיבים x -> ⌊x⌋.
Floor(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
מידע על StableHLO זמין במאמר StableHLO - floor.
פיוז'ן
מידע נוסף זמין במאמר בנושא HloInstruction::CreateFusion.
הפעולה Fusion מייצגת הוראות HLO ומשמשת כפרימיטיב ב-HLO.
יכול להיות שהאופציה הזו תופיע בפריקות של HLO, אבל היא לא מיועדת ליצירה ידנית על ידי משתמשי קצה.
איסוף
הפעולה gather של XLA מחברת כמה פרוסות (כל פרוסה עם היסט שונה בזמן הריצה) של מערך קלט.
מידע על StableHLO זמין במאמר StableHLO - gather.
סמנטיקה כללית
מידע נוסף זמין במאמר בנושא XlaBuilder::Gather.
תיאור פשוט יותר מופיע בקטע 'תיאור לא רשמי' שבהמשך.
gather(operand, start_indices, dimension_numbers, slice_sizes,
indices_are_sorted)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand
|
XlaOp
|
המערך שממנו אנחנו אוספים את הנתונים. |
start_indices
|
XlaOp
|
מערך שמכיל את אינדקס ההתחלה של הפרוסות שאנחנו אוספים. |
dimension_numbers
|
GatherDimensionNumbers
|
המימד ב-start_indices שמכיל את אינדקס ההתחלה. בהמשך מופיע תיאור מפורט. |
slice_sizes
|
ArraySlice<int64>
|
slice_sizes[i] הוא הגבולות של הפלח במאפיין i. |
indices_are_sorted
|
bool
|
הארגומנט שקובע אם מובטח שהאינדקסים ממוינים לפי הפונקציה שקוראת לפונקציה הנוכחית. |
כדי שיהיה לכם נוח, אנחנו מוסיפים למאפיינים במערך הפלט שלא נמצאים ב-offset_dims
תווית batch_dims.
הפלט הוא מערך עם batch_dims.size + offset_dims.size ממדים.
הערך operand.rank חייב להיות שווה לסכום של offset_dims.size ושל collapsed_slice_dims.size. בנוסף, הערך של slice_sizes.size צריך להיות שווה לערך של operand.rank.
אם index_vector_dim שווה ל-start_indices.rank, אנחנו מתייחסים באופן מרומז ל-start_indices כאל טנזור עם מימד נגרר 1 (כלומר, אם הצורה של start_indices היא [6,7] ו-index_vector_dim הוא 2, אנחנו מתייחסים באופן מרומז לצורה של start_indices כאל [6,7,1]).
הגבולות של מערך הפלט לאורך המימד i מחושבים באופן הבא:
אם
iמופיע ב-batch_dims(כלומר, שווה ל-batch_dims[k]עבורkכלשהו), אנחנו בוחרים את גבולות המאפיין המתאימים מתוךstart_indices.shape, ומדלגים עלindex_vector_dim(כלומר, בוחריםstart_indices.shape.dims[k] אםk<index_vector_dim, ואחרת בוחריםstart_indices.shape.dims[k+1]).אם
iמופיע ב-offset_dims(כלומר, שווה ל-offset_dims[k] עבורkמסוים), אנחנו בוחרים את הגבול המתאים מתוךslice_sizesאחרי שמתחשבים ב-collapsed_slice_dims(כלומר, אנחנו בוחריםadjusted_slice_sizes[k] כאשרadjusted_slice_sizesהואslice_sizesעם הגבולות במדדיםcollapsed_slice_dimsשהוסרו).
באופן רשמי, אינדקס האופרנד In שמתאים לאינדקס פלט נתון Out מחושב באופן הבא:
Let
G= {Out[k] forkinbatch_dims}. UseGto slice out a vectorSsuch thatS[i] =start_indices[Combine(G,i)] where Combine(A, b) inserts b at positionindex_vector_diminto A. שימו לב שההגדרה הזו ברורה גם אםGריק: אםGריק, אזS=start_indices.יצירת אינדקס התחלתי,
Sin, ב-operandבאמצעותSעל ידי פיזורSבאמצעותstart_index_map. באופן ספציפי יותר:Sin[start_index_map[k]] =S[k] ifk<start_index_map.size.
Sin[_] =0אחרת.
יוצרים אינדקס
Oinלתוךoperandעל ידי פיזור האינדקסים בהיסט של המימדים ב-Outבהתאם לסטcollapsed_slice_dims. באופן ספציפי יותר:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]] ifk<offset_dims.size(remapped_offset_dimsis defined below).
Oin[_] =0אחרת.
InהואOin+Sinכאשר + הוא חיבור של כל רכיב בנפרד.
remapped_offset_dims היא פונקציה מונוטונית עם תחום [0, offset_dims.size) וטווח [0, operand.rank) \ collapsed_slice_dims. לדוגמה, offset_dims.size הוא 4, operand.rank הוא 6 ו-collapsed_slice_dims הוא {0, 2}, אז remapped_offset_dims הוא {0→1, 1→3, 2→4, 3→5}.
אם המדיניות indices_are_sorted מוגדרת כ-True, XLA יכול להניח שהמשתמש מיין את start_indices (בסדר עולה, אחרי פיזור הערכים לפי start_index_map). אם לא, הסמנטיקה מוגדרת בהטמעה.
תיאור לא רשמי ודוגמאות
באופן לא רשמי, כל אינדקס Out במערך הפלט תואם לאלמנט E במערך האופרנד, והוא מחושב באופן הבא:
אנחנו משתמשים במאפייני האצווה ב-
Outכדי לחפש אינדקס התחלתי מ-start_indices.אנחנו משתמשים ב-
start_index_mapכדי למפות את אינדקס ההתחלה (שהגודל שלו עשוי להיות קטן מ-operand.rank) לאינדקס התחלה 'מלא' ב-operand.אנחנו יוצרים פרוסה באופן דינמי בגודל
slice_sizesבאמצעות אינדקס ההתחלה המלא.אנחנו משנים את הצורה של הפלח על ידי כיווץ המאפיינים
collapsed_slice_dims. מכיוון שכל המאפיינים של הפרוסות המכווצות חייבים להיות בגודל 1, השינוי הזה תמיד חוקי.אנחנו משתמשים בממדי ההזזה ב-
Outכדי ליצור אינדקס בפלח הזה ולקבל את רכיב הקלט,E, שמתאים לאינדקס הפלטOut.
הערך של index_vector_dim מוגדר ל-start_indices.rank – 1 בכל הדוגמאות שבהמשך. ערכים מעניינים יותר של index_vector_dim לא משנים את הפעולה באופן מהותי, אבל הופכים את הייצוג החזותי למסורבל יותר.
כדי להבין איך כל מה שצוין למעלה מתחבר יחד, נסתכל על דוגמה שבה נאספים 5 פרוסות בצורה [8,6] ממערך [16,11]. המיקום של פרוסה במערך [16,11] יכול להיות מיוצג כווקטור אינדקס בצורה S64[2], כך שקבוצה של 5 מיקומים יכולה להיות מיוצגת כמערך S64[5,2].
אפשר לתאר את אופן הפעולה של gather כטרנספורמציה של אינדקס שלוקחת [G,O0,O1], אינדקס בצורת הפלט וממפה אותו לרכיב במערך הקלט באופן הבא:
קודם בוחרים וקטור (X,Y) ממערך האינדקסים של הפעולה gather באמצעות G.
הרכיב במערך הפלט באינדקס [G,O0,O1] הוא הרכיב במערך הקלט באינדקס [X+O0,Y+O1].
slice_sizes הוא [8,6], שקובע את הטווח של O0 ו-O1, והוא בתורו קובע את הגבולות של הפלח.
פעולת האיסוף הזו פועלת כמו פלח דינמי של אצווה עם G כממד האצווה.
האינדקסים של איסוף הנתונים יכולים להיות רב-ממדיים. לדוגמה, גרסה כללית יותר של הדוגמה שלמעלה שמשתמשת במערך 'איסוף אינדקסים' בצורה [4,5,2] תתרגם אינדקסים באופן הבא:
שוב, זה פועל כפלח דינמי של קבוצה G0 וG1 כמאפייני הקבוצה. גודל הפלח הוא עדיין [8,6].
הפעולה gather ב-XLA מכלילה את הסמנטיקה הלא פורמלית שמתוארת למעלה בדרכים הבאות:
אנחנו יכולים להגדיר אילו מימדים בצורת הפלט הם מימדי ההיסט (מימדים שמכילים
O0,O1בדוגמה האחרונה). מאפייני אצווה של פלט (מאפיינים שמכיליםG0,G1בדוגמה האחרונה) מוגדרים כמאפייני הפלט שלא מוגדרים כמאפייני היסט.יכול להיות שמספר המאפיינים של היסט הפלט שמוצגים באופן מפורש בצורת הפלט קטן ממספר המאפיינים של הקלט. למאפיינים ה'חסרים' האלה, שמופיעים במפורש כ-
collapsed_slice_dims, צריך להיות גודל פלח של1. מכיוון שגודל הפרוסה שלהם הוא1, האינדקס התקף היחיד שלהם הוא0, והשמטה שלהם לא יוצרת עמימות.יכול להיות שלפרוסה שחולצה מהמערך Gather Indices (מספרים
Xו-Yבדוגמה האחרונה) יהיו פחות רכיבים ממספר המימדים של מערך הקלט, ומיפוי מפורש קובע איך להרחיב את האינדקס כך שיהיה לו אותו מספר מימדים כמו לקלט.
כדוגמה אחרונה, אנחנו משתמשים ב-(2) וב-(3) כדי להטמיע את tf.gather_nd:
הפרמטרים G0 ו-G1 משמשים לחיתוך אינדקס התחלתי ממערך האינדקסים של הפעולה gather כרגיל, אלא שהאינדקס ההתחלתי מכיל רק רכיב אחד, X. באופן דומה, יש רק אינדקס אחד של היסט בפלט עם הערך O0. עם זאת, לפני השימוש בהם כאינדקסים במערך הקלט, הם מורחבים בהתאם ל-Gather Index Mapping (start_index_map בתיאור הרשמי) ול-Offset Mapping (remapped_offset_dims בתיאור הרשמי) ל-[X,0] ול-[0,O0] בהתאמה, ומתקבל [X,O0]. במילים אחרות, אינדקס הפלט [G0,G1,O0] ממופה לאינדקס הקלט [GatherIndices[G0,G1,0],O0], וזה נותן לנו את הסמנטיקה של tf.gather_nd.
מספר הפנייה שלך הוא slice_sizes.[1,11] באופן אינטואיטיבי, המשמעות היא שכל אינדקס X במערך האינדקסים של הפעולה gather בוחר שורה שלמה, והתוצאה היא שרשור של כל השורות האלה.
GetDimensionSize
מידע נוסף זמין במאמר בנושא XlaBuilder::GetDimensionSize.
הפונקציה מחזירה את הגודל של המימד הנתון של האופרנד. האופרנד חייב להיות בצורת מערך.
GetDimensionSize(operand, dimension)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך קלט n ממדי |
dimension
|
int64
|
ערך במרווח [0, n) שמציין את המאפיין |
מידע על StableHLO זמין במאמר StableHLO – get_dimension_size.
GetTupleElement
מידע נוסף זמין במאמר בנושא XlaBuilder::GetTupleElement.
אינדקסים לתוך טאפל עם ערך קבוע בזמן ההידור.
הערך חייב להיות קבוע בזמן ההידור, כדי שהסקת הצורה תוכל לקבוע את סוג הערך שמתקבל.
זה דומה ל-std::get<int N>(t) ב-C++. באופן עקרוני:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
מידע נוסף מופיע במאמר tf.tuple.
GetTupleElement(tuple_data, index)
| ארגומנט | סוג | סמנטיקה |
|---|---|---|
tuple_data |
XlaOP |
הטופל |
index |
int64 |
אינדקס של צורת טאפל |
מידע על StableHLO זמין במאמר StableHLO – get_tuple_element.
Imag
מידע נוסף זמין במאמר בנושא XlaBuilder::Imag.
החלק המדומה של צורה מרוכבת (או ממשית) לפי אלמנט. x -> imag(x). אם האופרנד הוא מסוג נקודה צפה, הפונקציה מחזירה 0.
Imag(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
מידע על StableHLO זמין במאמר בנושא StableHLO - imag.
בתוך הפיד
מידע נוסף זמין במאמר בנושא XlaBuilder::Infeed.
Infeed(shape, config)
| ארגומנט | סוג | סמנטיקה |
|---|---|---|
shape
|
Shape
|
צורת הנתונים שנקראים מממשק Infeed. השדה layout של הצורה צריך להיות מוגדר כך שיתאים לפריסה של הנתונים שנשלחים למכשיר. אחרת, ההתנהגות שלו לא מוגדרת. |
config |
אופציונלי string |
ההגדרה של הפעולה. |
קוראת פריט נתונים יחיד מממשק הסטרימינג המרומז של Infeed במכשיר, מפרשת את הנתונים כצורה הנתונה והפריסה שלהם ומחזירה XlaOp של הנתונים. מותר להשתמש בכמה פעולות Infeed בחישוב, אבל צריך להיות סדר כולל בין הפעולות האלה. לדוגמה, שני Infeed בקוד שלמטה מסודרים בסדר מלא כי יש תלות בין לולאות ה-while.
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
אין תמיכה בצורות של טאפל מוטמע. במקרה של צורת טופל ריקה, הפעולה Infeed היא למעשה פעולה ללא פעולה (no-op) והיא ממשיכה בלי לקרוא נתונים מה-Infeed של המכשיר.
מידע על StableHLO זמין במאמר StableHLO - infeed.
Iota
מידע נוסף זמין במאמר בנושא XlaBuilder::Iota.
Iota(shape, iota_dimension)
יוצר מחרוזת קבועה במכשיר במקום העברה פוטנציאלית גדולה של מארח. יוצרת מערך עם צורה שצוינה ומכילה ערכים שמתחילים מאפס ועולים באחד לאורך המימד שצוין. במקרים של סוגי נתונים של נקודה צפה, המערך שנוצר שווה ל-ConvertElementType(Iota(...)), כאשר Iota הוא סוג נתונים של מספר שלם וההמרה היא לסוג נתונים של נקודה צפה.
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
shape |
Shape |
הצורה של המערך שנוצר על ידי Iota() |
iota_dimension |
int64 |
המאפיין שלפיו יבוצע הגידול. |
לדוגמה, הפקודה Iota(s32[4, 8], 0) מחזירה
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
אפשרות החזרה במחיר Iota(s32[4, 8], 1)
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
מידע על StableHLO זמין במאמר בנושא StableHLO – iota.
IsFinite
מידע נוסף זמין במאמר בנושא XlaBuilder::IsFinite.
הפונקציה בודקת אם כל רכיב של operand הוא סופי, כלומר לא אינסוף חיובי או שלילי, ולא NaN. הפונקציה מחזירה מערך של ערכים PRED עם אותה צורה כמו הקלט, כאשר כל אלמנט הוא true אם ורק אם אלמנט הקלט התואם הוא סופי.
IsFinite(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
מידע על StableHLO זמין במאמר StableHLO – is_finite.
יומן
מידע נוסף זמין במאמר בנושא XlaBuilder::Log.
לוגריתם טבעי של כל רכיב x -> ln(x).
Log(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Log תומכת גם בארגומנט האופציונלי result_accuracy:
Log(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
מידע על StableHLO זמין במאמר בנושא StableHLO – יומן.
Log1p
מידע נוסף זמין במאמר בנושא XlaBuilder::Log1p.
לוגריתם טבעי מוזז לפי רכיב x -> ln(1+x).
Log1p(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Log1p תומכת גם בארגומנט האופציונלי result_accuracy:
Log1p(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
מידע על StableHLO זמין במאמר StableHLO - log_plus_one.
לוגיסטי
מידע נוסף זמין במאמר בנושא XlaBuilder::Logistic.
חישוב פונקציה לוגיסטית לפי רכיבים x -> logistic(x).
Logistic(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Logistic תומכת גם בארגומנט האופציונלי result_accuracy:
Logistic(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
מידע על StableHLO זמין במאמר StableHLO – לוגיסטיקה.
מפה
מידע נוסף זמין במאמר בנושא XlaBuilder::Map.
Map(operands..., computation, dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands |
רצף של N XlaOps |
N מערכים מהסוגים T0..T{N-1} |
computation
|
XlaComputation
|
חישוב מסוג T_0, T_1,
.., T_{N + M -1} -> S עם N פרמטרים מסוג T ו-M פרמטרים מסוג שרירותי. |
dimensions |
int64 array |
מערך של מימדי מיפוי |
static_operands
|
רצף של N XlaOps
|
פעולות סטטיות לפעולת המפה |
הפונקציה מחילה פונקציה סקלרית על המערכים operands שצוינו, ומחזירה מערך באותם ממדים שבהם כל רכיב הוא התוצאה של הפונקציה הממופה שהוחלה על הרכיבים התואמים במערכי הקלט.
הפונקציה הממופה היא חישוב שרירותי עם ההגבלה שיש לה N קלטים מסוג סקלרי T ופלט יחיד מסוג S. לפלט יש את אותם הממדים כמו לאופרנדים, רק שסוג הרכיב T מוחלף ב-S.
לדוגמה: Map(op1, op2, op3, computation, par1) ממפה את elem_out <-
computation(elem1, elem2, elem3, par1) בכל אינדקס (רב-ממדי) במערכי הקלט כדי ליצור את מערך הפלט.
מידע על StableHLO זמין במאמר StableHLO – map.
מקסימום
מידע נוסף זמין במאמר בנושא XlaBuilder::Max.
מבצעת פעולת מקסימום לפי רכיבים בטנסורים lhs ו-rhs.
Max(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בשידור בממדים שונים ל-Max:
Max(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
למידע על StableHLO, ראו StableHLO – maximum.
מינימום
מידע נוסף זמין במאמר בנושא XlaBuilder::Min.
מבצעת פעולת min לפי רכיבים ב-lhs וב-rhs.
Min(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בשידור מממד אחר עבור Min:
Min(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר StableHLO – מינימום.
Mul
מידע נוסף זמין במאמר בנושא XlaBuilder::Mul.
מבצעת מכפלה של כל רכיב ב-lhs עם הרכיב התואם ב-rhs.
Mul(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בהרחבת שידור מממד שונה עבור Mul:
Mul(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר בנושא StableHLO – multiply.
Neg
מידע נוסף זמין במאמר בנושא XlaBuilder::Neg.
שלילה של כל רכיב x -> -x.
Neg(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
למידע על StableHLO, ראו StableHLO – negate
לא
מידע נוסף זמין במאמר בנושא XlaBuilder::Not.
שלילה לוגית לפי רכיבים x -> !(x).
Not(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
מידע על StableHLO זמין במאמר StableHLO - not.
OptimizationBarrier
מידע נוסף זמין במאמר בנושא XlaBuilder::OptimizationBarrier.
חוסם כל מעבר אופטימיזציה של חישובים מעבר למחסום.
OptimizationBarrier(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה מוודאת שכל ערכי הקלט מוערכים לפני כל האופרטורים שתלויים בפלט של המחסום.
מידע על StableHLO זמין במאמר StableHLO - optimization_barrier.
או
מידע נוסף זמין במאמר בנושא XlaBuilder::Or.
מבצעת פעולת OR בין כל רכיב ב-lhs לבין הרכיב התואם ב-rhs .
Or(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בשידור עם ממדים שונים עבור Or:
Or(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר StableHLO - or.
הזנת נתונים
מידע נוסף זמין במאמר בנושא XlaBuilder::Outfeed.
כותב את הקלט לפיד.
Outfeed(operand, shape_with_layout, outfeed_config)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T |
shape_with_layout |
Shape |
הגדרה של פריסת הנתונים שמועברים |
outfeed_config |
string |
קבוע של הגדרה להוראה Outfeed |
shape_with_layout מעביר את הצורה שרוצים להוציא.
מידע על StableHLO זמין במאמר StableHLO - outfeed.
רפידה
מידע נוסף זמין במאמר בנושא XlaBuilder::Pad.
Pad(operand, padding_value, padding_config)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T |
padding_value
|
XlaOp
|
סקלר מסוג T למילוי הריפוד שנוסף |
padding_config
|
PaddingConfig
|
כמות הריווח בשני הקצוות (נמוך, גבוה) ובין הרכיבים של כל מימד |
הפונקציה מרחיבה את המערך operand שצוין על ידי הוספת ערכי מילוי מסביב למערך וגם בין הרכיבים של המערך עם הערך padding_value שצוין. padding_config
מציין את כמות הריווח בשוליים ואת הריווח הפנימי לכל מימד.
PaddingConfig הוא שדה חוזר של PaddingConfigDimension, שמכיל שלושה שדות לכל מאפיין: edge_padding_low, edge_padding_high ו-interior_padding.
הערכים edge_padding_low ו-edge_padding_high מציינים את כמות הריווח שנוספה בקצה הנמוך (ליד אינדקס 0) ובקצה הגבוה (ליד האינדקס הגבוה ביותר) של כל מימד, בהתאמה. הערך של הריווח הפנימי יכול להיות שלילי. הערך המוחלט של ריווח פנימי שלילי מציין את מספר הרכיבים שצריך להסיר מהמאפיין שצוין.
interior_padding מציין את כמות הריווח שנוספה בין שני רכיבים בכל מימד. הערך לא יכול להיות שלילי. הריווח הפנימי מתבצע מבחינה לוגית לפני הריווח החיצוני, ולכן במקרה של ריווח חיצוני שלילי, הרכיבים מוסרים מהאופרנד עם הריווח הפנימי.
הפעולה הזו לא מבצעת כלום אם כל זוגות המרווחים הפנימיים בקצוות הם (0, 0) וכל ערכי המרווחים הפנימיים הם 0. בדוגמה הבאה מוצגים ערכים שונים של edge_padding ו-interior_padding במערך דו-ממדי.
מידע על StableHLO זמין במאמר StableHLO - pad.
פרמטר
מידע נוסף זמין במאמר בנושא XlaBuilder::Parameter.
Parameter מייצג ארגומנט שמוזן לחישוב.
PartitionID
מידע נוסף זמין במאמר בנושא XlaBuilder::BuildPartitionId.
יוצרת partition_id של התהליך הנוכחי.
PartitionID(shape)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
shape |
Shape |
צורת הנתונים |
המחרוזת PartitionID עשויה להופיע בקובצי dump של HLO, אבל היא לא מיועדת ליצירה ידנית על ידי משתמשי קצה.
מידע על StableHLO זמין במאמר בנושא StableHLO – partition_id.
PopulationCount
מידע נוסף זמין במאמר בנושא XlaBuilder::PopulationCount.
הפונקציה מחשבת את מספר הביטים שמוגדרים בכל רכיב של operand.
PopulationCount(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
למידע על StableHLO, ראו StableHLO – popcnt.
פאו
מידע נוסף זמין במאמר בנושא XlaBuilder::Pow.
מבצע העלאה בחזקה של lhs ב-rhs ברמת הרכיב.
Pow(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת גרסה חלופית עם תמיכה בשידור בממדים שונים עבור Pow:
Pow(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר StableHLO – power.
Real
מידע נוסף זמין במאמר בנושא XlaBuilder::Real.
החלק הממשי של צורה מרוכבת (או ממשי) לפי אלמנט. x -> real(x). אם האופרנד הוא מסוג נקודה צפה, הפונקציה Real מחזירה את אותו ערך.
Real(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
מידע על StableHLO זמין במאמר בנושא StableHLO - real.
Recv
מידע נוסף זמין במאמר בנושא XlaBuilder::Recv.
Recv, RecvWithTokens ו-RecvToHost הם פעולות שמשמשות כפרימיטיבים של תקשורת ב-HLO. הפעולות האלה מופיעות בדרך כלל בפריקות של HLO כחלק מהעברת קלט/פלט ברמה נמוכה או העברה בין מכשירים, אבל הן לא מיועדות לבנייה ידנית על ידי משתמשי קצה.
Recv(shape, handle)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
shape |
Shape |
צורת הנתונים שיתקבלו |
handle |
ChannelHandle |
מזהה ייחודי לכל זוג של שליחה/קבלה |
מקבל נתונים מהצורה שצוינה מהוראת Send בחישוב אחר שמשתמש באותו שם של ערוץ. מחזירה XlaOp לנתונים שהתקבלו.
מידע על StableHLO זמין במאמר StableHLO - recv.
RecvDone
מידע נוסף זמין במאמרים בנושא HloInstruction::CreateRecv וHloInstruction::CreateRecvDone.
בדומה ל-Send, פעולת Recv של לקוח ה-API מייצגת תקשורת סינכרונית. עם זאת, ההוראה מפורקת באופן פנימי ל-2 הוראות HLO (Recv ו-RecvDone) כדי לאפשר העברות נתונים אסינכרוניות.
Recv(const Shape& shape, int64 channel_id)
הפונקציה מקצה את המשאבים שנדרשים לקבלת נתונים מהוראה Send עם אותו channel_id. מחזירה הקשר למשאבים שהוקצו, שמשמש בהוראה הבאה RecvDone להמתנה להשלמת העברת הנתונים. ההקשר הוא טאפל של {מאגר לקליטת נתונים (צורה), מזהה בקשה (U32)} ואפשר להשתמש בו רק בהוראה RecvDone.
בהינתן הקשר שנוצר על ידי הוראה Recv, המערכת ממתינה להשלמת העברת הנתונים ומחזירה את הנתונים שהתקבלו.
הקטנה
מידע נוסף זמין במאמר בנושא XlaBuilder::Reduce.
מפעילה פונקציית צמצום על מערך אחד או יותר במקביל.
Reduce(operands..., init_values..., computation, dimensions_to_reduce)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands
|
רצף של N XlaOp
|
N מערכים מסוג T_0,...,
T_{N-1}. |
init_values
|
רצף של N XlaOp
|
N סקלרים מהסוגים
T_0,..., T_{N-1}. |
computation
|
XlaComputation
|
חישוב מסוג
T_0,..., T_{N-1}, T_0,
...,T_{N-1} ->
Collate(T_0,...,
T_{N-1}). |
dimensions_to_reduce
|
int64 array
|
מערך לא מסודר של מימדים לצמצום. |
כאשר:
- הערך של n חייב להיות גדול מ-1 או שווה לו.
- החישוב צריך להיות אסוציאטיבי בקירוב (ראו בהמשך).
- לכל מערכי הקלט צריכים להיות אותם ממדים.
- כל הערכים ההתחלתיים צריכים ליצור זהות תחת
computation. - אם
N = 1, אזCollate(T)הואT. - אם
N > 1,Collate(T_0, ..., T_{N-1})הוא טאפל שלNרכיבים מסוגT.
הפעולה הזו מצמצמת מימד אחד או יותר של כל מערך קלט לערכים סקלריים.
מספר המימדים של כל מערך שמוחזר הוא number_of_dimensions(operand) - len(dimensions). הפלט של הפעולה הוא Collate(Q_0, ..., Q_N), כאשר Q_i הוא מערך מסוג T_i, והממדים שלו מתוארים בהמשך.
מותר לשייך מחדש את חישוב ההפחתה למערכות עורפיות שונות. הדבר עלול להוביל להבדלים מספריים, כי חלק מפונקציות הצמצום כמו חיבור לא אסוציאטיביות עבור מספרים ממשיים. עם זאת, אם טווח הנתונים מוגבל, פעולת החיבור של מספרים ממשיים קרובה מספיק להיות אסוציאטיבית לרוב השימושים המעשיים.
מידע על StableHLO זמין במאמר בנושא StableHLO – reduce.
דוגמאות
כשמצמצמים לאורך מימד אחד במערך חד-ממדי יחיד עם הערכים [10, 11,
12, 13], עם פונקציית הצמצום f (זה computation), אפשר לחשב את זה כך:
f(10, f(11, f(12, f(init_value, 13)))
אבל יש גם הרבה אפשרויות אחרות, למשל:
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
הדוגמה הבאה היא פסאודו-קוד גס שמראה איך אפשר להטמיע צמצום, באמצעות סיכום כחישוב הצמצום עם ערך התחלתי של 0.
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
דוגמה לצמצום של מערך דו-ממדי (מטריצה). לצורה יש 2 מימדים, מימד 0 בגודל 2 ומימד 1 בגודל 3:
תוצאות של צמצום מאפיינים 0 או 1 באמצעות פונקציית 'הוספה':

שימו לב ששתי תוצאות הצמצום הן מערכים חד-ממדיים. בתרשים, אחד מוצג כעמודה והשני כשורה רק לצורך נוחות ויזואלית.
דוגמה מורכבת יותר: מערך תלת-ממדי. מספר המאפיינים הוא 3, מאפיין 0 בגודל 4, מאפיין 1 בגודל 2 ומאפיין 2 בגודל 3. כדי לפשט את הדברים, הערכים 1 עד 6 משוכפלים במאפיין 0.
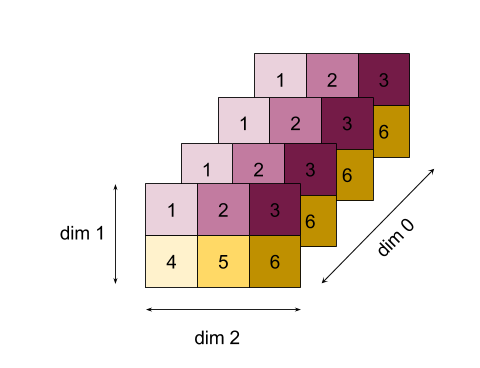
בדומה לדוגמה הדו-ממדית, אפשר לצמצם רק ממד אחד. אם מצמצמים את מאפיין 0, למשל, מקבלים מערך דו-ממדי שבו כל הערכים במאפיין 0 קופלו לתוך סקלר:
| 4 8 12 |
| 16 20 24 |
אם נצמצם את מאפיין 2, נקבל גם מערך דו-ממדי שבו כל הערכים במאפיין 2 קופלו לערך סקלרי:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
שימו לב: הסדר היחסי בין המאפיינים שנותרו בקלט נשמר בפלט, אבל יכול להיות שלחלק מהמאפיינים יוקצו מספרים חדשים (כי מספר המאפיינים משתנה).
אפשר גם לצמצם כמה מאפיינים. הוספה של מאפיינים מצמצמים 0 ו-1 יוצרת את המערך החד-ממדי [20, 28, 36].
צמצום המערך התלת-ממדי בכל המימדים שלו יוצר את הסקלר 84.
Variadic Reduce
כשמשתמשים ב-N > 1, הפונקציה reduce קצת יותר מורכבת, כי היא מופעלת בו-זמנית על כל ערכי הקלט. האופרנדים מסופקים לחישוב בסדר הבא:
- הפעלת ערך מופחת לאופרנד הראשון
- ...
- הפעלת ערך מופחת לאופרנד ה-N
- ערך הקלט של האופרנד הראשון
- ...
- ערך הקלט של האופרנד ה-N
לדוגמה, נניח שיש לכם את פונקציית הצמצום הבאה, שאפשר להשתמש בה כדי לחשב את המקסימום ואת argmax של מערך חד-ממדי במקביל:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
עבור מערכי קלט חד-ממדיים V = Float[N], K = Int[N] וערכי אתחול I_V = Float, I_K = Int, התוצאה f_(N-1) של צמצום המערך לאורך מימד הקלט היחיד שווה לשימוש הרקורסיבי הבא:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
הפעלת הפונקציה הזו על מערך של ערכים ועל מערך של אינדקסים עוקבים (כלומר iota) תגרום לאיטרציה משותפת על המערכים, ותחזיר טופל שמכיל את הערך המקסימלי ואת האינדקס התואם.
ReducePrecision
מידע נוסף זמין במאמר בנושא XlaBuilder::ReducePrecision.
הפונקציה מדמה את ההשפעה של המרת ערכים של נקודה צפה לפורמט עם דיוק נמוך יותר (כמו IEEE-FP16) וחזרה לפורמט המקורי. אפשר לציין באופן שרירותי את מספר הסיביות של המעריך והמנטיסה בפורמט עם דיוק נמוך יותר, אבל יכול להיות שלא כל גדלי הסיביות נתמכים בכל יישומי החומרה.
ReducePrecision(operand, exponent_bits, mantissa_bits)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג נקודה צפה T. |
exponent_bits |
int32 |
מספר הביטים של המעריך בפורמט עם דיוק נמוך יותר |
mantissa_bits |
int32 |
מספר הביטים של המנטיסה בפורמט עם דיוק נמוך יותר |
התוצאה היא מערך מסוג T. ערכי הקלט מעוגלים לערך הקרוב ביותר שאפשר לייצג עם מספר הביטים של המנטיסה שצוין (באמצעות סמנטיקה של 'עיגול למספר הזוגי הקרוב ביותר'), וכל הערכים שחורגים מהטווח שצוין על ידי מספר הביטים של המעריך מוצמדים לאינסוף חיובי או שלילי. הערכים של NaN נשמרים, אבל יכול להיות שהם יומרו לערכים קנוניים של NaN.
בפורמט עם הדיוק הנמוך יותר צריך להיות לפחות ביט אחד של חזקה (כדי להבחין בין ערך אפס לבין אינסוף, כי לשניהם יש מנטיסה אפסית), ומספר הביטים של המנטיסה צריך להיות לא שלילי. יכול להיות שמספר הביטים של המעריך או המנטיסה יהיה גדול מהערך המתאים לסוג T. במקרה כזה, החלק המתאים של ההמרה פשוט לא יבצע פעולה.
למידע על StableHLO, אפשר לעיין במאמר בנושא StableHLO – reduce_precision.
ReduceScatter
מידע נוסף זמין במאמר בנושא XlaBuilder::ReduceScatter.
ReduceScatter היא פעולה קולקטיבית שמבצעת למעשה AllReduce ואז מפזרת את התוצאה על ידי פיצול שלה ל-shard_count בלוקים לאורך scatter_dimension, והרפליקה i בקבוצת הרפליקות מקבלת את ה-shard ith.
ReduceScatter(operand, computation, scatter_dimension, shard_count,
replica_groups, channel_id, layout, use_global_device_ids)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand
|
XlaOp
|
מערך או טופל לא ריק של מערכים לצמצום בין העותקים. |
computation |
XlaComputation |
חישוב הצמצום |
scatter_dimension |
int64 |
המאפיין לפיזור. |
shard_count
|
int64
|
מספר הבלוקים לפיצול
scatter_dimension |
replica_groups
|
ReplicaGroup וקטור
|
קבוצות שביניהן מתבצעות ההפחתות |
channel_id
|
אופציונלי
ChannelHandle |
מזהה ערוץ אופציונלי לתקשורת בין מודולים |
layout
|
אופציונלי Layout
|
פריסת זיכרון שמוגדרת על ידי המשתמש |
use_global_device_ids |
אופציונלי bool |
סימון שהוגדר על ידי המשתמש |
- אם
operandהוא טאפל של מערכים, הפעולה reduce-scatter מתבצעת על כל רכיב בטאפל. -
replica_groupsהיא רשימה של קבוצות העתקים שביניהן מתבצעת ההפחתה (אפשר לאחזר את מזהה ההעתק של ההעתק הנוכחי באמצעותReplicaId). הסדר של ההעתקים בכל קבוצה קובע את הסדר שבו התוצאה של פעולת ה-all-reduce תפוזר.replica_groupsהשדה צריך להיות ריק (ואז כל העותקים שייכים לקבוצה אחת), או להכיל את אותו מספר רכיבים כמו מספר העותקים. אם יש יותר מקבוצת העתקים, כולן צריכות להיות באותו גודל. לדוגמה,replica_groups = {0, 2}, {1, 3}מבצע צמצום בין העותקים0ו-2, ובין1ו-3, ואז מפזר את התוצאה. -
shard_countהוא הגודל של כל קבוצת עותקים. אנחנו צריכים את זה במקרים שבהם השדותreplica_groupsריקים. אםreplica_groupsלא ריק,shard_countחייב להיות שווה לגודל של כל קבוצת עותקים. -
channel_idמשמש לתקשורת בין מודולים: רק פעולותreduce-scatterעם אותוchannel_idיכולות לתקשר ביניהן. layoutמידע נוסף על פריסות זמין במאמר xla::shapes.-
use_global_device_idsהוא דגל שצוין על ידי המשתמש. כש-false(ברירת מחדל) המספרים ב-replica_groupsהםReplicaIdכש-trueהמספרים ב-replica_groupsמייצגים מזהה גלובלי של (ReplicaID*partition_count+partition_id). לדוגמה:- עם 2 עותקים ו-4 מחיצות,
- replica_groups={ {0,1,4,5},{2,3,6,7} } and use_global_device_ids=true
- group[0] = (0,0), (0,1), (1,0), (1,1)
- group[1] = (0,2), (0,3), (1,2), (1,3)
- כאשר כל צמד הוא (replica_id, partition_id).
צורת הפלט היא צורת הקלט עם scatter_dimension שהוקטן פי shard_count. לדוגמה, אם יש שני עותקים והאופרנד הוא [1.0, 2.25] ו-[3.0, 5.25] בהתאמה בשני העותקים, ערך הפלט מהפעולה הזו שבה scatter_dim הוא 0 יהיה [4.0] בעותק הראשון ו-[7.5] בעותק השני.
מידע על StableHLO זמין במאמר בנושא StableHLO – reduce_scatter.
ReduceScatter - Example 1 - StableHLO
בדוגמה שלמעלה, יש 2 רפליקות שמשתתפות ב-ReduceScatter. בכל עותק, לאופרנד יש צורה f32[2,4]. מתבצעת פעולת all-reduce (סכום) בין העותקים, ונוצר ערך מוקטן של צורה f32[2,4] בכל עותק. לאחר מכן, הערך המצומצם הזה מפולח ל-2 חלקים לאורך מאפיין 1, כך שלכל חלק יש צורה f32[2,2]. כל רפליקה בקבוצת התהליכים מקבלת את החלק שמתאים למיקום שלה בקבוצה. כתוצאה מכך, הפלט בכל עותק הוא בצורה f32[2,2].
ReduceWindow
מידע נוסף זמין במאמר בנושא XlaBuilder::ReduceWindow.
הפונקציה מחילה פונקציית צמצום על כל הרכיבים בכל חלון של רצף של מערכים רב-ממדיים, ומפיקה מערך רב-ממדי יחיד או טופל של N מערכים רב-ממדיים כפלט. לכל מערך פלט יש את אותו מספר של רכיבים כמו מספר המיקומים התקינים של החלון. שכבת איגום יכולה להיות מיוצגת כ-ReduceWindow. בדומה ל-Reduce, הערך של computation שמוחל תמיד מועבר ל-init_values בצד ימין.
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands
|
N XlaOps
|
רצף של מערכים רב-ממדיים של סוגים T_0,..., T_{N-1}, כל אחד מהם מייצג את אזור הבסיס שבו החלון ממוקם. |
init_values
|
N XlaOps
|
N ערכי ההתחלה של הפעולה, אחד לכל אחד מ-N האופרנדים. פרטים נוספים מופיעים במאמר בנושא הפחתה. |
computation
|
XlaComputation
|
פונקציית צמצום מסוג T_0,
..., T_{N-1}, T_0, ..., T_{N-1}
-> Collate(T_0, ..., T_{N-1}), שמוחלת על רכיבים בכל חלון של כל האופרנדים של הקלט. |
window_dimensions
|
ArraySlice<int64>
|
מערך של מספרים שלמים לערכי מאפייני חלון |
window_strides
|
ArraySlice<int64>
|
מערך של מספרים שלמים לערכי הצעד של החלון |
base_dilations
|
ArraySlice<int64>
|
מערך של מספרים שלמים לערכי הרחבה של הבסיס |
window_dilations
|
ArraySlice<int64>
|
מערך של מספרים שלמים לערכי הרחבת חלון |
padding
|
Padding
|
סוג הריפוד של החלון (Padding::kSame, שמרפד כך שצורת הפלט תהיה זהה לצורת הקלט אם הצעד הוא 1, או Padding::kValid, שלא משתמש בריפוד ומפסיק את החלון ברגע שהוא כבר לא מתאים) |
כאשר:
- הערך של n חייב להיות גדול מ-1 או שווה לו.
- לכל מערכי הקלט צריכים להיות אותם ממדים.
- אם
N = 1, אזCollate(T)הואT. - אם
N > 1,Collate(T_0, ..., T_{N-1})הוא טאפל שלNרכיבים מסוג(T0,...T{N-1}).
מידע על StableHLO זמין במאמר בנושא StableHLO – reduce_window.
ReduceWindow – דוגמה 1
הקלט הוא מטריצה בגודל [4x6], והמימדים של window_dimensions ושל window_stride_dimensions הם [2x3].
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
צעד של 1 במאפיין מציין שהמיקום של חלון במאפיין הוא במרחק של אלמנט אחד מהחלון הסמוך לו. כדי לציין שלא יהיה חפיפה בין החלונות, הערך של window_stride_dimensions צריך להיות שווה לערך של window_dimensions. באיור שלמטה מוצג שימוש בשני ערכים שונים של stride. הריפוד מוחל על כל מאפיין של הקלט, והחישובים זהים לאלה שמתבצעים כאילו הקלט הגיע עם המאפיינים שיש לו אחרי הריפוד.
כדי לראות דוגמה לריפוד לא טריוויאלי, נניח שרוצים לחשב את הערך המינימלי של חלון ההפחתה (הערך ההתחלתי הוא MAX_FLOAT) עם המימד 3 והצעד 2 במערך הקלט [10000, 1000, 100, 10, 1]. הפונקציה Padding kValid מחשבת ערכי מינימום על פני שני חלונות תקפים: [10000, 1000, 100] ו-[100, 10, 1], והתוצאה היא הפלט [100, 1]. הפונקציה Padding kSame מוסיפה בהתחלה רכיבים למערך משני הצדדים, כך שהצורה אחרי הפונקציה reduce-window תהיה זהה לצורה של הקלט עבור הצעד הראשון, ומתקבל [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE]. הפעלת הפונקציה reduce-window על המערך עם הריפוד פועלת על שלושה חלונות [MAX_VALUE, 10000, 1000], [1000, 100, 10], [10, 1, MAX_VALUE] ומחזירה את הערך [1000, 10, 1].
סדר החישוב של פונקציית הצמצום הוא שרירותי ועשוי להיות לא דטרמיניסטי. לכן, פונקציית הצמצום לא צריכה להיות רגישה מדי לשיוך מחדש. פרטים נוספים מופיעים בדיון על אסוציאטיביות בהקשר של Reduce.
ReduceWindow – דוגמה 2 – StableHLO
בדוגמה שלמעלה:
קלט) לאופרנד יש צורת קלט של S32[3,2]. עם הערכים
[[1,2],[3,4],[5,6]]
שלב 1) הרחבה בסיסית עם פקטור 2 לאורך מימד השורה מוסיפה חורים בין כל שורה של האופרנד. אחרי ההרחבה, מוחל ריווח של 2 שורות בחלק העליון ושורה אחת בחלק התחתון. כתוצאה מכך, הטנסור הופך לגבוה יותר.
שלב 2) מוגדר חלון בצורה [2,1] עם הרחבת חלון [3,1]. המשמעות היא שבכל חלון נבחרים שני רכיבים מאותה עמודה, אבל הרכיב השני נלקח שלוש שורות מתחת לרכיב הראשון ולא ישירות מתחתיו.
שלב 3) החלונות מוזזים על פני האופרנד עם צעד [4,1]. כתוצאה מכך, החלון יזוז ארבע שורות למטה בכל פעם, ויזוז עמודה אחת בכל פעם אופקית. תאי הריפוד מלאים בערך init_value (במקרה הזה init_value = 0). המערכת מתעלמת מערכים ש 'נופלים' לתאי ההרחבה.
בגלל הצעד והריפוד, חלק מהחלונות חופפים רק לאפסים ולחורים, ואילו אחרים חופפים לערכי קלט אמיתיים.
שלב 4) בכל חלון, הרכיבים משולבים באמצעות פונקציית הצמצום (a, b) → a + b, החל מערך התחלתי של 0. שני החלונות העליונים רואים רק ריפוד וחורים, ולכן התוצאות שלהם הן 0. החלונות התחתונים מציגים את הערכים 3 ו-4 מהקלט ומחזירים אותם כתוצאות.
תוצאות) הפלט הסופי הוא בצורה S32[2,2], עם הערכים: [[0,0],[3,4]]
Rem
מידע נוסף זמין במאמר בנושא XlaBuilder::Rem.
מבצעת שארית חלוקה של דיבידנד lhs ומחלק rhs לפי אלמנטים.
הסימן של התוצאה נלקח מהמחולק, והערך המוחלט של התוצאה תמיד קטן מהערך המוחלט של המחלק.
Rem(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בשידור ממדים שונים עבור Rem:
Rem(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר בנושא StableHLO – שארית.
ReplicaId
מידע נוסף זמין במאמר בנושא XlaBuilder::ReplicaId.
מחזירה את המזהה הייחודי (סקלר U32) של העותק.
ReplicaId()
המזהה הייחודי של כל רפליקה הוא מספר שלם לא מסומן במרווח [0, N),
כאשר N הוא מספר הרפליקות. מכיוון שכל העותקים הרצים מריצים את אותה תוכנית, קריאה של ReplicaId() בתוכנית תחזיר ערך שונה בכל עותק רץ.
מידע על StableHLO זמין במאמר בנושא StableHLO – replica_id.
עיצוב מחדש
מידע נוסף זמין במאמר בנושא XlaBuilder::Reshape.
והפעולה Collapse.
משנה את הצורה של המערך לתצורה חדשה.
Reshape(operand, dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T |
dimensions |
int64 וקטור |
ווקטור של גדלים של מאפיינים חדשים |
מבחינה רעיונית, הפונקציה reshape משטחת קודם מערך לתוך וקטור חד-ממדי של ערכי נתונים, ואז משנה את הווקטור הזה לצורה חדשה. ארגומנטי הקלט הם מערך שרירותי מסוג T, וקטור קבוע בזמן הקומפילציה של אינדקסים של ממדים, ווקטור קבוע בזמן הקומפילציה של גדלים של ממדים לתוצאה.
הווקטור dimensions קובע את הגודל של מערך הפלט. הערך באינדקס 0 ב-dimensions הוא הגודל של מאפיין 0, הערך באינדקס 1 הוא הגודל של מאפיין 1, וכן הלאה. המכפלה של המימדים dimensions חייבת להיות שווה למכפלה של גדלי המימדים של האופרנד. כשמצמצמים את המערך המכווץ למערך הרב-ממדי שמוגדר על ידי dimensions, המימדים ב-dimensions מסודרים מהמימד עם השינוי הכי איטי (הכי משמעותי) למימד עם השינוי הכי מהיר (הכי פחות משמעותי).
לדוגמה, נניח ש-v הוא מערך של 24 רכיבים:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
במקרה מיוחד, הפונקציה reshape יכולה להפוך מערך עם רכיב יחיד לערך סקלרי ולהפך. לדוגמה,
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
מידע על StableHLO זמין במאמר בנושא StableHLO – reshape.
שינוי צורה (תוכן בוטה)
מידע נוסף זמין במאמר בנושא XlaBuilder::Reshape.
Reshape(shape, operand)
פעולת שינוי צורה שמשתמשת בצורת יעד מפורשת.
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
shape |
Shape |
צורת הפלט של סוג T |
operand |
XlaOp |
מערך מסוג T |
הפוך
מידע נוסף זמין במאמר בנושא XlaBuilder::Rev.
Rev(operand, dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T |
dimensions |
ArraySlice<int64> |
מאפיינים להחלפה |
הפונקציה הופכת את סדר הרכיבים במערך operand לאורך הציר dimensions שצוין, ויוצרת מערך פלט באותו הצורה. כל רכיב במערך האופרנד במדד רב-ממדי מאוחסן במערך הפלט במדד שעבר טרנספורמציה. האינדקס הרב-ממדי עובר טרנספורמציה על ידי היפוך האינדקס בכל ממד שצריך להפוך (כלומר, אם ממד בגודל N הוא אחד מהממדים שצריך להפוך, האינדקס שלו i עובר טרנספורמציה ל-N - 1 - i).
אחד השימושים בפעולה Rev הוא היפוך של מערך המשקלים של הקונבולוציה לאורך שני ממדי החלון במהלך חישוב הגרדיאנט ברשתות נוירונים.
מידע על StableHLO זמין במאמר בנושא StableHLO – reverse.
RngNormal
מידע נוסף זמין במאמר בנושא XlaBuilder::RngNormal.
יוצרת פלט בצורה נתונה עם מספרים אקראיים שנוצרו לפי \(N(\mu, \sigma)\) ההתפלגות הנורמלית. הפרמטרים \(\mu\) ו- \(\sigma\), וצורת הפלט צריכים להיות מסוג נקודה צפה. בנוסף, הפרמטרים צריכים להיות בעלי ערך סקלרי.
RngNormal(mu, sigma, shape)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
mu |
XlaOp |
סקלר מסוג T שמציין את הממוצע של המספרים שנוצרו |
sigma
|
XlaOp
|
סקלר מסוג T שמציין את סטיית התקן של |
shape |
Shape |
צורת הפלט של סוג T |
מידע על StableHLO זמין במאמר StableHLO - rng.
RngUniform
מידע נוסף זמין במאמר בנושא XlaBuilder::RngUniform.
יוצר פלט בצורה נתונה עם מספרים אקראיים שנוצרו לפי ההתפלגות האחידה במרווח \([a,b)\). הפרמטרים וסוג הרכיב של הפלט צריכים להיות מסוג בוליאני, מסוג של מספר שלם או מסוג של מספר עם נקודה עשרונית, והסוגים צריכים להיות עקביים. בשלב הזה, קצה העורף של המעבד ושל ה-GPU תומך רק ב-F64, F32, F16, BF16, S64, U64, S32 ו-U32. בנוסף, הפרמטרים צריכים להיות בעלי ערך סקלרי. אם \(b <= a\) התוצאה היא מוגדרת-הטמעה.
RngUniform(a, b, shape)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
a |
XlaOp |
ערך סקלרי מסוג T שמציין את הגבול התחתון של המרווח |
b |
XlaOp |
ערך סקלרי מסוג T שמציין את הגבול העליון של המרווח |
shape |
Shape |
צורת הפלט של סוג T |
מידע על StableHLO זמין במאמר StableHLO - rng.
RngBitGenerator
מידע נוסף זמין במאמר בנושא XlaBuilder::RngBitGenerator.
יוצר פלט עם צורה נתונה שממולאת בביטים אקראיים אחידים באמצעות האלגוריתם שצוין (או ברירת המחדל של העורף), ומחזיר מצב מעודכן (עם אותה צורה כמו המצב ההתחלתי) ואת הנתונים האקראיים שנוצרו.
המצב ההתחלתי הוא המצב ההתחלתי של יצירת המספר האקראי הנוכחית. הוא תלוי באלגוריתם שבו משתמשים, וגם בצורה הנדרשת ובערכים התקפים.
הפלט הוא פונקציה דטרמיניסטית של המצב ההתחלתי, אבל לא מובטח שהוא יהיה דטרמיניסטי בין קצה עורפי לבין גרסאות שונות של קומפיילר.
RngBitGenerator(algorithm, initial_state, shape)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
algorithm |
RandomAlgorithm |
אלגוריתם PRNG שבו יש להשתמש. |
initial_state |
XlaOp |
מצב התחלתי של אלגוריתם PRNG. |
shape |
Shape |
צורת הפלט של הנתונים שנוצרו. |
הערכים הזמינים של algorithm:
rng_default: אלגוריתם ספציפי ל-Backend עם דרישות ספציפיות לגבי הצורה של ה-Backend.
rng_three_fry: אלגוריתם PRNG מבוסס-מונה של ThreeFry. הצורהinitial_stateהיאu64[2]עם ערכים שרירותיים. Salmon et al. SC 2011. מספרים אקראיים מקבילים: קל ונוח.
rng_philox: אלגוריתם Philox ליצירת מספרים אקראיים במקביל. הצורהinitial_stateהיאu64[3]עם ערכים שרירותיים. Salmon et al. SC 2011. מספרים אקראיים מקבילים: קל ונוח.
מידע על StableHLO זמין במאמר StableHLO – rng_bit_generator.
RngGetAndUpdateState
מידע נוסף זמין במאמר בנושא HloInstruction::CreateRngGetAndUpdateState.
ממשק ה-API של הפעולות השונות ב-Rng מפורק באופן פנימי להוראות HLO, כולל RngGetAndUpdateState.
RngGetAndUpdateState משמש כפרימיטיב ב-HLO. האופרטור הזה עשוי להופיע בקובצי dump של HLO, אבל הוא לא מיועד לבנייה ידנית על ידי משתמשי קצה.
עגול
מידע נוסף זמין במאמר בנושא XlaBuilder::Round.
עיגול לפי רכיבים, במקרה של שוויון המרחק מהאפס.
Round(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
RoundNearestAfz
מידע נוסף זמין במאמר בנושא XlaBuilder::RoundNearestAfz.
הפונקציה מבצעת עיגול של כל רכיב למספר השלם הקרוב ביותר, והיא מעגלת מספרים שחציון שלהם הוא 0 לכיוון ההפוך מאפס.
RoundNearestAfz(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
מידע על StableHLO זמין במאמר בנושא StableHLO – round_nearest_afz.
RoundNearestEven
מידע נוסף זמין במאמר בנושא XlaBuilder::RoundNearestEven.
עיגול לפי רכיבים, במקרה של שוויון מעגלים למספר הזוגי הקרוב ביותר.
RoundNearestEven(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
מידע על StableHLO זמין במאמר StableHLO - round_nearest_even.
Rsqrt
מידע נוסף זמין במאמר בנושא XlaBuilder::Rsqrt.
ההופכי של השורש הריבועי של כל רכיב בנפרד, x -> 1.0 / sqrt(x).
Rsqrt(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Rsqrt תומכת גם בארגומנט האופציונלי result_accuracy:
Rsqrt(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
מידע על StableHLO זמין במאמר StableHLO – rsqrt.
סריקה
מידע נוסף זמין במאמר בנושא XlaBuilder::Scan.
הפונקציה מחילה פונקציית צמצום על מערך לאורך ממד נתון, ומייצרת מצב סופי ומערך של ערכי ביניים.
Scan(inputs..., inits..., to_apply, scan_dimension,
is_reverse, is_associative)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
inputs |
רצף של m XlaOp |
המערכים שייסרקו. |
inits |
רצף של k XlaOp |
העברות ראשוניות. |
to_apply |
XlaComputation |
חישוב מסוג i_0, ..., i_{m-1}, c_0, ..., c_{k-1} -> (o_0, ..., o_{n-1}, c'_0, ..., c'_{k-1}). |
scan_dimension |
int64 |
המאפיין שצריך לסרוק. |
is_reverse |
bool |
אם הערך הוא true, הסריקה מתבצעת בסדר הפוך. |
is_associative |
bool (שלושה מצבים) |
אם הערך הוא true, הפעולה היא אסוציאטיבית. |
הפונקציה to_apply מוחלת באופן עקבי על רכיבים ב-inputs לאורך scan_dimension. אם הערך של is_reverse הוא false, הרכיבים מעובדים לפי הסדר 0 עד N-1, כאשר N הוא הגודל של scan_dimension. אם הערך של is_reverse הוא true, הרכיבים מעובדים מ-N-1 עד 0.
הפונקציה to_apply מקבלת m + k אופרנדים:
mאלמנטים נוכחיים מתוךinputs.kערכי הנשיאה מהשלב הקודם (אוinitsעבור הרכיב הראשון).
הפונקציה to_apply מחזירה טאפל של n + k ערכים:
- רכיבי
nשלoutputs. kערכים חדשים של העברה.
פעולת הסריקה יוצרת טאפל של n + k ערכים:
- מערכי הפלט
n, שמכילים את ערכי הפלט לכל שלב. - הערכים הסופיים של
kהם הערכים שמתקבלים אחרי עיבוד כל הרכיבים.
הסוגים של הקלט m צריכים להיות זהים לסוגים של הפרמטרים הראשונים m של
to_apply עם מאפיין סריקה נוסף. הסוגים של הפלטים של n צריכים להיות זהים לסוגים של ערכי ההחזרה הראשונים של to_apply עם מימד סריקה נוסף.n הגודל של המימד הנוסף בסריקה צריך להיות זהה N בכל הקלט והפלט. הסוגים של הפרמטרים האחרונים k וערכי ההחזרה של to_apply וגם של k init צריכים להיות זהים.
לדוגמה (m, n, k == 1, N == 3), כדי להעביר את הערך הראשוני i, מזינים [a, b, c], פונקציה f(x, c) -> (y, c') ו-scan_dimension=0, is_reverse=false:
- שלב 0:
f(a, i) -> (y0, c0) - שלב 1:
f(b, c0) -> (y1, c1) - שלב 2:
f(c, c1) -> (y2, c2)
הפלט של Scan הוא ([y0, y1, y2], c2).
פיזור
מידע נוסף זמין במאמר בנושא XlaBuilder::Scatter.
פעולת הפיזור של XLA יוצרת רצף של תוצאות שהן הערכים של מערך הקלט operands, עם כמה פרוסות (באינדקסים שצוינו על ידי scatter_indices) שמעודכנות ברצף הערכים ב-updates באמצעות update_computation.
Scatter(operands..., scatter_indices, updates..., update_computation,
dimension_numbers, indices_are_sorted, unique_indices)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands |
רצף של N XlaOp |
N מערכים מסוג T_0, ..., T_N לפיזור. |
scatter_indices |
XlaOp |
מערך שמכיל את אינדקס ההתחלה של הפרוסות שצריך לפזר. |
updates |
רצף של N XlaOp |
N מערכים מסוג T_0, ..., T_N. updates[i] מכיל את הערכים שצריך להשתמש בהם לפיזור operands[i]. |
update_computation |
XlaComputation |
חישוב שישמש לשילוב הערכים הקיימים במערך הקלט והעדכונים במהלך הפיזור. החישוב הזה צריך להיות מסוג T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N). |
index_vector_dim |
int64 |
המאפיין ב-scatter_indices שמכיל את האינדקסים ההתחלתיים. |
update_window_dims |
ArraySlice<int64> |
קבוצת המאפיינים בצורה updates שהם מאפייני חלון. |
inserted_window_dims |
ArraySlice<int64> |
קבוצת מידות החלון שצריך להוסיף לצורה updates. |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
מיפוי של המאפיינים ממדדי הפיזור למרחב של מדדי האופרנד. המערך הזה מתפרש כמיפוי של i ל-scatter_dims_to_operand_dims[i] . המיפוי צריך להיות מלא וחד-חד-ערכי. |
dimension_number |
ScatterDimensionNumbers |
מספרי מאפיינים לפעולת פיזור |
indices_are_sorted |
bool |
הארגומנט שקובע אם המדדים ממוינים על ידי הפונקציה שקוראת לפונקציה הנוכחית. |
unique_indices |
bool |
האם המדדים מובטחים להיות ייחודיים על ידי המתקשר. |
כאשר:
- הערך של n חייב להיות גדול מ-1 או שווה לו.
- כל המאפיינים
operands[0], ...,operands[N-1] חייבים להיות באותן מידות. - כל המאפיינים
updates[0], ...,updates[N-1] חייבים להיות באותן מידות. - אם
N = 1, אזCollate(T)הואT. - אם
N > 1,Collate(T_0, ..., T_N)הוא טאפל של רכיביNמסוגT.
אם index_vector_dim שווה ל-scatter_indices.rank, אנחנו מניחים באופן מרומז של-scatter_indices יש מאפיין 1 בסוף.
אנחנו מגדירים את update_scatter_dims מסוג ArraySlice<int64> כקבוצת המאפיינים של הצורה updates שלא נמצאים ב-update_window_dims, בסדר עולה.
הארגומנטים של scatter צריכים לעמוד במגבלות הבאות:
לכל מערך
updatesצריכות להיותupdate_window_dims.size + scatter_indices.rank - 1מידות.הגבולות של מאפיין
iבכל מערךupdatesצריכים להיות בהתאם לדרישות הבאות:- אם
iמופיע ב-update_window_dims(כלומר, שווה ל-update_window_dims[k] עבורkמסוים), אז הגבול של המאפייןiב-updatesלא יכול להיות גדול מהגבול התואם שלoperandאחרי שמתחשבים ב-inserted_window_dims(כלומר,adjusted_window_bounds[k], כאשרadjusted_window_boundsמכיל את הגבולות שלoperandעם הגבולות במדדיםinserted_window_dimsשהוסרו). - אם
iמופיע ב-update_scatter_dims(כלומר, שווה ל-update_scatter_dims[k] עבור ערך מסוים שלk), אז הגבול של המימדiב-updatesחייב להיות שווה לגבול המתאים שלscatter_indices, תוך דילוג עלindex_vector_dim(כלומר,scatter_indices.shape.dims[k], אםk<index_vector_dim, ו-scatter_indices.shape.dims[k+1] אחרת).
- אם
המספרים
update_window_dimsצריכים להיות בסדר עולה, לא יכולים להיות מספרי מאפיינים חוזרים, והם צריכים להיות בטווח[0, updates.rank).המספרים
inserted_window_dimsצריכים להיות בסדר עולה, לא יכולים להיות מספרי מאפיינים חוזרים, והם צריכים להיות בטווח[0, operand.rank).הערך של
operand.rankחייב להיות שווה לסכום שלupdate_window_dims.sizeושלinserted_window_dims.size.הערך של
scatter_dims_to_operand_dims.sizeצריך להיות שווה לערך שלscatter_indices.shape.dims[index_vector_dim], והערכים שלו צריכים להיות בטווח[0, operand.rank).
לכל אינדקס U במערך updates, האינדקס התואם I במערך operands שאליו צריך להחיל את העדכון הזה מחושב באופן הבא:
- Let
G= {U[k] forkinupdate_scatter_dims}. UseGto look up an index vectorSin thescatter_indicesarray such thatS[i] =scatter_indices[Combine(G,i)] where Combine(A, b) inserts b at positionsindex_vector_diminto A. - תצור אינדקס
Sinב-operandבאמצעותSעל ידי פיזורSבאמצעות המפהscatter_dims_to_operand_dims. בצורה רשמית יותר:Sin[scatter_dims_to_operand_dims[k]] =S[k] ifk<scatter_dims_to_operand_dims.size.-
Sin[_] =0אחרת.
- יוצרים אינדקס
Winלכל מערךoperandsעל ידי פיזור האינדקסים ב-update_window_dimsב-Uבהתאם ל-inserted_window_dims. בצורה רשמית יותר:-
Win[window_dims_to_operand_dims(k)] =U[k] ifkis inupdate_window_dims, wherewindow_dims_to_operand_dimsis the monotonic function with domain [0,update_window_dims.size) and range [0,operand.rank) \inserted_window_dims. (לדוגמה, אםupdate_window_dims.sizeהוא4, operand.rankהוא6ו-inserted_window_dimsהוא {0,2}, אזwindow_dims_to_operand_dimsהוא {0→1,1→3,2→4,3→5}). -
Win[_] =0אחרת.
-
-
IהואWin+Sinכאשר + הוא חיבור של כל רכיב בנפרד.
לסיכום, אפשר להגדיר את פעולת הפיזור באופן הבא.
- מאתחלים את
outputעםoperands, כלומר לכל האינדקסיםJ, לכל האינדקסיםOבמערךoperands[J]:
output[J][O] =operands[J][O] - לכל אינדקס
Uבמערךupdates[J] ולאינדקס התואםOבמערךoperand[J], אםOהוא אינדקס תקין עבורoutput:
(output[0][O], ...,output[N-1][O]) =update_computation(output[0][O], ..., ,output[N-1][O],updates[0][U], ...,updates[N-1][U])
סדר העדכונים לא קבוע. לכן, אם כמה אינדקסים ב-updates מפנים לאותו אינדקס ב-operands, הערך התואם ב-output יהיה לא דטרמיניסטי.
שימו לב שהפרמטר הראשון שמועבר אל update_computation תמיד יהיה הערך הנוכחי מהמערך output, והפרמטר השני תמיד יהיה הערך מהמערך updates. זה חשוב במיוחד במקרים שבהם update_computation הוא לא קומוטטיבי.
אם המדיניות indices_are_sorted מוגדרת כ-True, XLA יכול להניח שהמשתמש מיין את scatter_indices (בסדר עולה, אחרי פיזור הערכים לפי scatter_dims_to_operand_dims). אם הם לא כאלה, הסמנטיקה מוגדרת על ידי ההטמעה.
אם הערך של unique_indices הוא true, XLA יכול להניח שכל האלמנטים שמועברים הם ייחודיים. לכן, יכול להיות ש-XLA ישתמש בפעולות לא אטומיות. אם הערך של unique_indices הוא true והאינדקסים שמועברים אליהם לא ייחודיים, הסמנטיקה מוגדרת בהטמעה.
באופן לא רשמי, אפשר לראות את פעולת הפיזור כהיפוך של פעולת האיסוף, כלומר, פעולת הפיזור מעדכנת את הרכיבים בקלט שמחולצים על ידי פעולת האיסוף התואמת.
תיאור לא רשמי מפורט ודוגמאות זמינים בקטע 'תיאור לא רשמי' במאמר Gather.
מידע על StableHLO זמין במאמר StableHLO – scatter.
Scatter – דוגמה 1 – StableHLO
בתמונה שלמעלה, כל שורה בטבלה היא דוגמה לעדכון של אינדקס. בואו נבדוק את התהליך משמאל(עדכון האינדקס) לימין(תוצאת האינדקס):
הקלט) input הוא בצורה S32[2,3,4,2]. scatter_indices have shape
S64[2,2,3,2]. updates יש צורה S32[2,2,3,1,2].
עדכון האינדקס) כחלק מהקלט שקיבלנו update_window_dims:[3,4]. השורה הזו
מציינת שהמאפיינים dim 3 ו-dim 4 של updates הם מידות החלון, והם מסומנים
בצהוב. כך אנחנו יכולים להסיק ש-update_scatter_dims = [0,1,2].
עדכון מדד הפיזור) מוצגות לנו התוצאות שחולצו updated_scatter_dims לכל אחת מהן.
(החלק שלא צבוע בצהוב בעמודה Update Index)
אינדקס התחלה) אם נסתכל על תמונת הטנסור scatter_indices, נוכל לראות שהערכים מהשלב הקודם (עדכון אינדקס הפיזור) מציינים את המיקום של אינדקס ההתחלה. מ-index_vector_dim אנחנו גם מקבלים את המימד של starting_indices שמכיל את אינדקס ההתחלה, שהוא 3 עם גודל 2 עבור scatter_indices.
Full Start Index) scatter_dims_to_operand_dims = [2,1] אומר לנו שהרכיב הראשון של וקטור האינדקס עובר לאופרנד dim 2. האלמנט השני של וקטור האינדקס עובר לממד 1 של האופרנד. המאפיינים הנותרים של האופרנד ימולאו ב-0.
מדד אצווה מלא) אפשר לראות שהאזור הסגול המודגש מוצג בעמודה הזו(מדד אצווה מלא), בעמודת מדד פיזור העדכון ובעמודת מדד העדכון.
אינדקס המסך המלא) מחושב מתוך update_window_dimensions [3,4].
אינדקס התוצאה) סכום של אינדקס ההתחלה המלא, אינדקס האצווה המלא ואינדקס החלון המלא בטנזור operand. שימו לב שהאזורים שמודגשים בירוק תואמים גם לנתונים בoperand. השורה האחרונה מושמטת כי היא לא נכללת בטנזור operand.
בחירה
מידע נוסף זמין במאמר בנושא XlaBuilder::Select.
הפונקציה יוצרת מערך פלט מתוך רכיבים של שני מערכי קלט, על סמך הערכים של מערך פרדיקטים.
Select(pred, on_true, on_false)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
pred |
XlaOp |
מערך מסוג PRED |
on_true |
XlaOp |
מערך מסוג T |
on_false |
XlaOp |
מערך מסוג T |
למערכים on_true ו-on_false צריך להיות אותו מבנה. זה גם הצורה של מערך הפלט. למערך pred חייב להיות אותו מספר ממדים כמו למערכים on_true ו-on_false, עם סוג הרכיב PRED.
לכל אלמנט P ב-pred, האלמנט התואם במערך הפלט נלקח מ-on_true אם הערך של P הוא true, ומ-on_false אם הערך של P הוא false. pred יכול להיות סקלר מסוג PRED, כצורה מוגבלת של שידור. במקרה הזה, מערך הפלט נלקח כולו מ-on_true אם pred הוא true, ומ-on_false אם pred הוא false.
דוגמה עם ערך לא סקלרי pred:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
דוגמה עם סקלר pred:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
יש תמיכה בבחירות בין טאפלים. למטרה הזו, טאפלים נחשבים לסוגים סקלריים. אם on_true ו-on_false הם טאפלים (שחייבים להיות באותו הצורה!), אז pred חייב להיות סקלר מסוג PRED.
מידע על StableHLO זמין במאמר StableHLO - select
SelectAndScatter
מידע נוסף זמין במאמר בנושא XlaBuilder::SelectAndScatter.
אפשר להתייחס לפעולה הזו כאל פעולה מורכבת שמחשבת קודם את ReduceWindow במערך operand כדי לבחור רכיב מכל חלון, ואז מפזרת את מערך source לאינדקסים של הרכיבים שנבחרו כדי ליצור מערך פלט עם אותה צורה כמו מערך האופרנד. הפונקציה הבינארית
select משמשת לבחירת רכיב מכל חלון על ידי החלתה על כל חלון, והיא מופעלת עם המאפיין שבו וקטור האינדקס של הפרמטר הראשון קטן לקסיקוגרפית מווקטור האינדקס של הפרמטר השני. הפונקציה select מחזירה true אם הפרמטר הראשון נבחר, ומחזירה false אם הפרמטר השני נבחר. הפונקציה צריכה להיות טרנזיטיבית (כלומר, אם select(a, b) ו-select(b, c) הם true, אז גם select(a, c) הוא true), כדי שהרכיב שנבחר לא יהיה תלוי בסדר של הרכיבים שמועברים בחלון נתון.
הפונקציה scatter מוחלת על כל אינדקס שנבחר במערך הפלט. היא מקבלת שני פרמטרים סקלריים:
- הערך הנוכחי באינדקס שנבחר במערך הפלט
- ערך הפיזור מ-
sourceשחל על האינדקס שנבחר
הפונקציה משלבת את שני הפרמטרים ומחזירה ערך סקלרי שמשמש לעדכון הערך באינדקס שנבחר במערך הפלט. בהתחלה, כל האינדקסים של מערך הפלט מוגדרים ל-init_value.
למערך הפלט יש את אותו הצורה כמו למערך operand, ולמערך source
צריכה להיות אותה צורה כמו לתוצאה של הפעלת פעולה ReduceWindow על המערך operand. אפשר להשתמש ב-SelectAndScatter כדי להעביר לאחור את ערכי הגרדיאנט לשכבת איגום ברשת עצבית.
SelectAndScatter(operand, select, window_dimensions, window_strides, padding,
source, init_value, scatter)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand
|
XlaOp
|
מערך מסוג T שחלונות הזמן נעים לאורכו |
select
|
XlaComputation
|
חישוב בינארי מהסוג T, T
-> PRED, שחל על כל האלמנטים בכל חלון. הפונקציה מחזירה true אם הפרמטר הראשון נבחר, ומחזירה false אם הפרמטר השני נבחר. |
window_dimensions
|
ArraySlice<int64>
|
מערך של מספרים שלמים לערכי מאפייני חלון |
window_strides
|
ArraySlice<int64>
|
מערך של מספרים שלמים לערכי הצעד של החלון |
padding
|
Padding
|
סוג הריפוד של החלון (Padding::kSame או Padding::kValid) |
source
|
XlaOp
|
מערך מסוג T עם הערכים לפיזור |
init_value
|
XlaOp
|
ערך סקלרי מסוג T לערך ההתחלתי של מערך הפלט |
scatter
|
XlaComputation
|
חישוב בינארי מסוג T, T
-> T, כדי להחיל כל רכיב של מקור הפיזור עם רכיב היעד שלו |
באיור הבא מוצגות דוגמאות לשימוש בפונקציה SelectAndScatter, כאשר הפונקציה select מחשבת את הערך המקסימלי מבין הפרמטרים שלה. שימו לב: כשהחלונות חופפים, כמו באיור (2) שלמטה, יכול להיות שאינדקס של מערך operand ייבחר כמה פעמים על ידי חלונות שונים. באיור, הרכיב עם הערך 9 נבחר על ידי שני החלונות העליונים (הכחול והאדום), והפונקציה של החיבור הבינארי scatter יוצרת את רכיב הפלט עם הערך 8 (2 + 6).
סדר החישוב של הפונקציה scatter הוא שרירותי ולא דטרמיניסטי. לכן, הפונקציה scatter לא צריכה להיות רגישה מדי לשיוך מחדש. פרטים נוספים מופיעים בדיון על אסוציאטיביות בהקשר של Reduce.
מידע על StableHLO זמין במאמר בנושא StableHLO – select_and_scatter.
שליחה
מידע נוסף זמין במאמר בנושא XlaBuilder::Send.
Send, SendWithTokens ו-SendToHost הם פעולות שמשמשות כפרימיטיבים של תקשורת ב-HLO. הפעולות האלה מופיעות בדרך כלל בפריקות של HLO כחלק מהעברת קלט/פלט ברמה נמוכה או העברה בין מכשירים, אבל הן לא מיועדות לבנייה ידנית על ידי משתמשי קצה.
Send(operand, handle)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
הנתונים לשליחה (מערך מסוג T) |
handle |
ChannelHandle |
מזהה ייחודי לכל זוג של שליחה/קבלה |
שולחת את נתוני האופרנד שצוינו להוראה Recv בחישוב אחר שמשתמש באותו שם ערוץ. לא מוחזרים נתונים.
בדומה לפעולה Recv, ממשק ה-API של הלקוח של הפעולה Send מייצג תקשורת סינכרונית, והוא מפורק באופן פנימי ל-2 הוראות HLO (Send ו-SendDone) כדי לאפשר העברות נתונים אסינכרוניות. ראו גם HloInstruction::CreateSend ו-HloInstruction::CreateSendDone.
Send(HloInstruction operand, int64 channel_id)
מתחילה העברה אסינכרונית של האופרנד למשאבים שהוקצו על ידי ההוראה Recv עם אותו מזהה ערוץ. הפונקציה מחזירה הקשר, שמשמש את ההוראה הבאה SendDone להמתנה להשלמת העברת הנתונים. ההקשר הוא טאפל של {אופרנד (צורה), מזהה בקשה (U32)} ואפשר להשתמש בו רק בהוראה SendDone.
מידע על StableHLO זמין במאמר בנושא StableHLO – send.
SendDone
מידע נוסף זמין במאמר בנושא HloInstruction::CreateSendDone.
SendDone(HloInstruction context)
בהינתן הקשר שנוצר על ידי הוראה Send, המערכת ממתינה לסיום העברת הנתונים. ההוראה לא מחזירה נתונים.
תזמון של הוראות בערוץ
סדר הביצוע של 4 ההוראות לכל ערוץ (Recv, RecvDone, Send, SendDone) הוא כמו שמופיע בהמשך.
RecvלפניSendSendלפניRecvDoneRecvלפניRecvDoneSendלפניSendDone
כשמהדרים של העורף יוצרים תזמון לינארי לכל חישוב שמתבצע באמצעות הוראות לערוץ, לא יכולים להיות מחזורים בחישובים. לדוגמה, התזמונים הבאים מובילים לקיפאון.
SetDimensionSize
מידע נוסף זמין במאמר בנושא XlaBuilder::SetDimensionSize.
הפעולה מגדירה את הגודל הדינמי של המימד שצוין ב-XlaOp. האופרנד חייב להיות בצורת מערך.
SetDimensionSize(operand, val, dimension)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך קלט n-ממדי. |
val |
XlaOp |
int32 שמייצג את הגודל הדינמי של זמן הריצה. |
dimension
|
int64
|
ערך במרווח [0, n) שמציין את המאפיין. |
הפונקציה מעבירה את האופרנד כתוצאה, עם מאפיין דינמי שמתבצע אחריו מעקב על ידי הקומפיילר.
המערכת תתעלם מערכים עם ריווח בפעולות צמצום בהמשך.
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
ShiftLeft
מידע נוסף זמין במאמר בנושא XlaBuilder::ShiftLeft.
מבצעת פעולת הזזה שמאלה לפי רכיב ב-lhs לפי מספר הסיביות rhs.
ShiftLeft(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בהעברה בשידור עם ממדים שונים ל-ShiftLeft:
ShiftLeft(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר StableHLO - shift_left.
ShiftRightArithmetic
מידע נוסף זמין במאמר בנושא XlaBuilder::ShiftRightArithmetic.
מבצעת פעולת הזזה אריתמטית ימינה ברמת הרכיב ב-lhs במספר rhs של סיביות.
ShiftRightArithmetic(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בהעברה בשידור עם ממדים שונים עבור ShiftRightArithmetic:
ShiftRightArithmetic(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר StableHLO - shift_right_arithmetic.
ShiftRightLogical
מידע נוסף זמין במאמר בנושא XlaBuilder::ShiftRightLogical.
מבצעת פעולת הזזה לוגית ימינה ברמת הרכיב ב-lhs במספר rhs של סיביות.
ShiftRightLogical(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בהעברה רחבה של מימדים שונים עבור ShiftRightLogical:
ShiftRightLogical(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר StableHLO - shift_right_logical.
לחתימה
מידע נוסף זמין במאמר בנושא XlaBuilder::Sign.
Sign(operand) פעולת חתימה לפי רכיב x -> sgn(x) כאשר
\[\text{sgn}(x) = \begin{cases} -1 & x < 0\\ -0 & x = -0\\ NaN & x = NaN\\ +0 & x = +0\\ 1 & x > 0 \end{cases}\]
באמצעות אופרטור ההשוואה של סוג הרכיב operand.
Sign(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
מידע על StableHLO זמין במאמר בנושא StableHLO – sign.
חטא
Sin(operand) Element-wise sine x -> sin(x).
מידע נוסף זמין במאמר בנושא XlaBuilder::Sin.
Sin(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Sin תומכת גם בארגומנט האופציונלי result_accuracy:
Sin(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
מידע על StableHLO זמין במאמר StableHLO - sine.
תבנית של תוכן דינמי
מידע נוסף זמין במאמר בנושא XlaBuilder::Slice.
הפונקציה Slicing מחלצת תת-מערך ממערך הקלט. למערך המשנה יש אותו מספר ממדים כמו לקלט, והוא מכיל את הערכים בתוך תיבת תוחמת במערך הקלט, כאשר הממדים והאינדקסים של התיבה התוחמת ניתנים כארגומנטים לפעולת החיתוך.
Slice(operand, start_indices, limit_indices, strides)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך N ממדי מסוג T |
start_indices
|
ArraySlice<int64>
|
רשימה של N מספרים שלמים שמכילה את האינדקסים ההתחלתיים של הפרוסה לכל מימד. הערכים חייבים להיות גדולים מ-0 או שווים ל-0. |
limit_indices
|
ArraySlice<int64>
|
רשימה של N מספרים שלמים שמכילים את האינדקסים של סוף הפרוסה (לא כולל) לכל מאפיין. כל ערך צריך להיות גדול מהערך המתאים של start_indices במאפיין או שווה לו, וקטן מגודל המאפיין או שווה לו. |
strides
|
ArraySlice<int64>
|
רשימה של N מספרים שלמים שקובעת את קפיצת הקלט של הפרוסה. הפונקציה slice בוחרת כל רכיב strides[d] במאפיין d. |
דוגמה חד-ממדית:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4})
// Result: {2.0, 3.0}
דוגמה דו-ממדית:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3})
// Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
מידע על StableHLO זמין במאמר StableHLO - slice.
מיון
מידע נוסף זמין במאמר בנושא XlaBuilder::Sort.
Sort(operands, comparator, dimension, is_stable)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands |
ArraySlice<XlaOp> |
האופרנדים למיון. |
comparator |
XlaComputation |
החישוב של ההשוואה שבו רוצים להשתמש. |
dimension |
int64 |
המאפיין שלפיו רוצים למיין. |
is_stable |
bool |
מציינת אם להשתמש במיון יציב. |
אם מציינים רק אופרנד אחד:
אם האופרנד הוא טנזור חד-ממדי (מערך), התוצאה היא מערך ממוין. אם רוצים למיין את המערך בסדר עולה, פונקציית ההשוואה צריכה לבצע השוואה של 'קטן מ'. באופן רשמי, אחרי המיון של המערך, מתקיים לכל מיקומי האינדקס
i, jעםi < jאחד מהתנאים הבאים:comparator(value[i], value[j]) = comparator(value[j], value[i]) = falseאוcomparator(value[i], value[j]) = true.אם לאופרנד יש מספר גבוה יותר של מאפיינים, האופרנד ממוין לאורך המאפיין שצוין. לדוגמה, עבור טנזור דו-ממדי (מטריצה), ערך המאפיין
0ימיין באופן עצמאי כל עמודה, וערך המאפיין1ימיין באופן עצמאי כל שורה. אם לא מציינים מספר מאפיין, המערכת בוחרת כברירת מחדל את המאפיין האחרון. למאפיין שממוין, חל אותו סדר מיון כמו במקרה של מימד אחד.
אם מספקים אופרנדים של n > 1:
כל האופרנדים של
nצריכים להיות טנסורים עם אותם ממדים. יכול להיות שסוגי הרכיבים של הטנסורים יהיו שונים.כל האופרנדים ממוינים יחד, ולא בנפרד. מבחינה מושגית, האופרנדים נחשבים לטופל. כשבודקים אם צריך להחליף בין הרכיבים של כל אופרנד במיקומי האינדקס
iו-j, מתבצעת קריאה לפונקציית ההשוואה עם2 * nפרמטרים סקלריים, כאשר הפרמטר2 * kתואם לערך במיקוםiמהאופרנדk-th, והפרמטר2 * k + 1תואם לערך במיקוםjמהאופרנדk-th. בדרך כלל, פעולת ההשוואה תתבצע בין הפרמטרים2 * kו-2 * k + 1, ואולי גם בין זוגות אחרים של פרמטרים כדי להכריע במקרה של שוויון.התוצאה היא טופל שמורכב מהאופרנדים בסדר ממוין (לאורך המאפיין שצוין, כמו בדוגמה שלמעלה). האופרנד
i-thשל ה-tuple תואם לאופרנדi-thשל Sort.
לדוגמה, אם יש שלושה אופרנדים operand0 = [3, 1], operand1 = [42, 50], operand2 = [-3.0, 1.1], והפונקציה להשוואה משווה רק את הערכים של operand0 עם האופרטור 'קטן מ', הפלט של המיון הוא ה-tuple ([1, 3], [50, 42], [1.1, -3.0]).
אם הערך של is_stable הוא true, המיון יציב. כלומר, אם יש רכיבים שנחשבים שווים על ידי פונקציית ההשוואה, הסדר היחסי של הערכים השווים נשמר. שני אלמנטים e1 ו-e2 שווים אם ורק אם comparator(e1, e2) = comparator(e2, e1) = false. כברירת מחדל, is_stable מוגדר כ-false.
מידע על StableHLO זמין במאמר בנושא StableHLO – sort.
Sqrt
מידע נוסף זמין במאמר בנושא XlaBuilder::Sqrt.
פעולת שורש ריבועי לפי רכיב x -> sqrt(x).
Sqrt(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Sqrt תומכת גם בארגומנט האופציונלי result_accuracy:
Sqrt(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
מידע על StableHLO זמין במאמר בנושא StableHLO – sqrt.
תת-נכס
מידע נוסף זמין במאמר בנושא XlaBuilder::Sub.
מבצעת חיסור של lhs ו-rhs לפי אלמנטים.
Sub(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בשידור בממדים שונים עבור Sub:
Sub(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר בנושא StableHLO – subtract.
חום צהבהב
מידע נוסף זמין במאמר בנושא XlaBuilder::Tan.
טנגנס של כל רכיב x -> tan(x).
Tan(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Tan תומכת גם בארגומנט האופציונלי result_accuracy:
Tan(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
מידע על StableHLO זמין במאמר StableHLO - tan.
Tanh
מידע נוסף זמין במאמר בנושא XlaBuilder::Tanh.
טנגנס היפרבולי של כל רכיב x -> tanh(x).
Tanh(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה Tanh תומכת גם בארגומנט האופציונלי result_accuracy:
Tanh(operand, result_accuracy)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
result_accuracy
|
אופציונלי ResultAccuracy
|
סוגי הדיוק שהמשתמש יכול לבקש עבור פעולות אונריות עם כמה הטמעות |
מידע נוסף על result_accuracy זמין במאמר דיוק התוצאות.
למידע על StableHLO, ראו StableHLO – tanh.
TopK
מידע נוסף זמין במאמר בנושא XlaBuilder::TopK.
TopK מוצאת את הערכים והאינדקסים של k הרכיבים הגדולים או הקטנים ביותר בממד האחרון של הטנזור הנתון.
TopK(operand, k, largest)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand
|
XlaOp
|
הטנזור שממנו יש לחלץ את k הרכיבים העליונים.
ל-Tensor חייבים להיות לפחות מימד אחד. הגודל של המימד האחרון של הטנזור חייב להיות גדול מ-k או שווה לו. |
k |
int64 |
מספר הרכיבים לחילוץ. |
largest
|
bool
|
האם לחלץ את k
הרכיבים הגדולים או הקטנים ביותר. |
עבור טנסור קלט חד-ממדי (מערך), הפונקציה מוצאת את k הערכים הגדולים או הקטנים ביותר במערך ומחזירה טאפל של שני מערכים (values, indices). לכן, values[j] הוא הערך ה-j בגודל או בקטן ביותר ב-operand, והאינדקס שלו הוא indices[j].
עבור טנסור קלט עם יותר ממימד אחד, הפונקציה מחשבת את k הרשומות המובילות לאורך המימד האחרון, ושומרת את כל המימדים האחרים (שורות) בפלט.
לכן, עבור אופרנד בצורה [A, B, ..., P, Q] כאשר Q >= k הפלט הוא טאפל (values, indices) כאשר:
values.shape = indices.shape = [A, B, ..., P, k]
אם שני אלמנטים בשורה שווים, האלמנט עם האינדקס הנמוך יותר מופיע ראשון.
החלפה
כדאי לעיין גם בפעולה tf.reshape.
Transpose(operand, permutation)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד שצריך לשנות את המיקום שלו. |
permutation |
ArraySlice<int64> |
איך מבצעים פרמוטציה של המאפיינים. |
מבצעת פרמוטציה של המאפיינים של האופרנד עם הפרמוטציה שצוינה, כך שמתקבל ∀ i . 0 ≤ i < number of dimensions ⇒
input_dimensions[permutation[i]] = output_dimensions[i].
הפונקציה הזו זהה לפונקציה Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)).
מידע על StableHLO זמין במאמר StableHLO – transpose.
TriangularSolve
מידע נוסף זמין במאמר בנושא XlaBuilder::TriangularSolve.
פותר מערכות של משוואות ליניאריות עם מטריצות מקדמים משולשות עליונות או תחתונות באמצעות החלפה קדימה או אחורה. השגרה הזו משדרת לאורך הממדים המובילים, ופותרת אחת ממערכות המטריצות op(a) * x =
b או x * op(a) = b עבור המשתנה x, בהינתן a ו-b, כאשר op(a) הוא op(a) = a, או op(a) = Transpose(a), או op(a) = Conj(Transpose(a)).
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
a
|
XlaOp
|
מערך דו-ממדי של מספרים מרוכבים או מספרים עם נקודה צפה, עם צורה [..., M,
M]. |
b
|
XlaOp
|
a > מערך דו-ממדי מאותו סוג עם צורה [..., M, K] אם left_side הוא true, אחרת [..., K, M]. |
left_side
|
bool
|
מציין אם לפתור מערכת מהצורה op(a) * x = b (true) או x *
op(a) = b (false). |
lower
|
bool
|
אם להשתמש במשולש העליון או התחתון של a. |
unit_diagonal
|
bool
|
אם true, הרכיבים האלכסוניים של a הם 1 ולא מתבצעת אליהם גישה. |
transpose_a
|
Transpose
|
האם להשתמש ב-a כמו שהוא, לבצע לו טרנספוזיציה או
לקחת את הטרנספוזיציה הצמודה שלו. |
נתוני הקלט נקראים רק מהמשולש התחתון או העליון של a, בהתאם לערך של lower. המערכת מתעלמת מהערכים מהמשולש השני. נתוני הפלט מוחזרים באותו המשולש. הערכים במשולש השני מוגדרים בהטמעה ויכולים להיות כל דבר.
אם מספר המימדים של a ו-b גדול מ-2, המערכת מתייחסת אליהם כאל קבוצות של מטריצות, שבהן כל המימדים מלבד 2 המימדים המשניים הם מימדי קבוצה. המידות של המנות a ו-b צריכות להיות זהות.
מידע על StableHLO זמין במאמר StableHLO – triangular_solve.
טופל
מידע נוסף זמין במאמר בנושא XlaBuilder::Tuple.
טופל שמכיל מספר משתנה של נקודות אחיזה לנתונים, שלכל אחת מהן יש צורה משלה.
Tuple(elements)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
elements |
וקטור של XlaOp |
מערך N מסוג T |
זה דומה ל-std::tuple ב-C++. באופן עקרוני:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
אפשר לפרק טאפלים (לגשת אליהם) באמצעות הפעולה GetTupleElement.
מידע על StableHLO זמין במאמר בנושא StableHLO – tuple.
אף שהפונקציה
מידע נוסף זמין במאמר בנושא XlaBuilder::While.
While(condition, body, init)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
condition
|
XlaComputation
|
XlaComputation מסוג T -> PRED שמגדיר את תנאי הסיום של הלולאה. |
body
|
XlaComputation
|
XlaComputation מסוג T -> T שמגדיר את גוף הלולאה. |
init
|
T
|
הערך הראשוני של הפרמטר של condition ושל body. |
מבצע את הפעולות של body ברצף עד שהפעולה של condition נכשלת. הלולאה הזו דומה ללולאת while טיפוסית בשפות רבות אחרות, למעט ההבדלים וההגבלות שמפורטים בהמשך.
- צומת
Whileמחזיר ערך מסוגT, שהוא התוצאה מההפעלה האחרונה שלbody. - הצורה של הסוג
Tנקבעת באופן סטטי וחייבת להיות זהה בכל האיטרציות.
הפרמטרים T של החישובים מאותחלים עם הערך init באיטרציה הראשונה, ומעודכנים אוטומטית לתוצאה החדשה מ-body בכל איטרציה עוקבת.
מקרה שימוש מרכזי אחד של צומת While הוא הטמעה של ביצוע חוזר של אימון ברשתות עצביות. בהמשך מוצג קוד מדומה פשוט עם תרשים שמייצג את החישוב. הקוד נמצא בכתובת while_test.cc.
הסוג T בדוגמה הזו הוא Tuple שמורכב מ-int32 לספירת האיטרציות ומ-vector[10] לאקומולטור. ב-1,000 איטרציות, הלולאה ממשיכה להוסיף וקטור קבוע לאוגר.
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}
מידע על StableHLO זמין במאמר StableHLO - while.
Xor
מידע נוסף זמין במאמר בנושא XlaBuilder::Xor.
מבצעת XOR לפי רכיבים של lhs ו-rhs.
Xor(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | אופרנד בצד ימין: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי התיעוד בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא מערך שנוצר משידור של שני מערכי הקלט. בגרסה הזו, פעולות בין מערכים בדרגות שונות לא נתמכות, אלא אם אחד מהאופרנדים הוא סקלר.
קיימת וריאציה חלופית עם תמיכה בשידור רב-ממדי עבור Xor:
Xor(lhs,rhs, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
| lhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| rhs | XlaOp | האופרנד בצד ימין: מערך מסוג T |
| broadcast_dimension | ArraySlice |
איזה מאפיין בצורת היעד תואם לכל מאפיין בצורת האופרנד |
צריך להשתמש בווריאנט הזה של הפעולה לפעולות אריתמטיות בין מערכים בדרגות שונות (כמו הוספת מטריצה לווקטור).
האופרנד הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמציינת את המימדים שבהם יש להשתמש לשידור האופרנדים. הסמנטיקה מתוארת בפירוט בדף השידור.
מידע על StableHLO זמין במאמר StableHLO – xor.








