下文介绍了 XlaBuilder 接口中定义的操作的语义。通常,这些操作与 xla_data.proto 中 RPC 接口内定义的操作一一对应。
关于命名惯例的说明:XLA 处理的广义数据类型是 N 维数组,其中包含某种统一类型的元素(例如 32 位浮点数)。在整个文档中,数组用于表示任意维度的数组。为方便起见,特殊情况具有更具体且更熟悉的名称;例如,向量是一维数组,矩阵是二维数组。
腹肌
另请参阅 XlaBuilder::Abs。
按元素取绝对值 x -> |x|。
Abs(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
如需了解 StableHLO,请参阅 StableHLO - abs。
添加
另请参阅 XlaBuilder::Add。
对 lhs 和 rhs 执行逐元素加法。
Add(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Add,存在支持不同维度广播的替代变体:
Add(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - 添加。
AddDependency
另请参阅 HloInstruction::AddDependency。
AddDependency 可能会出现在 HLO 转储中,但最终用户不应手动构建它们。
AfterAll
另请参阅 XlaBuilder::AfterAll。
AfterAll 接受数量可变的 token,并生成单个 token。令牌是可以在有副作用的操作之间传递以强制执行顺序的原始类型。AfterAll 可用作令牌的联接,用于在执行一组操作后对操作进行排序。
AfterAll(tokens)
| 参数 | 类型 | 语义 |
|---|---|---|
tokens |
XlaOp 的矢量 |
可变数量的令牌 |
如需了解 StableHLO,请参阅 StableHLO - after_all。
AllGather
另请参阅 XlaBuilder::AllGather。
跨副本执行串联。
AllGather(operand, all_gather_dimension, shard_count, replica_groups,
channel_id, layout, use_global_device_ids)
| 参数 | 类型 | 语义 |
|---|---|---|
operand
|
XlaOp
|
要在各个副本中串联的数组 |
all_gather_dimension |
int64 |
串联维度 |
shard_count
|
int64
|
每个副本组的大小 |
replica_groups
|
int64 的向量的向量 |
执行串联的组 |
channel_id
|
可选
ChannelHandle |
用于跨模块通信的可选渠道 ID |
layout
|
可选 Layout
|
创建布局模式,用于捕获实参中匹配的布局 |
use_global_device_ids
|
可选 bool
|
如果 ReplicaGroup 配置中的 ID 表示全局 ID,则返回 true |
replica_groups是执行串联的副本组列表(可以使用ReplicaId检索当前副本的副本 ID)。每个组中副本的顺序决定了它们在结果中输入的位置顺序。replica_groups必须为空(在这种情况下,所有副本都属于一个组,按从0到N - 1的顺序排列),或者包含的元素数量与副本数量相同。例如,replica_groups = {0, 2}, {1, 3}在副本0和2之间以及1和3之间执行串联。shard_count是每个副本组的大小。如果replica_groups为空,则需要此值。channel_id用于跨模块通信:只有具有相同channel_id的all-gather操作才能相互通信。use_global_device_ids如果 ReplicaGroup 配置中的 ID 表示的是全局 ID(replica_id * partition_count + partition_id),而不是副本 ID,则返回 true。如果此 all-reduce 同时跨分区和跨副本,则可以更灵活地对设备进行分组。
输出形状是输入形状,其中 all_gather_dimension 扩大了 shard_count 倍。例如,如果有两个副本,并且操作数在两个副本上的值分别为 [1.0, 2.5] 和 [3.0, 5.25],那么当 all_gather_dim 为 0 时,此操作的输出值在两个副本上都将为 [1.0, 2.5, 3.0,5.25]。
AllGather 的 API 在内部分解为 2 个 HLO 指令(AllGatherStart 和 AllGatherDone)。
另请参阅 HloInstruction::CreateAllGatherStart。
AllGatherStart、AllGatherDone 用作 HLO 中的基元。这些操作可能会出现在 HLO 转储中,但最终用户不应手动构建它们。
如需了解 StableHLO,请参阅 StableHLO - all_gather。
AllReduce
另请参阅 XlaBuilder::AllReduce。
跨副本执行自定义计算。
AllReduce(operand, computation, replica_groups, channel_id,
shape_with_layout, use_global_device_ids)
| 参数 | 类型 | 语义 |
|---|---|---|
operand
|
XlaOp
|
要跨副本缩减的数组或非空数组元组 |
computation |
XlaComputation |
减幅计算 |
replica_groups
|
ReplicaGroup vector
|
执行归约操作的组 |
channel_id
|
可选
ChannelHandle |
用于跨模块通信的可选渠道 ID |
shape_with_layout
|
可选 Shape
|
定义所传输数据的布局 |
use_global_device_ids
|
可选 bool
|
如果 ReplicaGroup 配置中的 ID 表示全局 ID,则返回 true |
- 如果
operand是一个数组元组,则对元组的每个元素执行 all-reduce 操作。 replica_groups是执行缩减的副本组列表(可以使用ReplicaId检索当前副本的副本 ID)。replica_groups必须为空(在这种情况下,所有副本都属于一个组),或者包含的元素数量与副本数量相同。例如,replica_groups = {0, 2}, {1, 3}在副本0和2之间以及1和3之间执行缩减。channel_id用于跨模块通信:只有具有相同channel_id的all-reduce操作才能相互通信。shape_with_layout:强制将 AllReduce 的布局设置为给定的布局。 用于保证一组单独编译的 AllReduce 操作具有相同的布局。use_global_device_ids如果 ReplicaGroup 配置中的 ID 表示的是全局 ID(replica_id * partition_count + partition_id),而不是副本 ID,则返回 true。如果此 all-reduce 同时跨分区和跨副本,则可以更灵活地对设备进行分组。
输出形状与输入形状相同。例如,如果有两个副本,并且操作数在两个副本上分别具有值 [1.0, 2.5] 和 [3.0, 5.25],那么此操作和求和计算的输出值在两个副本上都将为 [4.0, 7.75]。如果输入是元组,则输出也是元组。
计算 AllReduce 的结果需要每个副本都提供一个输入,因此如果一个副本执行 AllReduce 节点的次数比另一个副本多,则前者将永远等待。由于所有副本都运行相同的程序,因此这种情况发生的可能性不大,但当 while 循环的条件依赖于来自 infeed 的数据时,如果 infeed 中的数据导致一个副本上的 while 循环比另一个副本上的 while 循环迭代更多次,则可能会发生这种情况。
AllReduce 的 API 在内部分解为 2 个 HLO 指令(AllReduceStart 和 AllReduceDone)。
另请参阅 HloInstruction::CreateAllReduceStart。
AllReduceStart 和 AllReduceDone 用作 HLO 中的基元。这些操作可能会出现在 HLO 转储中,但最终用户不应手动构建它们。
CrossReplicaSum
另请参阅 XlaBuilder::CrossReplicaSum。
执行求和计算的 AllReduce。
CrossReplicaSum(operand, replica_groups)
| 参数 | 类型 | 语义 |
|---|---|---|
operand
|
XlaOp | 要跨副本缩减的数组或非空数组元组 |
replica_groups
|
向量的向量,其中包含 int64 |
执行归约操作的组 |
返回每个副本子组中操作数值的总和。所有副本都为总和提供一个输入,并且所有副本都会接收每个子群组的最终总和。
AllToAll
另请参阅 XlaBuilder::AllToAll。
AllToAll 是一种集体操作,可将数据从所有核心发送到所有核心。该方法分两步来实现:
- 分散阶段。在每个核心上,操作数沿
split_dimensions分成split_count个块,这些块会分散到所有核心,例如,第 i 个块会发送到第 i 个核心。 - 收集阶段。每个核心都会沿
concat_dimension连接接收到的块。
参与的核心可以通过以下方式进行配置:
replica_groups:每个 ReplicaGroup 都包含参与计算的副本 ID 列表(可以使用ReplicaId检索当前副本的副本 ID)。AllToAll 将按指定顺序在子组内应用。例如,replica_groups = { {1,2,3}, {4,5,0} }表示将在副本{1, 2, 3}内应用 AllToAll,并且在收集阶段,接收到的块将按 1、2、3 的相同顺序串联。然后,在副本 4、5、0 中应用另一个 AllToAll,串联顺序也是 4、5、0。如果replica_groups为空,则所有副本都属于一个组,按其出现的串联顺序排列。
前提条件:
split_dimension上操作数的维度大小可被split_count整除。- 操作数的形状不是元组。
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups, layout, channel_id)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
n 维输入数组 |
split_dimension
|
int64
|
区间 [0,n) 中的一个值,用于指明操作数拆分的维度 |
concat_dimension
|
int64
|
区间 [0,n) 中的一个值,用于指定串联拆分块的维度 |
split_count
|
int64
|
参与此操作的核心数。如果 replica_groups 为空,则此值应为副本数;否则,此值应等于每个组中的副本数。 |
replica_groups
|
ReplicaGroupvector
|
每个组都包含一个副本 ID 列表。 |
layout |
可选 Layout |
用户指定的内存布局 |
channel_id
|
可选 ChannelHandle
|
每个发送/接收对的唯一标识符 |
如需详细了解形状和布局,请参阅 xla::shapes。
如需了解 StableHLO,请参阅 StableHLO - all_to_all。
AllToAll - 示例 1。
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(
x,
/*split_dimension=*/ 1,
/*concat_dimension=*/ 0,
/*split_count=*/ 4);
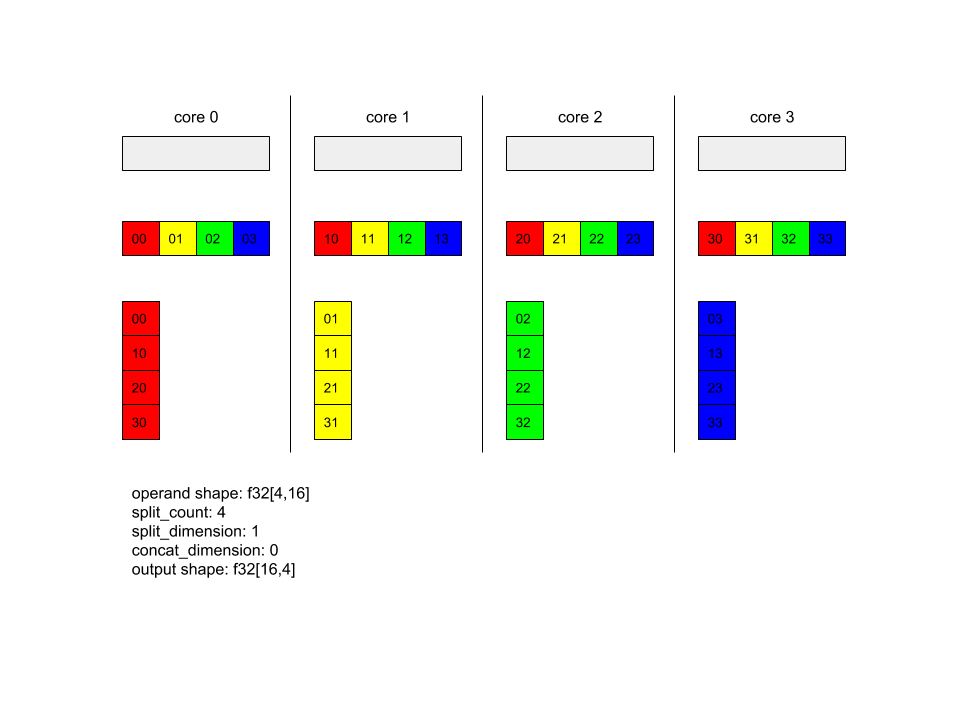
在上面的示例中,有 4 个核心参与 Alltoall。在每个核心上,操作数沿维度 1 拆分为 4 个部分,因此每个部分的形状为 f32[4,4]。这 4 个部分会分散到所有核心。然后,每个核心按核心 0-4 的顺序沿维度 0 连接接收到的部分。因此,每个核心上的输出的形状为 f32[16,4]。
AllToAll - 示例 2 - StableHLO
在上面的示例中,有 2 个副本参与 AllToAll。在每个副本上,操作数的形状为 f32[2,4]。操作数沿维度 1 拆分为 2 个部分,因此每个部分的形状为 f32[2,2]。然后,这两个部分会根据它们在副本组中的位置在各个副本之间进行交换。每个副本都会从两个操作数中收集相应的部分,并沿维度 0 将它们串联起来。因此,每个副本上的输出的形状为 f32[4,2]。
RaggedAllToAll
另请参阅 XlaBuilder::RaggedAllToAll。
RaggedAllToAll 执行集体全到全操作,其中输入和输出是不规则张量。
RaggedAllToAll(input, input_offsets, send_sizes, output, output_offsets,
recv_sizes, replica_groups, channel_id)
| 参数 | 类型 | 语义 |
|---|---|---|
input |
XlaOp |
类型为 T 的 N 数组 |
input_offsets |
XlaOp |
类型为 T 的 N 数组 |
send_sizes |
XlaOp |
类型为 T 的 N 数组 |
output |
XlaOp |
类型为 T 的 N 数组 |
output_offsets |
XlaOp |
类型为 T 的 N 数组 |
recv_sizes |
XlaOp |
类型为 T 的 N 数组 |
replica_groups
|
ReplicaGroup vector
|
每个组都包含一个副本 ID 列表。 |
channel_id
|
可选 ChannelHandle
|
每个发送/接收对的唯一标识符 |
不规则张量由一组三个张量定义:
data:data张量沿其最外层维度是“不规则”的,沿该维度每个索引元素的尺寸各不相同。offsets':offsets张量用于为data张量的最外层维度编制索引,并表示data张量的每个不规则元素的起始偏移量。sizes:sizes张量表示data张量的每个不规则元素的规模,其中规模以子元素为单位指定。子元素定义为通过移除最外层的“不规则”维度而获得的“数据”张量形状的后缀。offsets和sizes张量的大小必须相同。
一个不规则张量示例:
data: [8,3] =
{ {a,b,c},{d,e,f},{g,h,i},{j,k,l},{m,n,o},{p,q,r},{s,t,u},{v,w,x} }
offsets: [3] = {0, 1, 4}
sizes: [3] = {1, 3, 4}
// Index 'data' at 'offsets'[0], 'sizes'[0]' // {a,b,c}
// Index 'data' at 'offsets'[1], 'sizes'[1]' // {d,e,f},{g,h,i},{j,k,l}
// Index 'data' at 'offsets'[2], 'sizes'[2]' // {m,n,o},{p,q,r},{s,t,u},{v,w,x}
必须以这样一种方式对 output_offsets 进行分片,即每个副本都具有目标副本输出视角中的偏移量。
对于第 i 个输出偏移量,当前副本将向第 i 个副本发送 input[input_offsets[i]:input_offsets[i]+input_sizes[i]] 更新,该更新将写入第 i 个副本中的 output_i[output_offsets[i]:output_offsets[i]+send_sizes[i]] output。
例如,如果我们有 2 个副本:
replica 0:
input: [1, 2, 2]
output:[0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 2]
output_offsets: [0, 0]
recv_sizes: [1, 1]
replica 1:
input: [3, 4, 0]
output: [0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 1]
output_offsets: [1, 2]
recv_sizes: [2, 1]
// replica 0's result will be: [1, 3, 0, 0]
// replica 1's result will be: [2, 2, 4, 0]
不规则全到全 HLO 具有以下实参:
input:不规则的输入数据张量。output:不规则输出数据张量。input_offsets:不规则输入偏移量张量。send_sizes:不规则发送大小张量。output_offsets:目标副本输出中的不规则偏移数组。recv_sizes:不规则接收大小张量。
*_offsets 和 *_sizes 张量必须具有相同的形状。
*_offsets 和 *_sizes 张量支持以下两种形状:
[num_devices],其中 ragged-all-to-all 最多可向复制组中的每个远程设备发送一次更新。例如:
for (remote_device_id : replica_group) {
SEND input[input_offsets[remote_device_id]],
output[output_offsets[remote_device_id]],
send_sizes[remote_device_id] }
[num_devices, num_updates]其中,对于复制组中的每个远程设备,不规则的全到全通信可能会向同一远程设备发送最多num_updates个更新(每个更新具有不同的偏移量)。
例如:
for (remote_device_id : replica_group) {
for (update_idx : num_updates) {
SEND input[input_offsets[remote_device_id][update_idx]],
output[output_offsets[remote_device_id][update_idx]]],
send_sizes[remote_device_id][update_idx] } }
且
另请参阅 XlaBuilder::And。
对两个张量 lhs 和 rhs 执行按元素 AND 运算。
And(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 And,存在一种支持不同维度广播的替代变体:
And(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO -。
异步
另请参阅 HloInstruction::CreateAsyncStart、HloInstruction::CreateAsyncUpdate、HloInstruction::CreateAsyncDone。
AsyncDone、AsyncStart 和 AsyncUpdate 是用于异步操作的内部 HLO 指令,在 HLO 中充当基元。这些操作可能会出现在 HLO 转储中,但最终用户不应手动构建它们。
Atan2
另请参阅 XlaBuilder::Atan2。
对 lhs 和 rhs 执行逐元素 atan2 运算。
Atan2(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Atan2,存在一种具有不同维度广播支持的替代变体:
Atan2(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - atan2。
BatchNormGrad
如需详细了解该算法,另请参阅 XlaBuilder::BatchNormGrad 和原始的批次归一化论文。
计算批次归一化的梯度。
BatchNormGrad(operand, scale, batch_mean, batch_var, grad_output, epsilon,
feature_index)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp | 要归一化的 n 维数组 (x) |
scale |
XlaOp | 1 维数组 (\(\gamma\)) |
batch_mean |
XlaOp | 1 维数组 (\(\mu\)) |
batch_var |
XlaOp | 1 维数组 (\(\sigma^2\)) |
grad_output |
XlaOp | 传递给 BatchNormTraining 的梯度 (\(\nabla y\)) |
epsilon |
float |
Epsilon 值 (\(\epsilon\)) |
feature_index |
int64 |
operand 中特征维度的索引 |
对于特征维度中的每个特征(feature_index 是 operand 中特征维度的索引),该操作会计算相对于 operand、offset 和 scale 的梯度(跨所有其他维度)。feature_index 必须是 operand 中特征维度的有效索引。
这三个梯度由以下公式定义(假设 4 维数组为 operand,特征维度指数为 l,批次大小为 m,空间大小为 w 和 h):
\[ \begin{split} c_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sigma^2_l+\epsilon} \right) \\\\ d_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \\\\ \nabla x_{ijkl} &= \frac{\gamma_{l} }{\sqrt{\sigma^2_{l}+\epsilon} } \left( \nabla y_{ijkl} - d_l - c_l (x_{ijkl} - \mu_{l}) \right) \\\\ \nabla \gamma_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sqrt{\sigma^2_{l}+\epsilon} } \right) \\\\\ \nabla \beta_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \end{split} \]
输入 batch_mean 和 batch_var 表示批次和空间维度上的矩值。
输出类型是包含三个句柄的元组:
| 输出 | 类型 | 语义 |
|---|---|---|
grad_operand
|
XlaOp | 相对于输入 operand 的梯度(\(\nabla x\)) |
grad_scale
|
XlaOp | 相对于输入 **scale ** 的梯度 (\(\nabla\gamma\)) |
grad_offset
|
XlaOp | 相对于输入offset(\(\nabla\beta\)) 的梯度 |
如需了解 StableHLO,请参阅 StableHLO - batch_norm_grad。
BatchNormInference
如需详细了解该算法,另请参阅 XlaBuilder::BatchNormInference 和原始的批次归一化论文。
跨批次和空间维度对数组进行归一化。
BatchNormInference(operand, scale, offset, mean, variance, epsilon,
feature_index)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp | 要归一化的 n 维数组 |
scale |
XlaOp | 一维数组 |
offset |
XlaOp | 一维数组 |
mean |
XlaOp | 一维数组 |
variance |
XlaOp | 一维数组 |
epsilon |
float |
Epsilon 值 |
feature_index |
int64 |
operand 中特征维度的索引 |
对于特征维度中的每个特征(feature_index 是 operand 中特征维度的索引),该操作会计算所有其他维度上的平均值和方差,并使用这些平均值和方差来归一化 operand 中的每个元素。feature_index 必须是 operand 中特征维度的有效索引。
BatchNormInference 等效于调用 BatchNormTraining,但不会为每个批次计算 mean 和 variance。它会改用输入 mean 和 variance 作为估计值。此操作的目的是减少推理延迟,因此命名为 BatchNormInference。
输出是一个 n 维归一化数组,其形状与输入 operand 相同。
如需了解 StableHLO,请参阅 StableHLO - batch_norm_inference。
BatchNormTraining
如需详细了解该算法,另请参阅 XlaBuilder::BatchNormTraining 和 the original batch normalization paper。
跨批次和空间维度对数组进行归一化。
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
要归一化的 n 维数组 (x) |
scale |
XlaOp |
1 维数组 (\(\gamma\)) |
offset |
XlaOp |
1 维数组 (\(\beta\)) |
epsilon |
float |
Epsilon 值 (\(\epsilon\)) |
feature_index |
int64 |
operand 中特征维度的索引 |
对于特征维度中的每个特征(feature_index 是 operand 中特征维度的索引),该操作会计算所有其他维度上的平均值和方差,并使用这些平均值和方差来归一化 operand 中的每个元素。feature_index 必须是 operand 中特征维度的有效索引。
对于 operand \(x\) 中的每个批次(包含 m 个元素,空间维度的大小为 w 和 h,假设 operand 是一个 4 维数组),该算法的运行方式如下:
计算特征维度中每个特征
l的批次平均值 \(\mu_l\) :\(\mu_l=\frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h x_{ijkl}\)计算批次方差 \(\sigma^2_l\):$\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
归一化、缩放和平移: \(y_{ijkl}=\frac{\gamma_l(x_{ijkl}-\mu_l)}{\sqrt[2]{\sigma^2_l+\epsilon} }+\beta_l\)
添加 epsilon 值(通常是一个较小的数字)是为了避免出现除以零错误。
输出类型是包含三个 XlaOp 的元组:
| 输出 | 类型 | 语义 |
|---|---|---|
output
|
XlaOp
|
与输入 operand (y) 具有相同形状的 n 维数组 |
batch_mean |
XlaOp |
1 维数组 (\(\mu\)) |
batch_var |
XlaOp |
1 维数组 (\(\sigma^2\)) |
batch_mean 和 batch_var 是使用上述公式在批次维度和空间维度上计算出的矩。
如需了解 StableHLO,请参阅 StableHLO - batch_norm_training。
Bitcast
另请参阅 HloInstruction::CreateBitcast。
Bitcast 可能会出现在 HLO 转储中,但最终用户不应手动构建它们。
BitcastConvertType
另请参阅 XlaBuilder::BitcastConvertType。
与 TensorFlow 中的 tf.bitcast 类似,执行从数据形状到目标形状的逐元素位转换操作。输入和输出大小必须一致:例如,s32 元素通过 bitcast 例程变为 f32 元素,一个 s32 元素将变为四个 s8 元素。Bitcast 是作为低级转换实现的,因此具有不同浮点表示的机器会给出不同的结果。
BitcastConvertType(operand, new_element_type)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
具有维度 D 的 T 类型数组 |
new_element_type |
PrimitiveType |
U 型 |
操作数和目标形状的维度必须一致,但最后一个维度除外,该维度将根据转换前后原型的尺寸比发生变化。
源元素类型和目标元素类型不得为元组。
如需了解 StableHLO,请参阅 StableHLO - bitcast_convert。
以不同宽度转换为基元类型的 Bitcast
BitcastConvert HLO 指令支持输出元素类型 T' 的大小不等于输入元素 T 的大小的情况。由于整个操作在概念上是位广播,不会更改底层字节,因此输出元素的形状必须发生变化。对于 B = sizeof(T), B' =
sizeof(T'),可能存在两种情况。
首先,当 B > B' 时,输出形状会获得一个大小为 B/B' 的新最次要维度。例如:
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
有效标量的规则保持不变:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
或者,对于 B' > B,该指令要求输入形状的最后一个逻辑维度等于 B'/B,并且在转换期间会舍弃此维度:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
请注意,不同位宽之间的转换不是按元素进行的。
广播
另请参阅 XlaBuilder::Broadcast。
通过复制数组中的数据,向数组添加维度。
Broadcast(operand, broadcast_sizes)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
要复制的数组 |
broadcast_sizes |
ArraySlice<int64> |
新维度的大小 |
新维度会插入到左侧,也就是说,如果 broadcast_sizes 的值为 {a0, ..., aN},而操作数形状的维度为 {b0, ..., bM},那么输出的形状维度为 {a0, ..., aN, b0, ..., bM}。
新维度会索引到操作数的副本中,即
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
例如,如果 operand 是值为 2.0f 的标量 f32,且 broadcast_sizes 为 {2, 3},则结果将是一个形状为 f32[2, 3] 的数组,并且结果中的所有值都将为 2.0f。
如需了解 StableHLO,请参阅 StableHLO - 广播。
BroadcastInDim
另请参阅 XlaBuilder::BroadcastInDim。
通过复制数组中的数据来扩大数组的大小和维度数量。
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
要复制的数组 |
out_dim_size
|
ArraySlice<int64>
|
目标形状的维度大小 |
broadcast_dimensions
|
ArraySlice<int64>
|
操作数形状的每个维度对应于目标形状中的哪个维度 |
与广播类似,但允许在任意位置添加维度,并扩展大小为 1 的现有维度。
operand 会广播到 out_dim_size 所描述的形状。
broadcast_dimensions 将 operand 的维度映射到目标形状的维度,即运算数的第 i 个维度映射到输出形状的 broadcast_dimension[i] 个维度。operand 的维度必须具有大小 1,或者与它们映射到的输出形状中的维度大小相同。其余维度会填充大小为 1 的维度。然后,退化维度广播会沿着这些退化维度进行广播,以达到输出形状。如需详细了解语义,请参阅广播页面。
致电
另请参阅 XlaBuilder::Call。
使用给定的实参调用计算。
Call(computation, operands...)
| 参数 | 类型 | 语义 |
|---|---|---|
computation
|
XlaComputation
|
具有任意类型 N 个形参的 T_0, T_1, ...,
T_{N-1} -> S 类型计算 |
operands |
N 个 XlaOp 的序列 |
N 个任意类型的实参 |
operands 的元数和类型必须与 computation 的形参相匹配。允许没有 operands。
CompositeCall
另请参阅 XlaBuilder::CompositeCall。
封装了由其他 StableHLO 操作组成的(复合)操作,该操作接受输入和 composite_attributes 并生成结果。相应运算的语义由分解属性实现。复合操作可以替换为其分解,而不会改变程序语义。如果内嵌分解无法提供相同的运算语义,则最好使用 custom_call。
版本字段(默认为 0)用于表示复合语义何时发生变化。
此操作实现为具有属性 is_composite=true 的 kCall。decomposition 字段由 computation 属性指定。前端属性存储以 composite. 为前缀的其余属性。
CompositeCall 操作示例:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
CompositeCall(computation, operands..., name, attributes, version)
| 参数 | 类型 | 语义 |
|---|---|---|
computation
|
XlaComputation
|
具有任意类型 N 个形参的 T_0, T_1, ...,
T_{N-1} -> S 类型计算 |
operands |
N 个 XlaOp 的序列 |
可变数量的值 |
name |
string |
复合的名称 |
attributes
|
可选 string
|
可选的属性字符串化字典 |
version
|
可选 int64
|
数到版本更新到复合操作的语义 |
相应操作的 decomposition 不是调用的字段,而是显示为指向包含较低级别实现的函数的 to_apply 属性,即 to_apply=%funcname
如需详细了解组合和分解,请参阅 StableHLO 规范。
Cbrt
另请参阅 XlaBuilder::Cbrt。
元素级立方根运算 x -> cbrt(x)。
Cbrt(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Cbrt 还支持可选的 result_accuracy 实参:
Cbrt(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
如需了解 StableHLO 信息,请参阅 StableHLO - cbrt。
向上取整
另请参阅 XlaBuilder::Ceil。
按元素取上限 x -> ⌈x⌉。
Ceil(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
如需了解 StableHLO,请参阅 StableHLO - ceil。
Cholesky
另请参阅 XlaBuilder::Cholesky。
计算一批对称(Hermitian)正定矩阵的 Cholesky 分解。
Cholesky(a, lower)
| 参数 | 类型 | 语义 |
|---|---|---|
a
|
XlaOp
|
一种具有 2 个以上维度且类型为复数或浮点数的数组。 |
lower |
bool |
是否使用 a 的上三角或下三角。 |
如果 lower 为 true,则计算下三角矩阵 l,使 $a = l .
l^T$。如果 lower 为 false,则计算上三角矩阵 u,使得\(a = u^T . u\)。
输入数据仅从 a 的下/上三角读取,具体取决于 lower 的值。系统会忽略另一个三角形中的值。输出数据在同一三角形中返回;另一三角形中的值由实现定义,可以是任何值。
如果 a 的维度大于 2,则 a 会被视为一批矩阵,其中除了次要的 2 个维度之外,所有维度都是批次维度。
如果 a 不是对称(Hermitian)正定矩阵,则结果由实现定义。
如需了解 StableHLO 信息,请参阅 StableHLO - cholesky。
限制取值范围
另请参阅 XlaBuilder::Clamp。
将操作数限制在最小值和最大值之间的范围内。
Clamp(min, operand, max)
| 参数 | 类型 | 语义 |
|---|---|---|
min |
XlaOp |
类型为 T 的数组 |
operand |
XlaOp |
类型为 T 的数组 |
max |
XlaOp |
类型为 T 的数组 |
给定一个操作数以及最小值和最大值,如果操作数在最小值和最大值之间的范围内,则返回该操作数;否则,如果操作数低于此范围,则返回最小值;如果操作数高于此范围,则返回最大值。即 clamp(a, x, b) = min(max(a, x), b)。
这三个数组必须具有相同的形状。或者,作为一种受限形式的广播,min 和/或 max 可以是 T 类型的标量。
包含标量 min 和 max 的示例:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
如需了解 StableHLO,请参阅 StableHLO - clamp。
收起
另请参阅 XlaBuilder::Collapse。
以及 tf.reshape 操作。
将数组的维度折叠为一个维度。
Collapse(operand, dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
类型为 T 的数组 |
dimensions |
int64 vector |
T 的维度按顺序排列的连续子集。 |
Collapse 将操作数给定子集的维度替换为单个维度。输入实参是任意类型的数组 T 和维度索引的编译时常量向量。维度指数必须是 T 的维度的有序(从低到高维度编号)连续子集。因此,{0, 1, 2}、{0, 1} 或 {1, 2} 都是有效的维度集,但 {1, 0} 或 {0, 2} 不是。它们会被一个新维度取代,该新维度在维度序列中的位置与被取代的维度相同,且新维度的大小等于原始维度大小的乘积。dimensions 中最低的维度编号是循环嵌套中变化最慢(最主要)的维度,这些维度会折叠,而最高的维度编号是变化最快(最次要)的维度。如果需要更通用的折叠顺序,请参阅 tf.reshape 运算符。
例如,假设 v 是一个包含 24 个元素的数组:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
Clz
另请参阅 XlaBuilder::Clz。
按元素计算前导零。
Clz(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
CollectiveBroadcast
另请参阅 XlaBuilder::CollectiveBroadcast。
跨副本广播数据。数据会从每个组中的第一个副本 ID 发送到同一组中的其他 ID。如果某个副本 ID 不在任何副本组中,则相应副本上的输出是 shape 中包含 0 的张量。
CollectiveBroadcast(operand, replica_groups, channel_id)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
replica_groups
|
ReplicaGroupvector
|
每个组都包含一个副本 ID 列表 |
channel_id
|
可选 ChannelHandle
|
每个发送/接收对的唯一标识符 |
如需了解 StableHLO,请参阅 StableHLO - collective_broadcast。
CollectivePermute
另请参阅 XlaBuilder::CollectivePermute。
CollectivePermute 是一种集体操作,可在各个副本之间发送和接收数据。
CollectivePermute(operand, source_target_pairs, channel_id, inplace)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
n 维输入数组 |
source_target_pairs
|
<int64, int64> vector
|
(source_replica_id, target_replica_id) 对的列表。 对于每对,操作数都会从源副本发送到目标副本。 |
channel_id
|
可选 ChannelHandle
|
用于跨模块通信的可选渠道 ID |
inplace
|
可选 bool
|
标志是否应就地进行排列 |
请注意,source_target_pairs 存在以下限制:
- 任意两个配对不应具有相同的目标副本 ID,也不应具有相同的源副本 ID。
- 如果某个副本 ID 不是任何配对中的目标,则相应副本上的输出是一个由 0 组成的张量,其形状与输入相同。
CollectivePermute 操作的 API 在内部分解为 2 个 HLO 指令(CollectivePermuteStart 和 CollectivePermuteDone)。
另请参阅 HloInstruction::CreateCollectivePermuteStart。
CollectivePermuteStart 和 CollectivePermuteDone 在 HLO 中充当基元。
这些操作可能会出现在 HLO 转储中,但最终用户不应手动构建它们。
如需了解 StableHLO,请参阅 StableHLO - collective_permute。
比较
另请参阅 XlaBuilder::Compare。
按元素对 lhs 和 rhs 执行以下比较:
Eq
另请参阅 XlaBuilder::Eq。
对 lhs 和 rhs 执行逐元素 等于比较。
\(lhs = rhs\)
Eq(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Eq,存在一种具有不同维度广播支持的替代变体:
Eq(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
通过强制执行以下条件,支持浮点数上的总顺序(针对 Eq):
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
EqTotalOrder(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
如需了解 StableHLO,请参阅 StableHLO - 比较。
Ne
另请参阅 XlaBuilder::Ne。
对 lhs 和 rhs 执行逐元素不等于比较。
\(lhs != rhs\)
Ne(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Ne,存在一种支持不同维度广播的替代变体:
Ne(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
通过强制执行以下操作,支持 Ne 的浮点数总订单:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
NeTotalOrder(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
如需了解 StableHLO,请参阅 StableHLO - 比较。
Ge
另请参阅 XlaBuilder::Ge。
对 lhs 和 rhs 执行逐元素greater-or-equal-than比较。
\(lhs >= rhs\)
Ge(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Ge,存在一种具有不同维度广播支持的替代变体:
Ge(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
通过强制执行以下条件,支持对 Gt 的浮点数进行全序比较:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
GtTotalOrder(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
如需了解 StableHLO,请参阅 StableHLO - 比较。
Gt
另请参阅 XlaBuilder::Gt。
对 lhs 和 rhs 执行逐元素的大于比较。
\(lhs > rhs\)
Gt(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Gt,存在一种具有不同维度广播支持的替代变体:
Gt(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - 比较。
Le
另请参阅 XlaBuilder::Le。
对 lhs 和 rhs 执行逐元素less-or-equal-than比较。
\(lhs <= rhs\)
Le(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Le,存在一种支持不同维度广播的替代变体:
Le(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
通过强制执行以下操作,支持 Le 的浮点数总订单:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LeTotalOrder(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
如需了解 StableHLO,请参阅 StableHLO - 比较。
Lt
另请参阅 XlaBuilder::Lt。
对 lhs 和 rhs 执行逐元素小于比较。
\(lhs < rhs\)
Lt(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Lt,存在一种支持不同维度广播的替代变体:
Lt(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
通过强制执行以下操作,支持总订单数大于浮点数(对于 Lt):
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LtTotalOrder(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
如需了解 StableHLO,请参阅 StableHLO - 比较。
复杂
另请参阅 XlaBuilder::Complex。
根据实数值和虚数值对 lhs 和 rhs 执行逐元素转换,以生成复数值。
Complex(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于复数,存在支持不同维度广播的替代变体:
Complex(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - 复杂。
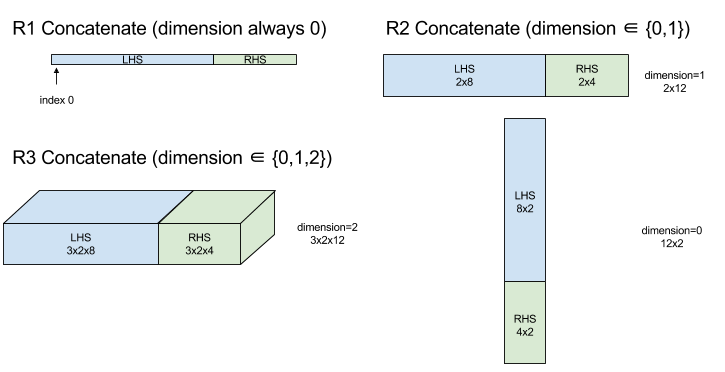
ConcatInDim(串联)
另请参阅 XlaBuilder::ConcatInDim。
Concatenate 从多个数组运算对象中组成一个数组。该数组的维度数与每个输入数组实参(必须具有相同的维度数)的维度数相同,并且包含按指定顺序排列的实参。
Concatenate(operands..., dimension)
| 参数 | 类型 | 语义 |
|---|---|---|
operands
|
N 个 XlaOp 的序列
|
维度为 [L0, L1, ...] 的 N 个类型为 T 的数组。要求 N >= 1。 |
dimension
|
int64
|
区间 [0, N) 中的一个值,用于指定要串联的维度(介于 operands 之间)。 |
除了 dimension 之外,所有维度都必须相同。这是因为 XLA 不支持“不规则”数组。另请注意,无法串联 0 维值(因为无法命名串联发生的维度)。
1 维示例:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
//Output: {2, 3, 4, 5, 6, 7}
二维示例:
let a = { {1, 2},
{3, 4},
{5, 6} };
let b = { {7, 8} };
Concat({a, b}, 0)
//Output: { {1, 2},
// {3, 4},
// {5, 6},
// {7, 8} }
图表:
如需了解 StableHLO,请参阅 StableHLO - 连接。
基于条件
另请参阅 XlaBuilder::Conditional。
Conditional(predicate, true_operand, true_computation, false_operand,
false_computation)
| 参数 | 类型 | 语义 |
|---|---|---|
predicate |
XlaOp |
类型为 PRED 的标量 |
true_operand |
XlaOp |
类型为 \(T_0\)的实参 |
true_computation |
XlaComputation |
类型为 \(T_0 \to S\)的 XlaComputation |
false_operand |
XlaOp |
类型为 \(T_1\)的实参 |
false_computation |
XlaComputation |
类型为 \(T_1 \to S\)的 XlaComputation |
如果 predicate 为 true,则执行 true_computation;如果 predicate 为 false,则执行 false_computation,并返回结果。
true_computation 必须接受类型为 \(T_0\) 的单个实参,并且将使用 true_operand(必须是同一类型)进行调用。false_computation 必须接受类型为 \(T_1\) 的单个实参,并且将使用 false_operand(必须是同一类型)进行调用。true_computation 和 false_computation 的返回值类型必须相同。
请注意,系统只会执行 true_computation 和 false_computation 中的一个,具体取决于 predicate 的值。
Conditional(branch_index, branch_computations, branch_operands)
| 参数 | 类型 | 语义 |
|---|---|---|
branch_index |
XlaOp |
类型为 S32 的标量 |
branch_computations |
N 个 XlaComputation 的序列 |
类型为 \(T_0 \to S , T_1 \to S , ..., T_{N-1} \to S\)的 XlaComputation |
branch_operands |
N 个 XlaOp 的序列 |
类型为 \(T_0 , T_1 , ..., T_{N-1}\)的实参 |
执行 branch_computations[branch_index],并返回结果。如果 branch_index 是小于 0 或大于等于 N 的 S32,则执行 branch_computations[N-1] 作为默认分支。
每个 branch_computations[b] 都必须接受一个类型为 \(T_b\) 的实参,并使用 branch_operands[b](必须是相同类型)进行调用。每个 branch_computations[b] 的返回值类型必须相同。
请注意,系统将根据 branch_index 的值仅执行其中一个 branch_computations。
如需了解 StableHLO,请参阅 StableHLO - if。
常量
另请参阅 XlaBuilder::ConstantLiteral。
从常量 literal 生成 output。
Constant(literal)
| 参数 | 类型 | 语义 |
|---|---|---|
literal |
LiteralSlice |
现有 Literal 的常量视图 |
如需了解 StableHLO,请参阅 StableHLO - 常量。
ConvertElementType
另请参阅 XlaBuilder::ConvertElementType。
与 C++ 中的逐元素 static_cast 类似,ConvertElementType 会执行从数据形状到目标形状的逐元素转换操作。维度必须一致,并且转换是逐元素的;例如,s32 个元素通过 s32 到 f32 的转换例程变为 f32 个元素。
ConvertElementType(operand, new_element_type)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
具有维度 D 的 T 类型数组 |
new_element_type |
PrimitiveType |
U 型 |
操作数的维度必须与目标形状一致。源元素类型和目标元素类型不得为元组。
从 T=s32 到 U=f32 的转换将执行归一化 int 到 float 的转换例程,例如最近舍入到偶数。
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
如需了解 StableHLO,请参阅 StableHLO - 转换。
Conv(卷积)
另请参阅 XlaBuilder::Conv。
计算神经网络中使用的卷积。在这里,卷积可以看作是一个 n 维窗口在 n 维基本区域上移动,并针对窗口的每个可能位置执行计算。
Conv 将卷积指令排入计算队列,该指令使用默认的卷积维度编号,且不进行扩张。
填充以简写方式指定为 SAME 或 VALID。SAME 填充会用零填充输入 (lhs),以便在不考虑步幅的情况下,输出与输入具有相同的形状。VALID 填充只是意味着没有填充。
Conv(lhs, rhs, window_strides, padding, feature_group_count,
batch_group_count, precision_config, preferred_element_type)
| 参数 | 类型 | 语义 |
|---|---|---|
lhs
|
XlaOp
|
(n+2) 维输入数组 |
rhs
|
XlaOp
|
内核权重的 (n+2) 维数组 |
window_strides |
ArraySlice<int64> |
n 维内核步幅数组 |
padding |
Padding |
填充枚举 |
feature_group_count
|
int64 | 特征组的数量 |
batch_group_count |
int64 | 批次组的数量 |
precision_config
|
可选
PrecisionConfig |
精确度枚举 |
preferred_element_type
|
可选
PrimitiveType |
标量元素类型的枚举 |
Conv 提供以下不同程度的控制:
假设 n 为空间维度的数量。lhs 实参是一个 (n+2) 维数组,用于描述基本面积。这称为输入,尽管当然 rhs 也是输入。在神经网络中,这些是输入激活。n+2 个维度按以下顺序排列:
batch:此维度中的每个坐标都表示一个独立的输入,将针对该输入执行卷积。z/depth/features:基础区域中的每个 (y,x) 位置都关联有一个向量,该向量会进入此维度。spatial_dims:描述定义窗口移动所跨越的基本区域的n空间维度。
rhs 实参是一个 (n+2) 维数组,用于描述卷积滤波器/内核/窗口。维度按以下顺序排列:
output-z:输出的z维度。input-z:此维度的大小乘以feature_group_count应等于左侧z维度的大小。spatial_dims:描述定义在基本区域上移动的 n 维窗口的n空间维度。
window_strides 实参用于指定卷积窗口在空间维度上的步幅。例如,如果第一个空间维度中的步幅为 3,则窗口只能放置在第一个空间指数可被 3 整除的坐标处。
padding 实参用于指定要应用于基本区域的零填充量。填充量可以为负值,负填充的绝对值表示在进行卷积之前要从指定维度中移除的元素数量。padding[0] 用于指定维度 y 的填充,padding[1] 用于指定维度 x 的填充。每个对组的第一个元素是低内边距,第二个元素是高内边距。低边衬区应用于较低索引的方向,而高边衬区应用于较高索引的方向。例如,如果 padding[1] 为 (2,3),则在第二个空间维度中,左侧将填充 2 个零,右侧将填充 3 个零。使用填充相当于在进行卷积之前将这些相同的零值插入到输入 (lhs) 中。
lhs_dilation 和 rhs_dilation 实参分别指定要应用于左侧和右侧的扩张系数(在每个空间维度中)。如果空间维度中的扩张率为 d,则在该维度中,每个条目之间会隐式放置 d-1 个空洞,从而增加数组的大小。这些空洞会填充一个空操作值,对于卷积而言,这意味着填充零。
右侧的扩张也称为空洞卷积。如需了解详情,请参阅 tf.nn.atrous_conv2d。左侧的扩张也称为转置卷积。如需了解详情,请参阅 tf.nn.conv2d_transpose。
feature_group_count 实参(默认值为 1)可用于分组卷积。feature_group_count 需要是输入和输出特征维度的除数。如果 feature_group_count 大于 1,则表示从概念上讲,输入和输出特征维度以及 rhs 输出特征维度会均匀拆分为多个 feature_group_count 组,每组包含一个连续的特征子序列。rhs 的输入特征维度需要等于 lhs 输入特征维度除以 feature_group_count(因此它已经具有一组输入特征的大小)。第 i 个组一起用于计算多个单独卷积的 feature_group_count。这些卷积的结果会串联在一起,形成输出特征维度。
对于深度可分离卷积,feature_group_count 实参将设置为输入特征维度,并且滤镜将从 [filter_height, filter_width, in_channels, channel_multiplier] 重塑为 [filter_height, filter_width, 1, in_channels * channel_multiplier]。如需了解详情,请参阅 tf.nn.depthwise_conv2d。
batch_group_count(默认值为 1)实参可用于反向传播期间的分组过滤。batch_group_count 必须是 lhs(输入)批次维度大小的除数。如果 batch_group_count 大于 1,则表示输出批次维度的大小应为 input batch
/ batch_group_count。batch_group_count 必须是输出特征大小的除数。
输出形状具有以下维度(按此顺序):
batch:此维度的大小乘以batch_group_count应等于左侧实参中batch维度的大小。z:与内核上的output-z大小相同 (rhs)。spatial_dims:每个有效的卷积窗口放置位置对应一个值。
上图显示了 batch_group_count 字段的运作方式。实际上,我们将每个左侧批次切分为 batch_group_count 个组,并对输出特征执行相同的操作。然后,我们对每个组进行成对卷积,并沿输出特征维度串联输出。所有其他维度(特征和空间)的运行语义保持不变。
卷积窗口的有效放置位置由步幅和填充后的基本区域大小决定。
为了描述卷积的作用,我们以 2D 卷积为例,并在输出中选择一些固定的 batch、z、y、x 坐标。然后,(y,x) 是窗口在基本区域内的某个角的位置(例如左上角,具体取决于您如何解读空间维度)。现在,我们有了一个从基本区域提取的二维窗口,其中每个二维点都与一个一维向量相关联,因此我们得到了一个三维框。从卷积核来看,由于我们固定了输出坐标 z,因此我们也有一个 3D 框。这两个框的维度相同,因此我们可以计算这两个框之间对应元素的乘积之和(类似于点积)。这就是输出值。
请注意,如果 output-z 是例如 5,则窗口的每个位置都会在输出的 z 维度中生成 5 个值。这些值的不同之处在于所使用的卷积核部分不同 - 每个 output-z 坐标都使用一个单独的 3D 值框。因此,您可以将其视为 5 个单独的卷积,每个卷积都有不同的滤镜。
以下是具有填充和步幅的 2D 卷积的伪代码:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
precision_config 用于指示精度配置。该级别决定了硬件是否应尝试生成更多机器代码指令,以便在需要时提供更准确的 dtype 模拟(即在仅支持 bf16 matmul 的 TPU 上模拟 f32)。值可以是 DEFAULT、HIGH、HIGHEST。MXU 部分中的其他详细信息。
preferred_element_type 是一种用于累积的更高/更低精度输出类型的标量元素。preferred_element_type 建议为指定操作使用累积类型,但无法保证。这样一来,某些硬件后端就可以先以其他类型累积,然后再转换为首选输出类型。
如需了解 StableHLO,请参阅 StableHLO - 卷积。
ConvWithGeneralPadding
另请参阅 XlaBuilder::ConvWithGeneralPadding。
ConvWithGeneralPadding(lhs, rhs, window_strides, padding,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
与 Conv 相同,其中填充配置是显式的。
| 参数 | 类型 | 语义 |
|---|---|---|
lhs
|
XlaOp
|
(n+2) 维输入数组 |
rhs
|
XlaOp
|
内核权重的 (n+2) 维数组 |
window_strides |
ArraySlice<int64> |
n 维内核步幅数组 |
padding
|
ArraySlice<
pair<int64,int64>> |
(low, high) 填充的 n 维数组 |
feature_group_count
|
int64 | 特征组的数量 |
batch_group_count |
int64 | 批次组的数量 |
precision_config
|
可选
PrecisionConfig |
精确度枚举 |
preferred_element_type
|
可选
PrimitiveType |
标量元素类型的枚举 |
ConvWithGeneralDimensions
另请参阅 XlaBuilder::ConvWithGeneralDimensions。
ConvWithGeneralDimensions(lhs, rhs, window_strides, padding,
dimension_numbers, feature_group_count, batch_group_count, precision_config,
preferred_element_type)
与 Conv 相同,其中维度编号是明确的。
| 参数 | 类型 | 语义 |
|---|---|---|
lhs
|
XlaOp
|
(n+2) 维输入数组 |
rhs
|
XlaOp
|
(n+2) 维的内核权重数组 |
window_strides
|
ArraySlice<int64>
|
内核步长的 n 维数组 |
padding |
Padding |
填充枚举 |
dimension_numbers
|
ConvolutionDimensionNumbers
|
维度数量 |
feature_group_count
|
int64 | 特征组的数量 |
batch_group_count
|
int64 | 批次组的数量 |
precision_config
|
可选 PrecisionConfig
|
表示精确度级别的枚举 |
preferred_element_type
|
可选 PrimitiveType
|
标量元素类型的枚举 |
ConvGeneral
另请参阅 XlaBuilder::ConvGeneral。
ConvGeneral(lhs, rhs, window_strides, padding, dimension_numbers,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
与 Conv 相同,其中维度编号和填充配置是明确的
| 参数 | 类型 | 语义 |
|---|---|---|
lhs
|
XlaOp
|
(n+2) 维输入数组 |
rhs
|
XlaOp
|
(n+2) 维的内核权重数组 |
window_strides
|
ArraySlice<int64>
|
内核步长的 n 维数组 |
padding
|
ArraySlice<
pair<int64,int64>>
|
(low, high) 内边距的 n 维数组 |
dimension_numbers
|
ConvolutionDimensionNumbers
|
维度数量 |
feature_group_count
|
int64 | 特征组的数量 |
batch_group_count
|
int64 | 批次组的数量 |
precision_config
|
可选 PrecisionConfig
|
表示精确度级别的枚举 |
preferred_element_type
|
可选 PrimitiveType
|
标量元素类型的枚举 |
ConvGeneralDilated
另请参阅 XlaBuilder::ConvGeneralDilated。
ConvGeneralDilated(lhs, rhs, window_strides, padding, lhs_dilation,
rhs_dilation, dimension_numbers, feature_group_count, batch_group_count,
precision_config, preferred_element_type, window_reversal)
与 Conv 相同,其中填充配置、扩张系数和维度数量是明确的。
| 参数 | 类型 | 语义 |
|---|---|---|
lhs
|
XlaOp
|
(n+2) 维输入数组 |
rhs
|
XlaOp
|
(n+2) 维的内核权重数组 |
window_strides
|
ArraySlice<int64>
|
内核步长的 n 维数组 |
padding
|
ArraySlice<
pair<int64,int64>>
|
(low, high) 内边距的 n 维数组 |
lhs_dilation
|
ArraySlice<int64>
|
n-d lhs 扩张系数数组 |
rhs_dilation
|
ArraySlice<int64>
|
n-d 右侧形变系数数组 |
dimension_numbers
|
ConvolutionDimensionNumbers
|
维度数量 |
feature_group_count
|
int64 | 特征组的数量 |
batch_group_count
|
int64 | 批次组的数量 |
precision_config
|
可选 PrecisionConfig
|
表示精确度级别的枚举 |
preferred_element_type
|
可选 PrimitiveType
|
标量元素类型的枚举 |
window_reversal
|
可选 vector<bool>
|
用于在应用卷积之前以逻辑方式反转维度的标志 |
复制
另请参阅 HloInstruction::CreateCopyStart。
Copy 在内部分解为 2 个 HLO 指令 CopyStart 和 CopyDone。Copy 以及 CopyStart 和 CopyDone 在 HLO 中充当基元。这些操作可能会出现在 HLO 转储中,但最终用户不应手动构建它们。
COS
另请参阅XlaBuilder::Cos。
按元素计算的余弦 x -> cos(x)。
Cos(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Cos 还支持可选的 result_accuracy 实参:
Cos(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
如需了解 StableHLO,请参阅 StableHLO - 余弦。
Cosh
另请参阅 XlaBuilder::Cosh。
按元素计算的双曲余弦 x -> cosh(x)。
Cosh(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Cosh 还支持可选的 result_accuracy 实参:
Cosh(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
CustomCall
另请参阅 XlaBuilder::CustomCall。
在计算中调用用户提供的函数。
如需查看 CustomCall 文档,请参阅开发者详细信息 - XLA 自定义调用
如需了解 StableHLO,请参阅 StableHLO - custom_call。
分组
另请参阅 XlaBuilder::Div。
对被除数 lhs 和除数 rhs 执行逐元素除法。
Div(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
整数除法溢出(有符号/无符号除法/余数为零或有符号除法/余数为 INT_SMIN 除以 -1)会产生由实现定义的值。
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Div,存在一种具有不同维度广播支持的替代变体:
Div(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - 除法。
网域
另请参阅 HloInstruction::CreateDomain。
Domain 可能会出现在 HLO 转储中,但最终用户不应手动构建它。
点
另请参阅 XlaBuilder::Dot。
Dot(lhs, rhs, precision_config, preferred_element_type)
| 参数 | 类型 | 语义 |
|---|---|---|
lhs |
XlaOp |
类型为 T 的数组 |
rhs |
XlaOp |
类型为 T 的数组 |
precision_config
|
可选
PrecisionConfig |
精确度枚举 |
preferred_element_type
|
可选
PrimitiveType |
标量元素类型的枚举 |
此操作的确切语义取决于操作数的秩:
| 输入 | 输出 | 语义 |
|---|---|---|
vector [n] dot vector [n] |
标量 | 向量点积 |
矩阵 [m x k] dot 向量 [k] |
vector [m] | 矩阵-向量乘法 |
矩阵 [m x k] dot 矩阵 [k x n] |
矩阵 [m x n] | 矩阵-矩阵乘法 |
该运算对 lhs 的第二个维度(如果 lhs 只有 1 个维度,则为第一个维度)和 rhs 的第一个维度执行乘积求和。这些是“收缩”维度。lhs 和 rhs 的缩并维度必须具有相同的大小。在实践中,它可以用于执行向量之间的点积、向量/矩阵乘法或矩阵/矩阵乘法。
precision_config 用于指示精度配置。该级别决定了硬件是否应尝试生成更多机器代码指令,以便在需要时提供更准确的 dtype 模拟(即在仅支持 bf16 matmul 的 TPU 上模拟 f32)。值可以是 DEFAULT、HIGH、HIGHEST。MXU 部分中的其他详细信息。
preferred_element_type 是一种用于累积的更高/更低精度输出类型的标量元素。preferred_element_type 建议为指定操作使用累积类型,但无法保证。这样一来,某些硬件后端就可以先以其他类型累积,然后再转换为首选输出类型。
如需了解 StableHLO,请参阅 StableHLO - 点。
DotGeneral
另请参阅 XlaBuilder::DotGeneral。
DotGeneral(lhs, rhs, dimension_numbers, precision_config,
preferred_element_type)
| 参数 | 类型 | 语义 |
|---|---|---|
lhs |
XlaOp |
类型为 T 的数组 |
rhs |
XlaOp |
类型为 T 的数组 |
dimension_numbers
|
DotDimensionNumbers
|
合同和批次维度编号 |
precision_config
|
可选
PrecisionConfig |
表示精确度级别的枚举 |
preferred_element_type
|
可选
PrimitiveType |
标量元素类型的枚举 |
与 Dot 类似,但允许为 lhs 和 rhs 指定收缩维度和批次维度编号。
| DotDimensionNumbers 字段 | 类型 | 语义 |
|---|---|---|
lhs_contracting_dimensions
|
repeated int64 | lhs 收缩维度数 |
rhs_contracting_dimensions
|
repeated int64 | rhs 收缩维度数 |
lhs_batch_dimensions
|
repeated int64 | lhs 批次维度数 |
rhs_batch_dimensions
|
repeated int64 | rhs 批次维度数 |
DotGeneral 会对 dimension_numbers 中指定的收缩维度执行乘积求和。
lhs 和 rhs 中的关联收缩维度编号不必相同,但必须具有相同的维度大小。
缩小维度数量的示例:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { { 6.0, 12.0},
{15.0, 30.0} }
lhs 和 rhs 中的关联批次维度编号必须具有相同的维度大小。
包含批次维度编号的示例(批次大小为 2,2x2 矩阵):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> {
{ {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| 输入 | 输出 | 语义 |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | 批次矩阵乘法 |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | 批次矩阵乘法 |
因此,生成的维度编号从批次维度开始,然后是 lhs 非收缩/非批次维度,最后是 rhs 非收缩/非批次维度。
precision_config 用于指示精度配置。该级别决定了硬件是否应尝试生成更多机器代码指令,以便在需要时提供更准确的 dtype 模拟(即在仅支持 bf16 matmul 的 TPU 上模拟 f32)。值可以是 DEFAULT、HIGH、HIGHEST。如需了解更多详情,请参阅 MXU 部分。
preferred_element_type 是一种用于累积的更高/更低精度输出类型的标量元素。preferred_element_type 建议为指定操作使用累积类型,但无法保证。这样一来,某些硬件后端就可以先以其他类型累积,然后再转换为首选输出类型。
如需了解 StableHLO,请参阅 StableHLO - dot_general。
ScaledDot
另请参阅 XlaBuilder::ScaledDot。
ScaledDot(lhs, lhs_scale, rhs, rhs_scale, dimension_number,
precision_config,preferred_element_type)
| 参数 | 类型 | 语义 |
|---|---|---|
lhs |
XlaOp |
类型为 T 的数组 |
rhs |
XlaOp |
类型为 T 的数组 |
lhs_scale |
XlaOp |
类型为 T 的数组 |
rhs_scale |
XlaOp |
类型为 T 的数组 |
dimension_number
|
ScatterDimensionNumbers
|
分散操作的维度编号 |
precision_config
|
PrecisionConfig
|
表示精确度级别的枚举 |
preferred_element_type
|
可选 PrimitiveType
|
标量元素类型的枚举 |
与 DotGeneral 类似。
使用操作数“lhs”“lhs_scale”“rhs”和“rhs_scale”创建一个缩放点运算,其中收缩维度和批次维度在“dimension_numbers”中指定。
RaggedDot
另请参阅 XlaBuilder::RaggedDot。
如需详细了解 RaggedDot 计算,请参阅 StableHLO - chlo.ragged_dot
DynamicReshape
另请参阅 XlaBuilder::DynamicReshape。
此操作在功能上与 reshape 相同,但结果形状是通过 output_shape 动态指定的。
DynamicReshape(operand, dim_sizes, new_size_bounds, dims_are_dynamic)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
类型为 T 的 N 维数组 |
dim_sizes |
XlaOP 的矢量 |
N 维向量大小 |
new_size_bounds |
int63 的矢量 |
N 维边界向量 |
dims_are_dynamic |
bool 的矢量 |
N 维动态 dim |
如需了解 StableHLO,请参阅 StableHLO - dynamic_reshape。
DynamicSlice
另请参阅 XlaBuilder::DynamicSlice。
DynamicSlice 会从动态 start_indices 处的输入数组中提取一个子数组。每个维度中切片的大小在 size_indices 中传递,该参数用于指定每个维度中不含端点的切片区间的端点:[start, start + size)。start_indices 的形状必须是一维的,维度大小等于 operand 的维度数。
DynamicSlice(operand, start_indices, slice_sizes)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
类型为 T 的 N 维数组 |
start_indices
|
N 个 XlaOp 的序列
|
包含每个维度的切片起始索引的 N 个标量整数的列表。 值必须大于或等于零。 |
size_indices
|
ArraySlice<int64>
|
包含每个维度的切片大小的 N 个整数的列表。 每个值都必须严格大于零,并且 start + size 必须小于或等于相应维度的大小,以避免出现环绕模维度大小的情况。 |
在执行切片之前,通过对 [1, N) 中的每个指数 i 应用以下转换来计算有效切片指数:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - slice_sizes[i])
这可确保提取的切片始终在操作数数组的范围内。如果切片在应用转换之前位于界限内,则转换不会产生任何影响。
1 维示例:
let a = {0.0, 1.0, 2.0, 3.0, 4.0};
let s = {2};
DynamicSlice(a, s, {2});
// Result: {2.0, 3.0}
二维示例:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2});
//Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
如需了解 StableHLO,请参阅 StableHLO - dynamic_slice。
DynamicUpdateSlice
另请参阅 XlaBuilder::DynamicUpdateSlice。
DynamicUpdateSlice 生成的结果是输入数组 operand 的值,其中切片 update 在 start_indices 处被覆盖。update 的形状决定了要更新的结果子数组的形状。
start_indices 的形状必须是一维的,维度大小等于 operand 的维度数。
DynamicUpdateSlice(operand, update, start_indices)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
类型为 T 的 N 维数组 |
update
|
XlaOp
|
包含切片更新的 T 类型 N 维数组。更新形状的每个维度都必须严格大于零,并且 start + update 必须小于或等于每个维度的运算数大小,以避免生成越界更新索引。 |
start_indices
|
N 个 XlaOp 的序列
|
包含每个维度的切片起始索引的 N 个标量整数的列表。 值必须大于或等于零。 |
在执行切片之前,通过对 [1, N) 中的每个指数 i 应用以下转换来计算有效切片指数:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
这样可确保更新后的切片始终在操作数数组的范围内。如果切片在应用转换之前位于界限内,则转换不会产生任何影响。
1 维示例:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s)
// Result: {0.0, 1.0, 5.0, 6.0, 4.0}
二维示例:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s)
// Result:
// { {0.0, 1.0, 2.0},
// {3.0, 12.0, 13.0},
// {6.0, 14.0, 15.0},
// {9.0, 16.0, 17.0} }
如需了解 StableHLO,请参阅 StableHLO - dynamic_update_slice。
Erf
另请参阅 XlaBuilder::Erf。
按元素计算的误差函数 x -> erf(x),其中:
\(\text{erf}(x) = \frac{2}{\sqrt{\pi} }\int_0^x e^{-t^2} \, dt\)。
Erf(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Erf 还支持可选的 result_accuracy 实参:
Erf(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
指数
另请参阅 XlaBuilder::Exp。
按元素计算的自然指数 x -> e^x。
Exp(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Exp 还支持可选的 result_accuracy 实参:
Exp(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
如需了解 StableHLO,请参阅 StableHLO - 指数。
Expm1
另请参阅 XlaBuilder::Expm1。
按元素计算的自然指数减一 x -> e^x - 1。
Expm1(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Expm1 还支持可选的 result_accuracy 实参:
Expm1(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
如需了解 StableHLO,请参阅 StableHLO - exponential_minus_one。
Fft
另请参阅 XlaBuilder::Fft。
XLA FFT 操作可针对实数和复数输入/输出实现正向和反向傅里叶转换。支持最多 3 个轴上的多维 FFT。
Fft(operand, ftt_type, fft_length)
| 参数 | 类型 | 语义 |
|---|---|---|
operand
|
XlaOp
|
要进行傅里叶转换的数组。 |
fft_type |
FftType |
请参见下表。 |
fft_length
|
ArraySlice<int64>
|
要转换的轴的时域长度。这对于 IRFFT 正确调整最内侧轴的大小尤为必要,因为 RFFT(fft_length=[16]) 的输出形状与 RFFT(fft_length=[17]) 相同。 |
FftType |
语义 |
|---|---|
FFT |
正向复数到复数 FFT。形状保持不变。 |
IFFT |
反向复数到复数 FFT。形状保持不变。 |
RFFT
|
正向实数到复数 FFT。如果 fft_length[-1] 是非零值,则最内侧轴的形状会缩减为 fft_length[-1] // 2 + 1,从而省略超出奈奎斯特频率的转换后信号的反向共轭部分。 |
IRFFT
|
逆实数到复数 FFT(即,接受复数,返回实数)。如果 fft_length[-1] 是非零值,则将最内侧轴的形状扩展为 fft_length[-1],从 1 到 fft_length[-1] // 2 + 1 条目的反向共轭推断出超出奈奎斯特频率的转换信号部分。 |
如需了解 StableHLO,请参阅 StableHLO - fft。
多维 FFT
如果提供多个 fft_length,则相当于对每个最内侧轴应用一系列 FFT 操作。请注意,对于实数到复数和复数到实数的情况,最内侧轴转换(实际上)先执行(RFFT;IRFFT 最后执行),这就是最内侧轴大小发生变化的原因。其他轴转换将为复数到复数。
实现细节
CPU FFT 由 Eigen 的 TensorFFT 提供支持。GPU FFT 使用 cuFFT。
楼层
另请参阅 XlaBuilder::Floor。
按元素取下限 x -> ⌊x⌋。
Floor(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
如需了解 StableHLO,请参阅 StableHLO - 下限。
Fusion
另请参阅 HloInstruction::CreateFusion。
Fusion 操作表示 HLO 指令,并用作 HLO 中的原语。此操作可能会出现在 HLO 转储中,但最终用户不应手动构建此操作。
收集
XLA gather 操作将输入数组的多个切片(每个切片可能具有不同的运行时偏移量)拼接在一起。
如需了解 StableHLO,请参阅 StableHLO - gather。
一般语义
另请参阅 XlaBuilder::Gather。
如需查看更直观的说明,请参阅下方的“非正式说明”部分。
gather(operand, start_indices, dimension_numbers, slice_sizes,
indices_are_sorted)
| 参数 | 类型 | 语义 |
|---|---|---|
operand
|
XlaOp
|
我们正在从中收集数据的数组。 |
start_indices
|
XlaOp
|
包含所收集切片的起始索引的数组。 |
dimension_numbers
|
GatherDimensionNumbers
|
start_indices 中“包含”起始索引的维度。如需详细说明,请参阅下文。 |
slice_sizes
|
ArraySlice<int64>
|
slice_sizes[i] 是维度 i 上切片的界限。 |
indices_are_sorted
|
bool
|
索引是否保证由调用方排序。 |
为方便起见,我们将输出数组中不在 offset_dims 中的维度标记为 batch_dims。
输出是一个具有 batch_dims.size + offset_dims.size 维度的数组。
operand.rank 必须等于 offset_dims.size 和 collapsed_slice_dims.size 的总和。此外,slice_sizes.size 必须等于 operand.rank。
如果 index_vector_dim 等于 start_indices.rank,我们会隐式地认为 start_indices 具有尾随的 1 维度(即,如果 start_indices 的形状为 [6,7] 且 index_vector_dim 为 2,那么我们会隐式地认为 start_indices 的形状为 [6,7,1])。
沿维度 i 的输出数组的边界计算方式如下:
如果
i存在于batch_dims中(即对于某个k,i等于batch_dims[k]),则从start_indices.shape中选择相应的维度界限,跳过index_vector_dim(即,如果k<index_vector_dim,则选择start_indices.shape.dims[k],否则选择start_indices.shape.dims[k+1])。如果
i存在于offset_dims中(即对于某个k,i等于offset_dims[k]),那么我们在考虑collapsed_slice_dims后,从slice_sizes中选择相应的界限(即我们选择adjusted_slice_sizes[k],其中adjusted_slice_sizes是移除了索引collapsed_slice_dims处的界限的slice_sizes)。
从形式上讲,与给定输出指数 Out 对应的操作数指数 In 的计算方式如下:
令
G= {Out[k] forkinbatch_dims}。使用G切分向量S,使得S[i] =start_indices[Combine(G,i)],其中 Combine(A, b) 将 b 插入到 A 中的位置index_vector_dim。请注意,即使G为空,此值也已明确定义:如果G为空,则S=start_indices。通过使用
start_index_map散布S,使用S在operand中创建起始索引Sin。更准确地说:Sin[start_index_map[k]] =S[k] ifk<start_index_map.size。Sin[_] =0,否则。
通过根据
collapsed_slice_dims集在Out中的偏移维度上分散索引,在operand中创建索引Oin。更准确地说:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]](如果k<offset_dims.size,remapped_offset_dims的定义见下文)。Oin[_] =0,否则。
In是Oin+Sin,其中 + 是按元素相加。
remapped_offset_dims 是一个单调函数,其定义域为 [0, offset_dims.size),值域为 [0, operand.rank) \ collapsed_slice_dims。因此,如果例如offset_dims.size 为 4,operand.rank 为 6,collapsed_slice_dims 为 {0, 2},则 remapped_offset_dims 为 {0→1、1→3、2→4、3→5}。
如果 indices_are_sorted 设置为 true,则 XLA 可以假设用户已对 start_indices 进行排序(按升序,在根据 start_index_map 分散其值之后)。如果不是,则语义由实现定义。
非正式说明和示例
简单来说,输出数组中的每个索引 Out 都对应于操作数数组中的一个元素 E,计算方式如下:
我们使用
Out中的批次维度从start_indices中查找起始索引。我们使用
start_index_map将起始索引(其大小可能小于操作数 rank)映射到operand中的“完整”起始索引。我们使用完整的起始索引动态切分出一个大小为
slice_sizes的切片。我们通过折叠
collapsed_slice_dims维度来重塑切片。 由于所有折叠切片维度都必须具有 1 的边界,因此这种重塑始终是合法的。我们使用
Out中的偏移维度来索引此切片,以获取与输出索引Out对应的输入元素E。
在以下所有示例中,index_vector_dim 都设置为 start_indices.rank - 1。更复杂的 index_vector_dim 值不会从根本上改变运算,但会使视觉呈现更加繁琐。
为了直观了解上述所有内容如何结合在一起,我们来看一个示例,该示例从 [16,11] 数组中收集 5 个形状为 [8,6] 的切片。切片在 [16,11] 数组中的位置可以表示为形状为 S64[2] 的索引向量,因此 5 个位置的集合可以表示为 S64[5,2] 数组。
然后,可以按如下方式将收集操作的行为描述为一种索引转换,该转换接受 [G,O0,O1](输出形状中的索引),并将其映射到输入数组中的元素:
我们首先使用 G 从收集索引数组中选择一个 (X,Y) 向量。输出数组中索引为 [G,O0,O1] 的元素随后会成为输入数组中索引为 [X+O0,Y+O1] 的元素。
slice_sizes 为 [8,6],用于确定 O0 和 O1 的范围,进而确定切片的边界。
此收集操作充当以 G 为批次维度的批次动态切片。
收集的索引可以是多维的。例如,上述示例的更通用版本使用形状为 [4,5,2] 的“收集索引”数组,会将索引转换为如下形式:
同样,这会充当批次动态切片 G0 和 G1(作为批次维度)。切片大小仍为 [8,6]。
XLA 中的收集操作通过以下方式概括了上述非正式语义:
我们可以配置输出形状中的哪些维度是偏移维度(包含最后一个示例中的
O0、O1)。输出批次维度(包含G0、G1的维度,如最后一个示例所示)定义为非偏移维度的输出维度。输出形状中明确存在的输出偏移维度数量可能小于输入维度数量。这些明确列为
collapsed_slice_dims的“缺失”维度必须具有1的切片大小。由于它们的切片大小为1,因此唯一有效的索引是0,省略它们不会造成歧义。从“Gather Indices”数组中提取的切片(最后一个示例中的 (
X,Y))的元素数量可能少于输入数组的维度数量,并且显式映射会规定应如何扩展索引,使其具有与输入相同的维度数量。
作为最后一个示例,我们使用 (2) 和 (3) 来实现 tf.gather_nd:
G0 和 G1 用于像往常一样从收集索引数组中切分出起始索引,只不过起始索引只有一个元素 X。同样,只有一个输出偏移量指数,其值为 O0。不过,在用作输入数组的索引之前,这些索引会根据“Gather Index Mapping”(正式说明中的 start_index_map)和“Offset Mapping”(正式说明中的 remapped_offset_dims)分别扩展为 [X,0] 和 [0,O0],总共为 [X,O0]。换句话说,输出索引 [G0,G1,O0] 会映射到输入索引 [GatherIndices[G0,G1,0],O0],这为 tf.gather_nd 提供了语义。
此情形下的 slice_sizes 为 [1,11]。直观地说,这意味着收集索引数组中的每个索引 X 都会选择一整行,而结果是所有这些行的串联。
GetDimensionSize
另请参阅 XlaBuilder::GetDimensionSize。
返回操作数指定维度的大小。操作数必须是数组形状。
GetDimensionSize(operand, dimension)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
n 维输入数组 |
dimension
|
int64
|
区间 [0, n) 中的一个值,用于指定维度 |
如需了解 StableHLO,请参阅 StableHLO - get_dimension_size。
GetTupleElement
另请参阅 XlaBuilder::GetTupleElement。
使用编译时常量值对元组进行索引。
该值必须是编译时常量,以便形状推断可以确定结果值的类型。
这类似于 C++ 中的 std::get<int N>(t)。从概念上讲:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
另请参阅 tf.tuple。
GetTupleElement(tuple_data, index)
| 参数 | 类型 | 语义 |
|---|---|---|
tuple_data |
XlaOP |
元组 |
index |
int64 |
元组形状的索引 |
如需了解 StableHLO,请参阅 StableHLO - get_tuple_element。
Imag
另请参阅 XlaBuilder::Imag。
复数(或实数)形状的逐元素虚部。x -> imag(x)。如果操作数是浮点类型,则返回 0。
Imag(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
如需了解 StableHLO,请参阅 StableHLO - imag。
Infeed
另请参阅 XlaBuilder::Infeed。
Infeed(shape, config)
| 参数 | 类型 | 语义 |
|---|---|---|
shape
|
Shape
|
从 Infeed 接口读取的数据的形状。形状的布局字段必须设置为与发送到设备的数据的布局相匹配;否则,其行为是未定义的。 |
config |
可选 string |
相应操作的配置。 |
从设备的隐式 Infeed 流式传输接口读取单个数据项,将数据解释为给定的形状及其布局,并返回数据的 XlaOp。一次计算中可以有多个 Infeed 操作,但这些 Infeed 操作之间必须存在全序关系。例如,以下代码中的两个 Infeed 具有全序,因为 while 循环之间存在依赖关系。
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
不支持嵌套的元组形状。对于空元组形状,Infeed 操作实际上是一个空操作,并且在不从设备的 Infeed 读取任何数据的情况下继续进行。
如需了解 StableHLO,请参阅 StableHLO - infeed。
Iota
另请参阅 XlaBuilder::Iota。
Iota(shape, iota_dimension)
在设备上构建常量字面值,而不是潜在的大型主机传输。创建一个具有指定形状的数组,该数组包含从零开始并沿指定维度递增 1 的值。对于浮点类型,生成的数组等效于 ConvertElementType(Iota(...)),其中 Iota 为整数类型,转换是到浮点类型的转换。
| 参数 | 类型 | 语义 |
|---|---|---|
shape |
Shape |
由 Iota() 创建的数组的形状 |
iota_dimension |
int64 |
要沿哪个维度递增。 |
例如,Iota(s32[4, 8], 0) 会返回
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
退货费用 Iota(s32[4, 8], 1)
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
如需了解 StableHLO,请参阅 StableHLO - iota。
IsFinite
另请参阅 XlaBuilder::IsFinite。
测试 operand 的每个元素是否为有限值,即不是正无穷大或负无穷大,也不是 NaN。返回一个与输入具有相同形状的 PRED 值数组,其中每个元素都是 true,当且仅当对应的输入元素是有限值时。
IsFinite(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
如需了解 StableHLO,请参阅 StableHLO - is_finite。
日志
另请参阅 XlaBuilder::Log。
按元素求自然对数 x -> ln(x)。
Log(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
日志记录还支持可选的 result_accuracy 实参:
Log(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
如需了解 StableHLO,请参阅 StableHLO - 日志。
Log1p
另请参阅 XlaBuilder::Log1p。
按元素计算的偏移自然对数 x -> ln(1+x)。
Log1p(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Log1p 还支持可选的 result_accuracy 实参:
Log1p(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
如需了解 StableHLO,请参阅 StableHLO - log_plus_one。
物流
另请参阅 XlaBuilder::Logistic。
元素级逻辑斯谛函数计算 x -> logistic(x)。
Logistic(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Logistic 还支持可选的 result_accuracy 实参:
Logistic(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
如需了解 StableHLO,请参阅 StableHLO - 后勤。
地图
另请参阅 XlaBuilder::Map。
Map(operands..., computation, dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
operands |
N 个 XlaOp 的序列 |
类型为 T0..T{N-1} 的 N 个数组 |
computation
|
XlaComputation
|
计算类型为 T_0, T_1,
.., T_{N + M -1} -> S,具有 N 个类型为 T 的形参和 M 个任意类型的形参。 |
dimensions |
int64 数组 |
地图维度数组 |
static_operands
|
N 个 XlaOp 的序列
|
地图操作的静态操作 |
对给定的 operands 数组应用标量函数,生成一个相同维度的数组,其中每个元素都是将映射函数应用于输入数组中相应元素的结果。
映射函数是一种任意计算,但限制是它具有 N 个标量类型 T 的输入和一个类型为 S 的输出。输出与操作数具有相同的维度,只是元素类型 T 替换为 S。
例如:Map(op1, op2, op3, computation, par1) 会映射输入数组中每个(多维)索引处的 elem_out <-
computation(elem1, elem2, elem3, par1),以生成输出数组。
如需了解 StableHLO,请参阅 StableHLO - 映射。
最大值
另请参阅 XlaBuilder::Max。
对张量 lhs 和 rhs 执行元素级最大值运算。
Max(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
Max 有一个支持不同维度广播的替代变体:
Max(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - 最大限度。
最小值
另请参阅 XlaBuilder::Min。
对 lhs 和 rhs 执行元素级最小值运算。
Min(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Min,存在一种支持不同维度广播的替代变体:
Min(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - 最低版本。
Mul
另请参阅 XlaBuilder::Mul。
按元素执行 lhs 和 rhs 的乘积。
Mul(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
Mul 有一个支持不同维度广播的替代变体:
Mul(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - multiply。
Neg
另请参阅 XlaBuilder::Neg。
按元素求反 x -> -x。
Neg(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
如需了解 StableHLO,请参阅 StableHLO - negate
非
另请参阅 XlaBuilder::Not。
逐元素的逻辑非 x -> !(x)。
Not(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
如需了解 StableHLO,请参阅 StableHLO - 不。
OptimizationBarrier
另请参阅 XlaBuilder::OptimizationBarrier。
阻止任何优化传递跨越屏障移动计算。
OptimizationBarrier(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
确保在任何依赖于屏障输出的运算符之前评估所有输入。
如需了解 StableHLO,请参阅 StableHLO - optimization_barrier。
或
另请参阅 XlaBuilder::Or。
对 lhs 和 rhs 执行按元素 OR 运算。
Or(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Or,存在支持不同维度广播的替代变体:
Or(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - 或。
Outfeed
另请参阅 XlaBuilder::Outfeed。
将输入写入出馈。
Outfeed(operand, shape_with_layout, outfeed_config)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
类型为 T 的数组 |
shape_with_layout |
Shape |
定义所传输数据的布局 |
outfeed_config |
string |
出料指令的配置常量 |
shape_with_layout 用于传达我们想要出料的铺设形状。
如需了解 StableHLO,请参阅 StableHLO - outfeed。
垫
另请参阅 XlaBuilder::Pad。
Pad(operand, padding_value, padding_config)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
类型为 T 的数组 |
padding_value
|
XlaOp
|
用于填充添加的填充的 T 类型的标量 |
padding_config
|
PaddingConfig
|
两个边缘(低、高)和每个维度元素之间的内边距量 |
通过在给定 operand 数组周围以及数组元素之间填充给定的 padding_value 来扩展该数组。padding_config 用于指定每个维度的边缘边衬区和内部边衬区的大小。
PaddingConfig 是 PaddingConfigDimension 的重复字段,其中包含每个维度的三个字段:edge_padding_low、edge_padding_high 和 interior_padding。
edge_padding_low 和 edge_padding_high 分别指定在每个维度的低端(紧邻索引 0)和高端(紧邻最高索引)添加的填充量。边缘内边距的大小可以为负值,负内边距的绝对值表示要从指定维度中移除的元素数量。
interior_padding 用于指定在每个维度中任意两个元素之间添加的内边距量;不得为负值。内部填充在逻辑上位于边缘填充之前,因此如果边缘填充为负值,则会从内部填充后的操作数中移除元素。
如果边缘填充对均为 (0, 0) 且内部填充值均为 0,则此操作为无操作。下图显示了二维数组的不同 edge_padding 和 interior_padding 值示例。
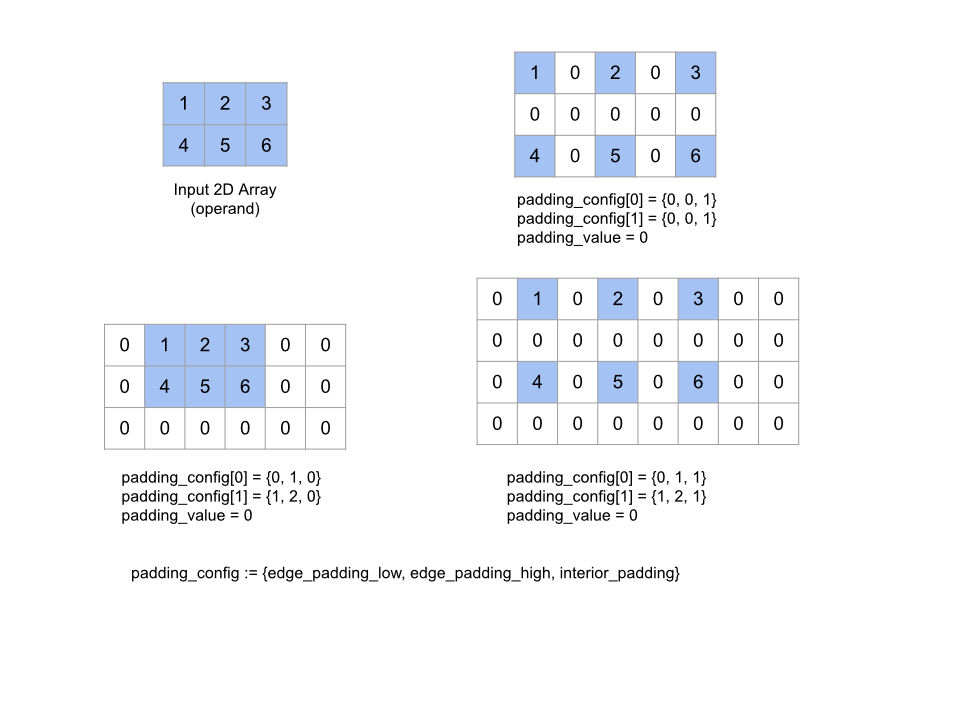
如需了解 StableHLO,请参阅 StableHLO - pad。
参数
另请参阅 XlaBuilder::Parameter。
Parameter 表示计算的实参输入。
PartitionID
另请参阅 XlaBuilder::BuildPartitionId。
生成当前进程的 partition_id。
PartitionID(shape)
| 参数 | 类型 | 语义 |
|---|---|---|
shape |
Shape |
数据形状 |
PartitionID 可能会出现在 HLO 转储中,但最终用户不应手动构建它。
如需了解 StableHLO,请参阅 StableHLO - partition_id。
PopulationCount
另请参阅 XlaBuilder::PopulationCount。
计算 operand 中每个元素中设置的位数。
PopulationCount(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
如需了解 StableHLO,请参阅 StableHLO - popcnt。
Pow
另请参阅 XlaBuilder::Pow。
对 lhs 执行按元素的指数运算,指数为 rhs。
Pow(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Pow,存在一种支持不同维度广播的替代变体:
Pow(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - 功率。
Real
另请参阅 XlaBuilder::Real。
复数(或实数)形状的逐元素实部。x -> real(x)。如果操作数是浮点类型,则 Real 返回相同的值。
Real(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
如需了解 StableHLO,请参阅 StableHLO - 真实。
Recv
另请参阅 XlaBuilder::Recv。
Recv、RecvWithTokens 和 RecvToHost 是在 HLO 中充当通信基元的操作。这些操作通常在 HLO 转储中显示为低级输入/输出或跨设备转移的一部分,但最终用户不应手动构建这些操作。
Recv(shape, handle)
| 参数 | 类型 | 语义 |
|---|---|---|
shape |
Shape |
要接收的数据的形状 |
handle |
ChannelHandle |
每个发送/接收对的唯一标识符 |
从共享同一渠道句柄的另一计算中的 Send 指令接收指定形状的数据。返回接收到的数据的 XlaOp。
如需了解 StableHLO,请参阅 StableHLO - recv。
RecvDone
另请参阅 HloInstruction::CreateRecv 和 HloInstruction::CreateRecvDone。
与 Send 类似,Recv 操作的客户端 API 表示同步通信。不过,该指令会在内部分解为 2 个 HLO 指令(Recv 和 RecvDone),以实现异步数据传输。
Recv(const Shape& shape, int64 channel_id)
分配接收来自具有相同 channel_id 的 Send 指令的数据所需的资源。返回已分配资源的上下文,后续的 RecvDone 指令会使用该上下文来等待数据传输完成。上下文是一个元组,包含 {接收缓冲区(形状)、请求标识符 (U32)},只能由 RecvDone 指令使用。
给定由 Recv 指令创建的上下文,等待数据传输完成并返回接收到的数据。
减少
另请参阅 XlaBuilder::Reduce。
并行对一个或多个数组应用归约函数。
Reduce(operands..., init_values..., computation, dimensions_to_reduce)
| 参数 | 类型 | 语义 |
|---|---|---|
operands
|
N 个 XlaOp 的序列
|
类型为 T_0,...,
T_{N-1} 的 N 个数组。 |
init_values
|
N 个 XlaOp 的序列
|
类型为 T_0,..., T_{N-1} 的 N 个标量。 |
computation
|
XlaComputation
|
类型为 T_0,..., T_{N-1}, T_0,
...,T_{N-1} -> 的计算
Collate(T_0,...,
T_{N-1})。 |
dimensions_to_reduce
|
int64 数组
|
要缩减的维度的无序数组。 |
其中:
- N 必须大于或等于 1。
- 计算必须“大致”符合结合律(见下文)。
- 所有输入数组的维度必须相同。
- 所有初始值都必须在
computation下形成一个恒等元素。 - 如果
N = 1,则Collate(T)为T。 - 如果
N > 1,Collate(T_0, ..., T_{N-1})是一个由N个T类型元素组成的元组。
此操作会将每个输入数组的一个或多个维度缩减为标量。
每个返回的数组的维度数为 number_of_dimensions(operand) - len(dimensions)。相应运算的输出为 Collate(Q_0, ..., Q_N),其中 Q_i 是 T_i 类型的数组,其维度如下所述。
不同的后端可以重新关联归约计算。这可能会导致数值差异,因为某些归约函数(例如加法)对于浮点数来说不具有结合律。不过,如果数据范围有限,浮点加法在大多数实际应用中都足够接近于关联。
如需了解 StableHLO,请参阅 StableHLO - 减少。
示例
当使用缩减函数 f(即 computation)缩减具有值 [10, 11,
12, 13] 的单个一维数组中的一个维度时,可以按如下方式计算:
f(10, f(11, f(12, f(init_value, 13)))
但也有许多其他可能性,例如
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
以下是一个粗略的伪代码示例,展示了如何实现归约,其中使用求和作为归约计算,初始值为 0。
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
下面是一个缩减二维数组(矩阵)的示例。该形状有 2 个维度,维度 0 的大小为 2,维度 1 的大小为 3:
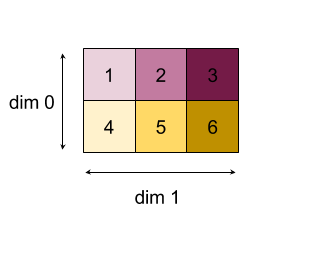
使用“add”函数缩减维度 0 或 1 的结果:
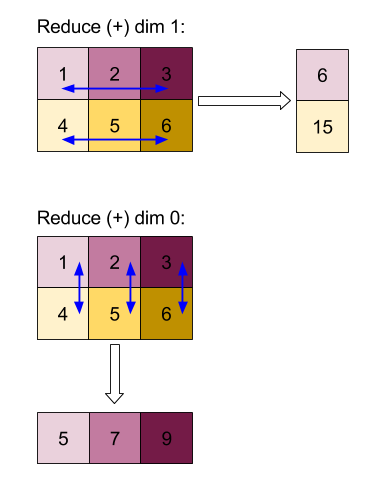
请注意,这两个缩减结果都是一维数组。该图表仅为方便直观显示而将一个显示为列,另一个显示为行。
下面是一个更复杂的示例,其中包含一个三维数组。它的维度数为 3,维度 0 的大小为 4,维度 1 的大小为 2,维度 2 的大小为 3。为简单起见,值 1 到 6 会在维度 0 中复制。
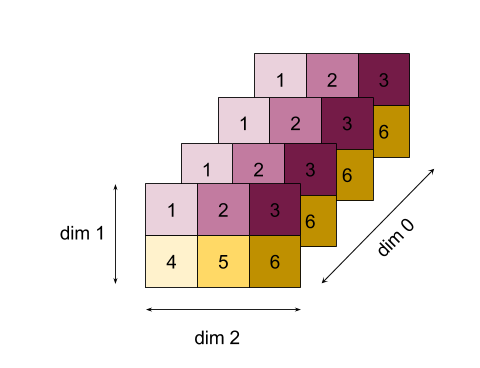
与 2D 示例类似,我们也可以仅减少一个维度。例如,如果我们减少维度 0,我们会得到一个二维数组,其中维度 0 的所有值都折叠成一个标量:
| 4 8 12 |
| 16 20 24 |
如果我们缩减维度 2,我们还会得到一个二维数组,其中维度 2 中的所有值都折叠成一个标量:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
请注意,输入中剩余维度之间的相对顺序在输出中会保留,但某些维度可能会被分配新的编号(因为维度数量会发生变化)。
我们还可以减少多个维度。添加缩减维度 0 和 1 会生成一维数组 [20, 28, 36]。
在所有维度上缩减 3D 数组会生成标量 84。
变参 Reduce
当 N > 1 时,reduce 函数应用会稍微复杂一些,因为它会同时应用于所有输入。操作数按以下顺序提供给计算:
- 第一个操作数的运行缩减值
- …
- 为第 N 个操作数运行了缩减值
- 第一个操作数的输入值
- …
- 第 N 个运算数的输入值
例如,请考虑以下归约函数,该函数可用于并行计算一维数组的最大值和 argmax:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
对于一维输入数组 V = Float[N], K = Int[N] 和初始值 I_V = Float, I_K = Int,对唯一输入维度进行归约的结果 f_(N-1) 等效于以下递归应用:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
将此缩减函数应用于值数组和顺序索引数组(即 iota)时,将共同迭代这两个数组,并返回一个包含最大值和匹配索引的元组。
ReducePrecision
另请参阅 XlaBuilder::ReducePrecision。
用于模拟将浮点值转换为低精度格式(例如 IEEE-FP16)并转换回原始格式的效果。低精度格式中的指数和尾数位数可以任意指定,不过并非所有硬件实现都支持所有位大小。
ReducePrecision(operand, exponent_bits, mantissa_bits)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
浮点类型 T 的数组。 |
exponent_bits |
int32 |
低精度格式中的指数位数 |
mantissa_bits |
int32 |
低精度格式中的尾数位数 |
结果是 T 类型的数组。输入值会舍入为可用指定数量的尾数位表示的最接近的值(使用“四舍六入五成双”语义),并且任何超出指数位数量所指定范围的值都会被限制为正无穷大或负无穷大。NaN 值会保留,但可能会转换为规范的 NaN 值。
较低精度格式必须至少有一个指数位(以便区分零值和无穷大,因为两者都具有零尾数),并且必须具有非负数量的尾数位。指数或尾数位数可能超过类型 T 的相应值;转换的相应部分随后会变成空操作。
如需了解 StableHLO,请参阅 StableHLO - reduce_precision。
ReduceScatter
另请参阅 XlaBuilder::ReduceScatter。
ReduceScatter 是一种集体操作,可有效执行 AllReduce,然后沿 scatter_dimension 将结果拆分为 shard_count 个块,从而分散结果,并且复制组中的复制 i 会接收 ith 分片。
ReduceScatter(operand, computation, scatter_dimension, shard_count,
replica_groups, channel_id, layout, use_global_device_ids)
| 参数 | 类型 | 语义 |
|---|---|---|
operand
|
XlaOp
|
要跨复制副本缩减的数组或非空数组元组。 |
computation |
XlaComputation |
减幅计算 |
scatter_dimension |
int64 |
要散布的维度。 |
shard_count
|
int64
|
要拆分的块数
scatter_dimension |
replica_groups
|
ReplicaGroup vector
|
执行归约操作的组 |
channel_id
|
可选
ChannelHandle |
用于跨模块通信的可选渠道 ID |
layout
|
可选 Layout
|
用户指定的内存布局 |
use_global_device_ids |
可选 bool |
用户指定的标志 |
- 如果
operand是一个数组元组,则对元组的每个元素执行 reduce-scatter。 replica_groups是执行缩减的副本组列表(可以使用ReplicaId检索当前副本的副本 ID)。每个组中副本的顺序决定了全缩减结果的分散顺序。replica_groups必须为空(在这种情况下,所有副本都属于一个组),或者包含的元素数量与副本数量相同。如果有多个副本组,则它们的大小必须相同。例如,replica_groups = {0, 2}, {1, 3}会在副本0和2之间以及1和3之间执行归约,然后分散结果。shard_count是每个副本组的大小。如果replica_groups为空,则需要此值。如果replica_groups不为空,则shard_count必须等于每个副本组的大小。channel_id用于跨模块通信:只有具有相同channel_id的reduce-scatter操作才能相互通信。layout如需详细了解布局,请参阅 xla::shapes。use_global_device_ids是用户指定的标志。当false(默认)时,replica_groups中的数字为ReplicaId;当true时,replica_groups表示 (ReplicaID*partition_count+partition_id) 的全局 ID。例如:- 如果使用 2 个副本和 4 个分区,
- replica_groups={ {0,1,4,5},{2,3,6,7} } and use_global_device_ids=true
- group[0] = (0,0)、(0,1)、(1,0)、(1,1)
- group[1] = (0,2), (0,3), (1,2), (1,3)
- 其中,每个对都是(副本 ID、分区 ID)。
输出形状是输入形状,但 scatter_dimension 缩小了 shard_count 倍。例如,如果有两个副本,并且操作数在两个副本上分别具有 [1.0, 2.25] 和 [3.0, 5.25] 值,那么当 scatter_dim 为 0 时,此操作的输出值对于第一个副本将为 [4.0],对于第二个副本将为 [7.5]。
如需了解 StableHLO,请参阅 StableHLO - reduce_scatter。
ReduceScatter - 示例 1 - StableHLO
在上面的示例中,有 2 个副本参与 ReduceScatter。 在每个副本上,操作数的形状为 f32[2,4]。在各个副本之间执行全归约(求和),从而在每个副本上生成形状为 f32[2,4] 的归约值。然后,沿维度 1 将此缩减后的值拆分为 2 个部分,因此每个部分的形状为 f32[2,2]。进程组中的每个副本都会收到与其在组中的位置对应的部分。因此,每个副本上的输出的形状为 f32[2,2]。
ReduceWindow
另请参阅 XlaBuilder::ReduceWindow。
对 N 个多维数组序列中每个窗口的所有元素应用归约函数,生成单个或 N 个多维数组的元组作为输出。每个输出数组的元素数量与窗口的有效位置数量相同。池化层可以表示为 ReduceWindow。与 Reduce 类似,应用的 computation 始终传递到左侧的 init_values。
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| 参数 | 类型 | 语义 |
|---|---|---|
operands
|
N XlaOps
|
一个包含 N 个多维数组(类型为 T_0,..., T_{N-1})的序列,每个数组表示放置窗口的基本区域。 |
init_values
|
N XlaOps
|
缩减的 N 个起始值,每个操作数对应一个。如需了解详情,请参阅减少。 |
computation
|
XlaComputation
|
类型为 T_0,
..., T_{N-1}, T_0, ..., T_{N-1}
-> Collate(T_0, ..., T_{N-1}) 的缩减函数,用于应用于所有输入操作数的每个窗口中的元素。 |
window_dimensions
|
ArraySlice<int64>
|
用于窗口维度值的整数数组 |
window_strides
|
ArraySlice<int64>
|
用于窗口步长值的整数数组 |
base_dilations
|
ArraySlice<int64>
|
用于基本空洞值的整数数组 |
window_dilations
|
ArraySlice<int64>
|
用于窗口扩张值的整数数组 |
padding
|
Padding
|
窗口的填充类型(Padding::kSame,如果步幅为 1,则填充以使输出形状与输入形状相同;Padding::kValid,不使用填充,并在窗口不再适合时“停止”) |
其中:
- N 必须大于或等于 1。
- 所有输入数组的维度必须相同。
- 如果
N = 1,则Collate(T)为T。 - 如果
N > 1,Collate(T_0, ..., T_{N-1})是一个由N个(T0,...T{N-1})类型元素组成的元组。
如需了解 StableHLO,请参阅 StableHLO - reduce_window。
ReduceWindow - 示例 1
输入是一个大小为 [4x6] 的矩阵,window_dimensions 和 window_stride_dimensions 均为 [2x3]。
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
某个维度中的步幅为 1 表示相应维度中一个窗口的位置与相邻窗口相隔 1 个元素。为了指定窗口之间不重叠,window_stride_dimensions 应等于 window_dimensions。下图展示了两种不同的步幅值。填充会应用于输入的每个维度,计算方式与输入在填充后具有相应维度时的计算方式相同。
对于一个非平凡的填充示例,请考虑计算输入数组 [10000, 1000, 100, 10, 1] 上维度为 3、步幅为 2 的缩减窗口最小值(初始值为 MAX_FLOAT)。填充 kValid 会计算两个有效窗口([10000, 1000, 100] 和 [100, 10, 1])的最小值,从而生成输出 [100, 1]。填充 kSame 首先填充数组,使缩减窗口后的形状与步幅为 1 的输入相同,方法是在两侧添加初始元素,得到 [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE]。对填充后的数组运行 reduce-window 会对三个窗口 [MAX_VALUE, 10000, 1000]、[1000, 100, 10]、[10, 1, MAX_VALUE] 进行操作,并生成 [1000, 10, 1]。
归约函数的评估顺序是任意的,并且可能具有不确定性。因此,缩减函数不应过于敏感地响应重新关联。如需了解详情,请参阅有关 Reduce 上下文中的关联性的讨论。
ReduceWindow - 示例 2 - StableHLO
在上述示例中:
输入)操作数的输入形状为 S32[3,2]。值为 [[1,2],[3,4],[5,6]]
第 1 步)沿行维度以 2 为系数进行基本扩张,在操作数的每行之间插入空洞。膨胀后,顶部填充 2 行,底部填充 1 行。这样一来,张量就会变高。
第 2 步)定义形状为 [2,1] 的窗口,窗口扩张为 [3,1]。这意味着每个窗口都会从同一列中选择两个元素,但第二个元素位于第一个元素下方三行,而不是直接位于其下方。
第 3 步)然后,以步幅 [4,1] 在操作数上滑动窗口。这会导致窗口每次向下移动 4 行,同时每次水平移动 1 列。填充单元格会填充 init_value(在本例中为 init_value = 0)。“落入”扩张单元格的值会被忽略。
由于步幅和填充,有些窗口仅重叠零和空洞,而另一些窗口则重叠实际输入值。
第 4 步)在每个窗口内,元素使用缩减函数 (a, b) → a + b(从初始值 0 开始)进行组合。前两个窗口仅包含填充和孔洞,因此其结果为 0。底部窗口从输入中捕获值 3 和 4,并将这些值作为结果返回。
结果)最终输出的形状为 S32[2,2],值如下:[[0,0],[3,4]]
Rem
另请参阅 XlaBuilder::Rem。
按元素计算被除数 lhs 和除数 rhs 的余数。
结果的符号与被除数的符号相同,结果的绝对值始终小于除数的绝对值。
Rem(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
Rem 有一个支持不同维度广播的替代变体:
Rem(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - 余数。
ReplicaId
另请参阅 XlaBuilder::ReplicaId。
返回副本的唯一 ID(U32 标量)。
ReplicaId()
每个副本的唯一 ID 是区间 [0, N) 中的无符号整数,其中 N 是副本数。由于所有副本都运行相同的程序,因此程序中的 ReplicaId() 调用会在每个副本上返回不同的值。
如需了解 StableHLO,请参阅 StableHLO - replica_id。
Reshape
另请参阅 XlaBuilder::Reshape。
以及 Collapse 操作。
将数组的维度重塑为新的配置。
Reshape(operand, dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
类型为 T 的数组 |
dimensions |
int64 vector |
新维度的尺寸向量 |
从概念上讲,reshape 首先将数组展平为一维数据值向量,然后将此向量细化为新形状。输入实参是任意类型为 T 的数组、维度索引的编译时常量向量,以及结果的维度大小的编译时常量向量。dimensions 向量决定了输出数组的大小。dimensions 中索引 0 处的值是维度 0 的大小,索引 1 处的值是维度 1 的大小,依此类推。dimensions 各维度的乘积必须等于操作数各维度大小的乘积。将折叠数组细化为由 dimensions 定义的多维数组时,dimensions 中的维度会按从变化最慢(最主要)到变化最快(最次要)的顺序排列。
例如,假设 v 是一个包含 24 个元素的数组:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
作为一种特殊情况,reshape 可以将单元素数组转换为标量,反之亦然。例如,
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
如需了解 StableHLO,请参阅 StableHLO - reshape。
Reshape(显式)
另请参阅 XlaBuilder::Reshape。
Reshape(shape, operand)
使用明确目标形状的 Reshape 操作。
| 参数 | 类型 | 语义 |
|---|---|---|
shape |
Shape |
类型为 T 的输出形状 |
operand |
XlaOp |
类型为 T 的数组 |
Rev(反向)
另请参阅 XlaBuilder::Rev。
Rev(operand, dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
类型为 T 的数组 |
dimensions |
ArraySlice<int64> |
要反转的维度 |
沿指定的 dimensions 反转 operand 数组中元素的顺序,生成形状相同的输出数组。操作数数组中位于多维索引处的每个元素都会存储到输出数组中位于转换后的索引处。通过反转每个要反转的维度中的索引来转换多维索引(即,如果大小为 N 的维度是要反转的维度之一,则其索引 i 会转换为 N - 1 - i)。
Rev 操作的一种用途是在神经网络中的梯度计算期间,沿两个窗口维度反转卷积权重数组。
如需了解 StableHLO,请参阅 StableHLO - 反向。
RngNormal
另请参阅 XlaBuilder::RngNormal。
构建一个具有给定形状的输出,其中包含按照 \(N(\mu, \sigma)\) 正态分布生成的随机数。形参 \(\mu\) 和 \(\sigma\)以及输出形状必须具有浮点元素类型。此外,参数还必须是标量值。
RngNormal(mu, sigma, shape)
| 参数 | 类型 | 语义 |
|---|---|---|
mu |
XlaOp |
类型为 T 的标量,用于指定生成数字的平均值 |
sigma
|
XlaOp
|
类型为 T 的标量,用于指定生成 |
shape |
Shape |
类型为 T 的输出形状 |
如需了解 StableHLO,请参阅 StableHLO - rng。
RngUniform
另请参阅 XlaBuilder::RngUniform。
构建一个具有给定形状的输出,其中包含按照区间 \([a,b)\)上的均匀分布生成的随机数。形参和输出元素类型必须是布尔类型、整数类型或浮点类型,并且类型必须一致。CPU 和 GPU 后端目前仅支持 F64、F32、F16、BF16、S64、U64、S32 和 U32。此外,参数必须是标量值。如果 \(b <= a\) 结果由实现定义。
RngUniform(a, b, shape)
| 参数 | 类型 | 语义 |
|---|---|---|
a |
XlaOp |
指定区间下限的 T 类型标量 |
b |
XlaOp |
指定区间上限的 T 类型标量 |
shape |
Shape |
类型为 T 的输出形状 |
如需了解 StableHLO,请参阅 StableHLO - rng。
RngBitGenerator
另请参阅 XlaBuilder::RngBitGenerator。
使用指定算法(或后端默认算法)生成具有给定形状且填充了均匀随机位的输出,并返回更新后的状态(与初始状态具有相同的形状)和生成的随机数据。
初始状态是当前随机数生成的初始状态。它以及所需的形状和有效值取决于所使用的算法。
输出保证是初始状态的确定性函数,但不保证在后端和不同编译器版本之间具有确定性。
RngBitGenerator(algorithm, initial_state, shape)
| 参数 | 类型 | 语义 |
|---|---|---|
algorithm |
RandomAlgorithm |
要使用的 PRNG 算法。 |
initial_state |
XlaOp |
PRNG 算法的初始状态。 |
shape |
Shape |
生成数据的输出形状。 |
algorithm 的可用值:
rng_default:具有后端特定形状要求的后端特定算法。rng_three_fry:基于 ThreeFry 计数器的 PRNG 算法。initial_state的形状为u64[2],具有任意值。Salmon 等,SC 2011。并行随机数:只需 3 步即可完成。rng_philox:用于并行生成随机数的 Philox 算法。initial_state的形状为u64[3],具有任意值。 Salmon 等,SC 2011。并行随机数:只需 3 步即可完成。
如需了解 StableHLO,请参阅 StableHLO - rng_bit_generator。
RngGetAndUpdateState
另请参阅 HloInstruction::CreateRngGetAndUpdateState。
各种 Rng 操作的 API 在内部会分解为 HLO 指令,包括 RngGetAndUpdateState。
RngGetAndUpdateState 在 HLO 中充当原语。此操作可能会出现在 HLO 转储中,但最终用户不应手动构建此操作。
圆形
另请参阅 XlaBuilder::Round。
按元素进行舍入,中间数向远离零的方向舍入。
Round(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
RoundNearestAfz
另请参阅 XlaBuilder::RoundNearestAfz。
执行按元素舍入到最接近的整数,舍入方式为远离零。
RoundNearestAfz(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
如需了解 StableHLO,请参阅 StableHLO - round_nearest_afz。
RoundNearestEven
另请参阅 XlaBuilder::RoundNearestEven。
按元素进行舍入,将结果舍入为最接近的偶数。
RoundNearestEven(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
如需了解 StableHLO 信息,请参阅 StableHLO - round_nearest_even。
Rsqrt
另请参阅 XlaBuilder::Rsqrt。
元素级平方根倒数运算 x -> 1.0 / sqrt(x)。
Rsqrt(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Rsqrt 还支持可选的 result_accuracy 实参:
Rsqrt(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
如需了解 StableHLO,请参阅 StableHLO - rsqrt。
扫描
另请参阅 XlaBuilder::Scan。
沿指定维度对数组应用缩减函数,生成最终状态和中间值数组。
Scan(inputs..., inits..., to_apply, scan_dimension,
is_reverse, is_associative)
| 参数 | 类型 | 语义 |
|---|---|---|
inputs |
m XlaOp 的序列 |
要扫描的数组。 |
inits |
k XlaOp 的序列 |
初始携带。 |
to_apply |
XlaComputation |
类型为 i_0, ..., i_{m-1}, c_0, ..., c_{k-1} -> (o_0, ..., o_{n-1}, c'_0, ..., c'_{k-1}) 的计算。 |
scan_dimension |
int64 |
要扫描的维度。 |
is_reverse |
bool |
如果为 true,则按相反顺序扫描。 |
is_associative |
bool(三态) |
如果为 true,则表示相应运算是关联的。 |
函数 to_apply 会按顺序应用于 inputs 中沿 scan_dimension 的元素。如果 is_reverse 为 false,则按顺序处理元素 0 到 N-1,其中 N 是 scan_dimension 的大小。如果 is_reverse 为 true,则从 N-1 到 0 处理元素。
to_apply 函数采用 m + k 个操作数:
m来自inputs的当前元素。k携带上一步中的值(或第一个元素的inits)。
to_apply 函数会返回一个包含 n + k 值的元组:
outputs的n元素。k新的进位值。
扫描操作会生成一个包含 n + k 值的元组:
n输出数组,包含每个步长的输出值。- 处理完所有元素后的最终
k进位值。
m 输入的类型必须与 to_apply 的前 m 个形参的类型一致,并具有额外的扫描维度。n 输出的类型必须与 to_apply 的第一个 n 返回值的类型相匹配,并具有额外的扫描维度。所有输入和输出中的额外扫描维度必须具有相同的大小 N。to_apply 的最后 k 个形参和返回值以及 k 个初始化的类型必须匹配。
例如 (m, n, k == 1, N == 3),对于初始进位 i、输入 [a, b, c]、函数 f(x, c) -> (y, c') 和 scan_dimension=0,is_reverse=false:
- 第 0 步:
f(a, i) -> (y0, c0) - 第 1 步:
f(b, c0) -> (y1, c1) - 第 2 步:
f(c, c1) -> (y2, c2)
Scan 的输出为 ([y0, y1, y2], c2)。
散点图
另请参阅 XlaBuilder::Scatter。
XLA scatter 操作会生成一系列结果,这些结果是输入数组 operands 的值,其中有几个切片(位于 scatter_indices 指定的索引处)使用 update_computation 通过 updates 中的一系列值进行更新。
Scatter(operands..., scatter_indices, updates..., update_computation,
dimension_numbers, indices_are_sorted, unique_indices)
| 参数 | 类型 | 语义 |
|---|---|---|
operands |
N 个 XlaOp 的序列 |
要分散到的 N 个 T_0, ..., T_N 类型的数组。 |
scatter_indices |
XlaOp |
包含必须分散到的切片的起始索引的数组。 |
updates |
N 个 XlaOp 的序列 |
类型为 T_0, ..., T_N 的 N 个数组。updates[i] 包含必须用于分散 operands[i] 的值。 |
update_computation |
XlaComputation |
用于在分散期间合并输入数组中的现有值和更新的计算。此计算应为 T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N) 类型。 |
index_vector_dim |
int64 |
scatter_indices 中包含起始索引的维度。 |
update_window_dims |
ArraySlice<int64> |
updates 形的维度集,即窗口维度。 |
inserted_window_dims |
ArraySlice<int64> |
必须插入到 updates 形状中的一组窗口尺寸。 |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
从分散索引到操作数索引空间的维度映射。此数组会被解读为将 i 映射到 scatter_dims_to_operand_dims[i]。必须是一对一且完全的。 |
dimension_number |
ScatterDimensionNumbers |
分散操作的维度编号 |
indices_are_sorted |
bool |
调用方是否保证索引已排序。 |
unique_indices |
bool |
调用方是否保证索引是唯一的。 |
其中:
- N 必须大于或等于 1。
operands[0]、...、operands[N-1] 必须都具有相同的维度。updates[0]、...、updates[N-1] 必须都具有相同的维度。- 如果
N = 1,则Collate(T)为T。 - 如果
N > 1,Collate(T_0, ..., T_N)是一个由N个T类型元素组成的元组。
如果 index_vector_dim 等于 scatter_indices.rank,我们会隐式地认为 scatter_indices 具有尾随的 1 维度。
我们将类型为 ArraySlice<int64> 的 update_scatter_dims 定义为 updates 形状中不在 update_window_dims 中的维度集合,并按升序排列。
scatter 的实参应遵循以下限制:
每个
updates数组都必须具有update_window_dims.size + scatter_indices.rank - 1个维度。每个
updates数组中维度i的边界必须符合以下条件:- 如果
i存在于update_window_dims中(即对于某个k,i等于update_window_dims[k]),则在考虑inserted_window_dims后,updates中维度i的边界不得超过operand的相应边界(即adjusted_window_bounds[k],其中adjusted_window_bounds包含operand的边界,但移除了索引为inserted_window_dims的边界)。 - 如果
i存在于update_scatter_dims中(即等于某个k的update_scatter_dims[k]),则updates中维度i的界限必须等于scatter_indices的相应界限(跳过index_vector_dim,即scatter_indices.shape.dims[k],如果k<index_vector_dim,否则为scatter_indices.shape.dims[k+1])。
- 如果
update_window_dims必须按升序排列,不得有任何重复的维度编号,且必须在[0, updates.rank)范围内。inserted_window_dims必须按升序排列,不得有任何重复的维度编号,且必须在[0, operand.rank)范围内。operand.rank必须等于update_window_dims.size和inserted_window_dims.size的总和。scatter_dims_to_operand_dims.size必须等于scatter_indices.shape.dims[index_vector_dim],并且其值必须在[0, operand.rank)范围内。
对于每个 updates 数组中的给定索引 U,相应 operands 数组中必须应用此更新的对应索引 I 的计算方式如下:
- 令
G= {U[k] forkinupdate_scatter_dims}。使用G在scatter_indices数组中查找索引向量S,使得S[i] =scatter_indices[Combine(G,i)],其中 Combine(A, b) 将 b 插入到 A 中的位置index_vector_dim。 - 使用
scatter_dims_to_operand_dims映射通过分散S来创建operand的索引Sin。S更正式的说法:Sin[scatter_dims_to_operand_dims[k]] =S[k] ifk<scatter_dims_to_operand_dims.size.Sin[_] =0,否则。
- 通过根据
inserted_window_dims散布U中位于update_window_dims的索引,为每个operands数组创建一个索引Win。更正式的说法:- 如果
k位于update_window_dims中,则Win[window_dims_to_operand_dims(k)] =U[k],其中window_dims_to_operand_dims是一个单调函数,其域为 [0,update_window_dims.size),值域为 [0,operand.rank) \inserted_window_dims。(例如,如果update_window_dims.size为4,operand.rank为6,inserted_window_dims为 {0,2},则window_dims_to_operand_dims为 {0→1,1→3,2→4,3→5})。 Win[_] =0,否则。
- 如果
I是Win+Sin,其中 + 是按元素相加。
总而言之,分散操作可以定义如下。
- 使用
operands初始化output,即对于所有指数J,对于operands[J] 数组中的所有指数O:
output[J][O] =operands[J][O] - 对于
updates[J] 数组中的每个索引U和operand[J] 数组中的对应索引O,如果O是output的有效索引,则:
((output[0][O], ...,output[N-1][O]) =update_computation(output[0][O], ...,output[N-1][O],updates[0][U], ...,updates[N-1][U])
应用更新的顺序是不确定的。因此,当 updates 中的多个索引引用 operands 中的同一索引时,output 中的相应值将是不确定的。
请注意,传递到 update_computation 中的第一个参数始终是 output 数组中的当前值,第二个参数始终是 updates 数组中的值。这对于 update_computation 不可交换的情况尤为重要。
如果 indices_are_sorted 设置为 true,则 XLA 可以假设用户已对 scatter_indices 进行排序(按升序,在根据 scatter_dims_to_operand_dims 分散其值之后)。如果不是,则语义由实现定义。
如果 unique_indices 设置为 true,则 XLA 可以假定分散到的所有元素都是唯一的。因此,XLA 可以使用非原子操作。如果 unique_indices 设置为 true,并且要分散到的索引不是唯一的,则语义由实现定义。
从非正式的角度来看,scatter 操作可以视为 gather 操作的逆运算,也就是说,scatter 操作会更新输入中由相应 gather 操作提取的元素。
如需详细的非正式说明和示例,请参阅 Gather 下的“非正式说明”部分。
如需了解 StableHLO,请参阅 StableHLO - scatter。
Scatter - 示例 1 - StableHLO
在上图中,表格的每一行都是一个更新索引示例。我们从左侧(更新索引)到右侧(结果索引)逐步进行查看:
输入)input 的形状为 S32[2,3,4,2]。scatter_indices 的形状为 S64[2,2,3,2]。updates 的形状为 S32[2,2,3,1,2]。
更新索引)作为输入的一部分,我们获得了 update_window_dims:[3,4]。这表明 updates 的维度 3 和维度 4 是窗口维度,以黄色突出显示。这样我们就可以得出 update_scatter_dims = [0,1,2]。
更新散点图指数)显示了每个实体的提取 updated_scatter_dims。
(“更新索引”列的非黄色部分)
开始索引)查看 scatter_indices 张量图片,我们可以看到上一步(更新分散索引)中的值给出了开始索引的位置。从 index_vector_dim 中,我们还可以得知包含起始索引的 starting_indices 的维度,对于 scatter_indices,该维度为 3,大小为 2。
Full Start Index) scatter_dims_to_operand_dims = [2,1] 表示索引向量的第一个元素会传递给操作数维度 2。索引向量的第二个元素会传递给操作数维度 1。其余操作数维度填充为 0。
完整批处理指数)我们可以看到,紫色突出显示的区域显示在此列(完整批处理指数)、更新分散指数列和更新指数列中。
全窗口指数)根据 update_window_dimensions [3,4] 计算得出。
结果索引)operand 张量中添加了完整起始索引、完整批处理索引和完整窗口索引。请注意,绿色突出显示的区域也与 operand 图相对应。由于最后一行超出 operand 张量的范围,因此系统会跳过该行。
选择
另请参阅 XlaBuilder::Select。
根据谓词数组的值,从两个输入数组的元素构造一个输出数组。
Select(pred, on_true, on_false)
| 参数 | 类型 | 语义 |
|---|---|---|
pred |
XlaOp |
PRED 类型的数组 |
on_true |
XlaOp |
类型为 T 的数组 |
on_false |
XlaOp |
类型为 T 的数组 |
数组 on_true 和 on_false 必须具有相同的形状。这也是输出数组的形状。数组 pred 必须与 on_true 和 on_false 具有相同的维度,且元素类型为 PRED。
对于 pred 的每个元素 P,如果 P 的值为 true,则输出数组的对应元素取自 on_true;如果 P 的值为 false,则输出数组的对应元素取自 on_false。作为一种受限形式的广播,pred 可以是 PRED 类型的标量。在这种情况下,如果 pred 为 true,则输出数组完全取自 on_true;如果 pred 为 false,则输出数组完全取自 on_false。
使用非标量 pred 的示例:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
使用标量 pred 的示例:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
支持在元组之间进行选择。就此而言,元组被视为标量类型。如果 on_true 和 on_false 是元组(必须具有相同的形状!),则 pred 必须是 PRED 类型的标量。
如需了解 StableHLO,请参阅 StableHLO - 选择
SelectAndScatter
另请参阅 XlaBuilder::SelectAndScatter。
此操作可以视为一种复合操作,它首先计算 operand 数组的 ReduceWindow,以从每个窗口中选择一个元素,然后将 source 数组分散到所选元素的索引,以构建与操作数数组具有相同形状的输出数组。二元 select 函数用于通过在每个窗口中应用该函数来从每个窗口中选择一个元素,并且该函数在调用时具有以下属性:第一个形参的索引向量在字典编排上小于第二个形参的索引向量。如果选择第一个形参,select 函数会返回 true;如果选择第二个形参,则返回 false。该函数必须保持传递性(即,如果 select(a, b) 和 select(b, c) 为 true,则 select(a, c) 也为 true),这样一来,所选元素就不会依赖于给定窗口中遍历元素的顺序。
函数 scatter 会应用于输出数组中的每个所选索引。它接受两个标量参数:
- 输出数组中选定索引处的当前值
source中适用于所选索引的散列值
它会合并这两个形参,并返回一个标量值,用于更新输出数组中选定索引处的值。最初,输出数组的所有指数都设置为 init_value。
输出数组的形状与 operand 数组相同,并且 source 数组的形状必须与对 operand 数组应用 ReduceWindow 运算的结果相同。SelectAndScatter 可用于反向传播神经网络中池化层的梯度值。
SelectAndScatter(operand, select, window_dimensions, window_strides, padding,
source, init_value, scatter)
| 参数 | 类型 | 语义 |
|---|---|---|
operand
|
XlaOp
|
窗口滑动的 T 类型数组 |
select
|
XlaComputation
|
类型为 T, T
-> PRED 的二元计算,应用于每个窗口中的所有元素;如果选择第一个形参,则返回 true;如果选择第二个形参,则返回 false |
window_dimensions
|
ArraySlice<int64>
|
用于窗口维度值的整数数组 |
window_strides
|
ArraySlice<int64>
|
用于窗口步长值的整数数组 |
padding
|
Padding
|
窗口的填充类型(Padding::kSame 或 Padding::kValid) |
source
|
XlaOp
|
要分散的值的 T 类型数组 |
init_value
|
XlaOp
|
输出数组初始值的 T 类型标量值 |
scatter
|
XlaComputation
|
类型为 T, T
-> T 的二元计算,用于将每个分散源元素与其目标元素进行应用 |
下图展示了使用 SelectAndScatter 的示例,其中 select 函数用于计算其参数中的最大值。请注意,当窗口重叠时(如下图 [2] 所示),operand 数组的某个索引可能会被多个不同的窗口多次选中。在该图中,值为 9 的元素同时被顶部窗口(蓝色和红色)选中,而二元加法 scatter 函数会生成值为 8 (2 + 6) 的输出元素。
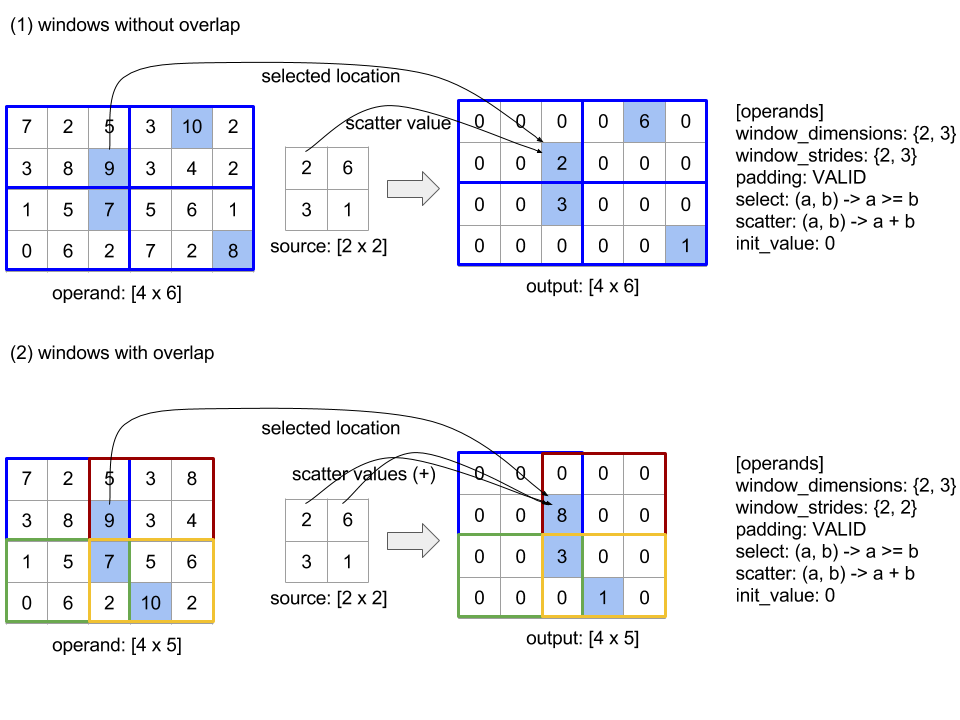
scatter 函数的评估顺序是任意的,可能具有不确定性。因此,scatter 函数不应过于敏感地对待重新关联。如需了解详情,请参阅有关 Reduce 上下文中的关联性的讨论。
如需了解 StableHLO,请参阅 StableHLO - select_and_scatter。
发送
另请参阅 XlaBuilder::Send。
Send、SendWithTokens 和 SendToHost 是在 HLO 中充当通信基元的操作。这些操作通常在 HLO 转储中显示为低级输入/输出或跨设备转移的一部分,但最终用户不应手动构建这些操作。
Send(operand, handle)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
要发送的数据(类型为 T 的数组) |
handle |
ChannelHandle |
每个发送/接收对的唯一标识符 |
将给定的操作数数据发送到共享同一渠道句柄的另一计算中的 Recv 指令。不返回任何数据。
与 Recv 操作类似,Send 操作的客户端 API 表示同步通信,并在内部分解为 2 个 HLO 指令(Send 和 SendDone),以实现异步数据传输。另请参阅 HloInstruction::CreateSend 和 HloInstruction::CreateSendDone。
Send(HloInstruction operand, int64 channel_id)
启动操作数到由具有相同通道 ID 的 Recv 指令分配的资源之间的异步转移。返回一个上下文,后续的 SendDone 指令会使用该上下文来等待数据传输完成。上下文是一个元组,包含 {操作数(形状)、请求标识符 (U32)},只能由 SendDone 指令使用。
如需了解 StableHLO,请参阅 StableHLO - 发送。
SendDone
另请参阅 HloInstruction::CreateSendDone。
SendDone(HloInstruction context)
给定由 Send 指令创建的上下文,等待数据传输完成。该指令不会返回任何数据。
频道指令的调度
每个渠道(Recv、RecvDone、Send、SendDone)的 4 条指令的执行顺序如下。
Recv发生在Send之前Send发生在RecvDone之前Recv发生在RecvDone之前Send发生在SendDone之前
当后端编译器为每个通过渠道指令进行通信的计算生成线性调度时,计算之间不得存在环路。例如,以下调度会导致死锁。
SetDimensionSize
另请参阅 XlaBuilder::SetDimensionSize。
设置给定维度的 XlaOp 的动态大小。操作数必须是数组形状。
SetDimensionSize(operand, val, dimension)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
n 维输入数组。 |
val |
XlaOp |
表示运行时动态大小的 int32。 |
dimension
|
int64
|
区间 [0, n) 中的一个值,用于指定维度。 |
将操作数作为结果传递,并由编译器跟踪动态维度。
填充值将被下游缩减操作忽略。
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
ShiftLeft
另请参阅 XlaBuilder::ShiftLeft。
对 lhs 执行元素级左移运算,移动位数为 rhs。
ShiftLeft(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
ShiftLeft 有一个支持不同维度广播的替代变体:
ShiftLeft(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - shift_left。
ShiftRightArithmetic
另请参阅 XlaBuilder::ShiftRightArithmetic。
对 lhs 执行按位算术右移运算,移动位数为 rhs。
ShiftRightArithmetic(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
ShiftRightArithmetic 存在另一种支持不同维度广播的变体:
ShiftRightArithmetic(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - shift_right_arithmetic。
ShiftRightLogical
另请参阅 XlaBuilder::ShiftRightLogical。
对 lhs 执行元素级逻辑右移运算,移动位数为 rhs。
ShiftRightLogical(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 ShiftRightLogical,存在一种支持不同维度广播的替代变体:
ShiftRightLogical(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - shift_right_logical。
签名
另请参阅 XlaBuilder::Sign。
Sign(operand) 元素级符号运算 x -> sgn(x),其中
\[\text{sgn}(x) = \begin{cases} -1 & x < 0\\ -0 & x = -0\\ NaN & x = NaN\\ +0 & x = +0\\ 1 & x > 0 \end{cases}\]
使用 operand 的元素类型的比较运算符。
Sign(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
如需了解 StableHLO,请参阅 StableHLO - 签名。
Sin
Sin(operand) 逐元素正弦 x -> sin(x)。
另请参阅 XlaBuilder::Sin。
Sin(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Sin 还支持可选的 result_accuracy 实参:
Sin(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
如需了解 StableHLO,请参阅 StableHLO - 正弦。
切片
另请参阅 XlaBuilder::Slice。
切片可从输入数组中提取子数组。子数组的维度数与输入相同,并且包含输入数组中边界框内的值,其中边界框的维度和索引作为切片运算的实参给出。
Slice(operand, start_indices, limit_indices, strides)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
类型为 T 的 N 维数组 |
start_indices
|
ArraySlice<int64>
|
包含每个维度的切片起始索引的 N 个整数的列表。值必须大于或等于零。 |
limit_indices
|
ArraySlice<int64>
|
包含 N 个整数的列表,其中包含每个维度的切片的结束索引(不含)。每个值都必须大于或等于相应维度的 start_indices 值,且小于或等于相应维度的大小。 |
strides
|
ArraySlice<int64>
|
一个包含 N 个整数的列表,用于决定切片的输入步幅。切片会选择维度 d 中的每个 strides[d] 元素。 |
1 维示例:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4})
// Result: {2.0, 3.0}
二维示例:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3})
// Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
如需了解 StableHLO,请参阅 StableHLO - slice。
排序
另请参阅 XlaBuilder::Sort。
Sort(operands, comparator, dimension, is_stable)
| 参数 | 类型 | 语义 |
|---|---|---|
operands |
ArraySlice<XlaOp> |
要排序的实参。 |
comparator |
XlaComputation |
要使用的比较器计算。 |
dimension |
int64 |
要排序的维度。 |
is_stable |
bool |
是否应使用稳定排序。 |
如果仅提供一个操作数:
如果操作数是一维张量(数组),则结果是排序后的数组。如果您想按升序对数组进行排序,比较器应执行小于比较。从形式上讲,在对数组进行排序后,对于所有索引位置
i, j(其中i < j为comparator(value[i], value[j]) = comparator(value[j], value[i]) = false或comparator(value[i], value[j]) = true),该数组都成立。如果操作数的维度数较高,则沿提供的维度对操作数进行排序。例如,对于二维张量(矩阵),维度值为
0将独立对每个列进行排序,维度值为1将独立对每个行进行排序。如果未提供维度编号,则默认选择最后一个维度。对于已排序的维度,排序顺序与一维情况下的排序顺序相同。
如果提供了 n > 1 实参:
所有
n操作数都必须是具有相同维度的张量。张量的元素类型可能不同。所有操作数一起排序,而不是单独排序。从概念上讲,操作数被视为一个元组。在检查索引位置
i和j处每个操作数的元素是否需要交换时,系统会使用2 * n标量参数调用比较器,其中参数2 * k对应于k-th操作数中位置i处的值,参数2 * k + 1对应于k-th操作数中位置j处的值。因此,比较器通常会比较参数2 * k和2 * k + 1,并可能会使用其他参数对作为平局决胜因素。结果是一个元组,其中包含按排序顺序排列的运算对象(沿提供的维度,如上所示)。元组的
i-th运算数对应于 Sort 的i-th运算数。
例如,如果有三个操作数 operand0 = [3, 1]、operand1 = [42, 50]、operand2 = [-3.0, 1.1],并且比较器仅使用小于运算符比较 operand0 的值,则排序的输出为元组 ([1, 3], [50, 42], [1.1, -3.0])。
如果 is_stable 设置为 true,则保证排序是稳定的,也就是说,如果比较器认为存在相等的元素,则会保留相等值的相对顺序。当且仅当 comparator(e1, e2) = comparator(e2, e1) = false 时,两个元素 e1 和 e2 相等。默认情况下,is_stable 设置为 false。
如需了解 StableHLO,请参阅 StableHLO - 排序。
Sqrt
另请参阅 XlaBuilder::Sqrt。
元素级平方根运算 x -> sqrt(x)。
Sqrt(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Sqrt 还支持可选的 result_accuracy 实参:
Sqrt(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
如需了解 StableHLO,请参阅 StableHLO - sqrt。
子级
另请参阅 XlaBuilder::Sub。
对 lhs 和 rhs 执行逐元素减法。
Sub(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Sub,存在一种具有不同维度广播支持的替代变体:
Sub(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - subtract。
棕黄色
另请参阅 XlaBuilder::Tan。
按元素求正切 x -> tan(x)。
Tan(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Tan 还支持可选的 result_accuracy 实参:
Tan(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
如需了解 StableHLO,请参阅 StableHLO - tan。
Tanh
另请参阅 XlaBuilder::Tanh。
按元素计算的双曲正切 x -> tanh(x)。
Tanh(operand)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
Tanh 还支持可选的 result_accuracy 实参:
Tanh(operand, result_accuracy)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
函数的实参 |
result_accuracy
|
可选 ResultAccuracy
|
用户可以为具有多种实现的单目运算请求的准确度类型 |
如需详细了解 result_accuracy,请参阅结果准确性。
如需了解 StableHLO,请参阅 StableHLO - tanh。
TopK
另请参阅 XlaBuilder::TopK。
TopK 用于查找给定张量最后一个维度中 k 个最大或最小元素的值和索引。
TopK(operand, k, largest)
| 参数 | 类型 | 语义 |
|---|---|---|
operand
|
XlaOp
|
要从中提取前 k 个元素的张量。
张量的维度必须大于或等于 1。张量最后一个维度的大小必须大于或等于 k。 |
k |
int64 |
要提取的元素数量。 |
largest
|
bool
|
是否提取最大或最小的 k 个元素。 |
对于一维输入张量(数组),查找数组中 k 个最大或最小的条目,并输出包含两个数组 (values, indices) 的元组。因此,values[j] 是 operand 中第 j 大/小的条目,其指数为 indices[j]。
对于维度数大于 1 的输入张量,沿最后一个维度计算前 k 个条目,并在输出中保留所有其他维度(行)。
因此,对于形状为 [A, B, ..., P, Q](其中 Q >= k)的操作数,输出是一个元组 (values, indices),其中:
values.shape = indices.shape = [A, B, ..., P, k]
如果某行中的两个元素相等,则索引较低的元素会先显示。
Transpose
另请参阅 tf.reshape 操作。
Transpose(operand, permutation)
| 参数 | 类型 | 语义 |
|---|---|---|
operand |
XlaOp |
要转置的操作数。 |
permutation |
ArraySlice<int64> |
如何对维度进行置换。 |
使用给定的置换来置换操作数维度,因此 ∀ i . 0 ≤ i < number of dimensions ⇒
input_dimensions[permutation[i]] = output_dimensions[i]。
这与 Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)) 相同。
如需了解 StableHLO,请参阅 StableHLO - 转置。
TriangularSolve
另请参阅 XlaBuilder::TriangularSolve。
通过前向或后向替换来求解具有下三角或上三角系数矩阵的线性方程组。此例程沿前导维度进行广播,用于求解矩阵系统 op(a) * x =
b 或 x * op(a) = b 中的变量 x(给定 a 和 b),其中 op(a) 为 op(a) = a、op(a) = Transpose(a) 或 op(a) = Conj(Transpose(a))。
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| 参数 | 类型 | 语义 |
|---|---|---|
a
|
XlaOp
|
维度大于 2 的复数或浮点类型数组,形状为 [..., M,
M]。 |
b
|
XlaOp
|
如果 left_side 为 true,则为形状为 [..., M, K] 的同类型多维数组(维度数 > 2);否则为 [..., K, M]。 |
left_side
|
bool
|
用于指明是求解 op(a) * x = b (true) 形式的系统还是 x *
op(a) = b (false) 形式的系统。 |
lower
|
bool
|
是否使用 a 的上三角或下三角。 |
unit_diagonal
|
bool
|
如果为 true,则假定 a 的对角线元素为 1,并且不会访问这些元素。 |
transpose_a
|
Transpose
|
是按原样使用 a,还是对其进行转置或共轭转置。 |
输入数据仅从 a 的下/上三角读取,具体取决于 lower 的值。系统会忽略另一个三角形中的值。输出数据在同一三角形中返回;另一三角形中的值由实现定义,可以是任何值。
如果 a 和 b 的维度数大于 2,则它们会被视为矩阵批次,其中除了次要的 2 个维度之外,所有维度都是批次维度。a 和 b 必须具有相同的批次维度。
如需了解 StableHLO,请参阅 StableHLO - triangular_solve。
元组
另请参阅 XlaBuilder::Tuple。
一个元组,包含数量可变的数据句柄,每个句柄都有自己的形状。
Tuple(elements)
| 参数 | 类型 | 语义 |
|---|---|---|
elements |
XlaOp 的矢量 |
类型为 T 的 N 数组 |
这类似于 C++ 中的 std::tuple。从概念上讲:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
可以通过 GetTupleElement 操作解构(访问)元组。
如需了解 StableHLO,请参阅 StableHLO - 元组。
虽然
另请参阅 XlaBuilder::While。
While(condition, body, init)
| 参数 | 类型 | 语义 |
|---|---|---|
condition
|
XlaComputation
|
类型为 T -> PRED 的 XlaComputation,用于定义循环的终止条件。 |
body
|
XlaComputation
|
类型为 T -> T 的 XlaComputation,用于定义循环的正文。 |
init
|
T
|
condition 和 body 参数的初始值。 |
按顺序执行 body,直到 condition 失败。这与许多其他语言中的典型 while 循环类似,但存在以下列出的区别和限制。
While节点会返回T类型的值,该值是body的最后一次执行结果。- 类型为
T的形状是静态确定的,并且在所有迭代中必须相同。
计算的 T 形参在第一次迭代时会初始化为 init 值,并在后续每次迭代时自动更新为 body 的新结果。
While 节点的一个主要用例是实现神经网络中训练的重复执行。下面的简化伪代码显示了一个表示计算的图。您可以在 while_test.cc 中找到该代码。
此示例中的类型 T 是一个 Tuple,包含用于迭代次数的 int32 和用于累加器的 vector[10]。对于 1, 000 次迭代,循环会不断向累加器添加一个常量向量。
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}
如需了解 StableHLO,请参阅 StableHLO - while。
Xor
另请参阅 XlaBuilder::Xor。
对 lhs 和 rhs 执行按元素异或运算。
Xor(lhs, rhs)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
实参的形状必须相似或兼容。如需了解形状兼容性的含义,请参阅有关广播的文档。运算结果的形状是广播两个输入数组的结果。在此变体中,不支持不同秩的数组之间的运算,除非其中一个操作数是标量。
对于 Xor,存在一种具有不同维度广播支持的替代变体:
Xor(lhs,rhs, broadcast_dimensions)
| 参数 | 类型 | 语义 |
|---|---|---|
| lhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| rhs | XlaOp | 左侧操作数:类型为 T 的数组 |
| broadcast_dimension | ArraySlice |
操作数形状的每个维度对应于目标形状中的哪个维度 |
此变体应用于不同秩的数组之间的算术运算(例如将矩阵添加到向量)。
额外的 broadcast_dimensions 操作数是一个整数切片,用于指定广播操作数时要使用的维度。广播页面上详细介绍了这些语义。
如需了解 StableHLO,请参阅 StableHLO - xor。








