다음은 XlaBuilder 인터페이스에 정의된 작업의 시맨틱을 설명합니다. 일반적으로 이러한 작업은 xla_data.proto의 RPC 인터페이스에 정의된 작업에 일대일로 매핑됩니다.
명명법에 관한 참고사항: XLA가 처리하는 일반화된 데이터 유형은 균일한 유형 (예: 32비트 부동 소수점)의 요소를 보유하는 N차원 배열입니다. 문서 전체에서 배열은 임의 차원 배열을 나타내는 데 사용됩니다. 편의를 위해 특수한 사례에는 더 구체적이고 친숙한 이름이 있습니다. 예를 들어 벡터는 1차원 배열이고 행렬은 2차원 배열입니다.
모양 및 레이아웃과 타일식 레이아웃에서 작업의 구조에 대해 자세히 알아보세요.
복근
XlaBuilder::Abs도 참고하세요.
요소별 abs x -> |x|.
Abs(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
StableHLO 정보는 StableHLO - abs를 참고하세요.
추가
XlaBuilder::Add도 참고하세요.
lhs과 rhs의 요소별 덧셈을 실행합니다.
Add(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
추가의 경우 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Add(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - 추가를 참고하세요.
AddDependency
HloInstruction::AddDependency도 참고하세요.
AddDependency는 HLO 덤프에 표시될 수 있지만 최종 사용자가 수동으로 구성하도록 설계되지 않았습니다.
AfterAll
XlaBuilder::AfterAll도 참고하세요.
AfterAll은 가변 개수의 토큰을 가져와 단일 토큰을 생성합니다. 토큰은 순서를 적용하기 위해 부작용이 있는 작업 간에 스레딩할 수 있는 기본 유형입니다. AfterAll는 일련의 작업 후 작업을 정렬하기 위한 토큰의 조인으로 사용할 수 있습니다.
AfterAll(tokens)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
tokens |
XlaOp 벡터 |
가변 개수의 토큰 |
StableHLO 정보는 StableHLO - after_all을 참고하세요.
AllGather
XlaBuilder::AllGather도 참고하세요.
복제본 간에 연결을 실행합니다.
AllGather(operand, all_gather_dimension, shard_count, replica_groups,
channel_id, layout, use_global_device_ids)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand
|
XlaOp
|
복제본에서 연결할 배열 |
all_gather_dimension |
int64 |
연결 측정기준 |
shard_count
|
int64
|
각 복제본 그룹의 크기 |
replica_groups
|
벡터의 벡터
int64 |
연결이 수행되는 그룹 |
channel_id
|
선택사항
ChannelHandle |
크로스 모듈 통신을 위한 선택적 채널 ID |
layout
|
선택사항 Layout
|
인수에서 일치하는 레이아웃을 캡처하는 레이아웃 패턴을 만듭니다. |
use_global_device_ids
|
선택사항 bool
|
ReplicaGroup 구성의 ID가 전역 ID를 나타내는 경우 true를 반환합니다. |
replica_groups는 연결이 실행되는 복제본 그룹 목록입니다 (현재 복제본의 복제본 ID는ReplicaId를 사용하여 가져올 수 있음). 각 그룹의 복제본 순서에 따라 결과에서 입력이 배치되는 순서가 결정됩니다.replica_groups는 비어 있거나 (이 경우 모든 복제본이0에서N - 1까지 순서대로 단일 그룹에 속함) 복제본 수와 동일한 수의 요소를 포함해야 합니다. 예를 들어replica_groups = {0, 2}, {1, 3}는 복제본0와2,1와3간에 연결을 실행합니다.shard_count은 각 복제본 그룹의 크기입니다.replica_groups가 비어 있는 경우에 필요합니다.channel_id는 교차 모듈 통신에 사용됩니다. 동일한channel_id를 사용하는all-gather작업만 서로 통신할 수 있습니다.use_global_device_ids복제본 ID 대신 ReplicaGroup 구성의 ID가 (replica_id * partition_count + partition_id)의 전역 ID를 나타내는 경우 true를 반환합니다. 이 경우 모든 축소가 파티션 간 및 복제본 간에 모두 적용되면 기기를 더 유연하게 그룹화할 수 있습니다.
출력 모양은 all_gather_dimension이 shard_count배 커진 입력 모양입니다. 예를 들어 복제본이 두 개 있고 피연산자의 값이 두 복제본에서 각각 [1.0, 2.5] 및 [3.0, 5.25]인 경우 all_gather_dim이 0인 이 작업의 출력 값은 두 복제본에서 [1.0, 2.5, 3.0,5.25]가 됩니다.
AllGather API는 내부적으로 2개의 HLO 명령(AllGatherStart 및 AllGatherDone)으로 분해됩니다.
HloInstruction::CreateAllGatherStart도 참고하세요.
AllGatherStart, AllGatherDone은 HLO에서 프리미티브로 사용됩니다. 이러한 작업은 HLO 덤프에 표시될 수 있지만 최종 사용자가 수동으로 구성하도록 설계되지 않았습니다.
StableHLO 정보는 StableHLO - all_gather를 참고하세요.
AllReduce
XlaBuilder::AllReduce도 참고하세요.
복제본 전반에서 맞춤 계산을 실행합니다.
AllReduce(operand, computation, replica_groups, channel_id,
shape_with_layout, use_global_device_ids)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand
|
XlaOp
|
복제본에서 축소할 배열 또는 비어 있지 않은 배열 튜플 |
computation |
XlaComputation |
감소 계산 |
replica_groups
|
ReplicaGroup 벡터
|
축소가 실행되는 그룹 |
channel_id
|
선택사항
ChannelHandle |
크로스 모듈 통신을 위한 선택적 채널 ID |
shape_with_layout
|
선택사항 Shape
|
전송된 데이터의 레이아웃을 정의합니다. |
use_global_device_ids
|
선택사항 bool
|
ReplicaGroup 구성의 ID가 전역 ID를 나타내는 경우 true를 반환합니다. |
operand이 배열 튜플인 경우 튜플의 각 요소에서 all-reduce가 실행됩니다.replica_groups는 축소가 실행되는 복제본 그룹의 목록입니다 (현재 복제본의 복제본 ID는ReplicaId를 사용하여 가져올 수 있음).replica_groups는 비어 있거나 (이 경우 모든 복제본이 단일 그룹에 속함) 복제본 수와 동일한 수의 요소를 포함해야 합니다. 예를 들어replica_groups = {0, 2}, {1, 3}는 복제본0와2,1와3간에 축소를 실행합니다.channel_id는 교차 모듈 통신에 사용됩니다. 동일한channel_id를 사용하는all-reduce작업만 서로 통신할 수 있습니다.shape_with_layout: AllReduce의 레이아웃을 지정된 레이아웃으로 강제합니다. 별도로 컴파일된 AllReduce 작업 그룹에 동일한 레이아웃을 보장하는 데 사용됩니다.use_global_device_ids복제본 ID 대신 ReplicaGroup 구성의 ID가 (replica_id * partition_count + partition_id)의 전역 ID를 나타내는 경우 true를 반환합니다. 이 경우 모든 축소가 파티션 간 및 복제본 간에 모두 적용되면 기기를 더 유연하게 그룹화할 수 있습니다.
출력 모양은 입력 모양과 동일합니다. 예를 들어 복제본이 두 개 있고 피연산자의 값이 두 복제본에서 각각 [1.0, 2.5] 및 [3.0, 5.25]인 경우 이 작업과 합계 계산의 출력 값은 두 복제본 모두에서 [4.0, 7.75]가 됩니다. 입력이 튜플이면 출력도 튜플입니다.
AllReduce 결과를 계산하려면 각 복제본의 입력이 하나씩 있어야 하므로 한 복제본이 다른 복제본보다 AllReduce 노드를 더 많이 실행하면 전자의 복제본이 영원히 대기합니다. 복제본이 모두 동일한 프로그램을 실행하므로 이러한 상황이 발생할 가능성은 크지 않지만, while 루프의 조건이 infeed의 데이터에 따라 달라지고 infeed의 데이터로 인해 한 복제본에서 다른 복제본보다 while 루프가 더 많이 반복되는 경우 가능합니다.
AllReduce API는 내부적으로 2개의 HLO 명령(AllReduceStart 및 AllReduceDone)으로 분해됩니다.
HloInstruction::CreateAllReduceStart도 참고하세요.
AllReduceStart 및 AllReduceDone는 HLO에서 기본 요소로 사용됩니다. 이러한 작업은 HLO 덤프에 표시될 수 있지만 최종 사용자가 수동으로 구성하도록 설계되지 않았습니다.
CrossReplicaSum
XlaBuilder::CrossReplicaSum도 참고하세요.
합계 계산을 사용하여 AllReduce을 실행합니다.
CrossReplicaSum(operand, replica_groups)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand
|
XlaOp | 복제본에서 축소할 배열 또는 비어 있지 않은 배열 튜플 |
replica_groups
|
int64 벡터의 벡터 |
축소가 실행되는 그룹 |
복제본의 각 하위 그룹 내 피연산자 값의 합계를 반환합니다. 모든 복제본은 합계에 하나의 입력을 제공하고 모든 복제본은 각 하위 그룹의 결과 합계를 수신합니다.
AllToAll
XlaBuilder::AllToAll도 참고하세요.
AllToAll은 모든 코어에서 모든 코어로 데이터를 전송하는 집단 연산입니다. 두 단계로 구성됩니다.
- 분산 단계 각 코어에서 피연산자는
split_dimensions를 따라split_count개의 블록으로 분할되고 블록은 모든 코어에 분산됩니다. 예를 들어 i번째 블록은 i번째 코어로 전송됩니다. - 수집 단계 각 코어는
concat_dimension를 따라 수신된 블록을 연결합니다.
참여하는 코어는 다음을 통해 구성할 수 있습니다.
replica_groups: 각 ReplicaGroup에는 계산에 참여하는 복제본 ID 목록이 포함됩니다 (현재 복제본의 복제본 ID는ReplicaId를 사용하여 가져올 수 있음). AllToAll은 지정된 순서로 하위 그룹 내에서 적용됩니다. 예를 들어replica_groups = { {1,2,3}, {4,5,0} }는 AllToAll이 복제본{1, 2, 3}내에서 수집 단계에 적용되며 수신된 블록이 1, 2, 3과 동일한 순서로 연결됨을 의미합니다. 그런 다음 복제본 4, 5, 0 내에서 또 다른 AllToAll이 적용되고 연결 순서도 4, 5, 0입니다.replica_groups이 비어 있으면 모든 복제본이 표시되는 연결 순서대로 하나의 그룹에 속합니다.
기본 요건:
split_dimension의 피연산자 차원 크기는split_count로 나눌 수 있습니다.- 피연산자의 모양이 튜플이 아닙니다.
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups, layout, channel_id)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
n차원 입력 배열 |
split_dimension
|
int64
|
피연산자가 분할되는 차원의 이름을 지정하는 [0,n) 간격의 값 |
concat_dimension
|
int64
|
[0,n) 간격의 값으로, 분할 블록이 연결되는 측정기준의 이름을 지정합니다. |
split_count
|
int64
|
이 작업에 참여하는 코어 수입니다. replica_groups이 비어 있으면 복제본 수여야 하고, 그렇지 않으면 각 그룹의 복제본 수와 같아야 합니다. |
replica_groups
|
ReplicaGroupvector
|
각 그룹에는 복제본 ID 목록이 포함됩니다. |
layout |
선택사항 Layout |
사용자 지정 메모리 레이아웃 |
channel_id
|
선택사항 ChannelHandle
|
각 송수신 쌍의 고유 식별자 |
모양 및 레이아웃에 관한 자세한 내용은 xla::shapes를 참고하세요.
StableHLO 정보는 StableHLO - all_to_all을 참고하세요.
AllToAll - 예 1.
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(
x,
/*split_dimension=*/ 1,
/*concat_dimension=*/ 0,
/*split_count=*/ 4);
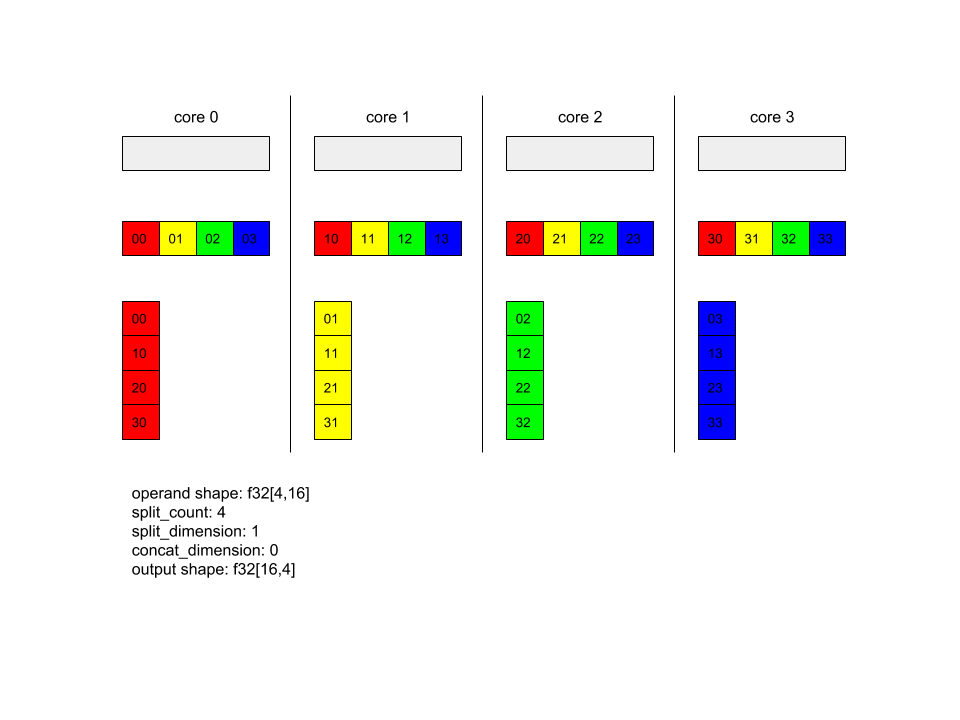
위 예에서는 Alltoall에 참여하는 코어가 4개 있습니다. 각 코어에서 피연산자는 1차원을 따라 4개 부분으로 분할되므로 각 부분의 모양은 f32[4,4]입니다. 4개의 파트가 모든 코어에 분산됩니다. 그런 다음 각 코어는 코어 0~4 순서로 수신된 부분을 0번째 차원을 따라 연결합니다. 따라서 각 코어의 출력에는 f32[16,4] 모양이 있습니다.
AllToAll - 예 2 - StableHLO
위의 예에서는 AllToAll에 참여하는 복제본이 2개 있습니다. 각 복제본에서 피연산자의 모양은 f32[2,4]입니다. 피연산자는 차원 1을 따라 2개 부분으로 분할되므로 각 부분의 모양은 f32[2,2]입니다. 그런 다음 두 부분이 복제본 그룹에서의 위치에 따라 복제본 간에 교환됩니다. 각 복제본은 두 피연산자에서 해당 부분을 수집하고 0번째 차원을 따라 연결합니다. 따라서 각 복제본의 출력은 f32[4,2] 모양을 갖습니다.
RaggedAllToAll
XlaBuilder::RaggedAllToAll도 참고하세요.
RaggedAllToAll은 입력과 출력이 러그드 텐서인 집단 all-to-all 작업을 실행합니다.
RaggedAllToAll(input, input_offsets, send_sizes, output, output_offsets,
recv_sizes, replica_groups, channel_id)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
input |
XlaOp |
T 유형의 N 배열 |
input_offsets |
XlaOp |
T 유형의 N 배열 |
send_sizes |
XlaOp |
T 유형의 N 배열 |
output |
XlaOp |
T 유형의 N 배열 |
output_offsets |
XlaOp |
T 유형의 N 배열 |
recv_sizes |
XlaOp |
T 유형의 N 배열 |
replica_groups
|
ReplicaGroup 벡터
|
각 그룹에는 복제본 ID 목록이 포함됩니다. |
channel_id
|
선택사항 ChannelHandle
|
각 송수신 쌍의 고유 식별자 |
러그드 텐서는 다음 세 텐서의 집합으로 정의됩니다.
data:data텐서가 가장 바깥쪽 차원을 따라 '러그드'합니다. 이 차원을 따라 각 색인 요소의 크기가 가변적입니다.offsets':offsets텐서는data텐서의 가장 바깥쪽 차원을 색인화하고data텐서의 각 러그드 요소의 시작 오프셋을 나타냅니다.sizes:sizes텐서는data텐서의 각 러그드 요소의 크기를 나타내며, 크기는 하위 요소 단위로 지정됩니다. 하위 요소는 가장 바깥쪽의 '러그드' 차원을 삭제하여 얻은 '데이터' 텐서 모양의 접미사로 정의됩니다.offsets및sizes텐서의 크기는 동일해야 합니다.
러그드 텐서의 예:
data: [8,3] =
{ {a,b,c},{d,e,f},{g,h,i},{j,k,l},{m,n,o},{p,q,r},{s,t,u},{v,w,x} }
offsets: [3] = {0, 1, 4}
sizes: [3] = {1, 3, 4}
// Index 'data' at 'offsets'[0], 'sizes'[0]' // {a,b,c}
// Index 'data' at 'offsets'[1], 'sizes'[1]' // {d,e,f},{g,h,i},{j,k,l}
// Index 'data' at 'offsets'[2], 'sizes'[2]' // {m,n,o},{p,q,r},{s,t,u},{v,w,x}
output_offsets는 각 복제본이 타겟 복제본 출력 관점에서 오프셋을 갖도록 샤딩되어야 합니다.
i번째 출력 오프셋의 경우 현재 복제본은 i번째 복제본에 input[input_offsets[i]:input_offsets[i]+input_sizes[i]] 업데이트를 전송하며, 이는 i번째 복제본 output의 output_i[output_offsets[i]:output_offsets[i]+send_sizes[i]]에 기록됩니다.
예를 들어 복제본이 2개인 경우
replica 0:
input: [1, 2, 2]
output:[0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 2]
output_offsets: [0, 0]
recv_sizes: [1, 1]
replica 1:
input: [3, 4, 0]
output: [0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 1]
output_offsets: [1, 2]
recv_sizes: [2, 1]
// replica 0's result will be: [1, 3, 0, 0]
// replica 1's result will be: [2, 2, 4, 0]
불규칙한 all-to-all HLO에는 다음 인수가 있습니다.
input: 비정형 입력 데이터 텐서입니다.output: 러그 출력 데이터 텐서입니다.input_offsets: 비정형 입력 오프셋 텐서입니다.send_sizes: 비정형 전송 크기 텐서입니다.output_offsets: 타겟 복제본 출력의 불규칙한 오프셋 배열입니다.recv_sizes: 러그드 recv 크기 텐서입니다.
*_offsets 및 *_sizes 텐서의 모양은 모두 동일해야 합니다.
*_offsets 및 *_sizes 텐서에는 두 가지 모양이 지원됩니다.
[num_devices]. 여기서 ragged-all-to-all은 복제본 그룹의 각 원격 기기에 최대 하나의 업데이트를 보낼 수 있습니다. 예를 들면 다음과 같습니다.
for (remote_device_id : replica_group) {
SEND input[input_offsets[remote_device_id]],
output[output_offsets[remote_device_id]],
send_sizes[remote_device_id] }
[num_devices, num_updates]: 모든 기기에 불균형한 경우 최대num_updates업데이트를 동일한 원격 기기에 전송할 수 있습니다 (각각 다른 오프셋에서). 복제본 그룹의 각 원격 기기에 대해
예를 들면 다음과 같습니다.
for (remote_device_id : replica_group) {
for (update_idx : num_updates) {
SEND input[input_offsets[remote_device_id][update_idx]],
output[output_offsets[remote_device_id][update_idx]]],
send_sizes[remote_device_id][update_idx] } }
그리고
XlaBuilder::And도 참고하세요.
두 텐서 lhs와 rhs의 요소별 AND를 실행합니다.
And(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
And의 경우 다양한 차원의 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
And(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - and를 참고하세요.
비동기식
HloInstruction::CreateAsyncStart,
HloInstruction::CreateAsyncUpdate,
HloInstruction::CreateAsyncDone도 참고하세요.
AsyncDone, AsyncStart, AsyncUpdate는 비동기 작업에 사용되는 내부 HLO 명령어이며 HLO의 기본 요소로 사용됩니다. 이러한 작업은 HLO 덤프에 표시될 수 있지만 최종 사용자가 수동으로 구성해서는 안 됩니다.
Atan2
XlaBuilder::Atan2도 참고하세요.
lhs 및 rhs에 대해 요소별 atan2 연산을 실행합니다.
Atan2(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Atan2의 경우 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Atan2(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - atan2를 참고하세요.
BatchNormGrad
알고리즘에 관한 자세한 설명은 XlaBuilder::BatchNormGrad 및 원래 배치 정규화 논문을 참고하세요.
배치 정규화의 그라데이션을 계산합니다.
BatchNormGrad(operand, scale, batch_mean, batch_var, grad_output, epsilon,
feature_index)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp | 정규화할 n차원 배열 (x) |
scale |
XlaOp | 1차원 배열 (\(\gamma\)) |
batch_mean |
XlaOp | 1차원 배열 (\(\mu\)) |
batch_var |
XlaOp | 1차원 배열 (\(\sigma^2\)) |
grad_output |
XlaOp | BatchNormTraining (\(\nabla y\))에 전달된 그라데이션 |
epsilon |
float |
엡실론 값 (\(\epsilon\)) |
feature_index |
int64 |
operand의 특성 차원 색인 |
기능 측정기준 (operand에서 기능 측정기준의 색인은 feature_index)의 각 기능에 대해 이 작업은 다른 모든 측정기준에서 operand, offset, scale에 관한 그라데이션을 계산합니다. feature_index은 operand의 기능 측정기준에 대한 유효한 색인이어야 합니다.
세 가지 그라데이션은 다음 공식으로 정의됩니다 (4차원 배열을 operand로 가정하고 특징 차원 색인 l, 배치 크기 m, 공간 크기 w 및 h 사용).
\[ \begin{split} c_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sigma^2_l+\epsilon} \right) \\\\ d_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \\\\ \nabla x_{ijkl} &= \frac{\gamma_{l} }{\sqrt{\sigma^2_{l}+\epsilon} } \left( \nabla y_{ijkl} - d_l - c_l (x_{ijkl} - \mu_{l}) \right) \\\\ \nabla \gamma_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sqrt{\sigma^2_{l}+\epsilon} } \right) \\\\\ \nabla \beta_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \end{split} \]
입력 batch_mean 및 batch_var은 배치 및 공간 차원에 걸친 모멘트 값을 나타냅니다.
출력 유형은 다음 세 핸들의 튜플입니다.
| 출력 | 유형 | 시맨틱스 |
|---|---|---|
grad_operand
|
XlaOp | 입력 operand(\(\nabla x\))에 관한 그라데이션 |
grad_scale
|
XlaOp | 입력 **scale **에 관한 그라데이션(\(\nabla\gamma\)) |
grad_offset
|
XlaOp | 입력 offset(\(\nabla\beta\))에 관한 그라데이션 |
StableHLO 정보는 StableHLO - batch_norm_grad를 참고하세요.
BatchNormInference
알고리즘에 관한 자세한 설명은 XlaBuilder::BatchNormInference 및 원래 배치 정규화 논문을 참고하세요.
배치 및 공간 차원에서 배열을 정규화합니다.
BatchNormInference(operand, scale, offset, mean, variance, epsilon,
feature_index)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp | 정규화할 n차원 배열 |
scale |
XlaOp | 1차원 배열 |
offset |
XlaOp | 1차원 배열 |
mean |
XlaOp | 1차원 배열 |
variance |
XlaOp | 1차원 배열 |
epsilon |
float |
엡실론 값 |
feature_index |
int64 |
operand의 특성 차원 색인 |
이 작업은 특성 차원 (feature_index은 operand의 특성 차원 색인)의 각 특성에 대해 다른 모든 차원에서 평균과 분산을 계산하고 평균과 분산을 사용하여 operand의 각 요소를 정규화합니다. feature_index은 operand의 특징 차원에 대한 유효한 색인이어야 합니다.
BatchNormInference은 각 배치에 대해 mean 및 variance를 계산하지 않고 BatchNormTraining를 호출하는 것과 같습니다. 대신 입력 mean 및 variance를 추정된 값으로 사용합니다. 이 작업의 목적은 추론의 지연 시간을 줄이는 것이므로 이름이 BatchNormInference입니다.
출력은 입력 operand와 모양이 동일한 n차원 정규화된 배열입니다.
StableHLO 정보는 StableHLO - batch_norm_inference를 참고하세요.
BatchNormTraining
알고리즘에 대한 자세한 설명은 XlaBuilder::BatchNormTraining 및 the original batch normalization paper도 참고하세요.
배치 및 공간 차원에서 배열을 정규화합니다.
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
정규화할 n차원 배열 (x) |
scale |
XlaOp |
1차원 배열 (\(\gamma\)) |
offset |
XlaOp |
1차원 배열 (\(\beta\)) |
epsilon |
float |
엡실론 값 (\(\epsilon\)) |
feature_index |
int64 |
operand의 특성 차원 색인 |
특성 차원 (feature_index은 operand의 특성 차원 색인)의 각 특성에 대해 이 작업은 다른 모든 차원에서 평균과 분산을 계산하고 평균과 분산을 사용하여 operand의 각 요소를 정규화합니다. feature_index은 operand의 특징 차원에 대한 유효한 색인이어야 합니다.
w 및 h이 공간 차원의 크기인 m 요소를 포함하는 operand \(x\) 의 각 배치에 대해 알고리즘은 다음과 같이 진행됩니다 (operand이 4차원 배열이라고 가정).
특성 차원에서 각 특성
l의 배치 평균 \(\mu_l\) 을 계산합니다. \(\mu_l=\frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h x_{ijkl}\)배치 분산을 계산합니다. \(\sigma^2_l\): $\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
정규화, 스케일링, 이동: \(y_{ijkl}=\frac{\gamma_l(x_{ijkl}-\mu_l)}{\sqrt[2]{\sigma^2_l+\epsilon} }+\beta_l\)
일반적으로 작은 숫자인 엡실론 값은 0으로 나누기 오류를 방지하기 위해 추가됩니다.
출력 유형은 세 개의 XlaOp 튜플입니다.
| 출력 | 유형 | 시맨틱스 |
|---|---|---|
output
|
XlaOp
|
입력 operand (y)와 모양이 동일한 n차원 배열 |
batch_mean |
XlaOp |
1차원 배열 (\(\mu\)) |
batch_var |
XlaOp |
1차원 배열 (\(\sigma^2\)) |
batch_mean 및 batch_var은 위의 공식을 사용하여 배치 및 공간 차원에서 계산된 모멘트입니다.
StableHLO 정보는 StableHLO - batch_norm_training을 참고하세요.
Bitcast
HloInstruction::CreateBitcast도 참고하세요.
Bitcast는 HLO 덤프에 표시될 수 있지만 최종 사용자가 수동으로 구성하도록 설계되지 않았습니다.
BitcastConvertType
XlaBuilder::BitcastConvertType도 참고하세요.
TensorFlow의 tf.bitcast와 유사하게 데이터 모양에서 타겟 모양으로 요소별 bitcast 작업을 실행합니다. 입력 및 출력 크기가 일치해야 합니다. 예를 들어 s32 요소는 비트캐스트 루틴을 통해 f32 요소가 되고 하나의 s32 요소는 4개의 s8 요소가 됩니다. 비트캐스트는 하위 수준 캐스트로 구현되므로 부동 소수점 표현이 다른 머신은 다른 결과를 제공합니다.
BitcastConvertType(operand, new_element_type)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
차원 D가 있는 T 유형의 배열 |
new_element_type |
PrimitiveType |
type U |
피연산자와 타겟 모양의 차원은 변환 전후의 기본 크기 비율에 따라 변경되는 마지막 차원을 제외하고 일치해야 합니다.
소스 및 대상 요소 유형은 튜플이 아니어야 합니다.
StableHLO 정보는 StableHLO - bitcast_convert를 참고하세요.
너비가 다른 기본 유형으로 bitcast 변환
BitcastConvert HLO 명령어는 출력 요소 유형 T'의 크기가 입력 요소 T의 크기와 같지 않은 경우를 지원합니다. 전체 작업이 개념적으로 비트캐스트이고 기본 바이트를 변경하지 않으므로 출력 요소의 모양이 변경되어야 합니다. B = sizeof(T), B' =
sizeof(T')의 경우 두 가지 경우가 있습니다.
첫째, B > B'인 경우 출력 모양에 크기가 B/B'인 새로운 가장 작은 차원이 추가됩니다. 예를 들면 다음과 같습니다.
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
유효 스칼라의 규칙은 다음과 같이 동일하게 유지됩니다.
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
또는 B' > B의 경우 입력 모양의 마지막 논리적 차원이 B'/B와 같아야 하며 이 차원은 변환 중에 삭제됩니다.
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
서로 다른 비트 너비 간의 변환은 요소별로 이루어지지 않습니다.
방송
XlaBuilder::Broadcast도 참고하세요.
배열의 데이터를 복제하여 배열에 측정기준을 추가합니다.
Broadcast(operand, broadcast_sizes)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
복제할 배열 |
broadcast_sizes |
ArraySlice<int64> |
새 측정기준의 크기 |
새로운 차원은 왼쪽에 삽입됩니다. 즉, broadcast_sizes에 {a0, ..., aN} 값이 있고 피연산자 모양에 {b0, ..., bM} 차원이 있으면 출력 모양에 {a0, ..., aN, b0, ..., bM} 차원이 있습니다.
새 측정기준은 피연산자의 사본으로 색인화됩니다. 즉,
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
예를 들어 operand이 값 2.0f가 있는 스칼라 f32이고 broadcast_sizes이 {2, 3}이면 결과는 모양이 f32[2, 3]인 배열이 되며 결과의 모든 값은 2.0f가 됩니다.
StableHLO 정보는 StableHLO - 브로드캐스트를 참고하세요.
BroadcastInDim
XlaBuilder::BroadcastInDim도 참고하세요.
배열의 데이터를 복제하여 배열의 크기와 차원 수를 확장합니다.
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
복제할 배열 |
out_dim_size
|
ArraySlice<int64>
|
타겟 모양의 측정기준 크기 |
broadcast_dimensions
|
ArraySlice<int64>
|
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
브로드캐스트와 유사하지만 어디에나 차원을 추가하고 크기가 1인 기존 차원을 확장할 수 있습니다.
operand은 out_dim_size로 설명된 모양에 브로드캐스트됩니다.
broadcast_dimensions는 operand의 차원을 타겟 모양의 차원에 매핑합니다. 즉, 피연산자의 i번째 차원은 broadcast_dimension[i]번째 출력 모양의 차원에 매핑됩니다. operand의 차원 크기는 1이거나 매핑되는 출력 모양의 차원 크기와 동일해야 합니다. 나머지 차원은 크기가 1인 차원으로 채워집니다. 그런 다음 퇴화된 차원 브로드캐스팅은 이러한 퇴화된 차원을 따라 브로드캐스팅하여 출력 모양에 도달합니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
통화
XlaBuilder::Call도 참고하세요.
지정된 인수로 계산을 호출합니다.
Call(computation, operands...)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
computation
|
XlaComputation
|
임의 유형의 N 파라미터가 있는 T_0, T_1, ...,
T_{N-1} -> S 유형의 계산 |
operands |
N개의 XlaOp 시퀀스 |
임의 유형의 N 인수 |
operands의 arity와 유형은 computation의 매개변수와 일치해야 합니다. operands이 없어도 됩니다.
CompositeCall
XlaBuilder::CompositeCall도 참고하세요.
입력과 composite_attributes를 가져오고 결과를 생성하는 다른 StableHLO 작업으로 구성된 작업을 캡슐화합니다. 작업의 시맨틱은 분해 속성으로 구현됩니다. 복합 작업은 프로그램 의미 체계를 변경하지 않고 분해로 대체할 수 있습니다. 분해를 인라인으로 처리해도 동일한 작업 의미가 제공되지 않는 경우 custom_call을 사용하는 것이 좋습니다.
버전 필드 (기본값은 0)는 컴포지트의 의미가 변경되는 시점을 나타내는 데 사용됩니다.
이 작업은 속성 is_composite=true이 있는 kCall로 구현됩니다. decomposition 필드는 computation 속성으로 지정됩니다. 프런트엔드 속성은 composite.이 접두사로 붙은 나머지 속성을 저장합니다.
CompositeCall 작업의 예:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
CompositeCall(computation, operands..., name, attributes, version)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
computation
|
XlaComputation
|
임의 유형의 N 파라미터가 있는 T_0, T_1, ...,
T_{N-1} -> S 유형의 계산 |
operands |
N개의 XlaOp 시퀀스 |
가변 개수의 값 |
name |
string |
컴포지션 이름 |
attributes
|
선택사항 string
|
속성의 선택적 문자열화된 사전 |
version
|
선택사항 int64
|
복합 작업의 의미 체계에 대한 버전 업데이트 번호 |
작업의 decomposition는 호출되는 필드가 아니라 하위 수준 구현(즉, to_apply=%funcname)이 포함된 함수를 가리키는 to_apply 속성으로 표시됩니다.
합성 및 분해에 관한 자세한 내용은 StableHLO 사양을 참고하세요.
Cbrt
XlaBuilder::Cbrt도 참고하세요.
요소별 세제곱근 연산 x -> cbrt(x).
Cbrt(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
Cbrt는 선택적 result_accuracy 인수도 지원합니다.
Cbrt(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
StableHLO 정보는 StableHLO - cbrt를 참고하세요.
올림
XlaBuilder::Ceil도 참고하세요.
요소별 올림 x -> ⌈x⌉
Ceil(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
StableHLO 정보는 StableHLO - ceil을 참고하세요.
Cholesky
XlaBuilder::Cholesky도 참고하세요.
대칭 (에르미트) 양의 정부호 행렬의 배치에 대한 촐레스키 분해를 계산합니다.
Cholesky(a, lower)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
a
|
XlaOp
|
2개 이상의 차원이 있는 복소수 또는 부동 소수점 유형의 배열 |
lower |
bool |
a의 위쪽 또는 아래쪽 삼각형을 사용할지 여부입니다. |
lower이 true인 경우 $a = l .l
l^T$. lower이 false인 경우\(a = u^T . u\)인 상삼각 행렬 u를 계산합니다.
입력 데이터는 lower 값에 따라 a의 하단/상단 삼각형에서만 읽습니다. 다른 삼각형의 값은 무시됩니다. 출력 데이터는 동일한 삼각형에 반환됩니다. 다른 삼각형의 값은 구현에 따라 정의되며 어떤 값이든 될 수 있습니다.
a의 차원이 2보다 큰 경우 a은 행렬 배치로 취급되며, 여기서 하위 2개 차원을 제외한 모든 차원은 배치 차원입니다.
a가 대칭 (에르미트) 양의 정부가 아닌 경우 결과는 구현에 따라 다릅니다.
StableHLO 정보는 StableHLO - cholesky를 참고하세요.
고정
XlaBuilder::Clamp도 참고하세요.
피연산자를 최솟값과 최댓값 사이의 범위로 제한합니다.
Clamp(min, operand, max)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
min |
XlaOp |
T 유형의 배열 |
operand |
XlaOp |
T 유형의 배열 |
max |
XlaOp |
T 유형의 배열 |
피연산자와 최소값 및 최대값이 주어지면 피연산자가 최소값과 최대값 사이의 범위에 있는 경우 피연산자를 반환하고, 피연산자가 이 범위 미만인 경우 최소값을 반환하고, 피연산자가 이 범위 초과인 경우 최대값을 반환합니다. 즉, clamp(a, x, b) = min(max(a, x), b)입니다.
세 배열의 모양이 모두 동일해야 합니다. 또는 브로드캐스팅의 제한된 형태로서 min 및/또는 max가 T 유형의 스칼라일 수 있습니다.
스칼라 min 및 max의 예:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
StableHLO 정보는 StableHLO - clamp를 참고하세요.
접기
XlaBuilder::Collapse도 참고하세요.
tf.reshape 작업입니다.
배열의 차원을 하나의 차원으로 축소합니다.
Collapse(operand, dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
T 유형의 배열 |
dimensions |
int64 벡터 |
T의 측정기준의 순서대로 연속된 하위 집합입니다. |
Collapse는 피연산자의 지정된 하위 집합을 단일 차원으로 대체합니다. 입력 인수는 T 유형의 임의 배열과 컴파일 시간 상수 차원 색인 벡터입니다. 측정기준 색인은 T의 측정기준의 순서대로 (낮은 측정기준 번호에서 높은 측정기준 번호로) 연속된 하위 집합이어야 합니다. 따라서 {0, 1, 2}, {0, 1}, {1, 2}는 모두 유효한 차원 집합이지만 {1, 0} 또는 {0, 2}는 유효하지 않습니다. 이러한 측정기준은 대체하는 측정기준과 동일한 위치에 있는 단일 새 측정기준으로 대체되며, 새 측정기준 크기는 원래 측정기준 크기의 곱과 같습니다. dimensions의 가장 낮은 차원 번호는 이러한 차원을 축소하는 루프 중첩에서 가장 느리게 변하는 차원 (가장 주요)이고 가장 높은 차원 번호는 가장 빠르게 변하는 차원 (가장 사소)입니다. 더 일반적인 접기 순서가 필요한 경우 tf.reshape 연산자를 참고하세요.
예를 들어 v가 24개 요소의 배열이라고 가정해 보겠습니다.
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
Clz
XlaBuilder::Clz도 참고하세요.
요소별 선행 0 개수를 계산합니다.
Clz(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
CollectiveBroadcast
XlaBuilder::CollectiveBroadcast도 참고하세요.
복제본 간에 데이터를 브로드캐스트합니다. 데이터는 각 그룹의 첫 번째 복제본 ID에서 동일한 그룹의 다른 ID로 전송됩니다. 복제본 ID가 복제본 그룹에 없으면 해당 복제본의 출력은 shape의 0으로 구성된 텐서입니다.
CollectiveBroadcast(operand, replica_groups, channel_id)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
replica_groups
|
ReplicaGroupvector
|
각 그룹에는 복제본 ID 목록이 포함됩니다. |
channel_id
|
선택사항 ChannelHandle
|
각 송수신 쌍의 고유 식별자 |
StableHLO 정보는 StableHLO - collective_broadcast를 참고하세요.
CollectivePermute
XlaBuilder::CollectivePermute도 참고하세요.
CollectivePermute는 복제본 간에 데이터를 전송하고 수신하는 집단 연산입니다.
CollectivePermute(operand, source_target_pairs, channel_id, inplace)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
n차원 입력 배열 |
source_target_pairs
|
<int64, int64> 벡터
|
(source_replica_id, target_replica_id) 쌍 목록입니다. 각 쌍에 대해 피연산자는 소스 복제본에서 타겟 복제본으로 전송됩니다. |
channel_id
|
선택사항 ChannelHandle
|
크로스 모듈 통신을 위한 선택적 채널 ID |
inplace
|
선택사항 bool
|
순열을 제자리에서 실행해야 하는지 여부를 나타내는 플래그 |
source_target_pairs에는 다음과 같은 제한사항이 있습니다.
- 두 쌍의 타겟 복제본 ID가 동일해서는 안 되며 소스 복제본 ID가 동일해서도 안 됩니다.
- 복제본 ID가 어떤 쌍에서도 타겟이 아닌 경우 해당 복제본의 출력은 입력과 모양이 동일한 0으로 구성된 텐서입니다.
CollectivePermute 작업의 API는 내부적으로 2개의 HLO 명령 (CollectivePermuteStart 및 CollectivePermuteDone)으로 분해됩니다.
HloInstruction::CreateCollectivePermuteStart도 참고하세요.
CollectivePermuteStart 및 CollectivePermuteDone는 HLO에서 기본 요소로 사용됩니다.
이러한 작업은 HLO 덤프에 표시될 수 있지만 최종 사용자가 수동으로 구성하도록 설계되지 않았습니다.
StableHLO 정보는 StableHLO - collective_permute를 참고하세요.
비교
XlaBuilder::Compare도 참고하세요.
다음의 lhs과 rhs을 요소별로 비교합니다.
Eq
XlaBuilder::Eq도 참고하세요.
lhs와 rhs의 요소별 같음 비교를 수행합니다.
\(lhs = rhs\)
Eq(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Eq의 경우 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Eq(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
부동 소수점 수에 대한 전체 순서 지원은 다음을 적용하여 Eq에 존재합니다.
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
EqTotalOrder(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
StableHLO 정보는 StableHLO - 비교를 참고하세요.
Ne
XlaBuilder::Ne도 참고하세요.
lhs와 rhs의 요소별 같지 않음 비교를 수행합니다.
\(lhs != rhs\)
Ne(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Ne에는 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Ne(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
부동 소수점 수에 대한 전체 순서 지원은 다음을 적용하여 Ne에 존재합니다.
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
NeTotalOrder(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
StableHLO 정보는 StableHLO - 비교를 참고하세요.
Ge
XlaBuilder::Ge도 참고하세요.
lhs와 rhs의 요소별 greater-or-equal-than 비교를 실행합니다.
\(lhs >= rhs\)
Ge(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Ge에는 다양한 차원의 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Ge(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
부동 소수점 수에 대한 전체 순서 지원은 다음을 적용하여 Gt에 존재합니다.
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
GtTotalOrder(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
StableHLO 정보는 StableHLO - 비교를 참고하세요.
Gt
XlaBuilder::Gt도 참고하세요.
lhs와 rhs의 요소별 보다 큼 비교를 실행합니다.
\(lhs > rhs\)
Gt(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Gt에는 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Gt(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - 비교를 참고하세요.
Le
XlaBuilder::Le도 참고하세요.
lhs와 rhs의 요소별 less-or-equal-than 비교를 실행합니다.
\(lhs <= rhs\)
Le(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Le의 경우 다양한 차원의 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Le(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
부동 소수점 수에 대한 전체 순서가 다음을 적용하여 Le에 존재하도록 지원합니다.
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LeTotalOrder(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
StableHLO 정보는 StableHLO - 비교를 참고하세요.
Lt
XlaBuilder::Lt도 참고하세요.
lhs와 rhs의 요소별 보다 작음 비교를 실행합니다.
\(lhs < rhs\)
Lt(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Lt의 경우 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Lt(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
부동 소수점 수에 대한 총 주문이 Lt에 지원됩니다. 다음을 적용하여
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LtTotalOrder(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
StableHLO 정보는 StableHLO - 비교를 참고하세요.
복잡
XlaBuilder::Complex도 참고하세요.
실수 값과 허수 값의 쌍(lhs 및 rhs)에서 복소수 값으로 요소별 변환을 실행합니다.
Complex(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Complex의 경우 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Complex(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - complex를 참고하세요.
ConcatInDim (연결)
XlaBuilder::ConcatInDim도 참고하세요.
Concatenate는 여러 배열 피연산자에서 배열을 구성합니다. 배열의 차원 수는 각 입력 배열 피연산자 (서로 차원 수가 같아야 함)의 차원 수와 같으며, 지정된 순서대로 인수를 포함합니다.
Concatenate(operands..., dimension)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operands
|
N개의 XlaOp 시퀀스
|
[L0, L1, ...] 차원의 T 유형 배열 N개입니다. N >= 1이 필요합니다. |
dimension
|
int64
|
operands 사이에 연결할 측정기준의 이름을 지정하는 [0, N)의 값입니다. |
dimension를 제외한 모든 측정기준은 동일해야 합니다. 이는 XLA가 '러그드' 배열을 지원하지 않기 때문입니다. 또한 0차원 값은 연결할 수 없습니다 (연결이 발생하는 차원의 이름을 지정할 수 없기 때문).
1차원 예:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
//Output: {2, 3, 4, 5, 6, 7}
2차원 예:
let a = { {1, 2},
{3, 4},
{5, 6} };
let b = { {7, 8} };
Concat({a, b}, 0)
//Output: { {1, 2},
// {3, 4},
// {5, 6},
// {7, 8} }
다이어그램:
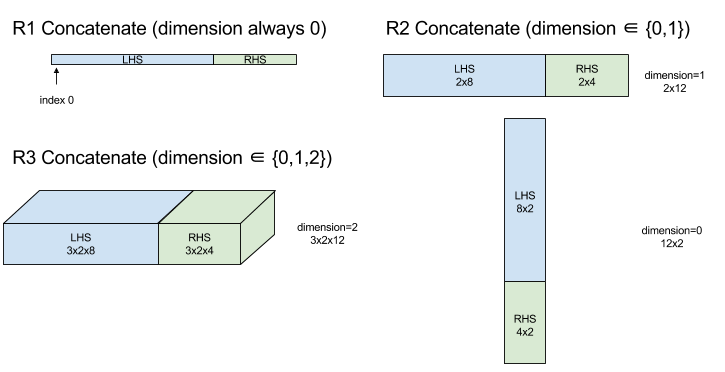
StableHLO 정보는 StableHLO - concatenate를 참고하세요.
조건부
XlaBuilder::Conditional도 참고하세요.
Conditional(predicate, true_operand, true_computation, false_operand,
false_computation)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
predicate |
XlaOp |
PRED 유형의 스칼라 |
true_operand |
XlaOp |
\(T_0\)유형의 인수 |
true_computation |
XlaComputation |
\(T_0 \to S\)유형의 XlaComputation |
false_operand |
XlaOp |
\(T_1\)유형의 인수 |
false_computation |
XlaComputation |
\(T_1 \to S\)유형의 XlaComputation |
predicate이 true이면 true_computation를 실행하고, predicate이 false이면 false_computation를 실행하고 결과를 반환합니다.
true_computation는 \(T_0\) 유형의 단일 인수를 사용해야 하며 동일한 유형이어야 하는 true_operand로 호출됩니다. false_computation는 \(T_1\) 유형의 단일 인수를 사용해야 하며 동일한 유형이어야 하는 false_operand로 호출됩니다. true_computation 및 false_computation의 반환 값 유형은 동일해야 합니다.
predicate 값에 따라 true_computation 및 false_computation 중 하나만 실행됩니다.
Conditional(branch_index, branch_computations, branch_operands)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
branch_index |
XlaOp |
S32 유형의 스칼라 |
branch_computations |
N개의 XlaComputation 시퀀스 |
\(T_0 \to S , T_1 \to S , ..., T_{N-1} \to S\)유형의 XlaComputations |
branch_operands |
N개의 XlaOp 시퀀스 |
\(T_0 , T_1 , ..., T_{N-1}\)유형의 인수 |
branch_computations[branch_index]을 실행하고 결과를 반환합니다. branch_index이 0보다 작거나 N보다 큰 S32이면 branch_computations[N-1]이 기본 분기로 실행됩니다.
각 branch_computations[b]는 \(T_b\) 유형의 단일 인수를 사용해야 하며 동일한 유형이어야 하는 branch_operands[b]로 호출됩니다. 각 branch_computations[b]의 반환 값 유형은 동일해야 합니다.
branch_index 값에 따라 branch_computations 중 하나만 실행됩니다.
StableHLO 정보는 StableHLO - if를 참고하세요.
상수
XlaBuilder::ConstantLiteral도 참고하세요.
상수 literal에서 output을 생성합니다.
Constant(literal)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
literal |
LiteralSlice |
기존 Literal의 상수 뷰 |
StableHLO 정보는 StableHLO - 상수를 참고하세요.
ConvertElementType
XlaBuilder::ConvertElementType도 참고하세요.
C++의 요소별 static_cast와 마찬가지로 ConvertElementType는 데이터 모양에서 타겟 모양으로 요소별 변환 작업을 실행합니다. 차원이 일치해야 하며 변환은 요소별로 이루어집니다. 예를 들어 s32 요소는 s32-to-f32 변환 루틴을 통해 f32 요소가 됩니다.
ConvertElementType(operand, new_element_type)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
차원 D가 있는 T 유형의 배열 |
new_element_type |
PrimitiveType |
type U |
피연산자와 타겟 모양의 차원이 일치해야 합니다. 소스 및 대상 요소 유형은 튜플이 아니어야 합니다.
T=s32에서 U=f32로의 변환은 가장 가까운 짝수로 반올림과 같은 정규화된 int-to-float 변환 루틴을 실행합니다.
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
StableHLO 정보는 StableHLO - 변환을 참고하세요.
Conv (컨볼루션)
XlaBuilder::Conv도 참고하세요.
신경망에서 사용되는 종류의 컨볼루션을 계산합니다. 여기서 컨볼루션은 n차원 기본 영역을 가로지르는 n차원 윈도우로 생각할 수 있으며 윈도우의 가능한 각 위치에 대해 계산이 실행됩니다.
Conv 팽창 없이 기본 컨볼루션 차원 번호를 사용하는 컨볼루션 명령어를 계산에 대기열에 추가합니다.
패딩은 SAME 또는 VALID로 약식으로 지정됩니다. SAME 패딩은 스트라이드를 고려하지 않을 때 출력이 입력과 동일한 모양을 갖도록 0으로 입력을 패딩합니다 (lhs). 유효한 패딩은 패딩이 없음을 의미합니다.
Conv(lhs, rhs, window_strides, padding, feature_group_count,
batch_group_count, precision_config, preferred_element_type)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
lhs
|
XlaOp
|
입력의 (n+2)차원 배열 |
rhs
|
XlaOp
|
커널 가중치의 (n+2)차원 배열 |
window_strides |
ArraySlice<int64> |
커널 스트라이드의 n차원 배열 |
padding |
Padding |
패딩 열거형 |
feature_group_count
|
int64 | 기능 그룹 수 |
batch_group_count |
int64 | 일괄 그룹 수 |
precision_config
|
선택사항
PrecisionConfig |
정밀도 수준의 enum |
preferred_element_type
|
선택사항
PrimitiveType |
스칼라 요소 유형의 enum |
Conv에 사용할 수 있는 제어 수준은 다음과 같습니다.
n을 공간 차원 수라고 하겠습니다. lhs 인수는 기본 영역을 설명하는 (n+2)차원 배열입니다. 물론 rhs도 입력이지만 이를 입력이라고 합니다. 신경망에서 이는 입력 활성화입니다. n+2개의 측정기준은 다음 순서로 표시됩니다.
batch: 이 차원의 각 좌표는 컨볼루션이 실행되는 독립적인 입력을 나타냅니다.z/depth/features: 기본 영역의 각 (y,x) 위치에는 이 차원으로 이동하는 벡터가 연결되어 있습니다.spatial_dims: 창이 이동하는 기본 영역을 정의하는n공간 크기를 설명합니다.
rhs 인수는 컨볼루션 필터/커널/창을 설명하는 (n+2)차원 배열입니다. 측정기준은 다음 순서로 표시됩니다.
output-z: 출력의z차원입니다.input-z: 이 차원의 크기에feature_group_count을 곱한 값은 lhs의z차원의 크기와 같아야 합니다.spatial_dims: 기본 영역을 가로질러 이동하는 n차원 창을 정의하는n공간 차원을 설명합니다.
window_strides 인수는 공간 차원에서 컨볼루션 창의 보폭을 지정합니다. 예를 들어 첫 번째 공간 차원의 보폭이 3이면 첫 번째 공간 색인이 3으로 나누어지는 좌표에만 창을 배치할 수 있습니다.
padding 인수는 기본 영역에 적용할 0 패딩의 양을 지정합니다. 패딩 양수는 음수일 수 있습니다. 음수 패딩의 절대값은 컨볼루션을 실행하기 전에 지정된 차원에서 삭제할 요소의 수를 나타냅니다. padding[0]은 y 측정기준의 패딩을 지정하고 padding[1]은 x 측정기준의 패딩을 지정합니다. 각 쌍에는 첫 번째 요소로 하위 패딩이 있고 두 번째 요소로 상위 패딩이 있습니다. 낮은 패딩은 낮은 색인 방향으로 적용되고 높은 패딩은 높은 색인 방향으로 적용됩니다. 예를 들어 padding[1]이 (2,3)이면 두 번째 공간 차원에서 왼쪽에 0이 2개, 오른쪽에 0이 3개 패딩됩니다. 패딩을 사용하는 것은 컨볼루션을 실행하기 전에 입력 (lhs)에 동일한 0 값을 삽입하는 것과 같습니다.
lhs_dilation 및 rhs_dilation 인수는 각 공간 차원에서 lhs와 rhs에 각각 적용할 팽창 계수를 지정합니다. 공간 차원의 팽창 계수가 d인 경우 해당 차원의 각 항목 사이에 d-1개의 홀이 암시적으로 배치되어 배열의 크기가 증가합니다. 홀은 no-op 값으로 채워지며, 이는 컨볼루션의 경우 0을 의미합니다.
rhs의 팽창을 atrous convolution이라고도 합니다. 자세한 내용은 tf.nn.atrous_conv2d를 참고하세요. lhs의 팽창을 트랜스포즈된 컨볼루션이라고도 합니다. 자세한 내용은 tf.nn.conv2d_transpose를 참고하세요.
feature_group_count 인수 (기본값 1)는 그룹화된 컨볼루션에 사용할 수 있습니다. feature_group_count는 입력 및 출력 특징 차원의 약수여야 합니다. feature_group_count이 1보다 크면 개념적으로 입력 및 출력 특성 차원과 rhs 출력 특성 차원이 여러 feature_group_count 그룹으로 균등하게 분할되며 각 그룹은 연속된 특성 하위 시퀀스로 구성됩니다. rhs의 입력 특성 차원은 lhs 입력 특성 차원을 feature_group_count로 나눈 값과 같아야 합니다 (따라서 이미 입력 특성 그룹의 크기가 있음). i번째 그룹은 여러 개별 컨볼루션의 feature_group_count를 계산하는 데 함께 사용됩니다. 이러한 컨볼루션의 결과는 출력 특징 차원에서 연결됩니다.
깊이별 컨볼루션의 경우 feature_group_count 인수가 입력 특성 차원으로 설정되고 필터가 [filter_height, filter_width, in_channels, channel_multiplier]에서 [filter_height, filter_width, 1, in_channels * channel_multiplier]로 재구성됩니다. 자세한 내용은 tf.nn.depthwise_conv2d를 참고하세요.
batch_group_count (기본값 1) 인수는 역전파 중에 그룹화된 필터에 사용할 수 있습니다. batch_group_count은 lhs (입력) 배치 크기의 약수여야 합니다. batch_group_count가 1보다 크면 출력 배치 차원의 크기가 input batch
/ batch_group_count이어야 합니다. batch_group_count는 출력 기능 크기의 약수여야 합니다.
출력 형태에는 다음 순서로 이러한 차원이 있습니다.
batch: 이 차원의 크기에batch_group_count을 곱한 값은 lhs의batch차원의 크기와 같아야 합니다.z: 커널 (rhs)의output-z과 동일한 크기입니다.spatial_dims: 컨볼루션 창의 유효한 배치마다 하나의 값입니다.
위 그림은 batch_group_count 필드의 작동 방식을 보여줍니다. 효과적으로 각 lhs 배치를 batch_group_count 그룹으로 슬라이스하고 출력 기능에 대해서도 동일한 작업을 실행합니다. 그런 다음 이러한 각 그룹에 대해 쌍별 합성곱을 수행하고 출력 특성 차원을 따라 출력을 연결합니다. 다른 모든 측정기준 (기능 및 공간)의 작동 의미는 동일하게 유지됩니다.
컨볼루션 창의 유효한 배치는 패딩 후의 보폭과 기본 영역의 크기에 따라 결정됩니다.
컨볼루션의 기능을 설명하기 위해 2D 컨볼루션을 고려하고 출력에서 고정된 batch, z, y, x 좌표를 선택합니다. 그러면 (y,x)는 기본 영역 내 창의 모서리 위치입니다 (예: 공간 치수를 해석하는 방식에 따라 왼쪽 상단 모서리). 이제 기본 영역에서 가져온 2D 창이 있으며 각 2D 포인트는 1D 벡터와 연결되어 있으므로 3D 상자가 표시됩니다. 컨볼루션 커널에서 출력 좌표 z를 고정했으므로 3D 상자도 있습니다. 두 상자의 크기가 동일하므로 두 상자 간의 요소별 곱의 합을 구할 수 있습니다 (내적과 유사). 이것이 출력 값입니다.
output-z이 예를 들어 5인 경우 윈도우의 각 위치는 출력의 z 측정기준에 5개의 값을 생성합니다. 이러한 값은 컨볼루션 커널의 어떤 부분이 사용되는지에 따라 달라집니다. 각 output-z 좌표에 사용되는 별도의 3D 값 상자가 있습니다. 따라서 각각 다른 필터를 사용하는 5개의 별도 컨볼루션으로 생각할 수 있습니다.
패딩과 스트라이딩이 있는 2D 컨볼루션의 의사 코드는 다음과 같습니다.
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
precision_config는 정밀도 구성을 나타내는 데 사용됩니다. 이 수준은 필요할 때 더 정확한 dtype 에뮬레이션을 제공하기 위해 하드웨어에서 더 많은 머신 코드 명령어를 생성하려고 시도해야 하는지 여부를 나타냅니다 (예: bf16 matmul만 지원하는 TPU에서 f32 에뮬레이션). 값은 DEFAULT, HIGH, HIGHEST일 수 있습니다. MXU 섹션에서 자세한 내용을 확인하세요.
preferred_element_type는 누적에 사용되는 정밀도가 높거나 낮은 출력 유형의 스칼라 요소입니다. preferred_element_type는 지정된 작업에 누적 유형을 권장하지만 보장되지는 않습니다. 이를 통해 일부 하드웨어 백엔드는 대신 다른 유형으로 누적되고 선호하는 출력 유형으로 변환될 수 있습니다.
StableHLO 정보는 StableHLO - 컨볼루션을 참고하세요.
ConvWithGeneralPadding
XlaBuilder::ConvWithGeneralPadding도 참고하세요.
ConvWithGeneralPadding(lhs, rhs, window_strides, padding,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
패딩 구성이 명시적인 경우 Conv과 동일합니다.
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
lhs
|
XlaOp
|
입력의 (n+2)차원 배열 |
rhs
|
XlaOp
|
커널 가중치의 (n+2)차원 배열 |
window_strides |
ArraySlice<int64> |
커널 스트라이드의 n차원 배열 |
padding
|
ArraySlice<
pair<int64,int64>> |
(low, high) 패딩의 n차원 배열 |
feature_group_count
|
int64 | 기능 그룹 수 |
batch_group_count |
int64 | 일괄 그룹 수 |
precision_config
|
선택사항
PrecisionConfig |
정밀도 수준의 enum |
preferred_element_type
|
선택사항
PrimitiveType |
스칼라 요소 유형의 enum |
ConvWithGeneralDimensions
XlaBuilder::ConvWithGeneralDimensions도 참고하세요.
ConvWithGeneralDimensions(lhs, rhs, window_strides, padding,
dimension_numbers, feature_group_count, batch_group_count, precision_config,
preferred_element_type)
차원 번호가 명시적인 경우 Conv과 동일합니다.
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
lhs
|
XlaOp
|
입력의 (n+2)차원 배열 |
rhs
|
XlaOp
|
커널 가중치의 (n+2)차원 배열 |
window_strides
|
ArraySlice<int64>
|
커널 스트라이드의 n차원 배열 |
padding |
Padding |
패딩 열거형 |
dimension_numbers
|
ConvolutionDimensionNumbers
|
차원 수 |
feature_group_count
|
int64 | 특성 그룹 수 |
batch_group_count
|
int64 | 일괄 그룹 수 |
precision_config
|
선택사항 PrecisionConfig
|
정밀도 수준의 enum |
preferred_element_type
|
선택사항 PrimitiveType
|
스칼라 요소 유형의 enum |
ConvGeneral
XlaBuilder::ConvGeneral도 참고하세요.
ConvGeneral(lhs, rhs, window_strides, padding, dimension_numbers,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
차원 번호와 패딩 구성이 명시적인 Conv과 동일합니다.
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
lhs
|
XlaOp
|
입력의 (n+2)차원 배열 |
rhs
|
XlaOp
|
커널 가중치의 (n+2)차원 배열 |
window_strides
|
ArraySlice<int64>
|
커널 스트라이드의 n차원 배열 |
padding
|
ArraySlice<
pair<int64,int64>>
|
(low, high) 패딩의 n차원 배열 |
dimension_numbers
|
ConvolutionDimensionNumbers
|
차원 수 |
feature_group_count
|
int64 | 특성 그룹 수 |
batch_group_count
|
int64 | 일괄 그룹 수 |
precision_config
|
선택사항 PrecisionConfig
|
정밀도 수준의 enum |
preferred_element_type
|
선택사항 PrimitiveType
|
스칼라 요소 유형의 enum |
ConvGeneralDilated
XlaBuilder::ConvGeneralDilated도 참고하세요.
ConvGeneralDilated(lhs, rhs, window_strides, padding, lhs_dilation,
rhs_dilation, dimension_numbers, feature_group_count, batch_group_count,
precision_config, preferred_element_type, window_reversal)
패딩 구성, 팽창 계수, 차원 번호가 명시적인 Conv와 동일합니다.
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
lhs
|
XlaOp
|
입력의 (n+2)차원 배열 |
rhs
|
XlaOp
|
커널 가중치의 (n+2)차원 배열 |
window_strides
|
ArraySlice<int64>
|
커널 스트라이드의 n차원 배열 |
padding
|
ArraySlice<
pair<int64,int64>>
|
(low, high) 패딩의 n차원 배열 |
lhs_dilation
|
ArraySlice<int64>
|
n-d lhs dilation factor array |
rhs_dilation
|
ArraySlice<int64>
|
n-d rhs 팽창 요소 배열 |
dimension_numbers
|
ConvolutionDimensionNumbers
|
차원 수 |
feature_group_count
|
int64 | 특성 그룹 수 |
batch_group_count
|
int64 | 일괄 그룹 수 |
precision_config
|
선택사항 PrecisionConfig
|
정밀도 수준의 enum |
preferred_element_type
|
선택사항 PrimitiveType
|
스칼라 요소 유형의 enum |
window_reversal
|
선택사항 vector<bool>
|
컨볼루션을 적용하기 전에 논리적으로 차원을 반전하는 데 사용되는 플래그 |
복사
HloInstruction::CreateCopyStart도 참고하세요.
Copy는 내부적으로 2개의 HLO 명령 CopyStart 및 CopyDone로 분해됩니다. Copy은 CopyStart, CopyDone과 함께 HLO에서 프리미티브 역할을 합니다. 이러한 작업은 HLO 덤프에 표시될 수 있지만 최종 사용자가 수동으로 구성해서는 안 됩니다.
COS
XlaBuilder::Cos도 참고하세요.
요소별 코사인 x -> cos(x).
Cos(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
Cos는 선택적 result_accuracy 인수도 지원합니다.
Cos(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
StableHLO 정보는 StableHLO - cosine을 참고하세요.
Cosh
XlaBuilder::Cosh도 참고하세요.
요소별 쌍곡선 코사인 x -> cosh(x)입니다.
Cosh(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
Cosh는 선택적 result_accuracy 인수도 지원합니다.
Cosh(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
CustomCall
XlaBuilder::CustomCall도 참고하세요.
계산 내에서 사용자 제공 함수를 호출합니다.
CustomCall 문서는 개발자 세부정보 - XLA 맞춤 호출에 제공됩니다.
StableHLO 정보는 StableHLO - custom_call을 참고하세요.
디비전
XlaBuilder::Div도 참고하세요.
피제수 lhs와 제수 rhs의 요소별 나눗셈을 실행합니다.
Div(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
정수 나눗셈 오버플로 (0으로 부호 있는/부호 없는 나눗셈/나머지 또는 -1로 INT_SMIN의 부호 있는 나눗셈/나머지)는 구현 정의 값을 생성합니다.
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Div의 경우 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Div(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - divide를 참고하세요.
도메인
HloInstruction::CreateDomain도 참고하세요.
Domain는 HLO 덤프에 표시될 수 있지만 최종 사용자가 수동으로 구성해서는 안 됩니다.
점
XlaBuilder::Dot도 참고하세요.
Dot(lhs, rhs, precision_config, preferred_element_type)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
lhs |
XlaOp |
T 유형의 배열 |
rhs |
XlaOp |
T 유형의 배열 |
precision_config
|
선택사항
PrecisionConfig |
정밀도 수준의 enum |
preferred_element_type
|
선택사항
PrimitiveType |
스칼라 요소 유형의 enum |
이 작업의 정확한 시맨틱은 피연산자의 순위에 따라 다릅니다.
| 입력 | 출력 | 시맨틱스 |
|---|---|---|
vector [n] dot vector [n] |
스칼라 | 벡터 내적 |
행렬 [m x k] dot 벡터
[k] |
벡터 [m] | 행렬-벡터 곱셈 |
행렬 [m x k] dot 행렬
[k x n] |
행렬 [m x n] | 행렬-행렬 곱셈 |
이 작업은 lhs의 두 번째 차원 (또는 1차원인 경우 첫 번째 차원)과 rhs의 첫 번째 차원에 걸쳐 곱의 합을 실행합니다. 이러한 측정기준을 '축약된' 측정기준이라고 합니다. lhs 및 rhs의 축소된 크기는 동일해야 합니다. 실제로 벡터 간의 점곱, 벡터/행렬 곱셈 또는 행렬/행렬 곱셈을 실행하는 데 사용할 수 있습니다.
precision_config는 정밀도 구성을 나타내는 데 사용됩니다. 이 수준은 필요할 때 더 정확한 dtype 에뮬레이션을 제공하기 위해 하드웨어에서 더 많은 머신 코드 명령어를 생성하려고 시도해야 하는지 여부를 나타냅니다 (예: bf16 matmul만 지원하는 TPU에서 f32 에뮬레이션). 값은 DEFAULT, HIGH, HIGHEST일 수 있습니다. MXU 섹션에서 자세한 내용을 확인하세요.
preferred_element_type는 누적에 사용되는 정밀도가 높거나 낮은 출력 유형의 스칼라 요소입니다. preferred_element_type는 지정된 작업에 누적 유형을 권장하지만 보장되지는 않습니다. 이를 통해 일부 하드웨어 백엔드는 대신 다른 유형으로 누적되고 선호하는 출력 유형으로 변환될 수 있습니다.
StableHLO 정보는 StableHLO - dot을 참고하세요.
DotGeneral
XlaBuilder::DotGeneral도 참고하세요.
DotGeneral(lhs, rhs, dimension_numbers, precision_config,
preferred_element_type)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
lhs |
XlaOp |
T 유형의 배열 |
rhs |
XlaOp |
T 유형의 배열 |
dimension_numbers
|
DotDimensionNumbers
|
계약 및 배치 측정기준 번호 |
precision_config
|
선택사항
PrecisionConfig |
정밀도 수준의 enum |
preferred_element_type
|
선택사항
PrimitiveType |
스칼라 요소 유형의 enum |
Dot과 유사하지만 lhs 및 rhs 모두에 대해 축소 및 배치 차원 번호를 지정할 수 있습니다.
| DotDimensionNumbers 필드 | 유형 | 시맨틱스 |
|---|---|---|
lhs_contracting_dimensions
|
repeated int64 | lhs 계약 측정기준 번호 |
rhs_contracting_dimensions
|
repeated int64 | rhs 계약 측정기준 번호 |
lhs_batch_dimensions
|
repeated int64 | lhs 배치 측정기준 번호 |
rhs_batch_dimensions
|
repeated int64 | rhs 배치 측정기준 번호 |
DotGeneral은 dimension_numbers에 지정된 축소 측정기준에 대한 제품의 합계를 실행합니다.
lhs 및 rhs의 연결된 축소 측정기준 번호는 동일하지 않아도 되지만 측정기준 크기는 동일해야 합니다.
축소된 측정기준 번호의 예:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { { 6.0, 12.0},
{15.0, 30.0} }
lhs 및 rhs의 연결된 배치 차원 번호는 차원 크기가 동일해야 합니다.
배치 측정기준 번호가 있는 예 (배치 크기 2, 2x2 행렬):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> {
{ {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| 입력 | 출력 | 시맨틱스 |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | 배치 행렬 곱 |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | 배치 행렬 곱 |
결과 측정기준 번호는 배치 측정기준으로 시작하고, lhs 비축소/비배치 측정기준이 뒤따르며, 마지막으로 rhs 비축소/비배치 측정기준이 뒤따릅니다.
precision_config는 정밀도 구성을 나타내는 데 사용됩니다. 이 수준은 필요할 때 더 정확한 dtype 에뮬레이션을 제공하기 위해 하드웨어에서 더 많은 머신 코드 명령어를 생성하려고 시도해야 하는지 여부를 나타냅니다 (예: bf16 matmul만 지원하는 TPU에서 f32 에뮬레이션). 값은 DEFAULT, HIGH, HIGHEST일 수 있습니다. 자세한 내용은 MXU 섹션에서 확인하세요.
preferred_element_type는 누적에 사용되는 정밀도가 높거나 낮은 출력 유형의 스칼라 요소입니다. preferred_element_type는 지정된 작업에 누적 유형을 권장하지만 보장되지는 않습니다. 이를 통해 일부 하드웨어 백엔드는 대신 다른 유형으로 누적되고 선호하는 출력 유형으로 변환될 수 있습니다.
StableHLO 정보는 StableHLO - dot_general을 참고하세요.
ScaledDot
XlaBuilder::ScaledDot도 참고하세요.
ScaledDot(lhs, lhs_scale, rhs, rhs_scale, dimension_number,
precision_config,preferred_element_type)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
lhs |
XlaOp |
T 유형의 배열 |
rhs |
XlaOp |
T 유형의 배열 |
lhs_scale |
XlaOp |
T 유형의 배열 |
rhs_scale |
XlaOp |
T 유형의 배열 |
dimension_number
|
ScatterDimensionNumbers
|
분산 작업의 측정기준 번호 |
precision_config
|
PrecisionConfig
|
정확도 수준의 열거형 |
preferred_element_type
|
선택사항 PrimitiveType
|
스칼라 요소 유형의 enum |
DotGeneral과 유사합니다.
'dimension_numbers'에 지정된 축소 및 배치 차원을 사용하여 피연산자 'lhs', 'lhs_scale', 'rhs', 'rhs_scale'로 확장된 점 곱 연산을 만듭니다.
RaggedDot
XlaBuilder::RaggedDot도 참고하세요.
RaggedDot 계산의 분석은 StableHLO - chlo.ragged_dot을 참고하세요.
DynamicReshape
XlaBuilder::DynamicReshape도 참고하세요.
이 작업은 기능적으로 reshape와 동일하지만 결과 모양은 output_shape를 통해 동적으로 지정됩니다.
DynamicReshape(operand, dim_sizes, new_size_bounds, dims_are_dynamic)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
T 유형의 N차원 배열 |
dim_sizes |
XlaOP 벡터 |
N차원 벡터 크기 |
new_size_bounds |
int63 벡터 |
경계의 N차원 벡터 |
dims_are_dynamic |
bool 벡터 |
N차원 동적 차원 |
StableHLO 정보는 StableHLO - dynamic_reshape를 참고하세요.
DynamicSlice
XlaBuilder::DynamicSlice도 참고하세요.
DynamicSlice는 동적 start_indices에서 입력 배열의 하위 배열을 추출합니다. 각 차원의 슬라이스 크기는 size_indices에 전달되며, 이는 각 차원에서 배타적 슬라이스 간격의 끝점을 지정합니다([start, start + size)). start_indices의 모양은 1차원이어야 하며, 차원 크기는 operand의 차원 수와 같아야 합니다.
DynamicSlice(operand, start_indices, slice_sizes)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
T 유형의 N차원 배열 |
start_indices
|
N개의 XlaOp 시퀀스
|
각 차원의 슬라이스 시작 색인을 포함하는 N개의 스칼라 정수 목록입니다. 값은 0 이상이어야 합니다. |
size_indices
|
ArraySlice<int64>
|
각 차원의 슬라이스 크기가 포함된 N개의 정수 목록입니다. 각 값은 0보다 커야 하며, 시작 + 크기는 모듈로 차원 크기 래핑을 방지하기 위해 차원 크기보다 작거나 같아야 합니다. |
효과적인 슬라이스 색인은 슬라이스를 실행하기 전에 [1, N)의 각 색인 i에 다음 변환을 적용하여 계산됩니다.
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - slice_sizes[i])
이렇게 하면 추출된 슬라이스가 항상 피연산자 배열의 범위 내에 있게 됩니다. 변환이 적용되기 전에 슬라이스가 경계 내에 있으면 변환이 적용되지 않습니다.
1차원 예:
let a = {0.0, 1.0, 2.0, 3.0, 4.0};
let s = {2};
DynamicSlice(a, s, {2});
// Result: {2.0, 3.0}
2차원 예:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2});
//Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
StableHLO 정보는 StableHLO - dynamic_slice를 참고하세요.
DynamicUpdateSlice
XlaBuilder::DynamicUpdateSlice도 참고하세요.
DynamicUpdateSlice는 start_indices에서 update 슬라이스가 덮어쓰여진 입력 배열 operand의 값인 결과를 생성합니다.
update의 모양에 따라 업데이트되는 결과의 하위 배열 모양이 결정됩니다.
start_indices의 모양은 1차원이어야 하며, 차원 크기는 operand의 차원 수와 같아야 합니다.
DynamicUpdateSlice(operand, update, start_indices)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
T 유형의 N차원 배열 |
update
|
XlaOp
|
슬라이스 업데이트가 포함된 T 유형의 N차원 배열입니다. 업데이트 셰이프의 각 측정기준은 0보다 커야 하며, 경계 외 업데이트 색인이 생성되지 않도록 시작 + 업데이트는 각 측정기준의 피연산자 크기보다 작거나 같아야 합니다. |
start_indices
|
N개의 XlaOp 시퀀스
|
각 차원의 슬라이스 시작 색인을 포함하는 N개의 스칼라 정수 목록입니다. 값은 0 이상이어야 합니다. |
효과적인 슬라이스 색인은 슬라이스를 실행하기 전에 [1, N)의 각 색인 i에 다음 변환을 적용하여 계산됩니다.
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
이렇게 하면 업데이트된 슬라이스가 항상 피연산자 배열의 범위 내에 있게 됩니다. 변환이 적용되기 전에 슬라이스가 경계 내에 있으면 변환이 적용되지 않습니다.
1차원 예:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s)
// Result: {0.0, 1.0, 5.0, 6.0, 4.0}
2차원 예:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s)
// Result:
// { {0.0, 1.0, 2.0},
// {3.0, 12.0, 13.0},
// {6.0, 14.0, 15.0},
// {9.0, 16.0, 17.0} }
StableHLO 정보는 StableHLO - dynamic_update_slice를 참고하세요.
Erf
XlaBuilder::Erf도 참고하세요.
요소별 오차 함수 x -> erf(x)(여기서)
\(\text{erf}(x) = \frac{2}{\sqrt{\pi} }\int_0^x e^{-t^2} \, dt\).
Erf(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
Erf는 선택적 result_accuracy 인수도 지원합니다.
Erf(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
지수
XlaBuilder::Exp도 참고하세요.
요소별 자연 지수 x -> e^x
Exp(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
Exp는 선택적 result_accuracy 인수도 지원합니다.
Exp(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
StableHLO 정보는 StableHLO - 지수를 참고하세요.
Expm1
XlaBuilder::Expm1도 참고하세요.
요소별 자연 지수 빼기 1 x -> e^x - 1
Expm1(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
Expm1은 선택적 result_accuracy 인수도 지원합니다.
Expm1(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
StableHLO 정보는 StableHLO - exponential_minus_one을 참고하세요.
Fft
XlaBuilder::Fft도 참고하세요.
XLA FFT 작업은 실수 및 복소수 입력/출력에 대한 순방향 및 역방향 푸리에 변환을 구현합니다. 최대 3개 축의 다차원 FFT가 지원됩니다.
Fft(operand, ftt_type, fft_length)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand
|
XlaOp
|
푸리에 변환할 배열입니다. |
fft_type |
FftType |
아래의 표를 참조하세요. |
fft_length
|
ArraySlice<int64>
|
변환되는 축의 시간 영역 길이입니다. 이는 특히 IRFFT가 가장 안쪽 축의 크기를 적절하게 조정하는 데 필요합니다. RFFT(fft_length=[16])의 출력 모양이 RFFT(fft_length=[17])와 동일하기 때문입니다. |
FftType |
시맨틱스 |
|---|---|
FFT |
복소수-복소수 FFT를 전달합니다. 모양이 변경되지 않았습니다. |
IFFT |
복소수-복소수 역 FFT입니다. 모양이 변경되지 않았습니다. |
RFFT
|
실수-복소수 FFT를 전달합니다. fft_length[-1]이 0이 아닌 값인 경우 가장 안쪽 축의 모양이 fft_length[-1] // 2 + 1로 줄어들어 나이퀴스트 주파수를 초과하는 변환된 신호의 반전된 공액 부분이 생략됩니다. |
IRFFT
|
실수-복소수 역 FFT입니다 (복소수를 취하고 실수를 반환함).
fft_length[-1]이 0이 아닌 값인 경우 가장 안쪽 축의 모양이 fft_length[-1]로 확장되어 1~fft_length[-1] // 2 + 1 항목의 역 공액에서 나이퀴스트 주파수를 초과하는 변환된 신호의 부분이 추론됩니다. |
StableHLO 정보는 StableHLO - fft를 참고하세요.
다차원 FFT
fft_length가 두 개 이상 제공되면 가장 안쪽 축 각각에 FFT 작업의 캐스케이드가 적용되는 것과 같습니다. 실수->복소수 및 복소수->실수 사례의 경우 가장 안쪽 축 변환이 먼저 실행됩니다(RFFT의 경우 마지막, IRFFT의 경우 처음). 따라서 가장 안쪽 축의 크기가 변경됩니다. 다른 축 변환은 복소수->복소수가 됩니다.
구현 세부정보
CPU FFT는 Eigen의 TensorFFT로 지원됩니다. GPU FFT는 cuFFT를 사용합니다.
층
XlaBuilder::Floor도 참고하세요.
요소별 하한 x -> ⌊x⌋
Floor(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
StableHLO 정보는 StableHLO - floor를 참고하세요.
Fusion
HloInstruction::CreateFusion도 참고하세요.
Fusion 작업은 HLO 명령어를 나타내며 HLO의 기본 요소 역할을 합니다.
이 작업은 HLO 덤프에 표시될 수 있지만 최종 사용자가 수동으로 구성해서는 안 됩니다.
수집
XLA gather 작업은 입력 배열의 여러 슬라이스 (각 슬라이스는 잠재적으로 다른 런타임 오프셋에 있음)를 함께 연결합니다.
StableHLO 정보는 StableHLO - gather를 참고하세요.
일반 시맨틱스
XlaBuilder::Gather도 참고하세요.
더 직관적인 설명은 아래의 '비공식 설명' 섹션을 참고하세요.
gather(operand, start_indices, dimension_numbers, slice_sizes,
indices_are_sorted)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand
|
XlaOp
|
수집할 배열입니다. |
start_indices
|
XlaOp
|
수집하는 슬라이스의 시작 색인을 포함하는 배열입니다. |
dimension_numbers
|
GatherDimensionNumbers
|
시작 색인을 '포함'하는 start_indices의 측정기준입니다. 자세한 설명은 아래를 참고하세요. |
slice_sizes
|
ArraySlice<int64>
|
slice_sizes[i]은 i 차원의 슬라이스 경계입니다. |
indices_are_sorted
|
bool
|
호출자가 색인을 정렬하도록 보장되는지 여부입니다. |
편의를 위해 출력 배열에서 offset_dims에 없는 측정기준에 batch_dims 라벨을 지정합니다.
출력은 batch_dims.size + offset_dims.size 차원의 배열입니다.
operand.rank은 offset_dims.size과 collapsed_slice_dims.size의 합과 같아야 합니다. 또한 slice_sizes.size은 operand.rank와 같아야 합니다.
index_vector_dim가 start_indices.rank와 같으면 start_indices에 후행 1 차원이 있는 것으로 간주합니다 (예: start_indices의 모양이 [6,7]이고 index_vector_dim가 2이면 start_indices의 모양이 [6,7,1]인 것으로 간주합니다).
i 차원을 따라 출력 배열의 경계는 다음과 같이 계산됩니다.
i이batch_dims에 있으면 (즉, 일부k에 대해batch_dims[k]와 같음)start_indices.shape에서 해당 측정기준 경계를 선택하고index_vector_dim는 건너뜁니다 (즉,k<index_vector_dim이면start_indices.shape.dims[k] 를 선택하고 그렇지 않으면start_indices.shape.dims[k+1] 를 선택).i가offset_dims에 있는 경우 (즉, 일부k의 경우offset_dims[k] 와 같음)collapsed_slice_dims를 고려한 후slice_sizes에서 해당 바운드를 선택합니다 (즉,adjusted_slice_sizes가 색인collapsed_slice_dims의 바운드가 삭제된slice_sizes인 경우adjusted_slice_sizes[k] 를 선택합니다).
형식적으로 지정된 출력 색인 Out에 해당하는 피연산자 색인 In은 다음과 같이 계산됩니다.
G= {Out[k] forkinbatch_dims}라고 가정합니다.G를 사용하여S[i] =start_indices[Combine(G,i)] 이 되도록 벡터S를 슬라이스합니다. 여기서 Combine(A, b)는index_vector_dim위치에 b를 A에 삽입합니다.G가 비어 있는 경우에도 잘 정의됩니다.G가 비어 있으면S=start_indices입니다.start_index_map를 사용하여S를 분산하여S를 사용하여operand에 시작 색인Sin을 만듭니다. 더 정확하게 말하면 다음과 같습니다.Sin[start_index_map[k]] =S[k](k<start_index_map.size인 경우)그렇지 않으면
Sin[_] =0입니다.
collapsed_slice_dims세트에 따라Out의 오프셋 차원에서 색인을 분산하여operand에 색인Oin을 만듭니다. 더 정확하게 말하면 다음과 같습니다.Oin[remapped_offset_dims(k)] =Out[offset_dims[k]] ifk<offset_dims.size(remapped_offset_dims은 아래에 정의됨)그렇지 않으면
Oin[_] =0입니다.
In는Oin+Sin입니다. 여기서 +는 요소별 덧셈입니다.
remapped_offset_dims는 도메인이 [0, offset_dims.size)이고 범위가 [0, operand.rank) \ collapsed_slice_dims인 단조 함수입니다. 예를 들어 offset_dims.size이 4이고 operand.rank이 6이며 collapsed_slice_dims이 {0, 2}이면 remapped_offset_dims은 {0→1, 1→3, 2→4, 3→5}입니다.
indices_are_sorted이 true로 설정되면 XLA는 사용자가 start_indices을 start_index_map에 따라 값을 분산한 후 오름차순으로 정렬했다고 가정할 수 있습니다. 그렇지 않으면 시맨틱스는 구현 정의됩니다.
비공식 설명 및 예
비공식적으로 출력 배열의 모든 색인 Out은 피연산자 배열의 요소 E에 해당하며 다음과 같이 계산됩니다.
Out의 배치 차원을 사용하여start_indices에서 시작 색인을 조회합니다.start_index_map는 시작 색인 (크기가 피연산자.rank보다 작을 수 있음)을operand의 '전체' 시작 색인에 매핑하는 데 사용됩니다.전체 시작 인덱스를 사용하여 크기가
slice_sizes인 슬라이스를 동적으로 슬라이스합니다.collapsed_slice_dims측정기준을 접어 슬라이스의 모양을 변경합니다. 축소된 모든 슬라이스 측정기준의 바운드가 1이어야 하므로 이 재형성은 항상 허용됩니다.Out의 오프셋 치수를 사용하여 이 슬라이스를 색인화하여 출력 색인Out에 해당하는 입력 요소E를 가져옵니다.
index_vector_dim은 이어지는 모든 예에서 start_indices.rank~1로 설정됩니다. index_vector_dim의 더 흥미로운 값은 작업을 근본적으로 변경하지는 않지만 시각적 표현을 더 번거롭게 만듭니다.
위의 모든 요소가 어떻게 결합되는지 직관적으로 이해하기 위해 [16,11] 배열에서 [8,6] 모양의 슬라이스 5개를 수집하는 예를 살펴보겠습니다. [16,11] 배열로의 슬라이스 위치는 S64[2] 모양의 색인 벡터로 나타낼 수 있으므로 5개 위치의 집합은 S64[5,2] 배열로 나타낼 수 있습니다.
그러면 gather 작업의 동작을 출력 모양의 색인 [G,O0,O1]을 가져와 다음과 같은 방식으로 입력 배열의 요소에 매핑하는 색인 변환으로 묘사할 수 있습니다.
먼저 G를 사용하여 수집 색인 배열에서 (X,Y) 벡터를 선택합니다.
그러면 색인 [G,O0,O1] 의 출력 배열에 있는 요소는 색인 [X+O0,Y+O1]의 입력 배열에 있는 요소입니다.
slice_sizes는 O0 및 O1의 범위를 결정하는 [8,6]이며, 이는 슬라이스의 경계를 결정합니다.
이 수집 작업은 G를 배치 차원으로 사용하는 배치 동적 슬라이스로 작동합니다.
수집된 색인은 다차원일 수 있습니다. 예를 들어 [4,5,2] 모양의 '색인 수집' 배열을 사용하는 위의 예의 더 일반적인 버전은 다음과 같이 색인을 변환합니다.
여기서도 배치 측정기준으로 배치 동적 슬라이스 G0 및 G1가 사용됩니다. 슬라이스 크기는 여전히 [8,6]입니다.
XLA의 gather 작업은 위에서 설명한 비공식 시맨틱스를 다음과 같은 방식으로 일반화합니다.
출력 모양의 어떤 측정기준이 오프셋 측정기준인지 구성할 수 있습니다 (마지막 예의
O0,O1이 포함된 측정기준). 출력 배치 차원 (마지막 예에서G0,G1이 포함된 차원)은 오프셋 차원이 아닌 출력 차원으로 정의됩니다.출력 모양에 명시적으로 표시된 출력 오프셋 차원 수가 입력 차원 수보다 작을 수 있습니다.
collapsed_slice_dims로 명시적으로 나열된 이러한 '누락된' 측정기준의 슬라이스 크기는1이어야 합니다. 슬라이스 크기가1이므로 유효한 색인은0뿐이며 이를 생략해도 모호성이 발생하지 않습니다.'Gather Indices' 배열에서 추출된 슬라이스(마지막 예의 (
X,Y))의 요소 수가 입력 배열의 차원 수보다 적을 수 있으며, 명시적 매핑은 입력과 동일한 차원 수를 갖도록 색인을 확장하는 방법을 지정합니다.
마지막 예로 (2)와 (3)을 사용하여 tf.gather_nd를 구현합니다.
G0 및 G1는 시작 색인이 X 요소 하나만 있다는 점을 제외하고 평소와 같이 gather 색인 배열에서 시작 색인을 잘라내는 데 사용됩니다. 마찬가지로 값이 O0인 출력 오프셋 색인도 하나만 있습니다. 하지만 입력 배열의 색인으로 사용되기 전에 '색인 매핑 수집' (공식 설명의 start_index_map) 및 '오프셋 매핑' (공식 설명의 remapped_offset_dims)에 따라 각각 [X,0] 및 [0,O0] 로 확장되어 [X,O0]이 됩니다. 즉, 출력 색인 [G0,G1,O0] 은 입력 색인 [GatherIndices[G0,G1,0],O0]에 매핑되어 tf.gather_nd의 의미를 제공합니다.
이 경우의 slice_sizes은 [1,11]입니다. 직관적으로 이는 수집 색인 배열의 모든 색인 X이 전체 행을 선택하고 결과는 이러한 모든 행의 연결임을 의미합니다.
GetDimensionSize
XlaBuilder::GetDimensionSize도 참고하세요.
피연산자의 지정된 차원의 크기를 반환합니다. 피연산자는 배열 모양이어야 합니다.
GetDimensionSize(operand, dimension)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
n차원 입력 배열 |
dimension
|
int64
|
[0, n) 간격의 값으로, 차원을 지정합니다. |
StableHLO 정보는 StableHLO - get_dimension_size를 참고하세요.
GetTupleElement
XlaBuilder::GetTupleElement도 참고하세요.
컴파일 시간 상수 값을 사용하여 튜플로 색싱합니다.
모양 추론이 결과 값의 유형을 결정할 수 있도록 값은 컴파일 시간 상수여야 합니다.
이는 C++의 std::get<int N>(t)와 유사합니다. 개념적으로는 다음과 같습니다.
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
tf.tuple도 참고하세요.
GetTupleElement(tuple_data, index)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
tuple_data |
XlaOP |
튜플 |
index |
int64 |
튜플 모양의 색인 |
StableHLO 정보는 StableHLO - get_tuple_element를 참고하세요.
Imag
XlaBuilder::Imag도 참고하세요.
복소수 (또는 실수) 모양의 요소별 허수부입니다. x -> imag(x). 피연산자가 부동 소수점 유형인 경우 0을 반환합니다.
Imag(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
StableHLO 정보는 StableHLO - imag를 참고하세요.
인피드
XlaBuilder::Infeed도 참고하세요.
Infeed(shape, config)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
shape
|
Shape
|
인피드 인터페이스에서 읽은 데이터의 모양입니다. 모양의 레이아웃 필드는 기기에 전송된 데이터의 레이아웃과 일치하도록 설정해야 합니다. 그렇지 않으면 동작이 정의되지 않습니다. |
config |
선택사항 string |
작업의 구성입니다. |
기기의 암시적 인피드 스트리밍 인터페이스에서 단일 데이터 항목을 읽고 데이터를 지정된 모양과 레이아웃으로 해석하여 데이터의 XlaOp을 반환합니다. 하나의 계산에 여러 인피드 작업이 허용되지만 인피드 작업 간에 전체 순서가 있어야 합니다. 예를 들어 아래 코드의 두 Infeed에는 while 루프 간에 종속성이 있으므로 전체 순서가 있습니다.
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
중첩된 튜플 모양은 지원되지 않습니다. 빈 튜플 모양의 경우 인피드 작업은 사실상 no-op이며 기기의 인피드에서 데이터를 읽지 않고 진행됩니다.
StableHLO 정보는 StableHLO - 인피드를 참고하세요.
Iota
XlaBuilder::Iota도 참고하세요.
Iota(shape, iota_dimension)
잠재적으로 큰 호스트 전송이 아닌 기기에서 상수 리터럴을 빌드합니다. 지정된 모양을 가지며 0부터 시작하여 지정된 차원을 따라 1씩 증가하는 값을 보유하는 배열을 만듭니다. 부동 소수점 유형의 경우 생성된 배열은 ConvertElementType(Iota(...))와 동일합니다. 여기서 Iota는 정수 유형이고 변환은 부동 소수점 유형입니다.
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
shape |
Shape |
Iota()로 생성된 배열의 모양 |
iota_dimension |
int64 |
증가시킬 측정기준입니다. |
예를 들어 Iota(s32[4, 8], 0)는 다음을 반환합니다.
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
반품 가능, 수수료 Iota(s32[4, 8], 1)
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
StableHLO 정보는 StableHLO - iota를 참고하세요.
IsFinite
XlaBuilder::IsFinite도 참고하세요.
operand의 각 요소가 유한한지, 즉 양수 또는 음수 무한대가 아니고 NaN이 아닌지 테스트합니다. 입력과 모양이 동일한 PRED 값의 배열을 반환합니다. 여기서 각 요소는 해당 입력 요소가 유한한 경우에만 true입니다.
IsFinite(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
StableHLO 정보는 StableHLO - is_finite를 참고하세요.
로그
XlaBuilder::Log도 참고하세요.
요소별 자연 로그 x -> ln(x)입니다.
Log(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
로그는 선택적 result_accuracy 인수도 지원합니다.
Log(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
StableHLO 정보는 StableHLO - log를 참고하세요.
Log1p
XlaBuilder::Log1p도 참고하세요.
요소별로 이동된 자연 로그 x -> ln(1+x)입니다.
Log1p(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
Log1p는 선택적 result_accuracy 인수도 지원합니다.
Log1p(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
StableHLO 정보는 StableHLO - log_plus_one을 참고하세요.
물류
XlaBuilder::Logistic도 참고하세요.
요소별 로지스틱 함수 계산 x -> logistic(x)
Logistic(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
Logistic은 선택적 result_accuracy 인수도 지원합니다.
Logistic(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
StableHLO 정보는 StableHLO - 물류를 참고하세요.
지도
XlaBuilder::Map도 참고하세요.
Map(operands..., computation, dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operands |
N개의 XlaOp 시퀀스 |
T0..T{N-1} 유형의 N 배열 |
computation
|
XlaComputation
|
T 유형의 N 매개변수와 임의 유형의 M을 사용하여 T_0, T_1,
.., T_{N + M -1} -> S 유형을 계산합니다. |
dimensions |
int64 배열 |
지도 측정기준의 배열 |
static_operands
|
N개의 XlaOp 시퀀스
|
지도 작업의 정적 작업 |
주어진 operands 배열에 스칼라 함수를 적용하여 각 요소가 입력 배열의 해당 요소에 적용된 매핑된 함수의 결과인 동일한 차원의 배열을 생성합니다.
매핑된 함수는 스칼라 유형 T의 입력이 N개 있고 유형이 S인 단일 출력이 있다는 제한이 있는 임의의 계산입니다. 출력은 요소 유형 T가 S로 대체된다는 점을 제외하고 피연산자와 동일한 차원을 갖습니다.
예를 들어 Map(op1, op2, op3, computation, par1)는 입력 배열의 각 (다차원) 색인에서 elem_out <-
computation(elem1, elem2, elem3, par1)을 매핑하여 출력 배열을 생성합니다.
StableHLO 정보는 StableHLO - map을 참고하세요.
최대
XlaBuilder::Max도 참고하세요.
텐서 lhs 및 rhs에 요소별 최대 연산을 실행합니다.
Max(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Max에는 다양한 차원의 방송을 지원하는 대체 변형이 있습니다.
Max(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - 최대값을 참고하세요.
최소
XlaBuilder::Min도 참고하세요.
lhs 및 rhs에 대해 요소별 최소 연산을 실행합니다.
Min(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
다른 차원의 브로드캐스팅 지원이 있는 대체 변형이 Min에 있습니다.
Min(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - 최소를 참고하세요.
Mul
XlaBuilder::Mul도 참고하세요.
lhs와 rhs의 요소별 곱을 수행합니다.
Mul(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Mul의 경우 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Mul(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - multiply를 참고하세요.
Neg
XlaBuilder::Neg도 참고하세요.
요소별 부정 x -> -x
Neg(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
StableHLO 정보는 StableHLO - negate를 참고하세요.
제외
XlaBuilder::Not도 참고하세요.
요소별 논리 부정 x -> !(x)입니다.
Not(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
StableHLO 정보는 StableHLO - not을 참고하세요.
OptimizationBarrier
XlaBuilder::OptimizationBarrier도 참고하세요.
최적화 패스가 장벽을 넘어 계산을 이동하는 것을 차단합니다.
OptimizationBarrier(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
배리어의 출력에 종속된 연산자보다 먼저 모든 입력이 평가되도록 합니다.
StableHLO에 관한 자세한 내용은 StableHLO - optimization_barrier를 참고하세요.
또는
XlaBuilder::Or도 참고하세요.
lhs 및 rhs의 요소별 OR을 실행합니다 .
Or(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
다음과 같은 경우 다른 차원 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Or(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - or를 참고하세요.
아웃피드
XlaBuilder::Outfeed도 참고하세요.
입력을 아웃피드에 씁니다.
Outfeed(operand, shape_with_layout, outfeed_config)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
T 유형의 배열 |
shape_with_layout |
Shape |
전송된 데이터의 레이아웃을 정의합니다. |
outfeed_config |
string |
아웃피드 명령의 구성 상수 |
shape_with_layout는 배출하려는 레이아웃된 모양을 전달합니다.
StableHLO 정보는 StableHLO - outfeed를 참고하세요.
Pad
XlaBuilder::Pad도 참고하세요.
Pad(operand, padding_value, padding_config)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
T 유형의 배열 |
padding_value
|
XlaOp
|
추가된 패딩을 채우는 T 유형의 스칼라 |
padding_config
|
PaddingConfig
|
양쪽 가장자리 (낮음, 높음)와 각 차원의 요소 사이의 패딩 양 |
주어진 padding_value로 배열 주변과 배열 요소 사이에 패딩을 추가하여 주어진 operand 배열을 확장합니다. padding_config는 각 차원의 가장자리 패딩과 내부 패딩의 양을 지정합니다.
PaddingConfig는 PaddingConfigDimension의 반복 필드이며 각 측정기준에 대해 edge_padding_low, edge_padding_high, interior_padding의 세 필드를 포함합니다.
edge_padding_low 및 edge_padding_high는 각 차원의 하위 (색인 0 옆) 및 상위 (최고 색인 옆)에 추가된 패딩의 양을 각각 지정합니다. 가장자리 패딩의 양은 음수일 수 있습니다. 음수 패딩의 절대값은 지정된 차원에서 삭제할 요소의 수를 나타냅니다.
interior_padding는 각 차원의 두 요소 사이에 추가된 패딩의 양을 지정하며 음수일 수 없습니다. 내부 패딩은 논리적으로 가장자리 패딩보다 먼저 발생하므로 가장자리 패딩이 음수인 경우 요소가 내부 패딩 피연산자에서 삭제됩니다.
가장자리 패딩 쌍이 모두 (0, 0)이고 내부 패딩 값이 모두 0이면 이 작업은 no-op입니다. 아래 그림은 2차원 배열의 다양한 edge_padding 및 interior_padding 값의 예를 보여줍니다.
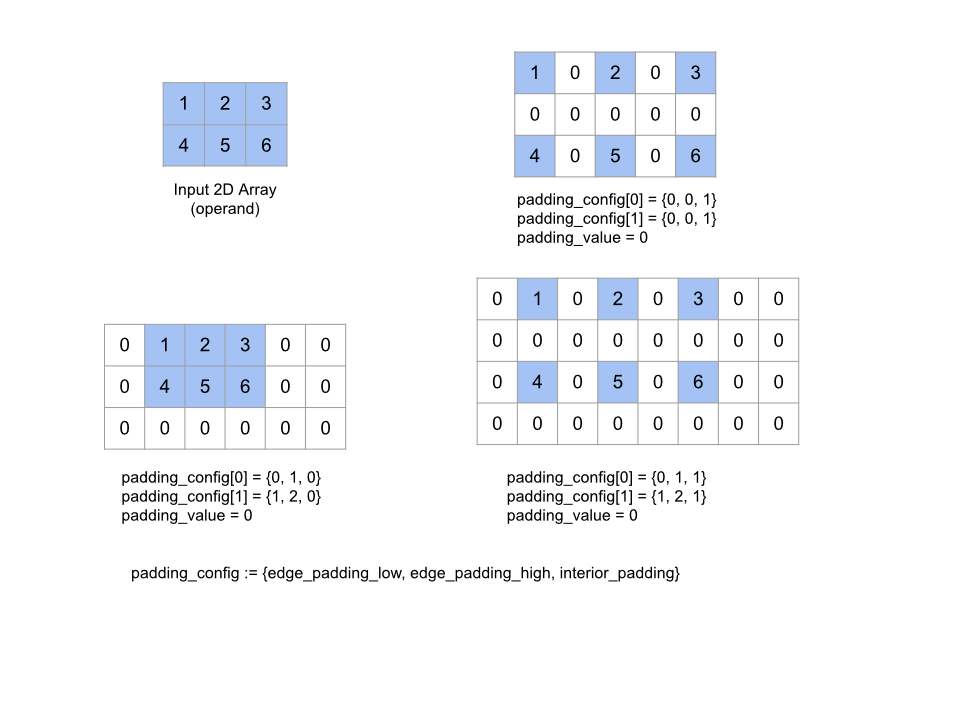
StableHLO 정보는 StableHLO - 패딩을 참고하세요.
매개변수
XlaBuilder::Parameter도 참고하세요.
Parameter는 계산에 대한 인수 입력을 나타냅니다.
PartitionID
XlaBuilder::BuildPartitionId도 참고하세요.
현재 프로세스의 partition_id을 생성합니다.
PartitionID(shape)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
shape |
Shape |
데이터 형태 |
PartitionID는 HLO 덤프에 표시될 수 있지만 최종 사용자가 수동으로 구성하도록 설계되지 않았습니다.
StableHLO 정보는 StableHLO - partition_id를 참고하세요.
PopulationCount
XlaBuilder::PopulationCount도 참고하세요.
operand의 각 요소에 설정된 비트 수를 계산합니다.
PopulationCount(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
StableHLO 정보는 StableHLO - popcnt를 참고하세요.
Pow
XlaBuilder::Pow도 참고하세요.
lhs을 rhs로 거듭제곱한 값을 요소별로 계산합니다.
Pow(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Pow의 경우 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Pow(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - power를 참고하세요.
실제
XlaBuilder::Real도 참고하세요.
복소수 (또는 실수) 모양의 요소별 실수부입니다. x -> real(x). 피연산자가 부동 소수점 유형인 경우 Real은 동일한 값을 반환합니다.
Real(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
StableHLO 정보는 StableHLO - 실제를 참고하세요.
Recv
XlaBuilder::Recv도 참고하세요.
Recv, RecvWithTokens, RecvToHost는 HLO에서 통신 프리미티브 역할을 하는 작업입니다. 이러한 작업은 일반적으로 HLO 덤프에 하위 수준 입력/출력 또는 교차 기기 전송의 일부로 표시되지만 최종 사용자가 수동으로 구성하도록 설계되지 않았습니다.
Recv(shape, handle)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
shape |
Shape |
수신할 데이터의 모양 |
handle |
ChannelHandle |
각 송수신 쌍의 고유 식별자 |
동일한 채널 핸들을 공유하는 다른 계산의 Send 명령어에서 지정된 모양의 데이터를 수신합니다. 수신된 데이터의 XlaOp를 반환합니다.
StableHLO 정보는 StableHLO - recv를 참고하세요.
RecvDone
HloInstruction::CreateRecv 및 HloInstruction::CreateRecvDone도 참고하세요.
Send와 마찬가지로 Recv 작업의 클라이언트 API는 동기 통신을 나타냅니다. 하지만 비동기 데이터 전송을 지원하기 위해 이 명령어는 내부적으로 2개의 HLO 명령어 (Recv 및 RecvDone)로 분해됩니다.
Recv(const Shape& shape, int64 channel_id)
동일한 channel_id를 사용하여 Send 명령에서 데이터를 수신하는 데 필요한 리소스를 할당합니다. 할당된 리소스의 컨텍스트를 반환합니다. 이 컨텍스트는 후속 RecvDone 명령어에서 데이터 전송이 완료될 때까지 기다리는 데 사용됩니다. 컨텍스트는 {수신 버퍼 (모양), 요청 식별자 (U32)} 튜플이며 RecvDone 명령어에서만 사용할 수 있습니다.
Recv 명령어로 생성된 컨텍스트가 주어지면 데이터 전송이 완료될 때까지 기다리고 수신된 데이터를 반환합니다.
방지(Reduce)
XlaBuilder::Reduce도 참고하세요.
하나 이상의 배열에 병렬로 축소 함수를 적용합니다.
Reduce(operands..., init_values..., computation, dimensions_to_reduce)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operands
|
N개의 XlaOp 시퀀스
|
T_0,...,
T_{N-1} 유형의 N 배열 |
init_values
|
N개의 XlaOp 시퀀스
|
T_0,..., T_{N-1} 유형의 스칼라 N개 |
computation
|
XlaComputation
|
T_0,..., T_{N-1}, T_0,
...,T_{N-1} ->
Collate(T_0,...,
T_{N-1}) 유형의 계산 |
dimensions_to_reduce
|
int64 배열
|
축소할 차원의 순서가 지정되지 않은 배열입니다. |
각 항목의 의미는 다음과 같습니다.
- N은 1 이상이어야 합니다.
- 계산은 '대략' 결합적이어야 합니다 (아래 참고).
- 모든 입력 배열의 크기가 동일해야 합니다.
- 모든 초기 값은
computation에서 ID를 형성해야 합니다. N = 1이면Collate(T)은T입니다.N > 1,Collate(T_0, ..., T_{N-1})이T유형의N요소로 구성된 튜플인 경우
이 작업은 각 입력 배열의 하나 이상의 차원을 스칼라로 축소합니다.
반환된 각 배열의 차원 수는 number_of_dimensions(operand) - len(dimensions)입니다. 작업의 출력은 Collate(Q_0, ..., Q_N)입니다. 여기서 Q_i는 T_i 유형의 배열이며 그 차원은 아래에 설명되어 있습니다.
다양한 백엔드에서 축소 계산을 다시 연결할 수 있습니다. 더하기와 같은 일부 축소 함수는 부동 소수점의 경우 결합적이지 않으므로 수치 차이가 발생할 수 있습니다. 하지만 데이터 범위가 제한적인 경우 부동 소수점 덧셈은 대부분의 실제 용도에 연관성이 충분히 있습니다.
StableHLO 정보는 StableHLO - reduce를 참고하세요.
예
값이 [10, 11,
12, 13]인 단일 1D 배열에서 한 측정기준을 따라 감소하고 감소 함수가 f (computation)인 경우 다음과 같이 계산할 수 있습니다.
f(10, f(11, f(12, f(init_value, 13)))
하지만 다음과 같은 다른 가능성도 많습니다.
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
다음은 합계를 초기값 0으로 사용하여 감소 계산으로 구현할 수 있는 감소의 대략적인 의사 코드 예입니다.
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
다음은 2D 배열 (행렬)을 축소하는 예입니다. 모양에는 크기가 2인 0번째 차원과 크기가 3인 1번째 차원의 두 차원이 있습니다.
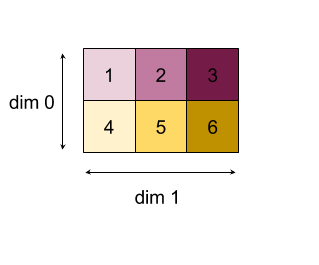
'add' 함수를 사용하여 차원 0 또는 1을 축소한 결과:
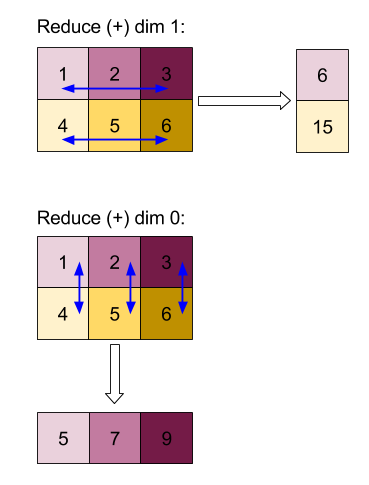
두 감소 결과 모두 1D 배열입니다. 다이어그램에서는 시각적 편의를 위해 하나는 열로, 다른 하나는 행으로 표시합니다.
더 복잡한 예로 3D 배열이 있습니다. 차원 수는 3이고, 크기가 4인 차원 0, 크기가 2인 차원 1, 크기가 3인 차원 2입니다. 간단하게 하기 위해 값 1~6은 차원 0에 복제됩니다.
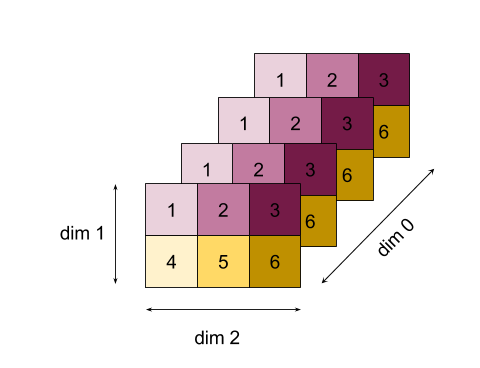
2D 예와 마찬가지로 한 차원만 줄일 수 있습니다. 예를 들어 차원 0을 축소하면 차원 0의 모든 값이 스칼라로 접힌 2차원 배열이 됩니다.
| 4 8 12 |
| 16 20 24 |
측정기준 2를 줄이면 측정기준 2의 모든 값이 스칼라로 접힌 2차원 배열도 얻을 수 있습니다.
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
입력의 나머지 측정기준 간의 상대적 순서는 출력에서 유지되지만 측정기준 수가 변경되므로 일부 측정기준에 새 번호가 할당될 수 있습니다.
여러 측정기준을 줄일 수도 있습니다. 0과 1을 축소하면 1D 배열 [20, 28, 36]가 생성됩니다.
모든 차원에서 3D 배열을 줄이면 스칼라 84가 생성됩니다.
가변 인자 감소
N > 1의 경우 함수 적용이 모든 입력에 동시에 적용되므로 약간 더 복잡합니다. 피연산자는 다음 순서로 계산에 제공됩니다.
- 첫 번째 피연산자의 감소된 값 실행
- ...
- N번째 피연산자에 대해 감소된 값을 실행합니다.
- 첫 번째 피연산자의 입력 값
- ...
- N번째 피연산자의 입력 값
예를 들어 다음 축소 함수를 사용하여 1차원 배열의 최대값과 argmax를 병렬로 계산할 수 있습니다.
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
1차원 입력 배열 V = Float[N], K = Int[N] 및 초기값 I_V = Float, I_K = Int의 경우 유일한 입력 차원에서 축소한 결과 f_(N-1)는 다음 재귀 적용과 같습니다.
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
값 배열과 순차 색인 배열 (즉, iota)에 이 축소를 적용하면 배열을 공동 반복하고 최대값과 일치하는 색인이 포함된 튜플을 반환합니다.
ReducePrecision
XlaBuilder::ReducePrecision도 참고하세요.
부동 소수점 값을 낮은 정밀도 형식 (예: IEEE-FP16)으로 변환한 후 원래 형식으로 다시 변환하는 효과를 모델링합니다. 낮은 정밀도 형식의 지수 및 가수 비트 수는 임의로 지정할 수 있지만 모든 비트 크기가 모든 하드웨어 구현에서 지원되지는 않을 수 있습니다.
ReducePrecision(operand, exponent_bits, mantissa_bits)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
부동 소수점 유형 T의 배열입니다. |
exponent_bits |
int32 |
낮은 정밀도 형식의 지수 비트 수 |
mantissa_bits |
int32 |
낮은 정밀도 형식의 가수 비트 수 |
결과는 T 유형의 배열입니다. 입력 값은 주어진 수의 가수 비트로 표현할 수 있는 가장 가까운 값으로 반올림되고('짝수 쪽으로 반올림' 의미 체계 사용), 지수 비트 수로 지정된 범위를 초과하는 값은 양의 무한대 또는 음의 무한대로 클램핑됩니다. NaN 값은 유지되지만 표준 NaN 값으로 변환될 수 있습니다.
정밀도가 낮은 형식에는 0 값과 무한대를 구분하기 위해 (둘 다 가수가 0임) 하나 이상의 지수 비트가 있어야 하며 음수가 아닌 가수 비트 수가 있어야 합니다. 지수 또는 가수 비트 수가 T 유형의 해당 값을 초과할 수 있습니다. 이 경우 변환의 해당 부분은 단순히 작업이 없습니다.
StableHLO 정보는 StableHLO - reduce_precision을 참고하세요.
ReduceScatter
XlaBuilder::ReduceScatter도 참고하세요.
ReduceScatter는 AllReduce를 효과적으로 실행한 다음 결과를 scatter_dimension을 따라 shard_count 블록으로 분할하여 분산하는 집단 작업이며 복제본 그룹의 복제본 i는 ith 샤드를 수신합니다.
ReduceScatter(operand, computation, scatter_dimension, shard_count,
replica_groups, channel_id, layout, use_global_device_ids)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand
|
XlaOp
|
복제본에서 축소할 배열 또는 비어 있지 않은 배열 튜플입니다. |
computation |
XlaComputation |
감소 계산 |
scatter_dimension |
int64 |
분산할 차원입니다. |
shard_count
|
int64
|
scatter_dimension을 분할할 블록 수 |
replica_groups
|
ReplicaGroup 벡터
|
축소가 실행되는 그룹 |
channel_id
|
선택사항
ChannelHandle |
크로스 모듈 통신을 위한 선택적 채널 ID |
layout
|
선택사항 Layout
|
사용자 지정 메모리 레이아웃 |
use_global_device_ids |
선택사항 bool |
사용자 지정 플래그 |
operand이 배열의 튜플인 경우 튜플의 각 요소에서 reduce-scatter가 실행됩니다.replica_groups은 축소가 실행되는 복제본 그룹의 목록입니다 (현재 복제본의 복제본 ID는ReplicaId를 사용하여 가져올 수 있음). 각 그룹의 복제본 순서에 따라 전체 감소 결과가 분산되는 순서가 결정됩니다.replica_groups는 비어 있거나 (이 경우 모든 복제본이 단일 그룹에 속함) 복제본 수와 동일한 수의 요소를 포함해야 합니다. 복제본 그룹이 두 개 이상인 경우 모두 크기가 동일해야 합니다. 예를 들어replica_groups = {0, 2}, {1, 3}는 복제본0와2,1와3간에 축소를 수행한 다음 결과를 분산합니다.shard_count은 각 복제본 그룹의 크기입니다.replica_groups가 비어 있는 경우에 필요합니다.replica_groups이 비어 있지 않으면shard_count은 각 복제본 그룹의 크기와 같아야 합니다.channel_id는 교차 모듈 통신에 사용됩니다. 동일한channel_id를 사용하는reduce-scatter작업만 서로 통신할 수 있습니다.layout레이아웃에 관한 자세한 내용은 xla::shapes를 참고하세요.use_global_device_ids는 사용자가 지정한 플래그입니다.false(기본값)인 경우true일 때replica_groups의 숫자는ReplicaId입니다.true일 때replica_groups은 (ReplicaID*partition_count+partition_id)의 전역 ID를 나타냅니다. 예를 들면 다음과 같습니다.- 복제본 2개와 파티션 4개를 사용하면
- replica_groups={ {0,1,4,5},{2,3,6,7} } and use_global_device_ids=true
- group[0] = (0,0), (0,1), (1,0), (1,1)
- group[1] = (0,2), (0,3), (1,2), (1,3)
- 여기서 각 쌍은 (replica_id, partition_id)입니다.
출력 모양은 scatter_dimension가 shard_count배 작아진 입력 모양입니다. 예를 들어 복제본이 두 개 있고 피연산자의 값이 두 복제본에서 각각 [1.0, 2.25] 및 [3.0, 5.25]인 경우 scatter_dim이 0인 이 작업의 출력 값은 첫 번째 복제본의 경우 [4.0], 두 번째 복제본의 경우 [7.5]이 됩니다.
StableHLO 정보는 StableHLO - reduce_scatter를 참고하세요.
ReduceScatter - 예 1 - StableHLO
위의 예에서는 ReduceScatter에 참여하는 복제본이 2개 있습니다. 각 복제본에서 피연산자의 모양은 f32[2,4]입니다. 복제본 전체에서 all-reduce (합계)가 실행되어 각 복제본에서 f32[2,4] 모양의 감소된 값이 생성됩니다. 이 감소된 값은 차원 1을 따라 두 부분으로 분할되므로 각 부분의 모양은 f32[2,2]입니다. 프로세스 그룹 내의 각 복제본은 그룹 내 위치에 해당하는 부분을 수신합니다. 따라서 각 복제본의 출력은 f32[2,2] 형태를 갖습니다.
ReduceWindow
XlaBuilder::ReduceWindow도 참고하세요.
N 다차원 배열 시퀀스의 각 윈도우에 있는 모든 요소에 감소 함수를 적용하여 단일 또는 N 다차원 배열 튜플을 출력으로 생성합니다. 각 출력 배열에는 창의 유효한 위치 수와 동일한 수의 요소가 있습니다. 풀링 레이어는 ReduceWindow로 표현할 수 있습니다. Reduce와 마찬가지로 적용된 computation는 항상 왼쪽의 init_values에 전달됩니다.
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operands
|
N XlaOps
|
타입 T_0,..., T_{N-1}의 N 다차원 배열 시퀀스로, 각 배열은 창이 배치되는 기본 영역을 나타냅니다. |
init_values
|
N XlaOps
|
축소의 N 시작 값입니다. 각 N 피연산자에 하나씩 있습니다. 자세한 내용은 줄이기를 참고하세요. |
computation
|
XlaComputation
|
모든 입력 피연산자의 각 윈도우에 있는 요소에 적용할 T_0,
..., T_{N-1}, T_0, ..., T_{N-1}
-> Collate(T_0, ..., T_{N-1}) 유형의 감소 함수입니다. |
window_dimensions
|
ArraySlice<int64>
|
창 측정기준 값의 정수 배열 |
window_strides
|
ArraySlice<int64>
|
윈도우 스트라이드 값의 정수 배열 |
base_dilations
|
ArraySlice<int64>
|
기본 팽창 값의 정수 배열 |
window_dilations
|
ArraySlice<int64>
|
창 팽창 값의 정수 배열 |
padding
|
Padding
|
창의 패딩 유형입니다(스트라이드가 1인 경우 입력과 동일한 출력 모양을 갖도록 패딩하는 Padding::kSame 또는 패딩을 사용하지 않고 더 이상 맞지 않으면 창을 '중지'하는 Padding::kValid). |
각 항목의 의미는 다음과 같습니다.
- N은 1 이상이어야 합니다.
- 모든 입력 배열의 크기가 동일해야 합니다.
N = 1이면Collate(T)은T입니다.N > 1,Collate(T_0, ..., T_{N-1})이(T0,...T{N-1})유형의N요소로 구성된 튜플인 경우
StableHLO 정보는 StableHLO - reduce_window를 참고하세요.
ReduceWindow - 예 1
입력은 [4x6] 크기의 행렬이고 window_dimensions와 window_stride_dimensions는 모두 [2x3]입니다.
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
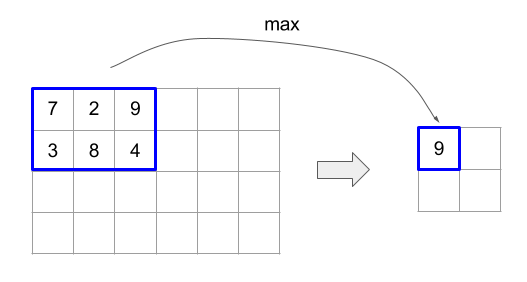
측정기준의 스트라이드 1은 측정기준의 윈도우 위치가 인접한 윈도우에서 1개 요소 떨어져 있음을 지정합니다. 창이 서로 겹치지 않도록 지정하려면 window_stride_dimensions가 window_dimensions와 같아야 합니다. 아래 그림은 두 가지 다른 보폭 값의 사용을 보여줍니다. 패딩은 입력의 각 차원에 적용되며 계산은 패딩 후의 차원을 가진 입력이 들어온 것과 동일합니다.
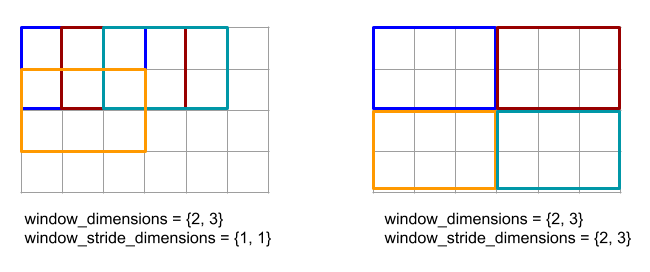
사소하지 않은 패딩 예시로 입력 배열 [10000, 1000, 100, 10, 1]에 대해 차원 3과 스트라이드 2로 reduce-window minimum(초기 값은 MAX_FLOAT)을 계산하는 것을 고려해 보세요. 패딩 kValid는 [10000, 1000, 100] 및 [100, 10, 1]의 두 유효한 구간에서 최솟값을 계산하여 [100, 1] 출력을 생성합니다. 패딩 kSame은 먼저 축소 창 후의 모양이 양쪽에 초기 요소를 추가하여 스트라이드 1의 입력과 동일하도록 배열을 패딩하여 [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE]을 얻습니다. 패딩된 배열에 reduce-window를 실행하면 세 개의 창 [MAX_VALUE, 10000, 1000], [1000, 100, 10], [10, 1, MAX_VALUE]에서 작동하고 [1000, 10, 1]이 생성됩니다.
축소 함수의 평가 순서는 임의적이며 확정적이지 않을 수 있습니다. 따라서 감소 함수는 재연결에 지나치게 민감해서는 안 됩니다. Reduce 컨텍스트의 결합성에 관한 토론을 참고하세요.
ReduceWindow - 예 2 - StableHLO
위의 예에서
입력) 피연산자의 입력 모양은 S32[3,2]입니다. 값이 [[1,2],[3,4],[5,6]]인 경우
1단계) 행 차원을 따라 계수 2로 기본 팽창을 적용하면 피연산자의 각 행 사이에 구멍이 삽입됩니다. 팽창 후 상단에 2개 행, 하단에 1개 행의 패딩이 적용됩니다. 따라서 텐서가 더 길어집니다.
2단계) 모양이 [2,1] 인 창이 정의되고 창 팽창은 [3,1]입니다. 즉, 각 윈도우는 동일한 열에서 두 요소를 선택하지만 두 번째 요소는 바로 아래가 아닌 첫 번째 요소 아래 3개 행에서 가져옵니다.
3단계) 그런 다음 윈도우가 스트라이드 [4,1]로 피연산자를 가로질러 슬라이드됩니다. 이렇게 하면 창이 한 번에 네 행씩 아래로 이동하고 한 번에 한 열씩 가로로 이동합니다. 패딩 셀은 init_value (이 경우 init_value = 0)로 채워집니다. 팽창 셀에 '속하는' 값은 무시됩니다.
보폭과 패딩으로 인해 일부 창은 0과 구멍만 겹치고 다른 창은 실제 입력 값을 겹칩니다.
4단계) 각 윈도우 내에서 요소는 감소 함수 (a, b) → a + b를 사용하여 결합되며, 초기값은 0입니다. 상위 두 창에는 패딩과 홀만 표시되므로 결과는 0입니다. 하단 창은 입력에서 값 3과 4를 캡처하고 이를 결과로 반환합니다.
결과) 최종 출력의 모양은 S32[2,2]이며 값은 다음과 같습니다. [[0,0],[3,4]]
Rem
XlaBuilder::Rem도 참고하세요.
피제수 lhs와 제수 rhs의 요소별 나머지를 계산합니다.
결과의 부호는 피제수에서 가져오며 결과의 절대값은 항상 제수의 절대값보다 작습니다.
Rem(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Rem의 경우 차원이 다른 브로드캐스팅을 지원하는 대체 변형이 있습니다.
Rem(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - 나머지를 참고하세요.
ReplicaId
XlaBuilder::ReplicaId도 참고하세요.
복제본의 고유 ID (U32 스칼라)를 반환합니다.
ReplicaId()
각 복제본의 고유 ID는 [0, N) 간격의 부호 없는 정수입니다. 여기서 N는 복제본 수입니다. 모든 복제본이 동일한 프로그램을 실행하므로 프로그램의 ReplicaId() 호출은 각 복제본에서 다른 값을 반환합니다.
StableHLO 정보는 StableHLO - replica_id를 참고하세요.
재구성
XlaBuilder::Reshape도 참고하세요.
Collapse 작업입니다.
배열의 차원을 새 구성으로 재구성합니다.
Reshape(operand, dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
T 유형의 배열 |
dimensions |
int64 벡터 |
새 차원의 크기 벡터 |
개념적으로 reshape는 먼저 배열을 데이터 값의 1차원 벡터로 평탄화한 다음 이 벡터를 새 모양으로 세분화합니다. 입력 인수는 T 유형의 임의 배열, 컴파일 시간 상수 차원 색인 벡터, 결과의 컴파일 시간 상수 차원 크기 벡터입니다.
dimensions 벡터는 출력 배열의 크기를 결정합니다. dimensions의 색인 0에 있는 값은 측정기준 0의 크기이고, 색인 1에 있는 값은 측정기준 1의 크기입니다. dimensions 차원의 곱은 피연산자의 차원 크기의 곱과 같아야 합니다. 축소된 배열을 dimensions로 정의된 다차원 배열로 구체화할 때 dimensions의 차원은 가장 느리게 변하는 것 (가장 주요)부터 가장 빠르게 변하는 것 (가장 사소)까지 순서대로 정렬됩니다.
예를 들어 v가 24개 요소의 배열이라고 가정해 보겠습니다.
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
특수한 경우 reshape는 단일 요소 배열을 스칼라로 변환할 수 있으며 그 반대도 가능합니다. 예를 들면 다음과 같습니다.
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
StableHLO 정보는 StableHLO - reshape을 참고하세요.
재구성 (명시적)
XlaBuilder::Reshape도 참고하세요.
Reshape(shape, operand)
명시적 타겟 모양을 사용하는 reshape 작업
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
shape |
Shape |
T 유형의 출력 셰이프 |
operand |
XlaOp |
T 유형의 배열 |
Rev (반전)
XlaBuilder::Rev도 참고하세요.
Rev(operand, dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
T 유형의 배열 |
dimensions |
ArraySlice<int64> |
반전할 측정기준 |
지정된 dimensions을 따라 operand 배열의 요소 순서를 반대로 하여 동일한 모양의 출력 배열을 생성합니다. 다차원 인덱스에 있는 피연산자 배열의 각 요소는 변환된 인덱스에 있는 출력 배열에 저장됩니다. 다차원 색인은 반전할 각 차원의 색인을 반전하여 변환됩니다 (즉, 크기가 N인 차원이 반전 차원 중 하나인 경우 색인 i는 N - 1 - i로 변환됨).
Rev 연산의 한 가지 용도는 신경망에서 그라데이션을 계산하는 동안 두 창 차원을 따라 컨볼루션 가중치 배열을 반전하는 것입니다.
StableHLO 정보는 StableHLO - reverse를 참고하세요.
RngNormal
XlaBuilder::RngNormal도 참고하세요.
\(N(\mu, \sigma)\) 정규 분포에 따라 생성된 난수로 지정된 모양의 출력을 구성합니다. \(\mu\) 및 \(\sigma\)매개변수와 출력 모양은 부동 소수점 요소 유형이어야 합니다. 또한 매개변수는 스칼라 값이어야 합니다.
RngNormal(mu, sigma, shape)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
mu |
XlaOp |
생성된 숫자의 평균을 지정하는 T 유형의 스칼라 |
sigma
|
XlaOp
|
생성된 |
shape |
Shape |
T 유형의 출력 셰이프 |
StableHLO 정보는 StableHLO - rng를 참고하세요.
RngUniform
XlaBuilder::RngUniform도 참고하세요.
\([a,b)\)구간에 걸쳐 균등 분포를 따르는 무작위 숫자로 주어진 모양의 출력을 구성합니다. 파라미터와 출력 요소 유형은 불리언 유형, 정수 유형 또는 부동 소수점 유형이어야 하며 유형이 일관되어야 합니다. CPU 및 GPU 백엔드는 현재 F64, F32, F16, BF16, S64, U64, S32, U32만 지원합니다. 또한 매개변수는 스칼라 값이어야 합니다. \(b <= a\) 결과는 구현에 따라 다릅니다.
RngUniform(a, b, shape)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
a |
XlaOp |
간격의 하한을 지정하는 T 유형의 스칼라 |
b |
XlaOp |
간격의 상한을 지정하는 T 유형의 스칼라 |
shape |
Shape |
T 유형의 출력 셰이프 |
StableHLO 정보는 StableHLO - rng를 참고하세요.
RngBitGenerator
XlaBuilder::RngBitGenerator도 참고하세요.
지정된 알고리즘 (또는 백엔드 기본값)을 사용하여 균일한 무작위 비트로 채워진 지정된 모양의 출력을 생성하고 업데이트된 상태 (초기 상태와 동일한 모양)와 생성된 무작위 데이터를 반환합니다.
초기 상태는 현재 난수 생성의 초기 상태입니다. 필수 모양과 유효한 값은 사용된 알고리즘에 따라 달라집니다.
출력은 초기 상태의 결정적 함수로 보장되지만 백엔드와 다양한 컴파일러 버전 간에 결정적이라고 보장되지는 않습니다.
RngBitGenerator(algorithm, initial_state, shape)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
algorithm |
RandomAlgorithm |
사용할 PRNG 알고리즘입니다. |
initial_state |
XlaOp |
PRNG 알고리즘의 초기 상태입니다. |
shape |
Shape |
생성된 데이터의 출력 셰이프입니다. |
algorithm에 사용할 수 있는 값은 다음과 같습니다.
rng_default: 백엔드별 모양 요구사항이 있는 백엔드별 알고리즘입니다.rng_three_fry: ThreeFry 카운터 기반 PRNG 알고리즘입니다.initial_state모양은 임의의 값을 갖는u64[2]입니다. Salmon et al. SC 2011. 병렬 난수: 1, 2, 3만큼 쉽습니다.rng_philox: 병렬로 난수를 생성하는 Philox 알고리즘입니다.initial_state모양은 임의의 값을 갖는u64[3]입니다. Salmon et al. SC 2011. 병렬 난수: 1, 2, 3만큼 쉽습니다.
StableHLO 정보는 StableHLO - rng_bit_generator를 참고하세요.
RngGetAndUpdateState
HloInstruction::CreateRngGetAndUpdateState도 참고하세요.
다양한 Rng 작업의 API는 내부적으로 RngGetAndUpdateState를 포함한 HLO 명령어로 분해됩니다.
RngGetAndUpdateState는 HLO에서 기본 요소로 사용됩니다. 이 작업은 HLO 덤프에 표시될 수 있지만 최종 사용자가 수동으로 구성하도록 설계되지는 않았습니다.
라운드
XlaBuilder::Round도 참고하세요.
요소별 반올림, 0에서 멀어지는 방향으로 동률 처리
Round(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
RoundNearestAfz
XlaBuilder::RoundNearestAfz도 참고하세요.
0에서 멀어지는 방향으로 동률을 깨면서 가장 가까운 정수로 요소별 반올림을 실행합니다.
RoundNearestAfz(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
StableHLO 정보는 StableHLO - round_nearest_afz를 참고하세요.
RoundNearestEven
XlaBuilder::RoundNearestEven도 참고하세요.
요소별 반올림, 가장 가까운 짝수로 반올림
RoundNearestEven(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
StableHLO 정보는 StableHLO - round_nearest_even을 참고하세요.
Rsqrt
XlaBuilder::Rsqrt도 참고하세요.
제곱근 연산 x -> 1.0 / sqrt(x)의 요소별 역수입니다.
Rsqrt(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
Rsqrt는 선택적 result_accuracy 인수도 지원합니다.
Rsqrt(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
StableHLO 정보는 StableHLO - rsqrt를 참고하세요.
스캔
XlaBuilder::Scan도 참고하세요.
지정된 측정기준에서 배열에 감소 함수를 적용하여 최종 상태와 중간 값의 배열을 생성합니다.
Scan(inputs..., inits..., to_apply, scan_dimension,
is_reverse, is_associative)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
inputs |
m XlaOp 시퀀스 |
스캔할 배열입니다. |
inits |
k XlaOp 시퀀스 |
초기 캐리 |
to_apply |
XlaComputation |
i_0, ..., i_{m-1}, c_0, ..., c_{k-1} -> (o_0, ..., o_{n-1}, c'_0, ..., c'_{k-1}) 유형의 계산입니다. |
scan_dimension |
int64 |
스캔할 측정기준입니다. |
is_reverse |
bool |
true인 경우 역순으로 스캔합니다. |
is_associative |
bool (3상태) |
true인 경우 작업은 결합적입니다. |
to_apply 함수는 scan_dimension를 따라 inputs의 요소에 순차적으로 적용됩니다. is_reverse이 false이면 요소는 0에서 N-1 순서로 처리되며 여기서 N은 scan_dimension의 크기입니다. is_reverse이 true이면 요소는 N-1에서 0까지 처리됩니다.
to_apply 함수는 m + k 피연산자를 사용합니다.
inputs의 현재 요소m개k는 이전 단계의 값을 전달합니다 (첫 번째 요소의 경우inits).
to_apply 함수는 n + k 값의 튜플을 반환합니다.
outputs의n요소k새로운 carry 값입니다.
스캔 작업은 n + k 값의 튜플을 생성합니다.
- 각 단계의 출력 값을 포함하는
n출력 배열입니다. - 모든 요소를 처리한 후의 최종
k캐리 값입니다.
m 입력의 유형은 추가 스캔 차원이 있는 to_apply의 첫 번째 m 매개변수의 유형과 일치해야 합니다. n 출력의 유형은 추가 스캔 차원이 있는 to_apply의 첫 번째 n 반환 값의 유형과 일치해야 합니다. 모든 입력과 출력의 추가 스캔 차원은 크기가 N로 동일해야 합니다. 마지막 k 매개변수와 to_apply의 반환 값 및 k init의 유형이 일치해야 합니다.
예를 들어 초기 캐리 i, 입력 [a, b, c], 함수 f(x, c) -> (y, c'), scan_dimension=0, is_reverse=false의 경우 (m, n, k == 1, N == 3)는 다음과 같습니다.
- 0단계:
f(a, i) -> (y0, c0) - 1단계:
f(b, c0) -> (y1, c1) - 2단계:
f(c, c1) -> (y2, c2)
Scan의 출력은 ([y0, y1, y2], c2)입니다.
분산형
XlaBuilder::Scatter도 참고하세요.
XLA 분산 작업은 입력 배열 operands의 값인 결과 시퀀스를 생성하며, 여러 슬라이스 (scatter_indices로 지정된 색인에 있음)는 update_computation를 사용하여 updates의 값 시퀀스로 업데이트됩니다.
Scatter(operands..., scatter_indices, updates..., update_computation,
dimension_numbers, indices_are_sorted, unique_indices)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operands |
N개의 XlaOp 시퀀스 |
T_0, ..., T_N 유형의 N개 배열로 분산됩니다. |
scatter_indices |
XlaOp |
분산해야 하는 슬라이스의 시작 색인이 포함된 배열입니다. |
updates |
N개의 XlaOp 시퀀스 |
T_0, ..., T_N 유형의 N 배열 updates[i]에는 operands[i]을 분산하는 데 사용해야 하는 값이 포함됩니다. |
update_computation |
XlaComputation |
입력 배열의 기존 값과 스캐터 중 업데이트를 결합하는 데 사용할 계산입니다. 이 계산은 T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N) 유형이어야 합니다. |
index_vector_dim |
int64 |
시작 인덱스를 포함하는 scatter_indices의 차원입니다. |
update_window_dims |
ArraySlice<int64> |
updates 모양의 측정기준 집합으로, 창 측정기준입니다. |
inserted_window_dims |
ArraySlice<int64> |
updates 모양에 삽입해야 하는 창 크기 집합 |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
분산 색인에서 피연산자 색인 공간으로의 차원 맵입니다. 이 배열은 i을 scatter_dims_to_operand_dims[i]에 매핑하는 것으로 해석됩니다 . 일대일 관계여야 하며 합계여야 합니다. |
dimension_number |
ScatterDimensionNumbers |
분산 작업을 위한 차원 번호 |
indices_are_sorted |
bool |
호출자가 색인을 정렬하도록 보장되는지 여부입니다. |
unique_indices |
bool |
호출자가 색인이 고유함을 보장하는지 여부입니다. |
각 항목의 의미는 다음과 같습니다.
- N은 1 이상이어야 합니다.
operands[0], ...,operands[N-1] 의 크기가 모두 동일해야 합니다.updates[0], ...,updates[N-1] 의 크기가 모두 동일해야 합니다.N = 1이면Collate(T)은T입니다.N > 1,Collate(T_0, ..., T_N)이T유형의N요소로 구성된 튜플인 경우
index_vector_dim이 scatter_indices.rank와 같으면 scatter_indices에 후행 1 차원이 있는 것으로 간주합니다.
ArraySlice<int64> 유형의 update_scatter_dims는 updates 모양의 차원 중 update_window_dims에 없는 차원의 집합으로 정의되며, 오름차순으로 정렬됩니다.
분산의 인수는 다음 제약 조건을 따라야 합니다.
각
updates배열에는update_window_dims.size + scatter_indices.rank - 1차원이 있어야 합니다.각
updates배열에서i측정기준의 경계는 다음을 준수해야 합니다.i이update_window_dims에 있으면 (즉, 일부k에 대해update_window_dims[k] 와 같음)updates의i측정기준의 경계가inserted_window_dims을 고려한 후operand의 해당 경계를 초과해서는 안 됩니다 (즉,adjusted_window_bounds[k], 여기서adjusted_window_bounds에는inserted_window_dims의 색인에 있는 경계가 삭제된operand의 경계가 포함됨).i이update_scatter_dims에 있는 경우 (즉, 일부k에 대해update_scatter_dims[k] 와 같음)updates의i차원의 경계는index_vector_dim를 건너뛰고scatter_indices의 해당 경계와 같아야 합니다 (즉,k<index_vector_dim인 경우scatter_indices.shape.dims[k], 그렇지 않은 경우scatter_indices.shape.dims[k+1]).
update_window_dims는 오름차순이어야 하고, 반복되는 측정기준 번호가 없어야 하며,[0, updates.rank)범위에 있어야 합니다.inserted_window_dims는 오름차순이어야 하고, 반복되는 측정기준 번호가 없어야 하며,[0, operand.rank)범위에 있어야 합니다.operand.rank는update_window_dims.size와inserted_window_dims.size의 합과 같아야 합니다.scatter_dims_to_operand_dims.size은scatter_indices.shape.dims[index_vector_dim]과 같아야 하며 값은[0, operand.rank)범위에 있어야 합니다.
각 updates 배열의 지정된 색인 U의 경우 이 업데이트를 적용해야 하는 해당 operands 배열의 해당 색인 I은 다음과 같이 계산됩니다.
G= {U[k] forkinupdate_scatter_dims}라고 가정합니다.G를 사용하여S[i] =scatter_indices[Combine(G,i)] 이 되도록scatter_indices배열에서 색인 벡터S를 조회합니다. 여기서 Combine(A, b)는index_vector_dim위치에 b를 A에 삽입합니다.scatter_dims_to_operand_dims맵을 사용하여S를 분산하여S를 사용하여operand에 색인Sin을 만듭니다. 더 공식적으로 표현하면 다음과 같습니다.Sin[scatter_dims_to_operand_dims[k]] =S[k](k<scatter_dims_to_operand_dims.size인 경우)- 그렇지 않으면
Sin[_] =0입니다.
inserted_window_dims에 따라U의update_window_dims에 있는 색인을 분산하여 각operands배열에 색인Win을 만듭니다. 더 공식적으로 표현하면 다음과 같습니다.Win[window_dims_to_operand_dims(k)] =U[k](k이update_window_dims에 있는 경우), 여기서window_dims_to_operand_dims은 도메인이 [0,update_window_dims.size)이고 범위가 [0,operand.rank) \inserted_window_dims인 단조 함수입니다. (예를 들어update_window_dims.size이4이고operand.rank이6이며inserted_window_dims이 {0,2}이면window_dims_to_operand_dims은 {0→1,1→3,2→4,3→5}입니다.)- 그렇지 않으면
Win[_] =0입니다.
I는Win+Sin입니다. 여기서 +는 요소별 덧셈입니다.
요약하면 분산 작업은 다음과 같이 정의할 수 있습니다.
operands으로output를 초기화합니다. 즉, 모든 색인J에 대해operands[J] 배열의 모든 색인O에 대해
output[J][O] =operands[J][O]updates[J] 배열의 모든 색인U와operand[J] 배열의 해당 색인O에 대해O이output의 유효한 색인인 경우
(output[0][O], ...,output[N-1][O]) =update_computation(output[0][O], ..., ,output[N-1][O],updates[0][U], ...,updates[N-1][U])
업데이트가 적용되는 순서는 비결정적입니다. 따라서 updates의 여러 색인이 operands의 동일한 색인을 참조하는 경우 output의 해당 값은 비결정적입니다.
update_computation에 전달되는 첫 번째 매개변수는 항상 output 배열의 현재 값이고 두 번째 매개변수는 항상 updates 배열의 값입니다. 이는 update_computation가 교환 가능하지 않은 경우에 특히 중요합니다.
indices_are_sorted이 true로 설정되면 XLA는 사용자가 scatter_indices을 정렬 (scatter_dims_to_operand_dims에 따라 값을 분산한 후에 오름차순)한다고 가정할 수 있습니다. 그렇지 않으면 시맨틱스는 구현에 따라 정의됩니다.
unique_indices이 true로 설정되면 XLA는 분산된 모든 요소가 고유하다고 가정할 수 있습니다. 따라서 XLA는 비원자적 작업을 사용할 수 있습니다. unique_indices이 true로 설정되고 분산되는 색인이 고유하지 않으면 시맨틱은 구현에 따라 정의됩니다.
비공식적으로 스캐터 작업은 게더 작업의 역으로 볼 수 있습니다. 즉, 스캐터 작업은 해당 게더 작업으로 추출된 입력의 요소를 업데이트합니다.
자세한 비공식 설명과 예는 Gather의 '비공식 설명' 섹션을 참고하세요.
StableHLO 정보는 StableHLO - scatter를 참고하세요.
분산 - 예 1 - StableHLO
위 이미지에서 표의 각 행은 업데이트 색인 예시 하나를 보여줍니다. 왼쪽(색인 업데이트)에서 오른쪽(결과 색인)으로 단계별로 검토해 보겠습니다.
입력) input의 모양은 S32[2,3,4,2]입니다. scatter_indices의 모양은 S64[2,2,3,2]입니다. updates의 모양은 S32[2,2,3,1,2]입니다.
색인 업데이트) 입력의 일부로 update_window_dims:[3,4]가 제공됩니다. 이를 통해 updates의 3번째 차원과 4번째 차원이 창 크기임을 알 수 있으며, 이는 노란색으로 강조 표시됩니다. 이를 통해 update_scatter_dims = [0,1,2]임을 알 수 있습니다.
업데이트된 산점도 색인) 각 항목에 대해 추출된 updated_scatter_dims을 보여줍니다.
(열 업데이트 색인의 노란색이 아닌 부분)
시작 색인) scatter_indices 텐서 이미지를 보면 이전 단계 (분산 색인 업데이트)의 값이 시작 색인의 위치를 제공합니다. index_vector_dim에서 시작 색인을 포함하는 starting_indices의 차원도 알 수 있습니다. scatter_indices의 경우 크기가 2인 3차원입니다.
전체 시작 색인) scatter_dims_to_operand_dims = [2,1] 은 색인 벡터의 첫 번째 요소가 피연산자 차원 2로 이동함을 나타냅니다. 색인 벡터의 두 번째 요소는 피연산자 dim 1로 이동합니다. 나머지 피연산자 차원은 0으로 채워집니다.
전체 일괄 처리 색인) 보라색으로 강조 표시된 영역이 이 열(전체 일괄 처리 색인), 업데이트 분산 색인 열, 업데이트 색인 열에 표시됩니다.
전체 창 색인) update_window_dimensions [3,4]에서 계산됩니다.
결과 색인) operand 텐서에 전체 시작 색인, 전체 배치 색인, 전체 창 색인이 추가됩니다. 녹색으로 강조 표시된 영역이 operand 그림에도 해당합니다. 마지막 행은 operand 텐서 외부에 있으므로 건너뜁니다.
선택
XlaBuilder::Select도 참고하세요.
술어 배열의 값을 기반으로 두 입력 배열의 요소에서 출력 배열을 구성합니다.
Select(pred, on_true, on_false)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
pred |
XlaOp |
PRED 유형의 배열 |
on_true |
XlaOp |
T 유형의 배열 |
on_false |
XlaOp |
T 유형의 배열 |
on_true 및 on_false 배열의 모양이 동일해야 합니다. 출력 배열의 모양이기도 합니다. pred 배열은 on_true 및 on_false와 동일한 차원을 가져야 하며 PRED 요소 유형을 가져야 합니다.
pred의 각 요소 P에 대해 P 값이 true인 경우 출력 배열의 해당 요소는 on_true에서 가져오고 P 값이 false인 경우 on_false에서 가져옵니다. 브로드캐스팅의 제한된 형태인 pred는 PRED 유형의 스칼라일 수 있습니다. 이 경우 pred이 true이면 출력 배열은 on_true에서 완전히 가져오고 pred이 false이면 on_false에서 가져옵니다.
비스칼라 pred의 예:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
스칼라 pred의 예:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
튜플 간 선택이 지원됩니다. 튜플은 이 용도로 스칼라 유형으로 간주됩니다. on_true와 on_false가 튜플 (모양이 동일해야 함)인 경우 pred는 PRED 유형의 스칼라여야 합니다.
StableHLO 정보는 StableHLO - select를 참고하세요.
SelectAndScatter
XlaBuilder::SelectAndScatter도 참고하세요.
이 작업은 먼저 operand 배열에서 ReduceWindow를 계산하여 각 윈도우에서 요소를 선택한 다음 source 배열을 선택한 요소의 색인에 분산하여 피연산자 배열과 모양이 동일한 출력 배열을 구성하는 복합 작업으로 간주할 수 있습니다. 바이너리 select 함수는 각 윈도우에 적용하여 각 윈도우에서 요소를 선택하는 데 사용되며, 첫 번째 매개변수의 색인 벡터가 두 번째 매개변수의 색인 벡터보다 사전순으로 작다는 속성으로 호출됩니다. select 함수는 첫 번째 매개변수가 선택되면 true을 반환하고 두 번째 매개변수가 선택되면 false을 반환하며, 선택된 요소가 지정된 창에서 순회된 요소의 순서에 종속되지 않도록 함수는 전이성을 유지해야 합니다 (즉, select(a, b) 및 select(b, c)이 true이면 select(a, c)도 true임).
scatter 함수는 출력 배열의 각 선택된 색인에 적용됩니다. 두 스칼라 매개변수를 사용합니다.
- 출력 배열에서 선택한 색인의 현재 값
- 선택한 색인에 적용되는
source의 분산 값
두 매개변수를 결합하고 출력 배열에서 선택한 색인의 값을 업데이트하는 데 사용되는 스칼라 값을 반환합니다. 처음에는 출력 배열의 모든 색인이 init_value으로 설정됩니다.
출력 배열은 operand 배열과 모양이 동일해야 하며 source 배열은 operand 배열에 ReduceWindow 연산을 적용한 결과와 모양이 동일해야 합니다. SelectAndScatter는 신경망의 풀링 레이어에 대한 그라데이션 값을 역전파하는 데 사용할 수 있습니다.
SelectAndScatter(operand, select, window_dimensions, window_strides, padding,
source, init_value, scatter)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand
|
XlaOp
|
창이 슬라이드되는 T 유형의 배열 |
select
|
XlaComputation
|
T, T
-> PRED 유형의 이진 계산으로, 각 창의 모든 요소에 적용됩니다. 첫 번째 매개변수가 선택되면 true를 반환하고 두 번째 매개변수가 선택되면 false를 반환합니다. |
window_dimensions
|
ArraySlice<int64>
|
창 측정기준 값의 정수 배열 |
window_strides
|
ArraySlice<int64>
|
윈도우 스트라이드 값의 정수 배열 |
padding
|
Padding
|
창의 패딩 유형(Padding::kSame 또는 Padding::kValid) |
source
|
XlaOp
|
분산할 값이 있는 T 유형의 배열 |
init_value
|
XlaOp
|
출력 배열의 초기 값에 대한 T 유형의 스칼라 값 |
scatter
|
XlaComputation
|
T, T
-> T 유형의 이진 계산을 사용하여 각 분산 소스 요소를 대상 요소에 적용합니다. |
아래 그림은 SelectAndScatter 사용의 예를 보여줍니다. select 함수는 매개변수 중 최대값을 계산합니다. 아래 그림 (2)와 같이 창이 겹치면 operand 배열의 색인이 서로 다른 창에서 여러 번 선택될 수 있습니다. 그림에서 값 9의 요소는 상단 창 (파란색 및 빨간색) 모두에 의해 선택되고 이진 덧셈 scatter 함수는 값 8 (2 + 6)의 출력 요소를 생성합니다.
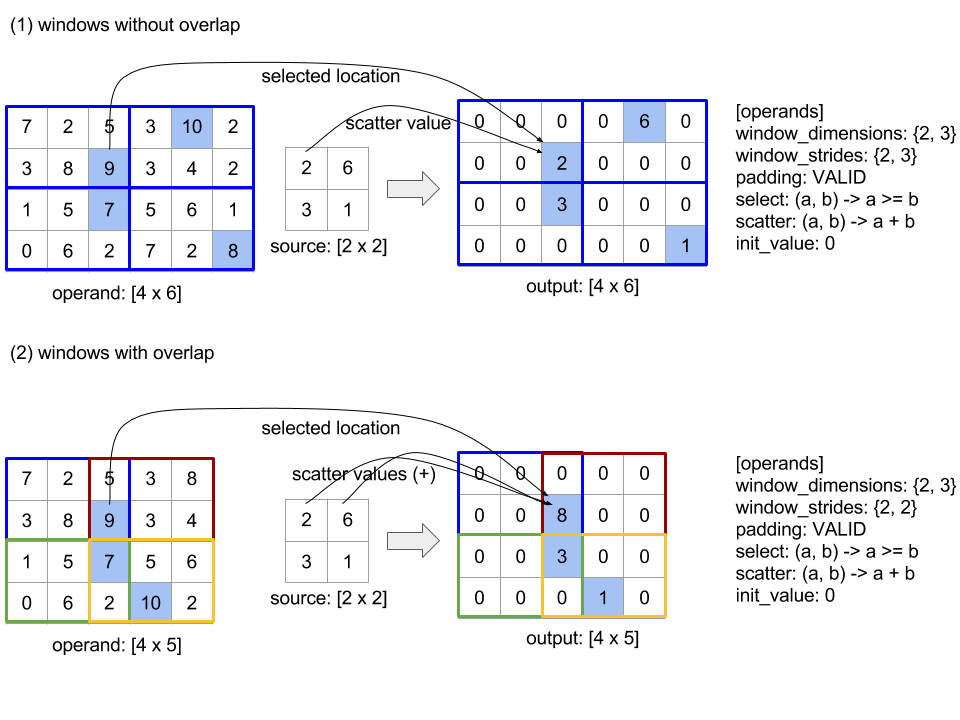
scatter 함수의 평가 순서는 임의적이며 확정되지 않을 수 있습니다. 따라서 scatter 함수는 재연결에 지나치게 민감해서는 안 됩니다. Reduce 컨텍스트의 결합성에 관한 토론을 참고하세요.
StableHLO 정보는 StableHLO - select_and_scatter를 참고하세요.
보내기
XlaBuilder::Send도 참고하세요.
Send, SendWithTokens, SendToHost는 HLO에서 통신 프리미티브 역할을 하는 작업입니다. 이러한 작업은 일반적으로 HLO 덤프에 하위 수준 입력/출력 또는 교차 기기 전송의 일부로 표시되지만 최종 사용자가 수동으로 구성하도록 설계되지 않았습니다.
Send(operand, handle)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
전송할 데이터 (T 유형의 배열) |
handle |
ChannelHandle |
각 송수신 쌍의 고유 식별자 |
동일한 채널 핸들을 공유하는 다른 계산의 Recv 명령어에 지정된 피연산자 데이터를 전송합니다. 데이터를 반환하지 않습니다.
Recv 작업과 마찬가지로 Send 작업의 클라이언트 API는 동기 통신을 나타내며 비동기 데이터 전송을 지원하기 위해 내부적으로 2개의 HLO 명령어 (Send 및 SendDone)로 분해됩니다. HloInstruction::CreateSend 및 HloInstruction::CreateSendDone도 참고하세요.
Send(HloInstruction operand, int64 channel_id)
동일한 채널 ID를 사용하여 Recv 명령어로 할당된 리소스로 피연산자의 비동기 전송을 시작합니다. 후속 SendDone 명령어가 데이터 전송이 완료될 때까지 기다리는 데 사용하는 컨텍스트를 반환합니다. 컨텍스트는 {피연산자 (모양), 요청 식별자(U32)} 튜플이며 SendDone 명령어에서만 사용할 수 있습니다.
StableHLO 정보는 StableHLO - send를 참고하세요.
SendDone
HloInstruction::CreateSendDone도 참고하세요.
SendDone(HloInstruction context)
Send 명령어로 생성된 컨텍스트가 주어지면 데이터 전송이 완료될 때까지 기다립니다. 명령어는 데이터를 반환하지 않습니다.
채널 안내 예약
각 채널 (Recv, RecvDone, Send, SendDone)의 4가지 명령어 실행 순서는 아래와 같습니다.
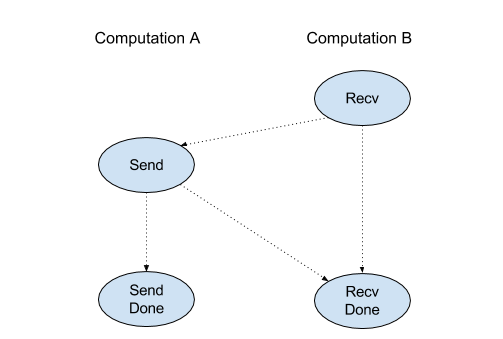
Recv이(가)Send보다 먼저 발생합니다.Send이(가)RecvDone보다 먼저 발생합니다.Recv이(가)RecvDone보다 먼저 발생합니다.Send이(가)SendDone보다 먼저 발생합니다.
백엔드 컴파일러가 채널 명령어를 통해 통신하는 각 계산에 대해 선형 일정을 생성할 때 계산 간에 사이클이 없어야 합니다. 예를 들어 아래 일정은 교착 상태를 유발합니다.
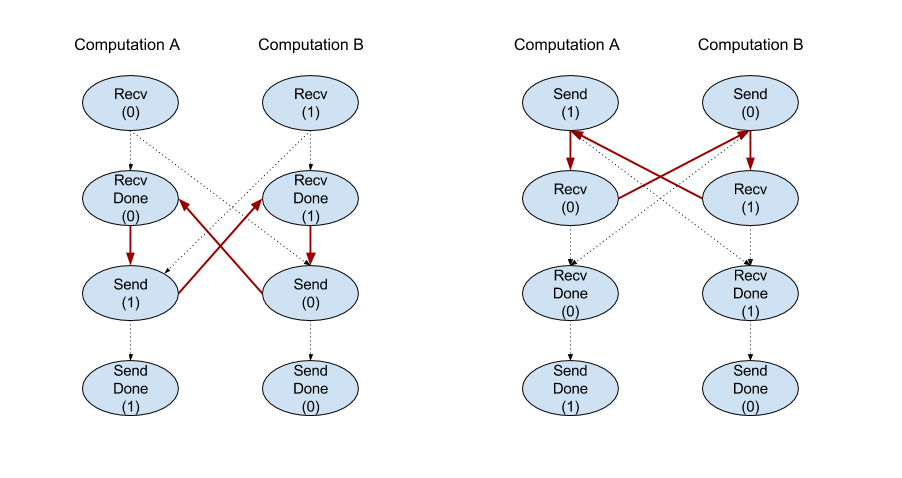
SetDimensionSize
XlaBuilder::SetDimensionSize도 참고하세요.
XlaOp의 지정된 차원의 동적 크기를 설정합니다. 피연산자는 배열 모양이어야 합니다.
SetDimensionSize(operand, val, dimension)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
n차원 입력 배열입니다. |
val |
XlaOp |
런타임 동적 크기를 나타내는 int32입니다. |
dimension
|
int64
|
[0, n) 간격의 값으로, 차원을 지정합니다. |
컴파일러에서 추적하는 동적 차원과 함께 피연산자를 결과로 전달합니다.
패딩된 값은 다운스트림 감소 작업에서 무시됩니다.
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
ShiftLeft
XlaBuilder::ShiftLeft도 참고하세요.
lhs에 대해 rhs 비트 수만큼 요소별 왼쪽 시프트 연산을 실행합니다.
ShiftLeft(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
ShiftLeft에는 다양한 차원의 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
ShiftLeft(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - shift_left를 참고하세요.
ShiftRightArithmetic
XlaBuilder::ShiftRightArithmetic도 참고하세요.
rhs 비트 수만큼 lhs에 요소별 산술 오른쪽 시프트 연산을 실행합니다.
ShiftRightArithmetic(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
ShiftRightArithmetic의 경우 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
ShiftRightArithmetic(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - shift_right_arithmetic을 참고하세요.
ShiftRightLogical
XlaBuilder::ShiftRightLogical도 참고하세요.
lhs에 대해 rhs 비트 수만큼 요소별 논리 오른쪽 시프트 연산을 실행합니다.
ShiftRightLogical(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
ShiftRightLogical의 경우 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
ShiftRightLogical(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - shift_right_logical을 참고하세요.
서명
XlaBuilder::Sign도 참고하세요.
Sign(operand) 요소별 부호 연산 x -> sgn(x)
\[\text{sgn}(x) = \begin{cases} -1 & x < 0\\ -0 & x = -0\\ NaN & x = NaN\\ +0 & x = +0\\ 1 & x > 0 \end{cases}\]
operand의 요소 유형의 비교 연산자를 사용합니다.
Sign(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
StableHLO 정보는 StableHLO - sign을 참고하세요.
Sin
Sin(operand) 요소별 사인 x -> sin(x).
XlaBuilder::Sin도 참고하세요.
Sin(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
Sin은 선택적 result_accuracy 인수도 지원합니다.
Sin(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
StableHLO 정보는 StableHLO - sine을 참고하세요.
슬라이스
XlaBuilder::Slice도 참고하세요.
슬라이싱은 입력 배열에서 하위 배열을 추출합니다. 하위 배열의 차원 수는 입력과 동일하며, 경계 상자의 차원과 색인이 슬라이스 작업에 인수로 제공되는 입력 배열 내 경계 상자 안의 값을 포함합니다.
Slice(operand, start_indices, limit_indices, strides)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
T 유형의 N차원 배열 |
start_indices
|
ArraySlice<int64>
|
각 차원의 슬라이스 시작 색인을 포함하는 N개의 정수 목록입니다. 값은 0 이상이어야 합니다. |
limit_indices
|
ArraySlice<int64>
|
각 차원의 슬라이스의 종료 색인 (포함되지 않음)이 포함된 N개의 정수 목록입니다. 각 값은 측정기준의 해당 start_indices 값보다 크거나 같아야 하고 측정기준의 크기보다 작거나 같아야 합니다. |
strides
|
ArraySlice<int64>
|
슬라이스의 입력 스트라이드를 결정하는 N개의 정수 목록입니다. 슬라이스는 d 차원의 모든 strides[d] 요소를 선택합니다. |
1차원 예:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4})
// Result: {2.0, 3.0}
2차원 예:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3})
// Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
StableHLO 정보는 StableHLO - 슬라이스를 참고하세요.
정렬
XlaBuilder::Sort도 참고하세요.
Sort(operands, comparator, dimension, is_stable)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operands |
ArraySlice<XlaOp> |
정렬할 피연산자입니다. |
comparator |
XlaComputation |
사용할 비교기 계산입니다. |
dimension |
int64 |
정렬할 측정기준입니다. |
is_stable |
bool |
안정적인 정렬을 사용해야 하는지 여부입니다. |
피연산자가 하나만 제공된 경우:
피연산자가 1차원 텐서 (배열)인 경우 결과는 정렬된 배열입니다. 배열을 오름차순으로 정렬하려면 비교기가 less-than 비교를 실행해야 합니다. 공식적으로 배열이 정렬된 후에는
comparator(value[i], value[j]) = comparator(value[j], value[i]) = false또는comparator(value[i], value[j]) = true인i < j이 있는 모든 색인 위치i, j에 대해 유지됩니다.피연산자의 차원 수가 더 많은 경우 피연산자는 제공된 차원을 따라 정렬됩니다. 예를 들어 2차원 텐서 (행렬)의 경우 측정기준 값
0은 각 열을 독립적으로 정렬하고 측정기준 값1은 각 행을 독립적으로 정렬합니다. 측정기준 번호를 제공하지 않으면 기본적으로 마지막 측정기준이 선택됩니다. 정렬된 측정기준의 경우 1차원 사례와 동일한 정렬 순서가 적용됩니다.
n > 1 피연산자가 제공되는 경우:
모든
n피연산자는 크기가 동일한 텐서여야 합니다. 텐서의 요소 유형이 다를 수 있습니다.모든 피연산자는 개별적으로가 아닌 함께 정렬됩니다. 개념적으로 피연산자는 튜플로 처리됩니다. 인덱스 위치
i및j에 있는 각 피연산자의 요소를 바꿔야 하는지 확인할 때 비교기는2 * n스칼라 매개변수와 함께 호출됩니다. 여기서 매개변수2 * k는k-th피연산자의 위치i에 있는 값에 해당하고 매개변수2 * k + 1는k-th피연산자의 위치j에 있는 값에 해당합니다. 따라서 일반적으로 비교기는2 * k및2 * k + 1매개변수를 서로 비교하고 다른 매개변수 쌍을 동점 방지용으로 사용할 수 있습니다.결과는 정렬된 순서의 피연산자로 구성된 튜플입니다 (위와 같이 제공된 차원을 따라). 튜플의
i-th피연산자는 Sort의i-th피연산자에 해당합니다.
예를 들어 피연산자 operand0 = [3, 1], operand1 = [42, 50], operand2 = [-3.0, 1.1]가 있고 비교기가 operand0의 값을 미만으로만 비교하는 경우 정렬의 출력은 튜플 ([1, 3], [50, 42], [1.1, -3.0])입니다.
is_stable가 true로 설정되면 정렬이 안정적으로 유지됩니다. 즉, 비교기에 의해 동일한 것으로 간주되는 요소가 있는 경우 동일한 값의 상대적 순서가 유지됩니다. 두 요소 e1와 e2는 comparator(e1, e2) = comparator(e2, e1) = false인 경우에만 동일합니다. 기본적으로 is_stable는 false로 설정됩니다.
StableHLO 정보는 StableHLO - sort를 참고하세요.
Sqrt
XlaBuilder::Sqrt도 참고하세요.
요소별 제곱근 연산 x -> sqrt(x).
Sqrt(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
Sqrt는 선택적 result_accuracy 인수도 지원합니다.
Sqrt(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
StableHLO 정보는 StableHLO - sqrt를 참고하세요.
하위
XlaBuilder::Sub도 참고하세요.
lhs과 rhs의 요소별 뺄셈을 실행합니다.
Sub(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Sub의 경우 차원이 다른 브로드캐스팅을 지원하는 대체 변형이 있습니다.
Sub(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - 빼기를 참고하세요.
황갈색
XlaBuilder::Tan도 참고하세요.
요소별 탄젠트 x -> tan(x)
Tan(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
Tan은 선택적 result_accuracy 인수도 지원합니다.
Tan(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
StableHLO 정보는 StableHLO - tan을 참고하세요.
Tanh
XlaBuilder::Tanh도 참고하세요.
요소별 쌍곡선 탄젠트 x -> tanh(x)입니다.
Tanh(operand)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
tanh는 선택적 result_accuracy 인수도 지원합니다.
Tanh(operand, result_accuracy)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
함수의 피연산자 |
result_accuracy
|
선택사항 ResultAccuracy
|
사용자가 구현이 여러 개인 단항 연산에 요청할 수 있는 정확도 유형 |
result_accuracy에 대한 자세한 내용은 결과 정확도를 참고하세요.
StableHLO 정보는 StableHLO - tanh를 참고하세요.
TopK
XlaBuilder::TopK도 참고하세요.
TopK는 지정된 텐서의 마지막 차원에서 k 가장 큰 요소 또는 가장 작은 요소의 값과 색인을 찾습니다.
TopK(operand, k, largest)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand
|
XlaOp
|
상위 k 요소를 추출할 텐서입니다.
텐서의 차원 수는 1 이상이어야 합니다. 텐서의 마지막 차원의 크기는 k 이상이어야 합니다. |
k |
int64 |
추출할 요소의 수입니다. |
largest
|
bool
|
가장 큰 k 요소를 추출할지 가장 작은 요소를 추출할지 여부입니다. |
1차원 입력 텐서 (배열)의 경우 배열에서 k 가장 큰 또는 가장 작은 항목을 찾아 두 배열의 튜플 (values, indices)을 출력합니다. 따라서 values[j]는 operand에서 j번째로 큰/작은 항목이며 색인은 indices[j]입니다.
차원이 2개 이상인 입력 텐서의 경우 마지막 차원을 따라 상위 k 항목을 계산하여 출력에서 다른 모든 차원 (행)을 유지합니다.
따라서 Q >= k 출력이 다음과 같은 튜플 (values, indices)인 [A, B, ..., P, Q] 모양의 피연산자의 경우:
values.shape = indices.shape = [A, B, ..., P, k]
행 내의 두 요소가 동일한 경우 인덱스가 낮은 요소가 먼저 표시됩니다.
전치행렬
tf.reshape 작업도 참고하세요.
Transpose(operand, permutation)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
operand |
XlaOp |
전치할 피연산자입니다. |
permutation |
ArraySlice<int64> |
측정기준을 순열하는 방법입니다. |
주어진 순열로 피연산자 차원을 순열합니다. ∀ i . 0 ≤ i < number of dimensions ⇒
input_dimensions[permutation[i]] = output_dimensions[i]
이는 Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions))과 동일합니다.
StableHLO 정보는 StableHLO - transpose를 참고하세요.
TriangularSolve
XlaBuilder::TriangularSolve도 참고하세요.
전방 또는 후방 대입을 통해 하삼각 또는 상삼각 계수 행렬이 있는 연립일차방정식을 풉니다. 선행 차원을 따라 브로드캐스팅하는 이 루틴은 a 및 b가 주어지고 op(a)이 op(a) = a 또는 op(a) = Transpose(a) 또는 op(a) = Conj(Transpose(a))인 경우 변수 x에 대해 행렬 시스템 op(a) * x =
b 또는 x * op(a) = b 중 하나를 해결합니다.
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
a
|
XlaOp
|
모양이 [..., M,
M]인 복소수 또는 부동 소수점 유형의 2차원 초과 배열 |
b
|
XlaOp
|
left_side이 true인 경우 [..., M, K] 모양을 갖는 동일한 유형의 2차원 이상의 배열, 그렇지 않은 경우 [..., K, M] |
left_side
|
bool
|
op(a) * x = b (true) 또는 x *
op(a) = b (false) 형식의 시스템을 풀지 여부를 나타냅니다. |
lower
|
bool
|
a의 위쪽 또는 아래쪽 삼각형을 사용할지 여부입니다. |
unit_diagonal
|
bool
|
true인 경우 a의 대각선 요소는 1로 간주되며 액세스되지 않습니다. |
transpose_a
|
Transpose
|
a를 그대로 사용할지, 전치할지, 공액 전치할지 여부입니다. |
입력 데이터는 lower 값에 따라 a의 하단/상단 삼각형에서만 읽습니다. 다른 삼각형의 값은 무시됩니다. 출력 데이터는 동일한 삼각형에 반환됩니다. 다른 삼각형의 값은 구현에 따라 정의되며 어떤 값이든 될 수 있습니다.
a 및 b의 차원 수가 2보다 크면 2개의 하위 차원을 제외한 모든 차원이 배치 차원인 행렬 배치로 처리됩니다. a와 b의 배치 차원이 동일해야 합니다.
StableHLO 정보는 StableHLO - triangular_solve를 참고하세요.
튜플
XlaBuilder::Tuple도 참고하세요.
각각 자체 모양이 있는 가변 데이터 핸들이 포함된 튜플입니다.
Tuple(elements)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
elements |
XlaOp 벡터 |
T 유형의 N 배열 |
이는 C++의 std::tuple와 유사합니다. 개념적으로는 다음과 같습니다.
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
튜플은 GetTupleElement 작업을 통해 구조를 해체 (액세스)할 수 있습니다.
StableHLO 정보는 StableHLO - 튜플을 참고하세요.
다음과 같은 경우
XlaBuilder::While도 참고하세요.
While(condition, body, init)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
condition
|
XlaComputation
|
루프의 종료 조건을 정의하는 T -> PRED 유형의 XlaComputation입니다. |
body
|
XlaComputation
|
루프 본문을 정의하는 T -> T 유형의 XlaComputation입니다. |
init
|
T
|
condition 및 body 매개변수의 초기 값입니다. |
condition이 실패할 때까지 body를 순차적으로 실행합니다. 이는 아래에 나열된 차이점과 제한사항을 제외하면 다른 많은 언어의 일반적인 while 루프와 유사합니다.
While노드는body의 마지막 실행 결과인T유형의 값을 반환합니다.T유형의 모양은 정적으로 결정되며 모든 반복에서 동일해야 합니다.
계산의 T 매개변수는 첫 번째 반복에서 init 값으로 초기화되며 각 후속 반복에서 body의 새 결과로 자동 업데이트됩니다.
While 노드의 한 가지 주요 사용 사례는 신경망에서 학습의 반복 실행을 구현하는 것입니다. 계산을 나타내는 그래프와 함께 단순화된 의사 코드가 아래에 표시되어 있습니다. 코드는 while_test.cc에서 확인할 수 있습니다.
이 예의 T 유형은 반복 횟수의 int32와 누적기의 vector[10]로 구성된 Tuple입니다. 1, 000회 반복의 경우 루프는 누적기에 상수 벡터를 계속 추가합니다.
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}
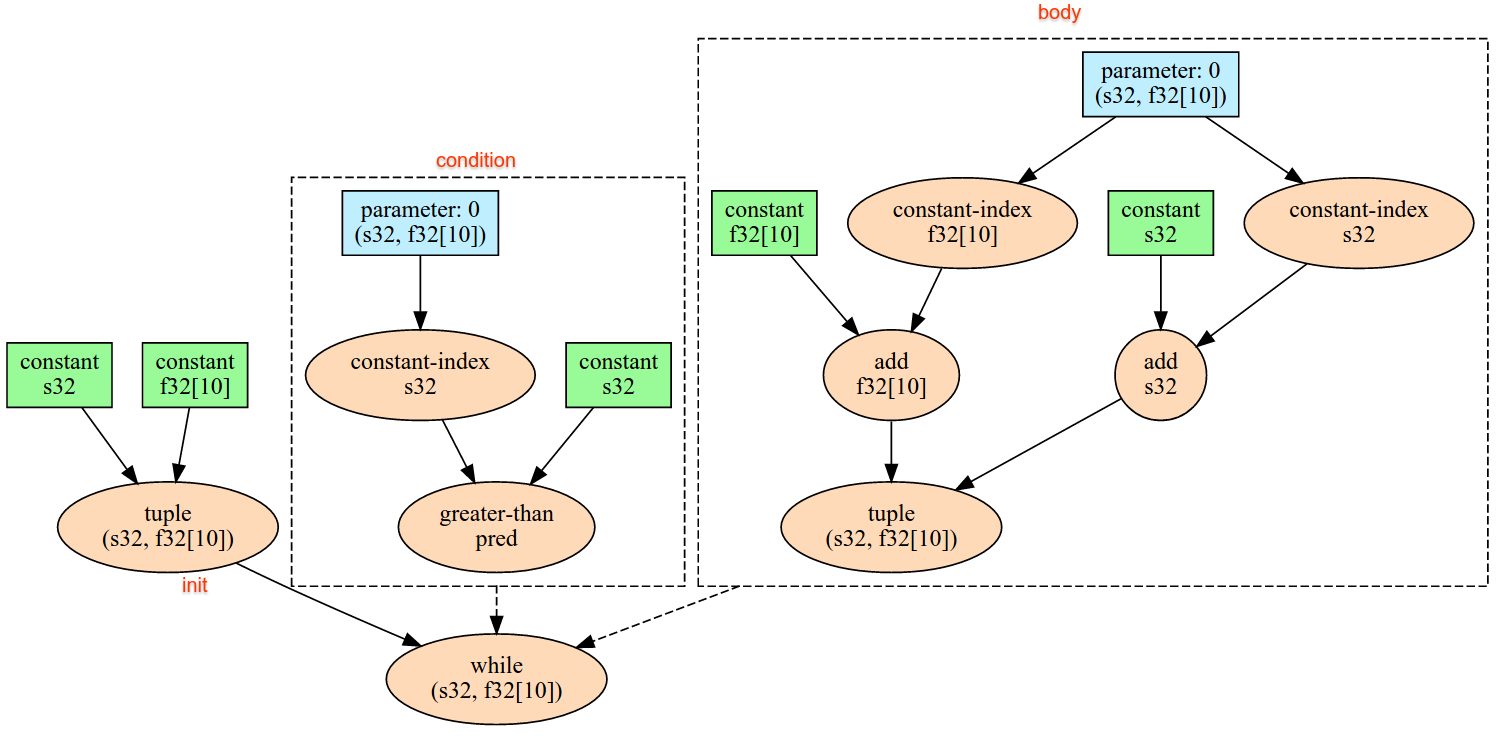
StableHLO 정보는 StableHLO - while을 참고하세요.
Xor
XlaBuilder::Xor도 참고하세요.
lhs 및 rhs의 요소별 XOR을 실행합니다.
Xor(lhs, rhs)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
인수의 모양은 유사하거나 호환되어야 합니다. 모양이 호환된다는 의미에 관한 내용은 브로드캐스팅 문서를 참고하세요. 작업의 결과는 두 입력 배열을 브로드캐스팅한 결과인 형태를 갖습니다. 이 변형에서는 피연산자 중 하나가 스칼라가 아닌 한 순위가 다른 배열 간 작업이 지원되지 않습니다.
Xor의 경우 차원이 다른 브로드캐스팅 지원이 있는 대체 변형이 있습니다.
Xor(lhs,rhs, broadcast_dimensions)
| 인수 | 유형 | 시맨틱스 |
|---|---|---|
| lhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| rhs | XlaOp | 왼쪽 피연산자: T 유형의 배열 |
| broadcast_dimension | ArraySlice |
타겟 모양의 어떤 차원이 피연산자 모양의 각 차원에 해당하는지 |
이 변형은 랭크가 다른 배열 간의 산술 연산 (예: 벡터에 행렬 추가)에 사용해야 합니다.
추가 broadcast_dimensions 피연산자는 피연산자를 브로드캐스팅하는 데 사용할 차원을 지정하는 정수 슬라이스입니다. 시맨틱스는 브로드캐스팅 페이지에 자세히 설명되어 있습니다.
StableHLO 정보는 StableHLO - xor을 참고하세요.








