A seguir, descrevemos a semântica das operações definidas na interface
XlaBuilder. Normalmente, essas operações são mapeadas de um para um para as operações definidas na interface RPC em xla_data.proto.
Uma observação sobre a nomenclatura: o tipo de dados generalizado com que a XLA trabalha é uma matriz N-dimensional que contém elementos de algum tipo uniforme (como ponto flutuante de 32 bits). Em toda a documentação, array é usado para denotar uma matriz de dimensão arbitrária. Para facilitar, os casos especiais têm nomes mais específicos e conhecidos. Por exemplo, um vetor é uma matriz unidimensional, e uma matriz é uma matriz bidimensional.
Saiba mais sobre a estrutura de uma operação em Formas e layout e Layout em blocos.
Abdômen
Consulte também
XlaBuilder::Abs.
Valor absoluto de elemento x -> |x|.
Abs(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Para informações sobre o StableHLO, consulte StableHLO: abs.
Adicionar
Consulte também
XlaBuilder::Add.
Executa a adição de elementos de lhs e rhs.
Add(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de diferentes dimensões para "Add":
Add(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO: adicionar.
AddDependency
Consulte também
HloInstruction::AddDependency.
AddDependency pode aparecer em despejos de HLO, mas não foi criado para ser construído manualmente por usuários finais.
AfterAll
Consulte também
XlaBuilder::AfterAll.
"AfterAll" usa um número variádico de tokens e produz um único token. Os tokens
são tipos primitivos que podem ser encadeados entre operações com efeitos colaterais para
impor a ordenação. AfterAll pode ser usado como uma junção de tokens para ordenar uma
operação após um conjunto de operações.
AfterAll(tokens)
| Argumentos | Tipo | Semântica |
|---|---|---|
tokens |
vetor de XlaOp |
número variádico de tokens |
Para informações sobre o StableHLO, consulte StableHLO - after_all.
AllGather
Consulte também
XlaBuilder::AllGather.
Realiza a concatenação entre réplicas.
AllGather(operand, all_gather_dimension, shard_count, replica_groups,
channel_id, layout, use_global_device_ids)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand
|
XlaOp
|
Matriz para concatenar em todas as réplicas |
all_gather_dimension |
int64 |
Dimensão de concatenação |
shard_count
|
int64
|
O tamanho de cada grupo de réplicas |
replica_groups
|
vetor de vetores de
int64 |
Grupos entre os quais a concatenação é realizada |
channel_id
|
opcional
ChannelHandle |
ID do canal opcional para comunicação entre módulos |
layout
|
opcional Layout
|
Cria um padrão de layout que captura o layout correspondente no argumento. |
use_global_device_ids
|
opcional bool
|
Retorna verdadeiro se os IDs na configuração ReplicaGroup representarem um ID global. |
replica_groupsé uma lista de grupos de réplicas entre os quais a concatenação é realizada. O ID da réplica atual pode ser recuperado usandoReplicaId. A ordem das réplicas em cada grupo determina a ordem em que as entradas são localizadas no resultado.replica_groupsprecisa estar vazio (nesse caso, todas as réplicas pertencem a um único grupo, ordenado de0aN - 1) ou conter o mesmo número de elementos que o número de réplicas. Por exemplo,replica_groups = {0, 2}, {1, 3}realiza a concatenação entre as réplicas0e2, e1e3.shard_counté o tamanho de cada grupo de réplicas. Precisamos disso nos casos em quereplica_groupsestão vazios.channel_idé usado para comunicação entre módulos: apenas operaçõesall-gathercom o mesmochannel_idpodem se comunicar entre si.use_global_device_idsRetorna "true" se os IDs na configuração do ReplicaGroup representarem um ID global de (replica_id * partition_count + partition_id) em vez de um ID de réplica. Isso permite um agrupamento mais flexível de dispositivos se essa redução total for entre partições e entre réplicas.
O formato de saída é o formato de entrada com o all_gather_dimension shard_count vezes maior. Por exemplo, se houver duas réplicas e o operando tiver o valor [1.0, 2.5] e [3.0, 5.25], respectivamente, nas duas réplicas, o valor de saída dessa operação em que all_gather_dim é 0 será [1.0, 2.5, 3.0,5.25] nas duas réplicas.
A API de AllGather é decomposta internamente em duas instruções HLO (AllGatherStart e AllGatherDone).
Consulte também
HloInstruction::CreateAllGatherStart.
AllGatherStart e AllGatherDone servem como primitivos em HLO. Essas operações podem aparecer em despejos de HLO, mas não devem ser criadas manualmente por usuários finais.
Para informações sobre o StableHLO, consulte StableHLO: all_gather.
AllReduce
Consulte também
XlaBuilder::AllReduce.
Realiza uma computação personalizada em várias réplicas.
AllReduce(operand, computation, replica_groups, channel_id,
shape_with_layout, use_global_device_ids)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand
|
XlaOp
|
Matriz ou tupla não vazia de matrizes para reduzir em réplicas. |
computation |
XlaComputation |
Cálculo de redução |
replica_groups
|
ReplicaGroup vetor
|
Grupos entre os quais as reduções são realizadas |
channel_id
|
opcional
ChannelHandle |
ID do canal opcional para comunicação entre módulos |
shape_with_layout
|
opcional Shape
|
Define o layout dos dados transferidos. |
use_global_device_ids
|
opcional bool
|
Retorna verdadeiro se os IDs na configuração ReplicaGroup representarem um ID global. |
- Quando
operandé uma tupla de matrizes, a redução completa é realizada em cada elemento da tupla. replica_groupsé uma lista de grupos de réplicas entre os quais a redução é realizada. O ID da réplica atual pode ser recuperado usandoReplicaId.replica_groupsprecisa estar vazio (nesse caso, todas as réplicas pertencem a um único grupo) ou conter o mesmo número de elementos que o número de réplicas. Por exemplo,replica_groups = {0, 2}, {1, 3}realiza a redução entre as réplicas0e2, e1e3.channel_idé usado para comunicação entre módulos: apenas operaçõesall-reducecom o mesmochannel_idpodem se comunicar entre si.shape_with_layout: força o layout do AllReduce para o layout especificado. Isso é usado para garantir o mesmo layout para um grupo de operações AllReduce compiladas separadamente.use_global_device_idsRetorna "true" se os IDs na configuração do ReplicaGroup representarem um ID global de (replica_id * partition_count + partition_id) em vez de um ID de réplica. Isso permite um agrupamento mais flexível de dispositivos se essa redução total for entre partições e entre réplicas.
O formato da saída é igual ao da entrada. Por exemplo, se houver duas réplicas e o operando tiver o valor [1.0, 2.5] e [3.0, 5.25], respectivamente, nas duas réplicas, o valor de saída dessa operação e o cálculo de soma serão [4.0, 7.75] nas duas réplicas. Se a entrada for uma tupla, a saída também será uma tupla.
Para calcular o resultado de AllReduce, é necessário ter uma entrada de cada réplica. Portanto, se uma réplica executar um nó AllReduce mais vezes do que outra, a primeira vai esperar para sempre. Como todas as réplicas executam o mesmo programa, não há muitas maneiras de isso acontecer. No entanto, é possível quando a condição de um loop "while" depende de dados de infeed e os dados que são infeed fazem com que o loop "while" itere mais vezes em uma réplica do que em outra.
A API de AllReduce é decomposta internamente em duas instruções HLO (AllReduceStart e AllReduceDone).
Consulte também
HloInstruction::CreateAllReduceStart.
AllReduceStart e AllReduceDone servem como primitivos em HLO. Essas operações podem aparecer em despejos de HLO, mas não devem ser criadas manualmente por usuários finais.
CrossReplicaSum
Consulte também
XlaBuilder::CrossReplicaSum.
Realiza AllReduce com um cálculo de soma.
CrossReplicaSum(operand, replica_groups)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand
|
XlaOp | Matriz ou tupla não vazia de matrizes para reduzir em todas as réplicas. |
replica_groups
|
vetor de vetores de
int64 |
Grupos entre os quais as reduções são realizadas |
Retorna a soma do valor do operando em cada subgrupo de réplicas. Todas as réplicas fornecem uma entrada para a soma e recebem o resultado para cada subgrupo.
AllToAll
Consulte também
XlaBuilder::AllToAll.
AllToAll é uma operação coletiva que envia dados de todos os núcleos para todos os núcleos. Ele tem duas fases:
- A fase de dispersão. Em cada núcleo, o operando é dividido em
split_countblocos ao longo dasplit_dimensions, e os blocos são distribuídos para todos os núcleos. Por exemplo, o iésimo bloco é enviado para o iésimo núcleo. - A fase de coleta. Cada núcleo concatena os blocos recebidos ao longo da
concat_dimension.
Os núcleos participantes podem ser configurados por:
replica_groups: cada ReplicaGroup contém uma lista de IDs de réplicas que participam da computação. O ID da réplica atual pode ser recuperado usandoReplicaId. O AllToAll será aplicado em subgrupos na ordem especificada. Por exemplo,replica_groups = { {1,2,3}, {4,5,0} }significa que um AllToAll será aplicado em réplicas{1, 2, 3}, na fase de coleta, e os blocos recebidos serão concatenados na mesma ordem de 1, 2, 3. Em seguida, outro AllToAll será aplicado nas réplicas 4, 5 e 0, e a ordem de concatenação também será 4, 5 e 0. Sereplica_groupsestiver vazio, todas as réplicas vão pertencer a um grupo, na ordem de concatenação da aparência delas.
Pré-requisitos:
- O tamanho da dimensão do operando em
split_dimensioné divisível porsplit_count. - O formato do operando não é uma tupla.
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups, layout, channel_id)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
matriz de entrada n-dimensional |
split_dimension
|
int64
|
Um valor no intervalo [0,n) que nomeia a dimensão ao longo da qual o operando é dividido. |
concat_dimension
|
int64
|
Um valor no intervalo [0,n) que nomeia a dimensão ao longo da qual os blocos de divisão são concatenados. |
split_count
|
int64
|
O número de núcleos que participam desta operação. Se replica_groups estiver vazio, esse valor será o número de réplicas. Caso contrário, ele será igual ao número de réplicas em cada grupo. |
replica_groups
|
ReplicaGroupvetor
|
Cada grupo contém uma lista de IDs de réplica. |
layout |
opcional Layout |
layout de memória especificado pelo usuário |
channel_id
|
opcional ChannelHandle
|
identificador exclusivo para cada par send/recv |
Consulte xla::shapes para mais informações sobre formas e layouts.
Para informações sobre o StableHLO, consulte StableHLO: all_to_all.
AllToAll: exemplo 1.
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(
x,
/*split_dimension=*/ 1,
/*concat_dimension=*/ 0,
/*split_count=*/ 4);
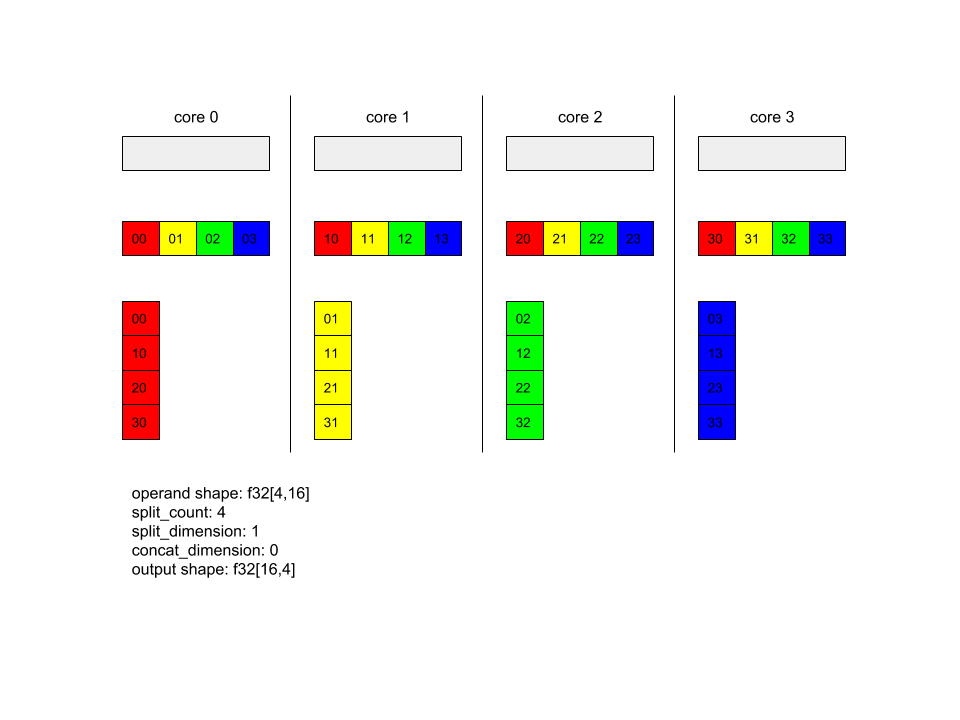
No exemplo acima, há quatro núcleos participando do Alltoall. Em cada núcleo, o operando é dividido em quatro partes ao longo da dimensão 1, de modo que cada parte tem formato f32[4,4]. As quatro partes são distribuídas para todos os núcleos. Em seguida, cada núcleo concatena as partes recebidas ao longo da dimensão 0, na ordem dos núcleos 0 a 4. Portanto, a saída em cada núcleo tem o formato f32[16,4].
AllToAll - Exemplo 2 - StableHLO
No exemplo acima, há duas réplicas participando do AllToAll. Em cada réplica, o operando tem a forma f32[2,4]. O operando é dividido em duas partes ao longo da dimensão 1, então cada parte tem a forma f32[2,2]. As duas partes são trocadas entre as réplicas de acordo com a posição delas no grupo. Cada réplica coleta a parte correspondente dos dois operandos e os concatena ao longo da dimensão 0. Como resultado, a saída em cada réplica tem o formato f32[4,2].
RaggedAllToAll
Consulte também
XlaBuilder::RaggedAllToAll.
O RaggedAllToAll realiza uma operação coletiva de todos para todos, em que a entrada e a saída são tensores irregulares.
RaggedAllToAll(input, input_offsets, send_sizes, output, output_offsets,
recv_sizes, replica_groups, channel_id)
| Argumentos | Tipo | Semântica |
|---|---|---|
input |
XlaOp |
Matriz N do tipo T |
input_offsets |
XlaOp |
Matriz N do tipo T |
send_sizes |
XlaOp |
Matriz N do tipo T |
output |
XlaOp |
Matriz N do tipo T |
output_offsets |
XlaOp |
Matriz N do tipo T |
recv_sizes |
XlaOp |
Matriz N do tipo T |
replica_groups
|
ReplicaGroup vetor
|
Cada grupo contém uma lista de IDs de réplica. |
channel_id
|
opcional ChannelHandle
|
identificador exclusivo para cada par send/recv |
Tensores irregulares são definidos por um conjunto de três tensores:
data: o tensordataé irregular ao longo da dimensão mais externa, em que cada elemento indexado tem tamanho variável.offsets: o tensoroffsetsindexa a dimensão mais externa do tensordatae representa o deslocamento inicial de cada elemento irregular do tensordata.sizes: o tensorsizesrepresenta o tamanho de cada elemento irregular do tensordata, em que o tamanho é especificado em unidades de subelementos. Um subelemento é definido como o sufixo da forma do tensor "data" obtido removendo a dimensão mais externa.- Os tensores
offsetsesizesprecisam ter o mesmo tamanho.
Exemplo de um tensor irregular:
data: [8,3] =
{ {a,b,c},{d,e,f},{g,h,i},{j,k,l},{m,n,o},{p,q,r},{s,t,u},{v,w,x} }
offsets: [3] = {0, 1, 4}
sizes: [3] = {1, 3, 4}
// Index 'data' at 'offsets'[0], 'sizes'[0]' // {a,b,c}
// Index 'data' at 'offsets'[1], 'sizes'[1]' // {d,e,f},{g,h,i},{j,k,l}
// Index 'data' at 'offsets'[2], 'sizes'[2]' // {m,n,o},{p,q,r},{s,t,u},{v,w,x}
output_offsets precisa ser fragmentado de forma que cada réplica tenha offsets na perspectiva de saída da réplica de destino.
Para o i-ésimo deslocamento de saída, a réplica atual vai enviar
a atualização input[input_offsets[i]:input_offsets[i]+input_sizes[i]] para a i-ésima
réplica, que será gravada em
output_i[output_offsets[i]:output_offsets[i]+send_sizes[i]] na i-ésima réplica
output.
Por exemplo, se tivermos duas réplicas:
replica 0:
input: [1, 2, 2]
output:[0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 2]
output_offsets: [0, 0]
recv_sizes: [1, 1]
replica 1:
input: [3, 4, 0]
output: [0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 1]
output_offsets: [1, 2]
recv_sizes: [2, 1]
// replica 0's result will be: [1, 3, 0, 0]
// replica 1's result will be: [2, 2, 4, 0]
O HLO irregular de todos para todos tem os seguintes argumentos:
input: tensor de dados de entrada irregulares.output: tensor de dados de saída irregulares.input_offsets: tensor de deslocamentos de entrada irregulares.send_sizes: tensor irregular de tamanhos de envio.output_offsets: matriz de intervalos irregulares na saída da réplica de destino.recv_sizes: tensor de tamanhos de recebimento irregulares.
Os tensores *_offsets e *_sizes precisam ter o mesmo formato.
Há duas formas compatíveis para os tensores *_offsets e *_sizes:
[num_devices]em que ragged-all-to-all pode enviar no máximo uma atualização para cada dispositivo remoto no grupo de réplicas. Exemplo:
for (remote_device_id : replica_group) {
SEND input[input_offsets[remote_device_id]],
output[output_offsets[remote_device_id]],
send_sizes[remote_device_id] }
[num_devices, num_updates]em que ragged-all-to-all pode enviar aténum_updatesatualizações para o mesmo dispositivo remoto (cada uma em diferentes offsets), para cada dispositivo remoto no grupo de réplicas.
Exemplo:
for (remote_device_id : replica_group) {
for (update_idx : num_updates) {
SEND input[input_offsets[remote_device_id][update_idx]],
output[output_offsets[remote_device_id][update_idx]]],
send_sizes[remote_device_id][update_idx] } }
E
Consulte também
XlaBuilder::And.
Executa um AND bit a bit de dois tensores lhs e rhs.
And(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para "And":
And(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO - and.
Assíncrona
Consulte também HloInstruction::CreateAsyncStart,
HloInstruction::CreateAsyncUpdate,
HloInstruction::CreateAsyncDone.
AsyncDone, AsyncStart e AsyncUpdate são instruções HLO internas usadas para operações assíncronas e servem como primitivos em HLO. Essas operações podem aparecer
em despejos de HLO, mas não devem ser construídas manualmente por usuários finais.
Atan2
Consulte também
XlaBuilder::Atan2.
Executa a operação atan2 elemento a elemento em lhs e rhs.
Atan2(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para Atan2:
Atan2(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO: atan2.
BatchNormGrad
Consulte também
XlaBuilder::BatchNormGrad
e o artigo original sobre normalização em lote
para uma descrição detalhada do algoritmo.
Calcula gradientes de normalização em lote.
BatchNormGrad(operand, scale, batch_mean, batch_var, grad_output, epsilon,
feature_index)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp | Matriz n-dimensional a ser normalizada (x) |
scale |
XlaOp | Matriz unidimensional (\(\gamma\)) |
batch_mean |
XlaOp | Matriz unidimensional (\(\mu\)) |
batch_var |
XlaOp | Matriz unidimensional (\(\sigma^2\)) |
grad_output |
XlaOp | Gradientes transmitidos para BatchNormTraining (\(\nabla y\)) |
epsilon |
float |
Valor de épsilon (\(\epsilon\)) |
feature_index |
int64 |
Indexação para dimensionar o recurso em operand |
Para cada recurso na dimensão de recurso (feature_index é o índice da dimensão de recurso em operand), a operação calcula os gradientes em relação a operand, offset e scale em todas as outras dimensões. O feature_index precisa ser um índice válido para a dimensão de recurso em operand.
Os três gradientes são definidos pelas seguintes fórmulas (supondo uma matriz de quatro dimensões como operand e com índice de dimensão de recurso l, tamanho do lote m e tamanhos espaciais w e h):
\[ \begin{split} c_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sigma^2_l+\epsilon} \right) \\\\ d_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \\\\ \nabla x_{ijkl} &= \frac{\gamma_{l} }{\sqrt{\sigma^2_{l}+\epsilon} } \left( \nabla y_{ijkl} - d_l - c_l (x_{ijkl} - \mu_{l}) \right) \\\\ \nabla \gamma_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sqrt{\sigma^2_{l}+\epsilon} } \right) \\\\\ \nabla \beta_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \end{split} \]
As entradas batch_mean e batch_var representam valores de momentos em dimensões espaciais e de lote.
O tipo de saída é uma tupla de três identificadores:
| Saídas | Tipo | Semântica |
|---|---|---|
grad_operand
|
XlaOp | gradiente em relação à entrada operand (\(\nabla x\)) |
grad_scale
|
XlaOp | gradiente em relação à entrada **scale ** (\(\nabla\gamma\)) |
grad_offset
|
XlaOp | gradiente em relação à entrada offset(\(\nabla\beta\)) |
Para informações sobre o StableHLO, consulte StableHLO - batch_norm_grad.
BatchNormInference
Consulte também
XlaBuilder::BatchNormInference
e o artigo original sobre normalização em lote
para uma descrição detalhada do algoritmo.
Normaliza uma matriz em lote e dimensões espaciais.
BatchNormInference(operand, scale, offset, mean, variance, epsilon,
feature_index)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp | Matriz n-dimensional a ser normalizada |
scale |
XlaOp | Matriz unidimensional |
offset |
XlaOp | Matriz unidimensional |
mean |
XlaOp | Matriz unidimensional |
variance |
XlaOp | Matriz unidimensional |
epsilon |
float |
Valor de épsilon |
feature_index |
int64 |
Indexação para dimensionar o recurso em operand |
Para cada recurso na dimensão de recurso (feature_index é o índice da dimensão de recurso em operand), a operação calcula a média e a variância em todas as outras dimensões e usa esses valores para normalizar cada elemento em operand. O feature_index precisa ser um índice válido para a dimensão de recurso em operand.
BatchNormInference é equivalente a chamar BatchNormTraining sem calcular mean e variance para cada lote. Em vez disso, ele usa as entradas mean e variance como valores estimados. O objetivo dessa operação é reduzir a latência na inferência, daí o nome BatchNormInference.
A saída é uma matriz normalizada n-dimensional com o mesmo formato da entrada operand.
Para informações sobre o StableHLO, consulte StableHLO - batch_norm_inference.
BatchNormTraining
Consulte também XlaBuilder::BatchNormTraining e the original batch normalization paper para uma descrição detalhada do algoritmo.
Normaliza uma matriz em lote e dimensões espaciais.
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
Matriz n-dimensional a ser normalizada (x) |
scale |
XlaOp |
Matriz unidimensional (\(\gamma\)) |
offset |
XlaOp |
Matriz unidimensional (\(\beta\)) |
epsilon |
float |
Valor de épsilon (\(\epsilon\)) |
feature_index |
int64 |
Indexação para dimensionar o recurso em operand |
Para cada recurso na dimensão de recurso (feature_index é o índice da dimensão de recurso em operand), a operação calcula a média e a variância em todas as outras dimensões e usa esses valores para normalizar cada elemento em operand. O feature_index precisa ser um índice válido para a dimensão de recurso em operand.
O algoritmo funciona da seguinte maneira para cada lote em operand \(x\) que contém melementos com w e h como o tamanho das dimensões espaciais (supondo que operandseja uma matriz de quatro dimensões):
Calcula a média do lote \(\mu_l\) para cada recurso
lna dimensão do recurso: \(\mu_l=\frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h x_{ijkl}\)Calcula a variância do lote \(\sigma^2_l\): $\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
Normaliza, dimensiona e muda: \(y_{ijkl}=\frac{\gamma_l(x_{ijkl}-\mu_l)}{\sqrt[2]{\sigma^2_l+\epsilon} }+\beta_l\)
O valor de epsilon, geralmente um número pequeno, é adicionado para evitar erros de divisão por zero.
O tipo de saída é uma tupla de três XlaOps:
| Saídas | Tipo | Semântica |
|---|---|---|
output
|
XlaOp
|
Matriz n-dimensional com a mesma forma da entrada operand (y) |
batch_mean |
XlaOp |
Matriz unidimensional (\(\mu\)) |
batch_var |
XlaOp |
Matriz unidimensional (\(\sigma^2\)) |
Os batch_mean e batch_var são momentos calculados em todas as dimensões espaciais e de lote usando as fórmulas acima.
Para informações sobre o StableHLO, consulte StableHLO - batch_norm_training.
Bitcast
Consulte também
HloInstruction::CreateBitcast.
Bitcast pode aparecer em despejos de HLO, mas não foi criado para ser construído
manualmente por usuários finais.
BitcastConvertType
Consulte também
XlaBuilder::BitcastConvertType.
Semelhante a um tf.bitcast no TensorFlow, realiza uma operação de bitcast de elemento a elemento de uma forma de dados para uma forma de destino. O tamanho da entrada e da saída precisa ser igual. Por exemplo, elementos s32 se tornam elementos f32 usando a rotina bitcast, e um elemento s32 se torna quatro elementos s8. O Bitcast é implementado como uma transmissão de baixo nível. Portanto, máquinas com representações de ponto flutuante diferentes vão gerar resultados diferentes.
BitcastConvertType(operand, new_element_type)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
matriz do tipo T com dimensões D |
new_element_type |
PrimitiveType |
tipo U |
As dimensões do operando e da forma de destino precisam corresponder, exceto a última dimensão, que vai mudar pela proporção do tamanho primitivo antes e depois da conversão.
Os tipos de elementos de origem e destino não podem ser tuplas.
Para mais informações sobre o StableHLO, consulte StableHLO - bitcast_convert.
Conversão de bitcast para tipo primitivo de largura diferente
A instrução BitcastConvert HLO é compatível com o caso em que o tamanho do tipo de elemento de saída T' não é igual ao tamanho do elemento de entrada T. Como toda a operação é conceitualmente um bitcast e não muda os bytes subjacentes, a forma do elemento de saída precisa mudar. Para B = sizeof(T), B' =
sizeof(T'), há dois casos possíveis.
Primeiro, quando B > B', o formato da saída recebe uma nova dimensão secundária de tamanho B/B'. Exemplo:
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
A regra permanece a mesma para escalares efetivos:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
Como alternativa, para B' > B, a instrução exige que a última dimensão lógica da forma de entrada seja igual a B'/B, e essa dimensão é descartada durante a conversão:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
As conversões entre diferentes larguras de bits não são feitas elemento a elemento.
Transmitir
Consulte também
XlaBuilder::Broadcast.
Adiciona dimensões a uma matriz duplicando os dados nela.
Broadcast(operand, broadcast_sizes)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
A matriz a ser duplicada. |
broadcast_sizes |
ArraySlice<int64> |
Os tamanhos das novas dimensões |
As novas dimensões são inseridas à esquerda. Por exemplo, se broadcast_sizes tiver valores {a0, ..., aN} e a forma do operando tiver dimensões {b0, ..., bM}, a forma da saída terá dimensões {a0, ..., aN, b0, ..., bM}.
O novo índice de dimensões em cópias do operando, ou seja,
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
Por exemplo, se operand for um escalar f32 com valor 2.0f, e broadcast_sizes for {2, 3}, o resultado será uma matriz com formato f32[2, 3] e todos os valores no resultado serão 2.0f.
Para informações sobre o StableHLO, consulte StableHLO: transmissão.
BroadcastInDim
Consulte também
XlaBuilder::BroadcastInDim.
Aumenta o tamanho e o número de dimensões de uma matriz duplicando os dados nela.
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
A matriz a ser duplicada. |
out_dim_size
|
ArraySlice<int64>
|
Os tamanhos das dimensões da forma de destino |
broadcast_dimensions
|
ArraySlice<int64>
|
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Semelhante à transmissão, mas permite adicionar dimensões em qualquer lugar e expandir as dimensões atuais com tamanho 1.
O operand é transmitido para a forma descrita por out_dim_size.
broadcast_dimensions mapeia as dimensões de operand para as dimensões da forma de destino. Ou seja, a i-ésima dimensão do operando é mapeada para a dimensão broadcast_dimension[i] da forma de saída. As dimensões de operand precisam ter tamanho 1 ou o mesmo tamanho da dimensão na forma de saída a que são mapeadas. As dimensões restantes são preenchidas com dimensões de tamanho 1. A transmissão de dimensões degeneradas é feita ao longo dessas dimensões para alcançar a forma de saída. A semântica é descrita em detalhes na
página de transmissão.
Ligar
Consulte também
XlaBuilder::Call.
Invoca um cálculo com os argumentos fornecidos.
Call(computation, operands...)
| Argumentos | Tipo | Semântica |
|---|---|---|
computation
|
XlaComputation
|
cálculo do tipo T_0, T_1, ...,
T_{N-1} -> S com N parâmetros de tipo arbitrário |
operands |
sequência de N XlaOps |
N argumentos de tipo arbitrário |
A aridade e os tipos de operands precisam corresponder aos parâmetros de computation. É permitido não ter operands.
CompositeCall
Consulte também
XlaBuilder::CompositeCall.
Encapsula uma operação composta por outras operações do StableHLO, recebendo entradas e composite_attributes e produzindo resultados. A semântica da operação é implementada pelo atributo de decomposição. A operação composta pode ser substituída pela decomposição sem mudar a semântica do programa. Nos casos em que a incorporação da decomposição não fornece a mesma semântica de operação, prefira usar custom_call.
O campo de versão (padrão é 0) é usado para indicar quando a semântica de um composto muda.
Essa operação é implementada como um kCall com o atributo is_composite=true. O campo
decomposition é especificado pelo atributo computation. Os atributos do front-end armazenam os atributos restantes prefixados com composite..
Exemplo de operação CompositeCall:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
CompositeCall(computation, operands..., name, attributes, version)
| Argumentos | Tipo | Semântica |
|---|---|---|
computation
|
XlaComputation
|
cálculo do tipo T_0, T_1, ...,
T_{N-1} -> S com N parâmetros de tipo arbitrário |
operands |
sequência de N XlaOps |
número variádico de valores |
name |
string |
nome do composto |
attributes
|
opcional string
|
dicionário opcional de atributos em formato de string |
version
|
opcional int64
|
número para atualizações de versão para semântica da operação composta |
O decomposition de uma operação não é um campo chamado, mas aparece como um atributo to_apply
que aponta para a função que contém a implementação
de nível inferior, ou seja, to_apply=%funcname.
Para mais informações sobre composição e decomposição, consulte a especificação do StableHLO.
Cbrt
Consulte também
XlaBuilder::Cbrt.
Operação de raiz cúbica com elementos x -> cbrt(x).
Cbrt(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
O Cbrt também é compatível com o argumento opcional result_accuracy:
Cbrt(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Para informações sobre o StableHLO, consulte StableHLO: cbrt.
Arredondar para cima
Consulte também
XlaBuilder::Ceil.
Teto de elemento a elemento x -> ⌈x⌉.
Ceil(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Para informações sobre o StableHLO, consulte StableHLO: ceil.
Cholesky
Consulte também
XlaBuilder::Cholesky.
Calcula a decomposição de Cholesky de um lote de matrizes simétricas (hermitianas) positivas definidas.
Cholesky(a, lower)
| Argumentos | Tipo | Semântica |
|---|---|---|
a
|
XlaOp
|
uma matriz de um tipo complexo ou de ponto flutuante com mais de duas dimensões. |
lower |
bool |
se o triângulo superior ou inferior de a será usado. |
Se lower for true, vai calcular matrizes triangulares inferiores l de forma que $a = l .
l^T$. Se lower for false, vai calcular matrizes triangulares superiores u de forma que\(a = u^T . u\).
Os dados de entrada são lidos apenas do triângulo inferior/superior de a, dependendo do valor de lower. Os valores do outro triângulo são ignorados. Os dados de saída são retornados no mesmo triângulo. Os valores no outro triângulo são definidos pela implementação e podem ser qualquer coisa.
Se a tiver mais de duas dimensões, ele será tratado como um lote de matrizes, em que todas, exceto as duas dimensões secundárias, são dimensões de lote.a
Se a não for simétrica (hermitiana) positiva definida, o resultado será definido pela implementação.
Para informações sobre o StableHLO, consulte StableHLO: cholesky.
Limitar
Consulte também
XlaBuilder::Clamp.
Restringe um operando ao intervalo entre um valor mínimo e máximo.
Clamp(min, operand, max)
| Argumentos | Tipo | Semântica |
|---|---|---|
min |
XlaOp |
matriz do tipo T |
operand |
XlaOp |
matriz do tipo T |
max |
XlaOp |
matriz do tipo T |
Dado um operando e valores mínimo e máximo, retorna o operando se ele estiver no intervalo entre o mínimo e o máximo. Caso contrário, retorna o valor mínimo se o operando estiver abaixo desse intervalo ou o valor máximo se o operando estiver acima desse intervalo. Ou seja, clamp(a, x, b) = min(max(a, x), b).
Todos os três precisam ter o mesmo formato. Como alternativa, como uma forma restrita de transmissão, min e/ou max podem ser um escalar do tipo T.
Exemplo com min e max escalares:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
Para informações sobre o StableHLO, consulte StableHLO: clamp.
Recolher
Consulte também
XlaBuilder::Collapse.
e a operação tf.reshape.
Reduz as dimensões de uma matriz em uma dimensão.
Collapse(operand, dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
matriz do tipo T |
dimensions |
int64 vetor |
em ordem, subconjunto consecutivo das dimensões de T. |
A redução substitui o subconjunto especificado das dimensões do operando por uma única dimensão. Os argumentos de entrada são uma matriz arbitrária do tipo T e um vetor constante de tempo de compilação de índices de dimensão. Os índices de dimensão precisam ser um subconjunto ordenado (números de dimensão de baixo para cima) e consecutivo das dimensões de T. Portanto, {0, 1, 2}, {0, 1} ou {1, 2} são conjuntos de dimensões válidos, mas {1, 0} ou {0, 2} não são. Elas são substituídas por uma única dimensão nova, na mesma posição na sequência de dimensões que as substituídas, com o tamanho da nova dimensão igual ao produto dos tamanhos das dimensões originais. O menor número de dimensão em dimensions é a dimensão de variação mais lenta (mais importante) no aninhamento de loop que recolhe essas dimensões, e o maior número de dimensão é a variação mais rápida (mais secundária). Consulte o operador tf.reshape se for necessário um ordenamento de redução mais geral.
Por exemplo, seja v uma matriz de 24 elementos:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
Clz
Consulte também
XlaBuilder::Clz.
Contagem de zeros à esquerda por elemento.
Clz(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
CollectiveBroadcast
Consulte também
XlaBuilder::CollectiveBroadcast.
Transmite dados entre réplicas. Os dados são enviados do primeiro ID de réplica em cada grupo para os outros IDs no mesmo grupo. Se um ID de réplica não estiver em nenhum grupo de réplicas, a saída nessa réplica será um tensor composto por 0s em shape.
CollectiveBroadcast(operand, replica_groups, channel_id)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
replica_groups
|
ReplicaGroupvetor
|
Cada grupo contém uma lista de IDs de réplica |
channel_id
|
opcional ChannelHandle
|
identificador exclusivo para cada par send/recv |
Para informações sobre o StableHLO, consulte StableHLO: collective_broadcast.
CollectivePermute
Consulte também
XlaBuilder::CollectivePermute.
CollectivePermute é uma operação coletiva que envia e recebe dados entre réplicas.
CollectivePermute(operand, source_target_pairs, channel_id, inplace)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
matriz de entrada n-dimensional |
source_target_pairs
|
<int64, int64> vetor
|
Uma lista de pares (source_replica_id, target_replica_id). Para cada par, o operando é enviado da réplica de origem para a réplica de destino. |
channel_id
|
opcional ChannelHandle
|
ID do canal opcional para comunicação entre módulos |
inplace
|
opcional bool
|
indica se a permutação deve ser feita no lugar |
Há as seguintes restrições no source_target_pairs:
- Dois pares não podem ter o mesmo ID de réplica de destino nem de origem.
- Se um ID de réplica não for um destino em nenhum par, a saída nessa réplica será um tensor composto de 0s com o mesmo formato da entrada.
A API da operação CollectivePermute é decomposta internamente em duas instruções HLO (CollectivePermuteStart e CollectivePermuteDone).
Consulte também
HloInstruction::CreateCollectivePermuteStart.
CollectivePermuteStart e CollectivePermuteDone servem como primitivos em HLO.
Essas operações podem aparecer em despejos de HLO, mas não devem ser construídas manualmente por usuários finais.
Para informações sobre o StableHLO, consulte StableHLO - collective_permute.
Comparar
Consulte também
XlaBuilder::Compare.
Executa uma comparação elemento a elemento de lhs e rhs do seguinte:
Eq
Consulte também
XlaBuilder::Eq.
Realiza uma comparação igual a por elemento de lhs e rhs.
\(lhs = rhs\)
Eq(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para a equação:
Eq(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Existe suporte para uma ordem total sobre os números de ponto flutuante para Eq, aplicando:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
EqTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Para informações sobre o StableHLO, consulte StableHLO: comparação.
Ne
Consulte também
XlaBuilder::Ne.
Executa uma comparação diferente de de elemento a elemento entre lhs e rhs.
\(lhs != rhs\)
Ne(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para Ne:
Ne(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Existe suporte para uma ordem total sobre os números de ponto flutuante para Ne, aplicando:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
NeTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Para informações sobre o StableHLO, consulte StableHLO: comparação.
Ge
Consulte também
XlaBuilder::Ge.
Executa uma comparação greater-or-equal-than elemento a elemento de lhs e rhs.
\(lhs >= rhs\)
Ge(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para Ge:
Ge(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Existe uma ordem total sobre os números de ponto flutuante para Gt, aplicando:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
GtTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Para informações sobre o StableHLO, consulte StableHLO: comparação.
Gt
Consulte também
XlaBuilder::Gt.
Executa uma comparação maior que de elemento a elemento de lhs e rhs.
\(lhs > rhs\)
Gt(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de diferentes dimensões para Gt:
Gt(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO: comparação.
Le
Consulte também
XlaBuilder::Le.
Executa uma comparação less-or-equal-than de elemento a elemento de lhs e rhs.
\(lhs <= rhs\)
Le(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para Le:
Le(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Existe uma ordem total sobre os números de ponto flutuante para Le, aplicando:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LeTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Para informações sobre o StableHLO, consulte StableHLO: comparação.
Lt
Consulte também
XlaBuilder::Lt.
Executa uma comparação menor que elemento a elemento de lhs e rhs.
\(lhs < rhs\)
Lt(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para Lt:
Lt(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Suporte a um pedido total sobre os números de ponto flutuante para Lt, aplicando:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LtTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Para informações sobre o StableHLO, consulte StableHLO: comparação.
Complexo
Consulte também
XlaBuilder::Complex.
Realiza a conversão de elemento por elemento para um valor complexo de um par de valores reais e imaginários, lhs e rhs.
Complex(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para números complexos:
Complex(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO: complex.
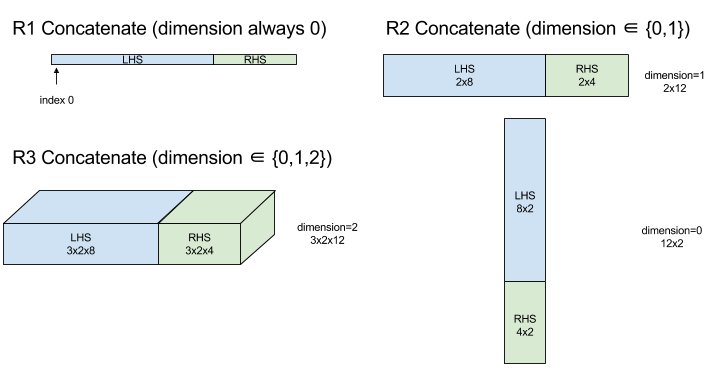
ConcatInDim (concatenação)
Consulte também
XlaBuilder::ConcatInDim.
A função CONCATENAR cria uma matriz com vários operandos de matriz. A matriz tem o mesmo número de dimensões que cada um dos operandos de matriz de entrada (que precisam ter o mesmo número de dimensões entre si) e contém os argumentos na ordem em que foram especificados.
Concatenate(operands..., dimension)
| Argumentos | Tipo | Semântica |
|---|---|---|
operands
|
sequência de N XlaOp
|
N matrizes do tipo T com dimensões [L0, L1, ...]. Exige N >= 1. |
dimension
|
int64
|
Um valor no intervalo [0, N) que nomeia a dimensão a ser concatenada entre os operands. |
Com exceção de dimension, todas as dimensões precisam ser iguais. Isso acontece porque o XLA não é compatível com matrizes irregulares. Além disso, valores de dimensão zero não podem ser concatenados, já que é impossível nomear a dimensão ao longo da qual a concatenação ocorre.
Exemplo unidimensional:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
//Output: {2, 3, 4, 5, 6, 7}
Exemplo bidimensional:
let a = { {1, 2},
{3, 4},
{5, 6} };
let b = { {7, 8} };
Concat({a, b}, 0)
//Output: { {1, 2},
// {3, 4},
// {5, 6},
// {7, 8} }
Diagrama:
Para mais informações sobre o StableHLO, consulte StableHLO: concatenar.
Condicional
Consulte também
XlaBuilder::Conditional.
Conditional(predicate, true_operand, true_computation, false_operand,
false_computation)
| Argumentos | Tipo | Semântica |
|---|---|---|
predicate |
XlaOp |
Escalar do tipo PRED |
true_operand |
XlaOp |
Argumento do tipo \(T_0\) |
true_computation |
XlaComputation |
XlaComputation do tipo \(T_0 \to S\) |
false_operand |
XlaOp |
Argumento do tipo \(T_1\) |
false_computation |
XlaComputation |
XlaComputation do tipo \(T_1 \to S\) |
Executa true_computation se predicate for true, false_computation se predicate for false e retorna o resultado.
O true_computation precisa receber um único argumento do tipo \(T_0\) e será
invocado com true_operand, que precisa ser do mesmo tipo. O
false_computation precisa usar um único argumento do tipo \(T_1\) e será
invocado com false_operand, que precisa ser do mesmo tipo. O tipo do valor retornado de true_computation e false_computation precisa ser o mesmo.
Apenas um de true_computation e false_computation será
executado, dependendo do valor de predicate.
Conditional(branch_index, branch_computations, branch_operands)
| Argumentos | Tipo | Semântica |
|---|---|---|
branch_index |
XlaOp |
Escalar do tipo S32 |
branch_computations |
sequência de N XlaComputation |
XlaComputations do tipo \(T_0 \to S , T_1 \to S , ..., T_{N-1} \to S\) |
branch_operands |
sequência de N XlaOp |
Argumentos do tipo \(T_0 , T_1 , ..., T_{N-1}\) |
Executa branch_computations[branch_index] e retorna o resultado. Se branch_index for um S32 que seja < 0 ou >= N, branch_computations[N-1] será executado como a ramificação padrão.
Cada branch_computations[b] precisa receber um único argumento do tipo \(T_b\) e será invocado com branch_operands[b], que precisa ser do mesmo tipo. O tipo do valor retornado de cada branch_computations[b] precisa ser o mesmo.
Apenas um dos branch_computations será executado, dependendo do valor de branch_index.
Para informações sobre o StableHLO, consulte StableHLO: if.
Constante
Consulte também
XlaBuilder::ConstantLiteral.
Produz um output de um literal constante.
Constant(literal)
| Argumentos | Tipo | Semântica |
|---|---|---|
literal |
LiteralSlice |
visualização constante de um Literal |
Para informações sobre o StableHLO, consulte StableHLO: constante.
ConvertElementType
Consulte também
XlaBuilder::ConvertElementType.
Semelhante a um static_cast independente em C++, o ConvertElementType realiza
uma operação de conversão independente de uma forma de dados para uma forma de destino. As dimensões precisam corresponder, e a conversão é elemento a elemento. Por exemplo, elementos s32 se tornam elementos f32 por uma rotina de conversão de s32 para f32.
ConvertElementType(operand, new_element_type)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
matriz do tipo T com dimensões D |
new_element_type |
PrimitiveType |
tipo U |
As dimensões do operando e do formato de destino precisam ser iguais. Os tipos de elementos de origem e destino não podem ser tuplas.
Uma conversão como T=s32 para U=f32 vai executar uma rotina de conversão de int para float normalizadora, como arredondamento para o número par mais próximo.
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
Para informações sobre o StableHLO, consulte StableHLO: converter.
Conv (convolução)
Consulte também
XlaBuilder::Conv.
Calcula uma convolução do tipo usado em redes neurais. Aqui, uma convolução pode ser considerada como uma janela n-dimensional que se move por uma área de base n-dimensional, e um cálculo é realizado para cada posição possível da janela.
Conv Enfileira uma instrução de convolução no cálculo, que usa os números de dimensão de convolução padrão sem dilatação.
O padding é especificado de forma abreviada como SAME ou VALID. O padding SAME preenche a entrada (lhs) com zeros para que a saída tenha o mesmo formato da entrada quando não considera o stride. O preenchimento VALID significa
que não há preenchimento.
Conv(lhs, rhs, window_strides, padding, feature_group_count,
batch_group_count, precision_config, preferred_element_type)
| Argumentos | Tipo | Semântica |
|---|---|---|
lhs
|
XlaOp
|
Matriz (n+2)-dimensional de entradas |
rhs
|
XlaOp
|
Matriz (n+2)-dimensional de pesos do kernel |
window_strides |
ArraySlice<int64> |
Matriz n-dimensional de strides do kernel |
padding |
Padding |
enum de padding |
feature_group_count
|
int64 | o número de grupos de recursos |
batch_group_count |
int64 | o número de grupos de lotes |
precision_config
|
opcional
PrecisionConfig |
enum para nível de precisão |
preferred_element_type
|
opcional
PrimitiveType |
enum do tipo de elemento escalar |
Há níveis crescentes de controles disponíveis para Conv:
Seja n o número de dimensões espaciais. O argumento lhs é uma matriz (n+2)-dimensional que descreve a área de base. Isso é chamado de entrada, embora o lado direito também seja uma entrada. Em uma rede neural, essas são as ativações de entrada. As dimensões n+2 são, nesta ordem:
batch: cada coordenada nessa dimensão representa uma entrada independente para a qual a convolução é realizada.z/depth/features: cada posição (y,x) na área de base tem um vetor associado a ela, que entra nessa dimensão.spatial_dims: descreve as dimensões espaciaisnque definem a área base em que a janela se move.
O argumento rhs é uma matriz (n+2)-dimensional que descreve o filtro/kernel/janela convolucional. As dimensões são, nesta ordem:
output-z: a dimensãozda saída.input-z: o tamanho dessa dimensão vezesfeature_group_countprecisa ser igual ao tamanho da dimensãozno lado esquerdo.spatial_dims: descreve as dimensões espaciaisnque definem a janela n-d que se move pela área de base.
O argumento window_strides especifica a extensão da janela convolucional
nas dimensões espaciais. Por exemplo, se o stride na primeira dimensão espacial for 3, a janela só poderá ser colocada em coordenadas em que o primeiro índice espacial seja divisível por 3.
O argumento padding especifica a quantidade de padding de zero a ser aplicada à área de base. A quantidade de padding pode ser negativa. O valor absoluto do padding negativo indica o número de elementos a serem removidos da dimensão especificada antes de fazer a convolução. padding[0] especifica o padding para a dimensão y, e padding[1] especifica o padding para a dimensão x. Cada par tem o padding baixo como o primeiro elemento e o padding alto como o segundo. O padding baixo é aplicado na direção de índices menores, enquanto o padding alto é aplicado na direção de índices maiores. Por exemplo, se padding[1] for (2,3), haverá um padding de dois zeros à esquerda e três zeros à direita na segunda dimensão espacial. Usar padding é equivalente a inserir esses mesmos valores zero na entrada (lhs) antes de fazer a convolução.
Os argumentos lhs_dilation e rhs_dilation especificam o fator de dilatação a ser aplicado ao lado esquerdo e direito, respectivamente, em cada dimensão espacial. Se o fator de dilatação em uma dimensão espacial for d, d-1 furos serão implicitamente colocados entre cada uma das entradas nessa dimensão, aumentando o tamanho da matriz. Os buracos são preenchidos com um valor nulo, que para convolução significa zeros.
A dilatação do rhs também é chamada de convolução atrous. Para mais detalhes, consulte
tf.nn.atrous_conv2d. A dilatação do lado esquerdo também é chamada de convolução transposta. Para mais detalhes, consulte tf.nn.conv2d_transpose.
O argumento feature_group_count (valor padrão 1) pode ser usado para convoluções agrupadas. feature_group_count precisa ser um divisor da dimensão de recurso de entrada e de saída. Se feature_group_count for maior que 1, isso significa que, conceitualmente, a dimensão do recurso de entrada e saída e a dimensão do recurso de saída rhs serão divididas igualmente em muitos grupos feature_group_count, cada um consistindo em uma subsequência consecutiva de recursos. A dimensão do recurso de entrada de rhs precisa ser igual à dimensão do recurso de entrada de lhs dividida por feature_group_count. Assim, ela já tem o tamanho de um grupo de recursos de entrada. Os grupos i-ésimos são usados juntos para calcular feature_group_count para muitas convoluções separadas. Os resultados dessas convoluções são concatenados na dimensão da característica de saída.
Para a convolução por profundidade, o argumento feature_group_count seria definido como a dimensão do recurso de entrada, e o filtro seria redimensionado de [filter_height, filter_width, in_channels, channel_multiplier] para [filter_height, filter_width, 1, in_channels * channel_multiplier]. Para mais detalhes, consulte tf.nn.depthwise_conv2d.
O argumento batch_group_count (valor padrão 1) pode ser usado para filtros agrupados durante a backpropagation. batch_group_count precisa ser um divisor do tamanho da dimensão do lote lhs (entrada). Se batch_group_count for maior que 1, isso significa que a dimensão do lote de saída deve ter o tamanho input batch
/ batch_group_count. O batch_group_count precisa ser um divisor do tamanho do recurso de saída.
O formato da saída tem estas dimensões, nesta ordem:
batch: o tamanho dessa dimensão vezesbatch_group_countprecisa ser igual ao tamanho da dimensãobatchem lhs.z: mesmo tamanho queoutput-zno kernel (rhs).spatial_dims: um valor para cada posição válida da janela convolucional.
A figura acima mostra como o campo batch_group_count funciona. Efetivamente, dividimos cada lote do lado esquerdo em batch_group_count grupos e fazemos o mesmo com os recursos de saída. Em seguida, para cada um desses grupos, fazemos convoluções aos pares e concatenamos a saída ao longo da dimensão do recurso de saída. A semântica operacional de todas as outras dimensões (recurso e espacial) permanece a mesma.
As posições válidas da janela convolucional são determinadas pelas strides e pelo tamanho da área da base após o padding.
Para descrever o que uma convolução faz, considere uma convolução 2D e escolha algumas coordenadas fixas batch, z, y, x na saída. Então, (y,x) é uma posição de um canto da janela dentro da área de base (por exemplo, o canto superior esquerdo, dependendo de como você interpreta as dimensões espaciais). Agora temos uma janela 2D, extraída da área de base, em que cada ponto 2D está associado a um vetor 1D, resultando em uma caixa 3D. Do kernel convolucional, como fixamos a coordenada de saída z, também temos uma caixa 3D. As duas caixas têm as mesmas dimensões. Portanto, podemos somar os produtos elemento a elemento entre elas (semelhante a um produto escalar). Esse é o valor de saída.
Se output-z for, por exemplo, 5, cada posição da janela produz cinco valores na saída para a dimensão z. Esses valores diferem na parte do kernel convolucional usada. Há uma caixa 3D separada de valores usada para cada coordenada output-z. Então, pense nisso como cinco convoluções separadas com um filtro diferente para cada uma delas.
Confira um pseudocódigo para uma convolução 2D com padding e stride:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
precision_config é usado para indicar a configuração de precisão. O nível
determina se o hardware deve tentar gerar mais instruções de código de máquina
para fornecer uma emulação de dtype mais precisa quando necessário (ou seja,
emular f32 em uma TPU que só aceita bf16 matmuls). Os valores podem ser
DEFAULT, HIGH, HIGHEST. Mais detalhes nas seções da MXU.
preferred_element_type é um elemento escalar de tipos de saída de precisão maior/menor usado para acumulação. preferred_element_type recomenda o tipo de acumulação para a operação especificada, mas não há garantia. Isso permite que alguns backends de hardware acumulem em um tipo diferente e convertam para o tipo de saída preferido.
Para informações sobre o StableHLO, consulte StableHLO: convolução.
ConvWithGeneralPadding
Consulte também
XlaBuilder::ConvWithGeneralPadding.
ConvWithGeneralPadding(lhs, rhs, window_strides, padding,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Igual a Conv, em que a configuração de padding é explícita.
| Argumentos | Tipo | Semântica |
|---|---|---|
lhs
|
XlaOp
|
Matriz (n+2)-dimensional de entradas |
rhs
|
XlaOp
|
Matriz (n+2)-dimensional de pesos do kernel |
window_strides |
ArraySlice<int64> |
Matriz n-dimensional de strides do kernel |
padding
|
ArraySlice<
pair<int64,int64>> |
Matriz n-d de padding (baixo, alto) |
feature_group_count
|
int64 | o número de grupos de recursos |
batch_group_count |
int64 | o número de grupos de lotes |
precision_config
|
opcional
PrecisionConfig |
enum para nível de precisão |
preferred_element_type
|
opcional
PrimitiveType |
enum do tipo de elemento escalar |
ConvWithGeneralDimensions
Consulte também
XlaBuilder::ConvWithGeneralDimensions.
ConvWithGeneralDimensions(lhs, rhs, window_strides, padding,
dimension_numbers, feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Igual a Conv, em que os números de dimensão são explícitos.
| Argumentos | Tipo | Semântica |
|---|---|---|
lhs
|
XlaOp
|
Matriz de entradas (n+2)-dimensional |
rhs
|
XlaOp
|
Matriz (n+2)-dimensional de pesos do kernel |
window_strides
|
ArraySlice<int64>
|
Matriz n-dimensional de strides do kernel |
padding |
Padding |
enum de padding |
dimension_numbers
|
ConvolutionDimensionNumbers
|
o número de dimensões |
feature_group_count
|
int64 | o número de grupos de recursos |
batch_group_count
|
int64 | o número de grupos de lotes |
precision_config
|
opcional PrecisionConfig
|
enum para nível de precisão |
preferred_element_type
|
opcional PrimitiveType
|
enum do tipo de elemento escalar |
ConvGeneral
Consulte também
XlaBuilder::ConvGeneral.
ConvGeneral(lhs, rhs, window_strides, padding, dimension_numbers,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Igual a Conv, em que os números de dimensão e a configuração de padding são explícitos.
| Argumentos | Tipo | Semântica |
|---|---|---|
lhs
|
XlaOp
|
Matriz de entradas (n+2)-dimensional |
rhs
|
XlaOp
|
Matriz (n+2)-dimensional de pesos do kernel |
window_strides
|
ArraySlice<int64>
|
Matriz n-dimensional de strides do kernel |
padding
|
ArraySlice<
pair<int64,int64>>
|
Matriz n-dimensional de padding (baixo, alto) |
dimension_numbers
|
ConvolutionDimensionNumbers
|
o número de dimensões |
feature_group_count
|
int64 | o número de grupos de recursos |
batch_group_count
|
int64 | o número de grupos de lotes |
precision_config
|
opcional PrecisionConfig
|
enum para nível de precisão |
preferred_element_type
|
opcional PrimitiveType
|
enum do tipo de elemento escalar |
ConvGeneralDilated
Consulte também
XlaBuilder::ConvGeneralDilated.
ConvGeneralDilated(lhs, rhs, window_strides, padding, lhs_dilation,
rhs_dilation, dimension_numbers, feature_group_count, batch_group_count,
precision_config, preferred_element_type, window_reversal)
Igual a Conv, em que a configuração de padding, os fatores de dilatação e os números de dimensão são explícitos.
| Argumentos | Tipo | Semântica |
|---|---|---|
lhs
|
XlaOp
|
Matriz de entradas (n+2)-dimensional |
rhs
|
XlaOp
|
Matriz (n+2)-dimensional de pesos do kernel |
window_strides
|
ArraySlice<int64>
|
Matriz n-dimensional de strides do kernel |
padding
|
ArraySlice<
pair<int64,int64>>
|
Matriz n-dimensional de padding (baixo, alto) |
lhs_dilation
|
ArraySlice<int64>
|
Matriz de fatores de dilatação do lado esquerdo n-d |
rhs_dilation
|
ArraySlice<int64>
|
Matriz de fatores de dilatação do RHS n-d |
dimension_numbers
|
ConvolutionDimensionNumbers
|
o número de dimensões |
feature_group_count
|
int64 | o número de grupos de recursos |
batch_group_count
|
int64 | o número de grupos de lotes |
precision_config
|
opcional PrecisionConfig
|
enum para nível de precisão |
preferred_element_type
|
opcional PrimitiveType
|
enum do tipo de elemento escalar |
window_reversal
|
opcional vector<bool>
|
flag usada para inverter logicamente a dimensão antes de aplicar a convolução |
Copiar
Consulte também
HloInstruction::CreateCopyStart.
O Copy é decomposto internamente em duas instruções HLO, CopyStart e CopyDone. Copy, CopyStart e CopyDone servem como primitivos em HLO. Essas operações podem aparecer em despejos de HLO, mas não devem ser construídas manualmente por usuários finais.
Cos
Consulte também XlaBuilder::Cos.
Cosseno elemento a elemento x -> cos(x).
Cos(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
A função Cos também aceita o argumento opcional result_accuracy:
Cos(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Para informações sobre o StableHLO, consulte StableHLO: cosseno.
Cosh
Consulte também
XlaBuilder::Cosh.
Cosseno hiperbólico x -> cosh(x) por elemento.
Cosh(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
A função Cosh também é compatível com o argumento opcional result_accuracy:
Cosh(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
CustomCall
Consulte também
XlaBuilder::CustomCall.
Chamar uma função fornecida pelo usuário em um cálculo.
A documentação do CustomCall está disponível em Detalhes do desenvolvedor: chamadas personalizadas do XLA
Para informações sobre o StableHLO, consulte StableHLO: custom_call.
Div
Consulte também
XlaBuilder::Div.
Realiza a divisão elemento a elemento do dividendo lhs e do divisor rhs.
Div(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
O estouro de divisão de números inteiros (divisão/resto com ou sem sinal por zero ou divisão/resto com sinal de INT_SMIN com -1) produz um valor definido pela implementação.
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte a transmissão de diferentes dimensões para Div:
Div(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO: divisão.
Domínio
Consulte também
HloInstruction::CreateDomain.
Domain pode aparecer em despejos de HLO, mas não foi criado para ser construído manualmente por usuários finais.
Escalar
Consulte também
XlaBuilder::Dot.
Dot(lhs, rhs, precision_config, preferred_element_type)
| Argumentos | Tipo | Semântica |
|---|---|---|
lhs |
XlaOp |
matriz do tipo T |
rhs |
XlaOp |
matriz do tipo T |
precision_config
|
opcional
PrecisionConfig |
enum para nível de precisão |
preferred_element_type
|
opcional
PrimitiveType |
enum do tipo de elemento escalar |
A semântica exata dessa operação depende das classificações dos operandos:
| Entrada | Saída | Semântica |
|---|---|---|
vetor [n] dot vetor [n] |
escalar | produto escalar de vetor |
matriz [m x k] dot vetor [k] |
vetor [m] | multiplicação matriz-vetor |
matriz [m x k] dot matriz[k x n] |
matriz [m x n] | multiplicação de matriz por matriz |
A operação realiza a soma dos produtos na segunda dimensão de lhs (ou a primeira, se tiver uma dimensão) e na primeira dimensão de rhs. Essas são as dimensões "contraídas". As dimensões contraídas de lhs e rhs precisam ser do mesmo tamanho. Na prática, ele pode ser usado para realizar produtos escalares entre vetores, multiplicações de vetor/matriz ou multiplicações de matriz/matriz.
precision_config é usado para indicar a configuração de precisão. O nível
determina se o hardware deve tentar gerar mais instruções de código de máquina
para fornecer uma emulação de dtype mais precisa quando necessário (ou seja,
emular f32 em uma TPU que só aceita bf16 matmuls). Os valores podem ser
DEFAULT, HIGH, HIGHEST. Mais detalhes nas seções da MXU.
preferred_element_type é um elemento escalar de tipos de saída de precisão maior/menor usado para acumulação. preferred_element_type recomenda o tipo de acumulação para a operação especificada, mas não há garantia. Isso permite que alguns backends de hardware acumulem em um tipo diferente e convertam para o tipo de saída preferido.
Para informações sobre o StableHLO, consulte StableHLO - dot.
DotGeneral
Consulte também
XlaBuilder::DotGeneral.
DotGeneral(lhs, rhs, dimension_numbers, precision_config,
preferred_element_type)
| Argumentos | Tipo | Semântica |
|---|---|---|
lhs |
XlaOp |
matriz do tipo T |
rhs |
XlaOp |
matriz do tipo T |
dimension_numbers
|
DotDimensionNumbers
|
contratação e números de dimensão de lote |
precision_config
|
opcional
PrecisionConfig |
enum para nível de precisão |
preferred_element_type
|
opcional
PrimitiveType |
enum do tipo de elemento escalar |
Semelhante a "Dot", mas permite que números de dimensão de contração e lote sejam especificados para lhs e rhs.
| Campos DotDimensionNumbers | Tipo | Semântica |
|---|---|---|
lhs_contracting_dimensions
|
repeated int64 | lhs números de dimensão de contração |
rhs_contracting_dimensions
|
repeated int64 | rhs números de dimensão de contração |
lhs_batch_dimensions
|
repeated int64 | lhs números de dimensão em lote |
rhs_batch_dimensions
|
repeated int64 | rhs números de dimensão em lote |
O DotGeneral realiza a soma dos produtos nas dimensões de contração especificadas em dimension_numbers.
Os números de dimensão de contração associados de lhs e rhs não precisam ser iguais, mas precisam ter os mesmos tamanhos de dimensão.
Exemplo com números de dimensão de contração:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { { 6.0, 12.0},
{15.0, 30.0} }
Os números de dimensão de lote associados de lhs e rhs precisam ter os mesmos tamanhos de dimensão.
Exemplo com números de dimensão de lote (tamanho do lote 2, matrizes 2x2):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> {
{ {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| Entrada | Saída | Semântica |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | multiplicação de matrizes em lote |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | multiplicação de matrizes em lote |
Portanto, o número da dimensão resultante começa com a dimensão de lote, depois a dimensão lhs não contraída/não em lote e, por fim, a dimensão rhs não contraída/não em lote.
precision_config é usado para indicar a configuração de precisão. O nível
determina se o hardware deve tentar gerar mais instruções de código de máquina
para fornecer uma emulação de dtype mais precisa quando necessário (ou seja,
emular f32 em uma TPU que só aceita bf16 matmuls). Os valores podem ser
DEFAULT, HIGH, HIGHEST. Mais detalhes
podem ser encontrados nas seções de MXU.
preferred_element_type é um elemento escalar de tipos de saída de precisão maior/menor usado para acumulação. preferred_element_type recomenda o tipo de acumulação para a operação especificada, mas não há garantia. Isso permite que alguns backends de hardware acumulem em um tipo diferente e convertam para o tipo de saída preferido.
Para informações sobre o StableHLO, consulte StableHLO: dot_general.
ScaledDot
Consulte também
XlaBuilder::ScaledDot.
ScaledDot(lhs, lhs_scale, rhs, rhs_scale, dimension_number,
precision_config,preferred_element_type)
| Argumentos | Tipo | Semântica |
|---|---|---|
lhs |
XlaOp |
matriz do tipo T |
rhs |
XlaOp |
matriz do tipo T |
lhs_scale |
XlaOp |
matriz do tipo T |
rhs_scale |
XlaOp |
matriz do tipo T |
dimension_number
|
ScatterDimensionNumbers
|
Números de dimensão para operação de dispersão |
precision_config
|
PrecisionConfig
|
enum para nível de precisão |
preferred_element_type
|
opcional PrimitiveType
|
enum do tipo de elemento escalar |
Semelhante a DotGeneral.
Cria uma operação de ponto escalonado com os operandos "lhs", "lhs_scale", "rhs" e "rhs_scale", com dimensões de contração e lote especificadas em "dimension_numbers".
RaggedDot
Consulte também
XlaBuilder::RaggedDot.
Para uma análise detalhada do cálculo de RaggedDot, consulte
StableHLO - chlo.ragged_dot
DynamicReshape
Consulte também
XlaBuilder::DynamicReshape.
Essa operação é funcionalmente idêntica a reshape, mas o formato do resultado é especificado dinamicamente via output_shape.
DynamicReshape(operand, dim_sizes, new_size_bounds, dims_are_dynamic)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
Matriz N-dimensional do tipo T |
dim_sizes |
vetor de XlaOP |
Tamanhos de vetores N dimensionais |
new_size_bounds |
vetor de int63 |
Vetor N-dimensional de limites |
dims_are_dynamic |
vetor de bool |
Dimensão dinâmica N-dimensional |
Para informações sobre o StableHLO, consulte StableHLO: dynamic_reshape.
DynamicSlice
Consulte também
XlaBuilder::DynamicSlice.
O DynamicSlice extrai uma submatriz da matriz de entrada em start_indices dinâmico. O tamanho da fatia em cada dimensão é transmitido em size_indices, que especifica o ponto final dos intervalos de fatias exclusivas em cada dimensão: [início, início + tamanho). O formato de start_indices precisa ser unidimensional, com tamanho igual ao número de dimensões de operand.
DynamicSlice(operand, start_indices, slice_sizes)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
Matriz N-dimensional do tipo T |
start_indices
|
sequência de N XlaOp
|
Lista de N números inteiros escalares que contêm os índices iniciais da fração para cada dimensão. O valor precisa ser maior ou igual a zero. |
size_indices
|
ArraySlice<int64>
|
Lista de N números inteiros que contém o tamanho da fração para cada dimensão. Cada valor precisa ser estritamente maior que zero, e "start + size" precisa ser menor ou igual ao tamanho da dimensão para evitar o encapsulamento do tamanho da dimensão do módulo. |
Os índices de corte efetivos são calculados aplicando a seguinte transformação para cada índice i em [1, N) antes de realizar o corte:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - slice_sizes[i])
Isso garante que a fração extraída esteja sempre dentro dos limites em relação à matriz de operandos. Se a fatia estiver dentro dos limites antes da transformação, ela não terá efeito.
Exemplo unidimensional:
let a = {0.0, 1.0, 2.0, 3.0, 4.0};
let s = {2};
DynamicSlice(a, s, {2});
// Result: {2.0, 3.0}
Exemplo bidimensional:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2});
//Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
Para informações sobre o StableHLO, consulte StableHLO: dynamic_slice.
DynamicUpdateSlice
Consulte também
XlaBuilder::DynamicUpdateSlice.
O DynamicUpdateSlice gera um resultado que é o valor da matriz de entrada
operand, com uma fração update substituída em start_indices.
A forma de update determina a forma da submatriz do resultado que é atualizada.
O formato de start_indices precisa ser unidimensional, com tamanho igual ao número de dimensões de operand.
DynamicUpdateSlice(operand, update, start_indices)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
Matriz N-dimensional do tipo T |
update
|
XlaOp
|
Matriz N-dimensional do tipo T que contém a atualização da fração. Cada dimensão da forma de atualização precisa ser estritamente maior que zero, e start + update precisa ser menor ou igual ao tamanho do operando em cada dimensão para evitar a geração de índices de atualização fora dos limites. |
start_indices
|
sequência de N XlaOp
|
Lista de N números inteiros escalares que contêm os índices iniciais da fração para cada dimensão. O valor precisa ser maior ou igual a zero. |
Os índices de corte efetivos são calculados aplicando a seguinte transformação para cada índice i em [1, N) antes de realizar o corte:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
Isso garante que a fatia atualizada esteja sempre dentro dos limites em relação à matriz de operandos. Se a fatia estiver dentro dos limites antes da transformação, ela não terá efeito.
Exemplo unidimensional:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s)
// Result: {0.0, 1.0, 5.0, 6.0, 4.0}
Exemplo bidimensional:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s)
// Result:
// { {0.0, 1.0, 2.0},
// {3.0, 12.0, 13.0},
// {6.0, 14.0, 15.0},
// {9.0, 16.0, 17.0} }
Para informações sobre o StableHLO, consulte StableHLO: dynamic_update_slice.
Erf
Consulte também
XlaBuilder::Erf.
Função de erro elemento a elemento x -> erf(x) em que:
\(\text{erf}(x) = \frac{2}{\sqrt{\pi} }\int_0^x e^{-t^2} \, dt\).
Erf(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
A função erf também é compatível com o argumento opcional result_accuracy:
Erf(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Exp
Consulte também
XlaBuilder::Exp.
Exponencial natural x -> e^x por elemento.
Exp(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
A função exponencial também é compatível com o argumento opcional result_accuracy:
Exp(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Para informações sobre o StableHLO, consulte StableHLO: exponencial.
Expm1
Consulte também
XlaBuilder::Expm1.
Exponencial natural elemento a elemento menos um x -> e^x - 1.
Expm1(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
A função Expm1 também aceita o argumento opcional result_accuracy:
Expm1(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Para informações sobre o StableHLO, consulte StableHLO: exponential_minus_one.
Fft
Consulte também
XlaBuilder::Fft.
A operação FFT do XLA implementa as transformações de Fourier direta e inversa para entradas/saídas reais e complexas. FFTs multidimensionais em até três eixos são compatíveis.
Fft(operand, ftt_type, fft_length)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand
|
XlaOp
|
A matriz que estamos transformando com Fourier. |
fft_type |
FftType |
Consulte a tabela abaixo. |
fft_length
|
ArraySlice<int64>
|
Os comprimentos no domínio do tempo dos eixos que estão sendo transformados. Isso é necessário principalmente para que a IRFFT dimensione corretamente o eixo mais interno, já que RFFT(fft_length=[16]) tem o mesmo formato de saída que RFFT(fft_length=[17]). |
FftType |
Semântica |
|---|---|
FFT |
FFT complexa para complexa direta. A forma não foi alterada. |
IFFT |
FFT complexa para complexa inversa. A forma não foi alterada. |
RFFT
|
FFT real para complexa direta. O formato do eixo mais interno é reduzido para fft_length[-1] // 2 + 1 se fft_length[-1] for um valor diferente de zero, omitindo a parte conjugada invertida do sinal transformado além da frequência de Nyquist. |
IRFFT
|
Transformada rápida de Fourier inversa de real para complexo (ou seja, usa números complexos e retorna reais).
A dimensão do eixo mais interno é expandida para fft_length[-1] se fft_length[-1] for um valor diferente de zero, inferindo a parte do sinal transformado além da frequência de Nyquist do conjugado inverso das entradas 1 para fft_length[-1] // 2 + 1. |
Para informações sobre o StableHLO, consulte StableHLO: fft.
FFT multidimensional
Quando mais de um fft_length é fornecido, isso equivale a aplicar uma cascata de operações de FFT a cada um dos eixos mais internos. Nos casos real->complexo e complexo->real, a transformação do eixo mais interno é (efetivamente) realizada primeiro (RFFT; última para IRFFT). Por isso, o eixo mais interno é o que muda de tamanho. Outras transformações de eixo serão complexas -> complexas.
Detalhes da implementação
A FFT da CPU é compatível com o TensorFFT do Eigen. A FFT da GPU usa cuFFT.
Andar
Consulte também
XlaBuilder::Floor.
Função de piso x -> ⌊x⌋ por elemento.
Floor(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Para informações sobre o StableHLO, consulte StableHLO: floor.
Fusão
Consulte também
HloInstruction::CreateFusion.
A operação Fusion representa instruções HLO e serve como uma primitiva em HLO.
Essa operação pode aparecer em despejos de HLO, mas não deve ser construída manualmente por usuários finais.
Coletar
A operação de coleta do XLA une várias partes (cada uma em um deslocamento de tempo de execução potencialmente diferente) de uma matriz de entrada.
Para informações sobre o StableHLO, consulte StableHLO: gather.
Semântica geral
Consulte também
XlaBuilder::Gather.
Para uma descrição mais intuitiva, consulte a seção "Descrição informal" abaixo.
gather(operand, start_indices, dimension_numbers, slice_sizes,
indices_are_sorted)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand
|
XlaOp
|
A matriz de onde estamos coletando. |
start_indices
|
XlaOp
|
Matriz que contém os índices iniciais das fatias coletadas. |
dimension_numbers
|
GatherDimensionNumbers
|
A dimensão em start_indices que "contém" os índices iniciais. Confira uma descrição detalhada abaixo. |
slice_sizes
|
ArraySlice<int64>
|
slice_sizes[i] são os limites da fatia na dimensão i. |
indices_are_sorted
|
bool
|
Se os índices têm garantia de serem classificados pelo autor da chamada. |
Por conveniência, rotulamos as dimensões na matriz de saída que não estão em offset_dims como batch_dims.
A saída é uma matriz com batch_dims.size + offset_dims.size dimensões.
O operand.rank precisa ser igual à soma de offset_dims.size e collapsed_slice_dims.size. Além disso, slice_sizes.size precisa ser igual a operand.rank.
Se index_vector_dim for igual a start_indices.rank, vamos considerar implicitamente que start_indices tem uma dimensão 1 final. Por exemplo, se start_indices tiver o formato [6,7] e index_vector_dim for 2, vamos considerar implicitamente que o formato de start_indices é [6,7,1].
Os limites da matriz de saída ao longo da dimensão i são calculados da seguinte forma:
Se
iestiver presente embatch_dims(ou seja, for igual abatch_dims[k]para algumk), vamos escolher os limites de dimensão correspondentes emstart_indices.shape, ignorandoindex_vector_dim(ou seja, escolherstart_indices.shape.dims[k] sek<index_vector_dimestart_indices.shape.dims[k+1] caso contrário).Se
iestiver presente emoffset_dims(ou seja, igual aoffset_dims[k] para algumk), vamos escolher o limite correspondente deslice_sizesdepois de considerarcollapsed_slice_dims(ou seja, vamos escolheradjusted_slice_sizes[k], em queadjusted_slice_sizeséslice_sizescom os limites nos índicescollapsed_slice_dimsremovidos).
Formalmente, o índice do operando In correspondente a um determinado índice de saída Out é calculado da seguinte maneira:
Seja
G= {Out[k] parakembatch_dims}. UseGpara extrair um vetorSde forma queS[i] =start_indices[Combine(G,i)], em que Combine(A, b) insere b na posiçãoindex_vector_dimem A. Isso é bem definido mesmo queGesteja vazio: seGestiver vazio,S=start_indices.Crie um índice inicial,
Sin, emoperandusandoSao dispersarSusandostart_index_map. Mais precisamente:Sin[start_index_map[k]] =S[k] sek<start_index_map.size.Sin[_] =0caso contrário.
Crie um índice
Oinemoperanddispersando os índices nas dimensões de deslocamento emOutde acordo com o conjuntocollapsed_slice_dims. Mais precisamente:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]] sek<offset_dims.size(remapped_offset_dimsé definido abaixo).Oin[_] =0caso contrário.
InéOin+Sin, em que + é a adição de elemento a elemento.
remapped_offset_dims é uma função monotônica com domínio [0, offset_dims.size) e intervalo [0, operand.rank) \ collapsed_slice_dims. Então, se, por exemplo, offset_dims.size é 4, operand.rank é 6 e
collapsed_slice_dims é {0, 2}, então remapped_offset_dims é {0→1,
1→3, 2→4, 3→5}.
Se indices_are_sorted for definido como verdadeiro, o XLA poderá presumir que start_indices
estão classificados (em ordem crescente, após dispersar os valores de acordo com
start_index_map) pelo usuário. Caso contrário, a semântica será definida pela implementação.
Descrição informal e exemplos
De maneira informal, cada índice Out na matriz de saída corresponde a um elemento E na matriz de operandos, calculado da seguinte maneira:
Usamos as dimensões do lote em
Outpara pesquisar um índice inicial destart_indices.Usamos
start_index_mappara mapear o índice inicial (cujo tamanho pode ser menor que operand.rank) para um índice inicial "completo" nooperand.Fazemos uma segmentação dinâmica com tamanho
slice_sizesusando o índice inicial completo.Para isso, recolhemos as dimensões
collapsed_slice_dims. Como todas as dimensões de fatia recolhidas precisam ter um limite de 1, essa mudança de formato é sempre válida.Usamos as dimensões de deslocamento em
Outpara indexar essa fatia e receber o elemento de entrada,E, correspondente ao índice de saídaOut.
index_vector_dim é definido como start_indices.rank - 1 em todos os exemplos a seguir. Valores mais interessantes para index_vector_dim não mudam a operação fundamentalmente, mas tornam a representação visual mais complicada.
Para entender como tudo isso se encaixa, vamos analisar um exemplo que reúne cinco fatias de forma [8,6] de uma matriz [16,11]. A posição de uma fatia na matriz [16,11] pode ser representada como um vetor de índice de forma S64[2]. Assim, o conjunto de cinco posições pode ser representado como uma matriz S64[5,2].
O comportamento da operação de coleta pode ser descrito como uma transformação de índice que usa [G,O0,O1], um índice no formato de saída, e o mapeia para um elemento na matriz de entrada da seguinte maneira:
Primeiro, selecionamos um vetor (X,Y) da matriz de índices de coleta usando G.
O elemento na matriz de saída no índice [G,O0,O1] é o elemento na matriz de entrada no índice [X+O0,Y+O1].
slice_sizes é [8,6], que decide o intervalo de O0 e O1, e isso, por sua vez, decide os limites da fração.
Essa operação de coleta funciona como uma fração dinâmica em lote com G como a dimensão do lote.
Os índices de coleta podem ser multidimensionais. Por exemplo, uma versão mais geral do exemplo acima usando uma matriz "reunir índices" de forma [4,5,2] traduziria os índices assim:
Novamente, isso funciona como uma segmentação dinâmica em lote G0 e G1 como as dimensões do lote. O tamanho da fração ainda é [8,6].
A operação de coleta no XLA generaliza a semântica informal descrita acima das seguintes maneiras:
Podemos configurar quais dimensões na forma de saída são as dimensões de ajuste (dimensões que contêm
O0,O1no último exemplo). As dimensões de lote de saída (dimensões que contêmG0,G1no último exemplo) são definidas como as dimensões de saída que não são de compensação.O número de dimensões de deslocamento de saída explicitamente presentes na forma de saída pode ser menor do que o número de dimensões de entrada. Essas dimensões "ausentes", que são listadas explicitamente como
collapsed_slice_dims, precisam ter um tamanho de fração de1. Como eles têm um tamanho de fração de1, o único índice válido é0, e a omissão não causa ambiguidade.A fatia extraída da matriz "Gather Indices" ((
X,Y) no último exemplo) pode ter menos elementos do que o número de dimensões da matriz de entrada, e um mapeamento explícito determina como o índice deve ser expandido para ter o mesmo número de dimensões da entrada.
Como exemplo final, usamos (2) e (3) para implementar tf.gather_nd:
G0 e G1 são usados para extrair um índice inicial da matriz de índices de coleta como de costume, exceto que o índice inicial tem apenas um elemento, X. Da mesma forma, há apenas um índice de ajuste de saída com o valor O0. No entanto, antes de serem usados como índices na matriz de entrada, eles são expandidos de acordo com "Coletar mapeamento de índice" (start_index_map na descrição formal) e "Mapeamento de deslocamento" (remapped_offset_dims na descrição formal) em [X,0] e [0,O0], respectivamente, somando [X,O0]. Em outras palavras, o índice de saída [G0,G1,O0] é mapeado para o índice de entrada [GatherIndices[G0,G1,0],O0], o que nos dá a semântica para tf.gather_nd.
slice_sizes para este caso é [1,11]. Isso significa que cada índice X na matriz de índices de coleta escolhe uma linha inteira, e o resultado é a concatenação de todas essas linhas.
GetDimensionSize
Consulte também
XlaBuilder::GetDimensionSize.
Retorna o tamanho da dimensão especificada do operando. O operando precisa ter o formato de matriz.
GetDimensionSize(operand, dimension)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
matriz de entrada n-dimensional |
dimension
|
int64
|
Um valor no intervalo [0, n) que especifica a dimensão |
Para informações sobre o StableHLO, consulte StableHLO - get_dimension_size.
GetTupleElement
Consulte também
XlaBuilder::GetTupleElement.
Indexa uma tupla com um valor constante de tempo de compilação.
O valor precisa ser uma constante de tempo de compilação para que a inferência de forma possa determinar o tipo do valor resultante.
Isso é análogo a std::get<int N>(t) em C++. Conceitualmente:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
Consulte também tf.tuple.
GetTupleElement(tuple_data, index)
| Argumento | Tipo | Semântica |
|---|---|---|
tuple_data |
XlaOP |
A tupla |
index |
int64 |
Índice da forma da tupla |
Para informações sobre o StableHLO, consulte StableHLO: get_tuple_element.
Imag
Consulte também
XlaBuilder::Imag.
Parte imaginária de um elemento de uma forma complexa (ou real). x -> imag(x). Se o operando for um tipo de ponto flutuante, será retornado 0.
Imag(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Para informações sobre o StableHLO, consulte StableHLO - imag.
No feed
Consulte também
XlaBuilder::Infeed.
Infeed(shape, config)
| Argumento | Tipo | Semântica |
|---|---|---|
shape
|
Shape
|
Formato dos dados lidos da interface Infeed. O campo de layout da forma precisa ser definido para corresponder ao layout dos dados enviados ao dispositivo. Caso contrário, o comportamento será indefinido. |
config |
opcional string |
Configuração da operação. |
Lê um único item de dados da interface de streaming infeed implícita do
dispositivo, interpretando os dados como a forma e o layout especificados, e retorna um
XlaOp dos dados. Várias operações de feed são permitidas em um cálculo, mas é necessário haver uma ordem total entre elas. Por exemplo, dois Infeeds no código abaixo têm uma ordem total porque há uma dependência entre os loops "while".
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
Não é possível usar tuplas aninhadas. Para uma forma de tupla vazia, a operação Infeed é efetivamente uma operação nula e continua sem ler dados do Infeed do dispositivo.
Para informações sobre o StableHLO, consulte StableHLO - infeed.
Iota
Consulte também
XlaBuilder::Iota.
Iota(shape, iota_dimension)
Cria uma constante literal no dispositivo em vez de uma transferência de host potencialmente grande. Cria uma matriz com o formato especificado e contém valores que começam em zero e aumentam em um ao longo da dimensão especificada. Para tipos de ponto flutuante, a matriz produzida é equivalente a ConvertElementType(Iota(...)), em que Iota é do tipo integral e a conversão é para o tipo de ponto flutuante.
| Argumentos | Tipo | Semântica |
|---|---|---|
shape |
Shape |
Formato da matriz criada por Iota() |
iota_dimension |
int64 |
A dimensão a ser incrementada. |
Por exemplo, Iota(s32[4, 8], 0) retorna
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
Devolução por Iota(s32[4, 8], 1)
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
Para informações sobre o StableHLO, consulte StableHLO: iota.
IsFinite
Consulte também
XlaBuilder::IsFinite.
Testa se cada elemento de operand é finito, ou seja, não é infinito positivo ou negativo e não é NaN. Retorna uma matriz de valores PRED com o mesmo formato da entrada, em que cada elemento é true se e somente se o elemento de entrada correspondente for finito.
IsFinite(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Para informações sobre o StableHLO, consulte StableHLO: is_finite.
Registro
Consulte também
XlaBuilder::Log.
Logaritmo natural elemento a elemento x -> ln(x).
Log(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
O registro também é compatível com o argumento opcional result_accuracy:
Log(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Para mais informações sobre o StableHLO, consulte StableHLO: log.
Log1p
Consulte também
XlaBuilder::Log1p.
Logaritmo natural x -> ln(1+x) com deslocamento elemento a elemento.
Log1p(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
O Log1p também aceita o argumento opcional result_accuracy:
Log1p(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Para informações sobre o StableHLO, consulte StableHLO - log_plus_one.
Logística
Consulte também
XlaBuilder::Logistic.
Cálculo da função logística elemento a elemento x -> logistic(x).
Logistic(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
A logística também aceita o argumento opcional result_accuracy:
Logistic(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Para informações sobre o StableHLO, consulte StableHLO: logística.
Mapa
Consulte também
XlaBuilder::Map.
Map(operands..., computation, dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
operands |
sequência de N XlaOps |
N matrizes de tipos T0..T{N-1} |
computation
|
XlaComputation
|
Cálculo do tipo T_0, T_1,
.., T_{N + M -1} -> S com N parâmetros do tipo T e M de tipo arbitrário. |
dimensions |
Matriz int64 |
Matriz de dimensões do mapa |
static_operands
|
sequência de N XlaOps
|
Operações estáticas para a operação de mapa |
Aplica uma função escalar às matrizes operands fornecidas, produzindo uma matriz de mesmas dimensões em que cada elemento é o resultado da função mapeada aplicada aos elementos correspondentes nas matrizes de entrada.
A função mapeada é um cálculo arbitrário com a restrição de ter N entradas do tipo escalar T e uma única saída do tipo S. A saída tem as mesmas dimensões que os operandos, exceto que o tipo de elemento T é substituído por S.
Por exemplo, Map(op1, op2, op3, computation, par1) mapeia elem_out <-
computation(elem1, elem2, elem3, par1) em cada índice (multidimensional) nas matrizes de entrada para produzir a matriz de saída.
Para informações sobre o StableHLO, consulte StableHLO: mapa.
Máx.
Consulte também
XlaBuilder::Max.
Executa a operação de máximo por elemento nos tensores lhs e rhs.
Max(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para o Max:
Max(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO: máximo.
Mín.
Consulte também
XlaBuilder::Min.
Executa a operação de mínimo com elementos em lhs e rhs.
Min(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para Min:
Min(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO: mínimo.
Mul
Consulte também
XlaBuilder::Mul.
Realiza o produto elemento a elemento de lhs e rhs.
Mul(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para Mul:
Mul(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO: multiplicação.
Neg
Consulte também
XlaBuilder::Neg.
Negação de elemento por elemento x -> -x.
Neg(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Para informações sobre o StableHLO, consulte StableHLO: negação
Não
Consulte também
XlaBuilder::Not.
Negação lógica x -> !(x) referente a elemento.
Not(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Para informações sobre o StableHLO, consulte StableHLO - not.
OptimizationBarrier
Consulte também
XlaBuilder::OptimizationBarrier.
Impede que qualquer transmissão de otimização mova computações pela barreira.
OptimizationBarrier(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Garante que todas as entradas sejam avaliadas antes de qualquer operador que dependa das saídas da barreira.
Para informações sobre o StableHLO, consulte StableHLO: optimization_barrier.
Ou
Consulte também
XlaBuilder::Or.
Executa um OR bit a bit de lhs e rhs .
Or(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para "Or":
Or(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO - ou.
Outfeed
Consulte também
XlaBuilder::Outfeed.
Grava entradas no feed de saída.
Outfeed(operand, shape_with_layout, outfeed_config)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
matriz do tipo T |
shape_with_layout |
Shape |
Define o layout dos dados transferidos. |
outfeed_config |
string |
Constante de configuração para a instrução Outfeed. |
shape_with_layout comunica a forma disposta que queremos extrair.
Para informações sobre o StableHLO, consulte StableHLO: saída.
Pad
Consulte também
XlaBuilder::Pad.
Pad(operand, padding_value, padding_config)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
matriz do tipo T |
padding_value
|
XlaOp
|
escalar do tipo T para preencher o padding adicionado |
padding_config
|
PaddingConfig
|
quantidade de padding nas duas extremidades (baixa, alta) e entre os elementos de cada dimensão |
Adiciona padding à matriz operand fornecida ao redor dela e entre os elementos com o padding_value especificado. padding_config especifica a quantidade de padding de borda e o padding interno para cada dimensão.
PaddingConfig é um campo repetido de PaddingConfigDimension, que contém três campos para cada dimensão: edge_padding_low, edge_padding_high e interior_padding.
edge_padding_low e edge_padding_high especificam a quantidade de padding adicionada na extremidade inferior (próxima ao índice 0) e na extremidade superior (próxima ao índice mais alto) de cada dimensão, respectivamente. A quantidade de padding de borda pode ser negativa. O valor absoluto do padding negativo indica o número de elementos a serem removidos da dimensão especificada.
interior_padding especifica a quantidade de padding adicionada entre dois elementos em cada dimensão e não pode ser negativa. O padding interno ocorre logicamente antes do padding de borda. Portanto, no caso de padding de borda negativo, os elementos são removidos do operando com padding interno.
Essa operação não faz nada se todos os pares de padding de borda forem (0, 0) e os valores de padding interno forem todos 0. A figura abaixo mostra exemplos de diferentes valores de edge_padding e interior_padding para uma matriz bidimensional.
Para informações sobre o StableHLO, consulte StableHLO: pad.
Parâmetro
Consulte também
XlaBuilder::Parameter.
Parameter representa uma entrada de argumento para um cálculo.
PartitionID
Consulte também
XlaBuilder::BuildPartitionId.
Produz partition_id do processo atual.
PartitionID(shape)
| Argumentos | Tipo | Semântica |
|---|---|---|
shape |
Shape |
Formato dos dados |
PartitionID pode aparecer em despejos de HLO, mas não foi criado para ser construído
manualmente por usuários finais.
Para informações sobre o StableHLO, consulte StableHLO: partition_id.
PopulationCount
Consulte também
XlaBuilder::PopulationCount.
Calcula o número de bits definidos em cada elemento de operand.
PopulationCount(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Para informações sobre o StableHLO, consulte StableHLO: popcnt.
Pow
Consulte também
XlaBuilder::Pow.
Realiza a exponenciação elemento a elemento de lhs por rhs.
Pow(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para Pow:
Pow(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO: energia.
Real
Consulte também
XlaBuilder::Real.
Parte real de um elemento de uma forma complexa (ou real). x -> real(x). Se o operando for um tipo de ponto flutuante, Real vai retornar o mesmo valor.
Real(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Para informações sobre o StableHLO, consulte StableHLO: real.
Recv
Consulte também
XlaBuilder::Recv.
Recv, RecvWithTokens e RecvToHost são operações que servem como
primitivos de comunicação em HLO. Essas operações geralmente aparecem em despejos de HLO como parte de entrada/saída de baixo nível ou transferência entre dispositivos, mas não devem ser construídas manualmente pelos usuários finais.
Recv(shape, handle)
| Argumentos | Tipo | Semântica |
|---|---|---|
shape |
Shape |
formato dos dados a serem recebidos |
handle |
ChannelHandle |
identificador exclusivo para cada par de envio/recebimento |
Recebe dados da forma especificada de uma instrução Send em outro cálculo que compartilha o mesmo identificador de canal. Retorna um XlaOp para os dados recebidos.
Para informações sobre o StableHLO, consulte StableHLO: recv.
RecvDone
Consulte também
HloInstruction::CreateRecv e HloInstruction::CreateRecvDone.
Assim como Send, a API do cliente da operação Recv representa
a comunicação síncrona. No entanto, a instrução é decomposta internamente
em duas instruções HLO (Recv e RecvDone) para permitir transferências
de dados assíncronas.
Recv(const Shape& shape, int64 channel_id)
Aloca os recursos necessários para receber dados de uma instrução Send com o mesmo channel_id. Retorna um contexto para os recursos alocados, que
é usado por uma instrução RecvDone a seguir para aguardar a conclusão da
transferência de dados. O contexto é uma tupla de {buffer de recebimento (formato), identificador de solicitação (U32)} e só pode ser usado por uma instrução RecvDone.
Dado um contexto criado por uma instrução Recv, aguarda a conclusão da transferência de dados e retorna os dados recebidos.
Reduzir
Consulte também
XlaBuilder::Reduce.
Aplica uma função de redução a uma ou mais matrizes em paralelo.
Reduce(operands..., init_values..., computation, dimensions_to_reduce)
| Argumentos | Tipo | Semântica |
|---|---|---|
operands
|
Sequência de N XlaOp
|
N matrizes de tipos T_0,...,
T_{N-1}. |
init_values
|
Sequência de N XlaOp
|
N escalares dos tipos
T_0,..., T_{N-1}. |
computation
|
XlaComputation
|
cálculo do tipo
T_0,..., T_{N-1}, T_0,
...,T_{N-1} ->
Collate(T_0,...,
T_{N-1}). |
dimensions_to_reduce
|
Matriz int64
|
matriz não ordenada de dimensões a serem reduzidas. |
Em que:
- N precisa ser maior ou igual a 1.
- O cálculo precisa ser "aproximadamente" associativo (veja abaixo).
- Todas as matrizes de entrada precisam ter as mesmas dimensões.
- Todos os valores iniciais precisam formar uma identidade em
computation. - Se
N = 1,Collate(T)seráT. - Se
N > 1,Collate(T_0, ..., T_{N-1})for uma tupla de elementosNdo tipoT.
Essa operação reduz uma ou mais dimensões de cada matriz de entrada em escalares.
O número de dimensões de cada matriz retornada é number_of_dimensions(operand) - len(dimensions). A saída da operação é
Collate(Q_0, ..., Q_N), em que Q_i é uma matriz do tipo T_i, e as
dimensões são descritas abaixo.
Diferentes back-ends podem reassociar o cálculo de redução. Isso pode levar a diferenças numéricas, já que algumas funções de redução, como adição, não são associativas para números de ponto flutuante. No entanto, se o intervalo dos dados for limitado, a adição de ponto flutuante será associativa o suficiente para a maioria dos usos práticos.
Para informações sobre o StableHLO, consulte StableHLO: reduzir.
Exemplos
Ao reduzir uma dimensão em uma única matriz 1D com valores [10, 11,
12, 13] e função de redução f (que é computation), isso pode ser calculado como
f(10, f(11, f(12, f(init_value, 13)))
mas também há muitas outras possibilidades, por exemplo:
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
Confira a seguir um exemplo aproximado de pseudocódigo de como a redução pode ser implementada, usando a soma como o cálculo de redução com um valor inicial de 0.
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
Confira um exemplo de redução de uma matriz 2D. O formato tem duas dimensões, a dimensão 0 de tamanho 2 e a dimensão 1 de tamanho 3:
Resultados da redução das dimensões 0 ou 1 com uma função "add":
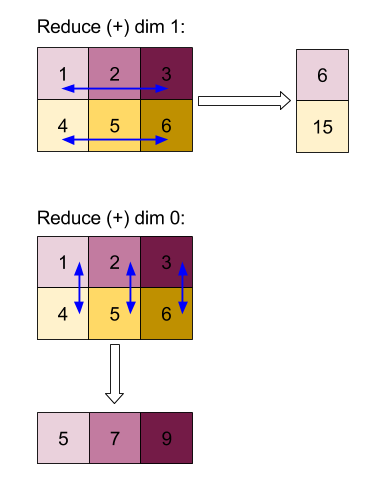
Os dois resultados de redução são matrizes unidimensionais. O diagrama mostra um como coluna e outro como linha apenas para conveniência visual.
Para um exemplo mais complexo, confira uma matriz 3D. O número de dimensões é 3, dimensão 0 de tamanho 4, dimensão 1 de tamanho 2 e dimensão 2 de tamanho 3. Para simplificar, os valores de 1 a 6 são replicados na dimensão 0.
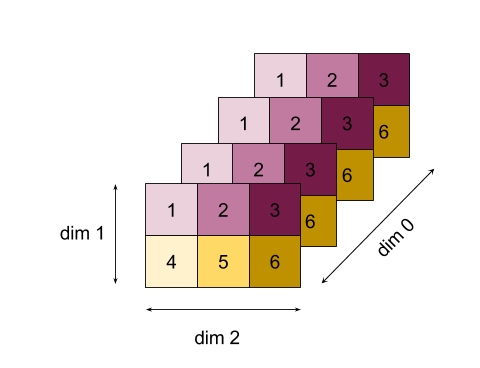
Assim como no exemplo 2D, podemos reduzir apenas uma dimensão. Se reduzirmos a dimensão 0, por exemplo, vamos ter uma matriz bidimensional em que todos os valores da dimensão 0 foram transformados em um escalar:
| 4 8 12 |
| 16 20 24 |
Se reduzirmos a dimensão 2, também vamos receber uma matriz bidimensional em que todos os valores na dimensão 2 foram agrupados em um escalar:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
A ordem relativa entre as dimensões restantes na entrada é preservada na saída, mas algumas dimensões podem receber novos números, já que o número de dimensões muda.
Também é possível reduzir várias dimensões. A adição de dimensões 0 e 1 reduzidas produz a matriz 1D [20, 28, 36].
Reduzir a matriz 3D em todas as dimensões produz o escalar 84.
Redução variádica
Quando N > 1, a aplicação da função de redução é um pouco mais complexa, já que é aplicada simultaneamente a todas as entradas. Os operandos são fornecidos ao cálculo na seguinte ordem:
- Execução do valor reduzido para o primeiro operando
- …
- Execução de valor reduzido para o Nésimo operando
- Valor de entrada do primeiro operando
- …
- Valor de entrada do N-ésimo operando
Por exemplo, considere a seguinte função de redução, que pode ser usada para calcular o máximo e o argmax de uma matriz unidimensional em paralelo:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
Para matrizes de entrada 1D V = Float[N], K = Int[N] e valores iniciais I_V = Float, I_K = Int, o resultado f_(N-1) da redução na única dimensão de entrada é equivalente à seguinte aplicação recursiva:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
Aplicar essa redução a uma matriz de valores e uma matriz de índices sequenciais (ou seja, iota) vai iterar em conjunto nas matrizes e retornar uma tupla que contém o valor máximo e o índice correspondente.
ReducePrecision
Consulte também
XlaBuilder::ReducePrecision.
Modela o efeito da conversão de valores de ponto flutuante para um formato de menor precisão (como IEEE-FP16) e de volta ao formato original. O número de bits de expoente e mantissa no formato de baixa precisão pode ser especificado arbitrariamente, embora nem todos os tamanhos de bits sejam compatíveis com todas as implementações de hardware.
ReducePrecision(operand, exponent_bits, mantissa_bits)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
matriz do tipo de ponto flutuante T. |
exponent_bits |
int32 |
número de bits de expoente no formato de baixa precisão |
mantissa_bits |
int32 |
número de bits da parte fracionária no formato de baixa precisão |
O resultado é uma matriz do tipo T. Os valores de entrada são arredondados para o valor representável mais próximo com o número de bits de mantissa especificado (usando a semântica "ties to even"), e todos os valores que excedem o intervalo especificado pelo número de bits de expoente são fixados como infinito positivo ou negativo. Os valores NaN são mantidos, mas podem ser convertidos em valores NaN canônicos.
O formato de menor precisão precisa ter pelo menos um bit de expoente (para distinguir um valor zero de um infinito, já que ambos têm uma mantissa zero) e um número não negativo de bits de mantissa. O número de bits de expoente ou mantissa pode exceder o valor correspondente para o tipo T. A parte correspondente da conversão é simplesmente uma operação nula.
Para informações sobre o StableHLO, consulte StableHLO: reduce_precision.
ReduceScatter
Consulte também
XlaBuilder::ReduceScatter.
O ReduceScatter é uma operação coletiva que faz um AllReduce e depois dispersa o resultado dividindo-o em shard_count blocos ao longo do scatter_dimension, e a réplica i no grupo de réplicas recebe o fragmento ith.
ReduceScatter(operand, computation, scatter_dimension, shard_count,
replica_groups, channel_id, layout, use_global_device_ids)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand
|
XlaOp
|
Matriz ou tupla não vazia de matrizes para reduzir em réplicas. |
computation |
XlaComputation |
Cálculo de redução |
scatter_dimension |
int64 |
Dimensão a ser dispersa. |
shard_count
|
int64
|
Número de blocos para dividir scatter_dimension. |
replica_groups
|
ReplicaGroup vetor
|
Grupos entre os quais as reduções são realizadas |
channel_id
|
opcional
ChannelHandle |
ID do canal opcional para comunicação entre módulos |
layout
|
opcional Layout
|
layout de memória especificado pelo usuário |
use_global_device_ids |
opcional bool |
flag especificada pelo usuário |
- Quando
operandé uma tupla de matrizes, o reduce-scatter é realizado em cada elemento da tupla. replica_groupsé uma lista de grupos de réplicas entre os quais a redução é realizada. O ID da réplica atual pode ser recuperado usandoReplicaId. A ordem das réplicas em cada grupo determina a ordem em que o resultado de redução total será disperso.replica_groupsprecisa estar vazio (nesse caso, todas as réplicas pertencem a um único grupo) ou conter o mesmo número de elementos que o número de réplicas. Quando há mais de um grupo de réplicas, todos precisam ter o mesmo tamanho. Por exemplo,replica_groups = {0, 2}, {1, 3}realiza a redução entre as réplicas0e2,1e3e, em seguida, dispersa o resultado.shard_counté o tamanho de cada grupo de réplicas. Precisamos disso nos casos em quereplica_groupsestão vazios. Sereplica_groupsnão estiver vazio,shard_countprecisará ser igual ao tamanho de cada grupo de réplicas.channel_idé usado para comunicação entre módulos: apenas operaçõesreduce-scattercom o mesmochannel_idpodem se comunicar entre si.layoutConsulte xla::shapes para mais informações sobre layouts.use_global_device_idsé uma flag especificada pelo usuário. Quandofalse(padrão), os números emreplica_groupssãoReplicaIdquandotrue, ereplica_groupsrepresenta um ID global de (ReplicaID*partition_count+partition_id). Por exemplo:- Com duas réplicas e quatro partições,
- replica_groups={ {0,1,4,5},{2,3,6,7} } and use_global_device_ids=true
- group[0] = (0,0), (0,1), (1,0), (1,1)
- group[1] = (0,2), (0,3), (1,2), (1,3)
- em que cada par é (replica_id, partition_id).
A forma de saída é a forma de entrada com o scatter_dimension shard_count vezes menor. Por exemplo, se houver duas réplicas e o operando tiver o valor [1.0, 2.25] e [3.0, 5.25], respectivamente, nas duas réplicas, o valor de saída dessa operação em que scatter_dim é 0 será [4.0] para a primeira réplica e [7.5] para a segunda.
Para informações sobre o StableHLO, consulte StableHLO: reduce_scatter.
ReduceScatter: exemplo 1 (StableHLO)
No exemplo acima, há duas réplicas participando do ReduceScatter. Em cada réplica, o operando tem o formato f32[2,4]. Uma redução total (soma) é realizada em todas as réplicas, produzindo um valor reduzido de forma f32[2,4] em cada réplica. Esse valor reduzido é dividido em duas partes ao longo da dimensão 1, de modo que cada parte tenha o formato f32[2,2]. Cada réplica no grupo de processos recebe a parte correspondente à sua posição no grupo. Como resultado, a saída em cada réplica tem o formato f32[2,2].
ReduceWindow
Consulte também
XlaBuilder::ReduceWindow.
Aplica uma função de redução a todos os elementos em cada janela de uma sequência de matrizes multidimensionais N, produzindo uma única matriz ou uma tupla de N matrizes multidimensionais como saída. Cada matriz de saída tem o mesmo número de elementos que o número de posições válidas da janela. Uma camada de pooling pode ser expressa como um
ReduceWindow. Assim como Reduce, o computation aplicado sempre é transmitido pelo init_values no lado esquerdo.
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| Argumentos | Tipo | Semântica |
|---|---|---|
operands
|
N XlaOps
|
Uma sequência de N matrizes multidimensionais de tipos T_0,..., T_{N-1}, cada uma representando a área de base em que a janela é colocada. |
init_values
|
N XlaOps
|
Os N valores iniciais para a redução, um para cada um dos N operandos. Consulte Reduzir para mais detalhes. |
computation
|
XlaComputation
|
Função de redução do tipo T_0,
..., T_{N-1}, T_0, ..., T_{N-1}
-> Collate(T_0, ..., T_{N-1}), a ser aplicada aos elementos em cada janela de todos os operandos de entrada. |
window_dimensions
|
ArraySlice<int64>
|
matriz de números inteiros para valores de dimensão da janela |
window_strides
|
ArraySlice<int64>
|
matriz de números inteiros para valores de stride da janela |
base_dilations
|
ArraySlice<int64>
|
matriz de números inteiros para valores de dilatação de base |
window_dilations
|
ArraySlice<int64>
|
matriz de números inteiros para valores de dilatação da janela |
padding
|
Padding
|
tipo de padding para janela (Padding::kSame, que faz padding para ter o mesmo formato de saída da entrada se o stride for 1, ou Padding::kValid, que não usa padding e "para" a janela quando ela não cabe mais) |
Em que:
- N precisa ser maior ou igual a 1.
- Todas as matrizes de entrada precisam ter as mesmas dimensões.
- Se
N = 1,Collate(T)seráT. - Se
N > 1,Collate(T_0, ..., T_{N-1})for uma tupla de elementosNdo tipo(T0,...T{N-1}).
Para informações sobre o StableHLO, consulte StableHLO: reduce_window.
ReduceWindow - Example 1
A entrada é uma matriz de tamanho [4x6], e window_dimensions e window_stride_dimensions são [2x3].
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
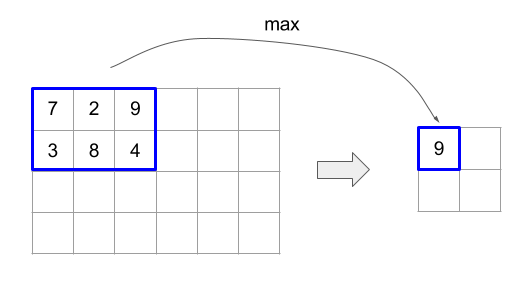
Uma passada de 1 em uma dimensão especifica que a posição de uma janela na dimensão está a um elemento de distância da janela adjacente. Para especificar que nenhuma janela se sobrepõe, window_stride_dimensions precisa ser igual a window_dimensions. A figura abaixo ilustra o uso de dois valores de stride diferentes. O padding é aplicado a cada dimensão da entrada, e os cálculos são os mesmos como se a entrada tivesse as dimensões que tem após o padding.
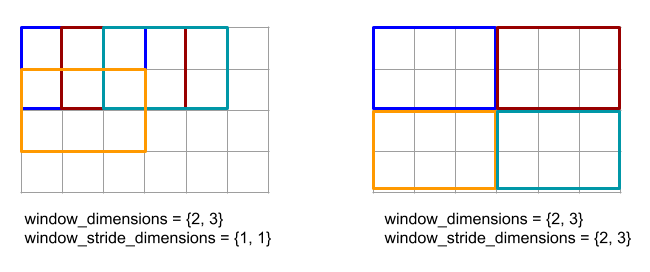
Para um exemplo de padding não trivial, considere calcular o mínimo da janela de redução (o valor inicial é MAX_FLOAT) com dimensão 3 e stride 2 na matriz de entrada [10000, 1000, 100, 10, 1]. O padding kValid calcula mínimos em duas janelas válidas: [10000, 1000, 100] e [100, 10, 1], resultando na saída [100, 1]. O padding kSame primeiro preenche a matriz para que a forma após a janela de redução seja igual à entrada para o stride 1, adicionando elementos iniciais nos dois lados, resultando em [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE]. Executar reduce-window na matriz com padding opera em três janelas [MAX_VALUE, 10000, 1000], [1000, 100, 10], [10, 1, MAX_VALUE] e gera [1000, 10, 1].
A ordem de avaliação da função de redução é arbitrária e pode ser não determinística. Portanto, a função de redução não pode ser muito sensível à reassociação. Consulte a discussão sobre associatividade no contexto de Reduce para mais detalhes.
ReduceWindow: exemplo 2 (StableHLO)
No exemplo acima:
Entrada) O operando tem um formato de entrada S32[3,2]. Com valores de
[[1,2],[3,4],[5,6]]
Etapa 1) A dilatação de base com fator 2 ao longo da dimensão da linha insere furos entre cada linha do operando. O padding de duas linhas na parte de cima e uma linha na parte de baixo é aplicado após a dilatação. Como resultado, o tensor fica mais alto.
Etapa 2) Uma janela de forma [2,1] é definida, com dilatação de janela [3,1]. Isso significa que cada janela seleciona dois elementos da mesma coluna, mas o segundo elemento é extraído três linhas abaixo do primeiro, em vez de diretamente abaixo dele.
Etapa 3) As janelas são deslizadas pelo operando com o incremento [4,1]. Isso faz com que a janela se mova quatro linhas por vez para baixo, enquanto muda uma coluna por vez horizontalmente. As células de padding são preenchidas com init_value (neste caso, init_value = 0). Os valores que "se enquadram" nas células de dilatação são ignorados.
Devido à extensão e ao padding, algumas janelas se sobrepõem apenas a zeros e buracos, enquanto outras se sobrepõem a valores de entrada reais.
Etapa 4) Em cada janela, os elementos são combinados usando a função de redução (a, b) → a + b, começando com um valor inicial de 0. As duas janelas de cima só veem preenchimento e furos, então os resultados são 0. As janelas de baixo capturam os valores 3 e 4 da entrada e os retornam como resultados.
Resultados) A saída final tem a forma S32[2,2], com valores: [[0,0],[3,4]]
Rem
Consulte também
XlaBuilder::Rem.
Realiza o restante da divisão do dividendo lhs e do divisor rhs elemento a elemento.
O sinal do resultado é retirado do dividendo, e o valor absoluto do resultado é sempre menor que o valor absoluto do divisor.
Rem(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para Rem:
Rem(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para mais informações sobre o StableHLO, consulte StableHLO: remainder.
ReplicaId
Consulte também
XlaBuilder::ReplicaId.
Retorna o ID exclusivo (escalar U32) da réplica.
ReplicaId()
O ID exclusivo de cada réplica é um número inteiro sem sinal no intervalo [0, N), em que N é o número de réplicas. Como todas as réplicas estão executando o mesmo programa, uma chamada ReplicaId() no programa vai retornar um valor diferente em cada réplica.
Para informações sobre o StableHLO, consulte StableHLO - replica_id.
Remodelação
Consulte também
XlaBuilder::Reshape.
e a operação Collapse.
Redimensiona as dimensões de uma matriz em uma nova configuração.
Reshape(operand, dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
matriz do tipo T |
dimensions |
int64 vetor |
vetor de tamanhos de novas dimensões |
Conceitualmente, o reshape primeiro achata uma matriz em um vetor unidimensional de valores de dados e depois refina esse vetor em um novo formato. Os argumentos de entrada são uma matriz arbitrária do tipo T, um vetor constante de tempo de compilação de índices de dimensão e um vetor constante de tempo de compilação de tamanhos de dimensão para o resultado.
O vetor dimensions determina o tamanho da matriz de saída. O valor no índice 0 em dimensions é o tamanho da dimensão 0, o valor no índice 1 é o tamanho da dimensão 1 e assim por diante. O produto das dimensões dimensions precisa ser igual ao produto dos tamanhos das dimensões do operando. Ao refinar a matriz recolhida na matriz multidimensional definida por dimensions, as dimensões em dimensions são ordenadas da variação mais lenta (mais importante) para a mais rápida (menos importante).
Por exemplo, seja v uma matriz de 24 elementos:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
Como um caso especial, a mudança de formato pode transformar uma matriz de elemento único em um escalar e vice-versa. Por exemplo,
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
Para informações sobre o StableHLO, consulte StableHLO: remodelagem.
Remodelar (explícito)
Consulte também
XlaBuilder::Reshape.
Reshape(shape, operand)
Operação de redimensionamento que usa uma forma de destino explícita.
| Argumentos | Tipo | Semântica |
|---|---|---|
shape |
Shape |
Formato de saída do tipo T |
operand |
XlaOp |
matriz do tipo T |
Rev (inversa)
Consulte também
XlaBuilder::Rev.
Rev(operand, dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
matriz do tipo T |
dimensions |
ArraySlice<int64> |
dimensões a serem invertidas |
Inverte a ordem dos elementos na matriz operand ao longo do dimensions especificado, gerando uma matriz de saída do mesmo formato. Cada elemento da matriz de operandos em um índice multidimensional é armazenado na matriz de saída em um índice transformado. O índice multidimensional é transformado invertendo o índice em cada dimensão a ser invertida. Por exemplo, se uma dimensão de tamanho N for uma das dimensões de inversão, o índice i será transformado em N - 1 - i.
Um uso da operação Rev é inverter a matriz de peso de convolução ao longo das duas dimensões da janela durante a computação de gradiente em redes neurais.
Para informações sobre o StableHLO, consulte StableHLO - reverse.
RngNormal
Consulte também
XlaBuilder::RngNormal.
Cria uma saída de uma determinada forma com números aleatórios gerados de acordo com a distribuição normal \(N(\mu, \sigma)\) . Os parâmetros \(\mu\) e \(\sigma\), e o formato de saída precisam ter um tipo de ponto flutuante. Além disso, os parâmetros precisam ser valores escalares.
RngNormal(mu, sigma, shape)
| Argumentos | Tipo | Semântica |
|---|---|---|
mu |
XlaOp |
Escalar do tipo T que especifica a média dos números gerados |
sigma
|
XlaOp
|
Escalar do tipo T que especifica o desvio padrão de |
shape |
Shape |
Formato de saída do tipo T |
Para informações sobre o StableHLO, consulte StableHLO: rng.
RngUniform
Consulte também
XlaBuilder::RngUniform.
Cria uma saída de uma determinada forma com números aleatórios gerados de acordo com a distribuição uniforme no intervalo \([a,b)\). Os parâmetros e o tipo de elemento de saída precisam ser um tipo booleano, um tipo integral ou um tipo de ponto flutuante, e os tipos precisam ser consistentes. No momento, os back-ends de CPU e GPU são compatíveis apenas com F64, F32, F16, BF16, S64, U64, S32 e U32. Além disso, os parâmetros precisam ser valores escalares. Se \(b <= a\) o resultado é definido pela implementação.
RngUniform(a, b, shape)
| Argumentos | Tipo | Semântica |
|---|---|---|
a |
XlaOp |
Escalar do tipo T que especifica o limite inferior do intervalo |
b |
XlaOp |
Escalar do tipo T que especifica o limite superior do intervalo |
shape |
Shape |
Formato de saída do tipo T |
Para informações sobre o StableHLO, consulte StableHLO: rng.
RngBitGenerator
Consulte também
XlaBuilder::RngBitGenerator.
Gera uma saída com uma determinada forma preenchida com bits aleatórios uniformes usando o algoritmo especificado (ou o padrão do back-end) e retorna um estado atualizado (com a mesma forma do estado inicial) e os dados aleatórios gerados.
O estado inicial é o estado inicial da geração atual de números aleatórios. e a forma necessária e os valores válidos dependem do algoritmo usado.
A saída é garantida como uma função determinista do estado inicial, mas não é garantida como determinista entre back-ends e diferentes versões de compilador.
RngBitGenerator(algorithm, initial_state, shape)
| Argumentos | Tipo | Semântica |
|---|---|---|
algorithm |
RandomAlgorithm |
Algoritmo PRNG a ser usado. |
initial_state |
XlaOp |
Estado inicial do algoritmo PRNG. |
shape |
Shape |
Formato de saída para dados gerados. |
Valores disponíveis para algorithm:
rng_default: algoritmo específico do back-end com requisitos de formato específicos do back-end.rng_three_fry: algoritmo PRNG baseado em contador ThreeFry. O formatoinitial_stateéu64[2]com valores arbitrários. Salmon et al. SC 2011. Números aleatórios paralelos: tão fácil quanto contar até três.rng_philox: algoritmo Philox para gerar números aleatórios em paralelo. O formatoinitial_stateéu64[3]com valores arbitrários. Salmon et al. SC 2011. Números aleatórios paralelos: tão fácil quanto contar até três.
Para informações sobre o StableHLO, consulte StableHLO: rng_bit_generator.
RngGetAndUpdateState
Consulte também
HloInstruction::CreateRngGetAndUpdateState.
A API das várias operações Rng é decomposta internamente em instruções HLO, incluindo RngGetAndUpdateState.
RngGetAndUpdateState serve como uma primitiva em HLO. Essa operação pode aparecer em despejos de HLO, mas não se destina a ser construída manualmente por usuários finais.
Rodada
Consulte também
XlaBuilder::Round.
Arredondamento elemento a elemento, desempates para longe de zero.
Round(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
RoundNearestAfz
Consulte também
XlaBuilder::RoundNearestAfz.
Realiza o arredondamento de elemento por elemento para o número inteiro mais próximo, resolvendo empates para longe de zero.
RoundNearestAfz(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Para informações sobre o StableHLO, consulte StableHLO: round_nearest_afz.
RoundNearestEven
Consulte também
XlaBuilder::RoundNearestEven.
Arredondamento elemento a elemento, empates para o número par mais próximo.
RoundNearestEven(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Para informações sobre o StableHLO, consulte StableHLO: round_nearest_even.
Rsqrt
Consulte também
XlaBuilder::Rsqrt.
Recíproco elemento a elemento da operação de raiz quadrada x -> 1.0 / sqrt(x).
Rsqrt(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Rsqrt também aceita o argumento opcional result_accuracy:
Rsqrt(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Para informações sobre o StableHLO, consulte StableHLO: rsqrt.
Verificar
Consulte também
XlaBuilder::Scan.
Aplica uma função de redução a uma matriz em uma determinada dimensão, produzindo um estado final e uma matriz de valores intermediários.
Scan(inputs..., inits..., to_apply, scan_dimension,
is_reverse, is_associative)
| Argumentos | Tipo | Semântica |
|---|---|---|
inputs |
Sequência de m XlaOps |
As matrizes a serem verificadas. |
inits |
Sequência de k XlaOps |
Atrelado à sua organização. |
to_apply |
XlaComputation |
Cálculo do tipo i_0, ..., i_{m-1}, c_0, ..., c_{k-1} -> (o_0, ..., o_{n-1}, c'_0, ..., c'_{k-1}). |
scan_dimension |
int64 |
A dimensão a ser verificada. |
is_reverse |
bool |
Se for verdadeiro, a verificação será feita em ordem inversa. |
is_associative |
bool (tristate) |
Se for "true", a operação será associativa. |
A função to_apply é aplicada sequencialmente aos elementos em inputs ao longo de scan_dimension. Se is_reverse for "false", os elementos serão processados na ordem
0 para N-1, em que N é o tamanho de scan_dimension. Se is_reverse for verdadeiro, os elementos serão processados de N-1 até 0.
A função to_apply usa operandos m + k:
melementos atuais deinputs.ktransmitem valores da etapa anterior (ouinitspara o primeiro elemento).
A função to_apply retorna uma tupla de valores n + k:
- Elementos
ndeoutputs. knovos valores de transferência.
A operação de verificação produz uma tupla de valores n + k:
- As matrizes de saída
n, que contêm os valores de saída de cada etapa. - Os valores finais de
ksão carregados após o processamento de todos os elementos.
Os tipos das entradas m precisam corresponder aos tipos dos primeiros parâmetros m de to_apply com uma dimensão de verificação extra. Os tipos das saídas n precisam corresponder aos tipos dos primeiros valores de retorno n de to_apply com uma dimensão de verificação extra. A dimensão de varredura extra entre todas as entradas e saídas precisa ter o mesmo tamanho N. Os tipos dos últimos parâmetros k e os valores de retorno de to_apply, bem como as inicializações k, precisam corresponder.
Por exemplo (m, n, k == 1, N == 3), para o transporte inicial i, entrada [a, b, c], função f(x, c) -> (y, c') e scan_dimension=0, is_reverse=false:
- Etapa 0:
f(a, i) -> (y0, c0) - Etapa 1:
f(b, c0) -> (y1, c1) - Etapa 2:
f(c, c1) -> (y2, c2)
A saída de Scan é ([y0, y1, y2], c2).
Dispersão
Consulte também
XlaBuilder::Scatter.
A operação de dispersão XLA gera uma sequência de resultados que são os valores da matriz de entrada operands, com várias slices (nos índices especificados por scatter_indices) atualizadas com a sequência de valores em updates usando update_computation.
Scatter(operands..., scatter_indices, updates..., update_computation,
dimension_numbers, indices_are_sorted, unique_indices)
| Argumentos | Tipo | Semântica |
|---|---|---|
operands |
Sequência de N XlaOp |
N matrizes de tipos T_0, ..., T_N em que serão dispersos. |
scatter_indices |
XlaOp |
Matriz que contém os índices iniciais das fatias que precisam ser dispersas. |
updates |
Sequência de N XlaOp |
N matrizes de tipos T_0, ..., T_N. updates[i] contém os valores que precisam ser usados para dispersão operands[i]. |
update_computation |
XlaComputation |
Cálculo a ser usado para combinar os valores atuais na matriz de entrada e as atualizações durante a dispersão. Esse cálculo precisa ser do tipo T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N). |
index_vector_dim |
int64 |
A dimensão em scatter_indices que contém os índices iniciais. |
update_window_dims |
ArraySlice<int64> |
O conjunto de dimensões na forma updates que são dimensões da janela. |
inserted_window_dims |
ArraySlice<int64> |
O conjunto de dimensões da janela que precisam ser inseridas na forma updates. |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
Um mapa de dimensões dos índices de dispersão para o espaço de índice do operando. Essa matriz é interpretada como um mapeamento de i para scatter_dims_to_operand_dims[i] . Ela precisa ser um para um e total. |
dimension_number |
ScatterDimensionNumbers |
Números de dimensão para operação de dispersão |
indices_are_sorted |
bool |
Se os índices são classificados pelo autor da chamada. |
unique_indices |
bool |
Se o caller garante que os índices são exclusivos. |
Em que:
- N precisa ser maior ou igual a 1.
operands[0], ...,operands[N-1] precisam ter as mesmas dimensões.updates[0], ...,updates[N-1] precisam ter as mesmas dimensões.- Se
N = 1,Collate(T)seráT. - Se
N > 1,Collate(T_0, ..., T_N)for uma tupla de elementosNdo tipoT.
Se index_vector_dim for igual a scatter_indices.rank, vamos considerar implicitamente que scatter_indices tem uma dimensão 1 final.
Definimos update_scatter_dims do tipo ArraySlice<int64> como o conjunto de dimensões na forma updates que não estão em update_window_dims, em ordem crescente.
Os argumentos de dispersão precisam seguir estas restrições:
Cada matriz
updatesprecisa ter dimensõesupdate_window_dims.size + scatter_indices.rank - 1.Os limites da dimensão
iem cada matrizupdatesprecisam obedecer ao seguinte:- Se
iestiver presente emupdate_window_dims(ou seja, for igual aupdate_window_dims[k] para algumk), o limite da dimensãoiemupdatesnão poderá exceder o limite correspondente deoperandapós a contabilização deinserted_window_dims(ou seja,adjusted_window_bounds[k], em queadjusted_window_boundscontém os limites deoperandcom os limites nos índicesinserted_window_dimsremovidos). - Se
iestiver presente emupdate_scatter_dims(ou seja, igual aupdate_scatter_dims[k] para algumk), o limite da dimensãoiemupdatesprecisará ser igual ao limite correspondente descatter_indices, ignorandoindex_vector_dim(ou seja,scatter_indices.shape.dims[k], sek<index_vector_dimescatter_indices.shape.dims[k+1] caso contrário).
- Se
update_window_dimsprecisa estar em ordem crescente, não ter números de dimensão repetidos e estar no intervalo[0, updates.rank).inserted_window_dimsprecisa estar em ordem crescente, não ter números de dimensão repetidos e estar no intervalo[0, operand.rank).operand.rankprecisa ser igual à soma deupdate_window_dims.sizeeinserted_window_dims.size.scatter_dims_to_operand_dims.sizeprecisa ser igual ascatter_indices.shape.dims[index_vector_dim], e os valores precisam estar no intervalo[0, operand.rank).
Para um determinado índice U em cada matriz updates, o índice I correspondente na matriz operands em que essa atualização precisa ser aplicada é calculado da seguinte maneira:
- Seja
G= {U[k] parakemupdate_scatter_dims}. UseGpara pesquisar um vetor de índiceSna matrizscatter_indicesde modo queS[i] =scatter_indices[Combine(G,i)], em que Combine(A, b) insere b nas posiçõesindex_vector_dimem A. - Crie um índice
SinemoperandusandoSao dispersarSusando o mapascatter_dims_to_operand_dims. De maneira mais formal:Sin[scatter_dims_to_operand_dims[k]] =S[k] sek<scatter_dims_to_operand_dims.size.Sin[_] =0caso contrário.
- Crie um índice
Winem cada matrizoperandsdispersando os índices emupdate_window_dimsemUde acordo cominserted_window_dims. De maneira mais formal:Win[window_dims_to_operand_dims(k)] =U[k] sekestiver emupdate_window_dims, em quewindow_dims_to_operand_dimsé a função monotônica com domínio [0,update_window_dims.size) e intervalo [0,operand.rank) \inserted_window_dims. Por exemplo, seupdate_window_dims.sizefor4,operand.rankfor6einserted_window_dimsfor {0,2}, entãowindow_dims_to_operand_dimsserá {0→1,1→3,2→4,3→5}.Win[_] =0caso contrário.
IéWin+Sin, em que + é a adição de elemento a elemento.
Em resumo, a operação de dispersão pode ser definida da seguinte maneira.
- Inicialize
outputcomoperands, ou seja, para todos os índicesJ, para todos os índicesOna matrizoperands[J]:
output[J][O] =operands[J][O] - Para cada índice
Una matrizupdates[J] e o índice correspondenteOna matrizoperand[J], seOfor um índice válido paraoutput:
((output[0][O], ...,output[N-1][O])=update_computation(output[0][O], ...,output[N-1][O],updates[0][U], ...,updates[N-1][U])
A ordem em que as atualizações são aplicadas não é determinista. Portanto, quando vários índices em updates se referem ao mesmo índice em operands, o valor correspondente em output não é determinista.
O primeiro parâmetro transmitido para update_computation sempre será o valor atual da matriz output, e o segundo parâmetro sempre será o valor da matriz updates. Isso é importante
especialmente para casos em que o update_computation não é comutativo.
Se indices_are_sorted for definido como verdadeiro, o XLA poderá presumir que scatter_indices será classificado (em ordem crescente, após dispersar os valores de acordo com scatter_dims_to_operand_dims) pelo usuário. Caso contrário, a semântica será definida pela implementação.
Se unique_indices for definido como verdadeiro, o XLA poderá presumir que todos os elementos dispersos são únicos. Assim, a XLA pode usar operações não atômicas. Se unique_indices for definido como verdadeiro e os índices que estão sendo dispersos não forem exclusivos, a semântica será definida pela implementação.
Informalmente, a operação de dispersão pode ser vista como um inverso da operação de coleta. Ou seja, a operação de dispersão atualiza os elementos na entrada extraídos pela operação de coleta correspondente.
Para uma descrição informal detalhada e exemplos, consulte a seção "Descrição informal" em Gather.
Para informações sobre o StableHLO, consulte StableHLO: scatter.
Dispersão – Exemplo 1 – StableHLO
Na imagem acima, cada linha da tabela é um exemplo de um índice de atualização. Vamos analisar etapa por etapa da esquerda(Atualizar índice) para a direita(Índice de resultados):
A entrada input tem o formato S32[2,3,4,2]. scatter_indices tem o formato S64[2,2,3,2]. updates tem o formato S32[2,2,3,1,2].
Atualizar índice) Como parte da entrada, recebemos update_window_dims:[3,4]. Isso indica que a dimensão 3 e a dimensão 4 de updates são dimensões de janela, destacadas em amarelo. Isso nos permite derivar que update_scatter_dims = [0,1,2].
Atualizar índice de dispersão) Mostra o updated_scatter_dims extraído para cada um.
(O não amarelo da coluna "Atualizar índice")
Índice inicial) Analisando a imagem do tensor scatter_indices, podemos ver que nossos valores da etapa anterior (índice de dispersão de atualização) nos dão a localização do índice inicial. Em index_vector_dim, também é informada a dimensão do starting_indices que contém os índices iniciais, que, para scatter_indices, é a dimensão 3 com tamanho 2.
Full Start Index) scatter_dims_to_operand_dims = [2,1] informa que o primeiro elemento do vetor de índice vai para a dimensão do operando 2. O segundo elemento do vetor de índice vai para a dimensão do operando 1. As dimensões restantes do operando são preenchidas com 0.
Índice de lote completo) Podemos ver que a área roxa destacada aparece nesta coluna(índice de lote completo), na coluna de índice de dispersão de atualização e na coluna de índice de atualização.
Índice de janela completa) calculado com base em update_window_dimensions [3,4].
Índice de resultado: a adição de índice de início completo, índice de lote completo e índice de janela completa no tensor operand. Observe que as regiões destacadas em verde também correspondem à figura operand. A última linha é ignorada porque está fora do tensor operand.
Selecionar
Consulte também
XlaBuilder::Select.
Cria uma matriz de saída com base nos elementos de duas matrizes de entrada, de acordo com os valores de uma matriz de predicado.
Select(pred, on_true, on_false)
| Argumentos | Tipo | Semântica |
|---|---|---|
pred |
XlaOp |
array do tipo PRED |
on_true |
XlaOp |
matriz do tipo T |
on_false |
XlaOp |
matriz do tipo T |
As matrizes on_true e on_false precisam ter o mesmo formato. Essa também é a forma da matriz de saída. A matriz pred precisa ter a mesma dimensionalidade que on_true e on_false, com o tipo de elemento PRED.
Para cada elemento P de pred, o elemento correspondente da matriz de saída é extraído de on_true se o valor de P for true e de on_false se o valor de P for false. Como uma forma restrita de transmissão,
pred pode ser um escalar do tipo PRED. Nesse caso, a matriz de saída é extraída
inteiramente de on_true se pred for true, e de on_false se pred for
false.
Exemplo com pred não escalar:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
Exemplo com pred escalar:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
Seleções entre tuplas são aceitas. As tuplas são consideradas tipos escalares para essa finalidade. Se on_true e on_false forem tuplas (que precisam ter o mesmo formato), pred terá que ser um escalar do tipo PRED.
Para informações sobre o StableHLO, consulte StableHLO: selecionar
SelectAndScatter
Consulte também
XlaBuilder::SelectAndScatter.
Essa operação pode ser considerada uma operação composta que primeiro calcula ReduceWindow na matriz operand para selecionar um elemento de cada janela e, em seguida, dispersa a matriz source nos índices dos elementos selecionados para construir uma matriz de saída com o mesmo formato da matriz de operandos. A função binária select é usada para selecionar um elemento de cada janela aplicando-o em todas elas. Ela é chamada com a propriedade de que o vetor de índice do primeiro parâmetro é lexicograficamente menor que o vetor de índice do segundo parâmetro. A função select retorna true se o primeiro parâmetro for selecionado e false se o segundo parâmetro for selecionado. Além disso, a função precisa manter a transitividade (ou seja, se select(a, b) e select(b, c) forem true, select(a, c) também será true) para que o elemento selecionado não dependa da ordem dos elementos percorridos em uma determinada janela.
A função scatter é aplicada a cada índice selecionado na matriz de saída. Ela
usa dois parâmetros escalares:
- Valor atual no índice selecionado da matriz de saída
- O valor de dispersão de
sourceque se aplica ao índice selecionado
Ele combina os dois parâmetros e retorna um valor escalar usado para atualizar o valor no índice selecionado na matriz de saída. Inicialmente, todos os índices da matriz de saída são definidos como init_value.
A matriz de saída tem o mesmo formato da matriz operand, e a matriz source precisa ter o mesmo formato do resultado da aplicação de uma operação ReduceWindow na matriz operand. O SelectAndScatter pode ser usado para fazer a backpropagation dos valores de gradiente de uma camada de pooling em uma rede neural.
SelectAndScatter(operand, select, window_dimensions, window_strides, padding,
source, init_value, scatter)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand
|
XlaOp
|
matriz do tipo T em que as janelas deslizam |
select
|
XlaComputation
|
cálculo binário do tipo T, T
-> PRED, a ser aplicado a todos os elementos em cada janela; retorna true se o primeiro parâmetro for selecionado e false se o segundo parâmetro for selecionado |
window_dimensions
|
ArraySlice<int64>
|
matriz de números inteiros para valores de dimensão da janela |
window_strides
|
ArraySlice<int64>
|
matriz de números inteiros para valores de stride da janela |
padding
|
Padding
|
tipo de padding para janela (Padding::kSame ou Padding::kValid) |
source
|
XlaOp
|
matriz do tipo T com os valores a serem dispersos |
init_value
|
XlaOp
|
valor escalar do tipo T para o valor inicial da matriz de saída |
scatter
|
XlaComputation
|
cálculo binário do tipo T, T
-> T para aplicar cada elemento de origem de dispersão com o elemento de destino |
A figura abaixo mostra exemplos de uso de SelectAndScatter, com a função select calculando o valor máximo entre os parâmetros. Quando as janelas se sobrepõem, como na figura (2) abaixo, um índice da matriz operand pode ser selecionado várias vezes por janelas diferentes. Na figura, o elemento de valor 9 é selecionado pelas duas janelas de cima (azul e vermelha), e a função de adição binária scatter produz o elemento de saída de valor 8 (2 + 6).
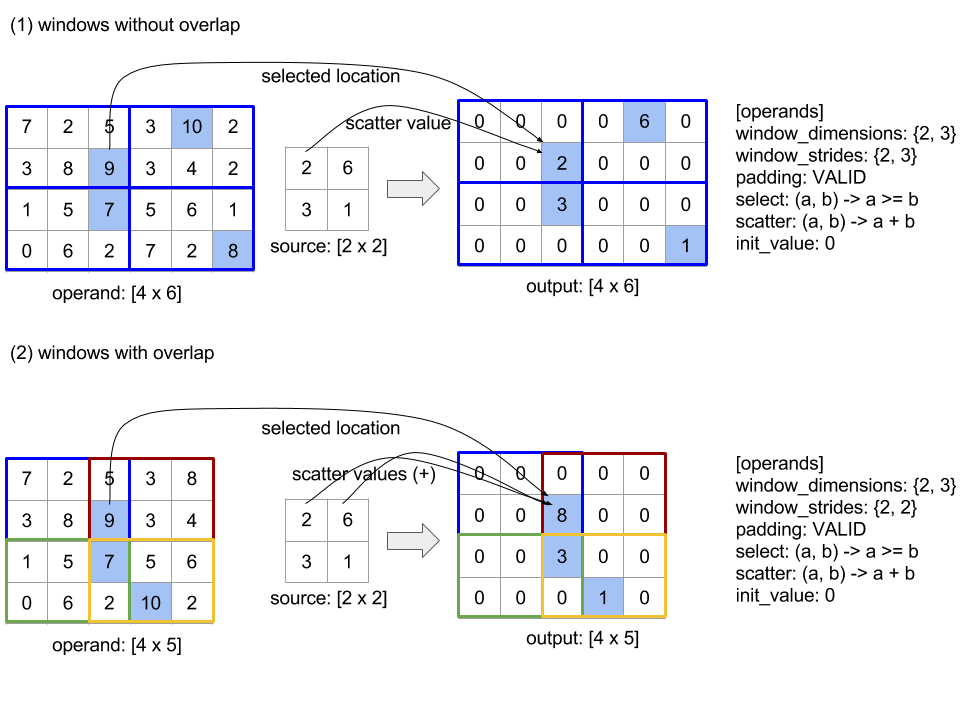
A ordem de avaliação da função scatter é arbitrária e pode ser não determinística. Portanto, a função scatter não pode ser muito sensível à reassociação. Consulte a discussão sobre associatividade no contexto de Reduce para mais detalhes.
Para informações sobre o StableHLO, consulte StableHLO: select_and_scatter.
Enviar
Consulte também
XlaBuilder::Send.
Send, SendWithTokens e SendToHost são operações que servem como
primitivos de comunicação em HLO. Essas operações geralmente aparecem em despejos de HLO como parte de entrada/saída de baixo nível ou transferência entre dispositivos, mas não devem ser construídas manualmente pelos usuários finais.
Send(operand, handle)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
dados a serem enviados (matriz do tipo T) |
handle |
ChannelHandle |
identificador exclusivo para cada par de envio/recebimento |
Envia os dados do operando especificado para uma instrução Recv em outro cálculo que compartilha o mesmo identificador de canal. Não retorna dados.
Semelhante à operação Recv, a API cliente da operação Send
representa a comunicação síncrona e é decomposta internamente em duas instruções
HLO (Send e SendDone) para permitir transferências de dados assíncronas. Consulte também HloInstruction::CreateSend e HloInstruction::CreateSendDone.
Send(HloInstruction operand, int64 channel_id)
Inicia uma transferência assíncrona do operando para os recursos alocados pela
instrução Recv com o mesmo ID do canal. Retorna um contexto, que é
usado por uma instrução SendDone a seguir para aguardar a conclusão da
transferência de dados. O contexto é uma tupla de {operando (formato), identificador de solicitação (U32)} e só pode ser usado por uma instrução SendDone.
Para informações sobre o StableHLO, consulte StableHLO: send.
SendDone
Consulte também
HloInstruction::CreateSendDone.
SendDone(HloInstruction context)
Dado um contexto criado por uma instrução Send, aguarda a conclusão da transferência de dados. A instrução não retorna dados.
Programação de instruções do canal
A ordem de execução das quatro instruções para cada canal (Recv, RecvDone, Send, SendDone) é a seguinte.
Recvacontece antes deSendSendacontece antes deRecvDoneRecvacontece antes deRecvDoneSendacontece antes deSendDone
Quando os compiladores de back-end geram uma programação linear para cada computação que se comunica por instruções de canal, não pode haver ciclos entre as computações. Por exemplo, as programações abaixo causam impasses.
SetDimensionSize
Consulte também
XlaBuilder::SetDimensionSize.
Define o tamanho dinâmico da dimensão especificada de XlaOp. O operando precisa ter o formato de matriz.
SetDimensionSize(operand, val, dimension)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
Matriz de entrada n-dimensional. |
val |
XlaOp |
int32 que representa o tamanho dinâmico de tempo de execução. |
dimension
|
int64
|
Um valor no intervalo [0, n) que especifica a dimensão. |
Transmita o operando como resultado, com a dimensão dinâmica rastreada pelo compilador.
Valores de padding serão ignorados pelas operações de redução downstream.
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
ShiftLeft
Consulte também
XlaBuilder::ShiftLeft.
Executa uma operação de deslocamento à esquerda bit a bit em lhs por rhs número de bits.
ShiftLeft(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para ShiftLeft:
ShiftLeft(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO: shift_left.
ShiftRightArithmetic
Consulte também
XlaBuilder::ShiftRightArithmetic.
Realiza uma operação de deslocamento aritmético à direita com elementos em lhs por rhs número de bits.
ShiftRightArithmetic(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte a transmissão de diferentes dimensões para ShiftRightArithmetic:
ShiftRightArithmetic(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO: shift_right_arithmetic.
ShiftRightLogical
Consulte também
XlaBuilder::ShiftRightLogical.
Executa a operação de deslocamento lógico à direita no nível do elemento em lhs por rhs número de bits.
ShiftRightLogical(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para ShiftRightLogical:
ShiftRightLogical(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO - shift_right_logical.
Assinar
Consulte também
XlaBuilder::Sign.
Sign(operand) Operação de sinal com elementos x -> sgn(x) em que
\[\text{sgn}(x) = \begin{cases} -1 & x < 0\\ -0 & x = -0\\ NaN & x = NaN\\ +0 & x = +0\\ 1 & x > 0 \end{cases}\]
usando o operador de comparação do tipo de elemento de operand.
Sign(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Para informações sobre o StableHLO, consulte StableHLO: sign.
Sin
Seno x -> sin(x) Sin(operand) elemento a elemento.
Consulte também
XlaBuilder::Sin.
Sin(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
A função seno também aceita o argumento opcional result_accuracy:
Sin(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Para informações sobre o StableHLO, consulte StableHLO: seno.
Fração
Consulte também
XlaBuilder::Slice.
A extração de fatias extrai uma submatriz da matriz de entrada. O subconjunto tem o mesmo número de dimensões da entrada e contém os valores dentro de uma caixa delimitadora na matriz de entrada, em que as dimensões e os índices da caixa delimitadora são fornecidos como argumentos para a operação de segmentação.
Slice(operand, start_indices, limit_indices, strides)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
Matriz N-dimensional do tipo T |
start_indices
|
ArraySlice<int64>
|
Lista de N números inteiros que contém os índices iniciais da fatia para cada dimensão. Os valores precisam ser maiores ou iguais a zero. |
limit_indices
|
ArraySlice<int64>
|
Lista de N números inteiros que contém os índices finais (exclusivos) da fração para cada dimensão. Cada valor precisa ser maior ou igual ao valor start_indices respectivo da dimensão e menor ou igual ao tamanho dela. |
strides
|
ArraySlice<int64>
|
Lista de N números inteiros que decide a
taxa de entrada da fatia. A fatia escolhe todos os elementos strides[d] na dimensão d. |
Exemplo unidimensional:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4})
// Result: {2.0, 3.0}
Exemplo bidimensional:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3})
// Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
Para informações sobre o StableHLO, consulte StableHLO: slice.
Classificar
Consulte também
XlaBuilder::Sort.
Sort(operands, comparator, dimension, is_stable)
| Argumentos | Tipo | Semântica |
|---|---|---|
operands |
ArraySlice<XlaOp> |
Os operandos a serem classificados. |
comparator |
XlaComputation |
O cálculo do comparador a ser usado. |
dimension |
int64 |
A dimensão ao longo da qual classificar. |
is_stable |
bool |
Indica se a classificação estável deve ser usada. |
Se apenas um operando for fornecido:
Se o operando for um tensor unidimensional (uma matriz), o resultado será uma matriz classificada. Se você quiser classificar a matriz em ordem crescente, o comparador precisa realizar uma comparação "menor que". Formalmente, depois que a matriz é classificada, ela é válida para todas as posições de índice
i, jcomi < jquecomparator(value[i], value[j]) = comparator(value[j], value[i]) = falseoucomparator(value[i], value[j]) = true.Se o operando tiver um número maior de dimensões, ele será classificado ao longo da dimensão fornecida. Por exemplo, para um tensor bidimensional (uma matriz), um valor de dimensão
0classifica de forma independente todas as colunas, e um valor de dimensão1classifica de forma independente cada linha. Se nenhum número de dimensão for fornecido, a última dimensão será escolhida por padrão. Para a dimensão classificada, a mesma ordem de classificação é aplicada como no caso unidimensional.
Se operandos n > 1 forem fornecidos:
Todos os operandos
nprecisam ser tensores com as mesmas dimensões. Os tipos de elementos dos tensores podem ser diferentes.Todos os operandos são classificados juntos, não individualmente. Conceitualmente, os operandos são tratados como uma tupla. Ao verificar se os elementos de cada operando nas posições de índice
iejprecisam ser trocados, o comparador é chamado com parâmetros escalares2 * n, em que o parâmetro2 * kcorresponde ao valor na posiçãoido operandok-th, e o parâmetro2 * k + 1corresponde ao valor na posiçãojdo operandok-th. Normalmente, o comparador compara os parâmetros2 * ke2 * k + 1entre si e pode usar outros pares de parâmetros como critério de desempate.O resultado é uma tupla que consiste nos operandos em ordem classificada (ao longo da dimensão fornecida, como acima). O operando
i-thda tupla corresponde ao operandoi-thde "Sort".
Por exemplo, se houver três operandos operand0 = [3, 1], operand1 = [42, 50], operand2 = [-3.0, 1.1] e o comparador comparar apenas os valores de operand0 com "menor que", a saída da classificação será a tupla ([1, 3], [50, 42], [1.1, -3.0]).
Se is_stable for definido como verdadeiro, a classificação será estável. Ou seja, se houver elementos considerados iguais pelo comparador, a ordem relativa dos valores iguais será preservada. Dois elementos e1 e e2 são iguais se e somente se comparator(e1, e2) = comparator(e2, e1) = false. Por padrão, is_stable é definido como "false".
Para mais informações sobre o StableHLO, consulte StableHLO: classificação.
Sqrt
Consulte também
XlaBuilder::Sqrt.
Operação de raiz quadrada com elementos x -> sqrt(x).
Sqrt(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
Sqrt também é compatível com o argumento opcional result_accuracy:
Sqrt(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações. |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Para informações sobre o StableHLO, consulte StableHLO: sqrt.
Sub
Consulte também
XlaBuilder::Sub.
Executa a subtração elemento a elemento de lhs e rhs.
Sub(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para Sub:
Sub(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO - subtract.
Marrom-médio
Consulte também
XlaBuilder::Tan.
Tangente x -> tan(x) por elemento.
Tan(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
A tangente também aceita o argumento opcional result_accuracy:
Tan(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Para informações sobre o StableHLO, consulte StableHLO: tan.
Tanh
Consulte também
XlaBuilder::Tanh.
Tangente hiperbólica x -> tanh(x) por elemento.
Tanh(operand)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
A função tanh também é compatível com o argumento opcional result_accuracy:
Tanh(operand, result_accuracy)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando da função |
result_accuracy
|
opcional ResultAccuracy
|
Os tipos de precisão que o usuário pode solicitar para operações unárias com várias implementações |
Para mais informações sobre result_accuracy, consulte
Precisão dos resultados.
Para informações sobre o StableHLO, consulte StableHLO: tanh.
TopK
Consulte também
XlaBuilder::TopK.
TopK encontra os valores e índices dos k maiores ou menores elementos da última dimensão do tensor especificado.
TopK(operand, k, largest)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand
|
XlaOp
|
O tensor de onde extrair os k elementos principais.
O tensor precisa ter uma ou mais dimensões. O tamanho da última dimensão do tensor precisa ser maior ou igual a k. |
k |
int64 |
O número de elementos a serem extraídos. |
largest
|
bool
|
Se extrair os elementos k maiores ou menores. |
Para um tensor de entrada unidimensional (uma matriz), encontra as kmaiores ou menores
entradas na matriz e gera uma tupla de duas matrizes (values, indices). Assim, values[j] é a jª maior/menor entrada em operand, e o índice dela é indices[j].
Para um tensor de entrada com mais de uma dimensão, calcula as principais entradas k ao longo da última dimensão, preservando todas as outras dimensões (linhas) na saída.
Assim, para um operando de forma [A, B, ..., P, Q] em que Q >= k, a saída é uma tupla (values, indices) em que:
values.shape = indices.shape = [A, B, ..., P, k]
Se dois elementos em uma linha forem iguais, o elemento de índice mais baixo vai aparecer primeiro.
Transposição
Consulte também a operação tf.reshape.
Transpose(operand, permutation)
| Argumentos | Tipo | Semântica |
|---|---|---|
operand |
XlaOp |
O operando a ser transposto. |
permutation |
ArraySlice<int64> |
Como permutar as dimensões. |
Permuta as dimensões do operando com a permutação especificada, de modo que ∀ i . 0 ≤ i < number of dimensions ⇒
input_dimensions[permutation[i]] = output_dimensions[i].
Isso é o mesmo que Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)).
Para informações sobre o StableHLO, consulte StableHLO: transposição.
TriangularSolve
Consulte também
XlaBuilder::TriangularSolve.
Resolve sistemas de equações lineares com matrizes de coeficientes triangulares inferior ou superior por substituição direta ou inversa. Transmitindo ao longo das principais dimensões, essa rotina resolve um dos sistemas de matrizes op(a) * x =
b ou x * op(a) = b para a variável x, considerando a e b, em que op(a) é op(a) = a, op(a) = Transpose(a) ou op(a) = Conj(Transpose(a)).
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| Argumentos | Tipo | Semântica |
|---|---|---|
a
|
XlaOp
|
uma matriz com mais de duas dimensões de um tipo complexo ou de ponto flutuante com a forma [..., M,
M]. |
b
|
XlaOp
|
uma matriz com mais de duas dimensões do mesmo tipo e formato [..., M, K] se left_side for verdadeiro, [..., K, M] caso contrário. |
left_side
|
bool
|
indica se é para resolver um sistema da forma op(a) * x = b (true) ou x *
op(a) = b (false). |
lower
|
bool
|
se o triângulo superior ou inferior de a será usado. |
unit_diagonal
|
bool
|
Se true, os elementos diagonais de a serão considerados 1 e não serão acessados. |
transpose_a
|
Transpose
|
se a será usado como está, transposto ou conjugado transposto. |
Os dados de entrada são lidos apenas do triângulo inferior/superior de a, dependendo do valor de lower. Os valores do outro triângulo são ignorados. Os dados de saída são retornados no mesmo triângulo. Os valores no outro triângulo são definidos pela implementação e podem ser qualquer coisa.
Se o número de dimensões de a e b for maior que 2, elas serão tratadas como lotes de matrizes, em que todas, exceto as duas dimensões secundárias, são dimensões de lote. a e b precisam ter dimensões de lote iguais.
Para informações sobre o StableHLO, consulte StableHLO: triangular_solve.
Tupla
Consulte também
XlaBuilder::Tuple.
Uma tupla que contém um número variável de identificadores de dados, cada um com seu próprio formato.
Tuple(elements)
| Argumentos | Tipo | Semântica |
|---|---|---|
elements |
vetor de XlaOp |
Matriz N do tipo T |
Isso é análogo a std::tuple em C++. Conceitualmente:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
As tuplas podem ser desconstruídas (acessadas) usando a operação GetTupleElement.
Para informações sobre o StableHLO, consulte StableHLO: tupla.
Embora
Consulte também
XlaBuilder::While.
While(condition, body, init)
| Argumentos | Tipo | Semântica |
|---|---|---|
condition
|
XlaComputation
|
XlaComputation do tipo T -> PRED que
define a condição de encerramento do
loop. |
body
|
XlaComputation
|
XlaComputation do tipo T -> T que
define o corpo do loop. |
init
|
T
|
Valor inicial para o parâmetro de condition e body. |
Executa sequencialmente o body até que o condition falhe. Isso é semelhante a um loop while típico em muitas outras linguagens, exceto pelas diferenças e restrições listadas abaixo.
- Um nó
Whileretorna um valor do tipoT, que é o resultado da última execução dobody. - A forma do tipo
Té determinada de maneira estática e precisa ser a mesma em todas as iterações.
Os parâmetros T dos cálculos são inicializados com o valor init na primeira iteração e são atualizados automaticamente para o novo resultado de body em cada iteração subsequente.
Um dos principais casos de uso do nó While é implementar a execução repetida do treinamento em redes neurais. O pseudocódigo simplificado é mostrado abaixo com um gráfico que representa a computação. O código pode ser encontrado em
while_test.cc.
O tipo T neste exemplo é um Tuple que consiste em um int32 para a contagem de iterações e um vector[10] para o acumulador. Para 1.000 iterações, o loop continua adicionando um vetor constante ao acumulador.
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}
Para informações sobre o StableHLO, consulte StableHLO: while.
Xor
Consulte também
XlaBuilder::Xor.
Executa XOR elemento a elemento de lhs e rhs.
Xor(lhs, rhs)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
As formas dos argumentos precisam ser semelhantes ou compatíveis. Consulte a documentação de transmissão para saber o que significa a compatibilidade de formas. O resultado de uma operação tem uma forma que é o resultado da transmissão das duas matrizes de entrada. Nessa variante, as operações entre matrizes de ranks diferentes não são aceitas, a menos que um dos operandos seja um escalar.
Existe uma variante alternativa com suporte de transmissão de dimensões diferentes para Xor:
Xor(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semântica |
|---|---|---|
| lhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| rhs | XlaOp | Operando do lado esquerdo: matriz do tipo T |
| broadcast_dimension | ArraySlice |
A qual dimensão na forma de destino cada dimensão da forma de operando corresponde |
Essa variante da operação deve ser usada para operações aritméticas entre matrizes de ranks diferentes (como adicionar uma matriz a um vetor).
O operando broadcast_dimensions adicional é uma fração de números inteiros que especifica as dimensões a serem usadas para transmissão dos operandos. A semântica é descrita em detalhes na página de transmissão.
Para informações sobre o StableHLO, consulte StableHLO: xor.








