Poniżej opisujemy semantykę operacji zdefiniowanych w interfejsie XlaBuilder. Zazwyczaj te operacje są mapowane 1:1 na operacje zdefiniowane w interfejsie RPC w xla_data.proto.
Uwaga dotycząca nazewnictwa: uogólniony typ danych XLA to tablica N-wymiarowa zawierająca elementy o jednolitym typie (np. 32-bitowe liczby zmiennoprzecinkowe). W dokumentacji termin tablica oznacza tablicę o dowolnej liczbie wymiarów. Dla wygody przypadki specjalne mają bardziej szczegółowe i znane nazwy. Na przykład wektor to tablica 1-wymiarowa, a macierz to tablica 2-wymiarowa.
Dowiedz się więcej o strukturze operacji w sekcjach Kształty i układ oraz Układ kafelkowy.
Brzuch
Zobacz też XlaBuilder::Abs.
Wartość bezwzględna każdego elementu x -> |x|.
Abs(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Informacje o StableHLO znajdziesz w artykule StableHLO – abs.
Dodaj
Zobacz też XlaBuilder::Add.
Wykonuje dodawanie elementów lhs i rhs.
Add(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywny wariant z obsługą emisji w różnych wymiarach w przypadku dodatku:
Add(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – dodawanie.
AddDependency
Zobacz też HloInstruction::AddDependency.
AddDependency może pojawiać się w zrzutach HLO, ale nie jest przeznaczony do ręcznego tworzenia przez użytkowników.
AfterAll
Zobacz też XlaBuilder::AfterAll.
Funkcja AfterAll przyjmuje zmienną liczbę tokenów i zwraca jeden token. Tokeny to typy pierwotne, które można przekazywać między operacjami wywołującymi efekty uboczne, aby wymusić kolejność. AfterAll może być używany jako łącznik tokenów do zamawiania operacji po wykonaniu zestawu operacji.
AfterAll(tokens)
| Argumenty | Typ | Semantyka |
|---|---|---|
tokens |
wektor XlaOp |
zmienna liczba tokenów, |
Więcej informacji o StableHLO znajdziesz w artykule StableHLO - after_all.
AllGather
Zobacz też XlaBuilder::AllGather.
Łączy repliki.
AllGather(operand, all_gather_dimension, shard_count, replica_groups,
channel_id, layout, use_global_device_ids)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand
|
XlaOp
|
Tablica do łączenia w wielu replikach |
all_gather_dimension |
int64 |
Wymiar łączenia |
shard_count
|
int64
|
rozmiar każdej grupy replik, |
replica_groups
|
wektor wektorów
int64 |
Grupy, między którymi wykonywane jest łączenie |
channel_id
|
opcjonalne
ChannelHandle |
Opcjonalny identyfikator kanału do komunikacji między modułami |
layout
|
opcjonalne Layout
|
Tworzy wzorzec układu, który przechwyci dopasowany układ w argumencie. |
use_global_device_ids
|
opcjonalne bool
|
Zwraca wartość „prawda”, jeśli identyfikatory w konfiguracji ReplicaGroup reprezentują identyfikator globalny. |
replica_groupsto lista grup replik, między którymi wykonywane jest łączenie (identyfikator repliki dla bieżącej repliki można pobrać za pomocą funkcjiReplicaId). Kolejność replik w każdej grupie określa kolejność, w jakiej ich dane wejściowe znajdują się w wyniku.replica_groupsmusi być puste (w takim przypadku wszystkie repliki należą do jednej grupy, uporządkowanej od0doN - 1) lub zawierać tyle samo elementów co liczba replik. Na przykładreplica_groups = {0, 2}, {1, 3}wykonuje łączenie między replikami0i2oraz1i3.shard_countto rozmiar każdej grupy replik. Jest to konieczne w przypadku, gdy polereplica_groupsjest puste.channel_idjest używany do komunikacji między modułami: tylko operacje z tym samymchannel_idmogą się ze sobą komunikować.all-gatheruse_global_device_idsZwraca wartość „prawda”, jeśli identyfikatory w konfiguracji ReplicaGroup reprezentują identyfikator globalny w postaci (replica_id * partition_count + partition_id) zamiast identyfikatora repliki. Umożliwia to bardziej elastyczne grupowanie urządzeń, jeśli ta operacja all-reduce jest wykonywana zarówno w ramach partycji, jak i replik.
Kształt wyjściowy to kształt wejściowy powiększony all_gather_dimensionshard_count razy. Jeśli na przykład są 2 repliki, a operand ma odpowiednio wartości [1.0, 2.5] i [3.0, 5.25] na tych 2 replikach, to wartość wyjściowa tego działania, w którym all_gather_dim to 0, będzie wynosić [1.0, 2.5, 3.0,5.25] na obu replikach.
Interfejs API funkcji AllGather jest wewnętrznie rozkładany na 2 instrukcje HLO (AllGatherStart i AllGatherDone).
Zobacz też HloInstruction::CreateAllGatherStart.
AllGatherStart, AllGatherDone służą jako elementy podstawowe w HLO. Te operacje mogą pojawiać się w zrzutach HLO, ale nie są przeznaczone do ręcznego tworzenia przez użytkowników.
Informacje o StableHLO znajdziesz w artykule StableHLO – all_gather.
AllReduce
Zobacz też XlaBuilder::AllReduce.
Wykonuje obliczenia niestandardowe na replikach.
AllReduce(operand, computation, replica_groups, channel_id,
shape_with_layout, use_global_device_ids)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand
|
XlaOp
|
Tablica lub niepusta krotka tablic do zredukowania w replikach. |
computation |
XlaComputation |
Obliczanie redukcji |
replica_groups
|
ReplicaGroup wektor
|
Grupy, między którymi przeprowadzane są redukcje |
channel_id
|
opcjonalne
ChannelHandle |
Opcjonalny identyfikator kanału do komunikacji między modułami |
shape_with_layout
|
opcjonalne Shape
|
Określa układ przesyłanych danych. |
use_global_device_ids
|
opcjonalne bool
|
Zwraca wartość „prawda”, jeśli identyfikatory w konfiguracji ReplicaGroup reprezentują identyfikator globalny. |
- Jeśli
operandjest krotką tablic, operacja all-reduce jest wykonywana na każdym elemencie krotki. replica_groupsto lista grup replik, między którymi przeprowadzana jest redukcja (identyfikator repliki dla bieżącej repliki można pobrać za pomocą funkcjiReplicaId). Listareplica_groupsmusi być pusta (w takim przypadku wszystkie repliki należą do jednej grupy) lub zawierać tyle samo elementów, ile jest replik. Na przykładreplica_groups = {0, 2}, {1, 3}wykonuje redukcję między replikami0i2oraz1i3.channel_idjest używany do komunikacji między modułami: tylko operacje z tym samymchannel_idmogą się ze sobą komunikować.all-reduceshape_with_layout: wymusza układ operacji AllReduce na podany układ. Służy do zagwarantowania tego samego układu dla grupy operacji AllReduce skompilowanych oddzielnie.use_global_device_idsZwraca wartość „prawda”, jeśli identyfikatory w konfiguracji ReplicaGroup reprezentują identyfikator globalny w postaci (replica_id * partition_count + partition_id) zamiast identyfikatora repliki. Umożliwia to bardziej elastyczne grupowanie urządzeń, jeśli ta operacja all-reduce jest wykonywana zarówno w ramach partycji, jak i replik.
Kształt danych wyjściowych jest taki sam jak kształt danych wejściowych. Jeśli na przykład są 2 repliki, a operand ma wartość [1.0, 2.5] i [3.0, 5.25] odpowiednio na tych 2 replikach, to wartość wyjściowa tego działania i obliczenia sumy wyniesie [4.0, 7.75] na obu replikach. Jeśli dane wejściowe są krotką, dane wyjściowe też będą krotką.
Obliczenie wyniku działania AllReduce wymaga danych wejściowych z każdej repliki, więc jeśli jedna replika wykona węzeł AllReduce więcej razy niż inna, pierwsza z nich będzie czekać w nieskończoność. Ponieważ repliki uruchamiają ten sam program, nie ma wielu sposobów na to, aby tak się stało, ale jest to możliwe, gdy warunek pętli while zależy od danych z infeed, a dane z infeed powodują, że pętla while wykonuje więcej iteracji na jednej replice niż na innej.
Interfejs API funkcji AllReduce jest wewnętrznie rozkładany na 2 instrukcje HLO (AllReduceStart i AllReduceDone).
Zobacz też HloInstruction::CreateAllReduceStart.
AllReduceStart i AllReduceDone są typami prostymi w HLO. Te operacje mogą pojawiać się w zrzutach HLO, ale nie są przeznaczone do ręcznego tworzenia przez użytkowników.
CrossReplicaSum
Zobacz też XlaBuilder::CrossReplicaSum.
Wykonuje AllReduce z obliczeniem sumy.
CrossReplicaSum(operand, replica_groups)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand
|
XlaOp | Tablica lub niepusta krotka tablic do zredukowania w replikach. |
replica_groups
|
wektor wektorów
int64 |
Grupy, między którymi przeprowadzane są redukcje |
Zwraca sumę wartości operandu w każdej podgrupie replik. Wszystkie repliki dostarczają jeden sygnał wejściowy do sumy, a wszystkie repliki otrzymują wynikową sumę dla każdej podgrupy.
AllToAll
Zobacz też XlaBuilder::AllToAll.
AllToAll to operacja zbiorowa, która wysyła dane ze wszystkich rdzeni do wszystkich rdzeni. Składa się z 2 faz:
- Faza rozproszenia. Na każdym rdzeniu operand jest dzielony na
split_countbloków wzdłuż osisplit_dimensions, a bloki są rozpraszane na wszystkie rdzenie, np. i-ty blok jest wysyłany do i-tego rdzenia. - Faza zbierania. Każdy rdzeń łączy otrzymane bloki wzdłuż osi
concat_dimension.
Uczestniczące rdzenie można skonfigurować:
replica_groups: każda grupa replik zawiera listę identyfikatorów replik uczestniczących w obliczeniach (identyfikator repliki bieżącej można pobrać za pomocą funkcjiReplicaId). Funkcja AllToAll będzie stosowana w podgrupach w określonej kolejności. Na przykładreplica_groups = { {1,2,3}, {4,5,0} }oznacza, że operacja AllToAll zostanie zastosowana w replikach{1, 2, 3}i w fazie zbierania, a otrzymane bloki zostaną połączone w tej samej kolejności 1, 2, 3. Następnie w replikach 4, 5, 0 zostanie zastosowana kolejna operacja AllToAll, a kolejność łączenia będzie wynosić 4, 5, 0. Jeśli polereplica_groupsjest puste, wszystkie repliki należą do jednej grupy w kolejności ich występowania.
Wymagania wstępne:
- Rozmiar wymiaru operandu w
split_dimensionjest podzielny przezsplit_count. - Kształt operandu nie jest krotką.
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups, layout, channel_id)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
n-wymiarowa tablica wejściowa |
split_dimension
|
int64
|
Wartość z przedziału
[0,n), która określa
wymiar, wzdłuż którego
dzielony jest operand. |
concat_dimension
|
int64
|
Wartość z przedziału
[0,n), która określa
wymiar, wzdłuż którego
łączone są
bloki podziału. |
split_count
|
int64
|
Liczba rdzeni, które biorą udział w tej operacji. Jeśli pole replica_groups jest puste, powinna to być liczba replik. W przeciwnym razie powinna być równa liczbie replik w każdej grupie. |
replica_groups
|
ReplicaGroupwektor
|
Każda grupa zawiera listę identyfikatorów replik. |
layout |
opcjonalne Layout |
układ pamięci określony przez użytkownika, |
channel_id
|
opcjonalne ChannelHandle
|
unikalny identyfikator każdej pary wysyłania/odbierania; |
Więcej informacji o kształtach i układach znajdziesz w xla::shapes.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – all_to_all.
AllToAll – przykład 1.
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(
x,
/*split_dimension=*/ 1,
/*concat_dimension=*/ 0,
/*split_count=*/ 4);
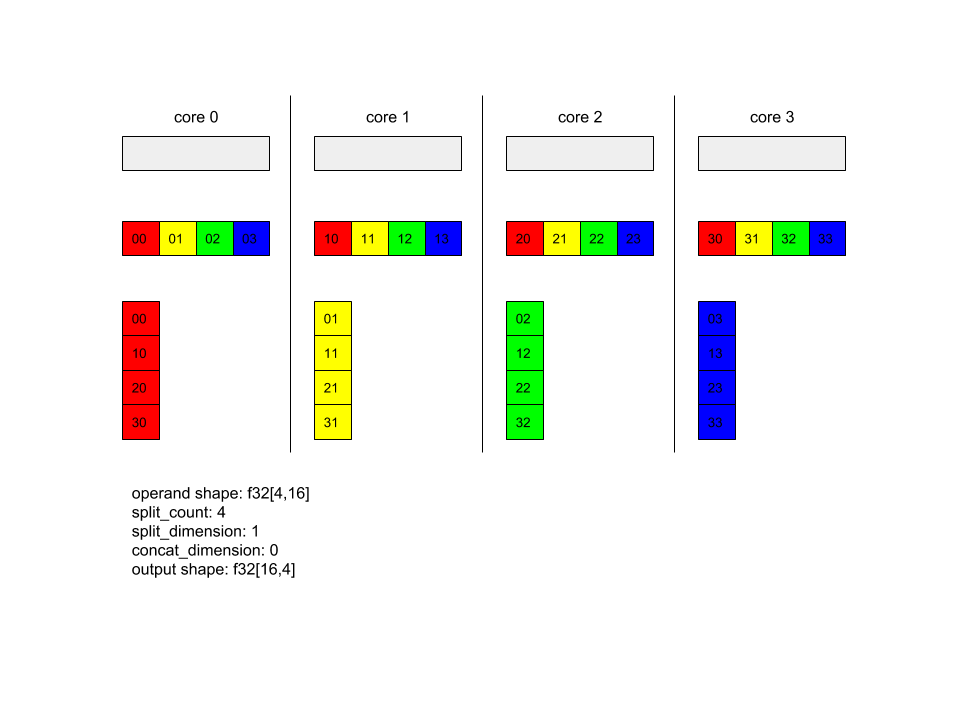
W przykładzie powyżej w operacji Alltoall uczestniczą 4 rdzenie. Na każdym rdzeniu operand jest dzielony na 4 części wzdłuż wymiaru 1, więc każda część ma kształt f32[4,4]. 4 części są rozproszone na wszystkie rdzenie. Następnie każdy rdzeń łączy otrzymane części wzdłuż wymiaru 0 w kolejności rdzeń 0–4. Dane wyjściowe na każdym rdzeniu mają kształt f32[16,4].
AllToAll - Example 2 - StableHLO
W przykładzie powyżej w operacji AllToAll uczestniczą 2 repliki. Na każdej replice operand ma kształt f32[2,4]. Operand jest dzielony na 2 części wzdłuż wymiaru 1, więc każda część ma kształt f32[2,2]. Następnie te 2 części są wymieniane między replikami zgodnie z ich pozycją w grupie replik. Każda replika pobiera odpowiednią część z obu operandów i łączy je wzdłuż wymiaru 0. W rezultacie dane wyjściowe na każdej replice mają kształt f32[4,2].
RaggedAllToAll
Zobacz też XlaBuilder::RaggedAllToAll.
RaggedAllToAll wykonuje zbiorową operację all-to-all, w której dane wejściowe i wyjściowe są tensorami poszarpanymi.
RaggedAllToAll(input, input_offsets, send_sizes, output, output_offsets,
recv_sizes, replica_groups, channel_id)
| Argumenty | Typ | Semantyka |
|---|---|---|
input |
XlaOp |
Tablica N typu T |
input_offsets |
XlaOp |
Tablica N typu T |
send_sizes |
XlaOp |
Tablica N typu T |
output |
XlaOp |
Tablica N typu T |
output_offsets |
XlaOp |
Tablica N typu T |
recv_sizes |
XlaOp |
Tablica N typu T |
replica_groups
|
ReplicaGroup wektor
|
Każda grupa zawiera listę identyfikatorów replik. |
channel_id
|
opcjonalne ChannelHandle
|
unikalny identyfikator każdej pary wysyłania/odbierania; |
Poszarpane tensory są zdefiniowane przez zestaw 3 tensorów:
data: tensordatajest „nierówny” wzdłuż najbardziej zewnętrznego wymiaru, wzdłuż którego każdy indeksowany element ma zmienny rozmiar.offsets: tensoroffsetsindeksuje najbardziej zewnętrzny wymiar tensoradatai reprezentuje początkowe przesunięcie każdego nierównego elementu tensoradata.sizes: tensorsizesreprezentuje rozmiar każdego nierównego elementu tensoradata, przy czym rozmiar jest określony w jednostkach elementów podrzędnych. Podrzędny element jest zdefiniowany jako sufiks kształtu tensora „data” uzyskany przez usunięcie najbardziej zewnętrznego „nierównego” wymiaru.- Tensory
offsetsisizesmuszą mieć ten sam rozmiar.
Przykładowy tensor nierówny:
data: [8,3] =
{ {a,b,c},{d,e,f},{g,h,i},{j,k,l},{m,n,o},{p,q,r},{s,t,u},{v,w,x} }
offsets: [3] = {0, 1, 4}
sizes: [3] = {1, 3, 4}
// Index 'data' at 'offsets'[0], 'sizes'[0]' // {a,b,c}
// Index 'data' at 'offsets'[1], 'sizes'[1]' // {d,e,f},{g,h,i},{j,k,l}
// Index 'data' at 'offsets'[2], 'sizes'[2]' // {m,n,o},{p,q,r},{s,t,u},{v,w,x}
output_offsets musi być podzielony w taki sposób, aby każda replika miała przesunięcia z perspektywy wyjściowej repliki docelowej.
W przypadku i-tego przesunięcia wyjściowego bieżąca replika wyśle aktualizację input[input_offsets[i]:input_offsets[i]+input_sizes[i]] do i-tej repliki, która zostanie zapisana w output_i[output_offsets[i]:output_offsets[i]+send_sizes[i]] w i-tej repliceoutput.
Jeśli na przykład mamy 2 repliki:
replica 0:
input: [1, 2, 2]
output:[0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 2]
output_offsets: [0, 0]
recv_sizes: [1, 1]
replica 1:
input: [3, 4, 0]
output: [0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 1]
output_offsets: [1, 2]
recv_sizes: [2, 1]
// replica 0's result will be: [1, 3, 0, 0]
// replica 1's result will be: [2, 2, 4, 0]
Funkcja ragged all-to-all HLO ma te argumenty:
input: nierówny tensor danych wejściowych.output: tensor danych wyjściowych o nieregularnym kształcie.input_offsets: tensor przesunięć nierównych danych wejściowych.send_sizes: tensor z nierównymi rozmiarami wysyłania.output_offsets: tablica nierównych przesunięć w danych wyjściowych repliki docelowej.recv_sizes: tensor z nierównymi rozmiarami odbioru.
Tensory *_offsets i *_sizes muszą mieć ten sam kształt.
W przypadku tensorów *_offsets i *_sizes obsługiwane są 2 kształty:
[num_devices], gdzie ragged-all-to-all może wysłać co najwyżej 1 aktualizację do każdego urządzenia zdalnego w grupie replik. Na przykład:
for (remote_device_id : replica_group) {
SEND input[input_offsets[remote_device_id]],
output[output_offsets[remote_device_id]],
send_sizes[remote_device_id] }
[num_devices, num_updates]gdzie ragged-all-to-all może wysyłać donum_updatesaktualizacji tego samego urządzenia zdalnego (każda z innym przesunięciem), dla każdego urządzenia zdalnego w grupie replik.
Na przykład:
for (remote_device_id : replica_group) {
for (update_idx : num_updates) {
SEND input[input_offsets[remote_device_id][update_idx]],
output[output_offsets[remote_device_id][update_idx]]],
send_sizes[remote_device_id][update_idx] } }
I
Zobacz też XlaBuilder::And.
Wykonuje operację AND na poszczególnych elementach 2 tensorów lhs i rhs.
And(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywna odmiana z obsługą transmisji o różnych wymiarach dla:
And(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Informacje o StableHLO znajdziesz w artykule StableHLO.
Dane asynchroniczne
Zobacz też HloInstruction::CreateAsyncStart,HloInstruction::CreateAsyncUpdate,HloInstruction::CreateAsyncDone.
AsyncDone, AsyncStart i AsyncUpdate to wewnętrzne instrukcje HLO używane w operacjach asynchronicznych, które służą jako elementy podstawowe w HLO. Te operacje mogą pojawiać się w zrzutach HLO, ale nie są przeznaczone do ręcznego tworzenia przez użytkowników.
Atan2
Zobacz też XlaBuilder::Atan2.
Wykonuje operację atan2 na poszczególnych elementach tensorów lhs i rhs.
Atan2(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywna wersja funkcji Atan2 z obsługą transmisji o różnych wymiarach:
Atan2(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – atan2.
BatchNormGrad
Szczegółowy opis algorytmu znajdziesz też w XlaBuilder::BatchNormGrad i oryginalnym artykule na temat normalizacji wsadowej.
Oblicza gradienty normalizacji wsadowej.
BatchNormGrad(operand, scale, batch_mean, batch_var, grad_output, epsilon,
feature_index)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp | n-wymiarowa tablica do normalizacji (x) |
scale |
XlaOp | Tablica jednowymiarowa (\(\gamma\)) |
batch_mean |
XlaOp | Tablica jednowymiarowa (\(\mu\)) |
batch_var |
XlaOp | Tablica jednowymiarowa (\(\sigma^2\)) |
grad_output |
XlaOp | Gradienty przekazane do: BatchNormTraining (\(\nabla y\)) |
epsilon |
float |
Wartość parametru epsilon (\(\epsilon\)) |
feature_index |
int64 |
Indeks wymiaru cechy w operand |
W przypadku każdej cechy w wymiarze cech (feature_index to indeks wymiaru cech w operand) operacja oblicza gradienty względem operand, offset i scale we wszystkich pozostałych wymiarach. Parametr feature_index musi być prawidłowym indeksem wymiaru cechy w parametrze operand.
Trzy gradienty są zdefiniowane przez te wzory (przy założeniu, że tablica 4-wymiarowa to operand, indeks wymiaru cechy to l, rozmiar partii to m, a rozmiary przestrzenne to w i h):
\[ \begin{split} c_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sigma^2_l+\epsilon} \right) \\\\ d_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \\\\ \nabla x_{ijkl} &= \frac{\gamma_{l} }{\sqrt{\sigma^2_{l}+\epsilon} } \left( \nabla y_{ijkl} - d_l - c_l (x_{ijkl} - \mu_{l}) \right) \\\\ \nabla \gamma_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sqrt{\sigma^2_{l}+\epsilon} } \right) \\\\\ \nabla \beta_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \end{split} \]
Dane wejściowe batch_mean i batch_var reprezentują wartości momentów w wymiarach przestrzennych i wymiarach partii.
Typem wyjściowym jest krotka 3 uchwytów:
| Wyniki | Typ | Semantyka |
|---|---|---|
grad_operand
|
XlaOp | gradient względem
danych wejściowych operand
(\(\nabla x\)) |
grad_scale
|
XlaOp | gradient względem
danych wejściowych **scale **
(\(\nabla\gamma\)) |
grad_offset
|
XlaOp | gradient względem
danych wejściowych
offset(\(\nabla\beta\)) |
Informacje o StableHLO znajdziesz w artykule StableHLO – batch_norm_grad.
BatchNormInference
Szczegółowy opis algorytmu znajdziesz też w XlaBuilder::BatchNormInference i oryginalnym artykule na temat normalizacji wsadowej.
Normalizuje tablicę w wymiarach partii i przestrzeni.
BatchNormInference(operand, scale, offset, mean, variance, epsilon,
feature_index)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp | n-wymiarowa tablica do znormalizowania |
scale |
XlaOp | Tablica jednowymiarowa |
offset |
XlaOp | Tablica jednowymiarowa |
mean |
XlaOp | Tablica jednowymiarowa |
variance |
XlaOp | Tablica jednowymiarowa |
epsilon |
float |
Wartość parametru epsilon |
feature_index |
int64 |
Indeks wymiaru cechy w operand |
Dla każdej cechy w wymiarze cech (feature_index to indeks wymiaru cech w operand) operacja oblicza średnią i wariancję we wszystkich pozostałych wymiarach, a następnie używa średniej i wariancji do normalizacji każdego elementu w operand. Parametr feature_index musi być prawidłowym indeksem wymiaru funkcji w parametrze operand.
Funkcja BatchNormInference jest odpowiednikiem wywołania funkcji BatchNormTraining bez obliczania wartości mean i variance dla każdej partii. Zamiast tego używa danych wejściowych mean i variance jako wartości szacunkowych. Celem tej operacji jest zmniejszenie opóźnienia w procesie wnioskowania, stąd nazwa BatchNormInference.
Wynikiem jest znormalizowana tablica n-wymiarowa o takim samym kształcie jak dane wejścioweoperand.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – batch_norm_inference.
BatchNormTraining
Szczegółowy opis algorytmu znajdziesz też w sekcjach XlaBuilder::BatchNormTraining i the original batch normalization paper.
Normalizuje tablicę w wymiarach partii i przestrzeni.
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
n-wymiarowa tablica do normalizacji (x) |
scale |
XlaOp |
Tablica jednowymiarowa (\(\gamma\)) |
offset |
XlaOp |
Tablica jednowymiarowa (\(\beta\)) |
epsilon |
float |
Wartość parametru epsilon (\(\epsilon\)) |
feature_index |
int64 |
Indeks wymiaru cechy w operand |
Dla każdej cechy w wymiarze cech (feature_index to indeks wymiaru cech w operand) operacja oblicza średnią i wariancję we wszystkich pozostałych wymiarach, a następnie używa średniej i wariancji do normalizacji każdego elementu w operand. Parametr feature_index musi być prawidłowym indeksem wymiaru funkcji w parametrze operand.
Dla każdej partii w operand \(x\) , która zawiera m elementy o rozmiarach wymiarów przestrzennych w i h (zakładając, że operand to 4-wymiarowa tablica), algorytm działa w ten sposób:
Oblicza średnią wsadową \(\mu_l\) dla każdej cechy
lw wymiarze cechy:\(\mu_l=\frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h x_{ijkl}\)Oblicza wariancję partii: \(\sigma^2_l\)$\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
Normalizuje, skaluje i przesuwa:\(y_{ijkl}=\frac{\gamma_l(x_{ijkl}-\mu_l)}{\sqrt[2]{\sigma^2_l+\epsilon} }+\beta_l\)
Wartość epsilon, zwykle mała liczba, jest dodawana, aby uniknąć błędów dzielenia przez zero.
Typem wyjściowym jest krotka 3 wartości XlaOp:
| Wyniki | Typ | Semantyka |
|---|---|---|
output
|
XlaOp
|
n-wymiarowa tablica o takim samym kształcie jak dane wejściowe
operand (y) |
batch_mean |
XlaOp |
Tablica jednowymiarowa (\(\mu\)) |
batch_var |
XlaOp |
Tablica jednowymiarowa (\(\sigma^2\)) |
Wartości batch_mean i batch_var są momentami obliczanymi w wymiarach przestrzennych i wymiarach partii za pomocą powyższych wzorów.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – batch_norm_training.
Bitcast
Zobacz też HloInstruction::CreateBitcast.
Bitcast mogą pojawiać się w zrzutach HLO, ale nie są przeznaczone do ręcznego tworzenia przez użytkowników.
BitcastConvertType
Zobacz też XlaBuilder::BitcastConvertType.
Podobnie jak tf.bitcast w TensorFlow wykonuje operację bitcast na poszczególnych elementach z kształtu danych do kształtu docelowego. Rozmiar danych wejściowych i wyjściowych musi być taki sam: np. elementy s32 stają się elementami f32 w wyniku procedury bitcast, a jeden element s32 staje się czterema elementami s8. Bitcast jest implementowany jako rzutowanie niskiego poziomu, więc maszyny z różnymi reprezentacjami zmiennoprzecinkowymi będą dawać różne wyniki.
BitcastConvertType(operand, new_element_type)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica typu T o wymiarach D |
new_element_type |
PrimitiveType |
typ U |
Wymiary operandu i kształtu docelowego muszą być zgodne, z wyjątkiem ostatniego wymiaru, który zmieni się o stosunek rozmiaru typu prostego przed i po konwersji.
Typy elementów źródłowych i docelowych nie mogą być krotkami.
Informacje o StableHLO znajdziesz w artykule StableHLO – bitcast_convert.
Konwersja bitcast na typ prosty o innej szerokości
BitcastConvert Instrukcja HLO obsługuje przypadek, w którym rozmiar typu elementu wyjściowego T' nie jest równy rozmiarowi elementu wejściowego T. Cała operacja jest koncepcyjnie bitcastem i nie zmienia podstawowych bajtów, więc musi się zmienić kształt elementu wyjściowego. W przypadku B = sizeof(T), B' =
sizeof(T') możliwe są 2 sytuacje.
Po pierwsze, gdy B > B', kształt wyjściowy zyskuje nowy wymiar o najmniejszym znaczeniu o rozmiarze B/B'. Na przykład:
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
W przypadku efektywnych skalarów reguła pozostaje taka sama:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
Alternatywnie w przypadku B' > B instrukcja wymaga, aby ostatni wymiar logiczny kształtu wejściowego był równy B'/B, a ten wymiar jest usuwany podczas konwersji:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
Pamiętaj, że konwersje między różnymi szerokościami bitowymi nie są wykonywane na poszczególnych elementach.
Transmisja
Zobacz też XlaBuilder::Broadcast.
Dodaje wymiary do tablicy, duplikując dane w tablicy.
Broadcast(operand, broadcast_sizes)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Tablica do zduplikowania |
broadcast_sizes |
ArraySlice<int64> |
Rozmiary nowych wymiarów |
Nowe wymiary są wstawiane po lewej stronie, tzn. jeśli broadcast_sizes ma wartości {a0, ..., aN}, a kształt operandu ma wymiary {b0, ..., bM}, to kształt wyniku ma wymiary {a0, ..., aN, b0, ..., bM}.
Nowe wymiary są indeksowane w kopiach operandu, tzn.
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
Jeśli na przykład operand jest skalarem f32 o wartości 2.0f, a broadcast_sizes to {2, 3}, wynikiem będzie tablica o kształcie f32[2, 3], a wszystkie wartości w niej będą równe 2.0f.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – broadcast.
BroadcastInDim
Zobacz też XlaBuilder::BroadcastInDim.
Zwiększa rozmiar i liczbę wymiarów tablicy przez zduplikowanie danych w tablicy.
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Tablica do zduplikowania |
out_dim_size
|
ArraySlice<int64>
|
Wymiary kształtu docelowego |
broadcast_dimensions
|
ArraySlice<int64>
|
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Podobna do funkcji Broadcast, ale umożliwia dodawanie wymiarów w dowolnym miejscu i rozszerzanie istniejących wymiarów o rozmiarze 1.
Wartość operand jest transmitowana do kształtu opisanego przez out_dim_size.
broadcast_dimensions mapuje wymiary operand na wymiary kształtu docelowego, tzn. i-ty wymiar operandu jest mapowany na broadcast_dimension[i]-ty wymiar kształtu wyjściowego. Wymiary elementu operand muszą mieć rozmiar 1 lub być takie same jak wymiary w kształcie wyjściowym, do którego są mapowane. Pozostałe wymiary są wypełniane wymiarami o rozmiarze 1. Rozgłaszanie w przypadku wymiarów zdegenerowanych rozgłasza wzdłuż tych wymiarów, aby uzyskać kształt wyjściowy. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Połączenie
Zobacz też XlaBuilder::Call.
Wywołuje obliczenia z podanymi argumentami.
Call(computation, operands...)
| Argumenty | Typ | Semantyka |
|---|---|---|
computation
|
XlaComputation
|
obliczenia typu T_0, T_1, ...,
T_{N-1} -> S z N parametrami dowolnego typu; |
operands |
sekwencja N znaków XlaOp, |
N argumentów dowolnego typu |
Liczność i typy argumentów funkcji operands muszą być zgodne z parametrami funkcji computation. Można nie podawać wartości operands.
CompositeCall
Zobacz też XlaBuilder::CompositeCall.
Zawiera operację składającą się z innych operacji StableHLO, która przyjmuje dane wejściowe i atrybuty złożone oraz zwraca wyniki. Semantyka operacji jest implementowana przez atrybut dekompozycji. Operację złożoną można zastąpić jej dekompozycją bez zmiany semantyki programu. W przypadkach, gdy wstawienie dekompozycji nie zapewnia tej samej semantyki operacji, zalecamy użycie funkcji custom_call.
Pole wersji (domyślnie 0) służy do oznaczania, kiedy zmienia się semantyka typu złożonego.
Ta operacja jest implementowana jako kCall z atrybutem is_composite=true. Pole decomposition jest określone przez atrybut computation. Atrybuty frontendowe przechowują pozostałe atrybuty z prefiksem composite..
Przykładowe wywołanie CompositeCall:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
CompositeCall(computation, operands..., name, attributes, version)
| Argumenty | Typ | Semantyka |
|---|---|---|
computation
|
XlaComputation
|
obliczenia typu T_0, T_1, ...,
T_{N-1} -> S z N parametrami dowolnego typu; |
operands |
sekwencja N znaków XlaOp, |
zmienna liczba wartości, |
name |
string |
nazwa elementu złożonego, |
attributes
|
opcjonalne string
|
opcjonalny słownik atrybutów w formie ciągu znaków. |
version
|
opcjonalne int64
|
numer wersji do zaktualizowania semantyka operacji złożonej |
Operacja decomposition nie jest polem, ale atrybutem to_apply, który wskazuje funkcję zawierającą implementację niższego poziomu, czyli to_apply=%funcname.
Więcej informacji o operacjach złożonych i dekompozycji znajdziesz w specyfikacji StableHLO.
Cbrt
Zobacz też XlaBuilder::Cbrt.
Operacja pierwiastka sześciennego na poszczególnych elementach x -> cbrt(x).
Cbrt(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja cbrt obsługuje też opcjonalny argument result_accuracy:
Cbrt(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Informacje o StableHLO znajdziesz w artykule StableHLO – cbrt.
ceil
Zobacz też XlaBuilder::Ceil.
Zaokrąglenie w górę każdego elementu x -> ⌈x⌉.
Ceil(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Informacje o StableHLO znajdziesz w artykule StableHLO – ceil.
Cholesky
Zobacz też XlaBuilder::Cholesky.
Oblicza rozkład Cholesky partii symetrycznych (hermitowskich) macierzy dodatnio określonych.
Cholesky(a, lower)
| Argumenty | Typ | Semantyka |
|---|---|---|
a
|
XlaOp
|
tablicę typu złożonego lub zmiennoprzecinkowego z > 2 wymiarami. |
lower |
bool |
czy użyć górnego czy dolnego trójkąta a. |
Jeśli lower to true, oblicza macierze dolnotrójkątne l takie, że $a = l .
l^T$. Jeśli lower to false, oblicza macierze górnotrójkątne u takie, że
\(a = u^T . u\).
Dane wejściowe są odczytywane tylko z dolnego lub górnego trójkąta macierzy a w zależności od wartości lower. Wartości z drugiego trójkąta są ignorowane. Dane wyjściowe są zwracane w tym samym trójkącie. Wartości w drugim trójkącie są zdefiniowane przez implementację i mogą być dowolne.
Jeśli a ma więcej niż 2 wymiary, jest traktowany jako partia macierzy, w której wszystkie wymiary oprócz 2 najmniejszych są wymiarami partii.a
Jeśli macierz a nie jest symetryczna (hermitowska) i dodatnio określona, wynik jest zdefiniowany przez implementację.
Informacje o StableHLO znajdziesz w artykule StableHLO – cholesky.
Ograniczanie zakresu
Zobacz też XlaBuilder::Clamp.
Ogranicza operand do zakresu między wartością minimalną a maksymalną.
Clamp(min, operand, max)
| Argumenty | Typ | Semantyka |
|---|---|---|
min |
XlaOp |
tablicę typu T, |
operand |
XlaOp |
tablicę typu T, |
max |
XlaOp |
tablicę typu T, |
Funkcja zwraca operand, jeśli mieści się on w zakresie między wartością minimalną a maksymalną. W przeciwnym razie zwraca wartość minimalną, jeśli operand jest poniżej tego zakresu, lub wartość maksymalną, jeśli operand jest powyżej tego zakresu. Czyli clamp(a, x, b) = min(max(a, x), b).
Wszystkie 3 tablice muszą mieć ten sam kształt. Alternatywnie, jako ograniczona forma nadawania, min lub max może być skalarem typu T.
Przykład ze skalarami min i max:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – clamp.
Zwiń
Zobacz też XlaBuilder::Collapse.
i operację tf.reshape.
Spłaszcza wymiary tablicy do jednego wymiaru.
Collapse(operand, dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablicę typu T, |
dimensions |
int64 wektor |
kolejny podzbiór wymiarów T. |
Operacja zwijania zastępuje podany podzbiór wymiarów operandu pojedynczym wymiarem. Argumentami wejściowymi są dowolna tablica typu T i wektor indeksów wymiarów stałych w czasie kompilacji. Indeksy wymiarów muszą być uporządkowanym (od najmniejszego do największego) i kolejnym podzbiorem wymiarów tensora T. Zatem {0, 1, 2}, {0, 1} i {1, 2} to prawidłowe zbiory wymiarów, ale {1, 0} i {0, 2} już nie. Zastępuje je jeden nowy wymiar, który znajduje się w tym samym miejscu w sekwencji wymiarów co zastępowane wymiary. Rozmiar nowego wymiaru jest równy iloczynowi rozmiarów pierwotnych wymiarów. Najmniejszy numer wymiaru w dimensions to wymiar o najwolniejszych zmianach (najważniejszy) w zagnieżdżeniu pętli, które zwija te wymiary, a największy numer wymiaru to wymiar o najszybszych zmianach (najmniej ważny). Jeśli potrzebujesz bardziej ogólnej kolejności zwijania, użyj operatora tf.reshape.
Niech na przykład v będzie tablicą 24 elementów:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
Clz
Zobacz też XlaBuilder::Clz.
Zliczanie zer z przodu w poszczególnych elementach.
Clz(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
CollectiveBroadcast
Zobacz też XlaBuilder::CollectiveBroadcast.
Przesyła dane do wszystkich replik. Dane są wysyłane z pierwszego identyfikatora repliki w każdej grupie do pozostałych identyfikatorów w tej samej grupie. Jeśli identyfikator repliki nie należy do żadnej grupy replik, dane wyjściowe na tej replice to tensor składający się z zer w shape.
CollectiveBroadcast(operand, replica_groups, channel_id)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
replica_groups
|
ReplicaGroupwektor
|
Każda grupa zawiera listę identyfikatorów replik. |
channel_id
|
opcjonalne ChannelHandle
|
unikalny identyfikator każdej pary wysyłania/odbierania; |
Informacje o StableHLO znajdziesz w artykule StableHLO – collective_broadcast.
CollectivePermute
Zobacz też XlaBuilder::CollectivePermute.
CollectivePermute to operacja zbiorowa, która wysyła i odbiera dane między replikami.
CollectivePermute(operand, source_target_pairs, channel_id, inplace)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
n-wymiarowa tablica wejściowa |
source_target_pairs
|
<int64, int64> wektor
|
Lista par (source_replica_id, target_replica_id). W przypadku każdej pary operand jest wysyłany z repliki źródłowej do repliki docelowej. |
channel_id
|
opcjonalne ChannelHandle
|
Opcjonalny identyfikator kanału do komunikacji między modułami |
inplace
|
opcjonalne bool
|
flaga z informacją, czy permutacja ma być wykonana w miejscu, |
Pamiętaj, że w przypadku symbolu source_target_pairs obowiązują te ograniczenia:
- Żadne 2 pary nie powinny mieć tego samego identyfikatora repliki docelowej ani tego samego identyfikatora repliki źródłowej.
- Jeśli identyfikator repliki nie jest celem w żadnej parze, dane wyjściowe na tej replice to tensor składający się z zer o takim samym kształcie jak dane wejściowe.
Interfejs API operacji CollectivePermute jest wewnętrznie rozkładany na 2 instrukcje HLO (CollectivePermuteStart i CollectivePermuteDone).
Zobacz też HloInstruction::CreateCollectivePermuteStart.
CollectivePermuteStart i CollectivePermuteDone są typami prostymi w HLO.
Te operacje mogą pojawiać się w zrzutach HLO, ale nie są przeznaczone do ręcznego tworzenia przez użytkowników.
Informacje o StableHLO znajdziesz w artykule StableHLO – collective_permute.
Porównaj
Zobacz też XlaBuilder::Compare.
Wykonuje porównanie elementów lhs i rhs w przypadku:
Eq
Zobacz też XlaBuilder::Eq.
Wykonuje porównanie równości elementów w lhs i rhs.
\(lhs = rhs\)
Eq(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywna wersja z obsługą transmisji w różnych wymiarach dla Eq:
Eq(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Obsługa łącznej liczby zamówień w przypadku liczb zmiennoprzecinkowych istnieje w przypadku funkcji Eq, poprzez wymuszenie:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
EqTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – porównanie.
Ne
Zobacz też XlaBuilder::Ne.
Wykonuje porównanie elementów różnych od w przypadku tensorów lhs i rhs.
\(lhs != rhs\)
Ne(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywna odmiana z obsługą transmisji w różnych wymiarach dla Ne:
Ne(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Obsługa całkowitego porządku liczb zmiennoprzecinkowych istnieje w przypadku Ne, poprzez wymuszenie:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
NeTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – porównanie.
Ge
Zobacz też XlaBuilder::Ge.
Wykonuje porównanie greater-or-equal-than elementów lhs i rhs.
\(lhs >= rhs\)
Ge(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Dla Ge istnieje alternatywna wersja z obsługą transmisji o różnych wymiarach:
Ge(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Obsługa łącznej liczby zamówień w przypadku liczb zmiennoprzecinkowych jest dostępna w przypadku wartości większych od zera, poprzez wymuszanie:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
GtTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – porównanie.
Gt
Zobacz też XlaBuilder::Gt.
Wykonuje porównanie elementów większych niż w przypadku tensorów lhs i rhs.
\(lhs > rhs\)
Gt(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Dla Gt istnieje alternatywny wariant z obsługą transmisji o różnych wymiarach:
Gt(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – porównanie.
Le
Zobacz też XlaBuilder::Le.
Wykonuje porównanie less-or-equal-than elementów lhs i rhs.
\(lhs <= rhs\)
Le(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Dla Le istnieje alternatywna wersja z obsługą transmisji o różnych wymiarach:
Le(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Obsługa całkowitego uporządkowania liczb zmiennoprzecinkowych istnieje w przypadku relacji ≤, ponieważ:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LeTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – porównanie.
Lt
Zobacz też XlaBuilder::Lt.
Przeprowadza porównanie mniejsze niż elementów lhs i rhs.
\(lhs < rhs\)
Lt(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Dla Lt istnieje alternatywny wariant z obsługą transmisji o różnych wymiarach:
Lt(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Obsługa całkowitego porządku liczb zmiennoprzecinkowych istnieje w przypadku relacji Lt, poprzez wymuszenie:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LtTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – porównanie.
Złożony
Zobacz też XlaBuilder::Complex.
Wykonuje konwersję poszczególnych elementów na wartość zespoloną z pary wartości rzeczywistych i urojonych, lhs i rhs.
Complex(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywna odmiana z obsługą transmisji o różnych wymiarach dla typu Complex:
Complex(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – złożone.
ConcatInDim (Concatenate)
Zobacz też XlaBuilder::ConcatInDim.
Funkcja ZŁĄCZ tworzy tablicę z wielu argumentów tablicowych. Tablica ma tyle samo wymiarów co każdy z argumentów wejściowych (które muszą mieć taką samą liczbę wymiarów) i zawiera argumenty w kolejności, w jakiej zostały podane.
Concatenate(operands..., dimension)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands
|
sekwencja N XlaOp
|
N tablic typu T o wymiarach [L0, L1, ...]. Wymaga N >= 1. |
dimension
|
int64
|
Wartość z przedziału [0, N), która określa wymiar do połączenia między operands. |
Z wyjątkiem dimension wszystkie wymiary muszą być takie same. Dzieje się tak, ponieważ XLA nie obsługuje „nierównych” tablic. Pamiętaj też, że wartości 0-wymiarowe nie mogą być łączone (ponieważ nie można nazwać wymiaru, wzdłuż którego następuje łączenie).
Przykład 1-wymiarowy:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
//Output: {2, 3, 4, 5, 6, 7}
Przykład dwuwymiarowy:
let a = { {1, 2},
{3, 4},
{5, 6} };
let b = { {7, 8} };
Concat({a, b}, 0)
//Output: { {1, 2},
// {3, 4},
// {5, 6},
// {7, 8} }
Diagram:
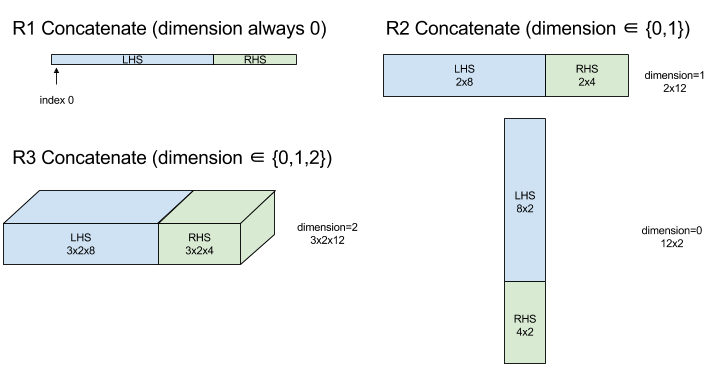
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – concatenate.
Warunkowy
Zobacz też XlaBuilder::Conditional.
Conditional(predicate, true_operand, true_computation, false_operand,
false_computation)
| Argumenty | Typ | Semantyka |
|---|---|---|
predicate |
XlaOp |
Skalar typu PRED |
true_operand |
XlaOp |
Argument typu \(T_0\) |
true_computation |
XlaComputation |
XlaComputation typu \(T_0 \to S\) |
false_operand |
XlaOp |
Argument typu \(T_1\) |
false_computation |
XlaComputation |
XlaComputation typu \(T_1 \to S\) |
Wykonuje true_computation, jeśli predicate ma wartość true, wykonuje false_computation, jeśli predicate ma wartość false, i zwraca wynik.
Funkcja true_computation musi przyjmować jeden argument typu \(T_0\) i będzie wywoływana z argumentem true_operand, który musi być tego samego typu. Funkcja false_computation musi przyjmować jeden argument typu \(T_1\) i będzie wywoływana z argumentem false_operand, który musi być tego samego typu. Typ zwracanej wartości true_computation i false_computation musi być taki sam.
Pamiętaj, że w zależności od wartości predicate zostanie wykonana tylko jedna z funkcji true_computation i false_computation.
Conditional(branch_index, branch_computations, branch_operands)
| Argumenty | Typ | Semantyka |
|---|---|---|
branch_index |
XlaOp |
Skalar typu S32 |
branch_computations |
sekwencja N XlaComputation |
XlaComputations typu \(T_0 \to S , T_1 \to S , ..., T_{N-1} \to S\) |
branch_operands |
sekwencja N XlaOp |
Argumenty typu \(T_0 , T_1 , ..., T_{N-1}\) |
Wykonuje branch_computations[branch_index] i zwraca wynik. Jeśli branch_index jest S32, a S32 < 0 lub >= N, to branch_computations[N-1] jest wykonywane jako gałąź domyślna.
Każda funkcja branch_computations[b] musi przyjmować jeden argument typu \(T_b\) i będzie wywoływana z argumentem branch_operands[b], który musi być tego samego typu. Typ zwracanej wartości każdego wyrażenia branch_computations[b] musi być taki sam.
Pamiętaj, że w zależności od wartości branch_index zostanie wykonana tylko jedna z funkcji branch_computations.
Informacje o StableHLO znajdziesz w artykule StableHLO – if.
Stała
Zobacz też XlaBuilder::ConstantLiteral.
Tworzy output ze stałej literal.
Constant(literal)
| Argumenty | Typ | Semantyka |
|---|---|---|
literal |
LiteralSlice |
stały widok istniejącego Literal, |
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – stała.
ConvertElementType
Zobacz też XlaBuilder::ConvertElementType.
Podobnie jak funkcja static_cast w C++, funkcja ConvertElementType wykonuje operację konwersji poszczególnych elementów z kształtu danych na kształt docelowy. Wymiary muszą być zgodne, a konwersja jest wykonywana na poziomie poszczególnych elementów, np. s32elementy stają się f32elementami w ramach procedury konwersji z s32 na f32.
ConvertElementType(operand, new_element_type)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica typu T o wymiarach D |
new_element_type |
PrimitiveType |
typ U |
Wymiary operandu i kształtu docelowego muszą być zgodne. Typy elementów źródłowego i docelowego nie mogą być krotkami.
Konwersja, np. T=s32 na U=f32, spowoduje wykonanie procedury normalizującej konwersję z liczby całkowitej na zmiennoprzecinkową, np. zaokrąglanie do najbliższej parzystej liczby.
celów.
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – convert.
Conv (splot)
Zobacz też XlaBuilder::Conv.
Oblicza splot podobny do tego, który jest używany w sieciach neuronowych. Splot można tu traktować jako n-wymiarowe okno przesuwające się po n-wymiarowym obszarze bazowym. Obliczenia są wykonywane dla każdej możliwej pozycji okna.
Conv Umieszcza w kolejce instrukcję splotu, która używa domyślnych numerów wymiarów splotu bez rozszerzenia.
Dopełnienie jest określane w skrócony sposób jako SAME lub VALID. SAME
padding uzupełnia dane wejściowe (lhs) zerami, aby dane wyjściowe miały taki sam kształt jak dane wejściowe, gdy nie uwzględnia się kroku. PRAWIDŁOWE dopełnienie oznacza po prostu brak dopełnienia.
Conv(lhs, rhs, window_strides, padding, feature_group_count,
batch_group_count, precision_config, preferred_element_type)
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs
|
XlaOp
|
Tablica wejściowa o wymiarach (n+2) |
rhs
|
XlaOp
|
(n+2)-wymiarowa tablica wag jądra |
window_strides |
ArraySlice<int64> |
n-wymiarowa tablica kroków jądra |
padding |
Padding |
wyliczenie dopełnienia |
feature_group_count
|
int64 | liczba grup cech, |
batch_group_count |
int64 | liczba grup plików do przetworzenia zbiorczego, |
precision_config
|
opcjonalne
PrecisionConfig |
wyliczenie poziomu precyzji |
preferred_element_type
|
opcjonalne
PrimitiveType |
enum typu elementu skalarnego |
W przypadku Conv dostępne są różne poziomy kontroli:
Niech n będzie liczbą wymiarów przestrzennych. Argument lhs to tablica (n+2)-wymiarowa opisująca obszar podstawy. Nazywamy to wejściem, choć oczywiście prawa strona też jest wejściem. W sieci neuronowej są to aktywacje wejściowe. Wymiary n+2 są w tej kolejności:
batch: Każda współrzędna w tym wymiarze reprezentuje niezależne dane wejściowe, dla których przeprowadzana jest konwolucja.z/depth/features: Każda pozycja (y,x) w obszarze podstawowym ma powiązany wektor, który wchodzi w ten wymiar.spatial_dims: opisujenwymiary przestrzenne, które określają obszar bazowy, po którym przesuwa się okno.
Argument rhs to tablica (n+2)-wymiarowa opisująca filtr/jądro/okno konwolucyjne. Wymiary są podane w tej kolejności:
output-z: wymiarzdanych wyjściowych.input-z: rozmiar tego wymiaru pomnożony przezfeature_group_countpowinien być równy rozmiarowi wymiaruzpo lewej stronie.spatial_dims: opisujenwymiary przestrzenne, które definiują n-wymiarowe okno przesuwające się po obszarze bazowym.
Argument window_strides określa krok okna splotu w wymiarach przestrzennych. Jeśli na przykład krok w pierwszym wymiarze przestrzennym wynosi 3, okno można umieścić tylko we współrzędnych, w których pierwszy indeks przestrzenny jest podzielny przez 3.
Argument padding określa ilość dopełnienia zerami, które ma zostać zastosowane do obszaru podstawowego. Wartość dopełnienia może być ujemna – wartość bezwzględna ujemnego dopełnienia wskazuje liczbę elementów do usunięcia z określonego wymiaru przed wykonaniem splotu. padding[0] określa dopełnienie wymiaru y, a padding[1] określa dopełnienie wymiaru x. Każda para zawiera najpierw dolny margines wewnętrzny, a potem górny. Dopełnienie o niskiej wartości jest stosowane w kierunku niższych indeksów, a dopełnienie o wysokiej wartości – w kierunku wyższych indeksów. Jeśli np. padding[1] to (2,3), w drugim wymiarze przestrzennym po lewej stronie zostaną dodane 2 zera, a po prawej – 3 zera. Użycie dopełnienia jest równoznaczne z wstawieniem tych samych wartości zerowych do danych wejściowych (lhs) przed wykonaniem splotu.
Argumenty lhs_dilation i rhs_dilation określają współczynnik rozszerzenia, który ma być zastosowany odpowiednio do lewej i prawej strony w każdym wymiarze przestrzennym. Jeśli współczynnik rozszerzenia w wymiarze przestrzennym wynosi d, między poszczególnymi elementami w tym wymiarze umieszcza się d-1 otworów, co zwiększa rozmiar tablicy. Luki są wypełniane wartością bez operacji, która w przypadku splotu oznacza zera.
Rozszerzenie prawej strony jest też nazywane konwolucją z dziurami. Więcej informacji znajdziesz w sekcji tf.nn.atrous_conv2d. Rozszerzenie lewej strony jest też nazywane transponowaną konwolucją. Więcej informacji znajdziesz w sekcji tf.nn.conv2d_transpose.
Argument feature_group_count (wartość domyślna to 1) może być używany w przypadku konwolucji grupowej. feature_group_count musi być dzielnikiem zarówno wymiaru cechy wejściowej, jak i wyjściowej. Jeśli feature_group_count jest większe niż 1, oznacza to, że wymiar cechy wejściowej i wyjściowej oraz wymiar cechy wyjściowej rhs są koncepcyjnie dzielone równomiernie na wiele grup feature_group_count, z których każda składa się z kolejnego podciągu cech. Wymiar cechy wejściowej elementu rhs musi być równy wymiarowi cechy wejściowej elementu lhs podzielonemu przez feature_group_count (czyli musi mieć rozmiar grupy cech wejściowych). i-te grupy są używane razem do obliczania
feature_group_count w przypadku wielu oddzielnych operacji splotu. Wyniki tych operacji splotu są łączone w wymiarze cechy wyjściowej.
W przypadku konwolucji przestrzennej argument feature_group_count byłby ustawiony na wymiar cechy wejściowej, a filtr zostałby przekształcony z [filter_height, filter_width, in_channels, channel_multiplier] na [filter_height, filter_width, 1, in_channels * channel_multiplier]. Więcej informacji znajdziesz w sekcji tf.nn.depthwise_conv2d.
Argument batch_group_count (wartość domyślna to 1) może być używany w przypadku zgrupowanych filtrów podczas propagacji wstecznej. batch_group_count musi być dzielnikiem rozmiaru wymiaru wsadu lhs (dane wejściowe). Jeśli batch_group_count jest większe niż 1, oznacza to, że wymiar wsadu wyjściowego powinien mieć rozmiar input batch
/ batch_group_count. Wartość batch_group_count musi być dzielnikiem rozmiaru cechy wyjściowej.
Kształt danych wyjściowych ma te wymiary w tej kolejności:
batch: rozmiar tego wymiaru pomnożony przezbatch_group_countpowinien być równy rozmiarowi wymiarubatchpo lewej stronie.z: taki sam rozmiar jakoutput-zna jądrze (rhs).spatial_dims: jedna wartość dla każdego prawidłowego umieszczenia okna konwolucyjnego.
Ilustracja powyżej pokazuje, jak działa pole batch_group_count. W praktyce dzielimy każdą partię lhs na batch_group_count grup i robimy to samo w przypadku cech wyjściowych. Następnie dla każdej z tych grup przeprowadzamy sploty parami i łączymy wyniki wzdłuż wymiaru cechy wyjściowej. Semantyka operacyjna wszystkich pozostałych wymiarów (funkcjonalnych i przestrzennych) pozostaje bez zmian.
Prawidłowe miejsca docelowe okna konwolucyjnego są określane przez krok i rozmiar obszaru bazowego po dopełnieniu.
Aby opisać, co robi konwolucja, rozważmy konwolucję 2D i wybierzmy stałe współrzędne batch, z, y, x w danych wyjściowych. Wtedy (y,x) to pozycja rogu okna w obszarze podstawowym (np. lewy górny róg, w zależności od interpretacji wymiarów przestrzennych). Mamy teraz okno 2D, które zostało wyodrębnione z obszaru podstawowego. Każdy punkt 2D jest powiązany z wektorem 1D, dzięki czemu otrzymujemy pole 3D. Z jądra konwolucyjnego, ponieważ ustaliliśmy współrzędną wyjściową z, mamy też trójwymiarowe pole. Oba pola mają te same wymiary, więc możemy obliczyć sumę iloczynów elementów między nimi (podobnie jak w przypadku iloczynu skalarnego). Jest to wartość wyjściowa.
Pamiętaj, że jeśli output-z to np. 5, to każda pozycja okna generuje 5 wartości w danych wyjściowych w wymiarze z. Wartości te różnią się tym, która część jądra splotowego jest używana – dla każdego współrzędnego output-z używane jest osobne trójwymiarowe pole wartości. Można to sobie wyobrazić jako 5 oddzielnych operacji splotu z różnymi filtrami.
Oto pseudokod dla konwolucji 2D z wypełnieniem i krokiem:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
precision_config służy do określania konfiguracji precyzji. Poziom określa, czy sprzęt powinien próbować generować więcej instrukcji kodu maszynowego, aby w razie potrzeby zapewnić dokładniejszą emulację typu danych (np. emulację typu f32 na TPU, który obsługuje tylko mnożenie macierzy typu bf16). Wartości mogą być DEFAULT, HIGH, HIGHEST. Dodatkowe informacje w sekcjach MXU.
preferred_element_type to element skalarny o wyższej lub niższej precyzji, który jest używany do akumulacji. preferred_element_type zaleca typ akumulacji w przypadku danej operacji, ale nie jest to gwarantowane. Dzięki temu niektóre platformy sprzętowe mogą gromadzić dane w innym typie i przekształcać je w preferowany typ wyjściowy.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – konwolucja.
ConvWithGeneralPadding
Zobacz też XlaBuilder::ConvWithGeneralPadding.
ConvWithGeneralPadding(lhs, rhs, window_strides, padding,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Tak samo jak Conv, gdzie konfiguracja dopełnienia jest jawna.
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs
|
XlaOp
|
Tablica wejściowa o wymiarach (n+2) |
rhs
|
XlaOp
|
(n+2)-wymiarowa tablica wag jądra |
window_strides |
ArraySlice<int64> |
n-wymiarowa tablica kroków jądra |
padding
|
ArraySlice<
pair<int64,int64>> |
n-wymiarowa tablica wartości (dolna, górna) dopełnienie |
feature_group_count
|
int64 | liczba grup cech, |
batch_group_count |
int64 | liczba grup plików do przetworzenia zbiorczego, |
precision_config
|
opcjonalne
PrecisionConfig |
wyliczenie poziomu precyzji |
preferred_element_type
|
opcjonalne
PrimitiveType |
enum typu elementu skalarnego |
ConvWithGeneralDimensions
Zobacz też XlaBuilder::ConvWithGeneralDimensions.
ConvWithGeneralDimensions(lhs, rhs, window_strides, padding,
dimension_numbers, feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Tak samo jak w przypadku Conv, gdzie numery wymiarów są podane wprost.
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-wymiarowa tablica danych wejściowych |
rhs
|
XlaOp
|
(n+2)-wymiarowa tablica wag jądra |
window_strides
|
ArraySlice<int64>
|
n-wymiarowa tablica kroków jądra |
padding |
Padding |
typ wyliczeniowy dopełnienia |
dimension_numbers
|
ConvolutionDimensionNumbers
|
liczba wymiarów, |
feature_group_count
|
int64 | liczba grup cech, |
batch_group_count
|
int64 | liczba grup plików wsadowych, |
precision_config
|
opcjonalne PrecisionConfig
|
wyliczenie poziomu precyzji |
preferred_element_type
|
opcjonalne PrimitiveType
|
enum typu elementu skalarnego |
ConvGeneral
Zobacz też XlaBuilder::ConvGeneral.
ConvGeneral(lhs, rhs, window_strides, padding, dimension_numbers,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Tak samo jak w przypadku Conv, gdzie numery wymiarów i konfiguracja dopełnienia są określone.
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-wymiarowa tablica danych wejściowych |
rhs
|
XlaOp
|
(n+2)-wymiarowa tablica wag jądra |
window_strides
|
ArraySlice<int64>
|
n-wymiarowa tablica kroków jądra |
padding
|
ArraySlice<
pair<int64,int64>>
|
tablica n-wymiarowa (low, high) dopełnienie |
dimension_numbers
|
ConvolutionDimensionNumbers
|
liczba wymiarów, |
feature_group_count
|
int64 | liczba grup cech, |
batch_group_count
|
int64 | liczba grup plików wsadowych, |
precision_config
|
opcjonalne PrecisionConfig
|
wyliczenie poziomu precyzji |
preferred_element_type
|
opcjonalne PrimitiveType
|
enum typu elementu skalarnego |
ConvGeneralDilated
Zobacz też XlaBuilder::ConvGeneralDilated.
ConvGeneralDilated(lhs, rhs, window_strides, padding, lhs_dilation,
rhs_dilation, dimension_numbers, feature_group_count, batch_group_count,
precision_config, preferred_element_type, window_reversal)
Podobnie jak w przypadku Conv, gdzie konfiguracja dopełnienia, współczynniki rozszerzenia i numery wymiarów są podane wprost.
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs
|
XlaOp
|
(n+2)-wymiarowa tablica danych wejściowych |
rhs
|
XlaOp
|
(n+2)-wymiarowa tablica wag jądra |
window_strides
|
ArraySlice<int64>
|
n-wymiarowa tablica kroków jądra |
padding
|
ArraySlice<
pair<int64,int64>>
|
tablica n-wymiarowa (low, high) dopełnienie |
lhs_dilation
|
ArraySlice<int64>
|
n-d lhs dilation factor array |
rhs_dilation
|
ArraySlice<int64>
|
tablica współczynników dylatacji n-wymiarowej po prawej stronie |
dimension_numbers
|
ConvolutionDimensionNumbers
|
liczba wymiarów, |
feature_group_count
|
int64 | liczba grup cech, |
batch_group_count
|
int64 | liczba grup plików wsadowych, |
precision_config
|
opcjonalne PrecisionConfig
|
wyliczenie poziomu precyzji |
preferred_element_type
|
opcjonalne PrimitiveType
|
enum typu elementu skalarnego |
window_reversal
|
opcjonalne vector<bool>
|
flaga używana do logicznego odwrócenia wymiaru przed zastosowaniem splotu |
Kopiuj
Zobacz też HloInstruction::CreateCopyStart.
Funkcja Copy jest wewnętrznie rozkładana na 2 instrukcje HLO: CopyStart i CopyDone. Copy wraz z CopyStart i CopyDone stanowią elementy podstawowe w HLO. Te operacje mogą pojawiać się w zrzutach HLO, ale nie są przeznaczone do ręcznego tworzenia przez użytkowników.
Cos
Zobacz teżXlaBuilder::Cos.
Podobieństwo kosinusowe elementów x -> cos(x).
Cos(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja cos obsługuje też opcjonalny argument result_accuracy:
Cos(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – cosine.
Cosh
Zobacz też XlaBuilder::Cosh.
Cosinus hiperboliczny każdego elementu x -> cosh(x).
Cosh(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja cosh obsługuje też opcjonalny argument result_accuracy:
Cosh(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
CustomCall
Zobacz też XlaBuilder::CustomCall.
Wywoływanie funkcji przekazanej przez użytkownika w obliczeniach.
Dokumentacja CustomCall jest dostępna w sekcji Szczegóły dla deweloperów – niestandardowe wywołania XLA.
Informacje o StableHLO znajdziesz w artykule StableHLO – custom_call.
Dyw
Zobacz też XlaBuilder::Div.
Wykonuje dzielenie elementów dywidendy lhs przez dzielnik rhs.
Div(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Przepełnienie dzielenia całkowitego (dzielenie/reszta z dzielenia przez zero ze znakiem lub bez znaku albo dzielenie/reszta z dzielenia liczby INT_SMIN przez -1 ze znakiem) daje wartość zdefiniowaną przez implementację.
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywna odmiana elementu Div, która obsługuje transmisję w różnych wymiarach:
Div(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – dzielenie.
Domena
Zobacz też HloInstruction::CreateDomain.
Domain może się pojawiać w zrzutach HLO, ale nie jest przeznaczony do ręcznego tworzenia przez użytkowników.
Kropka
Zobacz też XlaBuilder::Dot.
Dot(lhs, rhs, precision_config, preferred_element_type)
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs |
XlaOp |
tablicę typu T, |
rhs |
XlaOp |
tablicę typu T, |
precision_config
|
opcjonalne
PrecisionConfig |
wyliczenie poziomu precyzji |
preferred_element_type
|
opcjonalne
PrimitiveType |
enum typu elementu skalarnego |
Dokładna semantyka tej operacji zależy od rangi operandów:
| Dane wejściowe | Wyniki | Semantyka |
|---|---|---|
wektor [n] dot wektor [n] |
wartość skalarna | iloczyn skalarny wektorów, |
macierz [m x k] dot wektor[k] |
wektor [m] | mnożenie macierzy przez wektor, |
macierz [m × k] dot macierz [k × n] |
macierz [m x n] | mnożenie macierzy |
Operacja wykonuje sumę iloczynów wzdłuż drugiego wymiaru tensora lhs (lub pierwszego, jeśli ma 1 wymiar) i pierwszego wymiaru tensora rhs. Są to wymiary „skurczone”. Skurczone wymiary lhs i rhs muszą być tego samego rozmiaru. W praktyce można go używać do obliczania iloczynów skalarnych wektorów, mnożenia wektorów przez macierze lub mnożenia macierzy przez macierze.
precision_config służy do określania konfiguracji precyzji. Poziom określa, czy sprzęt powinien próbować generować więcej instrukcji kodu maszynowego, aby w razie potrzeby zapewnić dokładniejszą emulację typu danych (np. emulację typu f32 na TPU, który obsługuje tylko mnożenie macierzy typu bf16). Wartości mogą być DEFAULT, HIGH, HIGHEST. Dodatkowe informacje w sekcjach MXU.
preferred_element_type to element skalarny o wyższej lub niższej precyzji, który jest używany do akumulacji. preferred_element_type zaleca typ akumulacji w przypadku danej operacji, ale nie jest to gwarantowane. Dzięki temu niektóre platformy sprzętowe mogą gromadzić dane w innym typie i przekształcać je w preferowany typ wyjściowy.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – dot.
DotGeneral
Zobacz też XlaBuilder::DotGeneral.
DotGeneral(lhs, rhs, dimension_numbers, precision_config,
preferred_element_type)
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs |
XlaOp |
tablicę typu T, |
rhs |
XlaOp |
tablicę typu T, |
dimension_numbers
|
DotDimensionNumbers
|
numery wymiarów umów i partii, |
precision_config
|
opcjonalne
PrecisionConfig |
wyliczenie poziomu precyzji |
preferred_element_type
|
opcjonalne
PrimitiveType |
enum typu elementu skalarnego |
Podobna do Dot, ale umożliwia określenie numerów wymiarów kurczenia i partii zarówno dla lhs, jak i rhs.
| Pola DotDimensionNumbers | Typ | Semantyka |
|---|---|---|
lhs_contracting_dimensions
|
repeated int64 | lhs wymiaru kurczenia się
numerów |
rhs_contracting_dimensions
|
repeated int64 | rhs wymiaru kurczenia się
numerów |
lhs_batch_dimensions
|
repeated int64 | lhs wymiaru zbiorczego
numerów |
rhs_batch_dimensions
|
repeated int64 | rhs wymiaru zbiorczego
numerów |
Funkcja DotGeneral wykonuje sumę produktów w przypadku wymiarów kurczliwych określonych w dimension_numbers.
Powiązane numery wymiarów umowy z lhs i rhs nie muszą być takie same, ale muszą mieć te same rozmiary.
Przykład z numerami wymiarów umowy:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { { 6.0, 12.0},
{15.0, 30.0} }
Powiązane numery wymiarów wsadu z lhs i rhs muszą mieć te same rozmiary wymiarów.
Przykład z numerami wymiarów partii (rozmiar partii 2, macierze 2x2):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> {
{ {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| Dane wejściowe | Wyniki | Semantyka |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | batch matmul |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | batch matmul |
Wynikowa liczba wymiarów zaczyna się od wymiaru partii, następnie od wymiaru lhs niekurczliwego/niepartiowego, a na końcu od wymiaru rhs niekurczliwego/niepartiowego.
precision_config służy do określania konfiguracji precyzji. Poziom określa, czy sprzęt powinien próbować generować więcej instrukcji kodu maszynowego, aby w razie potrzeby zapewnić dokładniejszą emulację typu danych (np. emulację typu f32 na TPU, który obsługuje tylko mnożenie macierzy typu bf16). Wartości mogą być DEFAULT, HIGH, HIGHEST. Więcej informacji znajdziesz w sekcjach dotyczących MXU.
preferred_element_type to element skalarny o wyższej lub niższej precyzji, który jest używany do akumulacji. preferred_element_type zaleca typ akumulacji w przypadku danej operacji, ale nie jest to gwarantowane. Dzięki temu niektóre platformy sprzętowe mogą gromadzić dane w innym typie i przekształcać je w preferowany typ wyjściowy.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – dot_general.
ScaledDot
Zobacz też XlaBuilder::ScaledDot.
ScaledDot(lhs, lhs_scale, rhs, rhs_scale, dimension_number,
precision_config,preferred_element_type)
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs |
XlaOp |
tablicę typu T, |
rhs |
XlaOp |
tablicę typu T, |
lhs_scale |
XlaOp |
tablicę typu T, |
rhs_scale |
XlaOp |
tablicę typu T, |
dimension_number
|
ScatterDimensionNumbers
|
Numery wymiarów dla operacji rozpraszania |
precision_config
|
PrecisionConfig
|
wyliczenie poziomu precyzji |
preferred_element_type
|
opcjonalne PrimitiveType
|
enum typu elementu skalarnego |
Podobne do DotGeneral.
Tworzy operację skalowanego iloczynu skalarnego z operandami „lhs”, „lhs_scale”, „rhs” i „rhs_scale” oraz wymiarami kurczącymi i wymiarami wsadowymi określonymi w parametrze „dimension_numbers”.
RaggedDot
Zobacz też XlaBuilder::RaggedDot.
Szczegółowe informacje o obliczeniach RaggedDot znajdziesz w artykule StableHLO – chlo.ragged_dot.
DynamicReshape
Zobacz też XlaBuilder::DynamicReshape.
Ta operacja jest funkcjonalnie identyczna z operacją reshape, ale kształt wyniku jest określany dynamicznie za pomocą argumentu output_shape.
DynamicReshape(operand, dim_sizes, new_size_bounds, dims_are_dynamic)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
N-wymiarowa tablica typu T |
dim_sizes |
wektor XlaOP |
Rozmiary wektorów N-wymiarowych |
new_size_bounds |
wektor int63 |
N-wymiarowy wektor granic |
dims_are_dynamic |
wektor bool |
N-dimensional dynamic dim |
Informacje o StableHLO znajdziesz w artykule StableHLO – dynamic_reshape.
DynamicSlice
Zobacz też XlaBuilder::DynamicSlice.
Funkcja DynamicSlice wyodrębnia podtablicę z tablicy wejściowej w dynamicznym
start_indices. Rozmiar wycinka w każdym wymiarze jest przekazywany w size_indices, które określają punkt końcowy przedziałów wycinków w każdym wymiarze: [start, start + size). Kształt start_indices musi być jednowymiarowy, a rozmiar wymiaru musi być równy liczbie wymiarów operand.
DynamicSlice(operand, start_indices, slice_sizes)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
N-wymiarowa tablica typu T |
start_indices
|
sekwencja N XlaOp
|
Lista N liczb skalarnych całkowitych zawierających indeksy początkowe wycinka dla każdego wymiaru. Wartość musi być większa lub równa 0. |
size_indices
|
ArraySlice<int64>
|
Lista N liczb całkowitych zawierająca rozmiar wycinka dla każdego wymiaru. Każda wartość musi być większa od zera, a wartość start + size musi być mniejsza lub równa rozmiarowi wymiaru, aby uniknąć zawijania modulo rozmiar wymiaru. |
Efektywne indeksy wycinków są obliczane przez zastosowanie tej transformacji do każdego indeksu i w [1, N) przed wykonaniem wycinka:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - slice_sizes[i])
Dzięki temu wyodrębniony wycinek zawsze będzie mieścił się w zakresie tablicy operandów. Jeśli wycinek znajduje się w zakresie przed zastosowaniem przekształcenia, nie ma ono żadnego wpływu.
Przykład 1-wymiarowy:
let a = {0.0, 1.0, 2.0, 3.0, 4.0};
let s = {2};
DynamicSlice(a, s, {2});
// Result: {2.0, 3.0}
Przykład dwuwymiarowy:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2});
//Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
Informacje o StableHLO znajdziesz w artykule StableHLO – dynamic_slice.
DynamicUpdateSlice
Zobacz też XlaBuilder::DynamicUpdateSlice.
Funkcja DynamicUpdateSlice generuje wynik, który jest wartością tablicy wejściowej
operand, z zastąpionym wycinkiem update w miejscu start_indices.
Kształt argumentu update określa kształt podmacierzy wyniku, która jest aktualizowana.
Kształt start_indices musi być jednowymiarowy, a rozmiar wymiaru musi być równy liczbie wymiarów operand.
DynamicUpdateSlice(operand, update, start_indices)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
N-wymiarowa tablica typu T |
update
|
XlaOp
|
Wielowymiarowa tablica typu T zawierająca aktualizację wycinka. Każdy wymiar kształtu aktualizacji musi być ściśle większy od zera, a wartość start + update musi być mniejsza lub równa rozmiarowi operandu w przypadku każdego wymiaru, aby uniknąć generowania indeksów aktualizacji wykraczających poza zakres. |
start_indices
|
sekwencja N XlaOp
|
Lista N liczb skalarnych całkowitych zawierających indeksy początkowe wycinka dla każdego wymiaru. Wartość musi być większa lub równa 0. |
Efektywne indeksy wycinków są obliczane przez zastosowanie tej transformacji do każdego indeksu i w [1, N) przed wykonaniem wycinka:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
Dzięki temu zaktualizowany wycinek zawsze będzie mieścił się w zakresie tablicy operandów. Jeśli wycinek znajduje się w zakresie przed zastosowaniem przekształcenia, nie ma ono żadnego wpływu.
Przykład 1-wymiarowy:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s)
// Result: {0.0, 1.0, 5.0, 6.0, 4.0}
Przykład dwuwymiarowy:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s)
// Result:
// { {0.0, 1.0, 2.0},
// {3.0, 12.0, 13.0},
// {6.0, 14.0, 15.0},
// {9.0, 16.0, 17.0} }
Informacje o StableHLO znajdziesz w artykule StableHLO – dynamic_update_slice.
Erf
Zobacz też XlaBuilder::Erf.
Funkcja błędu dla poszczególnych elementów x -> erf(x), gdzie:
\(\text{erf}(x) = \frac{2}{\sqrt{\pi} }\int_0^x e^{-t^2} \, dt\).
Erf(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja Erf obsługuje też opcjonalny argument result_accuracy:
Erf(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Wykł.
Zobacz też XlaBuilder::Exp.
Wykładnik naturalny dla każdego elementu x -> e^x.
Exp(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja Exp obsługuje też opcjonalny argument result_accuracy:
Exp(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Informacje o StableHLO znajdziesz w artykule StableHLO – wykładniczy.
Expm1
Zobacz też XlaBuilder::Expm1.
Wykładnik naturalny każdego elementu pomniejszony o 1 x -> e^x - 1.
Expm1(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja expm1 obsługuje też opcjonalny argument result_accuracy:
Expm1(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Informacje o StableHLO znajdziesz w artykule StableHLO – exponential_minus_one.
FFT
Zobacz też XlaBuilder::Fft.
Operacja FFT w XLA implementuje transformaty Fouriera w przód i wstecz dla danych wejściowych i wyjściowych w postaci liczb rzeczywistych i zespolonych. Obsługiwane są wielowymiarowe FFT na maksymalnie 3 osiach.
Fft(operand, ftt_type, fft_length)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand
|
XlaOp
|
Tablica, którą przekształcamy za pomocą transformaty Fouriera. |
fft_type |
FftType |
Patrz tabela poniżej. |
fft_length
|
ArraySlice<int64>
|
Długości osi w dziedzinie czasu, które są przekształcane. Jest to szczególnie potrzebne w przypadku IRFFT, aby odpowiednio dopasować rozmiar wewnętrznej osi, ponieważ RFFT(fft_length=[16]) ma taki sam kształt wyjściowy jak RFFT(fft_length=[17]). |
FftType |
Semantyka |
|---|---|
FFT |
Szybka transformata Fouriera z liczb zespolonych na liczby zespolone. Kształt nie uległ zmianie. |
IFFT |
Odwrotna transformata FFT z liczb zespolonych na liczby zespolone. Kształt nie uległ zmianie. |
RFFT
|
Wykonuje szybką transformatę Fouriera z liczb rzeczywistych na zespolone. Kształt wewnętrznej osi jest
zredukowany do fft_length[-1] // 2 + 1, jeśli fft_length[-1] jest wartością
różną od zera, z pominięciem odwróconej części sprzężonej
przekształconego sygnału poza częstotliwością Nyquista. |
IRFFT
|
Odwrotna transformata FFT z liczb rzeczywistych na zespolone (pobiera liczby zespolone, zwraca rzeczywiste).
Kształt osi wewnętrznej jest rozszerzany do fft_length[-1], jeśli fft_length[-1] jest wartością niezerową, co oznacza, że część przekształconego sygnału poza częstotliwością Nyquista jest wywnioskowana z odwrotnego sprzężenia zespolonego wpisów od 1 do fft_length[-1] // 2 + 1. |
Informacje o StableHLO znajdziesz w artykule StableHLO – fft.
Wielowymiarowa szybka transformata Fouriera
Gdy podasz więcej niż 1 wartość fft_length, będzie to równoznaczne z zastosowaniem kaskady operacji FFT do każdej z najbardziej wewnętrznych osi. Zauważ, że w przypadku przekształceń rzeczywiste->zespolone i zespolone->rzeczywiste przekształcenie osi wewnętrznej jest (w zasadzie) wykonywane jako pierwsze (RFFT; ostatnie w przypadku IRFFT), dlatego to oś wewnętrzna zmienia rozmiar. Inne przekształcenia osi będą wtedy złożone -> złożone.
Szczegóły implementacji
FFT na procesorze jest obsługiwane przez TensorFFT z biblioteki Eigen. GPU FFT korzysta z cuFFT.
Piętro
Zobacz też XlaBuilder::Floor.
Funkcja podłogi dla poszczególnych elementów x -> ⌊x⌋.
Floor(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – floor.
Fusion
Zobacz też HloInstruction::CreateFusion.
Operacja Fusion reprezentuje instrukcje HLO i jest elementem podstawowym w HLO.
Ta operacja może pojawiać się w zrzutach HLO, ale nie jest przeznaczona do ręcznego tworzenia przez użytkowników.
Zbieranie
Operacja zbierania XLA łączy kilka wycinków (każdy wycinek może mieć inny przesunięcie w czasie wykonania) tablicy wejściowej.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – zbieranie.
Semantyka ogólna
Zobacz też XlaBuilder::Gather.
Bardziej intuicyjny opis znajdziesz w sekcji „Nieformalny opis” poniżej.
gather(operand, start_indices, dimension_numbers, slice_sizes,
indices_are_sorted)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand
|
XlaOp
|
Tablica, z której zbieramy dane. |
start_indices
|
XlaOp
|
Tablica zawierająca indeksy początkowe zbieranych przez nas wycinków. |
dimension_numbers
|
GatherDimensionNumbers
|
Wymiar w
start_indices, który
„zawiera” indeksy
początkowe. Szczegółowy opis znajdziesz poniżej. |
slice_sizes
|
ArraySlice<int64>
|
slice_sizes[i] to granice wycinka w wymiarze i. |
indices_are_sorted
|
bool
|
Określa, czy indeksy są posortowane przez wywołującego. |
Dla wygody wymiary w tablicy wyjściowej oznaczamy nie jako offset_dims, ale jako batch_dims.
Dane wyjściowe to tablica o wymiarach batch_dims.size + offset_dims.size.
Wartość operand.rank musi być równa sumie wartości offset_dims.size i collapsed_slice_dims.size. Poza tym wartość slice_sizes.size musi być równa operand.rank.
Jeśli index_vector_dim jest równe start_indices.rank, domyślnie przyjmujemy, że start_indices ma wymiar końcowy 1 (czyli jeśli start_indices ma kształt [6,7], a index_vector_dim to 2, domyślnie przyjmujemy, że kształt start_indices to [6,7,1]).
Granice tablicy wyjściowej wzdłuż wymiaru i są obliczane w ten sposób:
Jeśli
iwystępuje wbatch_dims(tzn. jest równebatch_dims[k]dla pewnegok), wybieramy odpowiednie granice wymiaru zstart_indices.shape, pomijającindex_vector_dim(tzn. wybieramystart_indices.shape.dims[k], jeślik<index_vector_dim, a w przeciwnym raziestart_indices.shape.dims[k+1]).Jeśli wartość
iwystępuje woffset_dims(czyli jest równaoffset_dims[k] dla pewnegok), wybieramy odpowiednią wartość graniczną zslice_sizespo uwzględnieniucollapsed_slice_dims(czyli wybieramyadjusted_slice_sizes[k], gdzieadjusted_slice_sizestoslice_sizesz usuniętymi wartościami granicznymi na indeksachcollapsed_slice_dims).
Formalnie indeks operandu In odpowiadający danemu indeksowi wyjściowemu Out jest obliczany w ten sposób:
Niech
G= {Out[k] dlakwbatch_dims}. UżyjG, aby wyodrębnić wektorStaki, żeS[i] =start_indices[Combine(G,i)], gdzie Combine(A, b) wstawia b na pozycjiindex_vector_dimdo A. Pamiętaj, że jest to dobrze zdefiniowane nawet wtedy, gdyGjest puste: jeśliGjest puste, toS=start_indices.Utwórz indeks początkowy
Sinwoperand, używającSprzez rozproszenieSza pomocąstart_index_map. Dokładniej:Sin[start_index_map[k]] =S[k] ifk<start_index_map.size.Sin[_] =0w innych przypadkach.
Utwórz indeks
Oinwoperand, rozpraszając indeksy w wymiarach przesunięcia wOutzgodnie z zestawemcollapsed_slice_dims. Dokładniej:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]] ifk<offset_dims.size(remapped_offset_dimsis defined below).Oin[_] =0w innych przypadkach.
IntoOin+Sin, gdzie + oznacza dodawanie elementów.
remapped_offset_dims to funkcja monotoniczna o dziedzinie [0, offset_dims.size) i zbiorze wartości [0, operand.rank) \ collapsed_slice_dims. Jeśli na przykład offset_dims.size to 4, operand.rank to 6 i collapsed_slice_dims to {0, 2}, to remapped_offset_dims to {0→1,
1→3, 2→4, 3→5}.
Jeśli zasada indices_are_sorted ma wartość Prawda, XLA może założyć, że start_indices są posortowane (w kolejności rosnącej, po rozproszeniu wartości zgodnie z zasadą start_index_map) przez użytkownika. W przeciwnym razie semantyka jest zdefiniowana przez implementację.
Nieformalny opis i przykłady
Nieformalnie każdy indeks Out w tablicy wyjściowej odpowiada elementowi E
w tablicy operandów, obliczonemu w ten sposób:
Wymiarów pakietu używamy w
Out, aby wyszukać indeks początkowy wstart_indices.Używamy
start_index_map, aby mapować indeks początkowy (którego rozmiar może być mniejszy niż operand.rank) na „pełny” indeks początkowy woperand.Dynamicznie wycinamy fragment o rozmiarze
slice_sizes, używając pełnego indeksu początkowego.Zmieniamy kształt wycinka, zwijając wymiary
collapsed_slice_dims. Ponieważ wszystkie wymiary zwiniętego wycinka muszą mieć wartość 1, ta zmiana kształtu jest zawsze prawidłowa.Używamy wymiarów przesunięcia w
Out, aby indeksować ten wycinek i uzyskać element wejściowyEodpowiadający indeksowi wyjściowemuOut.
index_vector_dim ma wartość start_indices.rank–1 we wszystkich poniższych przykładach. Bardziej interesujące wartości index_vector_dim nie zmieniają zasadniczo działania, ale utrudniają wizualizację.
Aby zrozumieć, jak to wszystko działa, przyjrzyjmy się przykładowi, w którym z tablicy [16,11] pobieranych jest 5 wycinków o kształcie [8,6]. Położenie wycinka w tablicy [16,11] można przedstawić jako wektor indeksu o kształcie S64[2], więc zbiór 5 położeń można przedstawić jako tablicę S64[5,2].
Działanie operacji gather można przedstawić jako przekształcenie indeksu,które przyjmuje [G,O0,O1], indeks w kształcie wyjściowym i mapuje go na element w tablicy wejściowej w ten sposób:
Najpierw wybieramy wektor (X,Y) z tablicy indeksów zbierania za pomocą funkcji G.
Element w tablicy wyjściowej o indeksie [G,O0,O1] jest elementem w tablicy wejściowej o indeksie [X+O0,Y+O1].
slice_sizes to [8,6], co decyduje o zakresie O0 i O1, a to z kolei decyduje o granicach wycinka.
Ta operacja zbierania działa jak dynamiczny wycinek wsadowy, w którym G jest wymiarem wsadowym.
Indeksy zbierania mogą być wielowymiarowe. Na przykład bardziej ogólna wersja powyższego przykładu, która używa tablicy „zbierz indeksy” o kształcie [4,5,2], przetłumaczy indeksy w ten sposób:
Ponownie będzie to dynamiczny wycinek wsadowy G0 i G1 jako wymiary wsadowe. Rozmiar wycinka to nadal [8,6].
Operacja zbierania w XLA uogólnia nieformalną semantykę opisaną powyżej w następujący sposób:
Możemy skonfigurować, które wymiary w kształcie wyjściowym są wymiarami przesunięcia (wymiary zawierające
O0,O1w ostatnim przykładzie). Wymiary wsadu wyjściowego (wymiary zawierająceG0,G1w ostatnim przykładzie) są zdefiniowane jako wymiary wyjściowe, które nie są wymiarami przesunięcia.Liczba wymiarów przesunięcia danych wyjściowych jawnie obecnych w kształcie danych wyjściowych może być mniejsza niż liczba wymiarów wejściowych. Wymiary „brakujące”, które są wyraźnie wymienione jako
collapsed_slice_dims, muszą mieć rozmiar wycinka1. Ponieważ mają one rozmiar wycinka1, jedynym prawidłowym indeksem jest0, a ich pominięcie nie wprowadza niejednoznaczności.Wyodrębniony z tablicy „Zbierz indeksy” wycinek ((
X,Y) w ostatnim przykładzie) może mieć mniej elementów niż liczba wymiarów tablicy wejściowej, a jawne mapowanie określa, jak indeks powinien zostać rozwinięty, aby mieć taką samą liczbę wymiarów jak dane wejściowe.
Na koniec używamy (2) i (3), aby zaimplementować tf.gather_nd:
G0 i G1 służą do wyodrębniania indeksu początkowego z tablicy indeksów zbierania w zwykły sposób, z tym wyjątkiem, że indeks początkowy ma tylko jeden element, X. Podobnie istnieje tylko jeden indeks przesunięcia danych wyjściowych o wartości O0. Zanim jednak zostaną użyte jako indeksy w tablicy wejściowej, są rozwijane zgodnie z zasadami „Mapowanie indeksu zbierania” (start_index_map w formalnym opisie) i „Mapowanie przesunięcia” (remapped_offset_dims w formalnym opisie) do postaci [X,0] i [0,O0], co daje w sumie [X,O0]. Innymi słowy,indeks wyjściowy [G0, G1,O0] jest mapowany na indeks wejściowy [GatherIndices[G0,G1,0],O0],co daje nam semantykę dla tf.gather_nd.
slice_sizes w tym przypadku to [1,11]. Intuicyjnie oznacza to, że każdy indeks X w tablicy indeksów zbierania wybiera cały wiersz, a wynikiem jest połączenie wszystkich tych wierszy.
GetDimensionSize
Zobacz też XlaBuilder::GetDimensionSize.
Zwraca rozmiar danego wymiaru argumentu. Operand musi mieć kształt tablicy.
GetDimensionSize(operand, dimension)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
n-wymiarowa tablica wejściowa |
dimension
|
int64
|
Wartość z przedziału [0, n) określająca wymiar. |
Informacje o StableHLO znajdziesz w artykule StableHLO – get_dimension_size.
GetTupleElement
Zobacz też XlaBuilder::GetTupleElement.
Indeksuje krotkę za pomocą wartości stałej w czasie kompilacji.
Wartość musi być stałą w czasie kompilacji, aby wnioskowanie o kształcie mogło określić typ wynikowej wartości.
Jest to analogiczne do std::get<int N>(t) w C++. Koncepcyjnie:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
Zobacz też tf.tuple.
GetTupleElement(tuple_data, index)
| Argument | Typ | Semantyka |
|---|---|---|
tuple_data |
XlaOP |
Krotka |
index |
int64 |
Indeks kształtu krotki |
Informacje o StableHLO znajdziesz w artykule StableHLO – get_tuple_element.
Imag
Zobacz też XlaBuilder::Imag.
Część urojona elementu kształtu zespolonego (lub rzeczywistego). x -> imag(x). Jeśli operand jest typu zmiennoprzecinkowego, zwraca 0.
Imag(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Informacje o StableHLO znajdziesz w artykule StableHLO – imag.
Infeed
Zobacz też XlaBuilder::Infeed.
Infeed(shape, config)
| Argument | Typ | Semantyka |
|---|---|---|
shape
|
Shape
|
Kształt danych odczytanych z interfejsu Infeed. Pole układu kształtu musi być ustawione tak, aby pasowało do układu danych wysyłanych na urządzenie. W przeciwnym razie jego działanie jest nieokreślone. |
config |
opcjonalne string |
Konfiguracja operacji. |
Odczytuje pojedynczy element danych z niejawnego interfejsu przesyłania strumieniowego Infeed urządzenia, interpretując dane jako podany kształt i jego układ, i zwraca XlaOp danych. W obliczeniach dozwolonych jest wiele operacji Infeed, ale musi między nimi istnieć porządek całkowity. Na przykład dwie zmienne w poniższym kodzie mają całkowity porządek, ponieważ istnieje zależność między pętlami while.Infeed
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
Zagnieżdżone kształty krotek nie są obsługiwane. W przypadku pustego kształtu krotki operacja Infeed jest w zasadzie bezczynna i przebiega bez odczytywania danych z kanału Infeed urządzenia.
Informacje o StableHLO znajdziesz w artykule StableHLO – infeed.
Iota
Zobacz też XlaBuilder::Iota.
Iota(shape, iota_dimension)
Tworzy stały literał na urządzeniu zamiast potencjalnie dużego transferu hosta. Tworzy tablicę o określonym kształcie, która zawiera wartości zaczynające się od zera i zwiększające się o jeden wzdłuż określonego wymiaru. W przypadku typów zmiennoprzecinkowych utworzona tablica jest równoważna ConvertElementType(Iota(...)), gdzie Iota jest typu całkowitego, a konwersja jest do typu zmiennoprzecinkowego.
| Argumenty | Typ | Semantyka |
|---|---|---|
shape |
Shape |
Kształt tablicy utworzonej przez Iota() |
iota_dimension |
int64 |
Wymiar, wzdłuż którego ma nastąpić przyrost. |
Na przykład Iota(s32[4, 8], 0) zwraca
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
Iota(s32[4, 8], 1) za możliwość zwrotu
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
Informacje o StableHLO znajdziesz w artykule StableHLO – iota.
IsFinite
Zobacz też XlaBuilder::IsFinite.
Sprawdza, czy każdy element operand jest skończony, tzn. nie jest dodatnią ani ujemną nieskończonością i nie jest wartością NaN. Zwraca tablicę wartości PRED o takim samym kształcie jak dane wejściowe, gdzie każdy element ma wartość true wtedy i tylko wtedy, gdy odpowiedni element wejściowy jest skończony.
IsFinite(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Informacje o StableHLO znajdziesz w artykule StableHLO – is_finite.
Log
Zobacz też XlaBuilder::Log.
Logarytm naturalny każdego elementu x -> ln(x).
Log(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja LOG obsługuje też opcjonalny argument result_accuracy:
Log(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – log.
Log1p
Zobacz też XlaBuilder::Log1p.
Przesunięty logarytm naturalny x -> ln(1+x).
Log1p(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja log1p obsługuje też opcjonalny argument result_accuracy:
Log1p(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – log_plus_one.
Logistyczna
Zobacz też XlaBuilder::Logistic.
Obliczenie funkcji logistycznej dla poszczególnych elementów x -> logistic(x).
Logistic(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja logistyczna obsługuje też opcjonalny argument result_accuracy:
Logistic(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – logistyka.
Mapa
Zobacz też XlaBuilder::Map.
Map(operands..., computation, dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands |
sekwencja N znaków XlaOp, |
N tablic typów T0..T{N-1} |
computation
|
XlaComputation
|
Obliczenia typu T_0, T_1,
.., T_{N + M -1} -> S z N parametrami typu T i M parametrami dowolnego typu. |
dimensions |
int64 tablica |
Tablica wymiarów mapy |
static_operands
|
sekwencja N znaków XlaOp,
|
Statyczne operacje na mapie |
Stosuje funkcję skalarną do podanych tablic operands, tworząc tablicę o tych samych wymiarach, w której każdy element jest wynikiem zastosowania funkcji mapowania do odpowiednich elementów w tablicach wejściowych.
Zmapowana funkcja to dowolne obliczenie z ograniczeniem, że ma N danych wejściowych typu skalarnego T i 1 dane wyjściowe typu S. Dane wyjściowe mają te same wymiary co operandy, z tym że typ elementu T jest zastępowany typem S.
Przykład: Map(op1, op2, op3, computation, par1) mapuje elem_out <-
computation(elem1, elem2, elem3, par1) przy każdym indeksie (wielowymiarowym) w tablicach wejściowych, aby utworzyć tablicę wyjściową.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – mapa.
Maks.
Zobacz też XlaBuilder::Max.
Wykonuje operację max na poszczególnych elementach tensorów lhs i rhs.
Max(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Dla Maxa dostępna jest alternatywna wersja z obsługą transmisji w różnych wymiarach:
Max(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Informacje o StableHLO znajdziesz w artykule StableHLO – maksimum.
Minimum
Zobacz też XlaBuilder::Min.
Wykonuje operację minimum na poszczególnych elementach tensorów lhs i rhs.
Min(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywna wersja z obsługą transmisji w różnych wymiarach dla:
Min(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Informacje o StableHLO znajdziesz w sekcji StableHLO – minimum.
Mul
Zobacz też XlaBuilder::Mul.
Wykonuje iloczyn elementów lhs i rhs.
Mul(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywna wersja z obsługą transmisji o różnych wymiarach dla Mul:
Mul(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – mnożenie.
Neg
Zobacz też XlaBuilder::Neg.
Negacja element po elemencie x -> -x.
Neg(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – negate.
Nie
Zobacz też XlaBuilder::Not.
Logiczne zaprzeczenie elementu x -> !(x).
Not(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Informacje o StableHLO znajdziesz w artykule StableHLO – not.
OptimizationBarrier
Zobacz też XlaBuilder::OptimizationBarrier.
Blokuje przenoszenie obliczeń przez barierę w ramach dowolnego etapu optymalizacji.
OptimizationBarrier(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Zapewnia, że wszystkie dane wejściowe są oceniane przed operatorami, którzy zależą od wyników bariery.
Informacje o StableHLO znajdziesz w sekcji StableHLO – optimization_barrier.
Lub
Zobacz też XlaBuilder::Or.
Wykonuje operację OR na poszczególnych elementach tensorów lhs i rhs .
Or(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje wariant alternatywny z obsługą transmisji w różnych wymiarach dla:
Or(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Informacje o StableHLO znajdziesz w artykule StableHLO.
Wyjście
Zobacz też XlaBuilder::Outfeed.
Zapisuje dane wejściowe w pliku wyjściowym.
Outfeed(operand, shape_with_layout, outfeed_config)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica typu T |
shape_with_layout |
Shape |
Określa układ przesyłanych danych. |
outfeed_config |
string |
Stała konfiguracji instrukcji Outfeed |
shape_with_layout określa kształt, który chcemy wygenerować.
Informacje o StableHLO znajdziesz w artykule StableHLO – dane wyjściowe.
Podkładka
Zobacz też XlaBuilder::Pad.
Pad(operand, padding_value, padding_config)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica typu T |
padding_value
|
XlaOp
|
skalar typu T, który wypełni dodane dopełnienie. |
padding_config
|
PaddingConfig
|
wartość dopełnienia na obu krawędziach (niska, wysoka) i między elementami każdego wymiaru. |
Rozszerza podaną tablicę operand, dodając do niej dopełnienie wokół niej i między jej elementami za pomocą podanego znaku padding_value. padding_config
określa ilość dopełnienia krawędzi i dopełnienia wewnętrznego dla każdego
wymiaru.
PaddingConfig to pole powtarzane w obiekcie PaddingConfigDimension, które zawiera 3 pola dla każdego wymiaru: edge_padding_low, edge_padding_high i interior_padding.
edge_padding_low i edge_padding_high określają ilość dopełnienia dodanego odpowiednio na początku (obok indeksu 0) i na końcu (obok najwyższego indeksu) każdego wymiaru. Wartość dopełnienia krawędzi może być ujemna. Wartość bezwzględna ujemnego dopełnienia wskazuje liczbę elementów do usunięcia z określonego wymiaru.
interior_padding określa ilość dopełnienia dodanego między dowolnymi 2 elementami w każdym wymiarze. Nie może być ujemna. Dopełnienie wewnętrzne występuje logicznie przed dopełnieniem krawędzi, więc w przypadku ujemnego dopełnienia krawędzi elementy są usuwane z operandu z dopełnieniem wewnętrznym.
Ta operacja nie ma wpływu na wynik, jeśli wszystkie pary dopełnienia krawędzi to (0, 0), a wartości dopełnienia wewnętrznego to 0. Na rysunku poniżej przedstawiono przykłady różnych wartości edge_padding i interior_padding w przypadku tablicy dwuwymiarowej.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – pad.
Parametr
Zobacz też XlaBuilder::Parameter.
Parameter reprezentuje argument wejściowy do obliczeń.
PartitionID
Zobacz też XlaBuilder::BuildPartitionId.
Generuje partition_id bieżącego procesu.
PartitionID(shape)
| Argumenty | Typ | Semantyka |
|---|---|---|
shape |
Shape |
Kształt danych |
Zapis PartitionID może się pojawiać w zrzutach HLO, ale nie jest przeznaczony do ręcznego tworzenia przez użytkowników.
Informacje o StableHLO znajdziesz w artykule StableHLO – partition_id.
PopulationCount
Zobacz też XlaBuilder::PopulationCount.
Oblicza liczbę ustawionych bitów w każdym elemencie operand.
PopulationCount(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – popcnt.
Pow
Zobacz też XlaBuilder::Pow.
Wykonuje potęgowanie elementów lhs przez rhs.
Pow(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywna odmiana z obsługą transmisji w różnych wymiarach dla Pow:
Pow(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – zasilanie.
Real
Zobacz też XlaBuilder::Real.
Część rzeczywista elementu złożonego (lub rzeczywistego). x -> real(x). Jeśli operand jest liczbą zmiennoprzecinkową, Real zwraca tę samą wartość.
Real(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Informacje o StableHLO znajdziesz w artykule StableHLO – rzeczywistość.
Recv
Zobacz też XlaBuilder::Recv.
Recv, RecvWithTokens i RecvToHost to operacje, które służą jako podstawowe elementy komunikacji w HLO. Te operacje zwykle pojawiają się w zrzutach HLO jako część operacji wejścia/wyjścia niskiego poziomu lub przesyłania danych między urządzeniami, ale nie są przeznaczone do ręcznego tworzenia przez użytkowników.
Recv(shape, handle)
| Argumenty | Typ | Semantyka |
|---|---|---|
shape |
Shape |
kształt danych do odebrania; |
handle |
ChannelHandle |
unikalny identyfikator każdej pary wysyłania/odbierania; |
Otrzymuje dane o podanym kształcie z instrukcji Send w innym obliczeniu, które korzysta z tego samego uchwytu kanału. Zwraca XlaOp dla otrzymanych danych.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – recv.
RecvDone
Zobacz też HloInstruction::CreateRecv i HloInstruction::CreateRecvDone.
Podobnie jak w przypadku operacji Send, interfejs API klienta operacji Recv reprezentuje komunikację synchroniczną. Instrukcja jest jednak wewnętrznie rozkładana na 2 instrukcje HLO (Recv i RecvDone), aby umożliwić asynchroniczne przesyłanie danych.
Recv(const Shape& shape, int64 channel_id)
Przydziela zasoby wymagane do odbierania danych z instrukcji Send o tym samym identyfikatorze kanału. Zwraca kontekst przydzielonych zasobów, który jest używany przez następną instrukcję RecvDone do oczekiwania na zakończenie przesyłania danych. Kontekst to krotka {bufor odbioru (kształt), identyfikator żądania (U32)}, która może być używana tylko przez instrukcję RecvDone.
W kontekście utworzonym przez instrukcję Recv czeka na zakończenie przesyłania danych i zwraca otrzymane dane.
Ograniczamy
Zobacz też XlaBuilder::Reduce.
Stosuje funkcję redukcji do co najmniej 1 tablicy równolegle.
Reduce(operands..., init_values..., computation, dimensions_to_reduce)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands
|
Sekwencja N XlaOp
|
N tablic typów T_0,...,
T_{N-1}. |
init_values
|
Sekwencja N XlaOp
|
N skalarów typów
T_0,..., T_{N-1}. |
computation
|
XlaComputation
|
obliczenia typu
T_0,..., T_{N-1}, T_0,
...,T_{N-1} ->
Collate(T_0,...,
T_{N-1}). |
dimensions_to_reduce
|
int64 tablica
|
nieuporządkowana tablica wymiarów do zredukowania. |
Gdzie:
- Wartość N musi być większa lub równa 1.
- Obliczenia muszą być „w przybliżeniu” łączne (patrz poniżej).
- Wszystkie tablice wejściowe muszą mieć te same wymiary.
- Wszystkie wartości początkowe muszą tworzyć tożsamość w ramach
computation. - Jeśli
N = 1,Collate(T)toT. - Jeśli
N > 1,Collate(T_0, ..., T_{N-1})jest krotkąNelementów typuT.
Ta operacja zmniejsza co najmniej 1 wymiar każdej tablicy wejściowej do skalarów.
Liczba wymiarów każdej zwróconej tablicy to number_of_dimensions(operand) - len(dimensions). Wynikiem działania tego operatora jest
Collate(Q_0, ..., Q_N), gdzie Q_i to tablica typu T_i, której
wymiary opisano poniżej.
Różne back-endy mogą ponownie powiązać obliczenia redukcji. Może to prowadzić do różnic liczbowych, ponieważ niektóre funkcje redukcji, takie jak dodawanie, nie są łączne w przypadku liczb zmiennoprzecinkowych. Jeśli jednak zakres danych jest ograniczony, dodawanie liczb zmiennoprzecinkowych jest wystarczająco łączne w większości praktycznych zastosowań.
Informacje o StableHLO znajdziesz w artykule StableHLO – reduce.
Przykłady
Gdy redukujesz w jednym wymiarze w pojedynczej tablicy 1D z wartościami [10, 11,
12, 13] za pomocą funkcji redukcji f (czyli computation), możesz to obliczyć w ten sposób:
f(10, f(11, f(12, f(init_value, 13)))
ale istnieje też wiele innych możliwości, np.
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
Poniżej znajdziesz przykładowy pseudokod, który pokazuje, jak można zaimplementować redukcję, używając sumowania jako obliczenia redukcji z wartością początkową 0.
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
Oto przykład zmniejszania tablicy dwuwymiarowej (macierzy). Kształt ma 2 wymiary: wymiar 0 o rozmiarze 2 i wymiar 1 o rozmiarze 3:
Wyniki redukcji wymiarów 0 lub 1 za pomocą funkcji „dodawanie”:
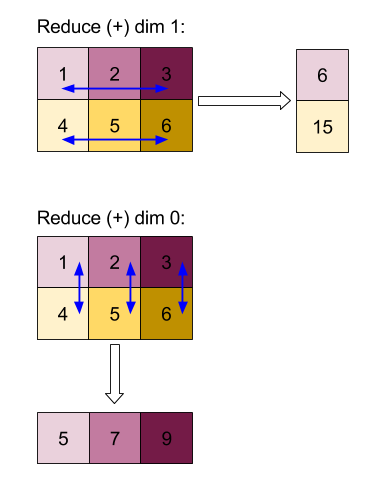
Pamiętaj, że oba wyniki redukcji to tablice 1D. Na diagramie jeden z nich jest przedstawiony jako kolumna, a drugi jako wiersz, co ułatwia wizualizację.
Oto bardziej złożony przykład tablicy 3D. Liczba wymiarów wynosi 3, wymiar 0 ma rozmiar 4, wymiar 1 ma rozmiar 2, a wymiar 2 ma rozmiar 3. Dla uproszczenia wartości od 1 do 6 są powielane w wymiarze 0.
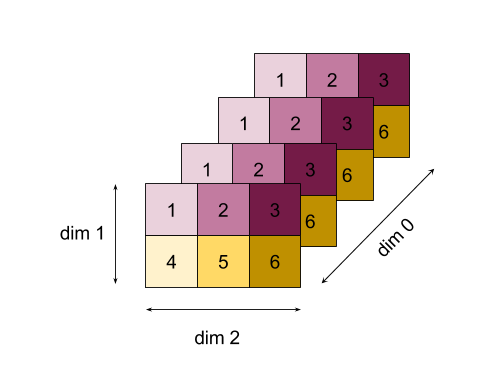
Podobnie jak w przypadku przykładu 2D możemy zmniejszyć tylko jeden wymiar. Jeśli np. zmniejszymy wymiar 0, otrzymamy tablicę dwuwymiarową, w której wszystkie wartości w wymiarze 0 zostały przekształcone w wartość skalarną:
| 4 8 12 |
| 16 20 24 |
Jeśli zmniejszymy wymiar 2, otrzymamy tablicę dwuwymiarową, w której wszystkie wartości w wymiarze 2 zostały przekształcone w wartość skalarną:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
Pamiętaj, że względna kolejność pozostałych wymiarów w danych wejściowych jest zachowywana w danych wyjściowych, ale niektóre wymiary mogą otrzymać nowe numery (ponieważ zmienia się liczba wymiarów).
Możemy też zmniejszyć liczbę wymiarów. Dodanie wymiarów 0 i 1 powoduje powstanie 1-wymiarowej tablicy [20, 28, 36].
Zmniejszenie tablicy 3D we wszystkich jej wymiarach daje skalar 84.
Variadic Reduce
Gdy N > 1, zastosowanie funkcji redukcji jest nieco bardziej złożone, ponieważ jest ona stosowana jednocześnie do wszystkich danych wejściowych. Operandy są przekazywane do obliczeń w tej kolejności:
- Uruchomienie zmniejszonej wartości pierwszego argumentu
- …
- Uruchomienie zmniejszonej wartości dla N-tego operandu
- Wartość wejściowa pierwszego argumentu
- …
- Wartość wejściowa N-tego operandu
Rozważmy na przykład tę funkcję redukcji, której można użyć do równoległego obliczania wartości maksymalnej i argumentu maksymalnego w tablicy 1D:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
W przypadku jednowymiarowych tablic wejściowych V = Float[N], K = Int[N] i wartości początkowych I_V = Float, I_K = Int wynik f_(N-1) redukcji w jedynym wymiarze wejściowym jest równoważny z następującym zastosowaniem rekurencyjnym:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
Zastosowanie tej redukcji do tablicy wartości i tablicy kolejnych indeksów (np. iota) spowoduje iterację po tablicach i zwrócenie krotki zawierającej maksymalną wartość i pasujący indeks.
ReducePrecision
Zobacz też XlaBuilder::ReducePrecision.
Modeluje efekt konwersji wartości zmiennoprzecinkowych na format o mniejszej precyzji (np. IEEE-FP16) i z powrotem na format pierwotny. Liczbę bitów wykładnika i mantysy w formacie o niższej precyzji można określić dowolnie, chociaż nie wszystkie rozmiary bitów mogą być obsługiwane we wszystkich implementacjach sprzętowych.
ReducePrecision(operand, exponent_bits, mantissa_bits)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica liczb zmiennoprzecinkowychT. |
exponent_bits |
int32 |
liczba bitów wykładnika w formacie o niższej precyzji; |
mantissa_bits |
int32 |
liczba bitów mantysy w formacie o mniejszej precyzji; |
Wynikiem jest tablica typu T. Wartości wejściowe są zaokrąglane do najbliższej wartości, którą można przedstawić za pomocą podanej liczby bitów mantysy (z użyciem semantyki „zaokrąglanie do najbliższej parzystej”), a wszystkie wartości przekraczające zakres określony przez liczbę bitów wykładnika są ograniczane do dodatniej lub ujemnej nieskończoności. Wartości NaN są zachowywane, chociaż mogą być przekształcane w kanoniczne wartości NaN.
Format o mniejszej precyzji musi mieć co najmniej 1 bit wykładnika (aby odróżnić wartość zero od nieskończoności, ponieważ obie mają mantysę równą zero) i nieujemną liczbę bitów mantysy. Liczba bitów wykładnika lub mantysy może przekraczać odpowiednią wartość dla typu T; odpowiednia część konwersji jest wtedy po prostu operacją bez efektu.
Informacje o StableHLO znajdziesz w sekcji StableHLO – reduce_precision.
ReduceScatter
Zobacz też XlaBuilder::ReduceScatter.
ReduceScatter to operacja zbiorowa, która skutecznie wykonuje AllReduce, a następnie rozprasza wynik, dzieląc go na shard_count bloków wzdłuż wymiaru scatter_dimension, a replika i w grupie replik otrzymuje fragment ith.
ReduceScatter(operand, computation, scatter_dimension, shard_count,
replica_groups, channel_id, layout, use_global_device_ids)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand
|
XlaOp
|
Tablica lub niepusta krotka tablic do zredukowania w replikach. |
computation |
XlaComputation |
Obliczanie redukcji |
scatter_dimension |
int64 |
Wymiar do rozproszenia. |
shard_count
|
int64
|
Liczba bloków do podziału
scatter_dimension |
replica_groups
|
ReplicaGroup wektor
|
Grupy, między którymi przeprowadzane są redukcje |
channel_id
|
opcjonalne
ChannelHandle |
Opcjonalny identyfikator kanału do komunikacji między modułami |
layout
|
opcjonalne Layout
|
układ pamięci określony przez użytkownika, |
use_global_device_ids |
opcjonalne bool |
flaga określona przez użytkownika, |
- Gdy
operandjest krotką tablic, operacja reduce-scatter jest wykonywana na każdym elemencie krotki. replica_groupsto lista grup replik, między którymi przeprowadzane jest zmniejszanie (identyfikator repliki dla bieżącej repliki można pobrać za pomocąReplicaId). Kolejność replik w każdej grupie określa kolejność, w jakiej zostanie rozproszony wynik operacji all-reduce.replica_groupsmusi być puste (w takim przypadku wszystkie repliki należą do jednej grupy) lub zawierać tyle samo elementów co liczba replik. Jeśli jest więcej niż jedna grupa replik, wszystkie muszą mieć ten sam rozmiar. Na przykład funkcjareplica_groups = {0, 2}, {1, 3}wykonuje redukcję między replikami0i2oraz1i3, a następnie rozprasza wynik.shard_countto rozmiar każdej grupy replik. Jest to konieczne w przypadku, gdy polereplica_groupsjest puste. Jeśli polereplica_groupsnie jest puste, wartośćshard_countmusi być równa rozmiarowi każdej grupy replik.channel_idjest używany do komunikacji między modułami: tylko operacjereduce-scatterz tym samymchannel_idmogą się ze sobą komunikować.layoutWięcej informacji o układach znajdziesz w sekcji xla::shapes.use_global_device_idsto flaga określona przez użytkownika. Gdyfalse(domyślnie) liczby wreplica_groupssąReplicaId, a gdytrueliczby wreplica_groupsreprezentują globalny identyfikator (ReplicaID*partition_count+partition_id). Przykład:- W przypadku 2 replik i 4 partycji
- replica_groups={ {0,1,4,5},{2,3,6,7} } and use_global_device_ids=true
- group[0] = (0,0), (0,1), (1,0), (1,1)
- group[1] = (0,2), (0,3), (1,2), (1,3)
- gdzie każda para to (replica_id, partition_id).
Kształt wyjściowy jest kształtem wejściowym zmniejszonym scatter_dimension razy.shard_count Jeśli na przykład są 2 repliki, a operand ma odpowiednio wartości [1.0, 2.25] i [3.0, 5.25] w tych 2 replikach, to wartość wyjściowa tego działania, w którym scatter_dim to 0, będzie wynosić [4.0] w przypadku pierwszej repliki i [7.5] w przypadku drugiej repliki.
Informacje o StableHLO znajdziesz w artykule StableHLO – reduce_scatter.
ReduceScatter - Example 1 - StableHLO
W przykładzie powyżej w operacji ReduceScatter uczestniczą 2 repliki. W każdej replice operand ma kształt f32[2,4]. Na replikach jest wykonywana operacja all-reduce (suma), która daje zredukowaną wartość o kształcie f32[2,4] na każdej replice. Zmniejszona wartość jest następnie dzielona na 2 części wzdłuż wymiaru 1, więc każda część ma kształt f32[2,2]. Każda replika w grupie procesów otrzymuje część odpowiadającą jej pozycji w grupie. W rezultacie dane wyjściowe na każdej replice mają kształt f32[2,2].
ReduceWindow
Zobacz też XlaBuilder::ReduceWindow.
Stosuje funkcję redukcji do wszystkich elementów w każdym oknie sekwencji N wielowymiarowych tablic, tworząc jako dane wyjściowe pojedynczą lub krotkę N wielowymiarowych tablic. Każda tablica wyjściowa ma tyle samo elementów, ile jest prawidłowych pozycji okna. Warstwę puli można wyrazić jako ReduceWindow. Podobnie jak w przypadku Reduce, zastosowany computation jest zawsze przekazywany do init_values po lewej stronie.
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands
|
N XlaOps
|
Ciąg N wielowymiarowych tablic typu T_0,..., T_{N-1}, z których każda reprezentuje obszar bazowy, na którym umieszczone jest okno. |
init_values
|
N XlaOps
|
N wartości początkowych redukcji, po jednej dla każdego z N operandów. Więcej informacji znajdziesz w sekcji Zmniejsz. |
computation
|
XlaComputation
|
Funkcja redukcji typu T_0,
..., T_{N-1}, T_0, ..., T_{N-1}
-> Collate(T_0, ..., T_{N-1}), która ma być stosowana do elementów w każdym oknie wszystkich operandów wejściowych. |
window_dimensions
|
ArraySlice<int64>
|
tablica liczb całkowitych dla wartości wymiaru okna |
window_strides
|
ArraySlice<int64>
|
tablica liczb całkowitych dla wartości okna kroku |
base_dilations
|
ArraySlice<int64>
|
tablica liczb całkowitych dla wartości dylatacji podstawy |
window_dilations
|
ArraySlice<int64>
|
tablica liczb całkowitych dla wartości dylatacji okna |
padding
|
Padding
|
typ dopełnienia okna (Padding::kSame, który dopełnia tak, aby kształt wyjściowy był taki sam jak kształt wejściowy, jeśli krok wynosi 1, lub Padding::kValid, który nie używa dopełnienia i „zatrzymuje” okno, gdy przestaje się mieścić); |
Gdzie:
- Wartość N musi być większa lub równa 1.
- Wszystkie tablice wejściowe muszą mieć te same wymiary.
- Jeśli
N = 1,Collate(T)toT. - Jeśli
N > 1,Collate(T_0, ..., T_{N-1})jest krotkąNelementów typu(T0,...T{N-1}).
Informacje o StableHLO znajdziesz w artykule StableHLO – reduce_window.
ReduceWindow – przykład 1
Dane wejściowe to macierz o rozmiarze [4x6], a zarówno window_dimensions, jak i window_stride_dimensions mają rozmiar [2x3].
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
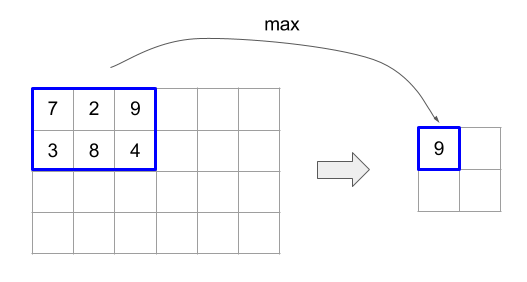
Krok 1 w wymiarze oznacza, że pozycja okna w tym wymiarze jest oddalona o 1 element od sąsiedniego okna. Aby określić, że okna nie nakładają się na siebie, wymiary_kroku_okna powinny być równe wymiarom_okna. Ilustracja poniżej pokazuje użycie dwóch różnych wartości parametru stride. Dopełnienie jest stosowane do każdego wymiaru danych wejściowych, a obliczenia są takie same, jak gdyby dane wejściowe miały wymiary po dopełnieniu.
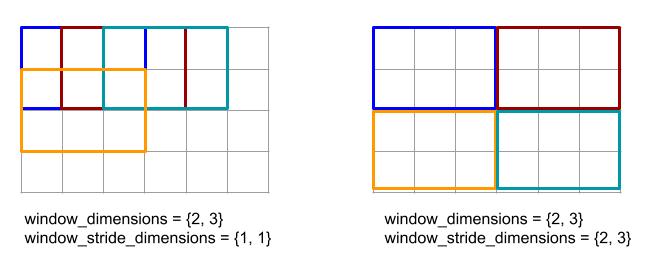
Aby zobaczyć nietrywialny przykład dopełnienia, rozważ obliczenie minimum w oknie redukcji (wartość początkowa to MAX_FLOAT) z wymiarem 3 i krokiem 2 na tablicy wejściowej [10000, 1000, 100, 10, 1]. Wypełnienie kValid oblicza wartości minimalne w 2 prawidłowych oknach: [10000, 1000, 100] i [100, 10, 1], co daje wynik [100, 1]. Wypełnienie kSame najpierw wypełnia tablicę, tak aby kształt po zastosowaniu funkcji reduce-window był taki sam jak dane wejściowe dla kroku 1, poprzez dodanie początkowych elementów po obu stronach, co daje [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE]. Zastosowanie funkcji reduce-window do wypełnionej tablicy powoduje utworzenie 3 okien: [MAX_VALUE, 10000, 1000], [1000, 100, 10] i [10, 1, MAX_VALUE], a w wyniku działania funkcji otrzymujemy [1000, 10, 1].
Kolejność obliczania funkcji redukcji jest dowolna i może być niedeterministyczna. Dlatego funkcja redukcji nie powinna być zbyt wrażliwa na ponowne powiązanie. Więcej informacji znajdziesz w omówieniu łączności w kontekście Reduce.
ReduceWindow - Example 2 - StableHLO
W powyższym przykładzie:
Dane wejściowe) Operand ma kształt wejściowy S32[3,2]. o wartościach
[[1,2],[3,4],[5,6]]
Krok 1. Rozszerzenie podstawowe ze współczynnikiem 2 wzdłuż wymiaru wiersza wstawia otwory między poszczególnymi wierszami operandu. Po rozszerzeniu dodawane jest dopełnienie w postaci 2 wierszy u góry i 1 wiersza u dołu. W efekcie tensor staje się wyższy.
Krok 2. Zdefiniowano okno o kształcie [2,1] z rozszerzeniem okna [3,1]. Oznacza to, że każde okno wybiera 2 elementy z tej samej kolumny, ale drugi element jest pobierany 3 wiersze poniżej pierwszego, a nie bezpośrednio pod nim.
Krok 3. Okna są następnie przesuwane po operandzie z krokiem [4,1]. Powoduje to przesunięcie okna o 4 wiersze w dół i o 1 kolumnę w poziomie. Komórki dopełniające są wypełniane znakiem init_value (w tym przypadku init_value = 0). Wartości „wpadające” do komórek rozszerzających są ignorowane.
Ze względu na krok i wypełnienie niektóre okna nakładają się tylko na zera i luki, a inne na rzeczywiste wartości wejściowe.
Krok 4. W każdym oknie elementy są łączone za pomocą funkcji redukcji (a, b) → a + b, zaczynając od wartości początkowej 0. Dwa pierwsze okna widzą tylko wypełnienie i dziury, więc ich wyniki wynoszą 0. Dolne okna pobierają wartości 3 i 4 z danych wejściowych i zwracają je jako wyniki.
Wyniki) Ostateczny wynik ma kształt S32[2,2] i wartości: [[0,0],[3,4]]
Faza REM
Zobacz też XlaBuilder::Rem.
Wykonuje operację reszty z dzielenia element po elemencie dla dzielnej lhs i dzielnika rhs.
Znak wyniku jest taki sam jak znak dzielnej, a wartość bezwzględna wyniku jest zawsze mniejsza niż wartość bezwzględna dzielnika.
Rem(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Dla Rem istnieje alternatywna wersja z obsługą transmisji w różnych wymiarach:
Rem(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – reszta.
ReplicaId
Zobacz też XlaBuilder::ReplicaId.
Zwraca unikalny identyfikator repliki (skalar U32).
ReplicaId()
Unikalny identyfikator każdej repliki to liczba całkowita bez znaku z przedziału [0, N), gdzie N to liczba replik. Ponieważ wszystkie repliki uruchamiają ten sam program, wywołanie ReplicaId() w programie zwróci inną wartość na każdej replice.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – replica_id.
Zmień kształt
Zobacz też XlaBuilder::Reshape.
i operację Collapse.
Zmienia kształt wymiarów tablicy na nową konfigurację.
Reshape(operand, dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablicę typu T, |
dimensions |
int64 wektor |
wektor rozmiarów nowych wymiarów |
Koncepcyjnie funkcja reshape najpierw spłaszcza tablicę do jednowymiarowego wektora wartości danych, a następnie przekształca ten wektor w nowy kształt. Argumenty wejściowe to dowolna tablica typu T, wektor indeksów wymiarów stałych w czasie kompilacji i wektor rozmiarów wymiarów stałych w czasie kompilacji dla wyniku.
Wektor dimensions określa rozmiar tablicy wyjściowej. Wartość pod indeksem 0 w dimensions to rozmiar wymiaru 0, wartość pod indeksem 1 to rozmiar wymiaru 1 itd. Iloczyn wymiarów dimensions musi być równy iloczynowi rozmiarów wymiarów operandu. Podczas przekształcania spłaszczonej tablicy w tablicę wielowymiarową zdefiniowaną przez dimensions wymiary w dimensions są uporządkowane od najwolniej zmieniającego się (najważniejszego) do najszybciej zmieniającego się (najmniej ważnego).
Niech na przykład v będzie tablicą 24 elementów:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
W szczególnym przypadku funkcja reshape może przekształcić tablicę jednoelementową w skalar i na odwrót. Na przykład
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – zmiana kształtu.
Zmiana kształtu (jawna)
Zobacz też XlaBuilder::Reshape.
Reshape(shape, operand)
Operacja zmiany kształtu, która używa jawnego kształtu docelowego.
| Argumenty | Typ | Semantyka |
|---|---|---|
shape |
Shape |
Kształt wyjściowy typu T |
operand |
XlaOp |
tablicę typu T, |
Rev (odwrócony)
Zobacz też XlaBuilder::Rev.
Rev(operand, dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablicę typu T, |
dimensions |
ArraySlice<int64> |
wymiary do odwrócenia, |
Odwraca kolejność elementów w tablicy operand wzdłuż określonej dimensions, generując tablicę wyjściową o tym samym kształcie. Każdy element tablicy operandów o indeksie wielowymiarowym jest zapisywany w tablicy wyjściowej pod przekształconym indeksem. Indeks wielowymiarowy jest przekształcany przez odwrócenie indeksu w każdym wymiarze, który ma zostać odwrócony (tzn. jeśli wymiar o rozmiarze N jest jednym z wymiarów odwracanych, jego indeks i jest przekształcany w N – 1 – i).
Jednym z zastosowań operacji Rev jest odwracanie tablicy wag konwolucji wzdłuż 2 wymiarów okna podczas obliczania gradientu w sieciach neuronowych.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – reverse.
RngNormal
Zobacz też XlaBuilder::RngNormal.
Tworzy dane wyjściowe o danym kształcie z losowymi liczbami wygenerowanymi zgodnie z \(N(\mu, \sigma)\) rozkładem normalnym. Parametry \(\mu\) i \(\sigma\)oraz kształt wyjściowy muszą mieć typ elementu zmiennoprzecinkowego. Parametry muszą mieć ponadto wartość skalarną.
RngNormal(mu, sigma, shape)
| Argumenty | Typ | Semantyka |
|---|---|---|
mu |
XlaOp |
Skalar typu T określający średnią wygenerowanych liczb. |
sigma
|
XlaOp
|
Skalar typu T określający odchylenie standardowe wygenerowanych |
shape |
Shape |
Kształt wyjściowy typu T |
Informacje o StableHLO znajdziesz w artykule StableHLO – rng.
RngUniform
Zobacz też XlaBuilder::RngUniform.
Tworzy dane wyjściowe o podanym kształcie z liczbami losowymi wygenerowanymi zgodnie z rozkładem jednostajnym w przedziale \([a,b)\). Parametry i typ elementu wyjściowego muszą być typem logicznym, typem całkowitym lub typem zmiennoprzecinkowym, a typy muszą być spójne. Obecnie backendy procesora i GPU obsługują tylko typy F64, F32, F16, BF16, S64, U64, S32 i U32. Ponadto parametry muszą mieć wartość skalarną. Jeśli \(b <= a\) wynik jest zdefiniowany przez implementację.
RngUniform(a, b, shape)
| Argumenty | Typ | Semantyka |
|---|---|---|
a |
XlaOp |
Skalar typu T określający dolną granicę przedziału |
b |
XlaOp |
Skalar typu T określający górny limit interwału |
shape |
Shape |
Kształt wyjściowy typu T |
Informacje o StableHLO znajdziesz w artykule StableHLO – rng.
RngBitGenerator
Zobacz też XlaBuilder::RngBitGenerator.
Generuje dane wyjściowe o podanym kształcie wypełnione jednolitymi losowymi bitami przy użyciu określonego algorytmu (lub domyślnego algorytmu backendu) i zwraca zaktualizowany stan (o takim samym kształcie jak stan początkowy) oraz wygenerowane dane losowe.
Stan początkowy to stan początkowy bieżącego generowania liczb losowych. Jego kształt i prawidłowe wartości zależą od użytego algorytmu.
Wynik jest deterministyczną funkcją stanu początkowego, ale nie musi być deterministyczny w przypadku różnych backendów i wersji kompilatora.
RngBitGenerator(algorithm, initial_state, shape)
| Argumenty | Typ | Semantyka |
|---|---|---|
algorithm |
RandomAlgorithm |
Algorytm PRNG, który ma być używany. |
initial_state |
XlaOp |
Stan początkowy algorytmu PRNG. |
shape |
Shape |
Kształt danych wyjściowych wygenerowanych danych. |
Dostępne wartości parametru algorithm:
rng_default: Algorytm specyficzny dla backendu z wymaganiami dotyczącymi kształtu specyficznymi dla backendu.rng_three_fry: algorytm PRNG oparty na liczniku ThreeFry. Kształtinitial_statema wymiaryu64[2]z dowolnymi wartościami. Salmon i in. SC 2011. Równoległe liczby losowe: to proste jak 1, 2, 3.rng_philox: algorytm Philox do równoległego generowania liczb losowych. Kształtinitial_statetou64[3]z dowolnymi wartościami. Salmon i in. SC 2011. Równoległe liczby losowe: to proste jak 1, 2, 3.
Informacje o StableHLO znajdziesz w artykule StableHLO – rng_bit_generator.
RngGetAndUpdateState
Zobacz też HloInstruction::CreateRngGetAndUpdateState.
Interfejs API różnych Rng operacji jest wewnętrznie rozkładany na instrukcje HLO, w tym RngGetAndUpdateState.
RngGetAndUpdateState jest elementem podstawowym w HLO. Ta operacja może pojawiać się w zrzutach HLO, ale nie jest przeznaczona do ręcznego tworzenia przez użytkowników.
Okrągłe
Zobacz też XlaBuilder::Round.
Zaokrąglanie elementów, zaokrąglanie w górę od zera.
Round(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
RoundNearestAfz
Zobacz też XlaBuilder::RoundNearestAfz.
Wykonuje zaokrąglanie elementów do najbliższej liczby całkowitej, a w przypadku remisu zaokrągla w kierunku zera.
RoundNearestAfz(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Informacje o StableHLO znajdziesz w artykule StableHLO – round_nearest_afz.
RoundNearestEven
Zobacz też XlaBuilder::RoundNearestEven.
Zaokrąglanie elementów, zaokrąglanie do najbliższej parzystej liczby.
RoundNearestEven(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – round_nearest_even.
Rsqrt
Zobacz też XlaBuilder::Rsqrt.
Operacja odwrotności pierwiastka kwadratowego x -> 1.0 / sqrt(x).
Rsqrt(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja Rsqrt obsługuje też opcjonalny argument result_accuracy:
Rsqrt(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – rsqrt.
Skanowanie
Zobacz też XlaBuilder::Scan.
Stosuje funkcję redukcji do tablicy wzdłuż danego wymiaru, tworząc stan końcowy i tablicę wartości pośrednich.
Scan(inputs..., inits..., to_apply, scan_dimension,
is_reverse, is_associative)
| Argumenty | Typ | Semantyka |
|---|---|---|
inputs |
Sekwencja m XlaOp |
Tablice do przeskanowania. |
inits |
Sekwencja k XlaOp |
Początkowe przeniesienia. |
to_apply |
XlaComputation |
Obliczenia typu i_0, ..., i_{m-1}, c_0, ..., c_{k-1} -> (o_0, ..., o_{n-1}, c'_0, ..., c'_{k-1}). |
scan_dimension |
int64 |
Wymiar, wzdłuż którego ma być przeprowadzane skanowanie. |
is_reverse |
bool |
Jeśli tak, skanuj w odwrotnej kolejności. |
is_associative |
bool (trójstanowy) |
Jeśli ma wartość Prawda, operacja jest łączna. |
Funkcja to_apply jest stosowana kolejno do elementów w inputs wzdłuż scan_dimension. Jeśli is_reverse ma wartość false, elementy są przetwarzane w kolejności od 0 do N-1, gdzie N to rozmiar scan_dimension. Jeśli wartość is_reverse to „true”, elementy są przetwarzane od N-1 do 0.
Funkcja to_apply przyjmuje m + k argumenty:
mbieżących elementów zinputs.kprzenosi wartości z poprzedniego kroku (lubinitsw przypadku pierwszego elementu).
Funkcja to_apply zwraca krotkę wartości n + k:
nelementów zoutputs.knowe wartości przeniesienia.
Operacja skanowania zwraca krotkę n + k wartości:
- Tablice wyjściowe
nzawierające wartości wyjściowe dla każdego kroku. - Ostateczne wartości
ksą przenoszone po przetworzeniu wszystkich elementów.
Typy danych wejściowych m muszą być zgodne z typami pierwszych parametrów m funkcji to_apply z dodatkowym wymiarem skanowania. Typy danych wyjściowych n muszą być zgodne z typami pierwszych wartości zwracanych n funkcji to_apply z dodatkowym wymiarem skanowania. Dodatkowy wymiar skanowania wśród wszystkich danych wejściowych i wyjściowych musi mieć ten sam rozmiar N. Typy ostatnich k parametrów i wartości zwracanych przez to_apply, a także k inicjatorów muszą być zgodne.
Na przykład (m, n, k == 1, N == 3) dla początkowego przeniesienia i, danych wejściowych [a, b, c], funkcji f(x, c) -> (y, c') oraz scan_dimension=0, is_reverse=false:
- Krok 0.
f(a, i) -> (y0, c0) - Krok 1.
f(b, c0) -> (y1, c1) - Krok 2.
f(c, c1) -> (y2, c2)
Wynikiem działania funkcji Scan jest ([y0, y1, y2], c2).
Punktowy
Zobacz też XlaBuilder::Scatter.
Operacja rozproszenia XLA generuje sekwencję wyników, które są wartościami tablicy wejściowej operands, przy czym kilka wycinków (w indeksach określonych przez scatter_indices) jest aktualizowanych za pomocą sekwencji wartości w updates przy użyciu update_computation.
Scatter(operands..., scatter_indices, updates..., update_computation,
dimension_numbers, indices_are_sorted, unique_indices)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands |
Sekwencja N XlaOp |
N tablic typu T_0, ..., T_N, do których mają zostać rozproszone dane. |
scatter_indices |
XlaOp |
Tablica zawierająca indeksy początkowe wycinków, które mają zostać rozproszone. |
updates |
Sekwencja N XlaOp |
N tablic typów T_0, ..., T_N. updates[i] zawiera wartości, które muszą być używane do rozpraszania operands[i]. |
update_computation |
XlaComputation |
Obliczenia, które mają być używane do łączenia istniejących wartości w tablicy wejściowej i aktualizacji podczas rozpraszania. Obliczenie powinno być typu T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N). |
index_vector_dim |
int64 |
Wymiar w scatter_indices, który zawiera indeksy początkowe. |
update_window_dims |
ArraySlice<int64> |
Zbiór wymiarów w kształcie updates, które są wymiarami okna. |
inserted_window_dims |
ArraySlice<int64> |
Zbiór wymiarów okna, które należy wstawić do kształtu updates. |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
Mapa wymiarów z indeksów rozproszenia do przestrzeni indeksu operandu. Ta tablica jest interpretowana jako mapowanie i na scatter_dims_to_operand_dims[i] . Musi to być relacja jeden do jednego i całkowita. |
dimension_number |
ScatterDimensionNumbers |
Numery wymiarów dla operacji rozpraszania |
indices_are_sorted |
bool |
Określa, czy indeksy są posortowane przez wywołującego. |
unique_indices |
bool |
Określa, czy indeksy są gwarantowane jako unikalne przez wywołującego. |
Gdzie:
- Wartość N musi być większa lub równa 1.
operands[0], ...,operands[N-1] muszą mieć te same wymiary.updates[0], ...,updates[N-1] muszą mieć te same wymiary.- Jeśli
N = 1,Collate(T)toT. - Jeśli
N > 1,Collate(T_0, ..., T_N)jest krotkąNelementów typuT.
Jeśli index_vector_dim jest równe scatter_indices.rank, przyjmujemy, że scatter_indices ma wymiar końcowy 1.
Zdefiniujmy update_scatter_dims typu ArraySlice<int64> jako zbiór wymiarów o kształcie updates, które nie należą do update_window_dims, w kolejności rosnącej.
Argumenty funkcji scatter powinny być zgodne z tymi ograniczeniami:
Każda tablica
updatesmusi miećupdate_window_dims.size + scatter_indices.rank - 1wymiary.Granice wymiaru
iw każdej tablicyupdatesmuszą być zgodne z tymi zasadami:- Jeśli
iwystępuje wupdate_window_dims(tzn. jest równeupdate_window_dims[k] dla pewnegok), to zakres wymiaruiwupdatesnie może przekraczać odpowiedniego zakresuoperandpo uwzględnieniuinserted_window_dims(tzn.adjusted_window_bounds[k], gdzieadjusted_window_boundszawiera zakresyoperandz zakresami w indeksachinserted_window_dims). - Jeśli wartość
iwystępuje wupdate_scatter_dims(tzn. jest równaupdate_scatter_dims[k] dla pewnegok), to zakres wymiaruiwupdatesmusi być równy odpowiedniemu zakresowiscatter_indicesz pominięciemindex_vector_dim(tzn.scatter_indices.shape.dims[k], jeślik<index_vector_dim, a w przeciwnym raziescatter_indices.shape.dims[k+1]).
- Jeśli
update_window_dimsmusi być uporządkowany rosnąco, nie może zawierać powtarzających się numerów wymiarów i musi mieścić się w zakresie[0, updates.rank).inserted_window_dimsmusi być uporządkowany rosnąco, nie może zawierać powtarzających się numerów wymiarów i musi mieścić się w zakresie[0, operand.rank).Wartość
operand.rankmusi być równa sumie wartościupdate_window_dims.sizeiinserted_window_dims.size.Wartość parametru
scatter_dims_to_operand_dims.sizemusi być równascatter_indices.shape.dims[index_vector_dim], a jego wartości muszą mieścić się w zakresie[0, operand.rank).
Dla danego indeksu U w każdej tablicy updates odpowiedni indeks I w odpowiedniej tablicy operands, do której należy zastosować tę aktualizację, jest obliczany w ten sposób:
- Niech
G= {U[k] dlakwupdate_scatter_dims}. UżyjG, aby wyszukać wektor indeksuSw tablicyscatter_indicestaki, żeS[i] =scatter_indices[Combine(G,i)], gdzie Combine(A, b) wstawia b w pozycjachindex_vector_dimdo A. - Utwórz indeks
Sinwoperandza pomocąSprzez rozproszenieSza pomocą mapyscatter_dims_to_operand_dims. Bardziej formalnie:Sin[scatter_dims_to_operand_dims[k]] =S[k] ifk<scatter_dims_to_operand_dims.size.Sin[_] =0w innych przypadkach.
- Utwórz indeks
Winw każdej tablicyoperands, rozpraszając indeksy wupdate_window_dimswUzgodnie zinserted_window_dims. Bardziej formalnie:Win[window_dims_to_operand_dims(k)] =U[k] ifkis inupdate_window_dims, wherewindow_dims_to_operand_dimsis the monotonic function with domain [0,update_window_dims.size) and range [0,operand.rank) \inserted_window_dims. (Na przykład, jeśliupdate_window_dims.sizeto4,operand.rankto6, ainserted_window_dimsto {0,2}, towindow_dims_to_operand_dimsto {0→1,1→3,2→4,3→5}).Win[_] =0w innych przypadkach.
ItoWin+Sin, gdzie + oznacza dodawanie elementów.
Podsumowując, operację rozproszenia można zdefiniować w ten sposób:
- Zainicjuj
outputwartościąoperands, tzn. dla wszystkich indeksówJ, dla wszystkich indeksówOw tablicyoperands[J]:
output[J][O] =operands[J][O] - Dla każdego indeksu
Uw tablicyupdates[J] i odpowiedniego indeksuOw tablicyoperand[J], jeśliOjest prawidłowym indeksem dlaoutput:
(output[0][O], ...,output[N-1][O]) =update_computation(output[0][O], ..., ,output[N-1][O],updates[0][U], ...,updates[N-1][U])
Kolejność stosowania aktualizacji jest niedeterministyczna. Jeśli więc wiele indeksów w updates odnosi się do tego samego indeksu w operands, odpowiednia wartość w output będzie niedeterministyczna.
Pamiętaj, że pierwszy parametr przekazywany do funkcji update_computation będzie zawsze bieżącą wartością z tablicy output, a drugi parametr będzie zawsze wartością z tablicy updates. Jest to ważne zwłaszcza w przypadku, gdy update_computation nie jest przemienne.
Jeśli zasada indices_are_sorted ma wartość Prawda, XLA może założyć, że wartości scatter_indices są posortowane (w porządku rosnącym, po rozproszeniu wartości zgodnie z scatter_dims_to_operand_dims) przez użytkownika. Jeśli nie, semantyka jest zdefiniowana przez implementację.
Jeśli wartość unique_indices to „true”, XLA może założyć, że wszystkie rozproszone elementy są unikalne. Dlatego XLA może używać operacji nieatomowych. Jeśli wartość unique_indices to „true” (prawda), a indeksy, do których są rozpraszane dane, nie są unikalne, semantyka jest zdefiniowana przez implementację.
Nieformalnie operację rozproszenia można traktować jako odwrotność operacji zbierania, tzn. operacja rozproszenia aktualizuje elementy w danych wejściowych, które są wyodrębniane przez odpowiednią operację zbierania.
Szczegółowy opis nieformalny i przykłady znajdziesz w sekcji „Opis nieformalny” w Gather.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – scatter.
Scatter - Example 1 - StableHLO
Na powyższym obrazie każdy wiersz tabeli to przykład jednego indeksu aktualizacji. Sprawdźmy krok po kroku od lewej(Update Index) do prawej(Result Index):
Input) input ma kształt S32[2,3,4,2]. scatter_indices ma kształt S64[2,2,3,2]. updates ma kształt S32[2,2,3,1,2].
Aktualizacja indeksu) W ramach danych wejściowych otrzymujemy update_window_dims:[3,4]. To oznacza, że wymiary 3 i 4 w updates to wymiary okna, które są wyróżnione na żółto. Dzięki temu możemy wywnioskować, że update_scatter_dims = [0,1,2].
Update Scatter Index) Pokazuje wyodrębnione updated_scatter_dims dla każdego z nich.
(nieżółta część kolumny Aktualizuj indeks)
Indeks początkowy) Patrząc na tensor scatter_indices, widzimy, że wartości z poprzedniego kroku (Aktualizacja indeksu rozproszenia) wskazują indeks początkowy. Z index_vector_dim dowiadujemy się też o wymiarze
starting_indices, który zawiera indeksy początkowe. W przypadku
scatter_indices jest to wymiar 3 o rozmiarze 2.
Pełny indeks początkowy) scatter_dims_to_operand_dims = [2,1] informuje, że pierwszy element wektora indeksu trafia do wymiaru operandu 2. Drugi element wektora indeksu trafia do wymiaru 1 operandu. Pozostałe wymiary operandu są wypełniane wartością 0.
Pełny indeks przetwarzania wsadowego) Widzimy, że fioletowy zaznaczony obszar jest widoczny w tej kolumnie(pełny indeks przetwarzania wsadowego), w kolumnie indeksu rozproszenia aktualizacji i w kolumnie indeksu aktualizacji.
Full Window Index) obliczany na podstawie update_window_dimensions [3,4].
Indeks wyniku) Suma indeksu pełnego początku, indeksu pełnego przetwarzania wsadowego i indeksu pełnego okna w tensorze operand. Zwróć uwagę, że zielone wyróżnione regiony odpowiadają też wartości operand. Ostatni wiersz jest pomijany, ponieważ
znajduje się poza tensorem operand.
Wybierz
Zobacz też XlaBuilder::Select.
Tworzy tablicę wyjściową z elementów 2 tablic wejściowych na podstawie wartości tablicy predykatu.
Select(pred, on_true, on_false)
| Argumenty | Typ | Semantyka |
|---|---|---|
pred |
XlaOp |
tablica typu PRED |
on_true |
XlaOp |
tablicę typu T, |
on_false |
XlaOp |
tablicę typu T, |
Tablice on_true i on_false muszą mieć ten sam kształt. Jest to również kształt tablicy wyjściowej. Tablica pred musi mieć taką samą liczbę wymiarów jak tablice on_true i on_false, a jej elementy muszą być typu PRED.
Dla każdego elementu P tablicy pred odpowiedni element tablicy wyjściowej jest pobierany z tablicy on_true, jeśli wartość elementu P to true, a z tablicy on_false, jeśli wartość elementu P to false. Jako ograniczona forma rozgłaszania wartość pred może być skalarem typu PRED. W tym przypadku tablica wyjściowa jest w całości pobierana z on_true, jeśli pred to true, a z on_false, jeśli pred to false.
Przykład z wartością nieskalarną pred:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
Przykład ze skalarem pred:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
Wybór między krotkami jest obsługiwany. Krotki są w tym przypadku traktowane jako typy skalarne. Jeśli on_true i on_false są krotkami (które muszą mieć ten sam kształt!), to pred musi być skalarem typu PRED.
Informacje o StableHLO znajdziesz w artykule StableHLO – wybór.
SelectAndScatter
Zobacz też XlaBuilder::SelectAndScatter.
Tę operację można uznać za operację złożoną, która najpierw oblicza ReduceWindow na tablicy operand, aby wybrać element z każdego okna, a następnie rozprasza tablicę source na indeksy wybranych elementów, aby utworzyć tablicę wyjściową o takim samym kształcie jak tablica operandów. Funkcja binarna select służy do wybierania elementu z każdego okna przez zastosowanie go w każdym oknie. Jest wywoływana z właściwością, że wektor indeksu pierwszego parametru jest leksykograficznie mniejszy niż wektor indeksu drugiego parametru. Funkcja select zwraca wartość true, jeśli wybrany jest pierwszy parametr, i wartość false, jeśli wybrany jest drugi parametr.Funkcja musi być przechodnia (tzn. jeśli select(a, b) i select(b, c) mają wartość true, to select(a, c) też ma wartość true), aby wybrany element nie zależał od kolejności elementów przechodzonych w danym oknie.
Funkcja scatter jest stosowana w przypadku każdego wybranego indeksu w tablicy wyjściowej. Przyjmuje 2 parametry skalarne:
- Bieżąca wartość w wybranym indeksie w tablicy wyjściowej.
- Wartość rozproszenia z
source, która odnosi się do wybranego indeksu
Łączy te 2 parametry i zwraca wartość skalarną, która jest używana do aktualizowania wartości w wybranym indeksie w tablicy wyjściowej. Początkowo wszystkie indeksy tablicy wyjściowej są ustawione na init_value.
Tablica wyjściowa ma taki sam kształt jak tablica operand, a tablica source musi mieć taki sam kształt jak wynik zastosowania operacji ReduceWindow na tablicy operand. SelectAndScatter może służyć do propagowania wstecznego wartości gradientu dla warstwy puli w sieci neuronowej.
SelectAndScatter(operand, select, window_dimensions, window_strides, padding,
source, init_value, scatter)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand
|
XlaOp
|
tablica typu T, po której przesuwają się okna |
select
|
XlaComputation
|
obliczenia binarne typu T, T
-> PRED, które mają być stosowane do wszystkich elementów w każdym oknie; zwraca true, jeśli wybrano pierwszy parametr, i false, jeśli wybrano drugi parametr. |
window_dimensions
|
ArraySlice<int64>
|
tablica liczb całkowitych dla wartości wymiaru okna |
window_strides
|
ArraySlice<int64>
|
tablica liczb całkowitych dla wartości okna kroku |
padding
|
Padding
|
typ dopełnienia okna (Padding::kSame lub Padding::kValid) |
source
|
XlaOp
|
tablica typu T z wartościami do rozproszenia; |
init_value
|
XlaOp
|
wartość skalarna typu T dla wartości początkowej tablicy wyjściowej. |
scatter
|
XlaComputation
|
obliczenia binarne typu T, T
-> T, aby zastosować każdy element źródłowy rozproszenia z odpowiednim elementem docelowym. |
Na rysunku poniżej przedstawiono przykłady użycia funkcji SelectAndScatter, w których funkcja select oblicza maksymalną wartość spośród swoich parametrów. Pamiętaj, że gdy okna się nakładają, jak na rysunku (2) poniżej, indeks tablicy operand może być wybierany wielokrotnie przez różne okna. Na rysunku element o wartości 9 jest wybierany przez oba okna górne (niebieskie i czerwone), a funkcja dodawania binarnego scatter tworzy element wyjściowy o wartości 8 (2 + 6).
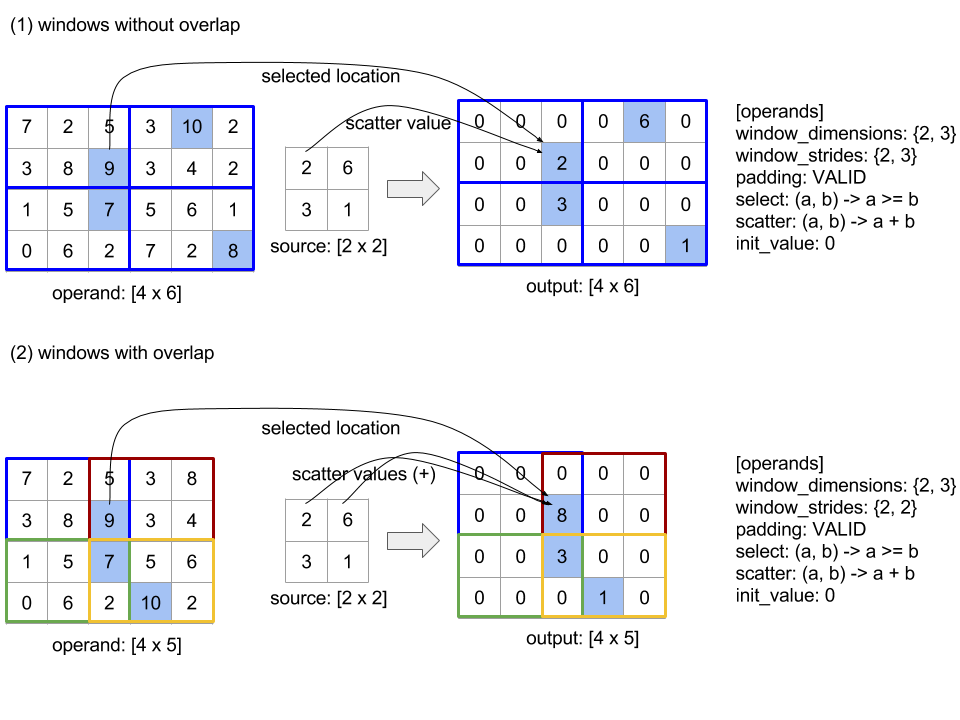
Kolejność obliczania funkcji scatter jest dowolna i może być niedeterministyczna. Dlatego funkcja scatter nie powinna być zbyt wrażliwa na ponowne powiązanie. Więcej informacji znajdziesz w omówieniu łączności w kontekście Reduce.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – select_and_scatter.
Wyślij
Zobacz też XlaBuilder::Send.
Send, SendWithTokens i SendToHost to operacje, które służą jako podstawowe elementy komunikacji w HLO. Te operacje zwykle pojawiają się w zrzutach HLO jako część operacji wejścia/wyjścia niskiego poziomu lub przesyłania danych między urządzeniami, ale nie są przeznaczone do ręcznego tworzenia przez użytkowników.
Send(operand, handle)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
dane do wysłania (tablica typu T); |
handle |
ChannelHandle |
unikalny identyfikator każdej pary wysyłania/odbierania; |
Wysyła podane dane operandu do instrukcji Recv w innym obliczeniu, które korzysta z tego samego uchwytu kanału. Nie zwraca żadnych danych.
Podobnie jak w przypadku operacji Recv, interfejs API klienta operacji Send reprezentuje komunikację synchroniczną i jest wewnętrznie rozkładany na 2 instrukcje HLO (Send i SendDone), aby umożliwić asynchroniczne przesyłanie danych. Zobacz też HloInstruction::CreateSend i HloInstruction::CreateSendDone.
Send(HloInstruction operand, int64 channel_id)
Inicjuje asynchroniczny transfer operandu do zasobów przydzielonych przez instrukcję Recv z tym samym identyfikatorem kanału. Zwraca kontekst, który jest używany przez następną instrukcję SendDone do oczekiwania na zakończenie przesyłania danych. Kontekst to krotka {operand (shape), request identifier
(U32)}, która może być używana tylko przez instrukcję SendDone.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – wysyłanie.
SendDone
Zobacz też HloInstruction::CreateSendDone.
SendDone(HloInstruction context)
W kontekście utworzonym przez instrukcję Send oczekuje na zakończenie przesyłania danych. Instrukcja nie zwraca żadnych danych.
Planowanie instrukcji dotyczących kanału
Kolejność wykonywania 4 instrukcji dla każdego kanału (Recv, RecvDone, Send, SendDone) jest następująca:
Recvjest wcześniejsza niżSendSendjest wcześniejsza niżRecvDoneRecvjest wcześniejsza niżRecvDoneSendjest wcześniejsza niżSendDone
Gdy kompilatory backendu generują liniowy harmonogram dla każdego obliczenia, które komunikuje się za pomocą instrukcji kanału, nie mogą występować cykle między obliczeniami. Na przykład poniższe harmonogramy prowadzą do zakleszczeń.
SetDimensionSize
Zobacz też XlaBuilder::SetDimensionSize.
Ustawia dynamiczny rozmiar danego wymiaru XlaOp. Operand musi mieć kształt tablicy.
SetDimensionSize(operand, val, dimension)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
n-wymiarowa tablica wejściowa. |
val |
XlaOp |
Liczba całkowita int32 reprezentująca dynamiczny rozmiar w czasie działania. |
dimension
|
int64
|
Wartość z przedziału [0, n), która określa wymiar. |
Przekazuje operand jako wynik, a kompilator śledzi dynamiczny wymiar.
Wartości dopełnione będą ignorowane przez operacje redukcji w dalszej części procesu.
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
ShiftLeft
Zobacz też XlaBuilder::ShiftLeft.
Wykonuje operację przesunięcia w lewo na poszczególnych elementach argumentu lhs o rhs bitów.
ShiftLeft(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje wariant alternatywny z obsługą transmisji o różnych wymiarach dla ShiftLeft:
ShiftLeft(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Informacje o StableHLO znajdziesz w artykule StableHLO – shift_left.
ShiftRightArithmetic
Zobacz też XlaBuilder::ShiftRightArithmetic.
Wykonuje operację arytmetycznego przesunięcia w prawo na poszczególnych elementach lhs o rhs bitów.
ShiftRightArithmetic(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywna odmiana z obsługą transmisji w różnych wymiarach dla funkcji ShiftRightArithmetic:
ShiftRightArithmetic(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – shift_right_arithmetic.
ShiftRightLogical
Zobacz też XlaBuilder::ShiftRightLogical.
Wykonuje operację logicznego przesunięcia w prawo na poszczególnych elementach lhs o rhs bitów.
ShiftRightLogical(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywna odmiana z obsługą transmisji o różnych wymiarach dla ShiftRightLogical:
ShiftRightLogical(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Informacje o StableHLO znajdziesz w artykule StableHLO – shift_right_logical.
Podpisz
Zobacz też XlaBuilder::Sign.
Sign(operand) Operacja znaku elementu x -> sgn(x), gdzie
\[\text{sgn}(x) = \begin{cases} -1 & x < 0\\ -0 & x = -0\\ NaN & x = NaN\\ +0 & x = +0\\ 1 & x > 0 \end{cases}\]
za pomocą operatora porównania typu elementu operand.
Sign(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Informacje o StableHLO znajdziesz w artykule StableHLO – sign.
Sinus
Sin(operand) Sinus każdego elementux -> sin(x)
Zobacz też XlaBuilder::Sin.
Sin(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja sin obsługuje też opcjonalny argument result_accuracy:
Sin(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Informacje o StableHLO znajdziesz w artykule StableHLO – sinus.
Wycinek
Zobacz też XlaBuilder::Slice.
Wycinanie wyodrębnia podtablicę z tablicy wejściowej. Podtablica ma taką samą liczbę wymiarów jak tablica wejściowa i zawiera wartości w ramce ograniczającej w tablicy wejściowej, w której wymiary i indeksy ramki ograniczającej są podane jako argumenty operacji wycinania.
Slice(operand, start_indices, limit_indices, strides)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
N-wymiarowa tablica typu T |
start_indices
|
ArraySlice<int64>
|
Lista N liczb całkowitych zawierająca indeksy początkowe wycinka dla każdego wymiaru. Wartości muszą być większe lub równe 0. |
limit_indices
|
ArraySlice<int64>
|
Lista N liczb całkowitych zawierająca indeksy końcowe (wyłączone) wycinka dla każdego wymiaru. Każda wartość musi być większa lub równa odpowiedniej wartości start_indices dla wymiaru i mniejsza lub równa rozmiarowi wymiaru. |
strides
|
ArraySlice<int64>
|
Lista N liczb całkowitych, która określa krok wejściowy wycinka. Funkcja slice wybiera każdy element strides[d] w wymiarze d. |
Przykład 1-wymiarowy:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4})
// Result: {2.0, 3.0}
Przykład dwuwymiarowy:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3})
// Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – slice.
Sortuj
Zobacz też XlaBuilder::Sort.
Sort(operands, comparator, dimension, is_stable)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands |
ArraySlice<XlaOp> |
Operandy do posortowania. |
comparator |
XlaComputation |
Obliczenia komparatora do użycia. |
dimension |
int64 |
Wymiar, według którego ma być przeprowadzane sortowanie. |
is_stable |
bool |
Określa, czy należy użyć stabilnego sortowania. |
Jeśli podano tylko 1 operand:
Jeśli operand jest tensorem 1-wymiarowym (tablicą), wynikiem jest posortowana tablica. Jeśli chcesz posortować tablicę w kolejności rosnącej, funkcja porównująca powinna przeprowadzać porównanie „mniejsze niż”. Formalnie po posortowaniu tablicy dla wszystkich pozycji indeksu
i, jzi < jzachodzi warunekcomparator(value[i], value[j]) = comparator(value[j], value[i]) = falselubcomparator(value[i], value[j]) = true.Jeśli operand ma większą liczbę wymiarów, jest sortowany wzdłuż podanego wymiaru. Na przykład w przypadku tensora dwuwymiarowego (macierzy) wartość wymiaru
0spowoduje niezależne sortowanie każdej kolumny, a wartość wymiaru1spowoduje niezależne sortowanie każdego wiersza. Jeśli nie podasz numeru wymiaru, domyślnie zostanie wybrany ostatni wymiar. W przypadku posortowanego wymiaru obowiązuje ten sam porządek sortowania co w przypadku 1-wymiarowego.
Jeśli podano operandy n > 1:
Wszystkie operandy
nmuszą być tensorami o tych samych wymiarach. Typy elementów tensorów mogą się różnić.Wszystkie operandy są sortowane razem, a nie osobno. Operandy są traktowane jako krotka. Podczas sprawdzania, czy elementy każdego argumentu na pozycjach indeksu
iijnależy zamienić, funkcja porównująca jest wywoływana z2 * nparametrami skalarnymi, gdzie parametr2 * kodpowiada wartości na pozycjiiw argumenciek-th, a parametr2 * k + 1odpowiada wartości na pozycjijw argumenciek-th. Zwykle komparator porównuje ze sobą parametry2 * ki2 * k + 1, a w przypadku remisu może używać innych par parametrów.Wynikiem jest krotka składająca się z operandów w kolejności posortowanej (wzdłuż podanego wymiaru, jak powyżej). Operand
i-thkrotki odpowiada operandowii-thw przypadku sortowania.
Jeśli np. są 3 operandy: operand0 = [3, 1], operand1 = [42, 50] i operand2 = [-3.0, 1.1], a komparator porównuje tylko wartości operand0 za pomocą operatora „mniejsze niż”, to wynikiem sortowania jest krotka ([1, 3], [50, 42], [1.1, -3.0]).
Jeśli wartość is_stable to „true”, sortowanie jest stabilne, tzn. jeśli komparator uzna elementy za równe, zachowana zostanie względna kolejność tych elementów. Dwa elementy e1 i e2 są równe wtedy i tylko wtedy, gdy comparator(e1, e2) = comparator(e2, e1) = false. Domyślnie wartość is_stable jest ustawiona na fałsz.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – sortowanie.
Sqrt
Zobacz też XlaBuilder::Sqrt.
Operacja pierwiastka kwadratowego na poszczególnych elementach x -> sqrt(x).
Sqrt(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja Sqrt obsługuje też opcjonalny argument result_accuracy:
Sqrt(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – sqrt.
Podrzędna
Zobacz też XlaBuilder::Sub.
Wykonuje odejmowanie elementów lhs i rhs.
Sub(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywna wersja z obsługą transmisji w różnych wymiarach dla subskrybenta:
Sub(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Informacje o StableHLO znajdziesz w artykule StableHLO – odejmowanie.
Jasnobrązowy
Zobacz też XlaBuilder::Tan.
Styczna elementu x -> tan(x).
Tan(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja tan obsługuje też opcjonalny argument result_accuracy:
Tan(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – tan.
Tanh
Zobacz też XlaBuilder::Tanh.
Tangens hiperboliczny każdego elementu x -> tanh(x).
Tanh(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja Tanh obsługuje też opcjonalny argument result_accuracy:
Tanh(operand, result_accuracy)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
result_accuracy
|
opcjonalne ResultAccuracy
|
Rodzaje dokładności, o jakie użytkownik może prosić w przypadku operacji jednoargumentowych z wieloma implementacjami. |
Więcej informacji o result_accuracy znajdziesz w sekcji Dokładność wyników.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – tanh.
TopK
Zobacz też XlaBuilder::TopK.
TopK znajduje wartości i indeksy k największych lub najmniejszych elementów w ostatnim wymiarze danego tensora.
TopK(operand, k, largest)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand
|
XlaOp
|
Tensor, z którego mają zostać wyodrębnione k największe elementy.
Tensor musi mieć co najmniej 1 wymiar. Rozmiar ostatniego wymiaru tensora musi być większy lub równy k. |
k |
int64 |
Liczba elementów do wyodrębnienia. |
largest
|
bool
|
Czy wyodrębniać największe czy najmniejsze k elementy. |
W przypadku 1-wymiarowego tensora wejściowego (tablicy) znajduje k największe lub najmniejsze
wartości w tablicy i zwraca krotkę 2 tablic (values, indices). Zatem
values[j] to j-ty największy/najmniejszy element w operand, a jego indeks to
indices[j].
W przypadku tensora wejściowego z więcej niż 1 wymiarem oblicza k największych wartości wzdłuż ostatniego wymiaru, zachowując wszystkie pozostałe wymiary (wiersze) w danych wyjściowych.
W przypadku operandu o kształcie [A, B, ..., P, Q], gdzie Q >= k, wynikiem jest krotka (values, indices), w której:
values.shape = indices.shape = [A, B, ..., P, k]
Jeśli 2 elementy w wierszu są równe, najpierw wyświetlany jest element o niższym indeksie.
Transponuj
Zobacz też operację tf.reshape.
Transpose(operand, permutation)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Operand do transponowania. |
permutation |
ArraySlice<int64> |
Jak przestawić wymiary. |
Przestawia wymiary operandu zgodnie z podaną permutacją, więc
∀ i . 0 ≤ i < number of dimensions ⇒
input_dimensions[permutation[i]] = output_dimensions[i].
Jest to to samo co Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)).
Więcej informacji o StableHLO znajdziesz w sekcji StableHLO – transpozycja.
TriangularSolve
Zobacz też XlaBuilder::TriangularSolve.
Rozwiązuje układy równań liniowych z macierzami współczynników trójkątnych dolnych lub górnych przez podstawianie do przodu lub do tyłu. Ta procedura, która działa w oparciu o rozgłaszanie wzdłuż wiodących wymiarów, rozwiązuje jeden z układów macierzy op(a) * x =
b lub x * op(a) = b dla zmiennej x, przy danych a i b, gdzie op(a) jest równe op(a) = a, op(a) = Transpose(a) lub op(a) = Conj(Transpose(a)).
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| Argumenty | Typ | Semantyka |
|---|---|---|
a
|
XlaOp
|
a > 2-wymiarowa tablica liczb zespolonych lub zmiennoprzecinkowych o kształcie [..., M,
M]. |
b
|
XlaOp
|
a > dwuwymiarowa tablica tego samego typu o kształcie [..., M, K], jeśli left_side ma wartość true, w przeciwnym razie [..., K, M]. |
left_side
|
bool
|
określa, czy rozwiązywać układ równań w postaci op(a) * x = b (true) czy x *
op(a) = b (false). |
lower
|
bool
|
czy używać górnego czy dolnego trójkąta
symbolu a. |
unit_diagonal
|
bool
|
jeśli true, elementy na przekątnej macierzy a są traktowane jako 1 i nie są dostępne. |
transpose_a
|
Transpose
|
czy użyć a w obecnej postaci, transponować ją czy obliczyć jej transpozycję sprzężoną. |
Dane wejściowe są odczytywane tylko z dolnego lub górnego trójkąta macierzy a w zależności od wartości lower. Wartości z drugiego trójkąta są ignorowane. Dane wyjściowe są zwracane w tym samym trójkącie. Wartości w drugim trójkącie są zdefiniowane przez implementację i mogą być dowolne.
Jeśli liczba wymiarów tensorów a i b jest większa niż 2, są one traktowane jako partie macierzy, w których wszystkie wymiary z wyjątkiem 2 mniejszych są wymiarami partii. a i b muszą mieć równe wymiary wsadu.
Informacje o StableHLO znajdziesz w artykule StableHLO – triangular_solve.
krotka,
Zobacz też XlaBuilder::Tuple.
Krotka zawierająca zmienną liczbę uchwytów danych, z których każdy ma własny kształt.
Tuple(elements)
| Argumenty | Typ | Semantyka |
|---|---|---|
elements |
wektor XlaOp |
Tablica N typu T |
Jest to analogiczne do std::tuple w C++. Koncepcyjnie:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
Krotki można rozkładać (uzyskiwać do nich dostęp) za pomocą operacji GetTupleElement.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – krotka.
z wyjątkiem funkcji custom_calls/get_tuple_element.
Podczas
Zobacz też XlaBuilder::While.
While(condition, body, init)
| Argumenty | Typ | Semantyka |
|---|---|---|
condition
|
XlaComputation
|
XlaComputation typu T -> PRED, który określa warunek zakończenia pętli. |
body
|
XlaComputation
|
XlaComputation typu T -> T, który określa treść pętli. |
init
|
T
|
Wartość początkowa parametru condition i body. |
Sekwencyjnie wykonuje body, dopóki condition nie zakończy się niepowodzeniem. Działa to podobnie do typowej pętli while w wielu innych językach, z wyjątkiem różnic i ograniczeń wymienionych poniżej.
- Węzeł
Whilezwraca wartość typuT, która jest wynikiem ostatniego wykonania węzłabody. - Kształt typu
Tjest określany statycznie i musi być taki sam we wszystkich iteracjach.
Parametry T obliczeń są inicjowane wartością init w pierwszej iteracji i automatycznie aktualizowane do nowego wyniku z body w każdej kolejnej iteracji.
Jednym z głównych zastosowań węzła While jest implementacja wielokrotnego wykonywania trenowania w sieciach neuronowych. Poniżej znajduje się uproszczony pseudokod z wykresem
przedstawiającym obliczenia. Kod znajdziesz w while_test.cc.
Typ T w tym przykładzie to Tuple składający się z int32 dla liczby iteracji i vector[10] dla akumulatora. W 1000 iteracji pętla stale dodaje do akumulatora stały wektor.
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – while.
Xor
Zobacz też XlaBuilder::Xor.
Wykonuje operację XOR na poszczególnych elementach lhs i rhs.
Xor(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej rozgłaszania. Wynik operacji ma kształt, który jest wynikiem rozgłaszania dwóch tablic wejściowych. W tym wariancie operacje między tablicami o różnych rangach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Istnieje alternatywny wariant z obsługą transmisji o różnych wymiarach dla operacji XOR:
Xor(lhs,rhs, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
| lhs | XlaOp | Lewy argument operacji: tablica typu T |
| rhs | XlaOp | Lewy argument operacji: tablica typu T |
| broadcast_dimension | ArraySlice |
który wymiar w kształcie docelowym odpowiada każdemu wymiarowi kształtu operandu. |
Ten wariant operacji należy stosować w przypadku operacji arytmetycznych między tablicami o różnych rangach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych określający wymiary, które mają być używane do rozgłaszania operandów. Semantyka jest szczegółowo opisana na stronie dotyczącej transmisji.
Więcej informacji o StableHLO znajdziesz w artykule StableHLO – xor.








