A continuación, se describe la semántica de las operaciones definidas en la interfaz XlaBuilder. Por lo general, estas operaciones se asignan de forma individual a las operaciones definidas en la interfaz de RPC en xla_data.proto.
Una nota sobre la nomenclatura: El tipo de datos generalizado con el que trabaja XLA es un array N-dimensional que contiene elementos de algún tipo uniforme (como un número de punto flotante de 32 bits). En toda la documentación, se usa array para denotar un array de dimensiones arbitrarias. Para mayor comodidad, los casos especiales tienen nombres más específicos y conocidos; por ejemplo, un vector es un array unidimensional y una matriz es un array bidimensional.
Obtén más información sobre la estructura de una operación en Formas y diseño y Diseño en mosaicos.
Abdominales
Consulta también XlaBuilder::Abs.
Valor absoluto de cada elemento de x -> |x|.
Abs(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Para obtener información sobre StableHLO, consulta StableHLO: abs.
Agregar
Consulta también XlaBuilder::Add.
Realiza la suma de lhs y rhs elemento por elemento.
Add(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad de transmisión multidimensional para Add:
Add(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: add.
AddDependency
Consulta también HloInstruction::AddDependency.
AddDependency puede aparecer en volcados de HLO, pero no está diseñado para que los usuarios finales lo construyan manualmente.
AfterAll
Consulta también XlaBuilder::AfterAll.
AfterAll toma una cantidad variable de tokens y produce un solo token. Los tokens son tipos primitivos que se pueden encadenar entre operaciones con efectos secundarios para aplicar un orden. AfterAll se puede usar como una unión de tokens para ordenar una operación después de un conjunto de operaciones.
AfterAll(tokens)
| Argumentos | Tipo | Semántica |
|---|---|---|
tokens |
vector de XlaOp |
Cantidad variable de tokens |
Para obtener información sobre StableHLO, consulta StableHLO - after_all.
AllGather
Consulta también XlaBuilder::AllGather.
Realiza la concatenación en las réplicas.
AllGather(operand, all_gather_dimension, shard_count, replica_groups,
channel_id, layout, use_global_device_ids)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand
|
XlaOp
|
Es el array que se concatenará en las réplicas. |
all_gather_dimension |
int64 |
Dimensión de concatenación |
shard_count
|
int64
|
El tamaño de cada grupo de réplicas |
replica_groups
|
vector de vectores de
int64 |
Son los grupos entre los que se realiza la concatenación. |
channel_id
|
opcional
ChannelHandle |
ID de canal opcional para la comunicación entre módulos |
layout
|
opcional Layout
|
Crea un patrón de diseño que capturará el diseño coincidente en el argumento. |
use_global_device_ids
|
opcional bool
|
Devuelve verdadero si los IDs en la configuración de ReplicaGroup representan un ID global. |
replica_groupses una lista de grupos de réplicas entre los que se realiza la concatenación (el ID de la réplica actual se puede recuperar conReplicaId). El orden de las réplicas en cada grupo determina el orden en el que se ubican sus entradas en el resultado.replica_groupsdebe estar vacío (en cuyo caso todas las réplicas pertenecen a un solo grupo, ordenado de0aN - 1) o contener la misma cantidad de elementos que la cantidad de réplicas. Por ejemplo,replica_groups = {0, 2}, {1, 3}realiza la concatenación entre las réplicas0y2, y1y3.shard_countes el tamaño de cada grupo de réplicas. Necesitamos este campo en los casos en quereplica_groupsesté vacío.channel_idse usa para la comunicación entre módulos: solo las operaciones deall-gathercon el mismochannel_idpueden comunicarse entre sí.use_global_device_idsDevuelve verdadero si los IDs de la configuración de ReplicaGroup representan un ID global de (replica_id * partition_count + partition_id) en lugar de un ID de réplica. Esto permite una agrupación más flexible de los dispositivos si esta operación de reducción total es tanto entre particiones como entre réplicas.
La forma de salida es la forma de entrada con el all_gather_dimension aumentado shard_count veces. Por ejemplo, si hay dos réplicas y el operando tiene el valor [1.0, 2.5] y [3.0, 5.25], respectivamente, en las dos réplicas, el valor de salida de esta operación en la que all_gather_dim es 0 será [1.0, 2.5, 3.0,5.25] en ambas réplicas.
Internamente, la API de AllGather se descompone en 2 instrucciones de HLO (AllGatherStart y AllGatherDone).
Consulta también HloInstruction::CreateAllGatherStart.
AllGatherStart y AllGatherDone sirven como primitivas en HLO. Estas operaciones pueden aparecer en volcados de HLO, pero no están diseñadas para que los usuarios finales las construyan manualmente.
Para obtener información sobre StableHLO, consulta StableHLO - all_gather.
AllReduce
Consulta también XlaBuilder::AllReduce.
Realiza un cálculo personalizado en todas las réplicas.
AllReduce(operand, computation, replica_groups, channel_id,
shape_with_layout, use_global_device_ids)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand
|
XlaOp
|
Es un array o una tupla no vacía de arrays para reducir en las réplicas. |
computation |
XlaComputation |
Cálculo de la reducción |
replica_groups
|
ReplicaGroup vector
|
Son los grupos entre los que se realizan las reducciones. |
channel_id
|
opcional
ChannelHandle |
ID de canal opcional para la comunicación entre módulos |
shape_with_layout
|
opcional Shape
|
Define el diseño de los datos transferidos. |
use_global_device_ids
|
opcional bool
|
Devuelve verdadero si los IDs en la configuración de ReplicaGroup representan un ID global. |
- Cuando
operandes una tupla de arrays, la reducción de todos se realiza en cada elemento de la tupla. replica_groupses una lista de grupos de réplicas entre los que se realiza la reducción (el ID de la réplica actual se puede recuperar conReplicaId).replica_groupsdebe estar vacío (en cuyo caso todas las réplicas pertenecen a un solo grupo) o contener la misma cantidad de elementos que la cantidad de réplicas. Por ejemplo,replica_groups = {0, 2}, {1, 3}realiza la reducción entre las réplicas0y2, y1y3.channel_idse usa para la comunicación entre módulos: solo las operaciones deall-reducecon el mismochannel_idpueden comunicarse entre sí.shape_with_layout: Fuerza el diseño de AllReduce al diseño determinado. Se usa para garantizar el mismo diseño para un grupo de operaciones de AllReduce compiladas por separado.use_global_device_idsDevuelve verdadero si los IDs de la configuración de ReplicaGroup representan un ID global de (replica_id * partition_count + partition_id) en lugar de un ID de réplica. Esto permite una agrupación más flexible de los dispositivos si esta operación de reducción total es tanto entre particiones como entre réplicas.
La forma de salida es la misma que la forma de entrada. Por ejemplo, si hay dos réplicas y el operando tiene el valor [1.0, 2.5] y [3.0, 5.25], respectivamente, en las dos réplicas, el valor de salida de esta operación y el cálculo de la suma serán [4.0, 7.75] en ambas réplicas. Si la entrada es una tupla, la salida también lo será.
Para calcular el resultado de AllReduce, se requiere una entrada de cada réplica, por lo que, si una réplica ejecuta un nodo AllReduce más veces que otra, la primera esperará indefinidamente. Dado que todas las réplicas ejecutan el mismo programa, no hay muchas formas en que esto pueda suceder, pero es posible cuando la condición de un bucle while depende de los datos de infeed y los datos que son infeed hacen que el bucle while itere más veces en una réplica que en otra.
Internamente, la API de AllReduce se descompone en 2 instrucciones de HLO (AllReduceStart y AllReduceDone).
Consulta también HloInstruction::CreateAllReduceStart.
AllReduceStart y AllReduceDone sirven como primitivas en HLO. Estas operaciones pueden aparecer en volcados de HLO, pero no están diseñadas para que los usuarios finales las construyan manualmente.
CrossReplicaSum
Consulta también XlaBuilder::CrossReplicaSum.
Realiza AllReduce con un cálculo de suma.
CrossReplicaSum(operand, replica_groups)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand
|
XlaOp | Es un array o una tupla no vacía de arrays para reducir en las réplicas. |
replica_groups
|
vector de vectores de int64 |
Son los grupos entre los que se realizan las reducciones. |
Devuelve la suma del valor del operando dentro de cada subgrupo de réplicas. Todas las réplicas proporcionan una entrada a la suma y todas las réplicas reciben la suma resultante para cada subgrupo.
AllToAll
Consulta también XlaBuilder::AllToAll.
AllToAll es una operación colectiva que envía datos de todos los núcleos a todos los núcleos. Tiene dos fases:
- La fase de dispersión. En cada núcleo, el operando se divide en
split_countbloques a lo largo desplit_dimensions, y los bloques se dispersan en todos los núcleos, p.ej., el bloque i-ésimo se envía al núcleo i-ésimo. - La fase de recopilación. Cada núcleo concatena los bloques recibidos a lo largo de
concat_dimension.
Los núcleos participantes se pueden configurar de las siguientes maneras:
replica_groups: Cada ReplicaGroup contiene una lista de IDs de réplica que participan en el cálculo (el ID de réplica de la réplica actual se puede recuperar conReplicaId). AllToAll se aplicará dentro de los subgrupos en el orden especificado. Por ejemplo,replica_groups = { {1,2,3}, {4,5,0} }significa que se aplicará un AllToAll dentro de las réplicas{1, 2, 3}y en la fase de recopilación, y los bloques recibidos se concatenarán en el mismo orden de 1, 2 y 3. Luego, se aplicará otro AllToAll dentro de las réplicas 4, 5 y 0, y el orden de concatenación también será 4, 5 y 0. Sireplica_groupsestá vacío, todas las réplicas pertenecen a un grupo, en el orden de concatenación de su aparición.
Requisitos previos:
- El tamaño de la dimensión del operando en
split_dimensiones divisible porsplit_count. - La forma del operando no es una tupla.
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups, layout, channel_id)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de entrada de n dimensiones. |
split_dimension
|
int64
|
Un valor en el intervalo [0,n) que nombra la dimensión a lo largo de la cual se divide el operando |
concat_dimension
|
int64
|
Un valor en el intervalo [0,n) que nombra la dimensión a lo largo de la cual se concatenan los bloques de división |
split_count
|
int64
|
Es la cantidad de núcleos que participan en esta operación. Si replica_groups está vacío, debe ser la cantidad de réplicas; de lo contrario, debe ser igual a la cantidad de réplicas en cada grupo. |
replica_groups
|
ReplicaGroupvector
|
Cada grupo contiene una lista de IDs de réplicas. |
layout |
opcional Layout |
Diseño de memoria especificado por el usuario |
channel_id
|
opcional ChannelHandle
|
Identificador único para cada par de envío y recepción |
Consulta xla::shapes para obtener más información sobre las formas y los diseños.
Para obtener información sobre StableHLO, consulta StableHLO: all_to_all.
AllToAll: ejemplo 1
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(
x,
/*split_dimension=*/ 1,
/*concat_dimension=*/ 0,
/*split_count=*/ 4);
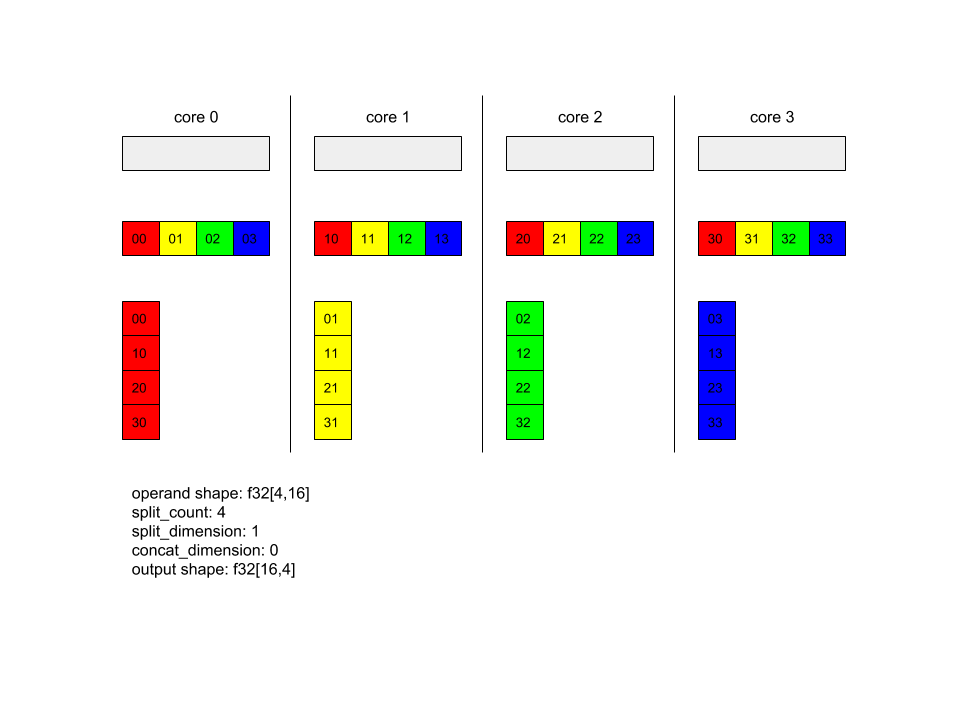
En el ejemplo anterior, hay 4 núcleos que participan en Alltoall. En cada núcleo, el operando se divide en 4 partes a lo largo de la dimensión 1, por lo que cada parte tiene la forma f32[4,4]. Las 4 partes se dispersan en todos los núcleos. Luego, cada núcleo concatena las partes recibidas a lo largo de la dimensión 0, en el orden de los núcleos del 0 al 4. Por lo tanto, el resultado en cada núcleo tiene la forma f32[16,4].
AllToAll, ejemplo 2, StableHLO
En el ejemplo anterior, hay 2 réplicas que participan en AllToAll. En cada réplica, el operando tiene la forma f32[2,4]. El operando se divide en 2 partes a lo largo de la dimensión 1, por lo que cada parte tiene la forma f32[2,2]. Luego, las 2 partes se intercambian entre las réplicas según su posición en el grupo de réplicas. Cada réplica recopila su parte correspondiente de ambos operandos y los concatena a lo largo de la dimensión 0. Como resultado, la salida en cada réplica tiene la forma f32[4,2].
RaggedAllToAll
Consulta también XlaBuilder::RaggedAllToAll.
RaggedAllToAll realiza una operación colectiva de todos a todos, en la que la entrada y la salida son tensores irregulares.
RaggedAllToAll(input, input_offsets, send_sizes, output, output_offsets,
recv_sizes, replica_groups, channel_id)
| Argumentos | Tipo | Semántica |
|---|---|---|
input |
XlaOp |
Es un array de N elementos de tipo T. |
input_offsets |
XlaOp |
Es un array de N elementos de tipo T. |
send_sizes |
XlaOp |
Es un array de N elementos de tipo T. |
output |
XlaOp |
Es un array de N elementos de tipo T. |
output_offsets |
XlaOp |
Es un array de N elementos de tipo T. |
recv_sizes |
XlaOp |
Es un array de N elementos de tipo T. |
replica_groups
|
ReplicaGroup vector
|
Cada grupo contiene una lista de IDs de réplica. |
channel_id
|
opcional ChannelHandle
|
Identificador único para cada par de envío y recepción |
Los tensores irregulares se definen con un conjunto de tres tensores:
data: El tensordataes “irregular” a lo largo de su dimensión más externa, a lo largo de la cual cada elemento indexado tiene un tamaño variable.offsets: El tensoroffsetsindexa la dimensión más externa del tensordatay representa el desplazamiento inicial de cada elemento irregular del tensordata.sizes: El tensorsizesrepresenta el tamaño de cada elemento irregular del tensordata, en el que el tamaño se especifica en unidades de subelementos. Un subelemento se define como el sufijo de la forma del tensor "data" que se obtiene quitando la dimensión "irregular" más externa.- Los tensores
offsetsysizesdeben tener el mismo tamaño.
Ejemplo de un tensor irregular:
data: [8,3] =
{ {a,b,c},{d,e,f},{g,h,i},{j,k,l},{m,n,o},{p,q,r},{s,t,u},{v,w,x} }
offsets: [3] = {0, 1, 4}
sizes: [3] = {1, 3, 4}
// Index 'data' at 'offsets'[0], 'sizes'[0]' // {a,b,c}
// Index 'data' at 'offsets'[1], 'sizes'[1]' // {d,e,f},{g,h,i},{j,k,l}
// Index 'data' at 'offsets'[2], 'sizes'[2]' // {m,n,o},{p,q,r},{s,t,u},{v,w,x}
output_offsets debe fragmentarse de manera que cada réplica tenga desplazamientos en la perspectiva de salida de la réplica de destino.
Para el desplazamiento de salida i-ésimo, la réplica actual enviará la actualización input[input_offsets[i]:input_offsets[i]+input_sizes[i]] a la réplica i-ésima que se escribirá en output_i[output_offsets[i]:output_offsets[i]+send_sizes[i]] en la réplica i-ésima output.
Por ejemplo, si tenemos 2 réplicas:
replica 0:
input: [1, 2, 2]
output:[0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 2]
output_offsets: [0, 0]
recv_sizes: [1, 1]
replica 1:
input: [3, 4, 0]
output: [0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 1]
output_offsets: [1, 2]
recv_sizes: [2, 1]
// replica 0's result will be: [1, 3, 0, 0]
// replica 1's result will be: [2, 2, 4, 0]
El HLO de todos a todos irregular tiene los siguientes argumentos:
input: Tensor de datos de entrada irregulares.output: Tensor de datos de salida irregulares.input_offsets: Tensor de desplazamiento de entrada irregular.send_sizes: Tensor de tamaños de envío irregulares.output_offsets: Es un array de desplazamientos irregulares en el resultado de la réplica de destino.recv_sizes: Es un tensor de tamaños de recv irregulares.
Todos los tensores *_offsets y *_sizes deben tener la misma forma.
Se admiten dos formas para los tensores *_offsets y *_sizes:
[num_devices], donde ragged-all-to-all puede enviar como máximo una actualización a cada dispositivo remoto del grupo de réplicas. Por ejemplo:
for (remote_device_id : replica_group) {
SEND input[input_offsets[remote_device_id]],
output[output_offsets[remote_device_id]],
send_sizes[remote_device_id] }
[num_devices, num_updates], donde ragged-all-to-all puede enviar hastanum_updatesactualizaciones al mismo dispositivo remoto (cada una con diferentes compensaciones), para cada dispositivo remoto del grupo de réplicas.
Por ejemplo:
for (remote_device_id : replica_group) {
for (update_idx : num_updates) {
SEND input[input_offsets[remote_device_id][update_idx]],
output[output_offsets[remote_device_id][update_idx]]],
send_sizes[remote_device_id][update_idx] } }
y
Consulta también XlaBuilder::And.
Realiza un AND a nivel de los elementos de dos tensores lhs y rhs.
And(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para And:
And(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: y.
Asíncrono
Consulta también HloInstruction::CreateAsyncStart, HloInstruction::CreateAsyncUpdate, HloInstruction::CreateAsyncDone.
AsyncDone, AsyncStart y AsyncUpdate son instrucciones internas de HLO que se usan para las operaciones asíncronas y sirven como primitivas en HLO. Estas operaciones pueden aparecer en volcados de HLO, pero no están diseñadas para que los usuarios finales las construyan manualmente.
Atan2
Consulta también XlaBuilder::Atan2.
Realiza la operación atan2 en términos de elementos en lhs y rhs.
Atan2(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Atan2:
Atan2(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: atan2.
BatchNormGrad
Consulta también XlaBuilder::BatchNormGrad y el informe original sobre la normalización por lotes para obtener una descripción detallada del algoritmo.
Calcula los gradientes de la normalización por lotes.
BatchNormGrad(operand, scale, batch_mean, batch_var, grad_output, epsilon,
feature_index)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp | Es un array de n dimensiones que se normalizará (x). |
scale |
XlaOp | Arreglo unidimensional (\(\gamma\)) |
batch_mean |
XlaOp | Arreglo unidimensional (\(\mu\)) |
batch_var |
XlaOp | Arreglo unidimensional (\(\sigma^2\)) |
grad_output |
XlaOp | Gradientes que se pasan a BatchNormTraining (\(\nabla y\)) |
epsilon |
float |
Valor de Epsilon (\(\epsilon\)) |
feature_index |
int64 |
Índice de la dimensión de la característica en operand |
Para cada atributo en la dimensión de atributos (feature_index es el índice de la dimensión de atributos en operand), la operación calcula los gradientes con respecto a operand, offset y scale en todas las demás dimensiones. El feature_index debe ser un índice válido para la dimensión del atributo en operand.
Los tres gradientes se definen con las siguientes fórmulas (suponiendo un array de 4 dimensiones como operand y con el índice de dimensión de la característica l, el tamaño del lote m y los tamaños espaciales w y h):
\[ \begin{split} c_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sigma^2_l+\epsilon} \right) \\\\ d_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \\\\ \nabla x_{ijkl} &= \frac{\gamma_{l} }{\sqrt{\sigma^2_{l}+\epsilon} } \left( \nabla y_{ijkl} - d_l - c_l (x_{ijkl} - \mu_{l}) \right) \\\\ \nabla \gamma_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sqrt{\sigma^2_{l}+\epsilon} } \right) \\\\\ \nabla \beta_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \end{split} \]
Las entradas batch_mean y batch_var representan valores de momentos en las dimensiones espaciales y de lote.
El tipo de salida es una tupla de tres identificadores:
| Salidas | Tipo | Semántica |
|---|---|---|
grad_operand
|
XlaOp | Gradiente con respecto a la entrada operand (\(\nabla x\)) |
grad_scale
|
XlaOp | Gradiente con respecto a la entrada **scale ** (\(\nabla\gamma\)) |
grad_offset
|
XlaOp | Gradiente con respecto a la entrada offset(\(\nabla\beta\)) |
Para obtener información sobre StableHLO, consulta StableHLO - batch_norm_grad.
BatchNormInference
Consulta también XlaBuilder::BatchNormInference y el informe original sobre la normalización por lotes para obtener una descripción detallada del algoritmo.
Normaliza un array en las dimensiones espaciales y de lote.
BatchNormInference(operand, scale, offset, mean, variance, epsilon,
feature_index)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp | Es un array de dimensión n que se normalizará. |
scale |
XlaOp | Array unidimensional |
offset |
XlaOp | Array unidimensional |
mean |
XlaOp | Array unidimensional |
variance |
XlaOp | Array unidimensional |
epsilon |
float |
Valor de Epsilon |
feature_index |
int64 |
Índice de la dimensión de la característica en operand |
Para cada atributo en la dimensión de atributos (feature_index es el índice de la dimensión de atributos en operand), la operación calcula la media y la varianza en todas las demás dimensiones y usa la media y la varianza para normalizar cada elemento en operand. El feature_index debe ser un índice válido para la dimensión de la característica en operand.
BatchNormInference equivale a llamar a BatchNormTraining sin calcular mean y variance para cada lote. En su lugar, usa las entradas mean y variance como valores estimados. El propósito de esta operación es reducir la latencia en la inferencia, de ahí el nombre BatchNormInference.
El resultado es un array normalizado de n dimensiones con la misma forma que la entrada operand.
Para obtener información sobre StableHLO, consulta StableHLO: batch_norm_inference.
BatchNormTraining
Consulta también XlaBuilder::BatchNormTraining y the original batch normalization paper para obtener una descripción detallada del algoritmo.
Normaliza un array en las dimensiones espaciales y de lote.
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de n dimensiones que se normalizará (x). |
scale |
XlaOp |
Arreglo unidimensional (\(\gamma\)) |
offset |
XlaOp |
Arreglo unidimensional (\(\beta\)) |
epsilon |
float |
Valor de Epsilon (\(\epsilon\)) |
feature_index |
int64 |
Índice de la dimensión de la característica en operand |
Para cada atributo en la dimensión de atributos (feature_index es el índice de la dimensión de atributos en operand), la operación calcula la media y la varianza en todas las demás dimensiones y usa la media y la varianza para normalizar cada elemento en operand. El feature_index debe ser un índice válido para la dimensión de la característica en operand.
El algoritmo funciona de la siguiente manera para cada lote en operand \(x\) que contiene elementos m con w y h como el tamaño de las dimensiones espaciales (suponiendo que operand es un array de 4 dimensiones):
Calcula la media del lote \(\mu_l\) para cada atributo
len la dimensión del atributo: \(\mu_l=\frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h x_{ijkl}\)Calcula la varianza del lote \(\sigma^2_l\): $\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
Normaliza, ajusta y desplaza los datos: \(y_{ijkl}=\frac{\gamma_l(x_{ijkl}-\mu_l)}{\sqrt[2]{\sigma^2_l+\epsilon} }+\beta_l\)
El valor de épsilon, que suele ser un número pequeño, se agrega para evitar errores de división por cero.
El tipo de salida es una tupla de tres XlaOp:
| Salidas | Tipo | Semántica |
|---|---|---|
output
|
XlaOp
|
Es un array de n dimensiones con la misma forma que el array de entrada operand (y). |
batch_mean |
XlaOp |
Arreglo unidimensional (\(\mu\)) |
batch_var |
XlaOp |
Arreglo unidimensional (\(\sigma^2\)) |
Los valores batch_mean y batch_var son momentos calculados en las dimensiones espaciales y de lote con las fórmulas anteriores.
Para obtener información sobre StableHLO, consulta StableHLO - batch_norm_training.
Bitcast
Consulta también HloInstruction::CreateBitcast.
Bitcast puede aparecer en los volcados de HLO, pero no está diseñado para que los usuarios finales lo construyan manualmente.
BitcastConvertType
Consulta también XlaBuilder::BitcastConvertType.
De manera similar a un tf.bitcast en TensorFlow, realiza una operación de bitcast elemento por elemento desde una forma de datos a una forma de destino. El tamaño de entrada y salida debe coincidir: p.ej., los elementos s32 se convierten en elementos f32 a través de la rutina de conversión de bits, y un elemento s32 se convertirá en cuatro elementos s8. Bitcast se implementa como una conversión de bajo nivel, por lo que las máquinas con diferentes representaciones de punto flotante arrojarán resultados diferentes.
BitcastConvertType(operand, new_element_type)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de tipo T con dimensiones D. |
new_element_type |
PrimitiveType |
tipo U |
Las dimensiones del operando y la forma objetivo deben coincidir, excepto la última dimensión, que cambiará según la proporción del tamaño primitivo antes y después de la conversión.
Los tipos de elementos de origen y destino no deben ser tuplas.
Para obtener información sobre StableHLO, consulta StableHLO - bitcast_convert.
Conversión de Bitcast a un tipo primitivo de ancho diferente
La instrucción BitcastConvert de HLO admite el caso en el que el tamaño del tipo de elemento de salida T' no es igual al tamaño del elemento de entrada T. Como toda la operación es, conceptualmente, una conversión de bits y no cambia los bytes subyacentes, la forma del elemento de salida debe cambiar. En el caso de B = sizeof(T), B' =
sizeof(T'), hay dos casos posibles.
Primero, cuando B > B', la forma de salida obtiene una nueva dimensión secundaria más pequeña de tamaño B/B'. Por ejemplo:
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
La regla sigue siendo la misma para los escalares efectivos:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
Como alternativa, para B' > B, la instrucción requiere que la última dimensión lógica de la forma de entrada sea igual a B'/B, y esta dimensión se descarta durante la conversión:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
Ten en cuenta que las conversiones entre diferentes anchos de bits no son elemento por elemento.
Transmisión
Consulta también XlaBuilder::Broadcast.
Agrega dimensiones a un array duplicando los datos en el array.
Broadcast(operand, broadcast_sizes)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el array que se duplicará. |
broadcast_sizes |
ArraySlice<int64> |
Los tamaños de las nuevas dimensiones |
Las nuevas dimensiones se insertan a la izquierda, es decir, si broadcast_sizes tiene valores {a0, ..., aN} y la forma del operando tiene dimensiones {b0, ..., bM}, entonces la forma del resultado tiene dimensiones {a0, ..., aN, b0, ..., bM}.
Los nuevos índices de dimensiones se copian en los operandos, es decir:
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
Por ejemplo, si operand es un escalar f32 con el valor 2.0f y broadcast_sizes es {2, 3}, el resultado será un array con la forma f32[2, 3] y todos los valores del resultado serán 2.0f.
Para obtener información sobre StableHLO, consulta StableHLO: broadcast.
BroadcastInDim
Consulta también XlaBuilder::BroadcastInDim.
Expande el tamaño y la cantidad de dimensiones de un array duplicando los datos en el array.
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el array que se duplicará. |
out_dim_size
|
ArraySlice<int64>
|
Los tamaños de las dimensiones de la forma objetivo |
broadcast_dimensions
|
ArraySlice<int64>
|
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Es similar a Broadcast, pero permite agregar dimensiones en cualquier lugar y expandir las dimensiones existentes con tamaño 1.
El operand se transmite a la forma que describe out_dim_size.
broadcast_dimensions asigna las dimensiones de operand a las dimensiones de la forma objetivo, es decir, la i-ésima dimensión del operando se asigna a la dimensión broadcast_dimension[i] de la forma de salida. Las dimensiones de operand deben tener un tamaño de 1 o el mismo tamaño que la dimensión en la forma de salida a la que se asignan. Las dimensiones restantes se completan con dimensiones de tamaño 1. Luego, la transmisión de dimensiones degeneradas se realiza a lo largo de estas dimensiones degeneradas para alcanzar la forma del resultado. La semántica se describe en detalle en la página de transmisión.
Llamar
Consulta también XlaBuilder::Call.
Invoca un cálculo con los argumentos proporcionados.
Call(computation, operands...)
| Argumentos | Tipo | Semántica |
|---|---|---|
computation
|
XlaComputation
|
cálculo de tipo T_0, T_1, ...,
T_{N-1} -> S con N parámetros de tipo arbitrario |
operands |
secuencia de N XlaOp |
N argumentos de tipo arbitrario |
La aridad y los tipos de operands deben coincidir con los parámetros de computation. Se permite no tener operands.
CompositeCall
Consulta también XlaBuilder::CompositeCall.
Encapsula una operación compuesta por otras operaciones de StableHLO, que toma entradas y composite_attributes y produce resultados. La semántica de la operación se implementa con el atributo de descomposición. La operación compuesta se puede reemplazar por su descomposición sin cambiar la semántica del programa. En los casos en que la incorporación de la descomposición no proporcione la misma semántica de la operación, se recomienda usar custom_call.
El campo de versión (que tiene el valor predeterminado 0) se usa para indicar cuándo cambian las semánticas de un elemento compuesto.
Este op se implementa como un kCall con el atributo is_composite=true. El campo decomposition se especifica con el atributo computation. Los atributos de frontend almacenan los atributos restantes con el prefijo composite..
Ejemplo de operación CompositeCall:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
CompositeCall(computation, operands..., name, attributes, version)
| Argumentos | Tipo | Semántica |
|---|---|---|
computation
|
XlaComputation
|
cálculo de tipo T_0, T_1, ...,
T_{N-1} -> S con N parámetros de tipo arbitrario |
operands |
secuencia de N XlaOp |
Cantidad variable de valores |
name |
string |
Nombre del compuesto |
attributes
|
opcional string
|
Diccionario opcional serializado de atributos |
version
|
opcional int64
|
Número para actualizar las versiones de la semántica de la operación compuesta |
El decomposition de una operación no es un campo llamado, sino que aparece como un atributo to_apply que apunta a la función que contiene la implementación de nivel inferior, es decir, to_apply=%funcname.
Puedes encontrar más información sobre la composición y la descomposición en la Especificación de StableHLO.
Cbrt
Consulta también XlaBuilder::Cbrt.
Operación de raíz cúbica para cada elemento x -> cbrt(x).
Cbrt(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Cbrt también admite el argumento opcional result_accuracy:
Cbrt(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Para obtener información sobre StableHLO, consulta StableHLO - cbrt.
Techo
Consulta también XlaBuilder::Ceil.
Función ceil para cada elemento x -> ⌈x⌉.
Ceil(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Para obtener información sobre StableHLO, consulta StableHLO: ceil.
Cholesky
Consulta también XlaBuilder::Cholesky.
Calcula la descomposición de Cholesky de un lote de matrices simétricas (hermitianas) definidas positivas.
Cholesky(a, lower)
| Argumentos | Tipo | Semántica |
|---|---|---|
a
|
XlaOp
|
Un array de un tipo complejo o de punto flotante con más de 2 dimensiones. |
lower |
bool |
Indica si se debe usar el triángulo superior o inferior de a. |
Si lower es true, calcula matrices triangulares inferiores l de modo que $a = l$ .
l^T$. Si lower es false, calcula matrices triangulares superiores u de modo que\(a = u^T . u\).
Los datos de entrada se leen solo desde el triángulo inferior o superior de a, según el valor de lower. Se ignoran los valores del otro triángulo. Los datos de salida se devuelven en el mismo triángulo; los valores del otro triángulo se definen según la implementación y pueden ser cualquier valor.
Si a tiene más de 2 dimensiones, se trata como un lote de matrices, en el que todas las dimensiones, excepto las 2 dimensiones secundarias, son dimensiones de lote.a
Si a no es simétrica (hermítica) y definida positiva, el resultado se define según la implementación.
Para obtener información sobre StableHLO, consulta StableHLO: cholesky.
Restringir
Consulta también XlaBuilder::Clamp.
Ajusta un operando dentro del rango entre un valor mínimo y uno máximo.
Clamp(min, operand, max)
| Argumentos | Tipo | Semántica |
|---|---|---|
min |
XlaOp |
Es un array de tipo T. |
operand |
XlaOp |
Es un array de tipo T. |
max |
XlaOp |
Es un array de tipo T. |
Dado un operando y valores mínimos y máximos, devuelve el operando si se encuentra en el rango entre el mínimo y el máximo; de lo contrario, devuelve el valor mínimo si el operando está por debajo de este rango o el valor máximo si el operando está por encima de este rango. Es decir, clamp(a, x, b) = min(max(a, x), b).
Los tres arrays deben tener la misma forma. Como alternativa, y como una forma restringida de transmisión, min o max pueden ser un escalar de tipo T.
Ejemplo con min y max escalares:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
Para obtener información sobre StableHLO, consulta StableHLO: clamp.
Contraer
Consulta también XlaBuilder::Collapse.
y la operación tf.reshape.
Reduce las dimensiones de un array a una sola dimensión.
Collapse(operand, dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de tipo T. |
dimensions |
int64 vector |
Subconjunto consecutivo y ordenado de las dimensiones de T. |
El colapso reemplaza el subconjunto determinado de las dimensiones del operando por una sola dimensión. Los argumentos de entrada son un array arbitrario de tipo T y un vector constante en tiempo de compilación de índices de dimensión. Los índices de dimensión deben ser un subconjunto consecutivo y ordenado (de menor a mayor) de las dimensiones de T. Por lo tanto, {0, 1, 2}, {0, 1} o {1, 2} son conjuntos de dimensiones válidos, pero {1, 0} o {0, 2} no lo son. Se reemplazan por una sola dimensión nueva, en la misma posición de la secuencia de dimensiones que las que reemplazan, con el tamaño de la nueva dimensión igual al producto de los tamaños de las dimensiones originales. El número de dimensión más bajo en dimensions es la dimensión de variación más lenta (la más importante) en el bucle anidado que contrae estas dimensiones, y el número de dimensión más alto es la dimensión de variación más rápida (la menos importante). Consulta el operador tf.reshape si necesitas un orden de contracción más general.
Por ejemplo, sea v un array de 24 elementos:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
Clz
Consulta también XlaBuilder::Clz.
Cuenta los ceros iniciales de cada elemento.
Clz(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
CollectiveBroadcast
Consulta también XlaBuilder::CollectiveBroadcast.
Difunde datos entre las réplicas. Los datos se envían desde el primer ID de réplica de cada grupo a los demás IDs del mismo grupo. Si un ID de réplica no está en ningún grupo de réplicas, el resultado en esa réplica es un tensor que consta de 0 en shape.
CollectiveBroadcast(operand, replica_groups, channel_id)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
replica_groups
|
ReplicaGroupvector
|
Cada grupo contiene una lista de IDs de réplicas. |
channel_id
|
opcional ChannelHandle
|
Identificador único para cada par de envío y recepción |
Para obtener información sobre StableHLO, consulta StableHLO - collective_broadcast.
CollectivePermute
Consulta también XlaBuilder::CollectivePermute.
CollectivePermute es una operación colectiva que envía y recibe datos entre réplicas.
CollectivePermute(operand, source_target_pairs, channel_id, inplace)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de entrada de n dimensiones. |
source_target_pairs
|
<int64, int64> vector
|
Es una lista de pares (source_replica_id, target_replica_id). Para cada par, el operando se envía desde la réplica de origen a la réplica de destino. |
channel_id
|
opcional ChannelHandle
|
ID de canal opcional para la comunicación entre módulos |
inplace
|
opcional bool
|
marca si la permutación se debe realizar en el lugar |
Ten en cuenta que existen las siguientes restricciones en source_target_pairs:
- Ningún par debe tener el mismo ID de réplica de destino ni el mismo ID de réplica de origen.
- Si un ID de réplica no es un destino en ningún par, el resultado en esa réplica es un tensor que consta de 0(s) con la misma forma que la entrada.
Internamente, la API de la operación CollectivePermute se descompone en 2 instrucciones de HLO (CollectivePermuteStart y CollectivePermuteDone).
Consulta también HloInstruction::CreateCollectivePermuteStart.
CollectivePermuteStart y CollectivePermuteDone sirven como primitivas en HLO.
Estas operaciones pueden aparecer en los volcados de HLO, pero no están diseñadas para que los usuarios finales las construyan manualmente.
Para obtener información sobre StableHLO, consulta StableHLO - collective_permute.
Comparar
Consulta también XlaBuilder::Compare.
Realiza una comparación elemento por elemento de lhs y rhs de lo siguiente:
Ec.
Consulta también XlaBuilder::Eq.
Realiza una comparación igual a elemento por elemento de lhs y rhs.
\(lhs = rhs\)
Eq(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Eq:
Eq(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Se admite un orden total sobre los números de punto flotante para Eq, ya que se aplica lo siguiente:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
EqTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Para obtener información sobre StableHLO, consulta StableHLO: Comparación.
Ne
Consulta también XlaBuilder::Ne.
Realiza una comparación de no igual a elemento por elemento de lhs y rhs.
\(lhs != rhs\)
Ne(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Ne:
Ne(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Existe un orden total sobre los números de punto flotante para Ne, ya que se aplica lo siguiente:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
NeTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Para obtener información sobre StableHLO, consulta StableHLO: Comparación.
Ge
Consulta también XlaBuilder::Ge.
Realiza una comparación greater-or-equal-than según cada elemento de lhs y rhs.
\(lhs >= rhs\)
Ge(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Ge:
Ge(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Existe un orden total sobre los números de punto flotante para Gt, ya que se aplica lo siguiente:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
GtTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Para obtener información sobre StableHLO, consulta StableHLO: Comparación.
Gt
Consulta también XlaBuilder::Gt.
Realiza una comparación mayor que a nivel del elemento de lhs y rhs.
\(lhs > rhs\)
Gt(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Gt:
Gt(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: Comparación.
Le
Consulta también XlaBuilder::Le.
Realiza una comparación less-or-equal-than a nivel del elemento de lhs y rhs.
\(lhs <= rhs\)
Le(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Le:
Le(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Existe un orden total sobre los números de punto flotante para Le, ya que se aplica lo siguiente:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LeTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Para obtener información sobre StableHLO, consulta StableHLO: Comparación.
Lt
Consulta también XlaBuilder::Lt.
Realiza una comparación menor que elemento por elemento de lhs y rhs.
\(lhs < rhs\)
Lt(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Lt:
Lt(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Existe un orden total sobre los números de punto flotante para Lt, ya que se aplica lo siguiente:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LtTotalOrder(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Para obtener información sobre StableHLO, consulta StableHLO: Comparación.
Complejo
Consulta también XlaBuilder::Complex.
Realiza una conversión de cada elemento a un valor complejo a partir de un par de valores reales e imaginarios, lhs y rhs.
Complex(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad de transmisión multidimensional para Complex:
Complex(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: complejo.
ConcatInDim (Concatenate)
Consulta también XlaBuilder::ConcatInDim.
La función CONCATENAR compone un array a partir de varios operandos de array. El array tiene la misma cantidad de dimensiones que cada uno de los operandos del array de entrada (que deben tener la misma cantidad de dimensiones entre sí) y contiene los argumentos en el orden en que se especificaron.
Concatenate(operands..., dimension)
| Argumentos | Tipo | Semántica |
|---|---|---|
operands
|
secuencia de N XlaOp
|
Es un array de N de tipo T con dimensiones [L0, L1, …]. Requiere N >= 1. |
dimension
|
int64
|
Es un valor en el intervalo [0, N) que nombra la dimensión que se concatenará entre los operands. |
Con la excepción de dimension, todas las dimensiones deben ser iguales. Esto se debe a que XLA no admite arrays "irregulares". También ten en cuenta que los valores de 0 dimensiones no se pueden concatenar (ya que es imposible nombrar la dimensión a lo largo de la cual se produce la concatenación).
Ejemplo unidimensional:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
//Output: {2, 3, 4, 5, 6, 7}
Ejemplo bidimensional:
let a = { {1, 2},
{3, 4},
{5, 6} };
let b = { {7, 8} };
Concat({a, b}, 0)
//Output: { {1, 2},
// {3, 4},
// {5, 6},
// {7, 8} }
Diagrama:
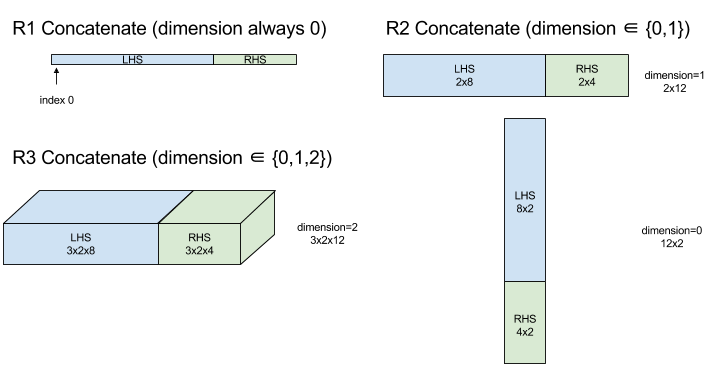
Para obtener información sobre StableHLO, consulta StableHLO: concatenate.
Condicional
Consulta también XlaBuilder::Conditional.
Conditional(predicate, true_operand, true_computation, false_operand,
false_computation)
| Argumentos | Tipo | Semántica |
|---|---|---|
predicate |
XlaOp |
Escalar de tipo PRED |
true_operand |
XlaOp |
Argumento de tipo \(T_0\) |
true_computation |
XlaComputation |
XlaComputation de tipo \(T_0 \to S\) |
false_operand |
XlaOp |
Argumento de tipo \(T_1\) |
false_computation |
XlaComputation |
XlaComputation de tipo \(T_1 \to S\) |
Ejecuta true_computation si predicate es true, false_computation si predicate es false y muestra el resultado.
El true_computation debe tomar un solo argumento del tipo \(T_0\) y se invocará con true_operand, que debe ser del mismo tipo. El false_computation debe tomar un solo argumento del tipo \(T_1\) y se invocará con false_operand, que debe ser del mismo tipo. El tipo del valor devuelto de true_computation y false_computation debe ser el mismo.
Ten en cuenta que solo se ejecutará uno de los valores true_computation y false_computation según el valor de predicate.
Conditional(branch_index, branch_computations, branch_operands)
| Argumentos | Tipo | Semántica |
|---|---|---|
branch_index |
XlaOp |
Escalar de tipo S32 |
branch_computations |
secuencia de N XlaComputation |
XlaComputations de tipo \(T_0 \to S , T_1 \to S , ..., T_{N-1} \to S\) |
branch_operands |
secuencia de N XlaOp |
Argumentos de tipo \(T_0 , T_1 , ..., T_{N-1}\) |
Ejecuta branch_computations[branch_index] y muestra el resultado. Si branch_index es un S32 que es < 0 o >= N, se ejecuta branch_computations[N-1] como la rama predeterminada.
Cada branch_computations[b] debe tomar un solo argumento del tipo \(T_b\) y se invocará con branch_operands[b], que debe ser del mismo tipo. El tipo del valor devuelto de cada branch_computations[b] debe ser el mismo.
Ten en cuenta que solo se ejecutará uno de los branch_computations según el valor de branch_index.
Para obtener información sobre StableHLO, consulta StableHLO: if.
Constante
Consulta también XlaBuilder::ConstantLiteral.
Produce un output a partir de un literal constante.
Constant(literal)
| Argumentos | Tipo | Semántica |
|---|---|---|
literal |
LiteralSlice |
Vista constante de un Literal existente |
Para obtener información sobre StableHLO, consulta StableHLO: constant.
ConvertElementType
Consulta también XlaBuilder::ConvertElementType.
Al igual que un static_cast por elemento en C++, ConvertElementType realiza una operación de conversión por elemento de una forma de datos a una forma de destino. Las dimensiones deben coincidir, y la conversión es elemento por elemento; p.ej., los elementos s32 se convierten en elementos f32 a través de una rutina de conversión de s32 a f32.
ConvertElementType(operand, new_element_type)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de tipo T con dimensiones D. |
new_element_type |
PrimitiveType |
tipo U |
Las dimensiones del operando y la forma objetivo deben coincidir. Los tipos de elementos de origen y destino no deben ser tuplas.
Una conversión como T=s32 a U=f32 realizará una rutina de conversión de int a float normalizadora, como redondear al número par más cercano.
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
Para obtener información sobre StableHLO, consulta StableHLO: convert.
Conv (convolución)
Consulta también XlaBuilder::Conv.
Calcula una convolución del tipo que se usa en las redes neuronales. Aquí, una convolución se puede considerar como una ventana de n dimensiones que se mueve por un área base de n dimensiones, y se realiza un cálculo para cada posición posible de la ventana.
Conv Pone en cola una instrucción de convolución en el cálculo, que usa los números de dimensión de convolución predeterminados sin dilatación.
El padding se especifica de forma abreviada como SAME o VALID. El padding SAME agrega ceros al tensor de entrada (lhs) para que el tensor de salida tenga la misma forma que el de entrada cuando no se tiene en cuenta el stride. El padding VALID simplemente significa que no hay padding.
Conv(lhs, rhs, window_strides, padding, feature_group_count,
batch_group_count, precision_config, preferred_element_type)
| Argumentos | Tipo | Semántica |
|---|---|---|
lhs
|
XlaOp
|
Es un array de entradas de (n+2) dimensiones. |
rhs
|
XlaOp
|
Es un array de (n+2) dimensiones de pesos del kernel. |
window_strides |
ArraySlice<int64> |
Es un array de n dimensiones de las separaciones del kernel. |
padding |
Padding |
enum de padding |
feature_group_count
|
int64 | la cantidad de grupos de funciones |
batch_group_count |
int64 | La cantidad de grupos de lotes |
precision_config
|
opcional
PrecisionConfig |
Es un enum para el nivel de precisión. |
preferred_element_type
|
opcional
PrimitiveType |
enum del tipo de elemento escalar |
Los niveles de controles disponibles para Conv son los siguientes:
Sea n la cantidad de dimensiones espaciales. El argumento lhs es un array de (n+2) dimensiones que describe el área base. Esto se denomina entrada, aunque, por supuesto, el lado derecho también es una entrada. En una red neuronal, estas son las activaciones de entrada. Las dimensiones n+2 son, en este orden:
batch: Cada coordenada en esta dimensión representa una entrada independiente para la que se lleva a cabo la convolución.z/depth/features: Cada posición (y,x) en el área base tiene un vector asociado, que se incluye en esta dimensión.spatial_dims: Describe las dimensiones espaciales denque definen el área base por la que se desplaza la ventana.
El argumento rhs es un array de (n+2) dimensiones que describe el filtro, el kernel o la ventana convolucional. Las dimensiones son, en este orden:
output-z: Es la dimensiónzdel resultado.input-z: El tamaño de esta dimensión multiplicado porfeature_group_countdebe ser igual al tamaño de la dimensiónzen el lado izquierdo.spatial_dims: Describe las dimensiones espacialesnque definen la ventana n-dimensional que se desplaza por el área base.
El argumento window_strides especifica el paso de la ventana convolucional en las dimensiones espaciales. Por ejemplo, si el stride en la primera dimensión espacial es 3, la ventana solo se puede colocar en coordenadas en las que el primer índice espacial sea divisible por 3.
El argumento padding especifica la cantidad de relleno con ceros que se aplicará al área base. La cantidad de padding puede ser negativa. El valor absoluto del padding negativo indica la cantidad de elementos que se deben quitar de la dimensión especificada antes de realizar la convolución. padding[0] especifica el padding para la dimensión y y padding[1] especifica el padding para la dimensión x. Cada par tiene el padding bajo como primer elemento y el padding alto como segundo elemento. El padding bajo se aplica en la dirección de los índices más bajos, mientras que el padding alto se aplica en la dirección de los índices más altos. Por ejemplo, si padding[1] es (2,3), habrá un relleno de 2 ceros a la izquierda y de 3 ceros a la derecha en la segunda dimensión espacial. Usar relleno equivale a insertar esos mismos valores cero en la entrada (lhs) antes de realizar la convolución.
Los argumentos lhs_dilation y rhs_dilation especifican el factor de dilatación que se aplicará al lado izquierdo y al lado derecho, respectivamente, en cada dimensión espacial. Si el factor de dilatación en una dimensión espacial es d, se colocan implícitamente d-1 agujeros entre cada una de las entradas en esa dimensión, lo que aumenta el tamaño del array. Los agujeros se rellenan con un valor no operativo, que para la convolución significa ceros.
La dilatación del RHS también se denomina convolución atrous. Para obtener más información, consulta tf.nn.atrous_conv2d. La dilatación del LHD también se conoce como convolución transpuesta. Para obtener más información, consulta tf.nn.conv2d_transpose.
El argumento feature_group_count (valor predeterminado 1) se puede usar para las convoluciones agrupadas. feature_group_count debe ser un divisor de la dimensión de la característica de entrada y de salida. Si feature_group_count es mayor que 1, significa que, conceptualmente, la dimensión de los atributos de entrada y salida y la dimensión de los atributos de salida rhs se dividen de manera uniforme en muchos grupos de feature_group_count, cada uno de los cuales consta de una subsecuencia consecutiva de atributos. La dimensión del atributo de entrada de rhs debe ser igual a la dimensión del atributo de entrada de lhs dividida por feature_group_count (por lo que ya tiene el tamaño de un grupo de atributos de entrada). Los i-ésimos grupos se usan juntos para calcular feature_group_count para muchas convoluciones separadas. Los resultados de estas convoluciones se concatenan en la dimensión de la característica de salida.
Para la convolución separable en profundidad, el argumento feature_group_count se establecería en la dimensión de la característica de entrada, y el filtro se cambiaría de forma de [filter_height, filter_width, in_channels, channel_multiplier] a [filter_height, filter_width, 1, in_channels * channel_multiplier]. Para obtener más información, consulta tf.nn.depthwise_conv2d.
El argumento batch_group_count (valor predeterminado 1) se puede usar para los filtros agrupados durante la retropropagación. batch_group_count debe ser un divisor del tamaño de la dimensión del lote de lhs (entrada). Si batch_group_count es mayor que 1, significa que la dimensión del lote de salida debe ser de tamaño input batch
/ batch_group_count. El valor de batch_group_count debe ser un divisor del tamaño de la función de salida.
La forma de salida tiene estas dimensiones, en este orden:
batch: El tamaño de esta dimensión multiplicado porbatch_group_countdebe ser igual al tamaño de la dimensiónbatchen el lado izquierdo.z: Tiene el mismo tamaño queoutput-zen el kernel (rhs).spatial_dims: Un valor para cada posición válida de la ventana convolucional.
En la figura anterior, se muestra cómo funciona el campo batch_group_count. De hecho, dividimos cada lote del lado izquierdo en grupos de batch_group_count y hacemos lo mismo con las características de salida. Luego, para cada uno de estos grupos, realizamos convoluciones por pares y concatenamos la salida a lo largo de la dimensión de atributos de salida. La semántica operativa de todas las demás dimensiones (espacial y de atributos) sigue siendo la misma.
Las posiciones válidas de la ventana convolucional se determinan según los pasos y el tamaño del área base después del padding.
Para describir lo que hace una convolución, considera una convolución 2D y elige algunas coordenadas fijas batch, z, y, x en el resultado. Luego, (y,x) es la posición de una esquina de la ventana dentro del área base (p.ej., la esquina superior izquierda, según cómo interpretes las dimensiones espaciales). Ahora tenemos una ventana 2D, tomada del área base, en la que cada punto 2D se asocia a un vector 1D, por lo que obtenemos una caja 3D. Desde el kernel convolucional, dado que fijamos la coordenada de salida z, también tenemos una caja 3D. Las dos cajas tienen las mismas dimensiones, por lo que podemos sumar los productos de los elementos correspondientes entre las dos cajas (de forma similar a un producto escalar). Ese es el valor de salida.
Ten en cuenta que, si output-z es, p.ej., 5, entonces cada posición de la ventana produce 5 valores en el resultado en la dimensión z del resultado. Estos valores difieren en qué parte del kernel convolucional se usa: hay una caja 3D separada de valores que se usa para cada coordenada output-z. Por lo tanto, podrías pensar en ella como 5 convoluciones separadas con un filtro diferente para cada una.
A continuación, se muestra el seudocódigo para una convolución 2D con padding y stride:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
precision_config se usa para indicar la configuración de precisión. El nivel indica si el hardware debe intentar generar más instrucciones de código de máquina para proporcionar una emulación de dtype más precisa cuando sea necesario (es decir, emular f32 en una TPU que solo admite matmuls de bf16). Los valores pueden ser DEFAULT, HIGH o HIGHEST. Encontrarás detalles adicionales en las secciones de la MXU.
preferred_element_type es un elemento escalar de tipos de salida de precisión mayor o menor que se usa para la acumulación. preferred_element_type recomienda el tipo de acumulación para la operación determinada, pero no se garantiza. Esto permite que algunos backends de hardware se acumulen en un tipo diferente y se conviertan al tipo de salida preferido.
Para obtener información sobre StableHLO, consulta StableHLO: convolución.
ConvWithGeneralPadding
Consulta también XlaBuilder::ConvWithGeneralPadding.
ConvWithGeneralPadding(lhs, rhs, window_strides, padding,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Es igual que Conv, donde la configuración del padding es explícita.
| Argumentos | Tipo | Semántica |
|---|---|---|
lhs
|
XlaOp
|
Es un array de entradas de (n+2) dimensiones. |
rhs
|
XlaOp
|
Es un array de (n+2) dimensiones de pesos del kernel. |
window_strides |
ArraySlice<int64> |
Es un array de n dimensiones de las separaciones del kernel. |
padding
|
ArraySlice<
pair<int64,int64>> |
Es un array de n dimensiones que contiene el padding (inferior, superior). |
feature_group_count
|
int64 | la cantidad de grupos de funciones |
batch_group_count |
int64 | La cantidad de grupos de lotes |
precision_config
|
opcional
PrecisionConfig |
Es un enum para el nivel de precisión. |
preferred_element_type
|
opcional
PrimitiveType |
enum del tipo de elemento escalar |
ConvWithGeneralDimensions
Consulta también XlaBuilder::ConvWithGeneralDimensions.
ConvWithGeneralDimensions(lhs, rhs, window_strides, padding,
dimension_numbers, feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Es igual que Conv, donde los números de dimensión son explícitos.
| Argumentos | Tipo | Semántica |
|---|---|---|
lhs
|
XlaOp
|
Es un array de entradas de (n+2) dimensiones. |
rhs
|
XlaOp
|
Es un array de (n+2) dimensiones de pesos del kernel. |
window_strides
|
ArraySlice<int64>
|
Es un array de n dimensiones de las unidades de desplazamiento del kernel. |
padding |
Padding |
enum de padding |
dimension_numbers
|
ConvolutionDimensionNumbers
|
la cantidad de dimensiones |
feature_group_count
|
int64 | la cantidad de grupos de funciones |
batch_group_count
|
int64 | la cantidad de grupos de lotes |
precision_config
|
opcional PrecisionConfig
|
Es una enumeración para el nivel de precisión. |
preferred_element_type
|
opcional PrimitiveType
|
enum del tipo de elemento escalar |
ConvGeneral
Consulta también XlaBuilder::ConvGeneral.
ConvGeneral(lhs, rhs, window_strides, padding, dimension_numbers,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
Es igual que Conv, donde la configuración del padding y los números de dimensión son explícitos.
| Argumentos | Tipo | Semántica |
|---|---|---|
lhs
|
XlaOp
|
Es un array de entradas de (n+2) dimensiones. |
rhs
|
XlaOp
|
Es un array de (n+2) dimensiones de pesos del kernel. |
window_strides
|
ArraySlice<int64>
|
Es un array de n dimensiones de las unidades de desplazamiento del kernel. |
padding
|
ArraySlice<
pair<int64,int64>>
|
Es un array de n dimensiones que contiene el padding (inferior, superior) |
dimension_numbers
|
ConvolutionDimensionNumbers
|
la cantidad de dimensiones |
feature_group_count
|
int64 | la cantidad de grupos de funciones |
batch_group_count
|
int64 | la cantidad de grupos de lotes |
precision_config
|
opcional PrecisionConfig
|
Es una enumeración para el nivel de precisión. |
preferred_element_type
|
opcional PrimitiveType
|
enum del tipo de elemento escalar |
ConvGeneralDilated
Consulta también XlaBuilder::ConvGeneralDilated.
ConvGeneralDilated(lhs, rhs, window_strides, padding, lhs_dilation,
rhs_dilation, dimension_numbers, feature_group_count, batch_group_count,
precision_config, preferred_element_type, window_reversal)
Es igual que Conv, donde la configuración de padding, los factores de dilatación y los números de dimensión son explícitos.
| Argumentos | Tipo | Semántica |
|---|---|---|
lhs
|
XlaOp
|
Es un array de entradas de (n+2) dimensiones. |
rhs
|
XlaOp
|
Es un array de (n+2) dimensiones de pesos del kernel. |
window_strides
|
ArraySlice<int64>
|
Es un array de n dimensiones de las unidades de desplazamiento del kernel. |
padding
|
ArraySlice<
pair<int64,int64>>
|
Es un array de n dimensiones que contiene el padding (inferior, superior) |
lhs_dilation
|
ArraySlice<int64>
|
Es un array de factores de dilatación del LHS de n dimensiones. |
rhs_dilation
|
ArraySlice<int64>
|
Es un array de factores de dilatación del RHS de n dimensiones. |
dimension_numbers
|
ConvolutionDimensionNumbers
|
la cantidad de dimensiones |
feature_group_count
|
int64 | la cantidad de grupos de funciones |
batch_group_count
|
int64 | la cantidad de grupos de lotes |
precision_config
|
opcional PrecisionConfig
|
Es una enumeración para el nivel de precisión. |
preferred_element_type
|
opcional PrimitiveType
|
enum del tipo de elemento escalar |
window_reversal
|
opcional vector<bool>
|
Es una marca que se usa para invertir lógicamente la dimensión antes de aplicar la convolución. |
Copiar
Consulta también HloInstruction::CreateCopyStart.
Internamente, Copy se descompone en 2 instrucciones de HLO, CopyStart y CopyDone. Copy, junto con CopyStart y CopyDone, sirven como primitivas en HLO. Estas operaciones pueden aparecer en volcados de HLO, pero no están diseñadas para que los usuarios finales las construyan manualmente.
COS
Consulta tambiénXlaBuilder::Cos.
Coseno de elemento inteligente x -> cos(x).
Cos(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Cos también admite el argumento opcional result_accuracy:
Cos(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Para obtener información sobre StableHLO, consulta StableHLO: coseno.
Cosh
Consulta también XlaBuilder::Cosh.
Coseno hiperbólico x -> cosh(x) según cada elemento.
Cosh(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Cosh también admite el argumento opcional result_accuracy:
Cosh(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
CustomCall
Consulta también XlaBuilder::CustomCall.
Llama a una función proporcionada por el usuario dentro de un cálculo.
La documentación de CustomCall se proporciona en Detalles para desarrolladores: Llamadas personalizadas de XLA
Para obtener información sobre StableHLO, consulta StableHLO - custom_call.
Div
Consulta también XlaBuilder::Div.
Realiza la división de cada elemento del dividendo lhs y el divisor rhs.
Div(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
El desbordamiento de la división de números enteros (división o resto con signo/sin signo por cero o división o resto con signo de INT_SMIN con -1) produce un valor definido por la implementación.
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Div:
Div(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: divide.
Dominio
Consulta también HloInstruction::CreateDomain.
Domain puede aparecer en los volcados de HLO, pero no está diseñado para que los usuarios finales lo construyan manualmente.
Punto
Consulta también XlaBuilder::Dot.
Dot(lhs, rhs, precision_config, preferred_element_type)
| Argumentos | Tipo | Semántica |
|---|---|---|
lhs |
XlaOp |
Es un array de tipo T. |
rhs |
XlaOp |
Es un array de tipo T. |
precision_config
|
opcional
PrecisionConfig |
Es un enum para el nivel de precisión. |
preferred_element_type
|
opcional
PrimitiveType |
enum del tipo de elemento escalar |
La semántica exacta de esta operación depende de los rangos de los operandos:
| Entrada | Salida | Semántica |
|---|---|---|
vector [n] dot vector [n] |
escalar | producto escalar de vectores |
matriz [m x k] dot vector [k] |
vector [m] | multiplicación de matriz por vector |
matriz [m x k] dot matriz [k x n] |
matriz [m x n] | Multiplicación de matrices |
La operación realiza la suma de productos en la segunda dimensión de lhs (o la primera si tiene 1 dimensión) y la primera dimensión de rhs. Estas son las dimensiones "contraídas". Las dimensiones contraídas de lhs y rhs deben tener el mismo tamaño. En la práctica, se puede usar para realizar productos escalares entre vectores, multiplicaciones de vectores o matrices, o multiplicaciones de matrices.
precision_config se usa para indicar la configuración de precisión. El nivel indica si el hardware debe intentar generar más instrucciones de código de máquina para proporcionar una emulación de dtype más precisa cuando sea necesario (es decir, emular f32 en una TPU que solo admite matmuls de bf16). Los valores pueden ser DEFAULT, HIGH o HIGHEST. Encontrarás detalles adicionales en las secciones de la MXU.
preferred_element_type es un elemento escalar de tipos de salida de precisión mayor o menor que se usa para la acumulación. preferred_element_type recomienda el tipo de acumulación para la operación determinada, pero no se garantiza. Esto permite que algunos backends de hardware se acumulen en un tipo diferente y se conviertan al tipo de salida preferido.
Para obtener información sobre StableHLO, consulta StableHLO - dot.
DotGeneral
Consulta también XlaBuilder::DotGeneral.
DotGeneral(lhs, rhs, dimension_numbers, precision_config,
preferred_element_type)
| Argumentos | Tipo | Semántica |
|---|---|---|
lhs |
XlaOp |
Es un array de tipo T. |
rhs |
XlaOp |
Es un array de tipo T. |
dimension_numbers
|
DotDimensionNumbers
|
Números de contratación y de dimensiones de lotes |
precision_config
|
opcional
PrecisionConfig |
Es una enumeración para el nivel de precisión. |
preferred_element_type
|
opcional
PrimitiveType |
enum del tipo de elemento escalar |
Es similar a Dot, pero permite especificar números de dimensiones de contracción y de lote para lhs y rhs.
| Campos de DotDimensionNumbers | Tipo | Semántica |
|---|---|---|
lhs_contracting_dimensions
|
repeated int64 | lhs números de dimensión de contracción |
rhs_contracting_dimensions
|
repeated int64 | rhs números de dimensión de contracción |
lhs_batch_dimensions
|
repeated int64 | Números de dimensión de lhs |
rhs_batch_dimensions
|
repeated int64 | Números de dimensión de rhs |
DotGeneral realiza la suma de productos en las dimensiones de contracción especificadas en dimension_numbers.
No es necesario que los números de dimensión de contratación asociados de lhs y rhs sean los mismos, pero deben tener los mismos tamaños de dimensión.
Ejemplo con números de dimensiones contraídas:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { { 6.0, 12.0},
{15.0, 30.0} }
Los números de dimensión de lote asociados de lhs y rhs deben tener los mismos tamaños de dimensión.
Ejemplo con números de dimensión de lote (tamaño del lote 2, matrices de 2 x 2):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> {
{ {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| Entrada | Salida | Semántica |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | matmul por lotes |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | matmul por lotes |
De ello se deduce que el número de dimensión resultante comienza con la dimensión de lote, luego la dimensión lhs no contractiva/no de lote y, finalmente, la dimensión rhs no contractiva/no de lote.
precision_config se usa para indicar la configuración de precisión. El nivel indica si el hardware debe intentar generar más instrucciones de código de máquina para proporcionar una emulación de dtype más precisa cuando sea necesario (es decir, emular f32 en una TPU que solo admite matmuls de bf16). Los valores pueden ser DEFAULT, HIGH o HIGHEST. Encontrarás más detalles en las secciones de la MXU.
preferred_element_type es un elemento escalar de tipos de salida de precisión mayor o menor que se usa para la acumulación. preferred_element_type recomienda el tipo de acumulación para la operación determinada, pero no se garantiza. Esto permite que algunos backends de hardware se acumulen en un tipo diferente y se conviertan al tipo de salida preferido.
Para obtener información sobre StableHLO, consulta StableHLO - dot_general.
ScaledDot
Consulta también XlaBuilder::ScaledDot.
ScaledDot(lhs, lhs_scale, rhs, rhs_scale, dimension_number,
precision_config,preferred_element_type)
| Argumentos | Tipo | Semántica |
|---|---|---|
lhs |
XlaOp |
Es un array de tipo T. |
rhs |
XlaOp |
Es un array de tipo T. |
lhs_scale |
XlaOp |
Es un array de tipo T. |
rhs_scale |
XlaOp |
Es un array de tipo T. |
dimension_number
|
ScatterDimensionNumbers
|
Números de dimensión para la operación de dispersión |
precision_config
|
PrecisionConfig
|
Es una enumeración para el nivel de precisión. |
preferred_element_type
|
opcional PrimitiveType
|
enum del tipo de elemento escalar |
Es similar a DotGeneral.
Crea una operación de punto escalada con los operandos "lhs", "lhs_scale", "rhs" y "rhs_scale", con las dimensiones de contracción y lote especificadas en "dimension_numbers".
RaggedDot
Consulta también XlaBuilder::RaggedDot.
Para obtener un desglose del cálculo de RaggedDot, consulta StableHLO - chlo.ragged_dot.
DynamicReshape
Consulta también XlaBuilder::DynamicReshape.
Esta operación es funcionalmente idéntica a reshape, pero la forma del resultado se especifica de forma dinámica a través de output_shape.
DynamicReshape(operand, dim_sizes, new_size_bounds, dims_are_dynamic)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de N dimensiones del tipo T. |
dim_sizes |
vector de XlaOP |
Tamaños de vectores de N dimensiones |
new_size_bounds |
vector de int63 |
Vector de límites de N dimensiones |
dims_are_dynamic |
vector de bool |
Dim dinámica de N dimensiones |
Para obtener información sobre StableHLO, consulta StableHLO - dynamic_reshape.
DynamicSlice
Consulta también XlaBuilder::DynamicSlice.
DynamicSlice extrae un subarreglo del arreglo de entrada en start_indices dinámico. El tamaño de la segmentación en cada dimensión se pasa en size_indices, que especifica el extremo de los intervalos de segmentación exclusivos en cada dimensión: [inicio, inicio + tamaño). La forma de start_indices debe ser unidimensional, con un tamaño de dimensión igual a la cantidad de dimensiones de operand.
DynamicSlice(operand, start_indices, slice_sizes)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de N dimensiones del tipo T. |
start_indices
|
secuencia de N XlaOp
|
Lista de N números enteros escalares que contienen los índices iniciales del segmento para cada dimensión. El valor debe ser mayor o igual que cero. |
size_indices
|
ArraySlice<int64>
|
Lista de N números enteros que contiene el tamaño de la segmentación para cada dimensión. Cada valor debe ser estrictamente mayor que cero, y start + size debe ser menor o igual que el tamaño de la dimensión para evitar el ajuste del módulo del tamaño de la dimensión. |
Los índices de segmentación efectivos se calculan aplicando la siguiente transformación para cada índice i en [1, N) antes de realizar la segmentación:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - slice_sizes[i])
Esto garantiza que el segmento extraído siempre esté dentro de los límites con respecto al array de operandos. Si el segmento está dentro de los límites antes de que se aplique la transformación, esta no tendrá ningún efecto.
Ejemplo unidimensional:
let a = {0.0, 1.0, 2.0, 3.0, 4.0};
let s = {2};
DynamicSlice(a, s, {2});
// Result: {2.0, 3.0}
Ejemplo bidimensional:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2});
//Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
Para obtener información sobre StableHLO, consulta StableHLO - dynamic_slice.
DynamicUpdateSlice
Consulta también XlaBuilder::DynamicUpdateSlice.
DynamicUpdateSlice genera un resultado que es el valor del array de entrada operand, con un segmento update sobrescrito en start_indices.
La forma de update determina la forma del subarreglo del resultado que se actualiza.
La forma de start_indices debe ser unidimensional, con un tamaño de dimensión igual a la cantidad de dimensiones de operand.
DynamicUpdateSlice(operand, update, start_indices)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de N dimensiones de tipo T. |
update
|
XlaOp
|
Es un array de N dimensiones de tipo T que contiene la actualización de la segmentación. Cada dimensión de la forma de actualización debe ser estrictamente mayor que cero, y start + update debe ser menor o igual que el tamaño del operando para cada dimensión, de modo que no se generen índices de actualización fuera de los límites. |
start_indices
|
secuencia de N XlaOp
|
Lista de N números enteros escalares que contienen los índices iniciales del segmento para cada dimensión. El valor debe ser mayor o igual que cero. |
Los índices de segmentación efectivos se calculan aplicando la siguiente transformación para cada índice i en [1, N) antes de realizar la segmentación:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
Esto garantiza que el segmento actualizado siempre esté dentro de los límites con respecto al array de operandos. Si el segmento está dentro de los límites antes de que se aplique la transformación, esta no tendrá ningún efecto.
Ejemplo unidimensional:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s)
// Result: {0.0, 1.0, 5.0, 6.0, 4.0}
Ejemplo bidimensional:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s)
// Result:
// { {0.0, 1.0, 2.0},
// {3.0, 12.0, 13.0},
// {6.0, 14.0, 15.0},
// {9.0, 16.0, 17.0} }
Para obtener información sobre StableHLO, consulta StableHLO - dynamic_update_slice.
Erf
Consulta también XlaBuilder::Erf.
Función error x -> erf(x) para cada elemento, donde:
\(\text{erf}(x) = \frac{2}{\sqrt{\pi} }\int_0^x e^{-t^2} \, dt\).
Erf(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Erf también admite el argumento opcional result_accuracy:
Erf(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Exponencial
Consulta también XlaBuilder::Exp.
Exponencial natural x -> e^x para cada elemento.
Exp(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Exp también admite el argumento opcional result_accuracy:
Exp(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Para obtener información sobre StableHLO, consulta StableHLO: exponencial.
Expm1
Consulta también XlaBuilder::Expm1.
Exponencial natural menos uno x -> e^x - 1 para cada elemento.
Expm1(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
La función Expm1 también admite el argumento opcional result_accuracy:
Expm1(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Para obtener información sobre StableHLO, consulta StableHLO - exponential_minus_one.
Fft
Consulta también XlaBuilder::Fft.
La operación FFT de XLA implementa las transformaciones de Fourier directa e inversa para entradas y salidas reales y complejas. Se admiten FFT multidimensionales en hasta 3 ejes.
Fft(operand, ftt_type, fft_length)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand
|
XlaOp
|
Es el array al que le aplicamos la transformada de Fourier. |
fft_type |
FftType |
Consulta la tabla que se encuentra a continuación |
fft_length
|
ArraySlice<int64>
|
Son las longitudes del dominio temporal de los ejes que se transforman. Esto es necesario en particular para que IRFFT ajuste el tamaño del eje más interno, ya que RFFT(fft_length=[16]) tiene la misma forma de salida que RFFT(fft_length=[17]). |
FftType |
Semántica |
|---|---|
FFT |
Realiza la FFT de complejo a complejo. La forma no cambió. |
IFFT |
Es la FFT inversa de números complejos a números complejos. La forma no cambió. |
RFFT
|
Es la FFT de real a complejo directa. La forma del eje más interno se reduce a fft_length[-1] // 2 + 1 si fft_length[-1] es un valor distinto de cero, lo que omite la parte conjugada invertida de la señal transformada más allá de la frecuencia de Nyquist. |
IRFFT
|
Es la FFT inversa de real a complejo (es decir, toma números complejos y devuelve números reales).
La forma del eje más interno se expande a fft_length[-1] si fft_length[-1] es un valor distinto de cero, lo que infiere la parte de la señal transformada más allá de la frecuencia de Nyquist a partir del conjugado inverso de las entradas de 1 a fft_length[-1] // 2 + 1. |
Para obtener información sobre StableHLO, consulta StableHLO - fft.
FFT multidimensional
Cuando se proporciona más de 1 fft_length, esto equivale a aplicar una cascada de operaciones de FFT a cada uno de los ejes más internos. Ten en cuenta que, para los casos de real->complejo y complejo->real, la transformación del eje más interno se realiza (de manera efectiva) primero (FFT real a compleja; última para la FFT inversa de compleja a real), por lo que el eje más interno es el que cambia de tamaño. Las otras transformaciones de ejes serán de complejo a complejo.
Detalles de implementación
La FFT de CPU se basa en TensorFFT de Eigen. La FFT de la GPU usa cuFFT.
Piso
Consulta también XlaBuilder::Floor.
Función de piso para cada elemento x -> ⌊x⌋.
Floor(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Para obtener información sobre StableHLO, consulta StableHLO: piso.
Fusión
Consulta también HloInstruction::CreateFusion.
La operación Fusion representa instrucciones de HLO y sirve como primitiva en HLO.
Esta operación puede aparecer en volcados de HLO, pero no está diseñada para que los usuarios finales la construyan manualmente.
Recopila
La operación de recopilación de XLA une varias segmentaciones (cada una con un desplazamiento de tiempo de ejecución potencialmente diferente) de un array de entrada.
Para obtener información sobre StableHLO, consulta StableHLO: gather.
Semántica general
Consulta también XlaBuilder::Gather.
Para obtener una descripción más intuitiva, consulta la sección "Descripción informal" que se encuentra a continuación.
gather(operand, start_indices, dimension_numbers, slice_sizes,
indices_are_sorted)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand
|
XlaOp
|
Es el array del que recopilamos datos. |
start_indices
|
XlaOp
|
Es un array que contiene los índices iniciales de los segmentos que recopilamos. |
dimension_numbers
|
GatherDimensionNumbers
|
Dimensión en start_indices que "contiene" los índices iniciales. Consulta la siguiente descripción detallada. |
slice_sizes
|
ArraySlice<int64>
|
slice_sizes[i] son los límites del segmento en la dimensión i. |
indices_are_sorted
|
bool
|
Indica si el llamador garantiza que los índices están ordenados. |
Para mayor comodidad, etiquetamos las dimensiones del array de salida que no están en offset_dims como batch_dims.
El resultado es un array con dimensiones batch_dims.size + offset_dims.size.
El operand.rank debe ser igual a la suma de offset_dims.size y collapsed_slice_dims.size. Además, slice_sizes.size debe ser igual a operand.rank.
Si index_vector_dim es igual a start_indices.rank, consideramos implícitamente que start_indices tiene una dimensión final 1 (es decir, si start_indices tenía la forma [6,7] y index_vector_dim es 2, consideramos implícitamente que la forma de start_indices es [6,7,1]).
Los límites para el array de salida a lo largo de la dimensión i se calculan de la siguiente manera:
Si
iestá presente enbatch_dims(es decir, es igual abatch_dims[k]para algúnk), elegimos los límites de dimensión correspondientes destart_indices.shape, y omitimosindex_vector_dim(es decir, elegimosstart_indices.shape.dims[k] sik<index_vector_dimystart_indices.shape.dims[k+1] en caso contrario).Si
iestá presente enoffset_dims(es decir, es igual aoffset_dims[k] para algúnk), elegimos el límite correspondiente deslice_sizesdespués de tener en cuentacollapsed_slice_dims(es decir, elegimosadjusted_slice_sizes[k], dondeadjusted_slice_sizesesslice_sizescon los límites en los índicescollapsed_slice_dimsquitados).
Formalmente, el índice de operando In correspondiente a un índice de salida determinado Out se calcula de la siguiente manera:
Sea
G= {Out[k] parakenbatch_dims}. UsaGpara segmentar un vectorSde modo queS[i] =start_indices[Combine(G,i)], donde Combine(A, b) inserta b en la posiciónindex_vector_dimen A. Ten en cuenta que esto está bien definido incluso siGestá vacío: siGestá vacío, entoncesS=start_indices.Crea un índice inicial,
Sin, enoperandconSdispersandoSconstart_index_map. Más precisamente:Sin[start_index_map[k]] =S[k] sik<start_index_map.size.Sin[_] =0en caso contrario.
Crea un índice
Oinenoperanddispersando los índices en las dimensiones de desplazamiento enOutsegún el conjuntocollapsed_slice_dims. Más precisamente:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]] sik<offset_dims.size(remapped_offset_dimsse define a continuación).Oin[_] =0en caso contrario.
InesOin+Sin, donde + es la suma de cada elemento.
remapped_offset_dims es una función monótona con dominio [0, offset_dims.size) y rango [0, operand.rank) \ collapsed_slice_dims. Por ejemplo, si offset_dims.size es 4, operand.rank es 6 y collapsed_slice_dims es {0, 2}, entonces remapped_offset_dims es {0→1, 1→3, 2→4, 3→5}.
Si indices_are_sorted se establece como verdadero, XLA puede suponer que el usuario ordenó start_indices (en orden ascendente, después de dispersar sus valores según start_index_map). Si no lo son, la semántica se define según la implementación.
Descripción y ejemplos informales
De manera informal, cada índice Out en el array de salida corresponde a un elemento E en el array de operandos, que se calcula de la siguiente manera:
Usamos las dimensiones del lote en
Outpara buscar un índice inicial enstart_indices.Usamos
start_index_mappara correlacionar el índice inicial (cuyo tamaño puede ser menor que operand.rank) con un índice inicial "completo" enoperand.Realizamos un corte dinámico de un segmento con un tamaño de
slice_sizesusando el índice de inicio completo.Redimensionamos el segmento contrayendo las dimensiones
collapsed_slice_dims. Dado que todas las dimensiones de segmentación contraídas deben tener un límite de 1, este cambio de forma siempre es válido.Usamos las dimensiones de desplazamiento en
Outpara indexar esta división y obtener el elemento de entrada,E, que corresponde al índice de salidaOut.
index_vector_dim se establece en start_indices.rank - 1 en todos los ejemplos que se muestran a continuación. Los valores más interesantes para index_vector_dim no cambian la operación de forma fundamental, pero hacen que la representación visual sea más engorrosa.
Para comprender cómo se relacionan todos los elementos anteriores, veamos un ejemplo que recopila 5 segmentos de forma [8,6] de un array [16,11]. La posición de un segmento en el array [16,11] se puede representar como un vector de índice de forma S64[2], por lo que el conjunto de 5 posiciones se puede representar como un array S64[5,2].
Luego, el comportamiento de la operación de recopilación se puede representar como una transformación de índice que toma [G,O0,O1], un índice en la forma de salida, y lo asigna a un elemento en el array de entrada de la siguiente manera:
Primero, seleccionamos un vector (X,Y) del array de índices de recopilación con G.
El elemento del array de salida en el índice [G,O0,O1] es, entonces, el elemento del array de entrada en el índice [X+O0,Y+O1].
slice_sizes es [8,6], que decide el rango de O0 y O1, y esto, a su vez, decide los límites del segmento.
Esta operación de recopilación actúa como un segmento dinámico por lotes con G como dimensión de lote.
Los índices de recopilación pueden ser multidimensionales. Por ejemplo, una versión más general del ejemplo anterior que usa un array de "índices de recopilación" con la forma [4,5,2] traduciría los índices de la siguiente manera:
Nuevamente, esto actúa como un segmento dinámico por lotes G0 y G1 como las dimensiones del lote. El tamaño de la segmentación sigue siendo [8,6].
La operación de recopilación en XLA generaliza la semántica informal que se describió anteriormente de las siguientes maneras:
Podemos configurar qué dimensiones de la forma de salida son las dimensiones de desplazamiento (las dimensiones que contienen
O0yO1en el último ejemplo). Las dimensiones de lote de salida (dimensiones que contienenG0,G1en el último ejemplo) se definen como las dimensiones de salida que no son dimensiones de desplazamiento.La cantidad de dimensiones de desplazamiento de salida presentes de forma explícita en la forma de salida puede ser menor que la cantidad de dimensiones de entrada. Estas dimensiones "faltantes", que se indican explícitamente como
collapsed_slice_dims, deben tener un tamaño de segmentación de1. Dado que tienen un tamaño de segmento de1, el único índice válido para ellos es0, y omitirlos no genera ambigüedad.Es posible que el segmento extraído del array "Gather Indices" ((
X,Y) en el último ejemplo) tenga menos elementos que la cantidad de dimensiones del array de entrada, y una asignación explícita indica cómo se debe expandir el índice para tener la misma cantidad de dimensiones que la entrada.
Como ejemplo final, usamos (2) y (3) para implementar tf.gather_nd:
G0 y G1 se usan para segmentar un índice inicial del array de índices de recopilación como de costumbre, excepto que el índice inicial solo tiene un elemento, X. Del mismo modo, solo hay un índice de desplazamiento de salida con el valor O0. Sin embargo, antes de usarse como índices en el array de entrada, se expanden de acuerdo con "Asignación de índice de recopilación" (start_index_map en la descripción formal) y "Asignación de desplazamiento" (remapped_offset_dims en la descripción formal) en [X,0] y [0,O0], respectivamente, lo que suma [X,O0]. En otras palabras, el índice de salida [G0,G1,O0] se asigna al índice de entrada [GatherIndices[G0,G1,0],O0], lo que nos da la semántica para tf.gather_nd.
slice_sizes para este caso es [1,11]. Intuitivamente, esto significa que cada índice X en el array de índices de recopilación elige una fila completa y el resultado es la concatenación de todas estas filas.
GetDimensionSize
Consulta también XlaBuilder::GetDimensionSize.
Devuelve el tamaño de la dimensión especificada del operando. El operando debe tener forma de array.
GetDimensionSize(operand, dimension)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de entrada de n dimensiones. |
dimension
|
int64
|
Un valor en el intervalo [0, n) que especifica la dimensión |
Para obtener información sobre StableHLO, consulta StableHLO - get_dimension_size.
GetTupleElement
Consulta también XlaBuilder::GetTupleElement.
Indexa una tupla con un valor constante en tiempo de compilación.
El valor debe ser una constante de tiempo de compilación para que la inferencia de formas pueda determinar el tipo del valor resultante.
Esto es análogo a std::get<int N>(t) en C++. Conceptualmente:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
Consulta también tf.tuple.
GetTupleElement(tuple_data, index)
| Argumento | Tipo | Semántica |
|---|---|---|
tuple_data |
XlaOP |
La tupla |
index |
int64 |
Índice de la forma de la tupla |
Para obtener información sobre StableHLO, consulta StableHLO - get_tuple_element.
Imag
Consulta también XlaBuilder::Imag.
Parte imaginaria de cada elemento de una forma compleja (o real). x -> imag(x). Si el operando es de tipo de punto flotante, devuelve 0.
Imag(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Para obtener información sobre StableHLO, consulta StableHLO: imag.
In-feed
Consulta también XlaBuilder::Infeed.
Infeed(shape, config)
| Argumento | Tipo | Semántica |
|---|---|---|
shape
|
Shape
|
Es la forma de los datos leídos desde la interfaz de Infeed. El campo de diseño de la forma debe establecerse para que coincida con el diseño de los datos enviados al dispositivo; de lo contrario, su comportamiento no está definido. |
config |
opcional string |
Es la configuración de la operación. |
Lee un solo elemento de datos de la interfaz de transmisión Infeed implícita del dispositivo, interpreta los datos como la forma y el diseño determinados, y devuelve un XlaOp de los datos. Se permiten varias operaciones de Infeed en un cálculo, pero debe haber un orden total entre ellas. Por ejemplo, dos Infeed en el siguiente código tienen un orden total, ya que hay una dependencia entre los bucles while.
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
No se admiten las formas de tuplas anidadas. Para una forma de tupla vacía, la operación Infeed es, en efecto, una operación nula y continúa sin leer ningún dato de la Infeed del dispositivo.
Para obtener información sobre StableHLO, consulta StableHLO: Infeed.
Pizca
Consulta también XlaBuilder::Iota.
Iota(shape, iota_dimension)
Compila un literal constante en el dispositivo en lugar de una transferencia de host potencialmente grande. Crea un array que tiene la forma especificada y contiene valores que comienzan en cero y aumentan de uno en uno a lo largo de la dimensión especificada. Para los tipos de punto flotante, el array producido es equivalente a ConvertElementType(Iota(...)), en el que Iota es de tipo integral y la conversión es al tipo de punto flotante.
| Argumentos | Tipo | Semántica |
|---|---|---|
shape |
Shape |
Forma del array creado por Iota() |
iota_dimension |
int64 |
Es la dimensión a lo largo de la cual se incrementa. |
Por ejemplo, Iota(s32[4, 8], 0) devuelve
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
Devoluciones por Iota(s32[4, 8], 1)
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
Para obtener información sobre StableHLO, consulta StableHLO: Iota.
IsFinite
Consulta también XlaBuilder::IsFinite.
Comprueba si cada elemento de operand es finito, es decir, no es infinito positivo o negativo, y no es NaN. Devuelve un array de valores PRED con la misma forma que la entrada, en el que cada elemento es true si y solo si el elemento de entrada correspondiente es finito.
IsFinite(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Para obtener información sobre StableHLO, consulta StableHLO - is_finite.
Registro
Consulta también XlaBuilder::Log.
Logaritmo natural x -> ln(x) según cada elemento.
Log(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
El registro también admite el argumento opcional result_accuracy:
Log(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Para obtener información sobre StableHLO, consulta StableHLO: log.
Log1p
Consulta también XlaBuilder::Log1p.
Logaritmo natural desplazado x -> ln(1+x) para cada elemento.
Log1p(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Log1p también admite el argumento opcional result_accuracy:
Log1p(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Para obtener información sobre StableHLO, consulta StableHLO: log_plus_one.
Logística
Consulta también XlaBuilder::Logistic.
Cálculo de la función logística para cada elemento x -> logistic(x).
Logistic(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Logistic también admite el argumento opcional result_accuracy:
Logistic(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Para obtener información sobre StableHLO, consulta StableHLO: Logística.
Mapa
Consulta también XlaBuilder::Map.
Map(operands..., computation, dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
operands |
secuencia de N XlaOp |
N arrays de tipos T0..T{N-1} |
computation
|
XlaComputation
|
Es el cálculo de tipo T_0, T_1,
.., T_{N + M -1} -> S con N parámetros de tipo T y M de tipo arbitrario. |
dimensions |
Array de int64 |
Es un array de dimensiones del mapa. |
static_operands
|
secuencia de N XlaOp
|
Operaciones estáticas para la operación del mapa |
Aplica una función escalar a los arrays operands proporcionados, lo que genera un array de las mismas dimensiones en el que cada elemento es el resultado de la función asignada aplicada a los elementos correspondientes en los arrays de entrada.
La función asignada es un cálculo arbitrario con la restricción de que tiene N entradas de tipo escalar T y una sola salida con el tipo S. La salida tiene las mismas dimensiones que los operandos, excepto que el tipo de elemento T se reemplaza por S.
Por ejemplo, Map(op1, op2, op3, computation, par1) asigna elem_out <-
computation(elem1, elem2, elem3, par1) en cada índice (multidimensional) de los arrays de entrada para producir el array de salida.
Para obtener información sobre StableHLO, consulta StableHLO: mapa.
Máx.
Consulta también XlaBuilder::Max.
Realiza la operación de máximo para cada elemento en los tensores lhs y rhs.
Max(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Max:
Max(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: máximo.
Mín.
Consulta también XlaBuilder::Min.
Realiza una operación min en cada elemento de lhs y rhs.
Min(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Min:
Min(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: mínimo.
Mul
Consulta también XlaBuilder::Mul.
Realiza el producto de los elementos de lhs y rhs.
Mul(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Mul:
Mul(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: multiply.
Neg
Consulta también XlaBuilder::Neg.
Negación de cada elemento x -> -x.
Neg(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Para obtener información sobre StableHLO, consulta StableHLO: negate.
No
Consulta también XlaBuilder::Not.
Es la negación lógica de cada elemento x -> !(x).
Not(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Para obtener información sobre StableHLO, consulta StableHLO: No.
OptimizationBarrier
Consulta también XlaBuilder::OptimizationBarrier.
Impide que cualquier paso de optimización mueva los cálculos a través de la barrera.
OptimizationBarrier(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Garantiza que todas las entradas se evalúen antes de cualquier operador que dependa de los resultados de la barrera.
Para obtener información sobre StableHLO, consulta StableHLO: optimization_barrier.
O
Consulta también XlaBuilder::Or.
Realiza una operación OR a nivel del elemento de lhs y rhs .
Or(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Or:
Or(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: o.
Salida
Consulta también XlaBuilder::Outfeed.
Escribe las entradas en el feed externo.
Outfeed(operand, shape_with_layout, outfeed_config)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de tipo T. |
shape_with_layout |
Shape |
Define el diseño de los datos transferidos |
outfeed_config |
string |
Constante de configuración para la instrucción Outfeed |
shape_with_layout comunica la forma diseñada que queremos alimentar.
Para obtener información sobre StableHLO, consulta StableHLO: Outfeed.
Almohadilla
Consulta también XlaBuilder::Pad.
Pad(operand, padding_value, padding_config)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de tipo T. |
padding_value
|
XlaOp
|
valor escalar de tipo T para completar el padding agregado |
padding_config
|
PaddingConfig
|
Cantidad de relleno en ambos bordes (bajo, alto) y entre los elementos de cada dimensión |
Expande el array operand determinado agregando padding alrededor del array y entre los elementos del array con el padding_value determinado. padding_config especifica la cantidad de padding de borde y el padding interior para cada dimensión.
PaddingConfig es un campo repetido de PaddingConfigDimension que contiene tres campos para cada dimensión: edge_padding_low, edge_padding_high y interior_padding.
edge_padding_low y edge_padding_high especifican la cantidad de padding que se agrega en el extremo inferior (junto al índice 0) y el extremo superior (junto al índice más alto) de cada dimensión, respectivamente. La cantidad de padding de borde puede ser negativa. El valor absoluto del padding negativo indica la cantidad de elementos que se deben quitar de la dimensión especificada.
interior_padding especifica la cantidad de padding que se agrega entre dos elementos cualesquiera en cada dimensión; no puede ser negativo. El padding interior se produce lógicamente antes del padding de borde, por lo que, en el caso de un padding de borde negativo, los elementos se quitan del operando con padding interior.
Esta operación no hace nada si todos los pares de padding de borde son (0, 0) y todos los valores de padding interior son 0. En la siguiente figura, se muestran ejemplos de diferentes valores de edge_padding y interior_padding para un array bidimensional.
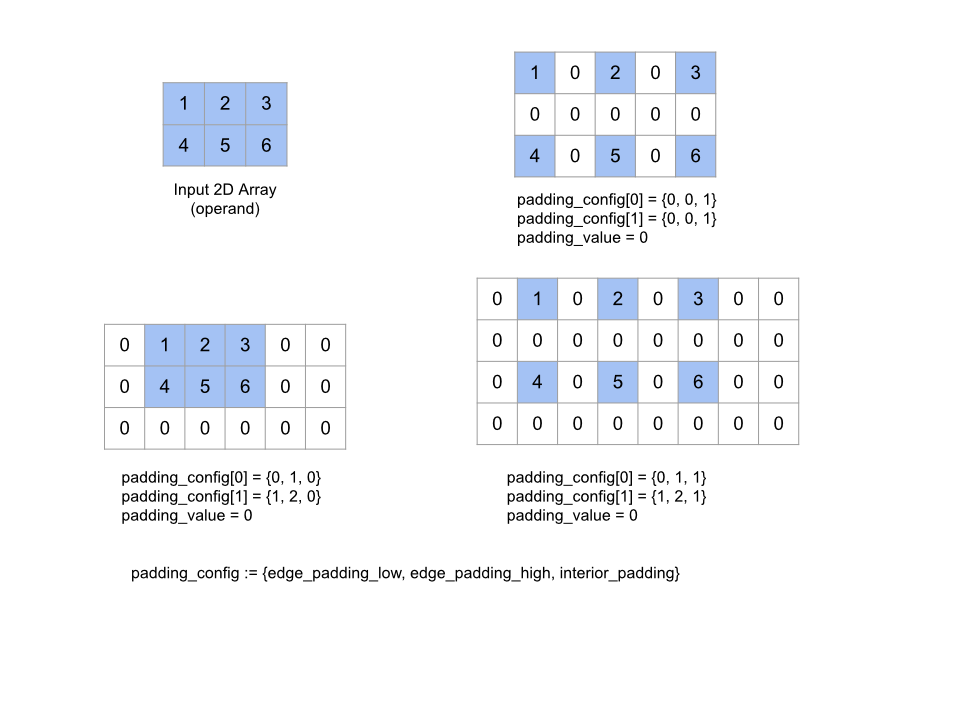
Para obtener información sobre StableHLO, consulta StableHLO: pad.
Parámetro
Consulta también XlaBuilder::Parameter.
Parameter representa un argumento de entrada para un cálculo.
PartitionID
Consulta también XlaBuilder::BuildPartitionId.
Produce partition_id del proceso actual.
PartitionID(shape)
| Argumentos | Tipo | Semántica |
|---|---|---|
shape |
Shape |
Forma de los datos |
PartitionID puede aparecer en los volcados de HLO, pero no está diseñado para que los usuarios finales lo construyan de forma manual.
Para obtener información sobre StableHLO, consulta StableHLO - partition_id.
PopulationCount
Consulta también XlaBuilder::PopulationCount.
Calcula la cantidad de bits establecidos en cada elemento de operand.
PopulationCount(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Para obtener información sobre StableHLO, consulta StableHLO: popcnt.
Pow
Consulta también XlaBuilder::Pow.
Realiza la exponenciación de lhs por rhs según cada elemento.
Pow(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Pow:
Pow(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: potencia.
Real
Consulta también XlaBuilder::Real.
Parte real de cada elemento de una forma compleja (o real). x -> real(x). Si el operando es de tipo de punto flotante, Real devuelve el mismo valor.
Real(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Para obtener información sobre StableHLO, consulta StableHLO: real.
Recv
Consulta también XlaBuilder::Recv.
Recv, RecvWithTokens y RecvToHost son operaciones que sirven como primitivas de comunicación en HLO. Por lo general, estas operaciones aparecen en los volcados de HLO como parte de la entrada/salida de bajo nivel o la transferencia entre dispositivos, pero no están diseñadas para que los usuarios finales las construyan de forma manual.
Recv(shape, handle)
| Argumentos | Tipo | Semántica |
|---|---|---|
shape |
Shape |
Forma de los datos que se recibirán |
handle |
ChannelHandle |
Identificador único para cada par de envío y recepción |
Recibe datos de la forma determinada a partir de una instrucción Send en otro cálculo que comparte el mismo identificador de canal. Devuelve un XlaOp para los datos recibidos.
Para obtener información sobre StableHLO, consulta StableHLO - recv.
RecvDone
Consulta también HloInstruction::CreateRecv y HloInstruction::CreateRecvDone.
Al igual que Send, la API de cliente de la operación Recv representa la comunicación síncrona. Sin embargo, la instrucción se descompone internamente en 2 instrucciones de HLO (Recv y RecvDone) para habilitar las transferencias de datos asíncronas.
Recv(const Shape& shape, int64 channel_id)
Asigna los recursos necesarios para recibir datos de una instrucción Send con el mismo channel_id. Devuelve un contexto para los recursos asignados, que una instrucción RecvDone posterior usa para esperar a que se complete la transferencia de datos. El contexto es una tupla de {búfer de recepción (forma), identificador de solicitud (U32)} y solo se puede usar con una instrucción RecvDone.
Dado un contexto creado por una instrucción Recv, espera a que se complete la transferencia de datos y devuelve los datos recibidos.
Reducir
Consulta también XlaBuilder::Reduce.
Aplica una función de reducción a uno o más arrays en paralelo.
Reduce(operands..., init_values..., computation, dimensions_to_reduce)
| Argumentos | Tipo | Semántica |
|---|---|---|
operands
|
Secuencia de N XlaOp
|
N arrays de tipos T_0,...,
T_{N-1}. |
init_values
|
Secuencia de N XlaOp
|
N valores escalares de tipos T_0,..., T_{N-1}. |
computation
|
XlaComputation
|
cálculo de tipo T_0,..., T_{N-1}, T_0,
...,T_{N-1} ->
Collate(T_0,...,
T_{N-1}). |
dimensions_to_reduce
|
Array de int64
|
Es un array no ordenado de dimensiones para reducir. |
Donde:
- N debe ser mayor o igual que 1.
- El cálculo debe ser "aproximadamente" asociativo (consulta a continuación).
- Todos los arrays de entrada deben tener las mismas dimensiones.
- Todos los valores iniciales deben formar una identidad en
computation. - Si es
N = 1,Collate(T)esT. - Si
N > 1,Collate(T_0, ..., T_{N-1})es una tupla de elementosNdel tipoT.
Esta operación reduce una o más dimensiones de cada array de entrada a escalares.
La cantidad de dimensiones de cada array devuelto es number_of_dimensions(operand) - len(dimensions). El resultado de la operación es Collate(Q_0, ..., Q_N), donde Q_i es un array de tipo T_i, cuyas dimensiones se describen a continuación.
Se permite que diferentes backends reasocien el cálculo de la reducción. Esto puede generar diferencias numéricas, ya que algunas funciones de reducción, como la suma, no son asociativas para los números de punto flotante. Sin embargo, si el rango de los datos es limitado, la suma de números de punto flotante es lo suficientemente asociativa para la mayoría de los usos prácticos.
Para obtener información sobre StableHLO, consulta StableHLO: reduce.
Ejemplos
Cuando se reduce en una dimensión en un solo array unidimensional con valores [10, 11,
12, 13], con la función de reducción f (esto es computation), se podría calcular de la siguiente manera:
f(10, f(11, f(12, f(init_value, 13)))
pero también hay muchas otras posibilidades, p.ej.,
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
A continuación, se muestra un ejemplo aproximado de pseudocódigo sobre cómo se podría implementar la reducción, usando la suma como el cálculo de reducción con un valor inicial de 0.
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
A continuación, se muestra un ejemplo de cómo reducir un array bidimensional (matriz). La forma tiene 2 dimensiones: la dimensión 0 de tamaño 2 y la dimensión 1 de tamaño 3:
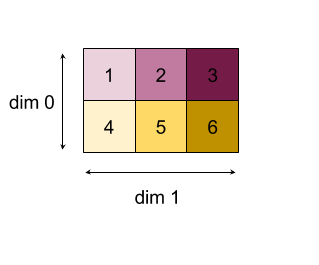
Resultados de la reducción de las dimensiones 0 o 1 con una función "add":
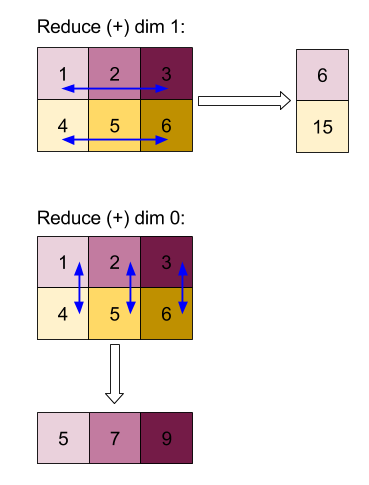
Ten en cuenta que ambos resultados de reducción son arrays unidimensionales. El diagrama muestra uno como columna y otro como fila solo para mayor comodidad visual.
Para un ejemplo más complejo, aquí tienes un array tridimensional. Su cantidad de dimensiones es 3: la dimensión 0 tiene un tamaño de 4, la dimensión 1 tiene un tamaño de 2 y la dimensión 2 tiene un tamaño de 3. Para simplificar, los valores del 1 al 6 se replican en la dimensión 0.
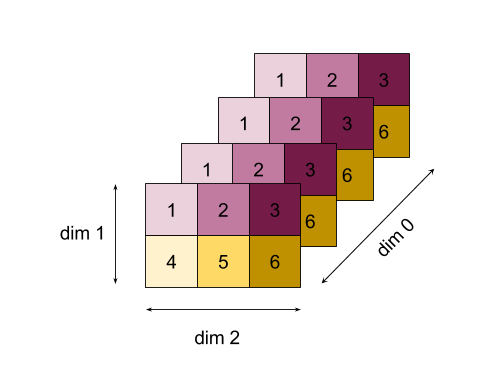
De manera similar al ejemplo en 2D, podemos reducir solo una dimensión. Si reducimos la dimensión 0, por ejemplo, obtenemos un array bidimensional en el que todos los valores de la dimensión 0 se plegaron en un escalar:
| 4 8 12 |
| 16 20 24 |
Si reducimos la dimensión 2, también obtenemos un array bidimensional en el que todos los valores de la dimensión 2 se plegaron en un escalar:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
Ten en cuenta que el orden relativo entre las dimensiones restantes en la entrada se conserva en la salida, pero es posible que a algunas dimensiones se les asignen números nuevos (ya que cambia la cantidad de dimensiones).
También podemos reducir varias dimensiones. La reducción de la suma de las dimensiones 0 y 1 produce el array unidimensional [20, 28, 36].
La reducción del array 3D en todas sus dimensiones produce el escalar 84.
Reducción variádica
Cuando es N > 1, la aplicación de la función de reducción es un poco más compleja, ya que se aplica simultáneamente a todas las entradas. Los operandos se proporcionan al cálculo en el siguiente orden:
- Valor reducido acumulado para el primer operando
- …
- Valor reducido en ejecución para el N-ésimo operando
- Valor de entrada del primer operando
- …
- Valor de entrada del N-ésimo operando
Por ejemplo, considera la siguiente función de reducción, que se puede usar para calcular el máximo y el argmax de un array unidimensional en paralelo:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
Para los arreglos de entrada V = Float[N], K = Int[N] de 1 dimensión y los valores de inicialización I_V = Float, I_K = Int, el resultado f_(N-1) de la reducción en la única dimensión de entrada es equivalente a la siguiente aplicación recursiva:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
Si se aplica esta reducción a un array de valores y a un array de índices secuenciales (es decir, iota), se realizará una coiteración sobre los arrays y se devolverá una tupla que contiene el valor máximo y el índice coincidente.
ReducePrecision
Consulta también XlaBuilder::ReducePrecision.
Modela el efecto de convertir valores de punto flotante a un formato de menor precisión (como IEEE-FP16) y volver al formato original. La cantidad de bits del exponente y la mantisa en el formato de menor precisión se puede especificar de forma arbitraria, aunque es posible que no todos los tamaños de bits sean compatibles con todas las implementaciones de hardware.
ReducePrecision(operand, exponent_bits, mantissa_bits)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de tipo de punto flotante T. |
exponent_bits |
int32 |
Cantidad de bits del exponente en el formato de menor precisión |
mantissa_bits |
int32 |
Cantidad de bits de mantisa en el formato de menor precisión |
El resultado es un array de tipo T. Los valores de entrada se redondean al valor representable más cercano con la cantidad determinada de bits de mantisa (con la semántica "empates a par"), y los valores que superan el rango especificado por la cantidad de bits de exponente se ajustan a infinito positivo o negativo. Los valores de NaN se conservan, aunque se pueden convertir en valores de NaN canónicos.
El formato de menor precisión debe tener al menos un bit de exponente (para distinguir un valor cero de un infinito, ya que ambos tienen una mantisa cero) y debe tener una cantidad no negativa de bits de mantisa. La cantidad de bits del exponente o la mantisa puede exceder el valor correspondiente para el tipo T; la porción correspondiente de la conversión es, entonces, simplemente una operación nula.
Para obtener información sobre StableHLO, consulta StableHLO: reduce_precision.
ReduceScatter
Consulta también XlaBuilder::ReduceScatter.
ReduceScatter es una operación colectiva que realiza de forma eficaz un AllReduce y, luego, dispersa el resultado dividiéndolo en bloques de shard_count a lo largo de scatter_dimension y la réplica i en el grupo de réplicas recibe el fragmento ith.
ReduceScatter(operand, computation, scatter_dimension, shard_count,
replica_groups, channel_id, layout, use_global_device_ids)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand
|
XlaOp
|
Es un array o una tupla no vacía de arrays para reducir en las réplicas. |
computation |
XlaComputation |
Cálculo de la reducción |
scatter_dimension |
int64 |
Es la dimensión para el diagrama de dispersión. |
shard_count
|
int64
|
Cantidad de bloques en los que se divide scatter_dimension |
replica_groups
|
ReplicaGroup vector
|
Son los grupos entre los que se realizan las reducciones. |
channel_id
|
opcional
ChannelHandle |
ID de canal opcional para la comunicación entre módulos |
layout
|
opcional Layout
|
Diseño de memoria especificado por el usuario |
use_global_device_ids |
opcional bool |
Marca especificada por el usuario |
- Cuando
operandes una tupla de arrays, la operación de reducción y dispersión se realiza en cada elemento de la tupla. replica_groupses una lista de grupos de réplicas entre los que se realiza la reducción (el ID de la réplica actual se puede recuperar conReplicaId). El orden de las réplicas en cada grupo determina el orden en el que se dispersará el resultado de la reducción total.replica_groupsdebe estar vacío (en cuyo caso todas las réplicas pertenecen a un solo grupo) o contener la misma cantidad de elementos que la cantidad de réplicas. Cuando hay más de un grupo de réplicas, todos deben tener el mismo tamaño. Por ejemplo,replica_groups = {0, 2}, {1, 3}realiza una reducción entre las réplicas0y2, y1y3, y, luego, dispersa el resultado.shard_countes el tamaño de cada grupo de réplicas. Necesitamos este campo en los casos en quereplica_groupsesté vacío. Sireplica_groupsno está vacío,shard_countdebe ser igual al tamaño de cada grupo de réplicas.channel_idse usa para la comunicación entre módulos: solo las operaciones dereduce-scattercon el mismochannel_idpueden comunicarse entre sí.layoutConsulta xla::shapes para obtener más información sobre los diseños.use_global_device_idses una marca especificada por el usuario. Cuando esfalse(predeterminado), los números enreplica_groupssonReplicaIdcuandotrue, yreplica_groupsrepresenta un ID global de (ReplicaID*partition_count+partition_id). Por ejemplo:- Con 2 réplicas y 4 particiones,
- replica_groups={ {0,1,4,5},{2,3,6,7} } and use_global_device_ids=true
- group[0] = (0,0), (0,1), (1,0), (1,1)
- group[1] = (0,2), (0,3), (1,2), (1,3)
- donde cada par es (replica_id, partition_id).
La forma de salida es la forma de entrada con el scatter_dimension reducido shard_count veces. Por ejemplo, si hay dos réplicas y el operando tiene el valor [1.0, 2.25] y [3.0, 5.25], respectivamente, en las dos réplicas, el valor de salida de esta operación en la que scatter_dim es 0 será [4.0] para la primera réplica y [7.5] para la segunda.
Para obtener información sobre StableHLO, consulta StableHLO - reduce_scatter.
ReduceScatter, ejemplo 1, StableHLO
En el ejemplo anterior, hay 2 réplicas que participan en ReduceScatter. En cada réplica, el operando tiene la forma f32[2,4]. Se realiza una reducción total (suma) en todas las réplicas, lo que produce un valor reducido de la forma f32[2,4] en cada réplica. Luego, este valor reducido se divide en 2 partes a lo largo de la dimensión 1, de modo que cada parte tenga la forma f32[2,2]. Cada réplica dentro del grupo de procesos recibe la parte correspondiente a su posición en el grupo. Como resultado, la salida en cada réplica tiene la forma f32[2,2].
ReduceWindow
Consulta también XlaBuilder::ReduceWindow.
Aplica una función de reducción a todos los elementos de cada ventana de una secuencia de arrays multidimensionales de N, lo que produce un solo array multidimensional o una tupla de N arrays multidimensionales como salida. Cada array de salida tiene la misma cantidad de elementos que la cantidad de posiciones válidas de la ventana. Una capa de agrupación se puede expresar como un ReduceWindow. Al igual que con Reduce, el computation aplicado siempre se pasa al init_values del lado izquierdo.
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| Argumentos | Tipo | Semántica |
|---|---|---|
operands
|
N XlaOps
|
Es una secuencia de N arrays multidimensionales de tipos T_0,..., T_{N-1}, cada uno de los cuales representa el área base sobre la que se coloca la ventana. |
init_values
|
N XlaOps
|
Son los N valores iniciales para la reducción, uno para cada uno de los N operandos. Consulta Reducir para obtener más detalles. |
computation
|
XlaComputation
|
Función de reducción de tipo T_0,
..., T_{N-1}, T_0, ..., T_{N-1}
-> Collate(T_0, ..., T_{N-1}) para aplicar a los elementos de cada ventana de todos los operandos de entrada. |
window_dimensions
|
ArraySlice<int64>
|
Es un array de números enteros para los valores de la dimensión de la ventana. |
window_strides
|
ArraySlice<int64>
|
Es un array de números enteros para los valores de la ventana de discretización. |
base_dilations
|
ArraySlice<int64>
|
Es un array de números enteros para los valores de dilatación base. |
window_dilations
|
ArraySlice<int64>
|
Es un array de números enteros para los valores de dilatación de la ventana. |
padding
|
Padding
|
Tipo de padding para la ventana (Padding::kSame, que agrega padding para tener la misma forma de salida que la entrada si la distancia es 1, o Padding::kValid, que no usa padding y "detiene" la ventana una vez que ya no cabe) |
Donde:
- N debe ser mayor o igual que 1.
- Todos los arrays de entrada deben tener las mismas dimensiones.
- Si es
N = 1,Collate(T)esT. - Si
N > 1,Collate(T_0, ..., T_{N-1})es una tupla de elementosNdel tipo(T0,...T{N-1}).
Para obtener información sobre StableHLO, consulta StableHLO - reduce_window.
ReduceWindow, ejemplo 1
La entrada es una matriz de tamaño [4x6], y tanto window_dimensions como window_stride_dimensions son [2x3].
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
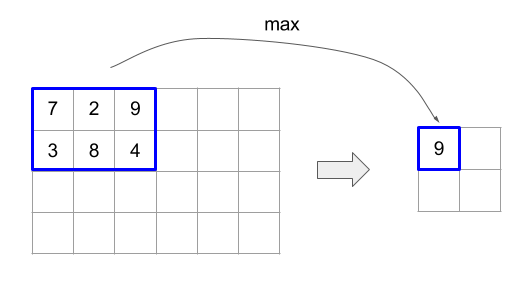
Un stride de 1 en una dimensión especifica que la posición de una ventana en la dimensión está a 1 elemento de distancia de su ventana adyacente. Para especificar que no se superpongan ventanas, window_stride_dimensions debe ser igual a window_dimensions. En la siguiente figura, se ilustra el uso de dos valores de stride diferentes. El padding se aplica a cada dimensión de la entrada, y los cálculos son los mismos que si la entrada llegara con las dimensiones que tiene después del padding.
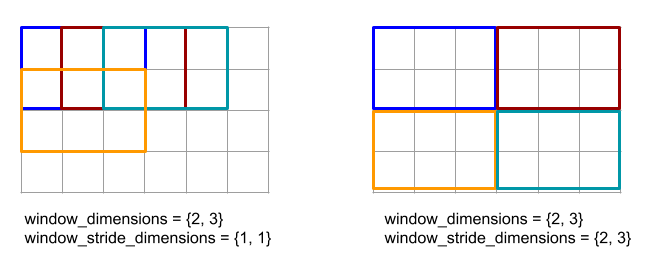
Para un ejemplo de padding no trivial, considera calcular el mínimo de la ventana de reducción (el valor inicial es MAX_FLOAT) con la dimensión 3 y el avance 2 sobre el array de entrada [10000, 1000, 100, 10, 1]. El padding kValid calcula los mínimos en dos ventanas válidas: [10000, 1000, 100] y [100, 10, 1], lo que genera el resultado [100, 1]. El padding kSame primero rellena el array para que la forma después de la ventana de reducción sea la misma que la entrada para el stride uno agregando elementos iniciales en ambos lados, lo que da como resultado [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE]. Ejecutar reduce-window en el array con padding opera en tres ventanas [MAX_VALUE, 10000, 1000], [1000, 100, 10] y [10, 1, MAX_VALUE], y genera [1000, 10, 1].
El orden de evaluación de la función de reducción es arbitrario y puede ser no determinístico. Por lo tanto, la función de reducción no debe ser demasiado sensible a la reasociación. Consulta el debate sobre la asociatividad en el contexto de Reduce para obtener más detalles.
ReduceWindow, ejemplo 2, StableHLO
En el ejemplo anterior, se muestra lo siguiente:
Entrada) El operando tiene una forma de entrada de S32[3,2]. Con valores de [[1,2],[3,4],[5,6]]
Paso 1: La dilatación base con un factor de 2 a lo largo de la dimensión de la fila inserta agujeros entre cada fila del operando. Después de la dilatación, se aplica un padding de 2 filas en la parte superior y 1 fila en la parte inferior. Como resultado, el tensor se vuelve más alto.
Paso 2: Se define una ventana con forma [2,1] y dilatación de ventana [3,1]. Esto significa que cada ventana selecciona dos elementos de la misma columna, pero el segundo elemento se toma tres filas debajo del primero en lugar de directamente debajo de él.
Paso 3: Luego, las ventanas se deslizan por el operando con un stride de [4,1]. Esto hace que la ventana se mueva cuatro filas hacia abajo a la vez, mientras se desplaza una columna a la vez de forma horizontal. Las celdas de padding se completan con el valor init_value (en este caso, init_value = 0). Se ignoran los valores que "caen en" las celdas de dilatación.
Debido al padding y al stride, algunas ventanas se superponen solo con ceros y agujeros, mientras que otras se superponen con valores de entrada reales.
Paso 4: Dentro de cada ventana, los elementos se combinan con la función de reducción (a, b) → a + b, a partir de un valor inicial de 0. Las dos ventanas superiores solo ven relleno y agujeros, por lo que sus resultados son 0. Las ventanas inferiores capturan los valores 3 y 4 de la entrada y los devuelven como resultados.
Resultados) El resultado final tiene la forma S32[2,2], con los siguientes valores: [[0,0],[3,4]]
Rem
Consulta también XlaBuilder::Rem.
Calcula el resto de la división, elemento por elemento, entre el dividendo lhs y el divisor rhs.
El signo del resultado se toma del dividendo, y el valor absoluto del resultado siempre es menor que el valor absoluto del divisor.
Rem(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Rem:
Rem(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: remainder.
ReplicaId
Consulta también XlaBuilder::ReplicaId.
Devuelve el ID único (escalar U32) de la réplica.
ReplicaId()
El ID único de cada réplica es un número entero sin signo en el intervalo [0, N), donde N es la cantidad de réplicas. Dado que todas las réplicas ejecutan el mismo programa, una llamada a ReplicaId() en el programa devolverá un valor diferente en cada réplica.
Para obtener información sobre StableHLO, consulta StableHLO - replica_id.
Reshape
Consulta también XlaBuilder::Reshape.
y la operación Collapse.
Cambia la forma de las dimensiones de un array en una configuración nueva.
Reshape(operand, dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de tipo T. |
dimensions |
int64 vector |
Vector de tamaños de las dimensiones nuevas |
Conceptualmente, reshape primero aplana un array en un vector unidimensional de valores de datos y, luego, refina este vector en una nueva forma. Los argumentos de entrada son un array arbitrario de tipo T, un vector constante en tiempo de compilación de índices de dimensión y un vector constante en tiempo de compilación de tamaños de dimensión para el resultado.
El vector dimensions determina el tamaño del array de salida. El valor en el índice 0 de dimensions es el tamaño de la dimensión 0, el valor en el índice 1 es el tamaño de la dimensión 1, y así sucesivamente. El producto de las dimensiones de dimensions debe ser igual al producto de los tamaños de las dimensiones del operando. Cuando se refina el array contraído en el array multidimensional definido por dimensions, las dimensiones en dimensions se ordenan desde la variación más lenta (más importante) hasta la variación más rápida (más secundaria).
Por ejemplo, sea v un array de 24 elementos:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
Como caso especial, reshape puede transformar un array de un solo elemento en un escalar y viceversa. Por ejemplo:
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
Para obtener información sobre StableHLO, consulta StableHLO: reshape.
Reshape (explícito)
Consulta también XlaBuilder::Reshape.
Reshape(shape, operand)
Es una operación de cambio de forma que usa una forma objetivo explícita.
| Argumentos | Tipo | Semántica |
|---|---|---|
shape |
Shape |
Forma de salida del tipo T |
operand |
XlaOp |
Es un array de tipo T. |
Rev (inversa)
Consulta también XlaBuilder::Rev.
Rev(operand, dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de tipo T. |
dimensions |
ArraySlice<int64> |
Dimensiones que se invertirán |
Invierte el orden de los elementos en el array operand a lo largo del dimensions especificado, lo que genera un array de salida con la misma forma. Cada elemento del array de operandos en un índice multidimensional se almacena en el array de salida en un índice transformado. El índice multidimensional se transforma invirtiendo el índice en cada dimensión que se debe invertir (es decir, si una dimensión de tamaño N es una de las dimensiones de inversión, su índice i se transforma en N - 1 - i).
Un uso de la operación Rev es invertir el array de pesos de convolución a lo largo de las dos dimensiones de la ventana durante el cálculo del gradiente en las redes neuronales.
Para obtener información sobre StableHLO, consulta StableHLO: Reverse.
RngNormal
Consulta también XlaBuilder::RngNormal.
Construye un resultado de una forma determinada con números aleatorios generados según la distribución normal \(N(\mu, \sigma)\) . Los parámetros \(\mu\) y \(\sigma\), y la forma de salida deben tener un tipo elemental de punto flotante. Además, los parámetros deben ser valores escalares.
RngNormal(mu, sigma, shape)
| Argumentos | Tipo | Semántica |
|---|---|---|
mu |
XlaOp |
Es un escalar de tipo T que especifica la media de los números generados. |
sigma
|
XlaOp
|
Es un escalar de tipo T que especifica la desviación estándar de los datos generados. |
shape |
Shape |
Forma de salida del tipo T |
Para obtener información sobre StableHLO, consulta StableHLO: rng.
RngUniform
Consulta también XlaBuilder::RngUniform.
Construye un tensor de salida con una forma determinada y números aleatorios generados según la distribución uniforme en el intervalo \([a,b)\). Los parámetros y el tipo de elemento de salida deben ser un tipo booleano, un tipo integral o tipos de punto flotante, y los tipos deben ser coherentes. Actualmente, los backends de CPU y GPU solo admiten F64, F32, F16, BF16, S64, U64, S32 y U32. Además, los parámetros deben ser valores escalares. Si \(b <= a\) el resultado está definido por la implementación.
RngUniform(a, b, shape)
| Argumentos | Tipo | Semántica |
|---|---|---|
a |
XlaOp |
Es un escalar de tipo T que especifica el límite inferior del intervalo. |
b |
XlaOp |
Es un escalar de tipo T que especifica el límite superior del intervalo. |
shape |
Shape |
Forma de salida del tipo T |
Para obtener información sobre StableHLO, consulta StableHLO: rng.
RngBitGenerator
Consulta también XlaBuilder::RngBitGenerator.
Genera un resultado con una forma determinada completada con bits aleatorios uniformes usando el algoritmo especificado (o el valor predeterminado del backend) y devuelve un estado actualizado (con la misma forma que el estado inicial) y los datos aleatorios generados.
El estado inicial es el estado inicial de la generación de números aleatorios actual. Tanto el valor como la forma requerida y los valores válidos dependen del algoritmo utilizado.
Se garantiza que el resultado es una función determinística del estado inicial, pero no se garantiza que sea determinístico entre diferentes backends y versiones del compilador.
RngBitGenerator(algorithm, initial_state, shape)
| Argumentos | Tipo | Semántica |
|---|---|---|
algorithm |
RandomAlgorithm |
Es el algoritmo de PRNG que se usará. |
initial_state |
XlaOp |
Es el estado inicial del algoritmo PRNG. |
shape |
Shape |
Es la forma de salida de los datos generados. |
Valores disponibles para algorithm:
rng_default: Es un algoritmo específico del backend con requisitos de forma específicos del backend.rng_three_fry: Algoritmo PRNG basado en el contador ThreeFry. La formainitial_stateesu64[2]con valores arbitrarios. Salmon et al. SC 2011. Números aleatorios paralelos: tan fácil como contar del 1 al 3.rng_philox: Algoritmo de Philox para generar números aleatorios en paralelo. La formainitial_stateesu64[3]con valores arbitrarios. Salmon et al. SC 2011. Números aleatorios paralelos: tan fácil como contar del 1 al 3.
Para obtener información sobre StableHLO, consulta StableHLO - rng_bit_generator.
RngGetAndUpdateState
Consulta también HloInstruction::CreateRngGetAndUpdateState.
Internamente, la API de las distintas operaciones de Rng se descompone en instrucciones de HLO, incluida RngGetAndUpdateState.
RngGetAndUpdateState funciona como primitiva en HLO. Esta operación puede aparecer en los volcados de HLO, pero no está diseñada para que los usuarios finales la construyan manualmente.
Ronda
Consulta también XlaBuilder::Round.
Redondeo según cada elemento, con desempate en dirección opuesta al cero.
Round(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
RoundNearestAfz
Consulta también XlaBuilder::RoundNearestAfz.
Realiza un redondeo según cada elemento hacia el número entero más cercano, y rompe los empates alejándose de cero.
RoundNearestAfz(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Para obtener información sobre StableHLO, consulta StableHLO - round_nearest_afz.
RoundNearestEven
Consulta también XlaBuilder::RoundNearestEven.
Redondeo según cada elemento, con empates al número par más cercano.
RoundNearestEven(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Para obtener información sobre StableHLO, consulta StableHLO - round_nearest_even.
Rsqrt
Consulta también XlaBuilder::Rsqrt.
Es el recíproco de la operación de raíz cuadrada x -> 1.0 / sqrt(x) para cada elemento.
Rsqrt(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Rsqrt también admite el argumento opcional result_accuracy:
Rsqrt(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Para obtener información sobre StableHLO, consulta StableHLO: rsqrt.
Escanear
Consulta también XlaBuilder::Scan.
Aplica una función de reducción a un array en una dimensión determinada, lo que genera un estado final y un array de valores intermedios.
Scan(inputs..., inits..., to_apply, scan_dimension,
is_reverse, is_associative)
| Argumentos | Tipo | Semántica |
|---|---|---|
inputs |
Secuencia de m XlaOps |
Son los arrays que se analizarán. |
inits |
Secuencia de k XlaOps |
Transporte inicial. |
to_apply |
XlaComputation |
Es un cálculo de tipo i_0, ..., i_{m-1}, c_0, ..., c_{k-1} -> (o_0, ..., o_{n-1}, c'_0, ..., c'_{k-1}). |
scan_dimension |
int64 |
Es la dimensión en la que se realizará el análisis. |
is_reverse |
bool |
Si es verdadero, se realiza el análisis en orden inverso. |
is_associative |
bool (tres estados) |
Si es verdadero, la operación es asociativa. |
La función to_apply se aplica de forma secuencial a los elementos de inputs a lo largo de scan_dimension. Si is_reverse es falso, los elementos se procesan en orden de 0 a N-1, donde N es el tamaño de scan_dimension. Si is_reverse es verdadero, los elementos se procesan desde N-1 hasta 0.
La función to_apply toma operandos m + k:
melementos actuales deinputsktransportan valores del paso anterior (oinitspara el primer elemento).
La función to_apply devuelve una tupla de valores n + k:
- Elementos
ndeoutputs. knuevos valores de transferencia.
La operación de análisis produce una tupla de valores n + k:
- Son los arrays de salida
n, que contienen los valores de salida para cada paso. - Son los valores finales de
kdespués de procesar todos los elementos.
Los tipos de las entradas de m deben coincidir con los tipos de los primeros parámetros de m de to_apply con una dimensión de exploración adicional. Los tipos de los resultados de n deben coincidir con los tipos de los primeros valores de retorno de n de to_apply con una dimensión de exploración adicional. La dimensión de exploración adicional entre todas las entradas y salidas debe tener el mismo tamaño N. Los tipos de los últimos parámetros k y los valores de retorno de to_apply, así como los inits de k, deben coincidir.
Por ejemplo (m, n, k == 1, N == 3), para el acarreo inicial i, la entrada [a, b, c], la función f(x, c) -> (y, c') y scan_dimension=0, is_reverse=false:
- Paso 0:
f(a, i) -> (y0, c0) - Paso 1:
f(b, c0) -> (y1, c1) - Paso 2:
f(c, c1) -> (y2, c2)
El resultado de Scan es ([y0, y1, y2], c2).
Dispersión
Consulta también XlaBuilder::Scatter.
La operación de dispersión de XLA genera una secuencia de resultados que son los valores del array de entrada operands, con varias segmentaciones (en los índices especificados por scatter_indices) actualizadas con la secuencia de valores en updates usando update_computation.
Scatter(operands..., scatter_indices, updates..., update_computation,
dimension_numbers, indices_are_sorted, unique_indices)
| Argumentos | Tipo | Semántica |
|---|---|---|
operands |
Secuencia de N XlaOp |
Es la cantidad de arrays de tipos T_0, ..., T_N que se dispersarán. |
scatter_indices |
XlaOp |
Es un array que contiene los índices iniciales de los segmentos que se deben dispersar. |
updates |
Secuencia de N XlaOp |
N arrays de tipos T_0, ..., T_N. updates[i] contiene los valores que se deben usar para la dispersión de operands[i]. |
update_computation |
XlaComputation |
Es el cálculo que se usará para combinar los valores existentes en el array de entrada y las actualizaciones durante la dispersión. Este cálculo debe ser del tipo T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N). |
index_vector_dim |
int64 |
Dimensión en scatter_indices que contiene los índices iniciales. |
update_window_dims |
ArraySlice<int64> |
Es el conjunto de dimensiones en forma de updates que son dimensiones de la ventana. |
inserted_window_dims |
ArraySlice<int64> |
Es el conjunto de dimensiones de la ventana que se deben insertar en la forma updates. |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
Es un mapa de dimensiones que va de los índices de dispersión al espacio de índices del operando. Este array se interpreta como una asignación de i a scatter_dims_to_operand_dims[i] . Debe ser uno a uno y total. |
dimension_number |
ScatterDimensionNumbers |
Números de dimensión para la operación de dispersión |
indices_are_sorted |
bool |
Indica si el llamador garantiza que los índices estén ordenados. |
unique_indices |
bool |
Indica si el llamador garantiza que los índices son únicos. |
Donde:
- N debe ser mayor o igual que 1.
operands[0], …,operands[N-1] deben tener las mismas dimensiones.updates[0], …,updates[N-1] deben tener las mismas dimensiones.- Si es
N = 1,Collate(T)esT. - Si
N > 1,Collate(T_0, ..., T_N)es una tupla de elementosNdel tipoT.
Si index_vector_dim es igual a scatter_indices.rank, consideramos implícitamente que scatter_indices tiene una dimensión 1 final.
Definimos update_scatter_dims de tipo ArraySlice<int64> como el conjunto de dimensiones en la forma updates que no están en update_window_dims, en orden ascendente.
Los argumentos de dispersión deben seguir estas restricciones:
Cada array
updatesdebe tener dimensionesupdate_window_dims.size + scatter_indices.rank - 1.Los límites de la dimensión
ien cada arrayupdatesdeben cumplir con lo siguiente:- Si
iestá presente enupdate_window_dims(es decir, es igual aupdate_window_dims[k] para algúnk), el límite de la dimensiónienupdatesno debe exceder el límite correspondiente deoperanddespués de tener en cuenta elinserted_window_dims(es decir,adjusted_window_bounds[k], dondeadjusted_window_boundscontiene los límites deoperandcon los límites en los índicesinserted_window_dimsquitados). - Si
iestá presente enupdate_scatter_dims(es decir, es igual aupdate_scatter_dims[k] para algúnk), el límite de la dimensiónienupdatesdebe ser igual al límite correspondiente descatter_indices, omitiendoindex_vector_dim(es decir,scatter_indices.shape.dims[k], sik<index_vector_dimyscatter_indices.shape.dims[k+1] en caso contrario).
- Si
update_window_dimsdebe estar en orden ascendente, no tener números de dimensión repetidos y estar en el rango[0, updates.rank).inserted_window_dimsdebe estar en orden ascendente, no tener números de dimensión repetidos y estar en el rango[0, operand.rank).operand.rankdebe ser igual a la suma deupdate_window_dims.sizeyinserted_window_dims.size.scatter_dims_to_operand_dims.sizedebe ser igual ascatter_indices.shape.dims[index_vector_dim], y sus valores deben estar en el rango[0, operand.rank).
Para un índice determinado U en cada matriz updates, el índice correspondiente I en la matriz operands correspondiente en la que se debe aplicar esta actualización se calcula de la siguiente manera:
- Sea
G= {U[k] parakenupdate_scatter_dims}. UsaGpara buscar un vector de índiceSen el arrayscatter_indicesde modo queS[i] =scatter_indices[Combine(G,i)], donde Combine(A, b) inserta b en las posicionesindex_vector_dimen A. - Crea un índice
SinenoperanddispersandoScon el mapascatter_dims_to_operand_dims.SDe manera más formal:Sin[scatter_dims_to_operand_dims[k]] =S[k] sik<scatter_dims_to_operand_dims.size.Sin[_] =0en caso contrario.
- Crea un índice
Winen cada arrayoperandsdispersando los índices enupdate_window_dimsenUsegúninserted_window_dims. De manera más formal:Win[window_dims_to_operand_dims(k)] =U[k] sikestá enupdate_window_dims, dondewindow_dims_to_operand_dimses la función monotónica con dominio [0,update_window_dims.size) y rango [0,operand.rank) \inserted_window_dims. (Por ejemplo, siupdate_window_dims.sizees4,operand.rankes6yinserted_window_dimses {0,2}, entonceswindow_dims_to_operand_dimses {0→1,1→3,2→4,3→5}).Win[_] =0en caso contrario.
IesWin+Sin, donde + es la suma de cada elemento.
En resumen, la operación de dispersión se puede definir de la siguiente manera.
- Inicializa
outputconoperands, es decir, para todos los índicesJy para todos los índicesOen el arrayoperands[J]:
output[J][O] =operands[J][O] - Para cada índice
Uen el arrayupdates[J] y el índice correspondienteOen el arrayoperand[J], siOes un índice válido paraoutput:
(output[0][O], …,output[N-1][O]) =update_computation(output[0][O], …, ,output[N-1][O],updates[0][U], …,updates[N-1][U])
El orden en el que se aplican las actualizaciones no es determinístico. Por lo tanto, cuando varios índices en updates hacen referencia al mismo índice en operands, el valor correspondiente en output no será determinístico.
Ten en cuenta que el primer parámetro que se pasa a update_computation siempre será el valor actual del array output y el segundo parámetro siempre será el valor del array updates. Esto es importante, en especial, en los casos en que update_computation no es conmutativo.
Si indices_are_sorted se establece como verdadero, XLA puede suponer que el usuario ordenó los scatter_indices (en orden ascendente, después de dispersar sus valores según scatter_dims_to_operand_dims). Si no lo son, la semántica se define según la implementación.
Si unique_indices se establece como verdadero, XLA puede suponer que todos los elementos dispersos son únicos. Por lo tanto, XLA podría usar operaciones no atómicas. Si unique_indices se establece como verdadero y los índices a los que se dispersan no son únicos, la semántica se define en la implementación.
De manera informal, la operación de dispersión se puede ver como una inversa de la operación de recopilación, es decir, la operación de dispersión actualiza los elementos de la entrada que se extraen con la operación de recopilación correspondiente.
Para obtener una descripción informal detallada y ejemplos, consulta la sección "Descripción informal" en Gather.
Para obtener información sobre StableHLO, consulta StableHLO: scatter.
Gráfico de dispersión: ejemplo 1, StableHLO
En la imagen anterior, cada fila de la tabla es un ejemplo de un índice de actualización. Revisemos paso a paso de izquierda(Actualizar índice) a derecha(Índice de resultados):
Input) input tiene la forma S32[2,3,4,2]. scatter_indices tiene la forma S64[2,2,3,2]. updates tiene la forma S32[2,2,3,1,2].
Actualizar índice) Como parte de la entrada, se nos proporciona update_window_dims:[3,4]. Esto nos indica que las dimensiones 3 y 4 de updates son dimensiones de ventana, destacadas en amarillo. Esto nos permite deducir que update_scatter_dims = [0,1,2].
Actualiza el índice de dispersión) Nos muestra el updated_scatter_dims extraído para cada uno.
(El no amarillo de la columna Update Index)
Índice de inicio): Si observamos la imagen del tensor scatter_indices, podemos ver que los valores del paso anterior (índice de dispersión de actualización) nos indican la ubicación del índice de inicio. En index_vector_dim, también se indica la dimensión de starting_indices, que contiene los índices iniciales, que, para scatter_indices, es la dimensión 3 con un tamaño de 2.
Índice de inicio completo) scatter_dims_to_operand_dims = [2,1] nos indica que el primer elemento del vector de índice va a la dimensión del operando 2. El segundo elemento del vector de índice va a la dimensión 1 del operando. Las dimensiones restantes del operando se completan con 0.
Índice de procesamiento por lotes completo) Podemos ver que el área destacada en morado se muestra en esta columna(índice de procesamiento por lotes completo), la columna del índice de dispersión de actualización y la columna del índice de actualización.
Índice de ventana completa) calculado a partir de update_window_dimensions [3,4].
Índice de resultado) La suma del índice de inicio completo, el índice de procesamiento por lotes completo y el índice de ventana completa en el tensor operand. Observa que las regiones destacadas en verde también corresponden a la figura operand. Se omite la última fila porque queda fuera del tensor operand.
Seleccionar
Consulta también XlaBuilder::Select.
Construye un array de salida a partir de elementos de dos arrays de entrada, según los valores de un array de predicado.
Select(pred, on_true, on_false)
| Argumentos | Tipo | Semántica |
|---|---|---|
pred |
XlaOp |
Es un array de tipo PRED. |
on_true |
XlaOp |
Es un array de tipo T. |
on_false |
XlaOp |
Es un array de tipo T. |
Los arrays on_true y on_false deben tener la misma forma. Esta también es la forma del array de salida. El array pred debe tener la misma dimensionalidad que on_true y on_false, con el tipo de elemento PRED.
Para cada elemento P de pred, el elemento correspondiente del array de salida se toma de on_true si el valor de P es true y de on_false si el valor de P es false. Como una forma restringida de transmisión, pred puede ser un escalar de tipo PRED. En este caso, el array de salida se toma por completo de on_true si pred es true, y de on_false si pred es false.
Ejemplo con pred no escalar:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
Ejemplo con pred escalar:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
Se admiten selecciones entre tuplas. A los efectos de este documento, las tuplas se consideran tipos escalares. Si on_true y on_false son tuplas (que deben tener la misma forma), pred debe ser un escalar de tipo PRED.
Para obtener información sobre StableHLO, consulta StableHLO: select.
SelectAndScatter
Consulta también XlaBuilder::SelectAndScatter.
Esta operación se puede considerar como una operación compuesta que primero calcula ReduceWindow en el array operand para seleccionar un elemento de cada ventana y, luego, dispersa el array source en los índices de los elementos seleccionados para construir un array de salida con la misma forma que el array de operandos. La función binaria select se usa para seleccionar un elemento de cada ventana aplicándolo en cada ventana, y se llama con la propiedad de que el vector de índice del primer parámetro es lexicográficamente menor que el vector de índice del segundo parámetro. La función select devuelve true si se selecciona el primer parámetro y devuelve false si se selecciona el segundo parámetro. Además, la función debe mantener la transitividad (es decir, si select(a, b) y select(b, c) son true, entonces select(a, c) también es true) para que el elemento seleccionado no dependa del orden de los elementos recorridos para una ventana determinada.
La función scatter se aplica en cada índice seleccionado del array de salida. Toma dos parámetros escalares:
- Valor actual en el índice seleccionado del array de salida
- El valor de dispersión de
sourceque se aplica al índice seleccionado
Combina los dos parámetros y devuelve un valor escalar que se usa para actualizar el valor en el índice seleccionado del array de salida. Inicialmente, todos los índices del array de salida se establecen en init_value.
El array de salida tiene la misma forma que el array operand, y el array source debe tener la misma forma que el resultado de aplicar una operación ReduceWindow en el array operand. SelectAndScatter se puede usar para propagar hacia atrás los valores del gradiente de una capa de agrupación en una red neuronal.
SelectAndScatter(operand, select, window_dimensions, window_strides, padding,
source, init_value, scatter)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand
|
XlaOp
|
Es un array de tipo T sobre el que se deslizan las ventanas. |
select
|
XlaComputation
|
Es el cálculo binario de tipo T, T
-> PRED que se aplica a todos los elementos de cada ventana. Muestra true si se selecciona el primer parámetro y false si se selecciona el segundo. |
window_dimensions
|
ArraySlice<int64>
|
Es un array de números enteros para los valores de la dimensión de la ventana. |
window_strides
|
ArraySlice<int64>
|
Es un array de números enteros para los valores de la ventana de discretización. |
padding
|
Padding
|
Tipo de padding para la ventana (Padding::kSame o Padding::kValid) |
source
|
XlaOp
|
Es un array de tipo T con los valores que se dispersarán. |
init_value
|
XlaOp
|
Valor escalar de tipo T para el valor inicial del array de salida |
scatter
|
XlaComputation
|
Cálculo binario de tipo T, T
-> T, para aplicar cada elemento de la fuente de dispersión con su elemento de destino |
En la siguiente figura, se muestran ejemplos del uso de SelectAndScatter, con la función select que calcula el valor máximo entre sus parámetros. Ten en cuenta que, cuando las ventanas se superponen, como en la figura (2) a continuación, un índice del array operand puede seleccionarse varias veces por diferentes ventanas. En la figura, el elemento con el valor 9 se selecciona en ambas ventanas superiores (azul y roja), y la función de suma binaria scatter produce el elemento de salida con el valor 8 (2 + 6).
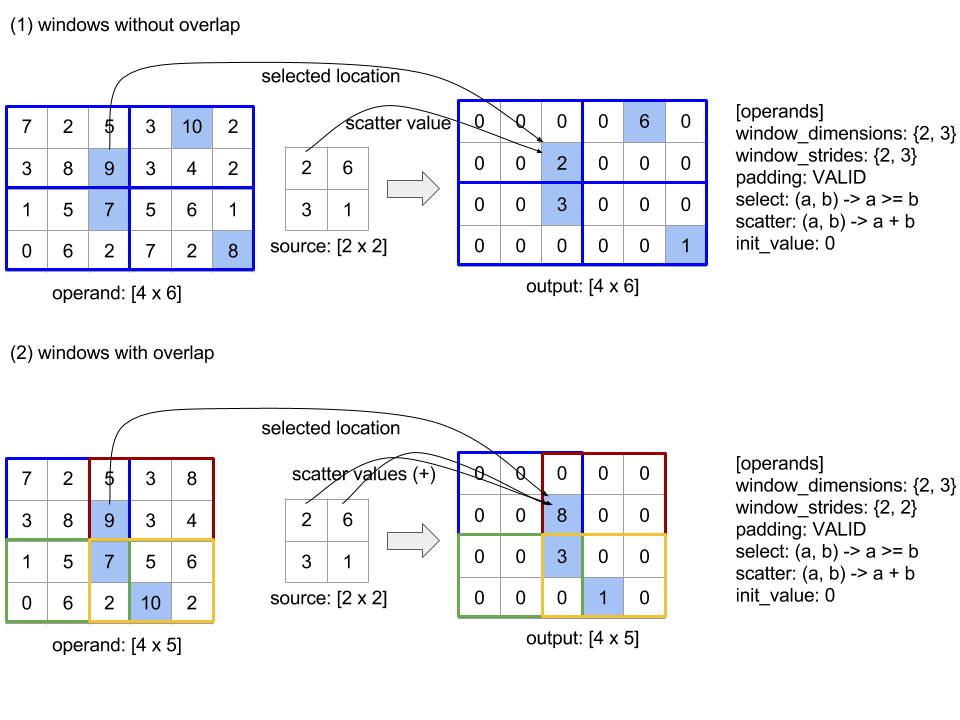
El orden de evaluación de la función scatter es arbitrario y puede ser no determinista. Por lo tanto, la función scatter no debe ser demasiado sensible a la reasociación. Consulta el debate sobre la asociatividad en el contexto de Reduce para obtener más detalles.
Para obtener información sobre StableHLO, consulta StableHLO: select_and_scatter.
Enviar
Consulta también XlaBuilder::Send.
Send, SendWithTokens y SendToHost son operaciones que sirven como primitivas de comunicación en HLO. Por lo general, estas operaciones aparecen en los volcados de HLO como parte de la entrada/salida de bajo nivel o la transferencia entre dispositivos, pero no están diseñadas para que los usuarios finales las construyan de forma manual.
Send(operand, handle)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Datos para enviar (array de tipo T) |
handle |
ChannelHandle |
Identificador único para cada par de envío y recepción |
Envía los datos del operando proporcionado a una instrucción Recv en otro cálculo que comparte el mismo identificador de canal. No devuelve ningún dato.
Al igual que la operación Recv, la API de cliente de la operación Send representa la comunicación síncrona y se descompone internamente en 2 instrucciones de HLO (Send y SendDone) para habilitar las transferencias de datos asíncronas. Consulta también HloInstruction::CreateSend y HloInstruction::CreateSendDone.
Send(HloInstruction operand, int64 channel_id)
Inicia una transferencia asíncrona del operando a los recursos asignados por la instrucción Recv con el mismo ID de canal. Devuelve un contexto que una instrucción SendDone posterior usa para esperar a que se complete la transferencia de datos. El contexto es una tupla de {operando (forma), identificador de solicitud (U32)} y solo se puede usar con una instrucción SendDone.
Para obtener información sobre StableHLO, consulta StableHLO: send.
SendDone
Consulta también HloInstruction::CreateSendDone.
SendDone(HloInstruction context)
Dado un contexto creado por una instrucción Send, espera a que se complete la transferencia de datos. La instrucción no devuelve ningún dato.
Programación de instrucciones del canal
El orden de ejecución de las 4 instrucciones para cada canal (Recv, RecvDone, Send, SendDone) es el siguiente.
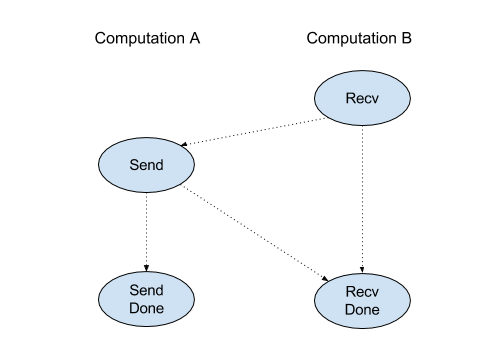
Recvocurre antes deSendSendocurre antes deRecvDoneRecvocurre antes deRecvDoneSendocurre antes deSendDone
Cuando los compiladores de backend generan una programación lineal para cada cálculo que se comunica a través de instrucciones de canal, no debe haber ciclos entre los cálculos. Por ejemplo, los siguientes programas generan interbloqueos.
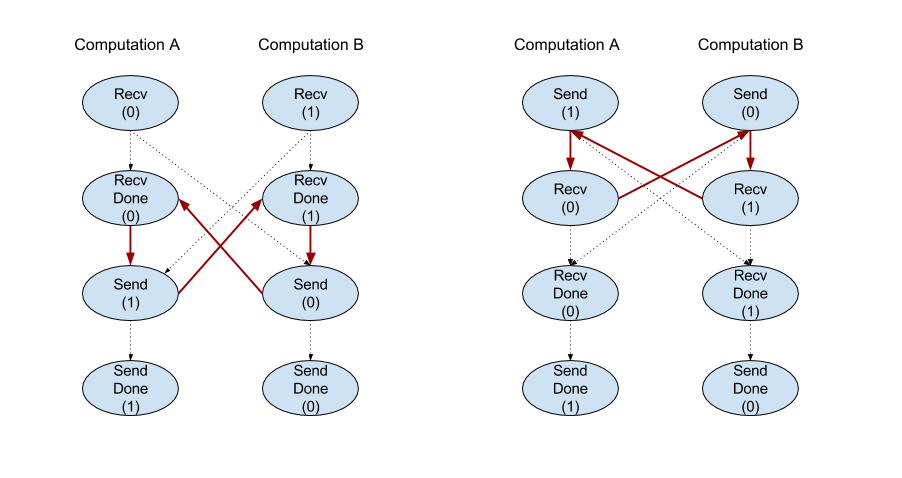
SetDimensionSize
Consulta también XlaBuilder::SetDimensionSize.
Establece el tamaño dinámico de la dimensión determinada de XlaOp. El operando debe tener forma de array.
SetDimensionSize(operand, val, dimension)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de entrada de dimensión n. |
val |
XlaOp |
Es un int32 que representa el tamaño dinámico del tiempo de ejecución. |
dimension
|
int64
|
Es un valor en el intervalo [0, n) que especifica la dimensión. |
Pasa el operando como resultado, con la dimensión dinámica que realiza el seguimiento del compilador.
Las operaciones de reducción posteriores ignorarán los valores de padding.
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
ShiftLeft
Consulta también XlaBuilder::ShiftLeft.
Realiza una operación de desplazamiento a la izquierda en cada elemento de lhs por una cantidad de bits igual a rhs.
ShiftLeft(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para ShiftLeft:
ShiftLeft(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO - shift_left.
ShiftRightArithmetic
Consulta también XlaBuilder::ShiftRightArithmetic.
Realiza una operación de desplazamiento a la derecha aritmético por elementos en lhs por una cantidad de bits de rhs.
ShiftRightArithmetic(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para ShiftRightArithmetic:
ShiftRightArithmetic(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO - shift_right_arithmetic.
ShiftRightLogical
Consulta también XlaBuilder::ShiftRightLogical.
Realiza la operación de desplazamiento lógico hacia la derecha bit a bit en lhs por la cantidad de bits de rhs.
ShiftRightLogical(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para ShiftRightLogical:
ShiftRightLogical(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO - shift_right_logical.
Firmar
Consulta también XlaBuilder::Sign.
Sign(operand) Operación de signo por elemento x -> sgn(x), donde
\[\text{sgn}(x) = \begin{cases} -1 & x < 0\\ -0 & x = -0\\ NaN & x = NaN\\ +0 & x = +0\\ 1 & x > 0 \end{cases}\]
con el operador de comparación del tipo de elemento de operand.
Sign(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Para obtener información sobre StableHLO, consulta StableHLO: sign.
Sin
Sin(operand) Seno de cada elemento x -> sin(x).
Consulta también XlaBuilder::Sin.
Sin(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
La función seno también admite el argumento opcional result_accuracy:
Sin(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Para obtener información sobre StableHLO, consulta StableHLO: seno.
Porción
Consulta también XlaBuilder::Slice.
El segmentado extrae un subarreglo del arreglo de entrada. El subarreglo tiene la misma cantidad de dimensiones que la entrada y contiene los valores dentro de un cuadro delimitador en el arreglo de entrada, en el que las dimensiones y los índices del cuadro delimitador se proporcionan como argumentos para la operación de segmentación.
Slice(operand, start_indices, limit_indices, strides)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es un array de N dimensiones del tipo T. |
start_indices
|
ArraySlice<int64>
|
Lista de N números enteros que contiene los índices iniciales de la segmentación para cada dimensión. Los valores deben ser mayores o iguales que cero. |
limit_indices
|
ArraySlice<int64>
|
Lista de N números enteros que contienen los índices finales (no inclusivos) del segmento para cada dimensión. Cada valor debe ser mayor o igual que el valor de start_indices respectivo para la dimensión y menor o igual que el tamaño de la dimensión. |
strides
|
ArraySlice<int64>
|
Lista de N números enteros que determina el avance de entrada del segmento. La segmentación selecciona cada elemento strides[d] en la dimensión d. |
Ejemplo unidimensional:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4})
// Result: {2.0, 3.0}
Ejemplo bidimensional:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3})
// Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
Para obtener información sobre StableHLO, consulta StableHLO: slice.
Ordenar
Consulta también XlaBuilder::Sort.
Sort(operands, comparator, dimension, is_stable)
| Argumentos | Tipo | Semántica |
|---|---|---|
operands |
ArraySlice<XlaOp> |
Son los operandos que se ordenarán. |
comparator |
XlaComputation |
Es el cálculo del comparador que se usará. |
dimension |
int64 |
Es la dimensión según la cual se ordenará. |
is_stable |
bool |
Indica si se debe usar la ordenación estable. |
Si solo se proporciona un operando, sucede lo siguiente:
Si el operando es un tensor unidimensional (un array), el resultado es un array ordenado. Si quieres ordenar el array de forma ascendente, el comparador debe realizar una comparación de menor que. Formalmente, después de ordenar el array, se cumple para todas las posiciones de índice
i, jconi < jquecomparator(value[i], value[j]) = comparator(value[j], value[i]) = falseocomparator(value[i], value[j]) = true.Si el operando tiene una mayor cantidad de dimensiones, se ordena según la dimensión proporcionada. Por ejemplo, para un tensor de 2 dimensiones (una matriz), un valor de dimensión de
0ordenará de forma independiente cada columna, y un valor de dimensión de1ordenará de forma independiente cada fila. Si no se proporciona ningún número de dimensión, se elige la última dimensión de forma predeterminada. Para la dimensión que se ordena, se aplica el mismo orden de clasificación que en el caso unidimensional.
Si se proporcionan operandos n > 1, ocurre lo siguiente:
Todos los operandos de
ndeben ser tensores con las mismas dimensiones. Los tipos de elementos de los tensores pueden ser diferentes.Todos los operandos se ordenan juntos, no de forma individual. Conceptualmente, los operandos se tratan como una tupla. Cuando se verifica si los elementos de cada operando en las posiciones de índice
iyjdeben intercambiarse, se llama al comparador con parámetros escalares2 * n, en los que el parámetro2 * kcorresponde al valor en la posiciónidel operandok-thy el parámetro2 * k + 1corresponde al valor en la posiciónjdel operandok-th. Por lo general, el comparador compararía los parámetros2 * ky2 * k + 1entre sí y, posiblemente, usaría otros pares de parámetros como desempate.El resultado es una tupla que consta de los operandos en orden de clasificación (a lo largo de la dimensión proporcionada, como se indicó anteriormente). El operando
i-thde la tupla corresponde al operandoi-thde Sort.
Por ejemplo, si hay tres operandos operand0 = [3, 1], operand1 = [42, 50] y operand2 = [-3.0, 1.1], y el comparador solo compara los valores de operand0 con el operador menor que, el resultado de la ordenación es la tupla ([1, 3], [50, 42], [1.1, -3.0]).
Si is_stable se establece como verdadero, se garantiza que la ordenación sea estable, es decir, si hay elementos que el comparador considera iguales, se conserva el orden relativo de los valores iguales. Dos elementos e1 y e2 son iguales si y solo si comparator(e1, e2) = comparator(e2, e1) = false. De forma predeterminada, is_stable se establece en falso.
Para obtener información sobre StableHLO, consulta StableHLO: sort.
Sqrt
Consulta también XlaBuilder::Sqrt.
Operación de raíz cuadrada en términos de elementos x -> sqrt(x).
Sqrt(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Sqrt también admite el argumento opcional result_accuracy:
Sqrt(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Para obtener información sobre StableHLO, consulta StableHLO - sqrt.
Subpropiedad
Consulta también XlaBuilder::Sub.
Realiza la resta de lhs y rhs elemento por elemento.
Sub(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Sub:
Sub(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: subtract.
Canela
Consulta también XlaBuilder::Tan.
Tangente de cada elemento x -> tan(x).
Tan(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
Tan también admite el argumento opcional result_accuracy:
Tan(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Son los tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones. |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Para obtener información sobre StableHLO, consulta StableHLO: tan.
tanh
Consulta también XlaBuilder::Tanh.
Tangente hiperbólica x -> tanh(x) para cada elemento.
Tanh(operand)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
La función tanh también admite el argumento opcional result_accuracy:
Tanh(operand, result_accuracy)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando de la función. |
result_accuracy
|
opcional ResultAccuracy
|
Tipos de precisión que el usuario puede solicitar para las operaciones unarias con varias implementaciones |
Para obtener más información sobre result_accuracy, consulta Precisión de los resultados.
Para obtener información sobre StableHLO, consulta StableHLO - tanh.
TopK
Consulta también XlaBuilder::TopK.
TopK encuentra los valores y los índices de los k elementos más grandes o más pequeños para la última dimensión del tensor determinado.
TopK(operand, k, largest)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand
|
XlaOp
|
Tensor del que se extraerán los principales elementos k.
El tensor debe tener una dimensión o más. El tamaño de la última dimensión del tensor debe ser mayor o igual que k. |
k |
int64 |
Cantidad de elementos que se extraerán. |
largest
|
bool
|
Indica si se deben extraer los elementos k más grandes o más pequeños. |
Para un tensor de entrada unidimensional (un array), encuentra las k entradas más grandes o más pequeñas del array y genera una tupla de dos arrays (values, indices). Por lo tanto, values[j] es la entrada j-ésima más grande o más pequeña en operand, y su índice es indices[j].
Para un tensor de entrada con más de 1 dimensión, calcula las primeras k entradas a lo largo de la última dimensión y conserva todas las demás dimensiones (filas) en el resultado.
Por lo tanto, para un operando con forma [A, B, ..., P, Q], en el que Q >= k, el resultado es una tupla (values, indices) en la que se cumple lo siguiente:
values.shape = indices.shape = [A, B, ..., P, k]
Si dos elementos dentro de una fila son iguales, el elemento con el índice más bajo aparece primero.
Transposición
Consulta también la operación tf.reshape.
Transpose(operand, permutation)
| Argumentos | Tipo | Semántica |
|---|---|---|
operand |
XlaOp |
Es el operando que se transpondrá. |
permutation |
ArraySlice<int64> |
Cómo permutar las dimensiones |
Permuta las dimensiones del operando con la permutación dada, de modo que ∀ i . 0 ≤ i < number of dimensions ⇒
input_dimensions[permutation[i]] = output_dimensions[i].
Esto es lo mismo que Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)).
Para obtener información sobre StableHLO, consulta StableHLO: transposición.
TriangularSolve
Consulta también XlaBuilder::TriangularSolve.
Resuelve sistemas de ecuaciones lineales con matrices de coeficientes triangulares inferiores o superiores por sustitución hacia adelante o hacia atrás. Esta rutina, que se transmite a lo largo de las dimensiones principales, resuelve uno de los sistemas de matrices op(a) * x =
b o x * op(a) = b para la variable x, dados a y b, donde op(a) es op(a) = a, op(a) = Transpose(a) o op(a) = Conj(Transpose(a)).
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| Argumentos | Tipo | Semántica |
|---|---|---|
a
|
XlaOp
|
Es un array de más de 2 dimensiones de un tipo complejo o de punto flotante con forma [..., M,
M]. |
b
|
XlaOp
|
Es un array de más de 2 dimensiones del mismo tipo con la forma [..., M, K] si left_side es verdadero o [..., K, M] en caso contrario. |
left_side
|
bool
|
Indica si se debe resolver un sistema de la forma op(a) * x = b (true) o x *
op(a) = b (false). |
lower
|
bool
|
Indica si se debe usar el triángulo superior o inferior de a. |
unit_diagonal
|
bool
|
Si es true, se supone que los elementos diagonales de a son 1 y no se accede a ellos. |
transpose_a
|
Transpose
|
Indica si se debe usar a tal como está, trasponerla o tomar su transpuesta conjugada. |
Los datos de entrada se leen solo desde el triángulo inferior o superior de a, según el valor de lower. Se ignoran los valores del otro triángulo. Los datos de salida se devuelven en el mismo triángulo; los valores del otro triángulo se definen según la implementación y pueden ser cualquier valor.
Si la cantidad de dimensiones de a y b es mayor que 2, se tratan como lotes de matrices, en los que todas las dimensiones, excepto las 2 dimensiones secundarias, son dimensiones de lote. a y b deben tener dimensiones de lote iguales.
Para obtener información sobre StableHLO, consulta StableHLO - triangular_solve.
Tupla
Consulta también XlaBuilder::Tuple.
Es una tupla que contiene una cantidad variable de identificadores de datos, cada uno con su propia forma.
Tuple(elements)
| Argumentos | Tipo | Semántica |
|---|---|---|
elements |
vector de XlaOp |
Es un array de N elementos de tipo T. |
Esto es análogo a std::tuple en C++. Conceptualmente:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
Las tuplas se pueden desconstruir (acceder) a través de la operación GetTupleElement.
Para obtener información sobre StableHLO, consulta StableHLO: tupla.
Si bien
Consulta también XlaBuilder::While.
While(condition, body, init)
| Argumentos | Tipo | Semántica |
|---|---|---|
condition
|
XlaComputation
|
XlaComputation de tipo T -> PRED que define la condición de finalización del bucle. |
body
|
XlaComputation
|
XlaComputation de tipo T -> T que define el cuerpo del bucle. |
init
|
T
|
Valor inicial para el parámetro de condition y body. |
Ejecuta body de forma secuencial hasta que falla condition. Esto es similar a un bucle while típico en muchos otros lenguajes, excepto por las diferencias y restricciones que se indican a continuación.
- Un nodo
Whiledevuelve un valor de tipoT, que es el resultado de la última ejecución debody. - La forma del tipo
Tse determina de forma estática y debe ser la misma en todas las iteraciones.
Los parámetros T de los cálculos se inicializan con el valor de init en la primera iteración y se actualizan automáticamente al nuevo resultado de body en cada iteración posterior.
Uno de los principales casos de uso del nodo While es implementar la ejecución repetida del entrenamiento en redes neuronales. A continuación, se muestra un pseudocódigo simplificado con un gráfico que representa el cálculo. El código se encuentra en while_test.cc.
El tipo T en este ejemplo es un Tuple que consta de un int32 para el recuento de iteraciones y un vector[10] para el acumulador. Durante 1,000 iteraciones, el bucle sigue agregando un vector constante al acumulador.
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}
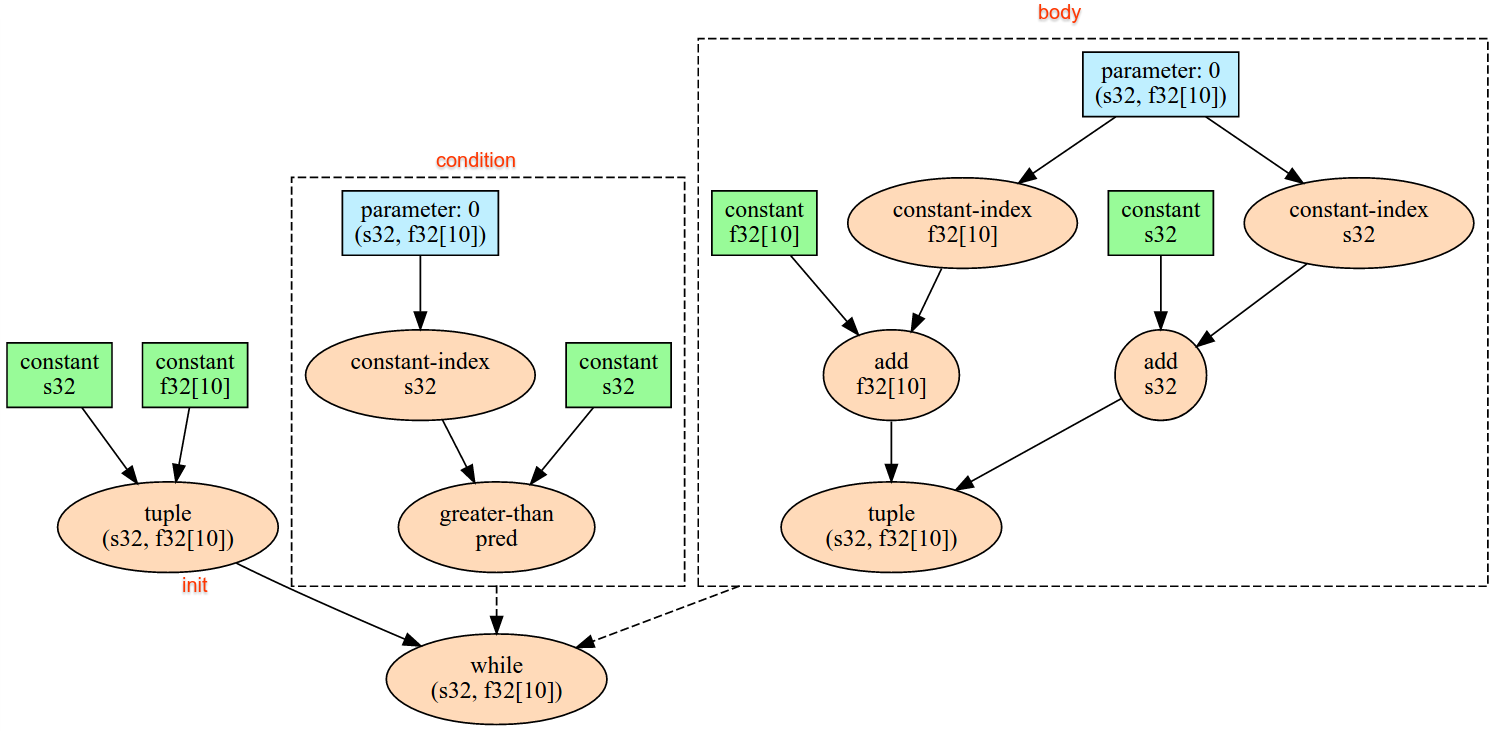
Para obtener información sobre StableHLO, consulta StableHLO: while.
Xor
Consulta también XlaBuilder::Xor.
Realiza una operación XOR a nivel de los elementos de lhs y rhs.
Xor(lhs, rhs)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
Las formas de los argumentos deben ser similares o compatibles. Consulta la documentación sobre transmisión para saber qué significa que las formas sean compatibles. El resultado de una operación tiene una forma que es el resultado de la transmisión de los dos arrays de entrada. En esta variante, no se admiten las operaciones entre arrays de diferentes rangos, a menos que uno de los operandos sea un escalar.
Existe una variante alternativa con compatibilidad para la transmisión de diferentes dimensiones para Xor:
Xor(lhs,rhs, broadcast_dimensions)
| Argumentos | Tipo | Semántica |
|---|---|---|
| lhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| rhs | XlaOp | Operando del lado izquierdo: Es un array de tipo T. |
| broadcast_dimension | ArraySlice |
A qué dimensión de la forma objetivo corresponde cada dimensión de la forma del operando |
Esta variante de la operación se debe usar para operaciones aritméticas entre arrays de diferentes rangos (como sumar una matriz a un vector).
El operando broadcast_dimensions adicional es un segmento de números enteros que especifica las dimensiones que se usarán para la transmisión de los operandos. La semántica se describe en detalle en la página de transmisión.
Para obtener información sobre StableHLO, consulta StableHLO: xor.








