下文說明 XlaBuilder 介面中定義的作業語意。通常這些作業會一對一對應至 xla_data.proto 中 RPC 介面定義的作業。
命名注意事項:XLA 處理的廣義資料型別是 N 維陣列,其中包含某種統一型別的元素 (例如 32 位元浮點數)。在整份文件中,陣列用於表示任意維度的陣列。為方便起見,特殊情況有更具體且熟悉的名稱,例如「向量」是 1 維陣列,「矩陣」是 2 維陣列。
進一步瞭解「形狀和版面配置」和「分塊版面配置」中的 Op 結構。
腹肌
另請參閱
XlaBuilder::Abs。
元素層級的絕對值 x -> |x|。
Abs(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
如需 StableHLO 資訊,請參閱「StableHLO - abs」。
新增
另請參閱
XlaBuilder::Add。
執行 lhs 和 rhs 的元素加法。
Add(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Add 有替代變體,支援不同維度的廣播:
Add(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 相關資訊,請參閱「StableHLO - add」。
AddDependency
另請參閱
HloInstruction::AddDependency。
AddDependency 可能會出現在 HLO 傾印中,但使用者不應手動建構這些項目。
AfterAll
另請參閱
XlaBuilder::AfterAll。
AfterAll 會採用可變數量的符記,並產生單一符記。權杖是原始型別,可在副作用作業之間建立執行緒,以強制執行排序。AfterAll 可做為權杖的聯結,用於在一組作業後排序作業。
AfterAll(tokens)
| 引數 | 類型 | 語意 |
|---|---|---|
tokens |
XlaOp 的向量 |
可變數量的權杖 |
如需 StableHLO 相關資訊,請參閱「StableHLO - after_all」。
AllGather
另請參閱
XlaBuilder::AllGather。
在備用資源之間執行串連作業。
AllGather(operand, all_gather_dimension, shard_count, replica_groups,
channel_id, layout, use_global_device_ids)
| 引數 | 類型 | 語意 |
|---|---|---|
operand
|
XlaOp
|
要跨副本串連的陣列 |
all_gather_dimension |
int64 |
串連維度 |
shard_count
|
int64
|
每個副本群組的大小 |
replica_groups
|
向量的向量
int64 |
執行串連的群組 |
channel_id
|
選填
ChannelHandle |
跨模組通訊的選用管道 ID |
layout
|
選填 Layout
|
建立版面配置模式,擷取引數中相符的版面配置 |
use_global_device_ids
|
選填 bool
|
如果 ReplicaGroup 設定中的 ID 代表全域 ID,則傳回 true |
replica_groups是執行串連作業的副本群組清單 (可以使用ReplicaId擷取目前副本的副本 ID)。每個群組中的副本順序會決定結果中輸入內容的順序。replica_groups必須為空白 (所有副本都屬於單一群組,並依0至N - 1的順序排列),或包含與副本數量相同的元素。舉例來說,replica_groups = {0, 2}, {1, 3}會在副本0和2之間,以及1和3之間執行串連作業。shard_count是每個副本群組的大小。如果replica_groups為空白,則必須提供這項資訊。channel_id用於跨模組通訊:只有具有相同channel_id的all-gather作業才能彼此通訊。use_global_device_ids如果 ReplicaGroup 設定中的 ID 代表 (replica_id * partition_count + partition_id) 的全域 ID,而非副本 ID,則傳回 true。如果這個全縮減作業是跨分割區和跨副本,就能更彈性地將裝置分組。
輸出形狀是輸入形狀放大 all_gather_dimension 倍後的結果。shard_count舉例來說,如果有兩個副本,而運算元在兩個副本上分別有 [1.0, 2.5] 和 [3.0, 5.25] 值,則當 all_gather_dim 為 0 時,這個作業的輸出值在兩個副本上都會是 [1.0, 2.5, 3.0,5.25]。
AllGather 的 API 會在內部分解為 2 個 HLO 指令 (AllGatherStart 和 AllGatherDone)。
另請參閱
HloInstruction::CreateAllGatherStart。
AllGatherStart 和 AllGatherDone 可做為 HLO 中的基本類型。這些作業可能會出現在 HLO 傾印中,但並非供使用者手動建構。
如需 StableHLO 相關資訊,請參閱「StableHLO - all_gather」。
AllReduce
另請參閱
XlaBuilder::AllReduce。
在備用資源之間執行自訂計算。
AllReduce(operand, computation, replica_groups, channel_id,
shape_with_layout, use_global_device_ids)
| 引數 | 類型 | 語意 |
|---|---|---|
operand
|
XlaOp
|
要跨備用資源縮減的陣列或非空白元組 (陣列) |
computation |
XlaComputation |
減免計算 |
replica_groups
|
ReplicaGroup vector
|
執行縮減作業的群組 |
channel_id
|
選填
ChannelHandle |
跨模組通訊的選用管道 ID |
shape_with_layout
|
選填 Shape
|
定義所轉移資料的版面配置 |
use_global_device_ids
|
選填 bool
|
如果 ReplicaGroup 設定中的 ID 代表全域 ID,則傳回 true |
- 如果
operand是陣列的元組,則會對元組的每個元素執行全縮減作業。 replica_groups是執行縮減作業的副本群組清單 (可以使用ReplicaId擷取目前副本的副本 ID)。replica_groups必須為空白 (所有副本都屬於單一群組),或包含與副本數量相同的元素數量。舉例來說,replica_groups = {0, 2}, {1, 3}會在副本0和2之間,以及1和3之間執行縮減作業。channel_id用於跨模組通訊:只有具有相同channel_id的all-reduce作業才能彼此通訊。shape_with_layout:強制將 AllReduce 的版面配置設為指定版面配置。這項設定可確保個別編譯的 AllReduce 作業群組採用相同版面配置。use_global_device_ids如果 ReplicaGroup 設定中的 ID 代表 (replica_id * partition_count + partition_id) 的全域 ID,而非副本 ID,則傳回 true。如果這個全縮減作業是跨分割區和跨副本,就能更彈性地將裝置分組。
輸出形狀與輸入形狀相同。舉例來說,如果有兩個副本,而運算元在兩個副本上的值分別為 [1.0, 2.5] 和 [3.0, 5.25],則這個運算和加總計算的輸出值在兩個副本上都會是 [4.0, 7.75]。如果輸入內容是元組,輸出內容也會是元組。
計算 AllReduce 的結果時,需要每個副本各提供一個輸入,因此如果一個副本執行 AllReduce 節點的次數比另一個副本多,前者就會永遠等待。由於所有副本都執行相同的程式,因此發生這種情況的機率不高,但如果 while 迴圈的條件取決於 infeed 中的資料,而該資料導致某個副本的 while 迴圈疊代次數多於其他副本,就可能發生這種情況。infeed
AllReduce 的 API 會在內部分解為 2 個 HLO 指令 (AllReduceStart 和 AllReduceDone)。
另請參閱
HloInstruction::CreateAllReduceStart。
AllReduceStart 和 AllReduceDone 在 HLO 中做為基本型別。這些作業可能會出現在 HLO 傾印中,但並非供使用者手動建構。
CrossReplicaSum
另請參閱
XlaBuilder::CrossReplicaSum。
執行 AllReduce,並計算總和。
CrossReplicaSum(operand, replica_groups)
| 引數 | 類型 | 語意 |
|---|---|---|
operand
|
XlaOp | 陣列或非空白的陣列元組,用於縮減副本 |
replica_groups
|
向量的向量,其中包含
int64 |
執行縮減作業的群組 |
傳回每個副本子群組中運算元值的總和。所有副本都會提供一個輸入內容給總和,且所有副本都會收到每個子群組的總和結果。
AllToAll
另請參閱
XlaBuilder::AllToAll。
AllToAll 是一種集體作業,可將所有核心的資料傳送至所有核心。這個方法包含下列兩個階段:
- 散布階段。在每個核心上,運算元會沿著
split_count分割成split_dimensions個區塊,並分散至所有核心,例如第 i 個區塊會傳送至第 i 個核心。 - 收集階段。每個核心都會沿著
concat_dimension串連收到的區塊。
參與的核心可透過下列方式設定:
replica_groups:每個 ReplicaGroup 都包含參與運算的副本 ID 清單 (目前副本的副本 ID 可使用ReplicaId擷取)。AllToAll 會依指定順序套用至子群組。舉例來說,replica_groups = { {1,2,3}, {4,5,0} }表示 AllToAll 會套用至副本{1, 2, 3}內,並在收集階段中,以 1、2、3 的順序串連收到的區塊。然後,系統會在副本 4、5、0 中套用另一個 AllToAll,串連順序也是 4、5、0。如果replica_groups為空白,所有副本會屬於一個群組,並依顯示順序串連。
需求條件:
- 運算元在
split_dimension上的維度大小可除以split_count。 - 運算元的形狀不是元組。
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups, layout, channel_id)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
n 維輸入陣列 |
split_dimension
|
int64
|
間隔 [0,n) 中的值,用於命名運算元分割的維度 |
concat_dimension
|
int64
|
間隔 [0,n) 中的值,用於命名分割區塊串連的維度 |
split_count
|
int64
|
參與這項作業的核心數量。如果 replica_groups 為空,則應為副本數量;否則應等於每個群組中的副本數量。 |
replica_groups
|
ReplicaGroupvector
|
每個群組都包含備用資源 ID 清單。 |
layout |
選填 Layout |
使用者指定的記憶體配置 |
channel_id
|
選填 ChannelHandle
|
每個傳送/接收配對的專屬 ID |
如要進一步瞭解形狀和版面配置,請參閱 xla::shapes。
如需 StableHLO 資訊,請參閱「StableHLO - all_to_all」。
AllToAll - 範例 1。
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(
x,
/*split_dimension=*/ 1,
/*concat_dimension=*/ 0,
/*split_count=*/ 4);
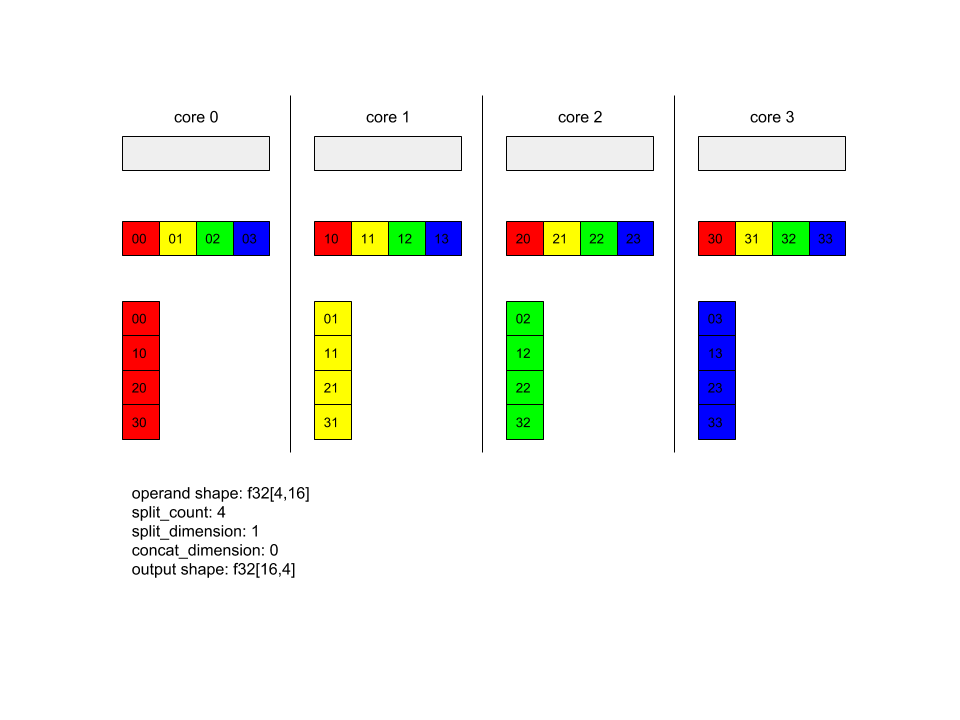
在上述範例中,有 4 個核心參與 Alltoall。在每個核心上,運算元會沿著維度 1 分成 4 個部分,因此每個部分的形狀為 f32[4,4]。這 4 個部分會分散到所有核心。然後每個核心會沿著維度 0 串連收到的部分,順序為核心 0 到 4。因此,每個核心的輸出內容形狀為 f32[16,4]。
AllToAll - 範例 2 - StableHLO
在上述範例中,有 2 個副本參與 AllToAll。在每個副本上,運算元的形狀為 f32[2,4]。運算元會沿著維度 1 分成 2 個部分,因此每個部分的形狀為 f32[2,2]。然後,這 2 個部分會根據副本群組中的位置,在副本之間交換。每個副本都會從兩個運算元收集對應部分,並沿著維度 0 串連這些部分。因此,每個副本的輸出內容形狀為 f32[4,2]。
RaggedAllToAll
另請參閱
XlaBuilder::RaggedAllToAll。
RaggedAllToAll 會執行集體全對全作業,其中輸入和輸出為參差不齊的張量。
RaggedAllToAll(input, input_offsets, send_sizes, output, output_offsets,
recv_sizes, replica_groups, channel_id)
| 引數 | 類型 | 語意 |
|---|---|---|
input |
XlaOp |
N 個 T 類型的陣列 |
input_offsets |
XlaOp |
N 個 T 類型的陣列 |
send_sizes |
XlaOp |
N 個 T 類型的陣列 |
output |
XlaOp |
N 個 T 類型的陣列 |
output_offsets |
XlaOp |
N 個 T 類型的陣列 |
recv_sizes |
XlaOp |
N 個 T 類型的陣列 |
replica_groups
|
ReplicaGroup vector
|
每個群組都包含副本 ID 清單。 |
channel_id
|
選填 ChannelHandle
|
每個傳送/接收配對的專屬 ID |
參差不齊的張量是由一組三個張量定義:
data:張量沿著最外層維度「不規則」,沿著該維度,每個索引元素的大小都不同。dataoffsets:offsets張量會為data張量的最外層維度建立索引,並代表data張量中每個參差不齊元素的起始偏移。sizes:sizes張量代表data張量的每個參差不齊元素大小,大小以子元素為單位指定。子元素定義為「資料」張量形狀的後置字元,方法是移除最外層的「不規則」維度。offsets和sizes張量的大小必須相同。
Ragged Tensor 範例:
data: [8,3] =
{ {a,b,c},{d,e,f},{g,h,i},{j,k,l},{m,n,o},{p,q,r},{s,t,u},{v,w,x} }
offsets: [3] = {0, 1, 4}
sizes: [3] = {1, 3, 4}
// Index 'data' at 'offsets'[0], 'sizes'[0]' // {a,b,c}
// Index 'data' at 'offsets'[1], 'sizes'[1]' // {d,e,f},{g,h,i},{j,k,l}
// Index 'data' at 'offsets'[2], 'sizes'[2]' // {m,n,o},{p,q,r},{s,t,u},{v,w,x}
output_offsets 必須以某種方式分片,讓每個副本都有目標副本輸出透視圖中的偏移。
對於第 i 個輸出偏移,目前的副本會將 input[input_offsets[i]:input_offsets[i]+input_sizes[i]] 更新傳送至第 i 個副本,並寫入第 i 個副本中的 output_i[output_offsets[i]:output_offsets[i]+send_sizes[i]]output。
舉例來說,如果我們有 2 個副本:
replica 0:
input: [1, 2, 2]
output:[0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 2]
output_offsets: [0, 0]
recv_sizes: [1, 1]
replica 1:
input: [3, 4, 0]
output: [0, 0, 0, 0]
input_offsets: [0, 1]
send_sizes: [1, 1]
output_offsets: [1, 2]
recv_sizes: [2, 1]
// replica 0's result will be: [1, 3, 0, 0]
// replica 1's result will be: [2, 2, 4, 0]
參差不齊的 all-to-all HLO 具有下列引數:
input:不規則輸入資料張量。output:不規則輸出資料張量。input_offsets:不規則輸入偏移張量。send_sizes:不規則傳送大小張量。output_offsets:目標副本輸出內容中的不規則偏移陣列。recv_sizes:不規則 recv 大小張量。
*_offsets 和 *_sizes 張量必須具有相同形狀。
*_offsets 和 *_sizes 張量支援兩種形狀:
[num_devices],其中 ragged-all-to-all 最多可將一次更新傳送至副本群組中的每個遠端裝置。例如:
for (remote_device_id : replica_group) {
SEND input[input_offsets[remote_device_id]],
output[output_offsets[remote_device_id]],
send_sizes[remote_device_id] }
[num_devices, num_updates],其中 ragged-all-to-all 最多可傳送num_updates更新至相同遠端裝置 (每個更新都有不同偏移), 適用於副本群組中的每個遠端裝置。
例如:
for (remote_device_id : replica_group) {
for (update_idx : num_updates) {
SEND input[input_offsets[remote_device_id][update_idx]],
output[output_offsets[remote_device_id][update_idx]]],
send_sizes[remote_device_id][update_idx] } }
和
另請參閱
XlaBuilder::And。
對兩個張量 lhs 和 rhs 執行元素層級的 AND 運算。
And(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
And 有支援不同維度廣播的替代變體:
And(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱「StableHLO - and」。
非同步
另請參閱 HloInstruction::CreateAsyncStart、HloInstruction::CreateAsyncUpdate、HloInstruction::CreateAsyncDone。
AsyncDone、AsyncStart 和 AsyncUpdate 是用於非同步作業的內部 HLO 指令,可做為 HLO 中的基本類型。這些作業可能會出現在 HLO 傾印中,但使用者不應手動建構這些作業。
Atan2
另請參閱
XlaBuilder::Atan2。
對 lhs 和 rhs 執行元素級別的 atan2 運算。
Atan2(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Atan2 有替代變體,支援不同維度的廣播:
Atan2(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱「StableHLO - atan2」。
BatchNormGrad
如需演算法的詳細說明,請參閱XlaBuilder::BatchNormGrad和原始的批次正規化論文。
計算批次正規化的梯度。
BatchNormGrad(operand, scale, batch_mean, batch_var, grad_output, epsilon,
feature_index)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp | 要正規化的 n 維陣列 (x) |
scale |
XlaOp | 1 維陣列 (\(\gamma\)) |
batch_mean |
XlaOp | 1 維陣列 (\(\mu\)) |
batch_var |
XlaOp | 1 維陣列 (\(\sigma^2\)) |
grad_output |
XlaOp | 傳遞至 BatchNormTraining (\(\nabla y\)) 的漸層 |
epsilon |
float |
隱私損失參數值 (\(\epsilon\)) |
feature_index |
int64 |
operand 中特徵維度的索引 |
針對特徵維度中的每個特徵 (feature_index 是 operand 中特徵維度的索引),這項作業會計算所有其他維度中,相對於 operand、offset 和 scale 的梯度。feature_index 必須是 operand 中特徵維度的有效索引。
以下公式定義了三種漸層 (假設 4 維陣列為 operand,且特徵維度索引為 l、批次大小為 m,空間大小為 w 和 h):
\[ \begin{split} c_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sigma^2_l+\epsilon} \right) \\\\ d_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \\\\ \nabla x_{ijkl} &= \frac{\gamma_{l} }{\sqrt{\sigma^2_{l}+\epsilon} } \left( \nabla y_{ijkl} - d_l - c_l (x_{ijkl} - \mu_{l}) \right) \\\\ \nabla \gamma_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sqrt{\sigma^2_{l}+\epsilon} } \right) \\\\\ \nabla \beta_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \end{split} \]
輸入 batch_mean 和 batch_var 代表批次和空間維度的時刻值。
輸出類型是三個控制代碼的元組:
| 輸出內容 | 類型 | 語意 |
|---|---|---|
grad_operand
|
XlaOp | 相對於輸入 operand 的梯度 (\(\nabla x\)) |
grad_scale
|
XlaOp | 相對於輸入 **scale ** 的梯度
(\(\nabla\gamma\)) |
grad_offset
|
XlaOp | 相對於輸入內容的梯度
offset(\(\nabla\beta\)) |
如需 StableHLO 資訊,請參閱「StableHLO - batch_norm_grad」。
BatchNormInference
如需演算法的詳細說明,請參閱XlaBuilder::BatchNormInference和原始的批次正規化論文。
在批次和空間維度中正規化陣列。
BatchNormInference(operand, scale, offset, mean, variance, epsilon,
feature_index)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp | 要正規化的 n 維陣列 |
scale |
XlaOp | 一維陣列 |
offset |
XlaOp | 一維陣列 |
mean |
XlaOp | 一維陣列 |
variance |
XlaOp | 一維陣列 |
epsilon |
float |
Epsilon 值 |
feature_index |
int64 |
operand 中特徵維度的索引 |
針對特徵維度中的每個特徵 (feature_index 是 operand 中特徵維度的索引),這項作業會計算所有其他維度的平均值和變異數,並使用平均值和變異數來正規化 operand 中的每個元素。feature_index 必須是 operand 中特徵維度的有效索引。
BatchNormInference 等於呼叫 BatchNormTraining,但不會為每個批次計算 mean 和 variance。而是使用輸入的 mean 和 variance 做為預估值。這個運算的目的是減少推論延遲,因此命名為 BatchNormInference。
輸出內容是 n 維度正規化陣列,形狀與輸入內容 operand 相同。
如需 StableHLO 資訊,請參閱「StableHLO - batch_norm_inference」。
BatchNormTraining
如需演算法的詳細說明,請參閱 XlaBuilder::BatchNormTraining 和 the original batch normalization paper。
在批次和空間維度中正規化陣列。
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
要正規化的 n 維陣列 (x) |
scale |
XlaOp |
1 維陣列 (\(\gamma\)) |
offset |
XlaOp |
1 維陣列 (\(\beta\)) |
epsilon |
float |
隱私損失參數值 (\(\epsilon\)) |
feature_index |
int64 |
operand 中特徵維度的索引 |
針對特徵維度中的每個特徵 (feature_index 是 operand 中特徵維度的索引),這項作業會計算所有其他維度的平均值和變異數,並使用平均值和變異數來正規化 operand 中的每個元素。feature_index 必須是 operand 中特徵維度的有效索引。
演算法會針對 operand \(x\) 中的每個批次執行下列步驟,其中包含 m 元素,且 w 和 h 是空間維度的大小 (假設 operand 是 4 維陣列):
計算特徵維度中每個特徵
l的批次平均值 \(\mu_l\) : \(\mu_l=\frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h x_{ijkl}\)計算批次變異數 \(\sigma^2_l\): $\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
正規化、縮放及位移: \(y_{ijkl}=\frac{\gamma_l(x_{ijkl}-\mu_l)}{\sqrt[2]{\sigma^2_l+\epsilon} }+\beta_l\)
為避免除以零錯誤,通常會加上 epsilon 值 (通常是小數字)。
輸出類型是三個 XlaOp 的元組:
| 輸出內容 | 類型 | 語意 |
|---|---|---|
output
|
XlaOp
|
n 維陣列,形狀與輸入的 operand (y) 相同 |
batch_mean |
XlaOp |
1 維陣列 (\(\mu\)) |
batch_var |
XlaOp |
1 維陣列 (\(\sigma^2\)) |
batch_mean 和 batch_var 是使用上述公式,針對批次和空間維度計算出的時刻。
如需 StableHLO 資訊,請參閱「StableHLO - batch_norm_training」。
Bitcast
另請參閱
HloInstruction::CreateBitcast。
Bitcast 可能會出現在 HLO 傾印中,但使用者不應手動建構這些項目。
BitcastConvertType
另請參閱
XlaBuilder::BitcastConvertType。
與 TensorFlow 中的 tf.bitcast 類似,會執行從資料形狀到目標形狀的元素層級 bitcast 運算。輸入和輸出大小必須相符:例如,s32 元素會透過位元轉換常式變成 f32 元素,而一個 s32 元素會變成四個 s8 元素。Bitcast 是以低階投放的形式實作,因此不同浮點表示法的機器會產生不同的結果。
BitcastConvertType(operand, new_element_type)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
具有 D 維度的 T 型陣列 |
new_element_type |
PrimitiveType |
U 型 |
運算元和目標形狀的維度必須相符,但最後一個維度除外,因為該維度會因轉換前後的原始大小比例而改變。
來源和目的地元素類型不得為元組。
如要瞭解 StableHLO,請參閱「StableHLO - bitcast_convert」。
Bitcast - 轉換為不同寬度的原始型別
BitcastConvert HLO 指令支援輸出元素類型 T' 的大小不等於輸入元素 T 大小的情況。由於整個作業在概念上是位元播送,不會變更基礎位元組,因此輸出元素的形狀必須變更。對於 B = sizeof(T), B' =
sizeof(T'),可能有兩種情況。
首先,當 B > B' 時,輸出形狀會取得大小為 B/B' 的新次要維度。例如:
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
有效純量的規則維持不變:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
或者,對於 B' > B 指令,輸入形狀的最後一個邏輯維度必須等於 B'/B,且這個維度會在轉換期間捨棄:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
請注意,不同位元寬度之間的轉換並非逐一元素轉換。
廣播
另請參閱
XlaBuilder::Broadcast。
藉由複製陣列中的資料,將維度新增至陣列。
Broadcast(operand, broadcast_sizes)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
要複製的陣列 |
broadcast_sizes |
ArraySlice<int64> |
新尺寸的大小 |
新維度會插入左側,也就是說,如果 broadcast_sizes 有值 {a0, ..., aN},而運算元形狀有維度 {b0, ..., bM},則輸出形狀的維度為 {a0, ..., aN, b0, ..., bM}。
新維度會索引至運算元的副本,也就是
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
舉例來說,如果 operand 是值為 2.0f 的純量 f32,且 broadcast_sizes 是 {2, 3},則結果會是形狀為 f32[2, 3] 的陣列,且結果中的所有值都會是 2.0f。
如需 StableHLO 資訊,請參閱「StableHLO - 廣播」。
BroadcastInDim
另請參閱
XlaBuilder::BroadcastInDim。
藉由複製陣列中的資料,擴大陣列的大小和維度數量。
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
要複製的陣列 |
out_dim_size
|
ArraySlice<int64>
|
目標形狀的維度大小 |
broadcast_dimensions
|
ArraySlice<int64>
|
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
與 Broadcast 類似,但允許在任何位置新增維度,並以大小 1 擴展現有維度。
operand 會廣播至 out_dim_size 所述的形狀。broadcast_dimensions 會將 operand 的維度對應至目標形狀的維度,也就是運算元的第 i 個維度會對應至輸出形狀的第 broadcast_dimension[i] 個維度。operand 的維度大小必須為 1,或與對應輸出形狀的維度大小相同。其餘維度則會填入大小為 1 的維度。然後,退化維度廣播會沿著這些退化維度廣播,以達到輸出形狀。如需詳細說明,請參閱廣播頁面。
撥打電話
另請參閱
XlaBuilder::Call。
使用指定引數叫用運算。
Call(computation, operands...)
| 引數 | 類型 | 語意 |
|---|---|---|
computation
|
XlaComputation
|
計算類型 T_0, T_1, ...,
T_{N-1} -> S,其中有 N 個任意類型的參數 |
operands |
N XlaOp 的序列 |
任意類型的 N 個引數 |
operands 的元數和型別必須與 computation 的參數相符。可以沒有 operands。
CompositeCall
另請參閱
XlaBuilder::CompositeCall。
封裝由其他 StableHLO 作業組成的作業,並接收輸入內容和 composite_attributes,然後產生結果。運算的語意是由分解屬性實作。複合運算子可替換為分解運算子,且不會變更程式語意。如果內嵌分解作業無法提供相同的作業語意,建議使用 custom_call。
版本欄位 (預設為 0) 用於表示複合項的語意何時變更。
這項作業會實作為具有 is_composite=true 屬性的 kCall。decomposition 欄位是由 computation 屬性指定。前端屬性會儲存其餘屬性,並加上 composite. 前置字串。
複合呼叫作業範例:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
CompositeCall(computation, operands..., name, attributes, version)
| 引數 | 類型 | 語意 |
|---|---|---|
computation
|
XlaComputation
|
計算類型 T_0, T_1, ...,
T_{N-1} -> S,其中有 N 個任意類型的參數 |
operands |
N XlaOp 的序列 |
可變數量的數值 |
name |
string |
複合名稱 |
attributes
|
選填 string
|
屬性的選用字串化字典 |
version
|
選填 int64
|
number to version updates to semantics of the composite op |
運算元的 decomposition 不是呼叫的欄位,而是顯示為指向函式的 to_apply 屬性,其中包含較低層級的實作項目,也就是 to_apply=%funcname
如要進一步瞭解複合和分解,請參閱 StableHLO 規格。
Cbrt
另請參閱
XlaBuilder::Cbrt。
元素級別的立方根運算 x -> cbrt(x)。
Cbrt(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Cbrt 也支援選用 result_accuracy 引數:
Cbrt(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
如需 StableHLO 資訊,請參閱「StableHLO - cbrt」。
向上取整
另請參閱
XlaBuilder::Ceil。
元素層面的 ceil x -> ⌈x⌉。
Ceil(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
如需 StableHLO 資訊,請參閱「StableHLO - ceil」。
Cholesky
另請參閱
XlaBuilder::Cholesky。
計算一批對稱 (Hermitian) 正定矩陣的 Cholesky 分解。
Cholesky(a, lower)
| 引數 | 類型 | 語意 |
|---|---|---|
a
|
XlaOp
|
維度大於 2 的複數或浮點類型陣列。 |
lower |
bool |
是否要使用 a 的上或下三角形。 |
如果 lower 為 true,則計算下三角矩陣 l,使 $a = l .
l^T$。如果 lower 為 false,則會計算上三角矩陣 u,使\(a = u^T . u\)。
系統只會從 a 的下/上三角形讀取輸入資料,視 lower 的值而定。系統會忽略其他三角形的值。輸出資料會以相同三角形傳回;其他三角形中的值是由實作定義,可以是任何值。
如果 a 的維度大於 2,a 會視為矩陣批次,
其中除了次要 2 個維度外,其餘都是批次維度。
如果 a 不是對稱 (Hermitian) 正定,結果會由實作定義。
如需 StableHLO 資訊,請參閱「StableHLO - cholesky」。
限制取值範圍
另請參閱
XlaBuilder::Clamp。
將運算元限制在最小值和最大值之間的範圍內。
Clamp(min, operand, max)
| 引數 | 類型 | 語意 |
|---|---|---|
min |
XlaOp |
類型為 T 的陣列 |
operand |
XlaOp |
類型為 T 的陣列 |
max |
XlaOp |
類型為 T 的陣列 |
指定運算元和最小值/最大值後,如果運算元介於最小值和最大值之間,則傳回運算元;如果運算元小於這個範圍,則傳回最小值;如果運算元大於這個範圍,則傳回最大值。也就是 clamp(a, x, b) = min(max(a, x), b)。
這三個陣列的形狀必須相同。或者,做為廣播的受限形式,min 和/或 max 可以是 T 型別的純量。
純量 min 和 max 的範例:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
如需 StableHLO 資訊,請參閱「StableHLO - clamp」。
收合
另請參閱
XlaBuilder::Collapse。
和 tf.reshape 作業。
將陣列的維度摺疊成一個維度。
Collapse(operand, dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
類型為 T 的陣列 |
dimensions |
int64 向量 |
T 的維度依序排列的連續子集。 |
「摺疊」會將運算元維度的指定子集,替換為單一維度。輸入引數是任意 T 型別的陣列,以及維度索引的編譯時間常數向量。維度索引必須是 T 維度的連續子集,且維度編號依序遞增。因此,{0, 1, 2}、{0, 1} 或 {1, 2} 都是有效的維度集,但 {1, 0} 或 {0, 2} 則否。這些維度會由一個新的維度取代,且在維度序列中的位置與取代的維度相同,新維度的大小則等於原始維度大小的乘積。dimensions 中最低的維度編號是迴圈巢狀結構中變化最慢的維度 (最主要),最高的維度編號則是變化最快的維度 (最次要)。如需更多一般摺疊排序,請參閱 tf.reshape 運算子。
舉例來說,假設 v 是含有 24 個元素的陣列:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
Clz
另請參閱
XlaBuilder::Clz。
逐一計算前置零。
Clz(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
CollectiveBroadcast
另請參閱
XlaBuilder::CollectiveBroadcast。
將資料廣播至所有副本。每個群組中的第一個副本 ID 會將資料傳送至同一個群組中的其他 ID。如果副本 ID 不在任何副本群組中,該副本的輸出內容會是 shape 中的 0 所組成的張量。
CollectiveBroadcast(operand, replica_groups, channel_id)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
replica_groups
|
ReplicaGroupvector
|
每個群組都包含副本 ID 清單 |
channel_id
|
選填 ChannelHandle
|
每個傳送/接收配對的專屬 ID |
如需 StableHLO 資訊,請參閱「StableHLO - collective_broadcast」。
CollectivePermute
另請參閱
XlaBuilder::CollectivePermute。
CollectivePermute 是一種集體作業,可在副本之間傳送及接收資料。
CollectivePermute(operand, source_target_pairs, channel_id, inplace)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
n 維輸入陣列 |
source_target_pairs
|
<int64, int64> vector
|
(source_replica_id, target_replica_id) 組合清單。對於每組運算元,系統都會從來源副本傳送至目標副本。 |
channel_id
|
選填 ChannelHandle
|
用於跨模組通訊的選填管道 ID |
inplace
|
選填 bool
|
是否應就地執行排列 |
請注意,source_target_pairs 有下列限制:
- 任意兩組不得有相同的目標副本 ID,也不得有相同的來源副本 ID。
- 如果副本 ID 不是任何配對中的目標,則該副本的輸出內容是張量,由形狀與輸入內容相同的 0 組成。
CollectivePermute 作業的 API 會在內部分解為 2 個 HLO 指令 (CollectivePermuteStart 和 CollectivePermuteDone)。
另請參閱
HloInstruction::CreateCollectivePermuteStart。
CollectivePermuteStart 和 CollectivePermuteDone 在 HLO 中做為基本型別。這些作業可能會出現在 HLO 傾印中,但並非供使用者手動建構。
如需 StableHLO 資訊,請參閱「StableHLO - collective_permute」。
比較
另請參閱
XlaBuilder::Compare。
對下列項目的 lhs 和 rhs 執行元素層級的比較:
Eq
另請參閱
XlaBuilder::Eq。
對 lhs 和 rhs 執行元素層級的相等比較。
\(lhs = rhs\)
Eq(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Eq 有支援不同維度廣播的替代變體:
Eq(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
支援浮點數的總訂單,方法是強制執行:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
EqTotalOrder(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
如要瞭解 StableHLO,請參閱比較 StableHLO。
Ne
另請參閱
XlaBuilder::Ne。
對 lhs 和 rhs 執行元素層級的不等於比較。
\(lhs != rhs\)
Ne(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Ne 有替代變體,支援不同維度的廣播:
Ne(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
Ne 支援總訂單超過浮點數,方法是強制執行:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
NeTotalOrder(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
如要瞭解 StableHLO,請參閱比較 StableHLO。
Ge
另請參閱
XlaBuilder::Ge。
對 lhs 和 rhs 執行元素層級的「大於或等於」greater-or-equal-than比較。
\(lhs >= rhs\)
Ge(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Ge 有替代變體,支援不同維度的廣播:
Ge(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
支援浮點數的總訂單,方法是強制執行:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
GtTotalOrder(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
如要瞭解 StableHLO,請參閱比較 StableHLO。
Gt
另請參閱
XlaBuilder::Gt。
對 lhs 和 rhs 執行元素層級的大於比較。
\(lhs > rhs\)
Gt(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Gt 有支援不同維度廣播的替代變體:
Gt(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如要瞭解 StableHLO,請參閱比較 StableHLO。
Le
另請參閱
XlaBuilder::Le。
對 lhs 和 rhs 執行元素層級的less-or-equal-than比較。
\(lhs <= rhs\)
Le(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Le 有支援不同維度廣播的替代變體:
Le(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
透過強制執行以下項目,支援 Le 的浮點數總訂單:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LeTotalOrder(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
如要瞭解 StableHLO,請參閱比較 StableHLO。
Lt
另請參閱
XlaBuilder::Lt。
對 lhs 和 rhs 執行元素層級的小於比較。
\(lhs < rhs\)
Lt(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Lt 另有支援不同維度廣播的替代變體:
Lt(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
支援 Lt 的浮點數總訂單,方法是強制執行:
\[-NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.\]
LtTotalOrder(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
如要瞭解 StableHLO,請參閱比較 StableHLO。
複雜
另請參閱
XlaBuilder::Complex。
從實數和虛數值 (lhs 和 rhs) 組合,逐一轉換為複數值。
Complex(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Complex 有替代變體,支援不同維度的廣播:
Complex(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱「StableHLO - complex」。
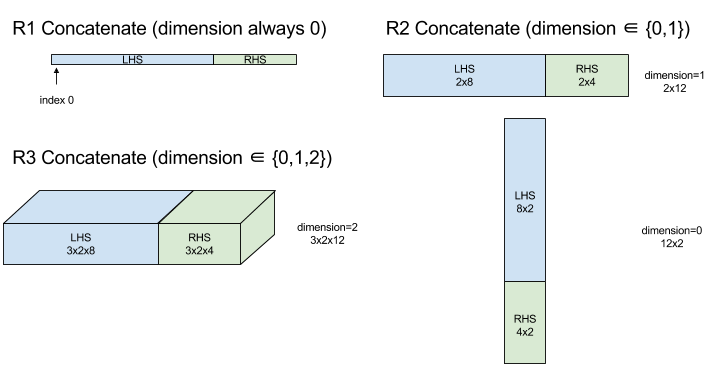
ConcatInDim (串連)
另請參閱
XlaBuilder::ConcatInDim。
Concatenate 會從多個陣列運算元組成一個陣列。這個陣列的維度數量與每個輸入陣列運算元相同 (這些運算元彼此的維度數量必須相同),且包含的引數順序與指定順序相同。
Concatenate(operands..., dimension)
| 引數 | 類型 | 語意 |
|---|---|---|
operands
|
N 序列 XlaOp
|
N 個 T 型別的陣列,維度為 [L0, L1, ...]。N 必須大於或等於 1。 |
dimension
|
int64
|
間隔 [0, N) 中的值,用於命名要串連的維度 (介於 operands 之間)。 |
除了 dimension 以外,所有維度都必須相同。這是因為 XLA 不支援「不規則」陣列。另請注意,0 維度值無法串連 (因為無法命名串連發生的維度)。
一維範例:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
//Output: {2, 3, 4, 5, 6, 7}
2 維範例:
let a = { {1, 2},
{3, 4},
{5, 6} };
let b = { {7, 8} };
Concat({a, b}, 0)
//Output: { {1, 2},
// {3, 4},
// {5, 6},
// {7, 8} }
圖表:
如需 StableHLO 相關資訊,請參閱「StableHLO - concatenate」。
條件式
另請參閱
XlaBuilder::Conditional。
Conditional(predicate, true_operand, true_computation, false_operand,
false_computation)
| 引數 | 類型 | 語意 |
|---|---|---|
predicate |
XlaOp |
PRED 型別的純量 |
true_operand |
XlaOp |
類型引數 \(T_0\) |
true_computation |
XlaComputation |
XlaComputation of type \(T_0 \to S\) |
false_operand |
XlaOp |
類型引數 \(T_1\) |
false_computation |
XlaComputation |
XlaComputation of type \(T_1 \to S\) |
如果 predicate 為 true,則執行 true_computation;如果 predicate 為 false,則執行 false_computation,並傳回結果。
true_computation 必須採用 \(T_0\) 類型的單一引數,並以 true_operand 叫用,而 true_operand 必須屬於相同類型。false_computation 必須採用 \(T_1\) 類型的單一引數,並以 false_operand 叫用,而 false_operand 必須屬於相同類型。true_computation 和 false_computation 的傳回值類型必須相同。
請注意,系統會根據 predicate 的值,只執行 true_computation 和 false_computation 其中一個。
Conditional(branch_index, branch_computations, branch_operands)
| 引數 | 類型 | 語意 |
|---|---|---|
branch_index |
XlaOp |
S32 型別的純量 |
branch_computations |
N XlaComputation 序列 |
XlaComputations of type \(T_0 \to S , T_1 \to S , ..., T_{N-1} \to S\) |
branch_operands |
N XlaOp 序列 |
類型為 \(T_0 , T_1 , ..., T_{N-1}\)的引數 |
執行 branch_computations[branch_index] 並傳回結果。如果 branch_index 是 < 0 或 >= N 的 S32,則 branch_computations[N-1] 會以預設分支執行。
每個 branch_computations[b] 都必須採用 \(T_b\) 類型的單一引數,並以 branch_operands[b] 叫用,而 branch_operands[b] 必須屬於相同類型。每個 branch_computations[b] 傳回的值必須是相同類型。
請注意,系統只會根據 branch_index 的值執行其中一個 branch_computations。
如需 StableHLO 資訊,請參閱「StableHLO - if」。
常數
另請參閱
XlaBuilder::ConstantLiteral。
從常數 literal 產生 output。
Constant(literal)
| 引數 | 類型 | 語意 |
|---|---|---|
literal |
LiteralSlice |
現有 Literal 的常數檢視畫面 |
如需 StableHLO 資訊,請參閱「StableHLO - constant」。
ConvertElementType
另請參閱
XlaBuilder::ConvertElementType。
與 C++ 中的元素式 static_cast 類似,ConvertElementType 會執行元素式轉換作業,將資料形狀轉換為目標形狀。維度必須相符,且轉換是逐一進行,例如 s32 元素會透過 s32 對 f32 的轉換常式變成 f32 元素。
ConvertElementType(operand, new_element_type)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
具有 D 維度的 T 型陣列 |
new_element_type |
PrimitiveType |
U 型 |
運算元和目標形狀的維度必須相符。來源和目的地元素類型不得為元組。
例如,從 T=s32 轉換為 U=f32 時,系統會執行正規化整數到浮點數的轉換常式,例如四捨五入到最接近的偶數。
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
如需 StableHLO 相關資訊,請參閱「StableHLO - convert」。
Conv (卷積)
另請參閱
XlaBuilder::Conv。
計算類神經網路中使用的捲積。在這裡,您可以將捲積視為在 n 維基礎區域中移動的 n 維視窗,並針對視窗的每個可能位置執行計算。
Conv 將捲積指令加入運算,使用預設捲積維度數字,不進行擴張。
填充內容會以簡短方式指定為 SAME 或 VALID。SAME
padding 會以零填補輸入 (lhs),因此在不考慮步幅的情況下,輸出與輸入的形狀相同。VALID 邊框間距只是指沒有邊框間距。
Conv(lhs, rhs, window_strides, padding, feature_group_count,
batch_group_count, precision_config, preferred_element_type)
| 引數 | 類型 | 語意 |
|---|---|---|
lhs
|
XlaOp
|
(n+2) 維輸入陣列 |
rhs
|
XlaOp
|
(n+2) 維度陣列,包含核心權重 |
window_strides |
ArraySlice<int64> |
核心步幅的 n 維陣列 |
padding |
Padding |
邊框間距列舉 |
feature_group_count
|
int64 | 特徵群組數量 |
batch_group_count |
int64 | 批次群組數量 |
precision_config
|
選填
PrecisionConfig |
精確程度的列舉 |
preferred_element_type
|
選填
PrimitiveType |
純量元素型別的列舉 |
Conv 提供以下控管層級:
假設 n 是空間維度的數量。lhs 引數是描述基本區域的 (n+2) 維陣列。這稱為輸入,當然,rhs 也是輸入。在類神經網路中,這些是輸入啟動。n+2 個維度依序為:
batch:這個維度中的每個座標都代表一個獨立的輸入,系統會對其執行捲積。z/depth/features:基本區域中的每個 (y,x) 位置都有相關聯的向量,會進入這個維度。spatial_dims:說明定義視窗移動基準區域的n空間尺寸。
rhs 引數是 (n+2) 維度陣列,用於說明捲積濾鏡/核心/視窗。維度依序為:
output-z:輸出的z維度。input-z:這個維度的大小乘以feature_group_count應等於左側z維度的大小。spatial_dims:說明定義 n 維視窗的n空間維度,該視窗會在基本區域中移動。
window_strides 引數會指定空間維度中捲積視窗的步幅。舉例來說,如果第一個空間維度的步幅為 3,則視窗只能放置在第一個空間索引可被 3 整除的座標。
padding 引數會指定要套用至基本區域的零邊框間距量。填補量可以是負值,負填補量的絕對值表示在執行捲積前,要從指定維度移除的元素數量。padding[0] 指定維度 y 的邊框間距,padding[1] 則指定維度 x 的邊框間距。每對值的第一個元素是低邊框間距,第二個元素是高邊框間距。低邊框間距會套用至索引較低的方向,高邊框間距則會套用至索引較高的方向。舉例來說,如果 padding[1] 是 (2,3),則第二個空間維度左側會以 2 個零填補,右側則以 3 個零填補。使用邊框間距等同於在執行捲積前,將相同的零值插入輸入 (lhs)。
lhs_dilation 和 rhs_dilation 引數會指定要套用至 lhs 和 rhs 的擴張因子,分別位於每個空間維度。如果空間維度的擴張係數為 d,則系統會在該維度的每個項目之間隱含地放置 d-1 個洞,增加陣列的大小。這些洞會填入無運算值,以卷積來說就是零。
rhs 的擴張也稱為 atrous 卷積。詳情請參閱 tf.nn.atrous_conv2d。左側的擴張也稱為轉置的捲積。詳情請參閱 tf.nn.conv2d_transpose。
feature_group_count 引數 (預設值為 1) 可用於分組的捲積。feature_group_count 必須是輸入和輸出特徵維度的除數。如果 feature_group_count 大於 1,表示輸入和輸出特徵維度以及 rhs 輸出特徵維度,在概念上會平均分成許多 feature_group_count 群組,每個群組都包含連續的特徵子序列。rhs 的輸入特徵維度必須等於 lhs 輸入特徵維度除以 feature_group_count (因此已具有一組輸入特徵的大小)。第 i 個群組會一起用於計算多個獨立的捲積。feature_group_count這些卷積的結果會串連在一起,並以輸出特徵維度呈現。
如果是深度方向的捲積,feature_group_count 引數會設為輸入特徵維度,而篩選器會從 [filter_height, filter_width, in_channels, channel_multiplier] 重新調整為 [filter_height, filter_width, 1, in_channels * channel_multiplier]。詳情請參閱 tf.nn.depthwise_conv2d。
batch_group_count (預設值為 1) 引數可用於反向傳播期間的分組篩選器。batch_group_count 必須是 lhs (輸入) 批次維度大小的除數。如果 batch_group_count 大於 1,表示輸出批次維度的大小應為 input batch
/ batch_group_count。batch_group_count 必須是輸出特徵大小的除數。
輸出形狀的維度如下 (依序):
batch:這個維度的尺寸乘以batch_group_count應等於左側batch維度的尺寸。z:與核心上的output-z大小相同 (rhs)。spatial_dims:每個有效放置的捲積視窗各有一個值。
上圖顯示 batch_group_count 欄位的運作方式。實際上,我們會將每個 lhs 批次切分成 batch_group_count 個群組,並對輸出特徵執行相同操作。接著,我們會對每個群組執行成對的捲積,並沿著輸出特徵維度串連輸出內容。所有其他維度 (特徵和空間) 的運算語意維持不變。
卷積視窗的有效位置取決於步幅和填補後底面積的大小。
如要說明卷積的用途,請考慮 2D 卷積,並在輸出中選取一些固定的 batch、z、y、x 座標。則為視窗在基本區域內的角落位置 (例如左上角,視您如何解讀空間尺寸而定)。(y,x)現在我們有一個 2D 視窗,取自基本區域,其中每個 2D 點都與 1D 向量相關聯,因此我們得到一個 3D 方塊。從卷積核心來看,由於我們修正了輸出座標 z,因此也有 3D 方塊。這兩個方塊的尺寸相同,因此我們可以取這兩個方塊之間元素乘積的總和 (類似於點積)。這就是輸出值。
請注意,如果 output-z 是 5,則視窗的每個位置都會在輸出內容的 z 維度中產生 5 個值。這些值使用的卷積核心部分不同,每個 output-z 座標都有各自的 3D 值方塊。因此,您可以將其視為 5 個獨立的迴旋,每個迴旋都有不同的濾鏡。
以下是使用填補和步幅的 2D 捲積虛擬程式碼:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
precision_config 用於指出精確度設定。這個層級會決定硬體是否應嘗試產生更多機器碼指令,以便在需要時提供更準確的 dtype 模擬 (也就是在僅支援 bf16 matmul 的 TPU 上模擬 f32)。值可能為 DEFAULT、HIGH、HIGHEST。詳情請參閱 MXU 專區。
preferred_element_type 是用於累加的較高/較低精確度輸出型別的純量元素。preferred_element_type 會建議指定作業的累積類型,但無法保證。這可讓某些硬體後端改為以不同類型累加,並轉換為偏好的輸出類型。
如需 StableHLO 資訊,請參閱「StableHLO - 卷積」。
ConvWithGeneralPadding
另請參閱
XlaBuilder::ConvWithGeneralPadding。
ConvWithGeneralPadding(lhs, rhs, window_strides, padding,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
與 Conv 相同,但邊框間距設定是明確的。
| 引數 | 類型 | 語意 |
|---|---|---|
lhs
|
XlaOp
|
(n+2) 維輸入陣列 |
rhs
|
XlaOp
|
(n+2) 維度陣列,包含核心權重 |
window_strides |
ArraySlice<int64> |
核心步幅的 n 維陣列 |
padding
|
ArraySlice<
pair<int64,int64>> |
(low, high) 的 n 維陣列 padding |
feature_group_count
|
int64 | 特徵群組數量 |
batch_group_count |
int64 | 批次群組數量 |
precision_config
|
選填
PrecisionConfig |
精確程度的列舉 |
preferred_element_type
|
選填
PrimitiveType |
純量元素型別的列舉 |
ConvWithGeneralDimensions
另請參閱
XlaBuilder::ConvWithGeneralDimensions。
ConvWithGeneralDimensions(lhs, rhs, window_strides, padding,
dimension_numbers, feature_group_count, batch_group_count, precision_config,
preferred_element_type)
與 Conv 相同,但維度編號是明確的。
| 引數 | 類型 | 語意 |
|---|---|---|
lhs
|
XlaOp
|
(n+2) 維輸入陣列 |
rhs
|
XlaOp
|
(n+2) 維度核心權重陣列 |
window_strides
|
ArraySlice<int64>
|
核心步幅的 n 維陣列 |
padding |
Padding |
邊框間距列舉 |
dimension_numbers
|
ConvolutionDimensionNumbers
|
維度數量 |
feature_group_count
|
int64 | 特徵群組數量 |
batch_group_count
|
int64 | 批次群組數量 |
precision_config
|
選填 PrecisionConfig
|
精確程度的列舉 |
preferred_element_type
|
選填 PrimitiveType
|
純量 元素型別的列舉 |
ConvGeneral
另請參閱
XlaBuilder::ConvGeneral。
ConvGeneral(lhs, rhs, window_strides, padding, dimension_numbers,
feature_group_count, batch_group_count, precision_config,
preferred_element_type)
與 Conv 相同,其中維度編號和邊框間距設定為明確
| 引數 | 類型 | 語意 |
|---|---|---|
lhs
|
XlaOp
|
(n+2) 維輸入陣列 |
rhs
|
XlaOp
|
(n+2) 維度核心權重陣列 |
window_strides
|
ArraySlice<int64>
|
核心步幅的 n 維陣列 |
padding
|
ArraySlice<
pair<int64,int64>>
|
n 維陣列,包含 (低、高) 邊框間距 |
dimension_numbers
|
ConvolutionDimensionNumbers
|
維度數量 |
feature_group_count
|
int64 | 特徵群組數量 |
batch_group_count
|
int64 | 批次群組數量 |
precision_config
|
選填 PrecisionConfig
|
精確程度的列舉 |
preferred_element_type
|
選填 PrimitiveType
|
純量 元素型別的列舉 |
ConvGeneralDilated
另請參閱
XlaBuilder::ConvGeneralDilated。
ConvGeneralDilated(lhs, rhs, window_strides, padding, lhs_dilation,
rhs_dilation, dimension_numbers, feature_group_count, batch_group_count,
precision_config, preferred_element_type, window_reversal)
與 Conv 相同,其中填補設定、擴張係數和維度編號都是明確的。
| 引數 | 類型 | 語意 |
|---|---|---|
lhs
|
XlaOp
|
(n+2) 維輸入陣列 |
rhs
|
XlaOp
|
(n+2) 維度核心權重陣列 |
window_strides
|
ArraySlice<int64>
|
核心步幅的 n 維陣列 |
padding
|
ArraySlice<
pair<int64,int64>>
|
n 維陣列,包含 (低、高) 邊框間距 |
lhs_dilation
|
ArraySlice<int64>
|
n-d lhs dilation factor array |
rhs_dilation
|
ArraySlice<int64>
|
n-d rhs dilation factor array |
dimension_numbers
|
ConvolutionDimensionNumbers
|
維度數量 |
feature_group_count
|
int64 | 特徵群組數量 |
batch_group_count
|
int64 | 批次群組數量 |
precision_config
|
選填 PrecisionConfig
|
精確程度的列舉 |
preferred_element_type
|
選填 PrimitiveType
|
純量 元素型別的列舉 |
window_reversal
|
選填 vector<bool>
|
旗標,用於在套用捲積前,以邏輯方式反轉維度 |
複製
另請參閱
HloInstruction::CreateCopyStart。
Copy 會在內部分解為 2 個 HLO 指令 CopyStart 和 CopyDone。Copy 以及 CopyStart 和 CopyDone,在 HLO 中做為基本型別。這些作業可能會出現在 HLO 傾印中,但使用者不應手動建構這些作業。
COS
另請參閱XlaBuilder::Cos。
元素層級餘弦 x -> cos(x)。
Cos(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Cos 也支援選用 result_accuracy 引數:
Cos(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
如需 StableHLO 資訊,請參閱「StableHLO - 餘弦」。
Cosh
另請參閱
XlaBuilder::Cosh。
逐一計算雙曲餘弦 x -> cosh(x)。
Cosh(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Cosh 也支援選用 result_accuracy 引數:
Cosh(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
CustomCall
另請參閱
XlaBuilder::CustomCall。
在運算中呼叫使用者提供的函式。
如需 CustomCall 說明文件,請參閱開發人員詳細資料 - XLA 自訂通話
如要瞭解 StableHLO,請參閱「StableHLO - custom_call」。
DIV
另請參閱
XlaBuilder::Div。
執行被除數 lhs 和除數 rhs 的元素層級除法。
Div(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
整數除法溢位 (有號/無號除法/餘數為零,或有號除法/餘數為 INT_SMIN 除以 -1) 會產生實作定義的值。
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Div 有替代變體,支援不同維度的廣播:
Div(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱「StableHLO - divide」。
網域
另請參閱
HloInstruction::CreateDomain。
Domain 可能會出現在 HLO 傾印中,但使用者不應手動建構。
Dot
另請參閱
XlaBuilder::Dot。
Dot(lhs, rhs, precision_config, preferred_element_type)
| 引數 | 類型 | 語意 |
|---|---|---|
lhs |
XlaOp |
類型為 T 的陣列 |
rhs |
XlaOp |
類型為 T 的陣列 |
precision_config
|
選填
PrecisionConfig |
精確程度的列舉 |
preferred_element_type
|
選填
PrimitiveType |
純量元素型別的列舉 |
這項作業的確切語意取決於運算元的等級:
| 輸入 | 輸出 | 語意 |
|---|---|---|
vector [n] dot vector [n] |
純量 | 向量點積 |
矩陣 [m x k] dot 向量
[k] |
向量 [m] | 矩陣向量乘法 |
矩陣 [m x k] dot 矩陣
[k x n] |
矩陣 [m x n] | 矩陣相乘 |
這項作業會對 lhs 的第二個維度 (或第一個維度,如果只有 1 個維度) 和 rhs 的第一個維度執行乘積總和。這些是「合約」維度。lhs 和 rhs 的收縮維度必須大小相同。在實務上,這項作業可用於執行向量之間的點積、向量/矩陣乘法或矩陣/矩陣乘法。
precision_config 用於指出精確度設定。這個層級會決定硬體是否應嘗試產生更多機器碼指令,以便在需要時提供更準確的 dtype 模擬 (也就是在僅支援 bf16 matmul 的 TPU 上模擬 f32)。值可能為 DEFAULT、HIGH、HIGHEST。詳情請參閱 MXU 專區。
preferred_element_type 是用於累加的較高/較低精確度輸出型別的純量元素。preferred_element_type 會建議指定作業的累積類型,但無法保證。這可讓某些硬體後端改為以不同類型累加,並轉換為偏好的輸出類型。
如需 StableHLO 資訊,請參閱 StableHLO - dot。
DotGeneral
另請參閱
XlaBuilder::DotGeneral。
DotGeneral(lhs, rhs, dimension_numbers, precision_config,
preferred_element_type)
| 引數 | 類型 | 語意 |
|---|---|---|
lhs |
XlaOp |
類型為 T 的陣列 |
rhs |
XlaOp |
類型為 T 的陣列 |
dimension_numbers
|
DotDimensionNumbers
|
合約和批次維度號碼 |
precision_config
|
選填
PrecisionConfig |
精確程度的列舉 |
preferred_element_type
|
選填
PrimitiveType |
純量元素型別的列舉 |
與 Dot 類似,但可指定 lhs 和 rhs 的合約和批次維度編號。
| DotDimensionNumbers 欄位 | 類型 | 語意 |
|---|---|---|
lhs_contracting_dimensions
|
repeated int64 | lhs 合約維度編號 |
rhs_contracting_dimensions
|
repeated int64 | rhs 合約維度編號 |
lhs_batch_dimensions
|
repeated int64 | lhs 批次維度
號碼 |
rhs_batch_dimensions
|
repeated int64 | rhs 批次維度
號碼 |
DotGeneral 會對 dimension_numbers 中指定的收縮維度執行產品總和。
lhs 和 rhs 的相關收縮尺寸編號不必相同,但尺寸大小必須相同。
以下是維度編號縮減的範例:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { { 6.0, 12.0},
{15.0, 30.0} }
lhs 和 rhs 中的相關批次維度編號必須具有相同的維度大小。
以下是批次維度數字的範例 (批次大小為 2,2x2 矩陣):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> {
{ {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| 輸入 | 輸出 | 語意 |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | 批次矩陣乘法 |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | 批次矩陣乘法 |
因此,產生的維度編號會先是批次維度,接著是 lhs 非收縮/非批次維度,最後是 rhs 非收縮/非批次維度。
precision_config 用於指出精確度設定。這個層級會決定硬體是否應嘗試產生更多機器碼指令,以便在需要時提供更準確的 dtype 模擬 (也就是在僅支援 bf16 matmul 的 TPU 上模擬 f32)。值可能為 DEFAULT、HIGH、HIGHEST。詳情請參閱 MXU 專區。
preferred_element_type 是用於累加的較高/較低精確度輸出型別的純量元素。preferred_element_type 會建議指定作業的累積類型,但無法保證。這可讓某些硬體後端改為以不同類型累加,並轉換為偏好的輸出類型。
如需 StableHLO 資訊,請參閱「StableHLO - dot_general」。
ScaledDot
另請參閱
XlaBuilder::ScaledDot。
ScaledDot(lhs, lhs_scale, rhs, rhs_scale, dimension_number,
precision_config,preferred_element_type)
| 引數 | 類型 | 語意 |
|---|---|---|
lhs |
XlaOp |
類型為 T 的陣列 |
rhs |
XlaOp |
類型為 T 的陣列 |
lhs_scale |
XlaOp |
類型為 T 的陣列 |
rhs_scale |
XlaOp |
類型為 T 的陣列 |
dimension_number
|
ScatterDimensionNumbers
|
散布作業的維度編號 |
precision_config
|
PrecisionConfig
|
精確程度的列舉 |
preferred_element_type
|
選填 PrimitiveType
|
純量 元素型別的列舉 |
類似於 DotGeneral。
使用運算元「lhs」、「lhs_scale」、「rhs」和「rhs_scale」建立縮放點積運算,並在「dimension_numbers」中指定收縮和批次維度。
RaggedDot
另請參閱
XlaBuilder::RaggedDot。
如要瞭解 RaggedDot 的計算方式,請參閱
StableHLO - chlo.ragged_dot
DynamicReshape
另請參閱
XlaBuilder::DynamicReshape。
這項作業在功能上與 reshape 相同,但結果形狀是透過 output_shape 動態指定。
DynamicReshape(operand, dim_sizes, new_size_bounds, dims_are_dynamic)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
型別為 T 的 N 維陣列 |
dim_sizes |
XlaOP 的向量 |
N 維向量大小 |
new_size_bounds |
int63 的向量 |
N 維度邊界向量 |
dims_are_dynamic |
bool 的向量 |
N 維度動態調暗 |
如需 StableHLO 相關資訊,請參閱「StableHLO - dynamic_reshape」。
DynamicSlice
另請參閱
XlaBuilder::DynamicSlice。
DynamicSlice 會從輸入陣列中擷取動態位置的子陣列。start_indices每個維度的切片大小都會傳遞至 size_indices,指定每個維度中不含結尾的切片間隔:[start, start + size)。start_indices 的形狀必須是 1 維,且維度大小等於 operand 的維度數量。
DynamicSlice(operand, start_indices, slice_sizes)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
型別為 T 的 N 維陣列 |
start_indices
|
N 序列 XlaOp
|
N 個純量整數的清單,其中包含每個維度的切片起始索引。值必須大於或等於零。 |
size_indices
|
ArraySlice<int64>
|
包含每個維度的切片大小的 N 個整數清單。每個值都必須嚴格大於零,且 start + size 必須小於或等於維度大小,以免包裝模數維度大小。 |
執行切片前,請先對 [1, N) 中的每個索引 i 進行下列轉換,計算有效切片索引:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - slice_sizes[i])
這可確保擷取的切片一律在運算元陣列的界線內。如果切片在套用轉換前位於界內,轉換不會產生任何效果。
一維範例:
let a = {0.0, 1.0, 2.0, 3.0, 4.0};
let s = {2};
DynamicSlice(a, s, {2});
// Result: {2.0, 3.0}
2 維範例:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2});
//Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
如需 StableHLO 資訊,請參閱「StableHLO - dynamic_slice」。
DynamicUpdateSlice
另請參閱
XlaBuilder::DynamicUpdateSlice。
DynamicUpdateSlice 會產生結果,也就是輸入陣列 operand 的值,並在 start_indices 覆寫部分 update。update 的形狀會決定結果中更新的子陣列形狀。start_indices 的形狀必須是一維,且維度大小等於 operand 的維度數量。
DynamicUpdateSlice(operand, update, start_indices)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
型別為 T 的 N 維陣列 |
update
|
XlaOp
|
包含切片更新的 T 型 N 維陣列。更新形狀的每個維度都必須嚴格大於零,且每個維度的開始 + 更新必須小於或等於運算元大小,才能避免產生超出範圍的更新索引。 |
start_indices
|
N 序列 XlaOp
|
N 個純量整數的清單,其中包含每個維度的切片起始索引。值必須大於或等於零。 |
執行切片前,請先對 [1, N) 中的每個索引 i 進行下列轉換,計算有效切片索引:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
這可確保更新後的切片一律在運算元陣列的界限內。如果切片在套用轉換前位於界內,轉換不會產生任何效果。
一維範例:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s)
// Result: {0.0, 1.0, 5.0, 6.0, 4.0}
2 維範例:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s)
// Result:
// { {0.0, 1.0, 2.0},
// {3.0, 12.0, 13.0},
// {6.0, 14.0, 15.0},
// {9.0, 16.0, 17.0} }
如需 StableHLO 資訊,請參閱「StableHLO - dynamic_update_slice」。
Erf
另請參閱
XlaBuilder::Erf。
元素級別誤差函式 x -> erf(x),其中:
\(\text{erf}(x) = \frac{2}{\sqrt{\pi} }\int_0^x e^{-t^2} \, dt\)。
Erf(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Erf 也支援選用的 result_accuracy 引數:
Erf(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
指數
另請參閱
XlaBuilder::Exp。
逐一計算元素的自然指數 x -> e^x。
Exp(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Exp 也支援選用的 result_accuracy 引數:
Exp(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
如需 StableHLO 資訊,請參閱「StableHLO - 指數」。
Expm1
另請參閱
XlaBuilder::Expm1。
元素層級的自然指數減一 x -> e^x - 1。
Expm1(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Expm1 也支援選用的 result_accuracy 引數:
Expm1(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
如需 StableHLO 相關資訊,請參閱「StableHLO - exponential_minus_one」。
Fft
另請參閱
XlaBuilder::Fft。
XLA FFT 運算會針對實數和複數輸入/輸出,實作正向和反向傅立葉轉換。支援最多 3 個軸的多維度 FFT。
Fft(operand, ftt_type, fft_length)
| 引數 | 類型 | 語意 |
|---|---|---|
operand
|
XlaOp
|
要進行傅立葉轉換的陣列。 |
fft_type |
FftType |
請參閱下表。 |
fft_length
|
ArraySlice<int64>
|
要轉換的軸的時間域長度。特別是 IRFFT 需要這個值,才能正確調整最內層軸的大小,因為 RFFT(fft_length=[16]) 的輸出形狀與 RFFT(fft_length=[17]) 相同。 |
FftType |
語意 |
|---|---|
FFT |
轉送複數到複數的 FFT。形狀未變更。 |
IFFT |
複數對複數 FFT 反轉換。形狀未變更。 |
RFFT
|
轉送實數到複數的 FFT。如果 fft_length[-1] 是非零值,最內層軸的形狀會縮減為 fft_length[-1] // 2 + 1,並省略超出奈奎斯特頻率的轉換訊號反向共軛部分。 |
IRFFT
|
實數到複數 FFT 的反向運算 (即輸入複數,回傳實數)。最內層軸的形狀會擴展為 fft_length[-1] (如果 fft_length[-1] 是非零值),並從 1 到 fft_length[-1] // 2 + 1 項目的反向共軛推斷轉換訊號中超出奈奎斯特頻率的部分。 |
如要瞭解 StableHLO,請參閱「StableHLO - fft」。
多維度 FFT
如果提供超過 1 個 fft_length,這相當於對每個最內層的軸套用一連串的 FFT 作業。請注意,在實數 -> 複數和複數 -> 實數的情況下,最內層的軸轉換會 (有效) 先執行 (RFFT;IRFFT 則為最後執行),因此最內層的軸會改變大小。其他軸轉換作業隨後會變成 complex->complex。
實作詳情
CPU FFT 由 Eigen 的 TensorFFT 支援。GPU FFT 使用 cuFFT。
樓層
另請參閱
XlaBuilder::Floor。
元素層級的底價 x -> ⌊x⌋。
Floor(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
如需 StableHLO 相關資訊,請參閱「StableHLO - floor」。
Fusion
另請參閱
HloInstruction::CreateFusion。
Fusion 作業代表 HLO 指令,並做為 HLO 中的基本項目。這個作業可能會出現在 HLO 傾印中,但使用者不應手動建構。
收集
XLA 收集作業會將輸入陣列的數個切片 (每個切片可能位於不同的執行階段偏移) 縫合在一起。
如需 StableHLO 相關資訊,請參閱「StableHLO - gather」。
一般語意
另請參閱
XlaBuilder::Gather。
如需更直覺的說明,請參閱下方的「非正式說明」一節。
gather(operand, start_indices, dimension_numbers, slice_sizes,
indices_are_sorted)
| 引數 | 類型 | 語意 |
|---|---|---|
operand
|
XlaOp
|
要從中收集資料的陣列。 |
start_indices
|
XlaOp
|
包含所收集切片的起始索引的陣列。 |
dimension_numbers
|
GatherDimensionNumbers
|
包含起始索引的維度。start_indices詳情請參閱下文。 |
slice_sizes
|
ArraySlice<int64>
|
slice_sizes[i] 是維度 i 上切片的界線。 |
indices_are_sorted
|
bool
|
索引是否保證由呼叫端排序。 |
為方便起見,我們將輸出陣列中不在 offset_dims 中的維度標示為 batch_dims。
輸出內容是具有 batch_dims.size + offset_dims.size 維度的陣列。
operand.rank 必須等於 offset_dims.size 和 collapsed_slice_dims.size 的總和。此外,slice_sizes.size 必須等於 operand.rank。
如果 index_vector_dim 等於 start_indices.rank,我們會隱含地將 start_indices 視為具有尾端 1 維度 (也就是說,如果 start_indices 的形狀為 [6,7],且 index_vector_dim 為 2,我們會隱含地將 start_indices 的形狀視為 [6,7,1])。
沿著維度 i 的輸出陣列界限計算方式如下:
如果
i出現在batch_dims中 (即等於某個batch_dims[k]k),我們會從start_indices.shape中挑選對應的維度界限,並略過index_vector_dim(即如果k<index_vector_dim,則挑選start_indices.shape.dims[k],否則挑選start_indices.shape.dims[k+1])。如果
i存在於offset_dims中 (即等於某些k的offset_dims[k]),則在考量collapsed_slice_dims後,我們會從slice_sizes中挑選對應的界線 (即挑選adjusted_slice_sizes[k],其中adjusted_slice_sizes是slice_sizes,且已移除索引collapsed_slice_dims的界線)。
正式來說,對應指定輸出索引 Out 的運算元索引 In 計算方式如下:
令
G= {Out[k] forkinbatch_dims}。使用G切出向量S,使S[i] =start_indices[Combine(G,i)],其中 Combine(A, b) 會將 b 插入 A 的index_vector_dim位置。請注意,即使G為空,這項定義仍適用:如果G為空,則S=start_indices。使用
start_index_map散布S,在operand中建立起始索引Sin。S更精確地說:Sin[start_index_map[k]] =S[k] ifk<start_index_map.size.Sin[_] =0,否則為0。
根據
collapsed_slice_dims集,將Out中偏移維度的索引分散到operand中,藉此建立索引Oin。更精確地說:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]] ifk<offset_dims.size(remapped_offset_dimsis defined below)。Oin[_] =0,否則為0。
In為Oin+Sin,其中 + 是元素加法。
remapped_offset_dims 是單調函式,網域為 [0, offset_dims.size),範圍為 [0, operand.rank) \ collapsed_slice_dims。因此,舉例來說,offset_dims.size 為 4,operand.rank 為 6,且 collapsed_slice_dims 為 {0, 2},則 remapped_offset_dims 為 {0→1、1→3、2→4、3→5}。
如果 indices_are_sorted 設為 true,XLA 可以假設 start_indices 是由使用者排序 (遞增順序,在根據 start_index_map 散佈其值之後)。如果不是,則語意是由實作定義。
非正式說明和範例
非正式地說,輸出陣列中的每個索引 Out 都對應至運算元陣列中的元素 E,計算方式如下:
我們會使用
Out中的批次維度,從start_indices查閱起始索引。我們會使用
start_index_map,將起始索引 (大小可能小於運算元等級) 對應至operand中的「完整」起始索引。我們會使用完整起始索引,動態切出大小為
slice_sizes的切片。我們透過摺疊
collapsed_slice_dims維度來重塑切片。 由於所有摺疊切片維度都必須有 1 的界限,因此這種重塑方式一律合法。我們會使用
Out中的偏移尺寸建立這個切片的索引,以取得對應於輸出索引Out的輸入元素E。
在後續所有範例中,index_vector_dim 都會設為 start_indices.rank - 1。index_vector_dim 的其他有趣值不會從根本上改變作業,但會使視覺呈現更加繁瑣。
如要瞭解上述所有內容如何搭配使用,請查看以下範例,該範例會從 [16,11] 陣列收集 5 個 [8,6] 形狀的切片。切片在 [16,11] 陣列中的位置可以表示為 S64[2] 形狀的索引向量,因此 5 個位置的集合可以表示為 S64[5,2] 陣列。
接著,可將收集作業的行為描述為索引轉換,該轉換會採用 [G,O0,O1]、輸出形狀中的索引,並以下列方式將其對應至輸入陣列中的元素:
我們首先使用 G,從收集索引陣列中選取 (X,Y) 向量。輸出陣列中索引 [G,O0,O1] 的元素,就是輸入陣列中索引 [X+O0,Y+O1] 的元素。
slice_sizes 是 [8,6],可決定 O0 和 O1 的範圍,進而決定切片的界限。
這項收集作業會做為批次動態切片,而 G 則做為批次維度。
收集索引可以是多維度。舉例來說,如果使用形狀為 [4,5,2] 的「收集索引」陣列,上述範例的更一般版本會像這樣轉換索引:
同樣地,這會做為批次動態切片 G0 和批次維度 G1。切片大小仍為 [8,6]。
XLA 中的收集作業會以以下方式,概括說明上述非正式語意:
我們可以設定輸出形狀中的哪些維度是偏移維度 (含有
O0、O1的維度,如上例所示)。輸出批次維度 (包含上一個範例中的G0、G1的維度) 定義為非偏移維度的輸出維度。輸出形狀中明確顯示的輸出偏移維度數量,可能小於輸入維度數量。這些「遺失」的維度 (明確列為
collapsed_slice_dims) 的切片大小必須為1。由於這些項目的大小為1,因此唯一有效的索引是 ,省略這些項目不會造成模稜兩可的情況。0從「Gather Indices」陣列擷取的切片 (上一個範例中的 (
X,Y)) 可能比輸入陣列的維度數量少,而明確的對應會決定索引應如何擴展,才能與輸入的維度數量相同。
最後一個範例是使用 (2) 和 (3) 實作 tf.gather_nd:
G0 和 G1 用於從收集索引陣列中切出起始索引,但起始索引只有一個元素 X。同樣地,只有一個輸出偏移索引,值為 O0。不過,在做為輸入陣列的索引之前,這些索引會根據「Gather Index Mapping」(正式說明中的 start_index_map) 和「Offset Mapping」(正式說明中的 remapped_offset_dims) 分別擴展為 [X,0] 和 [0,O0],加總為 [X,O0]。換句話說,輸出索引 [G0,G1,O0] 會對應至輸入索引 [GatherIndices[G0,G1,0],O0],這會提供 tf.gather_nd 的語意。
slice_sizes,這個案件的 ID 為 [1,11]。直覺上,這表示聚集索引陣列中的每個索引 X 都會選取整個資料列,而結果是所有這些資料列的串連。
GetDimensionSize
另請參閱
XlaBuilder::GetDimensionSize。
傳回運算元指定維度的大小。運算元必須是陣列形狀。
GetDimensionSize(operand, dimension)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
n 維輸入陣列 |
dimension
|
int64
|
間隔 [0, n) 中的值,用於指定維度 |
如需 StableHLO 資訊,請參閱 StableHLO - get_dimension_size。
GetTupleElement
另請參閱
XlaBuilder::GetTupleElement。
使用編譯時間常數值建立元組的索引。
這個值必須是編譯時間常數,形狀推斷才能判斷結果值的型別。
這類似於 C++ 中的 std::get<int N>(t)。概念上:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
另請參閱「tf.tuple」。
GetTupleElement(tuple_data, index)
| 引數 | 類型 | 語意 |
|---|---|---|
tuple_data |
XlaOP |
元組 |
index |
int64 |
元組形狀的索引 |
如需 StableHLO 資訊,請參閱「StableHLO - get_tuple_element」。
Imag
另請參閱
XlaBuilder::Imag。
複數 (或實數) 形狀的元素虛部。x -> imag(x)。如果運算元是浮點類型,則會傳回 0。
Imag(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
如要瞭解 StableHLO,請參閱「StableHLO - imag」。
動態內
另請參閱
XlaBuilder::Infeed。
Infeed(shape, config)
| 引數 | 類型 | 語意 |
|---|---|---|
shape
|
Shape
|
從 In-feed 介面讀取的資料形狀。形狀的版面配置欄位必須設為與傳送至裝置的資料版面配置相符,否則其行為未定義。 |
config |
選填 string |
作業的設定。 |
從裝置的隱含 Infeed 串流介面讀取單一資料項目,將資料解讀為指定形狀及其版面配置,並傳回資料的 XlaOp。計算中允許多個 Infeed 作業,但 Infeed 作業之間必須有總順序。舉例來說,以下程式碼中的兩個 Infeed 具有總順序,因為 while 迴圈之間存在依附元件。
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
系統不支援巢狀元組形狀。如果是空元組形狀,Infeed 作業實際上是無作業,會繼續進行,不會從裝置的 Infeed 讀取任何資料。
如需 StableHLO 相關資訊,請參閱這篇文章。
器皿打擊樂
另請參閱
XlaBuilder::Iota。
Iota(shape, iota_dimension)
在裝置上建構常數常值,而非可能很大的主機轉移。建立具有指定形狀的陣列,並從零開始沿指定維度遞增值。如果是浮點類型,產生的陣列相當於 ConvertElementType(Iota(...)),其中 Iota 是整數類型,轉換作業則是轉換為浮點類型。
| 引數 | 類型 | 語意 |
|---|---|---|
shape |
Shape |
Iota() 建立的陣列形狀 |
iota_dimension |
int64 |
要遞增的維度。 |
舉例來說,Iota(s32[4, 8], 0) 會傳回
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
可退貨 (費用:Iota(s32[4, 8], 1))
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
如需 StableHLO 相關資訊,請參閱「StableHLO - iota」。
IsFinite
另請參閱
XlaBuilder::IsFinite。
測試 operand 的每個元素是否為有限值,也就是不是正無限大或負無限大,也不是 NaN。傳回 PRED 值陣列,形狀與輸入內容相同,其中每個元素都是 true,但對應的輸入元素必須是有限值。
IsFinite(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
如需 StableHLO 資訊,請參閱「StableHLO - is_finite」。
記錄
另請參閱
XlaBuilder::Log。
元素級別自然對數 x -> ln(x)。
Log(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
記錄也支援選用的 result_accuracy 引數:
Log(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
如需 StableHLO 資訊,請參閱「StableHLO - log」。
Log1p
另請參閱
XlaBuilder::Log1p。
逐一元素移位的自然對數 x -> ln(1+x)。
Log1p(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Log1p 也支援選用的 result_accuracy 引數:
Log1p(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
如需 StableHLO 資訊,請參閱「StableHLO - log_plus_one」。
Logistic
另請參閱
XlaBuilder::Logistic。
計算元素級別的邏輯函式 x -> logistic(x)。
Logistic(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Logistic 也支援選用的 result_accuracy 引數:
Logistic(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
如需 StableHLO 資訊,請參閱 StableHLO - logistic。
地圖
另請參閱
XlaBuilder::Map。
Map(operands..., computation, dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
operands |
N XlaOp 的序列 |
N 個 T0..T{N-1} 型別的陣列 |
computation
|
XlaComputation
|
型別 T_0, T_1,
.., T_{N + M -1} -> S 的計算,其中 N 個參數的型別為 T,M 個參數的型別為任意型別。 |
dimensions |
int64 陣列 |
地圖尺寸陣列 |
static_operands
|
N XlaOps 序列
|
地圖作業的靜態作業 |
對指定 operands 陣列套用純量函式,產生相同維度的陣列,其中每個元素都是套用至輸入陣列中對應元素的對應函式結果。
對應函式是任意計算,但限制是必須有 N 個純量型別 T 的輸入,以及一個型別為 S 的輸出。輸出內容的維度與運算元相同,但元素類型 T 會替換為 S。
舉例來說,Map(op1, op2, op3, computation, par1) 會在輸入陣列的每個 (多維) 索引中對應 elem_out <-
computation(elem1, elem2, elem3, par1),以產生輸出陣列。
如需 StableHLO 相關資訊,請參閱「StableHLO - map」。
最大值
另請參閱
XlaBuilder::Max。
對張量 lhs 和 rhs 執行元素級別的 max 運算。
Max(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Max 另有替代版本,支援不同維度的播送:
Max(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱「StableHLO - maximum」。
最小值
另請參閱
XlaBuilder::Min。
對 lhs 和 rhs 執行元素級別的 min 運算。
Min(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Min 有替代變體,支援不同維度的廣播:
Min(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱「StableHLO - minimum」。
Mul
另請參閱
XlaBuilder::Mul。
執行 lhs 和 rhs 的元素乘積。
Mul(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Mul 有替代變體,支援不同維度的播送:
Mul(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱「StableHLO - multiply」。
Neg
另請參閱
XlaBuilder::Neg。
元素層級的否定 x -> -x。
Neg(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
如需 StableHLO 資訊,請參閱「StableHLO - negate」。
否
另請參閱
XlaBuilder::Not。
元素級別邏輯 NOT x -> !(x)。
Not(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
如需 StableHLO 資訊,請參閱「StableHLO - not」。
OptimizationBarrier
另請參閱
XlaBuilder::OptimizationBarrier。
禁止任何最佳化傳遞作業跨越障礙移動運算。
OptimizationBarrier(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
確保在任何依附於屏障輸出內容的運算子之前,評估所有輸入內容。
如需 StableHLO 資訊,請參閱「StableHLO - optimization_barrier」。
或
另請參閱
XlaBuilder::Or。
對 lhs 和 rhs 執行元素 OR 運算。
Or(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Or 有替代變體,支援不同維度的播送:
Or(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱StableHLO - or。
Outfeed
另請參閱
XlaBuilder::Outfeed。
將輸入內容寫入輸出饋給。
Outfeed(operand, shape_with_layout, outfeed_config)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
型別 T 的陣列 |
shape_with_layout |
Shape |
定義轉移資料的版面配置 |
outfeed_config |
string |
Outfeed 指令的設定常數 |
shape_with_layout 會傳達我們想要輸出的版面配置形狀。
如需 StableHLO 相關資訊,請參閱「StableHLO - outfeed」。
熱敷墊
另請參閱
XlaBuilder::Pad。
Pad(operand, padding_value, padding_config)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
型別 T 的陣列 |
padding_value
|
XlaOp
|
T 型別的純量,用於填入新增的邊框間距 |
padding_config
|
PaddingConfig
|
兩側的邊框間距量 (低、高),以及每個維度元素之間的邊框間距 |
擴展指定的 operand 陣列,方法是在陣列周圍以及陣列元素之間,填入指定的 padding_value。padding_config
指定每個維度的邊緣邊框間距和內部邊框間距量。
PaddingConfig 是 PaddingConfigDimension 的重複欄位,其中包含每個維度的三個欄位:edge_padding_low、edge_padding_high 和 interior_padding。
edge_padding_low 和 edge_padding_high 分別指定在每個維度的低端 (索引 0 旁) 和高端 (最高索引旁) 新增的邊框間距量。邊緣邊框間距量可以是負值,負邊框間距的絕對值表示要從指定維度移除的元素數量。
interior_padding 會指定在每個維度中,任意兩個元素之間新增的邊框間距量,不得為負值。內部邊框間距在邏輯上會先於邊緣邊框間距,因此如果邊緣邊框間距為負值,系統會從內部邊框間距的運算元中移除元素。
如果邊緣邊框間距配對全為 (0, 0),且內部邊框間距值全為 0,這項作業就不會執行任何動作。下圖顯示二維陣列的不同 edge_padding 和 interior_padding 值範例。
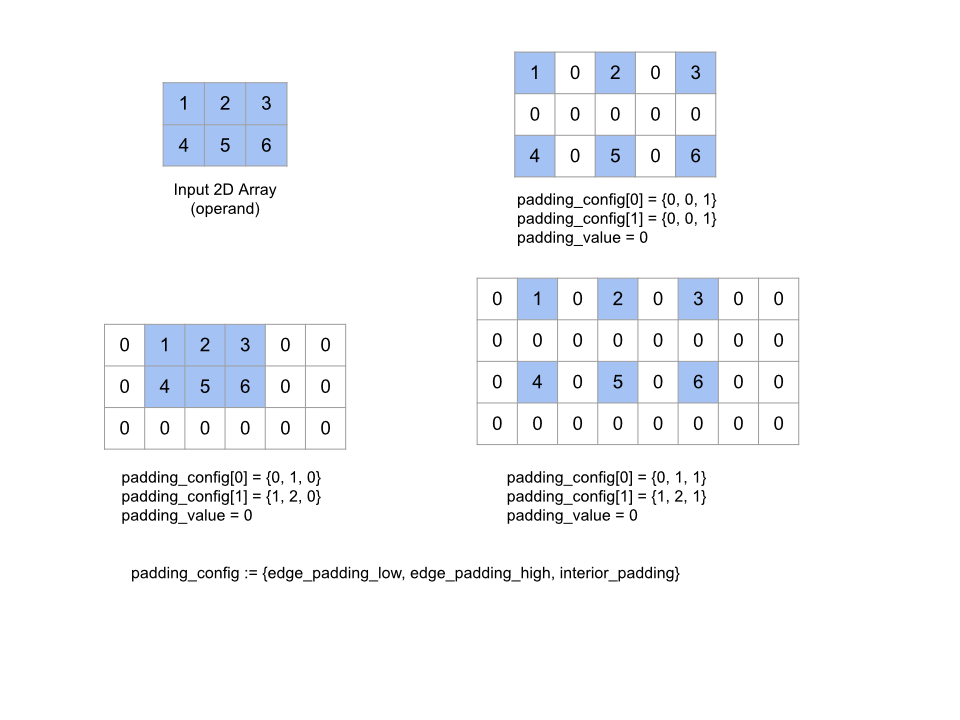
如需 StableHLO 資訊,請參閱「StableHLO - pad」。
參數
另請參閱
XlaBuilder::Parameter。
Parameter 代表運算的引數輸入。
PartitionID
另請參閱
XlaBuilder::BuildPartitionId。
產生目前程序的 partition_id。
PartitionID(shape)
| 引數 | 類型 | 語意 |
|---|---|---|
shape |
Shape |
資料形狀 |
PartitionID 可能會出現在 HLO 傾印中,但使用者不應手動建構。
如需 StableHLO 相關資訊,請參閱「StableHLO - partition_id」。
PopulationCount
另請參閱
XlaBuilder::PopulationCount。
計算 operand 每個元素中設定的位元數。
PopulationCount(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
如需 StableHLO 資訊,請參閱「StableHLO - popcnt」。
Pow
另請參閱
XlaBuilder::Pow。
對 lhs 執行元素層級的 rhs 次方運算。
Pow(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Pow 另有支援不同維度廣播的替代變體:
Pow(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱「StableHLO - power」。
真的
另請參閱
XlaBuilder::Real。
複數 (或實數) 形狀的元素級實部。x -> real(x)。如果運算元是浮點類型,Real 會傳回相同的值。
Real(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
如需 StableHLO 資訊,請參閱StableHLO - real。
Recv
另請參閱
XlaBuilder::Recv。
Recv、RecvWithTokens 和 RecvToHost 是 HLO 中的通訊基本類型作業。這些作業通常會出現在 HLO 傾印中,做為低階輸入/輸出或跨裝置轉移的一部分,但最終使用者不應手動建構這些作業。
Recv(shape, handle)
| 引數 | 類型 | 語意 |
|---|---|---|
shape |
Shape |
要接收的資料形狀 |
handle |
ChannelHandle |
每個傳送/接收配對的專屬 ID |
從另一個運算中的 Send 指令接收指定形狀的資料,這些運算共用相同的管道控制代碼。傳回接收資料的 XlaOp。
如需 StableHLO 資訊,請參閱「StableHLO - recv」。
RecvDone
另請參閱HloInstruction::CreateRecv和 HloInstruction::CreateRecvDone。
與 Send 類似,Recv 作業的用戶端 API 代表同步通訊。不過,這項指令會在內部分解為 2 個 HLO 指令 (Recv 和 RecvDone),以啟用非同步資料傳輸。
Recv(const Shape& shape, int64 channel_id)
分配從具有相同 channel_id 的 Send 指令接收資料所需的資源。傳回已分配資源的內容,後續的 RecvDone 指令會使用這個內容,等待資料傳輸完成。內容是 {接收緩衝區 (形狀)、要求 ID (U32)} 的元組,且只能由 RecvDone 指令使用。
指定由 Recv 指令建立的內容,等待資料傳輸完成並傳回收到的資料。
遏止
另請參閱
XlaBuilder::Reduce。
將縮減函式平行套用至一或多個陣列。
Reduce(operands..., init_values..., computation, dimensions_to_reduce)
| 引數 | 類型 | 語意 |
|---|---|---|
operands
|
N 的序列 XlaOp
|
N 個 T_0,...,
T_{N-1} 類型的陣列。 |
init_values
|
N 的序列 XlaOp
|
N 個型別的純量
T_0,..., T_{N-1}。 |
computation
|
XlaComputation
|
類型為
T_0,..., T_{N-1}, T_0,
...,T_{N-1} ->
Collate(T_0,...,
T_{N-1}) 的計算。 |
dimensions_to_reduce
|
int64 陣列
|
要縮減的維度無序陣列。 |
其中:
- N 必須大於或等於 1。
- 計算必須「大致」具有結合性 (請參閱下文)。
- 所有輸入陣列的維度必須相同。
- 所有初始值都必須在
computation下形成身分。 - 如果
N = 1,Collate(T)為T。 - 如果
N > 1,Collate(T_0, ..., T_{N-1})是T類型的N元素元組。
這項作業會將每個輸入陣列的一或多個維度縮減為純量。
每個傳回的陣列維度數量為 number_of_dimensions(operand) - len(dimensions)。運算元的輸出內容為 Collate(Q_0, ..., Q_N),其中 Q_i 是 T_i 類型的陣列,維度如下所述。
不同的後端可以重新關聯縮減運算。這可能會導致數值差異,因為加法等部分縮減函式不適用於浮點數。不過,如果資料範圍有限,浮點數加法就足以在大多數實用用途中成為關聯。
如需 StableHLO 資訊,請參閱「StableHLO - reduce」。
範例
在具有值 [10, 11,
12, 13] 的單一 1D 陣列中,使用縮減函式 f (這是 computation) 縮減一個維度時,可以計算為
f(10, f(11, f(12, f(init_value, 13)))
但也有許多其他可能性,例如:
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
以下是簡略的虛擬程式碼範例,說明如何實作縮減作業,並以加總做為縮減計算,初始值為 0。
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
以下是縮減 2D 陣列 (矩陣) 的範例。形狀有 2 個維度,維度 0 的大小為 2,維度 1 的大小為 3:
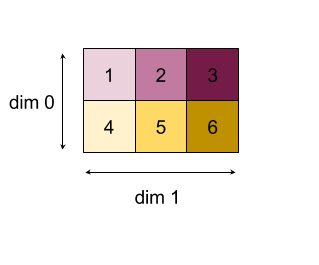
使用「add」函式縮減維度 0 或 1 的結果:
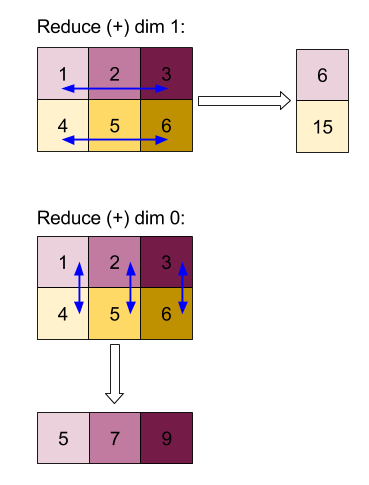
請注意,這兩個縮減結果都是 1D 陣列。為方便查看,圖表會將一個顯示為資料欄,另一個顯示為資料列。
如需更複雜的範例,請參閱以下 3D 陣列。維度數量為 3,維度 0 的大小為 4,維度 1 的大小為 2,維度 2 的大小為 3。為求簡單,值 1 到 6 會在維度 0 中複製。
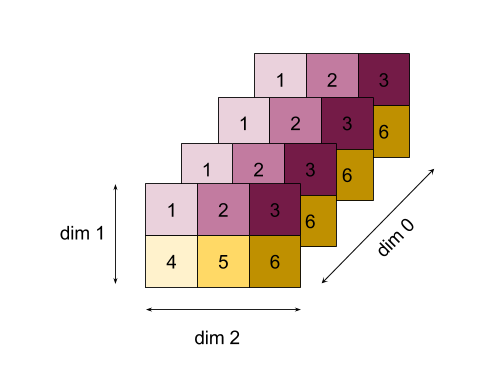
與 2D 範例類似,我們只能縮減一個維度。舉例來說,如果我們縮減維度 0,就會得到 2 維陣列,其中維度 0 的所有值都會摺疊成純量:
| 4 8 12 |
| 16 20 24 |
如果我們縮減維度 2,也會得到 2 維陣列,其中維度 2 的所有值都會摺疊成純量:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
請注意,輸入中其餘維度之間的相對順序會保留在輸出中,但部分維度可能會獲派新編號 (因為維度數量會變更)。
我們也可以減少多個維度。將維度 0 和 1 相加,會產生一維陣列 [20, 28, 36]。
在所有維度中縮減 3D 陣列,會產生純量 84。
Variadic Reduce
如果是 N > 1,由於會同時套用至所有輸入內容,因此縮減函式應用程式會稍微複雜一些。運算元會依下列順序提供給運算:
- 第一個運算元的遞減值
- ...
- 為第 N 個運算元執行縮減值
- 第一個運算元的輸入值
- ...
- 第 N 個運算元的輸入值
舉例來說,請看下列縮減函式,可用於平行計算 1 維陣列的最大值和 argmax:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
如果是 1 維輸入陣列 V = Float[N], K = Int[N] 和初始值 I_V = Float, I_K = Int,則在唯一輸入維度中縮減的結果 f_(N-1),等同於下列遞迴應用程式:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
將這項縮減套用至值陣列和連續索引陣列 (即 iota),即可共同疊代陣列,並傳回包含最大值和相符索引的元組。
ReducePrecision
另請參閱
XlaBuilder::ReducePrecision。
模擬將浮點值轉換為低精確度格式 (例如 IEEE-FP16),然後再轉換回原始格式的效果。您可以任意指定低精確度格式中的指數和尾數位元數,但並非所有硬體實作項目都支援所有位元大小。
ReducePrecision(operand, exponent_bits, mantissa_bits)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
浮點類型 T 的陣列。 |
exponent_bits |
int32 |
低精確度格式的指數位元數 |
mantissa_bits |
int32 |
低精確度格式中的尾數位元數 |
結果是 T 類型的陣列。輸入值會四捨五入至最接近的值,並以指定數量的尾數位元表示 (使用「ties to even」語意),而超出指數位元數量指定範圍的任何值,都會箝制為正無限大或負無限大。NaN 值,但可能會轉換為標準 NaN 值。
低精確度格式必須至少有一個指數位元 (為了區分零值和無限大,因為兩者都有零尾數),且尾數位元數不得為負數。指數或尾數的位元數可能超過型別 T 的對應值;轉換的對應部分隨後只會是無運算。
如需 StableHLO 資訊,請參閱「StableHLO - reduce_precision」。
ReduceScatter
另請參閱
XlaBuilder::ReduceScatter。
ReduceScatter 是一種集體作業,可有效執行 AllReduce,然後沿著副本群組中的 scatter_dimension 和副本 i,將結果分割成 shard_count 個區塊,並分散結果,副本 i 會收到 ith 分片。
ReduceScatter(operand, computation, scatter_dimension, shard_count,
replica_groups, channel_id, layout, use_global_device_ids)
| 引數 | 類型 | 語意 |
|---|---|---|
operand
|
XlaOp
|
要跨副本縮減的陣列或非空白陣列元組。 |
computation |
XlaComputation |
減免計算 |
scatter_dimension |
int64 |
要分散的維度。 |
shard_count
|
int64
|
要分割的區塊數量
scatter_dimension |
replica_groups
|
ReplicaGroup vector
|
執行縮減作業的群組 |
channel_id
|
選填
ChannelHandle |
跨模組通訊的選用管道 ID |
layout
|
選填 Layout
|
使用者指定的記憶體配置 |
use_global_device_ids |
選填 bool |
使用者指定的旗標 |
- 如果
operand是陣列的元組,則會對元組的每個元素執行縮減分散作業。 replica_groups是要執行縮減作業的副本群組清單 (可以使用ReplicaId擷取目前副本的副本 ID)。各群組中的副本順序會決定 all-reduce 結果的散布順序。replica_groups必須為空白 (所有副本都屬於單一群組),或包含與副本數量相同的元素。如果有多個副本群組,大小必須相同。舉例來說,replica_groups = {0, 2}, {1, 3}會在副本0和2之間執行縮減作業,以及1和3,然後分散結果。shard_count是每個副本群組的大小。如果replica_groups為空白,則必須提供這項資訊。如果replica_groups不為空,shard_count必須等於每個副本群組的大小。channel_id用於跨模組通訊:只有具有相同channel_id的reduce-scatter作業才能彼此通訊。layout如要進一步瞭解版面配置,請參閱 xla::shapes。use_global_device_ids是使用者指定的旗標。當false(預設)replica_groups中的數字是ReplicaId時,truereplica_groups代表 (ReplicaID*partition_count+partition_id) 的全域 ID。舉例來說:- 如果使用 2 個副本和 4 個分割區,
- replica_groups={ {0,1,4,5},{2,3,6,7} } and use_global_device_ids=true
- group[0] = (0,0), (0,1), (1,0), (1,1)
- group[1] = (0,2), (0,3), (1,2), (1,3)
- 其中每對都是 (replica_id, partition_id)。
輸出形狀是輸入形狀,但縮小了 scatter_dimension 倍。shard_count舉例來說,如果有兩個副本,而運算元在兩個副本上的值分別為 [1.0, 2.25] 和 [3.0, 5.25],則這個運算元的輸出值 (其中 scatter_dim 為 0) 會是第一個副本的 [4.0] 和第二個副本的 [7.5]。
如需 StableHLO 資訊,請參閱「StableHLO - reduce_scatter」。
ReduceScatter - 範例 1 - StableHLO
在上述範例中,有 2 個副本參與 ReduceScatter。 在每個副本上,運算元的形狀為 f32[2,4]。系統會在副本之間執行全縮減 (總和),在每個副本上產生形狀為 f32[2,4] 的縮減值。這個縮減值隨後會沿著維度 1 分成 2 個部分,因此每個部分的形狀為 f32[2,2]。程序群組中的每個副本都會收到與其在群組中的位置相應的部分。因此,每個副本的輸出內容形狀為 f32[2,2]。
ReduceWindow
另請參閱
XlaBuilder::ReduceWindow。
將縮減函式套用至 N 個多維度陣列序列中每個時間區間的所有元素,並產生單一或 N 個多維度陣列的元組做為輸出。每個輸出陣列的元素數量,與視窗的有效位置數量相同。集區層可以表示為 ReduceWindow。與 Reduce 類似,套用的 computation 一律會傳遞至左側的 init_values。
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| 引數 | 類型 | 語意 |
|---|---|---|
operands
|
N XlaOps
|
N 個多維度陣列的序列,類型為 T_0,..., T_{N-1},每個陣列代表放置視窗的基礎區域。 |
init_values
|
N XlaOps
|
縮減作業的 N 個起始值,每個運算元各有一個。詳情請參閱「調降」。 |
computation
|
XlaComputation
|
T_0,
..., T_{N-1}, T_0, ..., T_{N-1}
-> Collate(T_0, ..., T_{N-1}) 型別的縮減函式,用於套用至所有輸入運算元每個視窗中的元素。 |
window_dimensions
|
ArraySlice<int64>
|
視窗維度值的整數陣列 |
window_strides
|
ArraySlice<int64>
|
視窗步幅值的整數陣列 |
base_dilations
|
ArraySlice<int64>
|
基底的整數陣列 擴張值 |
window_dilations
|
ArraySlice<int64>
|
視窗擴張值的整數陣列 |
padding
|
Padding
|
視窗的邊框間距類型 (Padding::kSame,可填補邊框間距,使輸出形狀與輸入形狀相同 (如果步幅為 1),或 Padding::kValid,不使用邊框間距,並在視窗不再符合時「停止」視窗) |
其中:
- N 必須大於或等於 1。
- 所有輸入陣列的維度必須相同。
- 如果
N = 1,Collate(T)為T。 - 如果
N > 1,Collate(T_0, ..., T_{N-1})是(T0,...T{N-1})類型的N元素元組。
如需 StableHLO 資訊,請參閱「StableHLO - reduce_window」。
ReduceWindow - 範例 1
輸入內容是 [4x6] 大小的矩陣,window_dimensions 和 window_stride_dimensions 都是 [2x3]。
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
維度中的步幅為 1,表示視窗在維度中的位置與相鄰視窗相差 1 個元素。如要指定視窗彼此不重疊,window_stride_dimensions 應等於 window_dimensions。下圖說明如何使用兩種不同的步幅值。系統會對輸入內容的每個維度套用邊框間距,計算方式與輸入內容在套用邊框間距後具有的維度相同。
如要查看非簡單的填補範例,請考慮計算輸入陣列 [10000, 1000, 100, 10, 1] 的縮減視窗最小值 (初始值為 MAX_FLOAT),維度為 3,步幅為 2。Padding kValid 會計算兩個有效視窗的最小值:[10000, 1000, 100] 和 [100, 10, 1],並產生輸出 [100, 1]。Padding kSame 會先填補陣列,讓縮減視窗後的形狀與步幅為一的輸入內容相同,方法是在兩側新增初始元素,得到 [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE]。在經過填補的陣列上執行 reduce-window,會對三個視窗 [MAX_VALUE, 10000, 1000]、[1000, 100, 10]、[10, 1, MAX_VALUE] 進行運算,並產生 [1000, 10, 1]。
縮減函式的評估順序是任意的,可能不具決定性。因此,縮減函式不應對重新關聯過於敏感。詳情請參閱Reduce 關聯性討論。
ReduceWindow - 範例 2 - StableHLO
在上述範例中:
輸入) 運算元的輸入形狀為 S32[3,2]。值為
[[1,2],[3,4],[5,6]]
步驟 1) 沿著列維度以係數 2 為基礎擴張,在運算元的每一列之間插入洞。膨脹後,頂端會套用 2 列的邊框間距,底部則套用 1 列。因此張量會變高。
步驟 2) 定義形狀為 [2,1] 的視窗,視窗擴張為 [3,1]。也就是說,每個視窗都會從同一欄選取兩個元素,但第二個元素會取自第一個元素下方三列的位置,而不是直接取自下方。
步驟 3) 接著,視窗會以步幅 [4,1] 滑過運算元。這會導致視窗一次向下移動四列,同時水平移動一欄。填補儲存格會填入 init_value (本例為 init_value = 0)。系統會忽略「落入」擴張儲存格的值。由於步幅和填補,有些視窗只會重疊零和洞,而其他視窗則會重疊實際輸入值。
步驟 4) 在每個視窗中,系統會使用縮減函式 (a, b) → a + b 合併元素,初始值為 0。最上方的兩個視窗只會看到邊框間距和洞孔,因此結果為 0。底部視窗會從輸入內容擷取值 3 和 4,並將這些值做為結果傳回。
結果) 最終輸出內容的形狀為 S32[2,2],值為:[[0,0],[3,4]]
Rem
另請參閱
XlaBuilder::Rem。
執行被除數 lhs 和除數 rhs 的元素餘數。
結果的正負號與被除數相同,且結果的絕對值一律小於除數的絕對值。
Rem(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Rem 有替代版本,支援不同維度的廣播:
Rem(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱「StableHLO - remainder」。
ReplicaId
另請參閱
XlaBuilder::ReplicaId。
傳回副本的專屬 ID (U32 純量)。
ReplicaId()
每個副本的專屬 ID 都是 [0, N) 間隔內的無符號整數,其中 N 是副本數量。由於所有副本都執行相同的程式,因此程式中的 ReplicaId() 呼叫會在每個副本上傳回不同的值。
如需 StableHLO 資訊,請參閱「StableHLO - replica_id」。
重塑
另請參閱
XlaBuilder::Reshape。
和 Collapse 作業。
將陣列的維度重塑為新的設定。
Reshape(operand, dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
類型為 T 的陣列 |
dimensions |
int64 向量 |
新維度的向量大小 |
從概念上來說,reshape 會先將陣列扁平化為一維資料值向量,然後將這個向量精簡為新形狀。輸入引數是任意 T 型別的陣列、維度索引的編譯時間常數向量,以及結果的維度大小的編譯時間常數向量。dimensions 向量會決定輸出陣列的大小。dimensions 中索引 0 的值是維度 0 的大小,索引 1 的值是維度 1 的大小,依此類推。dimensions 維度的乘積必須等於運算元維度大小的乘積。將摺疊陣列精簡為 dimensions 定義的多維度陣列時,dimensions 中的維度會依變化速度排序,從最慢 (最主要) 到最快 (最次要)。
舉例來說,假設 v 是含有 24 個元素的陣列:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
在特殊情況下,reshape 可以將單一元素陣列轉換為純量,反之亦然。例如:
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
如需 StableHLO 資訊,請參閱「StableHLO - reshape」。
Reshape (明確)
另請參閱
XlaBuilder::Reshape。
Reshape(shape, operand)
使用明確目標形狀的 Reshape 作業。
| 引數 | 類型 | 語意 |
|---|---|---|
shape |
Shape |
類型 T 的輸出形狀 |
operand |
XlaOp |
類型為 T 的陣列 |
Rev (反向)
另請參閱
XlaBuilder::Rev。
Rev(operand, dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
類型為 T 的陣列 |
dimensions |
ArraySlice<int64> |
要反轉的維度 |
沿指定維度反轉 operand 陣列中的元素順序,產生形狀相同的輸出陣列。dimensions多維度索引處的運算元陣列中每個元素,都會儲存到轉換索引處的輸出陣列。多維度索引會經過轉換,方法是反轉每個要反轉的維度中的索引 (也就是說,如果大小為 N 的維度是反轉維度之一,其索引 i 會轉換為 N - 1 - i)。
Rev 運算的一項用途,是在類神經網路的梯度計算期間,沿著兩個視窗維度反轉迴旋權重陣列。
如需 StableHLO 資訊,請參閱「StableHLO - reverse」。
RngNormal
另請參閱
XlaBuilder::RngNormal。
建構指定形狀的輸出內容,並以 \(N(\mu, \sigma)\) 常態分布產生隨機數字。參數 \(\mu\) 和 \(\sigma\),以及輸出形狀,都必須具有浮點元素類型。此外,參數必須是純量值。
RngNormal(mu, sigma, shape)
| 引數 | 類型 | 語意 |
|---|---|---|
mu |
XlaOp |
類型為 T 的純量,指定產生的數字平均值 |
sigma
|
XlaOp
|
指定所產生隨機變數標準差的 T 型純量 |
shape |
Shape |
類型 T 的輸出形狀 |
如需 StableHLO 資訊,請參閱「StableHLO - rng」。
RngUniform
另請參閱
XlaBuilder::RngUniform。
使用在間隔 \([a,b)\)內依據均勻分布產生的隨機數字,建構指定形狀的輸出內容。參數和輸出元素類型必須是布林值、整數或浮點類型,且類型必須一致。CPU 和 GPU 後端目前僅支援 F64、F32、F16、BF16、S64、U64、S32 和 U32。此外,參數必須是純量值。如果 \(b <= a\) 結果是實作定義。
RngUniform(a, b, shape)
| 引數 | 類型 | 語意 |
|---|---|---|
a |
XlaOp |
類型 T 的純量,指定間隔的下限 |
b |
XlaOp |
指定間隔上限的 T 型純量 |
shape |
Shape |
類型 T 的輸出形狀 |
如需 StableHLO 資訊,請參閱「StableHLO - rng」。
RngBitGenerator
另請參閱
XlaBuilder::RngBitGenerator。
使用指定的演算法 (或後端預設值) 產生輸出內容,其中填入形狀相同的隨機位元,並傳回更新後的狀態 (與初始狀態的形狀相同) 和產生的隨機資料。
初始狀態是目前隨機數產生作業的初始狀態。這項屬性以及必要形狀和有效值取決於所用的演算法。
輸出內容保證是初始狀態的決定性函式,但不保證在後端和不同編譯器版本之間具有決定性。
RngBitGenerator(algorithm, initial_state, shape)
| 引數 | 類型 | 語意 |
|---|---|---|
algorithm |
RandomAlgorithm |
要使用的 PRNG 演算法。 |
initial_state |
XlaOp |
PRNG 演算法的初始狀態。 |
shape |
Shape |
生成資料的輸出形狀。 |
algorithm 的可用值:
rng_default:後端專屬演算法,具有後端專屬形狀需求。rng_three_fry:ThreeFry 計數器型 PRNG 演算法。initial_state形狀為u64[2],且具有任意值。Salmon et al. SC 2011. 平行隨機數:簡單 3 步驟即可完成。rng_philox:Philox 演算法,可平行產生隨機數字。initial_state形狀為u64[3],且具有任意值。Salmon et al. SC 2011. 平行隨機數:簡單 3 步驟即可完成。
如需 StableHLO 相關資訊,請參閱「StableHLO - rng_bit_generator」。
RngGetAndUpdateState
另請參閱
HloInstruction::CreateRngGetAndUpdateState。
各種 Rng 作業的 API 會在內部分解為 HLO 指令,包括 RngGetAndUpdateState。
RngGetAndUpdateState 做為 HLO 中的原始項目。這個作業可能會出現在 HLO 傾印中,但使用者不應手動建構。
回合
另請參閱
XlaBuilder::Round。
逐一對元素進行四捨五入,並捨去與零的距離。
Round(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
RoundNearestAfz
另請參閱
XlaBuilder::RoundNearestAfz。
執行元素層級的四捨五入,將值捨入至最接近的整數,並將中間值捨入至遠離零的值。
RoundNearestAfz(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
如需 StableHLO 資訊,請參閱「StableHLO - round_nearest_afz」。
RoundNearestEven
另請參閱
XlaBuilder::RoundNearestEven。
逐一捨入元素,捨入至最接近的偶數。
RoundNearestEven(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
如需 StableHLO 資訊,請參閱「StableHLO - round_nearest_even」。
Rsqrt
另請參閱
XlaBuilder::Rsqrt。
元素級別的平方根倒數運算 x -> 1.0 / sqrt(x)。
Rsqrt(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Rsqrt 也支援選用 result_accuracy 引數:
Rsqrt(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
如需 StableHLO 資訊,請參閱「StableHLO - rsqrt」。
掃描
另請參閱
XlaBuilder::Scan。
將縮減函式套用至指定維度的陣列,產生最終狀態和中繼值陣列。
Scan(inputs..., inits..., to_apply, scan_dimension,
is_reverse, is_associative)
| 引數 | 類型 | 語意 |
|---|---|---|
inputs |
m XlaOp 序列 |
要掃描的陣列。 |
inits |
k XlaOp 序列 |
初始運送。 |
to_apply |
XlaComputation |
類型 i_0, ..., i_{m-1}, c_0, ..., c_{k-1} -> (o_0, ..., o_{n-1}, c'_0, ..., c'_{k-1}) 的計算。 |
scan_dimension |
int64 |
要掃描的維度。 |
is_reverse |
bool |
如果為 true,則以反向順序掃描。 |
is_associative |
bool (三州) |
如果為 true,則作業為關聯。 |
函式 to_apply 會依序套用至 inputs 中的元素,並沿著 scan_dimension。如果 is_reverse 為 false,系統會依序處理 0 到 N-1 的元素,其中 N 是 scan_dimension 的大小。如果 is_reverse 為 true,系統會從 N-1 開始處理元素,直到 0 為止。
to_apply 函式會採用 m + k 運算元:
m目前的元素來自inputs。k從上一個步驟 (或第一個元素的inits) 攜帶值。
to_apply 函式會傳回 n + k 值的元組:
n元素。outputsk個新的結轉值。
掃描作業會產生 n + k 值的元組:
n輸出陣列,包含每個步驟的輸出值。- 處理完所有元素後,最終
k攜帶值。
m 輸入內容的型別必須與 to_apply 的第一個 m 參數型別相符,並加上額外的掃描維度。n 輸出的型別必須與 to_apply 的第一個 n 傳回值型別相符,並加上額外的掃描維度。所有輸入和輸出內容的額外掃描維度大小必須相同,即 N。最後一個 k 參數和 to_apply 的傳回值類型,以及 k 初始值必須相符。
舉例來說 (m, n, k == 1, N == 3),如要進行初始進位 i,請輸入 [a, b, c]、函式 f(x, c) -> (y, c') 和 scan_dimension=0、is_reverse=false:
- 步驟 0:
f(a, i) -> (y0, c0) - 步驟 1:
f(b, c0) -> (y1, c1) - 步驟 2:
f(c, c1) -> (y2, c2)
Scan 的輸出內容為 ([y0, y1, y2], c2)。
散布圖
另請參閱
XlaBuilder::Scatter。
XLA 散佈作業會產生一連串結果,這些結果是輸入陣列 operands 的值,其中有幾個切片 (位於 scatter_indices 指定的索引) 會使用 update_computation,以 updates 中的值序列更新。
Scatter(operands..., scatter_indices, updates..., update_computation,
dimension_numbers, indices_are_sorted, unique_indices)
| 引數 | 類型 | 語意 |
|---|---|---|
operands |
N 序列 XlaOp |
要分散至其中的 N 個型別 T_0, ..., T_N 的陣列。 |
scatter_indices |
XlaOp |
陣列,內含必須分散到的切片起始索引。 |
updates |
N 序列 XlaOp |
N 個 T_0, ..., T_N 類型的陣列。updates[i] 包含用於分散 operands[i] 的值。 |
update_computation |
XlaComputation |
用於合併輸入陣列中的現有值,以及分散期間的更新。這項計算應為 T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N) 類型。 |
index_vector_dim |
int64 |
包含起始索引的 scatter_indices 維度。 |
update_window_dims |
ArraySlice<int64> |
updates形狀中的維度集,即視窗維度。 |
inserted_window_dims |
ArraySlice<int64> |
必須插入 updates 形狀的視窗尺寸組合。 |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
從分散索引到運算元索引空間的維度對應。這個陣列會解讀為將 i 對應至 scatter_dims_to_operand_dims[i]。必須是一對一的完整對應。 |
dimension_number |
ScatterDimensionNumbers |
分散作業的維度編號 |
indices_are_sorted |
bool |
索引是否保證由呼叫端排序。 |
unique_indices |
bool |
呼叫端是否保證索引不重複。 |
其中:
- N 必須大於或等於 1。
operands[0]、...、operands[N-1] 的尺寸必須相同。updates[0]、...、updates[N-1] 的尺寸必須相同。- 如果
N = 1,Collate(T)為T。 - 如果
N > 1,Collate(T_0, ..., T_N)是T類型的N元素元組。
如果 index_vector_dim 等於 scatter_indices.rank,我們會隱含地將 scatter_indices 視為具有尾端 1 維度。
我們將 updates 形狀中不在 update_window_dims 的維度集定義為 update_scatter_dims,並以遞增順序排列。update_scatter_dims 的型別為 ArraySlice<int64>。
scatter 的引數應遵循下列限制:
每個
updates陣列都必須有update_window_dims.size + scatter_indices.rank - 1個維度。每個
updates陣列中維度i的界限必須符合下列條件:- 如果
i存在於update_window_dims中 (即等於某個k的update_window_dims[k]),則updates中維度i的界限不得超過operand的相應界限 (扣除inserted_window_dims後,即adjusted_window_bounds[k],其中adjusted_window_bounds包含operand的界限,且已移除索引inserted_window_dims的界限)。 - 如果
i存在於update_scatter_dims中 (即等於某個k的update_scatter_dims[k]),則updates中維度i的界限必須等於scatter_indices的對應界限,並略過index_vector_dim(即scatter_indices.shape.dims[k],如果k<index_vector_dim,否則為scatter_indices.shape.dims[k+1])。
- 如果
update_window_dims必須為遞增排序,不得有任何重複的維度編號,且須在[0, updates.rank)範圍內。inserted_window_dims必須為遞增排序,不得有任何重複的維度編號,且須在[0, operand.rank)範圍內。operand.rank必須等於update_window_dims.size和inserted_window_dims.size的總和。scatter_dims_to_operand_dims.size必須等於scatter_indices.shape.dims[index_vector_dim],且值必須介於[0, operand.rank)範圍內。
在每個 updates 陣列中,指定索引 U 時,對應的 operands 陣列中必須套用這項更新的索引 I 計算方式如下:
- 假設
G= {U[k] forkinupdate_scatter_dims}。使用G在scatter_indices陣列中查閱索引向量S,使S[i] =scatter_indices[Combine(G,i)],其中 Combine(A, b) 會將 b 插入 A 的index_vector_dim位置。 - 使用
scatter_dims_to_operand_dims地圖,將S散佈到operand中,藉此建立Sin的索引。S正式來說:Sin[scatter_dims_to_operand_dims[k]] =S[k] ifk<scatter_dims_to_operand_dims.size.Sin[_] =0,否則為0。
- 根據
inserted_window_dims,將U中的索引分散到update_window_dims,藉此在每個operands陣列中建立索引Win。正式來說:Win[window_dims_to_operand_dims(k)] =U[k] ifkis inupdate_window_dims, wherewindow_dims_to_operand_dimsis the monotonic function with domain [0,update_window_dims.size) and range [0,operand.rank) \inserted_window_dims. (舉例來說,如果update_window_dims.size是4,operand.rank是6,而inserted_window_dims是 {0,2},則window_dims_to_operand_dims是 {0→1,1→3,2→4,3→5})。Win[_] =0,否則為0。
I為Win+Sin,其中 + 是元素加法。
總而言之,散布作業可以定義如下。
- 使用
operands初始化output,也就是針對所有索引J,以及operands[J] 陣列中的所有索引O:
output[J][O] =operands[J][O] - 對於
updates[J] 陣列中的每個索引U,以及operand[J] 陣列中的對應索引O,如果O是output的有效索引:
(output[0][O], ...,output[N-1][O]) =update_computation(output[0][O], ..., ,output[N-1][O],updates[0][U], ...,updates[N-1][U])
更新的套用順序不確定。因此,當 updates 中的多個索引參照 operands 中的相同索引時,output 中的對應值會是不確定的。
請注意,傳遞至 update_computation 的第一個參數一律是 output 陣列中的目前值,第二個參數則一律是 updates 陣列中的值。如果 update_computation 不具交換律,這點就特別重要。
如果 indices_are_sorted 設為 true,XLA 可以假設 scatter_indices 是由使用者排序 (遞增順序,after 根據 scatter_dims_to_operand_dims 散佈其值)。如果不是,則語意是由實作定義。
如果 unique_indices 設為 true,XLA 可以假設分散的所有元素都是不重複的。因此 XLA 可以使用非不可分割的作業。如果 unique_indices 設為 true,且要分散的索引並非不重複,則語意是由實作定義。
非正式來說,散布運算子可以視為收集運算子的反向,也就是散布運算子會更新輸入內容中由對應收集運算子擷取的元素。
如需詳細的非正式說明和範例,請參閱 Gather 下方的「非正式說明」一節。
如需 StableHLO 資訊,請參閱「StableHLO - scatter」。
Scatter - 範例 1 - StableHLO
在上圖中,表格的每一列都是一個更新索引範例。讓我們從左側(更新索引) 到右側(結果索引) 逐步檢查:
輸入) input 的形狀為 S32[2,3,4,2]。scatter_indices 的形狀為 S64[2,2,3,2]。的形狀為 S32[2,2,3,1,2]。updates
更新索引) 做為我們收到的輸入內容 update_window_dims:[3,4]。這表示 updates 的 dim 3 和 dim 4 是視窗尺寸,以黃色醒目顯示。因此我們可以推導出 update_scatter_dims = [0,1,2]。
更新分散索引) 顯示每個項目的擷取 updated_scatter_dims。
(「更新索引」欄中非黃色的部分)
開始索引) 查看 scatter_indices 張量圖片,我們可以看到上一步 (更新分散索引) 的值,可提供開始索引的位置。從 index_vector_dim 我們也得知包含起始索引的 starting_indices 維度,也就是大小為 2 的維度 3。scatter_indices
完整開始索引) scatter_dims_to_operand_dims = [2,1] 表示索引向量的第一個元素會前往運算元維度 2。索引向量的第二個元素會傳送至運算元維度 1。剩餘的運算元維度會填入 0。
完整批次索引)。我們可以看到這個資料欄(完整批次索引)、更新分散索引資料欄和更新索引資料欄中,都顯示紫色醒目顯示區域。
全視窗索引),計算方式為 update_window_dimensions [3,4]。
結果索引)。在 operand 張量中加入完整開始索引、完整批次索引和完整視窗索引。請注意,綠色醒目顯示區域也對應 operand 圖。最後一列會遭到略過,因為該列超出 operand 張量範圍。
選取
另請參閱
XlaBuilder::Select。
根據述詞陣列的值,從兩個輸入陣列的元素建構輸出陣列。
Select(pred, on_true, on_false)
| 引數 | 類型 | 語意 |
|---|---|---|
pred |
XlaOp |
PRED 型別的陣列 |
on_true |
XlaOp |
類型為 T 的陣列 |
on_false |
XlaOp |
類型為 T 的陣列 |
陣列 on_true 和 on_false 的形狀必須相同。這也是輸出陣列的形狀。陣列 pred 的維度必須與 on_true 和 on_false 相同,且元素類型為 PRED。
對於 pred 的每個元素 P,如果 P 的值為 true,則輸出陣列的對應元素取自 on_true;如果 P 的值為 false,則取自 on_false。pred 是廣播的受限形式,可以是 PRED 類型的純量。在本例中,如果 pred 為 true,輸出陣列會完全取自 on_true;如果 pred 為 false,輸出陣列會完全取自 on_false。
非純量 pred 的範例:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
純量 pred 範例:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
支援元組之間的選取項目。就此目的而言,元組視為純量型別。如果 on_true 和 on_false 是元組 (必須具有相同形狀!),則 pred 必須是 PRED 類型的純量。
如需 StableHLO 資訊,請參閱 StableHLO - select
SelectAndScatter
另請參閱
XlaBuilder::SelectAndScatter。
這項作業可視為複合作業,首先會計算 ReduceWindow 陣列的 operand,從每個視窗選取元素,然後將 source 陣列分散至所選元素的索引,建構與運算元陣列形狀相同的輸出陣列。二進位 select 函式會套用至每個視窗,從中選取元素,並以第一個參數的索引向量在字典順序上小於第二個參數的索引向量的屬性呼叫。如果選取第一個參數,select 函式會傳回 true;如果選取第二個參數,則會傳回 false。此外,函式必須保留遞移性 (即如果 select(a, b) 和 select(b, c) 為 true,則 select(a, c) 也是 true),這樣所選元素就不會取決於特定視窗的元素遍歷順序。
函式 scatter 會套用至輸出陣列中的每個所選索引。並接受兩個純量參數:
- 輸出陣列中選定索引的目前值
- 適用於所選索引的
source散射值
這會合併兩個參數,並傳回用於更新輸出陣列中選定索引處值的純量值。輸出陣列的所有索引最初都會設為 init_value。
輸出陣列的形狀與 operand 陣列相同,且 source 陣列的形狀必須與對 operand 陣列套用 ReduceWindow 運算後產生的結果相同。SelectAndScatter 可用於類神經網路中,反向傳播集區層的梯度值。
SelectAndScatter(operand, select, window_dimensions, window_strides, padding,
source, init_value, scatter)
| 引數 | 類型 | 語意 |
|---|---|---|
operand
|
XlaOp
|
類型 T 的陣列,視窗會滑動此陣列 |
select
|
XlaComputation
|
T, T
-> PRED 類型的二進位運算,適用於每個視窗中的所有元素;如果選取第一個參數,則傳回 true,如果選取第二個參數,則傳回 false |
window_dimensions
|
ArraySlice<int64>
|
視窗維度值的整數陣列 |
window_strides
|
ArraySlice<int64>
|
視窗步幅值的整數陣列 |
padding
|
Padding
|
視窗的邊框間距類型 (Padding::kSame 或 Padding::kValid) |
source
|
XlaOp
|
要分散的值的 T 類型陣列 |
init_value
|
XlaOp
|
輸出陣列初始值的 T 型純量值 |
scatter
|
XlaComputation
|
T, T
-> T 類型的二進位運算,將每個分散來源元素套用至其目的地元素 |
下圖顯示使用 SelectAndScatter 的範例,其中 select 函式會計算參數中的最大值。請注意,當視窗重疊時 (如下圖 (2) 所示),不同視窗可能會多次選取 operand 陣列的索引。在圖中,值為 9 的元素會由頂端兩個視窗 (藍色和紅色) 選取,而二進位加法 scatter 函式會產生值為 8 (2 + 6) 的輸出元素。
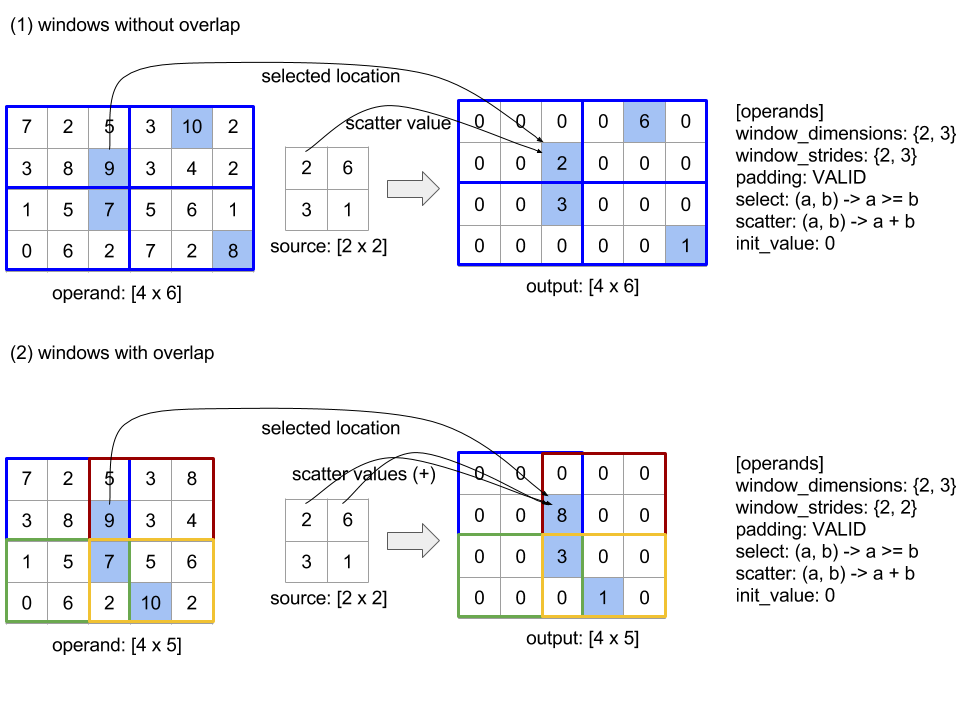
scatter 函式的評估順序是任意的,可能不具決定性。因此,scatter 函式不應對重新關聯過於敏感。詳情請參閱Reduce 關聯性討論。
如需 StableHLO 資訊,請參閱「StableHLO - select_and_scatter」。
傳送
另請參閱
XlaBuilder::Send。
Send、SendWithTokens 和 SendToHost 是 HLO 中的通訊基本類型作業。這些作業通常會出現在 HLO 傾印中,做為低階輸入/輸出或跨裝置轉移的一部分,但最終使用者不應手動建構這些作業。
Send(operand, handle)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
要傳送的資料 (T 類型的陣列) |
handle |
ChannelHandle |
每個傳送/接收配對的專屬 ID |
將指定的運算元資料傳送至另一個運算中的 Recv 指令,該指令共用相同的通道控制代碼。不會傳回任何資料。
與 Recv 作業類似,Send 作業的用戶端 API 代表同步通訊,且會在內部分解為 2 個 HLO 指令 (Send 和 SendDone),以啟用非同步資料轉移。另請參閱HloInstruction::CreateSend和HloInstruction::CreateSendDone。
Send(HloInstruction operand, int64 channel_id)
啟動運算元到 Recv 指令所分配資源的非同步轉移作業,並使用相同的通道 ID。傳回內容,後續的 SendDone 指令會使用此內容,等待資料傳輸完成。內容是 {運算元 (形狀)、要求 ID (U32)} 的元組,只能由 SendDone 指令使用。
如需 StableHLO 資訊,請參閱「StableHLO - send」。
SendDone
另請參閱
HloInstruction::CreateSendDone。
SendDone(HloInstruction context)
指定由 Send 指令建立的內容,等待資料移轉完成。指令不會傳回任何資料。
頻道指令排程
每個管道的 4 項指令 (Recv、RecvDone、Send、SendDone) 執行順序如下。
Recv發生在Send之前Send發生在RecvDone之前Recv發生在RecvDone之前Send發生在SendDone之前
後端編譯器為透過管道指令通訊的每個運算產生線性排程時,運算之間不得有週期。舉例來說,下列排程會導致死結。
SetDimensionSize
另請參閱
XlaBuilder::SetDimensionSize。
設定 XlaOp 指定維度的動態大小。運算元必須是陣列形狀。
SetDimensionSize(operand, val, dimension)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
n 維輸入陣列。 |
val |
XlaOp |
代表執行階段動態大小的 int32。 |
dimension
|
int64
|
間隔 [0, n) 中的值,用於指定維度。 |
將運算元做為結果傳遞,並由編譯器追蹤動態維度。
下游縮減作業會忽略填補值。
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
ShiftLeft
另請參閱
XlaBuilder::ShiftLeft。
對 lhs 執行元素級別的左移運算,移動位元數為 rhs。
ShiftLeft(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
ShiftLeft 另有替代變體,支援不同維度的廣播:
ShiftLeft(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱 StableHLO - shift_left。
ShiftRightArithmetic
另請參閱
XlaBuilder::ShiftRightArithmetic。
對 lhs 執行元素級別的算術右移運算,位元數為 rhs。
ShiftRightArithmetic(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
ShiftRightArithmetic 有替代變體,支援不同維度的廣播:
ShiftRightArithmetic(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱「StableHLO - shift_right_arithmetic」。
ShiftRightLogical
另請參閱
XlaBuilder::ShiftRightLogical。
對 lhs 執行元素級別的邏輯右移運算,位元數為 rhs。
ShiftRightLogical(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
ShiftRightLogical 有替代變體,支援不同維度的廣播:
ShiftRightLogical(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱「StableHLO - shift_right_logical」。
簽名
另請參閱
XlaBuilder::Sign。
Sign(operand) 元素級別的符號運算 x -> sgn(x),其中
\[\text{sgn}(x) = \begin{cases} -1 & x < 0\\ -0 & x = -0\\ NaN & x = NaN\\ +0 & x = +0\\ 1 & x > 0 \end{cases}\]
使用 operand 元素型別的比較運算子。
Sign(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
如需 StableHLO 資訊,請參閱「StableHLO - 簽章」。
Sin
Sin(operand) 元素層面的正弦 x -> sin(x)。
另請參閱
XlaBuilder::Sin。
Sin(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Sin 也支援選用 result_accuracy 引數:
Sin(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
如需 StableHLO 相關資訊,請參閱「StableHLO - sine」。
配量
另請參閱
XlaBuilder::Slice。
切片會從輸入陣列擷取子陣列。子陣列的維度數量與輸入相同,且包含輸入陣列中邊界方塊內的值,其中邊界方塊的維度和索引會做為引數提供給切片作業。
Slice(operand, start_indices, limit_indices, strides)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
型別為 T 的 N 維陣列 |
start_indices
|
ArraySlice<int64>
|
包含每個維度切片起始索引的 N 個整數清單。值必須大於或等於零。 |
limit_indices
|
ArraySlice<int64>
|
包含 N 個整數的清單,其中包含每個維度切片的結尾索引 (不含)。每個值都必須大於或等於維度的相應 start_indices 值,且小於或等於維度大小。 |
strides
|
ArraySlice<int64>
|
N 個整數的清單,用於決定切片的輸入步幅。切片會挑選維度 d 中的每個 strides[d] 元素。 |
一維範例:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4})
// Result: {2.0, 3.0}
2 維範例:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3})
// Result:
// { { 7.0, 8.0},
// {10.0, 11.0} }
如需 StableHLO 資訊,請參閱 StableHLO - slice。
排序
另請參閱
XlaBuilder::Sort。
Sort(operands, comparator, dimension, is_stable)
| 引數 | 類型 | 語意 |
|---|---|---|
operands |
ArraySlice<XlaOp> |
要排序的運算元。 |
comparator |
XlaComputation |
要使用的比較子計算。 |
dimension |
int64 |
要排序的維度。 |
is_stable |
bool |
是否應使用穩定排序。 |
如果只提供一個運算元:
如果運算元是 1 維張量 (陣列),結果會是排序後的陣列。如要將陣列排序為遞增順序,比較子應執行小於比較。正式來說,陣列排序後,所有索引位置
i, j都會保留i < j,且comparator(value[i], value[j]) = comparator(value[j], value[i]) = false或comparator(value[i], value[j]) = true。如果運算元具有較多的維度,系統會沿著提供的維度排序運算元。舉例來說,如果是 2 維張量 (矩陣),維度值
0會分別排序每個資料欄,維度值1則會分別排序每個資料列。如未提供維度編號,系統預設會選擇最後一個維度。如果是經過排序的維度,排序順序與一維情況相同。
如果提供 n > 1 運算元:
所有
n運算元都必須是相同維度的張量。張量的元素型別可能不同。所有運算元會一起排序,而不是個別排序。就概念上而言,運算元會視為元組。檢查索引位置
i和j的每個運算元元素是否需要交換時,系統會使用2 * n純量參數呼叫比較子,其中參數2 * k對應於k-th運算元中位置i的值,而參數2 * k + 1則對應於k-th運算元中位置j的值。因此,比較子通常會比較2 * k和2 * k + 1參數,並可能使用其他參數配對做為平手打破機制。結果是元組,由排序後的運算元組成 (如上所述,沿著提供的維度)。元組的
i-th運算元對應於 Sort 的i-th運算元。
舉例來說,假設有三個運算元 operand0 = [3, 1]、operand1 = [42, 50]、operand2 = [-3.0, 1.1],而比較子只會比較 operand0 的值是否小於其他值,則排序的輸出內容為元組 ([1, 3], [50, 42], [1.1, -3.0])。
如果 is_stable 設為 true,系統保證排序穩定,也就是說,如果比較子認為有元素相等,系統會保留相等值的相對順序。只有在 comparator(e1, e2) = comparator(e2, e1) = false 時,兩個元素 e1 和 e2 才會相等。根據預設,is_stable 會設為 false。
如需 StableHLO 資訊,請參閱「StableHLO - sort」。
Sqrt
另請參閱
XlaBuilder::Sqrt。
元素級別的平方根運算 x -> sqrt(x)。
Sqrt(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Sqrt 也支援選用 result_accuracy 引數:
Sqrt(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
如需 StableHLO 資訊,請參閱「StableHLO - sqrt」。
子項目
另請參閱
XlaBuilder::Sub。
執行 lhs 和 rhs 的元素減法。
Sub(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Sub 有替代版本,支援不同維度的廣播:
Sub(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱「StableHLO - subtract」。
棕褐色
另請參閱
XlaBuilder::Tan。
元素切線 x -> tan(x)。
Tan(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Tan 也支援選用 result_accuracy 引數:
Tan(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
如需 StableHLO 資訊,請參閱 StableHLO - tan。
Tanh
另請參閱
XlaBuilder::Tanh。
逐一計算雙曲正切 x -> tanh(x)。
Tanh(operand)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
Tanh 也支援選用 result_accuracy 引數:
Tanh(operand, result_accuracy)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
函式的運算元 |
result_accuracy
|
選填 ResultAccuracy
|
使用者可為具有多種實作方式的一元運算子要求準確度類型 |
如要進一步瞭解 result_accuracy,請參閱「結果準確度」。
如需 StableHLO 相關資訊,請參閱「StableHLO - tanh」。
TopK
另請參閱
XlaBuilder::TopK。
TopK 會找出指定張量最後一個維度的 k 最大或最小元素的值和索引。
TopK(operand, k, largest)
| 引數 | 類型 | 語意 |
|---|---|---|
operand
|
XlaOp
|
要從中擷取前 k 個元素的張量。
張量必須有一或多個維度。張量最後一個維度的大小必須大於或等於 k。 |
k |
int64 |
要擷取的元素數。 |
largest
|
bool
|
是否要擷取最大或最小的 k 元素。 |
如果是 1 維輸入張量 (陣列),則會找出陣列中 k 個最大或最小的項目,並輸出兩個陣列的元組 (values, indices)。因此,values[j] 是 operand 中第 j 大/小的項目,其索引為 indices[j]。
如果輸入張量超過 1 個維度,則沿著最後一個維度計算前 k 個項目,並保留輸出中的所有其他維度 (資料列)。因此,對於形狀為 [A, B, ..., P, Q] 的運算元 (其中 Q >= k),輸出內容是元組 (values, indices),其中:
values.shape = indices.shape = [A, B, ..., P, k]
如果同一列中的兩個元素相等,系統會先顯示索引較低的元素。
轉置
另請參閱 tf.reshape 作業。
Transpose(operand, permutation)
| 引數 | 類型 | 語意 |
|---|---|---|
operand |
XlaOp |
要轉置的運算元。 |
permutation |
ArraySlice<int64> |
如何排列維度。 |
使用指定排列方式排列運算元維度,因此 ∀ i . 0 ≤ i < number of dimensions ⇒
input_dimensions[permutation[i]] = output_dimensions[i]。
這與 Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)) 相同。
如需 StableHLO 資訊,請參閱「StableHLO - transpose」。
TriangularSolve
另請參閱
XlaBuilder::TriangularSolve。
透過前向或後向代入法,解開係數矩陣為上或下三角矩陣的聯立線性方程式。這個常式會沿著前導維度廣播,針對變數 x 求解其中一個矩陣系統 op(a) * x =
b 或 x * op(a) = b,並提供 a 和 b,其中 op(a) 是 op(a) = a、op(a) = Transpose(a) 或 op(a) = Conj(Transpose(a))。
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| 引數 | 類型 | 語意 |
|---|---|---|
a
|
XlaOp
|
形狀為 [..., M,
M] 的複數或浮點類型 > 2 維陣列。 |
b
|
XlaOp
|
如果 [..., M, K] 為 true,則為形狀為 [..., M, K] 的相同類型 2 維陣列,否則為 [..., K, M]。left_side |
left_side
|
bool
|
指出是否要解出 op(a) * x = b (true) 或 x *
op(a) = b (false) 形式的系統。 |
lower
|
bool
|
是否要使用 a 的上或下三角形。 |
unit_diagonal
|
bool
|
如果 true,則 a 的對角線元素會假設為 1,且不會存取。 |
transpose_a
|
Transpose
|
是否要照原樣使用 a、轉置或採用共軛轉置。 |
系統只會從 a 的下/上三角形讀取輸入資料,視 lower 的值而定。系統會忽略其他三角形的值。輸出資料會以相同三角形傳回;其他三角形中的值是由實作定義,可以是任何值。
如果 a 和 b 的維度數量大於 2,系統會將其視為矩陣批次,其中除了次要 2 個維度外,其餘都是批次維度。a 和 b 的批次維度必須相等。
如需 StableHLO 資訊,請參閱「StableHLO - triangular_solve」。
元組
另請參閱
XlaBuilder::Tuple。
包含不定數量資料控制代碼的元組,每個控制代碼都有自己的形狀。
Tuple(elements)
| 引數 | 類型 | 語意 |
|---|---|---|
elements |
XlaOp 的向量 |
N 個 T 類型的陣列 |
這類似於 C++ 中的 std::tuple。概念上:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
元組可透過 GetTupleElement 作業解構 (存取)。
如需 StableHLO 資訊,請參閱「StableHLO - 元組」。
雖然
另請參閱
XlaBuilder::While。
While(condition, body, init)
| 引數 | 類型 | 語意 |
|---|---|---|
condition
|
XlaComputation
|
類型為 T -> PRED 的 XlaComputation,用於定義迴圈的終止條件。 |
body
|
XlaComputation
|
XlaComputation (T -> T 型別),用於定義迴圈主體。 |
init
|
T
|
condition 和 body 參數的初始值。 |
依序執行 body,直到 condition 失敗為止。這與許多其他語言中的一般 while 迴圈類似,但有以下差異和限制。
While節點會傳回T類型的值,也就是上次執行body的結果。- 型別
T的形狀是靜態決定,且在所有疊代中都必須相同。
計算的 T 參數會在第一次疊代中以 init 值初始化,並在後續每次疊代中自動更新為 body 的新結果。
While 節點的主要用途之一,是在類神經網路中實作重複執行的訓練。下方顯示簡化的虛擬程式碼,以及代表運算的圖表。您可以在 while_test.cc 中找到程式碼。本例中的 T 型別是 Tuple,由疊代次數的 int32 和累加器的 vector[10] 組成。在 1000 次疊代中,迴圈會持續將常數向量新增至累加器。
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}
如需 StableHLO 資訊,請參閱StableHLO - while。
Xor
另請參閱
XlaBuilder::Xor。
對 lhs 和 rhs 執行元素層級的 XOR 運算。
Xor(lhs, rhs)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:T 型陣列 |
| rhs | XlaOp | 左側運算元:T 型陣列 |
引數的形狀必須相似或相容。如要瞭解形狀相容的意義,請參閱廣播說明文件。運算的結果形狀是廣播兩個輸入陣列的結果。在這個變體中,系統不支援不同等級的陣列間的運算,但其中一個運算元是純量的情況除外。
Xor 有替代變體,支援不同維度的廣播:
Xor(lhs,rhs, broadcast_dimensions)
| 引數 | 類型 | 語意 |
|---|---|---|
| lhs | XlaOp | 左側運算元:型別 T 的陣列 |
| rhs | XlaOp | 左側運算元:型別 T 的陣列 |
| broadcast_dimension | ArraySlice |
目標形狀中的哪個維度對應至運算元形狀的每個維度 |
這個運算變體應適用於不同等級的陣列之間的算術運算 (例如將矩陣加到向量)。
額外的 broadcast_dimensions 運算元是整數切片,用於指定要用於廣播運算元的維度。如需詳細說明,請參閱廣播頁面。
如需 StableHLO 資訊,請參閱 StableHLO - xor。








