این صفحه به‌وسیله ‏Cloud Translation API‏ ترجمه شده است.

تجزیه و تحلیل نمایه سازی

تجزیه و تحلیل نمایه سازی HLO یک تجزیه و تحلیل جریان داده است که چگونگی ارتباط عناصر یک تانسور با دیگری را از طریق "نقشه های نمایه سازی" توصیف می کند. به عنوان مثال، چگونه شاخص های یک دستور HLO خروجی به شاخص های عملوندهای دستورالعمل HLO نشان می دهد.

مثال

برای پخش از tensor<20xf32> به tensor<10x20x30xf32>

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

نقشه نمایه سازی از خروجی به ورودی (i, j, k) -> (j) برای i in [0, 10] ، j in [0, 20] و k in [0, 30] است.

انگیزه

XLA از چندین راه حل سفارشی برای استدلال در مورد طرح های ادغام، استفاده از عملوند و کاشی کاری استفاده می کند (جزئیات بیشتر در زیر). هدف از تجزیه و تحلیل نمایه سازی، ارائه یک جزء قابل استفاده مجدد برای چنین موارد استفاده است. تجزیه و تحلیل نمایه سازی بر اساس زیرساخت نقشه Affine MLIR ساخته شده است و معنای HLO را اضافه می کند.

ادغام

استدلال در مورد ادغام حافظه برای موارد غیر پیش پا افتاده امکان پذیر می شود، زمانی که می دانیم چه عناصر / برش هایی از ورودی ها برای محاسبه یک عنصر از خروجی خوانده می شوند.

استفاده از عملوند

استفاده از عملوند در XLA نشان می دهد که هر ورودی دستورالعمل با فرض استفاده کامل از خروجی آن چقدر استفاده می شود. در حال حاضر، استفاده برای یک مورد عمومی نیز محاسبه نمی شود. تجزیه و تحلیل نمایه سازی به ما امکان می دهد تا میزان استفاده را دقیقاً محاسبه کنیم.

کاشی کاری

کاشی/برش زیرمجموعه‌ای فرامستطیلی شکل از یک تانسور است که با انحراف‌ها، اندازه‌ها و گام‌ها پارامتر می‌شود. انتشار کاشی راهی برای محاسبه پارامترهای کاشی تولید کننده/مصرف کننده عملیات با استفاده از پارامترهای کاشی کاری خود op است. در حال حاضر کتابخانه ای وجود دارد که این کار را برای softmax و dot انجام می دهد. اگر از طریق نقشه های نمایه سازی بیان شود، انتشار کاشی می تواند عمومی تر و قوی تر شود.

نقشه نمایه سازی

نقشه نمایه سازی ترکیبی از

یک تابع نمادین بیان شده که هر عنصر یک تانسور A را به محدوده عناصر در تانسور B ترسیم می کند.
محدودیت در آرگومان های تابع معتبر، از جمله دامنه تابع.

آرگومان‌های تابع به 3 دسته تقسیم می‌شوند تا ماهیت خود را بهتر نشان دهند:

متغیرهای ابعاد تانسور A یا یک شبکه GPU که ما از آن نقشه برداری می کنیم. مقادیر به صورت ایستا شناخته می شوند. عناصر شاخص را متغیرهای بعد نیز می نامند.
متغیرهای محدوده آنها یک نگاشت یک به چند را تعریف می کنند و مجموعه ای از عناصر را در B مشخص می کنند که برای محاسبه یک مقدار واحد از A استفاده می شود. مقادیر به صورت ایستا شناخته می شوند. بعد انقباضی یک ضرب ماتریس نمونه ای از یک متغیر دامنه است.
متغیرهای زمان اجرا که فقط در هنگام اجرا شناخته می شوند. به عنوان مثال، آرگومان شاخص عملیات جمع آوری .

نتیجه تابع یک شاخص از تانسور B هدف است.

به طور خلاصه، یک تابع نمایه سازی از تانسور A به تانسور B برای عملیات x است

map_ab(index in A, range variables, runtime variables) -> index in B .

برای تفکیک بهتر انواع آرگومان های نگاشت آنها را به صورت زیر می نویسیم:

map_ab(index in A)[range variables]{runtime variables} -> (index in B)

به عنوان مثال، بیایید به نقشه های نمایه سازی برای عملیات کاهش نگاه کنیم f32[4, 8] out = reduce(f32[2, 4, 8, 16] in, 0), dimensions={0,3} :

برای نگاشت عناصر in to out تابع ما می تواند به صورت (d0, d1, d2, d3) -> (d1, d2) بیان شود. محدودیت های متغیرهای d0 in [0, 1], d1 in [0, 3], d2 in [0, 7], d3 in [0, 15] با شکل in تعریف می شوند.
برای نگاشت عناصر out to in : out فقط دو بعد دارد و کاهش دو متغیر محدوده را معرفی می کند که ابعاد کاهنده را پوشش می دهد. بنابراین تابع نگاشت (d0, d1)[s0, s1] -> (s0, d0, d1, s1) است که در آن (d0, d1) شاخص out است. s0 و s1 محدوده هایی هستند که با معنای عملیات و ابعاد دهانه 0 و 3 تانسور in تعریف می شوند. محدودیت ها d0 in [0, 3], d1 in [0, 7], s0 in [0,1], s1 in [0, 15] هستند.

توجه به این نکته مهم است که در اکثر سناریوها ما به نقشه برداری از عناصر خروجی علاقه مندیم. برای محاسبات

C = op1(A, B)
E = op2(C, D)

می توان در مورد "نمایه سازی B" به معنای "نقشه گذاری عناصر E به عناصر B " صحبت کرد. این ممکن است در مقایسه با انواع دیگر تجزیه و تحلیل جریان داده که از ورودی به خروجی کار می کنند، غیر شهودی باشد.

محدودیت‌های متغیرها فرصت‌های بهینه‌سازی را فراهم می‌کنند و به تولید کد کمک می‌کنند. در اسناد و محدودیت‌های پیاده‌سازی به عنوان دامنه نیز نامیده می‌شود زیرا همه ترکیب‌های معتبر یا مقادیر آرگومان تابع نگاشت را تعریف می‌کنند. برای بسیاری از عملیات، محدودیت ها به سادگی ابعاد تانسورها را توصیف می کنند، اما برای برخی عملیات ممکن است پیچیده تر باشند. نمونه های زیر را ببینید

با داشتن توابع و محدودیت‌های آرگومان که به صورت نمادین بیان می‌شوند و قادر به ترکیب توابع و محدودیت‌ها هستیم، می‌توانیم یک نگاشت نمایه‌سازی فشرده برای یک محاسبات بزرگ دلخواه (فوژن) محاسبه کنیم.

بیان تابع نمادین و محدودیت ها تعادلی بین پیچیدگی پیاده سازی و دستاوردهای بهینه سازی است که از داشتن یک نمایش دقیق تر به دست می آوریم. برای برخی از عملیات HLO ما الگوهای دسترسی را فقط تقریباً می‌گیریم.

پیاده سازی

از آنجایی که می خواهیم محاسبه مجدد را به حداقل برسانیم، به یک کتابخانه برای محاسبات نمادین نیاز داریم. XLA قبلاً به MLIR وابسته است، بنابراین ما به جای نوشتن یک کتابخانه حسابی نمادین دیگر از mlir::AffineMap استفاده می کنیم.

یک AffineMap معمولی به نظر می رسد

(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)

AffineMap دو نوع پارامتر دارد: ابعاد و نمادها . ابعاد مربوط به متغیرهای بعد d ; نمادها با متغیرهای محدوده r و متغیرهای زمان اجرا rt مطابقت دارند. AffineMap حاوی هیچ ابرداده ای در مورد محدودیت های پارامترها نیست، بنابراین باید آنها را جداگانه ارائه کنیم.

struct Interval {
 int64_t lower;
 int64_t upper;
};

class IndexingMap {
   // Variable represents dimension, range or runtime variable.
  struct Variable {
    Interval bounds;
    // Name of the variable is used for nicer printing.
    std::string name = "";
  };

  mlir::AffineMap affine_map_;

  // DimVars represent dimensions of a tensor or of a GPU grid.
  std::vector<Variable> dim_vars_;

  // RangeVars represent ranges of values, e.g. to compute a single element of
  // the reduction's result we need a range of values from the input tensor.
  std::vector<Variable> range_vars_;

  // RTVars represent runtime values, e.g. a dynamic offset in
  // HLO dynamic-update-slice op.
  std::vector<Variable> rt_vars_;
  llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};

dim_vars_ محدودیت‌های جعبه شامل متغیرهای بعد d نقشه نمایه‌سازی را رمزگذاری می‌کند، که معمولاً با شکل تانسور خروجی برای عملیات‌هایی مانند transpose، reduce، elementwise، dot منطبق است، اما استثناهایی مانند HloConcatenateInstruction وجود دارد.

range_vars_ همه مقادیری که متغیرهای محدوده می گیرند. متغیرهای محدوده زمانی مورد نیاز هستند که مقادیر متعددی برای محاسبه یک عنصر منفرد از تانسوری که ما از آن نقشه‌برداری می‌کنیم ضروری است، به عنوان مثال برای نقشه نمایه‌سازی خروجی-> ورودی کاهش یا نقشه ورودی-> خروجی برای پخش.

rt_vars_ مقادیر قابل اجرا را در زمان اجرا رمزگذاری می کند. به عنوان مثال، افست برای یک دستورالعمل 1 بعدی HloDynamicSliceInstruction پویا است. RTVar مربوطه مقادیر قابل اجرا بین 0 و tensor_size - slice_size - 1 خواهد داشت.

constraints_ روابط بین مقادیر را به شکل <expression> in <range> می گیرد، به عنوان مثال d0 + s0 in [0, 20] . آنها همراه با Variable.bounds "دامنه" تابع نمایه سازی را تعریف می کنند.

بیایید به صورت مثال مطالعه کنیم تا بفهمیم همه موارد بالا واقعاً به چه معنا هستند.

نمایه سازی نقشه ها برای عملیات های Unfused

از نظر عنصری

برای عملیات عنصری، نقشه نمایه سازی یک هویت است.

  p0 = f32[10, 20] parameter(0)
  p1 = f32[10, 20] parameter(1)
  output = f32[10, 20] add(p0, p1)

خروجی به output -> p0 :

(d0, d1) -> (d0, d1),
domain:
d0 in [0, 9],
d1 in [0, 19]

ورودی به خروجی نقشه p0 -> output :

(d0, d1) -> (d0, d1),
domain:
d0 in [0, 9],
d1 in [0, 19]

پخش می شود

پخش به این معنی است که وقتی خروجی را به ورودی نگاشت می کنیم برخی از ابعاد حذف می شود و وقتی ورودی به خروجی را نگاشت می کنیم اضافه می شود.

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

نقشه خروجی به ورودی:

(d0, d1, d2) -> (d1),
domain:
d0 in [0, 9],
d1 in [0, 19],
d2 in [0, 29]

نقشه ورودی به خروجی:

(d0)[s0, s1] -> (s0, d0, s1),
domain:
d0 in [0, 19],
s0 in [0, 9],
s1 in [0, 29]

توجه داشته باشید که اکنون متغیرهای محدوده s را در سمت راست برای نگاشت ورودی به خروجی داریم. اینها نمادهایی هستند که محدوده ای از مقادیر را نشان می دهند. به عنوان مثال، در این مورد خاص، هر عنصر ورودی با شاخص d0 به یک برش 10x1x30 از خروجی نگاشت می شود.

آیوتا

آیوتا عملوند تانسور ورودی ندارد، بنابراین هیچ آرگومان شاخص ورودی وجود ندارد.

iota = f32[2,4] iota(), dimensions={1}

نقشه خروجی به ورودی:

(d0, d1) -> ()
domain:
d0 in [0, 1]
d1 in [0, 3]

نقشه ورودی به خروجی:

()[s0, s1] -> (s0, s1)
domain:
s0 in [0, 1]
s1 in [0, 3]

DynamicSlice

DynamicSlice دارای افست هایی است که فقط در زمان اجرا شناخته می شوند.

src = s32[2, 2, 258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = s32[1, 2, 32] dynamic-slice(src, of1, of2, of3), dynamic_slice_sizes={1, 2, 32}

خروجی نقشه ورودی از ds به src :

(d0, d1, d2){rt0, rt1, rt2} -> (d0 + rt0, d1 + rt1, d2 + rt2),
domain:
d0 in [0, 0],
d1 in [0, 1],
d2 in [0, 31],
rt0 in [0, 1],
rt1 in [0, 0],
rt2 in [0, 226]

توجه داشته باشید که اکنون rt را در سمت راست برای نگاشت ورودی به خروجی داریم. اینها نمادهایی هستند که مقادیر زمان اجرا را نشان می دهند. به عنوان مثال، در این مورد خاص برای هر عنصر خروجی با شاخص‌های d0, d1, d2 ما به انحراف‌های برش of1 ، of2 و of3 برای محاسبه شاخص ورودی دسترسی داریم. فواصل متغیرهای زمان اجرا با این فرض به دست می‌آیند که کل برش در محدوده باقی می‌ماند.

خروجی نقشه ورودی برای of1 ، of2 و of3 :

(d0, d1, d2) -> (),
domain:
d0 in [0, 0],
d1 in [0, 1],
d2 in [0, 31]

DynamicUpdateSlice

src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
    s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)

خروجی نقشه ورودی برای src بی اهمیت است. می توان آن را با محدود کردن دامنه به شاخص های به روز نشده دقیق تر کرد، اما در حال حاضر نقشه های نمایه سازی از محدودیت های نابرابری پشتیبانی نمی کنند.

(d0, d1) -> (d0, d1),
domain:
d0 in [0, 19],
d1 in [0, 29]

خروجی نقشه ورودی برای upd :

(d0, d1){rt0, rt1} -> (d0 - rt0, d1 - rt1),
domain:
d0 in [0, 19],
d1 in [0, 29],
rt0 in [0, 15],
rt1 in [0, 20]

توجه داشته باشید که اکنون rt0 و rt1 داریم که مقادیر زمان اجرا را نشان می دهند. در این مورد خاص برای هر عنصر خروجی با شاخص‌های d0, d1 ما به انحراف‌های برش of1 و of2 برای محاسبه شاخص ورودی دسترسی داریم. فواصل متغیرهای زمان اجرا با این فرض به دست می‌آیند که کل برش در محدوده باقی می‌ماند.

خروجی نقشه ورودی برای of1 و of2 :

(d0, d1) -> (),
domain:
d0 in [0, 19],
d1 in [0, 29]

جمع کنید

فقط جمع ساده شده پشتیبانی می شود. collect_simplifier.h را ببینید.

operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
  offset_dims={1,2,3},
  collapsed_slice_dims={},
  start_index_map={0,1},
  index_vector_dim=1,
  slice_sizes={7,8,4}

خروجی نقشه ورودی برای operand :

(d0, d1, d2, d3){rt0, rt1} -> (d1 + rt0, d2 + rt1, d3),
domain:
d0 in [0, 1805],
d1 in [0, 6],
d2 in [0, 7],
d3 in [0, 3],
rt0 in [0, 26],
rt1 in [0, 68]

توجه داشته باشید که اکنون نمادهای rt داریم که مقادیر زمان اجرا را نشان می دهند.

خروجی به نقشه ورودی برای indices :

(d0, d1, d2, d3)[s0] -> (d0, s0),
domain:
d0 in [0, 1805],
d1 in [0, 6],
d2 in [0, 7],
d3 in [0, 3],
s0 in [0, 1]

متغیر محدوده s0 نشان می دهد که برای محاسبه یک عنصر از خروجی به کل ردیف (d0, *) تانسور indices نیاز داریم.

جابجا شود

نقشه نمایه سازی برای جابجایی، جایگشتی از ابعاد ورودی/خروجی است.

p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}

نقشه خروجی به ورودی:

(d0, d1, d2, d3) -> (d0, d3, d1, d2),
domain:
d0 in [0, 2],
d1 in [0, 5],
d2 in [0, 127],
d3 in [0, 12287],

نقشه ورودی به خروجی:

(d0, d1, d2, d3) -> (d0, d2, d3, d1),
domain:
d0 in [0, 2],
d1 in [0, 12287],
d2 in [0, 5],
d3 in [0, 127]

معکوس

نمایه سازی نقشه برای معکوس، ابعاد برگردانده شده را به upper_bound(d_i) - d_i :

p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}

نقشه خروجی به ورودی:

(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3),
domain:
d0 in [0, 0],
d1 in [0, 16],
d2 in [0, 8],
d3 in [0, 8]

نقشه ورودی به خروجی:

(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3),
domain:
d0 in [0, 0],
d1 in [0, 16],
d2 in [0, 8],
d3 in [0, 8]

(Variadic)کاهش دادن

کاهش متغیر دارای چندین ورودی و چندین مقدار اولیه است، نقشه از خروجی به ورودی ابعاد کاهش یافته را اضافه می کند.

p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
out = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
  dimensions={0}, to_apply=max

خروجی نقشه های ورودی:

out[0] -> p0 :

(d0)[s0] -> (s0, d0),
domain:
d0 in [0, 9],
s0 in [0, 255]

out[0] -> p0_init :

(d0) -> (),
domain:
d0 in [0, 9]

ورودی نقشه های خروجی:

p0 -> out[0] :

(d0, d1) -> (d1),
domain:
d0 in [0, 255],
d1 in [0, 9]

p0_init -> out[0] :

()[s0] -> (s0),
domain:
s0 in [0, 9]

برش

نمایه سازی از خروجی به ورودی برای برش منجر به یک نقشه نمایه سازی گام به گام می شود که برای هر عنصر خروجی معتبر است. نگاشت از ورودی به خروجی به محدوده ای از عناصر موجود در ورودی محدود می شود.

p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
  slice={[5:10:1], [3:20:7], [0:50:2]}

نقشه خروجی به ورودی:

(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2),
domain:
d0 in [0, 4],
d1 in [0, 2],
d2 in [0, 24]

نقشه ورودی به خروجی:

(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2),
domain:
d0 in [5, 9],
d1 in [3, 17],
d2 in [0, 48],
(d1 - 3) mod 7 in [0, 0],
d2 mod 2 in [0, 0]

تغییر شکل دهید

تغییر شکل ها طعم های مختلفی دارند.

شکل فرو ریختن

این یک تغییر شکل "خطی" از ND به 1D است.

p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)

نقشه خروجی به ورودی:

(d0) -> (d0 floordiv 8, d0 mod 8),
domain:
d0 in [0, 31]

نقشه ورودی به خروجی:

(d0, d1) -> (d0 * 8 + d1),
domain:
d0 in [0, 3],
d1 in [0, 7]

شکل را گسترش دهید

این یک عملیات معکوس "شکل فروپاشی" است، یک ورودی 1 بعدی را به خروجی ND تغییر شکل می دهد.

p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)

نقشه خروجی به ورودی:

(d0, d1) -> (d0 * 8 + d1),
domain:
d0 in [0, 3],
d1 in [0, 7]

نقشه ورودی به خروجی:

(d0) -> (d0 floordiv 8, d0 mod 8),
domain:
d0 in [0, 31]

تغییر شکل عمومی

اینها عملیات تغییر شکلی هستند که نمی‌توان آنها را به صورت یک شکل منبسط یا فروپاشی نشان داد. آنها را فقط می توان به عنوان ترکیبی از 2 یا بیشتر شکل گسترش یا فروپاشی نشان داد.

مثال 1: خطی سازی-خطی سازی.

p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)

این تغییر شکل را می توان به صورت ترکیبی از شکل فروپاشی tensor<4x8xf32> به tensor<32xf32> و سپس گسترش شکل به tensor<2x4x4xf32> نشان داد.

نقشه خروجی به ورودی:

(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4),
domain:
d0 in [0, 1],
d1 in [0, 3],
d2 in [0, 3]

نقشه ورودی به خروجی:

(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4),
domain:
d0 in [0, 3],
d1 in [0, 7]

مثال 2: شکل های فرعی منبسط و جمع شده

p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)

این تغییر شکل را می توان به عنوان ترکیبی از دو تغییر شکل نشان داد. اولی بیرونی ترین tensor<4x8x12xf32> به tensor<32x12xf32> می ریزد و دومی داخلی ترین tensor<32x12xf32> به tensor<32x3x4xf32> گسترش می دهد.

نقشه خروجی به ورودی:

(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2),
domain:
d0 in [0, 31],
d1 in [0, 2]
d2 in [0, 3]

نقشه ورودی به خروجی:

(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4),
domain:
d0 in [0, 3],
d1 in [0, 7],
d2 in [0, 11]

بیت کست

یک عملیات بیت‌کست را می‌توان به صورت دنباله‌ای از transpose-reshape-transpose نشان داد. بنابراین، نقشه های نمایه سازی آن فقط ترکیبی از نقشه های نمایه سازی برای این دنباله است.

الحاق

نگاشت خروجی به ورودی برای concat برای همه ورودی ها تعریف شده است، اما با دامنه های غیر همپوشانی، یعنی تنها یکی از ورودی ها در یک زمان استفاده می شود.

p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT output = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}

خروجی نقشه های ورودی:

output -> p0 :

(d0, d1, d2) -> (d0, d1, d2),
domain:
d0 in [0, 1],
d1 in [0, 4],
d2 in [0, 6]

output -> p1 :

(d0, d1, d2) -> (d0, d1 - 5, d2),
domain:
d0 in [0, 1],
d1 in [5, 15],
d2 in [0, 6]

output -> p2 :

(d0, d1, d2) -> (d0, d1 - 16, d2),
domain:
d0 in [0, 1],
d1 in [16, 32],
d2 in [0, 6]

ورودی های نقشه های خروجی:

p0 -> output :

(d0, d1, d2) -> (d0, d1, d2),
domain:
d0 in [0, 1],
d1 in [0, 4],
d2 in [0, 6]

p1 -> output :

(d0, d1, d2) -> (d0, d1 + 5, d2),
domain:
d0 in [0, 1],
d1 in [0, 10],
d2 in [0, 6]

p2 -> output :

(d0, d1, d2) -> (d0, d1 + 16, d2),
domain:
d0 in [0, 1],
d1 in [0, 16],
d2 in [0, 6]

نقطه

نقشه های نمایه سازی برای نقطه بسیار شبیه نقشه های کاهش است.

p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
output = f32[4, 128, 64] dot(p0, p1),
  lhs_batch_dims={0}, rhs_batch_dims={0},
  lhs_contracting_dims={2}, rhs_contracting_dims={1}

خروجی نقشه های ورودی:

خروجی -> p0:

(d0, d1, d2)[s0] -> (d0, d1, s0),
domain:
d0 in [0, 3],
d1 in [0, 127],
d2 in [0, 63],
s0 in [0, 255]

خروجی -> p1:

(d0, d1, d2)[s0] -> (d0, s0, d2),
domain:
d0 in [0, 3],
d1 in [0, 127],
d2 in [0, 63],
s0 in [0, 255]

ورودی های نقشه های خروجی:

p0 -> خروجی:

(d0, d1, d2)[s0] -> (d0, d1, s0),
domain:
d0 in [0, 3],
d1 in [0, 127],
d2 in [0, 255],
s0 in [0, 63]

p1 -> خروجی:

(d0, d1, d2)[s0] -> (d0, s0, d1),
domain:
d0 in [0, 3],
d1 in [0, 255],
d2 in [0, 63],
s0 in [0, 127]

پد

نمایه سازی PadOp معکوس نمایه سازی SliceOp است.

p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0

پیکربندی padding 1_4_1x4_8_0 نشان دهنده lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1 است.

خروجی نقشه های ورودی:

خروجی -> p0:

(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4),
domain:
d0 in [1, 7],
d1 in [4, 7],
(d0 - 1) mod 2 in [0, 0]

خروجی -> p1:

(d0, d1) -> (),
domain:
d0 in [0, 11],
d1 in [0, 15]

ReduceWindow

ReduceWindow در XLA نیز padding را انجام می دهد. بنابراین، نقشه های نمایه سازی را می توان به عنوان ترکیبی از نمایه سازی ReduceWindow محاسبه کرد که هیچ گونه padding و نمایه سازی PadOp را انجام نمی دهد.

c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
outpu = f32[1024, 3] reduce-window(p0, c_inf),
  window={size=1x512 pad=0_0x0_0}, to_apply=max

خروجی نقشه های ورودی:

output -> p0 :

(d0, d1)[s0] -> (d0, d1 + s0),
domain:
d0 in [0, 1023],
d1 in [0, 2],
s0 in [0, 511]

output -> c_inf :

(d0, d1) -> (),
domain:
d0 in [0, 1023],
d1 in [0, 2]

نمایه سازی نقشه ها برای فیوژن

نقشه نمایه سازی برای fusion op ترکیبی از نقشه های نمایه سازی برای هر عملیات در خوشه است. ممکن است برخی از ورودی ها چندین بار با الگوهای دسترسی متفاوت خوانده شوند.

یک ورودی، چندین نقشه نمایه سازی

در اینجا یک مثال برای p0 + transpose(p0) آورده شده است.

f {
  p0 = f32[1000, 1000] parameter(0)
  transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
  ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}

نقشه های نمایه سازی خروجی به ورودی برای p0 (d0, d1) -> (d0, d1) و (d0, d1) -> (d1, d0) خواهد بود. به این معنی که برای محاسبه یک عنصر از خروجی ممکن است لازم باشد پارامتر ورودی را دو بار بخوانیم.

یک ورودی، نقشه نمایه سازی کپی شده

مواردی وجود دارد که نقشه های نمایه سازی در واقع یکسان هستند، حتی اگر بلافاصله مشخص نباشد.

f {
  p0 = f32[20, 10, 50] parameter(0)
  lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
  lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
  lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
  rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
  rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
  rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
  ROOT output = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}

نقشه نمایه سازی خروجی به ورودی برای p0 در این مورد فقط (d0, d1, d2) -> (d2, d0, d1) است.

سافت مکس

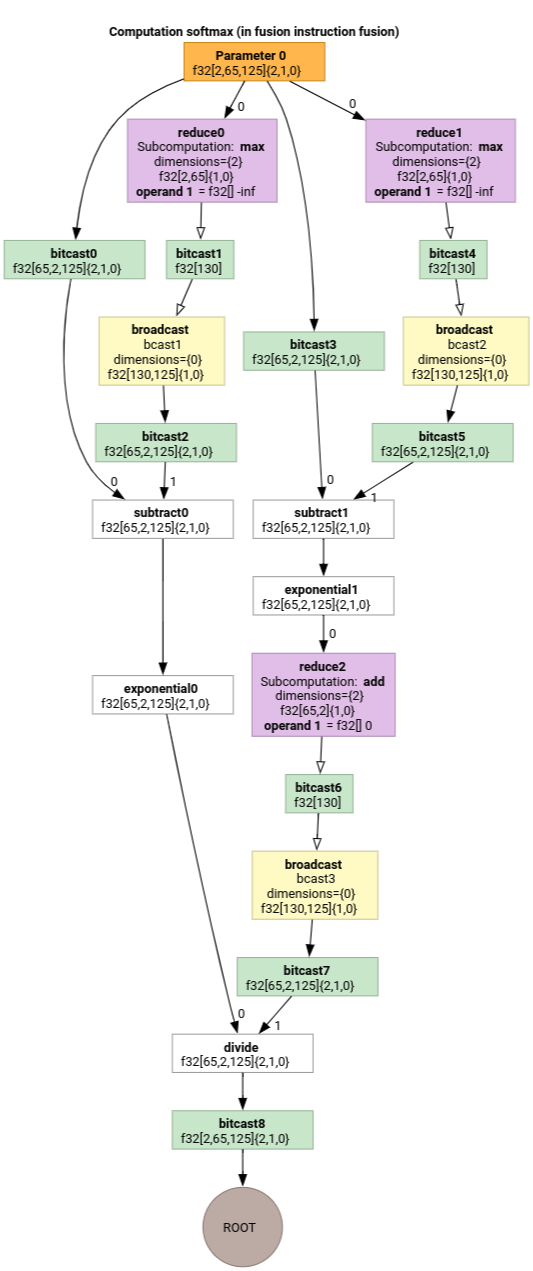
نقشه های نمایه سازی خروجی به ورودی برای parameter 0 برای softmax:

(d0, d1, d2)[s0] -> (d0, d1, s0),
domain:
d0 in [0, 1],
d1 in [0, 64],
d2 in [0, 124],
s0 in [0, 124]

(d0, d1, d2) -> (d0, d1, d2),
domain:
d0 in [0, 1],
d1 in [0, 64],
d2 in [0, 124]

که در آن s0 به درونی ترین بعد ورودی اشاره دارد.

برای مثال‌های بیشتر به indexing_analysis_test.cc مراجعه کنید.

نمایه سازی ساده کننده نقشه

ساده‌کننده پیش‌فرض mlir::AffineMap upstream نمی‌تواند هیچ فرضی در مورد محدوده ابعاد/نمادها داشته باشد. بنابراین، نمی تواند عبارات را با mod و div به طور موثر ساده کند.

ما می‌توانیم از دانش در مورد کران‌های پایین و بالای عبارات فرعی در نقشه‌های وابسته استفاده کنیم تا آنها را حتی بیشتر ساده کنیم.

ساده کننده می تواند عبارات زیر را بازنویسی کند.

(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16) برای d در [0, 6] x [0, 14] می شود (d0, d1) -> (d0, d1)
(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10) برای di in [0, 9] می شود (d0, d1, d2) -> (d0, d1, d2) .
(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8) برای d_i in [0, 9] می شود (d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8) .
(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9) برای d در [0, 9] x [0, 10] می شود (d0, d1) -> (d0) .

ساده‌ساز نقشه نمایه‌سازی به ما امکان می‌دهد بفهمیم که برخی از شکل‌های زنجیره‌ای در HLO یکدیگر را خنثی می‌کنند.

p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)

پس از ترکیب نقشه های نمایه سازی و ساده سازی آنها به دست خواهیم آورد

(d0, d1, d2) -> (d0, d1, d2) .

ساده سازی نقشه نمایه سازی محدودیت ها را نیز ساده می کند.

محدودیت های نوع lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_bound به صورت updated_lower_bound <= affine_expr <= updated_upped_bound بازنویسی می شوند.
محدودیت هایی که همیشه ارضا می شوند، به عنوان مثال d0 + s0 in [0, 20] برای d0 in [0, 5] و s0 in [1, 3] حذف می شوند.
عبارات Affine در محدودیت ها به عنوان نقشه affine نمایه سازی در بالا بهینه شده اند.

برای مثال‌های بیشتر به indexing_map_test.cc مراجعه کنید.

تجزیه و تحلیل نمایه سازی با مجموعه‌ها، منظم بمانید ذخیره و طبقه‌بندی محتوا براساس اولویت‌های شما.

مثال

انگیزه

ادغام

استفاده از عملوند

کاشی کاری

نقشه نمایه سازی

پیاده سازی

نمایه سازی نقشه ها برای عملیات های Unfused

از نظر عنصری

شکل فرو ریختن

شکل را گسترش دهید

تغییر شکل عمومی

مثال 1: خطی سازی-خطی سازی.

مثال 2: شکل های فرعی منبسط و جمع شده

بیت کست

نمایه سازی نقشه ها برای فیوژن

یک ورودی، چندین نقشه نمایه سازی

یک ورودی، نقشه نمایه سازی کپی شده

سافت مکس

نمایه سازی ساده کننده نقشه

تجزیه و تحلیل نمایه سازی