หน้านี้ได้รับการแปลโดย Cloud Translation API

การวิเคราะห์การจัดทำดัชนี

เอกสารนี้อธิบายการวิเคราะห์การจัดทำดัชนี HLO ซึ่งช่วยให้คุณ แมปการจัดทำดัชนีการประมวลผลสำหรับการดำเนินการ HLO แผนที่การระบุอินเด็กซ์คือฟังก์ชันที่แมปอินเด็กซ์ของเทมพอลลิ่งหนึ่งกับอินเด็กซ์ของเทมพอลลิ่งอื่น เช่น อินเด็กซ์ของเอาต์พุตคำสั่ง HLO กับอินเด็กซ์ของอินพุตคำสั่ง HLO หรือในทางกลับกัน

ตัวอย่าง

สำหรับประกาศจาก tensor<20xf32> ถึง tensor<10x20x30xf32>

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

แมปการจัดทำดัชนีจากเอาต์พุตไปยังอินพุตคือ (i, j, k) -> (j) สำหรับ i in [0, 10], j in [0, 20] และ k in [0, 30]

แรงจูงใจ

GPU ของ XLA ใช้โซลูชันที่ออกแบบมาโดยเฉพาะหลายรายการเพื่อพิจารณาการรวม การใช้ประโยชน์จากโอเปอเรนด์ และรูปแบบการแบ่งพื้นที่ (ดูรายละเอียดเพิ่มเติมด้านล่าง) เป้าหมายของการจัดทำดัชนี ซึ่งจะให้คอมโพเนนต์ที่นำมาใช้ใหม่ได้สำหรับกรณีการใช้งานดังกล่าว การวิเคราะห์การจัดทำดัชนี สร้างขึ้นบนโครงสร้างพื้นฐาน Affine Map ของ MLIR และเพิ่มความหมายของ HLO

การรวม

การหาเหตุผลเกี่ยวกับการรวมหน่วยความจำจะเป็นไปได้สำหรับกรณีที่ซับซ้อน เมื่อเราทราบว่ามีการอ่านองค์ประกอบ/ส่วนใดของอินพุตเพื่อคํานวณองค์ประกอบของเอาต์พุต

การใช้งาน Operand

การใช้ Operand ใน XLA บ่งบอกถึงปริมาณการใช้อินพุตแต่ละรายการของคำสั่งโดยสมมติว่ามีการใช้เอาต์พุตอย่างเต็มรูปแบบ ในปัจจุบัน การใช้งานก็ไม่ได้ สำหรับกรณีทั่วไป การวิเคราะห์การจัดทำดัชนีช่วยให้ใช้งานการประมวลผลได้ ได้อย่างแม่นยำ

การแปลงรหัสวิดีโอโดยใช้ไทล์

ไทล์/ส่วนคือชุดย่อยสี่เหลี่ยมผืนผ้าไฮเปอร์ของเทนเซอร์ที่กำหนดพารามิเตอร์ตามการเลื่อน <2fr>ขนาด และระยะห่าง การเผยแพร่ชิ้นส่วนย่อยคือวิธีประมวลผลพารามิเตอร์ไทล์ของ ผู้ผลิต/ผู้บริโภคของหน่วยงานที่ใช้พารามิเตอร์การแบ่งชิ้นส่วนของสหภาพเอง มี เป็น แล้ว คลัง ที่ทำหน้าที่ของ softmax และ จุด การนำไปใช้งานของไทล์สามารถทําให้ทั่วไปและมีประสิทธิภาพมากขึ้นได้หากแสดงผ่านแผนที่การจัดทำดัชนี

ฟังก์ชันและโดเมน

การแมปการจัดทำดัชนีคือฟังก์ชัน f(x) = f(d, r, rt) ที่แมป d หลายดัชนีของ tensor A กับองค์ประกอบ/ช่วงของ tensor B พารามิเตอร์ r หมายถึงช่วงของดัชนี มิติข้อมูลที่มีอยู่ใน tensor B แต่ไม่ใช่ใน tensor A พารามิเตอร์ rt หมายถึงค่ารันไทม์ เช่น ดัชนีสำหรับการชุมนุม

ตัวอย่างเช่น หากมีการลดจาก tensor<2x4x8x16xf32> เป็น tensor<4x8xf32> แผนที่การจัดทำดัชนีจากเอาต์พุต 2 มิติไปยังอินพุต 4 มิติจะเป็น (d0, d1) -> (r0, d0, d1, r1) โดยที่ d_i คือตัวแปรมิติข้อมูลที่ตรงกับดัชนีของเทนเซอร์เอาต์พุต การเข้ารหัสตัวแปรช่วง r_j หลายค่า เช่น ในการคำนวณเอลิเมนต์ (d0, d1) ของเอาต์พุต (r0, d0, d1, r1) ของอินพุต โดยที่ r0 in [0, 1] และ r1 in [0, 15]

การแมปนี้สามารถสร้างจากแอตทริบิวต์ของคำสั่ง HLO หรือ สามารถสร้างการแมปของคำสั่งที่ไม่ได้รวมเข้าด้วยกันเพื่อรับการจัดทำดัชนีสำหรับฟิวชันได้ การแมปยังมีโดเมน ซึ่งระบุองค์ประกอบของเทนเซอร์ที่มีการแมป

f(x) s.t.

lb <= g(x) <= ub

เนื่องจากเราต้องการลดการคำนวณใหม่ให้น้อยที่สุด เราจึงต้องมีไลบรารีสำหรับสัญลักษณ์ การคำนวณ XLA อาศัย MLIR อยู่แล้ว เราจึงใช้ mlir::AffineMap แทนที่จะเขียนห้องสมุดเลขคณิตเชิงสัญลักษณ์

AffineMap ปกติมีลักษณะ

(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)

AffineMapมีพารามิเตอร์ 2 ประเภท ได้แก่ มิติข้อมูลและสัญลักษณ์ มิติข้อมูลจะสอดคล้องกับตัวแปรมิติข้อมูล d, สัญลักษณ์จะสอดคล้องกับตัวแปรช่วง r และตัวแปร RT rt AffineMap ไม่มีข้อมูลเมตาเกี่ยวกับช่วงของมิติข้อมูล เราจึงต้องระบุข้อมูลนี้ด้วยตนเอง

struct Interval {
 int64_t lower;
 int64_t upper;
};

// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
  Interval bounds;
};

// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
  Interval range;
};

// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
  Interval feasible_values;
  const HloInstruction* hlo;
  // This is a map from the iteration space of the corresponding indexing map to
  // the iteration space of `hlo`. It shows what element of `hlo` we need to
  // extract to get the runtime value for the RTVar.
  mlir::AffineMap map;
};

class IndexingMap {
  mlir::AffineMap affine_map_;
  std::vector<DimVar> dim_vars_;
  std::vector<RangeVar> range_vars_;
  std::vector<RTVar> rt_vars_;
  llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};

dim_vars_ เข้ารหัสข้อจำกัดช่องรวมสำหรับมิติข้อมูล ตัวแปร d ของแผนที่การจัดทำดัชนี ซึ่งมักจะตรงกับ รูปร่างของ Tensor เอาต์พุตสำหรับการดำเนินการ เช่น สับเปลี่ยนตำแหน่ง, ลด, ธาตุ, จุด แต่ มีข้อยกเว้นบางอย่าง เช่น HloConcatenateInstruction

range_vars_ เข้ารหัสค่าที่เป็นไปได้ที่พารามิเตอร์ r รับได้

rt_vars_ จัดเก็บคำสั่ง hlo ที่เชื่อมโยงไว้พร้อมกับรูปแบบการเข้าถึงและค่าที่เป็นไปได้ในรันไทม์ เช่น ออฟเซตเป็นแบบไดนามิกสําหรับ HloDynamicSliceInstruction 1 มิติ RTVar ที่เกี่ยวข้องจะมี HloInstruction* ที่สร้าง Tensor อันดับ 0 ที่มีรูปแบบการเข้าถึง (d0) -> () เนื่องจากสำหรับองค์ประกอบทั้งหมดของเอาต์พุต เราจะดึงองค์ประกอบเดียวกันจาก Tensor ออฟเซตเพื่อคํานวณดัชนีของอินพุต เราสามารถสันนิษฐาน ค่าออฟเซ็ตของสไลซ์จะอยู่ระหว่าง 0 กับ tensor_size - slice_size - 1

มาศึกษาด้วยตัวอย่างเพื่อทําความเข้าใจความหมายของข้อความข้างต้นกัน

การจัดทำดัชนีแผนที่สําหรับการดําเนินการแบบไม่ผสาน

ตามองค์ประกอบ

สําหรับการดำเนินการแบบองค์ประกอบ แผนที่การระบุตัวจะเป็นตัวระบุ

  p0 = f32[10, 20] parameter(0)
  p1 = f32[10, 20] parameter(1)
  add = f32[10, 20] add(p0, p1)

เอาต์พุตสำหรับอินพุตแผนที่:

output -> input_i:

(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]

อินพุตสำหรับเอาต์พุตแผนที่

input_i -> output:

(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]

ออกอากาศ

การกระจายข้อมูลหมายความว่ามิติข้อมูลบางส่วนจะถูกลบออกเมื่อเราทำแผนที่ เอาต์พุตไปยังอินพุตและเพิ่มเมื่อเราแมปอินพุตกับเอาต์พุต

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

เอาต์พุตสำหรับอินพุตแผนที่:

(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]

แผนที่อินพุตไปยังเอาต์พุต

(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]

โปรดทราบว่าตอนนี้เรามี s ที่ด้านขวาสำหรับอินพุตไปยังเอาต์พุตแล้ว การแมป สัญลักษณ์เหล่านี้แสดงถึงช่วงของค่า ตัวอย่างเช่น ในกรณีนี้ องค์ประกอบอินพุตทุกรายการที่มีดัชนี d0 จะแมปกับส่วน 10x1x30 ของเอาต์พุต

Constant และ Iota

ไฟล์เหล่านี้ไม่มีพารามิเตอร์อินพุต จึงไม่ต้องคำนวณการจัดทําดัชนี

DynamicSlice

DynamicSlice มีลักษณะเหมือนกับสไลซ์ แต่ออฟเซ็ตจะเป็นแบบไดนามิก

src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}

แผนที่เอาต์พุตไปยังอินพุตสำหรับ src

(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
  hlo: of1 = s32[] parameter(1)
  (d0, d1, d2)  -> ()
s1 in [0, 0]
  hlo: of2 = s32[] parameter(2)
  (d0, d1, d2)  -> ()
s2 in [0, 226]
  hlo: of3 = s32[] parameter(3)
  (d0, d1, d2) -> ()

โปรดทราบว่าตอนนี้เรามี s ทางด้านขวาสําหรับการแมปอินพุตกับเอาต์พุต สัญลักษณ์เหล่านี้แสดงค่ารันไทม์ ตัวอย่างเช่น ในกรณีนี้สำหรับองค์ประกอบทั้งหมดของเอาต์พุตที่มีดัชนี d0, d1, d2 เราจะเข้าถึงออฟเซตส่วนของข้อมูล of1, of2 และ of3 เพื่อคํานวณดัชนีของอินพุต ช่วงเวลาของตัวแปรรันไทม์จะมาจากสมมติฐานว่าทั้งส่วนอยู่ในขอบเขต

เอาต์พุตไปยังแผนที่อินพุตสำหรับ of1, of2 และ of3:

(d0, d1, d2)  -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]

DynamicUpdateSlice

src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
    s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)

เอาต์พุตสำหรับอินพุตแผนที่สำหรับ src เพียงเล็กน้อย คุณสามารถเพิ่มความแม่นยำได้โดยจำกัดโดเมนให้อยู่ในดัชนีที่ไม่ได้อัปเดต แต่ตอนนี้การจัดทำดัชนีแผนที่ไม่รองรับข้อจำกัดความเท่าเทียม

(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]

เอาต์พุตไปยังแผนที่อินพุตสำหรับ upd:

(d0, d1)[s0, s1]  -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
  hlo: of1 = s32[] parameter(2)
  (d0, d1)  -> ()
s1 in [0, 20]
  hlo: of2 = s32[] parameter(3)
  (d0, d1)  -> ()

โปรดทราบว่าตอนนี้เรามี s ที่ด้านขวาสำหรับการแมปอินพุตกับเอาต์พุตแล้ว สัญลักษณ์เหล่านี้คือสัญลักษณ์ที่แทนค่ารันไทม์ ตัวอย่างเช่น ในกรณีนี้สำหรับองค์ประกอบทั้งหมดของเอาต์พุตที่มีดัชนี d0, d1 เราจะเข้าถึงออฟเซตส่วน of1 และ of2 เพื่อคํานวณดัชนีของอินพุต ช่วงเวลาของตัวแปรรันไทม์จะมาจากสมมติฐานว่าทั้งส่วนอยู่ในขอบเขต

แมปเอาต์พุตกับอินพุตสำหรับ of1 และ of2

(d0, d1)  -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]

รวบรวม

ระบบรองรับเฉพาะการเก็บรวบรวมแบบง่ายเท่านั้น ดู [gather_simplifier] (https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h)

operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
  offset_dims={1,2,3},
  collapsed_slice_dims={},
  start_index_map={0,1},
  index_vector_dim=1,
  slice_sizes={7,8,4}

เอาต์พุตไปยังแผนที่อินพุตสำหรับ operand:


(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
  hlo: indices = s32[1806,2]{1,0} parameter(1)
  (d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
  hlo: indices = s32[1806,2]{1,0} parameter(1)
  (d0, d1, d2, d3) -> (d0, 1)

โปรดทราบว่าตอนนี้เรามี s ทางด้านขวาสําหรับการแมปอินพุตกับเอาต์พุต สัญลักษณ์เหล่านี้แสดงค่ารันไทม์ ตัวอย่างเช่น ในกรณีนี้สำหรับองค์ประกอบทั้งหมดของเอาต์พุตที่มีอินเด็กซ์ d0, d1, d2, d3 เราจะดึงองค์ประกอบ (d0, 0) และ (d0, 1) ออกจากเทนเซอร์ indices

แผนที่เอาต์พุตไปยังอินพุตสำหรับ indices

  (d0, d1, d2, d3)[s0] -> (d0, s0)
  domain:
  d0 in [0, 1805]
  d1 in [0, 6]
  d2 in [0, 7]
  d3 in [0, 3]
  s0 in [0, 1]

ตัวแปรช่วง s0 แสดงให้เห็นว่าเราต้องการทั้งแถว (d0, *) ของค่า indices Tensor เพื่อคำนวณองค์ประกอบของเอาต์พุต

สลับตำแหน่ง

การแมปการจัดทำดัชนีสำหรับการเปลี่ยนรูปแบบคือการเรียงสับเปลี่ยนมิติข้อมูลอินพุต/เอาต์พุต

p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}

แมปเอาต์พุตไปยังอินพุต

(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]

อินพุตไปยังเอาต์พุตแผนที่:

(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]

ย้อนกลับ

แผนที่การจัดทำดัชนีสำหรับการเปลี่ยนกลับจะเปลี่ยนมิติข้อมูลที่เปลี่ยนกลับเป็น upper_bound(d_i) - d_i ดังนี้

p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}

เอาต์พุตสำหรับอินพุตแผนที่:

(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]

อินพุตสำหรับเอาต์พุตแผนที่:

(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]

(Variadic)Reduce (ลด)

การลดตามตัวแปรมีอินพุตหลายรายการและอินสแตนซ์หลายรายการ แผนที่จากเอาต์พุตไปยัง อินพุตจะเพิ่มขนาดที่ลดลง ดังนั้น การดำเนินการนี้จะทำงานแบบกลับกันกับประกาศในบางแง่

p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
  dimensions={0}, to_apply=max

เอาต์พุตสำหรับอินพุตแผนที่:

output -> input_j:

(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]

output -> init_j:

(d0) -> ()
domain:
d0 in [0, 9]

อินพุตสำหรับเอาต์พุตการจับคู่:

Input_i -> output_j:

(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]

init_i -> output_j:

()[s0] -> (s0)
domain:
s0 in [0, 9]

for i, j = 0, ... INPUT_COUNT

สไลซ์

การจัดทำดัชนีจากเอาต์พุตไปยังอินพุตสำหรับส่วนของผลลัพธ์จะทำให้เกิดแผนที่การจัดทำดัชนีแบบเพิ่มระยะ ซึ่งใช้ได้กับองค์ประกอบทั้งหมดของเอาต์พุต การแมปจากอินพุตไปยังเอาต์พุตจะจำกัดอยู่ในช่วงที่มีการสตรีดที่มาจากองค์ประกอบในอินพุต

p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
  slice={[5:10:1], [3:20:7], [0:50:2]}

แมปเอาต์พุตไปยังอินพุต

(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]

แผนที่อินพุตไปยังเอาต์พุต

(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]

ปรับรูปร่าง

การเปลี่ยนรูปแบบมีหลายรูปแบบ

ยุบรูปร่าง

นี่คือ "การทำให้เป็นเชิงเส้น" จะปรับรูปร่างจาก N-D เป็น 1D

p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)

แมปเอาต์พุตไปยังอินพุต

(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]

อินพุตไปยังเอาต์พุตแผนที่:

(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]

ขยายรูปร่าง

การดำเนินการนี้เป็นการดำเนินการ "ยุบรูปร่าง" แบบย้อนกลับ ซึ่งจะเปลี่ยนรูปร่างอินพุต 1 มิติให้เป็นเอาต์พุต N มิติ

p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)

เอาต์พุตสำหรับอินพุตแผนที่:

(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]

แผนที่อินพุตไปยังเอาต์พุต

(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]

การเปลี่ยนรูปร่างทั่วไป

นี่คือการดำเนินการปรับรูปร่างที่ไม่สามารถแสดงเป็นการขยายรายการเดียว หรือ ยุบรูปร่าง และต้องแสดงเป็นองค์ประกอบของรูปร่างแบบขยายหรือยุบอย่างน้อย 2 รายการเท่านั้น

ตัวอย่างที่ 1: การเปลี่ยนรูปแบบเป็นเชิงเส้นและการแปลงกลับ

p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)

การเปลี่ยนรูปร่างนี้สามารถแสดงเป็นองค์ประกอบของรูปร่างที่ยุบจาก tensor<4x8xf32> เป็น tensor<32xf32> แล้วขยายรูปร่างเป็น tensor<2x4x4xf32>

เอาต์พุตสำหรับอินพุตแผนที่:

(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]

อินพุตสำหรับเอาต์พุตแผนที่:

(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]

ตัวอย่างที่ 2: รูปร่างย่อยที่ขยายและยุบ

p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)

ซึ่งการ reshape นี้สามารถแสดงเป็นองค์ประกอบของการ reshape 2 รายการ รายการแรก ยุบมิติข้อมูลด้านนอกสุด tensor<4x8x12xf32> เป็น tensor<32x12xf32> และอันที่ 2 ขยายมิติข้อมูลด้านในสุด tensor<32x12xf32> เป็น tensor<32x3x4xf32>

เอาต์พุตสำหรับอินพุตแผนที่:

(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]

แผนที่อินพุตไปยังเอาต์พุต

(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]

บิตแคสต์

การดำเนินการเปลี่ยนประเภทข้อมูลแบบบิตสามารถแสดงเป็นลําดับการเปลี่ยนรูปแบบการเรียงลําดับการเปลี่ยนรูปแบบ ดังนั้น แผนที่การจัดทำดัชนีของลำดับดังกล่าวจึงเป็นเพียงการประกอบแผนที่การจัดทำดัชนี

Concatenate

การแมปเอาต์พุตกับอินพุตสำหรับ concat จะกำหนดไว้สำหรับอินพุตทั้งหมด แต่มีโดเมนที่ไม่ทับซ้อนกัน กล่าวคือจะใช้อินพุตเพียงรายการเดียวในแต่ละครั้ง

p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}

การแมปเอาต์พุตกับอินพุต

เอาต์พุต -> อินพุต 1:

(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]

เอาต์พุต -> อินพุต 2:

(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]

เอาต์พุต -> อินพุต 3:

(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]

อินพุตสำหรับแผนที่เอาต์พุต

อินพุต 1 -> เอาต์พุต

(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]

อินพุต 2 -> เอาต์พุต:

(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]

อินพุต 3 -> เอาต์พุต:

(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]

จุด

แผนที่การจัดทำดัชนีสำหรับจุดจะคล้ายกับแผนที่ของ Reduce อย่างมาก

p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
  lhs_batch_dims={0}, rhs_batch_dims={0},
  lhs_contracting_dims={2}, rhs_contracting_dims={1}

การจับคู่เอาต์พุตไปยังอินพุต:

เอาต์พุต -> input_1:

(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]

output -> input_2:

(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]

อินพุตสำหรับแผนที่เอาต์พุต

input_1 -> output:

(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]

Input_2 -> เอาต์พุต:

(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]

Pad

การจัดทำดัชนีของ PadOp จะผกผันกับการจัดทำดัชนีของ SliceOp

p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0

การกําหนดค่าระยะห่างจากขอบ 1_4_1x4_8_0 หมายถึง lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1

การแมปเอาต์พุตกับอินพุต

เอาต์พุต -> อินพุต

(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]

เอาต์พุต -> init:

(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]

ReduceWindow

ReduceWindow ใน XLA ยังเพิ่มระยะห่างจากขอบด้วย ดังนั้นแมปการจัดทำดัชนีอาจ คํานวณเป็นองค์ประกอบของการจัดทำดัชนี ReduceWindow ที่ไม่ได้ใช้ Padding ใดๆ และการจัดทำดัชนีของ PadOp

c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
  window={size=1x512 pad=0_0x0_0}, to_apply=max

เอาต์พุตสำหรับอินพุตแผนที่:

เอาต์พุต -> อินพุต

(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]

เอาต์พุต -> init:

(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]

การจัดทำดัชนีแผนที่สําหรับฟิวชัน

แผนที่การจัดทำดัชนีสําหรับการดําเนินการแบบฟิวชันคือองค์ประกอบของแผนที่การจัดทำดัชนีสําหรับการดําเนินการทุกรายการในคลัสเตอร์ ระบบอาจอ่านอินพุตบางรายการหลายครั้งด้วยรูปแบบการเข้าถึงที่แตกต่างกัน

อินพุต 1 รายการ แผนที่การจัดทำดัชนีหลายรายการ

นี่คือตัวอย่างสำหรับ p0 + transpose(p0)

f {
  p0 = f32[1000, 1000] parameter(0)
  transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
  ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}

การแมปการจัดทำดัชนีเอาต์พุตกับอินพุตสำหรับ p0 จะเป็น (d0, d1) -> (d0, d1) และ (d0, d1) -> (d1, d0) หมายความว่า การจะประมวลผลธาตุหนึ่ง ของเอาต์พุต เราอาจต้องอ่านพารามิเตอร์อินพุต 2 ครั้ง

อินพุต 1 รายการ แมปการจัดทำดัชนีที่กรองข้อมูลที่ซ้ำกันออกแล้ว

มีบางกรณีที่การแมปการจัดทำดัชนีเหมือนกัน แม้ว่าจะดูไม่ออกในทันที

f {
  p0 = f32[20, 10, 50] parameter(0)
  lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
  lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
  lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
  rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
  rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
  rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
  ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}

แผนที่การจัดทำดัชนีเอาต์พุตเป็นอินพุตสำหรับ p0 ในกรณีนี้คือแค่ (d0, d1, d2) -> (d2, d0, d1)

Softmax

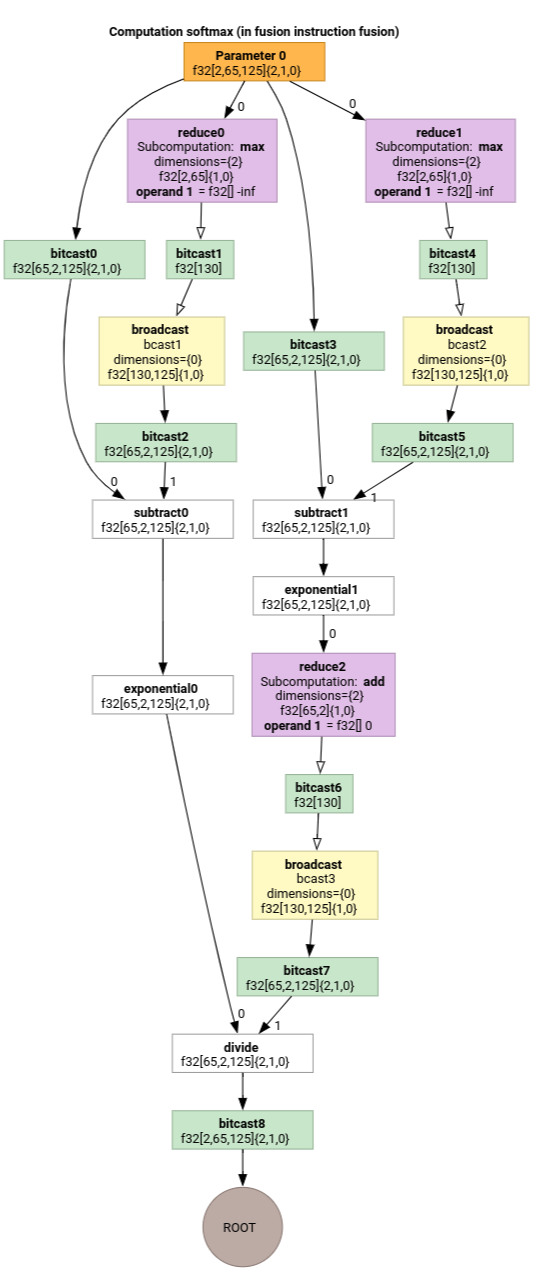
การแมปการจัดทำดัชนีเอาต์พุตกับอินพุตสําหรับ parameter 0 สําหรับ Softmax

(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]

และ

(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]

โดยที่ s0 หมายถึงมิติข้อมูลด้านในสุดของอินพุต

ตัวช่วยจัดทำดัชนีแผนที่

ตัวดำเนินการแบบง่ายเริ่มต้นสำหรับต้นทาง mlir::AffineMap ไม่สามารถสร้าง สมมติฐานเกี่ยวกับช่วงของมิติข้อมูล/สัญลักษณ์ ดังนั้นจึงไม่สามารถลดความซับซ้อนของนิพจน์ที่มี mod และ div ได้อย่างมีประสิทธิภาพ

เราสามารถใช้ประโยชน์จากความรู้เกี่ยวกับขอบเขตต่ำสุดและระดับบนของ ของนิพจน์ย่อยในแผนที่แบบแนบง่ายเพื่อลดความซับซ้อนของนิพจน์ย่อย

ตัวช่วยเขียนสูตรให้เข้าใจง่ายสามารถเขียนนิพจน์ต่อไปนี้ใหม่ได้

(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16) สำหรับ d ใน [0, 6] x [0, 14] เปลี่ยนเป็น (d0, d1) -> (d0, d1)
(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10) สำหรับ di in [0, 9] เปลี่ยนเป็น (d0, d1, d2) -> (d0, d1, d2)
(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8) สำหรับ d_i in [0, 9] เปลี่ยนเป็น (d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8)
(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9) สำหรับ d ใน [0, 9] x [0, 10] เปลี่ยนเป็น (d0, d1) -> (d0)

เครื่องมือจัดทำแผนที่การจัดทำดัชนีอย่างง่ายช่วยให้เราเข้าใจว่า การปรับรูปร่างใน HLO จะยกเลิกกันและกัน

p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)

หลังจากการประกอบแผนที่การจัดทำดัชนีและการทำให้แผนที่เรียบง่ายแล้ว เราจะได้

(d0, d1, d2) -> (d0, d1, d2)

การลดความซับซ้อนของแผนที่การจัดทำดัชนียังช่วยลดข้อจำกัดด้วย

ระบบจะเขียนข้อจำกัดประเภท lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_bound ใหม่เป็น updated_lower_bound <= affine_expr <= updated_upped_bound
เป็นข้อจำกัดที่ใช้ได้เสมอ เช่น d0 + s0 in [0, 20] สำหรับ d0 in [0, 5] และ s0 in [1, 3] จะหายไป
นิพจน์ Affine ในข้อจำกัดจะได้รับการเพิ่มประสิทธิภาพเป็นสัมพรรคภาพการจัดทำดัชนี แผนที่ด้านบน

ดูตัวอย่างเพิ่มเติมได้ที่ indexing_map_test.cc