이 문서에서는 HLO 연산의 색인 매핑을 기호적으로 계산할 수 있는 HLO 색인 분석을 설명합니다. 색인 매핑은 한 텐서의 색인을 다른 텐서의 색인에 매핑하는 함수입니다(예: HLO 명령어 출력의 색인을 HLO 명령어 입력의 색인에 매핑하거나 그 반대로 매핑).
예
tensor<20xf32>에서 tensor<10x20x30xf32>로의 브로드캐스트
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
출력에서 입력으로의 색인 매핑은 i in
[0, 10], j in [0, 20], k in [0, 30]의 경우 (i, j, k) -> (j)입니다.
동기
XLA GPU는 여러 맞춤 솔루션을 사용하여 병합, 피연산자 활용, 카드 레이아웃 스킴에 관해 추론합니다(아래에서 자세히 알아보기). 색인 분석의 목표는 이러한 사용 사례에 재사용 가능한 구성요소를 제공하는 것입니다. 색인 분석은 MLIR의 Affine Map 인프라를 기반으로 하며 HLO 시맨틱스를 추가합니다.
병합
메모리 병합에 관한 추론은 요소의 요소를 계산하기 위해 입력의 어떤 요소/슬라이스를 읽어야 하는지 출력됩니다.
피연산자 사용률
XLA의 피연산자 사용률은 명령어의 각 입력이 출력이 완전히 사용되었다는 가정 하에 사용됩니다. 현재 일반 사례의 경우에도 사용률이 계산되지 않습니다. 색인 분석을 통해 정확하게 사용률을 계산할 수 있습니다.
타일식:
타일/슬라이스는 오프셋으로 매개변수화된 텐서의 초직각형 하위 집합입니다. 큰 도움이 됩니다. 타일 전파는 오퍼레이션 자체의 타일링 매개변수를 사용하여 오퍼레이션의 생산자/소비자. 거기 은(는) 이미 라이브러리 소프트맥스와 닷에 대해 이 작업을 수행합니다 타일 전파는 더 일반적이고 지도 인덱싱을 통해 표현될 때 더욱 강력해집니다.
함수 및 도메인
색인 생성 맵은 함수 f(x) = f(d, r, rt)입니다.
텐서 A의 다중 색인 d를
텐서 B입니다. 매개변수 r은
텐서 B에는 있지만 텐서 A에는 없는 차원입니다. 이
매개변수 rt는 런타임 값을 나타냅니다. 예: 지표가 표시됩니다
예를 들어 tensor<2x4x8x16xf32>에서
tensor<4x8xf32>이면 2D 출력에서 4D 입력으로의 색인 생성 맵은
(d0, d1) -> (r0, d0, d1, r1), 여기서 d_i는
출력 텐서의 색인에 해당합니다. 범위 변수 r_j는 여러 값을 인코딩합니다. 즉, 출력의 (d0, d1) 요소를 계산하려면 입력의 (r0, d0, d1, r1) 요소(여기서 r0 in [0, 1] 및 r1 in [0, 15])가 필요합니다.
이 매핑은 HLO 명령어의 속성에서 구성할 수 있으며 융합되지 않은 명령어의 매핑을 구성하여 융합의 색인을 가져올 수 있습니다. 매핑에는 또한 텐서의 요소를 지정하는 도메인이 있습니다. 매핑이 존재하는지 확인합니다
f(x) s.t.
lb <= g(x) <= ub
재계산을 최소화하려면 기호화된 전처리를 위한 라이브러리가 필요합니다. 있습니다. XLA는 이미 MLIR에 종속되므로 mlir::AffineMap 을 사용해야 했습니다.
일반적인 AffineMap는 다음과 같습니다.
(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)
AffineMap에는 측정기준과 기호라는 두 가지 유형의 매개변수가 있습니다. 이
측정기준은 측정기준 변수 d, 기호는
범위 변수 r 및 RT 변수 rt입니다. AffineMap이(가) 포함되지 않음
메타데이터로 확인할 수 있으므로 이 데이터를
도움이 될 수 있습니다
struct Interval {
int64_t lower;
int64_t upper;
};
// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
Interval bounds;
};
// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
Interval range;
};
// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
Interval feasible_values;
const HloInstruction* hlo;
// This is a map from the iteration space of the corresponding indexing map to
// the iteration space of `hlo`. It shows what element of `hlo` we need to
// extract to get the runtime value for the RTVar.
mlir::AffineMap map;
};
class IndexingMap {
mlir::AffineMap affine_map_;
std::vector<DimVar> dim_vars_;
std::vector<RangeVar> range_vars_;
std::vector<RTVar> rt_vars_;
llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};
dim_vars_는 색인 생성 맵의 크기 변수 d에 관한 포함적 상자 제약 조건을 인코딩합니다. 이는 일반적으로 전치, 감소, 요소별, 내적과 같은 연산의 출력 텐서 모양과 일치하지만 HloConcatenateInstruction과 같은 몇 가지 예외가 있습니다.
range_vars_는 r 매개변수가 취할 수 있는 가능한 값을 인코딩합니다.
rt_vars_는 관련 hlo 명령을 액세스와 함께 저장
실행 가능한 값이 포함됩니다. 예를 들어 오프셋은 동적입니다.
1D HloDynamicSliceInstruction의 경우 상응하는 RTVar에는
(d0) -> () 액세스 권한으로 순위 0 텐서를 생성하는 HloInstruction*
이는 출력의 모든 요소에 대해 동일한 요소를 추출하고
오프셋 텐서에서 입력 색인을 계산합니다. 슬라이스의 오프셋이 항상 0과 tensor_size - slice_size - 1 사이라고 가정할 수도 있습니다.
예시를 통해 위의 내용이 실제로 무엇을 의미하는지 알아보겠습니다.
융합되지 않은 작업을 위한 지도 색인 생성
요소별
요소별 작업의 경우 색인 생성 맵은 ID입니다.
p0 = f32[10, 20] parameter(0)
p1 = f32[10, 20] parameter(1)
add = f32[10, 20] add(p0, p1)
입력 맵의 출력은 다음과 같습니다.
- 출력 -> input_i:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
입력-출력 매핑
- input_i -> output:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
방송
브로드캐스트는 출력을 입력에 매핑할 때 일부 측정기준이 삭제되고 입력을 출력에 매핑할 때 추가된다는 것을 의미합니다.
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
입력 맵의 출력은 다음과 같습니다.
(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]
입력-출력 맵
(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]
이제 오른쪽에 입력-출력을 위한 s가 있습니다.
있습니다. 값의 범위를 나타내는 기호입니다. 예를 들어 이 특정 경우에는 색인이 d0인 입력의 모든 요소가 출력의 10x1x30 슬라이스에 매핑됩니다.
상수 및 Iota
편리하게도 입력 매개변수가 없으므로 색인을 계산할 대상이 없습니다.
DynamicSlice
DynamicSlice는 Slice와 비슷하지만 오프셋은 동적입니다.
src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}
src의 입력 맵 출력은 다음과 같습니다.
(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
hlo: of1 = s32[] parameter(1)
(d0, d1, d2) -> ()
s1 in [0, 0]
hlo: of2 = s32[] parameter(2)
(d0, d1, d2) -> ()
s2 in [0, 226]
hlo: of3 = s32[] parameter(3)
(d0, d1, d2) -> ()
이제 입력-출력 매핑을 위한 s가 오른쪽에 있습니다.
런타임 값을 나타내는 기호입니다. 예를 들어 이
색인이 d0, d1, d2인 출력의 모든 요소에 대해
슬라이스 오프셋 of1, of2, of3에 액세스하여 입력 색인을 계산합니다.
런타임 변수의 간격은 전체 슬라이스가 경계 내에 있다고 가정하여 파생됩니다.
of1, of2, of3의 입력 맵 출력은 다음과 같습니다.
(d0, d1, d2) -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
DynamicUpdateSlice
src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)
src의 입력 맵으로의 출력은 간단합니다.
도메인을 업데이트되지 않은 색인으로 제한하지만 현재는 지도의 색인을 생성합니다.
비균등 제약조건을 지원하지 않습니다.
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]
upd의 출력-입력 맵:
(d0, d1)[s0, s1] -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
hlo: of1 = s32[] parameter(2)
(d0, d1) -> ()
s1 in [0, 20]
hlo: of2 = s32[] parameter(3)
(d0, d1) -> ()
이제 입력-출력 매핑을 위한 s가 오른쪽에 있습니다.
이는 런타임 값을 나타내는 기호입니다. 예를 들어 이
액세스하는 색인이 있는 d0, d1 출력의 모든 요소에 대한 특정 사례
슬라이스 오프셋 of1 및 of2로 입력 색인을 계산합니다. 간격
는 전체 슬라이스가
경계
of1 및 of2의 출력-입력 매핑:
(d0, d1) -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]
수집
단순화된 수집만 지원됩니다. [gather_simplifier].(https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h)를 참조하세요.
operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
offset_dims={1,2,3},
collapsed_slice_dims={},
start_index_map={0,1},
index_vector_dim=1,
slice_sizes={7,8,4}
operand의 입력 맵 출력은 다음과 같습니다.
(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 1)
이제 입력-출력 매핑을 위한 s가 오른쪽에 있습니다.
런타임 값을 나타내는 기호입니다. 예를 들어 이 특정 경우에는 색인이 d0, d1, d2, d3인 출력의 모든 요소에 대해 indices 텐서에서 요소 (d0, 0) 및 (d0, 1)을 추출합니다.
indices의 출력-입력 맵:
(d0, d1, d2, d3)[s0] -> (d0, s0)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 1]
범위 변수 s0는
출력 요소를 계산하는 indices 텐서.
전치
행열을 바꾸기 위한 지도 색인 생성은 입력/출력 차원의 순열입니다.
p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}
입력 맵에 대한 출력은 다음과 같습니다.
(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]
입력-출력 매핑은 다음과 같습니다.
(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]
역방향
역방향으로 되돌리기 위한 맵의 색인 생성은 되돌린 측정기준을 upper_bound(d_i) -
d_i로 변경합니다.
p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}
입력 맵의 출력은 다음과 같습니다.
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
입력-출력 맵:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
(Variadic)Reduce
변수 리덕션에는 여러 입력과 여러 인수가 있으며 출력에서 입력으로의 매핑은 축소된 차원을 추가합니다. 따라서 어떤 의미에서는 브로드캐스트의 역수처럼 작동합니다.
p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
dimensions={0}, to_apply=max
입력에 대한 출력은 다음과 같습니다.
- 출력 -> input_j:
(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]
- 출력 -> init_j:
(d0) -> ()
domain:
d0 in [0, 9]
입력-출력 매핑은 다음과 같습니다.
- 입력_i -> output_j:
(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]
- init_i -> output_j:
()[s0] -> (s0)
domain:
s0 in [0, 9]
for i, j = 0, ... INPUT_COUNT.
슬라이스
슬라이스의 출력에서 입력으로 색인을 생성하면 출력의 모든 요소에 유효한 획이 있는 색인 매핑이 생성됩니다. 입력에서 출력으로의 매핑은 입력에 있는 요소의 줄무늬 범위로 제한됩니다.
p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
slice={[5:10:1], [3:20:7], [0:50:2]}
입력 맵에 대한 출력은 다음과 같습니다.
(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]
입력-출력 매핑은 다음과 같습니다.
(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]
모양 변경
형태 변경에는 다양한 맛이 있습니다.
도형 접기
이는 N차원에서 1차원으로 '선형화' 리셰이프입니다.
p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)
입력 맵에 대한 출력은 다음과 같습니다.
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
입력-출력 매핑은 다음과 같습니다.
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
도형 펼치기
역 '도형 접기'입니다. 1D 입력을 N-D 출력으로 바꿉니다.
p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)
입력 맵에 대한 출력은 다음과 같습니다.
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
입력-출력 매핑은 다음과 같습니다.
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
일반 재구성
이는 단일 확장 또는 단일 호출로 표현할 수 없는 도형 접기 2개 이상의 펼치기 또는 접기 도형의 컴포지션으로만 표현할 수 있습니다.
예시 1: 선형화-선형화 취소
p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)
이 모양 변경은 tensor<4x8xf32>에서 tensor<32xf32>로 모양을 축소한 다음 tensor<2x4x4xf32>로 모양을 확장하는 컴포지션으로 나타낼 수 있습니다.
입력 맵의 출력은 다음과 같습니다.
(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]
입력-출력 매핑은 다음과 같습니다.
(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
예시 2: 펼쳐진 하위 도형과 접힌 하위 도형
p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)
이 리셰이프는 두 리셰이프의 합성으로 표현할 수 있습니다. 첫 번째 항목
가장 바깥쪽 크기 tensor<4x8x12xf32>을 tensor<32x12xf32>로 축소
두 번째는 가장 안쪽 치수 tensor<32x12xf32>를
tensor<32x3x4xf32>입니다.
입력 맵에 대한 출력은 다음과 같습니다.
(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]
입력-출력 맵:
(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]
비트캐스트
비트캐스트 작업은 전위-재형-전환 시퀀스 입니다. 따라서 색인 생성 맵은 이 시퀀스의 색인 생성 맵을 조합한 것에 불과합니다.
연결
concat을 위한 출력-입력 매핑은 모든 입력에 대해 정의되지만 겹치지 않는 도메인. 즉, 한 번에 하나의 입력만 사용됩니다.
p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}
입력에 대한 출력은 다음을 매핑합니다.
- 출력 -> 입력 1:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- 출력 -> 입력 2:
(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]
- 출력 -> 입력 3:
(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]
출력 맵의 입력은 다음과 같습니다.
- 입력 1 -> output:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- 입력 2 -> 출력:
(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]
- 입력 3 -> 출력:
(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]
점
점의 색인 생성 맵은 reduce의 색인 생성 맵과 매우 유사합니다.
p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
lhs_batch_dims={0}, rhs_batch_dims={0},
lhs_contracting_dims={2}, rhs_contracting_dims={1}
입력에 대한 출력은 다음을 매핑합니다.
- output -> input_1:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
- output -> input_2:
(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
출력 맵의 입력은 다음과 같습니다.
- 입력_1 -> output:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]
- input_2 -> output:
(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]
패드
PadOp의 색인은 SliceOp 색인의 역수입니다.
p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0
패딩 구성 1_4_1x4_8_0는 lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1를 나타냅니다.
입력에 대한 출력은 다음과 같습니다.
- 출력 -> 입력:
(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]
- 출력 -> init:
(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]
ReduceWindow
XLA의 ReduceWindow는 패딩도 수행합니다. 따라서 색인 생성 맵은 패딩을 수행하지 않는 ReduceWindow 색인 생성의 합성으로 계산됩니다. 색인을 생성합니다.
c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
window={size=1x512 pad=0_0x0_0}, to_apply=max
입력 맵의 출력은 다음과 같습니다.
- 출력 -> 입력:
(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]
- 출력 -> init:
(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]
Fusion용 지도 색인 생성
융합 연산의 색인 생성 맵은 클러스터의 모든 연산에 대한 색인 생성 맵의 조합입니다. 일부 입력은 다른 액세스 패턴으로 여러 번 읽힐 수 있습니다.
입력 1개, 색인 생성 맵 여러 개
다음은 p0 + transpose(p0)의 예입니다.
f {
p0 = f32[1000, 1000] parameter(0)
transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}
p0의 출력-입력 색인 매핑은 (d0, d1) -> (d0, d1) 및 (d0, d1) -> (d1, d0)입니다. 즉, 하나의 요소를 계산하려면
입력 매개변수를 두 번 읽어야 할 수도 있습니다.
중복 삭제된 색인 생성 맵 1개 입력
색인 생성 맵이 즉시 명확하지 않더라도 실제로 동일한 경우가 있습니다.
f {
p0 = f32[20, 10, 50] parameter(0)
lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}
여기서 p0의 출력-입력 색인 생성 맵은
(d0, d1, d2) -> (d2, d0, d1)입니다.
소프트맥스
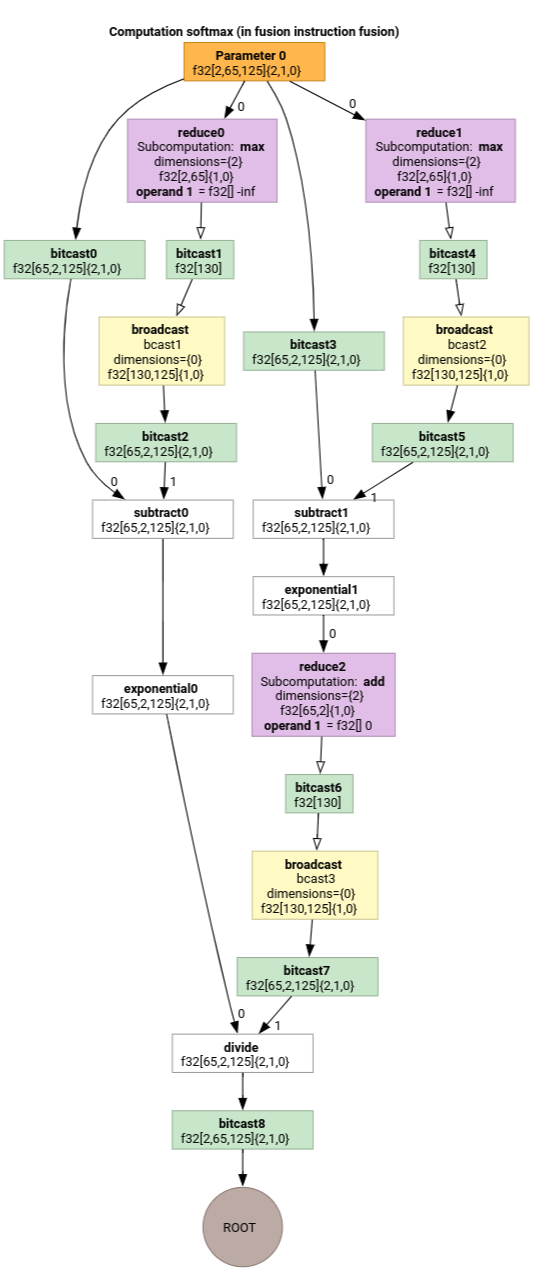
출력-입력 색인은 소프트맥스의 parameter 0에 매핑됩니다.
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]
및
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
여기서 s0는 입력의 가장 안쪽 크기를 나타냅니다.
색인 생성 지도 단순화 도구
mlir::AffineMap 업스트림의 기본 단순화 도구는 어떤 것도 만들 수 없습니다.
차원/기호 범위에 대한 가정. 따라서
mod를 사용하여 표현식을 div효율적으로 단순화합니다.
인코더-디코더 아키텍처의 하한 및 상한에 대한 하위 표현식을 사용하여 훨씬 더 단순화할 수 있게 되었습니다.
단순화 도구는 다음 표현식을 다시 작성할 수 있습니다.
[0, 6] x [0, 14]의 d에 대한(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16)가(d0, d1) -> (d0, d1)가 됩니다.di in [0, 9]의(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10)가(d0, d1, d2) -> (d0, d1, d2)로 변경됩니다.d_i in [0, 9]의(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8)가(d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8)로 변경됩니다.- d간
(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9)가[0, 9] x [0, 10]에(d0, d1) -> (d0)가 됩니다.
색인 생성 맵 단순화 도구를 사용하면 HLO에서 체이닝된 일부 변형이 서로 취소된다는 것을 알 수 있습니다.
p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)
색인 생성 맵을 구성하고 단순화한 후 다음과 같은 결과를 얻습니다.
(d0, d1, d2) -> (d0, d1, d2).
색인 지도를 단순화하면 제약 조건도 간소화됩니다.
- 유형의 제약조건
lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_bound:updated_lower_bound <= affine_expr <= updated_upped_bound(으)로 다시 작성되었습니다. - 항상 충족되는 제약 조건(예:
d0 + s0 in [0, 20]d0 in [0, 5]및s0 in [1, 3]에서 제거되었습니다. - 제약조건의 아핀 표현식은 색인 생성 아핀으로 최적화됩니다. 있습니다.
더 많은 예는 indexing_map_test.cc를 참고하세요.

