इस दस्तावेज़ में एचएलओ इंडेक्स के विश्लेषण के बारे में बताया गया है. इसकी मदद से, सिंबल के तौर पर HLO ops के लिए कंप्यूट इंडेक्सिंग मैप. इंडेक्स करने वाला मैप एक फ़ंक्शन है, जो मैप एक टेंसर के इंडेक्स से दूसरे टेंसर का इंडेक्स, जैसे कि किसी एचएलओ के इंडेक्स निर्देश आउटपुट को HLO निर्देश इनपुट के इंडेक्स पर या इसके उलटा.
उदाहरण
tensor<20xf32> से tensor<10x20x30xf32> तक ब्रॉडकास्ट के लिए
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
आउटपुट से इनपुट के लिए इंडेक्स मैप, i in
[0, 10], j in [0, 20], और k in [0, 30] के लिए (i, j, k) -> (j) है.
वजह
XLA जीपीयू, कोलेसिंग, ऑपरेंड के बारे में तर्क देने के लिए पसंद के मुताबिक कई समाधानों का इस्तेमाल करता है टाइलिंग स्कीम (ज़्यादा जानकारी नीचे दी गई है). इंडेक्स करने का मकसद विश्लेषण में ऐसे इस्तेमाल के लिए, फिर से इस्तेमाल किया जा सकने वाला कॉम्पोनेंट मिलता है. इंडेक्स करने का विश्लेषण को MLIR के Affine Map इन्फ़्रास्ट्रक्चर पर बनाया गया है और इसमें HLO सिमैंटिक जोड़ दिया गया है.
कोलेसिंग
मेमोरी को इकट्ठा किए जाने के बारे में तर्क करना गैर-मामूली मामलों में संभव हो जाता है, जब हमें पता है कि इनपुट के कौनसे एलिमेंट/स्लाइस को पढ़ा जाता है, ताकि आउटपुट.
ऑपरेंड यूटिलाइज़ेशन
XLA में ऑपर्च्यूनिटी के इस्तेमाल से पता चलता है कि निर्देश का हर इनपुट कितना है इस्तेमाल कर लिया जाएगा. फ़िलहाल, इस्तेमाल नहीं किया जा सकता इसकी गिनती सामान्य मामले के लिए की जाती है. इंडेक्स करने के विश्लेषण की मदद से, इस्तेमाल के हिसाब से सटीक जानकारी मिलती है.
टाइलिंग
टाइल/स्लाइस, ऑफ़सेट से पैरामीटर किए गए टेंसर का हाइपर-रेक्टैंग्युलर सबसेट है, पैरों के बीच की दूरी कम या ज़्यादा नहीं करना पड़ता. टाइल प्रोपगेशन, एक ऐसा तरीका है जिससे खुद ऑप के टाइलिंग पैरामीटर का इस्तेमाल करके, ऑप के निर्माता/उपभोक्ता. पहले से ही एक ऐसी लाइब्रेरी मौजूद है जो सॉफ़्टमैक्स और डॉट के लिए ऐसा करती है. टाइल का प्रॉपेगेशन, इंडेक्सिंग मैप के ज़रिए दिखाने पर, इसे ज़्यादा सामान्य और बेहतर बनाया जा सकता है.
फ़ंक्शन और डोमेन
इंडेक्स करने वाला मैप, f(x) = f(d, r, rt) फ़ंक्शन है
जो टेंसर A के मल्टी-इंडेक्स d को
टेंसर B. पैरामीटर r, इसके इंडेक्स की रेंज को दिखाता है
वे डाइमेंशन जो टेंसर B में मौजूद हैं, लेकिन टेंसर A में नहीं. कॉन्टेंट बनाने
पैरामीटर rt, रनटाइम की वैल्यू को दिखाता है, जैसे कि इकट्ठा करने की प्रोसेस के इंडेक्स
उदाहरण के लिए, अगर tensor<2x4x8x16xf32> से घटाकर tensor<4x8xf32> किया जाता है, तो 2D आउटपुट से 4D इनपुट में इंडेक्स करने वाला मैप (d0, d1) -> (r0, d0, d1, r1) होता है. यहां d_i ऐसे डाइमेंशन वैरिएबल होते हैं जो आउटपुट टेंसर के इंडेक्स से मेल खाते हैं. रेंज वैरिएबल r_j कोड में बदलें
एक से ज़्यादा वैल्यू, जैसे कि आउटपुट के (d0, d1) एलिमेंट की गणना करने के लिए, हमें
इनपुट के (r0, d0, d1, r1) एलिमेंट, जहां r0 in [0, 1] और
r1 in [0, 15].
इस मैपिंग को एचएलओ निर्देशों के एट्रिब्यूट से बनाया जा सकता है. इसके अलावा, फ़्यूज़ किए गए निर्देशों की मैपिंग को फ़्यूज़ करने के लिए इंडेक्स किया जा सकता है. मैपिंग में एक डोमेन भी होता है, जो टेंसर के किन एलिमेंट के लिए तय करता है मैपिंग मौजूद है.
f(x) ऐसा हो कि
lb <= g(x) <= ub
हम रीकंप्यूटेशन (फिर से गिनती) को कम करना चाहते हैं. इसलिए, हमें सिम्बॉलिक के लिए एक लाइब्रेरी की ज़रूरत है कंप्यूटेशन. XLA पहले से ही MLIR पर निर्भर है. इसलिए, हम कोई और सिंबलिक ऐरिथमेटिक लाइब्रेरी लिखने के बजाय, mlir::AffineMap का इस्तेमाल करते हैं.
आम AffineMap ऐसा दिखता है
(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)
AffineMap में दो तरह के पैरामीटर होते हैं: डाइमेंशन और सिंबल. डाइमेंशन, डाइमेंशन वैरिएबल d से जुड़े होते हैं. सिंबल, रेंज वैरिएबल r और आरटी वैरिएबल rt से जुड़े होते हैं. AffineMap में डाइमेंशन की रेंज के बारे में कोई मेटाडेटा नहीं होता, इसलिए हमें यह डेटा खुद उपलब्ध कराना होता है.
struct Interval {
int64_t lower;
int64_t upper;
};
// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
Interval bounds;
};
// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
Interval range;
};
// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
Interval feasible_values;
const HloInstruction* hlo;
// This is a map from the iteration space of the corresponding indexing map to
// the iteration space of `hlo`. It shows what element of `hlo` we need to
// extract to get the runtime value for the RTVar.
mlir::AffineMap map;
};
class IndexingMap {
mlir::AffineMap affine_map_;
std::vector<DimVar> dim_vars_;
std::vector<RangeVar> range_vars_;
std::vector<RTVar> rt_vars_;
llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};
dim_vars_ इंडेक्सिंग मैप के डाइमेंशन वैरिएबल d के लिए, शामिल करने वाले बॉक्स की पाबंदियों को कोड में बदलता है. आम तौर पर, ये पाबंदियां ट्रांसपोज़, रिड्यूस, एलिमेंट-वाइज़, बिंदु जैसे ऑपरेशन के लिए, आउटपुट टेंसर के आकार से मेल खाती हैं. हालांकि, HloConcatenateInstruction जैसे कुछ अपवाद हैं.
range_vars_, r पैरामीटर की संभावित वैल्यू को कोड में बदलता है.
rt_vars_, रनटाइम में उनके ऐक्सेस पैटर्न और काम की वैल्यू के साथ-साथ, उनसे जुड़े एचएलओ निर्देशों को सेव करता है. उदाहरण के लिए, ऑफ़सेट डाइनैमिक है
1D HloDynamicSliceInstruction के लिए. उससे जुड़े RTVar में एक ऐसा HloInstruction* होगा जो (d0) -> () ऐक्सेस पैटर्न के साथ रैंक-0 टेंसर बनाता है. ऐसा इसलिए होता है, क्योंकि आउटपुट के हर एलिमेंट के लिए, हम इनपुट के इंडेक्स का हिसाब लगाने के लिए, ऑफ़सेट टेंसर से एक ही एलिमेंट निकालते हैं. हम यह भी मान सकते हैं कि
स्लाइस का ऑफ़सेट हमेशा 0 और
tensor_size - slice_size - 1.
आइए, अलग-अलग उदाहरण के ज़रिए समझें कि ऊपर दिए गए सभी शब्दों का असल में क्या मतलब है.
Unfused Ops के लिए Maps को इंडेक्स करना
Elementwise
एलिमेंट के हिसाब से ऑपरेशन के लिए, इंडेक्सिंग मैप एक आइडेंटिटी है.
p0 = f32[10, 20] parameter(0)
p1 = f32[10, 20] parameter(1)
add = f32[10, 20] add(p0, p1)
मैप इनपुट करने के लिए आउटपुट:
- output -> input_i:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
इनपुट से आउटपुट मैप
- input_i -> output:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
ब्रॉडकास्ट
ब्रॉडकास्टिंग का मतलब है कि आउटपुट को इनपुट पर मैप करने पर, कुछ डाइमेंशन हटा दिए जाएंगे. वहीं, इनपुट को आउटपुट पर मैप करने पर, वे डाइमेंशन जोड़ दिए जाएंगे.
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
इनपुट मैप का आउटपुट:
(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]
आउटपुट मैप का इनपुट
(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]
ध्यान दें कि अब हमारे पास इनपुट-टू-आउटपुट मैपिंग के लिए, दाईं ओर s हैं. ये वे चिह्न हैं जो वैल्यू की रेंज दिखाते हैं. उदाहरण के लिए, इस मामले में इंडेक्स d0 वाले इनपुट का हर एलिमेंट, आउटपुट के 10x1x30 स्लाइस पर मैप किया जाता है.
कॉन्स्टेंट और आयोटा
आसानी से, इनमें कोई भी इनपुट पैरामीटर नहीं होता, इसलिए कंप्यूट इंडेक्स से जुड़ी जानकारी.
DynamicSlice
डाइनैमिक स्लाइस, स्लाइस की तरह है, लेकिन ऑफ़सेट डाइनैमिक हैं.
src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}
src के लिए मैप इनपुट करने का आउटपुट:
(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
hlo: of1 = s32[] parameter(1)
(d0, d1, d2) -> ()
s1 in [0, 0]
hlo: of2 = s32[] parameter(2)
(d0, d1, d2) -> ()
s2 in [0, 226]
hlo: of3 = s32[] parameter(3)
(d0, d1, d2) -> ()
ध्यान दें कि अब इनपुट-से-आउटपुट मैपिंग के लिए हमारे पास दाईं ओर s हैं.
ये वे चिह्न हैं जो रनटाइम की वैल्यू दिखाते हैं. उदाहरण के लिए, इस मामले में, इंडेक्स d0, d1, d2 वाले आउटपुट के हर एलिमेंट के लिए, हम इनपुट के इंडेक्स का हिसाब लगाने के लिए, स्लाइस ऑफ़सेट of1, of2, और of3 को ऐक्सेस करते हैं.
रनटाइम वैरिएबल के इंटरवल, इस आधार पर तय किए जाते हैं कि पूरा स्लाइस सीमाओं में बना रहे.
of1, of2 और of3 के लिए मैप इनपुट करने का आउटपुट:
(d0, d1, d2) -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
DynamicUpdateSlice
src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)
src के लिए मैप का आउटपुट बहुत छोटा है. इसे ज़्यादा सटीक बनाया जा सकता है
डोमेन को अपडेट नहीं किए गए इंडेक्स तक सीमित कर रहा है, लेकिन अभी मैप इंडेक्स कर रहा है
असमानता को बढ़ावा नहीं देती.
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]
upd के लिए मैप इनपुट करने का आउटपुट:
(d0, d1)[s0, s1] -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
hlo: of1 = s32[] parameter(2)
(d0, d1) -> ()
s1 in [0, 20]
hlo: of2 = s32[] parameter(3)
(d0, d1) -> ()
ध्यान दें कि अब इनपुट-से-आउटपुट मैपिंग के लिए हमारे पास दाईं ओर s हैं.
ये वे चिह्न हैं जो रनटाइम की वैल्यू दिखाते हैं. उदाहरण के लिए, इस
खास मामले, जहां इंडेक्स d0, d1 वाले आउटपुट के हर एलिमेंट के लिए हम ऐक्सेस करते हैं
स्लाइस ऑफ़सेट of1 और of2 इनपुट के इंडेक्स की गणना करने के लिए. रनटाइम वैरिएबल के लिए इंटरवल, इस आधार पर तय किए जाते हैं कि पूरी स्लाइस सीमाओं में बनी रहे.
of1 और of2 के लिए, आउटपुट से इनपुट मैप:
(d0, d1) -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]
इकट्ठा करना
सिर्फ़ आसान तरीके से इकट्ठा किए गए कलेक्शन का इस्तेमाल किया जा सकता है. [gather_simplifier] देखें.(https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h).
operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
offset_dims={1,2,3},
collapsed_slice_dims={},
start_index_map={0,1},
index_vector_dim=1,
slice_sizes={7,8,4}
operand के लिए, इनपुट मैप का आउटपुट:
(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 1)
ध्यान दें कि अब इनपुट-से-आउटपुट मैपिंग के लिए हमारे पास दाईं ओर s हैं.
ये ऐसे सिंबल हैं जो रनटाइम वैल्यू दिखाते हैं. उदाहरण के लिए, इस मामले में, इंडेक्स d0, d1, d2, d3 वाले आउटपुट के हर एलिमेंट के लिए, हम indices टेंसर से एलिमेंट (d0, 0) और (d0, 1) निकालते हैं.
indices के लिए, इनपुट मैप का आउटपुट:
(d0, d1, d2, d3)[s0] -> (d0, s0)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 1]
रेंज वैरिएबल s0 से पता चलता है कि हमें आउटपुट के किसी एलिमेंट का हिसाब लगाने के लिए, indices टेंसर की पूरी लाइन (d0, *) की ज़रूरत है.
ट्रांसपोज़ करना
ट्रांसपोज़ के लिए इंडेक्सिंग मैप, इनपुट/आउटपुट डाइमेंशन का क्रम बदलना है.
p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}
इनपुट मैप का आउटपुट:
(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]
इनपुट से आउटपुट मैप:
(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]
वापस जाएं
मैप को रिवर्स के लिए इंडेक्स करने से, पहले जैसे किए गए डाइमेंशन upper_bound(d_i) -
d_i में बदल जाते हैं:
p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}
इनपुट मैप का आउटपुट:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
इनपुट से आउटपुट मैप:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
(वैरियाडिक)घटाना
वैरिएडिक रिडक्शन में कई इनपुट और कई इनिट होते हैं. आउटपुट से इनपुट में मैप करने पर, कम किए गए डाइमेंशन जुड़ जाते हैं. इसलिए, यह कुछ हद तक ब्रॉडकास्ट के उलट काम करता है.
p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
dimensions={0}, to_apply=max
इनपुट मैप का आउटपुट:
- आउटपुट -> input_j:
(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]
- आउटपुट -> init_j:
(d0) -> ()
domain:
d0 in [0, 9]
इनपुट से आउटपुट मैप:
- इनपुट_i -> output_j:
(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]
- init_i -> output_j:
()[s0] -> (s0)
domain:
s0 in [0, 9]
for i, j = 0, ... INPUT_COUNT.
स्लाइस
स्लाइस के नतीजों के लिए आउटपुट से इनपुट तक को इंडेक्स करने के लिए, इंडेक्स की गई लाइन वाले मैप का इस्तेमाल किया जाता है, आउटपुट के हर एलिमेंट के लिए मान्य है. इनपुट से आउटपुट में मैप करने की सुविधा, इनपुट में मौजूद एलिमेंट की स्ट्राइड वाली रेंज तक ही सीमित है.
p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
slice={[5:10:1], [3:20:7], [0:50:2]}
इनपुट मैप का आउटपुट:
(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]
इनपुट से आउटपुट मैप:
(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]
साइज़ बदलना
आकार अलग-अलग फ़्लेवर में आते हैं.
आकार छोटा करें
यह N-D से 1D में, "रैखिक" रीशेप है.
p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)
इनपुट मैप का आउटपुट:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
इनपुट से आउटपुट मैप:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
आकार को बड़ा करें
यह "आकार को छोटा करें" ऑपरेशन का उलटा है. यह 1D इनपुट को N-D आउटपुट में बदल देता है.
p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)
मैप इनपुट करने के लिए आउटपुट:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
आउटपुट मैप का इनपुट:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
सामान्य आकार
ये ऐसे रीशेप ऑपरेशन हैं जिन्हें एक ही आकार में बड़ा या छोटा नहीं किया जा सकता. इन्हें सिर्फ़ दो या उससे ज़्यादा ज़ूम इन या ज़ूम आउट किए जा सकने वाले आकारों के कॉम्पोज़िशन के तौर पर दिखाया जा सकता है.
पहला उदाहरण: लीनियराइज़ेशन-डिलीनियराइज़ेशन.
p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)
यह आकृति, संक्षिप्त आकार की संरचना के रूप में प्रदर्शित की जा सकती है
tensor<4x8xf32> से tensor<32xf32> तक और फिर आकार विस्तार
tensor<2x4x4xf32>.
इनपुट मैप का आउटपुट:
(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]
इनपुट से आउटपुट मैप:
(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
उदाहरण 2: बड़े और छोटे किए गए सब-शेप
p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)
इस आकार को दो आकृतियों को मिलाकर दिखाया जा सकता है. पहला विकल्प
सबसे बाहरी डाइमेंशन tensor<4x8x12xf32> को tensor<32x12xf32> में छोटा करता है
और दूसरा वाला सबसे अंदरूनी डाइमेंशन tensor<32x12xf32> को
tensor<32x3x4xf32>.
इनपुट मैप का आउटपुट:
(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]
इनपुट से आउटपुट मैप:
(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]
Bitcast
बिटकस्ट ऑपरेशन को ट्रांसपोज़-रीशेप-ट्रांसपोज़ के क्रम के तौर पर दिखाया जा सकता है. इसलिए, इसके इंडेक्सिंग मैप, इस क्रम के लिए इंडेक्सिंग मैप का सिर्फ़ एक कॉम्पोनेंट हैं.
जोड़ें
Concat के लिए आउटपुट-टू-इनपुट मैपिंग को सभी इनपुट के लिए तय किया जाता है, लेकिन नॉन-ओवरलैपिंग डोमेन, यानी एक बार में सिर्फ़ एक इनपुट का इस्तेमाल किया जाएगा.
p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}
इनपुट मैप का आउटपुट:
- आउटपुट -> इनपुट 1:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- आउटपुट -> इनपुट 2:
(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]
- आउटपुट -> इनपुट 3:
(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]
आउटपुट मैप के इनपुट:
- इनपुट 1 -> आउटपुट:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- इनपुट 2 -> आउटपुट:
(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]
- इनपुट 3 -> आउटपुट:
(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]
बिंदु
डॉट के लिए मैप को इंडेक्स करना, कम करने वाली प्रोसेस की तरह ही है.
p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
lhs_batch_dims={0}, rhs_batch_dims={0},
lhs_contracting_dims={2}, rhs_contracting_dims={1}
इनपुट मैप का आउटपुट:
- output -> input_1:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
- output -> input_2:
(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
आउटपुट मैप के इनपुट:
- इनपुट_1 -> आउटपुट:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]
- input_2 -> output:
(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]
पैड
padOp को इंडेक्स करना, SliceOp इंडेक्स से बिलकुल उलट है.
p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0
पैडिंग कॉन्फ़िगरेशन 1_4_1x4_8_0 से lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1 का पता चलता है.
मैप इनपुट करने के लिए आउटपुट:
- आउटपुट -> इनपुट:
(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]
- output -> init:
(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]
ReduceWindow
XLA में कम करने की सुविधा, पैडिंग (जगह) भी करती है. इसलिए, इंडेक्स करने वाले मैप को, पैडिंग नहीं करने वाले ReduceWindow इंडेक्सिंग और PadOp के इंडेक्सिंग के कॉम्पोज़िशन के तौर पर कैलकुलेट किया जा सकता है.
c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
window={size=1x512 pad=0_0x0_0}, to_apply=max
मैप इनपुट करने के लिए आउटपुट:
- आउटपुट -> इनपुट:
(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]
- आउटपुट -> init:
(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]
Fusion के लिए Maps को इंडेक्स करना
fusion op के लिए मैप को इंडेक्स करना, मैप में हर ऑप के लिए मैप को इंडेक्स करने का एक कंपोज़िशन है क्लस्टर. ऐसा हो सकता है कि कुछ इनपुट को अलग-अलग तरीके से कई बार पढ़ा जाए ऐक्सेस पैटर्न.
एक इनपुट, कई इंडेक्स करने वाले मैप
यहां p0 + transpose(p0) का एक उदाहरण दिया गया है.
f {
p0 = f32[1000, 1000] parameter(0)
transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}
p0 के लिए, आउटपुट से इनपुट इंडेक्स करने वाले मैप (d0, d1) -> (d0, d1) और
(d0, d1) -> (d1, d0) होंगे. इसका मतलब है कि आउटपुट के एक एलिमेंट का हिसाब लगाने के लिए, हमें इनपुट पैरामीटर को दो बार पढ़ना पड़ सकता है.
एक इनपुट, डुप्लीकेट कॉपी हटाने के बाद का इंडेक्सिंग मैप
ऐसे मामले भी होते हैं जहां इंडेक्स करने वाले मैप असल में एक जैसे ही होते हैं, भले ही साफ़ तौर पर नहीं बताया जा सकता.
f {
p0 = f32[20, 10, 50] parameter(0)
lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}
इस मामले में, p0 के लिए आउटपुट-टू-इनपुट इंडेक्स करने वाला मैप सिर्फ़
(d0, d1, d2) -> (d2, d0, d1).
Softmax
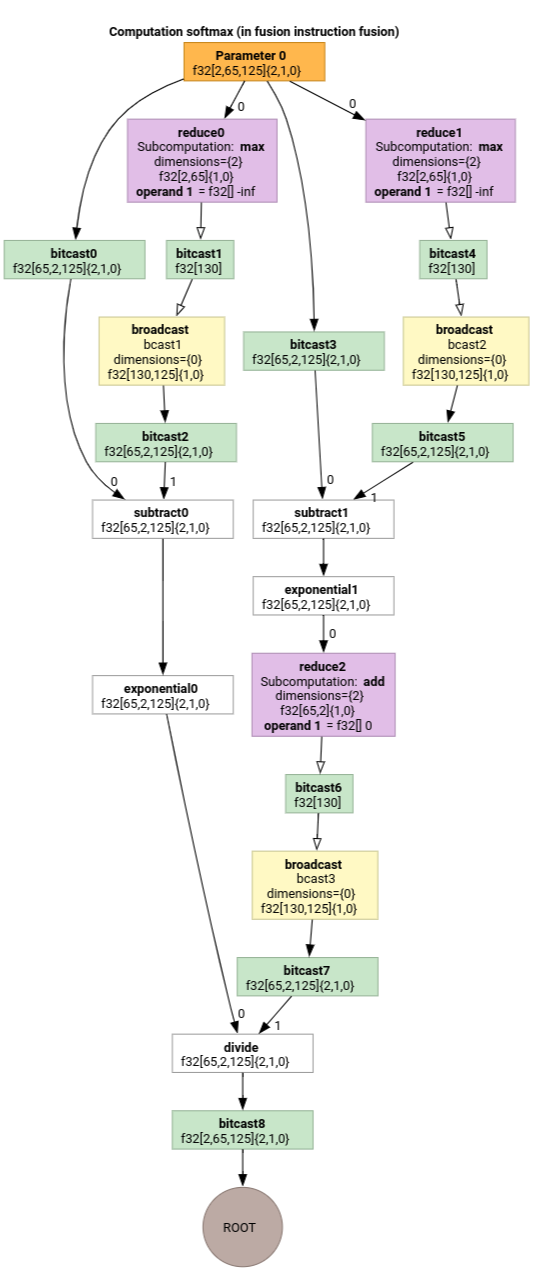
सॉफ़्टमैक्स के लिए parameter 0 के आउटपुट-टू-इनपुट इंडेक्सिंग मैप:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]
और
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
यहां s0, इनपुट के सबसे अंदरूनी डाइमेंशन को दिखाता है.
मैप सिंप्लीफ़ायर इंडेक्स करना
mlir::AffineMap अपस्ट्रीम के लिए डिफ़ॉल्ट सिंपलर, कोई वैल्यू नहीं बना सकता
डाइमेंशन/सिंबल की रेंज के बारे में लगाए गए अनुमान. इसलिए, यह नहीं कर सकता
mod और divका इस्तेमाल करके, एक्सप्रेशन को आसान बनाते हैं.
हम दुनिया भर की कंपनियों की निचली और ऊपरी सीमाओं की जानकारी का फ़ायदा ले सकते हैं अफ़ाइन मैप में सब-एक्सप्रेशन का इस्तेमाल करें, ताकि उन्हें और आसान बनाया जा सके.
सरल बनाने वाला टूल, इन व्यंजकों को फिर से लिख सकता है.
[0, 6] x [0, 14]में d के लिए(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16),(d0, d1) -> (d0, d1)हो जाता हैdi in [0, 9]के लिए(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10),(d0, d1, d2) -> (d0, d1, d2)हो जाएगा.d_i in [0, 9]के लिए(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8),(d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8)हो जाएगा.[0, 9] x [0, 10]में d के लिए(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9),(d0, d1) -> (d0)हो जाता है.
इंडेक्सिंग मैप को आसान बनाने वाले टूल की मदद से, हम यह समझ सकते हैं कि एचएलओ में चेन की गई कुछ रीशेप, एक-दूसरे को रद्द कर देती हैं.
p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)
मैप को इंडेक्स करने और उन्हें आसान बनाने के बाद, हम
(d0, d1, d2) -> (d0, d1, d2).
मैप को आसान बनाने की सुविधा को इंडेक्स करने से, सीमाएं भी आसान हो जाती हैं.
- टाइप की सीमाएं
lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_boundयह हैंupdated_lower_bound <= affine_expr <= updated_upped_boundके तौर पर फिर से लिखा गया. - हमेशा पूरी होने वाली शर्तें, जैसे कि
d0 in [0, 5]औरs0 in [1, 3]के लिएd0 + s0 in [0, 20]को हटा दिया जाता है. - पाबंदियों में मौजूद ऐफ़ाइन एक्सप्रेशन को, ऊपर दिए गए इंडेक्सिंग ऐफ़ाइन मैप के तौर पर ऑप्टिमाइज़ किया जाता है.
ज़्यादा उदाहरणों के लिए indexing_map_test.cc देखें.

