このドキュメントでは、HLO オペレーションのインデックス マップを記号的に計算できる HLO インデックス分析について説明します。インデックス マップは、あるテンソルのインデックスを別のテンソルのインデックスにマッピングする関数です。たとえば、HLO 命令出力のインデックスを HLO 命令入力のインデックスにマッピングします。
例
tensor<20xf32> から tensor<10x20x30xf32> へのブロードキャストの場合
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
出力から入力へのインデックス マップは、i in
[0, 10]、j in [0, 20]、k in [0, 30] の場合は (i, j, k) -> (j) です。
目的
XLA GPU は、いくつかのカスタム ソリューションを使用して、統合、オペランドの使用率、タイリング スキームを推論します(詳細は後述)。インデックス分析の目的は、このようなユースケースに再利用可能なコンポーネントを提供することです。インデックスの分析 MLIR の Affine Map インフラストラクチャ上に構築され、HLO セマンティクスを追加します。
合体
メモリ統合の推論は、出力の要素を計算するために読み取られる入力の要素 / スライスがわかっている場合、単純でないケースで実現可能になります。
オペランドの使用率
XLA のオペランド使用率は、命令の各入力がどのくらいの量か 使用されます。現在のところ、使用率も 一般的なケースで計算されますインデックス分析により、使用率を正確に計算できます。
並べ方
タイル/スライスは、オフセットでパラメータ化されたテンソルの超長方形のサブセットです。 ストライドを設定できます。タイルの伝播は、スペースのタイル パラメータを計算する方法です。 オペレーション自体のタイリング パラメータを使用して、オペレーションのプロデューサー/コンシューマに関連付けます。softmax と dot に対してこれを行うライブラリはすでにあります。インデックス マップを使用してタイル伝播を表現すると、より汎用性と堅牢性を高めることができます。
関数とドメイン
インデックス マップは関数 f(x) = f(d, r, rt) です。
テンソル A のマルチ インデックス d を次の要素/範囲にマッピングする
テンソル B です。パラメータ r は、
B テンソルには存在するが A テンソルには存在しない次元。「
パラメータ rt はランタイム値を指します。たとえば、収集します
たとえば、tensor<2x4x8x16xf32> から tensor<4x8xf32> への縮小がある場合、2D 出力から 4D 入力へのインデックス マップは (d0, d1) -> (r0, d0, d1, r1) です。ここで、d_i は出力テンソルのインデックスに対応するディメンション変数です。範囲変数 r_j エンコード
出力の (d0, d1) 要素を計算するには、
入力の (r0, d0, d1, r1) 要素。ここで r0 in [0, 1] と
r1 in [0, 15]。
このマッピングは、HLO 命令の属性から構築できます。また、統合されていない命令のマッピングを組み合わせて、統合のインデックスを取得することもできます。このマッピングにはドメインもあります。ドメインは、テンソルのどの要素を マッピングが存在することを示します。
f(x) s.t.
lb <= g(x) <= ub
再計算を最小限に抑えるため、記号計算用のライブラリが必要です。XLA はすでに MLIR に依存しているため、別の記号演算ライブラリを記述する代わりに mlir::AffineMap を使用します。
一般的な AffineMap は次のようになります
(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)
AffineMap には、ディメンションとシンボルの 2 種類のパラメータがあります。「
ディメンション はディメンション変数 d に、記号 は以下に対応します。
範囲変数 r と RT 変数 rt。「AffineMap」は何も含まない
追加する必要があります。このデータは
考えています
struct Interval {
int64_t lower;
int64_t upper;
};
// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
Interval bounds;
};
// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
Interval range;
};
// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
Interval feasible_values;
const HloInstruction* hlo;
// This is a map from the iteration space of the corresponding indexing map to
// the iteration space of `hlo`. It shows what element of `hlo` we need to
// extract to get the runtime value for the RTVar.
mlir::AffineMap map;
};
class IndexingMap {
mlir::AffineMap affine_map_;
std::vector<DimVar> dim_vars_;
std::vector<RangeVar> range_vars_;
std::vector<RTVar> rt_vars_;
llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};
dim_vars_ はディメンションのボックス制約をエンコードします。
インデックスマップの変数 d。通常、これはインデックスの
転置、削減、要素別、ドットなどの op の出力テンソルの形状ですが、
いくつかの例外があります
HloConcatenateInstruction。
range_vars_ は、r パラメータに取り得る値をエンコードします。
rt_vars_ は、関連する hlo 命令を、アクセス パターンと実行時に実行可能な値とともに保存します。たとえば、1D HloDynamicSliceInstruction の場合、オフセットは動的です。対応する RTVar には、
(d0) -> () アクセスで階数 0 のテンソルを生成する HloInstruction*
出力のすべての要素に対して同じ要素が抽出されるため、
入力のインデックスを計算します。また、スライスのオフセットは常に 0~tensor_size - slice_size - 1 の間にあると想定することもできます。
例を挙げて調べて、これらすべての意味を理解しましょう。
融合されていない運用のためのインデックス登録マップ
Elementwise
要素ごとのオペレーションでは、インデックス マップが ID です。
p0 = f32[10, 20] parameter(0)
p1 = f32[10, 20] parameter(1)
add = f32[10, 20] add(p0, p1)
出力から入力へのマッピング:
- 出力 ->input_i:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
入力から出力へのマッピング
- input_i -> output:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
ブロードキャスト
ブロードキャストとは、出力を入力にマッピングするときに一部のディメンションが削除され、入力を出力にマッピングするときに追加されることを意味します。
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
出力から入力へのマッピング:
(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]
入力から出力へのマップ
(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]
右側に入力から出力への s があることに注意してください。
あります。これらは値の範囲を表す記号です。たとえば、この特定のケースでは、インデックス d0 を持つ入力のすべての要素が、出力の 10x1x30 スライスにマッピングされます。
定数と Iota
便利なことに、入力パラメータがないため、追加の操作は必要ありません。 指定します。
DynamicSlice
Dynamic Slice は Slice に似ていますが、オフセットは動的です。
src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}
src の出力から入力へのマップ:
(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
hlo: of1 = s32[] parameter(1)
(d0, d1, d2) -> ()
s1 in [0, 0]
hlo: of2 = s32[] parameter(2)
(d0, d1, d2) -> ()
s2 in [0, 226]
hlo: of3 = s32[] parameter(3)
(d0, d1, d2) -> ()
入力から出力へのマッピングの右側に s があることに注意してください。
これらはランタイム値を表すシンボルです。たとえば、この特定のケースでは、インデックス d0, d1, d2 の出力のすべての要素に対して、スライス オフセット of1、of2、of3 にアクセスして入力のインデックスを計算します。ランタイム変数の区間は、スライス全体が境界内に収まることを前提として導出されます。
of1、of2、of3 の出力から入力マップ:
(d0, d1, d2) -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
DynamicUpdateSlice
src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)
src の入力マップへの出力は簡単です。ドメインを更新されていないインデックスに制限することで、より正確にできますが、現時点ではインデックス マップは不等式制約をサポートしていません。
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]
upd の出力から入力へのマップ:
(d0, d1)[s0, s1] -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
hlo: of1 = s32[] parameter(2)
(d0, d1) -> ()
s1 in [0, 20]
hlo: of2 = s32[] parameter(3)
(d0, d1) -> ()
入力と出力のマッピングの右側に s が追加されています。これらはランタイム値を表すシンボルです。たとえば、この特定のケースでは、インデックス d0, d1 の出力のすべての要素に対して、スライス オフセット of1 と of2 にアクセスして入力のインデックスを計算します。区間
ランタイム変数の変数は、スライス全体が
あります。
of1 と of2 の出力から入力へのマッピング:
(d0, d1) -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]
Gather
簡素化された収集のみがサポートされています。[gather_simplifier](https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h)をご覧ください。
operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
offset_dims={1,2,3},
collapsed_slice_dims={},
start_index_map={0,1},
index_vector_dim=1,
slice_sizes={7,8,4}
operand の出力から入力へのマップ:
(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 1)
入力から出力へのマッピングの右側に s があることに注意してください。
これらはランタイム値を表すシンボルです。たとえば、この例では
インデックス d0, d1, d2, d3 を持つ出力のすべての要素に対する特定のケース
indices テンソルから (d0, 0) と (d0, 1) の要素を抽出します。
indices の入力マップへの出力:
(d0, d1, d2, d3)[s0] -> (d0, s0)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 1]
範囲変数 s0 は、データセットの行全体(d0, *)が必要であることを示しています。
indices テンソル。出力の要素を計算します。
行 / 列の入れ替え
転置のインデックス マップは、入力 / 出力ディメンションの並べ替えです。
p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}
出力から入力へのマッピング:
(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]
入力から出力へのマップ:
(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]
反転
逆方向のインデックス マップは、元に戻されたディメンションを upper_bound(d_i) -
d_i に変更します。
p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}
出力から入力へのマッピング:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
入力と出力のマッピング:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
(Variadic)Reduce
可変長削減には複数の入力と複数の初期があります。出力から 入力値により縮小次元が追加されます。つまり、ブロードキャストの あります。
p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
dimensions={0}, to_apply=max
出力から入力へのマッピング:
- output -> input_j:
(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]
- 出力 ->init_j:
(d0) -> ()
domain:
d0 in [0, 9]
入力から出力へのマッピング:
- input_i ->output_j:
(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]
- init_i -> output_j:
()[s0] -> (s0)
domain:
s0 in [0, 9]
for i, j = 0, ... INPUT_COUNT.
スライス
スライスの出力から入力へのインデックスを作成すると、ストライドのインデックス マップになります。 出力のすべての要素に対して有効です。入力から出力へのマッピングは、入力内の要素のストライド範囲に制限されます。
p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
slice={[5:10:1], [3:20:7], [0:50:2]}
出力から入力へのマッピング:
(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]
入力から出力へのマップ:
(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]
再形成
リシェイプにはさまざまな種類があります。
シェイプを折りたたむ
これは、N 次元から 1 次元への「線形化」リシェイプです。
p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)
出力から入力へのマッピング:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
入力から出力へのマップ:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
シェイプを開く
これは「シェイプを圧縮」オペレーションの逆で、1D 入力を N-D 出力に再フォーマットします。
p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)
出力から入力へのマッピング:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
入力と出力のマッピング:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
一般的な Reshape
これらは、単一の拡張または圧縮シェイプとして表すことができない再構成オペレーションです。2 種類以上の組み合わせでしか表現できない クリックします。
例 1: 線形化と非線形化。
p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)
この再シェイプは、tensor<4x8xf32> を tensor<32xf32> に圧縮し、次に tensor<2x4x4xf32> に拡張するシェイプの合成として表すことができます。
出力から入力へのマッピング:
(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]
入力と出力のマッピング:
(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
例 2: サブシェイプの展開と折りたたみ
p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)
この再構成は、2 つの再構成の合成として表すことができます。1 つ目は、最も外側のディメンション tensor<4x8x12xf32> を tensor<32x12xf32> に折りたたみ、2 つ目は、最も内側のディメンション tensor<32x12xf32> を tensor<32x3x4xf32> に展開します。
出力から入力へのマッピング:
(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]
入力と出力のマッピング:
(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]
ビットキャスト
ビットキャスト演算は、転置 - 再構成 - 転置のシーケンスとして表すことができます。したがって、そのインデックス マップは、このシーケンスのインデックス マップの合成にすぎません。
連結
concat の出力から入力へのマッピングはすべての入力に対して定義されますが、ドメインが重複しません。つまり、一度に使用される入力は 1 つだけです。
p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}
出力から入力へのマッピング:
- 出力 ->入力 1:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- 出力 ->入力 2:
(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]
- 出力 ->入力 3:
(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]
出力マップへの入力:
- 入力 1 ->output:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- 入力 2 -> 出力:
(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]
- 入力 3 -> 出力:
(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]
ドット
dot のインデックス マップは、reduce のインデックス マップによく似ています。
p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
lhs_batch_dims={0}, rhs_batch_dims={0},
lhs_contracting_dims={2}, rhs_contracting_dims={1}
出力から入力へのマッピング:
- 出力 ->input_1:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
- 出力 ->input_2:
(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
入力から出力へのマッピング:
- 入力 1 ->output:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]
- input_2 -> output:
(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]
パッド
PadOp のインデックス作成は SliceOp のインデックス作成とは逆です。
p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0
パディング構成 1_4_1x4_8_0 は lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1 を示します。
出力から入力へのマッピング:
- output -> input:
(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]
- output -> init:
(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]
ReduceWindow
XLA の ReduceWindow もパディングを行います。したがって、インデックス マップは、パディングを行わない ReduceWindow インデックスと PadOp のインデックスの合成として計算できます。
c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
window={size=1x512 pad=0_0x0_0}, to_apply=max
出力から入力へのマッピング:
- output -> input:
(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]
- output -> init:
(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]
Fusion 用インデックス マップ
融合オペレーションのインデックス マップは、クラスタ内のすべてのオペレーションのインデックス マップの合成です。一部の入力が、異なるアクセス パターンで複数回読み取られることがあります。
1 つの入力、複数のインデックス マップ
p0 + transpose(p0) の例を次に示します。
f {
p0 = f32[1000, 1000] parameter(0)
transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}
p0 の出力から入力へのインデックス マップは (d0, d1) -> (d0, d1) になり、
(d0, d1) -> (d1, d0)。つまり、出力の 1 つの要素を計算するために、入力パラメータを 2 回読み取る必要がある場合があります。
1 つの入力、重複を排除したインデックス マップ
インデックス マップは実際には同じであるにもかかわらず、すぐには気づかない場合があります。
f {
p0 = f32[20, 10, 50] parameter(0)
lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}
この場合の p0 の出力から入力へのインデックス マップは、
(d0, d1, d2) -> (d2, d0, d1)。
ソフトマックス
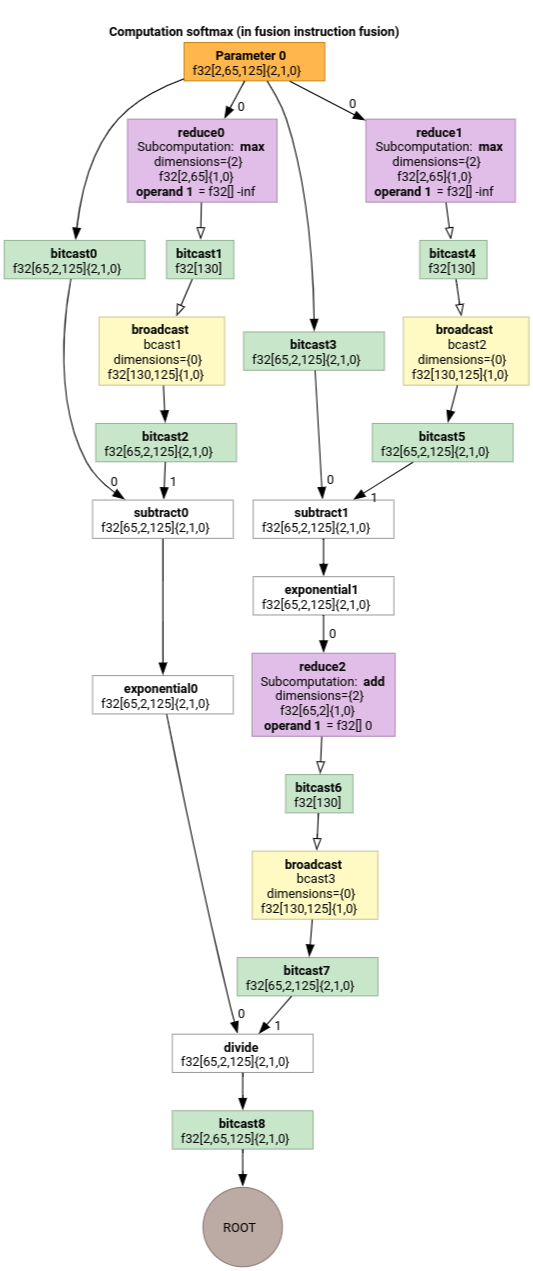
出力から入力へのインデックス作成は、ソフトマックスの parameter 0 に対応しています。
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]
と
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
ここで、s0 は入力の最も内側のディメンションを指します。
インデックス マップ簡素化
mlir::AffineMap のアップストリームのデフォルトの簡素化では、何も作成できません。
寸法/記号の範囲に関する前提条件があります。そのため、
mod と div を使用して式を効率的に簡素化します。
アフィン マップのサブ式の下限と上限に関する知識を利用して、さらに簡素化できます。
簡素化ツールは、次の式を書き換えることができます。
[0, 6] x [0, 14]の d の(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16)は(d0, d1) -> (d0, d1)になりますdi in [0, 9]の(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10)は(d0, d1, d2) -> (d0, d1, d2)になります。d_i in [0, 9]の(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8)は(d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8)になります。(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9)(日)[0, 9] x [0, 10]では(d0, d1) -> (d0)になります。
インデックス マップ簡素化ツールを使用すると、HLO 内の連鎖された一部の再シェイプが相互にキャンセルされることを把握できます。
p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)
インデックス マップの合成と簡素化の後、次のような結果が得られます。
(d0, d1, d2) -> (d0, d1, d2)。
インデックス マップの簡素化により、制約も簡素化されます。
- タイプの制約
lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_boundはupdated_lower_bound <= affine_expr <= updated_upped_boundと書き換えられます。 - 常に満たされる制約(例:
d0 + s0 in [0, 20]d0 in [0, 5]とs0 in [1, 3]が削除されます。 - 制約内のアフィン式は、上記のインデックス アフィン マップとして最適化されます。
その他の例については、indexing_map_test.cc をご覧ください。

