এইচএলও ইন্ডেক্সিং বিশ্লেষণ হল একটি ডেটাফ্লো বিশ্লেষণ যা বর্ণনা করে যে কীভাবে একটি টেনসরের উপাদানগুলি "ইনডেক্সিং ম্যাপ" এর মাধ্যমে অন্যটির সাথে সম্পর্কিত। উদাহরণস্বরূপ, কিভাবে HLO নির্দেশের আউটপুট ম্যাপের সূচকগুলি HLO নির্দেশনা অপারেন্ডের সূচকে।
উদাহরণ
tensor<20xf32> থেকে tensor<10x20x30xf32> সম্প্রচারের জন্য
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
আউটপুট থেকে ইনপুট পর্যন্ত ইন্ডেক্সিং ম্যাপ হল (i, j, k) -> (j) i in [0, 10] , j in [0, 20] এবং k in [0, 30] ।
প্রেরণা
কোলেসিং, অপারেন্ড ইউটিলাইজেশন, এবং টাইলিং স্কিম (নীচে আরও বিশদ বিবরণ) সম্পর্কে যুক্তির জন্য XLA বেশ কয়েকটি বেসপোক সমাধান ব্যবহার করে। ইন্ডেক্সিং বিশ্লেষণের লক্ষ্য হল এই ধরনের ব্যবহারের ক্ষেত্রে একটি পুনঃব্যবহারযোগ্য উপাদান প্রদান করা। ইন্ডেক্সিং বিশ্লেষণ MLIR এর Affine Map পরিকাঠামোর উপর নির্মিত এবং HLO শব্দার্থবিদ্যা যোগ করে।
কোলেসিং
মেমরি কোলেসিং সম্পর্কে যুক্তি অ-তুচ্ছ ক্ষেত্রে সম্ভব হয়ে ওঠে, যখন আমরা জানি আউটপুটের একটি উপাদান গণনা করার জন্য ইনপুটগুলির কোন উপাদান/স্লাইস পড়া হয়।
অপারেন্ড ইউটিলাইজেশন
XLA-তে অপারেন্ড ইউটিলাইজেশন নির্দেশ করে যে নির্দেশের প্রতিটি ইনপুট কতটা ব্যবহার করা হয়েছে অনুমান করে তার আউটপুট সম্পূর্ণরূপে ব্যবহৃত হয়েছে। বর্তমানে, একটি জেনেরিক ক্ষেত্রেও ব্যবহার গণনা করা হয় না। ইন্ডেক্সিং বিশ্লেষণ আমাদেরকে সঠিকভাবে ব্যবহার গণনা করতে দেয়।
টাইলিং
একটি টাইল/স্লাইস হল একটি টেনসরের হাইপার-আয়তক্ষেত্রাকার উপসেট যা অফসেট, আকার এবং স্ট্রাইড দ্বারা প্যারামিটারাইজ করা হয়। টাইল প্রচার হল অপের টাইলিং পরামিতি ব্যবহার করে অপের প্রযোজক/ভোক্তার টাইল প্যারামিটার গণনা করার একটি উপায়। ইতিমধ্যে একটি লাইব্রেরি রয়েছে যা এটি সফটম্যাক্স এবং ডটের জন্য করে। টাইল প্রচারকে আরও সাধারণ এবং শক্তিশালী করা যেতে পারে যদি এটি সূচীকরণ মানচিত্রের মাধ্যমে প্রকাশ করা হয়।
ইন্ডেক্সিং মানচিত্র
একটি ইন্ডেক্সিং মানচিত্র এর সংমিশ্রণ
- একটি প্রতীকীভাবে প্রকাশিত ফাংশন যা একটি টেনসর
Aএর প্রতিটি উপাদানকে টেনসরBএর উপাদানগুলির রেঞ্জে ম্যাপ করে; - ফাংশনের ডোমেন সহ বৈধ ফাংশন আর্গুমেন্টের সীমাবদ্ধতা।
ফাংশন আর্গুমেন্টগুলি তাদের প্রকৃতিকে আরও ভালভাবে যোগাযোগ করতে 3টি বিভাগে বিভক্ত করা হয়েছে:
টেনসর
Aবা একটি GPU গ্রিডের ডাইমেনশন ভেরিয়েবল যা থেকে আমরা ম্যাপিং করছি; মান স্ট্যাটিকভাবে পরিচিত হয়. সূচক উপাদানগুলিকে ডাইমেনশন ভেরিয়েবলও বলা হয়।পরিসীমা ভেরিয়েবল। তারা একটি থেকে একাধিক ম্যাপিং সংজ্ঞায়িত করে এবং
Aএর একটি একক মান গণনা করতে ব্যবহৃতBএ উপাদানগুলির একটি সেট নির্দিষ্ট করে; মান স্ট্যাটিকভাবে পরিচিত হয়. একটি ম্যাট্রিক্স গুণের সংকোচন মাত্রা একটি পরিসর পরিবর্তনশীলের একটি উদাহরণ।রানটাইম ভেরিয়েবল যা শুধুমাত্র এক্সিকিউশনের সময় পরিচিত। উদাহরণস্বরূপ, সংগ্রহ অপারেশনের সূচক আর্গুমেন্ট।
ফাংশনের ফলাফল লক্ষ্য B টেনসরের একটি সূচক।
সংক্ষেপে, অপারেশন x এর জন্য টেনসর A থেকে টেনসর B পর্যন্ত একটি ইন্ডেক্সিং ফাংশন
map_ab(index in A, range variables, runtime variables) -> index in B ।
ম্যাপিং আর্গুমেন্টের প্রকারগুলিকে আরও ভালভাবে আলাদা করতে আমরা সেগুলি লিখি:
map_ab(index in A)[range variables]{runtime variables} -> (index in B)
উদাহরণ স্বরূপ, চলুন কম অপারেশন f32[4, 8] out = reduce(f32[2, 4, 8, 16] in, 0), dimensions={0,3} জন্য ইন্ডেক্সিং ম্যাপ দেখি :
আমাদের ফাংশনের
inটুoutউপাদানগুলিকে ম্যাপ করার জন্য প্রকাশ করা যেতে পারে(d0, d1, d2, d3) -> (d1, d2)।d0 in [0, 1], d1 in [0, 3], d2 in [0, 7], d3 in [0, 15]এর সীমাবদ্ধতাগুলিinএর আকৃতি দ্বারা সংজ্ঞায়িত করা হয়েছে।outinএর এলিমেন্ট ম্যাপ করার জন্য:outমাত্র দুটি মাত্রা আছে এবং রিডাকশন দুটি পরিসরের ভেরিয়েবলের পরিচয় দেয় যা হ্রাসকারী মাত্রাগুলিকে কভার করে। এইভাবে ম্যাপিং ফাংশন হল(d0, d1)[s0, s1] -> (s0, d0, d1, s1), যেখানে(d0, d1)হলoutসূচক।s0,s1হল অপারেশনের শব্দার্থবিদ্যা এবংinস্প্যান মাত্রা 0 এবং 3 দ্বারা সংজ্ঞায়িত রেঞ্জ। সীমাবদ্ধতা হলd0 in [0, 3], d1 in [0, 7], s0 in [0,1], s1 in [0, 15]
এটি লক্ষ্য করা গুরুত্বপূর্ণ যে বেশিরভাগ পরিস্থিতিতে আমরা আউটপুটের উপাদানগুলি থেকে ম্যাপিং করতে আগ্রহী। গণনার জন্য
C = op1(A, B)
E = op2(C, D)
আমরা "B এর সূচীকরণ" সম্পর্কে কথা বলতে পারি যার অর্থ " B এর উপাদানগুলিতে E এর উপাদানগুলির ম্যাপিং"। এটি অন্যান্য ধরণের ডেটা-প্রবাহ বিশ্লেষণের তুলনায় পাল্টা-স্বজ্ঞাত হতে পারে যা ইনপুট থেকে আউটপুটের দিকে কাজ করে।
ভেরিয়েবলের সীমাবদ্ধতাগুলি অপ্টিমাইজেশনের সুযোগগুলি সক্ষম করে এবং কোড তৈরিতে সহায়তা করে। ডকুমেন্টেশন এবং বাস্তবায়নের সীমাবদ্ধতাগুলিকে ডোমেন হিসাবেও উল্লেখ করা হয় কারণ তারা ম্যাপিং ফাংশনের সমস্ত বৈধ সংমিশ্রণ বা যুক্তি মানগুলিকে সংজ্ঞায়িত করে। অনেক অপারেশনের জন্য, সীমাবদ্ধতাগুলি কেবল টেনসরের মাত্রা বর্ণনা করে কিন্তু কিছু অপারেশনের জন্য সেগুলি আরও জটিল হতে পারে; নীচে উদাহরণ দেখুন।
ফাংশন এবং আর্গুমেন্ট সীমাবদ্ধতা প্রতীকীভাবে প্রকাশ করে এবং ফাংশন এবং সীমাবদ্ধতা একত্রিত করতে সক্ষম হওয়ার মাধ্যমে আমরা একটি নির্বিচারে বড় গণনা (ফিউশন) এর জন্য একটি কমপ্যাক্ট ইনডেক্সিং ম্যাপিং গণনা করতে পারি।
সিম্বলিক ফাংশন এবং সীমাবদ্ধতার অভিব্যক্তি হল বাস্তবায়ন জটিলতা এবং অপ্টিমাইজেশান লাভের মধ্যে একটি ভারসাম্য যা আমরা আরও সুনির্দিষ্ট উপস্থাপনা থেকে পাই। কিছু HLO ক্রিয়াকলাপের জন্য আমরা কেবলমাত্র প্রায় অ্যাক্সেস প্যাটার্ন ক্যাপচার করি।
বাস্তবায়ন
যেহেতু আমরা পুনর্গণনা কমাতে চাই, তাই আমাদের প্রতীকী গণনার জন্য একটি লাইব্রেরি প্রয়োজন। XLA ইতিমধ্যেই MLIR-এর উপর নির্ভর করে, তাই আমরা mlir::AffineMap-এর পরিবর্তে অন্য একটি প্রতীকী গাণিতিক লাইব্রেরি লেখার পরিবর্তে ব্যবহার করি।
একটি সাধারণ AffineMap মত দেখায়
(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)
AffineMap দুটি ধরণের প্যারামিটার রয়েছে: মাত্রা এবং প্রতীক । মাত্রাগুলি মাত্রার ভেরিয়েবলের সাথে মিলে যায় d ; চিহ্নগুলি রেঞ্জ ভেরিয়েবল r এবং রানটাইম ভেরিয়েবল rt এর সাথে মিলে যায়। AffineMap প্যারামিটারের সীমাবদ্ধতা সম্পর্কে কোনো মেটাডেটা নেই, তাই আমাদের আলাদাভাবে সেগুলি প্রদান করতে হবে।
struct Interval {
int64_t lower;
int64_t upper;
};
class IndexingMap {
// Variable represents dimension, range or runtime variable.
struct Variable {
Interval bounds;
// Name of the variable is used for nicer printing.
std::string name = "";
};
mlir::AffineMap affine_map_;
// DimVars represent dimensions of a tensor or of a GPU grid.
std::vector<Variable> dim_vars_;
// RangeVars represent ranges of values, e.g. to compute a single element of
// the reduction's result we need a range of values from the input tensor.
std::vector<Variable> range_vars_;
// RTVars represent runtime values, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
std::vector<Variable> rt_vars_;
llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};
dim_vars_ ইনডেক্সিং ম্যাপের ডাইমেনশন ভেরিয়েবল d-এর জন্য ইনক্লুসিভ বক্স সীমাবদ্ধতাগুলিকে এনকোড করে, যা সাধারণত ট্রান্সপোজ, রিডুড, এলিমেন্টওয়াইজ, ডট-এর মতো অপ্সের জন্য আউটপুট টেনসরের আকারের সাথে মিলে যায়, কিন্তু কিছু ব্যতিক্রম আছে যেমন HloConcatenateInstruction ।
range_vars_ সমস্ত মান যে পরিসীমা ভেরিয়েবলগুলি গ্রহণ করে। পরিসীমা ভেরিয়েবলের প্রয়োজন হয় যখন আমরা যে টেনসর থেকে ম্যাপিং করছি তার একটি একক উপাদান গণনা করার জন্য একাধিক মান প্রয়োজন হয়, যেমন আউটপুট->ইনপুট ইনডেক্সিং ম্যাপ অব রিডাকশন বা ইনপুট-> সম্প্রচারের জন্য আউটপুট ম্যাপ।
rt_vars_ রানটাইমে সম্ভাব্য মান এনকোড করে। উদাহরণস্বরূপ, অফসেট একটি 1D HloDynamicSliceInstruction জন্য গতিশীল। সংশ্লিষ্ট RTVar 0 এবং tensor_size - slice_size - 1 মধ্যে সম্ভাব্য মান থাকবে।
constraints_ মানের মধ্যে সম্পর্ক ক্যাপচার করে <expression> in <range> , যেমন d0 + s0 in [0, 20] । Variable.bounds এর সাথে একসাথে তারা ইন্ডেক্সিং ফাংশনের "ডোমেন" সংজ্ঞায়িত করে।
উপরোক্ত সবকটির প্রকৃত অর্থ কী তা বোঝার জন্য আসুন উদাহরণ দ্বারা অধ্যয়ন করি।
Unfused Ops জন্য মানচিত্র সূচীকরণ
উপাদান অনুসারে
এলিমেন্টওয়াইজ অপারেশনের জন্য ইন্ডেক্সিং ম্যাপ হল একটি পরিচয়।
p0 = f32[10, 20] parameter(0)
p1 = f32[10, 20] parameter(1)
output = f32[10, 20] add(p0, p1)
মানচিত্র output -> p0 :
(d0, d1) -> (d0, d1),
domain:
d0 in [0, 9],
d1 in [0, 19]
আউটপুট মানচিত্র p0 -> output :
(d0, d1) -> (d0, d1),
domain:
d0 in [0, 9],
d1 in [0, 19]
সম্প্রচার
সম্প্রচারের অর্থ হল যখন আমরা আউটপুটকে ইনপুটে ম্যাপ করি এবং যখন আমরা ইনপুটকে আউটপুটে ম্যাপ করি তখন কিছু মাত্রা মুছে ফেলা হয়।
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
ইনপুট মানচিত্র আউটপুট:
(d0, d1, d2) -> (d1),
domain:
d0 in [0, 9],
d1 in [0, 19],
d2 in [0, 29]
আউটপুট মানচিত্রের ইনপুট:
(d0)[s0, s1] -> (s0, d0, s1),
domain:
d0 in [0, 19],
s0 in [0, 9],
s1 in [0, 29]
মনে রাখবেন যে ইনপুট-টু-আউটপুট ম্যাপিংয়ের জন্য এখন আমাদের ডানদিকে রেঞ্জ ভেরিয়েবল রয়েছে। সেগুলি হল চিহ্ন যা মানের রেঞ্জের প্রতিনিধিত্ব করে। উদাহরণস্বরূপ, এই বিশেষ ক্ষেত্রে ইনডেক্স d0 সহ ইনপুটের প্রতিটি উপাদান আউটপুটের 10x1x30 স্লাইসে ম্যাপ করা হয়।
আইওটা
Iota এর কোন ইনপুট টেনসর অপারেন্ড নেই, তাই কোন ইনপুট সূচক আর্গুমেন্ট নেই।
iota = f32[2,4] iota(), dimensions={1}
ইনপুট মানচিত্র আউটপুট:
(d0, d1) -> ()
domain:
d0 in [0, 1]
d1 in [0, 3]
আউটপুট মানচিত্রে ইনপুট:
()[s0, s1] -> (s0, s1)
domain:
s0 in [0, 1]
s1 in [0, 3]
ডাইনামিক স্লাইস
DynamicSlice শুধুমাত্র রানটাইমে পরিচিত অফসেট আছে.
src = s32[2, 2, 258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = s32[1, 2, 32] dynamic-slice(src, of1, of2, of3), dynamic_slice_sizes={1, 2, 32}
ds থেকে src এ ম্যাপ ইনপুট করার আউটপুট:
(d0, d1, d2){rt0, rt1, rt2} -> (d0 + rt0, d1 + rt1, d2 + rt2),
domain:
d0 in [0, 0],
d1 in [0, 1],
d2 in [0, 31],
rt0 in [0, 1],
rt1 in [0, 0],
rt2 in [0, 226]
মনে রাখবেন যে ইনপুট-টু-আউটপুট ম্যাপিংয়ের জন্য এখন আমাদের ডানদিকে rt আছে। সেগুলি হল চিহ্ন যা রানটাইম মান প্রতিনিধিত্ব করে। উদাহরণ স্বরূপ, এই বিশেষ ক্ষেত্রে আউটপুটের প্রতিটি উপাদানের জন্য সূচক d0, d1, d2 আমরা ইনপুটের সূচক গণনা করতে of1 , of2 এবং of3 এর স্লাইস অফসেটগুলি অ্যাক্সেস করি। রানটাইম ভেরিয়েবলের ব্যবধানগুলি অনুমান করে নেওয়া হয় যে পুরো স্লাইসটি সীমানায় থাকে।
of1 , of2 এবং of3 জন্য ইনপুট ম্যাপে আউটপুট:
(d0, d1, d2) -> (),
domain:
d0 in [0, 0],
d1 in [0, 1],
d2 in [0, 31]
ডাইনামিকআপডেট স্লাইস
src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)
src জন্য ইনপুট মানচিত্রের আউটপুট তুচ্ছ। ডোমেইনকে আপডেট করা হয়নি এমন সূচকগুলিতে সীমাবদ্ধ করে এটি আরও সুনির্দিষ্ট করা যেতে পারে, তবে এখনই সূচীকরণ মানচিত্রগুলি অসমতার সীমাবদ্ধতা সমর্থন করে না।
(d0, d1) -> (d0, d1),
domain:
d0 in [0, 19],
d1 in [0, 29]
upd জন্য ইনপুট ম্যাপে আউটপুট:
(d0, d1){rt0, rt1} -> (d0 - rt0, d1 - rt1),
domain:
d0 in [0, 19],
d1 in [0, 29],
rt0 in [0, 15],
rt1 in [0, 20]
মনে রাখবেন যে এখন আমাদের কাছে rt0 এবং rt1 রয়েছে যা রানটাইম মানগুলিকে উপস্থাপন করে। এই বিশেষ ক্ষেত্রে সূচক d0, d1 সহ আউটপুটের প্রতিটি উপাদানের জন্য আমরা ইনপুটের সূচক গণনা করতে of1 এবং of2 স্লাইস অফসেটগুলি অ্যাক্সেস করি। রানটাইম ভেরিয়েবলের ব্যবধানগুলি অনুমান করে নেওয়া হয় যে পুরো স্লাইসটি সীমানায় থাকে।
of1 এবং of2 জন্য ইনপুট ম্যাপে আউটপুট:
(d0, d1) -> (),
domain:
d0 in [0, 19],
d1 in [0, 29]
জড়ো করা
শুধুমাত্র সরলীকৃত জমায়েত সমর্থিত. gather_simplifier.h দেখুন।
operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
offset_dims={1,2,3},
collapsed_slice_dims={},
start_index_map={0,1},
index_vector_dim=1,
slice_sizes={7,8,4}
operand জন্য ইনপুট ম্যাপে আউটপুট:
(d0, d1, d2, d3){rt0, rt1} -> (d1 + rt0, d2 + rt1, d3),
domain:
d0 in [0, 1805],
d1 in [0, 6],
d2 in [0, 7],
d3 in [0, 3],
rt0 in [0, 26],
rt1 in [0, 68]
মনে রাখবেন যে এখন আমাদের কাছে rt চিহ্ন রয়েছে যা রানটাইম মানগুলিকে উপস্থাপন করে।
indices জন্য ইনপুট ম্যাপে আউটপুট:
(d0, d1, d2, d3)[s0] -> (d0, s0),
domain:
d0 in [0, 1805],
d1 in [0, 6],
d2 in [0, 7],
d3 in [0, 3],
s0 in [0, 1]
রেঞ্জ ভেরিয়েবল s0 দেখায় যে আউটপুটের একটি উপাদান গণনা করার জন্য আমাদের indices টেনসরের সম্পূর্ণ সারি (d0, *) প্রয়োজন।
স্থানান্তর
ট্রান্সপোজের জন্য ইন্ডেক্সিং ম্যাপ হল ইনপুট/আউটপুট মাত্রার একটি পরিবর্তন।
p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}
ইনপুট মানচিত্র আউটপুট:
(d0, d1, d2, d3) -> (d0, d3, d1, d2),
domain:
d0 in [0, 2],
d1 in [0, 5],
d2 in [0, 127],
d3 in [0, 12287],
আউটপুট মানচিত্রের ইনপুট:
(d0, d1, d2, d3) -> (d0, d2, d3, d1),
domain:
d0 in [0, 2],
d1 in [0, 12287],
d2 in [0, 5],
d3 in [0, 127]
বিপরীত
বিপরীতের জন্য ইন্ডেক্সিং মানচিত্র বিপরীত মাত্রাগুলিকে upper_bound(d_i) - d_i এ পরিবর্তন করে :
p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}
ইনপুট মানচিত্র আউটপুট:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3),
domain:
d0 in [0, 0],
d1 in [0, 16],
d2 in [0, 8],
d3 in [0, 8]
আউটপুট মানচিত্রের ইনপুট:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3),
domain:
d0 in [0, 0],
d1 in [0, 16],
d2 in [0, 8],
d3 in [0, 8]
(বৈচিত্র্যময়) হ্রাস করা
ভ্যারিয়াডিক রিডাকশনে বেশ কয়েকটি ইনপুট এবং বেশ কয়েকটি প্রাথমিক মান থাকে, আউটপুট থেকে ইনপুট পর্যন্ত মানচিত্র হ্রাসকৃত মাত্রা যোগ করে।
p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
out = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
dimensions={0}, to_apply=max
মানচিত্র ইনপুট করার আউটপুট:
-
out[0]->p0:
(d0)[s0] -> (s0, d0),
domain:
d0 in [0, 9],
s0 in [0, 255]
out[0]->p0_init:
(d0) -> (),
domain:
d0 in [0, 9]
আউটপুট মানচিত্র ইনপুট:
-
p0->out[0]:
(d0, d1) -> (d1),
domain:
d0 in [0, 255],
d1 in [0, 9]
p0_init->out[0]:
()[s0] -> (s0),
domain:
s0 in [0, 9]
স্লাইস
স্লাইসের জন্য আউটপুট থেকে ইনপুট পর্যন্ত সূচীকরণের ফলে একটি স্ট্রাইডেড ইনডেক্সিং ম্যাপ তৈরি হয় যা আউটপুটের প্রতিটি উপাদানের জন্য বৈধ। ইনপুট থেকে আউটপুটে ম্যাপিং ইনপুটের উপাদানগুলির একটি স্ট্রীড রেঞ্জের মধ্যে সীমাবদ্ধ।
p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
slice={[5:10:1], [3:20:7], [0:50:2]}
ইনপুট মানচিত্র আউটপুট:
(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2),
domain:
d0 in [0, 4],
d1 in [0, 2],
d2 in [0, 24]
আউটপুট মানচিত্রের ইনপুট:
(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2),
domain:
d0 in [5, 9],
d1 in [3, 17],
d2 in [0, 48],
(d1 - 3) mod 7 in [0, 0],
d2 mod 2 in [0, 0]
পুনরায় আকার দিন
রিশেপগুলি বিভিন্ন স্বাদে আসে।
আকৃতি সঙ্কুচিত করুন
এটি এনডি থেকে 1ডিতে একটি "লিনিয়ারাইজিং" রিশেপ।
p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)
ইনপুট মানচিত্র আউটপুট:
(d0) -> (d0 floordiv 8, d0 mod 8),
domain:
d0 in [0, 31]
আউটপুট মানচিত্রের ইনপুট:
(d0, d1) -> (d0 * 8 + d1),
domain:
d0 in [0, 3],
d1 in [0, 7]
আকৃতি প্রসারিত করুন
এটি একটি বিপরীত "পতনের আকৃতি" অপশন, এটি একটি 1D ইনপুটকে ND আউটপুটে পুনরায় আকার দেয়।
p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)
ইনপুট মানচিত্র আউটপুট:
(d0, d1) -> (d0 * 8 + d1),
domain:
d0 in [0, 3],
d1 in [0, 7]
আউটপুট মানচিত্রের ইনপুট:
(d0) -> (d0 floordiv 8, d0 mod 8),
domain:
d0 in [0, 31]
সাধারণ পুনঃআকৃতি
এগুলি হল রিশেপ অপ্স যেগুলিকে একক প্রসারিত বা ভেঙে পড়া আকৃতি হিসাবে উপস্থাপন করা যায় না। এগুলিকে শুধুমাত্র 2 বা তার বেশি প্রসারিত বা ভেঙে পড়া আকারের একটি রচনা হিসাবে উপস্থাপন করা যেতে পারে।
উদাহরণ 1: লিনিয়ারাইজেশন-রেখাকরণ।
p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)
এই রিশেপটিকে tensor<4x8xf32> থেকে tensor<32xf32> এবং তারপর tensor<2x4x4xf32> এর আকৃতি সম্প্রসারণের একটি রচনা হিসাবে উপস্থাপন করা যেতে পারে।
ইনপুট মানচিত্র আউটপুট:
(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4),
domain:
d0 in [0, 1],
d1 in [0, 3],
d2 in [0, 3]
আউটপুট মানচিত্রের ইনপুট:
(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4),
domain:
d0 in [0, 3],
d1 in [0, 7]
উদাহরণ 2: প্রসারিত এবং সংকুচিত সাবশেপ
p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)
এই পুনঃআকৃতি দুটি পুনঃআকৃতির একটি রচনা হিসাবে উপস্থাপন করা যেতে পারে। প্রথমটি বাইরেরতম মাত্রার tensor<4x8x12xf32> কে tensor<32x12xf32> ভেঙে ফেলে এবং দ্বিতীয়টি ভিতরেরতম মাত্রার tensor<32x12xf32> tensor<32x3x4xf32> প্রসারিত করে।
ইনপুট মানচিত্র আউটপুট:
(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2),
domain:
d0 in [0, 31],
d1 in [0, 2]
d2 in [0, 3]
আউটপুট মানচিত্রের ইনপুট:
(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4),
domain:
d0 in [0, 3],
d1 in [0, 7],
d2 in [0, 11]
বিটকাস্ট
একটি বিটকাস্ট অপকে ট্রান্সপোজ-রিশেপ-ট্রান্সপোজের একটি ক্রম হিসাবে উপস্থাপন করা যেতে পারে। অতএব, এর সূচীকরণ মানচিত্রগুলি এই অনুক্রমের জন্য ইন্ডেক্সিং মানচিত্রের একটি সংমিশ্রণ মাত্র।
সংযুক্ত করা
কনক্যাটের জন্য আউটপুট-টু-ইনপুট ম্যাপিং সমস্ত ইনপুটগুলির জন্য সংজ্ঞায়িত করা হয়েছে, তবে অ-ওভারল্যাপিং ডোমেনগুলির সাথে, অর্থাৎ একবারে শুধুমাত্র একটি ইনপুট ব্যবহার করা হবে৷
p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT output = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}
ইনপুট মানচিত্রের আউটপুট:
-
output->p0:
(d0, d1, d2) -> (d0, d1, d2),
domain:
d0 in [0, 1],
d1 in [0, 4],
d2 in [0, 6]
output->p1:
(d0, d1, d2) -> (d0, d1 - 5, d2),
domain:
d0 in [0, 1],
d1 in [5, 15],
d2 in [0, 6]
output->p2:
(d0, d1, d2) -> (d0, d1 - 16, d2),
domain:
d0 in [0, 1],
d1 in [16, 32],
d2 in [0, 6]
আউটপুট মানচিত্রের ইনপুট:
-
p0->output:
(d0, d1, d2) -> (d0, d1, d2),
domain:
d0 in [0, 1],
d1 in [0, 4],
d2 in [0, 6]
p1->output:
(d0, d1, d2) -> (d0, d1 + 5, d2),
domain:
d0 in [0, 1],
d1 in [0, 10],
d2 in [0, 6]
p2->output:
(d0, d1, d2) -> (d0, d1 + 16, d2),
domain:
d0 in [0, 1],
d1 in [0, 16],
d2 in [0, 6]
ডট
বিন্দুর জন্য ইন্ডেক্সিং মানচিত্রগুলি হ্রাসের সাথে খুব মিল।
p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
output = f32[4, 128, 64] dot(p0, p1),
lhs_batch_dims={0}, rhs_batch_dims={0},
lhs_contracting_dims={2}, rhs_contracting_dims={1}
ইনপুট মানচিত্রের আউটপুট:
- আউটপুট -> p0:
(d0, d1, d2)[s0] -> (d0, d1, s0),
domain:
d0 in [0, 3],
d1 in [0, 127],
d2 in [0, 63],
s0 in [0, 255]
- আউটপুট -> p1:
(d0, d1, d2)[s0] -> (d0, s0, d2),
domain:
d0 in [0, 3],
d1 in [0, 127],
d2 in [0, 63],
s0 in [0, 255]
আউটপুট মানচিত্রের ইনপুট:
- p0 -> আউটপুট:
(d0, d1, d2)[s0] -> (d0, d1, s0),
domain:
d0 in [0, 3],
d1 in [0, 127],
d2 in [0, 255],
s0 in [0, 63]
- p1 -> আউটপুট:
(d0, d1, d2)[s0] -> (d0, s0, d1),
domain:
d0 in [0, 3],
d1 in [0, 255],
d2 in [0, 63],
s0 in [0, 127]
প্যাড
PadOp-এর ইন্ডেক্সিং হল SliceOp ইন্ডেক্সিংয়ের বিপরীত।
p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0
প্যাডিং কনফিগারেশন 1_4_1x4_8_0 বোঝায় lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1 ।
মানচিত্র ইনপুট করার আউটপুট:
- আউটপুট -> p0:
(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4),
domain:
d0 in [1, 7],
d1 in [4, 7],
(d0 - 1) mod 2 in [0, 0]
- আউটপুট -> p1:
(d0, d1) -> (),
domain:
d0 in [0, 11],
d1 in [0, 15]
উইন্ডো হ্রাস করুন
XLA-তে ReduceWindow প্যাডিংও করে। তাই, ইনডেক্সিং ম্যাপগুলিকে ReduceWindow সূচীকরণের একটি রচনা হিসাবে গণনা করা যেতে পারে যা কোনও প্যাডিং এবং PadOp এর সূচীকরণ করে না।
c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
outpu = f32[1024, 3] reduce-window(p0, c_inf),
window={size=1x512 pad=0_0x0_0}, to_apply=max
মানচিত্র ইনপুট করার আউটপুট:
-
output -> p0:
(d0, d1)[s0] -> (d0, d1 + s0),
domain:
d0 in [0, 1023],
d1 in [0, 2],
s0 in [0, 511]
output -> c_inf:
(d0, d1) -> (),
domain:
d0 in [0, 1023],
d1 in [0, 2]
ফিউশনের জন্য ইন্ডেক্সিং ম্যাপ
ফিউশন অপের জন্য ইন্ডেক্সিং ম্যাপ হল ক্লাস্টারের প্রতিটি অপের জন্য ইন্ডেক্সিং ম্যাপের একটি সংমিশ্রণ। এটি ঘটতে পারে যে কিছু ইনপুট বিভিন্ন অ্যাক্সেস প্যাটার্ন সহ একাধিকবার পড়া হয়।
একটি ইনপুট, একাধিক ইন্ডেক্সিং ম্যাপ
এখানে p0 + transpose(p0) এর একটি উদাহরণ।
f {
p0 = f32[1000, 1000] parameter(0)
transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}
p0 এর জন্য আউটপুট-টু-ইনপুট ইন্ডেক্সিং মানচিত্র হবে (d0, d1) -> (d0, d1) এবং (d0, d1) -> (d1, d0) । এর অর্থ হল আউটপুটের একটি উপাদান গণনা করার জন্য আমাদের ইনপুট প্যারামিটারটি দুইবার পড়তে হবে।
একটি ইনপুট, অনুলিপি করা ইন্ডেক্সিং মানচিত্র
এমন কিছু ক্ষেত্রে আছে যখন ইনডেক্সিং মানচিত্রগুলি আসলে একই, যদিও তা অবিলম্বে স্পষ্ট নয়।
f {
p0 = f32[20, 10, 50] parameter(0)
lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
ROOT output = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}
এই ক্ষেত্রে p0 জন্য আউটপুট-টু-ইনপুট ইন্ডেক্সিং মানচিত্র হল (d0, d1, d2) -> (d2, d0, d1) ।
সফটম্যাক্স
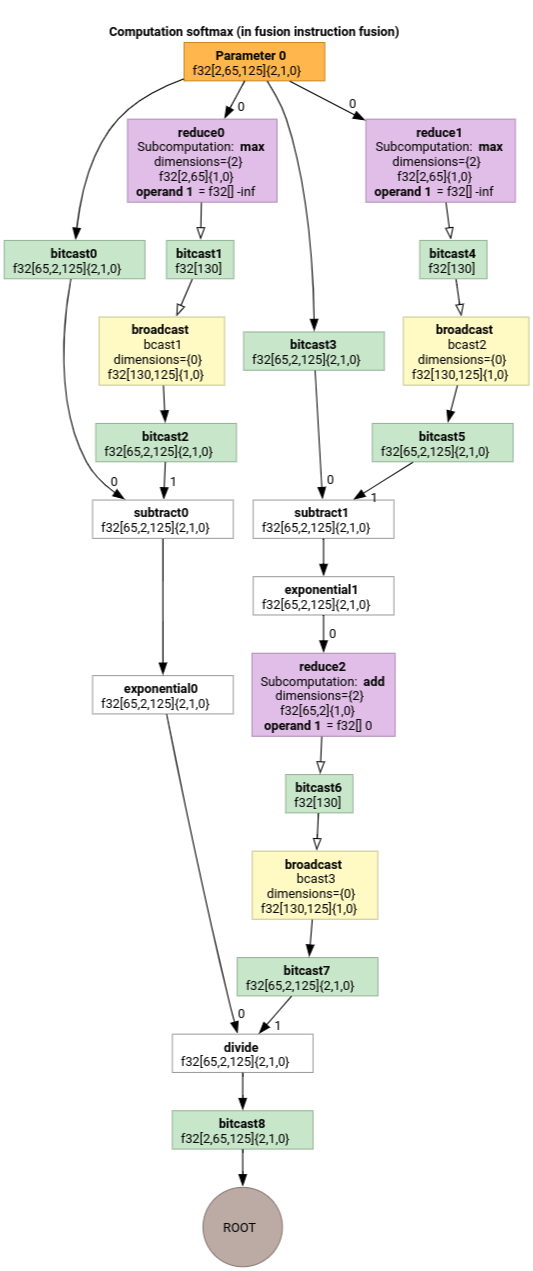
softmax-এর জন্য parameter 0 জন্য আউটপুট-টু-ইনপুট ইন্ডেক্সিং মানচিত্র:
(d0, d1, d2)[s0] -> (d0, d1, s0),
domain:
d0 in [0, 1],
d1 in [0, 64],
d2 in [0, 124],
s0 in [0, 124]
এবং
(d0, d1, d2) -> (d0, d1, d2),
domain:
d0 in [0, 1],
d1 in [0, 64],
d2 in [0, 124]
যেখানে s0 ইনপুটের অন্তর্নিহিত মাত্রাকে বোঝায়।
আরও উদাহরণের জন্য indexing_analysis_test.cc দেখুন।
ইন্ডেক্সিং ম্যাপ সিম্পলিফায়ার
mlir::AffineMap আপস্ট্রিমের জন্য ডিফল্ট সরলীকরণ মাত্রা/চিহ্নের পরিসর সম্পর্কে কোনো অনুমান করতে পারে না। অতএব, এটি দক্ষতার সাথে mod এবং div দিয়ে অভিব্যক্তিকে সরল করতে পারে না।
আমরা অ্যাফাইন ম্যাপে সাব-অভিব্যক্তির নিম্ন এবং উপরের সীমা সম্পর্কে জ্ঞান লাভ করতে পারি যাতে তাদের আরও সহজ করা যায়।
সরলীকরণকারী নিম্নলিখিত অভিব্যক্তিগুলি পুনরায় লিখতে পারে।
-
(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16)d- এর জন্য[0, 6] x [0, 14]হয়ে যায়(d0, d1) -> (d0, d1) -
(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10)di in [0, 9]জন্য ফ্লোরডিভ 10, d2 মোড 10) হয়ে যায়(d0, d1, d2) -> (d0, d1, d2). -
(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8)d_i in [0, 9]হয়ে যায়(d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8). -
(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9)d এর জন্য[0, 9] x [0, 10]হয়ে যায়(d0, d1) -> (d0)।
ইন্ডেক্সিং ম্যাপ সিম্পলিফায়ার আমাদের বুঝতে দেয় যে HLO-তে কিছু চেইন্ড রিশেপ একে অপরকে বাতিল করে।
p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)
ইনডেক্সিং ম্যাপ এবং তাদের সরলীকরণের পরে আমরা পাব
(d0, d1, d2) -> (d0, d1, d2) ।
ইন্ডেক্সিং মানচিত্র সরলীকরণ সীমাবদ্ধতাগুলিকেও সরল করে।
-
lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_boundপ্রকারের সীমাবদ্ধতাupdated_lower_bound <= affine_expr <= updated_upped_boundহিসাবে পুনরায় লেখা হয়। - যে সীমাবদ্ধতাগুলি সর্বদা সন্তুষ্ট থাকে, যেমন
d0 + s0 in [0, 20]জন্যd0 in [0, 5]এবংs0 in [1, 3]বাদ দেওয়া হয়। - সীমাবদ্ধতার মধ্যে Affine এক্সপ্রেশনগুলি উপরের সূচীকৃত affine মানচিত্র হিসাবে অপ্টিমাইজ করা হয়েছে।
আরও উদাহরণের জন্য indexing_map_test.cc দেখুন।


