Tài liệu này mô tả bản phân tích lập chỉ mục HLO, cho phép bạn sử dụng các biểu tượng bản đồ lập chỉ mục tính toán cho hoạt động HLO. Bản đồ lập chỉ mục là một hàm ánh xạ chỉ mục của tensor này với chỉ số của một tensor khác, ví dụ: chỉ mục của HLO đầu ra lệnh thành các chỉ mục của đầu vào lệnh HLO hoặc ngược lại.
Ví dụ:
Đối với thông báo từ tensor<20xf32> đến tensor<10x20x30xf32>
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
bản đồ lập chỉ mục từ đầu ra đến đầu vào là (i, j, k) -> (j) cho i in
[0, 10], j in [0, 20] và k in [0, 30].
Động lực
GPU XLA sử dụng một số giải pháp tuỳ chỉnh để lý giải về việc hợp nhất, sử dụng toán hạng và các lược đồ xếp kề (xem thêm thông tin chi tiết bên dưới). Mục tiêu của việc phân tích lập chỉ mục là cung cấp một thành phần có thể sử dụng lại cho các trường hợp sử dụng như vậy. Phân tích chỉ mục được xây dựng dựa trên cơ sở hạ tầng Affine Map của MLIR và thêm ngữ nghĩa HLO.
Hợp nhất
Việc suy luận về việc hợp nhất bộ nhớ trở nên khả thi đối với các trường hợp không quan trọng, khi chúng ta biết những phần tử/lát cắt của dữ liệu đầu vào được đọc để tính toán một phần tử của dữ liệu đầu ra.
Sử dụng Toán hạng
Mức sử dụng toán hạng trong XLA cho biết mức sử dụng của mỗi đầu vào của lệnh giả sử đầu ra của lệnh được sử dụng đầy đủ. Hiện tại, mức sử dụng cũng không được tính toán cho trường hợp chung. Dữ liệu phân tích lập chỉ mục giúp điện toán hoạt động sử dụng chính xác.
Cách phân ô
Hình khối/lát là tập con siêu hình chữ nhật của tensor được tham số bằng các giá trị bù trừ, kích cỡ và sải chân. Tính năng lan truyền thẻ thông tin là một cách để tính toán các tham số thẻ thông tin của nhà sản xuất/người tiêu dùng hoạt động bằng cách sử dụng các tham số xếp kề của chính vận hành đó. Đã có một thư viện thực hiện việc này cho softmax và dot. Có thể truyền tải thẻ thông tin chung chung hơn và mạnh mẽ nếu dữ liệu được thể hiện qua bản đồ lập chỉ mục.
Hàm và miền
Bản đồ lập chỉ mục là một hàm f(x) = f(d, r, rt)
ánh xạ đa chỉ mục d của tensor A với các phần tử/dải ô của
tensor B. Tham số r đề cập đến các dải chỉ mục của các phương diện có trong tensor B, nhưng không có trong tensor A. Tham số rt đề cập đến các giá trị thời gian chạy, ví dụ: chỉ mục cho một toán tử thu thập.
Ví dụ: nếu chúng ta giảm từ tensor<2x4x8x16xf32> xuống
tensor<4x8xf32>, thì bản đồ lập chỉ mục từ đầu ra 2D đến đầu vào 4D là
(d0, d1) -> (r0, d0, d1, r1), trong đó d_i là các biến kích thước
tương ứng với chỉ mục của tensor đầu ra. Mã hoá các biến phạm vi r_j
nhiều giá trị, tức là để tính toán phần tử (d0, d1) của đầu ra, chúng ta cần
Phần tử (r0, d0, d1, r1) của đầu vào, trong đó r0 in [0, 1] và
r1 in [0, 15].
Bạn có thể tạo mối liên kết này từ các thuộc tính của lệnh HLO hoặc có thể kết hợp các mối liên kết của lệnh chưa hợp nhất để lập chỉ mục cho một lệnh hợp nhất. Ánh xạ cũng có một miền chỉ định các phần tử của tensor ánh xạ đó tồn tại.
f(x) sao cho
lb <= g(x) <= ub
Vì muốn giảm thiểu việc tính toán lại, nên chúng ta cần một thư viện dành cho các phép tính. XLA đã phụ thuộc vào MLIR, vì vậy, chúng ta sử dụng mlir::AffineMap thay vì viết một thư viện số học tượng trưng khác.
AffineMap thông thường có dạng như sau
(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)
AffineMap có hai loại tham số: phương diện và ký hiệu. Chiến lược phát hành đĩa đơn
kích thước tương ứng với các biến thứ nguyên d, biểu tượng tương ứng với
các biến trong phạm vi r và biến RT rt. AffineMap không chứa bất kỳ
siêu dữ liệu về phạm vi của tham số, nên chúng tôi phải cung cấp dữ liệu này
của chúng tôi.
struct Interval {
int64_t lower;
int64_t upper;
};
// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
Interval bounds;
};
// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
Interval range;
};
// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
Interval feasible_values;
const HloInstruction* hlo;
// This is a map from the iteration space of the corresponding indexing map to
// the iteration space of `hlo`. It shows what element of `hlo` we need to
// extract to get the runtime value for the RTVar.
mlir::AffineMap map;
};
class IndexingMap {
mlir::AffineMap affine_map_;
std::vector<DimVar> dim_vars_;
std::vector<RangeVar> range_vars_;
std::vector<RTVar> rt_vars_;
llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};
dim_vars_ mã hoá các điều kiện ràng buộc hộp bao gồm cho phương diện
biến d của bản đồ lập chỉ mục, thường trùng với
hình dạng của tensor đầu ra cho các hoạt động như hoán vị, giảm, theo thành phần, dấu chấm, nhưng
có một số ngoại lệ như
HloConcatenateInstruction.
range_vars_ mã hoá các giá trị có thể mà tham số r có thể nhận.
rt_vars_ lưu trữ các hướng dẫn hlo được liên kết cùng với quyền truy cập của họ
và các giá trị khả thi trong thời gian chạy. Ví dụ: độ lệch là động
cho HloDynamicSliceInstruction 1D. RTVar tương ứng sẽ có
HloInstruction* tạo ra một tensor thứ hạng 0 với quyền truy cập (d0) -> ()
vì với mọi phần tử của dữ liệu đầu ra, chúng tôi trích xuất cùng một phần tử
từ tensor chênh lệch để tính toán chỉ số của đầu vào. Chúng ta cũng có thể giả định rằng độ dời của lát cắt luôn nằm trong khoảng từ 0 đến tensor_size - slice_size - 1.
Hãy cùng tìm hiểu qua ví dụ để hiểu rõ ý nghĩa của tất cả những nội dung trên.
Lập chỉ mục Maps cho Hoạt động không kết hợp
Elementwise
Đối với hoạt động kiểm thử phần tử, bản đồ lập chỉ mục là một danh tính.
p0 = f32[10, 20] parameter(0)
p1 = f32[10, 20] parameter(1)
add = f32[10, 20] add(p0, p1)
Dữ liệu đầu ra cho bản đồ đầu vào:
- đầu ra -> input_i:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Bản đồ đầu vào để đầu ra
- input_i -> output:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Truyền tin
Truyền tin có nghĩa là một số phương diện sẽ bị xoá khi chúng ta ánh xạ đầu ra đến đầu vào và được thêm khi chúng ta ánh xạ đầu vào đến đầu ra.
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
Đầu ra để nhập dữ liệu ánh xạ:
(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]
Bản đồ đầu vào đến đầu ra
(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]
Lưu ý rằng bây giờ chúng ta có s ở phía bên phải cho đầu vào đến đầu ra
ánh xạ. Đó là các ký hiệu đại diện cho phạm vi giá trị. Ví dụ: trong
trường hợp cụ thể này, mọi phần tử của đầu vào có chỉ mục d0 đều được ánh xạ tới
10x1x30 lát cắt của đầu ra.
Hằng số và Iota
Điểm thuận tiện là các API này không có tham số đầu vào nào nên sẽ không cần tính toán.
DynamicSlice
DynamicSlice giống như Slice, nhưng các độ dời là động.
src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}
Bản đồ đầu ra đến đầu vào cho src:
(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
hlo: of1 = s32[] parameter(1)
(d0, d1, d2) -> ()
s1 in [0, 0]
hlo: of2 = s32[] parameter(2)
(d0, d1, d2) -> ()
s2 in [0, 226]
hlo: of3 = s32[] parameter(3)
(d0, d1, d2) -> ()
Lưu ý rằng giờ đây, chúng ta có s ở bên phải để ánh xạ đầu vào với đầu ra.
Đó là các ký hiệu đại diện cho các giá trị thời gian chạy. Ví dụ: trong trường hợp này,
trường hợp cụ thể cho mỗi phần tử của đầu ra với các chỉ mục d0, d1, d2 chúng tôi
truy cập độ lệch của lát cắt of1, of2 và of3 để tính toán chỉ mục của đầu vào.
Khoảng thời gian cho các biến thời gian chạy được tính bằng cách giả định rằng toàn bộ
lát cắt vẫn nằm trong giới hạn.
Bản đồ đầu ra đến đầu vào cho of1, of2 và of3:
(d0, d1, d2) -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
DynamicUpdateSlice
src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)
Kết quả đầu ra bản đồ đầu vào cho src là không đáng kể. Bạn có thể làm cho truy vấn này chính xác hơn bằng cách hạn chế miền ở các chỉ mục chưa được cập nhật, nhưng hiện tại, bản đồ lập chỉ mục không hỗ trợ các quy tắc ràng buộc về bất đẳng thức.
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]
Bản đồ đầu ra đến đầu vào cho upd:
(d0, d1)[s0, s1] -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
hlo: of1 = s32[] parameter(2)
(d0, d1) -> ()
s1 in [0, 20]
hlo: of2 = s32[] parameter(3)
(d0, d1) -> ()
Lưu ý rằng giờ đây, chúng ta có s ở bên phải để ánh xạ đầu vào với đầu ra.
Đó là những ký hiệu thể hiện giá trị thời gian chạy. Ví dụ: trong trường hợp cụ thể này, đối với mọi phần tử của đầu ra có chỉ mục d0, d1, chúng ta truy cập vào độ dời lát cắt of1 và of2 để tính toán chỉ mục của dữ liệu đầu vào. Các khoảng thời gian cho biến thời gian chạy được lấy bằng cách giả định rằng toàn bộ lát cắt vẫn nằm trong giới hạn.
Đầu ra để nhập dữ liệu ánh xạ cho of1 và of2:
(d0, d1) -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]
Thu thập
Chỉ hỗ trợ tính năng thu thập dữ liệu đơn giản. Xem [gather_simplifier].(https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h).
operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
offset_dims={1,2,3},
collapsed_slice_dims={},
start_index_map={0,1},
index_vector_dim=1,
slice_sizes={7,8,4}
Bản đồ đầu ra đến đầu vào cho operand:
(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 1)
Lưu ý rằng giờ đây, chúng ta có s ở bên phải để ánh xạ đầu vào với đầu ra.
Đó là những ký hiệu thể hiện giá trị thời gian chạy. Ví dụ: trong trường hợp này,
trường hợp cụ thể cho mỗi phần tử của đầu ra với các chỉ mục d0, d1, d2, d3 chúng tôi
trích xuất các phần tử (d0, 0) và (d0, 1) từ tensor indices.
Bản đồ đầu ra đến đầu vào cho indices:
(d0, d1, d2, d3)[s0] -> (d0, s0)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 1]
Biến phạm vi s0 cho biết chúng ta cần toàn bộ hàng (d0, *) của
Tensor indices để tính toán một phần tử của đầu ra.
Chuyển mã
Bản đồ lập chỉ mục cho phép chuyển đổi là một phép hoán vị của các phương diện đầu vào/đầu ra.
p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}
Bản đồ đầu ra đến đầu vào:
(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]
Đầu vào để đầu ra bản đồ:
(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]
Đảo ngược
Bản đồ lập chỉ mục cho các thay đổi đảo ngược phương diện được huỷ bỏ về upper_bound(d_i) -
d_i:
p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}
Đầu ra để nhập dữ liệu ánh xạ:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
Đầu vào để đầu ra bản đồ:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
(Variadic)Giảm bớt
Phương thức giảm biến có một số đầu vào và một số giá trị khởi tạo, bản đồ từ đầu ra đến đầu vào sẽ thêm các phương diện đã giảm. Vì vậy, mã này hoạt động như một nghịch đảo của chương trình truyền tin theo một nghĩa nào đó.
p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
dimensions={0}, to_apply=max
Bản đồ đầu ra đến đầu vào:
- đầu ra -> input_j:
(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]
- đầu ra -> init_j:
(d0) -> ()
domain:
d0 in [0, 9]
Bản đồ đầu vào đến đầu ra:
- input_i -> output_j:
(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]
- init_i -> output_j:
()[s0] -> (s0)
domain:
s0 in [0, 9]
for i, j = 0, ... INPUT_COUNT.
Lát cắt
Việc lập chỉ mục từ đầu ra đến đầu vào cho lát cắt sẽ dẫn đến một bản đồ lập chỉ mục theo bước hợp lệ cho mọi phần tử của đầu ra. Việc ánh xạ từ đầu vào đến đầu ra bị hạn chế ở một phạm vi bước của các phần tử trong đầu vào.
p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
slice={[5:10:1], [3:20:7], [0:50:2]}
Bản đồ đầu ra đến đầu vào:
(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]
Bản đồ đầu vào đến đầu ra:
(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]
Tái định hình
Có nhiều cách định hình lại.
Thu gọn hình dạng
Đây là kỹ thuật "tuyến tính hoá" đổi hình từ N-D sang 1D.
p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)
Đầu ra để nhập dữ liệu ánh xạ:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
Đầu vào để đầu ra bản đồ:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
Mở rộng hình dạng
Đây là toán tử "rút gọn hình dạng" nghịch đảo, giúp định hình lại dữ liệu đầu vào 1 chiều thành dữ liệu đầu ra N chiều.
p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)
Đầu ra để nhập dữ liệu ánh xạ:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
Đầu vào để đầu ra bản đồ:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
Định hình lại chung
Đây là các hoạt động bị định hình lại không thể được biểu thị dưới dạng một mở rộng duy nhất hoặc thu gọn hình dạng. Chúng chỉ có thể được trình bày dưới dạng cấu trúc gồm 2 hoặc nhiều hơn mở rộng hoặc thu gọn hình dạng.
Ví dụ 1: Tuyến tính hoá – phi tuyến tính.
p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)
Bạn có thể biểu thị hình dạng mới này dưới dạng một thành phần kết hợp hình dạng thu gọn của tensor<4x8xf32> thành tensor<32xf32>, sau đó mở rộng hình dạng thành tensor<2x4x4xf32>.
Đầu ra để nhập dữ liệu ánh xạ:
(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]
Đầu vào để đầu ra bản đồ:
(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
Ví dụ 2: Hình dạng con mở rộng và thu gọn
p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)
Việc đổi hình dạng này có thể được biểu thị dưới dạng thành phần gồm 2 hình dạng lại. Mục đầu tiên
thu gọn kích thước ngoài cùng tensor<4x8x12xf32> thành tensor<32x12xf32>
và phương pháp thứ hai mở rộng chiều trong cùng tensor<32x12xf32> thành
tensor<32x3x4xf32>.
Bản đồ đầu ra đến đầu vào:
(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]
Đầu vào để đầu ra bản đồ:
(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]
Bitcast
Một bitcast op có thể được biểu diễn dưới dạng trình tự hoán vị-đổi hình. Do đó, bản đồ lập chỉ mục của Google chỉ là một tập hợp của các bản đồ lập chỉ mục cho trình tự.
Kết hợp
Ánh xạ đầu ra đến đầu vào cho concat được xác định cho tất cả đầu vào, nhưng với các miền không trùng lặp, tức là chỉ một trong số các đầu vào sẽ được sử dụng tại một thời điểm.
p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}
Đầu ra cho đầu vào liên kết:
- đầu ra -> đầu vào 1:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- đầu ra -> đầu vào 2:
(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]
- đầu ra -> đầu vào 3:
(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]
Dữ liệu đầu vào để tạo bản đồ đầu ra:
- đầu vào 1 -> đầu ra:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- đầu vào 2 -> đầu ra:
(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]
- đầu vào 3 -> đầu ra:
(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]
Dấu chấm
Bản đồ lập chỉ mục cho dấu chấm rất giống với bản đồ giảm.
p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
lhs_batch_dims={0}, rhs_batch_dims={0},
lhs_contracting_dims={2}, rhs_contracting_dims={1}
Đầu ra cho đầu vào liên kết:
- đầu ra -> input_1:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
- đầu ra -> input_2:
(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
Dữ liệu đầu vào để tạo bản đồ đầu ra:
- input_1 -> output:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]
- input_2 -> output:
(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]
Đệm
Việc lập chỉ mục PadOp là nghịch đảo của việc lập chỉ mục SliceOp.
p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0
Cấu hình khoảng đệm 1_4_1x4_8_0 biểu thị cho lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1.
Dữ liệu đầu ra cho bản đồ đầu vào:
- đầu ra -> đầu vào:
(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]
- đầu ra -> init:
(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]
ReduceWindow
GiảmWindow trong XLA cũng thực hiện khoảng đệm. Do đó, các bản đồ lập chỉ mục có thể được tính toán dưới dạng một thành phần của hoạt động lập chỉ mục ReduceWindow không thực hiện bất kỳ hoạt động đệm nào và hoạt động lập chỉ mục của PadOp.
c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
window={size=1x512 pad=0_0x0_0}, to_apply=max
Bản đồ đầu ra đến đầu vào:
- đầu ra -> đầu vào:
(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]
- output -> init:
(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]
Lập chỉ mục bản đồ cho Fusion
Bản đồ lập chỉ mục cho fusion op là một tập hợp các bản đồ lập chỉ mục cho mỗi hoạt động trong cụm. Có thể xảy ra trường hợp một số dữ liệu đầu vào được đọc nhiều lần với các mẫu truy cập khác nhau.
Một đầu vào, nhiều bản đồ lập chỉ mục
Sau đây là ví dụ về p0 + transpose(p0).
f {
p0 = f32[1000, 1000] parameter(0)
transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}
Bản đồ lập chỉ mục từ đầu vào đến đầu vào cho p0 sẽ là (d0, d1) -> (d0, d1) và
(d0, d1) -> (d1, d0). Điều này có nghĩa là để tính toán một phần tử
của đầu ra, chúng ta có thể cần đọc tham số đầu vào hai lần.
Một đầu vào, bản đồ lập chỉ mục đã loại bỏ trùng lặp
Có những trường hợp bản đồ lập chỉ mục thực sự giống nhau, mặc dù bản đồ không rõ ràng ngay lập tức.
f {
p0 = f32[20, 10, 50] parameter(0)
lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}
Bản đồ lập chỉ mục đầu ra đến đầu vào cho p0 trong trường hợp này chỉ là (d0, d1, d2) -> (d2, d0, d1).
Softmax
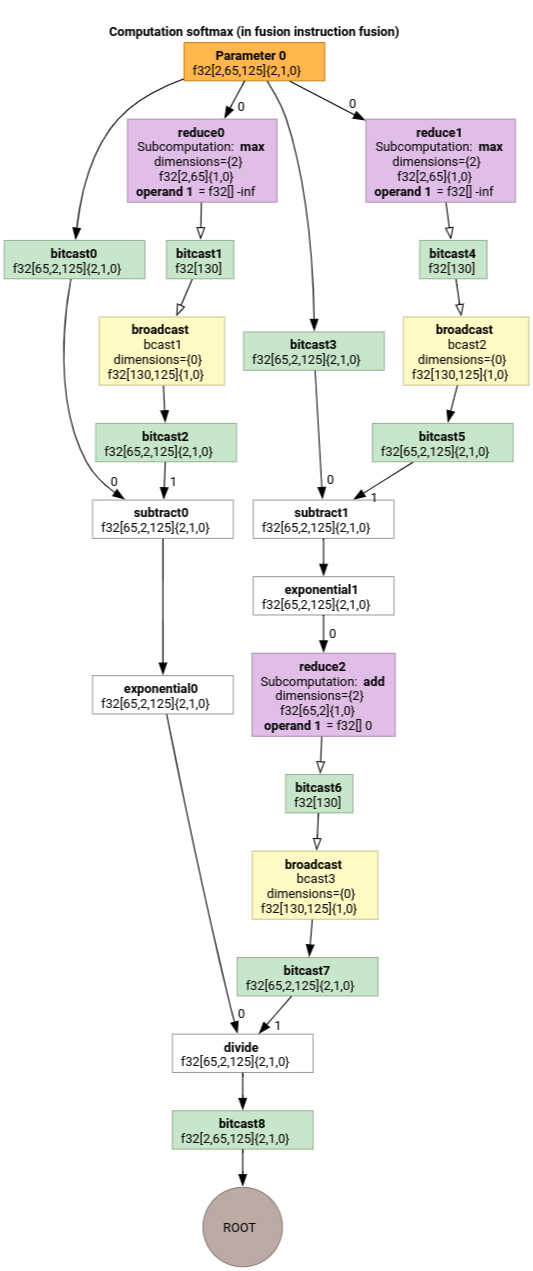
Liên kết lập chỉ mục từ đầu đến đến đầu vào của parameter 0 cho Softmax:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]
và
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
trong đó s0 là kích thước trong cùng của dữ liệu đầu vào.
Trình đơn giản hoá quy trình lập chỉ mục bản đồ
Trình đơn giản mặc định cho mlir::AffineMap ngược dòng không thể thực hiện bất kỳ
giả định về phạm vi kích thước/ký hiệu. Do đó, không thể
đơn giản hoá biểu thức bằng mod và divmột cách hiệu quả.
Chúng ta có thể tận dụng kiến thức về giới hạn dưới và giới hạn trên của biểu thức phụ trong bản đồ affine để đơn giản hoá chúng hơn nữa.
Trình đơn giản hoá có thể viết lại các biểu thức sau.
(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16)cho d trong[0, 6] x [0, 14]trở thành(d0, d1) -> (d0, d1)(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10)chodi in [0, 9]trở thành(d0, d1, d2) -> (d0, d1, d2).(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8)chod_i in [0, 9]trở thành(d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8).(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9)cho d trong[0, 9] x [0, 10]trở thành(d0, d1) -> (d0).
Trình bày bản đồ lập chỉ mục đơn giản hơn giúp chúng tôi hiểu rằng một số các hình dạng lại trong HLO sẽ huỷ lẫn nhau.
p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)
Sau khi kết hợp các bản đồ lập chỉ mục và đơn giản hoá các bản đồ đó, chúng ta sẽ có
(d0, d1, d2) -> (d0, d1, d2).
Việc đơn giản hoá bản đồ lập chỉ mục cũng giúp đơn giản hoá các hạn chế.
- Các hạn chế về kiểu
lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_boundlà được viết lại làupdated_lower_bound <= affine_expr <= updated_upped_bound. - Những quy tắc ràng buộc luôn được đáp ứng, ví dụ:
d0 + s0 in [0, 20]chod0 in [0, 5]vàs0 in [1, 3]bị loại. - Biểu thức affine trong các điều kiện ràng buộc được tối ưu hoá dưới dạng bản đồ affine lập chỉ mục ở trên.
Để biết thêm ví dụ, hãy truy cập vào indexing_map_test.cc.

