En este documento, se describe el análisis de indexación HLO, que te permite usar Procesar mapas de indexación para operaciones de HLO. El mapa de indexación es una función que asigna índices de un tensor a los índices de otro, p. ej., los índices de una salida de instrucción de HLO a los índices de las entradas de instrucción de HLO o viceversa.
Ejemplo
Para una transmisión de tensor<20xf32> a tensor<10x20x30xf32>
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
el mapa de indexación de la salida a la entrada es (i, j, k) -> (j) para i in
[0, 10], j in [0, 20] y k in [0, 30].
Motivación
La GPU de XLA usa varias soluciones personalizadas para razonar sobre la combinación, el uso de operandos y los esquemas de mosaico (más detalles a continuación). El objetivo de la indexación de datos es un componente reutilizable para esos casos de uso. Análisis de indexación se basa en la infraestructura de Affine Map de MLIR y agrega semántica de HLO.
Coalescing
El razonamiento sobre la coalescencia de memoria se vuelve factible para casos no triviales, cuando sabemos qué elementos o segmentos de las entradas se leen para calcular un elemento de la salida.
Utilización de operandos
El uso de operandos en XLA indica cuánto se usa cada entrada de la instrucción, siempre que se use por completo su salida. Actualmente, tampoco se calcula la utilización para un caso genérico. El análisis de indexación permite calcular el uso con precisión.
Mosaico
Una tarjeta o porción es un subconjunto hiperrectangular de un tensor parametrizado por desplazamientos, tamaños y pasos. La propagación de tarjetas es una forma de calcular los parámetros de mosaicos de las productor/consumidor de la operación con los parámetros de mosaicos de la propia operación. Ya existe una biblioteca que lo hace para softmax y punto. La propagación de mosaicos puede ser más genérica y sea sólida si se expresa a través de mapas de indexación.
Función y dominio
El mapa de indexación es una función f(x) = f(d, r, rt)
que asigna un d de varios índices de un tensor A a elementos o rangos de
tensor B. El parámetro r se refiere a los rangos de índices de las dimensiones que están presentes en el tensor B, pero no en el tensor A. El parámetro rt se refiere a los valores del entorno de ejecución, p. ej., los índices para una operación de recopilación.
Por ejemplo, si tenemos una reducción de tensor<2x4x8x16xf32> a tensor<4x8xf32>, el mapa de indexación del resultado 2D a la entrada 4D es (d0, d1) -> (r0, d0, d1, r1), donde d_i son las variables de dimensión que corresponden a los índices del tensor de salida. Codifican variables de rango r_j.
múltiples valores; es decir, para procesar un elemento (d0, d1) de la salida, necesitamos
Elementos (r0, d0, d1, r1) de la entrada, en los que r0 in [0, 1] y
r1 in [0, 15]
Esta asignación se puede construir a partir de los atributos de las instrucciones de HLO, o bien las asignaciones de instrucciones no fusionadas se pueden componer para obtener la indexación de una fusión. La asignación también tiene un dominio, que especifica para qué elementos del tensor existe la asignación.
f(x) de modo que
lb <= g(x) <= ub
Como queremos minimizar la reprocesamiento, necesitamos una biblioteca cálculos. XLA ya depende de MLIR, por lo que usamos mlir::AffineMap en lugar de escribir otra biblioteca aritmética simbólica.
Un AffineMap típico tiene este aspecto
(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)
AffineMap tiene dos tipos de parámetros: dimensiones y símbolos. Las dimensiones corresponden a las variables de dimensión d, los símbolos corresponden a las variables de rango r y las variables de RT rt. AffineMap no contiene metadatos sobre los rangos de las dimensiones, por lo que debemos proporcionar estos datos nosotros mismos.
struct Interval {
int64_t lower;
int64_t upper;
};
// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
Interval bounds;
};
// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
Interval range;
};
// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
Interval feasible_values;
const HloInstruction* hlo;
// This is a map from the iteration space of the corresponding indexing map to
// the iteration space of `hlo`. It shows what element of `hlo` we need to
// extract to get the runtime value for the RTVar.
mlir::AffineMap map;
};
class IndexingMap {
mlir::AffineMap affine_map_;
std::vector<DimVar> dim_vars_;
std::vector<RangeVar> range_vars_;
std::vector<RTVar> rt_vars_;
llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};
dim_vars_ codifica las restricciones de cuadro incluyente para las variables de dimensión d del mapa de indexación, que suelen coincidir con la forma del tensor de salida para operaciones como transponer, reducir, elemento a elemento, punto, pero hay algunas excepciones, como HloConcatenateInstruction.
range_vars_ codifica los valores posibles que pueden tomar los parámetros r.
rt_vars_ almacena las instrucciones hlo asociadas junto con sus patrones de acceso y los valores posibles en el entorno de ejecución. Por ejemplo, el desplazamiento es dinámico
para un HloDynamicSliceInstruction 1D. El RTVar correspondiente tendrá un HloInstruction* que produce un tensor de rango 0 con el patrón de acceso (d0) -> (), ya que para cada elemento de la salida extraemos el mismo elemento del tensor de offset para calcular el índice de la entrada. También podemos suponer
que el desplazamiento de la porción siempre está entre 0 y
tensor_size - slice_size - 1.
Estudiemos por ejemplo para comprender qué significa realmente todo lo anterior.
Indexación de mapas para operaciones no fusionadas
Por elemento
Para las operaciones por elementos, el mapa de indexación es una identidad.
p0 = f32[10, 20] parameter(0)
p1 = f32[10, 20] parameter(1)
add = f32[10, 20] add(p0, p1)
El resultado a las asignaciones de entrada:
- Salida -> entrada_i:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Las asignaciones de entrada a salida
- input_i -> output:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Anuncio
La transmisión implica que se quitarán algunas de las dimensiones cuando asignemos el valor salida a entrada y agregado cuando asignamos entrada a salida.
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
El mapa de salida a la entrada:
(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]
La entrada a la asignación de salida
(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]
Ten en cuenta que ahora tenemos s en el lado derecho para la entrada a salida.
la asignación. Esos son los símbolos que representan rangos de valores. Por ejemplo, en
este caso particular, cada elemento de entrada con el índice d0 se asigna a un
Porción de 10 × 1 × 30 del resultado
Constant y Iota
Convenientemente, no tienen ningún parámetro de entrada, por lo que no hay nada para calcular el indexado.
DynamicSlice
DynamicSlice es igual que Slice, pero los desplazamientos son dinámicos.
src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}
El mapa de salida a entrada para src:
(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
hlo: of1 = s32[] parameter(1)
(d0, d1, d2) -> ()
s1 in [0, 0]
hlo: of2 = s32[] parameter(2)
(d0, d1, d2) -> ()
s2 in [0, 226]
hlo: of3 = s32[] parameter(3)
(d0, d1, d2) -> ()
Observa que ahora tenemos s en el lado derecho para la asignación de entrada a salida.
Esos son los símbolos que representan los valores del entorno de ejecución. Por ejemplo, en este caso particular, para cada elemento de la salida con índices d0, d1, d2, accedemos a los desplazamientos de fragmento of1, of2 y of3 para calcular el índice de la entrada.
Los intervalos para las variables de entorno de ejecución se derivan suponiendo que se
porción permanezca dentro de los límites.
El resultado del mapa de entrada para of1, of2 y of3:
(d0, d1, d2) -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
DynamicUpdateSlice
src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)
El mapa de salida a entrada para src es trivial. Se puede hacer más preciso
restringiendo el dominio a índices no actualizados, pero ahora indexando mapas
y no admiten restricciones de igualdad.
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]
El resultado de la asignación de entrada para upd:
(d0, d1)[s0, s1] -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
hlo: of1 = s32[] parameter(2)
(d0, d1) -> ()
s1 in [0, 20]
hlo: of2 = s32[] parameter(3)
(d0, d1) -> ()
Observa que ahora tenemos s en el lado derecho para la asignación de entrada a salida.
Esos son los símbolos que representan los valores del entorno de ejecución. Por ejemplo, en este caso particular, para cada elemento de la salida con índices d0, d1, accedemos a los desplazamientos de fragmento of1 y of2 para calcular el índice de la entrada. Los intervalos para las variables del entorno de ejecución se derivan a partir de la suposición de que toda la porción permanece dentro de los límites.
El mapa de salida a entrada para of1 y of2:
(d0, d1) -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]
Reúne
Solo se admite la recopilación simplificada. Consulta [gather_simplifier].(https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h).
operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
offset_dims={1,2,3},
collapsed_slice_dims={},
start_index_map={0,1},
index_vector_dim=1,
slice_sizes={7,8,4}
El mapa de salida a entrada para operand:
(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 1)
Ten en cuenta que ahora tenemos s en el lado derecho para la asignación de entrada a salida.
Esos son los símbolos que representan los valores del entorno de ejecución. Por ejemplo, en esta
caso particular para cada elemento del resultado con índices d0, d1, d2, d3 que
extraer elementos (d0, 0) y (d0, 1) del tensor indices.
El mapa de salida a entrada para indices:
(d0, d1, d2, d3)[s0] -> (d0, s0)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 1]
La variable de rango s0 muestra que necesitamos toda la fila (d0, *) del tensor indices para calcular un elemento del resultado.
Transponer
El mapa de indexación para la transposición es una permutación de dimensiones de entrada y salida.
p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}
El mapa de salida a la entrada:
(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]
La entrada a la asignación de salida:
(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]
Inverso
El mapa de indexación para revertir cambia las dimensiones revertidas a upper_bound(d_i) -
d_i:
p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}
El mapa de salida a la entrada:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
El mapa de entrada a salida:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
Reduce (variadic)
La reducción variadica tiene varias entradas y varias inits, el mapa de salida a entrada agrega las dimensiones reducidas. Por lo tanto, se comporta como una cadena inversa a una transmisión en cierto sentido.
p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
dimensions={0}, to_apply=max
El resultado de los mapas de entrada:
- salida -> entrada_j:
(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]
- Salida -> init_j:
(d0) -> ()
domain:
d0 in [0, 9]
La entrada para generar mapas de salida:
- entrada_i -> salida_j:
(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]
- init_i -> output_j:
()[s0] -> (s0)
domain:
s0 in [0, 9]
para i, j = 0, ... INPUT_COUNT.
Porción
El indexado de salida a entrada para la porción genera un mapa de indexación con pasos que es válido para cada elemento de la salida. La asignación de la entrada a la salida se limita a un rango con paso de los elementos de la entrada.
p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
slice={[5:10:1], [3:20:7], [0:50:2]}
El resultado de la asignación de entrada es el siguiente:
(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]
La entrada a la asignación de salida:
(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]
Cambiar la forma
Los cambios de forma pueden tener diferentes formatos.
Contraer forma
Esta es una técnica de "linealización" cambiar de N-D a 1D.
p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)
El resultado de la asignación de entrada es el siguiente:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
El mapa de entrada a salida:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
Expandir forma
Esta es una operación inversa de "contraer forma", que cambia la forma de una entrada 1D en una salida de N dimensiones.
p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)
El mapa de salida a la entrada:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
El mapa de entrada a salida:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
Reestructuración genérica
Son las operaciones de cambio de forma que no se pueden representar como una sola operación de expansión contraer forma. Solo se pueden representar como una composición de 2 o más formas que se expanden o contraen.
Ejemplo 1: Linealización-deslinealización.
p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)
Esta reforma puede representarse como una composición de la forma contraída de
tensor<4x8xf32> hasta tensor<32xf32> y, luego, una expansión de forma hasta
tensor<2x4x4xf32>
El mapa de salida a la entrada:
(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]
El mapa de entrada a salida:
(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
Ejemplo 2: Subformas expandidas y contraídas
p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)
Esta transformación se puede representar como una composición de dos transformaciones. El primero contrae las dimensiones más externas tensor<4x8x12xf32> a tensor<32x12xf32> y el segundo expande la dimensión más interna tensor<32x12xf32> a tensor<32x3x4xf32>.
El mapa de salida a la entrada:
(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]
El mapa de entrada a salida:
(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]
Transmisión de bits
Una operación de transmisión de bits se puede representar como una secuencia de transposición, cambio de forma y transposición. Por lo tanto, sus mapas de indexación son solo una composición de los mapas de indexación para este secuencia.
Concatenar
La asignación de salida a entrada para concat se define para todas las entradas, pero con dominios que no se superponen, es decir, solo se usará una de las entradas a la vez.
p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}
La salida a las entradas asigna lo siguiente:
- salida -> entrada 1:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- resultado -> entrada 2:
(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]
- resultado -> entrada 3:
(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]
Las entradas a las asignaciones de salida son las siguientes:
- entrada 1 -> Resultado:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- entrada 2 -> salida:
(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]
- entrada 3 -> Resultado:
(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]
Dot
Los mapas de indexación para punto son muy similares a los de reducir.
p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
lhs_batch_dims={0}, rhs_batch_dims={0},
lhs_contracting_dims={2}, rhs_contracting_dims={1}
La salida a las asignaciones de entradas:
- output -> input_1:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
- resultado -> input_2:
(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
Las entradas para generar mapas de salida:
- input_1 -> Resultado:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]
- input_2 -> output:
(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]
Almohadilla
La indexación de PadOp es inversa a la indexación de SliceOp.
p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0
La configuración de padding 1_4_1x4_8_0 denota lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1.
El resultado de los mapas de entrada:
- resultado -> entrada:
(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]
- output -> init:
(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]
ReduceWindow
ReduceWindow en XLA también realiza rellenos. Por lo tanto, los mapas de indexación se pueden calcular como una composición de la indexación de ReduceWindow que no realiza ningún padding y la indexación de PadOp.
c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
window={size=1x512 pad=0_0x0_0}, to_apply=max
El resultado de los mapas de entrada:
- resultado -> entrada:
(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]
- output -> init:
(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]
Indexación de Maps para Fusion
El mapa de indexación para la operación de fusión es una composición de mapas de indexación para cada operación en el clúster. Puede suceder que algunas entradas se lean varias veces con diferentes patrones de acceso.
Una entrada, varios mapas de indexación
Este es un ejemplo de p0 + transpose(p0).
f {
p0 = f32[1000, 1000] parameter(0)
transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}
Los mapas de indexación de salida a entrada para p0 serán (d0, d1) -> (d0, d1) y
(d0, d1) -> (d1, d0) Esto significa que, para calcular un elemento
de la salida, es posible que debamos leer el parámetro de entrada dos veces.
Un mapa de indexación de entrada sin duplicados
Hay casos en los que los mapas de indexación son iguales, aunque no es obvio de manera inmediata.
f {
p0 = f32[20, 10, 50] parameter(0)
lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}
En este caso, el mapa de indexación de salida a entrada para p0 es solo (d0, d1, d2) -> (d2, d0, d1).
Softmax
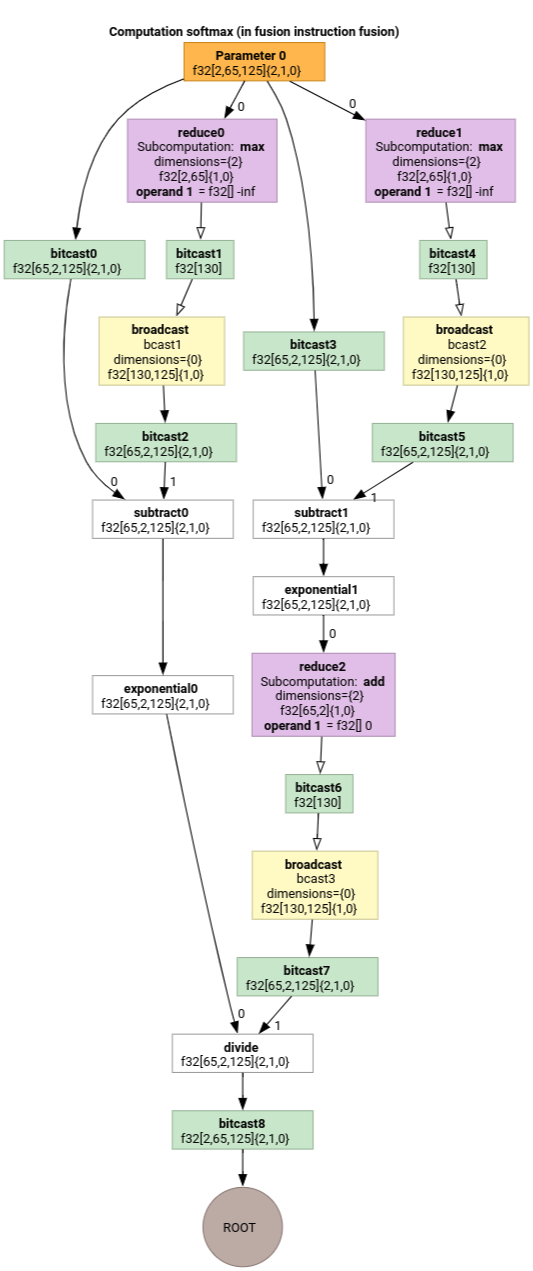
Los mapas de indexación de salida a entrada de parameter 0 para softmax:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]
y
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
donde s0 hace referencia a la dimensión más interna de la entrada.
Indexación del simplificador de mapas
El simplificador predeterminado para mlir::AffineMap upstream no puede hacer ninguna suposición sobre los rangos de dimensiones o símbolos. Por lo tanto, no puede
simplifica expresiones con mod y div de manera eficiente.
Podemos aprovechar el conocimiento sobre los límites inferior y superior de la subexpresiones en los mapas afines para simplificarlas aún más.
El simplificador puede reescribir las siguientes expresiones.
(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16)para d en[0, 6] x [0, 14]se convierte en(d0, d1) -> (d0, d1).(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10)paradi in [0, 9]se convierte en(d0, d1, d2) -> (d0, d1, d2).(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8)parad_i in [0, 9]se convierte en(d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8).(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9)para d en[0, 9] x [0, 10]se convierte en(d0, d1) -> (d0).
El simplificador de mapas de indexación nos permite comprender que algunos de los cambios de forma encadenados en HLO se cancelan entre sí.
p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)
Después de la composición de los mapas de indexación y su simplificación, obtendremos
(d0, d1, d2) -> (d0, d1, d2).
La simplificación del mapa de indexación también simplifica las restricciones.
- Restricciones de tipo
lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_boundson reescrito comoupdated_lower_bound <= affine_expr <= updated_upped_bound. - Se eliminan las restricciones que siempre se cumplen, p. ej.,
d0 + s0 in [0, 20]parad0 in [0, 5]ys0 in [1, 3]. - Las expresiones afín en las restricciones se optimizan como el mapa afín de indexación anterior.
Para ver más ejemplos, consulta indexing_map_test.cc.

