本頁面由 Cloud Translation API 翻譯而成。

索引分析

本文件說明 HLO 索引分析，可讓您以符號運算 HLO 運算的索引對應項目。索引對應是另一個張量的索引，例如：一系列 HLO 索引指示輸出與 HLO 指令輸入的索引，反之亦然。

範例

針對 tensor<20xf32> 到 tensor<10x20x30xf32> 的廣播訊息

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

從輸出到輸入的索引對應為 (i, j, k) -> (j) (i in [0, 10]、j in [0, 20] 和 k in [0, 30])。

動機

XLA GPU 使用數種輪輻式解決方案來推論共乘、運算元使用率和並排配置 (詳情請參閱下方說明)。建立索引的目標「分析」為這類用途提供可重複使用的元件索引分析是以 MLIR 的 Affine Map 基礎架構為基礎，並新增 HLO 語意。

煤炭

在非簡單的情況下，如果我們知道輸入內容的哪些元素/切片會讀取，即可推論記憶體合併。

運算元使用率

XLA 的運算元使用率代表每項指示輸入的程度便會先假設其輸出內容完全使用。目前，系統也不會針對一般情況計算使用率。索引分析可用於精確計算使用率。

圖塊

圖塊/切片是超矩形子集，由偏移、大小和步距參數化。圖塊傳播是一種方法，可使用作業本身的平鋪參數，計算作業的產生者/消費者的圖塊參數。我們已經有程式庫可執行軟性最大值和點運算。如果透過索引地圖表示，則可讓圖塊傳播更通用且健全。

功能和網域

索引對應是函式 f(x) = f(d, r, rt)，可將張量 A 的多重索引 d 對應至張量 B 的元素/範圍。參數 r 是指張量 B 中維度的索引範圍，但不包含張量 A。參數 rt 是指執行階段值，例如收集作業的索引。

舉例來說，假設我們從 tensor<2x4x8x16xf32> 減少為 tensor<4x8xf32>，那麼從 2D 輸出內容到 4D 輸入的索引對應會 (d0, d1) -> (r0, d0, d1, r1)，其中 d_i 是維度變數會對應至輸出張量的索引範圍變數 r_j 會對多個值進行編碼，也就是說，要計算輸出的 (d0, d1) 元素，我們需要輸入的 (r0, d0, d1, r1) 元素，其中 r0 in [0, 1] 和 r1 in [0, 15]。

這項對應可透過 HLO 指令的屬性建構，或是將未融合指令的對應組合，以便取得融合的索引。對應項目也具有網域，可指定對應項目存在於張量的哪些元素。

f(x) s.t.

lb <= g(x) <= ub

我們希望能盡量減少重新計算，因此需要建立符號的程式庫運算。XLA 已依附 MLIR，因此我們使用 mlir::AffineMap，而非編寫另一個符號算術程式庫。

一般 AffineMap 的樣子如下：

(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)

AffineMap 有兩種參數：尺寸和符號。維度會對應至維度變數 d，符號則對應至範圍變數 r 和 RT 變數 rt。AffineMap不含任何維度範圍的相關中繼資料，因此我們必須提供這些資料我們自己。

struct Interval {
 int64_t lower;
 int64_t upper;
};

// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
  Interval bounds;
};

// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
  Interval range;
};

// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
  Interval feasible_values;
  const HloInstruction* hlo;
  // This is a map from the iteration space of the corresponding indexing map to
  // the iteration space of `hlo`. It shows what element of `hlo` we need to
  // extract to get the runtime value for the RTVar.
  mlir::AffineMap map;
};

class IndexingMap {
  mlir::AffineMap affine_map_;
  std::vector<DimVar> dim_vars_;
  std::vector<RangeVar> range_vars_;
  std::vector<RTVar> rt_vars_;
  llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};

dim_vars_ 將維度的「大於」方塊限制編碼索引對應的變數「d」，通常會與輸出張量的形狀，例如轉置、縮減、元素時、點和有些例外狀況，例如 HloConcatenateInstruction。

range_vars_ 會編碼 r 參數可接受的可能值。

rt_vars_ 儲存相關聯的運動操作說明及其存取權以及執行階段中可行的值舉例來說，「偏移值」是動態值 1D HloDynamicSliceInstruction。對應的 RTVar 會獲得 HloInstruction* 會產生包含 (d0) -> () 存取權的「排名-0」張量而對於每個輸出元素，我們都會擷取相同的元素計算輸入的索引我們可以假設切片的偏移值一律介於 0 和 tensor_size - slice_size - 1。

我們透過範例來瞭解上述所有內容的實際意義。

為未合併的作業建立索引對應

Elementwise

就元素運算而言，索引對應表是一種身分。

  p0 = f32[10, 20] parameter(0)
  p1 = f32[10, 20] parameter(1)
  add = f32[10, 20] add(p0, p1)

輸出至輸入對應項目：

輸出 ->input_i:

(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]

輸出對應關係的輸入內容

input_i ->輸出：

(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]

廣播

廣播是指在將輸出內容對應至輸入內容時移除部分維度，並在將輸入內容對應至輸出內容時新增。

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

輸出至輸入對應關係：

(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]

輸出對應的輸入內容

(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]

請注意，現在輸入輸出至輸出的右側已有 s 對應。這些符號代表值的範圍。例如，在這種特定情況中，每個包含索引 d0 的輸入元素都會對應至 10x1x30 配量。

常數和 Iota

這些函式沒有任何輸入參數，因此不需要計算索引。

DynamicSlice

DynamicSlice 與 Slice 相同，但偏移量是動態的。

src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}

src 的輸出至輸入對應：

(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
  hlo: of1 = s32[] parameter(1)
  (d0, d1, d2)  -> ()
s1 in [0, 0]
  hlo: of2 = s32[] parameter(2)
  (d0, d1, d2)  -> ()
s2 in [0, 226]
  hlo: of3 = s32[] parameter(3)
  (d0, d1, d2) -> ()

請注意，現在右側有 s，用於輸入/輸出對應。這些是代表執行階段值的符號。例如，在這個例子中特定情況下，索引 d0, d1, d2 會特別說明輸出的每個元素存取切片偏移 of1、of2 和 of3 來計算輸入的索引。執行階段變數的間隔是假設整個切片保持界限

of1、of2 和 of3 的輸出至輸入對應：

(d0, d1, d2)  -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]

DynamicUpdateSlice

src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
    s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)

src 的輸入對應關係輸出內容相當簡單。因此可以更精確地辨識結果將網域限制在尚未更新的索引，但現在正在為地圖建立索引不支援不等式限制

(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]

upd 的輸出至輸入對應：

(d0, d1)[s0, s1]  -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
  hlo: of1 = s32[] parameter(2)
  (d0, d1)  -> ()
s1 in [0, 20]
  hlo: of2 = s32[] parameter(3)
  (d0, d1)  -> ()

請注意，現在輸入到輸出的對應關係右側有 s。這些符號代表執行階段值。舉例來說，在這個特殊情況中，對於具有索引 d0, d1 的輸出內容，我們會存取切片偏移量 of1 和 of2，以便計算輸入內容的索引。執行階段變數的間隔是假設整個切片都會保持在邊界內而衍生而來。

of1 和 of2 的輸入對應關係：

(d0, d1)  -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]

Gather

僅支援簡化的收集作業。請參閱 [gather_simplifier]。https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h

operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
  offset_dims={1,2,3},
  collapsed_slice_dims={},
  start_index_map={0,1},
  index_vector_dim=1,
  slice_sizes={7,8,4}

operand 的輸出至輸入對應：


(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
  hlo: indices = s32[1806,2]{1,0} parameter(1)
  (d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
  hlo: indices = s32[1806,2]{1,0} parameter(1)
  (d0, d1, d2, d3) -> (d0, 1)

請注意，現在輸入到輸出的對應關係右側有 s。這些是代表執行階段值的符號。例如，在這個例子中特定情況下，索引 d0, d1, d2, d3 會特別說明輸出的每個元素從 indices 張量擷取元素 (d0, 0) 和 (d0, 1)。

indices 的輸入對應關係：

  (d0, d1, d2, d3)[s0] -> (d0, s0)
  domain:
  d0 in [0, 1805]
  d1 in [0, 6]
  d2 in [0, 7]
  d3 in [0, 3]
  s0 in [0, 1]

範圍變數 s0 表示我們需要 indices 張量的整個資料列 (d0, *) 才能計算輸出的元素。

轉置

轉置的索引對應是輸入/輸出維度的排列。

p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}

輸入對應的輸出內容：

(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]

要輸出對應的輸入內容：

(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]

對調

反向索引對應會將已還原的維度變更為 upper_bound(d_i) - d_i：

p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}

輸入對應的輸出內容：

(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]

輸入至輸出對應：

(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]

(可變數)Reduce

減少血氧濃度會有一些輸入和系統會將維度縮減因此，在某種意義上，這項作業的行為類似於廣播的反向。

p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
  dimensions={0}, to_apply=max

輸出至輸入對應項目：

輸出 ->input_j:

(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]

output -> init_j：

(d0) -> ()
domain:
d0 in [0, 9]

輸入/輸出對應關係：

input_i ->output_j:

(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]

init_i -> output_j：

()[s0] -> (s0)
domain:
s0 in [0, 9]

for i, j = 0, ... INPUT_COUNT。

片段

為配量輸入將輸出建立索引和片段輸入，會產生階層式索引對應，對輸出的每個元素有效。從輸入到輸出的對應作業僅限於輸入元素的步進範圍。

p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
  slice={[5:10:1], [3:20:7], [0:50:2]}

輸入對應的輸出內容：

(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]

輸入/輸出對應：

(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]

Reshape

重塑有多種不同口味。

收合形狀

這就是「線性」將 N-D 轉變為 1D

p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)

輸出至輸入對應關係：

(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]

要輸出對應的輸入內容：

(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]

展開形狀

這是相反的「收合形狀」O 鍵，將 1D 輸入重塑為 N-D 輸出內容。

p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)

輸出至輸入對應關係：

(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]

要輸出對應的輸入內容：

(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]

通用重塑

這些是無法以單一展開或摺疊形狀表示的重新調整形狀作業。只能以 2 種以上的組合表示。展開或收合圖案。

範例 1：線性化-非線性化。

p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)

這項重塑作業可表示為 tensor<4x8xf32> 到 tensor<32xf32> 的折疊形狀組合，然後將形狀擴展至 tensor<2x4x4xf32>。

輸入對應的輸出內容：

(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]

輸入/輸出對應：

(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]

範例 2：展開和收合子形狀

p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)

這個重塑作業可視為兩個重塑作業的組合。第一份將最外層的維度 tensor<4x8x12xf32> 收合為 tensor<32x12xf32> 第二個則將最內層的 tensor<32x12xf32> 展開為 tensor<32x3x4xf32>。

輸入對應的輸出內容：

(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]

輸入至輸出對應：

(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]

比特卡

位元傳播運算可以表示因此，其索引地圖只是為地圖編列索引序列

串連

concat 的輸出至輸入對應項目會針對所有輸入項目定義，但使用非重疊的網域，也就是一次只會使用其中一個輸入項目。

p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}

輸出至輸入對應項目：

output -> input 1:

(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]

輸出 ->輸入 2：

(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]

output -> input 3：

(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]

輸出地圖的輸入內容：

輸入 1 ->輸出：

(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]

輸入 2 ->輸出：

(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]

輸入 3 ->輸出：

(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]

點線

點號的索引對應表與 reduce 的索引對應表非常相似。

p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
  lhs_batch_dims={0}, rhs_batch_dims={0},
  lhs_contracting_dims={2}, rhs_contracting_dims={1}

輸入的輸出內容對應：

輸出 ->input_1:

(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]

輸出 ->input_2:

(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]

輸出地圖的輸入內容：

輸入值_1 ->輸出：

(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]

輸入值_2 ->輸出：

(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]

巴德

PadOp 的索引與 SliceOp 索引相反。

p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0

邊框間距設定 1_4_1x4_8_0 代表 lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1。

輸入對應關係的輸出內容：

output -> input：

(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]

output -> init：

(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]

ReduceWindow

XLA 中的 ReduceWindow 也會執行邊框間距。因此，建立索引的地圖計算為不執行任何邊框間距的 ReduceWindow 索引和 PadOp 的索引建立功能

c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
  window={size=1x512 pad=0_0x0_0}, to_apply=max

輸出至輸入對應項目：

output -> input：

(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]

output -> init：

(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]

為地圖建立融合索引

融合運算的索引對應項目是叢集中每個運算的索引對應項目組合。有些輸入內容可能會以不同的存取模式讀取多次。

單一輸入內容、多個索引對應檔

以下是 p0 + transpose(p0) 的範例。

f {
  p0 = f32[1000, 1000] parameter(0)
  transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
  ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}

p0 的輸出至輸入索引對應項目為 (d0, d1) -> (d0, d1) 和 (d0, d1) -> (d1, d0)。也就是只計算一個元素因此可能需要讀取輸入參數兩次

一個輸入項目，已去除重複項目的索引對應

在某些情況下，雖然不容易察覺，但實際上索引對應項目是相同的。

f {
  p0 = f32[20, 10, 50] parameter(0)
  lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
  lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
  lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
  rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
  rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
  rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
  ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}

在本例中，p0 的輸出至輸入索引對應僅 (d0, d1, d2) -> (d2, d0, d1)。

Softmax

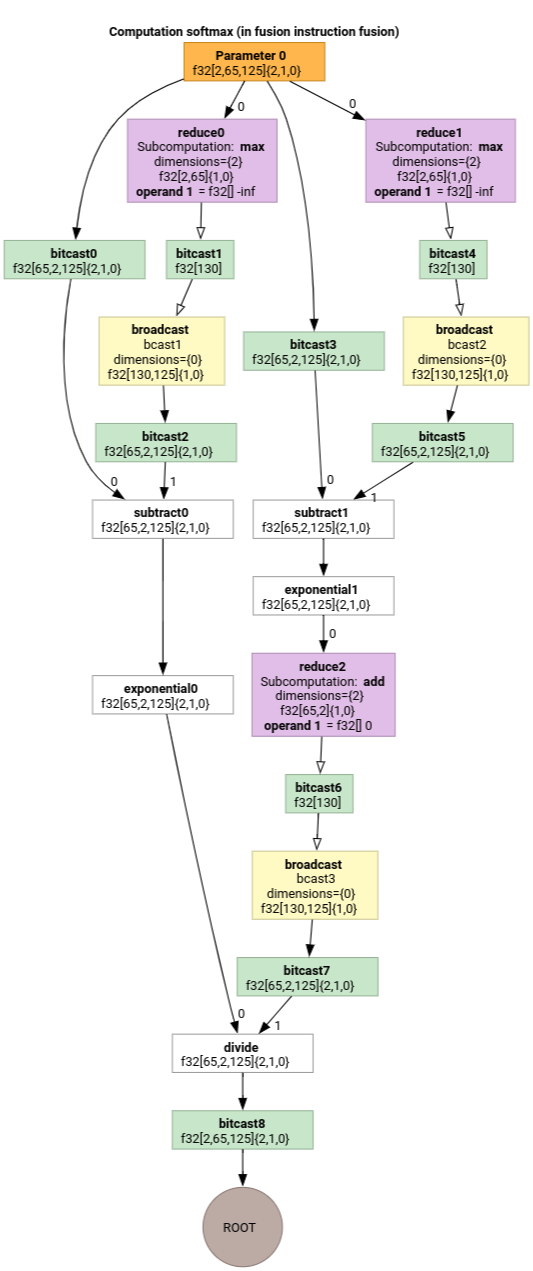
softmax 的 parameter 0 輸出至輸入索引對應：

(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]

和

(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]

其中 s0 是指輸入內容最內層的維度。

索引對應簡化器

mlir::AffineMap 上游的預設簡化器無法對維度/符號的範圍做出任何假設。因此不能使用 mod 和 div 有效率地簡化運算式。

我們可以運用相關知識進而簡化這些子運算式。

簡化器可改寫下列運算式。

[0, 6] x [0, 14] 中 d 的 (d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16) 會變成 (d0, d1) -> (d0, d1)
di in [0, 9] 的 (d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10) 會變成 (d0, d1, d2) -> (d0, d1, d2)。
d_i in [0, 9] 的 (d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8) 會變成 (d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8)。
[0, 9] x [0, 10] 中的 d (d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9) 會變成 (d0, d1) -> (d0)。

建立地圖簡化工具可讓我們理解在 HLO 中取消形狀會互相取消。

p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)

在建立索引地圖並簡化後，我們會得到

(d0, d1, d2) -> (d0, d1, d2)。

索引地圖簡化功能也會簡化限制。

類型的限制 lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_bound 是重寫為 updated_lower_bound <= affine_expr <= updated_upped_bound。
一律符合的條件，例如：d0 + s0 in [0, 20] 「d0 in [0, 5]」和「s0 in [1, 3]」的資料會遭到排除。
限制中的仿射式運算式會最佳化為上方的索引仿射對應。

如需更多範例，請參閱 indexing_map_test.cc。