Bu dokümanda, HLO dizine ekleme analizi açıklanmaktadır. HLO işlemleri için dizin oluşturma haritalarını kullanır. Dizine ekleme haritası, bir tensörün dizinlerini başka bir tensörün dizinleriyle eşleyen bir işlevdir (ör. bir HLO talimat çıkışının dizinlerini HLO talimat girişlerinin dizinleriyle veya tam tersini).
Örnek
tensor<20xf32> - tensor<10x20x30xf32> arası anons için
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
çıkıştan girişe kadar dizin haritası i in
[0, 10], j in [0, 20] ve k in [0, 30] için (i, j, k) -> (j).
Motivasyon
XLA GPU, birleştirme ve işlenen hakkında mantıksal işlem yapmak için farklı özel çözümler kullanır. ve döşeme şemaları hakkında daha fazla bilgi edinin (aşağıda daha ayrıntılı bilgi verilmiştir). Dizine ekleme hedefi analiz gibi kullanım alanları için yeniden kullanılabilir bir bileşen sağlar. Dizine ekleme analizi, MLIR'in Affine Map altyapısı üzerine kuruludur ve HLO semantiği ekler.
Birleştirme
Basit olmayan durumlarda bellek birleştirme hakkında akıl yürütme bir öğeyi hesaplamak için girişlerin hangi öğelerinin/dilimlerinin okunduğunu biliriz. çıktı.
İşlem Gören Kullanım
XLA'da işlem gören kullanım, her bir talimat girişinin ne kadar olduğunu gösterir tamamen kullanıldığı varsayılır. Şu anda genel bir durum için de kullanım oranı hesaplanmıyor. Dizine ekleme analizi, kullanımı tam olarak hesaplamanıza olanak tanır.
Döşeme
Parça/bölüm, ofsetler ile parametreleştirilmiş bir tensörün hiper dikdörtgen alt kümesidir. gerektiğini bileceksiniz. Karo yayma, işlemin karo parametrelerini kullanarak işlemin üreticisinin/tüketicisinin karo parametrelerini hesaplamanın bir yoludur. Orada zaten bir kitaplık tam da bunu yapıyor. Kart dağıtımı, dizine ekleme haritaları aracılığıyla ifade edilirse daha genel ve sağlam hale getirilebilir.
İşlev ve Alan Adı
Dizine ekleme haritası bir f(x) = f(d, r, rt) işlevidir
bir A tensörüne ait d çoklu dizinini
B tensörü r parametresi, B tenzorunda bulunan ancak A tenzorunda bulunmayan boyutların dizin aralıklarını ifade eder. rt parametresi, çalışma zamanı değerlerini (ör. bir toplama işleminin dizinleri) ifade eder.
Örneğin, tensor<2x4x8x16xf32> değerinden
tensor<4x8xf32> ise, 2D çıkışından 4D girişine giden dizine ekleme haritası şu şekildedir:
(d0, d1) -> (r0, d0, d1, r1) metriğidir. Burada d_i,
çıkış tensörünün indekslerine karşılık gelir. Aralık değişkenleri r_j birden fazla değeri kodlar. Yani çıkıştaki bir (d0, d1) öğesini hesaplamak için girişteki (r0, d0, d1, r1) öğesine ihtiyacımız vardır. Bu durumda r0 in [0, 1] ve r1 in [0, 15].
Bu eşleme, HLO talimatlarının özelliklerinden oluşturulabilir veya birleştirme için dizine ekleme işlemi yapmak üzere birleştirilmemiş talimatların eşlemeleri derlenebilir. Eşlemenin bir alanı da vardır. Bu alan, eşlemenin hangi tensör öğelerinde mevcut olduğunu belirtir.
f(x) s.t.
lb <= g(x) <= ub
Yeniden hesaplamayı en aza indirmek istediğimiz için simgesel ve hesaplamaları için de geçerlidir. XLA zaten MLIR'e bağlı olduğu için mlir::AffineMap kullanmaya başlayabilirsiniz.
Tipik bir AffineMap şu şekilde görünür:
(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)
AffineMap iki tür parametreye sahiptir: boyutlar ve simgeler. Boyutlar, boyut değişkenlerine d, simgeler ise aralık değişkenlerine r ve RT değişkenlerine rt karşılık gelir. AffineMap, boyutların aralıklarını içeren meta veriler içermediğinden bu verileri kendimiz sağlamamız gerekir.
struct Interval {
int64_t lower;
int64_t upper;
};
// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
Interval bounds;
};
// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
Interval range;
};
// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
Interval feasible_values;
const HloInstruction* hlo;
// This is a map from the iteration space of the corresponding indexing map to
// the iteration space of `hlo`. It shows what element of `hlo` we need to
// extract to get the runtime value for the RTVar.
mlir::AffineMap map;
};
class IndexingMap {
mlir::AffineMap affine_map_;
std::vector<DimVar> dim_vars_;
std::vector<RangeVar> range_vars_;
std::vector<RTVar> rt_vars_;
llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};
dim_vars_, boyutun kapsayıcı kutu kısıtlamalarını kodlar
dizine ekleme haritasının d değişkenleri. Bunlar genellikle
ters çevir, azalt, elemanlar, nokta, ancak gibi işlemler için çıkış tensörünün şekli
bazı istisnalar vardır
HloConcatenateInstruction.
range_vars_, r parametrelerinin alabileceği olası değerleri kodlar.
rt_vars_, ilişkili hlo talimatlarını erişimleriyle birlikte depolar
ve çalışma zamanındaki uygun değerleri kavrayacaksınız. Örneğin, ofset dinamiktir
1D HloDynamicSliceInstruction için. Çıktının her bir öğesi için girişin dizesini hesaplamak üzere ofset tenzorundan aynı öğeyi ayıkladığımızdan, karşılık gelen RTVar'te (d0) -> () erişim kalıbıyla 0. sıralı bir tenzor oluşturan bir HloInstruction* bulunur. Şunu da varsayabiliriz:
dilimin uzaklığı her zaman 0 ve
tensor_size - slice_size - 1.
Yukarıdakilerin hepsinin gerçekte ne anlama geldiğini anlamak için örnekleri adım adım inceleyelim.
Kaynaştırılmamış İşlemler için Haritaları Dizine Ekleme
Elementwise
Öğe bazında işlemler için dizine ekleme haritası bir kimliktir.
p0 = f32[10, 20] parameter(0)
p1 = f32[10, 20] parameter(1)
add = f32[10, 20] add(p0, p1)
Giriş haritalarının çıkışı:
- çıkış -> input_i:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Çıkış haritalarına giriş
- giriş_i -> çıkış:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Yayın
Yayın, eşleme yaptığımızda bazı boyutların kaldırılacağı anlamına gelir çıkışı girdiye ayarlanır ve girişi çıkışla eşlendiğinde eklenir.
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
Çıkışla giriş arasındaki eşleme:
(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]
Girişten çıkışa harita
(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]
Şimdi giriş-çıkış için sağ tarafta s harfinin olduğuna dikkat edin.
yardımcı olur. Bunlar, değer aralıklarını temsil eden sembollerdir. Örneğin, bu durumda d0 dizine sahip her giriş öğesi, çıktının 10x1x30 boyutunda bir dilimiyle eşlenir.
Constant ve Iota
Bu URL'lerin giriş parametresi olmadığı için dizine ekleme işlemini hesaplamak için hiçbir şey yoktur.
DynamicSlice
DynamicSlice, Slice'e benzer ancak ofsetler dinamiktir.
src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}
src için giriş haritasına çıkış:
(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
hlo: of1 = s32[] parameter(1)
(d0, d1, d2) -> ()
s1 in [0, 0]
hlo: of2 = s32[] parameter(2)
(d0, d1, d2) -> ()
s2 in [0, 226]
hlo: of3 = s32[] parameter(3)
(d0, d1, d2) -> ()
Şimdi giriş-çıkış eşleme için sağ tarafta s harfinin olduğuna dikkat edin.
Bunlar, çalışma zamanı değerlerini temsil eden simgelerdir. Örneğin, bu özel durumda, d0, d1, d2 dizine sahip çıkıştaki her öğe için girişin dizinini hesaplamak üzere dilim ofsetlerine of1, of2 ve of3 erişiriz.
Çalışma zamanı değişkenlerinin aralıkları, tüm
dilim sınırlar içinde kalıyor.
of1, of2 ve of3 için çıkıştan girişe harita:
(d0, d1, d2) -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
DynamicUpdateSlice
src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)
src için çıkıştan girişe harita önemsiz. Alan, güncellenmemiş dizinlerle sınırlandırılarak daha kesin hale getirilebilir ancak şu anda dizine ekleme haritaları eşitsizlik kısıtlamalarını desteklemez.
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]
upd için giriş eşlemesi çıkışı:
(d0, d1)[s0, s1] -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
hlo: of1 = s32[] parameter(2)
(d0, d1) -> ()
s1 in [0, 20]
hlo: of2 = s32[] parameter(3)
(d0, d1) -> ()
Girişten çıkışa eşleme için sağ tarafta artık s olduğunu unutmayın.
Bunlar, çalışma zamanı değerlerini temsil eden simgelerdir. Örneğin, bu özel durumda, d0, d1 dizinlerine sahip çıkışın her öğesi için girişin diznini hesaplamak üzere dilim ofsetlerine of1 ve of2 erişiriz. Çalışma zamanı değişkenlerinin aralıkları, dilimin tamamının sınırlar içinde kaldığı varsayılarak türetilir.
of1 ve of2 için giriş eşlemesi çıktı:
(d0, d1) -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]
Toplama
Yalnızca basitleştirilmiş toplama desteklenir. bkz. [gather_simplifier].(https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h).
operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
offset_dims={1,2,3},
collapsed_slice_dims={},
start_index_map={0,1},
index_vector_dim=1,
slice_sizes={7,8,4}
operand için giriş eşlemesi çıktı:
(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 1)
Şimdi giriş-çıkış eşleme için sağ tarafta s harfinin olduğuna dikkat edin.
Bunlar, çalışma zamanı değerlerini temsil eden simgelerdir. Örneğin bu
çıktının her bir öğesi için ayrı bir durum [ör. d0, d1, d2, d3]
indices tensöründen öğeleri (d0, 0) ve (d0, 1) ayıklayın.
indices için giriş eşlemesi çıkışı:
(d0, d1, d2, d3)[s0] -> (d0, s0)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 1]
s0 aralık değişkeni, çıktının bir öğesini hesaplamak için indices tenzorunun tüm satırına (d0, *) ihtiyacımız olduğunu gösterir.
Transpoze
Transpoze için dizine ekleme haritası, giriş/çıkış boyutlarının bir permütasyonudur.
p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}
Çıkışla giriş arasındaki eşleme:
(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]
Harita çıktısı girişi:
(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]
Ters
Haritayı tersine çevirmeniz için dizine ekleme, geri alınan boyutları upper_bound(d_i) -
d_i olarak değiştirir:
p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}
Çıkışla giriş arasındaki eşleme:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
Girişten çıkışa harita:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
(Çeşitli)Azaltma
Değişken indirgemenin birden fazla girdisi ve birkaç başlangıcı vardır. Bu girişler haritadan çıktıdan girdi, küçültülmüş boyutları ekler. Bu nedenle, bir bakıma yayının tersi gibi davranır.
p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
dimensions={0}, to_apply=max
Giriş haritalarının çıkışı:
- çıkış -> input_j:
(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]
- çıkış -> init_j:
(d0) -> ()
domain:
d0 in [0, 9]
Giriş ve çıkış haritaları:
- input_i -> output_j:
(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]
- init_i -> output_j:
()[s0] -> (s0)
domain:
s0 in [0, 9]
i, j = 0, ... INPUT_COUNT için.
Dilim
Dilim için çıkıştan girişe dizine ekleme işlemi, çıkışın her öğesi için geçerli olan sıçramalı dizine ekleme haritasıyla sonuçlanır. Girişten çıkışa eşleme, girişteki öğelerin sıçramalı bir aralığıyla sınırlıdır.
p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
slice={[5:10:1], [3:20:7], [0:50:2]}
Harita girişi için çıkış:
(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]
Girişten çıkışa harita:
(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]
Yeniden şekillendirme
Yeniden şekillendirmeler farklı aromalarda sunulur.
Şekli daralt
Bu bir "doğrusallaştırma"dır. yeniden şekillendirmektir.
p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)
Harita girişi için çıkış:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
Girişten çıkışa harita:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
Şekli genişlet
Bu, ters bir "şekli daraltma" işlemidir. 1 boyutlu bir girişi N boyutlu çıkışa yeniden şekillendirir.
p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)
Çıkışla giriş arasındaki eşleme:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
Harita çıktısı girişi:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
Genel yeniden şekillendirme
Bunlar, tek bir genişletme veya genişletme olarak temsil edilemeyen yeniden şekillendirme operasyonlarıdır. şekli daralt. Yalnızca 2 veya daha fazla öğeden oluşan bir bileşim olarak temsil edilebilirler. şekilleri genişletebilir veya daraltabilirsiniz.
1. Örnek: Doğrusallaştırma-doğrusallaştırmadan çıkarma.
p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)
Bu yeniden şekillenme,
tensor<4x8xf32> ile tensor<32xf32> arasında, ardından
tensor<2x4x4xf32>.
Harita girişi için çıkış:
(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]
Harita çıktısı girişi:
(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
2. örnek: Genişletilmiş ve daraltılmış alt şekiller
p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)
Bu yeniden şekillendirme, iki yeniden şekillendirmenin bileşimi olarak gösterilebilir. İlki
en dıştaki boyutları tensor<4x8x12xf32> ve tensor<32x12xf32> olacak şekilde daraltır
ikincisi ise en içteki tensor<32x12xf32> boyutunu
tensor<32x3x4xf32>.
Harita girişi için çıkış:
(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]
Harita çıktısı girişi:
(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]
Bitcast
Bitcast işlemi, transpoze-yeniden şekillendirme-transpoze dizisi olarak temsil edilebilir. Bu nedenle, dizine ekleme haritaları yalnızca bu dizinin dizine ekleme haritalarının bir bileşimidir.
Birleştir
Concat için çıkıştan girişe eşleme tüm girişler için tanımlanır ancak örtüşmeyen alan adları, yani tek seferde yalnızca bir giriş kullanılır.
p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}
Girişlere yönelik çıkışlar aşağıdakilerle eşlenir:
- çıkış -> giriş 1:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- çıkış -> giriş 2:
(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]
- çıkış -> giriş 3:
(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]
Çıkış eşleme girişleri:
- giriş 1 -> çıkış:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- giriş 2 -> çıkış:
(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]
- giriş 3 -> çıkış:
(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]
Nokta
nokta için dizine ekleme haritaları, azaltma haritalarına çok benzer.
p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
lhs_batch_dims={0}, rhs_batch_dims={0},
lhs_contracting_dims={2}, rhs_contracting_dims={1}
Girişlere yönelik çıkışlar aşağıdakilerle eşlenir:
- output -> input_1:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
- çıkış -> input_2:
(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
Çıkış eşleme girişleri:
- input_1 -> output:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]
- input_2 -> output:
(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]
Ped
PadOp dizine ekleme, SliceOp dizine ekleme işleminin tersidir.
p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0
Dolgu yapılandırması 1_4_1x4_8_0, lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1 anlamına geliyor.
Giriş için çıkış:
- output -> input:
(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]
- çıkış -> init:
(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]
ReduceWindow
XLA'daki ReduceWindow'u da dolgu yapar. Bu nedenle, dizine ekleme haritaları herhangi bir dolgu yapmayan ReduceWindow dizininin bir bileşimi olarak hesaplanır ve PadOp'un dizine eklenmesi.
c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
window={size=1x512 pad=0_0x0_0}, to_apply=max
Giriş için çıkış:
- output -> input:
(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]
- output -> init:
(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]
Fusion için Haritalar'ı dizine ekleme
Birleştirme işlemi için dizine ekleme haritası, kümedeki her işlem için dizine ekleme haritalarının bir birleşimidir. Bazı girişler farklı düzeylerde birkaç kez okunmuş olabilir. izin verir.
Bir giriş, birden fazla dizin haritası
p0 + transpose(p0) için bir örnek verilmiştir.
f {
p0 = f32[1000, 1000] parameter(0)
transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}
p0 için çıkıştan girişe dizine ekleme eşlemeleri (d0, d1) -> (d0, d1) ve
(d0, d1) -> (d1, d0). Yani, çıkışın bir öğesini hesaplamak için giriş parametresini iki kez okumamız gerekebilir.
Tek girişli, tekilleştirilmiş dizine ekleme haritası
Dizine ekleme haritalarının aslında aynı olduğu ancak bu durumun hemen anlaşılmadığı durumlar vardır.
f {
p0 = f32[20, 10, 50] parameter(0)
lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}
Bu durumda p0 için çıkıştan girişe dizine ekleme haritası yalnızca (d0, d1, d2) -> (d2, d0, d1)'tür.
Softmax
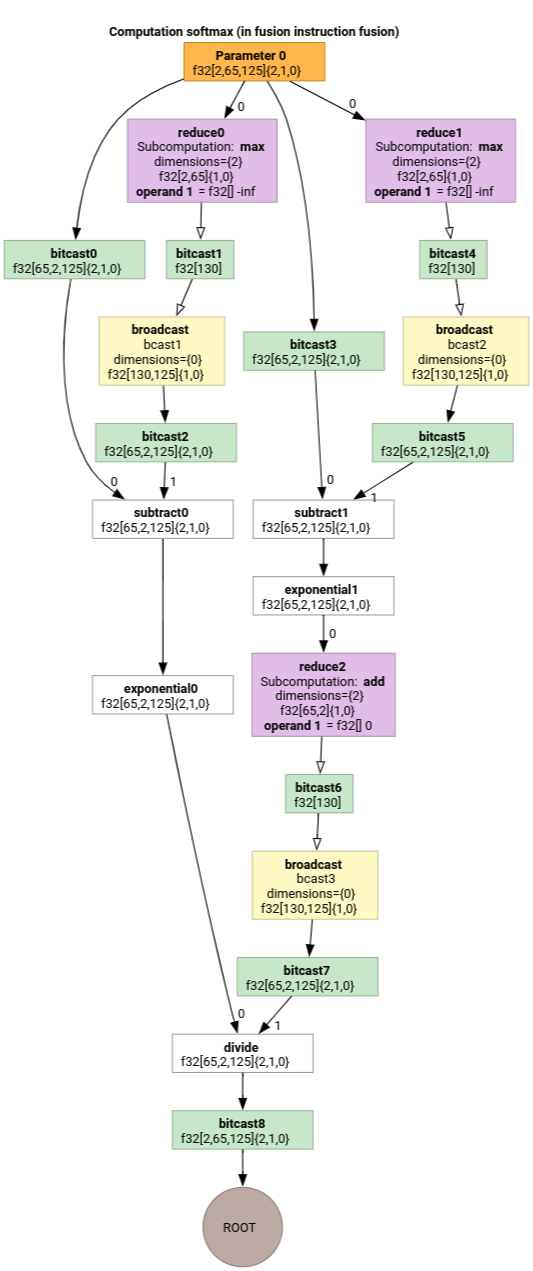
Softmax için parameter 0 çıkıştan girişe dizine ekleme eşlemeleri:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]
ve
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
Burada s0, girişin en iç boyutunu ifade eder.
Harita Dizine Ekleme Basitleştiricisi
mlir::AffineMap yukarı akış için varsayılan basitleştirici herhangi bir işlem yapamaz.
varsayımlar üzerinden yürütülür. Dolayısıyla,
mod ile ifadeleri verimli bir şekilde divve basit bir şekilde basitleştirin.
Sınırlamaların alt ve üst sınırları hakkındaki bilgilerimizden alt ifadeleri kullanarak bunları daha da basitleştirebilirsiniz.
Basitleştirici aşağıdaki ifadeleri yeniden yazabilir.
[0, 6] x [0, 14]bölgesinde d için(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16),(d0, d1) -> (d0, d1)olurdi in [0, 9]için(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10),(d0, d1, d2) -> (d0, d1, d2)olur.d_i in [0, 9]için(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8),(d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8)olur.[0, 9] x [0, 10]'daki d için(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9),(d0, d1) -> (d0)olur.
Dizine ekleme haritası basitleştirici, HLO'daki zincirlenmiş yeniden şekillendirme işlemlerinin bazılarının birbirini iptal ettiğini anlamamızı sağlar.
p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)
Dizine ekleme haritalarının oluşturulması ve basitleştirilmesinden sonra
(d0, d1, d2) -> (d0, d1, d2).
Haritayı dizine ekleme işlemi, kısıtlamaları da basitleştirir.
lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_boundtüründeki kısıtlamalarupdated_lower_bound <= affine_expr <= updated_upped_boundolarak yeniden yazılır.- Her zaman sağlanan kısıtlamalar, ör.
d0 + s0 in [0, 20]d0 in [0, 5]ves0 in [1, 3]elendi. - Kısıtlamalardaki afin ifadeleri, dizine ekleme afini olarak optimize edilir yukarıdaki haritada görebilirsiniz.
Daha fazla örnek için indexing_map_test.cc dosyasını inceleyin.

