Esta página foi traduzida pela API Cloud Translation.

Análise de indexação

Este documento descreve a análise de indexação do HLO, que permite calcular simbolicamente mapas de indexação para operações de HLO. O mapa de indexação é uma função que mapeia índices de um tensor para os índices de outro, por exemplo, índices de uma saída de instrução HLO para índices de entradas de instrução HLO ou vice-versa.

Exemplo

Para uma transmissão de tensor<20xf32> a tensor<10x20x30xf32>

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

o mapa de indexação da saída para a entrada é $(i, j, k) \mapsto (j)$ para $i \in [0, 10]$, $j \in [0, 20]$ and $k \in [0, 30]$.

Motivação

A GPU XLA usa várias soluções personalizadas para pensar sobre coalescência, utilização de operandos e esquemas de agrupamento (mais detalhes abaixo). O objetivo da análise de indexação é fornecer um componente reutilizável para esses casos de uso. A análise de indexação é criada na infraestrutura Affine Map do MLIR e adiciona semântica de HLO.

Coalescente

O raciocínio sobre a coalescência de memória se torna viável para casos não triviais, quando sabemos quais elementos/fatias das entradas são lidos para calcular um elemento da saída.

Utilização de operando

A utilização de operandos no XLA indica quanto cada entrada da instrução é usada, supondo que a saída seja totalmente usada. Atualmente, o uso também não é calculado para um caso genérico. A análise de indexação permite calcular com precisão a utilização.

Divisão

Um bloco/fatia é um subconjunto hiperretangular de um tensor parametrizado por deslocamentos, tamanhos e passos. A propagação de blocos é uma maneira de calcular os parâmetros de bloco do produtor/consumidor da operação usando os parâmetros de agrupamento da própria operação. Já existe uma biblioteca que faz isso para softmax e ponto. A propagação de blocos pode ser mais genérica e robusta se for expressa com mapas de indexação.

Função e domínio

O mapa de indexação é uma função $\boldsymbol{f}(\boldsymbol{d}, \boldsymbol{s})$ que mapeia um multiíndice $\boldsymbol{d}$ de um tensor $A$ para elementos/intervalos de tensor $B$. O parâmetro $\boldsymbol{s}$ se refere aos intervalos de índices das dimensões que estão presentes no tensor $B$, mas não no tensor $A$.

Por exemplo, se tivermos uma redução de tensor<2x4x8x16xf32> para tensor<4x8xf32>, o mapa de indexação da saída 2D para a entrada 4D será $(d_0, d_1) \mapsto (s_0, d_0, d_1, s_1)$, em que $d_i$ são os parâmetros de dimensão que correspondem aos índices do tensor de saída. Os parâmetros $s_j$ codificam vários valores. Por exemplo, para calcular um $(d_0, d_1)$ elemento da saída, precisamos de $(s_0, d_0, d_1, s_1)$ elementos da entrada, em que $s_0 \in [0, 2)$ e $s_1 \in [0, 16)$.

Esse mapeamento pode ser criado com base nos atributos das instruções de HLO, ou os mapeamentos de instruções não fundidas podem ser compostos para conseguir a indexação para uma fusão. O mapeamento também tem um domínio, que especifica para quais elementos do tensor o mapeamento existe.

\[ \begin{eqnarray} \boldsymbol{f}(\boldsymbol{d}, \boldsymbol{s})\; &s.t.& \\ \boldsymbol{lb}_d &\leq& \boldsymbol{d} \leq \boldsymbol{ub}_d \\ \boldsymbol{lb}_s &\leq& \boldsymbol{s} \leq \boldsymbol{ub}_s \\ \boldsymbol{lb}_g &\leq& \boldsymbol{g}(\boldsymbol{d}, \boldsymbol{s}) \leq \boldsymbol{ub}_g \end{eqnarray} \]

Como queremos minimizar a recomputação, precisamos de uma biblioteca para cálculos simbólicos. O XLA já depende de MLIR. Por isso, usamos mlir::AffineMap em vez de escrever uma biblioteca aritmética simbólica.

Um AffineMap típico se parece com

(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)

AffineMap tem dois tipos de parâmetros convenientemente: dimensões e símbolos, que podemos usar para $\boldsymbol d$ e $\boldsymbol s$ , respectivamente. AffineMap não contém metadados sobre intervalos das dimensões, então precisamos fornecer esses dados.

struct Range {
 int64_t lower_bound;
 int64_t upper_bound;
};

struct IndexingMap {
 mlir::AffineMap affine_map;
 std::vector<Range> dimension_ranges;
 std::vector<Range> symbol_ranges;
 llvm::DenseMap<mlir::AffineExpr, Range> expr_ranges;
};

dim_ranges codifica as restrições de caixa inclusiva para os parâmetros de dimensão $\boldsymbol{d}$ do mapa de indexação, que geralmente coincidem com a forma do tensor de saída para operações como transpor, reduzir, elemento a ponto, mas há algumas exceções, como HloConcatenateInstruction.

symbol_ranges codificam os valores possíveis que os parâmetros $\boldsymbol {s}$ podem assumir.

Vamos analisar cada exemplo para entender o que todas as opções acima significam.

Como indexar mapas para operações sem fusão

Elemento

Para operações com elementos, o mapa de indexação é uma identidade.

  p0 = f32[10, 20] parameter(0)
  p1 = f32[10, 20] parameter(1)
  add = f32[10, 20] add(p0, p1)

A saída dos mapas de entrada:

output -> input_0: $(d_0, d_1) \mapsto (d_0, d_1)$ para $\boldsymbol{d} \in [0,9] \times [0, 19]$, i.e. $\boldsymbol{d} \in {\rm Dom}(saída)$
output -> input_1: $(d_0, d_1) \mapsto (d_0, d_1)$ para $\boldsymbol{d} \in {\rm Dom} (output)$

A entrada para os mapas de saída

input_i -> output: $(d_0, d_1) \mapsto (d_0, d_1)$ para $\boldsymbol{d} \in {\rm Dom}(output)$

Transmitir

Com a transmissão, algumas dimensões serão removidas quando mapearmos a saída para a entrada e adicionadas quando mapearmos a entrada para a saída.

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

A saída do mapa de entrada:

output -> input: $(d_0, d_1, d_2) \mapsto (d_1)$ para $\boldsymbol{d} \in {\rm Dom}(output)$

O mapa de entrada para saída

input -> output: $(d_0) \mapsto (s_0, d_1, s_1)$ para $\boldsymbol{d} \in {\rm Dom}(output)$ and $\boldsymbol{s} \in [0, 9] \ttempos [0, 29]$.

Observe que agora temos $\boldsymbol s$ no lado direito do mapeamento de entrada para saída. Esses são os símbolos que representam intervalos de valores. Por exemplo, neste caso específico, cada elemento de entrada com índice $d_0$ é mapeado para uma fração de 10 x 1 x 30 da saída.

Constante e Iota

Convenientemente, elas não têm parâmetros de entrada, portanto, não há nada para calcular a indexação.

Transposição

O mapa de indexação para transposição é uma permutação de dimensões de entrada/saída.

p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}

A saída do mapa de entrada:

output -> input: $(d_0, d_1, d_2, d_3) \mapsto (d_0, d_3, d_1, d_2)$ para $\boldsymbol{d} \in {\rm Dom}(output)$.

O mapa de entrada para saída:

input -> output: $(d_0, d_1, d_2, d_3) \mapsto (d_0, d_2, d_3, d_1)$ para$\boldsymbol{d} \in {\rm Dom}(input)$.

Reverse

O mapa de indexação para reversão altera as dimensões revertidas para $upper_bound(d_i) - d_i$:

p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}

A saída do mapa de entrada:

saída -> input: $(d_0, d_1, d_2, d_3) \mapsto (d_0, -d_1 + 16, -d_2 + 8, d_3)$ for $\boldsymbol{d} \in {\rm Dom}(saída)$

O mapa de entrada para saída:

entrada -> saída: $(d_0, d_1, d_2, d_3) \mapsto (d_0, -d_1 + 16, -d_2 + 8, d_3)$ for $\boldsymbol{d} \in {\rm Dom}(entrada)$

(Variadica)Reduzir

A redução variada tem várias entradas e várias entradas, e o mapa da saída para a entrada adiciona as dimensões reduzidas. Ele se comporta como um inverso de uma transmissão.

p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
  dimensions={0}, to_apply=min

A saída dos mapas de entrada:

output -> input_j: $(d_0) \mapsto (s_0, d_0)$ para $\boldsymbol{d} \in {\rm Dom}(output)$ and $\boldsymbol{s} \in [0, 9]$
output -> init_j: $(d_0) \mapsto ()$ para $\boldsymbol{d} \in {\rm Dom}(output)$

A entrada para os mapas de saída:

input_i -> output_j: $(d_0, d_1) \mapsto (d_1)$ para $\boldsymbol{d} \in {\rm Dom}(input)$
init_i -> output_j: $() \mapsto (s_0)$ para $\boldsymbol{s} \in [0, 9]$

para $i, j = 0, \ldots, INPUT\\_COUNT$.

Fração

A indexação da saída à entrada para frações resulta em um mapa de indexação estrito que é válido para cada elemento da saída. O mapeamento da entrada para a saída é restrito a um intervalo estrito dos elementos na entrada.

p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
  slice={[5:10:1], [3:20:7], [0:50:2]}

A saída do mapa de entrada:

output -> input: $(d_0, d_1, d_2) \mapsto (d_0 + 5, 7d_1 + 3, 2d_2)$ para $\boldsymbol{d} \in {\rm Dom}(output)$.

O mapa de entrada para saída:

input -> output: $(d_0, d_1, d_2) \mapsto (d_0, d_1 / 7, d_2 / 2)$ para $\boldsymbol{d} \in [5, 9] \times [3, 19] \times [0, 49]$ com passos $[1, 7, 2]$.

A definir: indexação de entrada para saída

Remodelação

As remodelações têm variações diferentes.

Recolher forma

Este é um remodelamento "linearizante" de N-D para 1D.

p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)

A saída do mapa de entrada:

output -> input: $(d_0) \mapsto (d_0 / 8, d_0 \mod 8)$ para $\boldsymbol{d} \in {\rm Dom}(output)$

O mapa de entrada para saída:

input -> output: $(d_0, d_1) \mapsto (8 d_0 + d_1)$ para $\boldsymbol{d} \in {\rm Dom}(input)$.

Expandir forma

Essa é uma op inversa de "forma de recolhimento", ela remodela uma entrada 1D em uma saída N-D.

p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)

A saída do mapa de entrada:

output -> input: $(d_0, d_1) \mapsto (8 d_0 + d_1)$ para $\boldsymbol{d} \in {\rm Dom}(output)$

O mapa de entrada para saída:

input -> output: $(d_0) \mapsto (d_0 / 8, d_0 \mod 8)$ para $\boldsymbol{d} \in {\rm Dom}(input)$.

Remodelamento genérico

Essas são as operações de remodelamento que não podem ser representadas como uma única forma de expansão ou recolhimento. Eles só podem ser representados como uma composição de duas ou mais formas de expandir ou recolher.

Exemplo 1: deslinearização de linearização.

p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)

Essa remodelação pode ser representada como uma composição da forma recolhida de tensor<4x8xf32> para tensor<32xf32> e, em seguida, uma expansão de forma para tensor<2x4x4xf32>.

A saída do mapa de entrada:

saída -> input: $(d_0, d_1, d_2) \mapsto (2d_0 + (4d_1 + d_2) / 8, 4d_1 + d_2) \mod 8)$

por $\boldsymbol{d} \in {\rm Dom}(output)$

O mapa de entrada para saída:

entrada -> saída: $(d_0, d_1) \mapsto ((8d_0 + d_1) / 16, ((8d_0 + d_1) \mod 16) / 4, d_1 \mod 4)$

para $\boldsymbol{d} \in {\rm Dom}(input)$.

Exemplo 2: subformas expandidas e recolhidas

p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)

Essa remodelação pode ser representada como uma composição de duas remodelações. O primeiro recolhe as dimensões mais externas tensor<4x8x12xf32> para tensor<32x12xf32> e o segundo expande a dimensão mais interna tensor<32x12xf32> em tensor<32x3x4xf32>.

A saída do mapa de entrada:

output -> input: $(d_0, d_1, d_2) \mapsto (d_0 / 8, d_0 \mod 8, 4d_1 + d_2)$ para $\boldsymbol{d} \in {\rm Dom}(output)$.

O mapa de entrada para saída:

input -> output: $(d_0, d_1, d_2) \mapsto (8d_0 + d_1, d_2 / 4, d_2 \mod 4)$ para $\boldsymbol{d} \in {\rm Dom}(input)$.

Bitcast

Uma op de bitcast pode ser representada como uma sequência de transpose-reshape-transpose. Portanto, os mapas de indexação são apenas uma composição para essa sequência.

Concatenate

O mapeamento de saída para entrada para concat é definido para todas as entradas, mas com domínios não sobrepostos, ou seja, apenas uma das entradas será usada por vez.

p0 = f32[3,50] parameter(0)
p1 = f32[3,30] parameter(1)
concat = f32[3,80] concatenate(f32[3,50] p0, f32[3,30] p1),
  dimensions={1}

A saída do mapa de entrada:

saída -> entrada 1:

$(d_0, d_1) \mapsto (d_0, d_1)$ para $\boldsymbol{d} \in [0, 2] \times [0, 49]$

saída -> entrada 2:

$(d_0, d_1) \mapsto (d_0, d_1 - 50)$ para $\boldsymbol{d} \em [0, 2] \ttempos [50, 79]$

As entradas do mapa de saída:

input 1 -> output: $(d_0, d_1) \mapsto (d_0, d_1)$ para $\boldsymbol{d} \in {\rm Dom}(input_1)$.
entrada 2 -> output: $(d_0, d_1) \mapsto (d_0, d_1 + 50)$ para $\boldsymbol{d} \in {\rm Dom}(input_2)$.

Ponto (de saída para entrada implementada

Os mapas de indexação para pontos são muito semelhantes aos de reduz.

p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
  lhs_batch_dims={0}, rhs_batch_dims={0},
  lhs_contracting_dims={2}, rhs_contracting_dims={1}

A saída para os mapas de entrada é mapeada:

output -> input_1: $(d_0, d_1, d_2) \mapsto (d_0, d_1, s_0)$ para $\boldsymbol{d} \in {\rm Dom}(output)$ e $\boldsymbol{s} \in [0, 255]$.
output -> input_2: $(d_0, d_1, d_2) \mapsto (d_0, s_0, d_2)$ para $\boldsymbol{d} \in {\rm Dom}(output)$ e $\boldsymbol{s} \in [0, 255]$.

As entradas para os mapas de saída:

input_1 -> output: $(d_0, d_1, d_2) \mapsto (d_0, d_1, s_0)$ para$\boldsymbol{d} \in {\rm Dom}(input_1)$ e $\boldsymbol{s} \in [0, 63]$.
input_2 -> output: $(d_0, d_1, d_2) \mapsto (d_0, s_0, d_1)$ para$\boldsymbol{d} \in {\rm Dom}(input_2)$ e $\boldsymbol{s} \in [0, 127]$.

Reduzir janela (a definir)

Pad (a definir)

Como indexar o Maps for Fusion

O mapa de indexação da operação de fusão é uma composição de mapas de indexação para cada operação no cluster. Pode acontecer de algumas entradas serem lidas várias vezes com diferentes padrões de acesso.

Uma entrada, vários mapas de indexação

Confira um exemplo para $p_0 + p_0^T$

f {
  p0 = f32[1000, 1000] parameter(0)
  transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
  ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}

Os mapas de indexação de saída para entrada de p0 serão $(d_0, d_1) \mapsto (d_0, d_1)$ and $(d_0, d_1) \mapsto (d_1, d_0)$. Isso significa que, para calcular um elemento da saída, talvez seja preciso ler o parâmetro de entrada duas vezes.

Uma entrada, mapa de indexação sem duplicação

Há casos em que os mapas de indexação são iguais, mesmo que isso não seja imediatamente óbvio.

f {
  p0 = f32[20, 10, 50] parameter(0)
  lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
  lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
  lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
  rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
  rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
  rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
  ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}

Nesse caso, o mapa de indexação de saída para entrada para p0 é apenas $(d_0, d_1, d_2) \mapsto (d_2, d_0, d_1)$.

Softmax

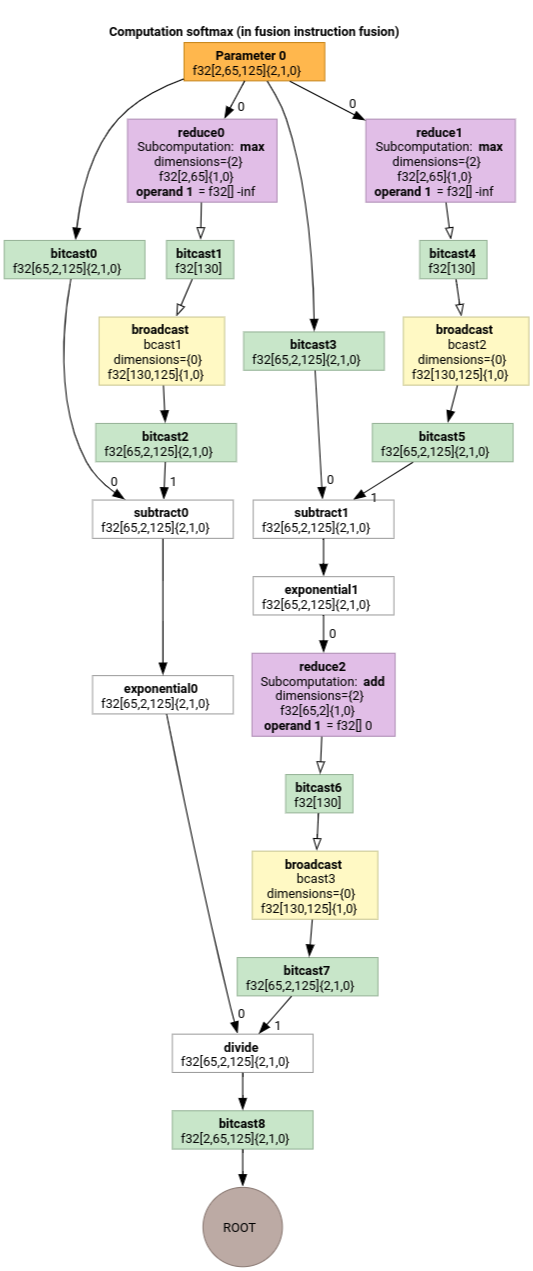
A indexação de saída para entrada é mapeada para parameter 0 para softmax:

$(d_0, d_1, d_2) \mapsto (d_0, d_1, d_2)$
$(d_0, d_1, d_2)[s_0] \mapsto (d_0, d_1, s_0)$

para $\boldsymbol{d} \in {\rm Dom}(output)$ e $\boldsymbol{s} \in [0, 124]$ refere-se à dimensão mais interna da entrada.

Simplificador de mapas de indexação

O simplificador padrão de mlir::AffineMap upstream não pode fazer nenhuma suposição sobre os intervalos de dimensões/símbolos. Portanto, ela não pode simplificar as expressões com mod e div de maneira eficiente.

Podemos aproveitar o conhecimento sobre os limites inferior e superior das subexpressões nos mapas afins para simplificá-los ainda mais.

O simplificador pode reescrever as expressões a seguir.

$(d_0, d_1) \mapsto (d_0 + d1 / 16, d1 \mod 16)$ para $\boldsymbol{d} \in [0, 6] \ttempos [0, 14]$ becomes $(d_0, d_1) \mapsto (d_0, d_1)$
$(d_0, d_1, d_2) \mapsto ((100d_0 + 10d_1 + d_2) /100, ((100d_0 + 10d_1 + d_2) \mod 100) / 10, d_2 \mod 10) \d_i, d_2 \mod_9)$ for $$ becomes $
$(d_0, d_1, d_2) \mapsto ((16d_0 + 4d_1 + d_2) /8, (16d_0 + 4d_1 + d_2) \mod 8)$ for $d_i \in [0, 9]$ becomes $(d_0, d_1, d_2) (d_1, d_2) (d_1, d_2)
$(d_0, d_1) \mapsto (-(-11d_0 - d_1 + 109) / 11 + 9)$ para $\boldsymbol{d} \em [0, 9] \ttempos [0, 10]$ becomes $(d_0, d_1) \mapsto (d_0)$.

O simplificador de mapa de indexação permite entender que algumas das reformas encadeadas no HLO cancelam umas às outras.

p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)

Depois da composição dos mapas de indexação e da simplificação deles, teremos

$(d_0, d_1, d_2) \mapsto (d_0, d_1, d_2)$.