Analiza indeksowania

W tym dokumencie opisujemy analizę indeksowania HLO, która umożliwia symboliczny i obliczać mapy indeksowania dla operacji HLO. Mapa indeksowania to funkcja, która umożliwia indeksy jednego tensora do indeksów innego, np. indeksy HLO dane wyjściowe instrukcji do indeksów wejściowych instrukcji HLO lub na odwrót.

Przykład

W przypadku transmisji z tensor<20xf32> do tensor<10x20x30xf32>

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

mapa indeksowania z danych wyjściowych do danych wejściowych ma wartość (i, j, k) -> (j) dla elementów i in [0, 10], j in [0, 20] i k in [0, 30].

Motywacja

GPU XLA korzysta z kilku rozwiązań dostosowanych do specyfikicznego wykorzystania danych, operandów i schematów układania (więcej informacji poniżej). Celem analizy indeksowania jest udostępnienie komponentu, który można wielokrotnie stosować w takich przypadkach. Analiza indeksowania jest zbudowana na podstawie infrastruktury mapy Affine w MLIR i dodaje semantykę HLO.

Koaleszja

W przypadku złożonych przypadków, gdy wiemy, które elementy lub fragmenty danych wejściowych są odczytywane do obliczenia elementu danych wyjściowych, można zastosować łączenie pamięci.

Wykorzystanie operacji

Wykorzystanie argumentu operacji w XLA wskazuje, na ile przydatne są poszczególne dane wejściowe instrukcji zakładając, że dane wyjściowe są w pełni wykorzystane. Wykorzystanie również nie jest obecnie obliczone dla przypadku ogólnego. Analiza indeksowania umożliwia dokładne obliczenie wykorzystania.

Segmentacja:

Płytka/wycinek to hiperprostokątny podzbiór tensora z parametrami przesunięć, rozmiarów i kroków. Rozpowszechnianie kafelków to sposób na obliczanie parametrów kafelków producenta/konsumenta operacji przy użyciu parametrów kafelków samego operacji. Biblioteka obsługuje już softmax i dot. Propagacja kafelków może być bardziej ogólna jeśli jest wyrażony w mapach indeksowania.

Funkcja i domena

Mapa indeksowania to funkcja f(x) = f(d, r, rt), która mapuje wieloindeks d tensora A na elementy lub zakresy tensora B. Parametr r odnosi się do zakresów indeksów wymiarów, które są obecne w tensorze B, ale nie w tensorze A. Parametr rt odnosi się do wartości na czas wykonywania, np. indeksów operacji zbierania.

Jeśli na przykład mamy redukcję z tensor<2x4x8x16xf32> na tensor<4x8xf32>, mapa indeksowania z wyjścia 2D na wejście 4D to (d0, d1) -> (r0, d0, d1, r1), gdzie d_i to zmienne wymiarów odpowiadające indeksom tensora wyjściowego. Zmienne zakresu r_j kodują wiele wartości, czyli aby obliczyć element (d0, d1) w wyniku, potrzebujemy (r0, d0, d1, r1) elementów wejściowych, gdzie r0 in [0, 1] i r1 in [0, 15].

Mapowanie można utworzyć z atrybutów instrukcji HLO lub mapowania niescalonych instrukcji w celu uzyskania indeksowania dla fuzji. Mapowanie ma też domenę, która określa, które elementy tensora mapowanie już istnieje.

f(x) s.t.

lb <= g(x) <= ub

Chcemy zminimalizować ponowne obliczenia, dlatego potrzebujemy biblioteki do obliczeń symbolicznych. XLA jest już zależna od MLIR, więc zamiast pisać kolejną symboliczną bibliotekę arytmetyczną, używamy funkcji mlir::AffineMap.

Typowa AffineMap wygląda tak

(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)

Funkcja AffineMap ma 2 typy parametrów: wymiary i symbole. wymiary odpowiadają zmiennym wymiaru d, a symbole odpowiadają zmienne zakresu r i zmienne RT rt. AffineMap nie zawiera żadnych metadanych zakresów wymiarów, więc musimy dostarczyć te dane, dla siebie.

struct Interval {
 int64_t lower;
 int64_t upper;
};

// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
  Interval bounds;
};

// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
  Interval range;
};

// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
  Interval feasible_values;
  const HloInstruction* hlo;
  // This is a map from the iteration space of the corresponding indexing map to
  // the iteration space of `hlo`. It shows what element of `hlo` we need to
  // extract to get the runtime value for the RTVar.
  mlir::AffineMap map;
};

class IndexingMap {
  mlir::AffineMap affine_map_;
  std::vector<DimVar> dim_vars_;
  std::vector<RangeVar> range_vars_;
  std::vector<RTVar> rt_vars_;
  llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};

dim_vars_ koduje ograniczenia pola włącznie dla wymiaru zmiennych d mapy indeksowania, które zwykle zbiegają się z wartością parametru kształt tensora wyjściowego dla operacji takich jak transponowanie, redukcja, elementwise, kropka, ale są wyjątki, HloConcatenateInstruction.

range_vars_ koduje możliwe wartości, które mogą przyjmować parametry r.

rt_vars_ przechowuje powiązane instrukcje hlo wraz z wzorami dostępu i możliwymi wartościami w czasie wykonywania. Na przykład przesunięcie jest dynamiczne, dla 1D HloDynamicSliceInstruction. Odpowiednie wartości w polu RTVar będą miały HloInstruction*, który tworzy tensor rankingu 0 z dostępem (d0) -> () wzorcem, ponieważ dla każdego elementu danych wyjściowych wyodrębniany jest ten sam element od tensora przesunięcia, aby obliczyć indeks danych wejściowych. Możemy też założyć, że przesunięcie wycinka znajduje się zawsze między 0 a tensor_size - slice_size - 1

Aby zrozumieć, co tak naprawdę oznaczają te wszystkie informacje, przyjrzyjmy się przykładom.

Mapy indeksowania na potrzeby nieujednoliconych operacji

Elementowa

W przypadku operacji elementowych mapa indeksowania jest tożsamościowa.

  p0 = f32[10, 20] parameter(0)
  p1 = f32[10, 20] parameter(1)
  add = f32[10, 20] add(p0, p1)

Mapowania wyjścia na dane wejściowe:

• dane wyjściowe -> input_i:

(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]

Dane wyjściowe map

• wejściowe_i -> dane wyjściowe:

(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]

Broadcast

Transmisja oznacza, że niektóre wymiary zostaną usunięte podczas mapowania dane wyjściowe do danych wejściowych i dodawane, gdy mapujemy dane wejściowe na dane wyjściowe.

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

Mapowanie wyjścia na dane wejściowe:

(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]

Mapa danych wejściowych i wyjściowych

(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]

Teraz po prawej stronie mamy s, czyli mapowanie danych wejściowych na dane wyjściowe. Są to symbole reprezentujące zakresy wartości. Na przykład w tym konkretnym przypadku każdy element danych wejściowych o indeksie d0 jest mapowany na wycinek danych wyjściowych o wymiarach 10 x 1 x 30.

Stała i Iota

Dla wygody nie mają one żadnych parametrów wejściowych, więc nie ma potrzeby, aby i generowania indeksowania.

DynamicSlice

DynamicSlice jest taki sam jak Slice, ale przesunięcia są dynamiczne.

src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}

Dane wyjściowe do mapy wejściowej dla funkcji src:

(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
  hlo: of1 = s32[] parameter(1)
  (d0, d1, d2)  -> ()
s1 in [0, 0]
  hlo: of2 = s32[] parameter(2)
  (d0, d1, d2)  -> ()
s2 in [0, 226]
  hlo: of3 = s32[] parameter(3)
  (d0, d1, d2) -> ()

Zwróć uwagę, że teraz po prawej stronie mamy s do mapowania wejścia-wyjścia. To symbole reprezentujące wartości w czasie wykonywania. Na przykład w tym konkretnym przypadku dla każdego elementu danych wyjściowych o indeksach d0, d1, d2 używamy przesunięć sekcji of1, of2 i of3, aby obliczyć indeks danych wejściowych. Przedziały dla zmiennych środowiska wykonawczego są obliczane przy założeniu, że cały parametr wycinek pozostaje w granicach.

Mapa wyjścia do wejścia dla of1, of2 i of3:

(d0, d1, d2)  -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]

DynamicUpdateSlice

src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
    s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)

Dane wyjściowe, które zostaną użyte w mapie wejściowej dla funkcji src, są proste. Można go dokładniej określić, ograniczając domenę do niezaktualizowanych indeksów, a obecnie indeksowanie map nie obsługują ograniczeń nierówności.

(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]

Dane wyjściowe do mapy wejściowej dla funkcji upd:

(d0, d1)[s0, s1]  -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
  hlo: of1 = s32[] parameter(2)
  (d0, d1)  -> ()
s1 in [0, 20]
  hlo: of2 = s32[] parameter(3)
  (d0, d1)  -> ()

Zwróć uwagę, że teraz po prawej stronie mamy s do mapowania wejścia-wyjścia. To symbole reprezentujące wartości w czasie wykonywania. Na przykład w tym konkretnym przypadku w przypadku każdego elementu danych wyjściowych o indeksach d0, d1 uzyskujemy dostęp do przesunięć of1 i of2, aby obliczyć indeks danych wejściowych. Przedziały zmiennych czasu wykonywania są wyznaczane z założenia, że cały wycinek pozostaje w zakresie.

Dane wyjściowe do mapy wejściowej dla funkcji of1 i of2:

(d0, d1)  -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]

Zbieraj

Obsługiwane jest tylko uproszczone zbieranie danych. Więcej informacji: [gather_simplifier] (https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h).

operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
  offset_dims={1,2,3},
  collapsed_slice_dims={},
  start_index_map={0,1},
  index_vector_dim=1,
  slice_sizes={7,8,4}

Dane wyjściowe do mapy wejściowej dla funkcji operand:

(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
  hlo: indices = s32[1806,2]{1,0} parameter(1)
  (d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
  hlo: indices = s32[1806,2]{1,0} parameter(1)
  (d0, d1, d2, d3) -> (d0, 1)

Zwróć uwagę, że po prawej stronie mamy teraz s, czyli mapowanie danych wejściowych na wyjściowe. To symbole reprezentujące wartości w czasie wykonywania. Na przykład w tym konkretnym przypadku dla każdego elementu danych wyjściowych z indeksami d0, d1, d2, d3 wyodrębniamy elementy (d0, 0) i (d0, 1) z tensora indices.

Mapowanie wyjścia na wejście w przypadku indices:

  (d0, d1, d2, d3)[s0] -> (d0, s0)
  domain:
  d0 in [0, 1805]
  d1 in [0, 6]
  d2 in [0, 7]
  d3 in [0, 3]
  s0 in [0, 1]

Zmienne zakresu s0 pokazuje, że do obliczenia elementu wyjściowego potrzebujemy całego wiersza (d0, *) tensora indices.

Transponuj

Mapowanie indeksów w przypadku transpozycji to permutacja wymiarów wejścia/wyjścia.

p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}

Dane wyjściowe do wprowadzenia mapy:

(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]

Dane wejściowe mapy wyjściowej:

(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]

Odwróć

Indeksowanie mapy w odwrotnej kolejności zmienia odwrócone wymiary na upper_bound(d_i) - d_i:

p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}

Mapowanie wyjścia na dane wejściowe:

(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]

Dane wejściowe mapy wyjściowej:

(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]

(Variadic)Reduce

Redukcja zmiennoprzecinkowa ma kilka danych wejściowych i kilka inicjacji, czyli mapowanie wartości od danych wyjściowych do dane wejściowe – o zmniejszonych wymiarach. Funkcja działa jak odwrotność transmisji, w pewnym sensie.

p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
  dimensions={0}, to_apply=max

Dane wyjściowe do wprowadzania map:

• output -> input_j:

(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]

• output -> init_j:

(d0) -> ()
domain:
d0 in [0, 9]

Dane wyjściowe map:

• wejściowe_i -> output_j:

(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]

• init_i -> output_j:

()[s0] -> (s0)
domain:
s0 in [0, 9]

dla i, j = 0, ... INPUT_COUNT.

Wycinek

Indeksowanie danych od wyjścia do danych wejściowych w przypadku wycinka powoduje utworzenie szybkiej mapy indeksowania, jest prawidłowa dla każdego elementu danych wyjściowych. Mapowanie z wejścia na wyjście jest ograniczone do zakresu skokowego elementów na wejściu.

p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
  slice={[5:10:1], [3:20:7], [0:50:2]}

Mapowanie wyjścia na dane wejściowe:

(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]

Mapowanie wejścia na wyjście:

(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]

Zmień kształt

Przekształcenia mają różne smaki.

Zwiń kształt

Jest to „liniowe” przekształcenie z N wymiarów na 1 wymiar.

p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)

Mapowanie wyjścia na dane wejściowe:

(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]

Mapa wejścia na wyjście:

(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]

Rozwiń kształt

To jest odwrotność „zwiniętego kształtu” zmienia kształt danych wejściowych 1D na wyjście N-D.

p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)

Dane wyjściowe do wprowadzenia mapy:

(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]

Mapa wejścia na wyjście:

(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]

Ogólne przekształcanie

Są to operacje zmiany kształtu, których nie można przedstawić jako pojedynczego rozwinięcia ani zwiń kształt. Mogą być reprezentowane tylko jako kompozycja co najmniej 2 kształtów.

Przykład 1. Przekształcenie liniowe i odwrotne.

p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)

Ta zmiana kształtu może być reprezentowana jako kompozycja złożenia kształtu tensor<4x8xf32> w tensor<32xf32>, a następnie rozszerzenia kształtu do tensor<2x4x4xf32>.

Mapowanie wyjścia na dane wejściowe:

(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]

Dane wejściowe mapy wyjściowej:

(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]

Przykład 2. Rozwinięte i zwinięte podkształty

p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)

Ten kształt może być przedstawiony jako kompozycja 2 kształtów. Pierwszy zwinie najbardziej zewnętrzne wymiary tensor<4x8x12xf32> do tensor<32x12xf32> a drugi rozwija najbardziej wewnętrzny wymiar tensor<32x12xf32> do tensor<32x3x4xf32>

Mapowanie wyjścia na dane wejściowe:

(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]

Dane wejściowe mapy wyjściowej:

(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]

Bitcast

Transmisja bitcastowa może być przedstawiona jako sekwencja typu transpose-reshape-transpose. Dlatego też mapy indeksowania to tylko kompozycja kolejne wartości.

Połącz

Mapowanie wyjścia na wejście w przypadku funkcji concat jest zdefiniowane dla wszystkich wejść, ale z nienakładającymi się domenami, co oznacza, że w danym momencie używane jest tylko jedno z wejść.

p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}

Dane wyjściowe do danych wejściowych:

• wyjście -> wejście 1:

(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]

• output -> input 2:

(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]

• wyjście -> wejście 3:

(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]

Dane wejściowe do wygenerowania map:

• wejście 1 -> dane wyjściowe:

(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]

• wejście 2 -> wyjście:

(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]

• wejście 3 -> dane wyjściowe:

(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]

Kropka

Mapy indeksowania dla kropki są bardzo podobne do map zmniejszania.

p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
  lhs_batch_dims={0}, rhs_batch_dims={0},
  lhs_contracting_dims={2}, rhs_contracting_dims={1}

Dane wyjściowe do danych wejściowych:

• dane wyjściowe -> input_1:

(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]

• dane wyjściowe -> input_2:

(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]

Dane wejściowe do wygenerowania map:

• wejście_1 -> dane wyjściowe:

(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]

• input_2 -> output:

(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]

Pad

Indeksowanie PadOp jest odwrotne do indeksowania SliceOp.

p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0

Konfiguracja dopełnienia 1_4_1x4_8_0 oznacza wartość lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1.

Dane wyjściowe do wprowadzania map:

• dane wyjściowe -> dane wejściowe:

(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]

• output -> init:

(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]

ReduceWindow

Funkcja ReduceWindow w XLA również wykonuje wypełnianie. Mapy indeksowania mogą więc być obliczone jako kompozycja indeksowania ReduceWindow bez żadnego dopełnienia i indeksowanie PadOp.

c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
  window={size=1x512 pad=0_0x0_0}, to_apply=max

Dane wyjściowe do wprowadzania map:

• dane wyjściowe -> dane wejściowe:

(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]

• dane wyjściowe -> init:

(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]

Indeksowanie Map dla Fusion

Mapa indeksowania operacji fuzji to kompozycja map indeksowania wszystkich operacji w klusterze. Może się zdarzyć, że niektóre dane wejściowe są odczytywane kilka razy z różnymi wzorców dostępu.

1 plik wejściowy, kilka map indeksowania

Oto przykład właściwości p0 + transpose(p0).

f {
  p0 = f32[1000, 1000] parameter(0)
  transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
  ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}

Mapy indeksowania wyjścia na wejście dla p0 to (d0, d1) -> (d0, d1) i (d0, d1) -> (d1, d0). Oznacza to, że do obliczenia jednego elementu danych wyjściowych może być konieczne dwukrotne odczytanie parametru wejściowego.

1 wejściowy, zdeduplikowana mapa indeksowania

Zdarza się, że mapy indeksowania są w istocie takie same, choć nie jest to od razu widoczne.

f {
  p0 = f32[20, 10, 50] parameter(0)
  lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
  lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
  lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
  rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
  rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
  rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
  ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}

W tym przypadku mapą indeksowania wyjścia na wejście dla p0 jest po prostu (d0, d1, d2) -> (d2, d0, d1).

Softmax

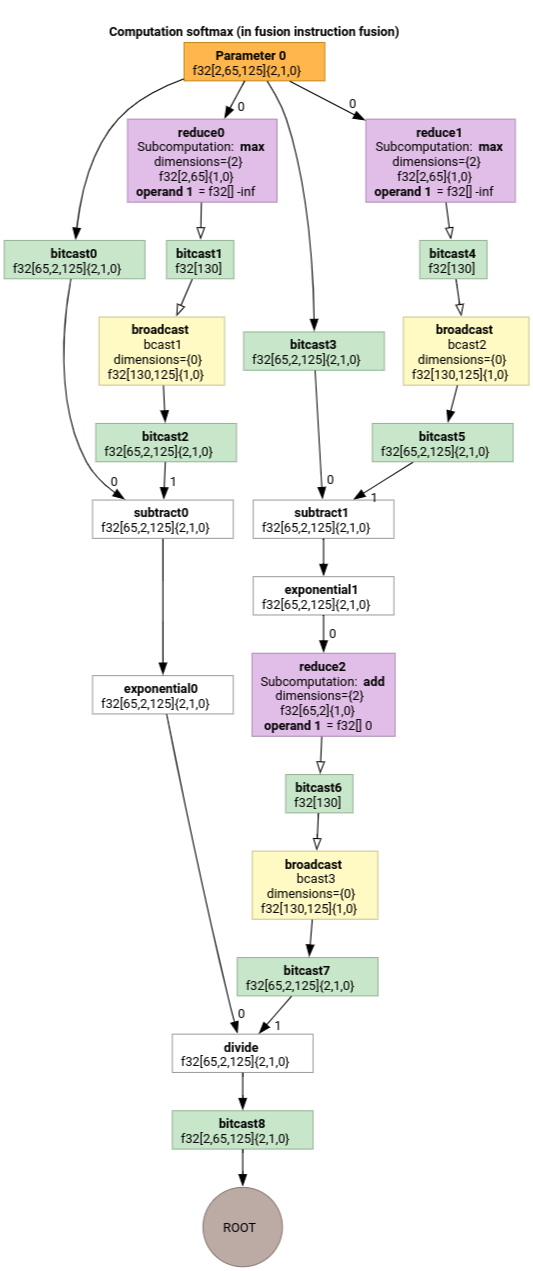
Mapy indeksowania danych wyjściowych dla danych wejściowych dla parameter 0 dla softmax:

(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]

i

(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]

gdzie s0 odnosi się do najbardziej wewnętrznego wymiaru danych wejściowych.

Uproszczony mapy indeksowania

Domyślny upraszczacz w przypadku mlir::AffineMap upstream nie może zakładać niczego na temat zakresów wymiarów lub symboli. Dlatego nie może efektywnie uprościć wyrażeń z użyciem funkcji mod i div.

Aby jeszcze bardziej uprościć mapy afiniczne, możemy wykorzystać informacje o dolnej i górnej granicy podwyrażeń.

Upraszczacz może przekształcić te wyrażenia.

1. (d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16) dla d w domenie [0, 6] x [0, 14] zmieni się na (d0, d1) -> (d0, d1)
2. (d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10) w domenie di in [0, 9] zmieni się na (d0, d1, d2) -> (d0, d1, d2).
3. (d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8) dla d_i in [0, 9] zmienia się na (d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8).
4. (d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9) w [0, 9] x [0, 10] zmienia się na (d0, d1) -> (d0).

Dzięki indeksowaniu upraszczania mapy możemy stwierdzić, że niektóre z połączonych przekształceń w HLO wzajemnie się anulują.

p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)

Po skomponowaniu map indeksowania i ich uproszczeniu otrzymamy

(d0, d1, d2) -> (d0, d1, d2).

Uproszczone indeksowanie mapy upraszcza też ograniczenia.

1. Ograniczenia typu lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_bound to przepisane jako updated_lower_bound <= affine_expr <= updated_upped_bound.
2. Ograniczenia, które są zawsze spełnione, np. d0 + s0 in [0, 20] for d0 in [0, 5] and s0 in [1, 3], są eliminowane.
3. Wyrażenia korelacyjne w ograniczeniach są optymalizowane jako afina indeksowania mapę powyżej.

Więcej przykładów znajdziesz na stronie indexing_map_test.cc.