Эта страница переведена с помощью Cloud Translation API.

Анализ индексации
Оптимизируйте свои подборки Сохраняйте и классифицируйте контент в соответствии со своими настройками.

Анализ индексации HLO — это анализ потока данных , который описывает, как элементы одного тензора связаны с другим посредством «карт индексации». Например, как индексы вывода инструкции HLO сопоставляются с индексами операндов инструкции HLO.

Пример

Для трансляции с tensor<20xf32> на tensor<10x20x30xf32>

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

карта индексации вывода на вход равна (i, j, k) -> (j) для i in [0, 10] , j in [0, 20] и k in [0, 30] .

Мотивация

XLA использует несколько индивидуальных решений для анализа объединений, использования операндов и схем листов (подробнее ниже). Целью индексного анализа является предоставление компонента многократного использования для таких случаев использования. Анализ индексирования построен на инфраструктуре Affine Map MLIR и добавляет семантику HLO.

Объединение

Рассуждения об объединении памяти становятся возможными в нетривиальных случаях, когда мы знаем, какие элементы/срезы входных данных считываются для вычисления элемента выходных данных.

Использование операндов

Использование операнда в XLA показывает, насколько сильно используется каждый вход инструкции, при условии, что ее выход полностью использован. В настоящее время использование также не рассчитывается для общего случая. Индексный анализ позволяет нам точно рассчитать загрузку.

Укладка плитки

Плитка/срез — это гиперпрямоугольное подмножество тензора, параметризованное смещениями, размерами и шагами. Распространение плиток — это способ вычисления параметров плитки производителя/потребителя операции с использованием параметров мозаики самой операции. Уже существует библиотека , которая делает это для softmax и dot. Распространение тайлов можно сделать более универсальным и надежным, если оно выражается через карты индексации.

Карта индексирования

Карта индексации представляет собой комбинацию

символически выраженная функция, которая отображает каждый элемент одного тензора A в диапазоны элементов в тензоре B ;
ограничения на допустимые аргументы функции, включая домен функции.

Аргументы функции разделены на 3 категории, чтобы лучше передать их природу:

размерные переменные тензора A или сетки графического процессора, из которой мы сопоставляем; значения известны статически. Элементы индекса также называются переменными измерения .
переменные диапазона . Они определяют отображение «один ко многим» и определяют набор элементов в B , используемых для вычисления одного значения A ; значения известны статически. Сжимающая размерность матричного умножения является примером переменной диапазона.
переменные времени выполнения , которые известны только во время выполнения. Например, аргумент индексов операции сбора .

Результатом функции является индекс целевого B тензора.

Короче говоря, индексная функция от тензора A к тензору B для операции x равна

map_ab(index in A, range variables, runtime variables) -> index in B .

Чтобы лучше разделить типы аргументов сопоставления, мы запишем их как:

map_ab(index in A)[range variables]{runtime variables} -> (index in B)

Например, давайте посмотрим на карты индексации для операции сокращения f32[4, 8] out = reduce(f32[2, 4, 8, 16] in, 0), dimensions={0,3} :

для сопоставления элементов in и out наша функция может быть выражена как (d0, d1, d2, d3) -> (d1, d2) . Ограничения переменных d0 in [0, 1], d1 in [0, 3], d2 in [0, 7], d3 in [0, 15] определяются формой in .
Чтобы сопоставить элементы out с in : out имеет только два измерения, а сокращение вводит две переменные диапазона, которые охватывают сокращающиеся измерения. Таким образом, функция отображения равна (d0, d1)[s0, s1] -> (s0, d0, d1, s1) , где (d0, d1) — индекс out . s0 , s1 — это диапазоны, определяемые семантикой операции и размерностью диапазона 0 и 3 in тензора. Ограничения: d0 in [0, 3], d1 in [0, 7], s0 in [0,1], s1 in [0, 15] .

Важно отметить, что в большинстве сценариев нас интересует сопоставление элементов вывода . Для вычислений

C = op1(A, B)
E = op2(C, D)

мы можем говорить об «индексации B», означающей «отображение элементов E в элементы B ». Это может показаться нелогичным по сравнению с другими типами анализа потока данных, которые работают от ввода к выводу.

Ограничения на переменные открывают возможности оптимизации и помогают при генерации кода. В документации и реализации ограничения также называются доменом , поскольку они определяют все допустимые комбинации или значения аргументов функции отображения. Для многих операций ограничения просто описывают размеры тензоров, но для некоторых операций они могут быть более сложными; см. примеры ниже.

Имея функции и ограничения аргументов, выраженные символически, и имея возможность комбинировать функции и ограничения, мы можем вычислить компактное индексное отображение для произвольного большого вычисления (слияния).

Выразительность символической функции и ограничений — это баланс между сложностью реализации и выигрышем от оптимизации, который мы получаем от более точного представления. Для некоторых операций HLO мы фиксируем шаблоны доступа лишь приблизительно.

Выполнение

Поскольку мы хотим минимизировать повторные вычисления, нам нужна библиотека для символьных вычислений. XLA уже зависит от MLIR, поэтому мы используем mlir::AffineMap вместо написания еще одной библиотеки символьной арифметики.

Типичный AffineMap выглядит так

(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)

AffineMap имеет два типа параметров: размеры и символы . Размеры соответствуют переменным размерности d ; символы соответствуют переменным диапазона r и переменным времени выполнения rt . AffineMap не содержит метаданных об ограничениях параметров, поэтому нам приходится предоставлять их отдельно.

struct Interval {
 int64_t lower;
 int64_t upper;
};

class IndexingMap {
   // Variable represents dimension, range or runtime variable.
  struct Variable {
    Interval bounds;
    // Name of the variable is used for nicer printing.
    std::string name = "";
  };

  mlir::AffineMap affine_map_;

  // DimVars represent dimensions of a tensor or of a GPU grid.
  std::vector<Variable> dim_vars_;

  // RangeVars represent ranges of values, e.g. to compute a single element of
  // the reduction's result we need a range of values from the input tensor.
  std::vector<Variable> range_vars_;

  // RTVars represent runtime values, e.g. a dynamic offset in
  // HLO dynamic-update-slice op.
  std::vector<Variable> rt_vars_;
  llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};

dim_vars_ кодируют ограничения инклюзивного блока для переменных измерения d карты индексации, которые обычно совпадают с формой выходного тензора для таких операций, как транспонирование, уменьшение, поэлементное, точечное, но есть некоторые исключения, такие как HloConcatenateInstruction .

range_vars_ все значения, которые принимают переменные диапазона. Переменные диапазона необходимы, когда необходимо несколько значений для вычисления одного элемента тензора, из которого мы сопоставляем, например, для карты индексации вывода->входа сокращений или карты ввода->вывода для широковещательных сообщений.

rt_vars_ кодирует возможные значения во время выполнения. Например, смещение является динамическим для 1D HloDynamicSliceInstruction . Соответствующий RTVar будет иметь допустимые значения от 0 до tensor_size - slice_size - 1 .

constraints_ фиксируют отношения между значениями в форме <expression> in <range> , например d0 + s0 in [0, 20] . Вместе с Variable.bounds они определяют «домен» функции индексирования.

Давайте рассмотрим пример, чтобы понять, что на самом деле означает все вышеперечисленное.

Индексирование карт для Unfused Ops

Поэлементно

Для поэлементных операций карта индексации является идентификатором.

  p0 = f32[10, 20] parameter(0)
  p1 = f32[10, 20] parameter(1)
  output = f32[10, 20] add(p0, p1)

Вывод на входной output -> p0 :

(d0, d1) -> (d0, d1),
domain:
d0 in [0, 9],
d1 in [0, 19]

Входная и выходная карта p0 -> output :

(d0, d1) -> (d0, d1),
domain:
d0 in [0, 9],
d1 in [0, 19]

Транслировать

Широковещательная передача означает, что некоторые измерения будут удалены, когда мы сопоставляем вывод с вводом, и добавлены, когда мы сопоставляем ввод с выводом.

p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}

Вывод на входную карту:

(d0, d1, d2) -> (d1),
domain:
d0 in [0, 9],
d1 in [0, 19],
d2 in [0, 29]

Входная и выходная карта:

(d0)[s0, s1] -> (s0, d0, s1),
domain:
d0 in [0, 19],
s0 in [0, 9],
s1 in [0, 29]

Обратите внимание, что теперь у нас есть переменные диапазона s с правой стороны для сопоставления ввода-вывода. Это символы, обозначающие диапазоны значений. Например, в этом конкретном случае каждый элемент ввода с индексом d0 сопоставляется с срезом вывода размером 10x1x30.

Йота

У Iota нет входного тензорного операнда, поэтому нет аргументов входного индекса.

iota = f32[2,4] iota(), dimensions={1}

Вывод на входную карту:

(d0, d1) -> ()
domain:
d0 in [0, 1]
d1 in [0, 3]

Вход в выходную карту:

()[s0, s1] -> (s0, s1)
domain:
s0 in [0, 1]
s1 in [0, 3]

Динамический срез

DynamicSlice имеет смещения, известные только во время выполнения.

src = s32[2, 2, 258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = s32[1, 2, 32] dynamic-slice(src, of1, of2, of3), dynamic_slice_sizes={1, 2, 32}

Вывод для ввода карты из ds в src :

(d0, d1, d2){rt0, rt1, rt2} -> (d0 + rt0, d1 + rt1, d2 + rt2),
domain:
d0 in [0, 0],
d1 in [0, 1],
d2 in [0, 31],
rt0 in [0, 1],
rt1 in [0, 0],
rt2 in [0, 226]

Обратите внимание, что теперь справа у нас есть rt для сопоставления ввода-вывода. Это символы, обозначающие значения времени выполнения. Например, в этом конкретном случае для каждого элемента вывода с индексами d0, d1, d2 мы получаем доступ к смещениям срезов of1 , of2 и of3 для вычисления индекса ввода. Интервалы для переменных времени выполнения определяются исходя из предположения, что весь срез остается в пределах.

Вывод на входную карту для of1 , of2 и of3 :

(d0, d1, d2) -> (),
domain:
d0 in [0, 0],
d1 in [0, 1],
d2 in [0, 31]

ДинамическийUpdateSlice

src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
    s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)

Вывод для ввода карты для src тривиален. Это можно сделать более точным, ограничив область необновляемыми индексами, но сейчас карты индексации не поддерживают ограничения неравенства.

(d0, d1) -> (d0, d1),
domain:
d0 in [0, 19],
d1 in [0, 29]

Вывод для ввода карты для upd :

(d0, d1){rt0, rt1} -> (d0 - rt0, d1 - rt1),
domain:
d0 in [0, 19],
d1 in [0, 29],
rt0 in [0, 15],
rt1 in [0, 20]

Обратите внимание, что теперь у нас есть rt0 и rt1 , которые представляют значения времени выполнения. В этом конкретном случае для каждого элемента вывода с индексами d0, d1 мы получаем доступ к смещениям срезов of1 и of2 для вычисления индекса ввода. Интервалы для переменных времени выполнения определяются исходя из предположения, что весь срез остается в пределах.

Вывод на входную карту для of1 и of2 :

(d0, d1) -> (),
domain:
d0 in [0, 19],
d1 in [0, 29]

Собирать

Поддерживается только упрощенная сборка. См. сбор_simplifier.h .

operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
  offset_dims={1,2,3},
  collapsed_slice_dims={},
  start_index_map={0,1},
  index_vector_dim=1,
  slice_sizes={7,8,4}

Вывод для входной карты для operand :

(d0, d1, d2, d3){rt0, rt1} -> (d1 + rt0, d2 + rt1, d3),
domain:
d0 in [0, 1805],
d1 in [0, 6],
d2 in [0, 7],
d3 in [0, 3],
rt0 in [0, 26],
rt1 in [0, 68]

Обратите внимание, что теперь у нас есть символы rt , которые представляют значения времени выполнения.

Вывод на входную карту для indices :

(d0, d1, d2, d3)[s0] -> (d0, s0),
domain:
d0 in [0, 1805],
d1 in [0, 6],
d2 in [0, 7],
d3 in [0, 3],
s0 in [0, 1]

Переменная диапазона s0 показывает, что нам нужна вся строка (d0, *) тензора indices для вычисления элемента вывода.

Транспонировать

Карта индексирования для транспонирования представляет собой перестановку измерений ввода/вывода.

p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}

Вывод на входную карту:

(d0, d1, d2, d3) -> (d0, d3, d1, d2),
domain:
d0 in [0, 2],
d1 in [0, 5],
d2 in [0, 127],
d3 in [0, 12287],

Входная и выходная карта:

(d0, d1, d2, d3) -> (d0, d2, d3, d1),
domain:
d0 in [0, 2],
d1 in [0, 12287],
d2 in [0, 5],
d3 in [0, 127]

Обеспечить регресс

Карта индексирования для обратного изменения изменяет возвращенные размеры на upper_bound(d_i) - d_i :

p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}

Вывод на входную карту:

(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3),
domain:
d0 in [0, 0],
d1 in [0, 16],
d2 in [0, 8],
d3 in [0, 8]

Входная и выходная карта:

(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3),
domain:
d0 in [0, 0],
d1 in [0, 16],
d2 in [0, 8],
d3 in [0, 8]

(Вариативный)Уменьшить

Вариативное сокращение имеет несколько входов и несколько начальных значений, карта от выхода ко входу добавляет уменьшенные измерения.

p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
out = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
  dimensions={0}, to_apply=max

Вывод для ввода карт:

out[0] -> p0 :

(d0)[s0] -> (s0, d0),
domain:
d0 in [0, 9],
s0 in [0, 255]

out[0] -> p0_init :

(d0) -> (),
domain:
d0 in [0, 9]

Входные и выходные карты:

p0 -> out[0] :

(d0, d1) -> (d1),
domain:
d0 in [0, 255],
d1 in [0, 9]

p0_init -> out[0] :

()[s0] -> (s0),
domain:
s0 in [0, 9]

Срез

Индексация от вывода ко входу для среза приводит к созданию карты пошаговой индексации, которая действительна для каждого элемента вывода. Сопоставление входа с выходом ограничено шагомерным диапазоном элементов на входе.

p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
  slice={[5:10:1], [3:20:7], [0:50:2]}

Вывод на входную карту:

(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2),
domain:
d0 in [0, 4],
d1 in [0, 2],
d2 in [0, 24]

Входная и выходная карта:

(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2),
domain:
d0 in [5, 9],
d1 in [3, 17],
d2 in [0, 48],
(d1 - 3) mod 7 in [0, 0],
d2 mod 2 in [0, 0]

Изменить форму

Изменения бывают разных вкусов.

Свернуть фигуру

Это «линеаризация» изменения формы от ND до 1D.

p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)

Вывод на входную карту:

(d0) -> (d0 floordiv 8, d0 mod 8),
domain:
d0 in [0, 31]

Входная и выходная карта:

(d0, d1) -> (d0 * 8 + d1),
domain:
d0 in [0, 3],
d1 in [0, 7]

Развернуть фигуру

Это обратная операция «свертывания формы», она преобразует входной сигнал 1D в выходной сигнал ND.

p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)

Вывод на входную карту:

(d0, d1) -> (d0 * 8 + d1),
domain:
d0 in [0, 3],
d1 in [0, 7]

Входная и выходная карта:

(d0) -> (d0 floordiv 8, d0 mod 8),
domain:
d0 in [0, 31]

Общее изменение формы

Это операции изменения формы, которые нельзя представить как одну фигуру развертывания или свертывания. Их можно представить только как композицию из двух или более фигур развертывания или свертывания.

Пример 1: Линеаризация-делинеаризация.

p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)

Это изменение формы можно представить как комбинацию формы свертывания tensor<4x8xf32> в tensor<32xf32> и последующего расширения формы до tensor<2x4x4xf32> .

Вывод на входную карту:

(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4),
domain:
d0 in [0, 1],
d1 in [0, 3],
d2 in [0, 3]

Входная и выходная карта:

(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4),
domain:
d0 in [0, 3],
d1 in [0, 7]

Пример 2. Развернутые и свернутые подфигуры

p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)

Это изменение формы можно представить как композицию двух изменений. Первый сжимает tensor<4x8x12xf32> самых внешних измерений до tensor<32x12xf32> , а второй расширяет tensor<32x12xf32> самых внутренних измерений в tensor<32x3x4xf32> .

Вывод на входную карту:

(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2),
domain:
d0 in [0, 31],
d1 in [0, 2]
d2 in [0, 3]

Входная и выходная карта:

(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4),
domain:
d0 in [0, 3],
d1 in [0, 7],
d2 in [0, 11]

Биткаст

Операцию битового вещания можно представить как последовательность транспонирования-изменения-транспонирования . Следовательно, его карты индексации представляют собой просто композицию карт индексации для этой последовательности.

Объединить

Сопоставление выходов и входов для concat определяется для всех входов, но с непересекающимися доменами, т. е. одновременно будет использоваться только один из входов.

p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT output = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}

Вывод на входные карты:

output -> p0 :

(d0, d1, d2) -> (d0, d1, d2),
domain:
d0 in [0, 1],
d1 in [0, 4],
d2 in [0, 6]

output -> p1 :

(d0, d1, d2) -> (d0, d1 - 5, d2),
domain:
d0 in [0, 1],
d1 in [5, 15],
d2 in [0, 6]

output -> p2 :

(d0, d1, d2) -> (d0, d1 - 16, d2),
domain:
d0 in [0, 1],
d1 in [16, 32],
d2 in [0, 6]

Входные данные для выходных карт:

p0 -> output :

(d0, d1, d2) -> (d0, d1, d2),
domain:
d0 in [0, 1],
d1 in [0, 4],
d2 in [0, 6]

p1 -> output :

(d0, d1, d2) -> (d0, d1 + 5, d2),
domain:
d0 in [0, 1],
d1 in [0, 10],
d2 in [0, 6]

p2 -> output :

(d0, d1, d2) -> (d0, d1 + 16, d2),
domain:
d0 in [0, 1],
d1 in [0, 16],
d2 in [0, 6]

Точка

Карты индексации для точки очень похожи на карты для уменьшения.

p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
output = f32[4, 128, 64] dot(p0, p1),
  lhs_batch_dims={0}, rhs_batch_dims={0},
  lhs_contracting_dims={2}, rhs_contracting_dims={1}

Вывод на входные карты:

выход -> p0:

(d0, d1, d2)[s0] -> (d0, d1, s0),
domain:
d0 in [0, 3],
d1 in [0, 127],
d2 in [0, 63],
s0 in [0, 255]

вывод -> p1:

(d0, d1, d2)[s0] -> (d0, s0, d2),
domain:
d0 in [0, 3],
d1 in [0, 127],
d2 in [0, 63],
s0 in [0, 255]

Входные данные для выходных карт:

p0 -> вывод:

(d0, d1, d2)[s0] -> (d0, d1, s0),
domain:
d0 in [0, 3],
d1 in [0, 127],
d2 in [0, 255],
s0 in [0, 63]

p1 -> вывод:

(d0, d1, d2)[s0] -> (d0, s0, d1),
domain:
d0 in [0, 3],
d1 in [0, 255],
d2 in [0, 63],
s0 in [0, 127]

Подушка

Индексирование PadOp является обратным индексированию SliceOp.

p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0

Конфигурация заполнения 1_4_1x4_8_0 обозначает lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1 .

Вывод для ввода карт:

выход -> p0:

(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4),
domain:
d0 in [1, 7],
d1 in [4, 7],
(d0 - 1) mod 2 in [0, 0]

вывод -> p1:

(d0, d1) -> (),
domain:
d0 in [0, 11],
d1 in [0, 15]

Уменьшить окно

РедуцированиеWindow в XLA также выполняет заполнение. Таким образом, карты индексации могут быть вычислены как комбинация индексации РедуцВиндов, которая не выполняет никаких дополнений, и индексации PadOp.

c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
outpu = f32[1024, 3] reduce-window(p0, c_inf),
  window={size=1x512 pad=0_0x0_0}, to_apply=max

Вывод для ввода карт:

output -> p0 :

(d0, d1)[s0] -> (d0, d1 + s0),
domain:
d0 in [0, 1023],
d1 in [0, 2],
s0 in [0, 511]

output -> c_inf :

(d0, d1) -> (),
domain:
d0 in [0, 1023],
d1 in [0, 2]

Индексирование карт для Fusion

Карта индексации для операции слияния — это композиция карт индексации для каждой операции в кластере. Может случиться так, что некоторые входные данные читаются несколько раз с разными шаблонами доступа.

Один вход, несколько карт индексации

Вот пример для p0 + transpose(p0) .

f {
  p0 = f32[1000, 1000] parameter(0)
  transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
  ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}

Карты индексации вывода-ввода для p0 будут (d0, d1) -> (d0, d1) и (d0, d1) -> (d1, d0) . Это означает, что для вычисления одного элемента вывода нам может потребоваться дважды прочитать входной параметр.

Один вход, дедуплицированная карта индексации

Бывают случаи, когда карты индексации на самом деле одинаковы, хотя это не сразу очевидно.

f {
  p0 = f32[20, 10, 50] parameter(0)
  lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
  lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
  lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
  rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
  rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
  rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
  ROOT output = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}

Карта индексации вывода-ввода для p0 в этом случае равна просто (d0, d1, d2) -> (d2, d0, d1) .

Софтмакс

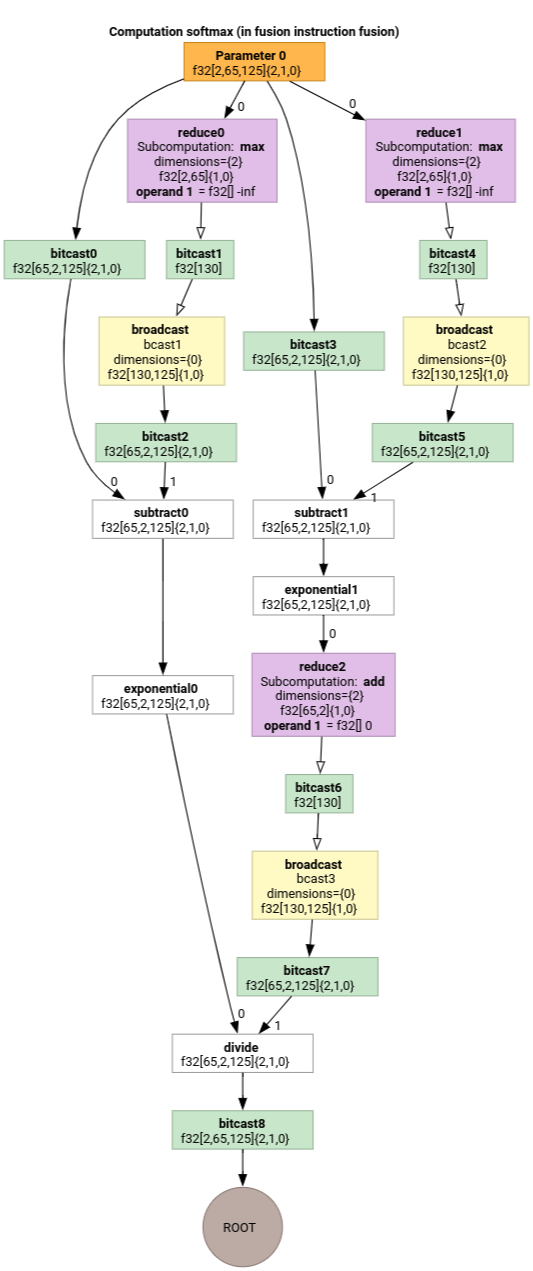
Сопоставления индексации вывода и ввода для parameter 0 для softmax:

(d0, d1, d2)[s0] -> (d0, d1, s0),
domain:
d0 in [0, 1],
d1 in [0, 64],
d2 in [0, 124],
s0 in [0, 124]

(d0, d1, d2) -> (d0, d1, d2),
domain:
d0 in [0, 1],
d1 in [0, 64],
d2 in [0, 124]

где s0 относится к самому внутреннему измерению ввода.

Дополнительные примеры см. в indexing_anaанализ_test.cc .

Упроститель карт индексирования

Упроститель по умолчанию для mlir::AffineMap в восходящем направлении не может делать никаких предположений о диапазонах размеров/символов. Следовательно, он не может эффективно упрощать выражения с помощью mod и div .

Мы можем использовать знания о нижних и верхних границах подвыражений в аффинных картах, чтобы еще больше их упростить.

Упроститель может переписать следующие выражения.

(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16) для d в [0, 6] x [0, 14] становится (d0, d1) -> (d0, d1)
(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10) для di in [0, 9] становится (d0, d1, d2) -> (d0, d1, d2) .
(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8) для d_i in [0, 9] становится (d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8) .
(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9) для d в [0, 9] x [0, 10] становится (d0, d1) -> (d0) .

Упроститель карты индексации позволяет нам понять, что некоторые цепочки изменений в HLO отменяют друг друга.

p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)

После составления карт индексации и их упрощения получим

(d0, d1, d2) -> (d0, d1, d2) .

Упрощение карты индексации также упрощает ограничения.

Ограничения типа lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_bound перезаписываются как updated_lower_bound <= affine_expr <= updated_upped_bound .
Ограничения, которые всегда выполняются, например, d0 + s0 in [0, 20] для d0 in [0, 5] и s0 in [1, 3] устраняются.
Аффинные выражения в ограничениях оптимизируются как аффинная карта индексации, приведенная выше.

Дополнительные примеры см. в indexing_map_test.cc .

Анализ индексации Оптимизируйте свои подборки Сохраняйте и классифицируйте контент в соответствии со своими настройками.

Пример

Мотивация

Объединение

Использование операндов

Укладка плитки

Карта индексирования

Выполнение

Индексирование карт для Unfused Ops

Поэлементно

Свернуть фигуру

Развернуть фигуру

Общее изменение формы

Пример 1: Линеаризация-делинеаризация.

Пример 2. Развернутые и свернутые подфигуры

Биткаст

Индексирование карт для Fusion

Один вход, несколько карт индексации

Один вход, дедуплицированная карта индексации

Софтмакс

Упроститель карт индексирования

Анализ индексации
Оптимизируйте свои подборки Сохраняйте и классифицируйте контент в соответствии со своими настройками.