Dokumen ini menjelaskan analisis pengindeksan HLO, yang memungkinkan Anda secara simbolis peta pengindeksan komputasi untuk operasi HLO. Peta pengindeksan adalah fungsi yang memetakan indeks satu tensor ke indeks lain, misalnya indeks HLO output instruksi dengan indeks input instruksi HLO atau sebaliknya.
Contoh
Untuk siaran dari tensor<20xf32> ke tensor<10x20x30xf32>
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
peta pengindeksan dari output ke input adalah (i, j, k) -> (j) untuk i in
[0, 10], j in [0, 20], dan k in [0, 30].
Motivasi
GPU XLA menggunakan beberapa solusi khusus untuk memahami penggabungan, penggunaan operand, dan skema tiling (detail selengkapnya di bawah). Sasaran analisis pengindeksan adalah menyediakan komponen yang dapat digunakan kembali untuk kasus penggunaan tersebut. Analisis pengindeksan dibangun di infrastruktur Peta Affine MLIR dan menambahkan semantik HLO.
Penggabungan
Penalaran tentang penggabungan memori dapat dilakukan untuk kasus-kasus non-trivial, kita tahu elemen/irisan input apa yang dibaca untuk menghitung elemen {i>output<i} tersebut.
Pemanfaatan Operand
Penggunaan operand di XLA menunjukkan seberapa banyak setiap input petunjuk digunakan dengan asumsi outputnya digunakan sepenuhnya. Saat ini, penggunaan juga tidak dihitung untuk kasus umum. Analisis pengindeksan memungkinkan penghitungan penggunaan secara akurat.
Susunan persegi
Kartu/irisan adalah subset hiper-persegi panjang dari tensor yang diparameterisasi oleh offset, dan langkah-langkahnya. Penyebaran kartu adalah cara untuk menghitung parameter kartu produser/konsumen op menggunakan parameter tiling op itu sendiri. Sudah ada library yang melakukannya untuk softmax dan dot. Propagasi {i>tiled <i}bisa dibuat lebih umum dan andal jika dinyatakan melalui peta pengindeksan.
Fungsi dan Domain
Peta pengindeksan adalah fungsi f(x) = f(d, r, rt)
yang memetakan multi-indeks d dari tensor A ke elemen/rentang
Tensor B. Parameter r mengacu pada rentang indeks dari
dimensi yang ada dalam tensor B, tetapi tidak pada tensor A. Tujuan
parameter rt mengacu pada nilai runtime, misalnya, indeks untuk operasi pengumpulan.
Misalnya, jika kita memiliki pengurangan dari tensor<2x4x8x16xf32> menjadi
tensor<4x8xf32>, maka peta pengindeksan dari output 2D ke input 4D akan
(d0, d1) -> (r0, d0, d1, r1), dengan d_i adalah variabel dimensi yang
sesuai dengan indeks tensor output. Enkode variabel rentang r_j
beberapa nilai, yaitu untuk menghitung elemen (d0, d1) dari output, kita perlu
(r0, d0, d1, r1) elemen input, dengan r0 in [0, 1] dan
r1 in [0, 15].
Pemetaan ini dapat dibuat dari atribut petunjuk HLO atau pemetaan petunjuk yang tidak digabungkan dapat disusun untuk mendapatkan pengindeksan untuk penggabungan. Pemetaan juga memiliki domain, yang menentukan elemen tensor mana yang ada pemetaan.
f(x) s.t.
lb <= g(x) <= ub
Karena kita ingin meminimalkan komputasi ulang, kita memerlukan library untuk komputasi simbolis. XLA sudah bergantung pada MLIR, jadi kami menggunakan mlir::AffineMap alih-alih menulis perpustakaan aritmatika simbolis lainnya.
AffineMap standar terlihat seperti
(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)
AffineMap memiliki dua jenis parameter: dimensi dan simbol. Dimensi
sesuai dengan variabel dimensi d, simbol sesuai dengan
variabel rentang r dan variabel RT rt. AffineMap tidak berisi
metadata apa pun tentang rentang dimensi, jadi kita harus menyediakan data ini
sendiri.
struct Interval {
int64_t lower;
int64_t upper;
};
// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
Interval bounds;
};
// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
Interval range;
};
// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
Interval feasible_values;
const HloInstruction* hlo;
// This is a map from the iteration space of the corresponding indexing map to
// the iteration space of `hlo`. It shows what element of `hlo` we need to
// extract to get the runtime value for the RTVar.
mlir::AffineMap map;
};
class IndexingMap {
mlir::AffineMap affine_map_;
std::vector<DimVar> dim_vars_;
std::vector<RangeVar> range_vars_;
std::vector<RTVar> rt_vars_;
llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};
dim_vars_ mengenkode batasan kotak inklusif untuk dimensi
variabel d dari peta pengindeksan, yang biasanya bertepatan dengan
bentuk tensor output untuk operasi seperti {i>transpose<i},
mengurangi, elementwise, titik, tetapi
ada beberapa pengecualian seperti
HloConcatenateInstruction.
range_vars_ mengenkode kemungkinan nilai yang dapat digunakan parameter r.
rt_vars_ menyimpan petunjuk hlo terkait beserta aksesnya
pola dan nilai yang layak dalam runtime. Misalnya, offset bersifat dinamis
untuk HloDynamicSliceInstruction 1D. RTVar yang sesuai akan memiliki
HloInstruction* yang menghasilkan tensor peringkat 0 dengan pola akses
(d0) -> (), karena untuk setiap elemen output, kita mengekstrak elemen yang sama
dari tensor offset untuk menghitung indeks input. Kita juga bisa berasumsi
bahwa offset irisan irisan selalu antara 0 dan
tensor_size - slice_size - 1.
Mari kita pelajari dengan contoh untuk memahami arti semua hal di atas.
Pengindeksan Maps untuk Operasi yang Tidak Menyatu
Elementwise
Untuk operasi elementwise, peta pengindeksan adalah identitas.
p0 = f32[10, 20] parameter(0)
p1 = f32[10, 20] parameter(1)
add = f32[10, 20] add(p0, p1)
Output ke peta input:
- {i>output<i} -> input_i:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Peta input ke output
- input_i -> {i>output<i}:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Siaran
Penyiaran berarti sebagian dimensi akan dihapus saat kita memetakan {i>output<i} ke input dan ditambahkan saat kita memetakan input ke {i>output<i}.
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
Peta output ke input:
(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]
Peta input ke output
(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]
Perhatikan, sekarang kita memiliki s di sisi kanan untuk input-ke-output
pemetaan peta Google. Simbol-simbol itu merepresentasikan rentang nilai. Misalnya, di
Dalam kasus ini, setiap elemen input dengan indeks d0 dipetakan ke
potongan 10x1x30 dari {i>output<i}.
Konstanta dan Iota
Mudah, mereka tidak memiliki parameter input apa pun, jadi tidak ada yang pengindeksan komputasi ini.
DynamicSlice
DynamicSlice sama seperti Slice, tetapi offsetnya dinamis.
src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}
Peta output ke input untuk src:
(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
hlo: of1 = s32[] parameter(1)
(d0, d1, d2) -> ()
s1 in [0, 0]
hlo: of2 = s32[] parameter(2)
(d0, d1, d2) -> ()
s2 in [0, 226]
hlo: of3 = s32[] parameter(3)
(d0, d1, d2) -> ()
Perhatikan bahwa sekarang kita memiliki s di sisi kanan untuk pemetaan input-ke-output.
Simbol tersebut mewakili nilai runtime. Misalnya, dalam
kasus tertentu untuk setiap elemen output dengan indeks d0, d1, d2 kita
offset slice akses of1, of2, dan of3 untuk menghitung indeks input.
Interval untuk variabel runtime diperoleh dengan mengasumsikan bahwa seluruh
slice tetap dalam batas.
Peta output ke input untuk of1, of2, dan of3:
(d0, d1, d2) -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
DynamicUpdateSlice
src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)
Output ke peta input untuk src kecil. Data tersebut dapat dibuat lebih tepat dengan
membatasi domain ke indeks yang tidak diperbarui, tetapi saat ini mengindeks peta
tidak mendukung batasan inqequality.
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]
Peta output ke input untuk upd:
(d0, d1)[s0, s1] -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
hlo: of1 = s32[] parameter(2)
(d0, d1) -> ()
s1 in [0, 20]
hlo: of2 = s32[] parameter(3)
(d0, d1) -> ()
Perhatikan bahwa sekarang kita memiliki s di sisi kanan untuk pemetaan input-ke-output.
Ini adalah simbol yang mewakili nilai runtime. Misalnya, dalam
kasus khusus ini untuk setiap elemen output dengan indeks d0, d1, kita mengakses
offset slice of1 dan of2 untuk menghitung indeks input. Interval
untuk variabel runtime diperoleh dengan asumsi bahwa seluruh slice tetap berada di
batas.
Output ke peta input untuk of1 dan of2:
(d0, d1) -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]
Berkumpul
Hanya pengumpulan yang disederhanakan yang didukung. Lihat [gather_simplifier].(https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h).
operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
offset_dims={1,2,3},
collapsed_slice_dims={},
start_index_map={0,1},
index_vector_dim=1,
slice_sizes={7,8,4}
Peta output ke input untuk operand:
(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 1)
Perhatikan bahwa sekarang kita memiliki s di sisi kanan untuk pemetaan input-ke-output.
Ini adalah simbol yang mewakili nilai runtime. Misalnya, dalam
kasus tertentu untuk setiap elemen output dengan indeks d0, d1, d2, d3 kita
ekstrak elemen (d0, 0) dan (d0, 1) dari tensor indices.
Output ke peta input untuk indices:
(d0, d1, d2, d3)[s0] -> (d0, s0)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 1]
Variabel rentang s0 menunjukkan bahwa kita membutuhkan seluruh baris (d0, *) dari
Tensor indices untuk menghitung elemen output.
Transpose
Peta pengindeksan untuk transposisi adalah permutasi dimensi input/output.
p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}
Peta output ke input:
(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]
Peta input ke output:
(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]
Balik
Peta pengindeksan untuk pengembalian mengubah dimensi yang dikembalikan ke upper_bound(d_i) -
d_i:
p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}
Peta output ke input:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
Peta input ke output:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
(Variadik)Mengurangi
Pengurangan variadik memiliki beberapa input dan beberapa inisialisasi, peta dari output ke input menambahkan dimensi yang dikurangi. Jadi, perilakunya seperti kebalikan dari broadcast dalam beberapa hal.
p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
dimensions={0}, to_apply=max
Output ke peta input:
- {i>output<i} -> input_j:
(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]
- {i>output<i} -> init_j:
(d0) -> ()
domain:
d0 in [0, 9]
Peta input ke output:
- input_i -> output_j:
(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]
- init_i -> output_j:
()[s0] -> (s0)
domain:
s0 in [0, 9]
for i, j = 0, ... INPUT_COUNT.
Potongan
Pengindeksan dari output ke input untuk potongan menghasilkan peta pengindeksan strided yang valid untuk setiap elemen output. Pemetaan dari input ke output dibatasi pada rentang elemen dengan stride dalam input.
p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
slice={[5:10:1], [3:20:7], [0:50:2]}
Peta output ke input:
(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]
Peta input ke output:
(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]
Bentuk ulang
Bentuk ulang hadir dalam berbagai bentuk.
Ciutkan bentuk
Ini adalah "linearisasi" yang mengubah bentuk dari N-D menjadi 1D.
p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)
Output untuk input peta:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
Peta input ke output:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
Memperluas bentuk
Ini adalah "bentuk penciutan" terbalik op, ia membentuk kembali input 1D menjadi {i>output<i} N-D.
p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)
Peta output ke input:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
Peta input ke output:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
Pembentukan ulang generik
Ini adalah operasi pembentukan ulang yang tidak dapat direpresentasikan sebagai satu bentuk luaskan atau ciutkan. Elemen ini hanya dapat direpresentasikan sebagai komposisi dari 2 atau lebih bentuk luaskan atau ciutkan.
Contoh 1: Linearisasi-delinearisasi.
p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)
Bentuk ulang ini dapat digambarkan sebagai
komposisi bentuk menciutkan
tensor<4x8xf32> ke tensor<32xf32>, lalu perluasan bentuk ke
tensor<2x4x4xf32>.
Output untuk input peta:
(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]
Peta input ke output:
(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
Contoh 2: Subbentuk yang diperluas dan diciutkan
p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)
Bentuk ulang ini dapat direpresentasikan sebagai komposisi dua bentuk ulang. Yang pertama
menyempitkan dimensi terluar tensor<4x8x12xf32> ke tensor<32x12xf32>
dan yang kedua memperluas dimensi terdalam tensor<32x12xf32> menjadi
tensor<32x3x4xf32>.
Peta output ke input:
(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]
Peta input ke output:
(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]
Bitcast
Operasi bitcast dapat direpresentasikan sebagai urutan transpose-reshape-transpose. Oleh karena itu, peta pengindeksan hanyalah komposisi peta pengindeksan untuk urutan ini.
Gabungkan
Pemetaan output-ke-input untuk concat ditentukan untuk semua input, tetapi dengan domain yang tidak tumpang-tindih, yaitu hanya satu input yang akan digunakan pada satu waktu.
p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}
Output ke input memetakan:
- {i>output<i} -> masukan 1:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- output -> input 2:
(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]
- output -> input 3:
(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]
Input ke output memetakan:
- input 1 -> output:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- masukan 2 -> {i>output<i}:
(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]
- masukan 3 -> {i>output<i}:
(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]
Titik
Peta pengindeksan untuk titik sangat mirip dengan peta pengindeksan untuk reduce.
p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
lhs_batch_dims={0}, rhs_batch_dims={0},
lhs_contracting_dims={2}, rhs_contracting_dims={1}
Output ke input memetakan:
- {i>output<i} -> input_1:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
- {i>output<i} -> input_2:
(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
Input ke output memetakan:
- input_1 -> {i>output<i}:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]
- input_2 -> {i>output<i}:
(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]
Pad
Pengindeksan PadOp adalah kebalikan dari pengindeksan SliceOp.
p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0
Konfigurasi padding 1_4_1x4_8_0 menunjukkan lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1.
Output ke peta input:
- {i>output<i} -> masukan:
(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]
- output -> init:
(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]
ReduceWindow
ReduceWindow di XLA juga melakukan padding. Oleh karena itu, peta pengindeksan dapat dihitung sebagai komposisi pengindeksan ReduceWindow yang tidak melakukan padding dan pengindeksan PadOp.
c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
window={size=1x512 pad=0_0x0_0}, to_apply=max
Output ke peta input:
- {i>output<i} -> masukan:
(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]
- {i>output<i} -> init:
(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]
Mengindek Maps untuk Fusion
Peta pengindeksan untuk operasi penggabungan adalah komposisi peta pengindeksan untuk setiap operasi dalam cluster. Beberapa input dapat dibaca beberapa kali dengan pola akses.
Satu input, beberapa peta pengindeksan
Berikut adalah contoh untuk p0 + transpose(p0).
f {
p0 = f32[1000, 1000] parameter(0)
transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}
Peta pengindeksan output ke input untuk p0 adalah (d0, d1) -> (d0, d1) dan
(d0, d1) -> (d1, d0). Artinya untuk menghitung satu elemen
{i>output<i} kita mungkin perlu
membaca parameter input dua kali.
Satu input, peta pengindeksan yang dihapus duplikatnya
Ada kalanya peta pengindeksan sebenarnya sama, meskipun tidak langsung terlihat.
f {
p0 = f32[20, 10, 50] parameter(0)
lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}
Peta pengindeksan output ke input untuk p0 dalam hal ini hanya
(d0, d1, d2) -> (d2, d0, d1).
Softmax
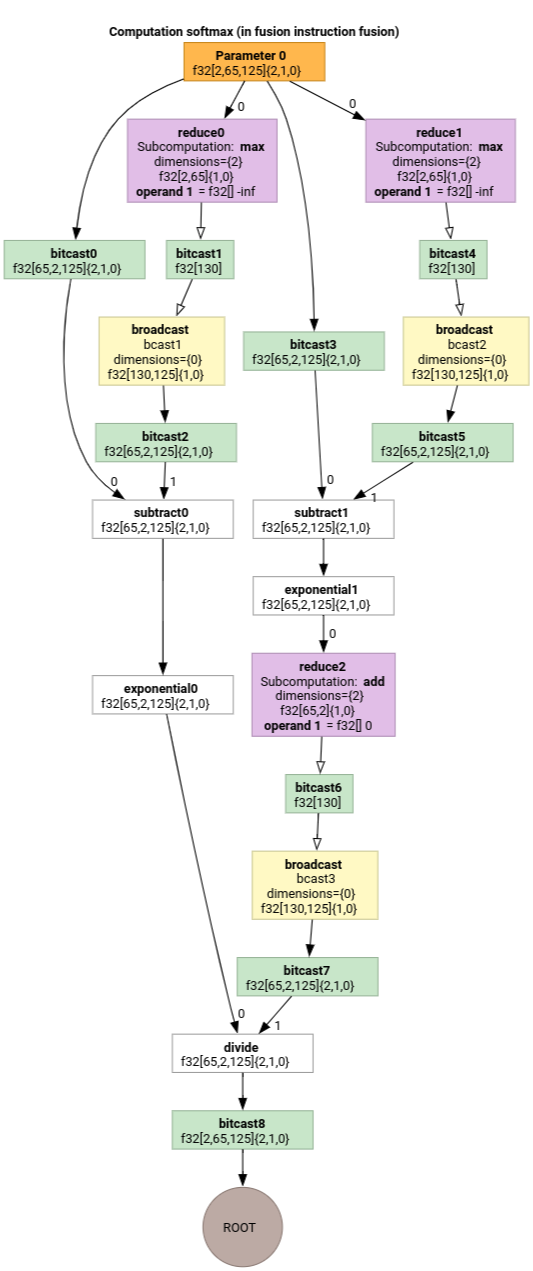
Peta pengindeksan output-ke-input untuk parameter 0 untuk softmax:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]
dan
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
dengan s0 mengacu pada dimensi input yang paling dalam.
Pengindeksan Peta Penyederhana
Penyederhana default untuk upstream mlir::AffineMap tidak dapat membuat
asumsi tentang rentang dimensi/simbol. Oleh karena itu,
menyederhanakan ekspresi dengan mod dan divsecara efisien.
Kita dapat memanfaatkan pengetahuan tentang batas bawah dan atas sub-ekspresi dalam peta afin untuk menyederhanakannya lebih lanjut.
Yang lebih sederhana dapat menulis ulang ekspresi berikut.
(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16)untuk d di[0, 6] x [0, 14]menjadi(d0, d1) -> (d0, d1)(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10)untukdi in [0, 9]menjadi(d0, d1, d2) -> (d0, d1, d2).(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8)untukd_i in [0, 9]menjadi(d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8).(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9)untuk d di[0, 9] x [0, 10]menjadi(d0, d1) -> (d0).
Pengindeksan pemecah peta memungkinkan kita memahami bahwa beberapa perubahan bentuk berantai di HLO saling membatalkan.
p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)
Setelah komposisi pengindeksan peta dan penyederhanaannya, kita akan mendapatkan
(d0, d1, d2) -> (d0, d1, d2).
Penyederhanaan peta pengindeksan juga menyederhanakan batasan.
- Batasan jenis
lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_boundditulis ulang sebagaiupdated_lower_bound <= affine_expr <= updated_upped_bound. - Batasan yang selalu terpenuhi, misalnya
d0 + s0 in [0, 20]untukd0 in [0, 5]dans0 in [1, 3]dieliminasi. - Ekspresi affine dalam batasan dioptimalkan sebagai affine pengindeksan peta di atas.
Untuk contoh lainnya, lihat indexing_map_test.cc.

