Questo documento descrive l'analisi dell'indicizzazione HLO, che consente di calcolare simbolicamente le mappe di indicizzazione per le operazioni HLO. La mappa di indicizzazione è una funzione che mappa gli indici di un tensore agli indici di un altro, ad esempio gli indici dell'output di un'istruzione HLO agli indici degli input delle istruzioni HLO o viceversa.
Esempio
Per una trasmissione da tensor<20xf32> a tensor<10x20x30xf32>
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
la mappa di indicizzazione dall'output all'input è (i, j, k) -> (j) per i in
[0, 10], j in [0, 20] e k in [0, 30].
Motivazione
La GPU XLA utilizza diverse soluzioni personalizzate per ragionare su unione, utilizzo degli operandi e schemi di suddivisione in riquadri (maggiori dettagli di seguito). Lo scopo dell'analisi dell'indicizzazione è fornire un componente riutilizzabile per questi casi d'uso. Analisi dell'indicizzazione si basa sull'infrastruttura Affine Map di MLIR e aggiunge la semantica dell'HLO.
Fusione
Il ragionamento sulla coalescenza della memoria diventa fattibile per casi non banali, quando sappiamo quali elementi/sezioni degli input vengono letti per calcolare un elemento dell'output.
Utilizzo operando
L'utilizzo dell'operando in XLA indica quanto viene utilizzato ogni input dell'istruzione, supponendo che l'output sia completamente utilizzato. Attualmente, inoltre, l'utilizzo viene calcolata per un caso generico. L'analisi dell'indicizzazione consente di calcolare con precisione l'utilizzo.
Riquadri:
Un riquadro/una frazione è un sottoinsieme iperrettangolare di un tensore parametrizzato da offset, dimensioni e passi. La propagazione dei riquadri è un modo per calcolare i parametri dei riquadri produttore/consumatore dell'operazione utilizzando i parametri di tiling dell'operazione stessa. Esiste già una libreria che esegue questa operazione per softmax e dot. La propagazione dei riquadri può essere resa più generica e solida se viene espressa tramite mappe di indicizzazione.
Funzione e dominio
La mappa di indicizzazione è una funzione f(x) = f(d, r, rt)
che mappa un d multiindice di un tensore A a elementi/intervalli di
tensore B. Il parametro r si riferisce agli intervalli di indici delle dimensioni presenti nel tensore B, ma non nel tensore A. Il parametro rt si riferisce ai valori di runtime, ad esempio gli indici per un'operazione di aggregazione.
Ad esempio, se abbiamo una riduzione da tensor<2x4x8x16xf32> a
tensor<4x8xf32>, la mappa di indicizzazione dall'output 2D all'input 4D è
(d0, d1) -> (r0, d0, d1, r1), dove d_i sono le variabili di dimensione che
corrispondono agli indici del tensore di output. Le variabili di intervallo r_j codificano più valori, ovvero per calcolare un elemento (d0, d1) dell'output, sono necessari elementi (r0, d0, d1, r1) dell'input, dove r0 in [0, 1] e
r1 in [0, 15].
Questa mappatura può essere costruita dagli attributi delle istruzioni HLO o le mappature delle istruzioni non fuse possono essere composte per ottenere l'indicizzazione per una fusione. La mappatura ha anche un dominio, che specifica per quali elementi del tensore esiste.
f(x) s.t.
lb <= g(x) <= ub
Poiché vogliamo ridurre al minimo il ricalcolo, abbiamo bisogno di una libreria per molto altro. La XLA dipende già dall'MLIR, quindi utilizziamo mlir::AffineMap invece di scrivere un'altra libreria aritmetica simbolica.
Un AffineMap tipico ha questo aspetto
(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)
AffineMap ha due tipi di parametri: dimensioni e simboli. La
dimensioni corrispondono alle variabili di dimensione d, i simboli corrispondono
le variabili di intervallo r e le variabili RT rt. AffineMap non contiene
metadati relativi agli intervalli delle dimensioni, quindi dobbiamo fornire questi dati
noi stessi.
struct Interval {
int64_t lower;
int64_t upper;
};
// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
Interval bounds;
};
// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
Interval range;
};
// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
Interval feasible_values;
const HloInstruction* hlo;
// This is a map from the iteration space of the corresponding indexing map to
// the iteration space of `hlo`. It shows what element of `hlo` we need to
// extract to get the runtime value for the RTVar.
mlir::AffineMap map;
};
class IndexingMap {
mlir::AffineMap affine_map_;
std::vector<DimVar> dim_vars_;
std::vector<RangeVar> range_vars_;
std::vector<RTVar> rt_vars_;
llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};
dim_vars_ codifica i vincoli della casella inclusiva per la dimensione
variabili d della mappa di indicizzazione, che di solito coincidono con il
forma del tensore di output per operazioni come trasposizione, riduzione, elemento, punto,
ci sono alcune eccezioni, ad esempio
HloConcatenateInstruction.
range_vars_ codificano i possibili valori che possono essere assunti dai parametri r.
rt_vars_ archivia le istruzioni HLO associate insieme al proprio accesso
pattern e i valori fattibili nel tempo di esecuzione. Ad esempio, l'offset è dinamico per un HloDynamicSliceInstruction 1D. L'elemento RTVar corrispondente avrà un
HloInstruction* che produce un tensore di rango 0 con accesso (d0) -> ()
pattern, perché per ogni elemento dell'output estraiamo lo stesso elemento
dal tensore di offset per calcolare l'indice dell'input. Possiamo anche assumere
che l'offset del segmento sia sempre compreso tra 0 e
tensor_size - slice_size - 1.
Analizziamo un esempio per capire cosa significano realmente tutti i punti precedenti.
Indicizzazione delle mappe per le operazioni unfused
Elemento per elemento
Per le operazioni elementari, la mappa di indicizzazione è un'identità.
p0 = f32[10, 20] parameter(0)
p1 = f32[10, 20] parameter(1)
add = f32[10, 20] add(p0, p1)
L'output per inserire le mappe:
- output -> input_i:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Le mappe di input e output
- input_i -> :
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
Annuncio
La trasmissione significa che alcune dimensioni verranno rimosse quando mappiamo l'output all'input e aggiunte quando mappiamo l'input all'output.
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
L'output per inserire la mappa:
(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]
La mappa da input a output
(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]
Tieni presente che ora abbiamo s sul lato destro per la mappatura da input a output. Questi sono i simboli che rappresentano gli intervalli di valori. Ad esempio, in questo caso specifico ogni elemento di input con indice d0 viene mappato a un segmento di 10 x 1 x 30 dell'output.
Costante e Iota
Per comodità, non hanno parametri di input, quindi non c'è nulla da l'indicizzazione in tempo reale.
DynamicSlice
DynamicSlice è come una sezione, ma gli offset sono dinamici.
src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}
La mappa di output all'input per src:
(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
hlo: of1 = s32[] parameter(1)
(d0, d1, d2) -> ()
s1 in [0, 0]
hlo: of2 = s32[] parameter(2)
(d0, d1, d2) -> ()
s2 in [0, 226]
hlo: of3 = s32[] parameter(3)
(d0, d1, d2) -> ()
Tieni presente che ora abbiamo s sul lato destro per la mappatura da input a output.
Questi sono i simboli che rappresentano i valori di runtime. Ad esempio, in questo
caso particolare per ogni elemento dell'output con indici d0, d1, d2 che
accedi agli offset della sezione of1, of2 e of3 per calcolare l'indice dell'input.
Gli intervalli per le variabili di runtime vengono derivati supponendo che l'intera
la sezione rimane entro i limiti.
La mappa di output per l'input per of1, of2 e of3:
(d0, d1, d2) -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
DynamicUpdateSlice
src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)
La mappa di output per input per src è banale. Può essere reso più preciso
restringendo il dominio agli indici non aggiornati, ma al momento indicizzando le mappe
non supportano i vincoli di disuguaglianza.
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]
La mappa di output all'input per upd:
(d0, d1)[s0, s1] -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
hlo: of1 = s32[] parameter(2)
(d0, d1) -> ()
s1 in [0, 20]
hlo: of2 = s32[] parameter(3)
(d0, d1) -> ()
Tieni presente che ora abbiamo s sul lato destro per il mapping da input a output.
Questi sono i simboli che rappresentano i valori di runtime. Ad esempio, in questo
caso particolare, per ogni elemento dell'output con indici d0, d1 accediamo
alle compensazioni delle sezioni of1 e of2 per calcolare l'indice dell'input. Gli intervalli
per le variabili di runtime vengono ricavati assumendo che l'intero segmento rimanga nei
limiti.
L'output per inserire la mappa per of1 e of2:
(d0, d1) -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]
Riunisci
È supportata solo la raccolta semplificata. Vedi [gather_simplifier].(https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h).
operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
offset_dims={1,2,3},
collapsed_slice_dims={},
start_index_map={0,1},
index_vector_dim=1,
slice_sizes={7,8,4}
L'output per inserire la mappa per operand:
(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 1)
Tieni presente che ora abbiamo s sul lato destro per il mapping da input a output.
Si tratta dei simboli che rappresentano i valori di runtime. Ad esempio, in questo
caso particolare per ogni elemento dell'output con indici d0, d1, d2, d3 che
estrarre elementi (d0, 0) e (d0, 1) dal tensore indices.
La mappa di output all'input per indices:
(d0, d1, d2, d3)[s0] -> (d0, s0)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 1]
La variabile di intervallo s0 mostra che abbiamo bisogno dell'intera riga (d0, *) della
tensore indices per calcolare un elemento dell'output.
Trasposta
La mappa di indicizzazione per la trasposizione è una permutazione delle dimensioni di input/output.
p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}
L'output per inserire la mappa:
(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]
La mappa di input/output:
(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]
Retro
La mappa di indicizzazione per l'inversione modifica le dimensioni ripristinate in upper_bound(d_i) -
d_i:
p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}
La mappa di output all'input:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
La mappa da input a output:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
(Variadica)Riduci
La riduzione variadica ha diversi input e diversi inits, la mappa dall'output all'input aggiunge le dimensioni ridotte. In un certo senso, si comporta come un annuncio opposto.
p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
dimensions={0}, to_apply=max
L'output per inserire le mappe:
- output -> input_j:
(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]
- output -> init_j:
(d0) -> ()
domain:
d0 in [0, 9]
L'input per le mappe di output:
- input_i -> output_j:
(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]
- init_i -> output_j:
()[s0] -> (s0)
domain:
s0 in [0, 9]
per i, j = 0, ... INPUT_COUNT.
Sezione
L'indice dall'output all'input per la frazione genera una mappa di indicizzazione con stride che è valida per ogni elemento dell'output. La mappatura dall'input all'output limitato a un intervallo striato degli elementi nell'input.
p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
slice={[5:10:1], [3:20:7], [0:50:2]}
La mappa di output all'input:
(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]
La mappa di input/output:
(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]
Rimodellare
Le rimodellamenti sono disponibili in diversi gusti.
Comprimi forma
Questa è una "linearizzazione" rimodellati da ND a 1D.
p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)
L'output per inserire la mappa:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
La mappa di input/output:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
Espandi forma
Questa è un'operazione "collassamento forma" inversa, che trasforma un input 1D in output N-D.
p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)
L'output per inserire la mappa:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
La mappa da input a output:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
Rimodellamento generico
Si tratta delle operazioni di rimodellamento che non possono essere rappresentate come una singola espansione comprimi forma. Possono essere rappresentati solo come una composizione di 2 o più espandi o comprimi forme.
Esempio 1: linearizzazione-delinearizzazione.
p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)
Questa nuova forma può essere rappresentata come una composizione di una forma compressa da tensor<4x8xf32> a tensor<32xf32> e poi di un'espansione della forma a tensor<2x4x4xf32>.
La mappa di output all'input:
(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]
La mappa da input a output:
(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
Esempio 2: sottoforme espanse e compresse
p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)
Questa trasformazione può essere rappresentata come una composizione di due trasformazioni. La prima comprimi le dimensioni più esterne tensor<4x8x12xf32> in tensor<32x12xf32> e la seconda espande la dimensione più interna tensor<32x12xf32> in tensor<32x3x4xf32>.
L'output per inserire la mappa:
(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]
La mappa da input a output:
(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]
Bitcast
Un'operazione di trasmissione di bit può essere rappresentata come una sequenza di trasposizione-rimodellamento-trasposizione. Pertanto, le relative mappe di indicizzazione sono solo una composizione di mappe di indicizzazione per questo sequenza.
Concatena
La mappatura da output a input per concat è definita per tutti gli input, ma con domini non sovrapposti, ovvero verrà utilizzato un solo input alla volta.
p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}
L'output alle mappe degli input:
- output -> input 1:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- output -> input 2:
(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]
- output -> input 3:
(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]
Gli input per le mappe di output:
- input 1 -> :
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- input 2 -> :
(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]
- input 3 -> output:
(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]
Punto
L'indicizzazione delle mappe per punto è molto simile a quelle per ridurre.
p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
lhs_batch_dims={0}, rhs_batch_dims={0},
lhs_contracting_dims={2}, rhs_contracting_dims={1}
Le mappe di output agli input:
- output -> input_1:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
- output -> input_2:
(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
Gli input per le mappe di output:
- input_1 -> output:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]
- input_2 -> output:
(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]
Pad
L'indicizzazione di PadOp è l'inverso dell'indicizzazione di SliceOp.
p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0
La configurazione della spaziatura interna 1_4_1x4_8_0 indica lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1.
L'output per inserire le mappe:
- output -> input:
(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]
- output -> init:
(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]
ReduceWindow
ReduceWindow in XLA esegue anche il riempimento. Di conseguenza, le mappe di indicizzazione possono essere calcolata come una composizione dell'indicizzazione ReduceWindow che non esegue alcuna spaziatura interna e l'indicizzazione di PadOp.
c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
window={size=1x512 pad=0_0x0_0}, to_apply=max
Le mappe di output per input:
- output -> input:
(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]
- output -> init:
(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]
Indicizzazione di Maps per Fusion
La mappa di indicizzazione per l'operazione di fusione è una composizione di mappe di indicizzazione per ogni operazione nel cluster. Può capitare che alcuni input vengano letti più volte con diversi schemi di accesso.
Un input, più mappe di indicizzazione
Ecco un esempio per p0 + transpose(p0).
f {
p0 = f32[1000, 1000] parameter(0)
transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}
Le mappe di indicizzazione da output a input per p0 saranno (d0, d1) -> (d0, d1) e
(d0, d1) -> (d1, d0). Ciò significa che per calcolare un elemento
dell'output potremmo dover leggere il parametro di input due volte.
Mappa di indicizzazione deduplicata in input
A volte le mappe di indicizzazione sono effettivamente le stesse, anche se non immediatamente evidente.
f {
p0 = f32[20, 10, 50] parameter(0)
lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}
In questo caso, la mappa di indicizzazione da output a input per p0 è semplicemente
(d0, d1, d2) -> (d2, d0, d1).
Softmax
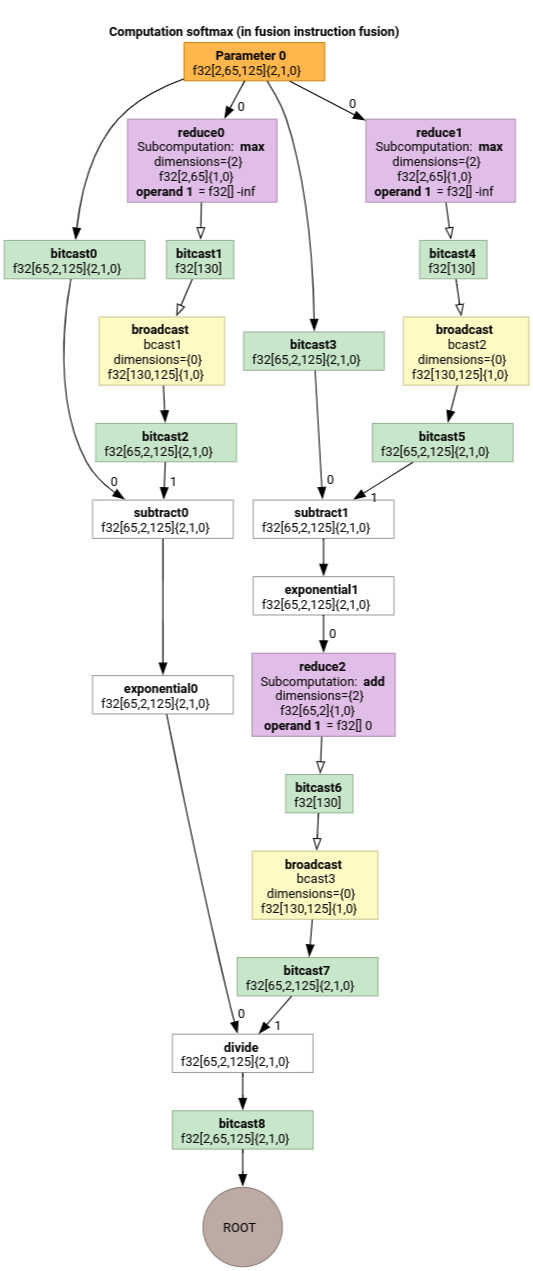
Le mappe di indicizzazione da output a input per parameter 0 per softmax:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]
e
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
dove s0 si riferisce alla dimensione più interna dell'input.
Semplificatore della mappa di indicizzazione
Lo semplificatore predefinito per mlir::AffineMap a monte non può fare alcuna ipotesi sugli intervalli di dimensioni/simboli. Pertanto, non può
simplificare in modo efficiente le espressioni con mod e div.
Possiamo sfruttare la conoscenza dei limiti inferiore e superiore del sottoespressioni nelle mappe affine per semplificarle ulteriormente.
Lo semplificatore può riscrivere le seguenti espressioni.
(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16)per d in[0, 6] x [0, 14]diventa(d0, d1) -> (d0, d1)(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10)perdi in [0, 9]diventa(d0, d1, d2) -> (d0, d1, d2).(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8)perd_i in [0, 9]diventa(d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8).(d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9)per d in[0, 9] x [0, 10]diventa(d0, d1) -> (d0).
Lo semplificatore della mappa di indicizzazione ci consente di capire che alcune delle ristrutturazioni concatenate in HLO si annullano a vicenda.
p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)
Dopo la composizione delle mappe di indicizzazione e la loro semplificazione,
(d0, d1, d2) -> (d0, d1, d2).
La semplificazione delle mappe di indicizzazione semplifica anche i vincoli.
- I vincoli di tipo
lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_boundvengono riscritti comeupdated_lower_bound <= affine_expr <= updated_upped_bound. - I vincoli che sono sempre soddisfatti, ad esempio
d0 + s0 in [0, 20]perd0 in [0, 5]es0 in [1, 3], vengono eliminati. - Le espressioni affine nei vincoli sono ottimizzate come affine di indicizzazione mappa qui sopra.
Per altri esempi, consulta indexing_map_test.cc.

