يصف هذا المستند تحليل الفهرسة في تعليمات HLO، والذي يتيح لك برمجيًا احتساب خرائط الفهرسة لعمليات HLO. خريطة الفهرسة هي دالة تربط بين فهرسَي مصفوفة تينسور معيّنَين، مثل فهرسَي ناتج تعليمات HLO وفهرسَي إدخالات تعليمات HLO أو العكس.
مثال
إذا كنت تريد بث المحتوى من tensor<20xf32> إلى tensor<10x20x30xf32>
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
خريطة الفهرسة من الإخراج إلى الإدخال هي (i, j, k) -> (j) لـ i in
[0, 10] وj in [0, 20] وk in [0, 30].
الحافز
تستخدم وحدة XLA GPU عدة حلول مخصّصة لتحديد عمليات الدمج واستخدام الم Operand وخطط التجميع (مزيد من التفاصيل أدناه). إنّ الهدف من تحليل الترتيب هو توفير مكوّن قابل لإعادة الاستخدام لحالات الاستخدام هذه. تحليل الفهرسة على البنية الأساسية لتطبيق Affine Map من MLIR، كما تضيف دلالات HLO.
الدمج
يصبح التفكير بشأن انسجام الذاكرة ممكنًا للحالات غير التافهة، عندما نعرف عناصر/شرائح المدخلات التي تتم قراءتها لحساب أحد عناصر الإخراج.
استخدام مرتبط
يشير استخدام الم Operand في XLA إلى مقدار استخدام كل إدخال من التعليمات بافتراض استخدام إخراجه بالكامل. في الوقت الحالي، لا يتم أيضًا حساب معدل الاستخدام لحالة عامة. يتيح تحليل الفهرسة احتساب الاستخدام بدقة.
التجزئة إلى أقسام عمودية:
المربّع أو الشريحة عبارة عن مجموعة فرعية مستطيلة الشكل من معامل موتّر مقسّمة حسب الإزاحة، الأحجام والخطوات. إنّ نشر التذاكر هو طريقة لاحتساب مَعلمات التذاكر الخاصة بالملف الشخصي لـ "المُنشئ" أو "المستهلك" للعملية باستخدام مَعلمات التذاكر للعملية نفسها. هناك مكتبة تُجري ذلك لعمليتي softmax وdot. يمكن جعل عملية نشر المربّعات أكثر عمومية و متانة إذا تم التعبير عنها من خلال خرائط الفهرسة.
الدالة والمجال
خريطة الفهرسة هي دالة f(x) = f(d، r، rt)
يعيّن فهرسًا متعدّد d في تنسور A إلى عناصر/نطاقات
متنسور B. تشير المَعلمة r إلى نطاقات فهارس
السمات المتوفّرة في مصفوفة B، ولكن ليس في مصفوفة A. تشير
المَعلمة rt إلى قيم وقت التشغيل، مثل فهارس عملية التجميع.
على سبيل المثال، إذا كان لدينا تخفيض من tensor<2x4x8x16xf32> إلى
tensor<4x8xf32>، تكون خريطة الفهرسة من المُخرج الثنائي الأبعاد إلى الإدخال رباعي الأبعاد
(d0, d1) -> (r0, d0, d1, r1)، حيث d_i هي متغيرات البُعد التي
مع مؤشرات مترابط الناتج. تُشفِّر متغيّرات النطاق r_j
قيمًا متعدّدة، أي أنّه لاحتساب عنصر (d0, d1) من الإخراج، نحتاج إلى
عناصر (r0, d0, d1, r1) من الإدخال، حيث r0 in [0, 1] و
r1 in [0, 15].
ويمكن إنشاء هذا التعيين من سمات تعليمات HLO أو يمكن إنشاء تعيينات للتعليمات غير المدمجة للحصول على فهرسة للدمج. كما أن التعيين له مجال، يحدد عناصر مترابطة التعيين موجود.
f(x) بحيث
lb <= g(x) <= ub
وبما أنّنا نريد تقليل عمليات إعادة الحساب، نحتاج إلى مكتبة للعمليات الحسابية الرمزية. يعتمد XLA بالفعل على MLIR، لذلك نستخدم mlir::AffineMap بدلاً من كتابة مكتبة حسابية رمزية حتى الآن.
الشكل المعتاد لـ AffineMap
(d0)[s0, s1] -> (s0 + 5, d0 * 2, s1 * 3 + 50)
يحتوي AffineMap على نوعَين من المَعلمات: السمات والرموز. تتوافق
السمات مع متغيّرات السمات d، وتتوافق الرموز مع
متغيّرات النطاق r ومتغيّرات RT rt. لا يحتوي AffineMap على أي
بيانات وصفية عن نطاقات السمات، لذا علينا تقديم هذه البيانات
بأنفسنا.
struct Interval {
int64_t lower;
int64_t upper;
};
// Dimension variable represents a dimension of a tensor or a GPU grid.
struct DimVar {
Interval bounds;
};
// RangeVar variable represents a range of values, e.g. to compute a single
// element of the reduction's result we need a range of values from the input
// tensor.
struct RangeVar {
Interval range;
};
// RTVar represents a runtime value, e.g. a dynamic offset in
// HLO dynamic-update-slice op.
struct RTVar {
Interval feasible_values;
const HloInstruction* hlo;
// This is a map from the iteration space of the corresponding indexing map to
// the iteration space of `hlo`. It shows what element of `hlo` we need to
// extract to get the runtime value for the RTVar.
mlir::AffineMap map;
};
class IndexingMap {
mlir::AffineMap affine_map_;
std::vector<DimVar> dim_vars_;
std::vector<RangeVar> range_vars_;
std::vector<RTVar> rt_vars_;
llvm::DenseMap<mlir::AffineExpr, Interval> constraints_;
};
dim_vars_ ترميز قيود المربّع الشاملة لسمات
السمة d لخريطة الفهرسة، والتي تتطابق عادةً مع
شكل مصفوفة الإخراج لعمليات مثل النقل والاختزال والعمليات على مستوى العنصر والنقطة، ولكن هناك
بعض الاستثناءات مثل
HloConcatenateInstruction.
تعمل range_vars_ على ترميز القيم المحتملة التي يمكن أن تتخذها المَعلمات r.
تخزِّن rt_vars_ تعليمات hlo المرتبطة مع أنماط الوصول
والقيم الممكنة في وقت التشغيل. على سبيل المثال، تكون الإزاحة ديناميكية
لمدة HloDynamicSliceInstruction يوم واحد سيكون للحقل RTVar المقابل
HloInstruction* الذي ينتج عنه متوتر ترتيب 0 مع إمكانية الوصول (d0) -> ()
نمط، لأنه لكل عنصر من عناصر المخرجات نستخرج نفس العنصر
من مقياس الإزاحة لحساب فهرس المُدخل. يمكننا أيضًا افتراض
أنّ القيمة المرجعية للشريحة تقع دائمًا بين 0 و
tensor_size - slice_size - 1.
لندرس كل مثال لفهم معنى كل ما سبق.
فهرسة الخرائط للعمليات غير المدمجة
حسب العنصر
وبالنسبة إلى العمليات الأساسية على الخريطة، تكون خريطة الفهرسة عبارة عن هوية.
p0 = f32[10, 20] parameter(0)
p1 = f32[10, 20] parameter(1)
add = f32[10, 20] add(p0, p1)
تعيين الإخراج إلى إدخال الخرائط:
- ناتج -> input_i:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
الإدخال في خرائط الإخراج
- إدخال_i -> الناتج:
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
الإعلان على جميع الأجهزة
يعني البث أنه ستتم إزالة بعض الأبعاد عند ربط المخرجات التي يتم إدخالها وتتم إضافتها عند تعيين الإدخال إلى المُخرج.
p0 = f32[20] parameter(0)
bc0 = f32[10, 20, 30] broadcast(p0), dimensions={1}
خريطة الإدخال إلى الإخراج:
(d0, d1, d2) -> (d1)
domain:
d0 in [0, 9]
d1 in [0, 19]
d2 in [0, 29]
خريطة الإدخال إلى الإخراج
(d0)[s0, s1] -> (s0, d0, s1)
domain:
d0 in [0, 19]
s0 in [0, 9]
s1 in [0, 29]
يُرجى العِلم أنّه لدينا الآن s على الجانب الأيمن لربط
الإدخال بالإخراج. هذه هي الرموز التي تمثل نطاقات القيم. على سبيل المثال، في
هذه الحالة المحدّدة، يتمّ ربط كلّ عنصر من مدخلات الفهرس d0 بقطعة
10x1x30 من الناتج.
الثابت وIota
على نحو ملائم، لا تحتوي هذه المفاتيح على أي معلَمات إدخال، لذا لن يكون هناك أي لحساب الفهرسة من أجله.
DynamicSlice
تشبه DynamicSlice دالة Slice، ولكنّ الفواصل الزمنية تكون ديناميكية.
src = s32[2,2,258] parameter(0)
of1 = s32[] parameter(1)
of2 = s32[] parameter(2)
of3 = s32[] parameter(3)
ds = dynamic-slice(s32[2,2,258] src, s32[] of1, s32[] of2, s32[] of3), dynamic_slice_sizes={1, 2, 32}
خريطة الإدخال إلى الإخراج لـ src:
(d0, d1, d2)[s0, s1, s2] -> (d0 + s0, d1 + s1, d2 + s2)
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
s0 in [0, 1]
hlo: of1 = s32[] parameter(1)
(d0, d1, d2) -> ()
s1 in [0, 0]
hlo: of2 = s32[] parameter(2)
(d0, d1, d2) -> ()
s2 in [0, 226]
hlo: of3 = s32[] parameter(3)
(d0, d1, d2) -> ()
يُرجى العِلم أنّه لدينا الآن s على الجانب الأيمن لربط الإدخال بالإخراج.
وهذه هي الرموز التي تمثل قيم بيئة التشغيل. على سبيل المثال، في هذه
حالة معيّنة لكل عنصر من عناصر المخرجات بالفهارس d0, d1, d2 التي
إزاحة شريحة الوصول of1 وof2 وof3 لاحتساب فهرس الإدخال.
يتم اشتقاق الفواصل الزمنية لمتغيرات بيئة التشغيل من خلال افتراض أن
تبقى الشريحة داخل الحدود.
خريطة الإخراج إلى الإدخال لكل من of1 وof2 وof3:
(d0, d1, d2) -> ()
domain:
d0 in [0, 0]
d1 in [0, 1]
d2 in [0, 31]
DynamicUpdateSlice
src = s32[20,30] parameter(0)
upd = s32[5,10] parameter(1)
of1 = s32[] parameter(2)
of2 = s32[] parameter(3)
dus = s32[20,30] dynamic-update-slice(
s32[20,30] src, s32[5,10] upd, s32[] of1, s32[] of2)
خريطة الإدخال إلى الإخراج لـ src بسيطة. يمكن جعلها أكثر دقة من خلال
حصر النطاق بالفهارس التي لم يتم تحديثها، ولكن تتم الآن فهرسة الخرائط
ولا تدعم قيود المساواة.
(d0, d1) -> (d0, d1)
domain:
d0 in [0, 19]
d1 in [0, 29]
ناتج إدخال الخريطة لـ upd:
(d0, d1)[s0, s1] -> (d0 - s0, d1 - s1)
domain:
d0 in [0, 19]
d1 in [0, 29]
s0 in [0, 15]
hlo: of1 = s32[] parameter(2)
(d0, d1) -> ()
s1 in [0, 20]
hlo: of2 = s32[] parameter(3)
(d0, d1) -> ()
يُرجى العِلم أنّه لدينا الآن s على الجانب الأيمن لربط الإدخال بالإخراج.
هذه هي الرموز التي تمثّل قيم وقت التشغيل. على سبيل المثال، في
هذه الحالة تحديدًا، لكل عنصر من عناصر الإخراج التي تحتوي على الفهرس d0, d1، نحصل على
إزاحات الشريحة of1 وof2 لاحتساب فهرس الإدخال. يتم اشتقاق الفواصل الزمنية
لمتغيّرات وقت التشغيل بافتراض أنّ الشريحة بأكملها تبقى ضمن
الحدود.
خريطة الإخراج إلى الإدخال لكلّ من of1 وof2:
(d0, d1) -> ()
domain:
d0 in [0, 19]
d1 in [0, 29]
Gather
لا تتوفّر سوى طريقة الالتقاط المبسّطة. يمكنك الاطّلاع على [gather_simplifier].(https://github.com/openxla/xla/blob/main/xla/hlo/transforms/simplifiers/gather_simplifier.h).
operand = f32[33,76,70] parameter(0)
indices = s32[1806,2] parameter(1)
gather = f32[1806,7,8,4] gather(operand, indices),
offset_dims={1,2,3},
collapsed_slice_dims={},
start_index_map={0,1},
index_vector_dim=1,
slice_sizes={7,8,4}
خريطة الإدخال إلى الإخراج لـ operand:
(d0, d1, d2, d3)[s0, s1] -> (d1 + s0, d2 + s1, d3)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 26]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 0)
s1 in [0, 68]
hlo: indices = s32[1806,2]{1,0} parameter(1)
(d0, d1, d2, d3) -> (d0, 1)
يُرجى العِلم أنّه لدينا الآن s على الجانب الأيمن لربط الإدخال بالإخراج.
وهذه هي الرموز التي تمثل قيم بيئة التشغيل. على سبيل المثال، في
هذه الحالة الخاصة لكل عنصر من عناصر الإخراج الذي يحتوي على الفهارس d0, d1, d2, d3، تتم
استخراج العنصرَين (d0, 0) و(d0, 1) من مصفوفة indices.
ناتج إدخال الخريطة لـ indices:
(d0, d1, d2, d3)[s0] -> (d0, s0)
domain:
d0 in [0, 1805]
d1 in [0, 6]
d2 in [0, 7]
d3 in [0, 3]
s0 in [0, 1]
يشير متغيّر النطاق s0 إلى أنّنا نحتاج إلى الصف بأكمله (d0, *) من مصفوفة indices لحساب عنصر من الإخراج.
تبديل الموضع
خارطة الفهرسة لعملية النقل هي تبديل لأبعاد الإدخال/الإخراج.
p0 = f32[3, 12288, 6, 128] parameter(0)
transpose = f32[3, 6, 128, 12288] transpose(p0), dimensions={0, 2, 3, 1}
مخرجات إدخال الخريطة:
(d0, d1, d2, d3) -> (d0, d3, d1, d2)
domain:
d0 in [0, 2]
d1 in [0, 5]
d2 in [0, 127]
d3 in [0, 12287]
الإدخال في خريطة الإخراج:
(d0, d1, d2, d3) -> (d0, d2, d3, d1)
domain:
d0 in [0, 2]
d1 in [0, 12287]
d2 in [0, 5]
d3 in [0, 127]
عكس
خريطة الفهرسة للتغييرات العكسية في السمات التي تم إرجاعها إلى upper_bound(d_i) -
d_i:
p0 = f32[1, 17, 9, 9] parameter(0)
reverse = f32[1, 17, 9, 9] reverse(p0), dimensions={1, 2}
خريطة الإدخال إلى الإخراج:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
الإدخال في خريطة الإخراج:
(d0, d1, d2, d3) -> (d0, -d1 + 16, -d2 + 8, d3)
domain:
d0 in [0, 0]
d1 in [0, 16]
d2 in [0, 8]
d3 in [0, 8]
(Variadic) تقليل
تحتوي دوال Variadic على العديد من المدخلات والعديد من الوحدات، فإن الخريطة من الإخراج إلى تضيف الأبعاد المخفّضة. وهو يتصرف كعكس للبث بطريقة ما.
p0 = f32[256,10] parameter(0)
p0_init = f32[] constant(-inf)
p1 = s32[256,10] parameter(1)
p1_init = s32[] constant(0)
reduce = (f32[10], s32[10]) reduce(p0, p1, p0_init, p1_init),
dimensions={0}, to_apply=max
تعيين الإخراج إلى إدخال الخرائط:
- ناتج -> input_j:
(d0)[s0] -> (s0, d0)
domain:
d0 in [0, 9]
s0 in [0, 255]
- ناتج -> init_j:
(d0) -> ()
domain:
d0 in [0, 9]
الإدخال في خرائط الإخراج:
- إدخال_i -> output_j:
(d0, d1) -> (d1)
domain:
d0 in [0, 255]
d1 in [0, 9]
- init_i -> output_j:
()[s0] -> (s0)
domain:
s0 in [0, 9]
بالنسبة إلى i، j = 0، ... INPUT_COUNT.
الشريحة
تؤدي الفهرسة من الناتج إلى الإدخال للشريحة إلى خريطة فهرسة متسلسلة صالحة لكل عنصر من الناتج. يقتصر الربط من الإدخال إلى الإخراج على نطاق متسلسل للعناصر في الإدخال.
p0 = f32[10, 20, 50] parameter(0)
slice = f32[5, 3, 25] slice(f32[10, 20, 50] p0),
slice={[5:10:1], [3:20:7], [0:50:2]}
الإخراج لإدخال الخريطة:
(d0, d1, d2) -> (d0 + 5, d1 * 7 + 3, d2 * 2)
domain:
d0 in [0, 4]
d1 in [0, 2]
d2 in [0, 24]
الإدخال في خريطة الإخراج:
(d0, d1, d2) -> (d0 - 5, (d1 - 3) floordiv 7, d2 floordiv 2)
domain:
d0 in [5, 9]
d1 in [3, 17]
d2 in [0, 48]
(d1 - 3) mod 7 in [0, 0]
d2 mod 2 in [0, 0]
إعادة التشكيل
تتوفر أشكال مختلفة من عمليات إعادة التشكيل.
تصغير الشكل
هذا هو "المساواة بين نقاط الاتصال" لإعادة الشكل من N-D إلى 1D.
p0 = f32[4,8] parameter(0)
reshape = f32[32] reshape(p0)
الإخراج لإدخال الخريطة:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
خريطة الإدخال إلى الإخراج:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
توسيع الشكل
هذه عملية عكسية من "تصغير الشكل"، وهي تعيد تشكيل إدخال أحادي الأبعاد إلى ناتج ذي أبعاد متعددة.
p0 = f32[32] parameter(0)
reshape = f32[4, 8] reshape(p0)
خريطة الإدخال إلى الإخراج:
(d0, d1) -> (d0 * 8 + d1)
domain:
d0 in [0, 3]
d1 in [0, 7]
الإدخال في خريطة الإخراج:
(d0) -> (d0 floordiv 8, d0 mod 8)
domain:
d0 in [0, 31]
إعادة تشكيل عامة
هذه هي عمليات إعادة التشكيل التي لا يمكن تمثيلها كشكل واحد للتوسيع أو التصغير. ولا يمكن تمثيلها سوى كمقطوعة من اثنتين أو أكثر. لتوسيع الأشكال أو تصغيرها.
المثال 1: التحويل إلى خطيّة والعكس
p0 = f32[4,8] parameter(0)
reshape = f32[2, 4, 4] reshape(p0)
يمكن تمثيل هذا الشكل الجديد كتركيب لشكل التصغير
من tensor<4x8xf32> إلى tensor<32xf32> ثم توسيع الشكل إلى
tensor<2x4x4xf32>
الإخراج لإدخال الخريطة:
(d0, d1, d2) -> (d0 * 2 + d1 floordiv 2, d2 + (d1 mod 2) * 4)
domain:
d0 in [0, 1]
d1 in [0, 3]
d2 in [0, 3]
الإدخال في خريطة الإخراج:
(d0, d1) -> (d0 floordiv 2, d1 floordiv 4 + (d0 mod 2) * 2, d1 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
المثال 2: الأشكال الفرعية الموسّعة والمصغرة
p0 = f32[4, 8, 12] parameter(0)
reshape = f32[32, 3, 4] reshape(p0)
يمكن تمثيل عملية إعادة التشكيل هذه على أنّها تركيب من عمليتَي إعادة تشكيل. الخيار الأول
تصغير الأبعاد الخارجية من tensor<4x8x12xf32> إلى tensor<32x12xf32>
والثاني يوسّع البعد الأعمق tensor<32x12xf32> إلى
tensor<32x3x4xf32>
خريطة الإدخال إلى الإخراج:
(d0, d1, d2) -> (d0 floordiv 8, d0 mod 8, d1 * 4 + d2)
domain:
d0 in [0, 31]
d1 in [0, 2]
d2 in [0, 3]
خريطة الإدخال إلى الإخراج:
(d0, d1, d2) -> (d0 * 8 + d1, d2 floordiv 4, d2 mod 4)
domain:
d0 in [0, 3]
d1 in [0, 7]
d2 in [0, 11]
Bitcast
يمكن تمثيل عملية تحويل الأرقام إلى ثنائية كأحد يلي: تسلسل من عمليات النقل-إعادة التشكيل-النقل. وبالتالي، فإن خرائط الفهرسة هي مجرد تركيبة من خرائط الفهرسة التسلسل.
التسلسل
يتمّ تحديد تعيين الإخراج إلى الإدخال لدالة concat لجميع الإدخالات، ولكن مع نطاقات غير متداخلة، أي سيتمّ استخدام إدخال واحد فقط في المرّة الواحدة.
p0 = f32[2, 5, 7] parameter(0)
p1 = f32[2, 11, 7] parameter(1)
p2 = f32[2, 17, 7] parameter(2)
ROOT concat = f32[2, 33, 7] concatenate(f32[2, 5, 7] p0, f32[2, 11, 7] p1, f32[2, 17, 7] p2), dimensions={1}
خرائط الإدخال:
- ناتج -> الإدخال 1:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- ناتج -> الإدخال 2:
(d0, d1, d2) -> (d0, d1 - 5, d2)
domain:
d0 in [0, 1]
d1 in [5, 15]
d2 in [0, 6]
- ناتج -> الإدخال 3:
(d0, d1, d2) -> (d0, d1 - 16, d2)
domain:
d0 in [0, 1]
d1 in [16, 32]
d2 in [0, 6]
مدخلات خرائط الإخراج:
- الإدخال 1 -> الإخراج:
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 4]
d2 in [0, 6]
- الإدخال 2 -> الإخراج:
(d0, d1, d2) -> (d0, d1 + 5, d2)
domain:
d0 in [0, 1]
d1 in [0, 10]
d2 in [0, 6]
- الإدخال 3 -> الإخراج:
(d0, d1, d2) -> (d0, d1 + 16, d2)
domain:
d0 in [0, 1]
d1 in [0, 16]
d2 in [0, 6]
النقطة
تتشابه خرائط الفهرسة لدالّة dot إلى حد كبير مع خرائط دالة reduce.
p0 = f32[4, 128, 256] parameter(0)
p1 = f32[4, 256, 64] parameter(1)
dot = f32[4, 128, 64] dot(p0, p1),
lhs_batch_dims={0}, rhs_batch_dims={0},
lhs_contracting_dims={2}, rhs_contracting_dims={1}
تُعرِض خريطة النتائج إلى المدخلات ما يلي:
- ناتج -> input_1:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
- ناتج -> input_2:
(d0, d1, d2)[s0] -> (d0, s0, d2)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 63]
s0 in [0, 255]
مدخلات خرائط النتائج:
- enter_1 -> الناتج:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 3]
d1 in [0, 127]
d2 in [0, 255]
s0 in [0, 63]
- input_2 -> output:
(d0, d1, d2)[s0] -> (d0, s0, d1)
domain:
d0 in [0, 3]
d1 in [0, 255]
d2 in [0, 63]
s0 in [0, 127]
اللوحة
فهرسة PadOp هي عكس فهرسة SliceOp.
p0 = f32[4, 4] parameter(0)
p1 = f32[] parameter(1)
pad = f32[12, 16] pad(p0, p1), padding=1_4_1x4_8_0
تشير إعدادات المساحة المتروكة 1_4_1x4_8_0 إلى lowPad_highPad_interiorPad_dim_0 x lowPad_highPad_interiorPad_dim_1.
ناتج إدخال الخرائط:
- الناتج -> الإدخال:
(d0, d1) -> ((d0 - 1) floordiv 2, d1 - 4)
domain:
d0 in [1, 7]
d1 in [4, 7]
(d0 - 1) mod 2 in [0, 0]
- ناتج -> init:
(d0, d1) -> ()
domain:
d0 in [0, 11]
d1 in [0, 15]
ReduceWindow
تُجري دالة ReduceWindow في XLA عملية الحشو أيضًا. لذلك، يمكن حساب خرائط الفهرسة كتركيبة من فهرسة ReduceWindow التي لا تُجري أيّ تعبئة وفهرسة PadOp.
c_inf = f32[] constant(-inf)
p0 = f32[1024, 514] parameter(0)
reduce-window = f32[1024, 3] reduce-window(p0, c_inf),
window={size=1x512 pad=0_0x0_0}, to_apply=max
ناتج إدخال الخرائط:
- الناتج -> الإدخال:
(d0, d1)[s0] -> (d0, d1 + s0)
domain:
d0 in [0, 1023]
d1 in [0, 2]
s0 in [0, 511]
- ناتج -> init:
(d0, d1) -> ()
domain:
d0 in [0, 1023]
d1 in [0, 2]
فهرسة الخرائط في Fusion
خريطة الفهرسة للتشغيل الشامل هي تركيبة من خرائط الفهرسة لكل عملية في تجميع. قد تتم قراءة بعض الإدخالات عدة مرات بأنماط وصول مختلفة.
إدخال واحد والعديد من خرائط الفهرسة
في ما يلي مثال على p0 + transpose(p0).
f {
p0 = f32[1000, 1000] parameter(0)
transpose_p0 = f32[1000, 1000]{0, 1} transpose(p0), dimensions={1, 0}
ROOT a0 = f32[1000, 1000] add(p0, transpose_p0)
}
ستكون خرائط الفهرسة من الناتج إلى المدخل لـ p0 هي (d0, d1) -> (d0, d1) و
(d0, d1) -> (d1, d0). وهذا يعني أنه لحساب عنصر واحد
من الناتج قد نحتاج إلى قراءة معلمة الإدخال مرتين.
إدخال واحد، خريطة الفهرسة التي تمّت إزالة تكرارها
هناك حالات تكون فيها خرائط الفهرسة متطابقة في الواقع، على الرغم من غير واضح على الفور.
f {
p0 = f32[20, 10, 50] parameter(0)
lhs_transpose_1 = f32[10, 20, 50] transpose(p0), dimensions={1, 0, 2}
lhs_e = f32[10, 20, 50] exponential(lhs_transpose_1)
lhs_transpose_2 = f32[10, 50, 20] transpose(lhs_e), dimensions={0, 2, 1}
rhs_transpose_1 = f32[50, 10, 20] transpose(p0), dimensions={2, 1, 0}
rhs_log = f32[50, 10, 20] exponential(rhs_transpose_1)
rhs_transpose_2 = f32[10, 50, 20] transpose(rhs_log), dimensions={1, 0, 2}
ROOT add = f32[10, 50, 20] add(lhs_transpose_2, rhs_transpose_2)
}
وفي هذه الحالة، ستكون خريطة فهرسة الإخراج إلى الإدخال في p0
(d0, d1, d2) -> (d2, d0, d1)
Softmax
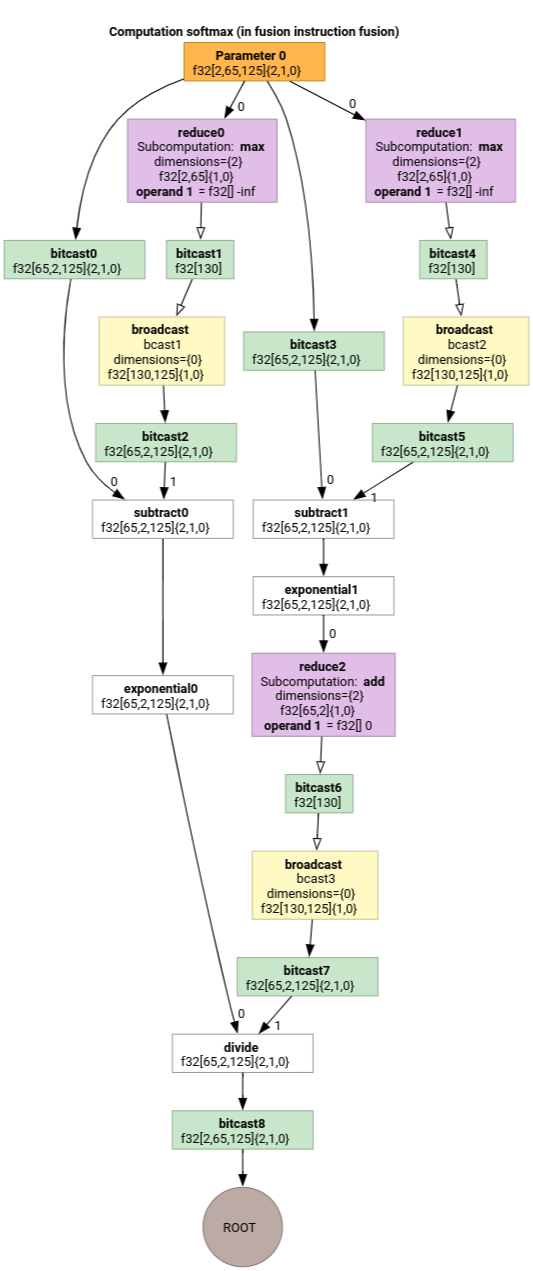
خرائط الفهرسة من أجل الإدخال والإخراج للدالة parameter 0 في softmax:
(d0, d1, d2)[s0] -> (d0, d1, s0)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
s0 in [0, 124]
و
(d0, d1, d2) -> (d0, d1, d2)
domain:
d0 in [0, 1]
d1 in [0, 64]
d2 in [0, 124]
حيث يشير s0 إلى السمة الداخلية للعنصر المُدخل.
أداة تبسيط خرائط الفهرسة
لا يمكن أن يجعل المُبسِّط التلقائي لسهم "mlir::AffineMap" الرئيسي أو المبسّط أي
افتراضات حول نطاقات الأبعاد/الرموز. ومن ثم، لا يمكن
تبسيط التعبيرات باستخدام mod وdivبكفاءة.
يمكننا الاستفادة من المعرفة حول الحدين الأدنى والعلوي التعبيرات الفرعية في خرائط التقارب لتبسيطها بشكل أكبر.
يمكن للمُبسط إعادة كتابة التعبيرات التالية.
(d0, d1) -> (d0 + d1 floordiv 16, d1 mod 16)لمدة d في[0, 6] x [0, 14]يصبح(d0, d1) -> (d0, d1)- يصبح
(d0, d1, d2) -> ((100d0 + 10d1 + d2) floorDiv 100, ((100d0 + 10d1 + d2) mod 100) floordiv 10, d2 mod 10)لحسابdi in [0, 9]هو(d0, d1, d2) -> (d0, d1, d2). - يصبح
(d0, d1, d2) -> ((16d0 + 4d1 + d2) floordiv 8, (16d0 + 4d1 + d2) mod 8)للنطاقd_i in [0, 9](d0, d1, d2) -> (2d0 + (4d1 + d2) floordiv 8,(4d1 + d2) mod 8). (d0, d1) -> (-(-11d0 - d1 + 109) floordiv 11 + 9)لمدة ي في[0, 9] x [0, 10]تصبح(d0, d1) -> (d0).
يتيح لنا مبسِّط خريطة الفهرسة فهم أنّ بعض عمليات إعادة التشكيل المقترنة في HLO تلغي بعضها.
p0 = f32[10, 10, 10] parameter(0)
reshape1 = f32[50, 20] reshape(p0)
reshape2 = f32[10, 10, 10] reshape(reshape1)
بعد إنشاء خرائط الفهرسة وتبسيطها، سنحصل على
(d0, d1, d2) -> (d0, d1, d2).
ويؤدي تبسيط خريطة الفهرسة إلى تبسيط القيود أيضًا.
- قيود النوع
lower_bound <= affine_expr (floordiv, +, -, *) constant <= upper_boundهي تمت إعادة كتابته باسمupdated_lower_bound <= affine_expr <= updated_upped_bound. - القيود التي يتم استيفاؤها دائمًا، على سبيل المثال
d0 + s0 in [0, 20]سيتم استبعادd0 in [0, 5]وs0 in [1, 3]. - يتم تحسين التعبيرات القريبة في القيود باعتبارها تقارب الفهرسة الخريطة أعلاه.
لمزيد من الأمثلة، راجِع indexing_map_test.cc.

