Vous trouverez ci-dessous la sémantique des opérations définies dans l'interface XlaBuilder. En règle générale, ces opérations sont mappées de manière individuelle aux opérations définies dans l'interface RPC dans xla_data.proto.
Remarque sur la nomenclature: le type de données généralisé que XLA traite est un tableau à N dimensions contenant des éléments d'un type uniforme (tel qu'un nombre à virgule flottante 32 bits). Dans l'ensemble de la documentation, le terme tableau est utilisé pour désigner un tableau à dimension arbitraire. Pour plus de commodité, les cas particuliers ont des noms plus spécifiques et plus familiers. Par exemple, un vecteur est un tableau à une dimension, et une matrice est un tableau à deux dimensions.
AfterAll
Consultez également XlaBuilder::AfterAll.
AfterAll prend un nombre variable de jetons et produit un seul jeton. Les jetons sont des types primitifs qui peuvent être enfilés entre des opérations à effet secondaire pour appliquer l'ordre. AfterAll peut être utilisé comme jointure de jetons pour ordonner une opération après une opération d'ensemble.
AfterAll(operands)
| Arguments | Type | Sémantique |
|---|---|---|
operands |
XlaOp |
nombre variable de jetons |
AllGather
Consultez également XlaBuilder::AllGather.
Effectue la concaténation entre les réplicas.
AllGather(operand, all_gather_dim, shard_count, replica_group_ids,
channel_id)
| Arguments | Type | Sémantique |
|---|---|---|
operand
|
XlaOp
|
Tableau à concaténer entre les réplicas |
all_gather_dim |
int64 |
Dimension de concaténation |
replica_groups
|
vecteur de vecteurs de
int64 |
Groupes entre lesquels la concaténation est effectuée |
channel_id
|
int64 facultatif
|
ID de canal facultatif pour la communication intermodule |
replica_groupsest une liste de groupes de réplicas entre lesquels la concaténation est effectuée (l'ID de réplica pour le réplica actuel peut être récupéré à l'aide deReplicaId). L'ordre des réplicas dans chaque groupe détermine l'ordre dans lequel leurs entrées se trouvent dans le résultat.replica_groupsdoit être vide (dans ce cas, tous les réplicas appartiennent à un seul groupe, ordonnés de0àN - 1) ou contenir le même nombre d'éléments que le nombre de réplicas. Par exemple,replica_groups = {0, 2}, {1, 3}effectue une concaténation entre les réplicas0et2, et1et3.shard_countcorrespond à la taille de chaque groupe de réplication. Nous en avons besoin lorsquereplica_groupsest vide.channel_idest utilisé pour la communication entre les modules: seules les opérationsall-gatheravec le mêmechannel_idpeuvent communiquer entre elles.
La forme de sortie est la forme d'entrée, avec all_gather_dim multiplié par shard_count. Par exemple, s'il existe deux réplicas et que l'opérande a les valeurs [1.0, 2.5] et [3.0, 5.25] respectivement sur les deux réplicas, la valeur de sortie de cette opération où all_gather_dim est 0 sera [1.0, 2.5, 3.0,
5.25] sur les deux réplicas.
AllReduce
Consultez également XlaBuilder::AllReduce.
Effectue un calcul personnalisé sur plusieurs réplicas.
AllReduce(operand, computation, replica_group_ids, channel_id)
| Arguments | Type | Sémantique |
|---|---|---|
operand
|
XlaOp
|
Tableau ou tuple non vide de tableaux à réduire entre les réplicas |
computation |
XlaComputation |
Calcul de la réduction |
replica_groups
|
vecteur de vecteurs de
int64 |
Groupes entre lesquels les réductions sont effectuées |
channel_id
|
facultatif int64
|
ID de canal facultatif pour la communication intermodule |
- Lorsque
operandest un tuple de tableaux, la réduction globale est effectuée sur chaque élément du tuple. replica_groupsest une liste de groupes de réplicas entre lesquels la réduction est effectuée (l'ID de réplica pour le réplica actuel peut être récupéré à l'aide deReplicaId).replica_groupsdoit être vide (dans ce cas, tous les réplicas appartiennent à un seul groupe) ou contenir le même nombre d'éléments que le nombre de réplicas. Par exemple,replica_groups = {0, 2}, {1, 3}effectue une réduction entre les réplicas0et2, et1et3.channel_idest utilisé pour la communication entre les modules: seules les opérationsall-reduceavec le mêmechannel_idpeuvent communiquer entre elles.
La forme de sortie est identique à celle de l'entrée. Par exemple, s'il existe deux réplicas et que l'opérande a la valeur [1.0, 2.5] et [3.0, 5.25] respectivement sur les deux réplicas, la valeur de sortie de cette opération et du calcul de la somme sera [4.0, 7.75] sur les deux réplicas. Si l'entrée est un tuple, la sortie est également un tuple.
Le calcul du résultat de AllReduce nécessite une entrée de chaque réplica, donc si un réplica exécute un nœud AllReduce plus de fois qu'un autre, l'ancien réplica attendra indéfiniment. Étant donné que les réplicas exécutent tous le même programme, il n'existe pas beaucoup de façons de procéder, mais cela est possible lorsque la condition d'une boucle while dépend des données de l'influx et que les données infusées entraînent l'itération de la boucle while plus de fois sur un réplica que sur un autre.
AllToAll
Consultez également XlaBuilder::AllToAll.
AllToAll est une opération collective qui envoie des données de tous les cœurs à tous les cœurs. Il comporte deux phases:
- Phase de dispersion. Sur chaque cœur, l'opérande est divisé en un nombre de blocs
split_countle long desplit_dimensions, et les blocs sont dispersés sur tous les cœurs (par exemple, le bloc i est envoyé au cœur i). - Phase de collecte. Chaque cœur concatène les blocs reçus le long de
concat_dimension.
Les cœurs participants peuvent être configurés comme suit:
replica_groups: chaque ReplicaGroup contient une liste d'ID de réplication participant au calcul (l'ID de réplication du réplica actuel peut être récupéré à l'aide deReplicaId). AllToAll sera appliqué dans les sous-groupes dans l'ordre spécifié. Par exemple,replica_groups = { {1,2,3}, {4,5,0} }signifie qu'une opération AllToAll sera appliquée dans les réplicas{1, 2, 3}et lors de la phase de collecte. Les blocs reçus seront ensuite concaténés dans l'ordre 1, 2, 3. Ensuite, une autre opération AllToAll est appliquée dans les réplicas 4, 5 et 0, et l'ordre de concaténation est également 4, 5 et 0. Sireplica_groupsest vide, tous les réplicas appartiennent à un seul groupe, dans l'ordre de concaténation de leur apparition.
Conditions préalables :
- La taille de dimension de l'opérande sur
split_dimensionest divisible parsplit_count. - La forme de l'opérande n'est pas un tuple.
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau d'entrée à n dimensions |
split_dimension
|
int64
|
Valeur de l'intervalle [0,
n) qui nomme la dimension le long de laquelle l'opérande est divisée |
concat_dimension
|
int64
|
Valeur de l'intervalle [0,
n) qui nomme la dimension le long de laquelle les blocs fractionnés sont concaténés |
split_count
|
int64
|
Nombre de cœurs participant à cette opération. Si replica_groups est vide, il doit s'agir du nombre de réplicas. Sinon, il doit être égal au nombre de réplicas de chaque groupe. |
replica_groups
|
Vecteur ReplicaGroup
|
Chaque groupe contient une liste d'ID de réplication. |
Vous trouverez ci-dessous un exemple d'Alltoall.
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(x, /*split_dimension=*/1, /*concat_dimension=*/0, /*split_count=*/4);

Dans cet exemple, quatre cœurs participent à l'opération Alltoall. Sur chaque cœur, l'opérande est divisé en quatre parties le long de la dimension 1. Chaque partie a donc la forme f32[4,4]. Les quatre parties sont réparties sur tous les cœurs. Chaque cœur concatène ensuite les parties reçues le long de la dimension 0, dans l'ordre des cœurs 0 à 4. La sortie de chaque cœur a donc la forme f32[16,4].
BatchNormGrad
Consultez également XlaBuilder::BatchNormGrad et l'article original sur la normalisation par lots pour obtenir une description détaillée de l'algorithme.
Calcule les gradients de la norme de lot.
BatchNormGrad(operand, scale, mean, variance, grad_output, epsilon,
feature_index)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau n dimensionnel à normaliser (x) |
scale |
XlaOp |
Tableau à une dimension (\(\gamma\)) |
mean |
XlaOp |
Tableau à une dimension (\(\mu\)) |
variance |
XlaOp |
Tableau à une dimension (\(\sigma^2\)) |
grad_output |
XlaOp |
Dégradés transmis à BatchNormTraining (\(\nabla y\)) |
epsilon |
float |
Valeur Epsilon (\(\epsilon\)) |
feature_index |
int64 |
Index de la dimension de caractéristique dans operand |
Pour chaque élément de la dimension d'éléments (feature_index est l'indice de la dimension d'éléments dans operand), l'opération calcule les gradients par rapport à operand, offset et scale dans toutes les autres dimensions. feature_index doit être un indice valide pour la dimension d'éléments géographiques dans operand.
Les trois gradients sont définis par les formules suivantes (en supposant un tableau à quatre dimensions comme operand et avec l'indice de dimension des éléments géographiques l, la taille de lot m et les tailles spatiales w et h):
\[ \begin{split} c_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sigma^2_l+\epsilon} \right) \\\\ d_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \\\\ \nabla x_{ijkl} &= \frac{\gamma_{l} }{\sqrt{\sigma^2_{l}+\epsilon} } \left( \nabla y_{ijkl} - d_l - c_l (x_{ijkl} - \mu_{l}) \right) \\\\ \nabla \gamma_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sqrt{\sigma^2_{l}+\epsilon} } \right) \\\\\ \nabla \beta_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \end{split} \]
Les entrées mean et variance représentent les valeurs des moments pour les dimensions de lot et spatiales.
Le type de sortie est un tuple de trois poignées:
| Sorties | Type | Sémantique |
|---|---|---|
grad_operand
|
XlaOp
|
gradient par rapport à l'entrée operand ($\nabla x$) |
grad_scale
|
XlaOp
|
gradient par rapport à l'entrée scale ($\nabla \gamma$) |
grad_offset
|
XlaOp
|
gradient par rapport à l'entrée offset($\nabla \beta$) |
BatchNormInference
Consultez également XlaBuilder::BatchNormInference et l'article original sur la normalisation par lots pour obtenir une description détaillée de l'algorithme.
Normalise un tableau pour les dimensions de lot et spatiales.
BatchNormInference(operand, scale, offset, mean, variance, epsilon,
feature_index)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau à n dimensions à normaliser |
scale |
XlaOp |
Tableau à une dimension |
offset |
XlaOp |
Tableau à une dimension |
mean |
XlaOp |
Tableau à une dimension |
variance |
XlaOp |
Tableau à une dimension |
epsilon |
float |
Valeur epsilon |
feature_index |
int64 |
Index de la dimension de caractéristique dans operand |
Pour chaque élément de la dimension d'éléments (feature_index est l'indice de la dimension d'éléments dans operand), l'opération calcule la moyenne et la variance pour toutes les autres dimensions, puis utilise la moyenne et la variance pour normaliser chaque élément dans operand. feature_index doit être un indice valide pour la dimension d'éléments géographiques dans operand.
BatchNormInference équivaut à appeler BatchNormTraining sans calculer mean et variance pour chaque lot. Il utilise plutôt les valeurs estimées mean et variance comme valeurs d'entrée. L'objectif de cette opération est de réduire la latence lors de l'inférence, d'où le nom BatchNormInference.
La sortie est un tableau normalisé n-dimensionnel de la même forme que l'entrée operand.
BatchNormTraining
Consultez également XlaBuilder::BatchNormTraining et the original batch normalization paper pour obtenir une description détaillée de l'algorithme.
Normalise un tableau pour les dimensions de lot et spatiales.
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau n dimensionnel à normaliser (x) |
scale |
XlaOp |
Tableau à une dimension (\(\gamma\)) |
offset |
XlaOp |
Tableau à une dimension (\(\beta\)) |
epsilon |
float |
Valeur Epsilon (\(\epsilon\)) |
feature_index |
int64 |
Index de la dimension de caractéristique dans operand |
Pour chaque élément de la dimension d'éléments (feature_index est l'indice de la dimension d'éléments dans operand), l'opération calcule la moyenne et la variance pour toutes les autres dimensions, puis utilise la moyenne et la variance pour normaliser chaque élément dans operand. feature_index doit être un indice valide pour la dimension d'éléments géographiques dans operand.
L'algorithme se présente comme suit pour chaque lot dans operand \(x\) qui contient des éléments m avec w et h comme taille des dimensions spatiales (en supposant que operand est un tableau à quatre dimensions):
Calcule la moyenne de lot \(\mu_l\) pour chaque élément géographique
ldans la dimension d'éléments géographiques : \(\mu_l=\frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h x_{ijkl}\)Calcule la variance par lot \(\sigma^2_l\) : $\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
Normalise, étale et décale : \(y_{ijkl}=\frac{\gamma_l(x_{ijkl}-\mu_l)}{\sqrt[2]{\sigma^2_l+\epsilon} }+\beta_l\)
La valeur epsilon, généralement un petit nombre, est ajoutée pour éviter les erreurs de division par zéro.
Le type de sortie est un tuple de trois XlaOp:
| Sorties | Type | Sémantique |
|---|---|---|
output
|
XlaOp
|
Tableau à n dimensions ayant la même forme que l'entrée operand (y) |
batch_mean |
XlaOp |
Tableau à une dimension (\(\mu\)) |
batch_var |
XlaOp |
Tableau à une dimension (\(\sigma^2\)) |
batch_mean et batch_var sont des moments calculés sur les dimensions de lot et spatiales à l'aide des formules ci-dessus.
BitcastConvertType
Consultez également XlaBuilder::BitcastConvertType.
Semblable à un tf.bitcast dans TensorFlow, effectue une opération de cast de bits par élément à partir d'une forme de données vers une forme cible. La taille d'entrée et de sortie doit correspondre: par exemple, les éléments s32 deviennent des éléments f32 via la routine de bitcast, et un élément s32 devient quatre éléments s8. Le cast de bits est implémenté en tant que cast de bas niveau. Par conséquent, les machines avec des représentations à virgule flottante différentes donneront des résultats différents.
BitcastConvertType(operand, new_element_type)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
tableau de type T avec dimensions D |
new_element_type |
PrimitiveType |
type U |
Les dimensions de l'opérande et de la forme cible doivent correspondre, à l'exception de la dernière dimension, qui changera en fonction du ratio de la taille primitive avant et après la conversion.
Les types d'éléments source et de destination ne doivent pas être des tupels.
Conversion par bitcast en type primitif de largeur différente
L'instruction HLO BitcastConvert prend en charge le cas où la taille du type d'élément de sortie T' n'est pas égale à la taille de l'élément d'entrée T. Étant donné que l'ensemble de l'opération est conceptuellement un cast de bits et ne modifie pas les octets sous-jacents, la forme de l'élément de sortie doit changer. Pour B = sizeof(T), B' =
sizeof(T'), deux cas sont possibles.
Tout d'abord, lorsque B > B', la forme de sortie reçoit une nouvelle dimension la plus petite de taille B/B'. Exemple :
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
La règle reste la même pour les scalaires effectifs:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
Pour B' > B, l'instruction exige que la dernière dimension logique de la forme d'entrée soit égale à B'/B, et cette dimension est supprimée lors de la conversion:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
Notez que les conversions entre différentes largeurs de bits ne sont pas élément par élément.
Annoncer
Consultez également XlaBuilder::Broadcast.
Ajoute des dimensions à un tableau en dupliquant les données du tableau.
Broadcast(operand, broadcast_sizes)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau à dupliquer |
broadcast_sizes |
ArraySlice<int64> |
Tailles des nouvelles dimensions |
Les nouvelles dimensions sont insérées à gauche. Autrement dit, si broadcast_sizes a les valeurs {a0, ..., aN} et que la forme de l'opérande a les dimensions {b0, ..., bM}, la forme de la sortie a les dimensions {a0, ..., aN, b0, ..., bM}.
Les nouvelles dimensions indexent des copies de l'opérande, c'est-à-dire
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
Par exemple, si operand est un scalaire f32 avec la valeur 2.0f et que broadcast_sizes est {2, 3}, le résultat est un tableau de forme f32[2, 3] et toutes les valeurs du résultat sont 2.0f.
BroadcastInDim
Consultez également XlaBuilder::BroadcastInDim.
Élargit la taille et le nombre de dimensions d'un tableau en dupliquant les données du tableau.
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau à dupliquer |
out_dim_size |
ArraySlice<int64> |
Tailles des dimensions de la forme cible |
broadcast_dimensions |
ArraySlice<int64> |
Dimension de la forme cible à laquelle chaque dimension de la forme opérande correspond |
Semblable à "Broadcast", mais permet d'ajouter des dimensions n'importe où et d'étendre les dimensions existantes de taille 1.
Le operand est diffusé sur la forme décrite par out_dim_size.
broadcast_dimensions mappe les dimensions de operand aux dimensions de la forme cible, c'est-à-dire que la i dimension de l'opérande est mappée sur la i dimension de la forme de sortie. Les dimensions de operand doivent avoir la taille 1 ou être de la même taille que la dimension de la forme de sortie à laquelle elles sont mappées. Les dimensions restantes sont remplies avec des dimensions de taille 1. La diffusion de dimensions dégénérées diffuse ensuite le long de ces dimensions dégénérées pour atteindre la forme de sortie. La sémantique est décrite en détail sur la page de diffusion.
Appeler
Consultez également XlaBuilder::Call.
Invoque un calcul avec les arguments donnés.
Call(computation, args...)
| Arguments | Type | Sémantique |
|---|---|---|
computation |
XlaComputation |
calcul de type T_0, T_1, ..., T_{N-1} -> S avec N paramètres de type arbitraire |
args |
séquence de N XlaOp |
N arguments de type arbitraire |
L'arité et les types de args doivent correspondre aux paramètres de computation. Il est autorisé de ne pas avoir de args.
CompositeCall
Consultez également XlaBuilder::CompositeCall.
Encapsule une opération composée d'autres opérations StableHLO, prenant des entrées et des attributs composites, et produisant des résultats. La sémantique de l'opération est implémentée par l'attribut de décomposition. L'opération composite peut être remplacée par sa décomposition sans modifier la sémantique du programme. Dans les cas où l'intégration de la décomposition ne fournit pas la même sémantique d'opération, privilégiez l'utilisation de custom_call.
Le champ de version (par défaut : 0) permet d'indiquer quand la sémantique d'un composite change.
Cette opération est implémentée en tant que kCall avec l'attribut is_composite=true. Le champ decomposition est spécifié par l'attribut computation. Les attributs de l'interface utilisateur stockent les attributs restants précédés du préfixe composite..
Exemple d'opération CompositeCall:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
Call(computation, args..., name, composite_attributes, version)
| Arguments | Type | Sémantique |
|---|---|---|
inputs |
XlaOp |
nombre de valeurs variable |
name |
string |
nom du composite |
composite_attributes |
string facultatif |
Dictionnaire d'attributs concaténé facultatif |
decomposition |
XlaComputation |
calcul de type T_0, T_1, ..., T_{N-1} -> S avec N paramètres de type arbitraire |
version |
int64. |
Mise à jour du nombre de versions de la sémantique de l'opération composite |
Cholesky
Consultez également XlaBuilder::Cholesky.
Calcule la décomposition de Cholesky d'un lot de matrices symétriques (hermitiennes) définies positives.
Cholesky(a, lower)
| Arguments | Type | Sémantique |
|---|---|---|
a |
XlaOp |
Un tableau de type complexe ou à virgule flottante avec plus de deux dimensions. |
lower |
bool |
d'utiliser le triangle supérieur ou inférieur de a. |
Si lower est true, calcule les matrices triangulaires inférieures l telles que $a = l .
l^T$. Si lower est false, calcule les matrices triangulaires supérieures u telles que\(a = u^T . u\).
Les données d'entrée ne sont lues que dans le triangle inférieur/supérieur de a, en fonction de la valeur de lower. Les valeurs de l'autre triangle sont ignorées. Les données de sortie sont renvoyées dans le même triangle. Les valeurs de l'autre triangle sont définies par l'implémentation et peuvent être n'importe quoi.
Si a comporte plus de deux dimensions, a est traité comme un lot de matrices, où toutes les dimensions, à l'exception des deux dimensions mineures, sont des dimensions de lot.
Si a n'est pas symétrique (hermitienne) définie positive, le résultat est défini par l'implémentation.
Limiter
Consultez également XlaBuilder::Clamp.
Écrête un opérande dans la plage comprise entre une valeur minimale et une valeur maximale.
Clamp(min, operand, max)
| Arguments | Type | Sémantique |
|---|---|---|
min |
XlaOp |
tableau de type T |
operand |
XlaOp |
tableau de type T |
max |
XlaOp |
tableau de type T |
À partir d'un opérande et de valeurs minimale et maximale, renvoie l'opérande s'il se trouve dans la plage comprise entre la valeur minimale et la valeur maximale, sinon renvoie la valeur minimale si l'opérande est inférieur à cette plage ou la valeur maximale si l'opérande est supérieur à cette plage. Par exemple, clamp(a, x, b) = min(max(a, x), b).
Les trois tableaux doivent avoir la même forme. En tant que forme restreinte de diffusion, min et/ou max peuvent également être un scalaire de type T.
Exemple avec les scalaires min et max:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
Réduire
Consultez également XlaBuilder::Collapse et l'opération tf.reshape.
Rassemble les dimensions d'un tableau en une seule dimension.
Collapse(operand, dimensions)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
tableau de type T |
dimensions |
Vecteur int64 |
sous-ensemble consécutif, dans l'ordre, des dimensions de T. |
La réduction remplace le sous-ensemble donné des dimensions de l'opérande par une seule dimension. Les arguments d'entrée sont un tableau arbitraire de type T et un vecteur constant au moment de la compilation d'indices de dimension. Les indices de dimension doivent être un sous-ensemble consécutif des dimensions de T, par ordre croissant (de faible à élevé). Ainsi, {0, 1, 2}, {0, 1} ou {1, 2} sont tous des ensembles de dimensions valides, mais {1, 0} ou {0, 2} ne le sont pas. Elles sont remplacées par une seule nouvelle dimension, à la même position dans la séquence de dimensions que celles qu'elles remplacent, et dont la taille est égale au produit des tailles des dimensions d'origine. Le numéro de dimension le plus bas dans dimensions est la dimension à variation la plus lente (la plus importante) dans le nid de boucles qui réduit ces dimensions, et le numéro de dimension le plus élevé est la variation la plus rapide (la plus mineure). Consultez l'opérateur tf.reshape si vous avez besoin d'un ordre de réduction plus général.
Par exemple, supposons que v soit un tableau de 24 éléments:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
CollectivePermute
Consultez également XlaBuilder::CollectivePermute.
CollectivePermute est une opération collective qui envoie et reçoit des données entre les réplications.
CollectivePermute(operand, source_target_pairs)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau d'entrée à n dimensions |
source_target_pairs |
Vecteur <int64, int64> |
Liste de paires (source_replica_id, target_replica_id). Pour chaque paire, l'opérande est envoyé du réplica source au réplica cible. |
Notez que les restrictions suivantes s'appliquent à source_target_pair:
- Aucune paire ne doit avoir le même ID de réplication cible ni le même ID de réplication source.
- Si un ID de réplication n'est pas une cible dans aucune paire, la sortie de ce réplica est un tenseur composé de 0(s) de la même forme que l'entrée.
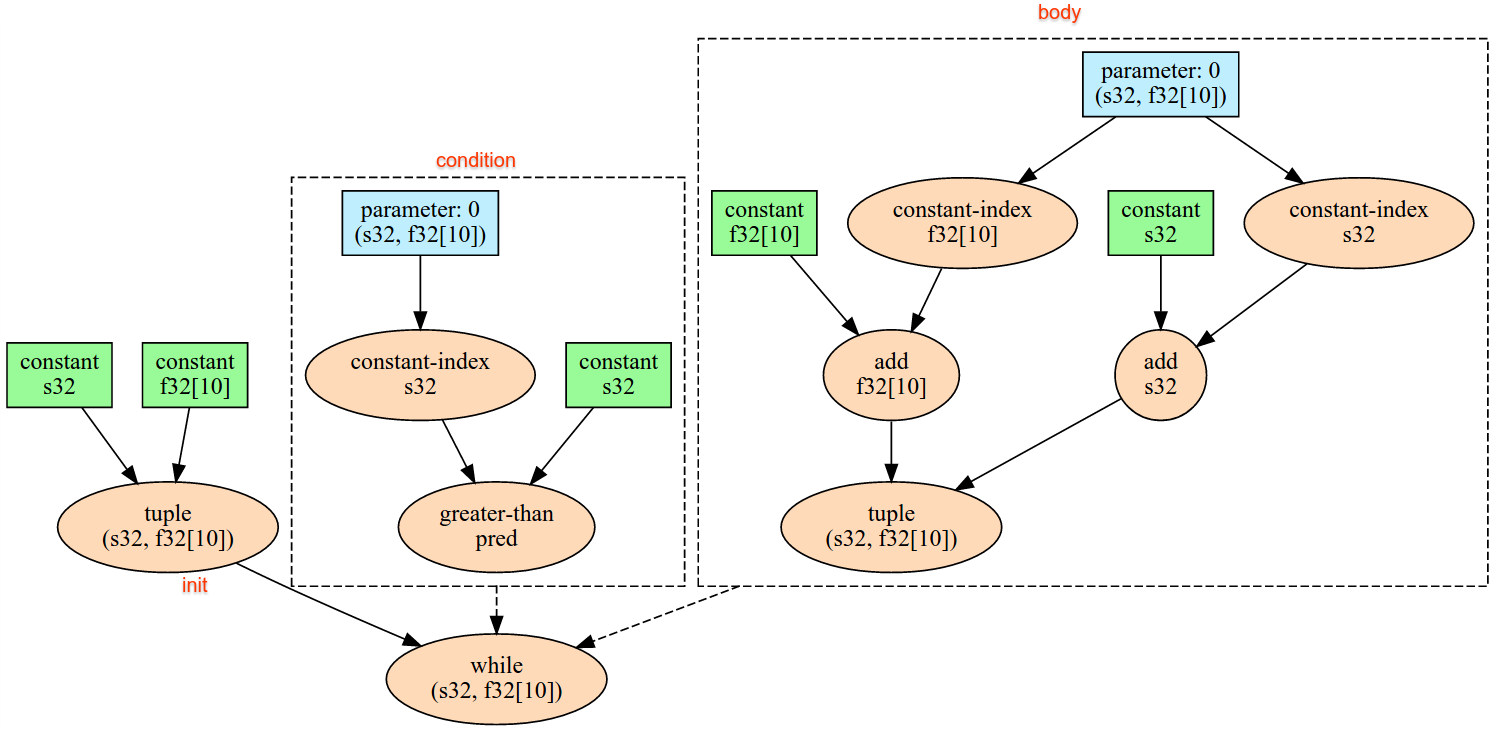
Concatenate
Consultez également XlaBuilder::ConcatInDim.
La concaténation compose un tableau à partir de plusieurs opérateurs de tableau. Le tableau a le même nombre de dimensions que chacun des opérandes de tableau d'entrée (qui doivent avoir le même nombre de dimensions les uns que les autres) et contient les arguments dans l'ordre dans lequel ils ont été spécifiés.
Concatenate(operands..., dimension)
| Arguments | Type | Sémantique |
|---|---|---|
operands |
séquence de N XlaOp |
N tableaux de type T avec des dimensions [L0, L1, ...]. N doit être supérieur ou égal à 1. |
dimension |
int64 |
Valeur comprise dans l'intervalle [0, N) qui nomme la dimension à concatenar entre les operands. |
À l'exception de dimension, toutes les dimensions doivent être identiques. En effet, XLA n'est pas compatible avec les tableaux "découpés". Notez également que les valeurs à dimension 0 ne peuvent pas être concaténées (car il est impossible de nommer la dimension le long de laquelle la concaténation se produit).
Exemple à une dimension:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
>>> {2, 3, 4, 5, 6, 7}
Exemple en deux dimensions:
let a = {
{1, 2},
{3, 4},
{5, 6},
};
let b = {
{7, 8},
};
Concat({a, b}, 0)
>>> {
{1, 2},
{3, 4},
{5, 6},
{7, 8},
}
Diagramme:
Conditionnel
Consultez également XlaBuilder::Conditional.
Conditional(pred, true_operand, true_computation, false_operand,
false_computation)
| Arguments | Type | Sémantique |
|---|---|---|
pred |
XlaOp |
Scalaire de type PRED |
true_operand |
XlaOp |
Argument de type \(T_0\) |
true_computation |
XlaComputation |
XlaComputation de type \(T_0 \to S\) |
false_operand |
XlaOp |
Argument de type \(T_1\) |
false_computation |
XlaComputation |
XlaComputation de type \(T_1 \to S\) |
Exécute true_computation si pred est true, false_computation si pred est false et renvoie le résultat.
true_computation doit utiliser un seul argument de type \(T_0\) et sera appelé avec true_operand, qui doit être du même type. false_computation doit recevoir un seul argument de type \(T_1\) et sera appelé avec false_operand, qui doit être du même type. Le type de la valeur renvoyée de true_computation et false_computation doit être le même.
Notez qu'un seul élément entre true_computation et false_computation sera exécuté en fonction de la valeur de pred.
Conditional(branch_index, branch_computations, branch_operands)
| Arguments | Type | Sémantique |
|---|---|---|
branch_index |
XlaOp |
Scalaire de type S32 |
branch_computations |
séquence de N XlaComputation |
XlaComputations de type \(T_0 \to S , T_1 \to S , ..., T_{N-1} \to S\) |
branch_operands |
séquence de N XlaOp |
Arguments de type \(T_0 , T_1 , ..., T_{N-1}\) |
Exécute branch_computations[branch_index] et renvoie le résultat. Si branch_index est un S32 inférieur à 0 ou supérieur ou égal à N, branch_computations[N-1] est exécuté en tant que branche par défaut.
Chaque branch_computations[b] doit accepter un seul argument de type \(T_b\) et sera appelé avec branch_operands[b], qui doit être du même type. Le type de la valeur renvoyée par chaque branch_computations[b] doit être le même.
Notez qu'un seul des branch_computations sera exécuté en fonction de la valeur de branch_index.
Conv (convolution)
Consultez également XlaBuilder::Conv.
Comme ConvWithGeneralPadding, mais le remplissage est spécifié de manière abrégée comme "SAME" ou "VALID". Le remplissage SAME remplit l'entrée (lhs) avec des zéros afin que la sortie ait la même forme que l'entrée lorsque l'on ne tient pas compte de la marche. La valeur "VALID" signifie simplement qu'il n'y a pas de marge intérieure.
ConvWithGeneralPadding (convolution)
Consultez également XlaBuilder::ConvWithGeneralPadding.
Calcule une convolution du type utilisé dans les réseaux de neurones. Ici, une convolution peut être considérée comme une fenêtre n-dimensionnelle se déplaçant sur une zone de base n-dimensionnelle, et un calcul est effectué pour chaque position possible de la fenêtre.
| Arguments | Type | Sémantique |
|---|---|---|
lhs |
XlaOp |
Tableau d'entrées à (n+2) dimensions |
rhs |
XlaOp |
Tableau (n+2) dimensionnel des poids du noyau |
window_strides |
ArraySlice<int64> |
Tableau n-d des pas de noyau |
padding |
ArraySlice< pair<int64,int64>> |
Tableau n-d de marge intérieure (bas, haut) |
lhs_dilation |
ArraySlice<int64> |
Tableau du facteur de dilatation de la gauche supérieure n-d |
rhs_dilation |
ArraySlice<int64> |
Tableau du facteur de dilatation de la partie droite n-d |
feature_group_count |
int64 | le nombre de groupes de caractéristiques ; |
batch_group_count |
int64 | le nombre de groupes de lots |
Soit n le nombre de dimensions spatiales. L'argument lhs est un tableau à (n + 2) dimensions décrivant la zone de base. C'est ce qu'on appelle l'entrée, même si, bien sûr, le membre de droite est également une entrée. Dans un réseau de neurones, il s'agit des activations d'entrée. Les dimensions n+2 sont les suivantes, dans l'ordre:
batch: chaque coordonnée de cette dimension représente une entrée indépendante pour laquelle la convolution est effectuée.z/depth/features: chaque position (y,x) de la zone de base est associée à un vecteur, qui entre dans cette dimension.spatial_dims: décrit les dimensions spatialesnqui définissent la zone de base sur laquelle la fenêtre se déplace.
L'argument rhs est un tableau à (n + 2) dimensions décrivant le filtre/noyau/fenêtre de convolution. Les dimensions sont les suivantes, dans l'ordre:
output-z: dimensionzde la sortie.input-z: la taille de cette dimension multipliée parfeature_group_countdoit être égale à la taille de la dimensionzdans lhs.spatial_dims: décrit les dimensions spatialesnqui définissent la fenêtre n-d qui se déplace dans la zone de base.
L'argument window_strides spécifie la longueur de la fenêtre de convolution dans les dimensions spatiales. Par exemple, si la longueur de pas de la première dimension spatiale est de 3, la fenêtre ne peut être placée qu'aux coordonnées où le premier indice spatial est divisible par 3.
L'argument padding spécifie la quantité de marge intérieure à appliquer à la zone de base. La quantité de remplissage peut être négative. La valeur absolue du remplissage négatif indique le nombre d'éléments à supprimer de la dimension spécifiée avant d'effectuer la convolution. padding[0] spécifie la marge intérieure pour la dimension y et padding[1] spécifie la marge intérieure pour la dimension x. Chaque paire comporte la marge intérieure basse comme premier élément et la marge intérieure haute comme deuxième élément. La marge intérieure basse est appliquée dans la direction des indices inférieurs, tandis que la marge intérieure haute est appliquée dans la direction des indices supérieurs. Par exemple, si padding[1] est (2,3), une marge intérieure de deux zéros est appliquée à gauche et de trois zéros à droite dans la deuxième dimension spatiale. L'utilisation du remplissage équivaut à insérer ces mêmes valeurs nulles dans l'entrée (lhs) avant d'effectuer la convolution.
Les arguments lhs_dilation et rhs_dilation spécifient le facteur de dilatation à appliquer à la partie gauche et à la partie droite, respectivement, dans chaque dimension spatiale. Si le facteur de dilatation dans une dimension spatiale est d, d-1 trous sont implicitement placés entre chacune des entrées de cette dimension, ce qui augmente la taille du tableau. Les trous sont remplis d'une valeur sans opération, ce qui signifie des zéros pour la convolution.
La dilatation du membre droit est également appelée convolution atrous. Pour en savoir plus, consultez tf.nn.atrous_conv2d. La dilatation du membre gauche est également appelée convolution transposée. Pour en savoir plus, consultez tf.nn.conv2d_transpose.
L'argument feature_group_count (valeur par défaut 1) peut être utilisé pour les convolutions groupées. feature_group_count doit être un diviseur à la fois de la dimension des éléments géographiques d'entrée et de sortie. Si feature_group_count est supérieur à 1, cela signifie que, conceptuellement, la dimension des caractéristiques d'entrée et de sortie et la dimension des caractéristiques de sortie rhs sont réparties uniformément en plusieurs groupes feature_group_count, chaque groupe étant constitué d'une sous-séquence consécutive de caractéristiques. La dimension des éléments géographiques d'entrée de rhs doit être égale à la dimension des éléments géographiques d'entrée de lhs divisée par feature_group_count (elle a donc déjà la taille d'un groupe d'éléments géographiques d'entrée). Les groupes i sont utilisés ensemble pour calculer feature_group_count pour de nombreuses convolutions distinctes. Les résultats de ces convolutions sont concatenatés dans la dimension des éléments géographiques de sortie.
Pour la convolution en profondeur, l'argument feature_group_count est défini sur la dimension des caractéristiques d'entrée, et le filtre est restructuré de [filter_height, filter_width, in_channels, channel_multiplier] à [filter_height, filter_width, 1, in_channels * channel_multiplier]. Pour en savoir plus, consultez tf.nn.depthwise_conv2d.
L'argument batch_group_count (valeur par défaut 1) peut être utilisé pour les filtres groupés lors de la rétropropagation. batch_group_count doit être un diviseur de la taille de la dimension de lot lhs (entrée). Si batch_group_count est supérieur à 1, cela signifie que la dimension de lot de sortie doit être de taille input batch
/ batch_group_count. batch_group_count doit être un diviseur de la taille des éléments géographiques de sortie.
La forme de sortie comporte les dimensions suivantes, dans l'ordre suivant:
batch: la taille de cette dimension multipliée parbatch_group_countdoit être égale à la taille de la dimensionbatchdans lhs.z: même taille queoutput-zsur le kernel (rhs).spatial_dims: une valeur pour chaque emplacement valide de la fenêtre de convolution.
La figure ci-dessus montre le fonctionnement du champ batch_group_count. En fait, nous découpons chaque lot lhs en groupes batch_group_count et faisons de même pour les éléments géographiques de sortie. Ensuite, pour chacun de ces groupes, nous effectuons des convolutions par paires et concaténons la sortie le long de la dimension des caractéristiques de sortie. La sémantique opérationnelle de toutes les autres dimensions (éléments géographiques et spatiales) reste inchangée.
Les emplacements valides de la fenêtre de convolution sont déterminés par les pas et la taille de la zone de base après le rembourrage.
Pour décrire ce qu'est une convolution, considérez une convolution 2D et choisissez des coordonnées batch, z, y et x fixes dans la sortie. (y,x) correspond alors à la position d'un angle de la fenêtre dans la zone de base (par exemple, l'angle supérieur gauche, selon la façon dont vous interprétez les dimensions spatiales). Nous avons maintenant une fenêtre 2D, extraite de la zone de base, où chaque point 2D est associé à un vecteur 1D. Nous obtenons ainsi une boîte 3D. À partir du noyau de convolution, comme nous avons fixé la coordonnée de sortie z, nous avons également une boîte 3D. Les deux boîtes ayant les mêmes dimensions, nous pouvons prendre la somme des produits par élément entre les deux boîtes (comme un produit scalaire). Il s'agit de la valeur de sortie.
Notez que si output-z est, par exemple, 5, chaque position de la fenêtre génère cinq valeurs dans la sortie dans la dimension z de la sortie. Ces valeurs diffèrent selon la partie du noyau de convolution utilisée. Une boîte 3D de valeurs distincte est utilisée pour chaque coordonnée output-z. Vous pouvez donc considérer qu'il s'agit de cinq convolutions distinctes, chacune avec un filtre différent.
Voici un pseudo-code pour une convolution 2D avec remplissage et pas de défilement:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
ConvertElementType
Consultez également XlaBuilder::ConvertElementType.
Semblable à une static_cast par élément en C++, effectue une opération de conversion par élément d'une forme de données vers une forme cible. Les dimensions doivent correspondre, et la conversion est effectuée par élément. Par exemple, les éléments s32 deviennent des éléments f32 via une routine de conversion s32 vers f32.
ConvertElementType(operand, new_element_type)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
tableau de type T avec dimensions D |
new_element_type |
PrimitiveType |
type U |
Les dimensions de l'opérande et de la forme cible doivent correspondre. Les types d'éléments source et de destination ne doivent pas être des tupels.
Une conversion telle que T=s32 en U=f32 effectue une routine de conversion d'entier en flottant normalisée, telle que l'arrondi à l'entier le plus proche.
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
CrossReplicaSum
Effectue AllReduce avec un calcul de somme.
CustomCall
Consultez également XlaBuilder::CustomCall.
Appeler une fonction fournie par l'utilisateur dans un calcul
CustomCall(target_name, args..., shape)
| Arguments | Type | Sémantique |
|---|---|---|
target_name |
string |
Nom de la fonction. Une instruction d'appel ciblant ce nom de symbole sera émise. |
args |
séquence de N XlaOp |
N arguments de type arbitraire, qui seront transmis à la fonction. |
shape |
Shape |
Forme de sortie de la fonction |
La signature de la fonction est la même, quelle que soit l'arité ou le type d'arguments:
extern "C" void target_name(void* out, void** in);
Par exemple, si CustomCall est utilisé comme suit:
let x = f32[2] {1,2};
let y = f32[2x3] { {10, 20, 30}, {40, 50, 60} };
CustomCall("myfunc", {x, y}, f32[3x3])
Voici un exemple d'implémentation de myfunc:
extern "C" void myfunc(void* out, void** in) {
float (&x)[2] = *static_cast<float(*)[2]>(in[0]);
float (&y)[2][3] = *static_cast<float(*)[2][3]>(in[1]);
EXPECT_EQ(1, x[0]);
EXPECT_EQ(2, x[1]);
EXPECT_EQ(10, y[0][0]);
EXPECT_EQ(20, y[0][1]);
EXPECT_EQ(30, y[0][2]);
EXPECT_EQ(40, y[1][0]);
EXPECT_EQ(50, y[1][1]);
EXPECT_EQ(60, y[1][2]);
float (&z)[3][3] = *static_cast<float(*)[3][3]>(out);
z[0][0] = x[1] + y[1][0];
// ...
}
La fonction fournie par l'utilisateur ne doit pas avoir d'effets secondaires, et son exécution doit être idempotente.
Point
Consultez également XlaBuilder::Dot.
Dot(lhs, rhs)
| Arguments | Type | Sémantique |
|---|---|---|
lhs |
XlaOp |
tableau de type T |
rhs |
XlaOp |
tableau de type T |
La sémantique exacte de cette opération dépend des rangs des opérandes:
| Entrée | Sortie | Sémantique |
|---|---|---|
vecteur [n] dot vecteur [n] |
scalaire | produit scalaire de vecteurs |
matrice [m x k] vecteur dot [k] |
vecteur [m] | multiplication matricielle-vectorielle |
matrice [m x k] dot matrice [k x n] |
matrice [m x n] | multiplication matricielle |
L'opération effectue la somme des produits sur la deuxième dimension de lhs (ou la première si elle comporte une seule dimension) et la première dimension de rhs. Il s'agit des dimensions "contractées". Les dimensions contractées de lhs et rhs doivent être de la même taille. En pratique, il peut être utilisé pour effectuer des produits scalaires entre des vecteurs, des multiplications vecteur/matrice ou des multiplications matrice/matrice.
DotGeneral
Consultez également XlaBuilder::DotGeneral.
DotGeneral(lhs, rhs, dimension_numbers)
| Arguments | Type | Sémantique |
|---|---|---|
lhs |
XlaOp |
tableau de type T |
rhs |
XlaOp |
tableau de type T |
dimension_numbers |
DotDimensionNumbers |
les numéros de dimension de sous-traitance et de lot ; |
Semblable à Dot, mais permet de spécifier des numéros de dimension de contrat et de lot pour lhs et rhs.
| Champs DotDimensionNumbers | Type | Sémantique |
|---|---|---|
lhs_contracting_dimensions
|
repeated int64 | lhs numéros de dimension contractante |
rhs_contracting_dimensions
|
repeated int64 | rhs numéros de dimension contractante |
lhs_batch_dimensions
|
repeated int64 | Numéros de dimension de lot lhs |
rhs_batch_dimensions
|
repeated int64 | Numéros de dimension de lot rhs |
DotGeneral effectue la somme des produits sur les dimensions de contraction spécifiées dans dimension_numbers.
Les numéros de dimension de contrat associés de lhs et rhs n'ont pas besoin d'être identiques, mais doivent avoir les mêmes tailles de dimension.
Exemple avec des numéros de dimension contractants:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { {6.0, 12.0},
{15.0, 30.0} }
Les numéros de dimension de lot associés de lhs et rhs doivent avoir les mêmes tailles de dimension.
Exemple avec des numéros de dimension de lot (taille de lot 2, matrices 2 x 2):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| Entrée | Sortie | Sémantique |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | matmul par lot |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | matmul par lot |
Par conséquent, le numéro de dimension obtenu commence par la dimension de lot, puis par la dimension lhs sans contrat/sans lot, et enfin par la dimension rhs sans contrat/sans lot.
DynamicSlice
Consultez également XlaBuilder::DynamicSlice.
DynamicSlice extrait un sous-tableau du tableau d'entrée à l'start_indices dynamique. La taille de la tranche dans chaque dimension est transmise dans size_indices, qui spécifie le point final des intervalles de tranche exclusifs dans chaque dimension: [start, start + size]. La forme de start_indices doit être unidimensionnelle, avec une taille de dimension égale au nombre de dimensions de operand.
DynamicSlice(operand, start_indices, size_indices)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau à N dimensions de type T |
start_indices |
séquence de N XlaOp |
Liste de N entiers scalaires contenant les indices de début de la tranche pour chaque dimension. La valeur doit être supérieure ou égale à zéro. |
size_indices |
ArraySlice<int64> |
Liste de N entiers contenant la taille de la tranche pour chaque dimension. Chaque valeur doit être strictement supérieure à zéro, et la valeur start + size doit être inférieure ou égale à la taille de la dimension pour éviter le retour à la ligne modulo la taille de la dimension. |
Les indices de tranche efficaces sont calculés en appliquant la transformation suivante pour chaque indice i dans [1, N) avant d'effectuer la tranche:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - size_indices[i])
Cela garantit que la tranche extraite est toujours dans les limites par rapport au tableau d'opérandes. Si la tranche est dans les limites avant l'application de la transformation, la transformation n'a aucun effet.
Exemple à une dimension:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let s = {2}
DynamicSlice(a, s, {2}) produces:
{2.0, 3.0}
Exemple en deux dimensions:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2}) produces:
{ { 7.0, 8.0},
{10.0, 11.0} }
DynamicUpdateSlice
Consultez également XlaBuilder::DynamicUpdateSlice.
DynamicUpdateSlice génère un résultat qui correspond à la valeur du tableau d'entrée operand, avec une tranche update écrasée à start_indices.
La forme de update détermine la forme du sous-tableau du résultat qui est mis à jour.
La forme de start_indices doit être unidimensionnelle, avec une taille de dimension égale au nombre de dimensions de operand.
DynamicUpdateSlice(operand, update, start_indices)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau à N dimensions de type T |
update |
XlaOp |
Tableau à N dimensions de type T contenant la mise à jour de la tranche. Chaque dimension de la forme de mise à jour doit être strictement supérieure à zéro, et le début + la mise à jour doit être inférieur ou égal à la taille de l'opérande pour chaque dimension afin d'éviter de générer des indices de mise à jour hors limites. |
start_indices |
séquence de N XlaOp |
Liste de N entiers scalaires contenant les indices de début de la tranche pour chaque dimension. La valeur doit être supérieure ou égale à zéro. |
Les indices de tranche efficaces sont calculés en appliquant la transformation suivante pour chaque indice i dans [1, N) avant d'effectuer la tranche:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
Cela garantit que la tranche mise à jour est toujours dans les limites par rapport au tableau d'opérandes. Si la tranche est dans les limites avant l'application de la transformation, la transformation n'a aucun effet.
Exemple à une dimension:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s) produces:
{0.0, 1.0, 5.0, 6.0, 4.0}
Exemple en deux dimensions:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s) produces:
{ {0.0, 1.0, 2.0},
{3.0, 12.0, 13.0},
{6.0, 14.0, 15.0},
{9.0, 16.0, 17.0} }
Opérations arithmétiques binaires au niveau des éléments
Consultez également XlaBuilder::Add.
Un ensemble d'opérations arithmétiques binaires au niveau des éléments est accepté.
Op(lhs, rhs)
Où Op est l'un des opérateurs suivants : Add (addition), Sub(soustraction), Mul (multiplication), Div (division), Pow (puissance), Rem (reste), Max (maximum), Min (minimum), And (AND logique), Or (OU logique), Xor (XOR logique), ShiftLeft (décalage à gauche), ShiftRightArithmetic (décalage à droite arithmétique), ShiftRightLogical (décalage à droite logique), Atan2 (arctangente à deux arguments) ou Complex (combine les parties réelle et imaginaire en un nombre complexe)
| Arguments | Type | Sémantique |
|---|---|---|
lhs |
XlaOp |
opérande de gauche: tableau de type T |
rhs |
XlaOp |
opérande de droite: tableau de type T |
Les formes des arguments doivent être similaires ou compatibles. Consultez la documentation sur la diffusion pour savoir ce que signifie la compatibilité des formes. Le résultat d'une opération a une forme qui est le résultat de la diffusion des deux tableaux d'entrée. Dans cette variante, les opérations entre des tableaux de différents rangs ne sont pas prises en charge, sauf si l'un des opérandes est un scalaire.
Lorsque Op est Rem, le signe du résultat est extrait du dividende, et la valeur absolue du résultat est toujours inférieure à la valeur absolue du diviseur.
Le débordement de la division entière (division/reste signé/non signé par zéro ou division/reste signé de INT_SMIN avec -1) produit une valeur définie par l'implémentation.
Une autre variante avec la prise en charge de la diffusion multidimensionnelle existe pour ces opérations:
Op(lhs, rhs, broadcast_dimensions)
Où Op est identique à ci-dessus. Cette variante de l'opération doit être utilisée pour les opérations arithmétiques entre des tableaux de différents rangs (par exemple, ajouter une matrice à un vecteur).
L'opérande broadcast_dimensions supplémentaire est une tranche d'entiers utilisée pour augmenter le nombre de dimensions de l'opérande à dimension inférieure jusqu'au nombre de dimensions de l'opérande à dimension supérieure. broadcast_dimensions mappe les dimensions de la forme à dimension inférieure aux dimensions de la forme à dimension supérieure. Les dimensions non mappées de la forme développée sont remplies de dimensions de taille 1. Le broadcasting de dimension dégénérée diffuse ensuite les formes le long de ces dimensions dégénérées pour égaliser les formes des deux opérandes. La sémantique est décrite en détail sur la page Diffusion.
Opérations de comparaison au niveau des éléments
Consultez également XlaBuilder::Eq.
Un ensemble d'opérations de comparaison binaires standards par élément est accepté. Notez que la sémantique de comparaison à virgule flottante standard IEEE 754 s'applique lors de la comparaison de types à virgule flottante.
Op(lhs, rhs)
Où Op est l'une des valeurs suivantes : Eq (égal à), Ne (différent de), Ge (supérieur ou égal à), Gt (supérieur à), Le (inférieur ou égal à) ou Lt (inférieur à). Un autre ensemble d'opérateurs, EqTotalOrder, NeTotalOrder, GeTotalOrder, GtTotalOrder, LeTotalOrder et LtTotalOrder, fournit les mêmes fonctionnalités, à l'exception qu'ils acceptent également un ordre total sur les nombres à virgule flottante, en appliquant -NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.
| Arguments | Type | Sémantique |
|---|---|---|
lhs |
XlaOp |
opérande de gauche: tableau de type T |
rhs |
XlaOp |
opérande de droite: tableau de type T |
Les formes des arguments doivent être similaires ou compatibles. Consultez la documentation sur la diffusion pour savoir ce que signifie la compatibilité des formes. Le résultat d'une opération a une forme qui est le résultat de la diffusion des deux tableaux d'entrée avec le type d'élément PRED. Dans cette variante, les opérations entre des tableaux de différents rangs ne sont pas prises en charge, sauf si l'un des opérandes est un scalaire.
Une autre variante avec la prise en charge de la diffusion multidimensionnelle existe pour ces opérations:
Op(lhs, rhs, broadcast_dimensions)
Où Op est identique à ci-dessus. Cette variante de l'opération doit être utilisée pour les opérations de comparaison entre des tableaux de différents rangs (par exemple, ajouter une matrice à un vecteur).
L'opérande broadcast_dimensions supplémentaire est une tranche d'entiers spécifiant les dimensions à utiliser pour la diffusion des opérandes. La sémantique est décrite en détail sur la page Diffusion.
Fonctions unaires au niveau des éléments
XlaBuilder accepte les fonctions unaires par élément suivantes:
Abs(operand) Valeur absolue élément par élément x -> |x|.
Cbrt(operand) Opération racine cubique au niveau des éléments x -> cbrt(x).
Ceil(operand) Plafond par élément x -> ⌈x⌉.
Clz(operand) Compte les zéros au début de chaque élément.
Cos(operand) Cosine par élément x -> cos(x).
Erf(operand) Fonction d'erreur au niveau des éléments x -> erf(x), où
\(\text{erf}(x) = \frac{2}{\sqrt{\pi} }\int_0^x e^{-t^2} \, dt\).
Exp(operand) Exponentielle naturelle par élément x -> e^x.
Expm1(operand) Exponentielle naturelle par élément moins un
x -> e^x - 1.
Floor(operand) Prix plancher par élément x -> ⌊x⌋.
Imag(operand) Partie imaginaire par élément d'une forme complexe (ou réelle). x -> imag(x). Si l'opérande est de type à virgule flottante, renvoie 0.
IsFinite(operand) Vérifie si chaque élément de operand est fini, c'est-à-dire qu'il ne correspond pas à l'infini positif ou négatif, et qu'il n'est pas NaN. Renvoie un tableau de valeurs PRED de la même forme que l'entrée, où chaque élément est true si et seulement si l'élément d'entrée correspondant est fini.
Log(operand) Logarithme naturel par élément x -> ln(x).
Log1p(operand) Logarithme naturel décalé par élément x -> ln(1+x).
Logistic(operand) Calcul de la fonction logistique par élément x ->
logistic(x).
Neg(operand) Négation élément par élément x -> -x.
Not(operand) Non logique par élément x -> !(x).
PopulationCount(operand) Calcule le nombre de bits définis dans chaque élément de operand.
Real(operand) Partie réelle par élément d'une forme complexe (ou réelle).
x -> real(x). Si l'opérande est de type à virgule flottante, renvoie la même valeur.
Round(operand) Arrondi élément par élément, les valeurs égales sont arrondies à l'écart de zéro.
RoundNearestEven(operand) Arrondi par élément, arrondi au chiffre pair le plus proche.
Rsqrt(operand) Inverse élément par élément de l'opération racine carrée x -> 1.0 / sqrt(x).
Sign(operand) : opération de signe au niveau des éléments x -> sgn(x), où
\[\text{sgn}(x) = \begin{cases} -1 & x < 0\\ -0 & x = -0\\ NaN & x = NaN\\ +0 & x = +0\\ 1 & x > 0 \end{cases}\]
à l'aide de l'opérateur de comparaison du type d'élément operand.
Sin(operand) Sinus élément par élément x -> sin(x).
Sqrt(operand) Opération racine carrée au niveau des éléments x -> sqrt(x).
Tan(operand) Tangente élément par élément x -> tan(x).
Tanh(operand) Tangente hyperbolique élément par élément x -> tanh(x).
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
L'opérande de la fonction |
La fonction est appliquée à chaque élément du tableau operand, ce qui génère un tableau de la même forme. operand peut être un scalaire (0 dimensionnel).
Fft
L'opération FFT XLA implémente les transformées de Fourier directe et inverse pour les entrées/sorties réelles et complexes. Les FFT multidimensionnelles sur jusqu'à trois axes sont acceptées.
Consultez également XlaBuilder::Fft.
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau que nous transformons en transformée de Fourier. |
fft_type |
FftType |
Consultez le tableau ci-dessous. |
fft_length |
ArraySlice<int64> |
Longueurs au domaine temporel des axes en cours de transformation. Cela est nécessaire en particulier pour que l'IRFFT ajuste la taille de l'axe le plus interne, car RFFT(fft_length=[16]) a la même forme de sortie que RFFT(fft_length=[17]). |
FftType |
Sémantique |
|---|---|
FFT |
FFT complexe à complexe en temps réel La forme reste inchangée. |
IFFT |
FFT inverse complexe à complexe. La forme reste inchangée. |
RFFT |
FFT directe réelle-complexe. La forme de l'axe le plus interne est réduite à fft_length[-1] // 2 + 1 si fft_length[-1] est une valeur non nulle, ce qui omet la partie conjuguée inversée du signal transformé au-delà de la fréquence Nyquist. |
IRFFT |
FFT inverse réel-complexe (c'est-à-dire qu'elle prend un complexe et renvoie un réel). La forme de l'axe le plus interne est étendue à fft_length[-1] si fft_length[-1] est une valeur non nulle, ce qui permet d'inférer la partie du signal transformé au-delà de la fréquence Nyquist à partir de la conjugaison inverse des entrées 1 à fft_length[-1] // 2 + 1. |
FFT multidimensionnelle
Lorsque plus d'un fft_length est fourni, cela équivaut à appliquer une cascade d'opérations FFT à chacun des axes les plus internes. Notez que pour les cas réel->complexe et complexe->réel, la transformation de l'axe le plus interne est (effectivement) effectuée en premier (RFFT, dernière pour IRFFT), c'est pourquoi l'axe le plus interne est celui qui change de taille. Les autres transformations d'axe seront alors de type complexe->complexe.
Détails de mise en œuvre
La FFT du processeur est prise en charge par TensorFFT d'Eigen. La FFT GPU utilise cuFFT.
Recueillir
L'opération de collecte XLA assemble plusieurs tranches (chaque tranche à un décalage d'exécution potentiellement différent) d'un tableau d'entrée.
Sémantique générale
Consultez également XlaBuilder::Gather.
Pour une description plus intuitive, consultez la section "Description informelle" ci-dessous.
gather(operand, start_indices, offset_dims, collapsed_slice_dims,
slice_sizes, start_index_map)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Le tableau à partir duquel nous collectons les données. |
start_indices |
XlaOp |
Tableau contenant les indices de début des tranches que nous recueillons. |
index_vector_dim |
int64 |
Dimension dans start_indices qui "contient" les indices de début. Vous trouverez une description détaillée ci-dessous. |
offset_dims |
ArraySlice<int64> |
Ensemble de dimensions dans la forme de sortie qui est décalé dans un tableau découpé à partir de l'opérande. |
slice_sizes |
ArraySlice<int64> |
slice_sizes[i] correspond aux limites du segment sur la dimension i. |
collapsed_slice_dims |
ArraySlice<int64> |
Ensemble des dimensions de chaque tranche qui sont réduites. Ces dimensions doivent avoir une taille de 1. |
start_index_map |
ArraySlice<int64> |
Carte décrivant comment mapper les indices dans start_indices sur des indices valides dans l'opérande. |
indices_are_sorted |
bool |
Indique si les indices sont triés par l'appelant. |
Pour plus de commodité, nous étiquetons les dimensions du tableau de sortie qui ne sont pas dans offset_dims comme batch_dims.
Le résultat est un tableau avec des dimensions batch_dims.size + offset_dims.size.
operand.rank doit être égal à la somme de offset_dims.size et collapsed_slice_dims.size. De plus, slice_sizes.size doit être égal à operand.rank.
Si index_vector_dim est égal à start_indices.rank, nous considérons implicitement que start_indices possède une dimension 1 en fin de chaîne (c'est-à-dire que si start_indices avait la forme [6,7] et que index_vector_dim est 2, nous considérons implicitement que la forme de start_indices est [6,7,1]).
Les limites du tableau de sortie le long de la dimension i sont calculées comme suit:
Si
iest présent dansbatch_dims(c'est-à-dire qu'il est égal àbatch_dims[k]pour certainsk), nous choisissons les limites de dimension correspondantes dansstart_indices.shape, en ignorantindex_vector_dim(c'est-à-dire que nous choisissonsstart_indices.shape.dims[k] sik<index_vector_dimetstart_indices.shape.dims[k+1] dans le cas contraire).Si
iest présent dansoffset_dims(c'est-à-dire égal àoffset_dims[k] pour certainsk), nous choisissons la borne correspondante dansslice_sizesaprès avoir pris en comptecollapsed_slice_dims(c'est-à-dire que nous choisissonsadjusted_slice_sizes[k] oùadjusted_slice_sizesestslice_sizesavec les bornes aux indicescollapsed_slice_dimssupprimées).
Formellement, l'indice d'opérande In correspondant à un indice de sortie Out donné est calculé comme suit:
Soit
G= {Out[k] pourkdansbatch_dims}. UtilisezGpour extraire un vecteurStel queS[i] =start_indices[Combine(G,i)] où Combine(A, b) insère b à la positionindex_vector_dimdans A. Notez que cette valeur est bien définie, même siGest vide: siGest vide,S=start_indices.Créez un indice de départ,
Sin, dansoperandà l'aide deSen dispersantSà l'aide destart_index_map. Plus précisément:Sin[start_index_map[k]] =S[k] sik<start_index_map.size.Sin[_] =0sinon.
Créez un index
Oindansoperanden dispersant les indices aux dimensions de décalage dansOuten fonction de l'ensemblecollapsed_slice_dims. Plus précisément:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]] sik<offset_dims.size(remapped_offset_dimsest défini ci-dessous).Oin[_] =0sinon.
InestOin+Sin, où + correspond à l'addition par élément.
remapped_offset_dims est une fonction monotone avec domaine [0, offset_dims.size) et plage [0, operand.rank) \ collapsed_slice_dims. Par exemple, Si offset_dims.size est 4, operand.rank est 6 et collapsed_slice_dims est {0, 2}, alors remapped_offset_dims est {0→1, 1→3, 2→4, 3→5}.
Si indices_are_sorted est défini sur "true", XLA peut supposer que start_indices est trié (par ordre croissant, après avoir dispersé ses valeurs en fonction de start_index_map) par l'utilisateur. Si ce n'est pas le cas, la sémantique est définie par l'implémentation.
Description informelle et exemples
De manière informelle, chaque indice Out du tableau de sortie correspond à un élément E du tableau d'opérandes, calculé comme suit:
Nous utilisons les dimensions de lot dans
Outpour rechercher un indice de début à partir destart_indices.Nous utilisons
start_index_mappour mapper l'index de départ (dont la taille peut être inférieure à operand.rank) sur un index de départ "complet" dansoperand.Nous extrayons de manière dynamique une tranche de taille
slice_sizesà l'aide de l'index de début complet.Nous remodellons la tranche en réduisant les dimensions
collapsed_slice_dims. Étant donné que toutes les dimensions de tranche tronquée doivent avoir une limite de 1, cette refonte est toujours légale.Nous utilisons les dimensions de décalage dans
Outpour indexer cette tranche afin d'obtenir l'élément d'entrée,E, correspondant à l'index de sortieOut.
index_vector_dim est défini sur start_indices.rank - 1 dans tous les exemples suivants. Les valeurs plus intéressantes pour index_vector_dim ne modifient pas fondamentalement l'opération, mais rendent la représentation visuelle plus lourde.
Pour comprendre comment tous les éléments ci-dessus s'intègrent, examinons un exemple qui rassemble cinq tranches de forme [8,6] à partir d'un tableau [16,11]. La position d'un segment dans le tableau [16,11] peut être représentée sous la forme d'un vecteur d'index de forme S64[2]. L'ensemble de cinq positions peut donc être représenté sous la forme d'un tableau S64[5,2].
Le comportement de l'opération de rassemblement peut ensuite être représenté comme une transformation d'index qui prend [G,O0,O1], un indice dans la forme de sortie, et le mappe sur un élément du tableau d'entrée comme suit:
Nous sélectionnons d'abord un vecteur (X,Y) à partir du tableau des indices de collecte à l'aide de G.
L'élément du tableau de sortie à l'index [G,O0,O1] est alors l'élément du tableau d'entrée à l'index [X+O0,Y+O1].
slice_sizes est [8,6], qui détermine la plage d'O0 et d'O1, ce qui détermine à son tour les limites de la tranche.
Cette opération de collecte agit comme une tranche dynamique par lot avec G comme dimension de lot.
Les indices de collecte peuvent être multidimensionnels. Par exemple, une version plus générale de l'exemple ci-dessus utilisant un tableau "indices de collecte" de forme [4,5,2] traduirait les indices comme suit:
Ici encore, il s'agit d'une tranche dynamique par lot G0 et G1 comme dimensions de lot. La taille de la tranche est toujours [8,6].
L'opération de collecte dans XLA généralise la sémantique informelle décrite ci-dessus comme suit:
Nous pouvons configurer les dimensions de la forme de sortie qui sont les dimensions de décalage (dimensions contenant
O0,O1dans le dernier exemple). Les dimensions de lot de sortie (dimensions contenantG0,G1dans le dernier exemple) sont définies comme étant les dimensions de sortie qui ne sont pas des dimensions de décalage.Le nombre de dimensions de décalage de sortie explicitement présentes dans la forme de sortie peut être inférieur au nombre de dimensions d'entrée. Ces dimensions "manquantes", qui sont listées explicitement comme
collapsed_slice_dims, doivent avoir une taille de tranche de1. Étant donné qu'elles ont une taille de tranche de1, le seul indice valide pour elles est0, et leur suppression n'introduit aucune ambiguïté.La tranche extraite du tableau "Indices de collecte" ("
X,Y" dans le dernier exemple) peut comporter moins d'éléments que le nombre de dimensions du tableau d'entrée, et un mappage explicite dicte comment l'index doit être développé pour avoir le même nombre de dimensions que l'entrée.
Pour finir, nous utilisons (2) et (3) pour implémenter tf.gather_nd:
G0 et G1 permettent de découper un indice de départ à partir du tableau des indices de collecte, comme d'habitude, sauf que l'indice de départ ne comporte qu'un seul élément, X. De même, il n'y a qu'un seul indice de décalage de sortie avec la valeur O0. Toutefois, avant d'être utilisés comme indices dans le tableau d'entrée, ils sont développés conformément à la "mise en correspondance de l'index de collecte" (start_index_map dans la description formelle) et à la "mise en correspondance de l'offset" (remapped_offset_dims dans la description formelle) dans [X,0] et [0,O0] respectivement, ce qui donne [X,O0]. En d'autres termes, l'index de sortie [G0,G1,O0] correspond à l'index d'entrée [GatherIndices[G0,G1,0],O0], ce qui nous donne la sémantique de tf.gather_nd.
slice_sizes dans ce cas est [1,11]. Intuitif, cela signifie que chaque indice X du tableau des indices de collecte sélectionne une ligne entière, et le résultat est la concaténation de toutes ces lignes.
GetDimensionSize
Consultez également XlaBuilder::GetDimensionSize.
Renvoie la taille de la dimension donnée de l'opérande. L'opérande doit être au format tableau.
GetDimensionSize(operand, dimension)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau d'entrée à n dimensions |
dimension |
int64 |
Valeur de l'intervalle [0, n) qui spécifie la dimension |
SetDimensionSize
Consultez également XlaBuilder::SetDimensionSize.
Définit la taille dynamique de la dimension donnée de XlaOp. L'opérande doit être au format tableau.
SetDimensionSize(operand, size, dimension)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau d'entrée à n dimensions. |
size |
XlaOp |
int32 représentant la taille dynamique d'exécution. |
dimension |
int64 |
Valeur de l'intervalle [0, n) qui spécifie la dimension. |
Transmettez l'opérande en tant que résultat, avec une dimension dynamique suivie par le compilateur.
Les valeurs mises en forme sont ignorées par les opérations de réduction en aval.
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
GetTupleElement
Consultez également XlaBuilder::GetTupleElement.
Indexe dans un tuple avec une valeur constante au moment de la compilation.
La valeur doit être une constante au moment de la compilation afin que l'inférence de forme puisse déterminer le type de la valeur résultante.
Cela équivaut à std::get<int N>(t) en C++. Conceptuellement:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
Consultez également tf.tuple.
In-Feed
Consultez également XlaBuilder::Infeed.
Infeed(shape)
| Argument | Type | Sémantique |
|---|---|---|
shape |
Shape |
Format des données lues à partir de l'interface Infeed. Le champ de mise en page de la forme doit être défini pour correspondre à la mise en page des données envoyées à l'appareil. Sinon, son comportement n'est pas défini. |
Lit un seul élément de données à partir de l'interface de streaming Infeed implicite de l'appareil, interprète les données en tant que forme donnée et sa mise en page, puis renvoie un XlaOp des données. Plusieurs opérations Infeed sont autorisées dans un calcul, mais il doit y avoir un ordre total entre les opérations Infeed. Par exemple, deux Infeeds dans le code ci-dessous ont un ordre total, car il existe une dépendance entre les boucles while.
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
Les formes de tuple imbriquées ne sont pas acceptées. Pour une forme de tuple vide, l'opération Infeed est en fait une opération sans effet et se poursuit sans lire aucune donnée de l'influx de l'appareil.
Iota
Consultez également XlaBuilder::Iota.
Iota(shape, iota_dimension)
Crée une valeur littérale constante sur l'appareil plutôt qu'un transfert hôte potentiellement important. Crée un tableau dont la forme est spécifiée et qui contient des valeurs commençant à zéro et augmentant de 1 selon la dimension spécifiée. Pour les types à virgule flottante, le tableau produit est équivalent à ConvertElementType(Iota(...)), où Iota est de type entier et la conversion est au type à virgule flottante.
| Arguments | Type | Sémantique |
|---|---|---|
shape |
Shape |
Forme du tableau créé par Iota() |
iota_dimension |
int64 |
Dimension à incrémenter. |
Par exemple, Iota(s32[4, 8], 0) renvoie
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
Retours pour Iota(s32[4, 8], 1)
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
Carte
Consultez également XlaBuilder::Map.
Map(operands..., computation)
| Arguments | Type | Sémantique |
|---|---|---|
operands |
séquence de N XlaOp |
N tableaux de types T0..T{N-1} |
computation |
XlaComputation |
calcul de type T_0, T_1, .., T_{N + M -1} -> S avec N paramètres de type T et M de type arbitraire |
dimensions |
Tableau int64 |
tableau des dimensions de la carte |
Applique une fonction scalaire aux tableaux operands donnés, produisant un tableau de mêmes dimensions où chaque élément est le résultat de la fonction mappée appliquée aux éléments correspondants des tableaux d'entrée.
La fonction mappée est un calcul arbitraire avec la restriction qu'elle comporte N entrées de type scalaire T et une seule sortie de type S. La sortie a les mêmes dimensions que les opérandes, à l'exception du type d'élément T, qui est remplacé par S.
Par exemple: Map(op1, op2, op3, computation, par1) mappe elem_out <-
computation(elem1, elem2, elem3, par1) à chaque indice (multidimensionnel) des tableaux d'entrée pour produire le tableau de sortie.
OptimizationBarrier
Empêche toute étape d'optimisation de déplacer des calculs au-delà de la barrière.
S'assure que toutes les entrées sont évaluées avant les opérateurs qui dépendent des sorties de la barrière.
Pad
Consultez également XlaBuilder::Pad.
Pad(operand, padding_value, padding_config)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
tableau de type T |
padding_value |
XlaOp |
scalaire de type T pour remplir la marge ajoutée |
padding_config |
PaddingConfig |
la quantité de marge intérieure sur les deux bords (faible, élevée) et entre les éléments de chaque dimension ; |
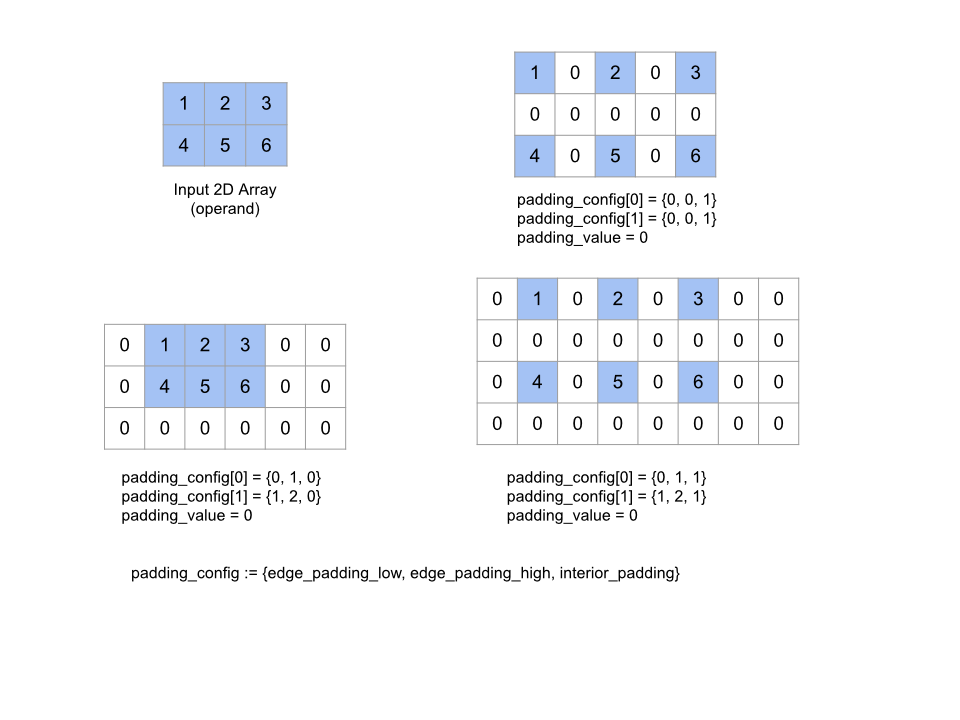
Élargit le tableau operand donné en ajoutant une marge interne autour du tableau et entre les éléments du tableau avec le padding_value donné. padding_config spécifie la quantité de marge intérieure et de marge extérieure pour chaque dimension.
PaddingConfig est un champ répété de PaddingConfigDimension, qui contient trois champs pour chaque dimension: edge_padding_low, edge_padding_high et interior_padding.
edge_padding_low et edge_padding_high spécifient respectivement la quantité de marge intérieure ajoutée à l'extrémité inférieure (à côté de l'indice 0) et à l'extrémité supérieure (à côté de l'indice le plus élevé) de chaque dimension. La valeur de la marge intérieure peut être négative. La valeur absolue de la marge intérieure négative indique le nombre d'éléments à supprimer de la dimension spécifiée.
interior_padding spécifie la quantité de marge intérieure ajoutée entre deux éléments de chaque dimension. Elle ne peut pas être négative. La marge intérieure se produit logiquement avant la marge extérieure. Par conséquent, en cas de marge extérieure négative, les éléments sont supprimés de l'opérande à marge intérieure.
Cette opération n'a aucun effet si les paires de marges extérieures sont toutes (0, 0) et que les valeurs de marge intérieure sont toutes égales à 0. La figure ci-dessous montre des exemples de valeurs edge_padding et interior_padding différentes pour un tableau à deux dimensions.
Recv
Consultez également XlaBuilder::Recv.
Recv(shape, channel_handle)
| Arguments | Type | Sémantique |
|---|---|---|
shape |
Shape |
forme des données à recevoir |
channel_handle |
ChannelHandle |
Identifiant unique pour chaque paire d'envoi/réception |
Réçoit les données de la forme donnée à partir d'une instruction Send dans un autre calcul qui partage le même canal. Renvoie un XlaOp pour les données reçues.
L'API cliente de l'opération Recv représente la communication synchrone.
Toutefois, l'instruction est décomposée en interne en deux instructions HLO (Recv et RecvDone) pour permettre les transferts de données asynchrones. Voir également HloInstruction::CreateRecv et HloInstruction::CreateRecvDone.
Recv(const Shape& shape, int64 channel_id)
Alloue les ressources requises pour recevoir des données à partir d'une instruction Send avec le même channel_id. Renvoie un contexte pour les ressources allouées, qui est utilisé par une instruction RecvDone suivante pour attendre la fin du transfert de données. Le contexte est un tuple de {tampon de réception (forme), identifiant de requête (U32)} et ne peut être utilisé que par une instruction RecvDone.
RecvDone(HloInstruction context)
Compte tenu d'un contexte créé par une instruction Recv, attend la fin du transfert de données et renvoie les données reçues.
Restreindre
Consultez également XlaBuilder::Reduce.
Applique une fonction de réduction à un ou plusieurs tableaux en parallèle.
Reduce(operands..., init_values..., computation, dimensions)
| Arguments | Type | Sémantique |
|---|---|---|
operands |
Séquence de N XlaOp |
N tableaux de types T_0, ..., T_{N-1}. |
init_values |
Séquence de N XlaOp |
N scalaires de types T_0, ..., T_{N-1}. |
computation |
XlaComputation |
calcul de type T_0, ..., T_{N-1}, T_0, ..., T_{N-1} -> Collate(T_0, ..., T_{N-1}). |
dimensions |
Tableau int64 |
Tableau non ordonné de dimensions à réduire. |
Où :
- N doit être supérieur ou égal à 1.
- Le calcul doit être "à peu près" associatif (voir ci-dessous).
- Tous les tableaux d'entrée doivent avoir les mêmes dimensions.
- Toutes les valeurs initiales doivent former une identité sous
computation. - Si
N = 1,Collate(T)estT. - Si
N > 1,Collate(T_0, ..., T_{N-1})est un tuple d'élémentsNde typeT.
Cette opération réduit une ou plusieurs dimensions de chaque tableau d'entrée en scalaires.
Le nombre de dimensions de chaque tableau renvoyé est number_of_dimensions(operand) - len(dimensions). La sortie de l'opération est Collate(Q_0, ..., Q_N), où Q_i est un tableau de type T_i, dont les dimensions sont décrites ci-dessous.
Différents backends sont autorisés à associer à nouveau le calcul de réduction. Cela peut entraîner des différences numériques, car certaines fonctions de réduction telles que l'addition ne sont pas associatives pour les nombres à virgule flottante. Toutefois, si la plage des données est limitée, l'addition à virgule flottante est suffisamment proche de l'associativité pour la plupart des utilisations pratiques.
Exemples
Lorsque vous effectuez une réduction sur une dimension dans un seul tableau 1D avec des valeurs [10, 11,
12, 13], avec la fonction de réduction f (il s'agit de computation), vous pouvez calculer la valeur comme suit :
f(10, f(11, f(12, f(init_value, 13)))
mais il existe également de nombreuses autres possibilités, par exemple :
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
Voici un exemple de pseudo-code approximatif de la façon dont la réduction peut être implémentée, en utilisant la somme comme calcul de réduction avec une valeur initiale de 0.
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
Voici un exemple de réduction d'une matrice (tableau à deux dimensions). La forme comporte deux dimensions, la dimension 0 de taille 2 et la dimension 1 de taille 3:
Résultats de la réduction des dimensions 0 ou 1 avec une fonction "add" :
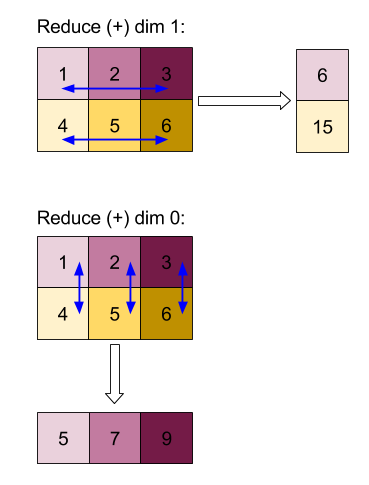
Notez que les deux résultats de réduction sont des tableaux 1D. Le diagramme en affiche une sous forme de colonne et l'autre sous forme de ligne, uniquement pour faciliter la visualisation.
Voici un exemple plus complexe d'une matrice 3D. Il comporte trois dimensions : la dimension 0 de taille 4, la dimension 1 de taille 2 et la dimension 2 de taille 3. Pour simplifier, les valeurs de 1 à 6 sont répliquées dans la dimension 0.
Comme dans l'exemple 2D, nous pouvons réduire une seule dimension. Si nous réduisons la dimension 0, par exemple, nous obtenons un tableau à deux dimensions dans lequel toutes les valeurs de la dimension 0 ont été pliées dans un scalaire:
| 4 8 12 |
| 16 20 24 |
Si nous réduisons la dimension 2, nous obtenons également un tableau à deux dimensions dans lequel toutes les valeurs de la dimension 2 ont été pliées dans un scalaire:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
Notez que l'ordre relatif entre les dimensions restantes de l'entrée est conservé dans la sortie, mais que de nouveaux numéros peuvent être attribués à certaines dimensions (puisque le nombre de dimensions change).
Nous pouvons également réduire plusieurs dimensions. Les dimensions de réduction d'ajout 0 et 1 génèrent le tableau 1D [20, 28, 36].
La réduction de la matrice 3D sur toutes ses dimensions produit le scalaire 84.
Réduction variadique
Avec N > 1, l'application de la fonction de réduction est légèrement plus complexe, car elle est appliquée simultanément à toutes les entrées. Les opérandes sont fournies au calcul dans l'ordre suivant:
- Valeur réduite en cours d'exécution pour le premier opérande
- …
- Valeur réduite en cours d'exécution pour l'opérande N
- Valeur d'entrée pour le premier opérande
- …
- Valeur d'entrée pour l'opérande N
Par exemple, considérons la fonction de réduction suivante, qui peut être utilisée pour calculer le maximum et l'argmax d'un tableau à dimension 1 en parallèle:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
Pour les tableaux d'entrée 1D V = Float[N], K = Int[N] et les valeurs d'initialisation I_V = Float, I_K = Int, le résultat f_(N-1) de la réduction sur la seule dimension d'entrée est équivalent à l'application récursive suivante:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
L'application de cette réduction à un tableau de valeurs et à un tableau d'indices séquentiels (c'est-à-dire iota) permet de co-itérer sur les tableaux et de renvoyer un tuple contenant la valeur maximale et l'indice correspondant.
ReducePrecision
Consultez également XlaBuilder::ReducePrecision.
Modélise l'effet de la conversion des valeurs à virgule flottante en un format à précision inférieure (tel que IEEE-FP16) et de leur retour au format d'origine. Le nombre de bits d'exposant et de mantisse dans le format à précision inférieure peut être spécifié de manière arbitraire, bien que toutes les tailles de bits ne soient pas compatibles avec toutes les implémentations matérielles.
ReducePrecision(operand, mantissa_bits, exponent_bits)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau de type à virgule flottante T. |
exponent_bits |
int32 |
Nombre de bits d'exposant au format à précision inférieure |
mantissa_bits |
int32 |
Nombre de bits de mantisse au format à précision inférieure |
Le résultat est un tableau de type T. Les valeurs d'entrée sont arrondies à la valeur la plus proche pouvant être représentée avec le nombre donné de bits de mantisse (à l'aide de la sémantique "égalités à pair"), et toutes les valeurs qui dépassent la plage spécifiée par le nombre de bits d'exposant sont limitées à l'infini positif ou négatif. Les valeurs NaN sont conservées, bien qu'elles puissent être converties en valeurs NaN canoniques.
Le format à précision inférieure doit comporter au moins un bit d'exposant (afin de distinguer une valeur nulle d'une infinité, car les deux ont une mantisse nulle) et un nombre non négatif de bits de mantisse. Le nombre de bits d'exposant ou de mantisse peut dépasser la valeur correspondante pour le type T. La partie correspondante de la conversion est alors simplement une opération sans effet.
ReduceScatter
Consultez également XlaBuilder::ReduceScatter.
ReduceScatter est une opération collective qui effectue effectivement une opération AllReduce, puis disperse le résultat en le divisant en blocs shard_count le long de scatter_dimension et le réplica i du groupe de réplicas reçoit le segment ith.
ReduceScatter(operand, computation, scatter_dim, shard_count,
replica_group_ids, channel_id)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau ou tuple de tableaux non vide à réduire entre les réplicas. |
computation |
XlaComputation |
Calcul de la réduction |
scatter_dimension |
int64 |
Dimension à disperser. |
shard_count |
int64 |
Nombre de blocs à diviser scatter_dimension |
replica_groups |
vecteur de vecteurs de int64 |
Groupes entre lesquels les réductions sont effectuées |
channel_id |
int64 facultatif |
ID de canal facultatif pour la communication inter-modules |
- Lorsque
operandest un tuple de tableaux, la réduction-dispersion est effectuée sur chaque élément du tuple. replica_groupsest une liste de groupes de réplicas entre lesquels la réduction est effectuée (l'ID de réplica pour le réplica actuel peut être récupéré à l'aide deReplicaId). L'ordre des réplicas dans chaque groupe détermine l'ordre dans lequel le résultat de la réduction globale sera dispersé.replica_groupsdoit être vide (dans ce cas, tous les réplicas appartiennent à un seul groupe) ou contenir le même nombre d'éléments que le nombre de réplicas. Lorsqu'il existe plusieurs groupes de réplication, ils doivent tous être de la même taille. Par exemple,replica_groups = {0, 2}, {1, 3}effectue une réduction entre les réplicas0et2, et1et3, puis disperse le résultat.shard_countcorrespond à la taille de chaque groupe de réplication. Nous en avons besoin lorsquereplica_groupsest vide. Sireplica_groupsn'est pas vide,shard_countdoit être égal à la taille de chaque groupe de réplicas.channel_idest utilisé pour la communication entre les modules: seules les opérationsreduce-scatteravec le mêmechannel_idpeuvent communiquer entre elles.
La forme de sortie est la forme d'entrée avec scatter_dimension réduit de shard_count fois. Par exemple, s'il existe deux réplications et que l'opérande a les valeurs [1.0, 2.25] et [3.0, 5.25] respectivement sur les deux réplications, la valeur de sortie de cette opération où scatter_dim est 0 sera [4.0] pour le premier réplica et [7.5] pour le second réplica.
ReduceWindow
Consultez également XlaBuilder::ReduceWindow.
Applique une fonction de réduction à tous les éléments de chaque fenêtre d'une séquence de N tableaux multidimensionnels, et produit un seul tableau multidimensionnel ou un tuple de N tableaux multidimensionnels en sortie. Chaque tableau de sortie comporte le même nombre d'éléments que le nombre de positions valides de la fenêtre. Une couche de pooling peut être exprimée sous la forme d'une ReduceWindow. Comme pour Reduce, le computation appliqué est toujours transmis au init_values sur la gauche.
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| Arguments | Type | Sémantique |
|---|---|---|
operands |
N XlaOps |
Séquence de N tableaux multidimensionnels de types T_0,..., T_{N-1}, chacun représentant la zone de base sur laquelle la fenêtre est placée. |
init_values |
N XlaOps |
Les N valeurs de départ de la réduction, une pour chacune des N opérandes. Pour en savoir plus, consultez Réduire. |
computation |
XlaComputation |
Fonction de réduction de type T_0, ..., T_{N-1}, T_0, ..., T_{N-1} -> Collate(T_0, ..., T_{N-1}), à appliquer aux éléments de chaque fenêtre de tous les opérandes d'entrée. |
window_dimensions |
ArraySlice<int64> |
Tableau d'entiers pour les valeurs de dimension de fenêtre |
window_strides |
ArraySlice<int64> |
Tableau d'entiers pour les valeurs de pas de fenêtre |
base_dilations |
ArraySlice<int64> |
Tableau d'entiers pour les valeurs de dilatation de base |
window_dilations |
ArraySlice<int64> |
Tableau d'entiers pour les valeurs de dilatation de la fenêtre |
padding |
Padding |
Type de marge intérieure pour la fenêtre (Padding::kSame, qui ajoute une marge intérieure pour avoir la même forme de sortie que l'entrée si la longueur de pas est de 1, ou Padding::kValid, qui n'utilise aucune marge intérieure et "arrête" la fenêtre une fois qu'elle ne convient plus) |
Où :
- N doit être supérieur ou égal à 1.
- Tous les tableaux d'entrée doivent avoir les mêmes dimensions.
- Si
N = 1,Collate(T)estT. - Si
N > 1,Collate(T_0, ..., T_{N-1})est un tuple d'élémentsNde type(T0,...T{N-1}).
Le code et l'image ci-dessous illustrent un exemple d'utilisation de ReduceWindow. L'entrée est une matrice de taille [4x6], et les dimensions de fenêtre et de pas de fenêtre sont [2x3].
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
Une valeur de pas de 1 dans une dimension indique que la position d'une fenêtre dans la dimension est à un élément de sa fenêtre adjacente. Pour spécifier qu'aucune fenêtre ne se chevauche, window_stride_dimensions doit être égal à window_dimensions. La figure ci-dessous illustre l'utilisation de deux valeurs de pas différentes. Le remplissage est appliqué à chaque dimension de l'entrée, et les calculs sont les mêmes que si l'entrée était fournie avec les dimensions qu'elle a après le remplissage.
Pour un exemple de remplissage non trivial, envisagez de calculer la valeur minimale de la fenêtre de réduction (valeur initiale : MAX_FLOAT) avec la dimension 3 et la longueur de pas 2 sur le tableau d'entrée [10000, 1000, 100, 10, 1]. Le remplissage kValid calcule les valeurs minimales sur deux fenêtres valides: [10000, 1000, 100] et [100, 10, 1], ce qui génère la sortie [100, 1]. Le remplissage kSame remplit d'abord le tableau afin que la forme après la fenêtre de réduction soit la même que l'entrée pour la première étape en ajoutant des éléments initiaux des deux côtés, ce qui donne [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE]. L'exécution de reduce-window sur le tableau rembourré s'effectue sur trois fenêtres [MAX_VALUE, 10000, 1000], [1000, 100, 10] et [10, 1, MAX_VALUE], et génère [1000, 10, 1].
L'ordre d'évaluation de la fonction de réduction est arbitraire et peut être non déterministe. Par conséquent, la fonction de réduction ne doit pas être trop sensible à la réassociation. Pour en savoir plus, consultez la discussion sur l'associativité dans le contexte de Reduce.
ReplicaId
Consultez également XlaBuilder::ReplicaId.
Renvoie l'identifiant unique (scalaire U32) du réplica.
ReplicaId()
L'ID unique de chaque réplica est un entier non signé dans l'intervalle [0, N), où N est le nombre de réplicas. Étant donné que tous les réplicas exécutent le même programme, un appel ReplicaId() dans le programme renvoie une valeur différente sur chaque réplica.
Remodeler
Consultez également XlaBuilder::Reshape et l'opération Collapse.
Remet en forme les dimensions d'un tableau dans une nouvelle configuration.
Reshape(operand, dimensions)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
tableau de type T |
dimensions |
Vecteur int64 |
vecteur des tailles des nouvelles dimensions |
Conceptuellement, la fonction reshape aplatit d'abord un tableau en un vecteur unidimensionnel de valeurs de données, puis affine ce vecteur en une nouvelle forme. Les arguments d'entrée sont un tableau arbitraire de type T, un vecteur constant au moment de la compilation d'indices de dimension et un vecteur constant au moment de la compilation de tailles de dimension pour le résultat.
Le vecteur dimensions détermine la taille du tableau de sortie. La valeur à l'index 0 dans dimensions correspond à la taille de la dimension 0, la valeur à l'index 1 correspond à la taille de la dimension 1, et ainsi de suite. Le produit des dimensions dimensions doit être égal au produit des tailles de dimension de l'opérande. Lorsque vous affinez le tableau condensé dans le tableau multidimensionnel défini par dimensions, les dimensions de dimensions sont triées de la variation la plus lente (la plus importante) à la variation la plus rapide (la plus mineure).
Par exemple, supposons que v soit un tableau de 24 éléments:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
Dans un cas particulier, reshape peut transformer un tableau à un seul élément en scalaire et inversement. Par exemple,
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
Rev (inverse)
Consultez également XlaBuilder::Rev.
Rev(operand, dimensions)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
tableau de type T |
dimensions |
ArraySlice<int64> |
dimensions à inverser |
Inverse l'ordre des éléments du tableau operand le long du dimensions spécifié, générant un tableau de sortie de la même forme. Chaque élément du tableau d'opérandes à un indice multidimensionnel est stocké dans le tableau de sortie à un indice transformé. L'indice multidimensionnel est transformé en inversant l'indice dans chaque dimension à inverser (c'est-à-dire que si une dimension de taille N est l'une des dimensions à inverser, son indice i est transformé en N-1-i).
L'opération Rev permet, entre autres, d'inverser le tableau de poids de convolution le long des deux dimensions de la fenêtre lors du calcul du gradient dans les réseaux de neurones.
RngNormal
Consultez également XlaBuilder::RngNormal.
Construit une sortie d'une forme donnée avec des nombres aléatoires générés selon la distribution normale \(N(\mu, \sigma)\) . Les paramètres \(\mu\) et \(\sigma\), ainsi que la forme de sortie, doivent avoir un type élémentaire à virgule flottante. De plus, les paramètres doivent être des valeurs scalaires.
RngNormal(mu, sigma, shape)
| Arguments | Type | Sémantique |
|---|---|---|
mu |
XlaOp |
Scalaire de type T spécifiant la moyenne des nombres générés |
sigma |
XlaOp |
Scalaire de type T spécifiant l'écart type de la valeur générée |
shape |
Shape |
Forme de sortie de type T |
RngUniform
Consultez également XlaBuilder::RngUniform.
Construit une sortie d'une forme donnée avec des nombres aléatoires générés selon la distribution uniforme sur l'intervalle \([a,b)\). Les paramètres et le type d'élément de sortie doivent être de type booléen, entier ou à virgule flottante, et les types doivent être cohérents. Les backends de processeur et de GPU ne sont actuellement compatibles qu'avec les types de données F64, F32, F16, BF16, S64, U64, S32 et U32. De plus, les paramètres doivent avoir une valeur scalaire. Si \(b <= a\) , le résultat est défini par l'implémentation.
RngUniform(a, b, shape)
| Arguments | Type | Sémantique |
|---|---|---|
a |
XlaOp |
Scalaire de type T spécifiant la limite inférieure de l'intervalle |
b |
XlaOp |
Scalaire de type T spécifiant la limite supérieure de l'intervalle |
shape |
Shape |
Forme de sortie de type T |
RngBitGenerator
Génère une sortie avec une forme donnée remplie de bits aléatoires uniformes à l'aide de l'algorithme spécifié (ou par défaut du backend) et renvoie un état mis à jour (avec la même forme que l'état initial) et les données aléatoires générées.
L'état initial correspond à l'état initial de la génération de nombres aléatoires actuelle. La forme et les valeurs valides requises, ainsi que la valeur, dépendent de l'algorithme utilisé.
La sortie est garantie comme étant une fonction déterministe de l'état initial, mais elle n'est pas garantie comme étant déterministe entre les backends et les différentes versions du compilateur.
RngBitGenerator(algorithm, key, shape)
| Arguments | Type | Sémantique |
|---|---|---|
algorithm |
RandomAlgorithm |
Algorithme de générateur de nombres pseudo-aléatoires à utiliser. |
initial_state |
XlaOp |
État initial de l'algorithme PRNG. |
shape |
Shape |
Forme de sortie des données générées. |
Valeurs disponibles pour algorithm:
rng_default: algorithme spécifique au backend avec des exigences de forme spécifiques au backend.rng_three_fry: algorithme PRNG basé sur un compteur ThreeFry. La formeinitial_stateestu64[2]avec des valeurs arbitraires. Salmon et al. SC 2011. Nombres aléatoires parallèles: un jeu d'enfant.rng_philox: algorithme Philox pour générer des nombres aléatoires en parallèle. La formeinitial_stateestu64[3]avec des valeurs arbitraires. Salmon et al. SC 2011. Nombres aléatoires parallèles: un jeu d'enfant.
Nuage de points
L'opération de dispersion XLA génère une séquence de résultats qui sont les valeurs du tableau d'entrée operands, avec plusieurs tranches (aux indices spécifiés par scatter_indices) mises à jour avec la séquence de valeurs dans updates à l'aide de update_computation.
Consultez également XlaBuilder::Scatter.
scatter(operands..., scatter_indices, updates..., update_computation,
index_vector_dim, update_window_dims, inserted_window_dims,
scatter_dims_to_operand_dims)
| Arguments | Type | Sémantique |
|---|---|---|
operands |
Séquence de N XlaOp |
N tableaux de types T_0, ..., T_N à répartir. |
scatter_indices |
XlaOp |
Tableau contenant les indices de début des tranches vers lesquelles les données doivent être dispersées. |
updates |
Séquence de N XlaOp |
N tableaux de types T_0, ..., T_N. updates[i] contient les valeurs à utiliser pour la diffusion operands[i]. |
update_computation |
XlaComputation |
Calcul à utiliser pour combiner les valeurs existantes du tableau d'entrée et les mises à jour lors de la dispersion. Ce calcul doit être de type T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N). |
index_vector_dim |
int64 |
Dimension dans scatter_indices contenant les indices de début. |
update_window_dims |
ArraySlice<int64> |
Ensemble de dimensions sous forme updates qui correspondent aux dimensions de la fenêtre. |
inserted_window_dims |
ArraySlice<int64> |
Ensemble des dimensions de la fenêtre à insérer dans la forme updates. |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
Mappage des dimensions des indices de dispersion sur l'espace d'index des opérandes. Ce tableau est interprété comme mappant i sur scatter_dims_to_operand_dims[i] . Il doit s'agir d'un contact direct et total. |
indices_are_sorted |
bool |
Indique si les indices sont triés par l'appelant. |
unique_indices |
bool |
Indique si l'appelant garantit que les indices sont uniques. |
Où :
- N doit être supérieur ou égal à 1.
operands[0], ...,operands[N-1] doivent tous avoir les mêmes dimensions.updates[0], ...,updates[N-1] doivent tous avoir les mêmes dimensions.- Si
N = 1,Collate(T)estT. - Si
N > 1,Collate(T_0, ..., T_N)est un tuple d'élémentsNde typeT.
Si index_vector_dim est égal à scatter_indices.rank, nous considérons implicitement que scatter_indices possède une dimension 1 à la fin.
Nous définissons update_scatter_dims de type ArraySlice<int64> comme l'ensemble des dimensions de forme updates qui ne sont pas dans update_window_dims, par ordre croissant.
Les arguments de la fonction scatter doivent respecter les contraintes suivantes:
Chaque tableau
updatesdoit avoir des dimensionsupdate_window_dims.size + scatter_indices.rank - 1.Les limites de la dimension
idans chaque tableauupdatesdoivent respecter les conditions suivantes:- Si
iest présent dansupdate_window_dims(c'est-à-dire égal àupdate_window_dims[k] pour certainsk), la limite de la dimensionidansupdatesne doit pas dépasser la limite correspondante deoperandaprès prise en compte deinserted_window_dims(c'est-à-direadjusted_window_bounds[k], oùadjusted_window_boundscontient les limites deoperandavec les limites aux indicesinserted_window_dimssupprimées). - Si
iest présent dansupdate_scatter_dims(c'est-à-dire égal àupdate_scatter_dims[k] pour certainsk), la limite de la dimensionidansupdatesdoit être égale à la limite correspondante descatter_indices, en ignorantindex_vector_dim(c'est-à-direscatter_indices.shape.dims[k], sik<index_vector_dimetscatter_indices.shape.dims[k+1] dans le cas contraire).
- Si
update_window_dimsdoit être trié par ordre croissant, ne pas contenir de numéros de dimension en double et être compris dans la plage[0, updates.rank).inserted_window_dimsdoit être trié par ordre croissant, ne pas contenir de numéros de dimension en double et être compris dans la plage[0, operand.rank).operand.rankdoit être égal à la somme deupdate_window_dims.sizeetinserted_window_dims.size.scatter_dims_to_operand_dims.sizedoit être égal àscatter_indices.shape.dims[index_vector_dim], et ses valeurs doivent être comprises dans la plage[0, operand.rank).
Pour un indice U donné dans chaque tableau updates, l'indice I correspondant dans le tableau operands correspondant auquel cette mise à jour doit être appliquée est calculé comme suit:
- Soit
G= {U[k] pourkdansupdate_scatter_dims}. UtilisezGpour rechercher un vecteur d'indexSdans le tableauscatter_indicesde sorte queS[i] =scatter_indices[Combine(G,i)] où Combine(A, b) insère b aux positionsindex_vector_dimdans A. - Créez un indice
Sindansoperandà l'aide deSen dispersantSà l'aide de la cartescatter_dims_to_operand_dims. Plus formellement :Sin[scatter_dims_to_operand_dims[k]] =S[k] sik<scatter_dims_to_operand_dims.size.Sin[_] =0sinon.
- Créez un index
Windans chaque tableauoperandsen dispersant les indices àupdate_window_dimsdansUseloninserted_window_dims. Plus formellement :Win[window_dims_to_operand_dims(k)] =U[k] sikappartient àupdate_window_dims, oùwindow_dims_to_operand_dimsest la fonction monotone avec domaine [0,update_window_dims.size) et plage [0,operand.rank) \inserted_window_dims. (Par exemple, siupdate_window_dims.sizeest4,operand.rankest6etinserted_window_dimsest {0,2},window_dims_to_operand_dimsest {0→1,1→3,2→4,3→5}).Win[_] =0sinon.
IestWin+Sin, où + correspond à l'addition par élément.
En résumé, l'opération de dispersion peut être définie comme suit.
- Initialisez
outputavecoperands, c'est-à-dire pour tous les indicesJ, pour tous les indicesOdans le tableauoperands[J] :
output[J][O] =operands[J][O] - Pour chaque index
Udans le tableauupdates[J] et l'indexOcorrespondant dans le tableauoperand[J], siOest un index valide pouroutput:
(output[0][O], ...,output[N-1][O]) =update_computation(output[0][O], ..., ,output[N-1][O],updates[0][U], ...,updates[N-1][U])
L'ordre dans lequel les mises à jour sont appliquées n'est pas déterministe. Ainsi, lorsque plusieurs indices dans updates font référence au même indice dans operands, la valeur correspondante dans output n'est pas déterministe.
Notez que le premier paramètre transmis à update_computation sera toujours la valeur actuelle du tableau output et que le deuxième paramètre sera toujours la valeur du tableau updates. Cela est particulièrement important lorsque update_computation n'est pas commutatif.
Si indices_are_sorted est défini sur "true", XLA peut supposer que l'utilisateur a trié les scatter_indices (par ordre croissant, après avoir dispersé ses valeurs en fonction de scatter_dims_to_operand_dims). Sinon, la sémantique est définie par l'implémentation.
Si unique_indices est défini sur "true", XLA peut supposer que tous les éléments dispersés sont uniques. XLA peut donc utiliser des opérations non atomiques. Si unique_indices est défini sur "true" et que les indices vers lesquels la diffusion est effectuée ne sont pas uniques, la sémantique est définie par l'implémentation.
De manière informelle, l'opération de dispersion peut être considérée comme l'inverse de l'opération de collecte, c'est-à-dire que l'opération de dispersion met à jour les éléments de l'entrée qui sont extraits par l'opération de collecte correspondante.
Pour obtenir une description informelle détaillée et des exemples, consultez la section "Description informelle" sous Gather.
Sélectionner
Consultez également XlaBuilder::Select.
Construit un tableau de sortie à partir des éléments de deux tableaux d'entrée, en fonction des valeurs d'un tableau de prédicats.
Select(pred, on_true, on_false)
| Arguments | Type | Sémantique |
|---|---|---|
pred |
XlaOp |
tableau de type PRED |
on_true |
XlaOp |
tableau de type T |
on_false |
XlaOp |
tableau de type T |
Les tableaux on_true et on_false doivent avoir la même forme. Il s'agit également de la forme du tableau de sortie. Le tableau pred doit avoir la même dimensionnalité que on_true et on_false, avec le type d'élément PRED.
Pour chaque élément P de pred, l'élément correspondant du tableau de sortie est extrait de on_true si la valeur de P est true, et de on_false si la valeur de P est false. En tant que forme restreinte de diffusion, pred peut être un scalaire de type PRED. Dans ce cas, le tableau de sortie est entièrement extrait de on_true si pred est true, et de on_false si pred est false.
Exemple avec pred non scalaire:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
Exemple avec un scalaire pred:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
Les sélections entre des tupels sont acceptées. À cette fin, les tupels sont considérés comme des types scalaires. Si on_true et on_false sont des tupels (qui doivent avoir la même forme), pred doit être un scalaire de type PRED.
SelectAndScatter
Consultez également XlaBuilder::SelectAndScatter.
Cette opération peut être considérée comme une opération composite qui calcule d'abord ReduceWindow sur le tableau operand pour sélectionner un élément de chaque fenêtre, puis disperse le tableau source sur les indices des éléments sélectionnés pour construire un tableau de sortie de la même forme que le tableau d'opérande. La fonction select binaire permet de sélectionner un élément de chaque fenêtre en l'appliquant à chaque fenêtre. Elle est appelée avec la propriété que le vecteur d'index du premier paramètre est lexicographiquement inférieur au vecteur d'index du deuxième paramètre. La fonction select renvoie true si le premier paramètre est sélectionné et false si le deuxième paramètre est sélectionné. La fonction doit respecter la transitivité (c'est-à-dire que si select(a, b) et select(b, c) sont true, select(a, c) est également true) afin que l'élément sélectionné ne dépende pas de l'ordre des éléments parcourus pour une fenêtre donnée.
La fonction scatter est appliquée à chaque indice sélectionné dans le tableau de sortie. Elle prend deux paramètres scalaires:
- Valeur actuelle à l'index sélectionné dans le tableau de sortie
- Valeur de dispersion de
sourcequi s'applique à l'indice sélectionné
Il combine les deux paramètres et renvoie une valeur scalaire utilisée pour mettre à jour la valeur à l'index sélectionné dans le tableau de sortie. Initialement, tous les indices du tableau de sortie sont définis sur init_value.
Le tableau de sortie a la même forme que le tableau operand, et le tableau source doit avoir la même forme que le résultat de l'application d'une opération ReduceWindow sur le tableau operand. SelectAndScatter peut être utilisé pour rétrodiffuser les valeurs de gradient pour une couche de pooling dans un réseau de neurones.
SelectAndScatter(operand, select, window_dimensions, window_strides,
padding, source, init_value, scatter)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
tableau de type T sur lequel les fenêtres glissent |
select |
XlaComputation |
Calcul binaire de type T, T -> PRED, à appliquer à tous les éléments de chaque fenêtre. Renvoie true si le premier paramètre est sélectionné et false si le deuxième paramètre est sélectionné. |
window_dimensions |
ArraySlice<int64> |
Tableau d'entiers pour les valeurs de dimension de fenêtre |
window_strides |
ArraySlice<int64> |
Tableau d'entiers pour les valeurs de pas de fenêtre |
padding |
Padding |
Type de marge intérieure pour la fenêtre (Padding::kSame ou Padding::kValid) |
source |
XlaOp |
Tableau de type T contenant les valeurs à disperser |
init_value |
XlaOp |
Valeur scalaire de type T pour la valeur initiale du tableau de sortie |
scatter |
XlaComputation |
Calcul binaire de type T, T -> T, pour appliquer chaque élément source de dispersion à son élément de destination |
La figure ci-dessous montre des exemples d'utilisation de SelectAndScatter, avec la fonction select qui calcule la valeur maximale parmi ses paramètres. Notez que lorsque les fenêtres se chevauchent, comme dans la figure 2 ci-dessous, un indice du tableau operand peut être sélectionné plusieurs fois par différentes fenêtres. Dans l'image, l'élément de valeur 9 est sélectionné par les deux fenêtres supérieures (bleue et rouge), et la fonction scatter d'addition binaire produit l'élément de sortie de valeur 8 (2 + 6).
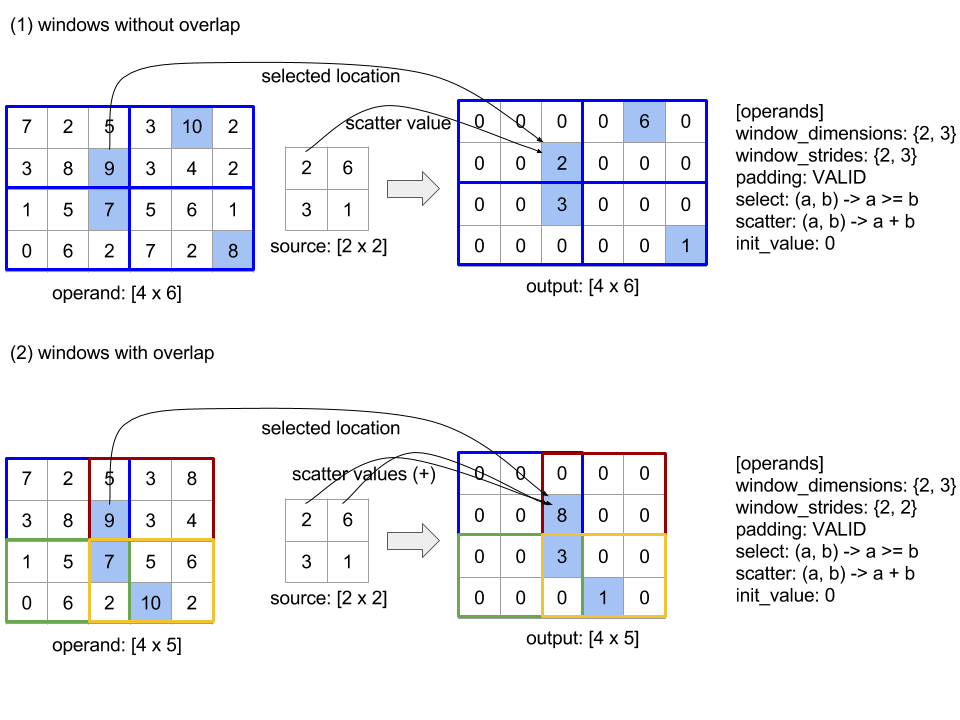
L'ordre d'évaluation de la fonction scatter est arbitraire et peut être non déterministe. Par conséquent, la fonction scatter ne doit pas être trop sensible à la réassociation. Pour en savoir plus, consultez la discussion sur l'associativité dans le contexte de Reduce.
Envoyer
Consultez également XlaBuilder::Send.
Send(operand, channel_handle)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Données à envoyer (tableau de type T) |
channel_handle |
ChannelHandle |
Identifiant unique pour chaque paire d'envoi/réception |
Envoie les données d'opérande données à une instruction Recv dans un autre calcul qui partage le même gestionnaire de canaux. ne renvoie aucune donnée ;
Comme pour l'opération Recv, l'API cliente de l'opération Send représente la communication synchrone et est décomposée en interne en deux instructions HLO (Send et SendDone) pour permettre les transferts de données asynchrones. Voir également HloInstruction::CreateSend et HloInstruction::CreateSendDone.
Send(HloInstruction operand, int64 channel_id)
Lance un transfert asynchrone de l'opérande vers les ressources allouées par l'instruction Recv avec le même ID de canal. Renvoie un contexte, qui est utilisé par une instruction SendDone suivante pour attendre la fin du transfert de données. Le contexte est un tuple de {operand (shape), request identifier (U32)} et ne peut être utilisé que par une instruction SendDone.
SendDone(HloInstruction context)
Compte tenu d'un contexte créé par une instruction Send, attend la fin du transfert de données. L'instruction ne renvoie aucune donnée.
Planifier des instructions de diffusion sur les chaînes
L'ordre d'exécution des quatre instructions pour chaque canal (Recv, RecvDone, Send et SendDone) est le suivant.
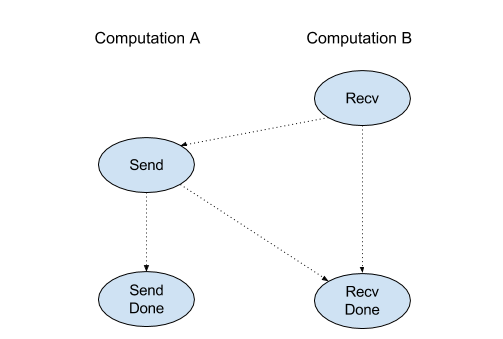
Recvse produit avantSendSendse produit avantRecvDoneRecvse produit avantRecvDoneSendse produit avantSendDone
Lorsque les compilateurs backend génèrent un calendrier linéaire pour chaque calcul qui communique via des instructions de canal, il ne doit pas y avoir de cycles dans les calculs. Par exemple, les planifications ci-dessous entraînent des interblocages.
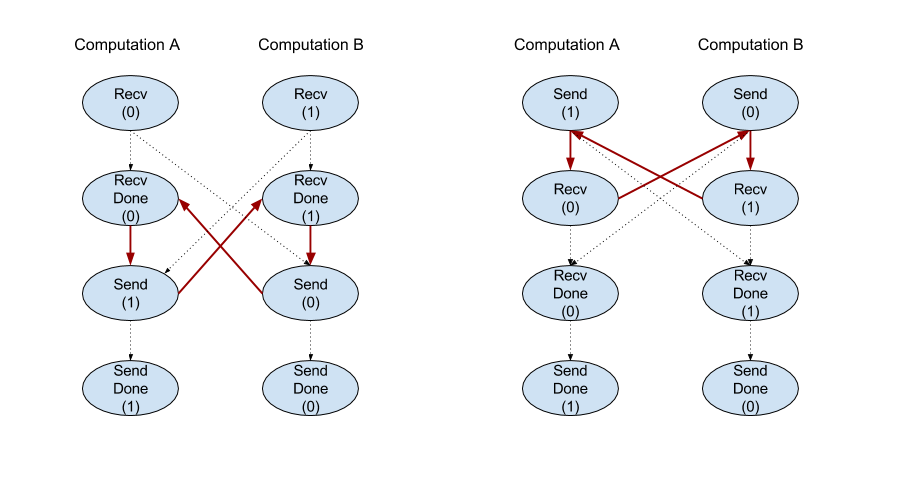
Notez que la contrainte sur les instructions ne s'applique qu'aux TPU au moment de l'exécution. Sur le GPU, send et recv bloquent et n'envoient aucune donnée réelle qu'après un échange de poignées de main entre les appareils source et cible.
Tranche
Consultez également XlaBuilder::Slice.
Le découpage extrait un sous-tableau du tableau d'entrée. Le sous-tableau a le même nombre de dimensions que l'entrée et contient les valeurs dans un rectangle englobant dans le tableau d'entrée, où les dimensions et les indices du rectangle englobant sont donnés comme arguments à l'opération de tranche.
Slice(operand, start_indices, limit_indices, strides)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tableau à N dimensions de type T |
start_indices |
ArraySlice<int64> |
Liste de N entiers contenant les indices de début de la tranche pour chaque dimension. Les valeurs doivent être supérieures ou égales à zéro. |
limit_indices |
ArraySlice<int64> |
Liste de N entiers contenant les indices de fin (exclusifs) de la tranche pour chaque dimension. Chaque valeur doit être supérieure ou égale à la valeur start_indices respective de la dimension, et inférieure ou égale à la taille de la dimension. |
strides |
ArraySlice<int64> |
Liste de N entiers qui déterminent la longueur de la ligne d'entrée de la tranche. La tranche sélectionne tous les éléments strides[d] de la dimension d. |
Exemple à une dimension:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4}) produces:
{2.0, 3.0}
Exemple en deux dimensions:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3}) produces:
{ { 7.0, 8.0},
{10.0, 11.0} }
Trier
Consultez également XlaBuilder::Sort.
Sort(operands, comparator, dimension, is_stable)
| Arguments | Type | Sémantique |
|---|---|---|
operands |
ArraySlice<XlaOp> |
Les opérandes à trier. |
comparator |
XlaComputation |
Calcul du comparateur à utiliser. |
dimension |
int64 |
Dimension à trier. |
is_stable |
bool |
Indique si le tri stable doit être utilisé. |
Si un seul opérande est fourni:
Si l'opérande est un tenseur à une dimension (un tableau), le résultat est un tableau trié. Si vous souhaitez trier le tableau par ordre croissant, le comparateur doit effectuer une comparaison inférieure. Formellement, une fois le tableau trié, il est vrai pour toutes les positions d'index
i, javeci < jquecomparator(value[i], value[j]) = comparator(value[j], value[i]) = falseoucomparator(value[i], value[j]) = true.Si l'opérande comporte un nombre de dimensions plus élevé, il est trié en fonction de la dimension fournie. Par exemple, pour un tenseur à deux dimensions (une matrice), une valeur de dimension de
0triera indépendamment chaque colonne, et une valeur de dimension de1triera indépendamment chaque ligne. Si aucun numéro de dimension n'est fourni, la dernière dimension est choisie par défaut. Pour la dimension triée, le même ordre de tri s'applique que dans le cas à une dimension.
Si des opérandes n > 1 sont fournies:
Tous les opérandes
ndoivent être des tenseurs de même dimension. Les types d'éléments des tenseurs peuvent être différents.Tous les opérandes sont triés ensemble, et non individuellement. D'un point de vue conceptuel, les opérandes sont traités comme un tuple. Lorsque vous vérifiez si les éléments de chaque opérande aux positions d'index
ietjdoivent être échangés, le comparateur est appelé avec des paramètres scalaires2 * n, où le paramètre2 * kcorrespond à la valeur à la positionide l'opérandek-th, et le paramètre2 * k + 1correspond à la valeur à la positionjde l'opérandek-th. En règle générale, le comparateur compare les paramètres2 * ket2 * k + 1entre eux et utilise éventuellement d'autres paires de paramètres comme briseurs d'égalité.Le résultat est un tuple composé des opérandes dans l'ordre trié (selon la dimension fournie, comme ci-dessus). L'opérande
i-thdu tuple correspond à l'opérandei-thde la fonction de tri.
Par exemple, s'il existe trois opérandes operand0 = [3, 1], operand1 = [42, 50] et operand2 = [-3.0, 1.1], et que le comparateur ne compare que les valeurs de operand0 avec "inférieur à", la sortie du tri est la tuple ([1, 3], [50, 42], [1.1, -3.0]).
Si is_stable est défini sur "true", le tri est garanti stable, c'est-à-dire que si des éléments sont considérés comme égaux par le comparateur, l'ordre relatif des valeurs égales est préservé. Deux éléments e1 et e2 sont égaux si et seulement si comparator(e1, e2) = comparator(e2, e1) = false. Par défaut, is_stable est défini sur "false".
TopK
Consultez également XlaBuilder::TopK.
TopK recherche les valeurs et les indices des k plus grands ou plus petits éléments pour la dernière dimension du tenseur donné.
TopK(operand, k, largest)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Tensor à partir duquel extraire les principaux éléments k. Le tenseur doit avoir au moins une dimension. La taille de la dernière dimension du tenseur doit être supérieure ou égale à k. |
k |
int64 |
Nombre d'éléments à extraire. |
largest |
bool |
Indique si les éléments k les plus grands ou les plus petits doivent être extraits. |
Pour un tenseur d'entrée à une dimension (un tableau), recherche les k plus grandes ou plus petites entrées du tableau et renvoie un tuple de deux tableaux (values, indices). Ainsi, values[j] est la je plus grande/petite entrée de operand, et son indice est indices[j].
Pour un tenseur d'entrée ayant plus d'une dimension, calcule les k premières entrées le long de la dernière dimension, en conservant toutes les autres dimensions (lignes) dans la sortie.
Ainsi, pour un opérande de forme [A, B, ..., P, Q] où Q >= k, la sortie est un tuple (values, indices) où:
values.shape = indices.shape = [A, B, ..., P, k]
Si deux éléments d'une ligne sont égaux, l'élément dont l'indice est le plus bas apparaît en premier.
Transposer
Consultez également l'opération tf.reshape.
Transpose(operand)
| Arguments | Type | Sémantique |
|---|---|---|
operand |
XlaOp |
Operande à transposer. |
permutation |
ArraySlice<int64> |
Permuter les dimensions |
Permute les dimensions de l'opérande avec la permutation donnée, soit ∀ i . 0 ≤ i < number of dimensions ⇒
input_dimensions[permutation[i]] = output_dimensions[i].
Cela revient à utiliser Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)).
TriangularSolve
Consultez également XlaBuilder::TriangularSolve.
Résout des systèmes d'équations linéaires avec des matrices de coefficients triangulaires inférieures ou supérieures par substitution directe ou inverse. En diffusant le long des dimensions principales, cette routine résout l'un des systèmes matriciels op(a) * x =
b ou x * op(a) = b pour la variable x, étant donné a et b, où op(a) est op(a) = a, op(a) = Transpose(a) ou op(a) = Conj(Transpose(a)).
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| Arguments | Type | Sémantique |
|---|---|---|
a |
XlaOp |
Un tableau à plus de deux dimensions d'un type complexe ou à virgule flottante de forme [..., M, M]. |
b |
XlaOp |
Un tableau à > 2 dimensions du même type avec la forme [..., M, K] si left_side est défini sur "true", [..., K, M] sinon. |
left_side |
bool |
Indique si un système de la forme op(a) * x = b (true) ou x * op(a) = b (false) doit être résolu. |
lower |
bool |
d'utiliser le triangle supérieur ou inférieur de a. |
unit_diagonal |
bool |
Si true, les éléments de la diagonale de a sont supposés être 1 et ne sont pas accessibles. |
transpose_a |
Transpose |
d'utiliser a tel quel, de le transposer ou de prendre sa transposée conjuguée. |
Les données d'entrée ne sont lues que dans le triangle inférieur/supérieur de a, en fonction de la valeur de lower. Les valeurs de l'autre triangle sont ignorées. Les données de sortie sont renvoyées dans le même triangle. Les valeurs de l'autre triangle sont définies par l'implémentation et peuvent être n'importe quoi.
Si le nombre de dimensions de a et b est supérieur à deux, elles sont traitées comme des lots de matrices, où toutes les dimensions, à l'exception des deux dimensions mineures, sont des dimensions de lot. a et b doivent avoir des dimensions de lot identiques.
Tuple
Consultez également XlaBuilder::Tuple.
Un tuple contenant un nombre variable de poignées de données, chacune ayant sa propre forme.
Cela équivaut à std::tuple en C++. Conceptuellement:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
Les tupels peuvent être déconstruits (accessibles) via l'opération GetTupleElement.
Bien que
Consultez également XlaBuilder::While.
While(condition, body, init)
| Arguments | Type | Sémantique |
|---|---|---|
condition |
XlaComputation |
XlaComputation de type T -> PRED qui définit la condition d'arrêt de la boucle. |
body |
XlaComputation |
XlaComputation de type T -> T qui définit le corps de la boucle. |
init |
T |
Valeur initiale du paramètre de condition et body. |
Exécute de manière séquentielle le body jusqu'à l'échec de l'condition. Il s'agit d'une boucle while typique dans de nombreuses autres langues, à l'exception des différences et des restrictions listées ci-dessous.
- Un nœud
Whilerenvoie une valeur de typeT, qui est le résultat de la dernière exécution debody. - La forme du type
Test déterminée de manière statique et doit être identique pour toutes les itérations.
Les paramètres T des calculs sont initialisés avec la valeur init lors de la première itération et sont automatiquement mis à jour avec le nouveau résultat de body à chaque itération ultérieure.
L'un des principaux cas d'utilisation du nœud While est l'implémentation de l'exécution répétée de l'entraînement dans les réseaux de neurones. Un pseudo-code simplifié est présenté ci-dessous avec un graphique représentant le calcul. Le code se trouve dans while_test.cc.
Le type T dans cet exemple est un Tuple composé d'un int32 pour le nombre d'itérations et d'un vector[10] pour l'accumulateur. Pendant 1 000 itérations, la boucle continue d'ajouter un vecteur constant à l'accumulateur.
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}