בהמשך מוסבר על הסמנטיקה של הפעולות שמוגדרות בממשק XlaBuilder. בדרך כלל, הפעולות האלה ממופות אחד לאחד לפעולות שמוגדרות בממשק ה-RPC ב-xla_data.proto.
הערה לגבי מונחים: סוג הנתונים הכללי ש-XLA מטפלת בו הוא מערך N-ממדי שמכיל רכיבים מסוג אחיד כלשהו (למשל, 32-bit float). במסמכי העזרה, המונח array משמש לציון מערך בעל מימדים שרירותיים. למקרים מיוחדים יש שמות ספציפיים ומוכרים יותר. לדוגמה, וקטור הוא מערך דו-מימדי ומטריצה היא מערך תלת-מימדי.
AfterAll
למידע נוסף: XlaBuilder::AfterAll
הפונקציה AfterAll מקבלת מספר משתנה של אסימונים ומפיקה טוקן יחיד. אסימונים הם סוגים פרימיטיביים שאפשר להוסיף לשרשור בין פעולות עם השפעות משניות כדי לאכוף את הסדר. אפשר להשתמש ב-AfterAll כצירוף של אסימונים כדי למיין פעולה אחרי פעולות של קבוצות.
AfterAll(operands)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands |
XlaOp |
מספר משתנה של אסימונים |
AllGather
למידע נוסף: XlaBuilder::AllGather
ביצוע שרשור בין הרפליקות.
AllGather(operand, all_gather_dim, shard_count, replica_group_ids,
channel_id)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand
|
XlaOp
|
מערך לשרשור בין הרפליקות |
all_gather_dim |
int64 |
מאפיין שרשור |
replica_groups
|
וקטור של וקטורים של
int64 |
הקבוצות שבין |
channel_id
|
אופציונלי int64
|
מזהה ערוץ אופציונלי לתקשורת בין מודולים |
replica_groupsהיא רשימה של קבוצות של רפליקות שביניהן מתבצעת הקונקטרציה (אפשר לאחזר את מזהה הרפליקה של הרפליקה הנוכחית באמצעותReplicaId). הסדר של הרפליקות בכל קבוצה קובע את הסדר שבו הקלט שלהן מופיע בתוצאה. השדהreplica_groupsחייב להיות ריק (במקרה כזה כל הרפליקות שייכות לקבוצה אחת, בסדר מ-0עדN - 1), או להכיל את אותו מספר רכיבים כמו מספר הרפליקות. לדוגמה,replica_groups = {0, 2}, {1, 3}מבצע שרשור בין הרפליקות0ו-2, וגם בין1ו-3.shard_countהוא הגודל של כל קבוצת רפליקות. אנחנו זקוקים לזה במקרים שבהם הערכים שלreplica_groupsריקים.- השדה
channel_idמשמש לתקשורת בין מודולים: רק פעולותall-gatherעם אותוchannel_idיכולות לתקשר זו עם זו.
צורת הפלט היא צורת הקלט, כאשר all_gather_dim גדולה פי shard_count. לדוגמה, אם יש שתי רפליקות והאופרטנד הוא [1.0, 2.5] ו-[3.0, 5.25], בהתאמה, בשתי הרפליקות, ערך הפלט של הפעולה הזו, כאשר all_gather_dim הוא 0, יהיה [1.0, 2.5, 3.0,
5.25] בשתי הרפליקות.
AllReduce
למידע נוסף: XlaBuilder::AllReduce
ביצוע חישוב מותאם אישית בין הרפליקות.
AllReduce(operand, computation, replica_group_ids, channel_id)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand
|
XlaOp
|
מערך או קבוצת מערכי tupe לא ריקה שרוצים לצמצם בין הרפליקות |
computation |
XlaComputation |
חישוב ההנחה |
replica_groups
|
וקטור של וקטורים של
int64 |
הקבוצות שביניהן מתבצעות ההנחות |
channel_id
|
אופציונלי int64
|
מזהה ערוץ אופציונלי לתקשורת בין מודולים |
- כש-
operandהוא קבוצה של מערכי משנה, הפעולה all-reduce מתבצעת על כל רכיב בקבוצה. replica_groupsהיא רשימה של קבוצות של רפליקות שביניהן מתבצעת ההפחתה (אפשר לאחזר את מזהה הרפליקה של הרפליקה הנוכחית באמצעותReplicaId).replica_groupsחייבת להיות ריקה (במקרה כזה, כל הרפליקות שייכות לקבוצה אחת) או להכיל את אותו מספר רכיבים כמו מספר הרפליקות. לדוגמה,replica_groups = {0, 2}, {1, 3}מבצע הפחתה בין הרפליקות0ו-2, וגם בין1ל-3.- השדה
channel_idמשמש לתקשורת בין מודולים: רק פעולותall-reduceעם אותוchannel_idיכולות לתקשר זו עם זו.
צורת הפלט זהה לצורת הקלט. לדוגמה, אם יש שתי רפליקות והאופרנד מכיל את הערכים [1.0, 2.5] ו-[3.0, 5.25] בשתי הרפליקות, ערך הפלט מהפעולה הזו ומחישוב הסיכום יהיה [4.0, 7.75] בשתי הרפליקות. אם הקלט הוא קבוצת ערכים, גם הפלט הוא קבוצת ערכים.
כדי לחשב את התוצאה של AllReduce, צריך קלט אחד מכל עותק, ולכן אם עותק אחד מפעיל צומת AllReduce יותר פעמים מאשר עותק אחר, העותק הראשון ימתין לנצח. מכיוון שכל הרפליקות מריצות את אותה תוכנית, יש מעט מאוד דרכים שבהן זה יכול לקרות, אבל זה אפשרי כשהתנאי של לולאת while תלוי בנתונים מה-infeed, והנתונים שמוזנים ל-infeed גורמים ללולאת while לבצע איטרציות יותר פעמים ברפליקה אחת מאשר ברפליקה אחרת.
AllToAll
למידע נוסף: XlaBuilder::AllToAll
AllToAll היא פעולה קולקטיבית ששולחת נתונים מכל הליבות לכל הליבות. הוא מורכב משני שלבים:
- שלב הפיזור. בכל ליבה, המשתנה מפוצל למספר הבלוקים
split_countלאורךsplit_dimensions, והבלוקים מפוזרים לכל הליבות, למשל, הבלוק ה-i נשלח לליבה ה-i. - שלב האיסוף. כל ליבה מקשרת את הבלוקים שהתקבלו לאורך
concat_dimension.
אפשר להגדיר את הליבות המשתתפות באמצעות:
replica_groups: כל ReplicaGroup מכיל רשימה של מזהי הרפליקות שמשתתפות בחישוב (אפשר לאחזר את מזהה הרפליקה של הרפליקה הנוכחית באמצעותReplicaId). AllToAll יחול בתוך קבוצות משנה בסדר שצוין. לדוגמה, הערךreplica_groups = { {1,2,3}, {4,5,0} }מציין ש-AllToAll יחול על הרפליקות{1, 2, 3}ובשלב האיסוף, והבלוקים שהתקבלו יקושרו באותו הסדר של 1, 2, 3. לאחר מכן, תתבצע פעולת AllToAll נוספת בתוך הרפליקות 4, 5 ו-0, וסדר השרשור יהיה גם 4, 5 ו-0. אם השדהreplica_groupsריק, כל הרפליקות שייכות לקבוצה אחת, לפי סדר השרשור שלהן.
דרישות מוקדמות:
- גודל המאפיין של המשתנה ב-
split_dimensionמתחלק ב-split_count. - הצורה של המשתנה המבצע היא לא קבוצת צמדי ערכים (tuple).
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך קלט n-ממדי |
split_dimension
|
int64
|
ערך במרווח [0,
n) שמציין את המאפיין שבו מתבצע הפיצול של האופרנד |
concat_dimension
|
int64
|
ערך במרווח [0,
n) שמציין את המאפיין שבו מחוברים הבלוקסים המפוצלים |
split_count
|
int64
|
מספר הליבות שמשתתפות בפעולה הזו. אם השדה replica_groups ריק, הערך צריך להיות מספר הרפליקות. אחרת, הערך צריך להיות שווה למספר הרפליקות בכל קבוצה. |
replica_groups
|
וקטור ReplicaGroup
|
כל קבוצה מכילה רשימה של מזהי רפליקות. |
בהמשך מוצגת דוגמה ל-Alltoall.
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(x, /*split_dimension=*/1, /*concat_dimension=*/0, /*split_count=*/4);
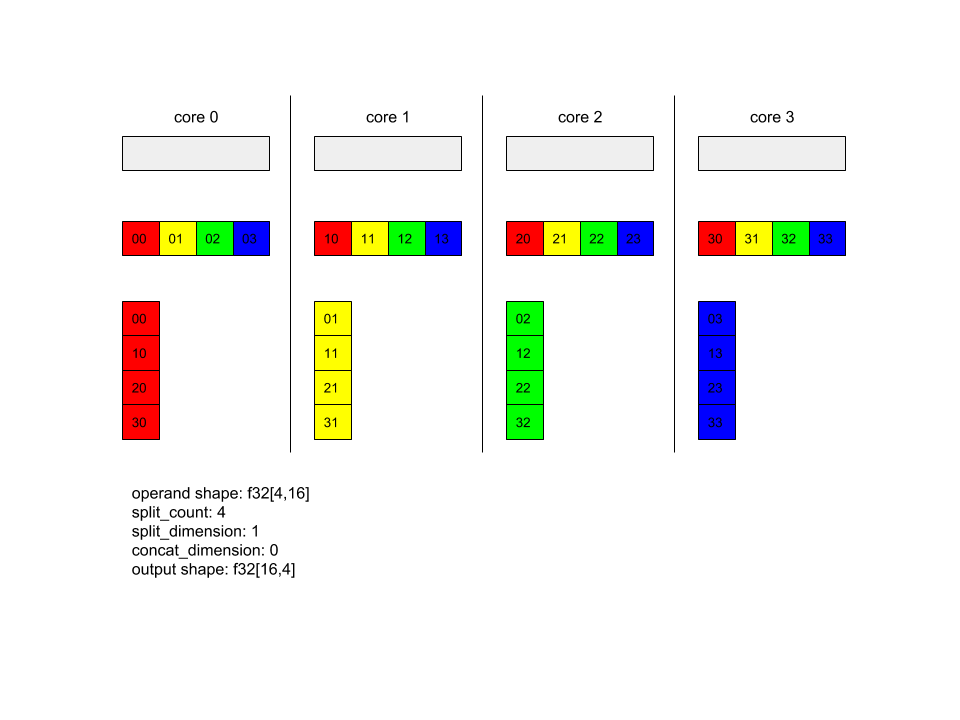
בדוגמה הזו, יש 4 ליבות שמשתתפות ב-Alltoall. בכל ליבה, המשתנה מחולק ל-4 חלקים לפי המאפיין 1, כך שכל חלק הוא מסוג f32[4,4]. 4 החלקים מפוזרים בין כל הליבות. לאחר מכן, כל ליבה מקשרת את החלקים שהתקבלו לפי המאפיין 0, בסדר של הליבה 0-4. לכן הפלט בכל ליבה הוא בפורמט f32[16,4].
BatchNormGrad
תיאור מפורט של האלגוריתם זמין גם במאמרים XlaBuilder::BatchNormGrad ובמאמר המקורי בנושא נורמליזציה באצווה.
חישוב נגזרות של רגולריזציה של קבוצות (batch normalization).
BatchNormGrad(operand, scale, mean, variance, grad_output, epsilon,
feature_index)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך n-מימדי לצורך נירמול (x) |
scale |
XlaOp |
מערך חד-מימדי (γ) |
mean |
XlaOp |
מערך חד-מימדי (μ) |
variance |
XlaOp |
מערך חד-מימדי (σ2) |
grad_output |
XlaOp |
שיפועים שהועברו אל BatchNormTraining (∇y) |
epsilon |
float |
ערך Epsilon (ϵ) |
feature_index |
int64 |
אינדקס למאפיין התכונה ב-operand |
לכל מאפיין במאפיין המאפיין (feature_index הוא המדד של מאפיין המאפיין ב-operand), הפעולה מחשבת את שיפועי השינוי ביחס ל-operand, ל-offset ול-scale בכל המאפיינים האחרים. הערך של feature_index חייב להיות אינדקס תקין למאפיין המאפיין ב-operand.
שלושת הגרדיאנטים מוגדרים לפי הנוסחאות הבאות (בהנחה שמשתמשים במערך 4-מימדי כ-operand, עם אינדקס של מאפיין המאפיין l, גודל האצווה m וגדלים מרחביים w ו-h):
cl=1mwhm∑i=1w∑j=1h∑k=1(∇yijklxijkl−μlσ2l+ϵ)dl=1mwhm∑i=1w∑j=1h∑k=1∇yijkl∇xijkl=γl√σ2l+ϵ(∇yijkl−dl−cl(xijkl−μl))∇γl=m∑i=1w∑j=1h∑k=1(∇yijklxijkl−μl√σ2l+ϵ) ∇βl=m∑i=1w∑j=1h∑k=1∇yijkl
הקלטים mean ו-variance מייצגים את ערכי הרגעים במאפיינים של קבוצות עיבוד נתונים ומאפיינים מרחביים.
סוג הפלט הוא קבוצה של שלושה כינויים:
| פלט | סוג | סמנטיקה |
|---|---|---|
grad_operand
|
XlaOp
|
שיפוע ביחס לקלט operand (∇x) |
grad_scale
|
XlaOp
|
שיפוע ביחס לקלט scale (∇γ) |
grad_offset
|
XlaOp
|
שיפוע ביחס לקלט offset(∇β) |
BatchNormInference
תיאור מפורט של האלגוריתם זמין גם במאמרים XlaBuilder::BatchNormInference ובמאמר המקורי בנושא נורמליזציה באצווה.
נורמליזציה של מערך במאפיינים של קבוצות עיבוד נתונים ומאפיינים מרחביים.
BatchNormInference(operand, scale, offset, mean, variance, epsilon,
feature_index)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך n-מימדי לצורך נירמול |
scale |
XlaOp |
מערך חד-מימדי |
offset |
XlaOp |
מערך חד-מימדי |
mean |
XlaOp |
מערך חד-מימדי |
variance |
XlaOp |
מערך חד-מימדי |
epsilon |
float |
ערך Epsilon |
feature_index |
int64 |
אינדקס למאפיין התכונה ב-operand |
לכל מאפיין במאפיין המאפיין (feature_index הוא האינדקס של מאפיין המאפיין ב-operand), הפעולה מחשבת את הממוצע והשונות בכל המאפיינים האחרים, ומשתמשת בממוצע ובשונות כדי לנרמל כל רכיב ב-operand. הערך של feature_index חייב להיות אינדקס חוקי למאפיין המאפיין ב-operand.
BatchNormInference היא שוות-ערך לקריאה ל-BatchNormTraining בלי לחשב את mean ו-variance לכל קבוצה. במקום זאת, המערכת משתמשת בערכים המשוערים של הקלט mean ו-variance. המטרה של הפעולה הזו היא לצמצם את זמן האחזור בתהליך ההסקה, ולכן השם שלה הוא BatchNormInference.
הפלט הוא מערך מנורמלי בעל n-ממדים באותה צורה כמו הקלט operand.
BatchNormTraining
תוכלו לקרוא גם את המאמרים XlaBuilder::BatchNormTraining ו-the original batch normalization paper כדי לקבל תיאור מפורט של האלגוריתם.
נורמליזציה של מערך במאפיינים של קבוצות עיבוד נתונים ומאפיינים מרחביים.
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך n-מימדי לצורך נירמול (x) |
scale |
XlaOp |
מערך חד-מימדי (γ) |
offset |
XlaOp |
מערך חד-מימדי (β) |
epsilon |
float |
ערך Epsilon (ϵ) |
feature_index |
int64 |
אינדקס למאפיין התכונה ב-operand |
לכל מאפיין במאפיין המאפיין (feature_index הוא האינדקס של מאפיין המאפיין ב-operand), הפעולה מחשבת את הממוצע והשונות בכל המאפיינים האחרים, ומשתמשת בממוצע ובשונות כדי לנרמל כל רכיב ב-operand. הערך של feature_index חייב להיות אינדקס חוקי למאפיין המאפיין ב-operand.
האלגוריתם פועל באופן הבא לכל קבוצה ב-operand x שמכילה m
אלמנטים עם w ו-h כגודל המאפיינים המרחביים (בהנחה ש-operand
הוא מערך 4-מימדי):
חישוב הממוצע של הקבוצה μl לכל מאפיין
lבמאפיין המאפיין: μl=1mwh∑mi=1∑wj=1∑hk=1xijklחישוב סטיית התקן של האצווה σ2l: $\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
נורמליזציה, שינוי קנה מידה והזזה: yijkl=γl(xijkl−μl)2√σ2l+ϵ+βl
ערך האפסילון, בדרך כלל מספר קטן, מתווסף כדי למנוע שגיאות של חלוקה באפס.
סוג הפלט הוא קבוצה של שלושה ערכים מסוג XlaOp:
| פלט | סוג | סמנטיקה |
|---|---|---|
output
|
XlaOp
|
מערך n-ממדי באותה צורה כמו הקלט operand (y) |
batch_mean |
XlaOp |
מערך חד-מימדי (μ) |
batch_var |
XlaOp |
מערך חד-מימדי (σ2) |
הערכים batch_mean ו-batch_var הם רגעים שמחושבים במאפיינים של האצווה והמרחב באמצעות הנוסחאות שלמעלה.
BitcastConvertType
למידע נוסף: XlaBuilder::BitcastConvertType
בדומה ל-tf.bitcast ב-TensorFlow, היא מבצעת פעולת העברת ביט ברמת הרכיב מצורת נתונים לצורת יעד. גודל הקלט והפלט חייב להיות זהה: לדוגמה, רכיבי s32 הופכים לרכיבי f32 באמצעות תוכנית bitcast, ורכיב s32 אחד הופך לארבעה רכיבי s8. ה-bitcast מיושם כ-cast ברמה נמוכה, כך שמכונות עם ייצוגים שונים של נקודות צפות יניבו תוצאות שונות.
BitcastConvertType(operand, new_element_type)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T עם מאפייני D |
new_element_type |
PrimitiveType |
סוג U |
המאפיינים של המשתנה המבצע את הפעולה ושל צורת היעד חייבים להיות זהים, מלבד המאפיין האחרון, שישתנה לפי היחס של גודל הרכיב הבסיסי לפני ההמרה ואחריה.
סוגי הרכיבים של המקור והיעד לא יכולים להיות צמדי ערכים (tuples).
המרה של Bitcast לסוג פרימיטיבי ברוחב שונה
הוראה BitcastConvert של HLO תומכת במקרה שבו הגודל של סוג רכיב הפלט T' לא שווה לגודל של רכיב הקלט T. מכיוון שהפעולה כולה היא בעצם bitcast ולא משתנה את הבייטים הבסיסיים, הצורה של רכיב הפלט צריכה להשתנות. עבור B = sizeof(T), B' =
sizeof(T'), יש שני מקרים אפשריים.
קודם, כש-B > B', לצורת הפלט מתווסף מאפיין משני חדש בגודל B/B'. לדוגמה:
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
הכלל נשאר זהה למשתנים סקלריים יעילים:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
לחלופין, עבור B' > B, ההוראה מחייבת שהמאפיין הלוגי האחרון של צורת הקלט יהיה שווה ל-B'/B, והמאפיין הזה יוסר במהלך ההמרה:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
חשוב לזכור שההמרות בין רוחב ביט שונה לא מתבצעות לפי רכיבים.
להודיע לכולם
למידע נוסף: XlaBuilder::Broadcast
הוספת מאפיינים למערך על ידי שכפול הנתונים במערך.
Broadcast(operand, broadcast_sizes)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
המערך שרוצים לשכפל |
broadcast_sizes |
ArraySlice<int64> |
הגדלים של המאפיינים החדשים |
המימדים החדשים מוכנסים בצד ימין, כלומר אם ל-broadcast_sizes יש ערכים {a0, ..., aN} ולמימד של המשתנה המבצע יש מימדים {b0, ..., bM}, אז למבנה הפלט יש מימדים {a0, ..., aN, b0, ..., bM}.
המאפיינים החדשים ממוינים בעותק של המשתנה, כלומר
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
לדוגמה, אם operand הוא סקלר f32 עם הערך 2.0f, ו-broadcast_sizes הוא {2, 3}, התוצאה תהיה מערך בפורמט f32[2, 3] וכל הערכים בתוצאה יהיו 2.0f.
BroadcastInDim
למידע נוסף: XlaBuilder::BroadcastInDim
הרחבת הגודל ומספר המאפיינים של מערך על ידי שכפול הנתונים במערך.
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
המערך שרוצים לשכפל |
out_dim_size |
ArraySlice<int64> |
הגדלים של המאפיינים של צורת היעד |
broadcast_dimensions |
ArraySlice<int64> |
המאפיין בצורת היעד שאליו מתאים כל מאפיין בצורת המשתנה |
דומה ל-Broadcast, אבל מאפשר להוסיף מאפיינים בכל מקום ולהרחיב מאפיינים קיימים בגודל 1.
הערך operand מופץ לצורה שמתוארת על ידי out_dim_size.
הפונקציה broadcast_dimensions ממפה את המאפיינים של operand למאפיינים של צורת היעד, כלומר המאפיין ה-i של המשתנה המבצע ממופה למאפיין ה-broadcast_dimension[i] של צורת הפלט. המאפיינים של operand חייבים להיות בגודל 1 או באותו גודל כמו המאפיין בצורת הפלט שאליו הם ממופה. שאר המאפיינים יתמלאו במאפיינים בגודל 1. לאחר מכן, השידור של המאפיינים המנוונים מתבצע לאורך המאפיינים המנוונים האלה כדי להגיע לצורת הפלט. הסמנטיקה מתוארת בפירוט בדף השידור.
התקשרות
למידע נוסף: XlaBuilder::Call
הפונקציה מפעילה חישוב עם הארגומנטים שצוינו.
Call(computation, args...)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
computation |
XlaComputation |
חישוב מסוג T_0, T_1, ..., T_{N-1} -> S עם N פרמטרים מסוג שרירותי |
args |
רצף של N XlaOps |
N ארגומנטים מסוג שרירותי |
האריתיות והסוגים של args צריכים להתאים לפרמטרים של computation. מותר שלא יהיה args.
CompositeCall
למידע נוסף: XlaBuilder::CompositeCall
אופרטור שמכיל בתוכו אופרטורים אחרים של StableHLO, ומקבל קלט ו-composite_attributes ומייצר תוצאות. הסמנטיקה של הפעולה מיושמת באמצעות מאפיין הפירוק. אפשר להחליף את הפעולה המורכבת בפירוק שלה בלי לשנות את הסמנטיקה של התוכנית. במקרים שבהם הטמעת הפירוק בקוד לא מספקת את אותה סמנטיקה של הפעולה, עדיף להשתמש ב-custom_call.
השדה version (ברירת המחדל היא 0) משמש לציון מתי הסמנטיקה של רכיב מורכב משתנה.
הפעולה הזו מוטמעת כ-kCall עם המאפיין is_composite=true. השדה decomposition מצוין על ידי המאפיין computation. המאפיינים של הקצה הקדמי מאחסנים את המאפיינים הנותרים עם הקידומת composite..
דוגמה לפעולה CompositeCall:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
Call(computation, args..., name, composite_attributes, version)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
inputs |
XlaOp |
מספר משתנה של ערכים |
name |
string |
השם של המאפיין המורכב |
composite_attributes |
אופציונלי string |
מילון אופציונלי של מאפיינים שמומר למחרוזת |
decomposition |
XlaComputation |
חישוב מסוג T_0, T_1, ..., T_{N-1} -> S עם N פרמטרים מסוג שרירותי |
version |
int64. |
מספר לעדכוני גרסה לסמנטיקה של הפעולה המשולבת |
Cholesky
למידע נוסף: XlaBuilder::Cholesky
הפונקציה מחשבת את הניתוח של Cholesky של קבוצה של מטריצות סימטריות (הרמיטיות) חיוביות מוגדרות.
Cholesky(a, lower)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
a |
XlaOp |
מערך מסוג מורכב או מסוג נקודה צפה עם יותר מ-2 מימדים. |
lower |
bool |
אם להשתמש במשולש העליון או התחתון של a. |
אם lower הוא true, מחשבים מטריצות משולש תחתון l כך ש- a=l.lT. אם lower הוא false, הפונקציה מחשבת מטריצות משושות עליונות u כך שa=uT.u.
נתוני הקלט נקראים רק מהמשולש התחתון/העליון של a, בהתאם לערך של lower. המערכת מתעלמת מערכים מהמשולש השני. נתוני הפלט מוחזרים באותו משולש. הערכים במשולש השני מוגדרים בהטמעה ויכולים להיות כל ערך שהוא.
אם ל-a יש יותר מ-2 מאפיינים, המערכת מתייחסת ל-a כאל קבוצה של מטריצות, שבהן כל המאפיינים חוץ משני המאפיינים המשניים הם מאפייני קבוצה.
אם המטריצה a לא סימטרית (הרמיטית) וחיובי-מוגדרת, התוצאה מוגדרת על ידי ההטמעה.
תיחום
למידע נוסף: XlaBuilder::Clamp
הפונקציה מגדירה ערך של אופרטנד בטווח שבין ערך מינימלי לערך מקסימלי.
Clamp(min, operand, max)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
min |
XlaOp |
מערך מסוג T |
operand |
XlaOp |
מערך מסוג T |
max |
XlaOp |
מערך מסוג T |
הפונקציה מקבלת אופרנד וערכים מינימלי ומקסימלי, ומחזירה את האופרנד אם הוא נמצא בטווח שבין הערך המינימלי לערך המקסימלי. אחרת, הפונקציה מחזירה את הערך המינימלי אם האופרנד נמוך מהטווח הזה, או את הערך המקסימלי אם האופרנד גבוה מהטווח הזה. כלומר, clamp(a, x, b) = min(max(a, x), b).
כל שלוש המערכות חייבות להיות באותו צורה. לחלופין, כצורה מוגבלת של שידור, הערכים של min ו/או max יכולים להיות סקלר מסוג T.
דוגמה עם רכיבים סקלריים min ו-max:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
כיווץ
אפשר לעיין גם במאמר XlaBuilder::Collapse ובפעולה tf.reshape.
צמצום המימדים של מערך למימד אחד.
Collapse(operand, dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T |
dimensions |
וקטור int64 |
קבוצת משנה עוקבת בסדר של המאפיינים של T. |
הפונקציה Collapse מחליפה את קבוצת המשנה הנתונה של המאפיינים של המשתנה ב-operand במימד יחיד. ארגומנטים הקלט הם מערך שרירותי מסוג T ווקטור קבוע בזמן הידור של אינדקסים של מאפיינים. אינדקסי המאפיינים חייבים להיות קבוצת משנה עוקבת של המאפיינים של T, לפי סדר (מספרים נמוכים של מאפיינים עד מספרים גבוהים). לכן, {0, 1, 2}, {0, 1} או {1, 2} הן קבוצות של מאפיינים חוקיות, אבל {1, 0} או {0, 2} לא חוקיות. הם מוחלפים במאפיין חדש יחיד, באותו מיקום ברצף המאפיינים שבו הם נמצאים, כאשר גודל המאפיין החדש שווה למכפלה של גדלי המאפיינים המקוריים. מספר המאפיין הנמוך ביותר ב-dimensions הוא המאפיין המשתנה האיטי ביותר (החשוב ביותר) בתוך ערימת הלולאות שמצמצמת את המאפיינים האלה, ומספר המאפיין הגבוה ביותר הוא המאפיין המשתנה המהיר ביותר (החשוב פחות). אם אתם צריכים סדר קריאה כללי יותר של התכונה 'קיבוץ', תוכלו לעיין באופרטור tf.reshape.
לדוגמה, נניח ש-v הוא מערך של 24 רכיבים:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
CollectivePermute
למידע נוסף: XlaBuilder::CollectivePermute
CollectivePermute היא פעולה קולקטיבית ששולחת ומקבלת נתונים בין רפליקות.
CollectivePermute(operand, source_target_pairs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך קלט n-ממדי |
source_target_pairs |
וקטור <int64, int64> |
רשימה של זוגות (source_replica_id, target_replica_id). לכל צמד, המשתנה נשלח מהרפליקה של המקור לרפליקה של היעד. |
שימו לב שיש את ההגבלות הבאות על source_target_pair:
- לשני זוגות לא יכול להיות אותו מזהה של רפליקת יעד, וגם לא אותו מזהה של רפליקת מקור.
- אם מזהה עותק לא נכלל כיעד באף זוג, הפלט של העותק הזה הוא טינסור שמכיל 0(s) באותו צורה כמו הקלט.
שרשור
למידע נוסף: XlaBuilder::ConcatInDim
הפונקציה Concatenate יוצרת מערך מכמה אופרטורים של מערך. למערך יש את אותו מספר מאפיינים כמו לכל אחד מאופרטורי מערך הקלט (שחייבים להיות בעלי אותו מספר מאפיינים זה לזה), והוא מכיל את הארגומנטים בסדר שבו הם צוינו.
Concatenate(operands..., dimension)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands |
רצף של N XlaOp |
N מערכים מסוג T עם המאפיינים [L0, L1, ...]. נדרש N >= 1. |
dimension |
int64 |
ערך במרווח [0, N) שמציין את השם של המאפיין שרוצים לשרשר בין ה-operands. |
כל המאפיינים חייבים להיות זהים, מלבד dimension. הסיבה לכך היא ש-XLA לא תומך במערכים 'לא סדירים'. חשוב לזכור שאי אפשר לשרשר ערכים עם מאפיין של מימד 0 (כי אי אפשר לתת שם למאפיין שבו מתבצעת השרשרת).
דוגמה במאפיין אחד:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
>>> {2, 3, 4, 5, 6, 7}
דוגמה דו-ממדית:
let a = {
{1, 2},
{3, 4},
{5, 6},
};
let b = {
{7, 8},
};
Concat({a, b}, 0)
>>> {
{1, 2},
{3, 4},
{5, 6},
{7, 8},
}
דיאגרמה:
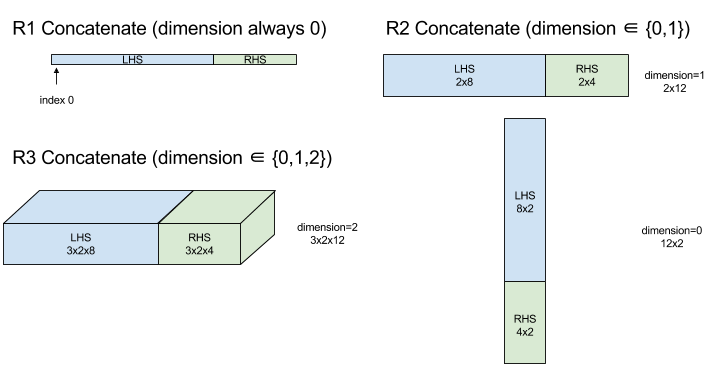
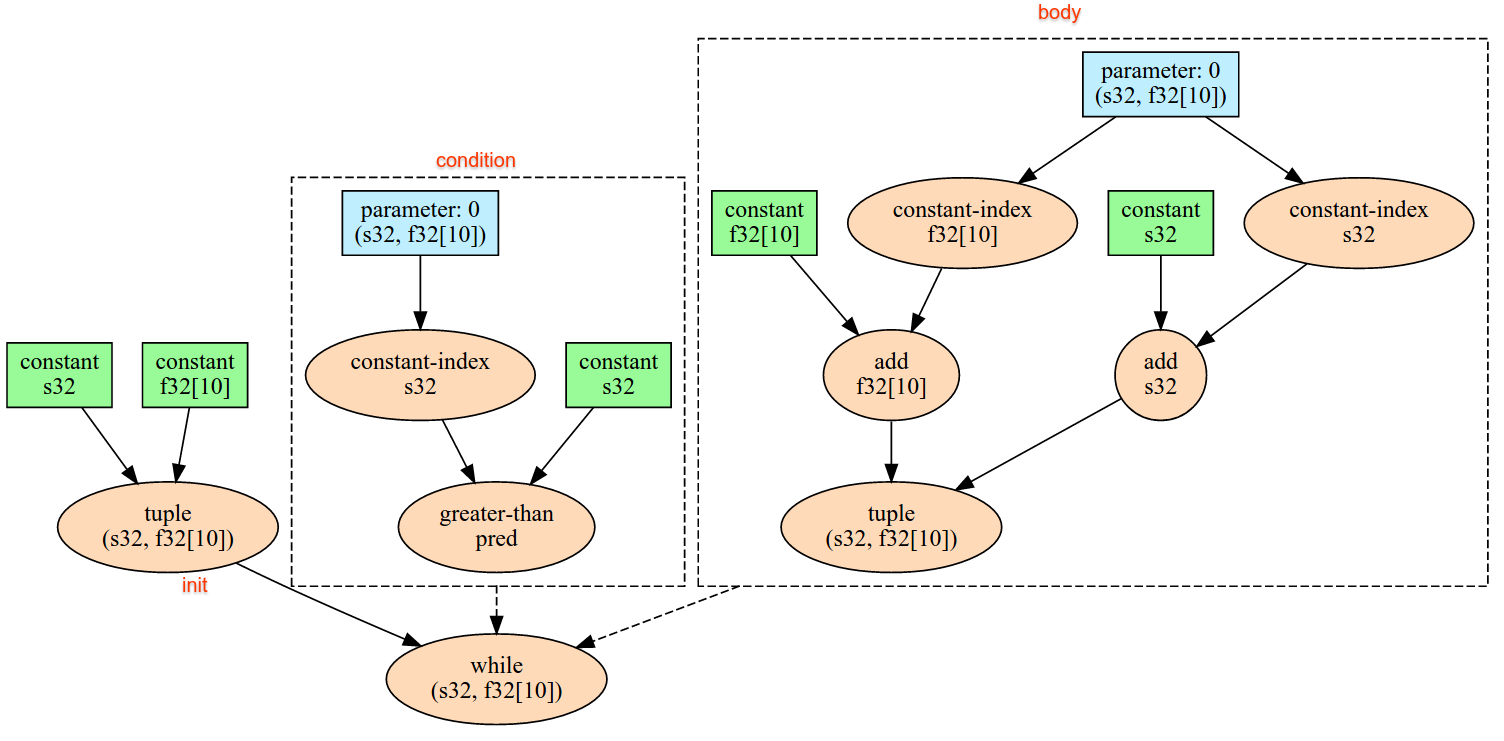
משפטי תנאי
למידע נוסף: XlaBuilder::Conditional
Conditional(pred, true_operand, true_computation, false_operand,
false_computation)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
pred |
XlaOp |
סקלר מסוג PRED |
true_operand |
XlaOp |
ארגומנט מסוג T0 |
true_computation |
XlaComputation |
XlaComputation מסוג T0→S |
false_operand |
XlaOp |
ארגומנט מסוג T1 |
false_computation |
XlaComputation |
XlaComputation מסוג T1→S |
הפונקציה מפעילה את true_computation אם הערך של pred הוא true, את false_computation אם הערך של pred הוא false ומחזירה את התוצאה.
הפונקציה true_computation חייבת לקבל ארגומנט יחיד מסוג T0 , והיא תופעל באמצעות true_operand, שגם הוא חייב להיות מאותו סוג. הפונקציה false_computation חייבת לקבל ארגומנט יחיד מסוג T1 , והיא תופעל באמצעות false_operand, שגם הוא חייב להיות מאותו סוג. הסוג של הערך המוחזר של true_computation ושל false_computation חייב להיות זהה.
שימו לב שרק אחת מהפונקציות true_computation ו-false_computation תוּפעל, בהתאם לערך של pred.
Conditional(branch_index, branch_computations, branch_operands)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
branch_index |
XlaOp |
סקלר מסוג S32 |
branch_computations |
רצף של N XlaComputation |
XlaComputations מסוג T0→S,T1→S,...,TN−1→S |
branch_operands |
רצף של N XlaOp |
ארגומנטים מסוג T0,T1,...,TN−1 |
הפונקציה מבצעת את branch_computations[branch_index] ומחזירה את התוצאה. אם branch_index הוא S32 שהוא < 0 או >= N, אז branch_computations[N-1] מופעל כענף ברירת המחדל.
כל פונקציית branch_computations[b] חייבת לקבל ארגומנט יחיד מסוג Tb , והיא תופעל באמצעות branch_operands[b] שחייב להיות מאותו סוג. הסוג של הערך המוחזר של כל branch_computations[b] חייב להיות זהה.
שימו לב שרק אחת מהפונקציות branch_computations תופעל, בהתאם לערך של branch_index.
Conv (convolution)
למידע נוסף: XlaBuilder::Conv
כמו ConvWithGeneralPadding, אבל ה-padding מצוין בקיצור כ-SAME או כ-VALID. בדילול SAME, הקלט (lhs) מתמלא באפסים כדי שהפלט יהיה באותו צורה כמו הקלט, בלי להביא בחשבון את ה-striding. 'VALID padding' (תוספת VALID) פירושה פשוט שאין תוספת.
ConvWithGeneralPadding (convolution)
למידע נוסף: XlaBuilder::ConvWithGeneralPadding
חישוב עיבוד נתונים מסוג 'קונטרולציה' (convolution) שנעשה בו שימוש ברשתות נוירונים. כאן, אפשר לחשוב על convolve כחלון n-ממדי שנע על פני אזור בסיס n-ממדי, ומתבצעת חישוב לכל מיקום אפשרי של החלון.
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs |
XlaOp |
מערך של קלט בממד (n+2) |
rhs |
XlaOp |
מערך של משקלים של גרעיני (n+2)-ממדיים |
window_strides |
ArraySlice<int64> |
מערך n-ממדי של צעדים של ליבה |
padding |
ArraySlice< pair<int64,int64>> |
מערך n-ממדי של מרווחים פנימיים (low, high) |
lhs_dilation |
ArraySlice<int64> |
מערך של גורם הרחבה של n-d lhs |
rhs_dilation |
ArraySlice<int64> |
מערך של גורם הרחבה של צד ימין ב-n-d |
feature_group_count |
int64 | מספר קבוצות המאפיינים |
batch_group_count |
int64 | מספר קבוצות האצווה |
נניח ש-n הוא מספר המימדים המרחביים. הארגומנט lhs הוא מערך (n+2)-ממדי שמתאר את שטח הבסיס. זה נקרא הקלט, למרות שגם הצד הימני הוא קלט. ברשת נוירונים, אלה הפעלות הקלט. המאפיינים n+2 הם, לפי הסדר הזה:
batch: כל קואורדינטה במאפיין הזה מייצגת קלט עצמאי שעליו מתבצעת עיבוד.z/depth/features: לכל מיקום (x,y) באזור הבסיס משויך וקטור שמשויך למאפיין הזה.spatial_dims: מתאר את המאפיינים המרחבייםnשמגדירים את אזור הבסיס שבו החלון נע.
הארגומנט rhs הוא מערך בעל (n+2) מימדים שמתאר את המסנן/הגרעין/החלון הקוונטי. המאפיינים הם, לפי הסדר הזה:
output-z: המאפייןzשל הפלט.input-z: הגודל של המאפיין הזה כפולfeature_group_countצריך להיות שווה לגודל של המאפייןzב-lhs.spatial_dims: מתאר את המאפיינים המרחבייםnשמגדירים את החלון n-ממדי שנע באזור הבסיס.
הארגומנט window_strides מציין את הצעדה של חלון הקוונטיל בממדים המרחביים. לדוגמה, אם הצעדה במאפיין המרחבי הראשון היא 3, אפשר למקם את החלון רק בקואורדינטות שבהן האינדקס המרחבי הראשון מתחלק ב-3.
הארגומנט padding מציין את כמות האפסים שצריך להוסיף לאזור הבסיס. כמות המילוי יכולה להיות שלילית – הערך המוחלט של המילוי השלילי מציין את מספר הרכיבים שצריך להסיר מהממד שצוין לפני ביצוע ההתמרה. padding[0] מציין את המילוי למאפיין y ו-padding[1] מציין את המילוי למאפיין x. כל זוג מכיל את ה-padding הנמוך כרכיב הראשון ואת ה-padding הגבוה כרכיב השני. ה-padding הנמוך מופעל לכיוון של אינדקסים נמוכים יותר, וה-padding הגבוה מופעל לכיוון של אינדקסים גבוהים יותר. לדוגמה, אם הערך של padding[1] הוא (2,3), תתבצע הוספת 2 אפסים בצד ימין ו-3 אפסים בצד שמאל במאפיין המרחבי השני. השימוש במילוי שווה ערך להוספת אותם ערכי אפס לקלט (lhs) לפני ביצוע ההתמרה.
הארגומנטים lhs_dilation ו-rhs_dilation מציינים את גורם ההרחבה שיחול על ה-lhs וה-rhs, בהתאמה, בכל מאפיין מרחבי. אם גורם ההרחבה במאפיין מרחבי הוא d, אז נוצרים d-1 חורים בין כל הרשומות במאפיין הזה, וכך הגודל של המערך גדל. החורים מתמלאים בערך no-op, שמשמעותו אפסים בגלול.
הרחבה של הצד הימני של המשוואה נקראת גם 'קונבולוציה אטרוסית'. למידע נוסף, ראו tf.nn.atrous_conv2d. הרחבה של ה-lhs נקראת גם טרנספוזיציה של convolve. פרטים נוספים זמינים במאמר tf.nn.conv2d_transpose.
אפשר להשתמש בארגומנט feature_group_count (ערך ברירת המחדל הוא 1) כדי לבצע עיבוד נתונים קבוצתי. הערך feature_group_count צריך להיות מחלק של מאפיין הקלט ושל מאפיין הפלט. אם הערך של feature_group_count גדול מ-1, המשמעות היא שקונספטואלית, מאפייני הקלט והפלט ומאפייני הפלט מסוג rhs מחולקים באופן שווה למספר רב של קבוצות feature_group_count, כאשר כל קבוצה מורכבת מרצף משנה רציף של מאפיינים. המאפיין של מאפיין הקלט rhs צריך להיות שווה למאפיין של מאפיין הקלט lhs חלקי feature_group_count (כך שהוא כבר בגודל של קבוצה של מאפייני קלט). הקבוצות ה-i משמשות יחד כדי לחשב את feature_group_count עבור עיבודים מרובים של convolve. התוצאות של ההתחברות הזו מחוברות זו לזו במאפיין הפלט.
עבור convolveion לעומק, הארגומנט feature_group_count יוגדר למאפיין של מאפיין הקלט, והמסנן ישתנה מ-[filter_height, filter_width, in_channels, channel_multiplier] ל-[filter_height, filter_width, 1, in_channels * channel_multiplier]. למידע נוסף, ראו tf.nn.depthwise_conv2d.
אפשר להשתמש בארגומנט batch_group_count (ערך ברירת המחדל הוא 1) למסננים מקובצים במהלך החזרה לאחור. הערך של batch_group_count צריך להיות חלוק של הגודל של מאפיין האצווה lhs (קלט). אם הערך של batch_group_count גדול מ-1, המשמעות היא שהמאפיין batch של הפלט צריך להיות בגודל input batch
/ batch_group_count. הערך של batch_group_count חייב להיות מחלק של גודל המאפיינים של הפלט.
צורת הפלט כוללת את המאפיינים הבאים, בסדר הזה:
batch: הגודל של המאפיין הזה כפולbatch_group_countצריך להיות שווה לגודל של המאפייןbatchב-lhs.z: באותו גודל כמוoutput-zבליבה (rhs).spatial_dims: ערך אחד לכל מיקום תקין של החלון הקוונטי.
באיור שלמעלה מוצג אופן הפעולה של השדה batch_group_count. למעשה, אנחנו מחלקים כל קבוצה של lhs ל-batch_group_count קבוצות, ועושים את אותו הדבר למאפייני הפלט. לאחר מכן, לכל אחת מהקבוצות האלה אנחנו מבצעים עיבוד קוונטי וביחד (convolution) ומקשרים את הפלט לפי מאפיין הפלט. הסמנטיקה התפעולית של כל המאפיינים האחרים (תכונות ומרחביים) נשארת ללא שינוי.
המיקומים התקינים של חלון ה-convolution נקבעים לפי הצעדים (strides) והגודל של אזור הבסיס אחרי הוספת הפסקה (padding).
כדי לתאר את הפעולה של קונבולציה, נבחן קונבולציה דו-מימדית ונבחר כמה קואורדינטות קבועות batch, z, y, x בפלט. במקרה כזה, הערך של (y,x) הוא המיקום של פינה של החלון בתוך אזור הבסיס (למשל, הפינה הימנית העליונה, בהתאם לאופן שבו מפרשים את המימדים המרחביים). עכשיו יש לנו חלון דו-מימדי, שנלקח מאזור הבסיס, שבו כל נקודה דו-מימדית משויכת לוקטור חד-מימדי, כך שאנחנו מקבלים תיבה תלת-מימדית. מתוך הליבה הקוונטית, מכיוון שתיקנו את קואורדינטת הפלט z, יש לנו גם תיבה תלת-ממדית. לשתי התיבות יש אותם מאפיינים, כך שאפשר לחשב את הסכום של המכפלות של הרכיבים בין שתי התיבות (בדומה למכפלה סקלרית). זהו ערך הפלט.
הערה: אם הערך של output-z הוא, למשל, 5, כל מיקום של החלון יוצר 5 ערכים בפלט במאפיין z של הפלט. הערכים האלה שונים בהתאם לחלק של הליבה הקוונטית שבו נעשה שימוש – יש תיבה נפרדת תלת-ממדית של ערכים שמשמשת לכל קואורדינטה output-z. אפשר לחשוב על זה בתור 5 convolve נפרד עם מסנן שונה לכל אחד מהם.
לפניכם קוד מדומה לערבול דו-מימדי עם מילוי ופסיעה:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
ConvertElementType
למידע נוסף: XlaBuilder::ConvertElementType
בדומה ל-static_cast לפי רכיב ב-C++, מבצעת פעולת המרה לפי רכיב מצורת נתונים לצורת יעד. המאפיינים חייבים להתאים, וההמרה מתבצעת לפי רכיבים. לדוגמה, רכיבי s32 הופכים לרכיבי f32 באמצעות תוכנית המרה מ-s32 ל-f32.
ConvertElementType(operand, new_element_type)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T עם מאפייני D |
new_element_type |
PrimitiveType |
סוג U |
המאפיינים של המשתנה המבצע והצורה של היעד חייבים להיות זהים. סוגי הרכיבים של המקור והיעד לא יכולים להיות צמדי ערכים (tuples).
המרה כמו T=s32 ל-U=f32 תבצע תוכנית רגילה של המרה של int ל-float, כמו עיגול ל-even הקרוב ביותר.
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
CrossReplicaSum
ביצוע AllReduce עם חישוב סכום.
CustomCall
למידע נוסף: XlaBuilder::CustomCall
קריאה לפונקציה שהמשתמש סיפק במסגרת חישוב.
CustomCall(target_name, args..., shape)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
target_name |
string |
שם הפונקציה. תופעל הוראה של קריאה שמטרגטת את שם הסמל הזה. |
args |
רצף של N XlaOps |
N ארגומנטים מסוג שרירותי, שיועברו לפונקציה. |
shape |
Shape |
צורת הפלט של הפונקציה |
חתימה הפונקציה זהה, ללא קשר לאריטי או לסוג של args:
extern "C" void target_name(void* out, void** in);
לדוגמה, אם משתמשים ב-CustomCall באופן הבא:
let x = f32[2] {1,2};
let y = f32[2x3] { {10, 20, 30}, {40, 50, 60} };
CustomCall("myfunc", {x, y}, f32[3x3])
דוגמה להטמעה של myfunc:
extern "C" void myfunc(void* out, void** in) {
float (&x)[2] = *static_cast<float(*)[2]>(in[0]);
float (&y)[2][3] = *static_cast<float(*)[2][3]>(in[1]);
EXPECT_EQ(1, x[0]);
EXPECT_EQ(2, x[1]);
EXPECT_EQ(10, y[0][0]);
EXPECT_EQ(20, y[0][1]);
EXPECT_EQ(30, y[0][2]);
EXPECT_EQ(40, y[1][0]);
EXPECT_EQ(50, y[1][1]);
EXPECT_EQ(60, y[1][2]);
float (&z)[3][3] = *static_cast<float(*)[3][3]>(out);
z[0][0] = x[1] + y[1][0];
// ...
}
אסור שתהיה לפונקציה שהמשתמש מספק השפעות לוואי, וההפעלה שלה צריכה להיות חזקה (idempotent).
נקודה
למידע נוסף: XlaBuilder::Dot
Dot(lhs, rhs)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs |
XlaOp |
מערך מסוג T |
rhs |
XlaOp |
מערך מסוג T |
הסמנטיקה המדויקת של הפעולה הזו תלויה ברמות של אופרטנדים:
| קלט | פלט | סמנטיקה |
|---|---|---|
vector [n] dot vector [n] |
סקלר | מכפלה סקלרית של וקטורים |
מטריצה [m x k] dot וקטור [k] |
וקטור [m] | כפל מטריצה-וקטור |
מטריצה [m x k] dot מטריצה [k x n] |
מטריצת [m x n] | כפל מטריצות |
הפעולה מבצעת סכום של מוצרים במאפיין השני של lhs (או במאפיין הראשון אם יש לו מאפיין אחד) ובמאפיין הראשון של rhs. אלה המאפיינים 'בהסכם'. המאפיינים המקוצרים של lhs ו-rhs חייבים להיות באותו גודל. בפועל, אפשר להשתמש בו כדי לבצע מכפלות נקודה בין וקטורים, מכפלות של וקטורים/מטריצות או מכפלות של מטריצות/מטריצות.
DotGeneral
למידע נוסף: XlaBuilder::DotGeneral
DotGeneral(lhs, rhs, dimension_numbers)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs |
XlaOp |
מערך מסוג T |
rhs |
XlaOp |
מערך מסוג T |
dimension_numbers |
DotDimensionNumbers |
מספרי מאפיינים של קבלנים ושל קבוצות |
דומה ל-Dot, אבל מאפשר לציין מספרים של מאפייני התכונה 'התכונה מתכוונת' ו'התכונה מקבילה' גם ב-lhs וגם ב-rhs.
| שדות DotDimensionNumbers | סוג | סמנטיקה |
|---|---|---|
lhs_contracting_dimensions
|
repeated int64 | lhs מספרי המאפיינים של הקבלן |
rhs_contracting_dimensions
|
repeated int64 | rhs מספרי המאפיינים של הקבלן |
lhs_batch_dimensions
|
repeated int64 | מספרי המאפיינים של lhs |
rhs_batch_dimensions
|
repeated int64 | מספרי המאפיינים של rhs |
הפונקציה DotGeneral מבצעת את סכום המכפלות של המאפיינים המצטמצמים שצוינו ב-dimension_numbers.
מספרי המאפיינים המשויכים של הקבלן מ-lhs ומ-rhs לא חייבים להיות זהים, אבל הם חייבים להיות באותו גודל.
דוגמה עם מספרי מאפיינים מתכווצים:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { {6.0, 12.0},
{15.0, 30.0} }
למספרי המאפיינים המשויכים של הקבוצה מהעמודות lhs ו-rhs צריכים להיות אותם גדלים של מאפיינים.
דוגמה עם מספרי מאפייני קבוצה (גודל קבוצה 2, מטריצות 2x2):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| קלט | פלט | סמנטיקה |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | batch matmul |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | batch matmul |
לכן, מספר המאפיין שנוצר מתחיל במאפיין האצווה, ואחריו המאפיין lhs ללא חוזה/ללא אצווה, ולבסוף המאפיין rhs ללא חוזה/ללא אצווה.
DynamicSlice
למידע נוסף: XlaBuilder::DynamicSlice
הפונקציה DynamicSlice מחלצת מערך משנה ממערך הקלט ב-start_indices דינמי. הגודל של הפלחים בכל מאפיין מועבר ב-size_indices, שמציין את נקודת הסיום של מרווחי הפלחים הבלעדיים בכל מאפיין: [start, start + size). הצורה של start_indices חייבת להיות בעלת מימד אחד, וגודלה צריך להיות שווה למספר המימדים של operand.
DynamicSlice(operand, start_indices, size_indices)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך N-מימדי מסוג T |
start_indices |
רצף של N XlaOp |
רשימה של N מספרים שלמים סקלריים שמכילה את אינדקסי ההתחלה של הפלחים בכל מאפיין. הערך חייב להיות גדול מ-0 או שווה ל-0. |
size_indices |
ArraySlice<int64> |
רשימה של N מספרים שלמים שמכילה את גודל הפרוסת לכל מאפיין. כל ערך חייב להיות גדול מאפס, והערך start + size חייב להיות קטן או שווה לגודל המאפיין כדי למנוע גלישת מודולים לפי גודל המאפיין. |
כדי לחשב את אינדקסי הפלחים היעילים, מחילים את הטרנספורמציה הבאה על כל אינדקס i ב-[1, N) לפני ביצוע הפלחים:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - size_indices[i])
כך אפשר לוודא שהפלח שחולץ תמיד נמצא בגבולות של מערך המשתנים. אם הפלחים נמצאים בתוך הגבולות לפני החלת הטרנספורמציה, לטרנספורמציה אין השפעה.
דוגמה במאפיין אחד:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let s = {2}
DynamicSlice(a, s, {2}) produces:
{2.0, 3.0}
דוגמה דו-ממדית:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2}) produces:
{ { 7.0, 8.0},
{10.0, 11.0} }
DynamicUpdateSlice
למידע נוסף: XlaBuilder::DynamicUpdateSlice
הפונקציה DynamicUpdateSlice יוצרת תוצאה שהיא הערך של מערך הקלט operand, עם פלחים של update שמחליפים את start_indices.
הצורה של update קובעת את הצורה של מערך המשנה של התוצאה שמתעדכנת.
הצורה של start_indices חייבת להיות בעלת מימד אחד, וגודל המאפיין צריך להיות שווה למספר המאפיינים של operand.
DynamicUpdateSlice(operand, update, start_indices)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך N-מימדי מסוג T |
update |
XlaOp |
מערך N-ממדי מסוג T שמכיל את עדכון הפלחים. כל מאפיין של צורת העדכון חייב להיות גדול מאפס, ו-start + update חייב להיות קטן או שווה לגודל המשתנה בכל מאפיין כדי למנוע יצירת אינדקסים של עדכונים מחוץ לטווח. |
start_indices |
רצף של N XlaOp |
רשימה של N מספרים שלמים סקלריים שמכילה את אינדקסי ההתחלה של הפלחים בכל מאפיין. הערך חייב להיות גדול מ-0 או שווה ל-0. |
כדי לחשב את אינדקסי הפלחים היעילים, מחילים את הטרנספורמציה הבאה על כל אינדקס i ב-[1, N) לפני ביצוע הפלחים:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
כך אפשר להבטיח שהפלח המעודכן תמיד יהיה בתוך גבולות המערך של המשתנה. אם הפלחים נמצאים בתוך הגבולות לפני החלת הטרנספורמציה, לטרנספורמציה אין השפעה.
דוגמה במאפיין אחד:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s) produces:
{0.0, 1.0, 5.0, 6.0, 4.0}
דוגמה דו-ממדית:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s) produces:
{ {0.0, 1.0, 2.0},
{3.0, 12.0, 13.0},
{6.0, 14.0, 15.0},
{9.0, 16.0, 17.0} }
פעולות אריתמטיות בינאריות לפי רכיבים
למידע נוסף: XlaBuilder::Add
יש תמיכה בקבוצה של פעולות אריתמטיות בינאריות לפי רכיבים.
Op(lhs, rhs)
כאשר Op הוא אחד מהפונקציות הבאות: Add (חיבור), Sub(חיסור), Mul (כפל), Div (חילוק), Pow (חזקה), Rem (שאר), Max (ערך מקסימלי), Min (ערך מינימלי), And (AND לוגי), Or (OR לוגי), Xor (XOR לוגי), ShiftLeft (הזזה ימינה), ShiftRightArithmetic (הזזה ימינה חשבונאית), ShiftRightLogical (הזזה ימינה לוגית), Atan2 (ארקטנגנט עם שני ארגומנטים) או Complex (שילוב של חלקים אמיתיים ודמיוניים למספר מורכב)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs |
XlaOp |
אופרנד בצד ימין: מערך מסוג T |
rhs |
XlaOp |
אופרנד בצד שמאל: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי העזרה בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא בצורה שמתקבלת מהשידור של שני מערכי הקלט. בגרסה הזו, אין תמיכה בפעולות בין מערכי משנה של דרגות שונות, אלא אם אחד מהאופרטנדים הוא סקלר.
כש-Op הוא Rem, סימן התוצאה נלקח מהמחלק, והערך המוחלט של התוצאה הוא תמיד קטן מהערך המוחלט של המחלק.
אם מתרחש חריגה ממלאי הזיכרון במהלך חילוק של מספר שלם (חילוק/שארית עם סימן או ללא סימן באפס, או חילוק/שארית עם סימן של INT_SMIN ב--1), מתקבל ערך שמוגדר על ידי ההטמעה.
יש גרסה חלופית עם תמיכה בשידור בממדים שונים לפעולות הבאות:
Op(lhs, rhs, broadcast_dimensions)
כאשר Op זהה ל-Op שלמעלה. צריך להשתמש בגרסת המשנה הזו של הפעולה לביצוע פעולות אריתמטיות בין מערכי משנה (arrays) של דרגות שונות (למשל, הוספת מטריקס לוקטור).
המשתנה הנוסף broadcast_dimensions הוא פרוסת מספרים שלמים שמשמשת להרחבת מספר המאפיינים של המשתנה בעל המאפיינים הנמוכים יותר עד למספר המאפיינים של המשתנה בעל המאפיינים הגבוהים יותר. broadcast_dimensions ממפה את המאפיינים של הצורה בעלת המאפיינים הנמוכים יותר למאפיינים של הצורה בעלת המאפיינים הגבוהים יותר. המאפיינים שלא מותאמים של הצורה המורחבת יתמלאו במאפיינים בגודל אחד. לאחר מכן, השידור של המאפיינים המנוונים מפיץ את הצורות לאורך המאפיינים המנוונים האלה כדי להשוות את הצורות של שני המשתנים. הסמנטיקה מתוארת בפירוט בדף השידור.
פעולות השוואה לפי רכיבים
למידע נוסף: XlaBuilder::Eq
יש תמיכה בקבוצה של פעולות השוואה בינאריות רגילות לפי רכיבים. חשוב לזכור שסמנטיקה רגילה של השוואה של נקודות צפות מסוג IEEE 754 חלה כשמשווים בין סוגי נקודות צפות.
Op(lhs, rhs)
כאשר Op הוא אחד מהערכים הבאים: Eq (שווה ל-), Ne (לא שווה ל-), Ge (גדול מ- או שווה ל-), Gt (גדול מ-), Le (קטן מ- או שווה ל-), Lt (קטן מ-). קבוצה אחרת של אופרטורים, EqTotalOrder, NeTotalOrder, GeTotalOrder, GtTotalOrder, LeTotalOrder ו-LtTotalOrder, מספקת את אותן פונקציות, מלבד התמיכה הנוספת בסדר מלא על מספרי נקודה צפה, על ידי אכיפה של -NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
lhs |
XlaOp |
אופרנד בצד ימין: מערך מסוג T |
rhs |
XlaOp |
אופרנד בצד שמאל: מערך מסוג T |
הצורות של הארגומנטים צריכות להיות דומות או תואמות. במסמכי העזרה בנושא שידור מוסבר מהי תאימות של צורות. התוצאה של פעולה היא בצורה שמתקבלת מהשידור של שני מערכי הקלט עם טיפוס הרכיב PRED. בגרסה הזו, אין תמיכה בפעולות בין מערכי משנה של דרגות שונות, אלא אם אחד מהאופרטנדים הוא סקלר.
יש גרסה חלופית עם תמיכה בשידור בממדים שונים לפעולות הבאות:
Op(lhs, rhs, broadcast_dimensions)
כאשר Op זהה ל-Op שלמעלה. צריך להשתמש בגרסת המשנה הזו של הפעולה לביצוע פעולות השוואה בין מערכי משנה (arrays) של דרגות שונות (למשל, הוספת מטריצה לוקטור).
המשתנה הנוסף broadcast_dimensions הוא פלחי מספרים שלמים שמציינים את המאפיינים שבהם יש להשתמש לשידור של המשתנים. בדף השידור מוסבר בפירוט על הסמנטיקה.
פונקציות יוניאריות לפי רכיב
XlaBuilder תומך בפונקציות היוניאריות הבאות לפי רכיבים:
Abs(operand) פונקציית abs x -> |x| לפי רכיבים.
Cbrt(operand) פעולת שורש שלישי של רכיבים x -> cbrt(x).
Ceil(operand) פונקציית ceil x -> ⌈x⌉ לפי רכיבים.
Clz(operand) ספירה של אפסים מובילים לפי רכיבים.
Cos(operand) קוסינוס של רכיבים x -> cos(x).
Erf(operand) פונקציית שגיאה לפי רכיבים x -> erf(x), כאשר
erf(x)=2√π∫x0e−t2dt.
Exp(operand) פונקציית מעריכית טבעית לפי רכיבים x -> e^x.
Expm1(operand) מעריכי טבעי לפי רכיבים פחות אחד
x -> e^x - 1.
Floor(operand) x -> ⌊x⌋ – רצפה לפי רכיבים.
Imag(operand) החלק המדומה של צורה מורכבת (או ממשית) לפי אלמנט. x -> imag(x). אם האופרנד הוא מסוג נקודה צפה, הפונקציה מחזירה 0.
IsFinite(operand) הפונקציה בודקת אם כל אלמנט ב-operand הוא סופי, כלומר, שהוא לא אינסוף חיובי או שלילי, והוא לא NaN. הפונקציה מחזירה מערך של ערכים מסוג PRED באותו צורה של הקלט, שבו כל רכיב הוא true אם ורק אם רכיב הקלט התואם הוא סופי.
Log(operand) לוגריתם טבעי לפי רכיבים x -> ln(x).
Log1p(operand) לוגריתם טבעי שהוזז לפי רכיבים x -> ln(1+x).
Logistic(operand) חישוב פונקציה לוגיסטית לפי רכיבים x ->
logistic(x).
Neg(operand) ביטול של רכיבים x -> -x.
Not(operand) שלילה לוגית של רכיבים x -> !(x).
PopulationCount(operand) חישוב מספר הסיביות שמוגדרים בכל רכיב של operand.
Real(operand) החלק הממשי של צורה מורכבת (או אמיתית) לפי אלמנט.
x -> real(x). אם האופרנד הוא מסוג נקודה צפה, הפונקציה מחזירה את אותו ערך.
Round(operand) עיגול לפי אלמנט, במקרה של שוויון עיגול הרחק מהאפס.
RoundNearestEven(operand) עיגול לפי רכיבים, קישור למספר השלם הזוגי הקרוב ביותר.
Rsqrt(operand) הופכית של פעולת השורש הריבועי ברמת האלמנטים
x -> 1.0 / sqrt(x).
Sign(operand) פעולת סימון לפי רכיבים x -> sgn(x) כאשר
sgn(x)={−1x<0−0x=−0NaNx=NaN+0x=+01x>0
באמצעות אופרטור ההשוואה של סוג הרכיב operand.
Sin(operand) סינוס של רכיבים x -> sin(x).
Sqrt(operand) פעולת שורש ריבועי לפי רכיבים x -> sqrt(x).
Tan(operand) נגזרת רכיבי x -> tan(x).
Tanh(operand) טנגנס היפרבולי של רכיבים x -> tanh(x).
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
האופרנד של הפונקציה |
הפונקציה חלה על כל רכיב במערך operand, וכתוצאה מכך נוצר מערך באותו צורה. מותר ל-operand להיות סקלר (בממד 0).
Fft
פעולת ה-FFT של XLA מיישמת את טרנספורמציית פורייה הישירה והפונקציה ההפוכה שלה לקלטים/פלטות אמיתיים ומעורבים. יש תמיכה ב-FFTs מרובי-מימדים ב-3 צירים לכל היותר.
למידע נוסף: XlaBuilder::Fft
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
המערך שאנחנו מבצעים עליו המרה לפורייה. |
fft_type |
FftType |
פרטים נוספים מופיעים בטבלה שבהמשך. |
fft_length |
ArraySlice<int64> |
האורך של הצירים שעוברים טרנספורמציה בתחום הזמן. הצורך בכך נובע במיוחד מכך ש-IRFFT צריך להתאים את הגודל של הציר הפנימי ביותר, כי ל-RFFT(fft_length=[16]) יש את אותו צורת פלט כמו ל-RFFT(fft_length=[17]). |
FftType |
סמנטיקה |
|---|---|
FFT |
FFT קדימה ממרוכב למרוכב. הצורה לא משתנה. |
IFFT |
FFT הפוך ממורכב למורכב. הצורה לא משתנה. |
RFFT |
FFT קדימה ממרחב ממשי למרוכב. הצורה של הציר הפנימי ביותר מצטמצמת ל-fft_length[-1] // 2 + 1 אם fft_length[-1] הוא ערך שאינו אפס, והחלק המנוגד (conjugate) של האות המומר מעבר לתדר Nyquist מושמט. |
IRFFT |
FFT הפוך ממשי למורכב (כלומר, מקבלת מורכב ומחזירה ממשי). הצורה של הציר הפנימי ביותר מורחבת ל-fft_length[-1] אם fft_length[-1] הוא ערך שאינו אפס, ומסקנת את החלק של האות המומר מעבר לתדר Nyquist מהערך הקונגרונטי ההפוך של הרשומות מ-1 ל-fft_length[-1] // 2 + 1. |
FFT רב-מימדי
אם מציינים יותר מ-fft_length אחד, הפעולה הזו שקולה להפעלת מפל של פעולות FFT בכל אחד מהצירים הפנימיים ביותר. שימו לב שבמקרים של המרה מ-real ל-complex ומ-complex ל-real, טרנספורמציית הציר הפנימי ביותר מתבצעת (למעשה) קודם (RFFT; אחרונה ב-IRFFT), ולכן הציר הפנימי ביותר הוא זה שמשתנה. לאחר מכן, טרנספורמציות ציר אחרות יהיו מסוג complex->complex.
פרטי ההטמעה
ה-FFT במעבד (CPU) נתמך על ידי TensorFFT של Eigen. ב-GPU FFT נעשה שימוש ב-cuFFT.
איסוף
פעולת האיסוף של XLA מחברת כמה פרוסות (כל פרוסה יכולה להיות במרווח זמן שונה בסביבת זמן הריצה) של מערך קלט.
סמנטיקה כללית
למידע נוסף: XlaBuilder::Gather
לתיאור אינטואיטיבי יותר, אפשר לעיין בקטע 'תיאור לא רשמי' שבהמשך.
gather(operand, start_indices, offset_dims, collapsed_slice_dims,
slice_sizes, start_index_map)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
המערך שממנו אנחנו אוספים את הנתונים. |
start_indices |
XlaOp |
מערך שמכיל את אינדקסי ההתחלה של הפרוסות שאנחנו אוספים. |
index_vector_dim |
int64 |
המאפיין ב-start_indices ש "מכיל" את האינדקסים ההתחלתיים. תיאור מפורט מופיע בהמשך. |
offset_dims |
ArraySlice<int64> |
קבוצת המאפיינים בפורמט הפלט שמשויכים למערך שנחתך מהאופרטנד. |
slice_sizes |
ArraySlice<int64> |
slice_sizes[i] הוא הגבולות של הפלחים במאפיין i. |
collapsed_slice_dims |
ArraySlice<int64> |
קבוצת המאפיינים בכל פרוסה שמכווצים. הגודל של המאפיינים האלה חייב להיות 1. |
start_index_map |
ArraySlice<int64> |
מפה שמתארת איך למפות אינדקסים ב-start_indices לאינדקסים חוקיים באופרטנד. |
indices_are_sorted |
bool |
האם יש ערובה שהאינדקסים ימוינו על ידי מבצע הקריאה החוזרת. |
כדי להקל עליך, אנחנו מסמנים את המאפיינים במערך הפלט שלא נמצאים ב-offset_dims בתור batch_dims.
הפלט הוא מערך עם batch_dims.size + offset_dims.size מאפיינים.
הערך operand.rank חייב להיות שווה לסכום של offset_dims.size ו-collapsed_slice_dims.size. בנוסף, הערך של slice_sizes.size צריך להיות שווה ל-operand.rank.
אם index_vector_dim שווה ל-start_indices.rank, אנחנו מתייחסים ל-start_indices כאל מאפיין עם מאפיין 1 בסופו (כלומר, אם start_indices היה בצורה [6,7] ו-index_vector_dim הוא 2, אנחנו מתייחסים ל-start_indices כאל [6,7,1]).
הגבולות של מערך הפלט לאורך המאפיין i מחושבים באופן הבא:
אם הערך
iנמצא ב-batch_dims(כלומר, הוא שווה ל-batch_dims[k]עבורkמסוים), בוחרים את גבולות המאפיין התואמים מתוךstart_indices.shape, ודילוגים עלindex_vector_dim(כלומר, בוחרים ב-start_indices.shape.dims[k] אםk<index_vector_dimוב-start_indices.shape.dims[k+1] במקרים אחרים).אם הערך
iנמצא ב-offset_dims(כלומר, הוא שווה ל-offset_dims[k] עבורkכלשהו), בוחרים את הגבול התואם מתוךslice_sizesאחרי שמביאים בחשבון אתcollapsed_slice_dims(כלומר, בוחרים את הערךadjusted_slice_sizes[k] כאשרadjusted_slice_sizesהואslice_sizesאחרי הסרת הגבולות באינדיקטוריםcollapsed_slice_dims).
באופן רשמי, אינדקס המשתנה In שתואם לאינדקס פלט Out נתון מחושב באופן הבא:
מגדירים את
G= {Out[k] forkinbatch_dims}. משתמשים ב-Gכדי לחתוך את הווקטורSכך ש-S[i] =start_indices[Combine(G,i)] כאשר Combine(A, b) מוסיף את b למיקוםindex_vector_dimב-A. שימו לב שההגדרה הזו תקפה גם אםGריק: אםGריק, אזS=start_indices.יוצרים אינדקס התחלה,
Sin, ב-operandבאמצעותSעל ידי פיזורSבאמצעותstart_index_map. באופן מדויק יותר:Sin[start_index_map[k]] =S[k] אםk<start_index_map.size.Sin[_] =0אחרת.
יוצרים אינדקס
Oinב-operandעל ידי פיזור האינדקסים במאפייני ה-offset ב-Outבהתאם לקבוצהcollapsed_slice_dims. באופן מדויק יותר:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]] אםk<offset_dims.size(remapped_offset_dimsמוגדר בהמשך).Oin[_] =0אחרת.
InהואOin+Sin, כאשר + הוא חיבור של רכיבים.
remapped_offset_dims היא פונקציה מונוטונית עם הדומיין [0,
offset_dims.size) והטווח [0, operand.rank) \ collapsed_slice_dims. למשל, אם offset_dims.size הוא 4, operand.rank הוא 6 ו-collapsed_slice_dims הוא {0, 2}, אז remapped_offset_dims הוא {0→1, 1→3, 2→4, 3→5}.
אם הערך של indices_are_sorted מוגדר כ-True, המערכת של XLA יכולה להניח שהמשתמש ממיין את start_indices (במספר עולה, אחרי פיזור הערכים שלו לפי start_index_map). אם לא, הסמנטיקה מוגדרת על ידי ההטמעה.
תיאור לא רשמי ודוגמאות
באופן לא רשמי, כל אינדקס Out במערך הפלט תואם לרכיב E במערך האופרנד, שמחושב באופן הבא:
אנחנו משתמשים במאפייני האצווה ב-
Outכדי לחפש אינדקס התחלה מ-start_indices.אנחנו משתמשים ב-
start_index_mapכדי למפות את אינדקס ההתחלה (שיכול להיות שהוא קטן מ-operand.rank) לאינדקס התחלה "מלא" ב-operand.אנחנו יוצרים פרוסה דינמית בגודל
slice_sizesבאמצעות אינדקס ההתחלה המלא.אנחנו משנים את הצורה של הפלחים על ידי צמצום המאפיינים
collapsed_slice_dims. מכיוון שכל המאפיינים של הפרוסה המקוצרת חייבים להיות מוגבלים ל-1, צורת ה-reshape הזו תמיד חוקית.אנחנו משתמשים במאפייני ההיסט ב-
Outכדי ליצור אינדקס בפרוסת הנתונים הזו, כדי לקבל את רכיב הקלט,E, שתואם לאינדקס הפלטOut.
הערך של index_vector_dim מוגדר ל-start_indices.rank – 1 בכל הדוגמאות שבהמשך. ערכים מעניינים יותר של index_vector_dim לא משנים את הפעולה באופן מהותי, אבל הם הופכים את הייצוג החזותי למסורבל יותר.
כדי להבין איך כל הרכיבים האלה משתלבים, נבחן דוגמה לאיסוף של 5 פרוסות בצורת [8,6] ממערך [16,11]. המיקום של פרוסה במערך [16,11] יכול להיות מיוצג כוקטור אינדקס בצורה S64[2], כך שקבוצה של 5 מיקומים יכולה להיות מיוצגת כמערך S64[5,2].
לאחר מכן, אפשר לתאר את ההתנהגות של פעולת ה-gather כטרנספורמציה של אינדקס שמקבלת את הערכים [G,O0,O1], אינדקס בפורמט הפלט, וממפה אותו לרכיב במערך הקלט באופן הבא:
קודם בוחרים וקטור (X,Y) ממערך אינדקסי האיסוף באמצעות G.
הרכיב במערך הפלט באינדקס [G,O0,O1] הוא הרכיב במערך הקלט באינדקס [X+O0,Y+O1].
הערך של slice_sizes הוא [8,6], שמחליט על הטווח של O0 ושל O1, ובתורו קובע את גבולות הפרוסה.
פעולת האיסוף הזו פועלת כפרוסה דינמית של אצווה, כאשר G הוא המאפיין של האצווה.
אינדקסי האיסוף יכולים להיות מרובת-ממדיים. לדוגמה, גרסה כללית יותר של הדוגמה שלמעלה, שמשתמשת במערך 'gather indices' בפורמט [4,5,2], תתרגם את המדדים כך:
שוב, הפונקציה הזו פועלת כפלח דינמי של קבוצה G0 ו-G1 כמאפייני הקבוצה. גודל הפלחים עדיין [8,6].
פעולת ה-gather ב-XLA מרחיבה את הסמנטיקה הבלתי רשמית שמפורטת למעלה בדרכים הבאות:
אפשר להגדיר אילו מאפיינים בפורמט הפלט הם מאפייני ההיסט (מאפיינים שמכילים את
O0,O1בדוגמה האחרונה). מאפייני האצווה של הפלט (מאפיינים שמכילים את הערכיםG0ו-G1בדוגמה האחרונה) מוגדרים כמאפייני הפלט שאינם מאפייני הזזה.יכול להיות שמספר מאפייני ההיסט של הפלט שקיימים באופן מפורש בפורמט הפלט יהיה קטן ממספר המאפיינים של הקלט. למאפיינים ה'חסרים' האלה, שמפורטים באופן מפורש כ-
collapsed_slice_dims, צריך להיות גודל פרוסת1. מכיוון שגודל הפלחים שלהם הוא1, האינדקס היחיד התקף בשבילם הוא0, והשמטת הפלחים לא יוצרת אי-בהירות.יכול להיות שבפרוסה שחולצה מהמערך Gather Indices ((
X,Y) בדוגמה האחרונה) יהיו פחות רכיבים ממספר המאפיינים של מערך הקלט, ומיפוי מפורש קובע איך צריך להרחיב את האינדקס כך שיכיל את אותו מספר מאפיינים כמו הקלט.
בדוגמה האחרונה, אנחנו משתמשים ב-(2) וב-(3) כדי להטמיע את tf.gather_nd:
G0 ו-G1 משמשים לחיתוך אינדקס התחלה ממערך אינדקסי האיסוף, כמו תמיד, אלא שהאינדקס ההתחלתי מכיל רק רכיב אחד, X. באופן דומה, יש רק אינדקס אחד של היסט פלט עם הערך O0. עם זאת, לפני שהם משמשים כאינדקסים במערך הקלט, הם מורחבים בהתאם למיפוי של אינדקס האיסוף (start_index_map בתיאור הפורמלי) ולמיפוי של ההיסט (remapped_offset_dims בתיאור הפורמלי) ל-[X,0] ול-[0,O0] בהתאמה, ומסתכמים ב-[X,O0]. במילים אחרות, אינדקס הפלט [G0,G1,O0] ממופה לאינדקס הקלט [GatherIndices[G0,G1,0],O0], שמספק את הסמנטיקה של tf.gather_nd.
slice_sizes של הפנייה הזו הוא [1,11]. באופן אינטואיטיבי, המשמעות היא שכל אינדקס X במערך של אינדקסי האיסוף בוחר שורה שלמה, והתוצאה היא שרשור של כל השורות האלה.
GetDimensionSize
למידע נוסף: XlaBuilder::GetDimensionSize
הפונקציה מחזירה את הגודל של המאפיין הנתון של המשתנה. האופרנד חייב להיות בצורת מערך.
GetDimensionSize(operand, dimension)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך קלט n-ממדי |
dimension |
int64 |
ערך בטווח [0, n) שקובע את המאפיין |
SetDimensionSize
למידע נוסף: XlaBuilder::SetDimensionSize
הגדרת הגודל הדינמי של המאפיין הנתון של XlaOp. האופרנד חייב להיות בצורת מערך.
SetDimensionSize(operand, size, dimension)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך קלט n-ממדי. |
size |
XlaOp |
int32 שמייצג את הגודל הדינמי בסביבת זמן הריצה. |
dimension |
int64 |
ערך בטווח [0, n) שקובע את המאפיין. |
העברת המשתנה כערך תוצאה, עם מעקב אחר המאפיין הדינמי על ידי המהדר.
פעולות הפחתה במורד הזרם יתעלמו מערכים עם תוספת שטח.
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
GetTupleElement
למידע נוסף: XlaBuilder::GetTupleElement
הוספת אינדקסים לקבוצת ערכים (tuple) עם ערך קבוע בזמן הידור.
הערך חייב להיות קבוע בזמן הידור כדי שאפשר יהיה להסיק את הצורה של הערך שנוצר.
זה דומה ל-std::get<int N>(t) ב-C++. באופן קונספטואלי:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
למידע נוסף: tf.tuple
Infeed
למידע נוסף: XlaBuilder::Infeed
Infeed(shape)
| ארגומנט | סוג | סמנטיקה |
|---|---|---|
shape |
Shape |
צורת הנתונים שנקראו מהממשק של המודעות שבתוכן. שדה הפריסה של הצורה צריך להיות מוגדר כך שיתאים לפריסה של הנתונים שנשלחים למכשיר. אחרת, ההתנהגות שלו לא מוגדרת. |
הפונקציה קוראת פריט נתונים יחיד מממשק הסטרימינג המשתמעים של ה-Infeed במכשיר, מפענחת את הנתונים לפי הצורה נתונה והפריסה שלה ומחזירה XlaOp של הנתונים. מותר להשתמש במספר פעולות Infeed במהלך חישוב, אבל חייב להיות סדר מוחלט בין פעולות ה-Infeed. לדוגמה, לשני מודעות In-feed בקוד שבהמשך יש סדר ביצוע מוחלט כי יש תלות בין לולאות ה-while.
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
אין תמיכה בצורות של צמדי ערכים (tuple) בתצוגת עץ. אם תבצעו פעולה על טופל (tuple) ריק, פעולת ה-Infeed תהיה למעשה פעולה ללא תוצאה (no-op) והיא תמשיך בלי לקרוא נתונים מה-Infeed של המכשיר.
Iota
למידע נוסף: XlaBuilder::Iota
Iota(shape, iota_dimension)
יצירת ליטרל קבוע במכשיר במקום העברה גדולה של מארח. יצירת מערך בצורה שצוינה, שמכיל ערכים שמתחילים באפס וממשיכים בעלייה של אחד לאורך המאפיין שצוין. לסוגים של נקודה צפה, המערך שנוצר שווה ל-ConvertElementType(Iota(...)), כאשר Iota הוא מסוג שלם וההמרה היא לסוג של נקודה צפה.
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
shape |
Shape |
הצורה של המערך שנוצר על ידי Iota() |
iota_dimension |
int64 |
המאפיין שבו רוצים להגדיל את הערך. |
לדוגמה, הפקודה Iota(s32[4, 8], 0) מחזירה
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
אפשרות החזרה במחיר Iota(s32[4, 8], 1)
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
מפה
למידע נוסף: XlaBuilder::Map
Map(operands..., computation)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands |
רצף של N XlaOps |
N מערכים מסוגים T0..T{N-1} |
computation |
XlaComputation |
חישוב מסוג T_0, T_1, .., T_{N + M -1} -> S עם N פרמטרים מסוג T ו-M מסוג שרירותי |
dimensions |
מערך int64 |
מערך של מאפייני מפה |
הפונקציה מחילה פונקציה סקלרית על מערכי operands הנתונים, ויוצרת מערך באותו המימדים שבו כל רכיב הוא התוצאה של הפונקציה הממופה שחלה על הרכיבים התואמים במערכים של הקלט.
הפונקציה הממופתת היא חישוב שרירותי עם ההגבלה שיש לה N מקורות קלט מסוג סקלר T ופלט יחיד מסוג S. לפלט יש את אותן מאפיינים כמו לאופרטורים, מלבד החלפת סוג הרכיב T ב-S.
לדוגמה: Map(op1, op2, op3, computation, par1) ממפה את elem_out <-
computation(elem1, elem2, elem3, par1) בכל אינדקס (רב-מימדי) במערכים של הקלט כדי ליצור את מערך הפלט.
OptimizationBarrier
מונעת מכל שלב אופטימיזציה להעביר חישובים מעבר למחסום.
מוודאים שכל הקלט מוערך לפני כל אופרטורים שתלויים בפלט של המחסום.
רפידה
למידע נוסף: XlaBuilder::Pad
Pad(operand, padding_value, padding_config)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T |
padding_value |
XlaOp |
סקלר מסוג T כדי למלא את המילוי שנוסף |
padding_config |
PaddingConfig |
כמות המרווח הפנימי בשני הקצוות (נמוך, גבוה) ובין הרכיבים של כל מאפיין |
הרחבה של מערך operand הנתון על ידי הוספת רווחים מסביב למערך וגם בין הרכיבים של המערך באמצעות הערך padding_value. padding_config מציין את כמות המילוי בקצוות ואת כמות המילוי הפנימי לכל מאפיין.
השדה PaddingConfig הוא שדה חוזר של PaddingConfigDimension, שמכיל שלושה שדות לכל מאפיין: edge_padding_low, edge_padding_high ו-interior_padding.
הערכים edge_padding_low ו-edge_padding_high מציינים את כמות המילוי שנוספה בקצה הנמוך (לצד המדד 0) ובקצה הגבוה (לצד המדד הגבוה ביותר) של כל מאפיין, בהתאמה. הערך של הפס ההשלמה בקצה יכול להיות שלילי – הערך המוחלט של הפס ההשלמה השלילי מציין את מספר הרכיבים שצריך להסיר מהמאפיין שצוין.
interior_padding מציין את כמות המרווח הפנימי שנוסף בין שני רכיבים בכל מאפיין. הערך לא יכול להיות שלילי. הוספת מרווח פנימי מתרחשת מבחינה לוגית לפני הוספת מרווח קצה, כך שבמקרה של הוספת מרווח קצה שלילי, הרכיבים יוסרו מהאופרטנד עם הוספת מרווח פנימי.
הפעולה הזו היא פעולה ללא תוצאה (no-op) אם כל זוגות המרווחים בקצוות הם (0, 0) וכל ערכי המרווחים הפנימיים הם 0. באיור הבא מוצגות דוגמאות לערכים שונים של edge_padding ו-interior_padding למערך דו-מימדי.

Recv
למידע נוסף: XlaBuilder::Recv
Recv(shape, channel_handle)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
shape |
Shape |
צורת הנתונים לקבלה |
channel_handle |
ChannelHandle |
מזהה ייחודי לכל זוג של שליחה/קבלה |
מקבל נתונים בפורמט הנתונים הנתון מפקודת Send במחשוב אחר שמשתמש באותו כינוי ערוץ. הפונקציה מחזירה XlaOp עבור הנתונים שהתקבלו.
ממשק ה-API של הלקוח של הפעולה Recv מייצג תקשורת סינכרונית.
עם זאת, ההוראה מפורקת באופן פנימי לשתי הוראות HLO (Recv ו-RecvDone) כדי לאפשר העברות נתונים אסינכררוניות. למידע נוסף, ראו HloInstruction::CreateRecv ו-HloInstruction::CreateRecvDone.
Recv(const Shape& shape, int64 channel_id)
הקצאת המשאבים הנדרשים לקבלת נתונים מהוראה Send עם אותו channel_id. הפונקציה מחזירה הקשר של המשאבים שהוקצו, שמשמש את ההוראה הבאה של RecvDone כדי להמתין להשלמת העברת הנתונים. ההקשר הוא קבוצה של {receive buffer (shape), request identifier (U32)}, וניתן להשתמש בו רק באמצעות הוראה RecvDone.
RecvDone(HloInstruction context)
בהתאם להקשר שנוצר על ידי הוראה Recv, הפונקציה ממתינה להשלמת העברת הנתונים ומחזירה את הנתונים שהתקבלו.
הקטנה
למידע נוסף: XlaBuilder::Reduce
החלת פונקציית הפחתה על מערך אחד או יותר במקביל.
Reduce(operands..., init_values..., computation, dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands |
רצף של N XlaOp |
N מערכים מסוגים T_0, ..., T_{N-1}. |
init_values |
רצף של N XlaOp |
N סקלריים מסוגים T_0, ..., T_{N-1}. |
computation |
XlaComputation |
חישוב מסוג T_0, ..., T_{N-1}, T_0, ..., T_{N-1} -> Collate(T_0, ..., T_{N-1}). |
dimensions |
מערך int64 |
מערך לא ממוין של מאפיינים לצמצום. |
כאשר:
- הערך של N חייב להיות שווה ל-1 או גדול ממנו.
- החישוב צריך להיות "בערך" אסוסיטיבי (ראו בהמשך).
- לכל מערכי הקלט צריכים להיות אותם מאפיינים.
- כל הערכים הראשוניים צריכים ליצור זהות ב-
computation. - אם
N = 1, הערך שלCollate(T)הואT. - אם
N > 1,Collate(T_0, ..., T_{N-1})הוא קבוצה של רכיביNמסוגT.
הפעולה הזו מפחיתה מימד אחד או יותר של כל מערך קלט למשתני סקלאר.
מספר המאפיינים בכל מערך מוחזר הוא number_of_dimensions(operand) - len(dimensions). הפלט של הפעולה הוא Collate(Q_0, ..., Q_N), כאשר Q_i הוא מערך מסוג T_i, שהמאפיינים שלו מתוארים בהמשך.
לקצוות עורפי שונים מותר לשייך מחדש את חישוב הפחתת הנתונים. כתוצאה מכך, יכולים להיות הבדלים מספריים, כי חלק מפונקציות הפחתה, כמו חיבור, לא הן פונקציות אסוסיאיטיביות למספרים מסוג float. עם זאת, אם טווח הנתונים מוגבל, הוספה של נקודה צפה קרובה מספיק להיות אסוציטיבית לרוב השימושים המעשיים.
דוגמאות
כשמצמצמים במאפיין אחד במערך יחיד של 1D עם הערכים [10, 11,
12, 13], עם פונקציית הפחתה f (זהו computation), אפשר לחשב את זה בתור
f(10, f(11, f(12, f(init_value, 13)))
אבל יש גם אפשרויות רבות אחרות, למשל:
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
בדוגמה הבאה מופיע פסאודו-קוד שמראה איך אפשר להטמיע הפחתה, באמצעות סיכום כחישוב ההפחתה עם ערך ראשוני של 0.
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
דוגמה לצמצום מערך דו-מימדי (מטריצה): לצורך יש 2 מימדים, מימד 0 בגודל 2 ומימד 1 בגודל 3:
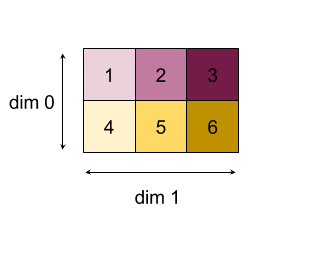
התוצאות של צמצום המאפיינים 0 או 1 באמצעות פונקציית add:

חשוב לזכור ששתי תוצאות הפחתת המידע הן מערכי 1D. הדיאגרמה מציגה את אחת מהן כעמודה ואת השנייה כשורה, רק מטעמי נוחות ויזואלית.
דוגמה מורכבת יותר היא מערך תלת-ממדי. מספר המאפיינים הוא 3, מאפיין 0 בגודל 4, מאפיין 1 בגודל 2 ומאפיין 2 בגודל 3. כדי לפשט את התמונה, הערכים 1 עד 6 מוכפלים במאפיין 0.

בדומה לדוגמה ב-2D, אפשר לצמצם רק מאפיין אחד. לדוגמה, אם מפחיתים את המאפיין 0, מקבלים מערך דו-מימדי שבו כל הערכים של המאפיין 0 מקופלים למערך סקלר:
| 4 8 12 |
| 16 20 24 |
אם נגביל את המאפיין השני, נקבל גם מערך דו-מימדי שבו כל הערכים במאפיין השני ימוקמו בערך סקלרי:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
שימו לב שהסדר היחסי בין המאפיינים שנותרו בקלט נשמר בפלט, אבל יכול להיות שיוקצו מספרים חדשים למאפיינים מסוימים (כי מספר המאפיינים משתנה).
אפשר גם לצמצם כמה מאפיינים. המאפיינים 0 ו-1 של הפחתת-הוספה יוצרים את המערך [20, 28, 36] שהוא מערך חד-ממדי.
צמצום המערך התלת-ממדי בכל המאפיינים שלו יוצר את המערך הסקלרי 84.
Reduce פוליגונומי
כש-N > 1, החלת הפונקציה reduce מורכבת יותר, כי היא חלה בו-זמנית על כל הקלט. אופרטנדים מסופקים לחישוב בסדר הבא:
- הפעלת ערך מופחת של המשתנה הראשון
- ...
- הפעלת ערך מופחת של המשתנה ה-N
- ערך הקלט של המשתנה הראשון
- ...
- ערך הקלט של האופרנד ה-N
לדוגמה, נבחן את פונקציית הפחתת הערכים הבאה, שבה אפשר להשתמש כדי לחשב את הערך המקסימלי ואת הערך argmax של מערך דו-מימדי במקביל:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
למערכי קלט חד-ממדיים V = Float[N], K = Int[N], ולערכים ראשוניים I_V = Float, I_K = Int, התוצאה f_(N-1) של הפחתה במאפיין הקלט היחיד שווה להפעלה הרקורסיבית הבאה:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
החלת הפחתה זו על מערך של ערכים ועל מערך של אינדקסים רציפים (כלומר iota) תבצע איטרציה משותפת על המערכים ותחזיר קבוצת ערכים (tuple) שמכילה את הערך המקסימלי ואת האינדקס התואם.
ReducePrecision
למידע נוסף: XlaBuilder::ReducePrecision
הדגמה של ההשפעה של המרת ערכים של נקודה צפה לפורמט עם דיוק נמוך יותר (כמו IEEE-FP16) וחזרה לפורמט המקורי. אפשר לציין באופן שרירותי את מספר הביטים של המונה והחזקה בפורמט ברמת הדיוק הנמוכה יותר, אבל יכול להיות שלא כל גדלי הביטים נתמכים בכל הטמעות החומרה.
ReducePrecision(operand, mantissa_bits, exponent_bits)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך של נקודה צפה מסוג T. |
exponent_bits |
int32 |
מספר הביטים של המעריך בפורמט עם דיוק נמוך יותר |
mantissa_bits |
int32 |
מספר הביטים של המנטיסה בפורמט עם דיוק נמוך יותר |
התוצאה היא מערך מסוג T. ערכי הקלט מעוגלים לערך הקרוב ביותר שאפשר לייצג במספר הביטים של המנטיסה (באמצעות סמנטיקה של 'קישור לזוגי'), וכל הערכים שחורגים מהטווח שצוין במספר הביטים של המעריך מוצמדים לאינסוף חיובי או שלילי. ערכי NaN נשמרים, אבל יכול להיות שהם יומרו לערכי NaN קנוניקליים.
בפורמט עם רמת הדיוק הנמוכה יותר חייב להיות לפחות ביט אחד של מעריך (כדי להבדיל בין ערך אפס לבין אינסוף, כי לשניהם יש חזקה אפס), וגם מספר לא שלילי של ביטים של חזקה. מספר הביטים של המעריך או של המנטיסה עשוי לחרוג מהערך התואם לסוג T. במקרה כזה, החלק המתאים של ההמרה הוא פשוט פעולה ללא תוצאה (no-op).
ReduceScatter
למידע נוסף: XlaBuilder::ReduceScatter
ReduceScatter היא פעולה קולקטיבית שמבצעת ביעילות AllReduce, ואז מפזרת את התוצאה על ידי פיצולה ל-shard_count בלוקים לאורך scatter_dimension, והרפליקה i בקבוצת הרפליקות מקבלת את הפלח ith.
ReduceScatter(operand, computation, scatter_dim, shard_count,
replica_group_ids, channel_id)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך או קבוצת מערכי tupliות לא ריקה שצריך לצמצם בין הרפליקות. |
computation |
XlaComputation |
חישוב ההנחה |
scatter_dimension |
int64 |
המאפיין ליצירת תרשים הפזורה. |
shard_count |
int64 |
מספר הבלוקטים לפצל scatter_dimension |
replica_groups |
וקטור של וקטורים של int64 |
הקבוצות שביניהן מתבצעות ההפחתות |
channel_id |
אופציונלי int64 |
מזהה ערוץ אופציונלי לתקשורת בין מודולים |
- כש-
operandהוא קבוצת צמדי ערכים (tuple) של מערכי נתונים, הפונקציה reduce-scatter מתבצעת על כל רכיב בקבוצת הצמדים. replica_groupsהיא רשימה של קבוצות של רפליקות שביניהן מתבצעת הפחתה (אפשר לאחזר את מזהה הרפליקה של הרפליקה הנוכחית באמצעותReplicaId). הסדר של הרפליקות בכל קבוצה קובע את הסדר שבו התוצאה של all-reduce תפוזר. השדהreplica_groupsחייב להיות ריק (במקרה כזה כל הרפליקות שייכות לקבוצה אחת) או להכיל את אותו מספר רכיבים כמו מספר הרפליקות. אם יש יותר מקבוצת רפליקות אחת, כולן צריכות להיות באותו גודל. לדוגמה,replica_groups = {0, 2}, {1, 3}מבצע הפחתה בין הרפליקות0ו-2, ו-1ו-3, ולאחר מכן מפזר את התוצאה.shard_countהוא הגודל של כל קבוצת רפליקות. אנחנו זקוקים לזה במקרים שבהם הערכים שלreplica_groupsריקים. אםreplica_groupsלא ריק, הערך שלshard_countחייב להיות שווה לגודל של כל קבוצת רפליקות.- השדה
channel_idמשמש לתקשורת בין מודולים: רק פעולותreduce-scatterעם אותוchannel_idיכולות לתקשר זו עם זו.
צורת הפלט היא צורת הקלט, כאשר scatter_dimension קטנה פי shard_count. לדוגמה, אם יש שתי רפליקות והאופרטנד הוא [1.0, 2.25] ו-[3.0, 5.25], בהתאמה, בשתי הרפליקות, ערך הפלט של הפעולה הזו, כאשר scatter_dim הוא 0, יהיה [4.0] ברפליקה הראשונה ו-[7.5] ברפליקה השנייה.
ReduceWindow
למידע נוסף: XlaBuilder::ReduceWindow
החלת פונקציית הפחתה על כל הרכיבים בכל חלון של רצף של N מערכים מרובי-ממדים, יצירת מערך יחיד או קבוצת ערכים (tuple) של N מערכים מרובי-ממדים כפלט. לכל מערך פלט יש את אותו מספר רכיבים כמו מספר המיקומים התקפים של החלון. אפשר לבטא שכבת צבירה בתור ReduceWindow. בדומה ל-Reduce, הערך של computation שהוחל תמיד מועבר ל-init_values בצד ימין.
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands |
N XlaOps |
רצף של N מערכים מרובי-מימדים מסוגים T_0,..., T_{N-1}, שכל אחד מהם מייצג את אזור הבסיס שבו ממוקם החלון. |
init_values |
N XlaOps |
הערכים ההתחלתיים של N לצורך הפחתה, אחד לכל אחד מ-N המשתנים. פרטים נוספים זמינים במאמר Reduce. |
computation |
XlaComputation |
פונקציית הפחתה מסוג T_0, ..., T_{N-1}, T_0, ..., T_{N-1} -> Collate(T_0, ..., T_{N-1}), שתחול על רכיבים בכל חלון של כל אופרטורי הקלט. |
window_dimensions |
ArraySlice<int64> |
מערך של מספרים שלמים לערכים של מאפייני חלון |
window_strides |
ArraySlice<int64> |
מערך של מספרים שלמים לערכים של חלון הצעדים |
base_dilations |
ArraySlice<int64> |
מערך של מספרים שלמים לערכים של התרחבות הבסיס |
window_dilations |
ArraySlice<int64> |
מערך של מספרים שלמים לערכים של הרחבת חלון |
padding |
Padding |
סוג המילוי של החלון (Padding::kSame, שמוסיף מילוי כדי שהצורה של הפלט תהיה זהה לזו של הקלט אם הצעידה היא 1, או Padding::kValid, שלא משתמש במילוי ו "עוצר" את החלון ברגע שהוא לא מתאים יותר) |
כאשר:
- הערך של N חייב להיות שווה ל-1 או גדול ממנו.
- לכל מערכי הקלט צריכים להיות אותם מאפיינים.
- אם
N = 1, הערך שלCollate(T)הואT. - אם
N > 1,Collate(T_0, ..., T_{N-1})הוא קבוצה של רכיביNמסוג(T0,...T{N-1}).
הקוד והאיור שבהמשך הם דוגמה לשימוש ב-ReduceWindow. הקלט הוא מטריקס בגודל [4x6], וגם window_dimensions וגם window_stride_dimensions הם בגודל [2x3].
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
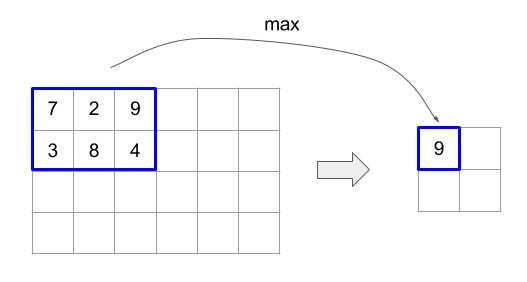
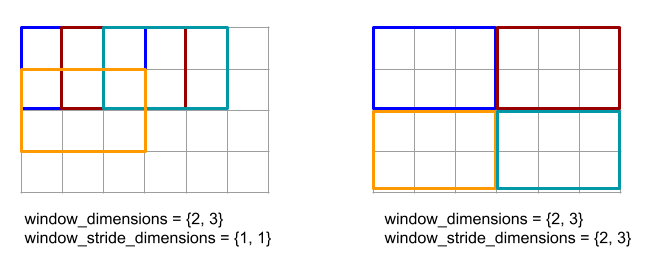
צעד של 1 במאפיין מציין שהמיקום של חלון במאפיין הוא רכיב אחד מהחלון הסמוך. כדי לציין שאין חפיפה בין החלונות, הערך של window_stride_dimensions צריך להיות שווה לערך של window_dimensions. באיור הבא מוצג השימוש בשני ערכים שונים של stride. הוספת הפסקה מתבצעת לכל מאפיין של הקלט, והחישובים זהים כאילו הקלט הגיע עם המאפיינים שלו אחרי הוספת הפסקה.
דוגמה לאיזומת מילוי לא טריוויאלית: חישוב המינימום של חלון הפחתה (הערך הראשוני הוא MAX_FLOAT) עם המאפיין 3 והמרחק 2 על מערך הקלט [10000, 1000, 100, 10, 1]. הפונקציה kValid מחשבת מינימומים בשני חלונות תקפים: [10000, 1000, 100] ו-[100, 10, 1], וכתוצאה מכך מתקבל הפלט [100, 1]. הפונקציה kSame מוסיפה תחילה לאלמנטים של המערך כדי שהצורה אחרי reduce-window תהיה זהה לקלט של צעד אחד, על ידי הוספת רכיבים ראשוניים משני הצדדים, ומקבלת את [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE]. הפעלת reduce-window על המערך המרופד פועלת על שלושה חלונות: [MAX_VALUE, 10000, 1000], [1000, 100, 10] ו-[10, 1, MAX_VALUE], ומניבה את הערך [1000, 10, 1].
סדר ההערכה של פונקציית הפחתה הוא שרירותי ויכול להיות לא דטרמיניסטי. לכן, פונקציית הפחתה לא צריכה להיות רגישה מדי לשיוך מחדש. פרטים נוספים זמינים בנושא שיוך בהקשר של Reduce.
ReplicaId
למידע נוסף: XlaBuilder::ReplicaId
הפונקציה מחזירה את המזהה הייחודי (סקלר U32) של הרפליקה.
ReplicaId()
המזהה הייחודי של כל עותק הוא מספר שלם ללא סימן במרווח [0, N),
כאשר N הוא מספר העותקים. מאחר שכל הרפליקות מריצות את אותה תוכנית, קריאה ל-ReplicaId() בתוכנית תחזיר ערך שונה בכל רפליקה.
עיצוב מחדש
אפשר לעיין גם במאמר XlaBuilder::Reshape ובפעולה Collapse.
שינוי הצורה של המאפיינים של מערך להגדרה חדשה.
Reshape(operand, dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T |
dimensions |
וקטור int64 |
וקטור של גדלים של מאפיינים חדשים |
באופן קונספטואלי, הפונקציה reshape קודם משטחת מערך וקובעת לו וקטור דו-מימדי של ערכים של נתונים, ולאחר מכן משייפת את הווקטור הזה לצורה חדשה. ארגומנטים הקלט הם מערך שרירותי מסוג T, וקבוע-זמן-קמפלור של אינדקסים של מאפיינים, וכן קבוע-זמן-קמפלור של גדלים של מאפיינים לתוצאה.
וקטור dimensions קובע את הגודל של מערך הפלט. הערך ב-index 0 ב-dimensions הוא הגודל של המאפיין 0, הערך ב-index 1 הוא הגודל של המאפיין 1 וכן הלאה. המכפלה של המאפיינים dimensions חייבת להיות שווה למכפלה של גדלי המאפיינים של המשתנה. כשמפיחים את המערך המכווץ למערך המימדי שמוגדר על ידי dimensions, המאפיינים ב-dimensions ממוינים מהשינויים האיטיים ביותר (השינויים המשמעותיים ביותר) לשינויים המהירים ביותר (השינויים הפחות משמעותיים).
לדוגמה, נניח ש-v הוא מערך של 24 רכיבים:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
במקרה מיוחד, הפונקציה reshape יכולה להפוך מערך של רכיב יחיד למערך סקלר ולהפך. לדוגמה,
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
Rev (הפוך)
למידע נוסף: XlaBuilder::Rev
Rev(operand, dimensions)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T |
dimensions |
ArraySlice<int64> |
המאפיינים שרוצים להפוך |
הפונקציה הופכת את הסדר של הרכיבים במערך operand לפי הערך שצוין ב-dimensions, ויוצרת מערך פלט באותו צורה. כל רכיב במערך האופרנד באינדקס רב-מימדי מאוחסן במערך הפלט באינדקס שהומר. כדי לבצע את הטרנספורמציה של המדד המימדי, הופכים את המדד בכל מאפיין שרוצים להפוך (כלומר, אם מאפיין בגודל N הוא אחד מהמאפיינים שרוצים להפוך, המדד שלו i הופך ל-N - 1 - i).
אחת מהשימושים של הפעולה Rev היא להפוך את מערך המשקלים של המפַתח לאורך שני המימדים של החלון במהלך חישוב השיפוע ברשתות נוירונליות.
RngNormal
למידע נוסף: XlaBuilder::RngNormal
יצירת פלט בצורה נתונה באמצעות מספרים אקראיים שנוצרו בהתאם לחלוקה הנורמלית N(μ,σ) . הפרמטרים μ ו- σוצורת הפלט צריכים להיות מסוג רכיב של נקודה צפה. בנוסף, הערכים של הפרמטרים צריכים להיות סקלריים.
RngNormal(mu, sigma, shape)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
mu |
XlaOp |
סקלר מסוג T שקובע את הממוצע של המספרים שנוצרו |
sigma |
XlaOp |
סקלר מסוג T שקובע את סטיית התקן של ה-generated |
shape |
Shape |
צורת הפלט מסוג T |
RngUniform
למידע נוסף: XlaBuilder::RngUniform
יצירת פלט בצורה נתונה עם מספרים אקראיים שנוצרו לפי התפלגות אחידה במרווח [a,b). הסוגים של הפרמטרים ורכיבי הפלט צריכים להיות בוליאניים, שלמים או של נקודות צפות, והם צריכים להיות עקביים. נכון לעכשיו, הקצוות העורפיים של המעבדים (CPU) ושל המעבדים הגרפיים (GPU) תומכים רק ב-F64, F32, F16, BF16, S64, U64, S32 ו-U32. בנוסף, הערכים של הפרמטרים צריכים להיות סקלריים. אם b<=a התוצאה מוגדרת בהטמעה.
RngUniform(a, b, shape)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
a |
XlaOp |
סקלר מסוג T שקובע את הגבול התחתון של מרווח |
b |
XlaOp |
סקלר מסוג T שקובע את הגבול העליון של מרווח |
shape |
Shape |
צורת הפלט מסוג T |
RngBitGenerator
הפונקציה יוצרת פלט בצורה נתונה שמלאה בביטים אקראיים אחידים באמצעות האלגוריתם שצוין (או ברירת המחדל לקצה העורפי), ומחזירה מצב מעודכן (באותה צורה כמו המצב הראשוני) ואת הנתונים האקראיים שנוצרו.
המצב הראשוני הוא המצב הראשוני של יצירת המספר האקראי הנוכחי. הוא והצורה הנדרשת והערכים התקפים תלויים באלגוריתם שבו נעשה שימוש.
מובטח שהפלט יהיה פונקציה גורמית (deterministic) של המצב הראשוני, אבל לא מובטח שהוא יהיה גורמי בין הקצוות העורפיים וגרסאות שונות של המהדר.
RngBitGenerator(algorithm, key, shape)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
algorithm |
RandomAlgorithm |
אלגוריתם ה-PRNG שבו יש להשתמש. |
initial_state |
XlaOp |
המצב הראשוני של אלגוריתם ה-PRNG. |
shape |
Shape |
צורת הפלט של הנתונים שנוצרו. |
הערכים הזמינים של algorithm:
rng_default: אלגוריתם ספציפי לקצה העורפי עם דרישות ספציפיות לקצה העורפי.rng_three_fry: אלגוריתם PRNG מבוסס-מונה של ThreeFry. הצורה שלinitial_stateהיאu64[2]עם ערכים שרירותיים. Salmon et al. SC 2011. מספרים אקראיים במקביל: קל כמו 1, 2, 3.rng_philox: אלגוריתם Philox ליצירת מספרים אקראיים במקביל. הצורהinitial_stateהיאu64[3]עם ערכים שרירותיים. Salmon et al. SC 2011. מספרים אקראיים במקביל: קל כמו 1, 2, 3.
פיזור
פעולת הפיזור של XLA יוצרת רצף של תוצאות שהן הערכים של מערך הקלט operands, עם כמה פרוסות (באינדקסים שצוינו על ידי scatter_indices) שמתעדכנות ברצף הערכים ב-updates באמצעות update_computation.
למידע נוסף: XlaBuilder::Scatter
scatter(operands..., scatter_indices, updates..., update_computation,
index_vector_dim, update_window_dims, inserted_window_dims,
scatter_dims_to_operand_dims)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands |
רצף של N XlaOp |
N מערכים מסוגים T_0, ..., T_N שרוצים לפזר אליהם. |
scatter_indices |
XlaOp |
מערך שמכיל את אינדקסי ההתחלה של הפרוסות שצריך לפזר אליהן. |
updates |
רצף של N XlaOp |
N מערכים מסוגים T_0, ..., T_N. updates[i] מכיל את הערכים שצריך להשתמש בהם כדי לבצע פיזור operands[i]. |
update_computation |
XlaComputation |
החישוב שישמש לשילוב הערכים הקיימים במערך הקלט והעדכונים במהלך הפיצול. החישוב הזה צריך להיות מסוג T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N). |
index_vector_dim |
int64 |
המאפיין ב-scatter_indices שמכיל את אינדקסי ההתחלה. |
update_window_dims |
ArraySlice<int64> |
קבוצת המאפיינים בצורה updates שהם מאפייני חלון. |
inserted_window_dims |
ArraySlice<int64> |
קבוצת המימדים של החלון שצריך להוסיף לצורה updates. |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
מפת מאפיינים מהאינדקסים של הפיזור למרחב של אינדקס המשתנים. המערך הזה מפורש כמיפוי של i אל scatter_dims_to_operand_dims[i] . היחס חייב להיות אחד לאחד וכוללות. |
indices_are_sorted |
bool |
האם יש ערובה שהאינדקסים ימוינו על ידי מבצע הקריאה החוזרת. |
unique_indices |
bool |
האם המפנה מבטיח שהאינדקסים יהיו ייחודיים. |
כאשר:
- הערך של N חייב להיות שווה ל-1 או גדול ממנו.
operands[0], ...,operands[N-1] חייבים להיות בעלי אותם מאפיינים.updates[0], ...,updates[N-1] חייבים להיות בעלי אותם מאפיינים.- אם
N = 1, הערך שלCollate(T)הואT. - אם
N > 1,Collate(T_0, ..., T_N)הוא קבוצה של רכיביNמסוגT.
אם הערך של index_vector_dim שווה ל-scatter_indices.rank, אנחנו מתייחסים ל-scatter_indices כאל מאפיין 1 עם תו אחריו.
אנחנו מגדירים את update_scatter_dims מסוג ArraySlice<int64> כקבוצת המאפיינים בפורמט updates שלא נמצאים ב-update_window_dims, בסדר עולה.
הארגומנטים של scatter צריכים לעמוד באילוצים הבאים:
כל מערך
updatesחייב לכלולupdate_window_dims.size + scatter_indices.rank - 1מאפיינים.גבולות המאפיין
iבכל מערךupdatesחייבים לעמוד בדרישות הבאות:- אם הערך
iנמצא ב-update_window_dims(כלומר, הוא שווה ל-update_window_dims[k] עבור ערך כלשהו שלk), אזי הגבול של המאפייןiב-updatesלא יכול לחרוג מהגבול התואם שלoperandאחרי שמביאים בחשבון אתinserted_window_dims(כלומר,adjusted_window_bounds[k], כאשרadjusted_window_boundsמכיל את הגבולות שלoperandאחרי הסרת הגבולות באינדיקטוריםinserted_window_dims). - אם הערך
iנמצא ב-update_scatter_dims(כלומר, הוא שווה ל-update_scatter_dims[k] עבור ערך כלשהו שלk), אז הגבול של המאפייןiב-updatesחייב להיות שווה לגבול התואם שלscatter_indices, תוך דילוג עלindex_vector_dim(כלומר,scatter_indices.shape.dims[k], אםk<index_vector_dim, ו-scatter_indices.shape.dims[k+1] במקרים אחרים).
- אם הערך
update_window_dimsחייב להיות בסדר עולה, בלי מספרי מאפיינים חוזרים, ובטווח[0, updates.rank).inserted_window_dimsחייב להיות בסדר עולה, בלי מספרי מאפיינים חוזרים, ובטווח[0, operand.rank).הערך
operand.rankחייב להיות שווה לסכום שלupdate_window_dims.sizeו-inserted_window_dims.size.הערך של
scatter_dims_to_operand_dims.sizeחייב להיות שווה ל-scatter_indices.shape.dims[index_vector_dim], והערכים שלו חייבים להיות בטווח[0, operand.rank).
עבור אינדקס U נתון בכל מערך updates, האינדקס התואם I במערך operands המתאים שאליו צריך להחיל את העדכון מחושב באופן הבא:
- מגדירים את
G= {U[k] forkinupdate_scatter_dims}. משתמשים ב-Gכדי לחפש וקטור אינדקסSבמערךscatter_indicesכך ש-S[i] =scatter_indices[Combine(G,i)] כאשר Combine(A, b) מוסיף את b למיקומיםindex_vector_dimב-A. - יוצרים אינדקס
Sinב-operandבאמצעותS, על ידי פיזור שלSבאמצעות המפהscatter_dims_to_operand_dims. באופן רשמי יותר:Sin[scatter_dims_to_operand_dims[k]] =S[k] אםk<scatter_dims_to_operand_dims.size.Sin[_] =0אחרת.
- יוצרים אינדקס
Winלכל מערךoperandsעל ידי פיזור האינדקסים ב-update_window_dimsב-Uבהתאם ל-inserted_window_dims. באופן רשמי יותר:Win[window_dims_to_operand_dims(k)] =U[k] אםkנמצא ב-update_window_dims, כאשרwindow_dims_to_operand_dimsהיא הפונקציה המונוטונית עם הדומיין [0,update_window_dims.size) והטווח [0,operand.rank) \inserted_window_dims. (לדוגמה, אםupdate_window_dims.sizeהוא4,operand.rankהוא6ו-inserted_window_dimsהוא {0,2}, אזwindow_dims_to_operand_dimsהוא {0→1,1→3,2→4,3→5}).Win[_] =0אחרת.
IהואWin+Sin, כאשר + הוא חיבור של רכיבים.
לסיכום, אפשר להגדיר את פעולת הפזורה באופן הבא.
- מאתחלים את
outputבאמצעותoperands, כלומר לכל האינדקסיםJ, לכל האינדקסיםOבמערךoperands[J]:
output[J][O] =operands[J][O] - לכל אינדקס
Uבמערךupdates[J] והאינדקס התואםOבמערךoperand[J], אםOהוא אינדקס תקין ל-output:
(output[0][O], ...,output[N-1][O]) =update_computation(output[0][O], ..., ,output[N-1][O],updates[0][U], ...,updates[N-1][U])
הסדר שבו העדכונים חלים הוא לא דטרמיניסטלי. לכן, כשמספר אינדקסים ב-updates מפנים לאותו אינדקס ב-operands, הערך התואם ב-output יהיה לא דטרמיניסטי.
שימו לב שהפרמטר הראשון שמוענק ל-update_computation יהיה תמיד הערך הנוכחי מהמערך output, והפרמטר השני יהיה תמיד הערך מהמערך updates. הדבר חשוב במיוחד במקרים שבהם הפונקציה update_computation לא מחליפת מקום.
אם הערך של indices_are_sorted מוגדר כ-True, המערכת של XLA יכולה להניח שהמשתמש ממיין את הערכים של scatter_indices (במספר עולה, אחרי פיזור הערכים לפי scatter_dims_to_operand_dims). אם לא, הסמנטיקה מוגדרת על ידי ההטמעה.
אם הערך של unique_indices מוגדר כ-True, ה-XLA יכול להניח שכל הרכיבים שמפוזרים הם ייחודיים. כך XLA יכול להשתמש בפעולות לא אטומיות. אם הערך של unique_indices מוגדר כ-true והאינדקסים שאליהם מתבצעת הפצת הנתונים הם לא ייחודיים, הסמנטיקה מוגדרת על ידי ההטמעה.
באופן לא רשמי, אפשר להתייחס לפעולת ה-scatter כהפוך של פעולת ה-gather, כלומר פעולת ה-scatter מעדכנת את הרכיבים בקלט שחולצו על ידי פעולת ה-gather התואמת.
לתיאור לא רשמי מפורט ולדוגמאות, אפשר לעיין בקטע 'תיאור לא רשמי' בקטע Gather.
בחירה
למידע נוסף: XlaBuilder::Select
יצירת מערך פלט מרכיבים של שני מערכי קלט, על סמך הערכים של מערך תנאי.
Select(pred, on_true, on_false)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
pred |
XlaOp |
מערך מסוג PRED |
on_true |
XlaOp |
מערך מסוג T |
on_false |
XlaOp |
מערך מסוג T |
המערך on_true והמערך on_false חייבים להיות באותו צורה. זהו גם הצורה של מערך הפלט. למערך pred צריכה להיות אותה מימדיות כמו של on_true ו-on_false, עם סוג הרכיב PRED.
לכל רכיב P של pred, הרכיב התואם של מערך הפלט נלקח מ-on_true אם הערך של P הוא true, ומ-on_false אם הערך של P הוא false. כצורה מוגבלת של שידור, הערך של pred יכול להיות סקלאר מסוג PRED. במקרה כזה, מערך הפלט נלקח כולו מ-on_true אם הערך של pred הוא true, ומ-on_false אם הערך של pred הוא false.
דוגמה עם pred שאינו סקלר:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
דוגמה עם רכיב סקלר pred:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
יש תמיכה בבחירות בין צמדי מידע. למטרה הזו, צמדי מפתחות נחשבים לסוגי סקלר. אם on_true ו-on_false הן קבוצות (שצריכות להיות באותו צורה), אז pred צריכה להיות סקלר מסוג PRED.
SelectAndScatter
למידע נוסף: XlaBuilder::SelectAndScatter
אפשר להתייחס לפעולה הזו כפעולה מורכבת שמחשבת קודם את ReduceWindow במערך operand כדי לבחור רכיב מכל חלון, ואז מפזרת את מערך source למערכי האינדקסים של הרכיבים שנבחרו כדי ליצור מערך פלט באותו צורה כמו מערך המשתנה. הפונקציה הבינארית select משמשת לבחירת רכיב מכל חלון על ידי החלתה על כל חלון, והיא נקראת עם המאפיין שוקטור האינדקס של הפרמטר הראשון נמוך מבחינה לקסיקוגרפית מוקטור האינדקס של הפרמטר השני. הפונקציה select מחזירה את הערך true אם הפרמטר הראשון נבחר, ומחזירה את הערך false אם הפרמטר השני נבחר. הפונקציה חייבת להיות טרנזיטיבית (כלומר, אם select(a, b) ו-select(b, c) הם true, אז גם select(a, c) הוא true) כדי שהרכיב שנבחר לא יהיה תלוי בסדר הרכיבים שעברתם בחלון נתון.
הפונקציה scatter חלה על כל אינדקס שנבחר במערך הפלט. הוא מקבל שני פרמטרים סקלריים:
- הערך הנוכחי באינדקס שנבחר במערך הפלט
- ערך הפיזור מ-
sourceשחלה על האינדקס שנבחר
הפונקציה משלבת את שני הפרמטרים ומחזירה ערך סקלר שמשמש לעדכון הערך במדד שנבחר במערך הפלט. בשלב הראשון, כל האינדקסים של מערך הפלט מוגדרים ל-init_value.
מערך הפלט הוא באותה צורה כמו מערך operand, ועל המערך source להיות באותה צורה כמו התוצאה של החלת הפעולה ReduceWindow על מערך operand. אפשר להשתמש ב-SelectAndScatter כדי להעביר חזרה (backpropagate) את ערכי המדרון של שכבת אגירה ברשת עצבית.
SelectAndScatter(operand, select, window_dimensions, window_strides,
padding, source, init_value, scatter)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך מסוג T שדרכו החלונות מחליקים |
select |
XlaComputation |
חישוב בינארי מסוג T, T -> PRED, שיוחל על כל הרכיבים בכל חלון. הפונקציה מחזירה את הערך true אם הפרמטר הראשון נבחר, ואת הערך false אם הפרמטר השני נבחר. |
window_dimensions |
ArraySlice<int64> |
מערך של מספרים שלמים לערכים של מאפייני חלון |
window_strides |
ArraySlice<int64> |
מערך של מספרים שלמים לערכים של חלון הצעדים |
padding |
Padding |
סוג המילוי של החלון (Padding::kSame או Padding::kValid) |
source |
XlaOp |
מערך מסוג T עם הערכים לפיזור |
init_value |
XlaOp |
ערך סקלרי מסוג T עבור הערך הראשוני של מערך הפלט |
scatter |
XlaComputation |
חישוב בינארי מסוג T, T -> T, כדי להחיל כל רכיב מקור של פיזור עם רכיב היעד שלו |
באיור הבא מוצגות דוגמאות לשימוש ב-SelectAndScatter, כאשר הפונקציה select מחשבת את הערך המקסימלי מבין הפרמטרים שלה. שימו לב שכאשר החלונות חופפים, כמו באיור (2) שבהמשך, יכול להיות שאינדקס של מערך operand יבחר כמה פעמים על ידי חלונות שונים. בתרשים, הרכיב עם הערך 9 נבחר על ידי שני החלונות העליונים (כחול ואדום), ופונקציית החיבור הבינארי scatter יוצרת את רכיב הפלט עם הערך 8 (2 + 6).
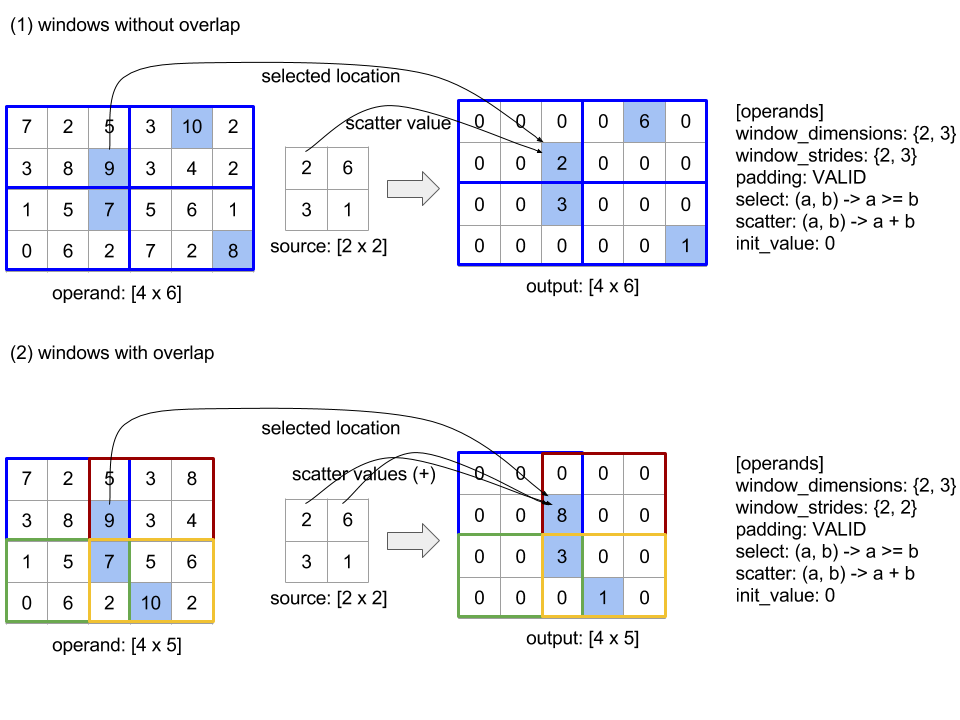
סדר ההערכה של הפונקציה scatter הוא שרירותי ויכול להיות לא דטרמיניסטי. לכן, הפונקציה scatter לא צריכה להיות רגישת מדי לשיוך מחדש. פרטים נוספים זמינים בנושא שיוך בהקשר של Reduce.
שליחה
למידע נוסף: XlaBuilder::Send
Send(operand, channel_handle)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
הנתונים לשליחה (מערך מסוג T) |
channel_handle |
ChannelHandle |
מזהה ייחודי לכל זוג של שליחה/קבלה |
הפונקציה שולחת את נתוני המשתנה שהוגדרו להוראת Recv במחשבה אחרת שמשתתפת באותו מזהה ערוץ. הפונקציה לא מחזירה נתונים.
בדומה לפעולה Recv, ממשק ה-API של הלקוח של הפעולה Send מייצג תקשורת סינכרונית, והוא מתפרק באופן פנימי לשתי הוראות HLO (Send ו-SendDone) כדי לאפשר העברות נתונים אסינכרוניות. למידע נוסף, ראו HloInstruction::CreateSend ו-HloInstruction::CreateSendDone.
Send(HloInstruction operand, int64 channel_id)
הפונקציה מפעילה העברה אסינכררונית של המשתנה למשאבים שהוקצו על ידי ההוראה Recv עם אותו מזהה ערוץ. הפונקציה מחזירה הקשר, שמשמש את ההוראה הבאה מסוג SendDone כדי להמתין להשלמת העברת הנתונים. ההקשר הוא קבוצה של {operand (shape), request identifier (U32)}, וניתן להשתמש בו רק באמצעות הוראה SendDone.
SendDone(HloInstruction context)
בהתאם להקשר שנוצר על ידי הוראה Send, הפונקציה ממתינה להשלמת העברת הנתונים. ההוראה לא מחזירה נתונים.
תזמון של הוראות לערוץ
סדר הביצוע של 4 ההוראות בכל ערוץ (Recv, RecvDone,
Send, SendDone) הוא כפי שמפורט בהמשך.
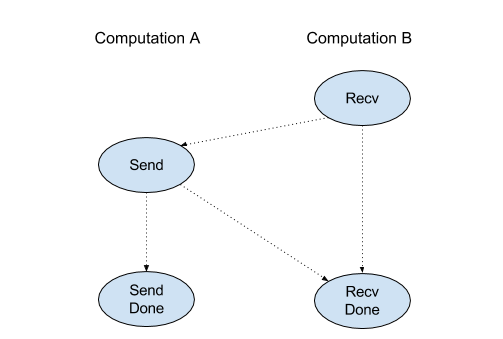
Recvמתרחש לפניSendSendמתרחש לפניRecvDoneRecvמתרחש לפניRecvDoneSendמתרחש לפניSendDone
כשמקודדי הקצה העורפי יוצרים לוח זמנים לינארי לכל חישוב שמתקשר באמצעות הוראות ערוץ, אסור שיהיו מחזורים בתוך החישובים. לדוגמה, לוחות הזמנים הבאים מובילים לנעילה מרובת משתמשים.
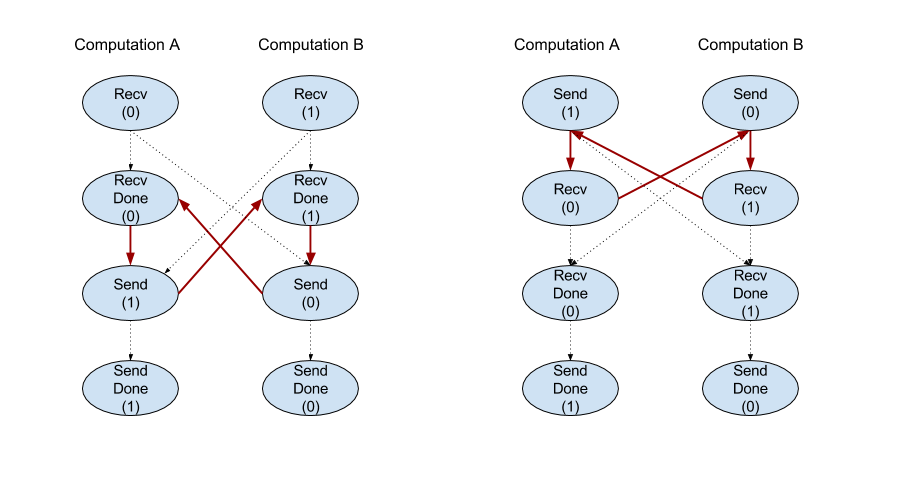
חשוב לזכור שהאילוץ על ההוראות חל רק על TPUs בזמן הריצה. ב-GPU, הערכים send ו-recv ייחסמו ולא ישלחו נתונים בפועל עד לאחר לחיצת יד בין מכשירי המקור והיעד.
תבנית של תוכן דינמי
למידע נוסף: XlaBuilder::Slice
חיתוך מחלץ מערך משנה ממערך הקלט. למערך המשנה יש את אותו מספר מאפיינים כמו הקלט, והוא מכיל את הערכים בתוך תיבת גבולות בתוך מערך הקלט, כאשר המאפיינים והאינדקסים של תיבת הגבולות ניתנים כארגומנטים לפעולה של החיתוך.
Slice(operand, start_indices, limit_indices, strides)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
מערך N-מימדי מסוג T |
start_indices |
ArraySlice<int64> |
רשימה של N מספרים שלמים שמכילה את אינדקסי ההתחלה של הפלחים בכל מאפיין. הערכים חייבים להיות גדולים מ-0 או שווים לו. |
limit_indices |
ArraySlice<int64> |
רשימה של N מספרים שלמים שמכילה את אינדקסי הסיום (לא כולל) של הפלחים לכל מאפיין. כל ערך צריך להיות גדול מ-start_indices או שווה לו עבור המאפיין, וקטן מגודל המאפיין או שווה לו. |
strides |
ArraySlice<int64> |
רשימה של N מספרים שלמים שמחליטים על צעד הקלט של הפלחים. בפלחים נבחרים כל הרכיבים של strides[d] במאפיין d. |
דוגמה במאפיין אחד:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4}) produces:
{2.0, 3.0}
דוגמה דו-ממדית:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3}) produces:
{ { 7.0, 8.0},
{10.0, 11.0} }
מיון
למידע נוסף: XlaBuilder::Sort
Sort(operands, comparator, dimension, is_stable)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operands |
ArraySlice<XlaOp> |
אופרטנדים למיון. |
comparator |
XlaComputation |
החישוב של המשווא להשוואה שבו צריך להשתמש. |
dimension |
int64 |
המאפיין שלפיו רוצים למיין. |
is_stable |
bool |
האם להשתמש במיון יציב. |
אם צוין רק אופרטנד אחד:
אם האופרנד הוא טינסור דו-מימדי (מערך), התוצאה היא מערך ממוין. אם רוצים למיין את המערך בסדר עולה, המבצע צריך לבצע השוואה של פחות מ-. באופן רשמי, אחרי שממיינים את המערך, הוא תקף לכל מיקומי האינדקס
i, jעםi < jששווה ל-comparator(value[i], value[j]) = comparator(value[j], value[i]) = falseאו ל-comparator(value[i], value[j]) = true.אם למשתנה המבצע יש מספר מאפיינים גבוה יותר, המשתנה המבצע ממוין לפי המאפיין שצוין. לדוגמה, בטנסור דו-מימדי (מטריצה), ערך המאפיין
0יסדר כל עמודה בנפרד, וערך המאפיין1יסדר כל שורה בנפרד. אם לא מציינים מספר מאפיין, המאפיין האחרון נבחר כברירת מחדל. למאפיין שממוין, חל אותו סדר מיון כמו במקרה של מאפיין אחד.
אם מציינים אופרטורים של n > 1:
כל המשתנים של
nחייבים להיות טינסורים עם אותם מאפיינים. סוגי הרכיבים של הטנסורים עשויים להיות שונים.כל המשתנים המבצעיים ממוינים יחד, ולא בנפרד. מבחינה מושגית, המשתנים המבצעיים נחשבים כקבוצה (tuple). כשבודקים אם צריך להחליף את הרכיבים של כל אופרנד במיקומי האינדקס
iו-j, מתבצעת קריאה למבצע ההשוואה עם2 * nפרמטרים סקלריים, כאשר הפרמטר2 * kתואם לערך במיקוםiמהאופרטורk-th, והפרמטר2 * k + 1תואם לערך במיקוםjמהאופרטורk-th. לכן, בדרך כלל המשווא המשווה תבדוק את הפרמטרים2 * kו-2 * k + 1ביניהם, ויכול להיות שתשתמש בזוגות פרמטרים אחרים כדי להכריע במקרה של תוצאה זהה.התוצאה היא קבוצת ערכים (tuple) שמכילה את אופרטנדים בסדר ממוין (לפי המאפיין שצוין, כפי שמתואר למעלה). המשתנה
i-thשל הטופל תואם למשתנהi-thשל Sort.
לדוגמה, אם יש שלושה אופרטנדים operand0 = [3, 1], operand1 = [42, 50] ו-operand2 = [-3.0, 1.1], והמתבצע משווה רק את הערכים של operand0 עם פחות מ-, הפלט של המיון הוא הטופל ([1, 3], [50, 42], [1.1, -3.0]).
אם הערך של is_stable מוגדר כ-true, אפשר להבטיח שהמיון יהיה יציב. כלומר, אם יש אלמנטים שנחשבים זהים על ידי המבצע, הסדר היחסי של הערכים הזהים נשמר. שני אלמנטים e1 ו-e2 שווים רק אם comparator(e1, e2) = comparator(e2, e1) = false. כברירת מחדל, הערך של is_stable מוגדר כ-false.
TopK
למידע נוסף: XlaBuilder::TopK
הפונקציה TopK מאתרת את הערכים והאינדקסים של k הרכיבים הגדולים או הקטנים ביותר במאפיין האחרון של הטנזור הנתון.
TopK(operand, k, largest)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
הטנזור שממנו יש לחלץ את k הרכיבים המובילים. למערך הטנזור חייב להיות לפחות מימד אחד. הגודל של המאפיין האחרון של הטנזור חייב להיות גדול מ-k או שווה לו. |
k |
int64 |
מספר הרכיבים לחילוץ. |
largest |
bool |
האם לחלץ את הרכיבים הגדולים ביותר או הקטנים ביותר של k. |
עבור טינסור קלט חד-מימדי (מערך), הפונקציה מאתרת את k הרשומות הגדולות או הקטנות ביותר במערך ומפיקה קבוצה של שני מערכים (values, indices). לכן, הערך values[j] הוא הערך הגדול/הקטן ביותר במקום ה-j ב-operand, והאינדקס שלו הוא indices[j].
עבור טינסור קלט עם יותר ממאפיין אחד, הפונקציה מחשבת את k הרשומות המובילות לפי המאפיין האחרון, תוך שמירה על כל שאר המאפיינים (השורות) בפלט.
לכן, עבור אופרטנד בצורה [A, B, ..., P, Q] כאשר Q >= k, הפלט הוא קבוצת ערכים (tuple) (values, indices) שבה:
values.shape = indices.shape = [A, B, ..., P, k]
אם שני אלמנטים בשורה זהים, האלמנט עם האינדקס הנמוך יותר מופיע קודם.
טרנספוזיציה
אפשר לעיין גם בפעולה tf.reshape.
Transpose(operand)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
operand |
XlaOp |
המשתנה שרוצים לבצע לו טרנספוזיציה. |
permutation |
ArraySlice<int64> |
איך לבצע תמורות של המאפיינים. |
הפונקציה מבצעת תמורה של המאפיינים של המשתנה לפי התמורה שצוינה, כך ש-∀ i . 0 ≤ i < number of dimensions ⇒
input_dimensions[permutation[i]] = output_dimensions[i].
הפונקציה הזו זהה לפונקציה Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)).
TriangularSolve
למידע נוסף: XlaBuilder::TriangularSolve
פתרון מערכות של משוואות ליניאריות עם מטריצות של גורמים משולשיים עליונים או תחתונים באמצעות החלפה קדימה או אחורה. באמצעות שידור (broadcasting) לפי המאפיינים המובילים, התכנית הזו פותרת אחת ממערכות המטריצות op(a) * x =
b או x * op(a) = b עבור המשתנה x, בהתאם ל-a ו-b, כאשר op(a) הוא op(a) = a, או op(a) = Transpose(a), או op(a) = Conj(Transpose(a)).
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
a |
XlaOp |
מערך דו-ממדי עם יותר מ-2 עמודות מסוג מורכב או נקודה צפה, בפורמט [..., M, M]. |
b |
XlaOp |
מערך בעל יותר מ-2 מימדים מאותו סוג עם הצורה [..., M, K] אם הערך של left_side הוא true, [..., K, M] אחרת. |
left_side |
bool |
מציין אם לפתור מערכת מהצורה op(a) * x = b (true) או x * op(a) = b (false). |
lower |
bool |
אם להשתמש במשולש העליון או התחתון של a. |
unit_diagonal |
bool |
אם true, האלמנטים באלכסון של a נחשבים ל-1 ולא מתבצעת גישה אליהם. |
transpose_a |
Transpose |
אם להשתמש ב-a כפי שהוא, לבצע בו טרנספוזיציה או לבצע טרנספוזיציה של הקונגרואנט שלו. |
נתוני הקלט נקראים רק מהמשולש התחתון/העליון של a, בהתאם לערך של lower. המערכת מתעלמת מערכים מהמשולש השני. נתוני הפלט מוחזרים באותו משולש. הערכים במשולש השני מוגדרים בהטמעה ויכולים להיות כל ערך שהוא.
אם מספר המאפיינים של a ו-b גדול מ-2, הם נחשבים כקבוצות של מטריצות, שבהן כל המאפיינים מלבד 2 המאפיינים המשניים הם מאפייני קבוצה. למאפייני האצווה של a ו-b צריכות להיות מאפיינים זהים.
קבוצה
למידע נוסף: XlaBuilder::Tuple
קבוצת ערכים (tuple) שמכילה מספר משתנה של מזהים של נתונים, לכל אחד מהם יש צורה משלו.
זה דומה ל-std::tuple ב-C++. באופן קונספטואלי:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
אפשר לפרק קבוצות של ערכים (ולגשת אליהן) באמצעות הפעולה GetTupleElement.
אף שהפונקציה
למידע נוסף: XlaBuilder::While
While(condition, body, init)
| ארגומנטים | סוג | סמנטיקה |
|---|---|---|
condition |
XlaComputation |
XlaComputation מסוג T -> PRED שמגדיר את תנאי הסיום של הלולאה. |
body |
XlaComputation |
XlaComputation מסוג T -> T שמגדיר את גוף הלולאה. |
init |
T |
הערך הראשוני של הפרמטר של condition ו-body. |
הפונקציה מבצעת את body ברצף עד שה-condition נכשל. הביטוי הזה דומה ל-while loop טיפוסי בשפות רבות אחרות, מלבד ההבדלים וההגבלות שמפורטים בהמשך.
- צומת
Whileמחזיר ערך מסוגT, שהוא התוצאה מההפעלה האחרונה שלbody. - הצורה של הסוג
Tנקבעת באופן סטטי וחובה שהיא תהיה זהה בכל האיטרציות.
הפרמטרים T של החישובים מופעלים עם הערך של init בחזרה הראשונה, ומעודכנים באופן אוטומטי לתוצאה החדשה מ-body בכל חזרה חוזרת.
אחד מהתרחישים העיקריים לשימוש בצומת While הוא להטמיע את הביצוע החוזר של אימון ברשתות נוירונליות. בהמשך מוצג קוד מדומה פשוט עם תרשים שמייצג את החישוב. הקוד מופיע ב-while_test.cc.
הסוג T בדוגמה הזו הוא Tuple שמורכב מ-int32 למספר החזרות ומ-vector[10] למצטבר. במשך 1,000 חזרות, הלולאה ממשיכה להוסיף וקטור קבוע למצטבר.
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}