Poniżej opisujemy semantykę operacji zdefiniowanych w interfejsie XlaBuilder. Zwykle operacje te są mapowane jeden do jednego na operacje zdefiniowane w interfejsie RPC w xla_data.proto.
Uwaga dotycząca nazewnictwa: ogólny typ danych XLA to tablica N-wymiarowa zawierająca elementy o jednolitym typie (np. 32-bitowa liczba zmiennoprzecinkowa). W całej dokumentacji termin tab. oznacza tablicę o dowolnej liczbie wymiarów. Dla wygody szczególne przypadki mają bardziej szczegółowe i znane nazwy. Na przykład wektory to tablice jednowymiarowe, a macierze to tablice dwuwymiarowe.
AfterAll
Zobacz też XlaBuilder::AfterAll.
Funkcja AfterAll przyjmuje zmienną liczbę tokenów i zwraca pojedynczy token. Tokeny to typy prymitywne, które można wplatywać między operacjami o efekcie ubocznym, aby wymuszać kolejność. AfterAll może służyć jako złączenie tokenów do sortowania operacji po zestawie operacji.
AfterAll(operands)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands |
XlaOp |
zmienna liczba tokenów |
AllGather
Zobacz też XlaBuilder::AllGather.
Przeprowadza konkatenację na replikach.
AllGather(operand, all_gather_dim, shard_count, replica_group_ids,
channel_id)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand
|
XlaOp
|
tablica do konkatenacji replik, |
all_gather_dim |
int64 |
Wymiar konkatenacji |
replica_groups
|
wektor wektorówint64 |
Grupy, między którymi wykonywane jest konkatenacja |
channel_id
|
opcjonalnie int64
|
Opcjonalny identyfikator kanału do komunikacji między modułami |
replica_groupsto lista grup replik, między którymi wykonywane jest konkatenowanie (identyfikator bieżącej repliki można pobrać za pomocą funkcjiReplicaId). Kolejność replik w każdej grupie określa kolejność, w jakiej ich dane wejściowe znajdują się w wyniku.replica_groupsmusi być pusty (w tym przypadku wszystkie repliki należą do jednej grupy, uporządkowanej od0doN - 1) lub zawierać taką samą liczbę elementów jak liczba replik. Na przykładreplica_groups = {0, 2}, {1, 3}wykonuje konkatenację replik0i2oraz1i3.shard_countto rozmiar każdej grupy replik. Potrzebujemy tego w przypadku pustych wartościreplica_groups.channel_idjest używany do komunikacji między modułami: tylko operacjeall-gatherz tym samymchannel_idmogą się ze sobą komunikować.
Kształt wyjściowy to kształt wejściowy powiększony o all_gather_dimshard_countrazy. Jeśli np. mamy 2 repliki, a operand ma odpowiednio wartości [1.0, 2.5] i [3.0, 5.25] na obu replikach, wartość wyjściowa z tego operatora, w którym all_gather_dim to 0, będzie wynosić [1.0, 2.5, 3.0,
5.25] na obu replikach.
AllReduce
Zobacz też XlaBuilder::AllReduce.
Wykonuje niestandardowe obliczenia na replikach.
AllReduce(operand, computation, replica_group_ids, channel_id)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand
|
XlaOp
|
Tablica lub niepusta tupla tablic do zredukowania na replikach |
computation |
XlaComputation |
Obliczanie redukcji |
replica_groups
|
wektor wektorówint64 |
Grupy, między którymi są przeprowadzane redukcje |
channel_id
|
opcjonalnie int64
|
Opcjonalny identyfikator kanału do komunikacji między modułami |
- Jeśli
operandto tablica tablic, operacja all-reduce jest wykonywana na każdym elemencie tablicy. replica_groupsto lista grup replik, między którymi wykonywane jest pomniejszenie (identyfikator repliki bieżącej repliki można pobrać za pomocąReplicaId).replica_groupsmusi być pusta (w tym przypadku wszystkie repliki należą do jednej grupy) lub zawierać taką samą liczbę elementów, jak liczba replik. Na przykładreplica_groups = {0, 2}, {1, 3}wykonuje redukcję między replikami0i2oraz1i3.channel_idjest używany do komunikacji między modułami: tylko operacjeall-reducez tym samymchannel_idmogą się ze sobą komunikować.
Kształt wyjściowy jest taki sam jak kształt wejściowy. Jeśli np. są 2 repliki i operand ma odpowiednio wartości [1.0, 2.5] i [3.0, 5.25] na obu replikach, wartość wyjściowa z tego operatora i obliczenia sumy będzie [4.0, 7.75] na obu replikach. Jeśli dane wejściowe to tuple, dane wyjściowe też będą tuple.
Obliczenie wyniku funkcji AllReduce wymaga podania jednego wejścia z każdej repliki, więc jeśli jedna z nich wykona węzeł AllReduce więcej razy niż druga, pierwsza będzie czekać w nieskończoność. Wszystkie repliki działają w ramach tego samego programu, więc nie ma zbyt wielu sposobów, aby to się stało, ale jest to możliwe, gdy warunek pętli while zależy od danych z infeedu, a dane te powodują, że pętla while jest wykonywana na jednej replice więcej razy niż na innej.
AllToAll
Zobacz też XlaBuilder::AllToAll.
AllToAll to operacja zbiorcza, która wysyła dane ze wszystkich rdzeni do wszystkich rdzeni. Składa się z 2 etapów:
- Faza rozrzutu. W każdym rdzeniu operand jest dzielony na
split_countbloków wzdłużsplit_dimensions, a bloki są rozproszone do wszystkich rdzeni, np. i-ty blok jest wysyłany do i-tego rdzenia. - Faza zbierania informacji. Każde jądro konkatenuje otrzymane bloki wzdłuż
concat_dimension.
Uczestniczących rdzeni można używać, konfigurując je w następujący sposób:
replica_groups: każda grupa replik zawiera listę identyfikatorów replik uczestniczących w obliczeniach (identyfikator repliki bieżącej repliki można pobrać za pomocą parametruReplicaId). Operacja AllToAll zostanie zastosowana w podgrupach w określonej kolejności. Na przykładreplica_groups = { {1,2,3}, {4,5,0} }oznacza, że operacja AllToAll zostanie zastosowana w ramach replik{1, 2, 3}, a w fazie zbierania otrzymane bloki zostaną złączone w tej samej kolejności: 1, 2, 3. Następnie zostanie zastosowany kolejny operator AllToAll w przypadku replik 4, 5, 0, a kolejność konkatenacji to również 4, 5, 0. Jeślireplica_groupsjest pusty, wszystkie repliki należą do jednej grupy w kolejności ich występowania.
Wymagania wstępne:
- Rozmiar wymiaru operanda w wyrażeniem
split_dimensionjest podzielny przezsplit_count. - Kształt operandu nie jest tablicą.
AllToAll(operand, split_dimension, concat_dimension, split_count,
replica_groups)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica wejściowa o n wymiarach |
split_dimension
|
int64
|
Wartość z przedziału [0,
n), która określa wymiar, wzdłuż którego operand jest dzielony. |
concat_dimension
|
int64
|
Wartość z przedziału [0,
n), która jest nazwą wymiaru, wzdłuż którego następuje konkatenacja bloków podzielonych |
split_count
|
int64
|
Liczba rdzeni, które biorą udział w tej operacji. Jeśli parametr replica_groups jest pusty, powinien on zawierać liczbę replik. W przeciwnym razie powinien być równy liczbie replik w każdej grupie. |
replica_groups
|
ReplicaGroup wektor
|
Każda grupa zawiera listę identyfikatorów replik. |
Poniżej znajduje się przykład Alltoall.
XlaBuilder b("alltoall");
auto x = Parameter(&b, 0, ShapeUtil::MakeShape(F32, {4, 16}), "x");
AllToAll(x, /*split_dimension=*/1, /*concat_dimension=*/0, /*split_count=*/4);

W tym przykładzie w operacji Alltoall biorą udział 4 rdzenie. Na każdym rdzeniu operand jest dzielony na 4 części wzdłuż wymiaru 1, więc każda część ma kształt f32[4,4]. 4 części są rozproszone po wszystkich rdzeniach. Następnie każda podstawa konkatenuje otrzymane części w wymiarach 0–4 w kolejności od 0 do 4. Dlatego dane wyjściowe każdego rdzenia mają postać f32[16,4].
BatchNormGrad
Szczegółowy opis algorytmu znajdziesz w artykule XlaBuilder::BatchNormGrad i pierwotnym artykule na temat normalizacji zbiorczej.
Oblicza gradienty normy zbiorczej.
BatchNormGrad(operand, scale, mean, variance, grad_output, epsilon,
feature_index)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica n-wymiarowa do znormalizowania (x) |
scale |
XlaOp |
Tablica jednowymiarowa (\(\gamma\)) |
mean |
XlaOp |
Tablica jednowymiarowa (\(\mu\)) |
variance |
XlaOp |
Tablica jednowymiarowa (\(\sigma^2\)) |
grad_output |
XlaOp |
Gradienty przekazane do BatchNormTraining (\(\nabla y\)) |
epsilon |
float |
Wartość epsilon (\(\epsilon\)) |
feature_index |
int64 |
Indeks do wymiaru cechy w operand |
W przypadku każdej cechy w wymiarze cech (feature_index to indeks wymiaru cech w operand) operacja oblicza gradienty względem operand, offset i scale we wszystkich pozostałych wymiarach. Wartość feature_index musi być prawidłowym indeksem wymiaru cechy w elementach operand.
Te 3 gradienty są zdefiniowane za pomocą tych wzorów (przy założeniu, że tablica 4-wymiarowa to operand, a indeks wymiaru funkcji to l, rozmiar partii to m, a rozmiary przestrzenne to w i h):
\[ \begin{split} c_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sigma^2_l+\epsilon} \right) \\\\ d_l&= \frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \\\\ \nabla x_{ijkl} &= \frac{\gamma_{l} }{\sqrt{\sigma^2_{l}+\epsilon} } \left( \nabla y_{ijkl} - d_l - c_l (x_{ijkl} - \mu_{l}) \right) \\\\ \nabla \gamma_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \left( \nabla y_{ijkl} \frac{x_{ijkl} - \mu_l}{\sqrt{\sigma^2_{l}+\epsilon} } \right) \\\\\ \nabla \beta_l &= \sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h \nabla y_{ijkl} \end{split} \]
Dane wejściowe mean i variance reprezentują wartości momentów w wymiarach zbiorczych i przestrzennych.
Typ danych wyjściowych to tupla 3 identyfikatorów:
| Wyniki | Typ | Semantyka |
|---|---|---|
grad_operand
|
XlaOp
|
gradient względem wejścia operand ($\nabla
x$) |
grad_scale
|
XlaOp
|
gradient względem wejścia scale ($\nabla
\gamma$) |
grad_offset
|
XlaOp
|
gradient względem wejścia offset($\nabla
\beta$) |
BatchNormInference
Szczegółowy opis algorytmu znajdziesz w artykule XlaBuilder::BatchNormInference i pierwotnym artykule na temat normalizacji zbiorczej.
Normalizuje tablicę w wymiarach zbiorczych i przestrzennych.
BatchNormInference(operand, scale, offset, mean, variance, epsilon,
feature_index)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica n-wymiarowa do znormalizowania |
scale |
XlaOp |
tablica jednowymiarowa, |
offset |
XlaOp |
tablica jednowymiarowa, |
mean |
XlaOp |
tablica jednowymiarowa, |
variance |
XlaOp |
tablica jednowymiarowa, |
epsilon |
float |
Wartość epsilon |
feature_index |
int64 |
Indeks do wymiaru cechy w operand |
W przypadku każdej cechy w wymiarze cech (feature_index to indeks wymiaru cech w wymiarze operand) operacja oblicza średnią i wariancję w przypadku wszystkich pozostałych wymiarów, a następnie używa średniej i wariacji do normalizacji każdego elementu w wymiarze operand. Wartość feature_index musi być prawidłowym indeksem wymiaru funkcji w parametrze operand.
Funkcja BatchNormInference jest odpowiednikiem funkcji BatchNormTraining bez obliczania wartości mean i variance dla każdej partii. Zamiast tego używa wartości wejściowych mean i variance jako wartości szacunkowych. Celem tej opcji jest zmniejszenie opóźnienia w inferencji, stąd nazwa BatchNormInference.
Dane wyjściowe to znormalizowany tablica n-wymiarowa o tej samej postaci co wejścieoperand.
BatchNormTraining
Szczegółowe informacje o algorytmie znajdziesz też w artykule XlaBuilder::BatchNormTraining i the original batch normalization paper.
Normalizuje tablicę w wymiarach zbiorczych i przestrzennych.
BatchNormTraining(operand, scale, offset, epsilon, feature_index)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica n-wymiarowa do znormalizowania (x) |
scale |
XlaOp |
Tablica jednowymiarowa (\(\gamma\)) |
offset |
XlaOp |
Tablica jednowymiarowa (\(\beta\)) |
epsilon |
float |
Wartość epsilon (\(\epsilon\)) |
feature_index |
int64 |
Indeks do wymiaru cechy w operand |
W przypadku każdej cechy w wymiarze cech (feature_index to indeks wymiaru cech w wymiarze operand) operacja oblicza średnią i wariancję w przypadku wszystkich pozostałych wymiarów, a następnie używa średniej i wariacji do normalizacji każdego elementu w wymiarze operand. Wartość feature_index musi być prawidłowym indeksem wymiaru funkcji w parametrze operand.
W przypadku każdego zbioru w tablicy operand \(x\) , który zawiera melementów o wymiarach przestrzennych w i h (przy założeniu, że operand to tablica 4-wymiarowa), algorytm działa w ten sposób:
Oblicza średnią zbiorczą \(\mu_l\) dla każdej cechy
lw wymiarze cech:\(\mu_l=\frac{1}{mwh}\sum_{i=1}^m\sum_{j=1}^w\sum_{k=1}^h x_{ijkl}\)Oblicza odchylenie standardowe partii: \(\sigma^2_l\) $\sigma^2l=\frac{1}{mwh}\sum{i=1}^m\sum{j=1}^w\sum{k=1}^h (x_{ijkl} - \mu_l)^2$
Normalizuje, skaluje i przesuwa:\(y_{ijkl}=\frac{\gamma_l(x_{ijkl}-\mu_l)}{\sqrt[2]{\sigma^2_l+\epsilon} }+\beta_l\)
Wartość epsilon, która zwykle jest niewielka, jest dodawana, aby uniknąć błędów dzielenia przez 0.
Typ danych wyjściowych to tupla 3 wartości XlaOp:
| Wyniki | Typ | Semantyka |
|---|---|---|
output
|
XlaOp
|
tablica n-wymiarowa o tym samym kształcie co wejście operand (y) |
batch_mean |
XlaOp |
Tablica jednowymiarowa (\(\mu\)) |
batch_var |
XlaOp |
Tablica jednowymiarowa (\(\sigma^2\)) |
Wartości batch_mean i batch_var to momenty obliczone na podstawie wymiarów zbiorczego i przestrzennego za pomocą podanych powyżej wzorów.
BitcastConvertType
Zobacz też XlaBuilder::BitcastConvertType.
Podobnie jak w przypadku funkcji tf.bitcast w TensorFlow, wykonuje ona bitową operację przesunięcia bitowego elementów z kształtu danych na kształt docelowy. Rozmiar danych wejściowych i wyjściowych musi być taki sam: np. elementy s32 stają się elementami f32 za pomocą rutyny bitowej, a jeden element s32 staje się 4 elementami s8. Przekształcanie bitowe jest implementowane jako przekształcanie na niskim poziomie, więc maszyny z różnymi reprezentacjami zmiennoprzecinkowymi będą dawać różne wyniki.
BitcastConvertType(operand, new_element_type)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica typu T o wymiarach D |
new_element_type |
PrimitiveType |
typ U |
Wymiary operandu i kształtu docelowego muszą być zgodne, z wyjątkiem ostatniego wymiaru, który zmieni się zgodnie z proporcją rozmiaru prymitywu przed i po konwersji.
Typy elementów źródłowego i docelowego nie mogą być tablicami.
Przekształcanie bitowe w prosty typ o innej szerokości
BitcastConvert Instrukcja HLO obsługuje przypadek, gdy rozmiar typu elementu wyjściowego T' nie jest równy rozmiarowi elementu wejściowego T. Cała operacja jest teoretycznie bitowym przesyłaniem i nie zmienia podstawowych bajtów, dlatego kształt elementu wyjściowego musi się zmienić. W przypadku B = sizeof(T), B' =
sizeof(T') są 2 możliwe scenariusze.
Po pierwsze, gdy B > B', kształt wyjściowy otrzymuje nowy wymiar o wymiary B/B'. Na przykład:
f16[10,2]{1,0} %output = f16[10,2]{1,0} bitcast-convert(f32[10]{0} %input)
W przypadku skutecznych wektorów reguła pozostaje taka sama:
f16[2]{0} %output = f16[2]{0} bitcast-convert(f32[] %input)
W przypadku instrukcji B' > B ostatni wymiar logiczny kształtu wejściowego musi być równy B'/B, a ten wymiar jest pomijany podczas konwersji:
f32[10]{0} %output = f32[10]{0} bitcast-convert(f16[10,2]{1,0} %input)
Pamiętaj, że konwersje między różnymi szerokościami bitów nie są wykonywane element po elemencie.
Transmisja
Zobacz też XlaBuilder::Broadcast.
Dodaje wymiary do tablicy, duplikując dane w niej.
Broadcast(operand, broadcast_sizes)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Tablica do powielenia |
broadcast_sizes |
ArraySlice<int64> |
rozmiary nowych wymiarów, |
Nowe wymiary są wstawiane po lewej stronie, czyli jeśli broadcast_sizes ma wartości {a0, ..., aN}, a kształt operandu ma wymiary {b0, ..., bM}, to kształt wyjściowy ma wymiary {a0, ..., aN, b0, ..., bM}.
Nowe wymiary indeksują kopie operandu, czyli
output[i0, ..., iN, j0, ..., jM] = operand[j0, ..., jM]
Jeśli na przykład operand to skalar f32 o wartości 2.0f, a broadcast_sizes to {2, 3}, wynik będzie tablicą o kształcie f32[2, 3], a wszystkie jej wartości będą miały wartość 2.0f.
BroadcastInDim
Zobacz też XlaBuilder::BroadcastInDim.
Zwiększa rozmiar i liczbę wymiarów tablicy przez powielanie danych w niej.
BroadcastInDim(operand, out_dim_size, broadcast_dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Tablica do powielenia |
out_dim_size |
ArraySlice<int64> |
Wymiary wymiarów kształtu docelowego |
broadcast_dimensions |
ArraySlice<int64> |
Do którego wymiaru kształtu docelowego ma być dopasowany każdy wymiar kształtu operandu |
Podobnie jak w przypadku transmisji, ale umożliwia dodawanie wymiarów w dowolnym miejscu i rozszerzanie dotychczasowych wymiarów o rozmiar 1.
Wartość operand jest nadawana do kształtu opisanego przez out_dim_size.
broadcast_dimensions mapuje wymiary funkcji operand na wymiary kształtu docelowego, tzn. i-ty wymiar operandu jest mapowany na i-ty wymiar kształtu wyjściowego (broadcast_dimension[i]). Wymiary operand muszą mieć rozmiar 1 lub taki sam jak wymiar w kształcie wyjściowym, do którego są mapowane. Pozostałe wymiary są wypełniane wymiarami o rozmiarze 1. Następnie przesyłanie danych za pomocą wymiarów zdegenerowanych, aby uzyskać kształt wyjściowy. Semantyka jest szczegółowo opisana na stronie z transmisją.
Połączenie
Zobacz też XlaBuilder::Call.
Wywołuje obliczenie z danymi argumentami.
Call(computation, args...)
| Argumenty | Typ | Semantyka |
|---|---|---|
computation |
XlaComputation |
obliczenia typu T_0, T_1, ..., T_{N-1} -> S z N parametrami dowolnego typu |
args |
sekwencja N XlaOp |
N argumentów dowolnego typu |
Liczba argumentów i typy funkcji args muszą być zgodne z parametrami funkcji
computation. Nie musi być elementu args.
CompositeCall
Zobacz też XlaBuilder::CompositeCall.
Zawiera operację złożoną z innych operacji StableHLO, która przyjmuje dane wejściowe i atrybuty złożone oraz zwraca wyniki. Semantyka operacji jest implementowana przez atrybut dekompozycji. Operację złożoną można zastąpić jej dekompozycją bez zmiany semantyki programu. Jeśli wstawienie dekompozycji nie zapewnia takiej samej semantyki funkcji, użyj funkcji custom_call.
Pole version (domyślnie 0) służy do wskazywania, kiedy zmienia się semantyka komponentu.
Ta opcja jest implementowana jako kCall z atrybutem is_composite=true. Pole decomposition jest określane przez atrybut computation. Pozostałe atrybuty są przechowywane w atrybutach interfejsu z przedrostkiem composite..
Przykład opcji CompositeCall:
f32[] call(f32[] %cst), to_apply=%computation, is_composite=true,
frontend_attributes = {
composite.name="foo.bar",
composite.attributes={n = 1 : i32, tensor = dense<1> : tensor<i32>},
composite.version="1"
}
Call(computation, args..., name, composite_attributes, version)
| Argumenty | Typ | Semantyka |
|---|---|---|
inputs |
XlaOp |
zmienna liczba wartości |
name |
string |
nazwa kompozycji; |
composite_attributes |
opcjonalnie string |
opcjonalny słownik atrybutów w postaci ciągu znaków; |
decomposition |
XlaComputation |
obliczenia typu T_0, T_1, ..., T_{N-1} -> S z N parametrami dowolnego typu |
version |
int64. |
number to version updates to semantics of the composite op |
Cholesky
Zobacz też XlaBuilder::Cholesky.
Oblicza dekomponację Choleskiego dla zbioru symetrycznych (hermickich) dodatnio określonych macierzy.
Cholesky(a, lower)
| Argumenty | Typ | Semantyka |
|---|---|---|
a |
XlaOp |
tablica typu złożonego lub zmiennoprzecinkowego o większej liczbie wymiarów niż 2. |
lower |
bool |
czy użyć górnego czy dolnego trójkąta w a. |
Jeśli lower to true, oblicza macierz dolny trójkątną l taką, że $a = l .
l^T$. Jeśli lower to false, oblicza górne macierze trójkątne u takie, że\(a = u^T . u\).
Dane wejściowe są odczytywane tylko z dolnego lub górnego trójkąta a w zależności od wartości parametru lower. Wartości z drugiego trójkąta są ignorowane. Dane wyjściowe są zwracane w tym samym trójkącie; wartości w drugim trójkącie są zdefiniowane przez implementację i mogą być dowolne.
Jeśli a ma więcej niż 2 wymiary, a jest traktowane jako zbiór macierzy,
gdzie wszystkie wymiary z wyjątkiem 2 mniejszych są wymiarami zbioru.
Jeśli a nie jest symetryczna (hermityczna) i oraz dodatnio określona, wynik jest zdefiniowany przez implementację.
Ograniczanie zakresu
Zobacz też XlaBuilder::Clamp.
Blokuje operand w zakresie między wartością minimalną a maksymalną.
Clamp(min, operand, max)
| Argumenty | Typ | Semantyka |
|---|---|---|
min |
XlaOp |
tablica typu T |
operand |
XlaOp |
tablica typu T |
max |
XlaOp |
tablica typu T |
Funkcja ta zwraca operanda, jeśli mieści się on w zakresie między wartością minimalną a maksymalną. W przeciwnym razie zwraca wartość minimalną, jeśli operand jest poniżej tego zakresu, lub wartość maksymalną, jeśli operand jest powyżej tego zakresu. Oznacza to, że clamp(a, x, b) = min(max(a, x), b).
Wszystkie 3 tablice muszą mieć ten sam kształt. Jako ograniczona forma transmisji zmienne min lub max mogą być skalarami typu T.
Przykład z elementami skalarnymi min i max:
let operand: s32[3] = {-1, 5, 9};
let min: s32 = 0;
let max: s32 = 6;
==>
Clamp(min, operand, max) = s32[3]{0, 5, 6};
Zwiń
Zobacz też XlaBuilder::Collapse i operację tf.reshape.
Łączy wymiary tablicy w jeden wymiar.
Collapse(operand, dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica typu T |
dimensions |
int64 wektor |
uporządkowany według kolejności ciągły podzbiór wymiarów T. |
Operacja Collapse zastępuje podzbiór wymiarów operandu pojedynczym wymiarem. Argumenty wejściowe to dowolna tablica typu T i wektory indeksów wymiarów stałe w czasie kompilacji. Indeksy wymiarów muszą być uporządkowane według numerów wymiarów (od niższych do wyższych), w kolejnym podzbiorze wymiarów T. Dlatego zestawy wymiarów {0, 1, 2}, {0, 1} i {1, 2} są prawidłowe, ale {1, 0} i {0, 2} – nie. Zostaną one zastąpione przez 1 nowy wymiar na tej samej pozycji w sekwencji wymiarów, co wymiary, które zastępują, a nowy rozmiar wymiaru będzie równy iloczynowi rozmiarów pierwotnych wymiarów. Najmniejsza liczba wymiaru w funkcji dimensions to wymiar o najwolniejszej zmienności (najbardziej ogólny) w gnieździe pętli, które zwija te wymiary, a największa liczba wymiaru to wymiar o najszybszej zmienności (najbardziej szczegółowy). Jeśli potrzebujesz bardziej ogólnego uporządkowania, użyj operatora tf.reshape.
Na przykład niech v będzie tablicą 24 elementów:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
// Collapse to a single dimension, leaving one dimension.
let v012 = Collapse(v, {0,1,2});
then v012 == f32[24] {10, 11, 12, 15, 16, 17,
20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37,
40, 41, 42, 45, 46, 47};
// Collapse the two lower dimensions, leaving two dimensions.
let v01 = Collapse(v, {0,1});
then v01 == f32[4x6] { {10, 11, 12, 15, 16, 17},
{20, 21, 22, 25, 26, 27},
{30, 31, 32, 35, 36, 37},
{40, 41, 42, 45, 46, 47} };
// Collapse the two higher dimensions, leaving two dimensions.
let v12 = Collapse(v, {1,2});
then v12 == f32[8x3] { {10, 11, 12},
{15, 16, 17},
{20, 21, 22},
{25, 26, 27},
{30, 31, 32},
{35, 36, 37},
{40, 41, 42},
{45, 46, 47} };
CollectivePermute
Zobacz też XlaBuilder::CollectivePermute.
CollectivePermute to operacja zbiorcza, która wysyła i odbiera dane z wielu replik.
CollectivePermute(operand, source_target_pairs)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica wejściowa o n wymiarach |
source_target_pairs |
<int64, int64> wektor |
Lista par (source_replica_id, target_replica_id). W przypadku każdej pary operand jest wysyłany z repliki źródłowej do docelowej. |
Pamiętaj, że w przypadku source_target_pair obowiązują następujące ograniczenia:
- Żadne 2 pary nie powinny mieć tego samego identyfikatora docelowej repliki ani tego samego identyfikatora źródłowej repliki.
- Jeśli identyfikator repliki nie jest celem w żadnej parze, wyjście na tej replice jest tensorem składającym się z 0(s) o tym samym kształcie co wejście.
Konkatenacja
Zobacz też XlaBuilder::ConcatInDim.
Funkcja CONCATENATE tworzy tablicę z wielu operandów tablicowych. Tablica ma taką samą liczbę wymiarów jak każdy z elementów wejściowych tablicy (które muszą mieć taką samą liczbę wymiarów jak inne) i zawiera argumenty w kolejności, w jakiej zostały określone.
Concatenate(operands..., dimension)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands |
sekwencja N XlaOp |
N tablic typu T o wymiarach [L0, L1, …]. Wymaga, aby N >= 1. |
dimension |
int64 |
Wartość z przedziału [0, N), która określa wymiar do złączenia w ramach operands. |
Z wyjątkiem wymiaru dimension wszystkie wymiary muszą być takie same. Dzieje się tak, ponieważ XLA nie obsługuje „rozdrobionych” tablic. Pamiętaj też, że wartości wymiaru 0-wymiarowego nie można konkatenować (ponieważ nie można podać nazwy wymiaru, w którym następuje konkatenacja).
Przykład jednowymiarowy:
Concat({ {2, 3}, {4, 5}, {6, 7} }, 0)
>>> {2, 3, 4, 5, 6, 7}
Przykład dwuwymiarowy:
let a = {
{1, 2},
{3, 4},
{5, 6},
};
let b = {
{7, 8},
};
Concat({a, b}, 0)
>>> {
{1, 2},
{3, 4},
{5, 6},
{7, 8},
}
Diagram:
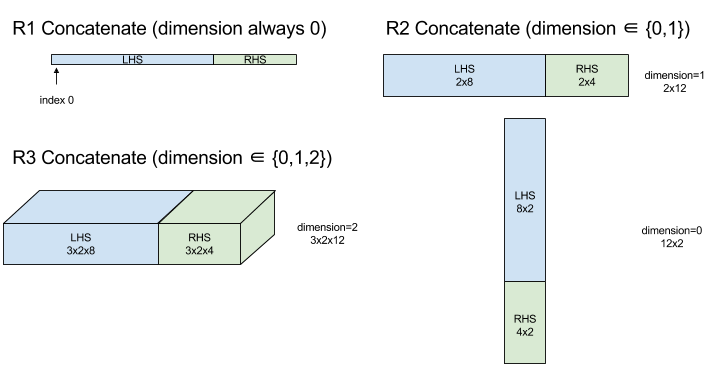
Warunkowy
Zobacz też XlaBuilder::Conditional.
Conditional(pred, true_operand, true_computation, false_operand,
false_computation)
| Argumenty | Typ | Semantyka |
|---|---|---|
pred |
XlaOp |
Typ skalarny: PRED |
true_operand |
XlaOp |
Argument typu \(T_0\) |
true_computation |
XlaComputation |
XlaComputation typu \(T_0 \to S\) |
false_operand |
XlaOp |
Argument typu \(T_1\) |
false_computation |
XlaComputation |
XlaComputation typu \(T_1 \to S\) |
Wykonuje instrukcję true_computation, jeśli pred ma wartość true, lub false_computation, jeśli pred ma wartość false, i zwraca wynik.
Funkcja true_computation musi przyjmować pojedynczy argument typu \(T_0\) i będzie wywoływana z parametrem true_operand, który musi być tego samego typu. Funkcja false_computation musi przyjmować pojedynczy argument typu \(T_1\) i będzie wywoływana z argumentem false_operand, który musi być tego samego typu. Typ zwracanej wartości true_computation i false_computation musi być taki sam.
Pamiętaj, że w zależności od wartości parametru pred zostanie wykonane tylko jedno z tych instrukcji: true_computation lub false_computation.
Conditional(branch_index, branch_computations, branch_operands)
| Argumenty | Typ | Semantyka |
|---|---|---|
branch_index |
XlaOp |
Typ skalarny: S32 |
branch_computations |
sekwencja N XlaComputation |
XlaComputations typu \(T_0 \to S , T_1 \to S , ..., T_{N-1} \to S\) |
branch_operands |
sekwencja N XlaOp |
Argumenty typu \(T_0 , T_1 , ..., T_{N-1}\) |
Wykonuje instrukcję branch_computations[branch_index] i zwraca jej wynik. Jeśli
branch_index jest S32, który jest mniejszy od 0 lub większy od N, wówczas branch_computations[N-1]
jest wykonywany jako gałąź domyślna.
Każda funkcja branch_computations[b] musi przyjmować 1 argument typu \(T_b\) i będzie wywoływana z argumentem branch_operands[b], który musi być tego samego typu. Typ zwracanej wartości każdego elementu branch_computations[b] musi być taki sam.
Pamiętaj, że w zależności od wartości branch_index zostanie wykonana tylko jedna z opcji branch_computations.
Konw. (splot)
Zobacz też XlaBuilder::Conv.
Podobnie jak w przypadku ConvWithGeneralPadding, ale wypełnienie jest określone w uproszczony sposób jako SAME lub VALID. SAME padding wypełnia dane wejściowe (lhs) zerami, aby dane wyjściowe miały taki sam kształt jak dane wejściowe, gdy nie uwzględnia się przesunięcia. VALID padding oznacza brak wypełnienia.
ConvWithGeneralPadding (convolution)
Zobacz też XlaBuilder::ConvWithGeneralPadding.
Oblicza splocenie tego typu, który jest używany w sieciach neuronowych. Konwolucję można tu traktować jako n-wymiarowe okno przesuwające się po n-wymiarowej podstawie. Obliczenia są wykonywane dla każdej możliwej pozycji okna.
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs |
XlaOp |
Tablica wejściowa o wymiarach (n+2) |
rhs |
XlaOp |
Tablica (n+2)-wymiarowa wag jądra |
window_strides |
ArraySlice<int64> |
tablica n-wymiarowa z skokowymi przesunięciami jądra |
padding |
ArraySlice< pair<int64,int64>> |
tablica n-wymiarowa z (niskim i wysokim) wypełnieniem |
lhs_dilation |
ArraySlice<int64> |
tablica współczynników rozszerzenia lewej strony równania w n-wymiarowej przestrzeni |
rhs_dilation |
ArraySlice<int64> |
tablica współczynników rozszerzenia po prawej stronie w n-wymiarach |
feature_group_count |
int64 | liczba grup cech; |
batch_group_count |
int64 | liczba grup zbiorczych |
Niech n będzie liczbą wymiarów przestrzennych. Argument lhs to tablica o wymiarach (n+2), która opisuje obszar bazowy. Nazywamy to wejściem, chociaż oczywiście prawe wyrażenie jest też wejściem. W sieci neuronowej są to aktywacje wejścia. Wymiary n + 2 to w tej kolejności:
batch: każda współrzędna w tym wymiarze reprezentuje niezależny element wejściowy, dla którego wykonywana jest operacja sprzężenia zwrotnego.z/depth/features: każda pozycja (y,x) w obszarze podstawowym ma powiązany wektor, który jest używany w tym wymiarze.spatial_dims: opisują wymiary przestrzennen, które definiują obszar bazowy, po którym porusza się okno.
Argument rhs to tablica o wymiarach (n + 2), która opisuje konwolucyjny filtr, jądro lub okno. Wymiary te są podawane w tej kolejności:
output-z: wymiarzdanych wyjściowych.input-z: rozmiar tego wymiaru pomnożony przezfeature_group_countpowinien być równy rozmiarowi wymiaruzpo lewej stronie.spatial_dims: opisnwymiarów przestrzennych, które definiują n-wymiarowe okno przesuwające się po obszarze bazowym.
Argument window_strides określa krok okna konwolucyjnego w wymiarach przestrzennych. Jeśli na przykład krok w pierwszym wymiarze przestrzennym wynosi 3, okno można umieścić tylko w współrzędnych, w których pierwszy indeks przestrzenny jest podzielny przez 3.
Argument padding określa ilość wypełniania zerami zerami zerowymi, które ma być stosowane do obszaru bazy. Ilość wypełnień może być ujemna – bezwzględna wartość ujemnego wypełnienia wskazuje liczbę elementów do usunięcia z wybranego wymiaru przed wykonaniem splotu. padding[0] określa wypełnienie wymiaru y, a padding[1] – wypełnienie wymiaru x. Każda para ma pierwszy element, który jest wypełnieniem dolnym, oraz drugi element, który jest wypełnieniem górnym. Dopełnienie dolne jest stosowane w kierunku niższych indeksów, a dopełnienie górne w kierunku wyższych indeksów. Jeśli na przykład padding[1] = (2,3), w drugim wymiarze przestrzennym zostanie dodane 2 zera z lewej strony i 3 zera z prawej strony. Użycie wypełnienia jest równoważne wstawianiu tych samych wartości zerowych do wejścia (lhs) przed wykonaniem splotu.
Argumenty lhs_dilation i rhs_dilation określają współczynnik rozszerzania, który ma być stosowany odpowiednio do wartości lhs i rhs w każdym wymiarze przestrzennym. Jeśli współczynnik powiększenia w wymiarze przestrzennym wynosi d, między każdymi wpisami w tym wymiarze umieszczane są domyślnie otwory o wielkości d-1, co zwiększa rozmiar tablicy. Dziury są wypełniane wartością no-op, która w przypadku splotu oznacza zera.
Dilatacja prawej strony nazywana jest też konwolucją atrosową. Więcej informacji znajdziesz w sekcji tf.nn.atrous_conv2d. Rozszerzenie lewej strony nazywane jest też transponowaną współczynnikiem. Więcej informacji znajdziesz w sekcji tf.nn.conv2d_transpose.
Argument feature_group_count (wartość domyślna 1) może być używany do zgrupowanych splotów. Wartość feature_group_count musi być dzielnikiem zarówno wymiaru danych wejściowych, jak i wymiaru danych wyjściowych. Jeśli feature_group_count jest większa niż 1, oznacza to, że wymiar cech wejściowych i wyjściowych oraz wymiar cech wyjściowych rhs są podzielone równomiernie na wiele grup feature_group_count, z których każda składa się z kolejnych podciągów cech. Wymiar cechy wejściowej rhs musi być równy wymiarowi cechy wejściowej lhs podzielonemu przez feature_group_count (czyli ma już rozmiar grupy cech wejściowych). Grupy i-te są używane razem do obliczania feature_group_count dla wielu osobnych splotów. Wyniki tych splotów są łączone w wymiarie funkcji wyjściowej.
W przypadku konwulsji w głębi argument feature_group_count jest ustawiany na wymiar funkcji wejściowych, a kształt filtra jest zmieniany z [filter_height, filter_width, in_channels, channel_multiplier] na [filter_height, filter_width, 1, in_channels * channel_multiplier]. Więcej informacji znajdziesz w sekcji tf.nn.depthwise_conv2d.
Argument batch_group_count (wartość domyślna 1) może być używany do filtrów grupowanych podczas propagacji wstecznej. Wartość batch_group_count musi być dzielnikiem rozmiaru wymiaru zbioru danych lhs (wejściowego). Jeśli batch_group_count jest większa niż 1, oznacza to, że wymiar wsad wyjściowego powinien mieć rozmiar input batch
/ batch_group_count. Wartość batch_group_count musi być dzielnikiem rozmiaru funkcji wyjściowej.
Wymiar wyjściowy ma te wymiary w takiej kolejności:
batch: rozmiar tego wymiaru pomnożony przezbatch_group_countpowinien być równy rozmiarowi wymiarubatchpo lewej stronie.z: ten sam rozmiar cooutput-zw jądrze (rhs).spatial_dims: jedna wartość dla każdej prawidłowej lokalizacji okna konwolucyjnego.
Rysunek powyżej pokazuje, jak działa pole batch_group_count. W efekcie dzielimy każdy zbiór danych lhs na grupy batch_group_count, a także robimy to samo w przypadku funkcji wyjściowych. Następnie dla każdej z tych grup wykonujemy konwolucję parową i konkatenujemy dane wyjściowe wzdłuż wymiaru cechy wyjściowej. Operacyjna semantyka wszystkich pozostałych wymiarów (funkcjonalnych i przestrzennych) pozostaje taka sama.
Prawidłowe pozycje okna konwolucyjnego są określane przez kroki i wielkość obszaru podstawy po wypełnieniu.
Aby opisać działanie splotu, rozważ splot 2D i wybierz w wyjściu stałe współrzędne batch, z, y, x. Następnie (y,x) to pozycja rogu okna w obszarze bazowym (np. lewy górny róg, w zależności od tego, jak interpretujesz wymiary przestrzenne). Mamy teraz okno 2D, pochodzące z obszaru podstawowego, w którym każdy punkt 2D jest powiązany z wektorem 1D, dzięki czemu otrzymujemy pudełko 3D. Z kernela konwolucyjnego, ponieważ stała jest współrzędna wyjściowa z, mamy też pole 3D. Obie skrzynki mają te same wymiary, więc możemy wziąć sumę iloczynów elementów między tymi skrzynkami (podobnie jak w przypadku iloczynu kropkowego). To jest wartość wyjściowa.
Pamiętaj, że jeśli output-z to na przykład 5, to każda pozycja okna wygeneruje 5 wartości w wyniku w wymiarze z. Różnią się one w zależności od tego, która część jądra convolacyjnego jest używana – dla każdej współrzędnej output-z jest osobna skrzynka 3D z wartościami. Możesz sobie wyobrazić, że są to 5 osobnych splotów z różnym filtrem dla każdego z nich.
Oto pseudokod konwekcji 2D z wypełnieniem i przeskakiwaniem:
for (b, oz, oy, ox) { // output coordinates
value = 0;
for (iz, ky, kx) { // kernel coordinates and input z
iy = oy*stride_y + ky - pad_low_y;
ix = ox*stride_x + kx - pad_low_x;
if ((iy, ix) inside the base area considered without padding) {
value += input(b, iz, iy, ix) * kernel(oz, iz, ky, kx);
}
}
output(b, oz, oy, ox) = value;
}
ConvertElementType
Zobacz też XlaBuilder::ConvertElementType.
Podobnie jak elementarna funkcja static_cast w C++, wykonuje elementarną operację konwersji z kształtu danych na kształt docelowy. Wymiary muszą być zgodne, a konwersja jest konwersją elementu. Przykładowo elementy s32 stają się elementami f32 za pomocą procedury konwersji s32 na f32.
ConvertElementType(operand, new_element_type)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica typu T o wymiarach D |
new_element_type |
PrimitiveType |
typ U |
Wymiary operandu i kształtu docelowego muszą być zgodne. Typy elementów źródła i docelowego nie mogą być tablicami.
Konwersja z wartości T=s32 na U=f32 spowoduje uruchomienie rutyny normalizacji konwersji int na float, np. zaokrąglania do najbliższej liczby parzystej.
let a: s32[3] = {0, 1, 2};
let b: f32[3] = convert(a, f32);
then b == f32[3]{0.0, 1.0, 2.0}
CrossReplicaSum
Wykonuje funkcję AllReduce z obliczeniem sumy.
CustomCall
Zobacz też XlaBuilder::CustomCall.
wywołać funkcję przekazaną przez użytkownika w ramach obliczeń;
CustomCall(target_name, args..., shape)
| Argumenty | Typ | Semantyka |
|---|---|---|
target_name |
string |
Nazwa funkcji. Zostanie wyemitowana instrukcja wywołania, która będzie kierować się na tę nazwę symbolu. |
args |
sekwencja N XlaOp |
N argumentów dowolnego typu, które zostaną przekazane funkcji. |
shape |
Shape |
Kształt wyjściowy funkcji |
Sygnatura funkcji jest taka sama niezależnie od liczby argumentów i ich typu:
extern "C" void target_name(void* out, void** in);
Jeśli na przykład funkcja CustomCall jest używana w ten sposób:
let x = f32[2] {1,2};
let y = f32[2x3] { {10, 20, 30}, {40, 50, 60} };
CustomCall("myfunc", {x, y}, f32[3x3])
Oto przykład implementacji funkcji myfunc:
extern "C" void myfunc(void* out, void** in) {
float (&x)[2] = *static_cast<float(*)[2]>(in[0]);
float (&y)[2][3] = *static_cast<float(*)[2][3]>(in[1]);
EXPECT_EQ(1, x[0]);
EXPECT_EQ(2, x[1]);
EXPECT_EQ(10, y[0][0]);
EXPECT_EQ(20, y[0][1]);
EXPECT_EQ(30, y[0][2]);
EXPECT_EQ(40, y[1][0]);
EXPECT_EQ(50, y[1][1]);
EXPECT_EQ(60, y[1][2]);
float (&z)[3][3] = *static_cast<float(*)[3][3]>(out);
z[0][0] = x[1] + y[1][0];
// ...
}
Funkcja dostarczona przez użytkownika nie może mieć efektów ubocznych, a jej wykonanie musi być idempotentne.
Kropka
Zobacz też XlaBuilder::Dot.
Dot(lhs, rhs)
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs |
XlaOp |
tablica typu T |
rhs |
XlaOp |
tablica typu T |
Dokładna semantyka tej operacji zależy od rang operandów:
| Dane wejściowe | Wyniki | Semantyka |
|---|---|---|
wektor [n] dot wektor [n] |
wartość skalarna | wektorowy iloczyn skalarny |
macierz [m x k] dot wektor [k] |
wektor [m] | mnożenie wektorów-macierzy, |
macierz [m x k] dot macierz [k x n] |
macierz [m x n] | mnożenie macierzy przez siebie, |
Operacja zwraca sumę produktów drugiego wymiaru funkcji lhs (lub pierwszego, jeśli ma ona 1 wymiar) i pierwszego wymiaru funkcji rhs. Są to „skrócone” wymiary. Wymiary lhs i rhs muszą być takie same. W praktyce można go używać do wykonywania iloczynów skalarnych wektorów, mnożenia wektorów przez macierze lub mnożenia macierzy przez macierze.
DotGeneral
Zobacz też XlaBuilder::DotGeneral.
DotGeneral(lhs, rhs, dimension_numbers)
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs |
XlaOp |
tablica typu T |
rhs |
XlaOp |
tablica typu T |
dimension_numbers |
DotDimensionNumbers |
numery wymiarów z kontraktu i zbioru danych; |
Podobnie jak w przypadku kropki, ale umożliwia określenie numerów wymiarów z grupowaniem i zbiorczo zarówno w przypadku lhs, jak i rhs.
| Pola DotDimensionNumbers | Typ | Semantyka |
|---|---|---|
lhs_contracting_dimensions
|
powtarzany typ int64 | lhs wymiaru z wyjątkiem liczb |
rhs_contracting_dimensions
|
powtarzany typ int64 | rhs wymiaru z wyjątkiem liczb |
lhs_batch_dimensions
|
powtarzany typ int64 | lhs wymiar zbiorczy: numery |
rhs_batch_dimensions
|
powtarzany typ int64 | rhs wymiar zbiorczy: numery |
DotGeneral zwraca sumę produktów w ramach wymiarów kontraktowania określonych w parametrye dimension_numbers.
Powiązane numery wymiarów kontraktowania w elementach lhs i rhs nie muszą być takie same, ale muszą mieć te same rozmiary wymiarów.
Przykład z wymiarami z obniżonym zakresem:
lhs = { {1.0, 2.0, 3.0},
{4.0, 5.0, 6.0} }
rhs = { {1.0, 1.0, 1.0},
{2.0, 2.0, 2.0} }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(1);
dnums.add_rhs_contracting_dimensions(1);
DotGeneral(lhs, rhs, dnums) -> { {6.0, 12.0},
{15.0, 30.0} }
Powiązane numery wymiarów partii w kolumnach lhs i rhs muszą mieć te same rozmiary wymiarów.
Przykład z liczbami wymiarów partii (partia o rozmiarze 2, macierze 2 x 2):
lhs = { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
rhs = { { {1.0, 0.0},
{0.0, 1.0} },
{ {1.0, 0.0},
{0.0, 1.0} } }
DotDimensionNumbers dnums;
dnums.add_lhs_contracting_dimensions(2);
dnums.add_rhs_contracting_dimensions(1);
dnums.add_lhs_batch_dimensions(0);
dnums.add_rhs_batch_dimensions(0);
DotGeneral(lhs, rhs, dnums) -> { { {1.0, 2.0},
{3.0, 4.0} },
{ {5.0, 6.0},
{7.0, 8.0} } }
| Dane wejściowe | Wyniki | Semantyka |
|---|---|---|
[b0, m, k] dot [b0, k, n] |
[b0, m, n] | batch matmul |
[b0, b1, m, k] dot [b0, b1, k, n] |
[b0, b1, m, n] | batch matmul |
Wynika z tego, że wynikowy numer wymiaru zaczyna się od wymiaru „partia”, następnie wymiaru „niezwiązany z kontraktem” lub „niezwiązany z partią” (lhs) i wreszcie wymiaru „niezwiązany z kontraktem” lub „niezwiązany z partią” (rhs).
DynamicSlice
Zobacz też XlaBuilder::DynamicSlice.
DynamicSlice wyodrębnia podtablicę z tablicy wejściowej w miejscu dynamicznegostart_indices. Rozmiar sekcji w każdym wymiarze jest przekazywany w elementach size_indices, które określają punkt końcowy wyłącznych przedziałów sekcji w każdym wymiarze: [start, start + size). Postać funkcji start_indices musi być jednowymiarowa, a wielkość wymiaru musi być równa liczbie wymiarów zbioru operand.
DynamicSlice(operand, start_indices, size_indices)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Tablica N-wymiarowa typu T |
start_indices |
sekwencja N XlaOp |
Lista N liczb całkowitych zawierających indeksy początkowe przekroju dla każdego wymiaru. Wartość nie może być mniejsza niż 0. |
size_indices |
ArraySlice<int64> |
Lista N liczb całkowitych zawierających rozmiar przedziału dla każdego wymiaru. Każda wartość musi być większa od zera, a wartość start + size musi być równa lub mniejsza od rozmiaru wymiaru, aby uniknąć zawijania modulo rozmiar wymiaru. |
Skuteczne indeksy przedziałów są obliczane przez zastosowanie tej transformacji do każdego indeksu i w [1, N) przed wykonaniem przedziału:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - size_indices[i])
Dzięki temu wyodrębniony wycinek zawsze mieści się w zakresie tablicy operanda. Jeśli przed zastosowaniem przekształcenia plaster mieści się w granicach, przekształcenie nie ma żadnego wpływu.
Przykład jednowymiarowy:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let s = {2}
DynamicSlice(a, s, {2}) produces:
{2.0, 3.0}
Przykład dwuwymiarowy:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let s = {2, 1}
DynamicSlice(b, s, {2, 2}) produces:
{ { 7.0, 8.0},
{10.0, 11.0} }
DynamicUpdateSlice
Zobacz też XlaBuilder::DynamicUpdateSlice.
DynamicUpdateSlice zwraca wynik, który jest wartością tablicy wejściowej operand, przy czym w miejscu start_indices zostanie zastąpiony fragment update.
Kształt argumentu update określa kształt podzbioru wyniku, który jest aktualizowany.
Postać funkcji start_indices musi być jednowymiarowa, a wielkość wymiaru musi być równa liczbie wymiarów funkcji operand.
DynamicUpdateSlice(operand, update, start_indices)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Tablica N-wymiarowa typu T |
update |
XlaOp |
Tablica N-wymiarowa typu T zawierająca aktualizację sekcji. Każdy wymiar kształtu aktualizacji musi być większy od zera, a wartość start + update musi być równa lub mniejsza od rozmiaru operandu w przypadku każdego wymiaru, aby uniknąć generowania indeksów aktualizacji spoza zakresu. |
start_indices |
sekwencja N XlaOp |
Lista N liczb całkowitych zawierających indeksy początkowe przekroju dla każdego wymiaru. Wartość nie może być mniejsza niż 0. |
Skuteczne indeksy przedziałów są obliczane przez zastosowanie tej transformacji do każdego indeksu i w [1, N) przed wykonaniem przedziału:
start_indices[i] = clamp(start_indices[i], 0, operand.dimension_size[i] - update.dimension_size[i])
Dzięki temu zaktualizowany wycinek zawsze mieści się w zakresie tablicy operanda. Jeśli przed zastosowaniem przekształcenia plaster mieści się w granicach, przekształcenie nie ma żadnego wpływu.
Przykład jednowymiarowy:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
let u = {5.0, 6.0}
let s = {2}
DynamicUpdateSlice(a, u, s) produces:
{0.0, 1.0, 5.0, 6.0, 4.0}
Przykład dwuwymiarowy:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
let u =
{ {12.0, 13.0},
{14.0, 15.0},
{16.0, 17.0} }
let s = {1, 1}
DynamicUpdateSlice(b, u, s) produces:
{ {0.0, 1.0, 2.0},
{3.0, 12.0, 13.0},
{6.0, 14.0, 15.0},
{9.0, 16.0, 17.0} }
Elementarne operacje arytmetyczne binarne
Zobacz też XlaBuilder::Add.
Obsługiwany jest zestaw operacji arytmetycznych binarnych na elementach.
Op(lhs, rhs)
Gdzie Op to jedna z funkcji: Add (dodawanie), Sub(odejmowanie), Mul (mnożenie), Div (dzielenie), Pow (potęga), Rem (reszta), Max (maksimum), Min (minimum), And (logiczne AND), Or (logiczne OR), Xor (logiczne XOR), ShiftLeft (przesunięcie w lewo), ShiftRightArithmetic (arytmetyczne przesunięcie w prawo), ShiftRightLogical (logiczne przesunięcie w prawo), Atan2 (2-argumentowa arctangesencja) lub Complex (łączy część rzeczywistą i urojona w liczbę zespoloną).
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs |
XlaOp |
argument po lewej stronie: tablica typu T; |
rhs |
XlaOp |
Prawy argument: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej transmisji. Wynik operacji ma kształt, który jest wynikiem rozgłoszenia dwóch tablic wejściowych. W tym wariancie operacje na tablicach o różnych wymiarach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
Gdy Op = Rem, znak wyniku jest zgodny ze znakiem dzielnika, a bezwzględna wartość wyniku jest zawsze mniejsza od bezwzględnej wartości dzielnika.
Przepełnienie dzielenia liczb całkowitych (dzielenie/reszta liczby całkowitej/nieoznaczonej przez 0 lub INT_SMIN z -1) zwraca wartość zdefiniowaną przez implementację.
W przypadku tych operacji istnieje alternatywny wariant z obsługą transmisji 2D:
Op(lhs, rhs, broadcast_dimensions)
Gdzie Op jest taki sam jak powyżej. Tego wariantu operacji należy używać do operacji arytmetycznych na tablicach o różnych wymiarach (np. dodawanie macierzy do wektora).
Dodatkowy operand broadcast_dimensions to wycinek liczb całkowitych służący do zwiększenia liczby wymiarów operandu o niższej wymiarowości do liczby wymiarów operandu o wyższej wymiarowości. broadcast_dimensionsprzypisuje wymiary kształtu o mniejszym wymiarze wymiarom kształtu o większym wymiarze. Niezmapowane wymiary rozwiniętego kształtu są wypełniane wymiarami o rozmiarze 1. Transmisja wymiarów zdegenerowanych następnie przekazuje kształty wzdłuż tych wymiarów zdegenerowanych, aby wyrównać kształty obu operandów. Semantyka jest szczegółowo opisana na stronie z transmisją.
Elementowe operacje porównywania
Zobacz też XlaBuilder::Eq.
Obsługiwany jest zestaw standardowych operacji binarnego porównywania elementów. Podczas porównywania typów zmiennoprzecinkowych obowiązuje standardowa semantyka porównywania typu zmiennoprzecinkowego IEEE 754.
Op(lhs, rhs)
Gdzie Op jest jedną z wartości Eq (równe), Ne (inne niż), Ge (jest większe lub równe), Gt (jest większe), Le (jest mniejsze lub równe), Lt (jest mniejsze). Inny zestaw operatorów, EqTotalOrder, NeTotalOrder, GeTotalOrder, GtTotalOrder, LeTotalOrder i LtTotalOrder, zapewnia te same funkcje, z tym że dodatkowo obsługuje całkowity porządek liczb zmiennoprzecinkowych, narzucając -NaN < -Inf < -Finite < -0 < +0 < +Finite < +Inf < +NaN.
| Argumenty | Typ | Semantyka |
|---|---|---|
lhs |
XlaOp |
argument po lewej stronie: tablica typu T; |
rhs |
XlaOp |
Prawy argument: tablica typu T |
Kształty argumentów muszą być podobne lub zgodne. Więcej informacji o tym, co oznacza zgodność kształtów, znajdziesz w dokumentacji dotyczącej transmisji. Wynik operacji ma kształt będący wynikiem rozgłoszenia 2 tablic wejściowych z typem elementu PRED. W tej wersji operacje na tablicach o różnych wymiarach nie są obsługiwane, chyba że jeden z operandów jest skalarem.
W przypadku tych operacji istnieje alternatywny wariant z obsługą transmisji 2D:
Op(lhs, rhs, broadcast_dimensions)
Gdzie Op jest taki sam jak powyżej. Tego wariantu operacji należy używać do operacji porównywania tablic o różnych wymiarach (np. dodawania macierzy do wektora).
Dodatkowy operand broadcast_dimensions to podzbiór liczb całkowitych określający wymiary, których należy używać do nadawania wartości operandów. Semantyka jest szczegółowo opisana na stronie z transmisją.
Elementarne funkcje jednoargumentowe
XlaBuilder obsługuje te funkcje jednoargumentowe elementowe:
Abs(operand) Absolwoty elementu x -> |x|.
Cbrt(operand) Elementowa operacja pierwiastka sześciennego x -> cbrt(x).
Ceil(operand) Element-wise ceil x -> ⌈x⌉.
Clz(operand) Policz zera na początku elementów.
Cos(operand) Element-wise cosine x -> cos(x).
Erf(operand) Funkcja błędu elementu x -> erf(x), gdzie
\(\text{erf}(x) = \frac{2}{\sqrt{\pi} }\int_0^x e^{-t^2} \, dt\).
Exp(operand) Elementarna potęga wykładnicza x -> e^x.
Expm1(operand) Elementarny wykładnik naturalny bez 1 x -> e^x - 1.
Floor(operand) Cena minimalna na element x -> ⌊x⌋.
Imag(operand) Element po elemencie część urojona kształtu złożonego (lub rzeczywistego). x -> imag(x). Jeśli operand jest typu zmiennoprzecinkowego, zwraca 0.
IsFinite(operand) Sprawdza, czy każdy element tablicy operand jest skończony, tzn. nie jest dodatnią ani ujemną nieskończonością i nie jest NaN. Zwraca tablicę wartości PRED o tym samym kształcie co wejście, w której każdy element jest true, o ile i tylko o ile odpowiadający element wejściowy jest skończony.
Log(operand) Elementowy logarytm naturalny x -> ln(x).
Log1p(operand) Element po element logarytm naturalny przesunięty o wartość x -> ln(1+x).
Logistic(operand) Obliczanie funkcji logistycznej element po elemencie x ->
logistic(x).
Neg(operand) Element-wise negation x -> -x.
Not(operand) Elementowy operator logiczny „nie” x -> !(x).
PopulationCount(operand) Oblicza liczbę bitów ustawionych w każdym elemencie operand.
Real(operand) Część rzeczywista elementów złożonej (lub rzeczywistej) formy.
x -> real(x). Jeśli operand jest typu zmiennoprzecinkowego, zwraca tę samą wartość.
Round(operand) Zaokrąglenie elementu, remisy z wartością 0.
RoundNearestEven(operand) Zaokrąglenie elementu do najbliższej parzystej.
Rsqrt(operand) Element po elementze odwrotność pierwiastka kwadratowego.
x -> 1.0 / sqrt(x)
Sign(operand) Operacja znaku elementu x -> sgn(x), gdzie
\[\text{sgn}(x) = \begin{cases} -1 & x < 0\\ -0 & x = -0\\ NaN & x = NaN\\ +0 & x = +0\\ 1 & x > 0 \end{cases}\]
za pomocą operatora porównania typu elementu operand.
Sin(operand) Sinus elementowy x -> sin(x).
Sqrt(operand) Elementowa operacja pierwiastka kwadratowego x -> sqrt(x).
Tan(operand) Tangens elementu x -> tan(x).
Tanh(operand) Elementowy tangens hiperboliczny x -> tanh(x).
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Argument funkcji |
Funkcja jest stosowana do każdego elementu w tablicy operand, co powoduje powstanie tablicy o tym samym kształcie. Zmienne operand może być typu skalarnego (0-wymiarowego).
Fft
Operacja XLA FFT implementuje bezpośrednią i odwrotną transformację Fouriera dla rzeczywistych i zespolonych wejść/wyjść. Obsługiwane są wielowymiarowe FFT na maksymalnie 3 osiach.
Zobacz też XlaBuilder::Fft.
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Tablica, którą przekształcamy za pomocą transformaty Fouriera. |
fft_type |
FftType |
Patrz tabela poniżej. |
fft_length |
ArraySlice<int64> |
Długości osi w domenie czasowej, które są przekształcane. Jest to konieczne, aby IRFFT mogła prawidłowo dostosować rozmiar wewnętrznej osi, ponieważ RFFT(fft_length=[16]) ma ten sam kształt wyjściowy co RFFT(fft_length=[17]). |
FftType |
Semantyka |
|---|---|
FFT |
Przesyłanie złożonej FFT do złożonej. Kształt się nie zmienił. |
IFFT |
odwrotna transformacja Fouriera z złożonej na złożoną; Kształt się nie zmienił. |
RFFT |
Przesyłanie FFT rzeczywistego na zespolony. Kształt wewnętrznej osi jest ograniczony do fft_length[-1] // 2 + 1, jeśli fft_length[-1] jest niezerową wartością, pomijając odwróconą część sprzężenia zwrotnego przekształconego sygnału poza częstotliwością Nyquista. |
IRFFT |
odwrotna transformacja FFT rzeczywistej na zespoloną (czyli przyjmuje zespoloną, zwraca rzeczywistą). Kształt wewnętrznej osi jest rozszerzony do fft_length[-1], jeśli fft_length[-1] ma wartość niezerową. Z konjugaty odwrotnej elementów 1 na fft_length[-1] // 2 + 1 wywnioskowano część przekształconego sygnału poza częstotliwością Nyquista. |
Wielowymiarowa transformata Fouriera
Jeśli podano więcej niż 1 wartość fft_length, jest to równoznaczne z zastosowaniem kaskady operacji FFT do każdej z najbardziej wewnętrznych osi. Pamiętaj, że w przypadku przekształceń rzeczywiste > zespolone i zespolone > rzeczywiste wewnętrzna transformacja osi jest (w zasadzie) wykonywana jako pierwsza (RFFT; jako ostatnia w przypadku IRFFT), dlatego wewnętrzna oś jest tą, która zmienia rozmiar. Inne transformacje osi będą wtedy miały wartość complex->complex.
Szczegóły implementacji
Obsługa FFT na procesorze jest obsługiwana przez TensorFFT w Eigen. FFT na GPU korzysta z cuFFT.
Zbieraj
Operacja zbierania XLA łączy ze sobą kilka kawałków (każdy kawałek o potencjalnie innym przesunięciu w czasie) tablicy wejściowej.
General Semantics
Zobacz też XlaBuilder::Gather.
Bardziej intuicyjny opis znajdziesz w sekcji „Nieformalny opis” poniżej.
gather(operand, start_indices, offset_dims, collapsed_slice_dims,
slice_sizes, start_index_map)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Tablica, z której pobieramy dane. |
start_indices |
XlaOp |
Tablica zawierająca indeksy początkowe przekroju, który gromadzimy. |
index_vector_dim |
int64 |
Wymiar w pliku start_indices, który „zawiera” indeksy początkowe. Poniżej znajdziesz szczegółowy opis. |
offset_dims |
ArraySlice<int64> |
Zbiór wymiarów w kształcie wyjściowym, który jest przesuwany do tablicy wyciętej z operanda. |
slice_sizes |
ArraySlice<int64> |
slice_sizes[i] to zakresy dla wycinka według wymiaru i. |
collapsed_slice_dims |
ArraySlice<int64> |
Zbiór wymiarów w każdej sekcji, które są zwinięte. Te wymiary muszą mieć rozmiar 1. |
start_index_map |
ArraySlice<int64> |
Mapowanie, które opisuje, jak mapować indeksy w definicji start_indices na prawidłowe indeksy w operandzie. |
indices_are_sorted |
bool |
Określa, czy indeksy są sortowane przez wywołującego. |
Dla wygody w tablicy wyników nie w wartości offset_dims, a w wartości batch_dims.
Wynik to tablica z wymiarami batch_dims.size + offset_dims.size.
Wartość operand.rank musi być równa sumie wartości offset_dims.size i collapsed_slice_dims.size. Ponadto wartość slice_sizes.size musi być równa wartości operand.rank.
Jeśli index_vector_dim jest równe start_indices.rank, uznajemy domyślnie, że start_indices ma wymiar dopełniający 1 (czyli jeśli start_indices ma kształt [6,7], a index_vector_dim ma wartość 2, uznajemy domyślnie, że kształt start_indices to [6,7,1]).
Granice tablicy wyjściowej wzdłuż wymiaru i są obliczane w ten sposób:
Jeśli
iwystępuje wbatch_dims(czyli jest równebatch_dims[k]dla niektórych wartościk), wybieramy odpowiednie przedziały wymiaru zstart_indices.shape, pomijającindex_vector_dim(czyli wybieramystart_indices.shape.dims[k], jeślik<index_vector_dim, a w przeciwnym raziestart_indices.shape.dims[k+1]).Jeśli
iwystępuje woffset_dims(czyli jest równeoffset_dims[k] dla dowolnegok), wybieramy odpowiednią granicę zslice_sizespo uwzględnieniucollapsed_slice_dims(czyli wybieramyadjusted_slice_sizes[k], gdzieadjusted_slice_sizesjestslice_sizesz usuniętymi granicami w indeksachcollapsed_slice_dims).
Formalnie indeks operanda In odpowiadający danemu indeksowi wyjściowemu Out jest obliczany w ten sposób:
Niech
G= {Out[k] dlakwbatch_dims}. UżyjG, aby wyodrębnić wektorStak, abyS[i] =start_indices[Combine(G,i)], gdzie Combine(A, b) wstawia b w pozycjiindex_vector_dimw A. Pamiętaj, że jest to dobrze zdefiniowane nawet wtedy, gdyGjest puste: jeśliGjest puste, toS=start_indices.Utwórz indeks początkowy
Sinwoperandza pomocąS, rozpraszającSza pomocąstart_index_map. Dokładniej:Sin[start_index_map[k]] =S[k] ifk<start_index_map.size.Sin[_] =0w innych przypadkach.
Utwórz indeks
Oinw tabelioperand, rozpraszając indeksy w wymiarach offsetowych w tabeliOutzgodnie z zbioremcollapsed_slice_dims. Dokładniej:Oin[remapped_offset_dims(k)] =Out[offset_dims[k]] jeślik<offset_dims.size(remapped_offset_dimsjest zdefiniowany poniżej).Oin[_] =0w innych przypadkach.
IntoOin+Sin, gdzie + oznacza dodawanie element po elemencie.
remapped_offset_dims to monotoniczna funkcja o domenie [0,offset_dims.size] i zakresie [0, operand.rank] \ collapsed_slice_dims. Jeśli na przykład offset_dims.size to 4, operand.rank to 6, a collapsed_slice_dims to {0, 2}, więc remapped_offset_dims to {0→1,
1→3, 2→4, 3→5}.
Jeśli parametr indices_are_sorted ma wartość Prawda, XLA może założyć, że elementy start_indices są posortowane (w kolejności rosnącej, po rozproszone według wartości start_index_map) przez użytkownika. Jeśli nie, semantyka jest definiowana przez implementację.
Opis nieformalny i przykłady
Nieformalnie każdy indeks Out w tablicy wyników odpowiada elementowi E w tablicy operandów, obliczonemu w ten sposób:
Używamy wymiarów partii w elementach
Out, aby pobrać indeks początkowy z elementustart_indices.Używamy funkcji
start_index_mapdo mapowania indeksu początkowego (którego rozmiar może być mniejszy niż operand.rank) na „pełny” indeks początkowy woperand.Wycinamy dynamicznie wycinek o rozmiarze
slice_sizes, używając pełnego indeksu początkowego.Zmieniamy kształt wycinka, zwijając wymiary
collapsed_slice_dims. Ponieważ wszystkie zwinięte wymiary sekcji muszą mieć ograniczenie 1, ta zmiana kształtu jest zawsze dozwolona.Używamy wymiarów offsetu w sekcji
Out, aby uzyskać indeks tego wycinka, który odpowiada elementowi wejściowemuEodpowiadającemu indeksowi wyjściowemuOut.
We wszystkich przykładach index_vector_dim ma wartość start_indices.rank – 1. Bardziej interesujące wartości dla index_vector_dim nie zmieniają zasadniczo operacji, ale powodują, że wizualizacja staje się bardziej skomplikowana.
Aby zrozumieć, jak wszystkie te elementy się ze sobą łączą, przyjrzyjmy się przykładowi, w którym z tablicy [16,11] wybieramy 5 elementów o kształcie [8,6]. Pozycja wycinka w tablicy [16,11] może być reprezentowana jako wektor indeksu o kształcie S64[2], więc zbiór 5 pozycji może być reprezentowany jako tablica S64[5,2].
Działanie operacji zbierania można przedstawić jako przekształcenie indeksu, które przyjmuje argument [G,O0,O1], czyli indeks w kształcie wyjściowym, i przypisuje go do elementu w tablicy wejściowej w następujący sposób:
Najpierw wybieramy wektor (X,Y) z tablicy indeksów zbiorczego za pomocą funkcji G.
Element w tablicy wyjściowej o indeksie [G,O0,O1] jest wtedy elementem w tablicy wejściowej o indeksie [X+O0,Y+O1].
slice_sizes to [8,6], który określa zakres O0 i O1, a to z kolei określa granice sekcji.
Ta operacja zbierania działa jako dynamiczny wycinek zbiorczego z użyciem wymiaru zbiorczego G.
Indeksy zbierania mogą być wielowymiarowe. Na przykład bardziej ogólna wersja powyższego przykładu, która używa tablicy „gather indices” o kształcie [4,5,2], przekształca indeksy w ten sposób:
Ponownie działa to jak dynamiczny wycinek zbiorczy G0 i G1 jako wymiary zbiorczego. Rozmiar sekcji to nadal [8,6].
Operacja zbierania w XLA generalizuje nieformalną semantykę opisaną powyżej w następujący sposób:
Możemy skonfigurować, które wymiary w kształcie wyjściowym są wymiarami przesunięcia (wymiary zawierające
O0,O1w ostatnim przykładzie). Wymiar wyjściowy zbioru danych (wymiary zawierająceG0lubG1w ostatnim przykładzie) jest zdefiniowany jako wymiar wyjściowy, który nie jest wymiarem offsetu.Liczba wymiarów przesunięcia danych wyjściowych, które są wyraźnie podane w kształcie danych wyjściowych, może być mniejsza niż liczba wymiarów wejściowych. Te „brakujące” wymiary, które są wymienione jako
collapsed_slice_dims, muszą mieć rozmiar1. Mają one rozmiar1, więc jedynym prawidłowym indeksem dla nich jest0, a ich pominięcie nie powoduje niejednoznaczności.Wycinek wyodrębniony z tablicy „Gather Indices” ((
X,Y) w ostatnim przykładzie) może mieć mniej elementów niż liczba wymiarów tablicy wejściowej. Wyraźne mapowanie określa, jak indeks powinien zostać rozszerzony, aby mieć taką samą liczbę wymiarów jak dane wejściowe.
W ostatnim przykładzie używamy elementów (2) i (3), aby zaimplementować tf.gather_nd:
G0 i G1 służą do wyodrębniania indeksu początkowego z tablicy indeksów zbiorczych w zwykły sposób, z tą różnicą, że indeks początkowy ma tylko jeden element, X. Podobnie jest z indeksem przesunięcia wyjścia, który ma tylko jedną wartość: O0. Jednak zanim zostaną użyte jako indeksy tablicy wejściowej, są one rozszerzane zgodnie z „mapowaniem indeksu zbiorczego” (start_index_map w opisie formalnym) i „mapowaniem przesunięcia” (remapped_offset_dims w opisie formalnym) odpowiednio na [X,0] i [0,O0], co daje w sumie [X,O0]. Innymi słowy,indeks wyjściowy [G0, G1,O0] jest mapowany na indeks wejściowy [GatherIndices[G0,G1,0],O0],co daje nam semantykę dla tf.gather_nd.
slice_sizes w tym przypadku to [1,11]. Oznacza to, że każdy indeks X w tablicy zbiorczych indeksów wybiera cały wiersz, a wynik jest konkatenacją wszystkich tych wierszy.
GetDimensionSize
Zobacz też XlaBuilder::GetDimensionSize.
Zwraca rozmiar danego wymiaru operanda. Operand musi mieć postać tablicy.
GetDimensionSize(operand, dimension)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica wejściowa o n wymiarach |
dimension |
int64 |
wartość z przedziału [0, n) określająca wymiar; |
SetDimensionSize
Zobacz też XlaBuilder::SetDimensionSize.
Ustawia dynamiczny rozmiar danego wymiaru XlaOp. Operand musi mieć postać tablicy.
SetDimensionSize(operand, size, dimension)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Tablica wejściowa o n wymiarach. |
size |
XlaOp |
int32 reprezentujący rozmiar dynamiczny w czasie wykonywania. |
dimension |
int64 |
Wartość z przedziału [0, n) określająca wymiar. |
Przekazywanie operandu jako wyniku z wykorzystaniem wymiaru dynamicznego śledzonego przez kompilator.
Wartości z dodatkiem zostaną zignorowane przez operacje redukcji w dół strumienia.
let v: f32[10] = f32[10]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
let five: s32 = 5;
let six: s32 = 6;
// Setting dynamic dimension size doesn't change the upper bound of the static
// shape.
let padded_v_five: f32[10] = set_dimension_size(v, five, /*dimension=*/0);
let padded_v_six: f32[10] = set_dimension_size(v, six, /*dimension=*/0);
// sum == 1 + 2 + 3 + 4 + 5
let sum:f32[] = reduce_sum(padded_v_five);
// product == 1 * 2 * 3 * 4 * 5
let product:f32[] = reduce_product(padded_v_five);
// Changing padding size will yield different result.
// sum == 1 + 2 + 3 + 4 + 5 + 6
let sum:f32[] = reduce_sum(padded_v_six);
GetTupleElement
Zobacz też XlaBuilder::GetTupleElement.
Indeksuje tablicę z wartością stałą w czasie kompilacji.
Wartość musi być stałą wartością kompilacji, aby inferencja kształtu mogła określić typ wartości wynikowej.
Jest to analogiczne do std::get<int N>(t) w C++. Koncepcyjnie:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
let element_1: s32 = gettupleelement(t, 1); // Inferred shape matches s32.
Zobacz też tf.tuple.
In-feed
Zobacz też XlaBuilder::Infeed.
Infeed(shape)
| Argument | Typ | Semantyka |
|---|---|---|
shape |
Shape |
Format danych odczytywanych z interfejsu Infeed. Pole układu kształtu musi być ustawione tak, aby odpowiadać układowi danych wysyłanych na urządzenie. W przeciwnym razie jego działanie nie będzie zdefiniowane. |
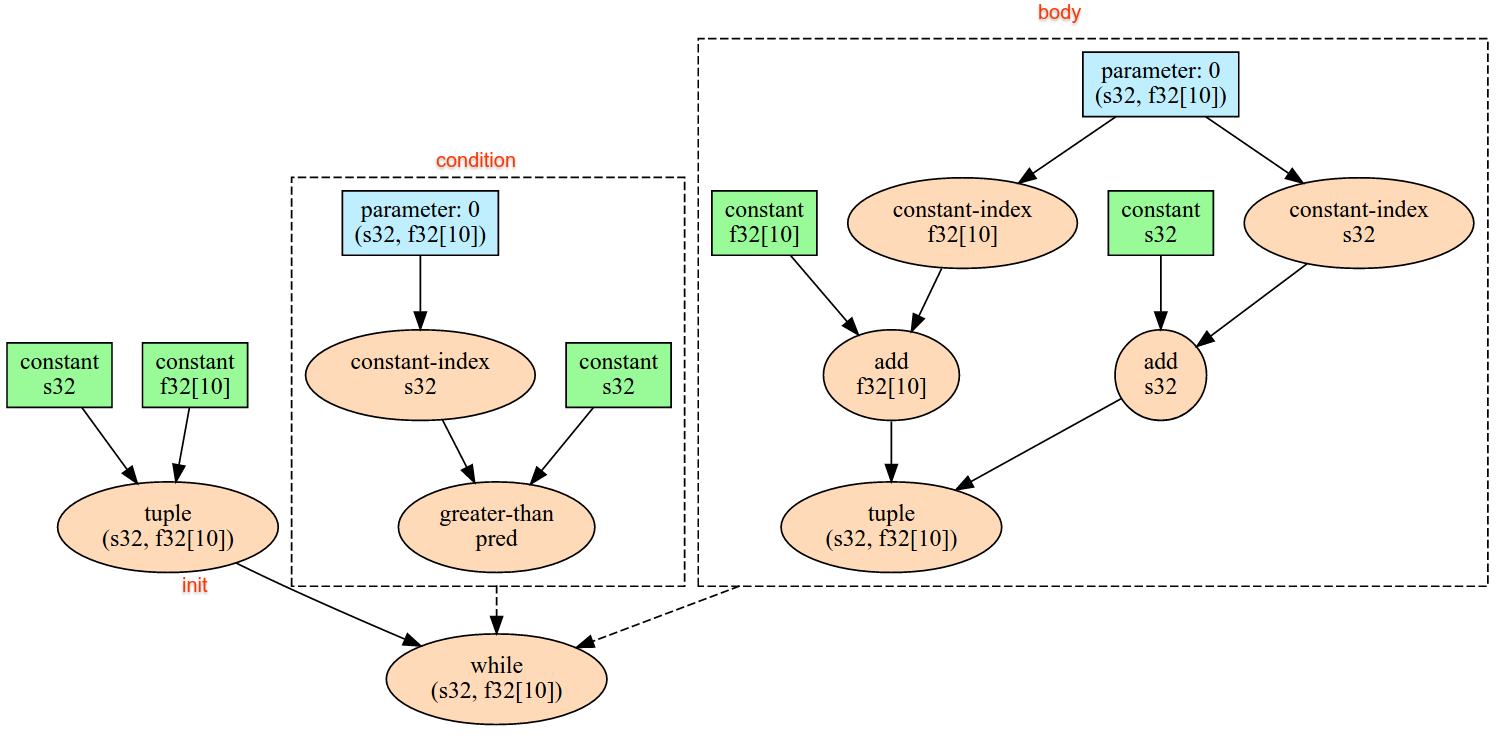
Odczytuje pojedynczy element danych z ukrytego interfejsu przesyłania danych w ramach InFeed na urządzeniu, interpretując dane jako określony kształt i jego układ, a następnie zwracaXlaOp danych. W obliczeniach można używać wielu operacji na danych wejściowych, ale muszą one być uporządkowane w ogólnym porządku. Na przykład 2 elementy danych wejściowych w poniższym kodzie mają całkowite zamówienie, ponieważ istnieje zależność między pętlami while.
result1 = while (condition, init = init_value) {
Infeed(shape)
}
result2 = while (condition, init = result1) {
Infeed(shape)
}
Zagnieżdżone kształty tuple nie są obsługiwane. W przypadku pustej tupla operacja na karcie Infeed jest operacją pustą i nie powoduje odczytu żadnych danych z karty Infeed urządzenia.
Iota
Zobacz też XlaBuilder::Iota.
Iota(shape, iota_dimension)
Tworzy stałą wartość dosłowną na urządzeniu, a nie potencjalnie duży transfer hosta. Tworzy tablicę o określonym kształcie, która zawiera wartości zaczynające się od 0 i wzrost o 1 w wymiarach określonych wymiarem. W przypadku typów zmiennoprzecinkowych utworzona tablica jest równoważna tablicy ConvertElementType(Iota(...)), w której Iota jest typu całkowitego, a konwersja jest typu zmiennoprzecinkowego.
| Argumenty | Typ | Semantyka |
|---|---|---|
shape |
Shape |
Kształt tablicy utworzonej przez Iota() |
iota_dimension |
int64 |
Wymiar, wzdłuż którego mają być dodawane wartości. |
Na przykład Iota(s32[4, 8], 0) zwraca
[[0, 0, 0, 0, 0, 0, 0, 0 ],
[1, 1, 1, 1, 1, 1, 1, 1 ],
[2, 2, 2, 2, 2, 2, 2, 2 ],
[3, 3, 3, 3, 3, 3, 3, 3 ]]
Iota(s32[4, 8], 1) za możliwość zwrotu
[[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ],
[0, 1, 2, 3, 4, 5, 6, 7 ]]
Mapa
Zobacz też XlaBuilder::Map.
Map(operands..., computation)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands |
sekwencja N XlaOp |
N tablic typów T0..T{N-1} |
computation |
XlaComputation |
obliczenia typu T_0, T_1, .., T_{N + M -1} -> S z N parametrami typu T i M o dowolnym typie |
dimensions |
int64 tablica |
tablica wymiarów mapy |
Stosuje funkcję skalarną do podanych tablic operands, tworząc tablicę o tych samych wymiarach, w której każdy element jest wynikiem zmapowanej funkcji zastosowanej do odpowiednich elementów w tablicach wejściowych.
Funkcja mapowana to dowolne obliczenie z ograniczeniem, że ma N wejść typu skalarnego T i jeden wyjście typu S. Wyjście ma te same wymiary co operandy, z tym że typ elementu T jest zastąpiony typem S.
Na przykład: Map(op1, op2, op3, computation, par1) mapuje elem_out <-
computation(elem1, elem2, elem3, par1) w każdym (wielowymiarowym) indeksie w tablicach wejściowych, aby utworzyć tablicę wyjściową.
OptimizationBarrier
Blokuje przenoszenie obliczeń przez barierę przez dowolny etap optymalizacji.
Sprawia, że wszystkie dane wejściowe są oceniane przed operatorami, które zależą od wyników funkcji barrier.
Podkładka
Zobacz też XlaBuilder::Pad.
Pad(operand, padding_value, padding_config)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica typu T |
padding_value |
XlaOp |
typu skalarnego T, aby wypełnić dodaną wyściółkę |
padding_config |
PaddingConfig |
ilość wypełnień po obu stronach (mała, duża) i między elementami każdego wymiaru; |
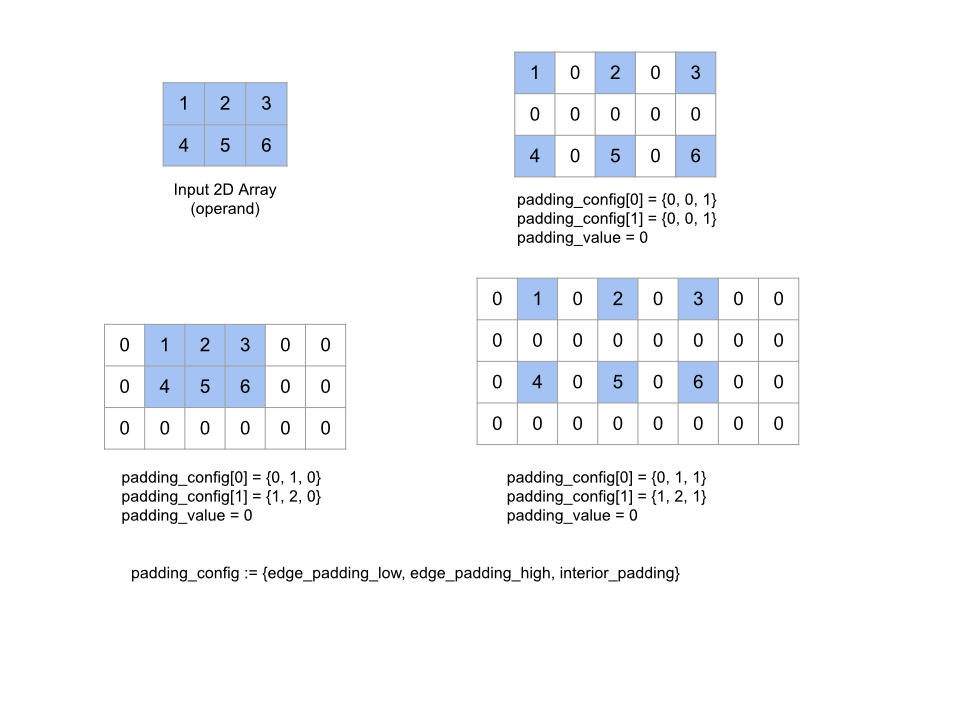
Rozszerza podany tablicę operand, dodając wypełnienie wokół tablicy oraz między elementami tablicy za pomocą podanego argumentu padding_value. padding_configokreśla ilość wypełnień krawędzi i wypełnień wewnętrznych dla każdego wymiaru.
PaddingConfig to powtarzalne pole obiektu PaddingConfigDimension, który zawiera 3 pola dla każdego wymiaru: edge_padding_low, edge_padding_high i interior_padding.
Parametry edge_padding_low i edge_padding_high określają ilość wypełnień dodawanych na niskich wartościach (obok indeksu 0) i na wysokich wartościach (obok najwyższego indeksu) w każdym wymiarze. Ilość wypełnień krawędzi może być ujemna – bezwzględna wartość ujemnego wypełnienia wskazuje liczbę elementów do usunięcia z wybranego wymiaru.
interior_padding określa ilość wypełniania dodanego między dowolnymi elementami w każdym wymiarze; nie może być ujemna. Dopełnienie wewnątrz występuje logicznie przed dopełnieniem krawędzi, więc w przypadku ujemnego dopełnienia krawędzi elementy są usuwane z operanda z dopełnieniem wewnątrz.
Ta operacja jest nieaktywna, jeśli pary wypełnień krawędzi mają wartości (0, 0), a wartości wypełnień wewnętrznych mają wartość 0. Rysunek poniżej przedstawia przykłady różnych wartości edge_padding i interior_padding w przypadku tablicy dwuwymiarowej.
Recv
Zobacz też XlaBuilder::Recv.
Recv(shape, channel_handle)
| Argumenty | Typ | Semantyka |
|---|---|---|
shape |
Shape |
format danych do odebrania; |
channel_handle |
ChannelHandle |
unikalny identyfikator dla każdej pary wysyłania/odbierania; |
Otrzymuje dane o określonym kształcie z instrukcji Send w innej operacji, która korzysta z tego samego identyfikatora kanału. Zwraca XlaOp dla otrzymanych danych.
Interfejs API klienta operacji Recv reprezentuje komunikację synchroniczną.
Jednak wewnętrznie instrukcja jest rozkładana na 2 instrukcje HLO (Recv i RecvDone), aby umożliwić asynchroniczne przesyłanie danych. Zobacz też HloInstruction::CreateRecv i HloInstruction::CreateRecvDone.
Recv(const Shape& shape, int64 channel_id)
Przydziela zasoby wymagane do odbierania danych z instrukcji Send o tym samym kanale_id. Zwraca kontekst dla przypisanych zasobów, który jest używany przez instrukcję RecvDone do oczekiwania na zakończenie przenoszenia danych. Kontekst to tupla {bufor odbioru (shape), identyfikator żądania (U32)} i może być używana tylko przez instrukcję RecvDone.
RecvDone(HloInstruction context)
Poczeka, aż zakończy się transfer danych utworzony przez instrukcję Recv, i zwróci otrzymane dane.
Ograniczamy
Zobacz też XlaBuilder::Reduce.
Stosuje funkcję redukcji do jednej lub większej liczby tablic równolegle.
Reduce(operands..., init_values..., computation, dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands |
Sekwencja N XlaOp |
N tablic typów T_0, ..., T_{N-1}. |
init_values |
Sekwencja N XlaOp |
N skalarów typu T_0, ..., T_{N-1}. |
computation |
XlaComputation |
obliczenia typu T_0, ..., T_{N-1}, T_0, ..., T_{N-1} -> Collate(T_0, ..., T_{N-1}). |
dimensions |
int64 tablica |
Nieuporządkowana tablica wymiarów do zredukowania. |
Gdzie:
- Wartość N musi być większa lub równa 1.
- Obliczenia muszą być „w przybliżeniu” asocjacyjne (patrz poniżej).
- Wszystkie tablice wejściowe muszą mieć te same wymiary.
- Wszystkie wartości początkowe muszą być identyczne w przypadku
computation. - Jeśli
N = 1,Collate(T)toT. - Jeśli
N > 1,Collate(T_0, ..., T_{N-1})jest tupla elementówNtypuT.
Ta operacja redukuje co najmniej 1 wymiar każdej tablicy wejściowej do skalarów.
Liczba wymiarów każdej zwróconej tablicy to number_of_dimensions(operand) - len(dimensions). Wyjście funkcji op to:
Collate(Q_0, ..., Q_N) gdzie Q_i to tablica typu T_i, której wymiary są opisane poniżej.
Inne backendy mogą ponownie powiązać obliczenia redukcji. Może to prowadzić do różnic numerycznych, ponieważ niektóre funkcje redukcji, takie jak dodawanie, nie są skojarzone z liczbami zmiennoprzecinkowymi. Jeśli jednak zakres danych jest ograniczony, dodawanie zmiennoprzecinkowe jest wystarczająco zbliżone do skojarzonego w większości praktycznych zastosowań.
Przykłady
Gdy redukujesz wymiar w pojedynczej tablicy 1D z wartościami [10, 11,
12, 13], przy użyciu funkcji redukcji f (czyli computation), można to obliczyć jako
f(10, f(11, f(12, f(init_value, 13)))
ale istnieje też wiele innych możliwości, np.
f(init_value, f(f(10, f(init_value, 11)), f(f(init_value, 12), f(init_value, 13))))
Poniżej znajduje się przykładowy pseudokod, który pokazuje, jak można zaimplementować redukcję, używając dodawania jako obliczenia redukcji z wartością początkową 0.
result_shape <- remove all dims in dimensions from operand_shape
# Iterate over all elements in result_shape. The number of r's here is equal
# to the number of dimensions of the result.
for r0 in range(result_shape[0]), r1 in range(result_shape[1]), ...:
# Initialize this result element
result[r0, r1...] <- 0
# Iterate over all the reduction dimensions
for d0 in range(dimensions[0]), d1 in range(dimensions[1]), ...:
# Increment the result element with the value of the operand's element.
# The index of the operand's element is constructed from all ri's and di's
# in the right order (by construction ri's and di's together index over the
# whole operand shape).
result[r0, r1...] += operand[ri... di]
Oto przykład zmniejszania tablicy dwuwymiarowej (macierzy). Kształt ma 2 wymiary: wymiar 0 o rozmiarze 2 i wymiar 1 o rozmiarze 3:
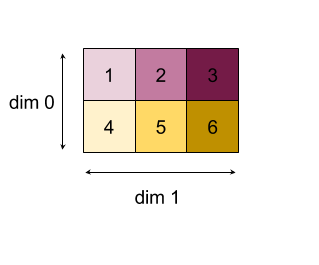
Wyniki redukcji wymiarów 0 i 1 za pomocą funkcji „dodawania”:

Pamiętaj, że oba wyniki redukcji to tablice jednowymiarowe. Diagram pokazuje jeden jako kolumnę, a drugi jako wiersz, co ułatwia wizualizację.
Oto bardziej złożony przykład tablicy 3D. Liczba wymiarów wynosi 3, wymiar 0 ma rozmiar 4, wymiar 1 ma rozmiar 2, a wymiar 2 ma rozmiar 3. Dla ułatwienia wartości od 1 do 6 są powielane w wymiarze 0.
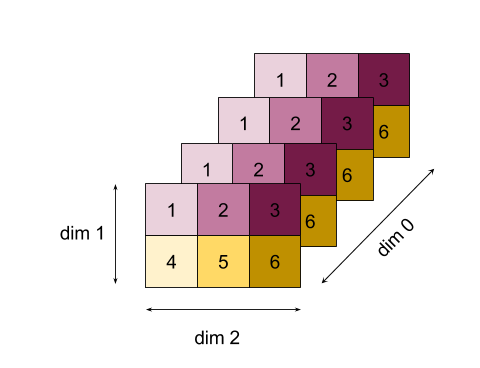
Podobnie jak w przypadku obrazu 2D, możemy zmniejszyć tylko jeden wymiar. Jeśli zredukujemy wymiar 0, otrzymamy tablicę dwuwymiarową, w której wszystkie wartości w wymiarze 0 zostały złożone w skalar:
| 4 8 12 |
| 16 20 24 |
Jeśli zredukujemy wymiar 2, otrzymamy też tablicę dwuwymiarową, w której wszystkie wartości w wymiarze 2 zostały złożone w skalar:
| 6 15 |
| 6 15 |
| 6 15 |
| 6 15 |
Pamiętaj, że względna kolejność pozostałych wymiarów w danych wejściowych jest zachowana w wynikach, ale niektóre wymiary mogą mieć przypisane nowe numery (ponieważ zmienia się liczba wymiarów).
Możemy też zmniejszyć liczbę wymiarów. Dodanie wymiarów 0 i 1 powoduje utworzenie tablicy jednowymiarowej [20, 28, 36].
Redukcja tablicy 3D we wszystkich wymiarach daje wartość skalarną 84.
Variadic Reduce
Gdy N > 1, zastosowanie funkcji reduce jest nieco bardziej skomplikowane, ponieważ jest stosowane jednocześnie do wszystkich danych wejściowych. Operandy są podawane do obliczeń w tej kolejności:
- Wartość zredukowana dla pierwszego operanda
- …
- Wartość zredukowana dla N-tego operanda
- Wartość wejściowa dla pierwszego operanda
- …
- Wartość wejściowa dla N-tego operandu
Rozważmy na przykład funkcję redukcji, która może służyć do równoległego obliczania wartości maksymalnej i argmax w tablicy jednowymiarowej:
f: (Float, Int, Float, Int) -> Float, Int
f(max, argmax, value, index):
if value >= max:
return (value, index)
else:
return (max, argmax)
W przypadku jednowymiarowych tablic wejściowych V = Float[N], K = Int[N] i wartości początkowych I_V = Float, I_K = Int wynik f_(N-1) z redukcji w jedynym wymiarze danych wejściowych jest równoważny z taką rekursywną aplikacją:
f_0 = f(I_V, I_K, V_0, K_0)
f_1 = f(f_0.first, f_0.second, V_1, K_1)
...
f_(N-1) = f(f_(N-2).first, f_(N-2).second, V_(N-1), K_(N-1))
Zastosowanie tego uproszczenia do tablicy wartości i tablicy sekwencyjnych indeksów (np. iota) spowoduje współiterację tablic i zwróci tuple zawierającą maksymalną wartość i odpowiadający jej indeks.
ReducePrecision
Zobacz też XlaBuilder::ReducePrecision.
Modeluje efekt konwersji wartości zmiennoprzecinkowych na format o niższej precyzji (np. IEEE-FP16) i z powrotem na format oryginalny. Liczba bitów wykładnika i manty w formacie o niższej precyzji może być dowolna, ale nie wszystkie rozmiary bitów mogą być obsługiwane przez wszystkie implementacje sprzętowe.
ReducePrecision(operand, mantissa_bits, exponent_bits)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica typu zmiennoprzecinkowego T. |
exponent_bits |
int32 |
liczba bitów wykładnika w formacie o niższej precyzji |
mantissa_bits |
int32 |
liczba bitów mantisy w formacie o niższej precyzji |
Wynikiem jest tablica typu T. Wartości wejściowe są zaokrąglane do najbliższej wartości, którą można przedstawić za pomocą określonej liczby bitów mantisy (z użyciem semantyki „wiązania do parzystej”), a wartości, które przekraczają zakres określony przez liczbę bitów wykładnika, są ograniczane do dodatniej lub ujemnej nieskończoności. Wartości NaN są zachowywane, ale mogą zostać przekonwertowane na kanoniczne wartości NaN.
Format o niższej precyzji musi mieć co najmniej 1 bit wykładnika (aby odróżnić wartość zerową od nieskończoności, ponieważ obie mają zerową mantisę) i musi mieć nieujemną liczbę bitów mantisy. Liczba bitów wykładnika lub mantisa może przekraczać odpowiednią wartość dla typu T; odpowiednia część konwersji jest wtedy po prostu pomijana.
ReduceScatter
Zobacz też XlaBuilder::ReduceScatter.
ReduceScatter to operacja zbiorcza, która skutecznie wykonuje AllReduce, a następnie rozprasza wynik, dzieląc go na bloki shard_count wzdłuż scatter_dimension, a replika i w grupie replik otrzymuje fragment ith.
ReduceScatter(operand, computation, scatter_dim, shard_count,
replica_group_ids, channel_id)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Tablica lub niepusta tupla tablic do zredukowania na replikach. |
computation |
XlaComputation |
Obliczanie redukcji |
scatter_dimension |
int64 |
Wymiar do zastosowania w rozrzucie. |
shard_count |
int64 |
Liczba bloków do podziału scatter_dimension |
replica_groups |
wektor wektorów int64 |
Grupy, między którymi są przeprowadzane redukcje |
channel_id |
opcjonalnie int64 |
Opcjonalny identyfikator kanału do komunikacji między modułami |
- Jeśli
operandto tablica tablic, operacja reduce-scatter jest wykonywana na każdym elemencie tablicy. replica_groupsto lista grup replik, między którymi wykonywane jest zredukowanie (identyfikator repliki bieżącej repliki można pobrać za pomocąReplicaId). Kolejność replik w każdej grupie określa kolejność, w jakiej wynik redukcji wszystkich replik zostanie rozproszony.replica_groupsmusi być pusty (w tym przypadku wszystkie repliki należą do jednej grupy) lub zawierać taką samą liczbę elementów jak liczba replik. Jeśli masz więcej niż jedną grupę replik, wszystkie muszą mieć ten sam rozmiar. Na przykładreplica_groups = {0, 2}, {1, 3}wykonuje redukcję między replikami0i2oraz1i3, a potem rozprasza wynik.shard_countto rozmiar każdej grupy replik. Potrzebujemy tego w przypadku pustych wartościreplica_groups. Jeślireplica_groupsnie jest pusty,shard_countmusi być równy rozmiarowi każdej grupy replik.channel_idjest używany do komunikacji między modułami: tylko operacjereduce-scatterz tym samymchannel_idmogą się ze sobą komunikować.
Kształt wyjściowy jest scatter_dimension razy mniejszy od kształtu wejściowego.shard_count Jeśli np. są 2 repliki, a operand ma odpowiednio wartości [1.0, 2.25] i [3.0, 5.25], wartość wyjściowa z tej operacji, w której scatter_dim to 0, będzie wynosić [4.0] w przypadku pierwszej repliki i [7.5] w przypadku drugiej repliki.
ReduceWindow
Zobacz też XlaBuilder::ReduceWindow.
Funkcja ta stosuje funkcję redukcji do wszystkich elementów w każdym oknie sekwencji N wielowymiarowych tablic, zwracając pojedynczą tablicę wielowymiarową lub wielowymiarową tablicę tuple. Każda tablica wyjściowa ma taką samą liczbę elementów jak liczba prawidłowych pozycji okna. Warstwę z wynikiem zrzutu można wyrazić jako ReduceWindow. Podobnie jak w przypadku Reduce, zastosowany computation jest zawsze przekazywany po lewej stronie init_values.
ReduceWindow(operands..., init_values..., computation, window_dimensions,
window_strides, padding)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands |
N XlaOps |
Sekwencja N wielowymiarowych tablic typu T_0,..., T_{N-1}, z których każda reprezentuje obszar podstawowy, na którym umieszczone jest okno. |
init_values |
N XlaOps |
N wartości początkowych reszty, po jednej dla każdego z N operandów. Więcej informacji znajdziesz w sekcji Zmniejszanie. |
computation |
XlaComputation |
Funkcja redukcji typu T_0, ..., T_{N-1}, T_0, ..., T_{N-1} -> Collate(T_0, ..., T_{N-1}), która ma być stosowana do elementów w każdym oknie wszystkich danych wejściowych. |
window_dimensions |
ArraySlice<int64> |
tablica liczb całkowitych dla wartości wymiaru okna |
window_strides |
ArraySlice<int64> |
tablica liczb całkowitych dla wartości kroku okna |
base_dilations |
ArraySlice<int64> |
tablica liczb całkowitych z wartościami rozszerzenia podstawowego |
window_dilations |
ArraySlice<int64> |
tablica liczb całkowitych dla wartości rozszerzenia okna |
padding |
Padding |
typ wypełnienia dla okna (Padding::kSame, który wypełnia tak, aby uzyskać taki sam kształt wyjściowy jak wejście, jeśli krok wynosi 1, lub Padding::kValid, który nie używa wypełnienia i „zatrzymuje” okno, gdy już się nie mieści); |
Gdzie:
- Wartość N musi być większa lub równa 1.
- Wszystkie tablice wejściowe muszą mieć te same wymiary.
- Jeśli
N = 1,Collate(T)toT. - Jeśli
N > 1,Collate(T_0, ..., T_{N-1})jest tupla elementówNtypu(T0,...T{N-1}).
Poniżej znajduje się kod i rysunek pokazujący przykład użycia funkcji ReduceWindow. Dane wejściowe to tablica o wymiarach [4 x 6], a obie zmienne window_dimensions i window_stride_dimensions mają wymiary [2 x 3].
// Create a computation for the reduction (maximum).
XlaComputation max;
{
XlaBuilder builder(client_, "max");
auto y = builder.Parameter(0, ShapeUtil::MakeShape(F32, {}), "y");
auto x = builder.Parameter(1, ShapeUtil::MakeShape(F32, {}), "x");
builder.Max(y, x);
max = builder.Build().value();
}
// Create a ReduceWindow computation with the max reduction computation.
XlaBuilder builder(client_, "reduce_window_2x3");
auto shape = ShapeUtil::MakeShape(F32, {4, 6});
auto input = builder.Parameter(0, shape, "input");
builder.ReduceWindow(
input,
/*init_val=*/builder.ConstantLiteral(LiteralUtil::MinValue(F32)),
*max,
/*window_dimensions=*/{2, 3},
/*window_stride_dimensions=*/{2, 3},
Padding::kValid);
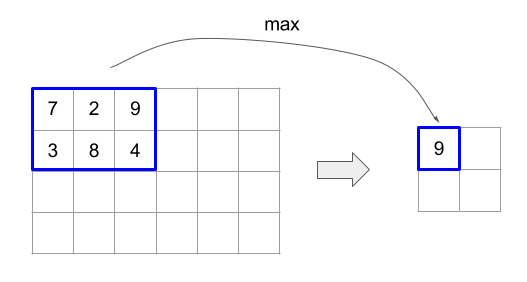
Krok 1 w wymiarze określa, że pozycja okna w wymiarze jest oddalona o 1 element od sąsiedniego okna. Aby określić, że żadne okna się nie nakładają, parametr window_stride_dimensions powinien być równy parametrowi window_dimensions. Rysunek poniżej pokazuje użycie 2 różnych wartości interwału. Dodanie wypełnień jest stosowane do każdego wymiaru danych wejściowych, a obliczenia są takie same, jak gdyby dane wejściowe miały wymiary po wypełnieniu.
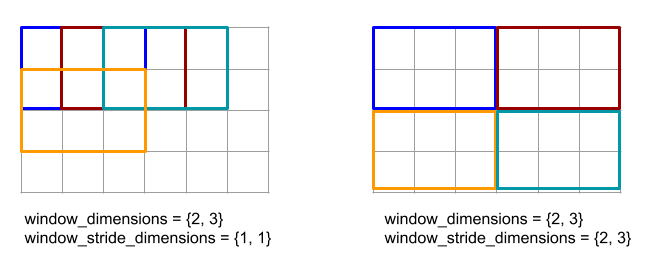
Przykładem nieoczywistego wypełniania może być obliczenie minimalnej wartości okna redukcyjnego (wartość początkowa to MAX_FLOAT) o wymiarach 3 i skoku 2 w wejściowym tablicy [10000, 1000, 100, 10, 1]. Funkcja Padding kValid oblicza minimum z 2 ważnych okien: [10000, 1000, 100] i [100, 10, 1], co daje wynik [100, 1]. Funkcja Padding kSame najpierw wypełnia tablicę, aby kształt po zmniejszeniu okna był taki sam jak dane wejściowe dla pierwszego kroku, dodając początkowe elementy po obu stronach i uzyskiwanie [MAX_VALUE, 10000, 1000, 100, 10, 1,
MAX_VALUE]. Uruchomienie funkcji reduce-window na wypełnionym tablicy działa na 3 oknach: [MAX_VALUE, 10000, 1000], [1000, 100, 10] i [10, 1, MAX_VALUE], przy czym zwraca wartość [1000, 10, 1].
Kolejność obliczania funkcji redukcji jest dowolna i może być niedeterministyczna. Dlatego funkcja redukcji nie powinna być zbyt wrażliwa na ponowne powiązanie. Aby dowiedzieć się więcej, zapoznaj się z dyskusją na temat asocjacyjności w kontekście Reduce.
ReplicaId
Zobacz też XlaBuilder::ReplicaId.
Zwraca unikalny identyfikator (skalarna U32) repliki.
ReplicaId()
Unikalny identyfikator każdej repliki to bezznakowa liczba całkowita z przedziału [0, N), gdzie N to liczba replik. Ponieważ na wszystkich replikach działa ten sam program, wywołanie ReplicaId() w programie zwróci inną wartość na każdej replice.
Kształtowanie
Zobacz też XlaBuilder::Reshape i operację Collapse.
Zmienia wymiary tablicy na nową konfigurację.
Reshape(operand, dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica typu T |
dimensions |
int64 wektor |
wektor rozmiarów nowych wymiarów |
Zmiana kształtu polega na spłaszczeniu tablicy do jednowymiarowego wektora wartości danych, a następnie na dopasowaniu tego wektora do nowego kształtu. Argumenty wejściowe to dowolny tablica typu T, wektor wymiarów będący stałą w czasie kompilacji oraz wektor wymiarów będący stałą w czasie kompilacji.
Wektor dimensions określa rozmiar tablicy wyjściowej. Wartość w indeksie 0 w tablicy dimensions to rozmiar wymiaru 0, wartość w indeksie 1 to rozmiar wymiaru 1 itd. Iloczyn wymiarów dimensions musi być równy iloczynowi rozmiarów wymiarów operandu. Gdy zawężenie złożonej tablicy do tablicy wielowymiarowej zdefiniowanej przez funkcję dimensions, wymiary w tablicy dimensions są uporządkowane od najmniej zmiennych (najbardziej istotnych) do najbardziej zmiennych (najmniej istotnych).
Na przykład niech v będzie tablicą 24 elementów:
let v = f32[4x2x3] { { {10, 11, 12}, {15, 16, 17} },
{ {20, 21, 22}, {25, 26, 27} },
{ {30, 31, 32}, {35, 36, 37} },
{ {40, 41, 42}, {45, 46, 47} } };
let v012_24 = Reshape(v, {24});
then v012_24 == f32[24] {10, 11, 12, 15, 16, 17, 20, 21, 22, 25, 26, 27,
30, 31, 32, 35, 36, 37, 40, 41, 42, 45, 46, 47};
let v012_83 = Reshape(v, {8,3});
then v012_83 == f32[8x3] { {10, 11, 12}, {15, 16, 17},
{20, 21, 22}, {25, 26, 27},
{30, 31, 32}, {35, 36, 37},
{40, 41, 42}, {45, 46, 47} };
W szczególnym przypadku funkcja reshape może przekształcić tablicę jednoelementową w skalar i odwrotnie. Na przykład
Reshape(f32[1x1] { {5} }, {}) == 5;
Reshape(5, {1,1}) == f32[1x1] { {5} };
Rev (wstecz)
Zobacz też XlaBuilder::Rev.
Rev(operand, dimensions)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica typu T |
dimensions |
ArraySlice<int64> |
wymiary do odwrócenia |
Odwraca kolejność elementów w tablicy operand wzdłuż określonej osi dimensions, generując tablicę wyjściową o tej samej strukturze. Każdy element tablicy operanda o wielowymiarowym indeksie jest zapisywany w tablicy wyjściowej o przekształconym indeksie. Indeks wielowymiarowy jest przekształcany przez odwrócenie indeksu w każdym wymiarze, który ma być odwrócony (czyli jeśli wymiar o rozmiarze N jest jednym z wymiarów odwracanych, jego indeks i jest przekształcany w N – 1 – i).
Operacja Rev może służyć do odwracania tablicy wag konwekcji wzdłuż 2 wymiarów okna podczas obliczania gradientu w sieciach neuronowych.
RngNormal
Zobacz też XlaBuilder::RngNormal.
Tworzy dane wyjściowe o określonym kształcie z losowymi liczbami wygenerowanymi zgodnie z \(N(\mu, \sigma)\) rozkładem normalnym. Parametry \(\mu\) i \(\sigma\)oraz kształt wyjściowy muszą mieć typ elementu liczby zmiennoprzecinkowej. Parametry muszą mieć wartość skalarną.
RngNormal(mu, sigma, shape)
| Argumenty | Typ | Semantyka |
|---|---|---|
mu |
XlaOp |
Typ T skalarny określający średnią wygenerowanych liczb |
sigma |
XlaOp |
Element typu T określający odchylenie standardowe wygenerowanego |
shape |
Shape |
Dane wyjściowe w postaci kształtu T |
RngUniform
Zobacz też XlaBuilder::RngUniform.
Tworzy dane wyjściowe o określonym kształcie za pomocą liczb losowych wygenerowanych zgodnie z rozkładem gęstości prawdopodobieństwa równego na przedziale \([a,b)\). Parametry i typ elementu wyjściowego muszą być typu logicznego, całkowitego lub zmiennoprzecinkowego. Typy muszą być spójne. Backendy procesora i procesora graficznego obsługują obecnie tylko formaty F64, F32, F16, BF16, S64, U64, S32 i U32. Ponadto parametry muszą mieć wartości skalarne. Jeśli \(b <= a\) wynik jest zdefiniowany przez implementację.
RngUniform(a, b, shape)
| Argumenty | Typ | Semantyka |
|---|---|---|
a |
XlaOp |
Element typu T określający dolną granicę przedziału |
b |
XlaOp |
Element typu T określający górną granicę przedziału |
shape |
Shape |
Dane wyjściowe w postaci kształtu T |
RngBitGenerator
Generuje dane wyjściowe o określonym kształcie wypełnione jednorodnymi losowymi bitami za pomocą określonego algorytmu (lub domyślnego algorytmu w backendzie) i zwraca zaktualizowany stan (o tym samym kształcie co stan początkowy) oraz wygenerowane losowe dane.
Stan początkowy to stan początkowy bieżącego generowania liczb losowych. Jego kształt i wymagane wartości zależą od użytego algorytmu.
Wyjście jest zdeterminowaną funkcją stanu początkowego, ale nie jest zdeterminowane między backendami i różnymi wersjami kompilatorów.
RngBitGenerator(algorithm, key, shape)
| Argumenty | Typ | Semantyka |
|---|---|---|
algorithm |
RandomAlgorithm |
Algorytm PRNG do użycia. |
initial_state |
XlaOp |
Stan początkowy algorytmu PRNG. |
shape |
Shape |
Format wyjściowy wygenerowanych danych. |
Dostępne wartości dla parametru algorithm:
rng_default: algorytm specyficzny dla backendu z wymaganiami dotyczącymi kształtu.rng_three_fry: algorytm PRNG oparty na liczniku ThreeFry. Kształtinitial_statejestu64[2]z dowolnymi wartościami. Salmon i in., SC 2011. Losowe liczby równoległe: to bardzo prosterng_philox: algorytm Philox do równoległego generowania liczb losowych. Kształtinitial_statetou64[3]z dowolnymi wartościami. Salmon i in., SC 2011. Losowe liczby równoległe: to bardzo proste
Punktowy
Operacja rozproszenia XLA generuje sekwencję wyników, które są wartościami tablicy wejściowej operands. Kilka przekrojów (w indeksach określonych przez scatter_indices) jest aktualizowanych za pomocą sekwencji wartości w tablicy updates za pomocą funkcji update_computation.
Zobacz też XlaBuilder::Scatter.
scatter(operands..., scatter_indices, updates..., update_computation,
index_vector_dim, update_window_dims, inserted_window_dims,
scatter_dims_to_operand_dims)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands |
Sekwencja N XlaOp |
N tablic typu T_0, ..., T_N, do których mają być rozproszone dane. |
scatter_indices |
XlaOp |
Tablica zawierająca początkowe indeksy przedziałów, do których należy wykonać rozproszenie. |
updates |
Sekwencja N XlaOp |
N tablic typów T_0, ..., T_N. updates[i] zawiera wartości, których należy używać do rozpraszania operands[i]. |
update_computation |
XlaComputation |
Obliczenie służące do łączenia dotychczasowych wartości w tablicy wejściowej i aktualizacji podczas rozpraszania. To obliczenie powinno być typu T_0, ..., T_N, T_0, ..., T_N -> Collate(T_0, ..., T_N). |
index_vector_dim |
int64 |
Wymiar w pozycji scatter_indices, który zawiera indeksy początkowe. |
update_window_dims |
ArraySlice<int64> |
Zbiór wymiarów w formie updates, które są wymiarami okna. |
inserted_window_dims |
ArraySlice<int64> |
Zestaw wymiarów okna, które należy wstawić do kształtu updates. |
scatter_dims_to_operand_dims |
ArraySlice<int64> |
Mapowanie wymiarów z indeksów rozproszonych na przestrzeń indeksu operandu. Ta tablica jest interpretowana jako mapowanie i na scatter_dims_to_operand_dims[i] . Musi być jeden do jednego i obejmuje wszystkich. |
indices_are_sorted |
bool |
Określa, czy indeksy są sortowane przez wywołującego. |
unique_indices |
bool |
Czy wywołujący może zagwarantować, że indeksy są unikalne. |
Gdzie:
- Wartość N musi być większa lub równa 1.
operands[0], ...,operands[N-1] muszą mieć te same wymiary.updates[0], ...,updates[N-1] muszą mieć te same wymiary.- Jeśli
N = 1,Collate(T)toT. - Jeśli
N > 1,Collate(T_0, ..., T_N)jest tablicą elementówNtypuT.
Jeśli index_vector_dim = scatter_indices.rank, zakładamy, że scatter_indices ma wymiar końcowy 1.
Definiujemy update_scatter_dims typu ArraySlice<int64> jako zbiór wymiarów w kształcie updates, które nie są w grupie update_window_dims, w porządku rosnącym.
Argumenty funkcji rozrzutu powinny być zgodne z tymi ograniczeniami:
Każda tablica
updatesmusi mieć wymiaryupdate_window_dims.size + scatter_indices.rank - 1.Granice wymiaru
iw każdej tablicyupdatesmuszą być zgodne z tymi wymaganiami:- Jeśli
iwystępuje wupdate_window_dims(czyli jest równeupdate_window_dims[k] dla dowolnegok), to górna granica wymiaruiwupdatesnie może przekraczać odpowiadającej jej górnej granicyoperandpo uwzględnieniuinserted_window_dims(czyliadjusted_window_bounds[k], gdzieadjusted_window_boundszawiera górne graniceoperandz usunięciem górnych granic w indeksachinserted_window_dims). - Jeśli w elementach zbioru
update_scatter_dimswystępuje elementi(czyli jest on równyupdate_scatter_dims[k] dla niektórych elementówk), to dolna granica wymiaruiw elementach zbioruupdatesmusi być równa odpowiadającej jej górnej granicy w elementach zbioruscatter_indices, pomijając elementindex_vector_dim(czyliscatter_indices.shape.dims[k], jeślik<index_vector_dim, a w przeciwnym raziescatter_indices.shape.dims[k+1]).
- Jeśli
update_window_dimsmusi być uporządkowana rosnąco, nie może zawierać powtarzających się numerów wymiarów i musi mieścić się w zakresie[0, updates.rank).inserted_window_dimsmusi być uporządkowana rosnąco, nie może zawierać powtarzających się numerów wymiarów i musi mieścić się w zakresie[0, operand.rank).Wartość
operand.rankmusi być równa sumie wartościupdate_window_dims.sizeiinserted_window_dims.size.scatter_dims_to_operand_dims.sizemusi być równescatter_indices.shape.dims[index_vector_dim], a jego wartości muszą mieścić się w zakresie[0, operand.rank).
Dla danego indeksu U w każdej tablicy updates odpowiedni indeks I w odpowiedniej tablicy operands, do której należy zastosować tę zmianę, jest obliczany w ten sposób:
- Niech
G= {U[k] dlakwupdate_scatter_dims}. UżyjG, aby wyszukać wektor indeksuSw tablicyscatter_indicestak, abyS[i] =scatter_indices[Combine(G,i)], gdzie Combine(A, b) wstawia b w pozycjiindex_vector_dimw tablicy A. - Utwórz indeks
Sinwoperand, używającS, rozpraszając elementySza pomocą mapyscatter_dims_to_operand_dims. Bardziej formalnie:Sin[scatter_dims_to_operand_dims[k]] =S[k], jeślik<scatter_dims_to_operand_dims.size.Sin[_] =0w innych przypadkach.
- Utwórz indeks
Winw każdej tablicyoperands, rozpraszając indeksy w pozycjiupdate_window_dimsw tablicyUzgodnie z wartościąinserted_window_dims. Bardziej formalnie:Win[window_dims_to_operand_dims(k)] =U[k], jeślikznajduje się wupdate_window_dims, gdziewindow_dims_to_operand_dimsjest monotoniczną funkcją o domenie [0,update_window_dims.size] i zakresie [0,operand.rank] \inserted_window_dims. (Jeśli na przykładupdate_window_dims.sizeto4,operand.rankto6, ainserted_window_dimsto {0,2}, towindow_dims_to_operand_dimsto {0→1,1→3,2→4,3→5}).Win[_] =0w innych przypadkach.
ItoWin+Sin, gdzie + oznacza dodawanie element po elemencie.
Operację rozpraszania można podsumować w ten sposób.
- Inicjalizacja
outputzoperands, czyli dla wszystkich indeksówJ, dla wszystkich indeksówOw tablicyoperands[J]:
output[J][O] =operands[J][O] - W przypadku każdego indeksu
Uw tablicyupdates[J] i odpowiadającego mu indeksuOw tablicyoperand[J], jeśliOjest prawidłowym indeksem dlaoutput:
(output[0][O], ...,output[N-1][O]) =update_computation(output[0][O], ..., ,output[N-1][O],updates[0][U], ...,updates[N-1][U])
Kolejność, w jakiej są one stosowane, nie jest określona. Dlatego, gdy wiele indeksów w updates odwołuje się do tego samego indeksu w operands, odpowiadająca mu wartość w output będzie niedeterministyczna.
Pamiętaj, że pierwszy parametr przekazywany do funkcji update_computation będzie zawsze bieżącą wartością z tablicy output, a drugi parametr będzie zawsze wartością z tablicy updates. Jest to ważne zwłaszcza w przypadku, gdy update_computation nie jest przemienna.
Jeśli indices_are_sorted ma wartość Prawda, XLA może założyć, że elementy scatter_indices są posortowane (w kolejności rosnącej, po rozproszeniu ich wartości zgodnie z scatter_dims_to_operand_dims) przez użytkownika. Jeśli nie, semantyka jest zdefiniowana przez implementację.
Jeśli parametr unique_indices ma wartość Prawda, XLA może założyć, że wszystkie elementy są unikalne. XLA może więc używać operacji nieatomowych. Jeśli parametr unique_indices ma wartość Prawda, a indeksy, do których jest wykonywane rozproszenie, nie są unikalne, semantyka jest definiowana przez implementację.
Operację rozproszenia można traktować jako odwrotność operacji zbierania, czyli operację aktualizującą elementy wejściowe, które zostały wyodrębnione przez odpowiadającą operację zbierania.
Szczegółowy opis i przykłady znajdziesz w sekcji „Opis nieformalny” w sekcji Gather.
Wybierz
Zobacz też XlaBuilder::Select.
Tworzy tablicę wyjściową z elementów dwóch tablic wejściowych na podstawie wartości tablicy z predykatem.
Select(pred, on_true, on_false)
| Argumenty | Typ | Semantyka |
|---|---|---|
pred |
XlaOp |
tablica typu PRED |
on_true |
XlaOp |
tablica typu T |
on_false |
XlaOp |
tablica typu T |
Tablice on_true i on_false muszą mieć ten sam kształt. Jest to też kształt tablicy wyjściowej. Tablica pred musi mieć taką samą wielowymiarowość jak tablice on_true i on_false oraz typ elementu PRED.
W przypadku każdego elementu P z tablicy pred odpowiedni element tablicy wyjściowej jest pobierany z tablicy on_true, jeśli wartość atrybutu P to true, i z tablicy on_false, jeśli wartość atrybutu P to false. Jako ograniczona forma nadawania,
pred może być skalarem typu PRED. W tym przypadku tablica wyjściowa jest pobierana wyłącznie z on_true, jeśli pred ma wartość true, i z on_false, jeśli pred ma wartość false.
Przykład z wartością nieskalarną pred:
let pred: PRED[4] = {true, false, false, true};
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 200, 300, 4};
Przykład z elementem skalarnym pred:
let pred: PRED = true;
let v1: s32[4] = {1, 2, 3, 4};
let v2: s32[4] = {100, 200, 300, 400};
==>
Select(pred, v1, v2) = s32[4]{1, 2, 3, 4};
Obsługiwane są zapytania dotyczące kolumn. W tym celu tuple są traktowane jako typy skalarne. Jeśli on_true i on_false to krotki (które muszą mieć ten sam kształt), to pred musi być skalarem typu PRED.
SelectAndScatter
Zobacz też XlaBuilder::SelectAndScatter.
Ta operacja może być traktowana jako operacja złożona, która najpierw oblicza ReduceWindow w tablicy operand, aby wybrać element z każdego okna, a potem rozprasza tablicę source do indeksów wybranych elementów, aby utworzyć tablicę wyjściową o tej samej formie co tablica operandów. Funkcja binarna
select służy do wybierania elementów z każdego okna przez zastosowanie w każdym z nich, a jest wywoływana z właściwością, która jest leksykalno-alfabetycznie mniejsza niż wektor indeksu pierwszego parametru w porównaniu z wektorem indeksu drugiego parametru. Funkcja select zwraca wartość true, jeśli wybrany jest pierwszy parametr, oraz false, jeśli wybrany jest drugi parametr. Funkcja musi być przechodnia (czyli jeśli select(a, b) i select(b, c) mają wartość true, to select(a, c) też ma wartość true), aby wybrany element nie zależał od kolejności elementów przemierzanych w danym oknie.
Funkcja scatter jest stosowana w przypadku każdego wybranego indeksu w tablicy wyjściowej. Funkcja ta przyjmuje 2 parametry skalarne:
- Bieżąca wartość w wybranym indeksie tablicy wyjściowej
- Wartość rozkładu z tabeli
source, która ma zastosowanie do wybranego indeksu
Łączy 2 parametry i zwraca wartość skalarną, która służy do aktualizowania wartości w wybranym indeksie w tablicy wyjściowej. Początkowo wszystkie indeksy tablicy wyjściowej mają wartość init_value.
Tablica wyjściowa ma ten sam kształt co tablica operand, a tablica source musi mieć ten sam kształt co wynik zastosowania operacji ReduceWindow do tablicy operand. SelectAndScatter można użyć do propagacji wstecznej wartości gradientu w warstwie zbiorczej w sieci neuronowej.
SelectAndScatter(operand, select, window_dimensions, window_strides,
padding, source, init_value, scatter)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
tablica typu T, na której przesuwają się okna |
select |
XlaComputation |
obliczenia binarne typu T, T -> PRED, które mają zastosowanie do wszystkich elementów w każdym oknie; zwraca true, jeśli wybrany jest pierwszy parametr, i zwraca false, jeśli wybrany jest drugi parametr |
window_dimensions |
ArraySlice<int64> |
tablica liczb całkowitych dla wartości wymiaru okna |
window_strides |
ArraySlice<int64> |
tablica liczb całkowitych dla wartości kroku okna |
padding |
Padding |
typ wypełnienia okna (Padding::kSame lub Padding::kValid) |
source |
XlaOp |
tablica typu T z wartościami do rozrzucenia |
init_value |
XlaOp |
wartość skalarna typu T dla wartości początkowej tablicy wyjściowej; |
scatter |
XlaComputation |
obliczenia binarne typu T, T -> T, aby zastosować każdy element źródłowy rozrzutu z elementem docelowym |
Rysunek poniżej przedstawia przykłady użycia funkcji SelectAndScatter, w której funkcja select oblicza maksymalną wartość spośród swoich parametrów. Pamiętaj, że gdy okna się nakładają, jak na rysunku (2) poniżej, indeks tablicy operand może być wybierany kilka razy przez różne okna. Na rysunku element o wartości 9 jest wybrany przez oba górne okna (niebieskie i czerwone), a funkcja binarna dodawania scatter generuje element wyjściowy o wartości 8 (2 + 6).
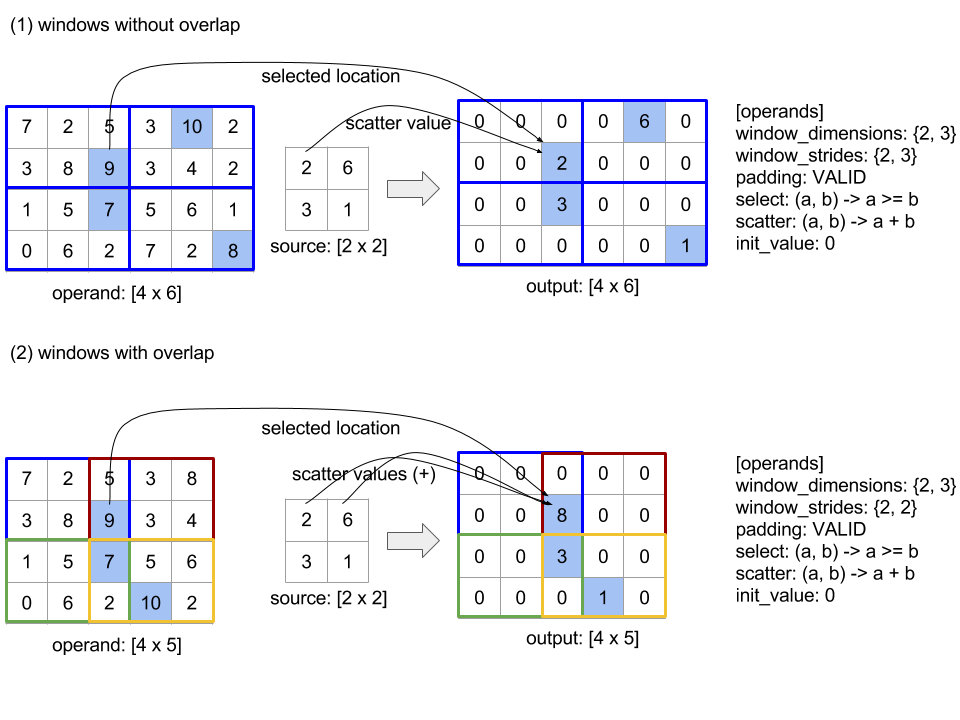
Kolejność obliczania funkcji scatter jest dowolna i może być niedeterministyczna. Dlatego funkcja scatter nie powinna być zbyt wrażliwa na ponowne powiązanie. Aby dowiedzieć się więcej, zapoznaj się z dyskusją na temat asocjacyjności w kontekście Reduce.
Wyślij
Zobacz też XlaBuilder::Send.
Send(operand, channel_handle)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
dane do wysłania (tabelka typu T) |
channel_handle |
ChannelHandle |
unikalny identyfikator dla każdej pary wysyłania/odbierania; |
Przesyła dane podanego operandu do instrukcji Recv w innej operacji, która korzysta z tego samego identyfikatora kanału. Nie zwraca żadnych danych.
Podobnie jak operacja Recv, interfejs API klienta operacji Send reprezentuje komunikację asynchroniczną i jest wewnętrznie rozkładany na 2 instrukcje HLO (Send i SendDone), aby umożliwić asynchroniczne przesyłanie danych. Zobacz też HloInstruction::CreateSend i HloInstruction::CreateSendDone.
Send(HloInstruction operand, int64 channel_id)
Inicjuje asynchroniczny transfer operandu do zasobów przydzielonych przez instrukcję Recv z tym samym identyfikatorem kanału. Zwraca kontekst, który jest używany przez instrukcję SendDone do oczekiwania na zakończenie transferu danych. Kontekst to tupla {operand (shape), request identifier
(U32)} i może być używana tylko przez instrukcję SendDone.
SendDone(HloInstruction context)
Po otrzymaniu kontekstu utworzonego przez instrukcję Send oczekuje na zakończenie przesyłania danych. Instrukcja nie zwraca żadnych danych.
Planowanie instrukcji dotyczących kanału
Kolejność wykonywania 4 instrukcji dla każdego kanału (Recv, RecvDone,
Send, SendDone) jest następująca:
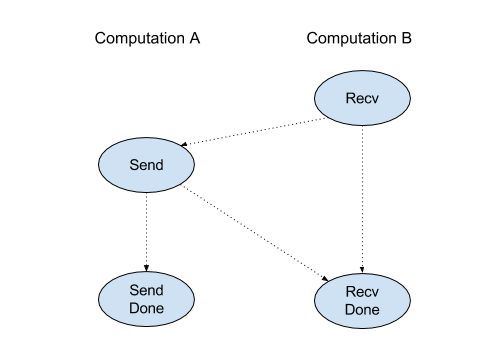
Recvma miejsce przedSendSendma miejsce przedRecvDoneRecvma miejsce przedRecvDoneSendma miejsce przedSendDone
Gdy kompilatory backendu generują harmonogram liniowy dla każdego obliczenia, które komunikuje się za pomocą instrukcji kanału, obliczenia nie mogą zawierać cykli. Na przykład harmonogramy poniżej powodują blokady.
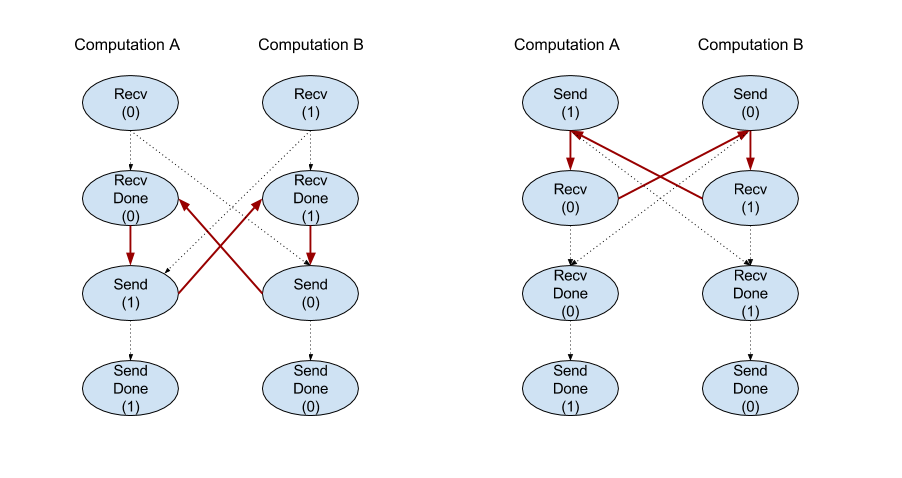
Pamiętaj, że ograniczenie dotyczące instrukcji dotyczy tylko TPU w czasie wykonywania. Na karcie GPU funkcje send i recv będą blokować i nie wysyłać żadnych danych, dopóki nie nastąpi wymiana danych między źródłem a urządzeniem docelowym.
Wycinek
Zobacz też XlaBuilder::Slice.
Slice wyodrębnia podtablicę z tablicy wejściowej. Podtablica ma taką samą liczbę wymiarów jak tablica wejściowa i zawiera wartości w ramce ograniczającej w tablicy wejściowej, gdzie wymiary i indeksy ramki ograniczającej są podawane jako argumenty operacji wycinania.
Slice(operand, start_indices, limit_indices, strides)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Tablica N-wymiarowa typu T |
start_indices |
ArraySlice<int64> |
Lista N liczb całkowitych zawierających indeksy początkowe przekroju dla każdego wymiaru. Wartości muszą być równe zeru lub większe. |
limit_indices |
ArraySlice<int64> |
Lista N liczb całkowitych zawierających indeksy końcowe (wykluczające) przekroju dla każdego wymiaru. Każda wartość musi być większa lub równa odpowiedniej wartości start_indices wymiaru i mniejsza lub równa rozmiarowi wymiaru. |
strides |
ArraySlice<int64> |
Lista N liczb całkowitych, która określa interwał wejściowy przekroju. Wycinka wybiera wszystkie elementy strides[d] w wymiarze d. |
Przykład jednowymiarowy:
let a = {0.0, 1.0, 2.0, 3.0, 4.0}
Slice(a, {2}, {4}) produces:
{2.0, 3.0}
Przykład dwuwymiarowy:
let b =
{ {0.0, 1.0, 2.0},
{3.0, 4.0, 5.0},
{6.0, 7.0, 8.0},
{9.0, 10.0, 11.0} }
Slice(b, {2, 1}, {4, 3}) produces:
{ { 7.0, 8.0},
{10.0, 11.0} }
Sortuj
Zobacz też XlaBuilder::Sort.
Sort(operands, comparator, dimension, is_stable)
| Argumenty | Typ | Semantyka |
|---|---|---|
operands |
ArraySlice<XlaOp> |
Operandy do posortowania. |
comparator |
XlaComputation |
Obliczenie porównywania do użycia. |
dimension |
int64 |
Wymiar, według którego chcesz sortować dane. |
is_stable |
bool |
Określa, czy należy użyć stabilnego sortowania. |
Jeśli podano tylko 1 operand:
Jeśli operand jest 1-wymiarowym tensorem (tablicą), wynik jest posortowaną tablicą. Jeśli chcesz posortować tablicę w kolejności rosnącej, porównywacz powinien wykonać porównanie mniejsze niż. Formalnie po posortowaniu tablicy jest to prawdziwe dla wszystkich pozycji indeksu
i, jzi < j, które są albocomparator(value[i], value[j]) = comparator(value[j], value[i]) = false, albocomparator(value[i], value[j]) = true.Jeśli operand ma większą liczbę wymiarów, jest sortowany według podanego wymiaru. Na przykład w przypadku 2-wymiarowego tensora (macierzy) wartość wymiaru
0spowoduje niezależne posortowanie każdej kolumny, a wartość wymiaru1spowoduje niezależne posortowanie każdego wiersza. Jeśli nie podasz numeru wymiaru, domyślnie zostanie wybrany ostatni wymiar. W przypadku wymiaru, który jest sortowany, obowiązuje ta sama kolejność sortowania co w przypadku wymiaru jednowymiarowego.
Jeśli podano operandy n > 1:
Wszystkie operandy
nmuszą być tensorami o tych samych wymiarach. Typy elementów tensorów mogą się różnić.Wszystkie operandy są sortowane razem, a nie osobno. Pojęcie operandów jest traktowane jako tuple. Podczas sprawdzania, czy elementy każdego operanda na pozycjach indeksu
iijnależy zamienić, wywoływany jest porównywacz z parametrami skalarnymi2 * n, gdzie parametr2 * kodpowiada wartości na pozycjiioperandak-th, a parametr2 * k + 1odpowiada wartości na pozycjijoperandak-th. Zwykle porównywarka porównuje parametry2 * ki2 * k + 1ze sobą oraz ewentualnie używa innych par parametrów jako kryteriów przełamania remisu.Wynikiem jest tupla złożona z operandów w uporządkowanej kolejności (zgodnie z podanym wymiarem, jak wyżej). Operand
i-thw tuplu odpowiada operandowii-thw funkcji Sort.
Jeśli np. istnieją 3 operandy operand0 = [3, 1], operand1 = [42, 50], operand2 = [-3.0, 1.1], a pośrednik porównuje tylko wartości operand0 z operatorem „mniejsze niż”, wyjściem sortowania jest tupla ([1, 3], [50, 42], [1.1, -3.0]).
Jeśli parametr is_stable ma wartość „true”, sortowanie jest stabilne, co oznacza, że jeśli są elementy, które są uważane za równe przez porównywacz, względna kolejność tych wartości jest zachowana. Dwa elementy e1 i e2 są równe wtedy i tylko wtedy, gdy comparator(e1, e2) = comparator(e2, e1) = false. Domyślnie is_stable ma wartość false.
TopK
Zobacz też XlaBuilder::TopK.
TopK znajduje wartości i indeksy k największych lub najmniejszych elementów w ostatnim wymiarze danego tensora.
TopK(operand, k, largest)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Tensor, z którego mają zostać wyodrębnione k elementy. Tensor musi mieć co najmniej 1 wymiar. Rozmiar ostatniej wymiary tensora musi być większy lub równy k. |
k |
int64 |
Liczba elementów do wyodrębnienia. |
largest |
bool |
Określa, czy wyodrębnić największe czy najmniejsze elementy k. |
W przypadku 1-wymiarowego wejściowego tensora (tablicy) znajduje k największe lub najmniejsze elementy w tablicy i wyprowadza parę złożoną z 2 tablic (values, indices). W ten sposób values[j] jest j-tym największym/najmniejszym wpisem w tablicy operand, a jego indeks to indices[j].
W przypadku wejściowego tensora o większej liczbie wymiarów oblicza k największe wpisy w ostatnim wymiarze, zachowując wszystkie pozostałe wymiary (wiersze) w wyjściu.
W przypadku operanda o postaci [A, B, ..., P, Q], gdzie Q >= k, wynikiem jest tuplet (values, indices), w którym:
values.shape = indices.shape = [A, B, ..., P, k]
Jeśli 2 elementy w wierszu są równe, najpierw wyświetla się element o niższym indeksie.
Transponuj
Zobacz też operację tf.reshape.
Transpose(operand)
| Argumenty | Typ | Semantyka |
|---|---|---|
operand |
XlaOp |
Operand do transponowania. |
permutation |
ArraySlice<int64> |
Jak zmieniać kolejność wymiarów. |
Przestawia wymiary operandów zgodnie z daną permutacją, czyli∀ i . 0 ≤ i < number of dimensions ⇒
input_dimensions[permutation[i]] = output_dimensions[i].
Jest to to samo co Reshape(operand, permutation, Permute(permutation, operand.shape.dimensions)).
TriangularSolve
Zobacz też XlaBuilder::TriangularSolve.
Rozwiązuje układy równań liniowych z macierzowymi współczynnikami o dolnej lub górnej części trójkąta za pomocą bezpośredniego lub odwrotnego podstawiania. Ta procedura rozwiązuje jeden z układów równań op(a) * x =
b lub x * op(a) = b dla zmiennej x, pod warunkiem że a i b, gdzie op(a) to op(a) = a, op(a) = Transpose(a) lub op(a) = Conj(Transpose(a)).
TriangularSolve(a, b, left_side, lower, unit_diagonal, transpose_a)
| Argumenty | Typ | Semantyka |
|---|---|---|
a |
XlaOp |
a > dwuwymiarowy tablica typu zespolonego lub zmiennoprzecinkowego o kształcie [..., M, M]. |
b |
XlaOp |
a > tablica dwuwymiarowa tego samego typu o kształcie [..., M, K], jeśli left_side ma wartość true, w przeciwnym razie [..., K, M]. |
left_side |
bool |
wskazuje, czy należy rozwiązać system o postaci op(a) * x = b (true) czy x * op(a) = b (false). |
lower |
bool |
czy użyć górnego czy dolnego trójkąta w a. |
unit_diagonal |
bool |
Jeśli true, przyjmuje się, że elementy diagonalne w elementach a mają wartość 1 i nie są dostępne. |
transpose_a |
Transpose |
czy ma być użyta wartość a w niezmienionej postaci, czy ma być transponowana, czy ma być pobrana jej sprzężona postać sprzężona. |
Dane wejściowe są odczytywane tylko z dolnego lub górnego trójkąta a w zależności od wartości parametru lower. Wartości z drugiego trójkąta są ignorowane. Dane wyjściowe są zwracane w tym samym trójkącie; wartości w drugim trójkącie są zdefiniowane przez implementację i mogą być dowolne.
Jeśli liczba wymiarów w przypadku a i b jest większa niż 2, są one traktowane jako grupy macierzy, w których wszystkie wymiary z wyjątkiem 2 mniejszych są wymiarami grupy. a i b muszą mieć te same wymiary wsadów.
tablice,
Zobacz też XlaBuilder::Tuple.
Tuple zawierający zmienną liczbę uchwytów danych, z których każdy ma swój kształt.
Jest to analogiczne do std::tuple w C++. Koncepcyjnie:
let v: f32[10] = f32[10]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
let s: s32 = 5;
let t: (f32[10], s32) = tuple(v, s);
Tupli można używać (dostęp do nich) za pomocą operacji GetTupleElement.
Podczas
Zobacz też XlaBuilder::While.
While(condition, body, init)
| Argumenty | Typ | Semantyka |
|---|---|---|
condition |
XlaComputation |
XlaComputation typu T -> PRED, który definiuje warunek zakończenia pętli. |
body |
XlaComputation |
XlaComputation typu T -> T, który definiuje ciało pętli. |
init |
T |
Wartość początkowa parametru condition i body. |
Sekwencyjnie wykonuje body, dopóki condition nie zakończy się niepowodzeniem. Jest to podobne do typowego pętli while w wielu innych językach, z tą różnicą i ograniczeniami, które zostały wymienione poniżej.
- Węzeł
Whilezwraca wartość typuT, która jest wynikiem ostatniego wykonania funkcjibody. - Kształt typu
Tjest określany statycznie i musi być taki sam we wszystkich iteracjach.
Parametry T obliczeń są inicjowane wartością init w pierwszej iteracji i automatycznie aktualizowane do nowego wyniku z funkcji body w każdej kolejnej iteracji.
Jednym z głównych zastosowań węzła While jest implementacja wielokrotnego wykonywania treningu w sieciach neuronowych. Poniżej przedstawiono uproszczony pseudokod z wykresem przedstawiającym obliczenia. Kod znajdziesz w while_test.cc.
W tym przykładzie typ T to Tuple, który składa się z elementu int32 odpowiadającego liczbie iteracji oraz elementu vector[10] odpowiadającego akumulatorowi. Przez 1000 iteracji pętla stale dodaje wektor stały do akumulatora.
// Pseudocode for the computation.
init = {0, zero_vector[10]} // Tuple of int32 and float[10].
result = init;
while (result(0) < 1000) {
iteration = result(0) + 1;
new_vector = result(1) + constant_vector[10];
result = {iteration, new_vector};
}