איור 1
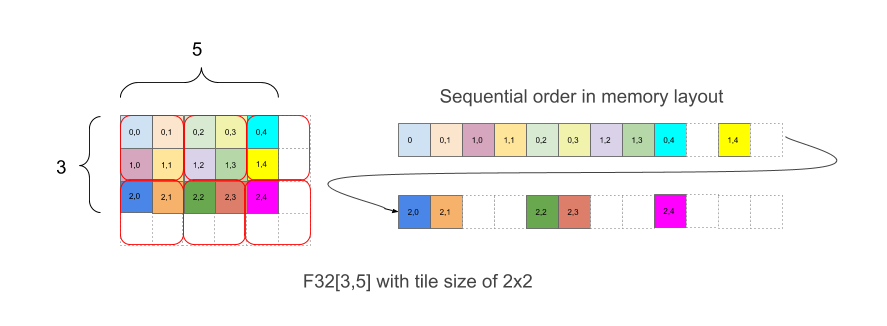
איור 1 מראה איך מערך F32[3,5] ערוך בזיכרון עם אריחים בגודל 2x2. בצורתminor_to_major
באופן אינטואיטיבי, האריחים פרוסים כדי לכסות את הצורה ולאחר מכן בתוך כל אריח, האלמנטים פרוסים ללא ריצוף, כמו בדוגמה למעלה, כאשר החלק הימני של הדוגמה מראה את הפריסה בזיכרון, כולל רכיבי המרווח הלבנים שנוספו כדי ליצור משבצות 2x2 מלאות, למרות שגבולות המערך המקורי אינם שווים.
האלמנטים הנוספים במרווח הפנימי לא חייבים להכיל ערך מסוים.
נוסחאות של אינדקס לינארי לפריסת צורה נתונה ומשבצת נתונה
בלי אריחים, רכיב e=(en, en-1, ... , e1) במערך עם גבולות המערך d=(dn, dn-1, ... , d1) (d1 הוא המאפיין המינורי ביותר) מפורט לפי הסדר ממז'ור למשנהו במיקום:
לינארי_index(e, d)
= לשדרג
n
כדי לשמור על פשטות הסימון במסמך הזה, נניח שלמשבצת יש אותו מספר מימדים כמו המערך. בתהליך ההטמעה של ריצוף XLA, הפריסה כוללת אריחים עם פחות מידות על ידי השארת המימדים הראשוניים הגדולים ביותר ללא שינוי והחלת האריחים רק על המאפיינים המינוריים ביותר, כך שהאריחים שצוינו יזכירו סיומת של המידות הפיזיקליות של הצורה שאותה מתבצעת ריצוף.
כשמתבצעת פריסה של גודל (tn, tn-1, ... , t1), רכיב במערך עם אינדקסים (en, en-1, ... , e1) ממופה למיקום הזה בפריסה הסופית:
Client_index_with_tile(e, d, t)
= ⌋, e/t⌋, e mod t), (⌈d/t⌉, t)) (arithmetic is elementwise, (a,b) הוא שרשור (a,b) הוא מחרוזות של
n
אפשר לדמות את הפריסה לשני חלקים: (⌊en/tn⌋, ... , ⌊e1/t1⌋), שתואם לאינדקס של משבצות במערך של אריחים בגודל (⌈dn/tn/tn⌋, ... , ⌊e1/t1⌋), שתואם לאינדקס של משבצות במערך של אריחים בגודל (⌈dn/tn, ... , ⌈d1), ... , ⌈d1 פונקציית ceil מופיעה ב-⌈di/ti⌉ כי אם האריחים חורגים מהגבולות של המערך הגדול יותר, המערכת מוסיפה מרווח פנימי כמו באיור 1. האריחים וגם הרכיבים שבתוך האריחים מסודרים באופן רקורסיבי, ללא ריצוף.
בדוגמה באיור 1, לאלמנט (2,3) יש אינדקס משבצות (1,1) ואינדקס בתוך אריחים (0,1), כדי לציין וקטור קואורדינטות משולב של (1,1,0,1). לאינדקסים של המשבצות יש גבולות (2,3) והמשבצת עצמה היא (2,2) לווקטור משולב של (2,3,2,2). אז האינדקס הלינארי עם אריח עבור האלמנט עם האינדקס (2,3) בצורה הלוגית הוא
· ·index_with_tile(2,3)
פריסה ושינוי של מרקם
פריסה המבוססת על פריסה פועלת באופן הבא:
שקול מערך של מאפיינים (dn, dn-1, ... , d1) (d1 הוא המאפיין המשני ביותר). כשהוא פרוס באמצעות ריצוף בגודל (tn, tn-1, ... , t1) (t1 הוא המאפיין המשני ביותר), אפשר לתאר את האריחים במונחים של שינוי צורה של פד.
- לאחר הוספת המערך ⌈dn/tn⌉tn, ... , ⌈d1/t1⌉t1).
- כל מימד i מחולק (⌈di/ti⌉,
ti), כלומר המערך מעוצב מחדש ל-
(⌈dn/tn⌉, tn, ... , ⌈d1/t1⌉, t1).
אין שינוי פריסה פיזית בעיצוב הזה לבדו, כך שהצורה הזו קצת יותר מושלמת. אם לא חושבים במפורש על ריצוף, ניתן לבטא כל צורה עם אותו מספר רכיבים כמו הצורה המרופדת. הדוגמה כאן היא איך לבטא אריח בדרך הזו. - טרנספורמציה מתרחשת על ידי העברת tn, ... , t1 לממדים המשניים ביותר תוך שמירה על הסדר היחסי שלהם, כך שסדר הממדים, מהעיקרון המינורי לרוב המינורי, הופך ל-
(⌈dn/tn⌉, ... , ⌈d1/t1⌉, ..., n1⌉, ...).
לצורה הסופית יש את הקידומת
(⌈dn/tn⌉, ... ,
⌈d1/t1⌉), שמתארת את מספר האריחים בכל ממד. רכיב במערך (en, ... , e1) ממופה לרכיב הזה בצורה הסופית:
(⌊en/tn⌋, ... ,
⌊e0/t0⌋, en mod tn, ... , e1). אפשר לראות בקלות שהאינדקס הלינארי של הרכיב תואם לנוסחה שלמעלה כמצופה.
אריחים חוזרים
הריצוף של XLA הופך לגמיש עוד יותר כי פורסים אותו שוב ושוב.
איור 2
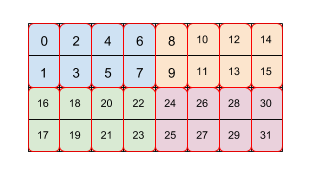
איור 2 מראה איך מערך בגודל 4x8 פרוס בשתי רמות של אריחים (קודם 2x4 ואז 2x1). אנחנו מייצגים את הריצוף החוזר הזה בתור (2,4)(2,1). כל צבע מציין אריח 2x4 וכל תיבת גבולות אדומה היא אריח 2x1. המספרים מציינים את האינדקס הלינארי בזיכרון של האלמנט הזה בפורמט משבצות. הפורמט הזה תואם לפורמט שבו נעשה שימוש ב-BF16 ב-TPU, אלא שהאריח הראשוני גדול יותר, כלומר הריצוף הוא (8,128)(2,1), שבו מטרת האריחים השנייה ב-2x1 היא לאסוף יחד שני ערכי 16 ביט כדי ליצור ערך אחד של 32 ביט באופן שתואם לארכיטקטורה של TPU.
שים לב שאריח שני או יותר יכול להתייחס לשני המימדים המשניים של האריחים, שפשוט מסדרים מחדש את הנתונים בתוך המשבצת, כמו בדוגמה הזו עם (8,128)(2,1), אבל גם יכול להתייחס למידות הראשיות של אריחים שונים מהאריחים הקודמים.
שילוב מימדים באמצעות אריחים
הריצוף של XLA תומך גם בשילוב מימדים. לדוגמה, הוא יכול לשלב מאפיינים ב-F32[2,7,8,11,10]{4,3,2,1,0} ב-F32[112,110]{1,0} לפני ריצוף באמצעות (2,3). האריח שבו נעשה שימוש הוא (כללית,1,2,בסס,3). כאן כוכבית במשבצת מרמזת על כך שלוקח את המאפיין הזה ומשלבים אותו עם המאפיין המינורי הבא. אפשר לכלול כמה מאפיינים סמוכים במאפיין אחד. מימד משויך מיוצג על ידי ערך משבצת של 1- במימד הזה של המשבצת, שאינו תקף בדרך אחרת במשבצת כגודל.
ליתר דיוק, אם מסירים את מאפיין i של הצורה באמצעות כוכבית באריחים, לפני החלת ההגדרה הקודמת של אריחים, המימד הזה מוסר גם מהצורה שניצבת וגם מהווקטור האריח, וגבולות המערך i-1 של הצורה גדלים מ-di-1 ל-didi-1. השלב הזה חוזר על עצמו עבור כל כוכבית בווקטור המשבצת.

