Halaman ini diterjemahkan oleh Cloud Translation API.

Tata letak {i>tiled Tetap teratur dengan koleksi Simpan dan kategorikan konten berdasarkan preferensi Anda.

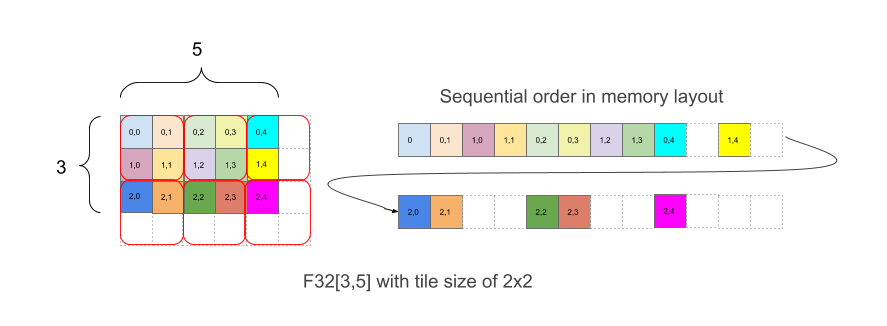
Gambar 1

Gambar 1 menunjukkan bagaimana array F32 [3,5] diletakkan dalam memori dengan ubin 2x2. Bentuk dengan tata letak ini ditulis sebagai F32[3,5]{1,0:T(2,2)}, dengan 1,0 berkaitan dengan urutan fisik dimensi (kolom minor_to_major dalam Layout) sedangkan (2,2) setelah titik dua menunjukkan ubin dimensi fisik dengan ubin 2x2.

Secara intuitif, ubin ditata untuk menutupi bentuk, lalu dalam setiap ubin, elemen kemudian ditata tanpa ubin, seperti pada contoh di atas, dengan bagian kanan dari contoh menunjukkan tata letak dalam memori, termasuk elemen padding putih yang ditambahkan untuk memiliki ubin 2x2 yang lengkap meskipun batas array aslinya tidak merata.

Elemen tambahan pada padding tidak perlu berisi nilai tertentu.

Rumus indeks linear untuk penyusunan ubin berdasarkan bentuk dan ubin

Tanpa penyusunan ubin, elemen e=(e_n, e_n-1, ... , e₁) dalam array dengan batas array d=(d_n, d_n-1, ... , d₁) (d1 adalah dimensi paling kecil) yang disusun berdasarkan urutan utama hingga minor pada posisi:

linear_index(e, d)
= linear_index((e_n, e_n-1, ... , e₁), (d_n, d_n-1, ... , d₁))
= e_nd_n-1...d₁ + _1-d₁

Untuk menyederhanakan notasi dalam dokumen ini, kami asumsikan kartu memiliki jumlah dimensi yang sama dengan array. Dalam penerapan pemasangan ubin XLA, hal ini umumnya terjadi pada ubin dengan dimensi yang lebih sedikit dengan membiarkan dimensi paling utama awal tidak berubah dan menerapkan perulangan hanya pada dimensi yang paling kecil, sehingga pemasangan ubin yang ditentukan menyebutkan akhiran dimensi fisik dari bentuk yang sedang dibuat.

Saat pembuatan ubin ukuran (t_n, t_n-1, ... , t₁) digunakan, elemen dalam array dengan indeks (e_n, e_n-1, ... , e₁) dipetakan ke posisi ini dalam tata letak akhir:

_n

Tata letak dapat dianggap memiliki dua bagian: (⌊e_n/t_n⌋, ... , ⌊e₁/t₁⌋), yang sesuai dengan indeks kartu dalam array kartu dengan ukuran (⌈d_n/t_n⌉, ... , ⌈d₁/t Fungsi ceil muncul dalam ⌈d_i/t_i⌉ karena jika ubin memenuhi batas array yang lebih besar, padding akan disisipkan seperti dalam Gambar 1. Ubin dan elemen dalam kartu disusun secara rekursif tanpa ubin.

Pada contoh pada Gambar 1, elemen (2,3) memiliki indeks ubin (1,1), dan indeks dalam ubin (0,1), untuk vektor koordinat gabungan (1,1,0,1). Indeks kartu memiliki batas (2,3) dan kartu itu sendiri adalah (2,2) untuk vektor gabungan (2,3,2,2). Indeks linear dengan ubin untuk elemen dengan indeks (2,3) dalam bentuk logis kemudian

linear_index_with_til((2,3), (3,5), (2,2))
= linear_index((1,1,0,1), (2,3,2,2))
= linear_index((1,1), (2,3)) ∙ 2 ∙ 2 + linear_index((0,1), (2,1))
=

Susun sebagai transposisi pad-reshape

Tata letak berbasis judul beroperasi sebagai berikut:
Pertimbangkan array dimensi (d_n, d_n-1, ... , d1) (d1 adalah dimensi yang paling kecil). Jika ditata dengan ubin dengan ukuran (t_n, t_n-1, ... , t₁) (t₁ adalah dimensi yang paling kecil), ubin tersebut dapat dijelaskan dalam bentuk pad-reshape-transpose dengan cara berikut.

1. Array diberi padding ke (⌈d_n/t_n⌉∙t_n, ... , ⌈d₁/t₁⌉∙t₁).
2. Setiap dimensi i dibagi menjadi (⌈d_i/ti⌉, t_i), yaitu array dibentuk ulang menjadi
   (⌈d_n/t_n⌉, t_n, ... , ⌈d₁/t₁⌉, t₁).
   Tidak ada perubahan tata letak fisik dalam bentuk ulang ini, sehingga pembentukan ulang ini merupakan bitcast. Jika seseorang tidak secara eksplisit memikirkan ubin, bentuk ulang ini dapat mengekspresikan bentuk apa pun dengan jumlah elemen yang sama dengan bentuk dengan padding - contoh di sini adalah cara mengekspresikan kartu dengan cara ini.
3. Transpos terjadi dengan memindahkan t_n, ... , t₁ ke dimensi yang paling kecil dengan tetap mempertahankan urutan relatifnya, sehingga urutan dimensi dari yang paling besar ke paling kecil menjadi
   (⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉, t_n, ).

Bentuk akhir memiliki awalan
(⌈d_n/t_n⌉, ... , ⌈d₁/t₁⌉), yang menjelaskan jumlah kartu di setiap dimensi. Elemen dalam array (e_n, ... , e₁) dipetakan ke elemen ini dalam bentuk akhir:
(⌊e_n/t_n⌋, ... , ⌊e₀/t₀⌋, e_n mod t_n, ... mod t e₁ ). Sangat mudah untuk melihat bahwa indeks linear elemen mengikuti formula di atas seperti yang diharapkan.

Pemasangan ubin berulang

Pemasangan ubin XLA menjadi lebih fleksibel dengan menerapkannya berulang kali.

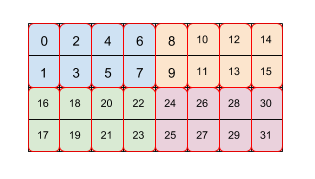
Gambar 2

Gambar 2 menunjukkan bagaimana array berukuran 4x8 disusun menggunakan dua tingkat perulangan (2x4 pertama, lalu 2x1). Kami menyatakan ubin berulang ini sebagai (2,4)(2,1). Setiap warna menunjukkan kartu 2x4 dan setiap kotak batas merah adalah kartu 2x1. Angka tersebut menunjukkan indeks linear dalam memori elemen tersebut dalam format tile. Format ini sesuai dengan format yang digunakan untuk BF16 di TPU, kecuali bahwa ubin awal lebih besar, yaitu ubinnya (8.128)(2,1), dengan tujuan penyusunan ubin kedua dengan 2x1 adalah untuk mengumpulkan dua nilai 16-bit untuk membentuk satu nilai 32-bit dengan cara yang sesuai dengan arsitektur TPU.

Perhatikan bahwa kartu kedua atau yang lebih baru dapat merujuk ke dimensi minor dalam kartu, yang hanya menyusun ulang data dalam kartu, seperti dalam contoh ini dengan (8.128)(2,1), tetapi juga dapat merujuk ke dimensi lintas-kartu utama dari petak sebelumnya.

Menggabungkan dimensi menggunakan tile

Pemasangan ubin XLA juga mendukung penggabungan dimensi. Misalnya, Transformer dapat menggabungkan dimensi di F32[2,7,8,11,10]{4,3,2,1,0} menjadi F32[112,110]{1,0} terlebih dahulu sebelum memberinya ubin dengan (2,3). Ubin yang digunakan adalah (∗,∗,2,∗,3). Di sini, tanda bintang dalam kartu menyiratkan mengambil dimensi tersebut dan menggabungkannya dengan dimensi minor berikutnya. Beberapa dimensi yang berdekatan dapat digabungkan menjadi satu dimensi. Dimensi yang disertakan direpresentasikan oleh nilai kartu -1 dalam dimensi kartu tersebut, yang tidak valid dalam kartu sebagai ukuran dimensi.

Lebih tepatnya, jika dimensi i pada bentuk dihilangkan melalui tanda bintang di ubin, maka sebelum definisi ubin sebelumnya diterapkan, dimensi tersebut akan dihapus dari bentuk yang disusun dan vektor ubin, dan dimensi i-1 dari bentuk tersebut memiliki batasan array yang meningkat dari d_i-1 ke d_id_i-1. Langkah ini diulang untuk setiap tanda bintang di vektor kartu.

Kirim masukan